B-site cation inter-diffusion in yttrium substituted barium zirconate

Abstract

B-site cation inter-diffusion in the ABO₃ perovskite yttrium-substituted barium zirconate (BZY) was studied at temperatures from 1100 to 1460 °C under reducing and oxidising conditions. The experiments followed two different approaches using Ce as a chemical tracer for Zr. By fitting diffusion profiles of the cation obtained by either Electron Probe Microanalysis (EPMA) or Time-of-Flight Secondary Ion Mass Spectrometry (ToF-SIMS), we determined bulk, grain-boundary and effective diffusion coefficients. The activation energies of bulk diffusion (4.5 ± 0.4 eV) are similar to the migration enthalpy obtained by a computational approach (∼4 eV). On this basis, we conclude that the activation energies correspond to the migration enthalpies, assuming that the concentration of Zr vacancies in the bulk was frozen-in. Grain-boundary diffusion coefficients were found to be more than four orders of magnitude higher than the corresponding bulk values, while the activation energies of grain-boundary diffusion are relatively similar to those for bulk. This was attributed to higher concentrations of cation vacancies in space-charge layers at the boundaries. Overall, the results show that BZY electrolytes are highly stable towards degradation related to B-site cation diffusion.

---

1. Introduction

Electrochemical potential gradients across the electrolyte of ceramic proton-conducting fuel cells and electrolyser cells are driving forces for cation transport—transport processes that may degrade the device by creep and demixing. Effects of cation diffusion on the long-term durability of proton-conducting ceramics have, however, been more or less neglected.

Compositions based on yttrium-substituted BaZrO₃ (BZY) are promising ceramic proton-conducting electrolyte materials for electrochemical energy conversion.^1–3 While still relatively unexplored, there are some studies of cation transport with relevance to this material. Sažinas et al. studied cation diffusion in BaZrO₃ (BZ) and related perovskites experimentally.^4–6 They performed tracer diffusion experiments on BZ, determining the diffusion profiles by means of Secondary Ion Mass Spectrometry (SIMS). The activation energies of Ba and Zr tracer diffusion in BZ were estimated to be (4.1 ± 0.5) eV and (4.5 ± 0.7) eV, respectively.⁶ Computational studies of diffusion in the perovskites LaGaO₃ by De Souza and Maier⁷ and in SrTiO₃ by Mizoguchi et al.⁸ showed that an A-site vacancy along the migration path promotes B-site diffusion.^7,8

In the present contribution the diffusion of Zr in BZY was studied by annealing inter-diffusion couples of either pellets of BZY and Y-substituted BaCeO₃ (BCY) facing each other, or BZY pellets coated with thin films of SrCeO₃ (SCO). The annealing experiments were performed in the temperature range 1100–1460 °C under reducing and oxidising conditions. The resulting cation diffusion profiles were measured by means of Electron Probe Micro Analysis (EPMA) or Time-of-Flight Secondary Ion Mass Spectrometry (ToF-SIMS). Subsequently, bulk inter-diffusion coefficients and grain-boundary diffusion coefficients were determined by fitting these profiles to appropriate solutions of Fick's second law.^9–14 The results are discussed with respect to effects of defect concentrations in bulk and grain-boundary regions and compared to results for other functional oxides reported in literature.

2. Methods

2.1. Synthesis and fabrication

BaZr_0.9Y_0.1O_3−δ and SrCeO₃ powders, prepared by spray pyrolysis followed by calcination, were obtained commercially (CerPoTech, Norway). BaCe_0.9Y_0.1O_3−δ powder was synthesised from BaCO₃ (99.95%), Ce(NO₃)₃ (99.99%) and Y(NO₃)₃ (99.9%) via the citric acid route with calcination at 900 °C in ambient air for 5 hours.¹⁵ The calcined powders were ball milled, mixed with a small amount of binder to improve green body density and strength, and finally pressed (isostatic) uniaxially into pellets. The BZY pellets were sintered for 10 hours in total; 3 hours at 1650 °C followed by 7 hours at 1600 °C in ambient air. The green bodies were covered with calcined BZY powder with a small excess of Ba in a closed alumina crucible to prevent Ba loss. The BCY pellets were sintered at 1550 °C for 5 hours and the SCO pellet to be used as a PLD-target was sintered at 1450 °C for 2 hours. Pellets of both materials were covered with sacrificial powder of the respective material and sintered in ambient air. The heating and cooling rates were 600 °C h⁻¹ and 300 °C h⁻¹, respectively. The relative densities of the sintered samples were 90–96% for BZY, 90–97% for BCY and ∼99% for SCO. The average grain sizes were ∼0.5 μm for BZY, ∼2 μm for BCY and ∼4 μm for SCO.

2.2. Diffusion experiments and data analysis

Inter-diffusion couples were annealed at temperatures from 1100 to 1460 °C under reducing (5% H₂ to 95% Ar) and oxidising (ambient air) conditions, following the two different approaches shown schematically in Fig. 1.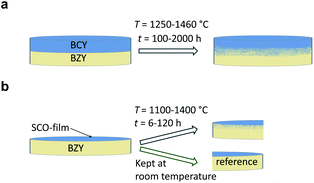

Fig. 1 Schematics showing the two approaches used for preparation and annealing of inter-diffusion couples suitable for measuring diffusion profiles by means of (a) EPMA and (b) SIMS.

Fig. 1a illustrates the inter-diffusion experiment with BZY and BCY pellets. The pellets were polished with SiC paper and diamond polish down to 5 μm and 0.25 μm particle sizes, respectively. Spring forces held the pellets in a ProboStat™ setup (NORECS, Norway) with the polished surfaces facing each other. The diffusion annealing were performed at 1250–1460 °C for 100–2000 hours. The heating and cooling rates were 200–300 °C h⁻¹, thus the ramping periods were short relative to the durations of the diffusion anneals. Effects of diffusion on the concentration profiles during ramping were consequently insignificant. After a successful experiment, there was proper adhesion between the two materials as observed by SEM. The diffusion couple was cut perpendicular to the interface, mounted in epoxy resin, polished down to 0.25 μm and coated with carbon. For each experiment, several X-ray line scans across the interface between the two materials were obtained with EPMA (Cameca SX100; acceleration voltage 15 kV, beam current 20 nA) to determine concentration profiles of the cations. To ensure that the region of the nominal stoichiometry was reached, the lengths of the line scans were varied from 10 to 60 μm, depending on the reaction parameters (duration and temperature). The concentrations of the cations were analysed every micrometre, except for the shortest diffusion profiles where the distance between each point of analyses was 1/3 of a micrometre.

Fig. 1b shows the specimen assembly of the second approach where BZY pellets were coated with thin films of SCO before the diffusion annealing. First, the surface of the BZY pellets was polished with SiC paper and diamond polish down to 5 μm and 0.25 μm particle sizes, respectively. The surface roughness of similar dense ceramics has been reported to be in the order of 40 nm following the same polishing protocol as we used.¹⁶ We determined the surface roughness (R_a) of our specimen to be ∼50 nm by means of an interference microscope (NT1100, Veeco). To establish the surface microstructure and promote that the defect concentrations correspond to equilibrium at the diffusion anneals, the BZY pellets were pre-annealed in the experimental conditions more than twice as long as for the actual diffusion experiment before being coated with SCO. Pulsed laser deposition (PLD) (SURFACE, Germany) was used to coat the polished side of the BZY pellets. A KrF excimer laser was utilised to make 3000 shots at the sintered SCO target (laser energy 300 mJ, laser frequency 5 Hz, substrate temperature 600 °C, gas pressure 0.02–0.07 mbar O₂), resulting in films with thicknesses between 30 and 70 nm. The use of SCO-film instead of BaCeO₃-film (BCO-film) was chosen aiming to obtain diffusion profiles for both A- and B-site cations from the same annealing experiments. However, obtaining diffusion profiles for A-site failed, probably because the film thickness, diffusion times and temperatures were not ideal. Thus we only report B-site diffusion coefficients in this paper. There are no indications in the diffusion data that using SCO-films instead of BCO-films does significantly affect the B-site diffusion.

The coated pellets were cut into two pieces. One part was kept as reference to determine the SCO film thickness and surface/interface roughness. The second part was annealed under oxidising conditions (ambient air) at different temperatures from 1100 to 1400 °C. The durations were varied from 120 to 6 hours to get similar lengths of the diffusion profiles at the different temperatures. The temperature ramps were sufficiently fast to avoid effects of diffusion from these periods on the diffusion profiles.

Intensity profiles of Ce were measured by means of ToF-SIMS. Secondary ions for analysis were created by a 25 keV Ga⁺ ion beam operated in bunched mode (analysis current ≈ 2 pA) and scanned over (62 × 62) μm² or (100 × 100) μm² areas in the centre of a larger crater. The larger craters were created by a 2 keV Cs⁺ ion beam utilised as a sputtering beam (sputtering current 110–140 nA) rastered over (300 × 300) μm² or (400 × 400) μm² areas to remove material. Negative secondary ions were monitored during depth profiling. The intensity profiles were normalised with respect to the intensity of ¹⁸O⁻ to correct for minor instabilities in analysis conditions. Several grains and grain boundaries were analysed since the probed volume is much larger than the grains (∼0.5 μm). The depths of the craters were determined using a Veeco Dektak 150 profilometer and used to convert the SIMS sputtering time to a sputter depth scale. The depth profiles were typically 0.5–1.5 μm.

Inter-diffusion coefficients describe the diffusion between compounds with different composition; here BZY and BCY for the EPMA approach and BZY and SCO for the SIMS approach. The chemical tracers, Ce and Zr, act essentially as isotope tracers in the respective materials under oxidising conditions.

Based on the ratio between grain size d, diffusion length and grain-boundary thickness ω Harrison classified three different regimes, A, B and C, to distinguish the influence of grain boundaries on solid state diffusion in a polycrystalline material.¹⁴ For experiments in the B-type regime both grain-boundary and bulk diffusion coefficients can be obtained whereas in the A-type regime only an effective diffusion coefficient can be determined.¹⁴

For the concentration profiles determined by EPMA, the bulk inter-diffusion coefficient (D_bulk) was extracted by fitting eqn (1), the solution of Fick's second law for diffusion from a constant source,^9,17

to the data. c represents the concentration of the diffusing cation, c_I and c_II represent the constant concentration far from the interface in the two phases (BZY and BCY), x is the distance from the original interface, t is the annealing time, and erfc denotes the complimentary error function. Eqn (1) is valid if the inter-diffusion displays negligible concentration dependence. This was verified to be the case for the present data set using Boltzmann–Matano analysis.¹⁷

The grain-boundary diffusion coefficient, D_gb, was estimated from the Whipple–Le Claire solution for in-diffusion from a constant source^11,12

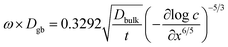where ω is the grain-boundary width (assumed to be 1 nm). According to eqn (2), D_gb can be calculated from the slope of the linear part of the depth profile's second feature in plots of log c versus x^6/5. The Whipple–Le Claire solution is valid for β ≥ 10 and 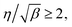where and ¹²

The boundary conditions in the approach with the SCO-film analysed with SIMS correspond to the thick film solution of Fick's second law.¹⁰

I is the normalised intensity, K is a constant, x is the depth, h is the film thickness and erf denotes the error function. σ is a SIMS mixing parameter which in this case is determined by the surface roughness of the samples as the ion beam mixing is negligible in comparison.¹⁰

The effective diffusion coefficient can be derived from the bulk and grain-boundary diffusion coefficients using the Hart equation¹⁴

D_eff = g × D_gb + (1 − g)D_bulk (4)

where g is given by the volume fraction of grain boundaries in the polycrystalline material (g = 3ω/d).

3. Results

3.1. Bulk diffusion

Fig. 2 shows typical concentration profiles of Zr and Ce determined by means of EPMA after the annealing of a BCY–BZY diffusion couple. The red lines in Fig. 2 represent the fit of eqn (1) to the experimental data. Element analysis by EPMA showed a slight Ba deficiency in the BCY samples (typically 1–2%) while no Ba deficiency was evident in the BZY samples.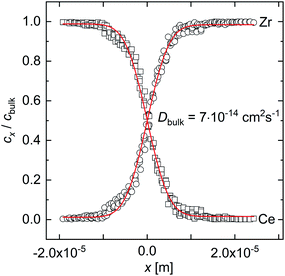

Fig. 2 Concentration profiles of Zr and Ce in the inter-diffusion couple BZY–BCY annealed at 1460 °C for 300 h in air determined by EPMA including the fit (red lines) of eqn (1).

Fig. 3 presents typical normalised intensity depth profiles obtained by SIMS for SCO-coated BZY from (a) a zero-time reference sample and (b) a diffusion-annealed sample. The interface between SCO and BZY in the reference sample is sharp, whereas for the annealed sample a substantial amount of Ce has diffused into BZY. Eqn (3) was first fitted to the intensity profile of the reference samples (t = 0) to obtain a value for the film thickness (h) and the SIMS mixing parameter (σ) (as shown in Fig. 3a). The values obtained for σ and h were then used when fitting eqn (3) to the intensity profiles of the diffusion-annealed samples to determine the bulk inter-diffusion coefficient, D_bulk (as shown in Fig. 3b).

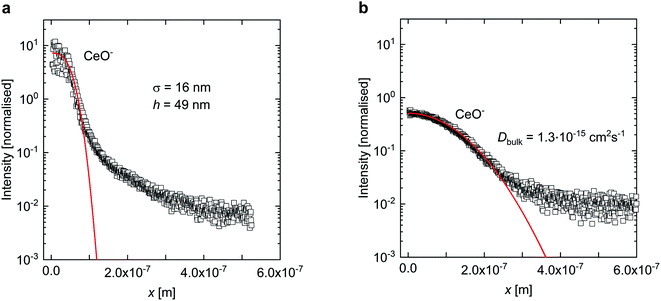Fig. 3 Normalised intensity profiles for a reference zero-time sample (a) and a sample annealed at 1350 °C for 10 h in air (b). The red curves corresponds to the fits of eqn (3) to the intensity profiles.

It should also be noted that after the annealing the intensity profile of Y shows a slight increase in Y concentration close to the surface, from 10% substitution in bulk to ∼13% substitution at the surface. This is not unexpected as Y segregation to the BZY surface has previously been reported by Sažinas et al.¹⁸ However, since this is only encountered in the vicinity of the surface, we do not expect that it will affect the cation diffusion to any extent.

Separate experiments were performed to rule out effects of annealing time on the extracted diffusion coefficients.

Fig. 4 displays the bulk diffusion coefficients in an Arrhenius representation. For EPMA, each point shown in the graph corresponds to a different annealing experiment, whereas for SIMS, data points at the same temperature correspond to different measurements on the same sample. Error bars are not included because there is not sufficient statistics for each point. However, the variation in the values of the diffusion coefficient, gives some indication as to the magnitude of the errors.

Fig. 4 Arrhenius plot of bulk diffusion coefficients. The lines correspond to least square fits to the data according to an Arrhenius behaviour, yielding activation energies. The solid lines are the separate fits of the different datasets and the dashed line is a fit of the data from both EPMA and SIMS under oxidising conditions combined.

The activation energies and the pre-exponentials of diffusion derived from the Arrhenius plot (Fig. 4) are presented in Table 1. The diffusion coefficients obtained by EPMA are systematically higher under reducing than under oxidising conditions, but activation energies are similar (5.4 ± 0.8) eV and (5.3 ± 0.4) eV, respectively. Because of the spread of the data between SIMS and EPMA under oxidising conditions, the activation energy from a fit including both datasets covering the whole temperature range is included. This fit gives an activation energy of (4.5 ± 0.4) eV (see Table 1).

Table 1 Activation energies and pre-exponentials for bulk diffusion. The errors given for the activation energies and the pre-exponentials are the errors obtained from the fitting procedure

Approach	Atmosphere	T [°C]	D 0,bulk [cm^2 s^−1]	E a,bulk [eV]
EPMA	Reducing	1250–1450	10^3 ± 2	5.4 ± 0.8
EPMA	Oxidising	1250–1460	10^2 ± 1	5.3 ± 0.4
SIMS	Oxidising	1100–1400	10^−3 ± 2	3.6 ± 0.5
SIMS & EPMA	Oxidising	1100–1460	10^−0.6 ± 1	4.5 ± 0.4

---

3.2. Grain-boundary diffusion

Fig. 5 shows by way of example the diffusion profile for Ce obtained by EPMA after annealing a BCY–BZY diffusion couple at 1310 °C for 800 hours, plotted according to the Whipple–Le Claire approach.¹¹

Fig. 5 The diffusion profile for Ce obtained by EPMA after annealing a diffusion couple at 1310 °C for 800 hours, plotted according to Whipple–Le Claire.¹¹ The line fitted to the linear part in deeper regions of the profile was used to estimate the grain-boundary diffusion coefficient.

The diffusion profiles obtained by SIMS are also consistent with fast grain-boundary diffusion, but the quality of the data does not allow for the quantitative analysis.

Fig. 6 presents the grain-boundary diffusion coefficients determined from the diffusion profiles obtained by EPMA. Grain-boundary data for both Ce diffusion in BZY and Zr diffusion in BCY were obtained. However, for simplicity, only the results for Ce in BZY are displayed in Fig. 6 since the grain-boundary diffusion coefficients of Zr in BCY and Ce in BZY were similar. As for the bulk diffusion, the grain-boundary diffusion is slightly higher in reducing than in oxidising atmosphere.

Fig. 6 Arrhenius plot of the grain-boundary diffusion coefficients. The grain-boundary width ω was assumed to be 1 nm. For simplicity, the graph only shows the coefficients for Ce in BZY. The lines shown correspond to least square fits to the data according to an Arrhenius behaviour, yielding activation energies.

The activation energies and pre-exponentials for grain-boundary diffusion are shown in Table 2. The activation energies obtained are lower or similar as those for bulk.

Table 2 Activation energies and pre-exponentials for grain-boundary diffusion of Ce in BZY obtained from the Arrhenius plot presented in Fig. 6. The error given is the error of the line fitting in the Arrhenius plot

Approach	Atmosphere	T [°C]	D 0,gb [cm^2 s^−1]	E a,gb [eV]
EPMA	Reducing	1250–1450	10^5 ± 2	4.5 ± 0.6
EPMA	Oxidising	1250–1460	10^2 ± 2	3.6 ± 0.7

---

4. Discussion

Cation diffusion in perovskite-type oxides generally occurs by cation vacancy mediated mechanisms.¹⁷ DFT NEB calculations show that the migration enthalpy of Zr in BZY is considerably reduced, from values >10 eV to ∼4 eV, when the migration mechanism also involves a Ba vacancy and not solely a Zr vacancy.⁶ Moreover, association between Zr, Ba and oxygen vacancies to form neutral clusters is energetically favourable. DFT calculations show that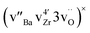 clusters facilitate the diffusion of Zr by slightly lowering the migration barrier of Zr to 3.4 eV.¹⁹ This migration enthalpy is lower than the activation energies obtained from the experiments (4.5 ± 0.4) eV for the present Y substituted BaZrO₃ and (4.5 ± 0.7) eV for nominal BaZrO₃.⁶

Although both Ba and Zr vacancies are essential for Zr migration, the concentration of Zr vacancies will still be governing the diffusion. The formation enthalpy of Zr vacancies is twice that of Ba vacancies thus the concentration of Zr vacancies will be much lower than the concentration of Ba vacancies.¹⁹ Any Ba loss during sintering would further reinforce this. Generally, the experimentally determined activation energy for diffusion comprises both the defect formation enthalpy and the migration enthalpy.¹⁷ However, the formation enthalpy of a Zr vacancy is higher than the activation energy we obtained experimentally for Zr diffusion. Presumably, the experimental activation energy for Zr bulk diffusion of ∼4.5 eV (see Table 1) therefore represents only the migration enthalpy. Accordingly, the concentration of Zr vacancies is considered constant at all temperatures explored in this work, representing a frozen-in cation defect concentration established during the sintering process. Similar conclusions were made by Sažinas et al. for nominal BZ and Vøllestad et al. for cation diffusion in lanthanum tungstate.^4,20 Schultz et al. obtained higher activation energies at higher temperatures than at lower temperatures in their tracer diffusion study of lanthanum gallate and explained it by a frozen in defect structure at the lower temperatures.²¹

The inter-diffusion coefficients are systematically higher in reducing than oxidising atmosphere (see Fig. 4 and 6), whereas the activation energies are within the experimental uncertainty. Generally, the cation vacancy concentrations decrease with decreasing p_O2, and that would result in lower diffusion coefficients, contrary to what is observed here. In reducing conditions and at high temperatures we expect partial reduction of Ce⁴⁺ to Ce³⁺ and one may speculate whether this influences the overall Ce transport. Thus, we cannot conclude about the effect of reducing conditions on diffusion of Zr in BZY while using Ce as a chemical tracer. To investigate the diffusion of Zr in reducing conditions an isotope tracer of Zr should therefore be used.

The effects of reducing conditions on the diffusion of Ce, may be interesting for commonly used electrolytes, containing both Ce and Zr; BaZr_1−x−yCe_xY_yO_3−δ (BZCY). DFT NEB calculations of Ce migrating in BZY have shown that Ce³⁺ is less unstable than Ce⁴⁺ at the transition state close to the vacant Ba-site in the BZY structure.¹⁹ Similarly, Da-Yong found by Raman spectroscopy that there is a small number of Ce³⁺ on A-site in the similar perovskite BaTi_1−xCe_xO₃ in oxidising conditions.²² Thus, Ce diffusion in reducing conditions may involve Ce³⁺ migrating partly along the Ba-site sublattice and thereby not be as dependent on Zr vacancies. However, if that was the case here, we would also expect to obtain a lower activation energy of diffusion from the experiments in reducing conditions, which was not the case.

To distinguish the contributions from bulk and grain-boundary diffusion on experimentally obtained diffusion profiles the measurements should be performed in the B-type regime according to Harrisons classification 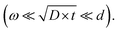As the grain sizes in BZY are small (∼0.5 μm) the diffusion lengths need to be even shorter. The EPMA diffusion experiments had diffusion lengths in the same order of magnitude as the grain size. As shown in Fig. 5 it was only possible to obtain a rough estimate of the grain-boundary diffusion coefficients from the profiles obtained by EPMA.

As expected, grain-boundary diffusion was significantly faster than bulk diffusion, more specifically; the diffusion coefficients are over four orders of magnitude higher than corresponding bulk values. The grain-boundary can be defined either as the actual junction between two grains, the grain-boundary core, or including also the region close to the core where the concentration of charged defects is different than in bulk, i.e. the so called space charge layer. Enhanced diffusivity can occur within the grain-boundary core, in the space charge layers along the grain-boundary core or both.

In barium zirconate and barium cerate, oxygen vacancies are known to accumulate in the grain-boundary core giving rise to an effectively positive core with adjacent space charge layers.^23–29 These space charge layers have the same structure as bulk, but to charge compensate the positive core, gradients in the concentration of charged defects develop: for dilute solutions effectively positive defects (oxygen vacancies and protons) gradually diminish and effectively negative defects (cation vacancies) accumulate, going from the bulk and towards the grain-boundary core. The higher concentration of cation vacancies in the space charge layer relative to bulk allows faster diffusion of Zr in the space charge layer along the grain-boundary.³⁰ Preliminary DFT calculations showed that the neutral vacancy cluster which favours Zr diffusion, tends to segregate from bulk to the grain-boundary core. The resulting higher concentration of these clusters in the grain-boundary core relative to the bulk, may potentially allow faster grain-boundary diffusion of Zr in the core. However, this would not explain why the obtained activation enthalpy of grain-boundary diffusion is similar to that of bulk diffusion, as we would expect the migration enthalpy in the grain-boundary core to be lower than in bulk.

It may seem controversial that the activation energies for grain-boundary transport is as high as or slightly lower than that for bulk (see Table 2), since it has been well accepted that the activation energy for diffusion along grain boundaries generally is significantly lower than for bulk diffusion.¹⁴ However, Parras and De Souza showed by continuum simulations that the activation enthalpy for diffusion along equilibrium space-charge layers in acceptor-doped MO₂ systems can be as high as that for bulk diffusion, but not higher.³⁰

Over time, the transport of ions across the inter-diffusion zone can lead to vacancy super saturation and pore formation on one side of the interface, so called Kirkendall porosity.¹⁷ This enhanced pore formation is indicative of vacancy-mediated inter-diffusion, with different effective diffusion coefficients in the two materials.¹⁷Fig. 7 shows that this type of porosity formed along the BCY–BZY interface on the BCY side and densification close to the materials interface on the BZY side. This observation indicates that the overall diffusion of Ce in BZY is higher than diffusion of Zr in BCY.

Fig. 7 BSE-SEM image of cross section of BZY (top) – BCY (bottom) diffusion couple after diffusion anneal at 1450 °C for 400 hours. Kirkendall porosity is seen along the interface in the BCY pellet.

As mentioned, Boltzmann–Matano analysis show that the bulk diffusion in the two materials are similar. Fig. 8 shows that this is also the case for the grain-boundary diffusion. To rationalize the observation of Kirkendall porosity we introduce the effective diffusion coefficient (eqn (4)), which accounts for differences in the grain sizes. Since the volume fraction of grain boundaries in BZY (d ∼ 0.5 μm) is higher compared to in BCY (d ∼ 2 μm), the effective diffusion of Ce in BZY is almost one order of magnitude larger than that of Zr in BCY. Fig. 8, comparing bulk, grain-boundary and effective diffusion coefficients, shows this for the BZY–BCY inter-diffusion couples annealed under oxidising conditions.

Fig. 8 Arrhenius plot of the bulk diffusion, the similar grain-boundary diffusion and the different effective diffusion of Ce in BZY and Zr in BCY, respectively.

In Fig. 9, B-site bulk diffusion coefficients in BZY are compared with relevant perovskites reported in the literature. B-site diffusion in nominal and 10% yttrium (Y) substituted barium zirconate is very similar.⁶ Consequently, it seems that Y³⁺ substitution for Zr⁴⁺ does not affect the B-site diffusion significantly. When Y resides along the migration path of Zr, the larger ionic radii of Y increases the steric repulsion, while the lower charge of Y decreases the electrostatic repulsion. Thus, the reason why the B-site diffusion of nominal and substituted barium zirconate is so similar could be that these two effects counteract each other. Zr diffusion in BZY has similar diffusion coefficients and activation energy as the B-site cation in BaTiO₃.³¹ The diffusion coefficients obtained under oxidising conditions are lower than in SrZrO₃ and CaZrO₃ and higher than in MgSiO₃ (La,Sr)TiO₃ and SrTiO₃.^4,32–34 Under reducing conditions the values for BZY are similar to those for CaZrO₃ under oxidising conditions.⁴ Further, Zr diffusion in BZY is slower and with higher activation energy than for most of the B-site cations in A^IIIB^IIIO₃ perovskites reported in literature.⁶ This was tentatively explained as being due to the higher charge of the B-site cation causing more electrostatic repulsion upon the migration of the four valent compared to the three valent cation.⁶ Finally, when comparing to highly stable fluorite-type oxides, such as yttrium stabilised zirconia (YSZ) it is seen that the B-site cation in BZY has similar diffusion coefficients and activation energies.⁶

Fig. 9 The results obtained in this study compared to relevant B-site bulk diffusion coefficients for A^IIB^IVO₃ perovskites reported in literature. (1): ⁹⁶Zr in CaZrO₃,⁴ (2): ⁹⁶Zr in SrZrO₃,⁴ (3): ⁹⁶Zr in BaZrO₃,⁴ (4): Si in MgSiO₃,³² (5): ⁴⁹Ti in (La,Sr)TiO₃,³³ (6): Zr in BaTiO₃,³¹ (7): Zr in SrTiO₃.³⁴

The time consuming experimental approaches generally limit the statistical basis of data on cation diffusion. Moreover, the experiments tend to carry rather high inherent uncertainties. This is evident here in the spread of the diffusion coefficients relative to a linear Arrhenius behaviour (see Fig. 4). The present results, however, still provide information about the magnitude and mechanism of cation diffusion, from which potential effects of cation transport on long-term durability and lifetime of ceramic devices can be evaluated. By assuming that the grain-boundary and bulk diffusion follow Arrhenius behaviour over wide temperature ranges, values of the effective diffusion coefficient can be extrapolated to give first estimates of cation transport under PCFC operating temperatures. As a first approximation with a grain size of 0.5 μm the effective diffusion coefficient will at 600 °C be in the order of 10⁻²⁰ to 10⁻³⁵ cm² s⁻¹, resulting in diffusion lengths 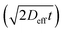in 20 years between 40 nm and <1 nm. Although such extrapolation over several hundred degrees carries considerable uncertainty, one may still conclude that B-site cation diffusion in BZY is slow and presently not the factor limiting the lifetime of fuel cells and electrolysers with BZY electrolytes. Sažinas et al. found that the diffusion coefficients of A-site cations are slightly higher than those of B-site cations in barium zirconate while the activation energies were slightly lower.⁶ As a first approximation with a grain size of 1 μm the effective diffusion coefficient will at 600 °C be in the order of 10⁻¹⁸ cm² s⁻¹, resulting in diffusion lengths in 20 years of ∼300 nm. Hence, barium zirconate is stable toward both A- and B-site cation diffusion related degradation.

As the grain-boundary diffusion is several orders of magnitude higher than the bulk diffusion, decreasing the volume fraction of grain boundaries would decrease the effective diffusion. By increasing the grain size from 0.5 μm to 4 μm, one would decrease the effective diffusion with almost one order of magnitude and the diffusion length to one third.

As the fast grain-boundary diffusion was attributed to higher concentrations of cation vacancies in the space charge layers along the grain-boundary core, it would be beneficial to decrease the positive charge of the core and thus also the accumulation of cation vacancies contributing to fast diffusion. The sintering temperature also affects the cation diffusion. Based on our results it seems the cation defect concentration is frozen-in at the equilibrium concentration at the sintering temperature. Thus, lowering the sintering temperature decreases cation vacancy concentration and slows down the diffusion.

5. Conclusions

The diffusion coefficients are slightly higher under reducing than under oxidising conditions and the activation energies are similar. The grain-boundary diffusion coefficients are more than four orders of magnitude higher than those for bulk diffusion (for 1250–1460 °C).

The activation energy of bulk diffusion under oxidising conditions was 4.5 ± 0.4 eV. Based on computational studies of the point defects governing the B-site cation transport in BZY, it was concluded that the bulk defect concentration is frozen-in and consequently, that this activation energy reflects the migration enthalpy of the mobile defect.

Higher concentration of cation vacancies in the space charge region along the grain-boundary rationalises both the high grain-boundary diffusivity and the activation energies of grain-boundary diffusion being relatively similar to those for bulk.

For the BCY–BZY diffusion couple, Kirkendall porosity forms in the BCY phase during the inter-diffusion process, supporting that the transport is vacancy mediated and indicating faster effective diffusion in BZY than in BCY. The latter is due to smaller grains and thus larger influence of the fast migration along grain boundaries in BZY.

BZY electrolytes are highly stable towards cation diffusion related degradation under PCFC operating temperatures. Increasing the grain size, decreasing the positive charge of the grain-boundary core and decreasing the sintering temperature would further increase the stability with respect to degradation due to B-site cation diffusion.

Author contributions

Ida Hasle: data curation, formal analysis, investigation, methodology, project administration, validation, visualisation, writing – original draft, Stephan P. Waldow: formal analysis, investigation, Ute N. Gries: formal analysis, investigation, Roger A. De Souza: funding acquisition, methodology, supervision, writing – review and editing, Einar Vøllestad: formal analysis, methodology, supervision, writing – review and editing, Reidar Haugsrud: conceptualisation, funding acquisition, methodology, supervision, validation, writing – review and editing.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

Muriel Marie Laure Erambert from the Department of Geosciences at the University of Oslo is gratefully acknowledged for acquisition of EPMA data. Financial support from the Research Council of Norway, project Nanomat/228355 “Functional oxides for clean energy technologies: fuel cells, gas separation membranes and electrolysers” (FOXCET) conducted by SINTEF, University of Oslo, and NTNU; and from the German Research Foundation (DFG), within the framework of the collaborative research centre SFB917, is gratefully acknowledged.

References

1. C. Duan, J. Tong, M. Shang, S. Nikodemski, M. Sanders, S. Ricote, A. Almansoori and R. O'Hayre, Readily processed protonic ceramic fuel cells with high performance at low temperatures, Science, 2015, 349(6254), 1321–1326.
2. S. Choi, C. J. Kucharczyk, Y. Liang, X. Zhang, I. Takeuchi, H.-I. Ji and S. M. Haile, Exceptional power density and stability at intermediate temperatures in protonic ceramic fuel cells, Nat. Energy, 2018, 202–210.
3. E. Vøllestad, R. Strandbakke, M. Tarach, D. Catalán-Martínez, M.-L. Fontaine, D. Beeaff, D. R. Clark, J. M. Serra and T. Norby, Mixed proton and electron conducting double perovskite anodes for stable and efficient tubular proton ceramic electrolysers, Nat. Mater., 2019, 18(7), 752–759.
4. R. Sažinas, I. Sakaguchi, M.-A. Einarsrud and T. Grande, ⁹⁶Zr Tracer Diffusion in AZrO₃ (A = Ca, Sr, Ba), Inorganics, 2018, 6(1), 14.
5. R. Sažinas, I. Sakaguchi, M.-A. Einarsrud and T. Grande, ¹³⁴Ba diffusion in polycrystalline BaMO₃ (M = Ti, Zr, Ce), AIP Adv., 2017, 7(11), 115024.
6. R. Sažinas, I. Sakaguchi, I. Hasle, J. M. Polfus, R. Haugsrud, M.-A. Einarsrud and T. Grande, Tracer diffusion of ⁹⁶Zr and ¹³⁴Ba in polycrystalline BaZrO₃, Phys. Chem. Chem. Phys., 2017, 19(32), 21878–21886.
7. R. A. De Souza and J. Maier, A computational study of cation defects in LaGaO₃, Phys. Chem. Chem. Phys., 2003, 5(4), 740–748.
8. T. Mizoguchi, N. Takahashi and H.-S. Lee, First-principles study on migration mechanism in SrTiO₃, Appl. Phys. Lett., 2011, 98(9), 091909.
9. J. Crank, The Mathematics of Diffusion, Clarendon Press, 1979.
10. S. P. Harvey, R. De Souza and M. Martin, Diffusion of La and Mn in Ba_0.5Sr_0.5Co_0.8Fe_0.2O_3−δ polycrystalline ceramics, Energy Environ. Sci., 2012, 5(2), 5803–5813.
11. R. Whipple, CXXXVIII. Concentration contours in grain boundary diffusion, London, Edinburgh Dublin Philos. Mag. J. Sci., 1954, 45(371), 1225–1236.
12. A. D. Le Claire, The analysis of grain boundary diffusion measurements, Br. J. Appl. Phys., 1963, 14(6), 351.
13. Y. C. Chung and B. J. Wuensch, An improved method, based on Whipple's exact solution, for obtaining accurate grain-boundary diffusion coefficients from shallow solute concentration gradients, J. Appl. Phys., 1996, 79(11), 8323–8329.
14. K. Inderjeet, J. Mišin and W. Gust, Fundamentals of grain and interphase boundary diffusion, Wiley, Chichester, 3rd edn, 1995.
15. D. W. Lee, J. H. Won and K. B. Shim, Low temperature synthesis of BaCeO₃ nano powders by the citrate process, Mater. Lett., 2003, 57(22–23), 3346–3351.
16. H. Téllez, J. Druce, Y.-W. Ju, J. Kilner and T. Ishihara, Surface chemistry evolution in LnBaCo₂O_5+δ double perovskites for oxygen electrodes, Int. J. Hydrogen Energy, 2014, 39(35), 20856–20863.
17. H. Mehrer, Diffusion in solids: fundamentals, methods, materials, diffusion-controlled processes, Springer Science & Business Media, 2007, vol. 155.
18. R. Sažinas, M. F. Sunding, A. Thøgersen, I. Sakaguchi, T. Norby, T. Grande and J. M. Polfus, Surface reactivity and cation non-stoichiometry in BaZr_1−xY_xO_3−δ (x = 0–0.2) exposed to CO₂ at elevated temperature, J. Mater. Chem. A, 2019, 7(8), 3848–3856.
19. I. Hasle, A. Matt, T. Bondevik, R. Haugsrud and J. M. Polfus, Cation Diffusion Mechanisms in Barium Zirconate and Related Perovskites by First-Principles Calculations, Manuscript under preparation.
20. E. Vøllestad, M. Teusner, R. A. De Souza and R. Haugsrud, Diffusion of Nd and Mo in lanthanum tungsten oxide, Solid State Ionics, 2015, 274, 128–133.
21. O. Schulz, M. Martin, C. Argirusis and G. Borchardt, Cation tracer diffusion of ¹³⁸La,⁸⁴Sr and ²⁵Mg in polycrystalline La_0.9Sr_0.1Ga_0.9Mg_0.1O_2.9, Phys. Chem. Chem. Phys., 2003, 5, 2308–2313.
22. D.-Y. Lu, D.-D. Han, X.-Y. Sun, X.-L. Zhuang and Y.-F. Zhang, Raman evidence for Ba-site Ce³⁺ in BaTiO₃, Jpn. J. Appl. Phys., 2013, 52(11R), 111501.
23. C. Kjølseth, H. Fjeld, Ø. Prytz, P. I. Dahl, C. Estournès, R. Haugsrud and T. Norby, Space-charge theory applied to the grain boundary impedance of proton conducting BaZr_0.9Y_0.1O_3−δ, Solid State Ionics, 2010, 181(5–7), 268–275.
24. M. Shirpour, R. Merkle and J. Maier, Space charge depletion in grain boundaries of BaZrO₃ proton conductors, Solid State Ionics, 2012, 225, 304–307.
25. E. E. Helgee, A. Lindman and G. Wahnström, Origin of Space Charge in Grain Boundaries of Proton-Conducting BaZrO₃, Fuel Cells, 2013, 13(1), 19–28.
26. B. J. Nyman, E. E. Helgee and G. Wahnström, Oxygen vacancy segregation and space-charge effects in grain boundaries of dry and hydrated BaZrO₃, Appl. Phys. Lett., 2012, 100(6), 061903.
27. R. De Souza, Z. A. Munir, S. Kim and M. Martin, Defect chemistry of grain boundaries in proton-conducting solid oxides, Solid State Ionics, 2011, 196(1), 1–8.
28. T. Bondevik, T. S. Bjørheim and T. Norby, Assessing common approximations in space charge modelling to estimate the proton resistance across grain boundaries in Y-doped BaZrO₃, Phys. Chem. Chem. Phys., 2020, 22(21), 11891–11902.
29. J. Polfus, K. Toyoura, F. Oba, I. Tanaka and R. Haugsrud, Defect chemistry of a BaZrO₃ Σ3 (111) grain boundary by first principles calculations and space-charge theory, Phys. Chem. Chem. Phys., 2012, 14(35), 12339.
30. J. P. Parras and R. A. De Souza, Grain-boundary diffusion of cations in fluorite-type oxides is faster but not always easier, Acta Mater., 2020, 195, 383–391.
31. S. Koerfer, R. A. De Souza, H.-I. Yoo and M. Martin, Diffusion of Sr and Zr in BaTiO₃ single crystals, Solid State Sci., 2008, 10(6), 725–734.
32. J. Xu, D. Yamazaki, T. Katsura, X. Wu, P. Remmert, H. Yurimoto and S. Chakraborty, Silicon and magnesium diffusion in a single crystal of MgSiO₃ perovskite, J. Geophys. Res.: Solid Earth, 2011, 116, B12205.
33. K. Gömann, G. Borchardt, A. Gunhold, W. Maus-Friedrichs and H. Baumann, Ti diffusion in La-doped SrTiO₃ single crystals, Phys. Chem. Chem. Phys., 2004, 6(13), 3639–3644.
34. U. N. Gries, M. Kessel, F. V. E. Hensling, R. Dittmann, M. Martin and R. A. De Souza, Behavior of cation vacancies in single-crystal and in thin-film SrTiO₃: the importance of strontium vacancies and their defect associates, Phys. Rev. Mater., 2020, 4(12), 123404.

---