The role of sodium in stabilizing tin–lead (Sn–Pb) alloyed perovskite quantum dots

Abstract

Narrow-bandgap CsSn_xPb_1−xI₃ perovskite quantum dots (QDs) show great promise for optoelectronic applications owing to their reduced use of toxic Pb, improved phase stability, and tunable band gaps in the visible and near-infrared range. The use of small ions has been proven beneficial in enhancing the stability and photoluminescence quantum yield (PLQY) of perovskite QDs. The introduction of sodium (Na) has succeeded in boosting the PLQY of CsSn_0.6Pb_0.4I₃ QDs. Unfortunately, the initial PLQY of the Na-doped QDs undergoes a fast degradation after one-day storage in solution, hindering their practical applications. Using density functional theory (DFT) calculations and ab initio molecular dynamics (AIMD) simulations, we study the effect of Na ions on the strength of surface bonds, defect formation energies, and the interactions between surface ligands and perovskite QDs. Our results suggest that Na ions enhance the covalent bonding of surface tin–iodine bonds and form strong ionic bonding with the neighboring iodine anions, thus suppressing the formation of I and Sn vacancies. Furthermore, Na ions also enhance the binding strength of the surface ligands with the perovskite QD surface. However, according to our AIMD simulations, the enhanced surface ligand binding is only effective on a selected surface configuration. While the position of Na ions remains intact on a CsI-terminated surface, they diffuse vigorously on an MI₂-terminated surface. As a result, the positive effect of Na vanishes with time, explaining the relatively short lifetime of the experimentally obtained high PLQYs. Our results indicate that engineering the surface termination of the QDs could be the next step in maintaining the favorable effect of Na doping for a high and stable PLQY of Sn–Pb QDs.

---

1. Introduction

Semiconductors with near-infrared absorption and emission have attracted tremendous attention for broad applications, including biological labeling, optical communication, and photovoltaics.^1–3 Metal-halide perovskites, a new class of optoelectronic materials, are developing rapidly because of their excellent photophysical properties and great success in photovoltaics.^4–10 Among various types of AMX₃ perovskites (A = Cs⁺, CH₃NH₃⁺, and CH₃(NH₂)₂⁺; M = Pb²⁺, Sn²⁺, Cu²⁺, Ge²⁺, and Mn²⁺; X = Cl⁻, Br⁻, and I⁻), ASnI₃ perovskites have attracted specific attention owing to their narrower optical band gaps (1.2–1.4 eV), allowing a strong response in the near-infrared spectral region.^11–13 The alloying of Sn with Pb at the M-site leads to the formation of an unusual band gap, which is lower than that of pure-Sn and -Pb perovskites, making the mixed Sn/Pb perovskites more attractive for application in high-efficiency tandem solar cells.^5,14–18 Additionally, mixing Sn and Pb is beneficial for stabilizing the fragile Sn-perovskite cubic phase and inhibiting the oxidation of Sn²⁺ to Sn⁴⁺.^14,19–23 As a result, the alloyed Sn–Pb perovskite solar cells have already shown enhanced phase stability and improved power conversion efficiency, making them attractive for various optoelectronic applications.^24–27

Reducing the crystallite size to the nanometer scale, for example, the quantum dot (QD) dimensions, further improves their phase stability because of the large contribution of surface energy and the protection by organic passivation ligands.^28–35 Moreover, owing to the increased exciton binding energy resulting from quantum confinement, excitons dominate against free carriers in these nano-sized semiconductor crystals, leading to enhanced radiative recombination and thus a high theoretical PLQY.³⁶ The synthesis of pure Sn or Sn–Pb alloyed perovskite QDs with reasonable luminescence efficiency is challenging. Even a slight incorporation of Sn in a Pb host would cause dramatic degradation of their radiative recombination, which usually leads to extremely low PLQYs of 0.3–3%.^37,38 The charge traps and recombination centers present in these Sn-contained QDs are believed to be the reasons for luminescence inefficiency.^39,40 It is generally accepted that the Sn vacancy defects are held accountable because of their low formation energy.⁴¹ However, previous computational studies suggested that Sn vacancies do not introduce deep-level traps inside the band gap. Hence, they are unlikely to produce such devastating consequences.^32,42,43 Another possible contribution to trap states in Sn–Pb alloyed QDs may come from surface halide vacancies, which will create under-coordinated metal ions. This resembles those cases in previous Pb-based perovskites where surface halide vacancies have been identified as the major defects negatively impacting their electronic properties.^44–50 However, from the viewpoint of the electronic structure, this is not the primary reason as deep-level states are present only in Cl-based perovskites, while in Br- and I-perovskites, the deficiency in surface halogen atoms will introduce only shallow defect levels.^44,51

Recent studies suggest that the formation of Sn vacancies and the oxidation of Sn²⁺ to Sn⁴⁺ are responsible for the overall degradation in Sn-containing perovskites.^52,53 Namely, the spontaneous oxidation starting from the bond breaking of Sn–I, and the under-coordinated Sn²⁺ can easily be oxidized to Sn⁴⁺. This accelerates the formation of Sn vacancies and finally converts the perovskite to the non-perovskite phase.^20,40,54,55 This indicates that the optimization of these defect-intolerant nanocrystals would require a significant suppression of the Sn vacancy formation and the oxidation of Sn²⁺ to Sn⁴⁺. A high PLQY of CsSnI₃ QDs, 59%, was achieved by using the kinetically controlled ion-exchange method by Yang et al.⁵⁶ They first synthesized the highly stable CsPbBr₃ QDs and then by introducing the SnI₂ precursor obtained the CsSnI₃ QDs with fewer defects and good structural stability. This demonstrates again the importance of defect suppression in Sn-containing perovskite QDs. Meanwhile, tailoring the QD synthesis route (with an ion-exchange reaction),^56,57 co-doping,^58,59 and inducing different ligands^60–62 have been investigated to improve the stability of perovskite QDs and increase the PLQY. For Sn-containing QDs, the stronger interaction between ligands and the surface has been proven to show a stabilization effect.^63–66 Overall, the prerequisite for retrieving the near-infrared emission of these Sn-containing QDs is to enhance the bonding strength between the Sn²⁺ and I⁻ ions and the passivation effect of surface ligands.

Doping of semiconductors has been proven to be a powerful tool to alter the structural and optoelectronic properties of both traditional semiconductors and perovskite nanocrystals.^67–74 Encouragingly, the lanthanide series (e.g. Yb³⁺ and Ce³⁺) were successfully doped into lattices of wide band-gap perovskite QDs, which demonstrated enhanced optical and electronic properties, leading to remarkably high PLQYs above 100%.^75–78 However, such an effect seems to be less effective in low band-gap perovskite QDs. For instance, mixing Br in CsPbCl₃ QDs caused a rapid drop in the PLQY.⁷⁶ Very recently, we found that ultra-low Na doping effectively improves the optoelectronic properties of Sn–Pb alloyed QDs, boosting the PLQY from ∼0.3% to 28%.⁷⁹ The X-ray photoelectron spectroscopy (XPS) analyses suggest that the Na dopant potentially enhances the chemical bonding of Sn²⁺ and I⁻ with surrounding ions and thus suppresses the formation of trapping states. However, the PLQY of the Na-doped QDs undergoes a fast degradation from ∼28% to 4% within 24 hours at room temperature. The atomistic origin of the improved luminescence efficiency of the Na doped Sn–Pb alloyed QDs and its subsequent degradation mechanisms remain unclear.

In this work, combining DFT calculations and AIMD simulations, we study the effect of Na ions on the strength of surface bonds, defect formation energies, and the interactions between surface ligands and perovskite QDs. We find that the Na dopant preferentially occupies the surface interstitial site, leading to the strengthened ionic bonding of Na with the surrounding I⁻ ions and enhanced covalent bonding of Sn²⁺ with I⁻ ions in [SnI₆]⁴⁻ octahedra. Both consequences suggest that the incorporation of Na effectively suppresses the formation of I and Sn vacancies. Furthermore, the binding energy of ligands with perovskites increases upon Na doping, resulting in a stronger passivation effect of the ligands and thus stabilizing the Sn–Pb perovskite QDs. The high mobility of the exotic Na dopant on an MI₂-terminated surface is observed from AIMD simulations, indicating that Na ions could not stabilize themselves in one out of the two surface terminations, causing the rapid decrease of PLQY.

2. Methods

2.1. Density functional theory calculation

Structural optimizations of all structures were performed using DFT implemented in the Vienna ab initio simulation package (VASP).⁸⁰ The Perdew–Burke–Ernzerhof (PBE) functional within the generalized gradient approximation (GGA) was used.⁸¹ The outermost s, p, and d (for Pb and Sn) electrons were treated as valence electrons, whose interactions with the remaining ions were modeled using pseudopotentials generated within the projector-augmented wave (PAW) method.^82,83 During the structural optimization, all ions were allowed to relax. An energy cutoff of 500 eV and a k-point scheme of 6 × 6 × 1 were used to achieve energy and force convergence of 0.01 meV and 20 meV Å⁻¹, respectively.

2.2. Ab initio molecular dynamics simulation

Ab initio molecular dynamics (AIMD) simulations were executed by using a canonical ensemble (NVT) with a Nosé–Hoover thermostat at 300 K,^84,85 as implemented in the VASP code. The PAW method was employed to describe the core-valence interaction, and the PBE exchange–correlation functional was used. A kinetic cutoff energy of 400 eV was used for the plane wave expansion. The energy and force convergence parameters were set at 0.01 meV and 20 meV Å⁻¹, respectively. A single k-point sampled at the Γ only was used to speed up the computations. The total simulation time of each calculation is 6 ps with a time step of 2 fs.

2.3. Chemical bonding analysis

An in-depth analysis of the chemical bonding was carried out to understand the chemical bonding of Na-doped perovskites. Of main interest was the bond between the Sn cation and the I anion. The strength of the chemical bonding was investigated by analyzing both the covalent and ionic bonding. The covalent contribution can be analyzed using the bond order, which correlates with the electron density value at the bond-critical point (saddle-points of electron density along the bond paths). The larger the bond order value, the stronger the covalent bond. The ionic contribution of a bond can be characterized by the net atomic charge, which quantifies the charge transfer between atoms. The positive net atomic charge of an atom indicates loss of electrons, and the negative one indicates gain of electrons. The bond order and net atomic charge calculations were carried out using DDEC6 charge partitioning implemented in the Chargemol code.^86–89

2.4. Structural models

The incorporation of Na⁺ at different locations on the surface and the bulk of QDs was investigated by using CsSn_0.6Pb_0.4I₃ surface models with the top and bottom surfaces being the [1 0 0] facets terminated by the CsI and MI₂ (M = Sn or Pb) layer, respectively (Fig. 1). The surfaces were modeled using slab models consisting of (2 × 2) cells in the x and y direction and 5 repeating units (20 Cs atoms, 12 Sn atoms, 8 Pb atoms, and 60 I atoms) with a vacuum of 15 Å in the z-direction. The dipole correction along the z-direction is considered. It should be noted that when using a quantum dot model,^90–92 a global view of the morphology of the perovskite QD surfaces and their interaction with ligands can be obtained. The surface structures, especially the surface bonds, show slightly different length and strength due to the quantum confinement effect.^93,94 However, such QD models are computationally expensive because of the need to simulate a large number of atoms. Therefore, slab models are often used as an alternative, as they are proven to be effective in correctly capturing the qualitative trends in such confinement effects.^95,96 The usage of slab models to investigate the properties of perovskite QDs has also led to many successes in previous studies.^63,66,97,98

Fig. 1 DFT optimized structures of the Na-doped CsSn_0.6Pb_0.4I₃ perovskite. In all structures, one Na ion (the yellow sphere) substitutes one Cs cation. (a–c) Side views and (d–f) top views of Na in the bulk, at the MI₂-terminated surface, and at the CsI-terminated surface (M: Pb or Sn). The (a) structure gives the highest energy. Using this as a reference, (b) has an energy of −0.22 eV, and (c) has an energy of −0.26 eV. The yellow, purple, grey, and blue spheres denote the Na⁺, I⁻, Pb²⁺, and Sn²⁺ ions, respectively.

To understand the surface ligand effect on the QDs, the slab model used above was passivated using oleylammonium (C₁₈H₃₅NH₃⁺: OLA) or oleate (C₁₈H₃₄O₂⁻: OA) on CsI or MI₂ termination, respectively. To validate our ligand slab model, we also calculated the ligand density and compared it with experimental data (Table S1†).⁹⁹ For DFT and AIMD simulations, atoms that were away from the ligand side (three repeating MI₆ octahedral layers) were fixed to mimic the bulk nature. The rest of the atoms, including the OLA and OA on top of the surface, were optimized. More computational details (e.g., vacancy formation energy, ligand binding energy, the charge displacement curve, and the diffusion coefficient) can be found in the ESI.† All structural models were visualized by using VESTA.¹⁰⁰

2.5. Experiments

We synthesized the undoped and Na-doped CsSn_0.6Pb_0.4I₃ colloidal QDs and performed X-ray photoelectron spectroscopy (XPS) characterization to analyze the surface environment of QDs. The experimental details can be found in the ESI.†

3. Results and discussion

3.1. Enhancing the surface Sn–I bonding strength

We first determine the possible atomistic locations of Na⁺ in the QDs. Fig. 1 depicts the three possible locations of Na in the QDs, where Na⁺ is found to be more stable on surfaces than in the bulk by 0.2 to 0.3 eV. On both CsI- and MI₂-terminated surfaces, Na⁺ preferentially occupies the interstitial site, rather than an A site. This is not unexpected considering the large difference in ionic radii of Na⁺ and Cs⁺ as well as the small size of Na⁺. In fact, previous studies also indicated that Na⁺ prefers to occupy an interstitial site in hybrid Pb perovskites.^101,102

Further zooming into the surface modification by Na, we found evident changes in the surface atomic structure as well as charge redistribution at the surface layers of the CsSn_0.6Pb_0.4I₃ perovskite. We found that the incorporation of Na does not affect the surface Pb–I bond strength because the bond order remains constant at 0.55. As the Sn²⁺ plays a more important role than Pb²⁺ in the stability of the QDs (see the Introduction section), we thus focus our study on the changes of the bonding state of the surface Sn²⁺ ions (Fig. 2a and b). We observe that the Sn–I bonds at the surface layer with Na are on average shorter than those without Na (one is shorter by 0.07 Å and the other slightly longer by 0.01 Å). Further chemical bonding analysis reveals an overall stronger covalent bonding between the Sn and the surface I atoms upon the incorporation of the Na dopant (Fig. 2c, S1 and Table S2†). For example, we see that the bond order of the Sn-11/I-52 bond has been increased from 0.60 to 0.66. Such an enhancement is also reflected in the electron localization function (Fig. 2e and f), where the electron cloud around the Sn²⁺ ion and I⁻ ion is more delocalized, which is a sign of a stronger covalent bonding in the Na-doped perovskite than that in the pristine one. The strengthened chemical bonding between the surface I and the Sn may originate from the newly formed strong Na–I ionic bonding on the subsurface layer, which induces a noticeable decrease in the covalent bonding between the subsurface I⁻ and the central Sn²⁺ ions (as evidenced by the decreased bond order in pairs such as Sn-11/I-50 and Sn-11/I-54). Overall, the introduction of Na⁺ induces charge redistribution, which is favorable for the formation of stronger covalent bonding of the surface Sn–I bonds.

Fig. 2 Atomistic view of the CsI-terminated surfaces of the CsSn_0.6Pb_0.4I₃ perovskite: (a) the clean (pure CsI) and (b) Na-doped (Na-CsI). The atom numbers are from the visualized model by using VESTA. The structure details with atomic coordinates can be found in the ESI.† (c) Average net atomic charges of the surface I⁻ and Sn²⁺ ions with and without incorporation of Na. (d) Comparison of the average bond order of surface Sn–I bonds with and without incorporation of Na. Electron localization function of the surface I⁻ and Sn²⁺ ions (e) without and (f) with the incorporation of Na. The arrows and dots indicate the magnitude of the electron delocalization around the Sn²⁺ and I⁻. (g) Formation energies of the Sn and I vacancies (on the top layer) in the pristine and Na-doped CsSn_0.6Pb_0.4I₃ perovskites.

We now analyze the impact of the incorporation of Na on the ionic bonding of the surrounding I⁻ and Sn²⁺. Overall, the ionic charge of I⁻ ions adjacent to the Na dopant increased, while that of the Sn²⁺ ions remained almost unchanged (see Fig. 2d). The ionic charge of I-51 increased from −0.53 to −0.55, and that of I-50 increased from −0.53 to −0.56. Consequently, a stronger chemical bonding of I⁻ with Na⁺ than that with Cs⁺ will be formed. The I⁻ with more atomic charges will form an enhanced ionic bonding with the neighboring Sn cations, which is expected to inhibit the formation of Sn⁴⁺. We also observe similar trends for the MI₂-terminated surface, and the details can be found in Fig. S2 and Table S3.†

To investigate the effect of the chemical bonding change on the behavior of defects, we then calculated the formation energies of I and Sn vacancies. We found that in the presence of Na, formation energies of those nearby I vacancies increased significantly: by 0.48 eV on the CsI-terminated surface (Fig. 2g) and by 0.89 eV on the MI₂-terminated surface. This increased vacancy formation energy of the subsurface I⁻ ions can be attributed to their stronger interaction with the Na dopant, as evidenced by both increased ionic and covalent interactions (the increased ionic charge on I⁻ ions and the larger bond order of Na–I than that of Cs–I, shown in Fig. S1 and Table S2†). Such enhanced bonding with neighboring atoms helps to suppress the diffusion of these anions.¹⁰² For those I⁻ ions sitting at the top layer of the CsI-terminated surface, we also found a high vacancy formation energy of 0.31 eV. This observation is also consistent with our earlier conclusion that the surface I⁻ ions form a stronger covalent bonding with the subsurface Sn²⁺ ions upon incorporation of the Na dopant. Previews studies showed that iodine vacancies do not create deleterious deep-level trap states within the band gap.^44,103 However, we consider that the suppression of I vacancies can be important for these Sn-containing perovskites. This is because I vacancies would exacerbate the problem of Sn⁴⁺ by exposing more uncoordinated Sn atoms, which are more susceptible to oxidation. As for Sn vacancies, we found that their formation energies are also moderately increased on both CsI- and MI₂-terminated surfaces by 0.11 eV and 0.44 eV, respectively, indicating that Na doping is also effective in suppressing the formation of these surface Sn vacancies. The increased formation energy of the Sn vacancies is a result of their enhanced chemical bonding with surrounding I⁻ ions, as discussed above.

To summarize, we have shown that the Na dopant enhances the chemical stability of Sn²⁺ and suppresses the formation of I and Sn vacancies. Both effects potentially inhibit the oxidation of Sn²⁺ to Sn⁴⁺ and the subsequent degradation of the perovskite compound, and therefore improve the optoelectronic properties of these Sn-containing perovskites.

3.2. Enhancing the ligand passivation effect

The surface ligand binding strength is another crucial factor contributing to the overall stability of perovskite QDs. The perovskite compounds will be significantly affected by the ligands due to the highly ionic and environmentally sensitive characteristics. We therefore speculate that the stability of the Sn–Pb alloyed perovskite QDs is related to the strength of chemical bonding between ligands and the surface. To examine this, we calculated the ligand binding energy (E_b) to evaluate the bond strength of ligands and the CsSn_0.6Pb_0.4I₃ QD surface, including the CsI- and MI₂-termination. The schemes of these two terminations are shown in Fig. 3a. The ligand type information is experimentally affirmed in our previous work,⁷⁹ and therefore, we built the CsSn_0.6Pb_0.4I₃ surface models that are capped with positively charged OLA and negatively charged OA, as shown in Fig. 3b. The ligand density of our model is 1.24 ligands per nm², which is close to the experimental results of Rossini et al. obtained by using solid-state NMR spectroscopy.⁹⁹

Fig. 3 (a) Idealized models of the surface termination of the as-synthesized CsSn_0.6Pb_0.4Br₃ QDs. Both surfaces are capped by cationic and anionic organic ligands at the outermost layer. (b) The considered cationic OLA and the anionic OA ligands in this study.

It is necessary to further explore the surface termination of CsSn_0.6Pb_0.4I₃ QDs owing to the different surface elemental compositions. Thus, we checked the surface composition by using XPS, as shown in Table S4.† The surface I/Cs chemical stoichiometric ratio is 2.65, which is smaller than the ratio in the chemical formula, I/Cs = 3. This implies that the CsSn_0.6Pb_0.4I₃ surface is mixed with both terminated surfaces but there are more CsI-terminations than MI₂-terminations. Thus, the two major terminations are both considered thereafter to study the surface ligand binding.

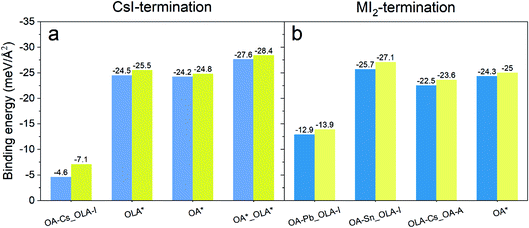
To investigate the effect of Na on the ligand binding strength, the E_b values were calculated for different binding modes of CsSn_0.6Pb_0.4I₃ surfaces and ligands without and with Na incorporation, which are schematically illustrated in Fig. 4. The ligands are assumed to attach or substitute the exposed Cs, Pb, Sn, or I surface atoms. For the CsI-terminated surface, four surface ligand configurations were considered: OLA attaches to I and OA attaches to Cs; OLA substitutes Cs; OA substitutes I; OLA substitutes I and OA substitutes Cs, shown in Fig. 4a and b from left to right. For the MI₂-terminated surface, four configurations were constructed too, that is, OLA attaches to the A cation and OA attaches to Pb; OLA attaches to the A cation and OA attaches to Sn; OLA and OA both attach to the A cation; OA substitutes I, shown in Fig. 4c and d from left to right.

Fig. 4 Schematic illustration of CsSn_0.6Pb_0.4I₃ QDs with a CsI-terminated surface (a) without and (b) with Na incorporation; MI₂-terminated surface (c) without and (d) with Na incorporation. The four different passivated configurations for the CsI-terminated surface are named OA-Cs_OLA-I, OLA*, OA*, and OA*_OLA* from left to right. Similarly, the four configurations for the MI₂-terminated surface are OA-Pb_OLA-I, OA-Sn_OLA-I, OLA-Cs_OA-A, and OA* from left to right. The * indicates the substitution of surface ions.

The calculated E_b values are all more negative after Na doping, regardless of the surface termination and the ligand interaction mode (see Fig. 5). For the CsI-terminated surface, the OLA attached to I and OA attached to Cs configurations show the smallest binding strength, while the OLA substituting Cs and OA substituting I show the largest value (see Fig. 5a). This suggests that the ligands prefer to substitute the surface ions rather than (OA substituting I and OLA substituting Cs) being physisorbed on the surface and interacting with the ions with opposite charge. For the MI₂-terminated surface, the interaction mode of OLA attached to the A cation and OA attached to Pb configurations shows the smallest binding strength, while the OLA attached to the A cation and OA attached to Sn configuration shows the largest value (see Fig. 5b). Overall, our results show that the binding strength between the surface and ligands is highly sensitive to the local atomic structure of the QDs. The incorporation of Na enhances the binding strength of the ligands with the perovskite surface, regardless of surface configurations. To investigate the genericity of alkali doping, we also studied the possible doping sites and binding energies of all other alkaline cations (see Table S5 and Fig. S6†), and the results show that only Na⁺ has such a positive effect. These results further elucidate the unique role of Na⁺ in enhancing the stability of the CsSn_0.6Pb_0.4I₃ QDs. We attribute the positive effect of Na⁺ to the ionic size. The Na⁺ has an apropos ionic size that could occupy the surface interstitial site and cause the stronger interaction with neighboring ions, enhancing the ligand binding strength.

Fig. 5 Binding energies of all ligand configurations of (a) CsI- and (b) MI₂-termination, respectively. The blue bar and yellow bar denote the original surface and the Na-incorporated surface, respectively.

To shed light on the enhanced ligand binding strength, we selected the configuration with the largest binding strength in each termination to analyze the charge transfer between the ligand and perovskite. We define Δρ_avg as the plane-averaged charge density difference and ΔQ as the charge displacement curve along the z-direction (see the ESI† for details). The results of charge transfer at two different terminations are displayed in Fig. 6. We found that the charge variations mainly occur at the interface region between the surface and ligands in both slab models. For the CsI-terminated surface shown in Fig. 6a, electrons are transferred from the ligand side to the perovskite layer in both undoped and Na-doped systems. The calculated ΔQ presented in Fig. 6c confirms this charge transfer behavior by the presence of a significant positive peak at the perovskite side but negative peaks at the side of the ligand. Moreover, an enhanced positive peak at the perovskite side and the reduced negative peaks at the ligand side are observed after Na doping. This means that a stronger charge transfer occurs at the surface after incorporating the Na, which indicates a stronger interaction between the ligand and perovskite. For the MI₂-terminated interface, a similar pattern is observed, where electrons are depleted near the ligands and accumulated at the exposed perovskite surface (see Fig. 6b). The calculated ΔQ also suggests the electron transfer from the ligands to the perovskite. The reduced negative peak at the interface and enhanced positive peak in the perovskite side after the Na incorporation in Fig. 6d indicate stronger interaction between the ligand and perovskite. Our analysis confirms that incorporating Na at the surfaces of perovskites strengthens the interaction of the ligand and perovskite by charge transfer from one to the other side.

Fig. 6 Plane-averaged charge density difference Δρ of the ligand–perovskite interfaces on (a) CsI- and (b) MI₂-terminated surfaces without and with doping. Charge displacement ΔQ of the ligand–perovskite interface on (c) CsI- and (d) MI₂-terminated surfaces without and with doping. The orange (+) and blue (−) spheres represent the depletion and accumulation of charges, respectively. The arrows represent the direction of the electron transfer. The inserted structure diagram shows the Na-doped CsI- and MI₂-terminated surfaces.

3.3. Interface dynamics on different terminations

The surface ligand binding is considered to be closely related to the thermal effect.¹⁰⁴ We thus also investigate the dynamics of the ligands on perovskite QD surfaces and the role of Na by using ab initio molecular dynamics (AIMD) simulations at room temperature, 300 K. The configurations with the largest binding strength in each termination are used as the starting point for the MD simulations. The temperature evolution during simulation time (see Fig. S3†) and the log (MSD) versus log (time) (see Fig. S4†) indicating the diffusivities of the systems reached equilibrium.

Fig. 7a and b show the mean square displacement (MSD) of all the diffusive ions in undoped and Na-doped systems. After incorporating the Na, the MSD for the CsI-terminated surface is reduced, while it is slightly increased for the MI₂-terminated surface. This difference suggests that the incorporation of Na ions has a different effect on the two terminations. Therefore, we zoom into the dynamics of specific ions. By tracking the dynamic positions of the tail-end N atom in OLA (N_OLA), the O atom in OA (O_OA) and Na, we obtain the diffusion coefficients of these ions (Fig. 7c and d). On the CsI-terminated surface, the N_OLA and O_OA have an overall lower diffusion coefficient with Na than without Na during the simulation and as well as at the end of 6 ps AIMD simulation (3.47 × 10⁻⁵ cm² s⁻¹vs. 5.13 × 10⁻⁵ cm² s⁻¹ for N_OLA and 4.23 × 10⁻⁵ cm² s⁻¹vs. 1.12 × 10⁻⁴ cm² s⁻¹ for O_OA), see Fig. 7c. In contrast, at the MI₂-terminated surface, the N_OLA and O_OA have an overall higher diffusion coefficient during the AIMD simulation after Na incorporation (Fig. 7d) as well as at the end of 6 ps AIMD simulation (1.22 × 10⁻⁴ cm² s⁻¹vs. 9.38 × 10⁻⁵ cm² s⁻¹ for N_OLA and 8.35 × 10⁻⁵ cm² s⁻¹vs. 6.64 × 10⁻⁵ cm² s⁻¹ for O_OA). It is worth noting that a large contrast is found in the diffusion coefficients of Na: the diffusion coefficient on the CsI-terminated surface is much smaller than that on the MI₂-terminated surface during AIMD simulation. The same is true for the final diffusion coefficient after 6 ps, which is two magnitudes smaller (3.34 × 10⁻⁶ cm² s⁻¹vs. 1.48 × 10⁻⁴ cm² s⁻¹).

Fig. 7 Mean-square displacement (MSD) of ligands and surface ion movement in (a) CsI- and (b) MI₂-terminated surfaces without and with Na doping. Diffusion coefficients of different ions on (c) CsI- and (d) MI₂-terminated surfaces without and with Na doping.

Fig. 8 illustrates the snapshots of the four models in the AIMD simulations. For the undoped models in Fig. 8a and b, the ligand and CsI-terminated perovskite closely interacted, while the ligand in the MI₂ terminated perovskite pulls the ions away from the surface, indicating the degradation of the perovskite. After doping Na on the surface of the perovskite, the CsI-termination maintains a stable binding interaction with ligands, while the degradation in the MI₂-termination is not mitigated as the Sn and adjacent I ions are pulled up by the OA, leading to the formation of Sn vacancies.

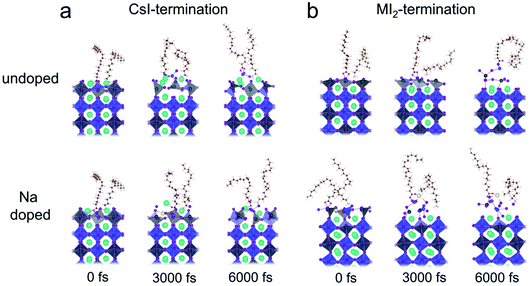Fig. 8 Snapshots of the interfaces after 6000 fs AIMD simulation of (a) CsI- and (b) MI₂-terminated surfaces without and with Na doping.

Furthermore, we found that Na is less mobile in the CsI-terminated model than in the MI₂-terminated model. This is evidenced by the time-dependent location distribution density analysis, which shows that Na⁺ is almost stationary on the CsI-terminated surface but diffuses violently on the MI₂-terminated surface (see Fig. S5†). The different diffusive behavior of Na⁺ on different terminations can be explained by the comparison of the net atomic charges of Na⁺ and adjacent I ions in the two terminations (see Fig. S6†). We found that the Na⁺ and adjacent I ions contain a larger amount of net charges, indicating the formation of a stronger ionic bond between Na and I ions in CsI-termination than in MI₂-termination, which manifests the much smaller Na⁺ mobility at CsI-termination.

4. Conclusions

To understand the role of Na ions in CsSn_0.6Pb_0.4I₃ perovskite QDs with enhanced photoluminescence and their subsequent photoluminescence degradation, we investigated the strength of surface bonds, defect formation energies, and the interaction of surface ligands and perovskite surfaces using first-principles DFT and MD calculations. Our results indicate that the Na doping has the following effects: first, Na ions prefer to locate at the surface and occupy the interstitial sites. This enhances covalent bonding of the surface Sn–I bonds and ionic bonding of Na⁺ with the neighboring Sn cations, and therefore improves the chemical stability of Sn²⁺ and suppresses the formation of I and Sn vacancies. Second, Na ions strengthen the ligand–QD surface binding and the two together passivate the surface dangling bonds of the QDs. Finally, AIMD simulations show that Na ions on the CsI-terminated surface tend to suppress the diffusion of surface ligands but do the opposite on the MI₂-terminated surface. The latter leads to the detachment of ligands and the perovskite surface layer, therefore causing the fast degradation of the MI₂-terminated surface. The above results indicate that the combination of the Na doping and CsI-termination of the QDs may result in the best improvement in maintaining a long lifetime of high photoluminescence efficiency. Therefore, we foresee that the surface termination engineering could offer a breakthrough in improving the efficiency and the lifetime of perovskite QDs for near-infrared applications. Moreover, in addition to the detrimental effect of Sn oxidation, the origin of the relatively low PLQY in infrared emitting CsSn_0.6Pb_0.4I₃ QDs could also be attributed to the constituents assembled imperfectly during the reaction process, which induced the structural defects that are challenging to eradicate only by adjusting the synthetic factors (e.g. reaction temperature and duration, and stoichiometry of reactants). We anticipate that tailoring the synthesis route, such as co-doping, or introducing different ligands may improve the stability of the Sn–Pb alloyed perovskite QDs further, meriting further experimental and theoretical studies.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

S. Tao and J. Jiang acknowledge funding by the Computational Sciences for Energy Research (CSER) tenure track program of Shell and NWO (Project number 15CST04-2) and NWO START-UP, the Netherlands. Q. Shen and F. Liu acknowledge funding by the Japan Science and Technology Agency (JST) Mirai program (JPMJMI17EA), MEXT KAKENHI Grant (Grant 17H02736, 18F18370, and 20H02565), and JSPS International Research Fellow (Faculty of Informatics and Engineering, UEC). Mr Zehua Chen is acknowledged for the constructive discussions. Dr Peter Klaver is acknowledged for his technical support in the computational study in this work.

References

1. P. W. Barone, S. Baik, D. A. Heller and M. S. Strano, Nat. Mater., 2005, 4, 86–92.
2. E. H. Sargent, Nat. Photonics, 2009, 3, 325–331.
3. S. Noda, K. Tomoda, N. Yamamoto and A. Chutinan, Science, 2000, 289, 604–606.
4. L. T. Dou, Y. Yang, J. B. You, Z. R. Hong, W. H. Chang, G. Li and Y. Yang, Nat. Commun., 2014, 5, 5404.
5. G. E. Eperon, T. Leijtens, K. A. Bush, R. Prasanna, T. Green, J. T. W. Wang, D. P. McMeekin, G. Volonakis, R. L. Milot, R. May, A. Palmstrom, D. J. Slotcavage, R. A. Belisle, J. B. Patel, E. S. Parrott, R. J. Sutton, W. Ma, F. Moghadam, B. Conings, A. Babayigit, H. G. Boyen, S. Bent, F. Giustino, L. M. Herz, M. B. Johnston, M. D. McGehee and H. J. Snaith, Science, 2016, 354, 861–865.
6. A. K. Jena, A. Kulkarni and T. Miyasaka, Chem. Rev., 2019, 119, 3036–3103.
7. J. Zhang, G. Hodes, Z. Jin and S. Liu, Angew. Chem., Int. Ed., 2019, 58, 15596–15618.
8. S. Yakunin, B. M. Benin, Y. Shynkarenko, O. Nazarenko, M. I. Bodnarchuk, D. N. Dirin, C. Hofer, S. Cattaneo and M. V. Kovalenko, Nat. Mater., 2019, 18, 846–852.
9. D. Zhang, Y. Yang, Y. Bekenstein, Y. Yu, N. A. Gibson, A. B. Wong, S. W. Eaton, N. Kornienko, Q. Kong, M. Lai, A. P. Alivisatos, S. R. Leone and P. Yang, J. Am. Chem. Soc., 2016, 138, 7236–7239.
10. Z. Xiao, Z. Song and Y. Yan, Adv. Mater., 2019, 31, 1803792.
11. W. Ke, C. C. Stoumpos and M. G. Kanatzidis, Adv. Mater., 2018, 31, 1803230.
12. G. Xing, M. H. Kumar, W. K. Chong, X. Liu, Y. Cai, H. Ding, M. Asta, M. Grätzel, S. Mhaisalkar, N. Mathews and T. C. Sum, Adv. Mater., 2016, 28, 8191–8196.
13. E. Jokar, C.-H. Chien, C.-M. Tsai, A. Fathi and E. W.-G. Diau, Adv. Mater., 2019, 31, 1804835.
14. F. Hao, C. C. Stoumpos, R. P. H. Chang and M. G. Kanatzidis, J. Am. Chem. Soc., 2014, 136, 8094–8099.
15. Y. Ogomi, A. Morita, S. Tsukamoto, T. Saitho, N. Fujikawa, Q. Shen, T. Toyoda, K. Yoshino, S. S. Pandey, T. L. Ma and S. Hayase, J. Phys. Chem. Lett., 2014, 5, 1004–1011.
16. M. Anaya, J. P. Correa-Baena, G. Lozano, M. Saliba, P. Anguita, B. Roose, A. Abate, U. Steiner, M. Gratzel, M. E. Calvo, A. Hagfeldt and H. Miguez, J. Mater. Chem. A, 2016, 4, 11214–11221.
17. W. Q. Liao, D. W. Zhao, Y. Yu, N. Shrestha, K. Ghimire, C. R. Grice, C. L. Wang, Y. Q. Xiao, A. J. Cimaroli, R. J. Ellingson, N. J. Podraza, K. Zhu, R. G. Xiong and Y. F. Yan, J. Am. Chem. Soc., 2016, 138, 12360–12363.
18. J. Tong, Z. Song, D. H. Kim, X. Chen, C. Chen, A. F. Palmstrom, P. F. Ndione, M. O. Reese, S. P. Dunfield, O. G. Reid, J. Liu, F. Zhang, S. P. Harvey, Z. Li, S. T. Christensen, G. Teeter, D. Zhao, M. M. Al-Jassim, M. F. A. M. van Hest, M. C. Beard, S. E. Shaheen, J. J. Berry, Y. Yan and K. Zhu, Science, 2019, 364, 475–479.
19. C. C. Stoumpos, C. D. Malliakas and M. G. Kanatzidis, Inorg. Chem., 2013, 52, 9019–9038.
20. T. Leijtens, R. Prasanna, A. Gold-Parker, M. F. Toney and M. D. McGehee, ACS Energy Lett., 2017, 2, 2159–2165.
21. K. Yamamoto, S. Iikubo, J. Yamasaki, Y. Ogomi and S. Hayase, J. Phys. Chem. C, 2017, 121, 27797–27804.
22. D. Guedes-Sobrinho, I. Guilhon, M. Marques and L. K. Teles, Sci. Rep., 2019, 9, 11061.
23. J. Jiang, F. Liu, I. Tranca, Q. Shen and S. Tao, ACS Appl. Energy Mater., 2020, 3, 11548–11558.
24. Y. Zong, Z. Zhou, M. Chen, N. P. Padture and Y. Zhou, Adv. Energy Mater., 2018, 8, 1800997.
25. S. Shao, Y. Cui, H. Duim, X. Qiu, J. Dong, G. H. ten Brink, G. Portale, R. C. Chiechi, S. Zhang, J. Hou and M. A. Loi, Adv. Mater., 2018, 30, 1803703.
26. R. Lin, K. Xiao, Z. Qin, Q. Han, C. Zhang, M. Wei, M. I. Saidaminov, Y. Gao, J. Xu, M. Xiao, A. Li, J. Zhu, E. H. Sargent and H. Tan, Nat. Energy, 2019, 4, 864–873.
27. M. Hu, M. Chen, P. Guo, H. Zhou, J. Deng, Y. Yao, Y. Jiang, J. Gong, Z. Dai, Y. Zhou, F. Qian, X. Chong, J. Feng, R. D. Schaller, K. Zhu, N. P. Padture and Y. Zhou, Nat. Commun., 2020, 11, 151.
28. L. Protesescu, S. Yakunin, M. I. Bodnarchuk, F. Krieg, R. Caputo, C. H. Hendon, R. X. Yang, A. Walsh and M. V. Kovalenko, Nano Lett., 2015, 15, 3692–3696.
29. A. Swarnkar, A. R. Marshall, E. M. Sanehira, B. D. Chernomordik, D. T. Moore, J. A. Christians, T. Chakrabarti and J. M. Luther, Science, 2016, 354, 92–95.
30. J. Xue, J.-W. Lee, Z. Dai, R. Wang, S. Nuryyeva, M. E. Liao, S.-Y. Chang, L. Meng, D. Meng, P. Sun, O. Lin, M. S. Goorsky and Y. Yang, Joule, 2018, 2, 1866–1878.
31. J. Huang, M. Lai, J. Lin and P. Yang, Adv. Mater., 2018, 30, 1802856.
32. A. B. Wong, Y. Bekenstein, J. Kang, C. S. Kley, D. Kim, N. A. Gibson, D. Zhang, Y. Yu, S. R. Leone, L.-W. Wang, A. P. Alivisatos and P. Yang, Nano Lett., 2018, 18, 2060–2066.
33. Z. Wang, A. M. Ganose, C. Niu and D. O. Scanlon, J. Mater. Chem. A, 2018, 6, 5652–5660.
34. J.-T. Lin, C.-C. Liao, C.-S. Hsu, D.-G. Chen, H.-M. Chen, M.-K. Tsai, P.-T. Chou and C.-W. Chiu, J. Am. Chem. Soc., 2019, 141, 10324–10330.
35. Q. Zhao, A. Hazarika, L. T. Schelhas, J. Liu, E. A. Gaulding, G. Li, M. Zhang, M. F. Toney, P. C. Sercel and J. M. Luther, ACS Energy Lett., 2020, 5, 238–247.
36. Y. Shirasaki, G. J. Supran, M. G. Bawendi and V. Bulovic, Nat. Photonics, 2013, 7, 13–23.
37. Y. Liao, H. Liu, W. Zhou, D. Yang, Y. Shang, Z. Shi, B. Li, X. Jiang, L. Zhang, L. N. Quan, R. Quintero-Bermudez, B. R. Sutherland, Q. Mi, E. H. Sargent and Z. Ning, J. Am. Chem. Soc., 2017, 139, 6693–6699.
38. T. C. Jellicoe, J. M. Richter, H. F. J. Glass, M. Tabachnyk, R. Brady, S. E. Dutton, A. Rao, R. H. Friend, D. Credgington, N. C. Greenham and M. L. Böhm, J. Am. Chem. Soc., 2016, 138, 2941–2944.
39. F. Liu, Y. Zhang, C. Ding, K. Kawabata, Y. Yoshihara, T. Toyoda, S. Hayase, T. Minemoto, R. Wang and Q. Shen, Chem. Mater., 2020, 32, 1089–1100.
40. Y. Yan, T. Pullerits, K. Zheng and Z. Liang, ACS Energy Lett., 2020, 5, 2052–2086.
41. I. Chung, J.-H. Song, J. Im, J. Androulakis, C. D. Malliakas, H. Li, A. J. Freeman, J. T. Kenney and M. G. Kanatzidis, J. Am. Chem. Soc., 2012, 134, 8579–8587.
42. P. Xu, S. Y. Chen, H. J. Xiang, X. G. Gong and S. H. Wei, Chem. Mater., 2014, 26, 6068–6072.
43. Z. Xiao and Y. Yan, Adv. Energy Mater., 2017, 7, 1701136.
44. D. P. Nenon, K. Pressler, J. Kang, B. A. Koscher, J. H. Olshansky, W. T. Osowiecki, M. A. Koc, L.-W. Wang and A. P. Alivisatos, J. Am. Chem. Soc., 2018, 140, 17760–17772.
45. A. Walsh, J. Phys. Chem. C, 2015, 119, 5755–5760.
46. F. Li, C. Zhang, J.-H. Huang, H. Fan, H. Wang, P. Wang, C. Zhan, C.-M. Liu, X. Li, L.-M. Yang, Y. Song and K.-J. Jiang, Angew. Chem., Int. Ed., 2019, 58, 6688–6692.
47. A. Walsh, D. O. Scanlon, S. Y. Chen, X. G. Gong and S. H. Wei, Angew. Chem., Int. Ed., 2015, 54, 1791–1794.
48. J. M. Ball and A. Petrozza, Nat. Energy, 2016, 1, 16149.
49. D. Yang, W. Ming, H. Shi, L. Zhang and M.-H. Du, Chem. Mater., 2016, 28, 4349–4357.
50. L. K. Ono, S. Liu and Y. Qi, Angew. Chem., Int. Ed., 2020, 59, 6676–6698.
51. Z.-J. Yong, S.-Q. Guo, J.-P. Ma, J.-Y. Zhang, Z.-Y. Li, Y.-M. Chen, B.-B. Zhang, Y. Zhou, J. Shu, J.-L. Gu, L.-R. Zheng, O. M. Bakr and H.-T. Sun, J. Am. Chem. Soc., 2018, 140, 9942–9951.
52. S. Shao, J. Liu, G. Portale, H.-H. Fang, G. R. Blake, G. H. ten Brink, L. J. A. Koster and M. A. Loi, Adv. Energy Mater., 2018, 8, 1702019.
53. J. Li, P. Hu, Y. Chen, Y. Li and M. Wei, ACS Sustainable Chem. Eng., 2020, 8, 8624–8628.
54. K. P. Marshall, M. Walker, R. I. Walton and R. A. Hatton, Nat. Energy, 2016, 1, 16178.
55. J. Jiang, C. K. Onwudinanti, R. A. Hatton, P. A. Bobbert and S. Tao, J. Phys. Chem. C, 2018, 122, 17660–17667.
56. M. Li, X. Zhang, K. Matras-Postolek, H.-S. Chen and P. Yang, J. Mater. Chem. C, 2018, 6, 5506–5513.
57. M. Imran, J. Ramade, F. Di Stasio, M. De Franco, J. Buha, S. Van Aert, L. Goldoni, S. Lauciello, M. Prato, I. Infante, S. Bals and L. Manna, Chem. Mater., 2020, 32, 10641–10652.
58. Y. Cheng, C. Shen, L. Shen, W. Xiang and X. Liang, ACS Appl. Mater. Interfaces, 2018, 10, 21434–21444.
59. Y. Zhai, X. Bai, G. Pan, J. Zhu, H. Shao, B. Dong, L. Xu and H. Song, Nanoscale, 2019, 11, 2484–2491.
60. T. Wu, Y. Wang, Z. Dai, D. Cui, T. Wang, X. Meng, E. Bi, X. Yang and L. Han, Adv. Mater., 2019, 31, 1900605.
61. Y. Wang, J. Yuan, X. Zhang, X. Ling, B. W. Larson, Q. Zhao, Y. Yang, Y. Shi, J. M. Luther and W. Ma, Adv. Mater., 2020, 32, 2000449.
62. Y. Hassan, J. H. Park, M. L. Crawford, A. Sadhanala, J. Lee, J. C. Sadighian, E. Mosconi, R. Shivanna, E. Radicchi, M. Jeong, C. Yang, H. Choi, S. H. Park, M. H. Song, F. De Angelis, C. Y. Wong, R. H. Friend, B. R. Lee and H. J. Snaith, Nature, 2021, 591, 72–77.
63. D. Yan, T. Shi, Z. Zang, T. Zhou, Z. Liu, Z. Zhang, J. Du, Y. Leng and X. Tang, Small, 2019, 15, 1901173.
64. D. Jia, J. Chen, M. Yu, J. Liu, E. M. J. Johansson, A. Hagfeldt and X. Zhang, Small, 2020, 16, 2001772.
65. J. Shamsi, D. Kubicki, M. Anaya, Y. Liu, K. Ji, K. Frohna, C. P. Grey, R. H. Friend and S. D. Stranks, ACS Energy Lett., 2020, 5, 1900–1907.
66. J. Shi, F. Li, Y. Jin, C. Liu, B. Cohen-Kleinstein, S. Yuan, Y. Li, Z.-K. Wang, J. Yuan and W. Ma, Angew. Chem., Int. Ed., 2020, 59, 22230–22237.
67. N. K. Kumawat, Z. Yuan, S. Bai and F. Gao, Isr. J. Chem., 2019, 59, 695–707.
68. A. Swarnkar, W. J. Mir and A. Nag, ACS Energy Lett., 2018, 3, 286–289.
69. E. A. Gaulding, J. Hao, H. S. Kang, E. M. Miller, S. N. Habisreutinger, Q. Zhao, A. Hazarika, P. C. Sercel, J. M. Luther and J. L. Blackburn, Adv. Mater., 2019, 31, 1902250.
70. K. Wang, W. S. Subhani, Y. Wang, X. Zuo, H. Wang, L. Duan and S. Liu, Adv. Mater., 2019, 31, 1902037.
71. S. Das Adhikari, S. K. Dutta, A. Dutta, A. K. Guria and N. Pradhan, Angew. Chem., Int. Ed., 2017, 56, 8746–8750.
72. M. I. Saidaminov, J. Kim, A. Jain, R. Quintero-Bermudez, H. Tan, G. Long, F. Tan, A. Johnston, Y. Zhao, O. Voznyy and E. H. Sargent, Nat. Energy, 2018, 3, 648–654.
73. S. Zou, Y. Liu, J. Li, C. Liu, R. Feng, F. Jiang, Y. Li, J. Song, H. Zeng, M. Hong and X. Chen, J. Am. Chem. Soc., 2017, 139, 11443–11450.
74. J. Luo, X. Wang, S. Li, J. Liu, Y. Guo, G. Niu, L. Yao, Y. Fu, L. Gao, Q. Dong, C. Zhao, M. Leng, F. Ma, W. Liang, L. Wang, S. Jin, J. Han, L. Zhang, J. Etheridge, J. Wang, Y. Yan, E. H. Sargent and J. Tang, Nature, 2018, 563, 541–545.
75. D. Zhou, D. Liu, G. Pan, X. Chen, D. Li, W. Xu, X. Bai and H. Song, Adv. Mater., 2017, 29, 1704149.
76. T. J. Milstein, K. T. Kluherz, D. M. Kroupa, C. S. Erickson, J. J. De Yoreo and D. R. Gamelin, Nano Lett., 2019, 19, 1931–1937.
77. D. Zhou, R. Sun, W. Xu, N. Ding, D. Li, X. Chen, G. Pan, X. Bai and H. Song, Nano Lett., 2019, 19, 6904–6913.
78. Q. Hu, Z. Li, Z. Tan, H. Song, C. Ge, G. Niu, J. Han and J. Tang, Adv. Opt. Mater., 2018, 6, 1700864.
79. F. Liu, J. Jiang, Y. Zhang, C. Ding, T. Toyoda, S. Hayase, R. Wang, S. Tao and Q. Shen, Angew. Chem., Int. Ed., 2020, 59, 8421–8424.
80. G. Kresse and J. Furthmüller, Comput. Mater. Sci., 1996, 6, 15–50.
81. J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865.
82. P. E. Blöchl, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50, 17953.
83. G. Kresse and D. Joubert, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 1758.
84. S. Nosé, J. Chem. Phys., 1984, 81, 511–519.
85. G. J. Martyna, M. L. Klein and M. Tuckerman, J. Chem. Phys., 1992, 97, 2635–2643.
86. T. A. Manz and N. G. Limas, RSC Adv., 2016, 6, 47771–47801.
87. N. G. Limas and T. A. Manz, RSC Adv., 2016, 6, 45727–45747.
88. T. A. Manz, RSC Adv., 2017, 7, 45552–45581.
89. T. Manz and N. G. Limas, http://ddec.sourceforge.net, 2016.
90. S. ten Brinck and I. Infante, ACS Energy Lett., 2016, 1, 1266–1272.
91. C. Giansante and I. Infante, J. Phys. Chem. Lett., 2017, 8, 5209–5215.
92. M. I. Bodnarchuk, S. C. Boehme, S. ten Brinck, C. Bernasconi, Y. Shynkarenko, F. Krieg, R. Widmer, B. Aeschlimann, D. Günther, M. V. Kovalenko and I. Infante, ACS Energy Lett., 2019, 4, 63–74.
93. F. Gao, Appl. Phys. Lett., 2011, 98, 193105.
94. Z. Lin, H. Li, A. Franceschetti and M. T. Lusk, ACS Nano, 2012, 6, 4029–4038.
95. H. Yu, J. Li, R. A. Loomis, L.-W. Wang and W. E. Buhro, Nat. Mater., 2003, 2, 517–520.
96. L. A. Cipriano, G. Di Liberto, S. Tosoni and G. Pacchioni, Nanoscale, 2020, 12, 17494–17501.
97. Y. Zheng, Z. Fang, M.-H. Shang, Z. Du, Z. Yang, K.-C. Chou, W. Yang, S. Wei and X. Hou, ACS Appl. Mater. Interfaces, 2020, 12, 34462–34469.
98. T. Binyamin, L. Pedesseau, S. Remennik, A. Sawahreh, J. Even and L. Etgar, Chem. Mater., 2020, 32, 1467–1474.
99. Y. Chen, S. R. Smock, A. H. Flintgruber, F. A. Perras, R. L. Brutchey and A. J. Rossini, J. Am. Chem. Soc., 2020, 142, 6117–6127.
100. K. Momma and F. Izumi, J. Appl. Crystallogr., 2011, 44, 1272–1276.
101. J. Cao, S. X. Tao, P. A. Bobbert, C.-P. Wong and N. Zhao, Adv. Mater., 2018, 30, 1707350.
102. N. Li, S. Tao, Y. Chen, X. Niu, C. K. Onwudinanti, C. Hu, Z. Qiu, Z. Xu, G. Zheng, L. Wang, Y. Zhang, L. Li, H. Liu, Y. Lun, J. Hong, X. Wang, Y. Liu, H. Xie, Y. Gao, Y. Bai, S. Yang, G. Brocks, Q. Chen and H. Zhou, Nat. Energy, 2019, 4, 408–415.
103. S. Tan, I. Yavuz, M. H. Weber, T. Huang, C.-H. Chen, R. Wang, H.-C. Wang, J. H. Ko, S. Nuryyeva, J. Xue, Y. Zhao, K.-H. Wei, J.-W. Lee and Y. Yang, Joule, 2020, 4, 2426–2442.
104. J. De Roo, M. Ibáñez, P. Geiregat, G. Nedelcu, W. Walravens, J. Maes, J. C. Martins, I. Van Driessche, M. V. Kovalenko and Z. Hens, ACS Nano, 2016, 10, 2071–2081.

---

Footnotes

† Electronic supplementary information (ESI) available: More computational details on vacancy formation energy, ligand binding energy, charge displacement curve, and diffusion coefficient; experimental details on the colloidal synthesis of undoped and Na-doped CsSn_0.6Pb_0.4I₃ QDs and XPS characterization; comparison of ligand density with experimental data; atomistic view, bond length, bond order, and net charge of the CsI-terminated and MI₂-terminated surfaces; surface atomistic composition from XPS data; temperature evolution and the plot of log(MSD) against log(time) of AIMD simulations; time-dependent location distribution density of Na ions; net atomic charges of the Na and adjacent I for ligand included models, the comparison of the introduction of alkaline cations (Li, Na, K, Rb, and Fr) with respect to doping site and binding energy, and the atomic coordinates for the CsSn_0.6Pb_0.4I₃ slab model without and with Na-doping at different surface terminations. See DOI: 10.1039/d1ta00955a

‡ These authors contributed equally to this work.

---