 Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Polymer-based hybrid battery electrolytes: theoretical insights, recent advances and challenges
Jelena
Popovic
 *a,
Daniel
Brandell
*a,
Daniel
Brandell
 b,
Sanyeuki
Ohno
b,
Sanyeuki
Ohno
 c,
Kelsey B.
Hatzell
c,
Kelsey B.
Hatzell
 d,
Jin
Zheng
e and
Yan-Yan
Hu
ef
d,
Jin
Zheng
e and
Yan-Yan
Hu
ef
aMax Planck Institute for Solid State Research, Stuttgart, Germany. E-mail: popovic@fkf.mpg.de
bDepartment of Chemistry – Ångström Laboratory, Uppsala University, Uppsala, Sweden
cDepartment of Applied Chemistry, Graduate School of Engineering, Kyushu University, Fukuoka, Japan
dDepartment of Chemical and Biochemical Engineering, Vanderbilt University, Nashville, USA
eDepartment of Chemistry and Biochemistry, Florida State University, Tallahassee, USA
fCenter of Interdisciplinary Magnetic Resonance, National High Magnetic Field Laboratory, Tallahassee, USA
First published on 11th February 2021
Abstract
Polymer-based hybrid electrolytes are a promissing class of materials for solid-state batteries due to their mechanical, physico-chemical and electrochemical properties. This paper gives an in-depth overview of possible ionic conduction mechanisms essential for good battery performance, and related relevant contemporary materials. The materials' preparation and characterization techniques are given in the light of necessity for deeper understanding of the structure–property relationship in such composites.
1. Introduction
Electrolyte materials are critical components in all battery systems because they enable fast and reversible ion transport between the anode and the cathode. Their chemical composition and energy landscape also regulates the electrode interface stabilization via solid electrolyte interphase (SEI) formation.5 Following the seminal work of Armand in the early 1980s, polymer-based electrolytes have been extensively investigated and commercially applied due to their high shear modulus providing mechanical rigidity, and low elastic modulus allowing flexibility. Moreover, they are generally lightweight, low-cost, inherently non-flammable, possess wide electrochemical windows, and are compatible with large-scale manufacturing processes.7–10 In comparison to the inorganic electrolytes, polymer-based electrolytes typically demonstrate better wetting with nanostructured and alkali metal electrodes, which results in lower interfacial resistances. Additionally, polymer electrolytes are versatile and can be synthesized directly on an electrode in situ from a liquid monomer or oligomer precursor. Compliant and conformal coating of an electrode is critical for achieving uniform ionic flux.The conventional salt-in-polymer electrolytes, e.g. polymer host (including poly(ethylene oxide), PEO, polyvinylidene fluoride, PVDF, and polyacrylonitrile, PAN) containing dissolved lithium salts, LiX, exhibits applicable ionic conductivities only at elevated temperatures, whereas a number of recently established Li inorganic electrolytes possess high ionic conductivities, which are even comparable to the conventional salt-in-solvent battery electrolytes at room temperature (>mS cm−1).14,15 Thus, a combination of these two solid electrolyte materials' classes could potentially solve the intrinsic problems of high energy density solid state batteries – polymers should give suitable mechanical properties while the inorganics can provide a rigid framework for fast ionic conduction.14 On the nanoscale, hybrid concepts in SEI formation have also addressed the issues of instability of solid-state electrolytes with alkali metal anodes and assisted the preparation of stable high energy density lithium metal batteries.18
There is a wide body of work that has elucidated the role non-conductive (e.g. inert) ceramic additives have in composite solid electrolytes. Typically, inert additives can affect local polymer structure (crystallinity) and/or can influence ion transport mechanisms. Historically, the first widely used polymer-based hybrid battery electrolytes was PEO mixed with oxide particles (e.g. Al2O3, SiO2), prepared by Weston and Steele, and further developed and popularized by the groups of Scrosati and Wieczorek in the 1990s.19–21 The inorganic particles plasticized the polymer, increased the volume fraction of amorphous domains on behalf of the non-conductive crystalline counterpart, and thereby increased the ionic conductivity by an order of magnitude. The group of Archer further advanced the bottom-up approach to composite synthesis by grafting oligomers on the surface of the SiO2 nanoparticles.22 Acid–base surface properties of oxide nanoparticles were put to the fore by the group of Maier to attain liquid–solid “soggy sand” electrolytes.23 In parallel, the group of Cui worked on the optimization of the 3D conductive network morphology.24,25 More recently, a considerable number of ionically conductive inorganic materials such as thiophosphates (e.g. Li10SnP2S12 (ref. 26 and 27)), garnet-type oxides (e.g., Li7La3Zr2O12 (ref. 2, 28–30)), NASICON-type phosphates (e.g., Li1+xAlxTi2−x(PO4)3 (ref. 12 and 31)), perovskite-type titanates (e.g., Li3xLa2/3−xTiO3 (ref. 32–34)) and some of their sodium counterparts35 have been investigated as potential inorganic constituents of polymer-based hybrid battery electrolytes for solid-state batteries, in particular in combination with alkali metal anodes.
This review provides a theoretical background on the ionic conduction mechanism and pathways in polymer-based hybrid electrolytes, most recent materials examples, and related synthesis procedures. The term hybrid is used to stress the inorganic-organic nature as well as the nano-/molecular level binding of these two classes of materials. We focus in detail on the properties of the above-mentioned materials, and present an overview of the most valuable experimental techniques, stressing their limitations.
2. Ionic conduction mechanisms: inorganic materials, polymers and interfaces
2.1 Inorganic ionic conductors
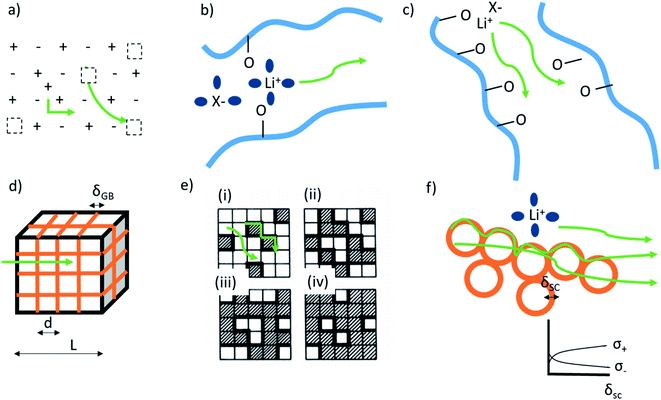
Ion transport in inorganic solids can be described by a classical diffusion model derived from statistical thermodynamic which describes ion transport in interconnected channels as a thermally activated process involving ion hopping from one lattice site to an adjacent vacant site (Fig. 1a). At the macroscopic scale, ionic conductivity is dependent on the charge (q) and density (c) of the mobile species, and their mobility (u) and typically exhibits an Arrhenius behaviour: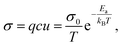 | (1) |
 | ||
| Fig. 1 Mechanisms of cation conduction (green lines) in: (a) ionic crystal of defective inorganic electrolyte. Schottky defect and interstitial doping are shown as typically occurring defects. Dotted squares represent charged vacancies. (b) Polymer materials wetted with solvent and displaying conductivity through vehicular diffusion. Blue lines and blue spheres represent polymer chains and solvent molecules, respectively. (c) Dry polymer materials through inter- and intramolecular chain transport. (d) Inorganic materials with blocking grain-boundaries (orange), where the ionic conductivity mechanism is through the bulk. The material is treated using a brick layer model. (e) The two-phase mixture on a square lattice for different concentration p of the insulating material, represented by the shaded regions. Bold lines mark the highly conducting bonds. (i) p < pc′, (ii) p = pc′ onset of interface percolation, (iii) p = pc′′ threshold for disruption of the conducting paths, and (iv) p > pc′′'. Reprinted with permission from ref. 6. (f) Hybrid materials consisting of conductive nanoparticles dispersed in electrolyte. The transport happens on the surface of insulating particles through formation of overlapping space charge zones (orange), and in the bulk of polymer and inorganic. The inset shows potentially occurring beneficial space charge zone formation. | ||
To bridge the macroscopic and microscopic ion transport, ionic conductivity can be related to the diffusion coefficient, D, through the Nernst–Einstein equation:
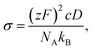 | (2) |
Within the classic hoping conduction formalism, ways of improving ionic conductivity in inorganic solids involve:
(i) increasing c through aliovalent doping37,38
(ii) Employment of the crystal structures with intrinsically low Ea (e.g. body-centered cubic anion packing39), Ea reduction by increasing lattice polarizability, by widening of the ion diffusion pathway, and through the introduction of frustration on the energy landscape.37,40
(iii) Increasing the dimensionality of the ion-conducting pathways to increase σ0.
When it comes to the device scale, the interfacial resistances typically arise from any solid/solid contact.
Recent studies propose a critical role of concerted migration of mobile ions and the lattice dynamics.41,42 In many cases, the inorganic ion conductors can be partially or completely amorphous (e.g. ionic glasses) highlighting the importance of understanding of the frustrated energy-landscape, in describing complex transport mechanisms.43,44
2.2 Polymeric ionic conductors
When dissolving a salt in a polymer, the formed material can consist of a multitude of phases: pure salt and pure polymer (both amorphous and crystalline), crystalline salt-polymer complexes of different ratios, and amorphous salt-polymer phases with varying concentrations. It is common that several of these phases co-exist, and that the material is often outside its thermodynamic equilibrium. Thus, transport properties are complex and likely demonstrate mixed behaviours depending on the specific composition, structure, and morphology. Traditionally, the crystalline regions have been considered insulating while the amorphous dominate ion transport.45 This picture, however, has changed in the recent years and crystalline or highly ordered salt-polymer ionic conductors have been widely reported in the literature.There is a number of distinct ion transport mechanisms in salt-polymer materials. Vehicular diffusion can be observed, but since macromolecules above the entanglement limit do not display such mobility in reasonable time-scales, this requires either the molecular weight, Mw, of the polymer to be low (i.e., the polymer chain is short) or a presence of additional low-Mw mobile solvent, where the ion is transported with a fixed or to some degree interchanging solvation shell (Fig. 1b). The later are the so-called ‘quasi-solid state electrolytes’ and can be found in many commercial devices. For high-energy density battery applications, the low-Mw counterpart is generally an organic carbonate, an ether or an ionic liquid, but many types of cationic-coordinating solvents have been considered.
Segmental-related mobility is the classical form of ionic mobility in polymers, related to the mobility of the coordinating polymer above its glass transition temperature (Tg) in its amorphous phase. Ion transport proceeds by coupled Brownian motion of the polymer chain segments in their rubbery state. This apparent worm-like motion is a consequence of solvation-desolvation of ions along the chains, where the coordination sphere of the cation contains anion and donor moieties from the polymer (Fig. 1c). This means that while the polymer electrolyte macroscopically behaves as a solid, at the molecular level the motion is more liquid-like. The transition from the liquid (vehicular) to polymer ionic conduction appears at the onset of chain entanglement at higher Mw values. Ionic conductivity commonly follows the empirical Vogel-Fulcher-Tammann equation above the Tg:
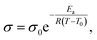 | (3) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) σ vs. 1/T), ion transport which is correlated to polymer segmental motion thereby displays an exponential shape in a similar plot.
σ vs. 1/T), ion transport which is correlated to polymer segmental motion thereby displays an exponential shape in a similar plot.
Several different transport modes can be described by segmental-related mobility. Ions can be coordinated to one or several polymer chains, and to anions. Changes in the coordination environments can promote new sites for cationic transport. This constitutes the basis for the dynamic bond percolation theory, a statistical thermodynamic model formulated by Ratner.47 Thus, the chemical structure of the polymer is its most important property that facilitates such site formation.48 In more recent work, it has been highlighted that interchain transfer of cations, rather than intrachain transport, impacts ionic conductivity in solvent-free polymer electrolytes.49,50 Nevertheless, if the ion mobility is controlled solely by the flexibility of the polymer, an extremely low Tg is necessary to achieve reasonable ionic conductivity (ca. 1 mS cm−1) at ambient temperatures. Low Tg will decrease the mechanical properties of the electrolyte and thus there is a delicate balance in terms of electrolyte design when considering both physical and transport properties.51 Strategies to overcome this problem include generating advanced polymer architectures comprised of mechanically rigid components (e.g., in the form of block-copolymers52,53) or by incorporating inorganic nano-particles into the polymer matrix. The later will be discussed throughout this review article.
Another type of ion mobility in polymer electrolytes is caused by ion hopping. In this case, the ion jumps between fixed sites. Unlike segmental-related mobility where changes in polymer/anion mobility impact ion transport, ion hopping mechanisms are governed by site specific properties. Such mechanisms are very similar to transport mechanisms exhibited in inorganic ion conductors and is often referred to as structural diffusion.54 Generally, this is an ionic movement which can occur below Tg, and should follow Arrhenius behavior.
It should be noted that there are no true fixed boundaries between different modes of ionic transport. For example, ion hopping can also be dependent on polymer mobility. Moreover, it can be difficult to distinguish these different modes of transport at short time-scales, as exemplified for many molecular dynamics (MD) studies of polymer-salt systems which are dominated by sub-diffusive mobility.55
Currently, polymer electrolytes demonstrate low room temperature conductivity (10−3 to 10−4 mS cm−1) which makes it challenging to integrate into real applications. A number of strategies have been explored to increase ion transport within these systems at ambient and sub-ambient environments. Generally, researchers look toward improving intrinsic material properties and/or tailoring transport mechanisms. Approaches to improve ionic conductivity in polymer electrolytes include:
(i) Addition of solvent, thus introducing an additional highly conductive liquid phase or plasticizing the polymer to increase its mobility.
(ii) Suppressing the polymer crystallinity through structural modification or heterogeneous doping leading to higher volume percentage of the conductive phase.
(iii) Decoupling ion-polymer motion through formation of ordered structures (e.g. nanochannels).56–58
(iv) Increasing the salt concentration until a percolating network is formed, which renders a conduction mechanism similar to a plasticized salt, and where ionic hopping is the dominating mechanism.59
Even dry salt-in-polymer electrolytes suffer from substantial anion conductivity which decreases the efficiency of cation transport and contributes to concentration polarization. A number of ionic species other than simple solvated ions may also exist, including neutral ion pairs [MX] or charged triple ions [M2X]+, [MX2]−. Depending on the specific chemistries, the cationic conductivity may be negatively affected by formation of neutral ionic species, large charged species with low ionic mobility, or mobile large charged species with negative charge. Additionally, the polymer chain length may affect the residence time of polymer in the vicinity of the cation, and thus directly govern ion–ion correlation and cationic transference number.60 Thus, it is important to define transference number for all species as the fraction of total current carried by particular ionic species:
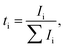 | (4) |
| Ii = ziFciuiX, | (5) |
2.3 Ionic conductivity at the interfaces and in composite materials
In the field of solid-states physics, particularly in the context of inorganic semiconductors, the concept of the space charge layer at the interfaces, where the defect concentration is altered from the bulk, is well known. When it comes to the inorganic ion conductors, the impact from the regions where the mobile carriers are depleted can be substantial when the volume fraction of such interfaces are high (e.g. if the inorganic particles are of nm size).64–66For polymer-based hybrid electrolytes, space charge layers/zones are to be expected at the following interfaces:
(i) Grain boundaries (GBs) of the polycrystalline inorganic electrolytes.
(ii) Ionic insulator/conductor interface.
(iii) Polymer/inorganic electrolyte interface.
In the first case, if cubic grains separated by GBs with homogeneous thickness and no parallel conduction pathways are assumed, a brick layer model (Fig. 1d) can be used to define the specific GB conductivity normal to the GB as:
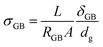 | (6) |
In insulator/ionic conductor dispersions without interfacial effects, effective conductivity can be expressed as:
| σm = (1 − φ)σ∞, | (7) |
Less is known on the formation of space charge zones at polymer/inorganic interface. Several models, including a multi-core model, has been developed in the field of flexible nanodielectric materials where such an interface is described for spherical inorganic particles dispersed in polymers and covered by several layers including:
(i) Chemically bonded layer closest to the inorganic material (ca. 1 nm thick).
(ii) Mechanically bound layer (up to 10 nm thick).
(iii) Loose layer with potentially different chain conformation, polymer mobility and free volume.
(iv) Electrochemical double layer (approximated by Gouy–Chapman or Debye–Hückel) overlapping the three layers (10 s of nm thick).71
The volume fraction of the interfacial region for such a model can be expressed by
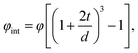 | (8) |
Interfaces between polymer and inorganic material can also be reactive, and solid-polymer electrolyte interphase (SPEI) may form, as termed by Janek, causing time-dependent changes in total conductivity.74 The SPEI is expected to be an organic–inorganic heterogenous multiphase material somewhat similar to the SEI, potentially possessing inherently higher ionic conductivity than the solid inorganic or the polymer itself.
In composite materials, ionic transport is typically composed of coupled mechanisms at different length scales (from Å to μm). Percolation theories are used to estimate the effective transport properties of randomly connected inhomogeneous composites, including ionic conductivity. The percolation threshold is a critical value of the occupation probability p above which a long-range infinite connectivity or percolation of one phase exists. The bond percolation models of composite ionic conductors consider a matrix of conducting, non-conducting and highly conducting bonds representing conductance of MX-crystals, A–A contacts and MX-A interfaces for dispersion of insulator phase in a conductive phase (Fig. 1e). In such a matrix, two critical percolation threshold probabilities exist, pc′ and pc′′ (below which probability is always 0 and above which probability is always 1) with values being 0 < pc′ < 0.5 and 0.5 < pc′′ < 1. Around pc′, conductivity behaviour is similar to a conductor-superconductor mixture, while close to pc′′ it is more similar to a conductor–insulator mixture. For such a three-phase system, the maximum of total conductivity variation with concentration of the second phase is found to be somewhere between pc′ and pc′′. Most of the percolation models are in praxis a combination of macroscopic statistical percolation model and the microscopic space-charge model.
In the 2D random-resistor-model, effective conductivity of the composite is derived to be
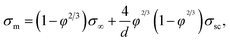 | (9) |
| σsc = zenu2ξ, | (10) |
An extension to eqn (7) in terms of parallel switching and 3D percolation is:
| σm = β∞(1 − φ)σ∞ + βαφασex, | (11) |
| σm = Aφpσp + Bφiσi + Cφscσsc | (12) |
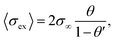 | (13) |
3. Materials components
Recently suggested materials with relevant room temperature ionic conductivities and good electrochemical stability vs. Li metal electrode are listed in Table 1.| Hybrid polymer-based electrolyte material | σ polymer/S cm−1 | σ inorganic/S cm−1 | σ composite/S cm−1 | Stability (vs. Li) | Reference |
|---|---|---|---|---|---|
| PEO–LiClO4–10 wt% SiO2 | ≈10−9 | — | 4.0 x 10−5 | 4.3 V | 80 |
| PVDF–PEO–LiTFSI–10 wt% Li7La3Zr2O12 | 1.4 × 10−5 | 2 × 10−3 | 9.5 × 10−4 | 5.2 V | 81 |
| PEO–LiTFSI– × wt% Li6.4La3Zr2Al0.2O12 | ≈10−3-10−6 | ≈10−3 | 2.5 × 10−4 | 6.0 V | 17 |
| PEO–LiClO4–78 wt% Li1.5Al0.5Ge1.5(PO4)3 | 1.5 × 10−6 | 2.5 × 10−4 | 2.0 × 10−5 | 5.2 V | 82 |
| PAN-LiClO4-15 wt% Li0.33La0.557TiO3 | 1 × 10−7 | 2.5 × 10−4 | 2.4 × 10−4 | N/A | 34 |
| PVDF-LiTFSI-80 wt% Li7La3Zr2O12 | N/A | 2 × 10−3 | Ca. 10−5 | 4.0 V | 83 |
| PEO–NaFSI–40 wt% Na3.4Zr1.8Mg0.2Si2PO12 | 3.7 × 10−6 | 1.6 × 10−3 | 4.4 × 10−5 | 4.4 V | 35 |
Generally, nanosized ceramic fillers agglomerate easily inside the polymer matrix due to inherent high surface energy, high van der Waals forces, high electrostatic forces, and/or due to entropic reasons. Compatibility between polymeric and inorganic phase can be enhanced via physical coating of nanoparticles, covalent bonding of organic modifiers by “grafting to” and “grafting on” approaches, and polycondensation reactions.77
3.1 Non-conductive inorganic component: crystallization of the polymer and acid-base effects on the inorganic particle surface
In LiClO4–PEO, serving as a model system, a room temperature conductivity enhancement of more than an order of magnitude was observed with the addition of inert TiO2 and Al2O3 powders around 5–10 nm in size, especially prevalent at low-temperature conditions.20,79 This discovery naturally sparked an immediate interest in the mechanistic background of the increase in global conductivity. The exact mechanism is still not completely understood. While salt-polymer-filler system appear simple in nature, complexity arises due to the wide range in constituent interactions that can manifest. Among these components, the salt displays a range of different cation–anion dissociation energies and corresponding differences in ion-polymer and ion–particle interactions. The ceramic particles, in turn, can display a range of Lewis acidity, neutrality and basicity (e.g. point of zero charge), large differences in dielectric properties and different sizes and shapes correlated to their effective surface area. Finally, the polymers can be either amorphous or semi-crystalline, depending on salt and particle concentration and the nature of the polymer itself, and also have different binding strengths to both the ionic components and to the particle surfaces. Moreover, there is considerable debate in the literature of the existence, size and nature of the interfacial layer formed between the dispersed nano-particles and the polymer matrix, as it is difficult to tackle experimentally. The most common approach to treat the addition of non-conductive inorganic components as additives, which are then benchmarked versus the corresponding salt-in-polymer system. In LiClO4–PEO, the conductivity increase was largely ascribed to the plasticizing effect of the particles, which after heating hindered the recrystallization of PEO. PEO-based electrolytes are otherwise known to form non-conductive crystalline phases below the melting temperature (ca. 70 °C). In this context, Best et al. studied a purely amorphous polymer (trifunctional polyether or poly(methylene ethylene oxide)), and saw no increase in conductivity with inorganic particles and only minor changes to transport properties when salt concentrations were varied.84,85 These observations suggest that the inorganic particles' primary role is in altering the polymer physics. However, when investigating electrolytes based on the semi-crystalline and low-Tg poly(caprolactone) polymer host, it was recently discovered that addition of neither nanosized TiO2 or Al2O3 resulted in any significant increase in ionic conductivity, despite a clear decrease in crystallinity.86 This highlights that the polymer plasticising cannot completely explain the conductivity increase. Instead, this work suggests that the interactions between the ceramic particle and polymer and subsequent interfacial region may have significant impact on transport.
Similar ideas have been frequently addressed in the last decades. Croce et al. stressed that the increase in conductivity was observed for LiClO4–PEO with Al2O3 and TiO2 not only at low-temperature, but also well above the Tm of PEO, where also the particle-free systems are completely amorphous.87 Instead, they hypothesized that the polar groups at the surface of the inorganic particles act as cross-linking centers for PEO and for the salt anion, which in turn lower the PEO reorganization tendency and promotes structures where the Li-ions can be transported through conducting pathways in the vicinity of the particle surface. Moreover, Lewis acid-base interactions between the ceramic surface and the ionic species could also increase the ion dissociation, and thereby increase the number of free charge carriers (see eqn (1)). By adjusting the Lewis acidity of the Al2O3 particles, a trend could be observed where the interaction between particles and both polymer and anions through hydrogen bonding was increased for the more acidic system, leading to higher conductivity.87 Similar observations were made for LiClO4–PAN system, where addition of Al2O3 helps separate ion pairs and Li+-nitrile interactions.88 Here it is important to note that in PAN-based composite the presence of dimethyformamide residue cannot be avoided.32 The basic particles, in contrast, displayed very little advantages as compared to the particle-free system, despite the obvious plasticizing effect.
Ion dissociation is impactful in describing transport properties in composite ion conductors. Sun et al. studied ferroelectric particles with high dielectric constants (BaTiO3, LiNbO3 and PbTiO3) as additives. These particles demonstrated an ion–ion screening interaction.89,90 To treat this case, electrostatic interactions between the polymer-salt complex and the ceramic are taken into account. If the polymer-salt complex is treated as a point charge (Q) in a dielectric medium dielectric constant ε1, at a distance D from the plane surface of ceramic medium with a dielectric constant ε2, the interaction energy can be expressed as:
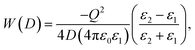 | (14) |
Interestingly, in a series of MD simulations of Al2O3 particles in different PEO-based electrolytes, Kasemägi et al. generally did not see any increased ionic mobility in the interface layer.94–97 Instead, an increased ionic clustering occurred, while the polymer and ionic mobility increased somewhat in the bulk region. These MD simulations were, however, performed for short simulation times, employing non-scaled charges and using monoatomic anions as well as low-εr Al2O3 nanoparticle in its non-acidic form, which could well influence the result. Resolving the actual transport mechanism, using contemporary computational techniques correlated with sophisticated experiments, could likely provide novel insights on ion transport in these electrolyte systems.
Nevertheless, it is believed that the interfacial region between polymer and inert filler is the key for an understanding of overall ionic transport. Studies that are more recent aimed at increasing the volume of this region and improving its connectivity through the electrolyte matrix – e.g. particles alignment, synthesis strategies preventing particle agglomeration, and specific preparation methods targeting chemical bonding rather than simple mechanical wrapping.80,98–100 Some of the investigated materials include LiTFSI-PEGDA with SiO2 aerogel, LiTFSI–PEO with vermiculite sheets or g-C3N4.101–104
Finally, since both spectroscopic and computational studies show that the polymers are more strongly coordinated at the very interface of the particles, the question arises if the mechanism is instead dominated by ion hopping at the surface. Most investigated systems, however, still display the VFT behaviour (corresponding to eqn (3)), which signals that the ionic mobility is rather correlated to the segmental motion of the polymer component. Second, however, the “interface region” can perhaps be more broadly defined and stretched out a considerable bit into the polymer bulk, where the free volume of the polymer de facto increases. The resulting general plasticisation of the polymeric system, the dielectric effects of the ceramic particles affecting the ion separation, and the surface interactions with the polymer and anions, could be incorporated into a unifying model, which can make sense of the data measured.
Hybrid electrolytes based on salt-in-solvent ionic liquids and non-conductive oxides fillers are often termed ‘ionogels’.110,111 Here, improved lithium transference numbers are possible through breaking of higher order aggregates, but room temperature ionic conductivity remains poor due to viscosity effects (ca. 10−6 S cm−1) unless additional solvent is added.112–114 Therefore, ionogels are typically used for applications above 60 °C since they also show enhanced thermal properties.115–117 As fillers, SiO2, Al2O3, metal organic frameworks, and boron nitride particles have been employed.118–120 Interestingly, ionogels can be prepared as thin films (ca. 600 nm) by spin coating.121
Solid/liquid electrolytes are believed to be beneficial for lithium metal batteries as they may increase Sand's time (e.g. time after which electroplating becomes unstable) for dendritic growth of lithium deposits or homogenise the current flow.122 Indeed, an anodic Al2O3 separator plays a crucial role in stable deposition of lithium metal from a 30 mol% LiF + LiTFSI/EC:DEC electrolyte.123 The ionic rectification is a more probable stabilization mechanism since the beneficial effect on lithium metal electrodes has been also observed in SiO2/salt-in-ionic liquid composites in which lithium transference is expected to be considerably lower compared to the “soggy sand” electrolytes (tLi < 0.2).124–127
3.2 Conductive inorganic component: importance of the 3D network formation and interfacial chemistry
Recent developments of inorganic solids possessing a high ionic conductivity at ambient temperature enables the use of conductive solids as fillers for hybrid electrolytes. While non-conductive fillers enhance ionic conductivity of the composite owing to the various interfacial (see Sections 2.3 and 3.1.2) and plasticizing effects,80 the achievable conductivity of dry systems remains low due to the low room temperature conductivity of polymers. The conductive fillers may open up another potentially dominant conduction pathway for ions when they percolate.11 Continuous conductive interfaces percolating through the composites can also further enhance the ion transport.There are two significant groups of conductive inorganic components: ion-conducting oxides and sulfides. The oxides tend to be chemically and electrochemically more stable, whereas sulfides typically exhibit higher ionic conductivities owing to their higher polarizability of the anion framework.42,128 Nevertheless, as both of ion-conducting inorganic solids are mechanically rigid and brittle, a so-called chemo-mechanical failure, caused by contact losses among the components due to the volume changes of active materials upon cycling, is one of the crucial failure mechanisms when solely inorganic solids are employed. Hence, the hybrid electrolytes composed of flexible polymers with highly conductive inorganic conductors can pave the way for complemental mechanical property and ionic transport for battery applications.
Improving key physical properties, e.g. ionic conductivity, adhesion, and strength, are paramount for further enhancement of hybrid electrolytes. In addition, structure (meso, micro, and nano) has also been shown to impact device performance. Therefore, a rational electrolyte design and optimization is necessary. The recent synthetic approaches for structuring the hybrid electrolytes with conductive oxides are summarized in Fig. 2.
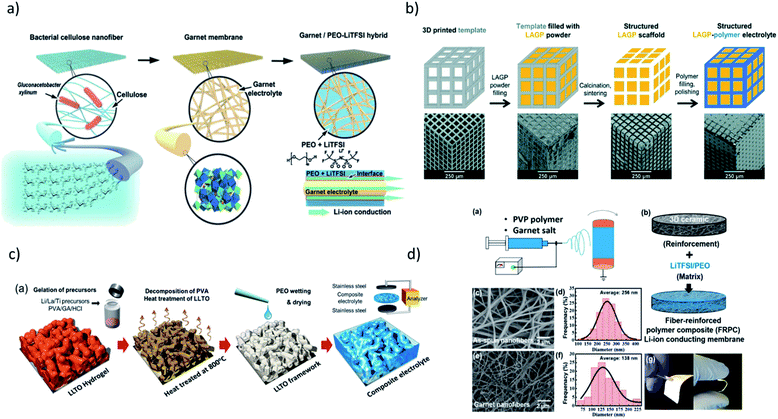 | ||
| Fig. 2 Synthetic procedures for preparation of hybrid electrolytes with conductive inorganic component resulting in different 3D network structures via: (a) hard templating using cellulose nanofiber to obtain PEO–LiTFSI–LLZO. Reproduced from ref. 1 with permission from John Wiley and Sons. (b) 3D printed hard template to obtain PEO–LAGP, Reproduced from ref. 12 with permission from The Royal Society of Chemistry. (c) Sol–gel chemistry to obtain PVA–LiTFSI–LLTO. Reprinted with permission from ref. 16 (d) electrospinning technique to obtain PEO–LiTFSI–LLZO. Reprinted with permission from ref. 17. | ||
Fu et al. constructed the first 3D Li-ion-conducting ceramic network based on Li6.4La3Zr2Al0.2O12 (LLZO) in PEO through fabricating the 3D network by electrospinning LLZO–PVP nanofibers (Fig. 1d).17 Considering the ionic conductivities of LLZO (∼1 × 10−3 S cm−1) and salt-in-polymer PEO (∼ 10−6 to 10−9 S cm−1), a reasonably high resulting ionic conductivity of the composite (2.5 × 10−4 S cm−1) is achieved with the mass ratio of polymer and filler of 4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1. The critical role of continuous filler network is further highlighted in work by Bae et al.33 They successfully constructed a continuous Li0.35La0.55TiO3 (LLTO) network by preparing porous LLTO framework through heat treatment of the LLTO hydrogel, followed by immersing it in the PEO matrix (Fig. 1c). The ionic conductivity of the resulting hybrid electrolyte is compared to that of the composite prepared with discontinuous LLTO nanoparticles, revealing almost an order of magnitude higher ionic conductivity with a continuous LLTO network (8.8 × 10−5 S cm−1 with 44 wt% of LLTO), despite the similar volume fractions of LLTO. The percolation model as a function of volume fraction of LLTO could fit the trend with continuous LLTO, further indicating the importance of the design of the component architecture.
1. The critical role of continuous filler network is further highlighted in work by Bae et al.33 They successfully constructed a continuous Li0.35La0.55TiO3 (LLTO) network by preparing porous LLTO framework through heat treatment of the LLTO hydrogel, followed by immersing it in the PEO matrix (Fig. 1c). The ionic conductivity of the resulting hybrid electrolyte is compared to that of the composite prepared with discontinuous LLTO nanoparticles, revealing almost an order of magnitude higher ionic conductivity with a continuous LLTO network (8.8 × 10−5 S cm−1 with 44 wt% of LLTO), despite the similar volume fractions of LLTO. The percolation model as a function of volume fraction of LLTO could fit the trend with continuous LLTO, further indicating the importance of the design of the component architecture.
Zekoll et al. further examine the impact of the component architecture through a precisely controlled microstructure of Li1.4Al0.4Ge1.6(PO4)3 (LAGP) with a 3D-printing technique.12 The LAGP scaffold was first constructed by filling the 3D template prepared by stereolithography. The polymers were filled in the channels of LAGP, followed by template removal. Four different microarchitectures of LAGP (cube, gyroid, diamond, and bijel-derived) with two different types of polymers were successfully constructed with almost identical volume fractions (Fig. 1b). Notably, there are significant variations in both the resulting polarization overpotential and susceptibility to fracture, highlighting the need for an optimally designed hybrid structure for ideal material and transport properties. A multitude of other research with conductive oxides as fillers have also been conducted with garnets,25,28,30,81,129–131 NASICONs,31,132–135 LISICONs,136 and perovskites.34,137–139
In comparison to the oxide-polymer hybrid electrolytes, there is only a limited amount of work on sulfide-polymer composites available. This is partly because highly conductive sulfides have been developed only recently, but also due to their low chemical and electrochemical stability, which makes the sample handling very demanding.140–142 For example, the highly conductive Li-thiophosphates, e.g. Li3PS4, Li6PS5Cl, and Li10GeP2S12 (LGPS), release H2S gas upon moisture exposure; therefore, any exposure to ambient air and residual moisture needs to be avoided.143 Phosphorous reduction and sulfur oxidation restrict the electrochemical stability window, often requiring a carefully tuned potential window for mitigating the evolution of interfacial resistances.144–146 Indeed, Li10SnP2S12 has recently shown to be unstable with PEO–LiTFSI electrolyte.147 It has been speculated that degradation reactions starts with polymerization of PS43− units, followed by reaction of released sulphur to form polysulfides and further on P–[S]n–P bridges. The oxidation of Li10SnP2S12 is enabled by the solubility of Li+ and polysulfides in PEO. Impurities in Li10SnP2S12 such as LiOH could act as PEO deprotonation agents. Also, PEO is highly hygroscopic, allowing for H2O residuals to react with sulphides.148 Nevertheless, some positive aspects and mechanistic understandings have been reported for ion-conducting sulfides in hybrid polymer electrolytes. For example, influences of β-Li3PS4,149 Li6PS5Cl,3 LGPS,150 and Li10SnP2S12 (LSnPS)26 fillers have been demonstrated to be beneficial for the effective ionic transport of the resulting composites. The major transport pathway in the LGPS–PEO composite has been identified to be at the solid/polymer interfaces, again highlighting the importance of the rationally designed composite structure.151 The interfacial instability of Li6PS5Cl in contact with PEO/LiTFSI has been confirmed by the combined spectroscopic measurements, corroborating the dominant products at the interface to be polysulfides and LiF.74 This work also reports the diffusion of the polysulfides from the Li6PS5Cl/polymer interface to the surface of Li metal, possibly enabling the use of Li-metal through formation of LixSy-rich artificial SEI. Very recently, Meirong Li et al.152 and Xue Li et al.26 demonstrated functioning Li–S batteries with Li-metal anode, enabled by the use of a hybrid electrolyte composed of PEO and LGPS or LSnPS. The enhanced cyclability of the resulting Li–S cells are attributed to the improved mechanical stability, as well as a mitigated detrimental effect from the anode interfaces. The here-mentioned work generally indicates the positive impact at the interface between electrolytes and Li–metal in terms of both chemical and chemo-mechanical stability.
While the employment of solid-polymer hybrid electrolytes with conductive solids is a promising strategy for boosting the performance of solid state batteries, there is still a vast room for further exploration and improvements including:
(i) Optimizing micro- and nano-structure design of the hybrids.
(ii) An in-depth assessment of the impact of surface of filler components.
(iii) Extension of the list of the candidate for conductive inorganic fillers.
Importantly, LLZO is prone to surface contamination via the formation of carbonate and oxide layers that hinder ionic transport between the inorganic and organic phases.153–155 When the designed filler structure becomes complex, the removal of the insulating Li2CO3 layer may require significant effort. The proton inclusion and conduction in the solids, e.g. NASICON, can also play a significant role in determining the conduction mechanisms.156 The nature of the interface surely changes when a new class of inorganic filler components is employed. Recently re-developed halide-based ion conductors are revealed to possess better electrochemical stability than sulfides, with comparably high ionic conductivity.157–159 The ion-conducting closo-borate and its relatives are also recently developed to be very promising class of materials with a larger electrochemical stability window than sulfides.160–162 Not to mention that Na-ion conducting solid-polymer hybrid electrolytes should be further explored with the hope of opening up another vast amount of candidate materials.117,163 Although further development and improvement are still required at the current stage, it is evident that there are numerous ways and vast amount of room to explore the hybrid electrolytes.
4. Overview of valuable characterization techniques and tools
4.1 Ionic transport experiments
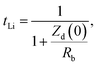 | (15) |
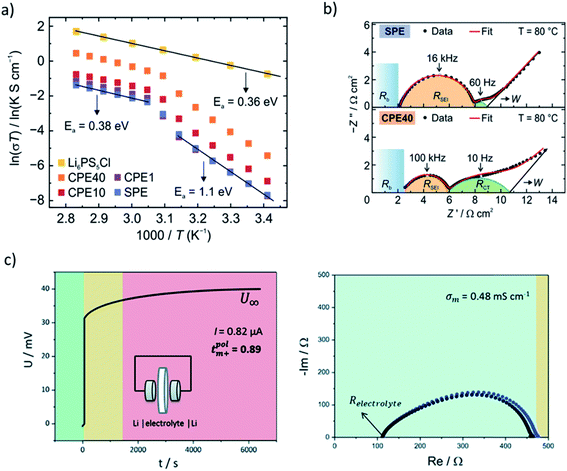 | ||
| Fig. 3 Electrochemical methods for characterization of hybrid electrolyte materials. (a) Temperature-dependent ionic conductivities measured by EIS in symmetric stainless steel cells. In composite electrolyte, two temperature regimes are fitted with Arrhenius equation to obtain Ea. (b) EIS from symmetric Li/electrolyte/Li cells showing the contributions of bulk composite electrolyte resistance (Rb), SEI resistance (RSEI) and charge transfer resistance (RCT). SPE corresponds to solid polymer electrolyte, CPE to composite polymer electrolyte with varied content of Li6PS5Cl (1–40 wt%). (a, b) Reprinted with permission from ref. 3. Copyright 2020 American Chemical Society. (c) Lithium transference number determination using galvanostatic polarization (left) in combination with EIS (right) in symmetric Li/triglyme-LiCF3SO3-AAO/Li cells. The observed semicircle corresponds to RSEI before and after polarization experiment. The colors represent different time regimes. Reproduced from ref. 13 with permission from The Royal Society of Chemistry. | ||
t Li can also be measured by combining the medium frequency EIS with dc polarization popularized by Bruce in the polymer electrolyte community:166
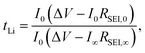 | (16) |
Symmetric Li/electrolyte/Li cells are also used to perform stripping-plating experiments which unlike dc polarization are designed to induce defects on lithium electrodes leading to dendrite formation and propagation through the electrolyte. Complex change of voltage in time in such experiments, however, also takes into account breaking and reformation of SEI, as well as appearance of “dead” lithium zones.
Although EIS has become a commonplace to address the ionic conductivity in solid ion conductors, the measured values of the same sample in some cases may vary depending on measurement condition and environment, e.g. sample and electrode geometry, pelletizing pressure, the pressure applied during the measurement, temperature ranges, applied frequency, the way the electrodes have been attached to the pellet, cell configuration, and even the sample history.167 A recent inter-laboratory reproducibility study via round robin test of thiophosphate-based electrolytes suggests a significant variation in the measured conductivity and Ea.168 Thus, it is worth noting that there may be a convoluted effect leading to considerable uncertainty in the results. Since the origin of the deviation is not straightforward to pinpoint, we highlight the importance of reproducibility of the observed trends. Even if an absolute value shows discrepancy, the trend seen in a series of samples measured in the same environment is more reliable. Overall, as long as one is aware of the potential reproducibility challenges, EIS is a useful routine for many researchers.
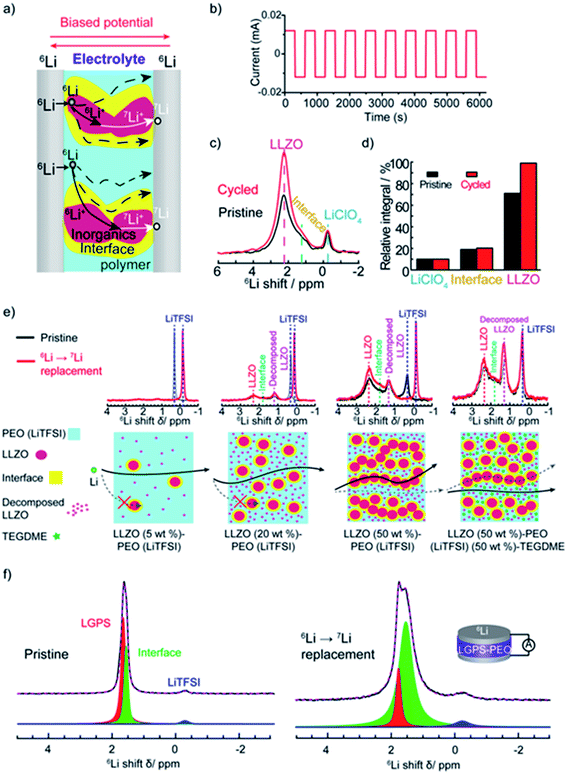 | ||
| Fig. 4 The tracer-exchange NMR method for characterizations of hybrid electrolytes. (a) Schematic of the symmetric 6Li/electrolyte/6Li battery and possible Li-ion transport pathways. (b) The current profile that is applied to drive Li ions to move from one 6Li-electrode to the other. (c) 6Li NMR spectra of LLZO–PEO before (pristine) and after (cycled) tracer-exchange. (d) Quantitative analysis of the 6Li amount in different components before and after tracer-exchange. (a)–(d) are reprinted with permission from ref. 2. (e) 6Li NMR comparison of pristine and tracer-exchanged LLZO–PEO composite electrolytes with different compositions (top) and the corresponding schematic illustrations of Li-ion transport pathways (bottom). Reprinted with permission from ref. 11. (f) 6Li NMR spectra and deconvolution results of LGPS–PEO composite electrolytes before (left) and after (right) tracer-exchange. Reprinted with permission from ref. 142. | ||
Variations in Li local environments often result in different ion dynamics. NMR relaxometry can be used to gauge ion mobility. For instance, 7Li spin-lattice relaxation time (T1) is measured to examine the Li-ion mobility in composite electrolytes.11,135,171–173 Wu et al. find that the addition of Gd0.1Ce0.9O1.95 (GCO), an oxygen-vacancy rich oxide, reduces 7Li T1 value of the LiTFSI in PEO from 0.55 to 0.25 s.172 For solid polymers with ionic conductivities <1 mS cm−1, empirically, Li+ ion motion lies in the slow motion region, i.e.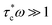 is where τc is the motion correlation time and ω is the Larmor frequency of Li NMR, according to the Bloembergen, Purcell, and Pound relaxation model.174,175 In the slow motion region, shorter T1 indicates faster ion motions. The results correlate with the enhanced ionic conductivity of GCO (5 wt%)–PEO composite (1.9 × 10−4 S cm−1) compared with PEO electrolyte (∼10−5 S cm−1) measured by EIS. However, high loading of ceramic particles limits the motion of Li ions.11,173 In LLZO (50 wt%)–PEO (LiTFSI), LLZO and LiTFSI exhibit longer 7Li T1, 1.33 and 0.73 s, respectively, than that of pure LLZO (0.45 s) and PEO (LiTFSI) (0.28 s), which is one of the reasons for the poor ionic conductivity.11 In composite electrolytes, Li ions can pass through inorganics, polymers, inorganic–polymer interface, or the combination of the two or three (Fig. 4a). To address this issue, some of us applied a new technique, tracer-exchange NMR, which tracks Li-ion transport pathways in solid electrolytes (Fig. 4a–d).2,11,135,151,171,176 Tracer-exchange NMR is a combination of 6Li → 7Li isotope replacement and high-resolution 6Li NMR. In the experimental setup, a solid electrolyte with Li in its natural abundance (7.6% 6Li and 92.4% 7Li) is assembled between two 6Li-enriched metal electrodes (Fig. 4a). The symmetric cell is imposed with a biased electric potential to drive 6Li ions to move from one 6Li-electrode to the other, passing through the electrolyte (Fig. 4b). Along their way, 6Li ions from the electrodes will partially replace 7Li ions in the electrolyte. In other words, the amount of 6Li on the ion transport path will increase due to tracer exchange, thus allowing the pathways to be revealed based on quantitative high-resolution 6Li NMR (Fig. 4c and d). Indeed, with tracer-exchange NMR, Li-ion transport pathways in LLZO–PEO composite electrolytes with various compositions have been determined (Fig. 4e).11 At low weight percentages of LLZO (e.g., 5 and 20 wt%), Li ions transport through PEO polymer matrix, especially in those regions where the presence of ceramic LLZO particles have prevented polymer crystallization. When more LLZO (e.g., 50 wt%) is incorporated into the composites, LLZO particles can form a percolated network and the majority of Li ions prefer going through the LLZO phase. It is worth noting that plasticizers, for instance, tetraethylene glycol dimethyl ether (TEGDME), can alter ion transport pathways. In LLZO–PEO–TEGDME electrolyte, most Li ions pass through the mixture of PEO–TEGDME instead of LLZO because of the improved ion mobility in PEO by TEGDME. In LLZO–PEO composites, LLZO–PEO interfaces barely contribute to Li-ion transport. It is likely due to the hardness of oxide electrolytes, which are difficult to form a coherent interface. On the other hand, sulfides are much softer in nature and more mechanically compatible with polymers. Tracer-exchange NMR results of LGPS–PEO composite electrolyte shows that 6Li is greatly enriched in LGPS–PEO interface after tracer-exchange (Fig. 4f), suggesting that Li-ion transport mainly takes place at LGPS–PEO interface.175
is where τc is the motion correlation time and ω is the Larmor frequency of Li NMR, according to the Bloembergen, Purcell, and Pound relaxation model.174,175 In the slow motion region, shorter T1 indicates faster ion motions. The results correlate with the enhanced ionic conductivity of GCO (5 wt%)–PEO composite (1.9 × 10−4 S cm−1) compared with PEO electrolyte (∼10−5 S cm−1) measured by EIS. However, high loading of ceramic particles limits the motion of Li ions.11,173 In LLZO (50 wt%)–PEO (LiTFSI), LLZO and LiTFSI exhibit longer 7Li T1, 1.33 and 0.73 s, respectively, than that of pure LLZO (0.45 s) and PEO (LiTFSI) (0.28 s), which is one of the reasons for the poor ionic conductivity.11 In composite electrolytes, Li ions can pass through inorganics, polymers, inorganic–polymer interface, or the combination of the two or three (Fig. 4a). To address this issue, some of us applied a new technique, tracer-exchange NMR, which tracks Li-ion transport pathways in solid electrolytes (Fig. 4a–d).2,11,135,151,171,176 Tracer-exchange NMR is a combination of 6Li → 7Li isotope replacement and high-resolution 6Li NMR. In the experimental setup, a solid electrolyte with Li in its natural abundance (7.6% 6Li and 92.4% 7Li) is assembled between two 6Li-enriched metal electrodes (Fig. 4a). The symmetric cell is imposed with a biased electric potential to drive 6Li ions to move from one 6Li-electrode to the other, passing through the electrolyte (Fig. 4b). Along their way, 6Li ions from the electrodes will partially replace 7Li ions in the electrolyte. In other words, the amount of 6Li on the ion transport path will increase due to tracer exchange, thus allowing the pathways to be revealed based on quantitative high-resolution 6Li NMR (Fig. 4c and d). Indeed, with tracer-exchange NMR, Li-ion transport pathways in LLZO–PEO composite electrolytes with various compositions have been determined (Fig. 4e).11 At low weight percentages of LLZO (e.g., 5 and 20 wt%), Li ions transport through PEO polymer matrix, especially in those regions where the presence of ceramic LLZO particles have prevented polymer crystallization. When more LLZO (e.g., 50 wt%) is incorporated into the composites, LLZO particles can form a percolated network and the majority of Li ions prefer going through the LLZO phase. It is worth noting that plasticizers, for instance, tetraethylene glycol dimethyl ether (TEGDME), can alter ion transport pathways. In LLZO–PEO–TEGDME electrolyte, most Li ions pass through the mixture of PEO–TEGDME instead of LLZO because of the improved ion mobility in PEO by TEGDME. In LLZO–PEO composites, LLZO–PEO interfaces barely contribute to Li-ion transport. It is likely due to the hardness of oxide electrolytes, which are difficult to form a coherent interface. On the other hand, sulfides are much softer in nature and more mechanically compatible with polymers. Tracer-exchange NMR results of LGPS–PEO composite electrolyte shows that 6Li is greatly enriched in LGPS–PEO interface after tracer-exchange (Fig. 4f), suggesting that Li-ion transport mainly takes place at LGPS–PEO interface.175
Other valuable NMR techniques also available for measurements of ion migration include pulse field gradient NMR (PFG-NMR) for studying lithium (or anion) self-diffusion, and electrophoretic NMR for studying self-diffusion under electric field.173,177–180 However, most of the conventional PFG-NMR techniques face difficulties when linked with highly inhomogeneous materials with variety of structural parameters, leading to microscopic diffusion anisotropy.181 Diffusion NMR with high spatial resolution will help to address these challenges.
In brief, NMR characterization offers insightful information to understand how composite electrolytes work, which facilitate the design and synthesis of new composite electrolytes with superior performance.
4.2 Visualization tools
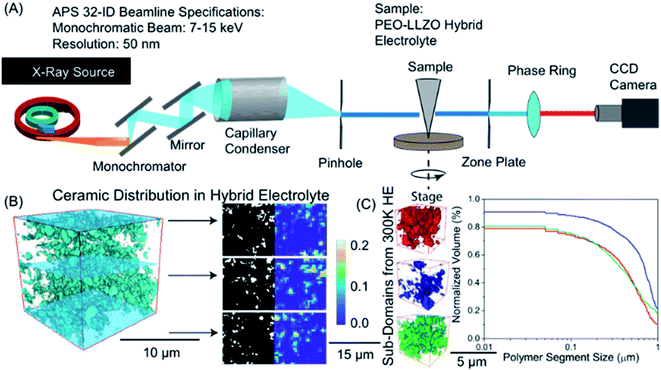 | ||
| Fig. 5 Visualization of ceramic distribution in hybrid polymer-based battery electrolyte based on nano-X-ray computed tomography: (A) sketch of the synchrotron setup used, (B) 3D tomograms showing ceramic distribution obtained by reconstruction of 2D images of different slices show on the right. In the right part, dark region corresponds to the polymer phase and white represents the inorganic particles. (C) Statistical analysis of multiple polymeric sub-volumes. Reproduced with permission from ref. 4. | ||
The segmentation process is a critical step in data processing which labels or assigns individual voxels to a specific material or phase (e.g. polymer or inorganic material). The segmentation process can introduce considerable uncertainty in the reconstructed images making quantitative analysis challenging. Deep learning techniques, such as convolutional neural networks have emerged as a pathway to dampen uncertainty in the segmentation process prior to simulation.187 Once images are reconstructed into 3D tomograms, physical properties (Young's moduli, stress distribution) and structural properties (vol% of the phase, pore size distribution, polymer size distribution, etc.) can be extracted. Fig. 5b demonstrates binarized data from different slices in a polymer ceramic electrolyte where the dark region represents the polymer phase and white represents the inorganic particles. Volumetric mapping of polymer or inorganic ceramic density can be averaged over the entire sample to visualize regions that are polymer rich and ceramic rich (Fig. 5b). Statistical analyses of multiple sub-volumes is typically necessary to account for uncertainty in segmentation and reconstruction (Fig. 5c). Some of us recently used nano-tomography to quantify the inorganic particle surface area within a hybrid solid electrolyte and found that the ionic conductivity of the composite was proportional to the accessible surface area,182 which suggests that transport between the inorganic and organic phases is ineffective.
X-ray techniques are powerful techniques for in situ, ex situ, and operando micro and nano-scale characterization of polymer-ceramic electrolyte. However, polymer degradation requires high energies and short exposure times. The latter can be achieved through controlled experimental design.
5. Conclusions and outlook
Hybrid polymer-based battery electrolytes are an emerging class of materials which promise to unify the beneficial electrochemical of inorganic nanoparticles with mechanical and/or surface properties of ionically conductive polymers. Despite an accelerated research effort in this area in recent years, however, there are still large uncertainties existing in the conduction mechanisms of this materials, and how they depend on the interplay between particle type, polymer host and the different concentrations and loadings. In this review, we show that when the inorganic particles are non-conductive, the synergy of these two materials' classes is mirrored by improvement of ionic conductivity in the polymer phase by inducing amorphicity, or in the formation of highly cationically conductive interfaces when adsorption properties of the particles are substantial. We also explain how different methodological approaches – both computational and experimental – can help to bring clarity into the mechanistic issues of ionic conductivity. Considering the effect of increased conductivity achieved also for melted and/or amorphous polymer hosts, or the lack of such an effect for certain semi-crystalline polymers, it can be concluded that it is not only a plasticizing effect that give rise to conductivity enhancement. Instead, the differences highlight that the ceramic–polymer interactions are of high importance for the electrochemical performances of these materials.In the case of conductive alkali-metal containing nanoparticles linked with polymers, the potential cation transport pathways are even more complex since the above-mentioned effects still may occur, but also grain boundaries and changes in the local chemical potentials in the particle vicinity may be substantial. While a number of systems have been suggested, the specific ionic pathways are highly dependent on the specific materials' chemistries and can hardly be generalized. In-depth understanding of both theoretical transport properties of individual materials as well as clever experimental design for composite materials' characterization on micro- and nanoscale is needed to be able to unveil them. In this review, we have highlighted the combined use of modelling, spectroscopy (e.g. EIS and NMR) and visualization tools, which has brought some clarity into these issues, and where percolation at micro-scale seem to be key for ionic transport – at least for some systems such as the well-studied LLZO–PEOxLiTFSI. With a broader portfolio of conductive composite materials, and more systematically investigated in terms of particle loading, temperature, etc., novel key findings can be expected in the near future.
Insights in surface and interface chemistry, chemical termination and chemical stability of both conductive and non-conductive inorganic particles is crucial for interpretation and prediction of their agglomeration and interaction with the polymer in the composite. However, it can be stated that controlled formation of percolating 3D networks of inorganic nanoparticles (or other nanostructures such as nanowires) by targeted synthesis is highly beneficial for the transport and mechanical properties of this class of materials. Specific chemical synthesis methods from the polymer chemistry spectrum, such as grafting on or to, can provide materials in which the inorganic-organic contact is chemically beneficial. On the other hand, physical deposition methods and nanotechnological techniques (e.g. nanolithography) could enable preparation of beneficial 3D structures. At the same time, development of in situ or operando non-destructive techniques to track the mass and charge transport, interfacial and changes in the materials' bulk structure (phases in the polymer part) upon cycling in cells is also of utmost importance.
Finally, in terms of potential application of hybrid polymer-based materials in commercial cells, further increase of room temperature ionic conductivity, cationic transference number, and electrochemical stability (in particular for coupling with high voltage cathodes and alkali metal anodes), is a clear goal for the next decades. Much of the research conducted on this category of electrolyte materials has been made under very controlled and electrochemically mild conditions. Elucidating their performance in realistic electrochemical cell will both provide novel insights into their physical chemistry, while also point out their potential usefulness in true solid-state energy storage systems.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
Douglas Fabini is thanked for reading the manuscript. KBH acknowledges support by the National Science Foundation under grants number 1847029. Reviewers are thanked for their suggestions for improvement of the manuscript. Open Access funding provided by the Max Planck Society.References
- H. Xie, C. Yang, K. Fu, Y. Yao, F. Jiang, E. Hitz, B. Liu, S. Wang and L. Hu, Adv. Energy Mater., 2018, 8, 1703474 CrossRef.
- J. Zheng, M. Tang and Y.-Y. Hu, Angew. Chem., Int. Ed., 2016, 55, 12538–12542 CrossRef CAS.
- F. J. Simon, M. Hanauer, F. H. Richter and J. Janek, ACS Appl. Mater. Interfaces, 2020, 12, 11713–11723 CrossRef CAS.
- M. B. Dixit, W. Zaman, N. Hortance, S. Vujic, B. Harkey, F. Shen, W.-Y. Tsai, V. De Andrade, X. C. Chen, N. Balke and K. B. Hatzell, Joule, 2020, 4, 207–221 CrossRef CAS.
- J. M. Tarascon and M. Armand, Nature, 2001, 414, 359–367 CrossRef CAS.
- H. E. Roman, A. Bunde and W. Dieterich, Phys. Rev. B: Condens. Matter Mater. Phys., 1986, 34, 3439–3445 CrossRef.
- M. Armand, Adv. Mater., 1990, 2, 278–286 CrossRef CAS.
- M. Armand, Solid State Ionics, 1994, 69, 309–319 CrossRef CAS.
- M. B. Armand, P. G. Bruce, M. Forsyth, B. Scrosati and W. Wieczorek, Polymer Electrolytes, John Wiley & Sons, 2011 Search PubMed.
- J. Mindemark, M. J. Lacey, T. Bowden and D. Brandell, Prog. Polym. Sci., 2018, 81, 114–143 CrossRef CAS.
- J. Zheng and Y.-Y. Hu, ACS Appl. Mater. Interfaces, 2018, 10, 4113–4120 CrossRef CAS.
- S. Zekoll, C. Marriner-Edwards, A. K. O. Hekselman, J. Kasemchainan, C. Kuss, D. E. J. Armstrong, D. Cai, R. J. Wallace, F. H. Richter, J. H. J. Thijssen and P. G. Bruce, Energy Environ. Sci., 2018, 11, 185–201 RSC.
- J. Popovic, G. Hasegawa, I. Moudrakovski and J. Maier, J. Mater. Chem. A, 2016, 4, 7135–7140 RSC.
- Y.-S. Hu, Nat. Energy, 2016, 1, 16042 CrossRef CAS.
- Z. Zhang, Y. Shao, B. Lotsch, Y.-S. Hu, H. Li, J. Janek, L. F. Nazar, C.-W. Nan, J. Maier, M. Armand and L. Chen, Energy Environ. Sci., 2018, 11, 1945–1976 RSC.
- J. Bae, Y. Li, J. Zhang, X. Zhou, F. Zhao, Y. Shi, J. B. Goodenough and G. Yu, Angew. Chem., Int. Ed., 2018, 57, 2096–2100 CrossRef CAS.
- K. Fu, Y. Gong, J. Dai, A. Gong, X. Han, Y. Yao, C. Wang, Y. Wang, Y. Chen, C. Yan, Y. Li, E. D. Wachsman and L. Hu, Proc. Natl. Acad. Sci. U. S. A., 2016, 113, 7094–7099 CrossRef CAS.
- Y. Gao, Z. Yan, J. L. Gray, X. He, D. Wang, T. Chen, Q. Huang, Y. C. Li, H. Wang, S. H. Kim, T. E. Mallouk and D. Wang, Nat. Mater., 2019, 18, 384–389 CrossRef CAS.
- F. Capuano, F. Croce and B. Scrosati, J. Electrochem. Soc., 1991, 138, 1918–1922 CrossRef CAS.
- F. Croce, G. B. Appetecchi, L. Persi and B. Scrosati, Nature, 1998, 394, 456–458 CrossRef CAS.
- J. E. Weston and B. C. H. Steele, Solid State Ionics, 1982, 7, 75–79 CrossRef CAS.
- J. L. Nugent, S. S. Moganty and L. A. Archer, Adv. Mater., 2010, 22, 3677–3680 CrossRef CAS.
- C. Pfaffenhuber, M. Göbel, J. Popovic and J. Maier, Phys. Chem. Chem. Phys., 2013, 15, 18318–18335 RSC.
- D. Lin, P. Y. Yuen, Y. Liu, W. Liu, N. Liu, R. H. Dauskardt and Y. Cui, Adv. Mater., 2018, 30, 1802661 CrossRef.
- J. Wan, J. Xie, X. Kong, Z. Liu, K. Liu, F. Shi, A. Pei, H. Chen, W. Chen, J. Chen, X. Zhang, L. Zong, J. Wang, L.-Q. Chen, J. Qin and Y. Cui, Nat. Nanotechnol., 2019, 14, 705–711 CrossRef CAS.
- X. Li, D. Wang, H. Wang, H. Yan, Z. Gong and Y. Yang, ACS Appl. Mater. Interfaces, 2019, 11, 22745–22753 CrossRef CAS.
- N. Riphaus, B. Stiaszny, H. Beyer, S. Indris, H. A. Gasteiger and S. J. Sedlmaier, J. Electrochem. Soc., 2019, 166, A975–A983 CrossRef CAS.
- Z. Li, W.-X. Sha and X. Guo, ACS Appl. Mater. Interfaces, 2019, 11, 26920–26927 CrossRef CAS.
- K. Fu, Y. Gong, J. Dai, A. Gong, X. Han, Y. Yao, C. Wang, Y. Wang, Y. Chen, C. Yan, Y. Li, E. D. Wachsman and L. Hu, Proc. Natl. Acad. Sci. U. S. A., 2016, 113, 7094–7099 CrossRef CAS.
- Z. Wan, D. Lei, W. Yang, C. Liu, K. Shi, X. Hao, L. Shen, W. Lv, B. Li, Q.-H. Yang, F. Kang and Y.-B. He, Adv. Funct. Mater., 2019, 29, 1805301 CrossRef.
- L. Yang, Z. Wang, Y. Feng, R. Tan, Y. Zuo, R. Gao, Y. Zhao, L. Han, Z. Wang and F. Pan, Adv. Energy Mater., 2017, 7, 1701437 CrossRef.
- W. Liu, S. W. Lee, D. Lin, F. Shi, S. Wang, A. D. Sendek and Y. Cui, Nat. Energy, 2017, 2, 17035 CrossRef CAS.
- J. Bae, Y. Li, J. Zhang, X. Zhou, F. Zhao, Y. Shi, J. B. Goodenough and G. Yu, Angew. Chem., Int. Ed., 2018, 57, 2096–2100 CrossRef CAS.
- W. Liu, N. Liu, J. Sun, P.-C. Hsu, Y. Li, H.-W. Lee and Y. Cui, Nano Lett., 2015, 15, 2740–2745 CrossRef CAS.
- Z. Zhang, Q. Zhang, C. Ren, F. Luo, Q. Ma, Y.-S. Hu, Z. Zhou, H. Li, X. Huang and L. Chen, J. Mater. Chem. A, 2016, 4, 15823–15828 RSC.
- J. Maier, J. Electrochem. Soc., 2015, 162, A2380–A2386 CrossRef CAS.
- A. Marcolongo and N. Marzari, Phys. Rev. Mater., 2017, 1, 025402 CrossRef.
- J. B. Goodenough, Solid State Ionics, 1997, 94, 17–25 CrossRef CAS.
- Y. Wang, W. D. Richards, S. P. Ong, L. J. Miara, J. C. Kim, Y. Mo and G. Ceder, Nat. Mater., 2015, 14, 1026–1031 CrossRef CAS.
- K. E. Kweon, J. B. Varley, P. Shea, N. Adelstein, P. Mehta, T. W. Heo, T. J. Udovic, V. Stavila and B. C. Wood, Chem. Mater., 2017, 29, 9142–9153 CrossRef CAS.
- X. He, Y. Zhu and Y. Mo, Nat. Commun., 2017, 8, 15893 CrossRef CAS.
- S. Muy, J. C. Bachman, L. Giordano, H.-H. Chang, D. L. Abernathy, D. Bansal, O. Delaire, S. Hori, R. Kanno, F. Maglia, S. Lupart, P. Lamp and Y. Shao-Horn, Energy Environ. Sci., 2018, 11, 850–859 RSC.
- C. Dietrich, D. A. Weber, S. J. Sedlmaier, S. Indris, S. P. Culver, D. Walter, J. Janek and W. G. Zeier, J. Mater. Chem. A, 2017, 5, 18111–18119 RSC.
- W. Wang, R. Christensen, B. Curtis, S. W. Martin and J. Kieffer, Phys. Chem. Chem. Phys., 2018, 20, 1629–1641 RSC.
- M. Armand, Solid State Ionics, 1983, 9–10, 745–754 CrossRef CAS.
- K. M. Diederichsen, H. G. Buss and B. D. McCloskey, Macromolecules, 2017, 50, 3831–3840 CrossRef CAS.
- M. A. Ratner and A. Nitzan, Faraday Discuss. Chem. Soc., 1989, 88, 19–42 RSC.
- M. Ebadi, T. Eriksson, P. Mandal, L. T. Costa, C. M. Araujo, J. Mindemark and D. Brandell, Macromolecules, 2020, 53, 764–774 CrossRef CAS.
- D. M. Pesko, M. A. Webb, Y. Jung, Q. Zheng, T. F. Miller, G. W. Coates and N. P. Balsara, Macromolecules, 2016, 49, 5244–5255 CrossRef CAS.
- D. J. Brooks, B. V. Merinov, W. A. Goddard, B. Kozinsky and J. Mailoa, Macromolecules, 2018, 51, 8987–8995 CrossRef CAS.
- C. A. Angell, Electrochim. Acta, 2017, 250, 368–375 CrossRef CAS.
- A. Bergfelt, G. Hernández, R. Mogensen, M. J. Lacey, J. Mindemark, D. Brandell and T. M. Bowden, ACS Appl. Polym. Mater., 2020, 2, 939–948 CrossRef CAS.
- R. Bouchet, S. Maria, R. Meziane, A. Aboulaich, L. Lienafa, J.-P. Bonnet, T. N. T. Phan, D. Bertin, D. Gigmes, D. Devaux, R. Denoyel and M. Armand, Nat. Mater., 2013, 12, 452–457 CrossRef CAS.
- D. Bresser, S. Lyonnard, C. Iojoiu, L. Picard and S. Passerini, Mol. Syst. Des. Eng., 2019, 4, 779–792 RSC.
- O. Borodin and G. D. Smith, Macromolecules, 2006, 39, 1620–1629 CrossRef CAS.
- A. L. Agapov and A. P. Sokolov, Macromolecules, 2011, 44, 4410–4414 CrossRef CAS.
- Z. Gadjourova, Y. G. Andreev, D. P. Tunstall and P. G. Bruce, Nature, 2001, 412, 520–523 CrossRef CAS.
- D. Golodnitsky and E. Peled, Electrochim. Acta, 2000, 45, 1431–1436 CrossRef CAS.
- M. Forsyth, J. Sun, D. R. Macfarlane and A. J. Hill, J. Polym. Sci., Part B: Polym. Phys., 2000, 38, 341–350 CrossRef CAS.
- D. Dong, F. Sälzer, B. Roling and D. Bedrov, Phys. Chem. Chem. Phys., 2018, 20, 29174–29183 RSC.
- D. M. Pesko, K. Timachova, R. Bhattacharya, M. C. Smith, I. Villaluenga, J. Newman and N. P. Balsara, J. Electrochem. Soc., 2017, 164, E3569–E3575 CrossRef CAS.
- M. Gouverneur, F. Schmidt and M. Schönhoff, Phys. Chem. Chem. Phys., 2018, 20, 7470–7478 RSC.
- Y. Ma, M. Doyle, T. F. Fuller, M. M. Doeff, L. C. De Jonghe and J. Newman, J. Electrochem. Soc., 1995, 142, 1859–1868 CrossRef CAS.
- J. Maier, Prog. Solid State Chem., 1995, 23, 171–263 CrossRef CAS.
- J. Maier, Nat. Mater., 2005, 4, 805–815 CrossRef CAS.
- N. J. J. de Klerk and M. Wagemaker, ACS Appl. Energy Mater., 2018, 1, 5609–5618 CAS.
- M. J. Verkerk, B. J. Middelhuis and A. J. Burggraaf, Solid State Ionics, 1982, 6, 159–170 CrossRef CAS.
- S. Yu and D. J. Siegel, Chem. Mater., 2017, 29, 9639–9647 CrossRef CAS.
- J. A. Dawson, P. Canepa, T. Famprikis, C. Masquelier and M. S. Islam, J. Am. Chem. Soc., 2018, 140, 362–368 CrossRef CAS.
- T. Jow, J. Electrochem. Soc., 1979, 126, 1963 CrossRef CAS.
- T. Tanaka, M. Kozako, N. Fuse and Y. Ohki, IEEE Trans. Dielectr. Electr. Insul., 2005, 12, 669–681 CrossRef CAS.
- X. Zhang, B.-W. Li, L. Dong, H. Liu, W. Chen, Y. Shen and C.-W. Nan, Adv. Mater. Interfaces, 2018, 5, 1800096 CrossRef.
- D. Brogioli, F. Langer, R. Kun and F. La Mantia, ACS Appl. Mater. Interfaces, 2019, 11, 11999–12007 CrossRef CAS.
- F. J. Simon, M. Hanauer, A. Henss, F. H. Richter and J. Janek, ACS Appl. Mater. Interfaces, 2019, 11, 42186–42196 CrossRef CAS.
- S. Jiang and J. B. Wagner, J. Phys. Chem. Solids, 1995, 56, 1101–1111 CrossRef CAS.
- W. Wang, E. Yi, A. J. Fici, R. M. Laine and J. Kieffer, J. Phys. Chem. C, 2017, 121, 2563–2573 CrossRef CAS.
- H. Luo, X. Zhou, C. Ellingford, Y. Zhang, S. Chen, K. Zhou, D. Zhang, C. R. Bowen and C. Wan, Chem. Soc. Rev., 2019, 48, 4424–4465 RSC.
- J. Przyluski, M. Siekierski and W. Wieczorek, Electrochim. Acta, 1995, 40, 2101–2108 CrossRef CAS.
- F. Croce, R. Curini, A. Martinelli, L. Persi, F. Ronci, B. Scrosati and R. Caminiti, J. Phys. Chem. B, 1999, 103, 10632–10638 CrossRef CAS.
- D. Lin, W. Liu, Y. Liu, H. R. Lee, P.-C. Hsu, K. Liu and Y. Cui, Nano Lett., 2016, 16, 459–465 CrossRef CAS.
- Y. Li, W. Zhang, Q. Dou, K. W. Wong and K. M. Ng, J. Mater. Chem. A, 2019, 7, 3391–3398 RSC.
- Y.-C. Jung, S.-M. Lee, J.-H. Choi, S. S. Jang and D.-W. Kim, J. Electrochem. Soc., 2015, 162, A704–A710 CrossRef CAS.
- J. Wu, X. Wu, W. Wang, Q. Wang, X. Zhou, Y. Liu and B. Guo, RSC Adv., 2020, 10, 22417–22421 RSC.
- A. S. Best, A. Ferry, D. R. MacFarlane and M. Forsyth, Solid State Ionics, 1999, 126, 269–276 CrossRef CAS.
- A. S. Best, J. Adebahr, P. Jacobsson, D. R. MacFarlane and M. Forsyth, Macromolecules, 2001, 34, 4549–4555 CrossRef CAS.
- T. Eriksson, J. Mindemark, M. Yue and D. Brandell, Electrochim. Acta, 2019, 300, 489–496 CrossRef CAS.
- F. Croce, L. Persi, B. Scrosati, F. Serraino-Fiory, E. Plichta and M. A. Hendrickson, Electrochim. Acta, 2001, 46, 2457–2461 CrossRef CAS.
- Z. Wang, X. Huang and L. Chen, Electrochem. Solid-State Lett., 2003, 6, E40 CrossRef CAS.
- H. Y. Sun, J. Electrochem. Soc., 1999, 146, 1672 CrossRef CAS.
- H. Y. Sun, Y. Takeda, N. Imanishi, O. Yamamoto and H. J. Sohn, J. Electrochem. Soc., 2000, 147, 2462 CrossRef CAS.
- K. F. Young and H. P. R. Frederikse, J. Phys. Chem. Ref. Data, 1973, 2, 313–410 CrossRef.
- O. Borodin, G. D. Smith, R. Bandyopadhyaya and O. Byutner, Macromolecules, 2003, 36, 7873–7883 CrossRef CAS.
- T. Dam, S. S. Jena and D. K. Pradhan, J. Phys. Chem. C, 2018, 122, 4133–4143 CrossRef CAS.
- H. Kasemägi, M. Klintenberg, A. Aabloo and J. O. Thomas, J. Mater. Chem., 2001, 11, 3191–3196 RSC.
- H. Kasemägi, M. Klintenberg, A. Aabloo and J. O. Thomas, Solid State Ionics, 2002, 147, 367–375 CrossRef.
- H. Kasemägi, M. Klintenberg, A. Aabloo and J. O. Thomas, Electrochim. Acta, 2003, 48, 2273–2278 CrossRef.
- H. Kasemägi, A. Aabloo, M. K. Klintenberg and J. O. Thomas, Solid State Ionics, 2004, 168, 249–254 CrossRef.
- D. Zhou, R. Liu, Y.-B. He, F. Li, M. Liu, B. Li, Q.-H. Yang, Q. Cai and F. Kang, Adv. Energy Mater., 2016, 6, 1502214 CrossRef.
- C.-H. Tsao, Y.-H. Hsiao, C.-H. Hsu and P.-L. Kuo, ACS Appl. Mater. Interfaces, 2016, 8, 15216–15224 CrossRef CAS.
- S. Choudhury, S. Stalin, Y. Deng and L. A. Archer, Chem. Mater., 2018, 30, 5996–6004 CrossRef CAS.
- D. Lin, P. Y. Yuen, Y. Liu, W. Liu, N. Liu, R. H. Dauskardt and Y. Cui, Adv. Mater., 2018, 30(32), 1802661 CrossRef.
- W. Tang, S. Tang, X. Guan, X. Zhang, Q. Xiang and J. Luo, Adv. Funct. Mater., 2019, 29, 1900648 CrossRef.
- C. Niu, J. Liu, G. Chen, C. Liu, T. Qian, J. Zhang, B. Cao, W. Shang, Y. Chen, J. Han, J. Du and Y. Chen, J. Power Sources, 2019, 417, 70–75 CrossRef CAS.
- Z. Sun, Y. Li, S. Zhang, L. Shi, H. Wu, H. Bu and S. Ding, J. Mater. Chem. A, 2019, 7, 11069–11076 RSC.
- C. Pfaffenhuber, F. Hoffmann, M. Fröba, J. Popovic and J. Maier, J. Mater. Chem. A, 2013, 1, 12560–12567 RSC.
- A. Jarosik, C. Pfaffenhuber, A. Bunde and J. Maier, Adv. Funct. Mater., 2011, 21, 3961–3966 CrossRef CAS.
- M. Nojabaee, J. Popovic and J. Maier, J. Mater. Chem. A, 2019, 7, 13331–13338 RSC.
- N. S. Grundish, C. D. Amos, A. Agrawal, H. Khani and J. B. Goodenough, Adv. Funct. Mater., 2019, 29, 1903550 CrossRef.
- C. M. Costa, Y.-H. Lee, J.-H. Kim, S.-Y. Lee and S. Lanceros-Méndez, Energy Storage Mater., 2019, 22, 346–375 CrossRef.
- J. Le Bideau, L. Viau and A. Vioux, Chem. Soc. Rev., 2011, 40, 907–925 RSC.
- N. Chen, H. Zhang, L. Li, R. Chen and S. Guo, Adv. Energy Mater., 2018, 8, 1702675 CrossRef.
- A. Guyomard-Lack, P. E. Delannoy, N. Dupré, C. V. Cerclier, B. Humbert and J. Le Bideau, Phys. Chem. Chem. Phys., 2014, 16, 23639–23645 RSC.
- S. Delacroix, F. Sauvage, M. Reynaud, M. Deschamps, S. Bruyère, M. Becuwe, D. Postel, J.-M. Tarascon and A. N. Van Nhien, Chem. Mater., 2015, 27, 7926–7933 CrossRef CAS.
- J. L. Schaefer, D. A. Yanga and L. A. Archer, Chem. Mater., 2013, 25, 834–839 CrossRef CAS.
- J. H. Lee, A. S. Lee, J.-C. Lee, S. M. Hong, S. S. Hwang and C. M. Koo, J. Mater. Chem. A, 2015, 3, 2226–2233 RSC.
- R. Chen, W. Qu, J. Qian, N. Chen, Y. Dai, C. Guo, Y. Huang, L. Li and F. Wu, J. Mater. Chem. A, 2017, 5, 24677–24685 RSC.
- S. Song, M. Kotobuki, F. Zheng, C. Xu, S. V. Savilov, N. Hu, L. Lu, Y. Wang and W. D. Z. Li, J. Mater. Chem. A, 2017, 5, 6424–6431 RSC.
- Z. Wang, R. Tan, H. Wang, L. Yang, J. Hu, H. Chen and F. Pan, Adv. Mater., 2018, 30, 1704436 CrossRef.
- W. J. Hyun, A. C. M. de Moraes, J.-M. Lim, J. R. Downing, K.-Y. Park, M. T. Z. Tan and M. C. Hersam, ACS Nano, 2019, 13, 9664–9672 CrossRef CAS.
- S. Wu, J. Yi, K. Zhu, S. Bai, Y. Liu, Y. Qiao, M. Ishida and H. Zhou, Adv. Energy Mater., 2017, 7, 1601759 CrossRef.
- D. S. Ashby, R. H. DeBlock, C.-H. Lai, C. S. Choi and B. S. Dunn, Joule, 2017, 1, 344–358 CrossRef CAS.
- J. Lee, H.-S. Lim, X. Cao, X. Ren, W.-J. Kwak, I. A. Rodríguez-Pérez, J.-G. Zhang, H. Lee and H.-T. Kim, ACS Appl. Mater. Interfaces, 2020, 12, 37188–37196 CrossRef CAS.
- Y. Lu, Z. Tu and L. A. Archer, Nat. Mater., 2014, 13, 961–969 CrossRef CAS.
- D. Zhou, R. Liu, Y.-B. He, F. Li, M. Liu, B. Li, Q.-H. Yang, Q. Cai and F. Kang, Adv. Energy Mater., 2016, 6(7), 1502214 CrossRef.
- Y. Lu, K. Korf, Y. Kambe, Z. Tu and L. A. Archer, Angew. Chem., Int. Ed., 2014, 53, 488–492 CrossRef CAS.
- Y. Lu, S. K. Das, S. S. Moganty and L. A. Archer, Adv. Mater., 2012, 24, 4430–4435 CrossRef CAS.
- F. Wu, N. Chen, R. Chen, Q. Zhu, J. Qian and L. Li, Chem. Mater., 2016, 28, 848–856 CrossRef CAS.
- S. Ohno, A. Banik, G. F. Dewald, M. A. Kraft, T. Krauskopf, N. Minafra, P. Till, M. Weiss and W. G. Zeier, Prog. Energy, 2020, 2, 022001 CrossRef.
- Z. Huang, W. Pang, P. Liang, Z. Jin, N. Grundish, Y. Li and C.-A. Wang, J. Mater. Chem. A, 2019, 7, 16425–16436 RSC.
- Z. Li, H.-M. Huang, J.-K. Zhu, J.-F. Wu, H. Yang, L. Wei and X. Guo, ACS Appl. Mater. Interfaces, 2019, 11, 784–791 CrossRef CAS.
- W. Zaman, N. Hortance, M. B. Dixit, V. De Andrade and K. B. Hatzell, J. Mater. Chem. A, 2019, 7, 23914–23921 RSC.
- M. Liu, Z. Cheng, S. Ganapathy, C. Wang, L. A. Haverkate, M. Tułodziecki, S. Unnikrishnan and M. Wagemaker, ACS Energy Lett., 2019, 4, 2336–2342 CrossRef CAS.
- J. Lee, T. Howell, M. Rottmayer, J. Boeckl and H. Huang, J. Electrochem. Soc., 2019, 166, A416–A422 CrossRef CAS.
- D. Li, L. Chen, T. Wang and L.-Z. Fan, ACS Appl. Mater. Interfaces, 2018, 10, 7069–7078 CrossRef CAS.
- N. Wu, P.-H. Chien, Y. Li, A. Dolocan, H. Xu, B. Xu, N. S. Grundish, H. Jin, Y.-Y. Hu and J. B. Goodenough, J. Am. Chem. Soc., 2020, 142, 2497–2505 CrossRef CAS.
- S. A. Ahmed, T. Pareek, S. Dwivedi, M. Badole and S. Kumar, J. Solid State Electrochem., 2020, 24, 2407–2417 CrossRef CAS.
- L. Zhu, P. Zhu, Q. Fang, M. Jing, X. Shen and L. Yang, Electrochim. Acta, 2018, 292, 718–726 CrossRef CAS.
- K.-Q. He, J.-W. Zha, P. Du, S. H.-S. Cheng, C. Liu, Z.-M. Dang and R. K. Y. Li, Dalton Trans., 2019, 48, 3263–3269 RSC.
- P. Zhu, C. Yan, M. Dirican, J. Zhu, J. Zang, R. K. Selvan, C.-C. Chung, H. Jia, Y. Li, Y. Kiyak, N. Wu and X. Zhang, J. Mater. Chem. A, 2018, 6, 4279–4285 RSC.
- G. F. Dewald, S. Ohno, M. A. Kraft, R. Koerver, P. Till, N. M. Vargas-Barbosa, J. Janek and W. G. Zeier, Chem. Mater., 2019, 31, 8328–8337 CrossRef CAS.
- S. Wenzel, S. J. Sedlmaier, C. Dietrich, W. G. Zeier and J. Janek, Solid State Ionics, 2018, 318, 102–112 CrossRef CAS.
- S. Wenzel, S. Randau, T. Leichtweiß, D. A. Weber, J. Sann, W. G. Zeier and J. Janek, Chem. Mater., 2016, 28, 2400–2407 CrossRef CAS.
- Y. Zhu and Y. Mo, Angew. Chem., Int. Ed., 2020, 132(40), 17625 CrossRef.
- D. H. S. Tan, E. A. Wu, H. Nguyen, Z. Chen, M. A. T. Marple, J.-M. Doux, X. Wang, H. Yang, A. Banerjee and Y. S. Meng, ACS Energy Lett., 2019, 4, 2418–2427 CrossRef CAS.
- T. K. Schwietert, V. A. Arszelewska, C. Wang, C. Yu, A. Vasileiadis, N. J. J. de Klerk, J. Hageman, T. Hupfer, I. Kerkamm, Y. Xu, E. van der Maas, E. M. Kelder, S. Ganapathy and M. Wagemaker, Nat. Mater., 2020, 19, 428–435 CrossRef CAS.
- F. Walther, S. Randau, Y. Schneider, J. Sann, M. Rohnke, F. H. Richter, W. G. Zeier and J. Janek, Chem. Mater., 2020, 32, 6123–6136 CrossRef CAS.
- N. Riphaus, B. Stiaszny, H. Beyer, S. Indris, H. A. Gasteiger and S. J. Sedlmaier, J. Electrochem. Soc., 2019, 166, A975–A983 CrossRef CAS.
- D. Mankovsky, D. Lepage, M. Lachal, L. Caradant, D. Aymé-Perrot and M. Dollé, Chem. Commun., 2020, 56, 10167–10170 RSC.
- S. Chen, J. Wang, Z. Zhang, L. Wu, L. Yao, Z. Wei, Y. Deng, D. Xie, X. Yao and X. Xu, J. Power Sources, 2018, 387, 72–80 CrossRef CAS.
- Y. Zhao, C. Wu, G. Peng, X. Chen, X. Yao, Y. Bai, F. Wu, S. Chen and X. Xu, J. Power Sources, 2016, 301, 47–53 CrossRef CAS.
- J. Zheng, P. Wang, H. Liu and Y.-Y. Hu, ACS Appl. Energy Mater., 2019, 2, 1452–1459 CrossRef CAS.
- M. Li, J. E. Frerichs, M. Kolek, W. Sun, D. Zhou, C. J. Huang, B. J. Hwang, M. R. Hansen, M. Winter and P. Bieker, Adv. Funct. Mater., 2020, 30, 1910123 CrossRef CAS.
- A. Sharafi, E. Kazyak, A. L. Davis, S. Yu, T. Thompson, D. J. Siegel, N. P. Dasgupta and J. Sakamoto, Chem. Mater., 2017, 29, 7961–7968 CrossRef CAS.
- C. Ma, Y. Cheng, K. Yin, J. Luo, A. Sharafi, J. Sakamoto, J. Li, K. L. More, N. J. Dudney and M. Chi, Nano Lett., 2016, 16, 7030–7036 CrossRef CAS.
- L. Cheng, E. J. Crumlin, W. Chen, R. Qiao, H. Hou, S. F. Lux, V. Zorba, R. Russo, R. Kostecki and Z. Liu, Phys. Chem. Chem. Phys., 2014, 16, 18294–18300 RSC.
- I. A. Stenina, I. Y. Pinus, A. I. Rebrov and A. B. Yaroslavtsev, Solid State Ionics, 2004, 175, 445–449 CrossRef CAS.
- T. Asano, A. Sakai, S. Ouchi, M. Sakaida, A. Miyazaki and S. Hasegawa, Adv. Mater., 2018, 30, 1803075 CrossRef.
- Z. Xu, X. Chen, K. Liu, R. Chen, X. Zeng and H. Zhu, Chem. Mater., 2019, 31, 7425–7433 CrossRef CAS.
- X. Li, J. Liang, J. Luo, M. Norouzi Banis, C. Wang, W. Li, S. Deng, C. Yu, F. Zhao, Y. Hu, T.-K. Sham, L. Zhang, S. Zhao, S. Lu, H. Huang, R. Li, K. R. Adair and X. Sun, Energy Environ. Sci., 2019, 12, 2665–2671 RSC.
- L. Duchêne, A. Remhof, H. Hagemann and C. Battaglia, Energy Storage Mater., 2020, 25, 782–794 CrossRef.
- S. Kim, H. Oguchi, N. Toyama, T. Sato, S. Takagi, T. Otomo, D. Arunkumar, N. Kuwata, J. Kawamura and S.-i. Orimo, Nat. Commun., 2019, 10, 1081 CrossRef.
- R. Asakura, L. Duchêne, R.-S. Kühnel, A. Remhof, H. Hagemann and C. Battaglia, ACS Appl. Energy Mater., 2019, 2, 6924–6930 CrossRef CAS.
- W. Ling, N. Fu, J. Yue, X.-X. Zeng, Q. Ma, Q. Deng, Y. Xiao, L.-J. Wan, Y.-G. Guo and X.-W. Wu, Adv. Energy Mater., 2020, 10, 1903966 CrossRef CAS.
- S. M. Haile, D. L. West and J. Campbell, J. Mater. Res., 1998, 13, 1576–1595 CrossRef CAS.
- J. Popovic, D. Höfler, J. P. Melchior, A. Münchinger, B. List and J. Maier, J. Phys. Chem. Lett., 2018, 9, 5116–5120 CrossRef CAS.
- J. Evans, C. A. Vincent and P. G. Bruce, Polymer, 1987, 28, 2324–2328 CrossRef CAS.
- T. Famprikis, Ö. U. Kudu, J. A. Dawson, P. Canepa, F. Fauth, E. Suard, M. Zbiri, D. Dambournet, O. J. Borkiewicz, H. Bouyanfif, S. P. Emge, S. Cretu, J.-N. Chotard, C. P. Grey, W. G. Zeier, M. S. Islam and C. Masquelier, J. Am. Chem. Soc., 2020, 142, 18422–18436 CrossRef CAS.
- S. Ohno, T. Bernges, J. Buchheim, M. Duchardt, A.-K. Hatz, M. A. Kraft, H. Kwak, A. L. Santhosha, Z. Liu, N. Minafra, F. Tsuji, A. Sakuda, R. Schlem, S. Xiong, Z. Zhang, P. Adelhelm, H. Chen, A. Hayashi, Y. S. Jung, B. V. Lotsch, B. Roling, N. M. Vargas-Barbosa and W. G. Zeier, ACS Energy Lett., 2020, 5, 910–915 CrossRef CAS.
- J. Zagórski, J. M. López del Amo, M. J. Cordill, F. Aguesse, L. Buannic and A. Llordés, ACS Appl. Energy Mater., 2019, 2, 1734–1746 CrossRef.
- I. Villaluenga, K. H. Wujcik, W. Tong, D. Devaux, D. H. C. Wong, J. M. DeSimone and N. P. Balsara, Proc. Natl. Acad. Sci. U. S. A., 2016, 113, 52–57 CrossRef CAS.
- J. Zheng, H. Dang, X. Feng, P.-H. Chien and Y.-Y. Hu, J. Mater. Chem. A, 2017, 5, 18457–18463 RSC.
- N. Wu, P.-H. Chien, Y. Qian, Y. Li, H. Xu, N. S. Grundish, B. Xu, H. Jin, Y.-Y. Hu, G. Yu and J. B. Goodenough, Angew. Chem., Int. Ed., 2020, 59, 4131–4137 CrossRef CAS.
- J. Peng, Y. Xiao, D. A. Clarkson, S. G. Greenbaum, T. A. Zawodzinski and X. C. Chen, ACS Appl. Polym. Mater., 2020, 2, 1180–1189 CrossRef CAS.
- N. Bloembergen, E. M. Purcell and R. V. Pound, Phys. Rev., 1948, 73, 679–712 CrossRef CAS.
- P. Wang, H. Liu, S. Patel, X. Feng, P.-H. Chien, Y. Wang and Y.-Y. Hu, Chem. Mater., 2020, 32, 3833–3840 CrossRef CAS.
- T. Yang, J. Zheng, Q. Cheng, Y.-Y. Hu and C. K. Chan, ACS Appl. Mater. Interfaces, 2017, 9, 21773–21780 CrossRef CAS.
- J. Adebahr, A. S. Best, N. Byrne, P. Jacobsson, D. R. MacFarlane and M. Forsyth, Phys. Chem. Chem. Phys., 2003, 5, 720–725 RSC.
- H. Al-Salih, A. Huang, C.-H. Yim, A. I. Freytag, G. R. Goward, E. Baranova and Y. Abu-Lebdeh, J. Electrochem. Soc., 2020, 167, 070557 CrossRef.
- H. J. Walls, P. S. Fedkiw, T. A. Zawodzinski and S. A. Khan, J. Electrochem. Soc., 2003, 150, E165 CrossRef CAS.
- S. Menkin, M. Lifshitz, A. Haimovich, M. Goor, R. Blanga, S. G. Greenbaum, A. Goldbourt and D. Golodnitsky, Electrochim. Acta, 2019, 304, 447–455 CrossRef CAS.
- D. Topgaard, in Diffusion NMR of Confined Systems: Fluid Transport in Porous Solids and Heterogeneous Materials, The Royal Society of Chemistry, 2017, pp. 226–259, 10.1039/9781782623779-00226.
- W. Zaman, N. M. Hortance, M. B. Dixit, V. De Andrande and K. B. Hatzell, J. Mater. Chem. A, 2019, 7, 23914–23921 RSC.
- M. B. Dixit, M. Regala, F. Shen, X. Xiao and K. B. Hatzell, ACS Appl. Mater. Interfaces, 2018, 11, 2022–2030 CrossRef.
- M. J. Palmer, S. Kalnaus, M. B. Dixit, A. S. Westover, K. B. Hatzell, N. J. Dudney and X. C. Chen, Energy Storage Mater., 2020, 26, 242–249 CrossRef.
- C. Martinez, K. M. Potter, M. D. Smith, E. A. Donahue, L. Collins, J. P. Korbin and S. A. Roberts, 2019.
- C. Norris, T. LaBonte, C. Martinez, S. A. Roberts and P. P. Mukherjee, arXiv:1910.10793v1.
- T. M. LaBonte, C. Martinez and S. A. Roberts, We Know Where We Don't Know: 3D Bayesian CNNs for Credible Geometric Uncertainty, Sandia National Lab. (SNL-NM), Albuquerque, NM (United States), 2020 Search PubMed.
- X. C. Chen, R. L. Sacci, N. C. Osti, M. Tyagi, Y. Wang, M. J. Palmer and N. J. Dudney, Mol. Syst. Des. Eng., 2019, 4, 379–385 RSC.
- S. K. Fullerton-Shirey and J. K. Maranas, Macromolecules, 2009, 42, 2142–2156 CrossRef CAS.
- G. Mao, R. F. Perea, W. S. Howells, D. L. Price and M.-L. Saboungi, Nature, 2000, 405, 163–165 CrossRef CAS.
- M. B. Dixit, W. Zaman, Y. Bootwala, Y. Zheng, M. C. Hatzell and K. B. Hatzell, ACS Appl. Mater. Interfaces, 2019, 11, 45087–45097 CrossRef CAS.
- W. Wang, E. Yi, A. J. Fici, R. M. Laine and J. Kieffer, J. Phys. Chem. C, 2017, 121, 2563–2573 CrossRef CAS.
- C. S. Jiang, N. Dunlap, Y. Li, H. Guthrey, P. Liu, S. H. Lee and M. M. Al-Jassim, Adv. Energy Mater., 2020, 10, 2000219 CrossRef CAS.
| This journal is © The Royal Society of Chemistry 2021 |






