Open Access Article
Open Access ArticleThermodynamic insights into strong metal–support interaction of transition metal nanoparticles on titania: simple descriptors for complex chemistry†
Xing
Wang
ab,
Arik
Beck
 ab,
Jeroen A.
van Bokhoven
ab,
Jeroen A.
van Bokhoven
 ab and
Dennis
Palagin
ab and
Dennis
Palagin
 *ab
*ab
aInstitute for Chemical and Bioengineering, ETH Zurich, Vladimir Prelog Weg 1, 8093 Zurich, Switzerland. E-mail: dennis.palagin@chem.ethz.ch
bLaboratory for Catalysis and Sustainable Chemistry, Paul Scherrer Institute, Forschungsstrasse 111, 5232 Villigen, Switzerland
First published on 13th January 2021
Abstract
The metal–support interaction plays a critical role in heterogeneous catalysis. Under reducing conditions, oxidic supports may interact with supported metal particles, by either forming an oxide overlayer or an alloy. The structure of both the support and the nanoparticle, as well as of the interface itself, changes in response to varying environmental conditions. Here, we present a fully ab initio approach to predict the structures and energetics of such systems for a range of transition metals (Me = Cu, Ru, Pd, Ag, Rh, Os, Ir, Pt, Au) supported on titania surfaces as a function of gas atmosphere composition. The competing formation of a monolayer comprising fully oxidized titania (TiO2), its reduced forms (Ti2O3, TiO), and the Ti–Me surface alloy, is investigated. The stability of each of these phases is found to be very sensitive to the environmental conditions and the supported metal. Encapsulation of metal, also known as classical strong metal–support interaction (SMSI), was predicted by thermodynamic driving force analysis. We show that a simple parameter, the Ti–Me alloy formation energy, is a good descriptor for the strength of the interaction between metal substrates and reduced titania monolayers and has predictive power towards the conditions under which an overlayer is stable. The presented thermochemical data and phase diagram analysis can be used to identify the structure and stability of supported metal catalysts under realistic conditions.
1 Introduction
Transition metal nanoparticles on oxide supports are among the most important heterogeneous catalysts and are widely used in chemicals transformation, environmental pollution control and sustainable energy systems.1,2 One of the basic roles of the oxide support is to enhance metal dispersion and prevent sintering.3 In many cases, the support is not chemically inert and participates in the catalytic cycle. The metal–support interaction (MSI) gives rise to unique phenomena at the interface between the metal and the oxide, such as electron transfer,4,5 chemical composition rearrangement,6,7 morphology reconstruction,8,9 and the formation of interfacial perimeter.10 These interfacial phenomena have a profound impact on both the stability and catalytic activity of supported metal catalysts, and render the MSI one of the most effective strategies to tune catalytic performance.11–16 A specific case of MSI is the encapsulation of metal particles by (partially) reduced oxide overlayers migrated from the support, also known as the strong metal–support interaction (SMSI), which was first introduced in 1978 by Tauster et al. for titania supported platinum catalysts.17 Since then, SMSI effects have been subject to intense investigation and significant debate.18–22 The effect of SMSI is multifold. On the one hand, it could be detrimental for the catalytic function, due to physical blocking of adsorption sites on nanoparticles.23,24 On the other hand, it opens a new way to decorate metal nanoparticles by oxide overlayers and/or form a novel interface between the nanoparticle and the support, thereby paving a novel pathway to deliberate altering of catalytic performance.25–28 SMSI is widely observed between Pt-group metals and reducible oxide supports, such as Nb2O5,29 Fe2O3,30 CeO2,31 V2O3 (ref. 32) and Ta2O5,33 and was further extended to non-reducible SiO2,34 transition-metal carbides35 and group IB metals.36The SMSI effect strongly depends on the gas atmosphere and shows a dynamic behavior under reactive environments.37 For instance, the thickness and the structure of TiOx overlayers on the Pd (111) surface are very sensitive to the partial pressure of oxygen and hydrogen, with dynamic formation and removal of TiOx oxide overlayers.37 Our recent work showed that the migration of reduced titanium oxide onto a platinum particle surface and the formation of an Ti–Pt alloy are competing mechanisms during high-temperature reduction.38
From the thermodynamic point of view, SMSI processes are driven by the minimization of the total free energy of the system. The influence of the bulk, surface and interface energy should be taken into consideration for accurate thermodynamic calculations. However, thermodynamic data on metal/oxide interfaces are rarely available, and, consequently, only bulk and surface data are typically used in the thermodynamic calculations as a reasonable first approximation.18 At the same time, for thin oxide overlayers, where the ratio of interface to bulk is large, the interface energy plays a significant role. Besides, chemical composition of the interfacial phases is often different from that of the bulk phase. The metal and the oxide can possess different stoichiometry and form complex phases at the interface.39 As a result, despite the importance of and the interest in SMSI, thermodynamic tools, capable of predicting the SMSI state under realistic conditions, are largely unexplored.
Utilizing ab initio density functional theory (DFT) to calculate the interface energies for every combination of oxide/metal interface can be very expensive and time-consuming. Identifying a simple, rule of thumb, descriptor, which depends only on properties of the oxide support and the metal, or the properties of bulk systems, would enable circumventing this difficulty and thus saving considerable amount of both computational and human time. Recently, prediction by theory has seen a lot of progress due to considerable advances in the development of materials science databases and machine learning tools.40–45 Previously, the adsorption energy of oxygen on metal surfaces and the formation energy of the metal oxide have been reported as reasonable descriptors for the interface strength between fully oxidized supports and metal substrates.9,46 For partially reduced supports, the stability of the formed overlayers has a linear scaling relation with the adsorption energy of the oxide-constituting metal atom on the corresponding metal surface.47
The goal of this study is to rationally understand the interaction of TiOx layers with metal surfaces, and to subsequently propose a universal descriptor, applicable to overlayers of different composition on a wide range of transition metals. In order to achieve this, we conducted a systematic ab initio investigation of the thermodynamics of SMSI phenomena between a range of surfaces, such as TiO2, Ti2O3, TiO, Ti–Me alloy, and a group of late transition metals (Pt, Pd, Ru, Os, Rh, Ir, Cu, Ag and Au). This study increased the complexity of the considered models step by step, to derive a suitable descriptor for the stability of overlayers. Initially, the stability of unsupported TiOx structures was studied to understand geometric arrangement of such a monolayer in comparison to its bulk structure and to assess its stability. Consequently, the layers were brought into contact with metal (111) surfaces, which drastically changes the stability and structure due to the newly formed TiOx–Me interface. Finally, these structures were considered under the influence of different gas phase and temperature conditions.
As a result, we were able to identify a simple, universal and easily calculable descriptor, the formation energy of the Me–Ti alloy, that accurately predicts the stability of reduced TiOx monolayers on metal substrates. Based on the stability of these monolayers, we were able to construct phase diagrams of all considered systems, which can be used to understand and predict the structure of supported metal catalysts observed under experimental conditions.
2 Results and discussion
2.1 Unsupported monolayers
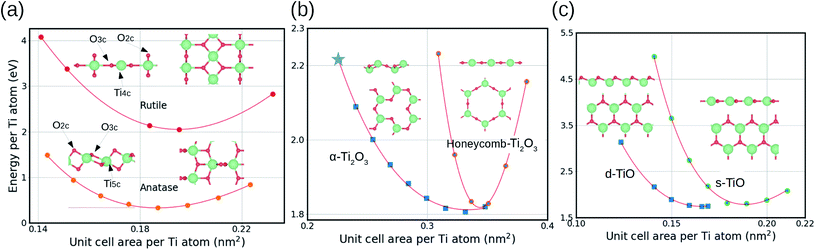
The TiO2 monolayers were cut from the thermodynamically most stable crystal facets of bulk rutile and anatase, which are the (110) and (101) facets, respectively. Fig. 1(a) shows that both rutile and anatase monolayers have two-coordinated oxygen atoms (O2c) at the top and the bottom, and three-coordinated oxygen atoms (O3c) in the middle. The main difference between the two monolayers is that titanium atoms are four-coordinated (Ti4c) in the rutile monolayer and five-coordinated (Ti5c) in the case of anatase. At the most stable geometry, the anatase monolayer has a slightly denser structure (0.187 nm2 per Ti atom) compared to the rutile monolayer (0.195 nm2 per Ti atom), due to the higher coordination number of titanium atoms in anatase.The stability of the single monolayer (ML) is calculated by:
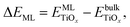 | (1) |
A Ti2O3 monolayer was cut from the (0001) facet of the most stable bulk structure (α-Ti2O3). Fig. 1(b) shows that the optimized monolayer maintains a hexagonal unit cell, with a two-coordinated oxygen atom (O2c) in the middle, and a three-coordinated titanium (Ti3c) atom at the top and the bottom, forming a rumpling structure. When the unit cell size increases, the α-Ti2O3 monolayer undergoes a slight transformation with a displacement of the top and the bottom titanium atoms into the middle of the structure, and of the oxygen atoms into the bridge sites between two titanium atoms. This eventually results in a conversion of the whole structure into a flat honeycomb configuration. This transformation makes the honeycomb monolayer 0.4 eV more stable than the original monolayer cut from the α-Ti2O3, which is marked by a star in Fig. 1(b).
A TiO monolayer was cut from the (111) facet of the rock-salt bulk TiO with cubic unit cell. Fig. 1(c) shows that the monolayer has a hexagonal unit cell, with a three-coordinated oxygen atom (O3c) and a three-coordinated titanium (Ti3c) atom. Similarly to the Ti2O3 monolayer, the TiO monolayer can have either a rumpling structure in a unit cell designated here as “dense” (d-TiO), or a flat structure in a unit cell designated as “sparse” (s-TiO). The stabilities of these two optimized monolayers are very close with only 0.1 eV difference.
2.2 Supported monolayers
Having derived the structure of unsupported TiOx monolayers, consequently, these structures as well as Ti–Me alloy layers are studied when positioned as topmost layer of metal surface. An anatase monolayer interacts with the metal surface mainly through forming the bond between aO2c oxygen and a metal atom, as shown in Fig. 2 (a, left). Rutile monolayer, on the other hand, binds strongly with the metal substrate through both O2c and Ti4c atoms, resulting in a dramatic geometry reconstruction. Fig. 2 (a, right) shows that the both anatase and rutile monolayers bind stronger to the metals located to the left in the transition metal series of the periodic table of elements (Ru > Rh > Pd > Ag, and Os > Ir ≫ Pt > Au), and stronger to 3d metals than to 4d and 5d ones (Cu > Ag > Au). This trend can be explained by the d-band model,50 which shows that the interaction between the metal substrate and the adsorbed oxygen atom is determined by the d-band center (with respect to the Fermi level) of metal substrate. A lower d-band center corresponds to an increase in filling of the anti-bonding state, leading to a weaker binding between the metal and the oxygen atom. The d-band center of transition metals decreases from left to right (Ru > Rh > Pd > Ag, and Os > Ir > Pt > Au) and from top to bottom (Cu > Ag > Au) along the periodic table.50 This is also consistent with previous literature, where both the adsorption energy of oxygen on metal and the formation energy of the metal oxide have been reported as reasonable descriptors for the interface strength between an oxide and a metal.9,46 Despite of the similar trend, rutile monolayer show large stability difference (around 0.4 eV) between Pt and Au surfaces, as well as between Pd and Ag surfaces. This difference can be attributed from the different binding strength between titanium atom and metal surfaces, which will be discussed in the following part. Overall, both supported rutile and anatase monolayers are less stable with respect to their bulk counterparts for all considered metals, indicating that fully oxidized titania is most stable in its bulk form.Both the Ti2O3 monolayer and the metal (111) surface have a hexagonal unit cell. Therefore, they can form a commensurate interface with titanium and oxygen atoms located in the high-symmetry sites (atop, bridge and hollow) on the (111) surface. Fig. 2 (b, left) shows that titanium atoms prefer to occupy the hollow surface sites, whereas oxygen atoms are located at the atop surface sites. There is a dramatic geometry reconstruction of the α-Ti2O3 monolayer, with the top titanium atoms moving close to the interface and forming a flat titanium plane instead of the rumpling structure observed in the unsupported case (Fig. 1(b)). The supported honeycomb monolayer also has a significant structural reordering compared to the unsupported one, with the oxygen atoms relaxing outwards and the titanium atoms approaching the (111) surface. The stability of the monolayer can be decomposed into two contributions: the first one is the energy gained upon the formation of the chemical bonds between the monolayer and the substrate, and the second one is the energy loss due to the strain to keep the lattice constants of the monolayer aligned with those of the substrate. The eventual monolayer structure is a result of the system trying to accommodate these two effects in an optimal way. Fig. 2 (b, right) shows that α-Ti2O3 monolayers is significantly less stable than the honeycomb monolayer, especially for copper surface which has the smallest lattice constant, indicating that high stain energy is responsible for the lower stability of α-Ti2O3 monolayers. In the case of honeycomb monolayers, Pd, Pt, Ag and Au prefer a commensurate interface, while Cu, Ru, Os, Rh and Ir prefer an incommensurate interface which could helps decreasing the strain further.
In contrast to TiO2, the partially reduced Ti2O3 shows a strong interaction with metal substrate, resulting in stable supported Ti2O3 monolayers with respect to their bulk counterparts in the cases of Ru, Rh, Pd, Os, Ir, Pt substrates. Besides, Fig. 2 (b, left) shows that the Ti2O3 monolayer interacts with metals substrate mainly through titanium–metal bonds, resulting in a different stability trend along the periodic table than the TiO2 monolayers. Ti2O3 monolayers bind weakly to the Cu, Ag and Au surfaces, while they bind strongly to the Ru, Rh, Pd, Os, Ir and Pt surfaces. Ti2O3 monolayers are slightly more stable on the 5d metals (Os, Ir, Pt, Au) than on the 4d metals (Ru, Rh, Pd, Ag), whereas TiO2 monolayers exhibit the opposite trend. Fig. S1(a)† shows the electron density difference for the Ti2O3 monolayer on Pt (111). The most visible effect is the accumulation of electron density in the interfacial region between the metal and the oxide. The excess electron density originates mainly from the Ti3+ cations and the metal atoms in the first layer of the substrate, which both display large negative difference densities. Fig. S1(b)† shows that the atom-like peak of the dz2 component of Ti3+ in the unsupported monolayer is pushed above the Fermi level and is entirely emptied when the monolayer is supported by Pt (111), indicating the electron is transferred from Ti3+ cations to the surface. Therefore, the titanium–metal bonds dominate the interfacial bonding here, as opposed to oxygen–metal bonds in the case of TiO2. Similar bonding character has previously been reported in the case of N2O5 and V2O3 honeycomb monolayers on metal (111) substrates.29,51
TiO monolayers can also form a commensurate interface with the metal (111) surface. Fig. 2 (c, left) shows the commensurate interface models of the dense (d-TiO) and sparse (s-TiO) TiO phases on the Pt (111) surface. Similarly to Ti2O3, the metal-supported monolayer interacts with a metal substrate through the titanium–metal bond, with the oxygen atoms relaxing outwards the (111) surface. In the dense TiO case, both the titanium and oxygen atoms are located at the hollow surface sites. The Ti–Ti distance is 2.80 Å, which is the same as the Pt–Pt bond length. In the sparse TiO case, one half of titanium atoms is located at the hollow sites, while the other half is located at the atop site, with a longer Ti–Ti distance of 3.24 Å. Fig. 2 (c, right) shows that on metal substrates with the larger unit cell, such as Au and Ag, TiO prefers to form the d-TiO monolayer, while for the metal substrates with smaller unit cells, the s-TiO monolayer is preferred. In all cases, TiO monolayers show a strong interaction with metal substrates. In the most stable case of platinum, the supported TiO monolayer is 1.1 eV more stable than its bulk counterpart. The stability of supported TiO monolayers exhibits a similar trend along the periodic table as was observed for the case of Ti2O3. TiO monolayers bind weakly to the Cu, Ag and Au, and bind stronger to the 5d metals than to the 4d metals.
A TiMe3 alloy monolayer was modeled by substituting surface metal atoms either in the top or in the second layer of the metal substrate with titanium. Fig. 2 (d, left) shows typical structures of such top- and second-layer surface alloys for the case of titanium on metal (111) surfaces. The relative stability of the TiMe3 overlayers compared to their bulk counterparts is given by:
| ΔGTiMe3/(111) = GTiMe3/(111) + GMe − GMe4/(111)−GTi, | (2) |
2.3 Descriptor
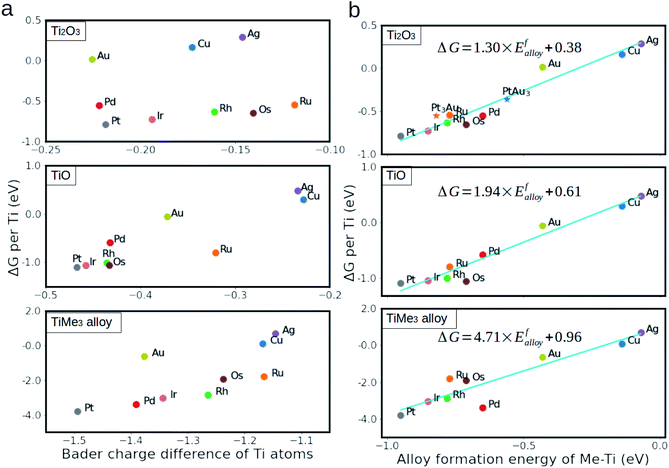
Having established the structures and the main trends in relative stability of different TiOx/metal phases, we proceed with identifying a descriptor suitable for predictive quality modeling of the binding strength at oxide/metal interfaces. In the case of reduced TiOx, the monolayer and metal substrate interaction is associated with the d electron transfer from the titanium cations towards the metal substrate. The amount of charge transferred can be estimated with the Bader charge analysis method.54Fig. 3(a) shows the monolayer stability as a function of the difference between the Bader charge on titanium atoms in the supported monolayer and the unsupported one. The negative charge difference on the titanium atoms indicates a charge transfer from the titanium to the metal substrate, which agrees with the electron density difference analysis in Fig. S1.† However, no single linear relationship successfully describes all considered substrate metals. Instead, the considered metals can be separated into two groups according to their stability. The first group, comprising Cu, Ag and Au, shows higher electron transfer but, at the same time, lower stability. This can be rationalized in terms of the d orbital of these metals being already full, thus the energy gained by the electron transfer from Ti atoms being small compared to the elements with lower d orbital occupation. These constitute the second group, comprising Pd, Pt, Ir, Rh, Os, and Ru. Similar trends to those outlined above for Ti2O3 are also observed in the case of the TiO monolayer and the TiMe3 surface alloy. Another possible descriptor is the surface energy of the metal substrates. Strong metal–support interaction is usually reported in systems with high surface energy, thus one would expect the oxide to interact stronger with the metal substrate with high surface energy.39 However, Fig. S2† shows that there is no clear relationship between the monolayer stability and the surface energy of the (111) metal surface.Since the titanium–metal bonds dominate the interfacial bonding, we investigated whether the interfacial binding strength is correlated to the formation energy of the Ti–Me alloy. As several alloys can be formed for a given Me–Ti binary system, the formation energy of the most stable one was chosen in each case (see Table S5†). For example, Fig. S3 in the ESI† demonstrates how this choice is made in the case of Ti–Pt alloy. The descriptor for a binary system is, therefore, defined as the formation energy of the most stable alloy phase, corresponding to this system. We found that, as shown in Fig. 3(b), the stability of Ti2O3, TiO and Ti–Me alloy monolayers increases linearly from metal to metal with the descriptor, shown by high R2 values of 0.95, 0.95 and 0.90, respectively. The slopes for the linear fitting equations are 1.30, 1.94 and 4.71 for Ti3+, Ti2+ and Ti0, respectively, suggesting that the more reduced the monolayer is, the stronger the metal–titanium bond is. Since the alloy formation energy can be computed very quickly, or even be found tabulated in various databases,55 it enables rapid prediction of the interfacial interaction strength and efficient pre-screening of the most favorable monolayer compositions.
The relatively poor prediction for some of the TiMe3 surface alloys, notably TiPd3 (see Fig. 3(a)), compared to the cases of Ti2O3 and TiO monolayers is partially arisen from the high strain energy, which was introduced upon replacing the surface metal atoms with titanium atoms. Whereas the strain energy in the cases of Ti2O3 and TiO monolayers is effectively minimized by using several interface models with different combinations of supercells, for the TiMe3 alloy this could not be achieved. This is especially obvious for the 4d metals (Ru, Rh and Pd), where large atomic radii of Pd compared to that of Ru and Rh increases the strain energy in the TiPd3 surface alloy, resulting in a smaller DFT calculated value of the alloy formation energy compared to the one predicted by the descriptor. As such, prediction of the SMSI through the formation energies of the alloys as a descriptor made for metals with significantly different atomic radii will be somewhat less reliable.
We further calculated the stability of the Ti2O3 monolayer on two Pt–Au alloy substrates (Pt3Au and PtAu3) as an example to validate the extent of the predictive power of this descriptor. The definition of the descriptor for Pt–Au alloys is given in the ESI.† The DFT calculated energies of the Ti2O3 monolayers, which are indicated by the stars in Fig. 3(b), fall into the previously predicted linear relationship, with the energy “error” smaller than 0.15 eV. Furthermore, the here suggested descriptor can also be successfully applied to alloys with more complex structures, such as Pt–Ag, Cu–Ag and Pt–Ir, for which the Pm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m structure was used. Fig. S4 in the ESI† shows that our descriptor predicted relative stability for TiOx monolayers versus the value calculated by DFT within 0.13 eV. We are, therefore, confident that the accuracy of the descriptor is adequate for prediction of the relative stabilities of the TiOx monolayers for all considered systems, and is general enough to extend the proposed model for other systems as well.
m structure was used. Fig. S4 in the ESI† shows that our descriptor predicted relative stability for TiOx monolayers versus the value calculated by DFT within 0.13 eV. We are, therefore, confident that the accuracy of the descriptor is adequate for prediction of the relative stabilities of the TiOx monolayers for all considered systems, and is general enough to extend the proposed model for other systems as well.
2.4 Phase diagrams of monolayers
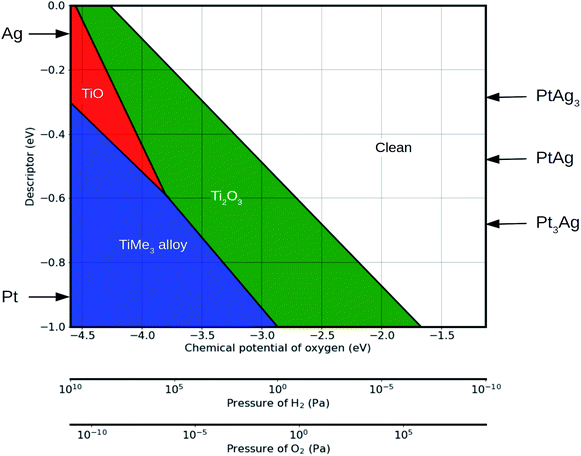
To understand the structure dependence on the gas environment, the effect of the gaseous composition on the relative stabilities of different monolayers on a range of metal substrates was investigated by ab initio atomistic thermodynamics modeling. The calculated Gibbs free energies for different monolayers on Me (111) surfaces at 600 °C as a function of hydrogen pressure are summarized in Fig. S3.† At lower hydrogen pressure (<10−6 Pa), all reduced monolayers are thermodynamically unstable and a clean metal surface is preferred. The Ti2O3 monolayers are the first to be formed as pressure increases. At the typical conditions for SMSI experiment (105 Pa hydrogen pressure and 600 °C),17,38 for Pt, Pd, Ru, Os, Rh and Ir, all reduced monolayers exhibit negative formation energies, indicating that encapsulation of these metal nanoparticles by a monolayer is thermodynamically favourable. For Au, Ag and Cu, the Ti2O3 monolayers has similar Gibbs free energies as the bulk TiO2, leading to the competition between an encapsulation state and a clean metal surface state.To illustrate more clearly these distinctions, we calculated the phase diagrams of the monolayers as a function of hydrogen pressure and temperature. Fig. 4 shows the phase diagrams of monolayers on the Pt (111), Au (111) and Ag (111) surfaces, representing strong, mediate and weak interactions with the reduced monolayers, respectively. Fig. S4† shows the phase diagrams for other metal surfaces (Cu, Ru, Rh, Pd, Os, Ir). The stability of TiOx strongly correlates with the strength of the bonding between titanium and the metal atoms of the support, and thus changes dramatically with the supporting surface. On the Pt (111) surface, Ti2O3 monolayer is stable at low temperature (0 °C) when PH2 > 10−2 Pa. At high temperature (600 °C), the presence of hydrogen makes the Ti2O3 monolayer stable already at partial pressures as low as 10−4 Pa. No stable range was found for the TiO monolayer on Pt (111) surface. On the Au (111) surface, Ti2O3 monolayer is not stable at low temperature (T < 200 °C) when PH2 < 1010 Pa. There is a stability range for TiO monolayer between Ti2O3 monolayer and the TiAu3 surface alloy. On the Ag (111) surface, the stability ranges of all monolayers shift towards high temperatures and hydrogen partial pressures. The TiAg3 surface alloy is only stable at very high temperatures and pressures. Overall, the stability of the monolayer is very sensitive to temperature and pressure. By either lowering the temperature or the hydrogen partial pressure, the monolayer stability transforms in the following order: alloy → (TiO) → Ti2O3 → clean surface.
Based on the linear relationship between the binding strength and the proposed descriptor, a phase diagram as a function of external conditions and of the descriptor can be constructed. As an illustration, Fig. 5 shows such a phase diagram at 600 °C (see Fig. S5† for the phase diagrams at 25 °C, 400 °C and 800 °C for comparison). Values of the descriptor for platinum and sliver are marked by the arrows. The stability ranges of Ti2O3 and TiMe3 monolayers increase with the absolute value of the descriptor, while the TiO monolayer is not stable on surfaces with a descriptor value higher than 0.6 eV, as in the case of Pt (111) surface, which agrees with the phase diagram in Fig. 4. The descriptor is not limited to pure metals. Values of the descriptor for Pt–Ag alloys, such as Pt3Ag, PtAg and PtAg3, can be calculated based on the linear combination of the descriptors for pure elements. The structure of an overlayer on these alloy surfaces can then be predicted based on the phase diagram.
With the external environmental conditions controlled experimentally, and with the descriptor reflecting the materials composition, such phase diagrams serve as a “structure–material–environment” map (Fig. 5). Using this map, one can choose the materials and the environmental conditions required to get the structure needed for a specific catalytic application.
3 Conclusions
In summary, this work presents a systematic ab initio investigation of fully oxidized and reduced titania monolayers deposited on Cu, Ru, Pd, Ag, Rh, Os, Ir, Pt and Au (111) surfaces. Titania monolayers with the anatase structure are more stable than those with the rutile structure. Reduced titania monolayers exhibit strong interaction with the metal through the electron transfer from the titanium cation to the metal substrate. The binding strength at the interfaces between the metal and the reduced titania varies substantially, ranging from particularly strong (Pt and Pd) to relatively weak (Cu and Ag).The alloy formation energy is a simple and reliable descriptor for the binding strength between a reduced titania monolayer and a metal substrate. The alloy formation energy descriptor reflects the material's composition at relevant environmental conditions, and thus can be used to identify the material structure at reactive conditions. In the case of alloys comprising metals with significantly different atomic radii, the descriptor might underestimate the effect of the increased strain energy. Notwithstanding this limitation, since alloy formation energies can either be found tabulated or easily computed, using them as a descriptor enables rapid pre-screening of the materials with the given interfacial interaction strength.
The analysis of the phase diagrams of various monolayers as a function of temperature and hydrogen pressure indicates that the stability range of monolayers are sensitive to the supporting metal, the temperature and the reducing atmosphere used to induce the SMSI. The constructed phase diagrams can be used to predict the complex dynamical behavior of SMSI, and may help to control the structure of supported metal catalysts.
4 Computational details
4.1 Electronic structure methodology
DFT calculations were performed using the Quickstep module in the CP2K simulation package.56 The generalized gradient approximation (GGA) using the Perdew, Burke and Ernzerhof (PBE) functional was chosen to evaluate the exchange–correlation energy.57 Valence electrons were treated explicitly, whereas interactions with the frozen atom core were described using Goedecker–Teter–Hutter (GTH) pseudo potentials.58 A double-zeta valence plus polarization (DZVP) basis set, optimized according to the Mol-Opt method,59 has been used. A cutoff of 500 Ry has been used for the auxiliary plane wave expansion of the charge density. Brillouin zone integration was performed with a reciprocal space mesh consisting of only the gamma point. A strict convergence criterion of 10−7 Ha was used for the SCF calculations. For transition metal oxides, DFT+U method is important to describe the electronic properties strong correlation effect from the d electrons. Detailed comparison of DFT+U on the key parameter of the current study, i.e. the relative stability of supported TiOx monolayers, indicates that it has only a small effect (see the ESI, Section S1†).4.2 Formation energy of alloy
Alloy formation energy Ef of a system of n atoms of element A and m atoms of element B is calculated as:| Ef = EAnBm−nEA − mEB, | (3) |
Geometrical structures of all considered alloys were taken from the Materials Project database.55 The formation energies were calculated using the computational setup described in Section 4.1.
The general way of calculating the energies of complex systems from first principles and comparing their relative stabilities has previously been discussed in great detail by the group of Ceder.60 This work uses an analogous methodology.
4.3 Ab initio thermodynamics
The effect of the gaseous environment on the relative stability of the considered surface structure was captured by the method of ab initio atomistic thermodynamics.61 The Gibbs free energy of a gas phase at temperature T and partial pressure P is given by:G(T,P) = EDFT + EZPE + ΔG(T,P0) + kBT![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln(P/P0), ln(P/P0), | (4) |
| ΔGTiOx/(111) = GTiOx/(111) − GTiOx − G(111), | (5) |
The equilibrium phase diagram for different surface structures, e.g. TiOm/Me (111) vs. TiOn/Me (111), is calculated by solving the following equation:
| GTiOm/Me(111)(T,P) − GTiOn/Me(111)(T,P) − (m − n)μO(T,P) = 0, | (6) |
4.4 Interface models
In this work, the face-centered cubic (FCC) structure and its closest packed (111) surfaces are considered. This choice is governed by the nature of the considered systems. For pure metals, we note that Rh, Ir, Ni, Pd, Pt, Cu, Ag, and Au have an FCC structure, while Ru and Os have a hexagonal closest packed (HCP) structure. Both FCC and HCP are closest packed structures, and their closest packed surfaces (the most stable surfaces) have the same structure, and the only difference between FCC and HCP is the packing sequence, with “–A–B–C–A–B–C–” for FCC and “–A–B–A–B–” for HCP. As a result, our choice corresponds to the most stable surfaces for all considered metals. Therefore, all the metal substrates were modeled by four FCC (111) atomic layers with the positions of two bottom layers fixed.The oxide monolayers were then deposited on top of metal substrates. Since metal substrates have a range of lattice constants, several oxide supercells were used to minimize the strain at the interfaces. Table 1 shows all interface models used in these calculations. A rectangular Me (111) unit cell (abbreviated as  ) was used for the rectangular TiO2 unit cell. It is important to note that the optimal lattice constants of the oxide monolayers on metal substrates can differ from those of the bulk oxides. Thus the lattice mismatch in Table 1 was used only as a reference to build the interface models that are as realistic as possible, and can not be used to estimate the real strain in the interface.
) was used for the rectangular TiO2 unit cell. It is important to note that the optimal lattice constants of the oxide monolayers on metal substrates can differ from those of the bulk oxides. Thus the lattice mismatch in Table 1 was used only as a reference to build the interface models that are as realistic as possible, and can not be used to estimate the real strain in the interface.
Conflicts of interest
The authors declare no conflicts of interest.Acknowledgements
We gratefully acknowledge the computational resources provided by the Paul Scherrer Institute (PSI) and the Swiss National Supercomputing Centre (CSCS). X. W. acknowledges financial support from the China Scholarships Council (No. 201506370019). A. B. and J. A. v. B. acknowledge the SNSF project 200021_178943.Notes and references
- J. R. Ross, Heterogeneous catalysis: fundamentals and applications, Elsevier, 2011 Search PubMed.
- R. Prins, A. Wang and X. Li, Introduction to Heterogeneous Catalysis, World Scientific Publishing Company, 2016, vol. 1 Search PubMed.
- J. A. Farmer and C. T. Campbell, Science, 2010, 329, 933–936 CrossRef CAS.
- Y. Lykhach, S. M. Kozlov, T. Skála, A. Tovt, V. Stetsovych, N. Tsud, F. Dvořák, V. Johánek, A. Neitzel, J. Mysliveček, S. Fabris, V. Matolín, K. M. Neyman and J. Libuda, Nat. Mater., 2016, 15, 284–288 CrossRef CAS.
- G. Pacchioni and H.-J. Freund, Chem. Soc. Rev., 2018, 47, 8474–8502 RSC.
- S. Zafeiratos, S. Piccinin and D. Teschner, Catal. Sci. Technol., 2012, 2, 1787–1801 RSC.
- S. Penner and M. Armbrüster, ChemCatChem, 2015, 7, 374–392 CrossRef CAS.
- M. Ahmadi, F. Behafarid and B. Roldan Cuenya, Nanoscale, 2016, 8, 11635–11641 RSC.
- S. L. Hemmingson and C. T. Campbell, ACS Nano, 2017, 11, 1196–1203 CrossRef CAS.
- L. B. Vilhelmsen and B. Hammer, ACS Catal., 2014, 4, 1626–1631 CrossRef CAS.
- T. W. v. Deelen, C. H. Mejía and K. P. d. Jong, Nat. Catal., 2019, 2, 955–970 CrossRef.
- X. Wang, J. A. van Bokhoven and D. Palagin, Phys. Chem. Chem. Phys., 2017, 19, 30513–30519 RSC.
- M. Kottwitz, Y. Li, R. M. Palomino, Z. Liu, G. Wang, Q. Wu, J. Huang, J. Timoshenko, S. D. Senanayake, M. Balasubramanian, D. Lu, R. G. Nuzzo and A. I. Frenkel, ACS Catal., 2019, 9, 8738–8748 CrossRef CAS.
- X. Wang, J. A. van Bokhoven and D. Palagin, Phys. Chem. Chem. Phys., 2020, 22, 28–38 RSC.
- J. Amsler, B. B. Sarma, G. Agostini, G. Prieto, P. N. Plessow and F. Studt, J. Am. Chem. Soc., 2020, 142, 5087–5096 CrossRef CAS.
- F. Maurer, J. Jelic, J. Wang, A. Gänzler, P. Dolcet, C. Wöll, Y. Wang, F. Studt, M. Casapu and J.-D. Grunwaldt, Nat. Catal., 2020, 3, 824–833 CrossRef CAS.
- S. J. Tauster, S. C. Fung and R. L. Garten, J. Am. Chem. Soc., 1978, 100, 170–175 CrossRef CAS.
- J.-M. Herrmann, J. Catal., 1989, 118, 43–52 CrossRef CAS.
- T. Suzuki and R. Souda, Surf. Sci., 2000, 448, 33–39 CrossRef CAS.
- Q. Fu, T. Wagner, S. Olliges and H.-D. Carstanjen, J. Phys. Chem. B, 2005, 109, 944–951 CrossRef CAS.
- X. Liu, M.-H. Liu, Y.-C. Luo, C.-Y. Mou, S. D. Lin, H. Cheng, J.-M. Chen, J.-F. Lee and T.-S. Lin, J. Am. Chem. Soc., 2012, 134, 10251–10258 CrossRef CAS.
- S. Tosoni and G. Pacchioni, J. Phys. Chem. C, 2019, 123, 7952–7960 CrossRef CAS.
- Z. Weng and F. Zaera, ACS Catal., 2018, 8, 8513–8524 CrossRef CAS.
- H. Tang, Y. Su, Y. Guo, L. Zhang, T. Li, K. Zang, F. Liu, L. Li, J. Luo, B. Qiao and J. Wang, Chem. Sci., 2018, 9, 6679–6684 RSC.
- A. Corma, P. Serna, P. Concepción and J. J. Calvino, J. Am. Chem. Soc., 2008, 130, 8748–8753 CrossRef CAS.
- M. Macino, A. J. Barnes, S. M. Althahban, R. Qu, E. K. Gibson, D. J. Morgan, S. J. Freakley, N. Dimitratos, C. J. Kiely, X. Gao, A. M. Beale, D. Bethell, Q. He, M. Sankar and G. J. Hutchings, Nat. Catal., 2019, 2, 873–881 CrossRef CAS.
- J. Zhang, H. Wang, L. Wang, S. Ali, C. Wang, L. Wang, X. Meng, B. Li, D. S. Su and F.-S. Xiao, J. Am. Chem. Soc., 2019, 141, 2975–2983 CrossRef CAS.
- Y. Zhang, X. Su, L. Li, H. Qi, C. Yang, W. Liu, X. Pan, X. Liu, X. Yang, Y. Huang and T. Zhang, ACS Catal., 2020, 10, 12967–12975 CrossRef CAS.
- S. Wang, J. Goniakowski, C. Noguera and M. R. Castell, Phys. Rev. B, 2019, 100, 125408 CrossRef CAS.
- K. Zhang, S. Shaikhutdinov and H.-J. Freund, ChemCatChem, 2015, 7, 3725–3730 CrossRef CAS.
- J. Graciani, A. B. Vidal, J. A. Rodriguez and J. F. Sanz, J. Phys. Chem. C, 2014, 118, 26931–26938 CrossRef CAS.
- S.-i. Ito, C. Chibana, K. Nagashima, S. Kameoka, K. Tomishige and K. Kunimori, Appl. Catal., A, 2002, 236, 113–120 CrossRef CAS.
- H. Sakamoto, T. Ohara, N. Yasumoto, Y. Shiraishi, S. Ichikawa, S. Tanaka and T. Hirai, J. Am. Chem. Soc., 2015, 137, 9324–9332 CrossRef CAS.
- L. Deng, H. Miura, T. Shishido, S. Hosokawa, K. Teramura and T. Tanaka, Chem. Commun., 2017, 53, 6937–6940 RSC.
- Z. Li, L. Yu, C. Milligan, T. Ma, L. Zhou, Y. Cui, Z. Qi, N. Libretto, B. Xu, J. Luo, E. Shi, Z. Wu, H. Xin, W. N. Delgass, J. T. Miller and Y. Wu, Nat. Commun., 2018, 9, 5258 CrossRef CAS.
- H. Tang, Y. Su, B. Zhang, A. F. Lee, M. A. Isaacs, K. Wilson, L. Li, Y. Ren, J. Huang, M. Haruta, B. Qiao, X. Liu, C. Jin, D. Su, J. Wang and T. Zhang, Sci. Adv., 2017, 3, e1700231 CrossRef.
- S. Zhang, P. N. Plessow, J. J. Willis, S. Dai, M. Xu, G. W. Graham, M. Cargnello, F. Abild-Pedersen and X. Pan, Nano Lett., 2016, 16, 4528–4534 CrossRef CAS.
- A. Beck, X. Huang, L. Artiglia, M. Zabilskiy, X. Wang, P. Rzepka, D. Palagin, M.-G. Willinger and J. A. van Bokhoven, Nat. Commun., 2020, 11, 3220 CrossRef CAS.
- Q. Fu and T. Wagner, Surf. Sci. Rep., 2007, 62, 431–498 CrossRef CAS.
- N. J. O'Connor, A. S. M. Jonayat, M. J. Janik and T. P. Senftle, Nat. Catal., 2018, 1, 531 CrossRef.
- D. Sharma, G. Gautam and S. Narasimhan, Appl. Surf. Sci., 2019, 492, 16–22 CrossRef CAS.
- L. A. Zotti, S. Sanvito and D. D. O'Regan, Mater. Des., 2018, 142, 158–165 CrossRef CAS.
- M. Capdevila-Cortada and N. López, ACS Catal., 2015, 5, 6473–6480 CrossRef CAS.
- Z.-J. Zhao, S. Liu, S. Zha, D. Cheng, F. Studt, G. Henkelman and J. Gong, Nat. Rev. Mater., 2019, 4, 792–804 CrossRef.
- C. F. Dickens, J. H. Montoya, A. R. Kulkarni, M. Bajdich and J. K. Nørskov, Surf. Sci., 2019, 681, 122–129 CrossRef CAS.
- E. M. Dietze and P. N. Plessow, J. Phys. Chem. C, 2019, 123, 20443–20450 CrossRef CAS.
- P. N. Plessow, M. Bajdich, J. Greene, A. Vojvodic and F. Abild-Pedersen, J. Phys. Chem. C, 2016, 120, 10351–10360 CrossRef CAS.
- H. Perron, C. Domain, J. Roques, R. Drot, E. Simoni and H. Catalette, Theor. Chem. Acc., 2007, 117, 565–574 Search PubMed.
- A. Vittadini and M. Casarin, Theor. Chem. Acc., 2008, 120, 551–556 Search PubMed.
- J. K. Nørskov, F. Studt, F. Abild-Pedersen and T. Bligaard, Fundamental concepts in heterogeneous catalysis, John Wiley & Sons, 2014 Search PubMed.
- J. Goniakowski and C. Noguera, J. Phys. Chem. C, 2019, 123, 9272–9281 CrossRef CAS.
- R. Tran, Z. Xu, B. Radhakrishnan, D. Winston, W. Sun, K. A. Persson and S. P. Ong, Sci. Data, 2016, 3, 1–13 CrossRef.
- N. Tsuboi, H. Okuyama, M. Nishijima and T. Aruga, Phys. Rev. B: Condens. Matter Mater. Phys., 2003, 68, 033408 CrossRef.
- G. Henkelman, A. Arnaldsson and H. Jónsson, Comput. Mater. Sci., 2006, 36, 354–360 CrossRef.
- A. Jain, S. P. Ong, G. Hautier, W. Chen, W. D. Richards, S. Dacek, S. Cholia, D. Gunter, D. Skinner, G. Ceder and K. a. Persson, APL Mater., 2013, 1, 011002 CrossRef.
- J. VandeVondele, M. Krack, F. Mohamed, M. Parrinello, T. Chassaing and J. Hutter, Comput. Phys. Commun., 2005, 167, 103–128 CrossRef CAS.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868 CrossRef CAS.
- S. Goedecker, M. Teter and J. Hutter, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 1703–1710 CrossRef CAS.
- G. Lippert, J. Hutter and M. Parrinello, Mol. Phys., 1997, 92, 477–488 CrossRef CAS.
- S. Ping Ong, L. Wang, B. Kang and G. Ceder, Chem. Mater., 2008, 20, 1798–1807 CrossRef.
- K. Reuter and M. Scheffler, Phys. Rev. Lett., 2003, 90, 046103 CrossRef.
- K. Reuter, C. Stampf and M. Scheffler, Ab Initio Atomistic Thermodynamics and Statistical Mechanics of Surface Properties and Functions, Springer Netherlands, Dordrecht, 2005, pp. 149–194 Search PubMed.
- A. H. Larsen, J. J. Mortensen, J. Blomqvist, I. E. Castelli, R. Christensen, M. Dułak, J. Friis, M. N. Groves, B. Hammer, C. Hargus, E. D. Hermes, P. C. Jennings, P. B. Jensen, J. Kermode, J. R. Kitchin, E. L. Kolsbjerg, J. Kubal, K. Kaasbjerg, S. Lysgaard, J. B. Maronsson, T. Maxson, T. Olsen, L. Pastewka, A. Peterson, C. Rostgaard, J. Schiøtz, O. Schütt, M. Strange, K. S. Thygesen, T. Vegge, L. Vilhelmsen, M. Walter, Z. Zeng and K. W. Jacobsen, J. Phys.: Condens. Matter, 2017, 29, 273002 CrossRef.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/d0ta11650e |
| This journal is © The Royal Society of Chemistry 2021 |



![[left over right harpoons]](https://www.rsc.org/images/entities/char_21cb.gif) H2O. Partial pressure of H2O is fixed to be 10−1 Pa, and temperature is fixed to be 600 °C.
H2O. Partial pressure of H2O is fixed to be 10−1 Pa, and temperature is fixed to be 600 °C.