Open Access Article
Open Access ArticleElucidating the nature of grain boundary resistance in lithium lanthanum titanate†
Adam R.
Symington
 *a,
Marco
Molinari
*a,
Marco
Molinari
 b,
James A.
Dawson
b,
James A.
Dawson
 cd,
Joel M.
Statham
a,
John
Purton
cd,
Joel M.
Statham
a,
John
Purton
 e,
Pieremanuele
Canepa
e,
Pieremanuele
Canepa
 *fg and
Stephen C.
Parker
*fg and
Stephen C.
Parker
 *a
*a
aDepartment of Chemistry, University of Bath, Claverton Down, Bath BA2 7AY, UK. E-mail: A.R.Symington@bath.ac.uk
bDepartment of Chemistry, University of Huddersfield, Huddersfield HD1 3DH, UK. E-mail: pcanepa@nus.edu.sg; S.C.Parker@bath.ac.uk
cChemistry – School of Natural and Environmental Sciences, Newcastle University, Newcastle upon Tyne, NE1 7RU, UK
dCentre for Energy, Newcastle University, Newcastle upon Tyne, NE1 7RU, UK
eScience and Technologies Facilities Council, Daresbury Laboratory, Keckwick Lane, Daresbury, WA4 4AD, UK
fDepartment of Materials Science and Engineering, The National University of Singapore, Singapore 117576, Singapore
gDepartment of Chemical and Biomolecular Engineering, The National University of Singapore, Singapore 117585, Singapore
First published on 29th January 2021
Abstract
Solid electrolytes for all-solid-state batteries are generating remarkable research interest as a means to improve the safety, stability and performance of rechargeable batteries. Solid electrolytes are often polycrystalline and the effect that grain boundaries have on the material properties is often not fully characterised. Here, we present a comprehensive molecular dynamics study that quantifies the effect of grain boundaries on Li-ion transport in perovskite Li3xLa(2/3)−xTiO3 (0 < x < 0.16) (LLTO). Our results predict that grain boundaries hinder Li-ion conductivity by 1 to 2 orders of magnitude compared to the bulk. We attribute the poor Li-ion conductivity of the grain boundaries to significant structural alterations at the grain boundaries. Our detailed analysis provides important insight into the influence of grain boundary structure on transport of Li-ions in solid electrolyte materials.
Introduction
Li-ion batteries are at the heart of modern technological innovation and key to current and future technologies, such as portable electronic devices,1 hybrid/electric vehicles,2 and stationary applications.3–7 Traditional Li-ion batteries have critical safety issues because of the highly flammable organic liquid electrolytes. These liquid electrolytes have low thermal stability, which introduces the risk of short circuit, cell failure, fire and in some cases explosion.8–10 Significant effort is directed towards replacing liquid electrolytes with solid electrolytes. Solid electrolytes have the potential to isolate the distinct chemistry of each electrode, and for example, reduce dendrite formation at the anode and to replace the current flammable liquid electrolytes,10–15 with safer materials that are free from leakage. However, this replacement in commercial Li-ion batteries introduces new challenges, such as insufficient ionic conductivity, narrow electrochemical stability windows and chiefly interfacial instabilities.12,16A range of materials have been investigated as solid electrolytes, based on garnet (Li7La3Zr2O12),17,18 NaSICON (NaxZr2Six−1P4−xO12), LiSICON (Li14Zn(GeO4)4),14 thio-LISICON (ternaries in Li2S–SiS2–Al2S3)19 and LGPS-like structures.15,20–22 The perovskite Li3xLa(2/3)−xTiO3 (0 < x < 0.16) (LLTO) was first studied as a solid electrolyte material and has become a viable alternative for next generation of all-solid-state batteries because of its unique physical and electrochemical behaviours.23–25 Crystalline LLTO exhibits a high ionic conductivity (1 × 10−3 S cm−1) at room temperature.10,23–26
LLTO is an A-site deficient perovskite with A-site vacancy partially filled with Li ions. Unless quenched at high temperatures,27 LLTO in Fig. 1 displays an alternate stacking of La-rich and Li-rich layers with A-site vacancies localised primarily in the Li-rich layers. The La-rich layers tend to block Li-ion conduction due to the small concentrations of Li-ions and charge carrying A-site vacancies. This limits Li-ion transport to be two dimensional and localised to the Li-rich layers.27
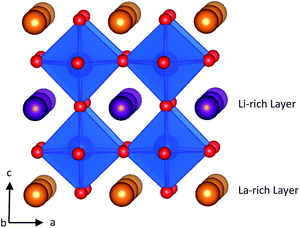 | ||
| Fig. 1 Structure of Li3xLa(2/3)−xTiO3. La atoms are shown in orange, Li in purple, O in red and TiO6 polyhedra are in blue. | ||
As for many ceramic materials, grain boundaries in LLTO play an important role on the overall ionic conductivity of the material.28 The applicability of LLTO is challenged by grain boundary resistance, which can reduce the ionic conductivity by 2–3 orders of magnitude.29–31 It has been suggested that a reduction in performance is due to structural changes that occurs at the grain boundaries, which may disrupt the Li-ion diffusion pathways within the Li-rich layers of LLTO.29 Grain boundary resistance is not unique to LLTO but is common for a range of solid electrolytes,13 as well as other ion-solid conductors.32–35 While there are many reports of the grain boundary blocking effects,30,31,36 these studies lack the structural description at the atomic scale structure, which is ultimately linked to the overall reduction of Li-ion conductivity. Understanding the effects of these structural extended defects in ceramic materials will provide clear guidance for the optimization of the synthesis and sintering procedures improving the overall ion transport of these materials.
With the task to understand the impact of grain boundaries on Li-ion transport in LLTO, we apply large-scale molecular dynamics simulations to a representative ceramic solid electrolyte material with formula Li3xLa(2/3)−xTiO3. We demonstrate that the formation energies of such grain boundaries are low, suggesting that grain boundaries are prevalent. Our findings elucidate that grain boundaries reduce Li-ion conductivity and concomitantly increase the activation energy for Li+ migration. We use these findings to establish a model that can quantify the effects of grain boundaries on the overall Li-ion conductivity of LLTO. These results provide a useful link between the atomic-scale insight and the role of grain boundaries on Li-ion transport of solid electrolytes. We establish a relationship between grain size and grain boundary resistance, which provides a heuristic principle to improve Li-ion conductivity and can be applied to all solid-state electrolytes.
Methodology
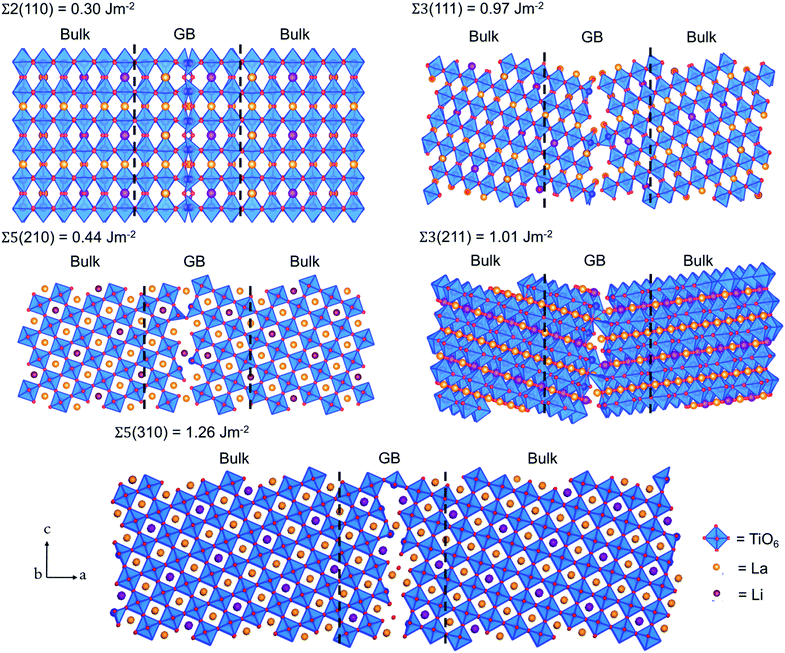
The grain boundary (GB) models were generated using the METADISE code.37,38 A complete procedure for the generation of the GB is given in the ESI.† The twin grain boundaries were constructed using coincidence site lattice theory, where two individual grains are titled by a given angle until their surface planes coincide. We explored the potential energy surfaces (Fig. S1†) of five symmetric tilt grain boundaries, namely, Σ2(110), Σ3(111), Σ5(210), Σ3(211) and Σ5(310). We find that the global minimum configurations of these grain boundaries resemble those described in detail in previous experimental and computational literature.32,33 In this notation, Σ is the coincidence index and the ratio of the coincidence unit cell volume to the primitive unit cell volume. These grain boundaries were selected because they have been observed in high concentrations in LLTO, as well as other perovskite materials, e.g., CaMnO3 and SrTiO3.39–43The grain boundary formation energy, γGB, is the energy needed to form the grain boundary from the bulk material per unit area:
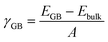 | (1) |
Using these GB models, molecular dynamics (MD) simulations were performed using the DL_POLY code.44 MD simulations of 5 ns were completed using a timestep of 1 fs with supercells of ∼8000 atoms (details are given in Table S2†) and a 10 Å potential cut-off. The equilibration was performed using the NPT ensemble until the cell volume had been converged. Production simulations were carried out within a temperature range of 300–1500 K at intervals of 100 K using the NVT ensemble. The Nose–Hoover thermostat (for NVT) and barostat (for NVT and NPT) were used.45,46
The self-diffusion coefficient of Li ions was derived from the mean square displacement (MSD), 〈ri2(t)〉, of Li ions as in eqn (2).
| 〈ri2(t)〉 = 6DLit | (2) |
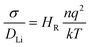 | (3) |
The electrostatic potential of the grain boundary structures is calculated from MD trajectories according to:
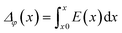 | (4) |
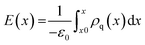 | (5) |
The structure generation and MD simulations employ a classical potential model, derived by Pedone et al. (details in Table S1†).47 The potential model used, accurately reproduced the lattice parameters and bond lengths of the LLTO perovskite structure.27 This model is based on rigid ions and partial charges and has been used extensively to investigate other materials and their GBs.32,33,48–53
It is accepted that altering the lithium content x value Li3xLa(2/3)−xTiO3 (0 < x < 0.16) affects the conductivity and activation energy of transport in LLTO. In this study, we set x to 0.05, corresponding to Li0.16La0.62TiO3.
Results
Grain boundary structures
The bulk tetragonal polymorph (with space group P4/nmm) of LLTO was simulated. The calculated lattice parameters show good agreement (a = b = 3.84 and c = 7.96 Å) with existing experimental work (a = b = 3.87 and c = 7.79 Å).54–56 We have constructed our GB models from this optimized structure.Five grain boundaries, namely, Σ2(110), Σ3(111), Σ5(210), Σ3(211) and Σ5(310), were constructed as outlined in the methodology.32,33,37 Using eqn (1), we estimated the thermodynamic propensity of such grain boundaries to form from LLTO bulk, which are shown in Fig. 2.
All grain boundary formation energies are relatively low (<1.3 J m−2) compared to other perovskite and polycrystalline materials,32,33,52,57–59 signifying that these GBs are likely present in high concentrations in the real material. The lowest energy was calculated for the Σ2(110) grain boundary (0.30 J m−2), while the least stable is the Σ5(310) structure (1.26 J m−2).
The relative stability of the grain boundaries and thus their concentration in the material is an important factor to consider when analysing the Li transport in LLTO. For example, it is likely to find a higher concentration of Σ2(110) grain boundaries than the Σ5(310) boundaries due to its lower energy.
Li-Ion conductivity in LLTO and its grain boundaries
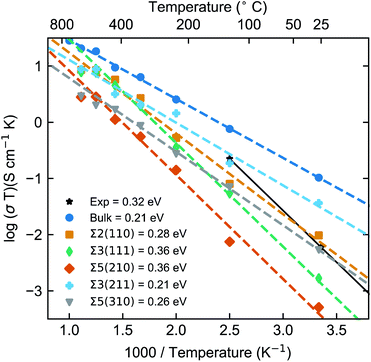
As noted previously, computational studies have not explored the effect of GBs on the observed grain boundary resistance in this material.MD simulations of the GB structures were performed to probe the impact of the GB resistance on the Li-ion conductivity in solid electrolytes, using LLTO as a model system. The Li+ diffusion coefficients were evaluated using the Nernst–Einstein equation of eqn (3). Fig. 3 shows the Arrhenius plots of the calculated Li-ion conductivities of each grain boundary compared to the bulk LLTO from the MD simulations computed between 300–900 K. Experimental data, calculated from A.C. impedance experiments for polycrystalline LLTO (with grain boundary and bulk contributions) is plotted for comparison.24
The calculated bulk LLTO conductivity at room temperature is 3.4 × 10−4 S cm−1, which is in good agreement with experimental studies examining single crystals.23,24,60,61 However, due to the variation in Li/La concentration, different synthesis and sample preparation techniques, a wide range of electrochemical impedance spectroscopy measurements have been reported in the literature.27
In general, the computed Li-ion conductivities of the five GBs appear lower than the bulk values at typical battery operating temperatures (∼25 to 150 °C). This effect was observed across the whole temperature range and confirms the high GB resistance in LLTO.
The Li-ion conductivities for the five GBs follow the order Σ3(211) > Σ2(110) > Σ5(310) > Σ3(111) > Σ5(210). Between 300 and 900 K, there are significant variations in the calculated grain boundary conductivities. For example, at 300 K the Li-ion conductivities were found to vary by approximately two orders of magnitude between the most conductive, Σ3(211) ∼1.2 × 10−4 S cm−1 and the least conductive GB, Σ5(210) ∼2.7 × 10−6 S cm−1. There is a small difference in conductivity between the bulk and the highest conducting GB, the Σ3(211), but a two order of magnitude difference between the bulk and the lowest conducting grain boundary, the Σ5(210). Inaguma et al. calculated the grain boundary conductivity (2 × 10−5 S cm−1) of LLTO at 300 K to be 2 orders of magnitude lower than that of the bulk (1 × 10−3 S cm−1).23
From Fig. 3, we could extract the activation energies, which follow the order Σ5(210) ≈ Σ3(111) > Σ2(110) > Σ5(310) > Σ3(211). This trend follows the order of Li-ion conductivities, except that the Σ5(310) and Σ2(110) switch their orders. An experimental activation energy of ∼0.32 eV was reported for polycrystalline LLTO and is clearly much larger than our calculated bulk activation energy. This is because the experimental value includes the contribution from both grain boundaries and bulk transport.
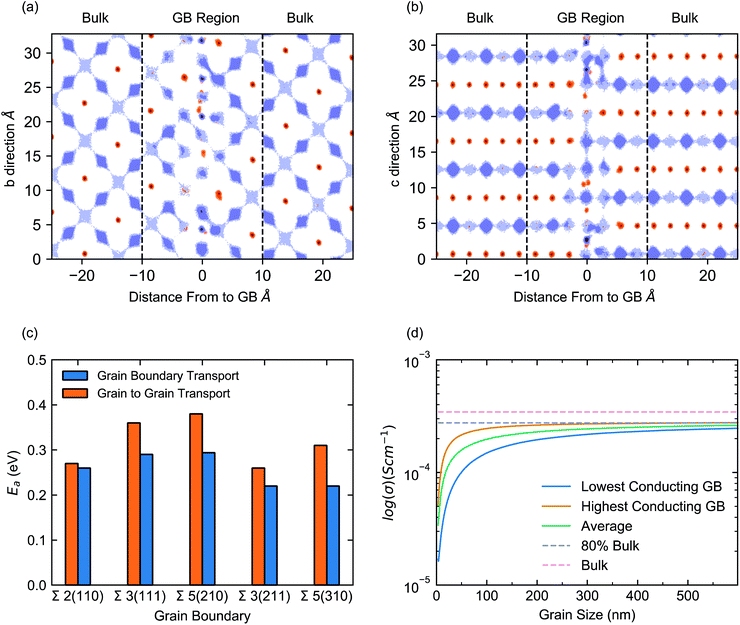
The directional dependence of the conductivity can be visualised by analysing the Li-ion trajectories of the MD simulations to produce Li-ion density maps, as shown for the Σ2(110) in Fig. 4a and b (plots for other grain boundaries can be found in S4–S8 of the ESI†). These plots illustrate the effect of the grain boundary structure on Li-ion diffusion channels in terms of both, diffusion within Li-rich layers and diffusion between Li-rich layers (via La-rich layers). The diffusion maps in Fig. 4a and b show the positions occupied by Li-ions (purple) and La-ions (orange) at all timesteps of the MD simulation and provide insight into the migration pathways of these atoms. To facilitate the visualization, the Σ2(110) grain boundary is placed at 0 Å and is shown from two viewpoints. The Li-rich layers can be clearly visualised (purple) and the mismatch between the layers of each grain at the grain boundary can also be observed.
These plots show clearly defined Li-ion migration channels in the bulk (Fig. 4a), with distinct Li-ion sites and interconnecting migration pathways. In contrast, at the grain boundary (Fig. 4b) these Li-ion sites and pathways are less clearly defined and, in many parts, non-existent, highlighting the heterogeneity of Li-ion conductivity between grains. Within the bulk, Li transport is restricted to the Li-rich layers and minimal transport occurs between these layers. However, at the grain boundary, a small number of Li-ions can be seen moving between such Li-rich layers. This is due to a misaligning between the Li-rich layers of each grain which instead, provides a continuous series of Li-ion sites. The effect introduced by this misalignment can be seen in Fig. 4c, which displays the activation energy for Li-ion conductivity along the grain boundaries (blue bars) and across grains via the grain boundary (orange bars). It is clear that the transport across grains (grain to grain) is hindered relative to transport along the grain boundaries.
Using our calculated Li-ion conductivities of LLTO, we have rationalised the effects of GBs on the overall ionic conductivity of a real polycrystalline sample, using a phenomenological model first derived for polycrystalline Li3OCl.52 The model is based on the equivalent circuit used in the interpretation of impedance data as in eqn (6).
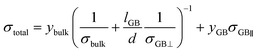 | (6) |
Fig. 4d plots the dependence of the total conductivity of a polycrystalline sample of LLTO against grain size. The orange line (Fig. 4d) corresponds to the total conductivity as a function of grain size, assuming the polycrystalline LLTO contains the most conductive grain boundaries (arithmetic average of Σ3(211) and Σ2(110)). In contrast, the blue line assumes the polycrystalline sample is dominated by the least conductive grain boundaries (using an arithmetic average of the ionic conductivities in Σ3(111) and Σ5(210)) and the green line is an arithmetic average (of all grain boundary conductivities). The pink dashed line identifies the bulk conductivity (3.4 × 10−4 S cm−1). From our analysis, the total conductivity above a ∼500 nm grain size is marked by a grey dashed line and corresponds to ∼80% of the bulk conductivity. The blue and orange bands around the lowest and highest polycrystalline conductivities represents two extreme cases calculated based on different densification behaviours, as discussed in Dawson et al.52
Fig. 4d reveals three main features. First, the Li-ion conductivity in the polycrystalline material increases with increasing grain size, as expected given the significant resistance of the GBs. Second, the influence of GB resistance is higher at very small grain sizes of <100 nm, with the highest value of Li-ion conductivity occurring at grain sizes exceeding 500 nm, as identified by the upper bound of the blue band. Third, for grain sizes < 100 nm, the total conductivity is dominated by GB contributions.
We have also investigated the mobility of individual Li ions depending on their location within the structure. We defined Li ions that move out of their starting A site to be mobile and those that do not to be immobile. In numerical terms, these immobile Li ions have a mean squared displacement of less than 4 Å2, which corresponds to the average the distance between the A sites in LLTO. This indicates that an Li-ion has not moved from its starting location or starting A-site during the entire simulation. Fig. S7† show the mobile and immobile Li-ions in LLTO grain boundary structures. The data shows that “immobile” Li-ions are present in the system and located primarily at the grain boundary.
Previous work has discussed the relationship between the size of the A-site and the associated bottleneck between A-sites, the cation coordination and the size of the cation.27 Li-ions in bulk LLTO are very mobile within the A-site and migrate between the 12 coordinate A-site and 4 coordinate tetrahedral sites within the A-site. Hence, the average coordination number of Li in bulk LLTO is less than the expected 12, typical of other perovskites. The comparatively large A-site allows diffusion of Li-ions between A-sites with ease. We find that the concentration of TiO6 polyhedra is greater in the grain boundary than in the bulk (Section S8 in the ESI†), and hence, the size of the A-site and associated bottleneck is reduced compared to the bulk structure.
Furthermore, our data suggest that the average coordination of Li is higher at the grain boundary than in the bulk, which indicates that the A-site is smaller, while Li-ions are not moving between tetrahedral sites in the A-site.
Voltage insights
In addition to the structural mismatch, described earlier that impacts the Li ion transport, the relaxed grain boundaries are also likely to modify the electric field through which Li ions move. Therefore, we examine the electrostatic potential experienced by Li ions to determine whether the grain boundaries generate barriers to ion diffusion. The electrostatic potential (V) is a property of a charged object, by virtue of its location in an electric field and is defined according to eqn (7).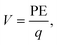 | (7) |
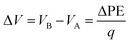 | (8) |
We have calculated the electrostatic potential of the five grain boundaries in order to determine how the presence of a grain boundary impacts the potential energy of Li ions. This quantity is crucial to elucidate the effects of grain boundaries on Li transport.
Fig. 5 shows the electrostatic potential calculated according to eqn (4) and (5) of five grain boundaries at 300 and 1000 K, respectively. To facilitate the discussion the grain boundary core is place at ∼0.0 Å on the x-axis (the non-periodic direction). The sharp oscillations along the x-axis are due to oppositely charged planes of cations and anions. Panels of Fig. 5 show oscillations in electrostatic potential between planes of cations and planes of anions in the grain boundary structures (region near ∼0.0 Å).
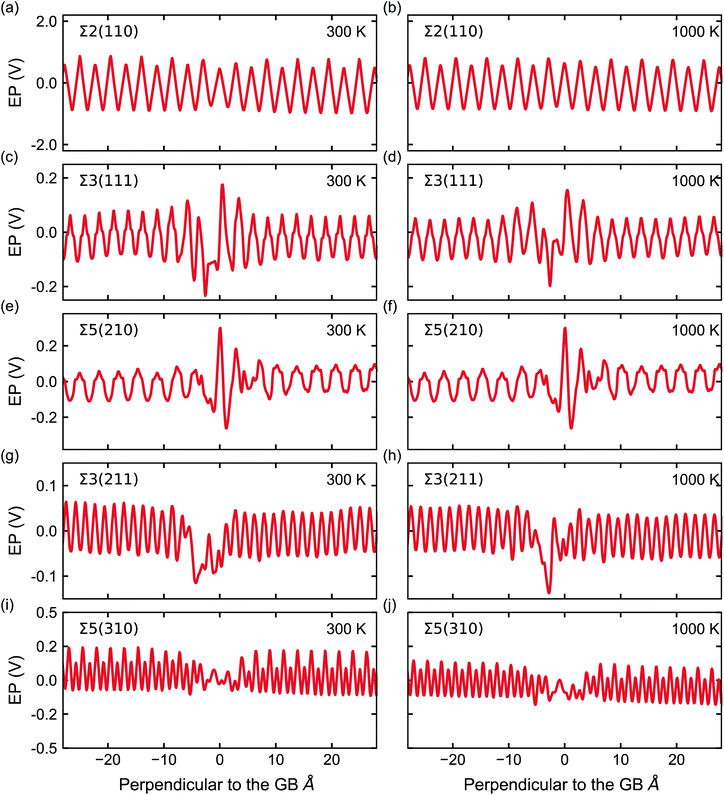 | ||
| Fig. 5 Electrostatic potential (EP) (solid red line) of the five GBs at 300 and 1000 K. The GB is located at 0 Å in these plots. Note, the scale of the y-axis varies across GBs. | ||
Fig. 6 summarises the average positive (negative) peak in the bulk and the largest positive (negative) peak in the grain boundary plotted in Fig. 5. Note, bulk refers to the region between grain boundaries in each simulation.
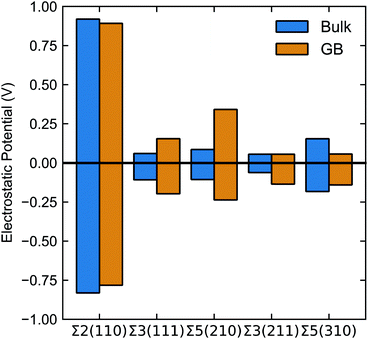 | ||
| Fig. 6 Maximum and minimum values of electrostatic potential (calculated according to eqn (7)) in the bulk (blue) and grain boundary (orange). Bulk refers to the region between grain boundaries in each simulation. | ||
The electrostatic potential profile is considerably different across the five grain boundaries, which led us to qualitatively separate them into two main categories: (i) with significant oscillations away from the bulk region, and (ii) with less pronounced oscillations in the GB area (∼0.0 Å in Fig. 5). The Σ3(211) and Σ5(310) GBs display a negative ΔV in the region of the grain boundary regions (see Fig. 5g, h, i, j, and 6). Thus, the profiles of these two grain boundaries vary considerably in the grain-boundary region compared to the bulk. In contrast, the Σ2(110) grain boundary (Fig. 5a and b) shows similar profiles to that of the bulk. The Σ3(111) and Σ5(210) grain boundaries have rather similar profiles and display distinct regions of negative ΔV and regions of positive ΔV relative to the bulk (Fig. 6). In particular, we observe that in both Σ3(111) (Fig. 5c and d) and Σ5(210) (Fig. 5e and f) grain boundaries there are regions of negative ΔV on either side of the GB region and areas with positive ΔV in the core of the grain boundary (x ∼ 0). We also find that temperature (left and right plots in Fig. 5) does not affect significantly the sign of ΔV in the GB studied.
These differences are better captured by analysing the widths of the distortion in the electrostatic potential caused by the grain boundaries. The width of the distortion field appears a unique feature of each grain boundary and follows the order Σ2(110) < Σ3(211) < Σ5(310) < Σ5(210) < Σ3(111) from smallest to largest, as in Fig. 5.
Discussion
Grain boundaries are a common structural motif found in ceramic oxides, and they can have a significant impact on the material properties.13,18,52,57,62 A significant body of research has investigated the impact of grain boundaries in a wide range of materials for different applications, e.g. Li-ion battery electrolytes,63 Li-ion battery cathodes,64 solid oxide fuel cells,32,65 solar cell ceramics66 and nuclear fuels.33 Grain boundaries have been shown to have a major impact on the defect chemistry of materials.67 In many materials it has been shown that grain boundaries contribute remarkably to high resistance to ionic conductivity.68In this work, we have focussed on the effect of grain boundaries on Li-ion conduction in a representative solid electrolyte material, i.e., Li0.16La0.62TiO3. To gain insights into the design of solid electrolytes for solid-state batteries, we have performed a comprehensive analysis of grain boundaries in LLTO across a range of typical temperature conditions.
We reported grain boundary energies (0.3–1.26 J m−2) which are consistently lower compared to other perovskite materials, notably, SrTiO3 (0.86–1.86 J m−2),57 BaTiO3 (1.03–1.57 J m−2),58 BaZrO3,59 Li3OCl (0.34–1.04 J m−2),39,52 as well as binary oxides, such as CeO2 (ref. 32) (1.16–2.10 J m−2) and UO2 (0.30–1.97 J m−2).33 These low grain boundary energies suggest their high concentrations within LLTO polycrystalline samples. This finding is in agreement with previous experimental work, which showed that Σ3/Σ5-type grain boundaries are prevalent and in high concentrations in LLTO.43 Therefore, our results, are representative of the overall structural properties of LLTO.
We predict an activation energy for bulk LLTO in good agreement with previous calculations on single crystals,23,24,61,69 but underestimate the electrochemical impedance spectroscopy values of ∼0.3 eV.23
It is generally accepted that grain boundary resistance is responsible for the discrepancy between the polycrystalline and single crystal measurements. Thus, our results highlight the importance of directly considering GB contributions to Li-ion conductivity in solid electrolyte materials. Depending on the grain boundary structure, we predicted grain boundary conductivities to range from 1 to 2 orders of magnitude lower than that of the bulk (3.4 × 10−4 S cm−1). This result aligns with experimental observations, which suggest that grain boundaries in LLTO are responsible for an increase in the resistance associated to Li-ion transport.
The calculated grain boundary conductivity is particularly low (1.2 × 10−4 to 2.7 × 10−6 S cm−1) compared to the bulk and appears in line with previous experimental observations.23,24,26,30,61,69–72 From an atomistic standpoint, we have shown that grain boundaries introduce significant structural alteration, with direct effects on the local coordination of Li+ ions and hence their mobility. This alteration corresponds to a mismatch between the Li-rich layers of the two grains (Fig. 4a and b). The mismatch between Li-rich layers at the grain boundary observed experimentally decreases Li-ion conductivity at grain boundaries followed by a breakdown of the layered motif.61 It has already been proposed that the alteration in the layered structure at the grain boundary is responsible for the reduction in conductivity in polycrystalline LLTO and our calculations provide evidence for this.31 Layered-type lithium conducting materials are common in battery research and similar reports of poor grain boundary conductivity can be explained by the misalignment of Li rich layers at the grain boundary.
We have used the electrostatic potential as a useful metric to understand the charge distribution within a structure. We have demonstrated that the electrostatic potential can be used to interpret the calculated conductivities. From the changes of electrostatic potential (ΔV) between the bulk and grain boundary (Fig. 5 and 6) four possible situations, types can be identified:
Type I – the electrostatic potential increases at the GB and ΔV is positive. This is regarded as the accumulation of positively charge species in the grain boundary core, e.g., anion vacancies or a local increase in cation concentration. In this case Li-ions in the bulk will experience a potential energy barrier that must be overcome to access the grain-boundary core. A potential barrier will hinder the percolation of the Li-ions between grains. In Li-ion batteries, ΔV being positive, suggests that there is a depletion of Li-ion vacancies (negative species) relative to the bulk. Li vacancies facilitate Li-ion transport and consequently the grain boundary conduction can be expected to be poor. Thus, in polycrystalline samples with small grain sizes and high concentrations of type I grain boundaries, Li-ion transport will be limited to conduction along the grain boundaries, resulting in samples with poor Li-ion conductivities.
Type II – the electrostatic potential decreases at the GB and ΔV is negative. This case suggests the accumulation of negatively charged species in the grain boundary core, e.g., cation (Li-ion) vacancies or an increase in anion concentration. In this case, the access of Li-ions to the GB from the bulk is barrierless. However, there exists a potential energy barrier for Li-ions to leave the GB. This effect may also suppress Li-ion conduction between grains. Hence, in this situation, we speculate that Li-ions can be “lost” orbiting near the GB surfaces. As with type I grain boundaries, in polycrystals with a small grain size and high concentrations of type II grain boundaries, conduction will be limited to the grain boundaries. However, because ΔV is negative, we expect the grain boundaries to contain a high concentration of Li vacancies (negative species) relative to the bulk. For this reason, Li-ion conduction in type II grain boundaries is expected to be better than in type I grain boundaries, because Li-ion vacancies are charge carriers for Li-ion diffusion.
Type III – there is a mixture of positive and negative ΔV regions in the grain boundary. This example is typically used when discussing space charge models. In this case there is a depletion of positive defects in the regions flanking the grain boundary core, leading to a negative ΔV and an accumulation of positive defects in the grain boundary core, leading to a positive ΔV.
Type IV – the trivial case where grain boundaries have no impact on the electrostatic potential and ΔV is 0. In this instance, the grain boundary will behave in the same manner as the bulk and there is no potential barrier.
None of the grain boundaries studied in LLTO can be classified as type I (with positive ΔV) or IV (ΔV = 0) alone. The Σ2(110), Σ3(211) and Σ5(310) boundaries have a negative ΔV and fall into the type II category. The negative ΔV is due to the depletion of Li-ions at the grain boundary, as depicted in Fig. 7. Lithium atoms in the grain boundary core (in the range −5 < x < 5 Å) experience a potential energy barrier to percolate from the core of the grain boundary into the bulk, and with notable effects on Li-ion transport between grains is curbed. However, the accumulation of Li-ion vacancies at the boundary facilitates Li-ion transport within the grain boundary core, which explains the high Li conductivity in the Σ2(110), Σ3(211) and Σ5(310) models.
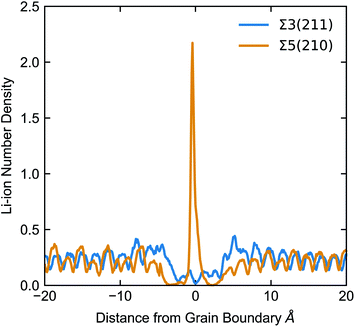 | ||
| Fig. 7 Number density of the centre of mass of Li-ions (total number of Li-ions in 0.1 Å histograms perpendicular to the GB) at the Σ5(210) and Σ3(211) boundaries. | ||
The Σ3(111) and Σ5(210) grain boundaries show a mixture of positive and negative ΔV across the GB and fall into the type III category. In these grain boundaries we find that there is a depletion of Li atoms (accumulation of Li vacancies) in the regions flanking the grain boundary core and an accumulation of Li ions at the GB core (depletion of Li vacancies). In this case there is a potential energy barrier for Li-ions to pass from one grain to the other.
In summary, Type III grain boundaries (Σ3(111) and Σ5(210)) are the least conductive boundaries studied, while the Type II grain boundaries ΔV (Σ2(110), Σ3(211) and Σ5(310)) are the most conductive. Nevertheless, in both cases our MD simulations suggest poor conductivity across the grain boundary when compared to the bulk.
Conclusions
The atomistic effects of grain boundaries are important to fully understand the transport properties of solid electrolytes for all-solid-state batteries. In this study, we have demonstrated the impact of grain boundaries in a widely used solid electrolyte, i.e., Li0.16La0.62TiO3 (LLTO). Our results revealed the following features.1. Low grain boundary formation energies indicate the presence of a high concentration of grain boundaries in polycrystalline LLTO.
2. The calculated bulk ionic conductivity is 0.68 × 10−4 S cm−1 at 300 K, in good agreement with impedance spectroscopy measurements. The grain boundaries studied appear 1–2 orders of magnitude less conductive that the bulk.
3. There is an increase in the Li-ion migration activation energy for all grain boundaries (0.22–0.29 eV) compared to the bulk (0.21 eV). These results help to rationalise on why previously calculated activation energies for bulk LLTO have been consistently underestimated compared to experiment.
4. Based upon our calculations, a model that describes the effect of grain size on the ionic conductivity has been used to show that the conductivity of the material is strongly linked to the grain size of the material.
The atomic-scale insights presented here qualify and quantify grain boundary resistance in a solid electrolyte for Li-ion battery applications and are generally application to a range of materials and applications, e.g., solid oxide fuel cells and electrolysers. Enhancing our understanding of grain boundaries and their influence on Li-ion transport is crucial for the future optimisation of new solid electrolytes for all-solid-state batteries.
Author contributions
ARS performed the calculations. ARS and PC discussed the data. ARS analysed the data. ARS and PC wrote the manuscript with contributions from all authors.Conflicts of interest
The authors declare no competing financial interest.Acknowledgements
Computations were run on Balena HPC facility at the University of Bath and the ARCHER UK National Supercomputing Service via our membership of the High-End Computing Materials Chemistry Consortium (HEC MCC) funded by the EPSRC (EP/L000202, EP/R029431). We are grateful to the UK Materials and Molecular Modelling Hub for computational resources, which is partially funded by the EPSRC (EP/P020194/1). P. C. acknowledges funding from the National Research Foundation under his NRF Fellowship NRFF12-2020-0012 and the ANR-NRF NRF2019-NRF-ANR073 Na-MASTER. The Monte Carlo calculations used computing resources provided by STFC Scientific Computing Department's SCARF cluster.References
- Y. Liang, C.-Z. Zhao, H. Yuan, Y. Chen, W. Zhang, J.-Q. Huang, D. Yu, Y. Liu, M.-M. Titirici, Y.-L. Chueh, H. Yu and Q. Zhang, A review of rechargeable batteries for portable electronic devices, InfoMat, 2019, 1(1), 6–32 CrossRef CAS.
- L. Lu, X. Han, J. Li, J. Hua and M. Ouyang, A review on the key issues for lithium-ion battery management in electric vehicles, J. Power Sources, 2013, 226, 272–288 CrossRef CAS.
- J. M. Tarascon and M. Armand, Issues and challenges facing rechargeable lithium batteries, Nature, 2001, 414(6861), 359–367 CrossRef CAS.
- M. Armand and J. M. Tarascon, Building better batteries, Nature, 2008, 451(7179), 652–657 CrossRef CAS.
- Y. Wang, W. D. Richards, S. P. Ong, L. J. Miara, J. C. Kim, Y. Mo and G. Ceder, Design principles for solid-state lithium superionic conductors, Nat. Mater., 2015, 14(10), 1026–1031 CrossRef CAS.
- N.-S. Choi, Z. Chen, S. A. Freunberger, X. Ji, Y.-K. Sun, K. Amine, G. Yushin, L. F. Nazar, J. Cho and P. G. Bruce, Challenges Facing Lithium Batteries and Electrical Double-Layer Capacitors, Angew. Chem., Int. Ed., 2012, 51(40), 9994–10024 CrossRef CAS.
- J. B. Goodenough and Y. Kim, Challenges for Rechargeable Li Batteries, Chem. Mater., 2010, 22(3), 587–603 CrossRef CAS.
- C. Arbizzani, G. Gabrielli and M. Mastragostino, Thermal stability and flammability of electrolytes for lithium-ion batteries, J. Power Sources, 2011, 196(10), 4801–4805 CrossRef CAS.
- D. D. MacNeil, Z. Lu, Z. Chen and J. R. Dahn, A comparison of the electrode/electrolyte reaction at elevated temperatures for various Li-ion battery cathodes, J. Power Sources, 2002, 108(1), 8–14 CrossRef CAS.
- J. C. Bachman, S. Muy, A. Grimaud, H.-H. Chang, N. Pour, S. F. Lux, O. Paschos, F. Maglia, S. Lupart, P. Lamp, L. Giordano and Y. Shao-Horn, Inorganic Solid-State Electrolytes for Lithium Batteries: Mechanisms and Properties Governing Ion Conduction, Chem. Rev., 2016, 116(1), 140–162 CrossRef CAS.
- M. D. Tikekar, S. Choudhury, Z. Tu and L. A. Archer, Design principles for electrolytes and interfaces for stable lithium-metal batteries, Nat. Energy, 2016, 1(9), 16114 CrossRef CAS.
- J. Janek and W. G. Zeier, A solid future for battery development, Nat. Energy, 2016, 1(9), 16141 CrossRef.
- T. Famprikis, P. Canepa, J. A. Dawson, M. S. Islam and C. Masquelier, Fundamentals of inorganic solid-state electrolytes for batteries, Nat. Mater., 2019, 18(12), 1278–1291 CrossRef CAS.
- P. Knauth, Inorganic solid Li ion conductors: An overview, Solid State Ionics, 2009, 180(14), 911–916 CrossRef CAS.
- N. Kamaya, K. Homma, Y. Yamakawa, M. Hirayama, R. Kanno, M. Yonemura, T. Kamiyama, Y. Kato, S. Hama, K. Kawamoto and A. Mitsui, A lithium superionic conductor, Nat. Mater., 2011, 10(9), 682–686 CrossRef CAS.
- S. Ohno, A. Banik, G. F. Dewald, M. A. Kraft, T. Krauskopf, N. Minafra, P. Till, M. Weiss and W. G. Zeier, Materials design of ionic conductors for solid state batteries, Prog. Energy, 2020, 2(2), 022001 CrossRef.
- R. Murugan, V. Thangadurai and W. Weppner, Fast Lithium Ion Conduction in Garnet-Type Li7La3Zr2O12, Angew. Chem., Int. Ed., 2007, 46(41), 7778–7781 CrossRef CAS.
- P. Canepa, J. A. Dawson, G. Sai Gautam, J. M. Statham, S. C. Parker and M. S. Islam, Particle Morphology and Lithium Segregation to Surfaces of the Li7La3Zr2O12 Solid Electrolyte, Chem. Mater., 2018, 30(9), 3019–3027 CrossRef CAS.
- M. Murayama, R. Kanno, M. Irie, S. Ito, T. Hata, N. Sonoyama and Y. Kawamoto, Synthesis of New Lithium Ionic Conductor Thio-LISICON—Lithium Silicon Sulfides System, J. Solid State Chem., 2002, 168(1), 140–148 CrossRef CAS.
- Y. Kato, S. Hori, T. Saito, K. Suzuki, M. Hirayama, A. Mitsui, M. Yonemura, H. Iba and R. Kanno, High-power all-solid-state batteries using sulfide superionic conductors, Nat. Energy, 2016, 1(4), 16030 CrossRef CAS.
- Y. Mo, S. P. Ong and G. Ceder, First Principles Study of the Li10GeP2S12 Lithium Super Ionic Conductor Material, Chem. Mater., 2012, 24(1), 15–17 CrossRef CAS.
- Z. Deng, G. Sai Gautam, S. K. Kolli, J.-N. Chotard, A. K. Cheetham, C. Masquelier and P. Canepa, Phase Behavior in Rhombohedral NaSiCON Electrolytes and Electrodes, Chem. Mater., 2020, 32(18), 7908–7920 CrossRef CAS.
- Y. Inaguma, C. Liquan, M. Itoh, T. Nakamura, T. Uchida, H. Ikuta and M. Wakihara, High ionic conductivity in lithium lanthanum titanate, Solid State Commun., 1993, 86(10), 689–693 CrossRef CAS.
- Y. Inaguma, L. Chen, M. Itoh and T. Nakamura, Candidate compounds with perovskite structure for high lithium ionic conductivity, Solid State Ionics, 1994, 70–71, 196–202 CrossRef CAS.
- M. Yashima, M. Itoh, Y. Inaguma and Y. Morii, Crystal Structure and Diffusion Path in the Fast Lithium-Ion Conductor La0.62Li0.16TiO3, J. Am. Chem. Soc., 2005, 127(10), 3491–3495 CrossRef CAS.
- Y. Zhang, Z. Zheng, X. Liu, M. Chi and Y. Wang, Fundamental Relationship of Microstructure and Ionic Conductivity of Amorphous LLTO as Solid Electrolyte Material, J. Electrochem. Soc., 2019, 166(4), A515–A520 CrossRef CAS.
- A. R. Symington, J. Purton, J. Statham, M. Molinari, M. S. Islam and S. C. Parker, Quantifying the impact of disorder on Li-ion and Na-ion transport in perovskite titanate solid electrolytes for solid-state batteries, J. Mater. Chem. A, 2020, 8(37), 19603–19611 RSC.
- G.-y. Adachi, N. Imanaka and S. Tamura, Ionic Conducting Lanthanide Oxides, Chem. Rev., 2002, 102(6), 2405–2430 CrossRef CAS.
- C. Ma, K. Chen, C. Liang, C.-W. Nan, R. Ishikawa, K. More and M. Chi, Atomic-scale origin of the large grain-boundary resistance in perovskite Li-ion-conducting solid electrolytes, Energy Environ. Sci., 2014, 7(5), 1638–1642 RSC.
- C. Uhlmann, P. Braun, J. Illig, A. Weber and E. Ivers-Tiffée, Interface and grain boundary resistance of a lithium lanthanum titanate (Li3xLa2/3−xTiO3, LLTO) solid electrolyte, J. Power Sources, 2016, 307, 578–586 CrossRef CAS.
- J.-F. Wu and X. Guo, Origin of the low grain boundary conductivity in lithium ion conducting perovskites: Li3xLa0.67−xTiO3, Phys. Chem. Chem. Phys., 2017, 19(8), 5880–5887 RSC.
- A. R. Symington, M. Molinari, J. Statham, J. Wu and S. C. Parker, The role of dopant segregation on the oxygen vacancy distribution and oxygen diffusion in CeO2 grain boundaries, J. Phys.: Energy, 2019, 1(4), 042005 CAS.
- A. R. Symington, M. Molinari, N. A. Brincat, N. R. Williams and S. C. Parker, Defect segregation facilitates oxygen transport at fluorite UO2 grain boundaries, Philos. Trans. R. Soc., A, 2019, 377(2152), 20190026 CrossRef CAS.
- Z.-P. Li, T. Mori, G. J. Auchterlonie, J. Zou and J. Drennan, Direct evidence of dopant segregation in Gd-doped ceria, Appl. Phys. Lett., 2011, 98(9), 093104 CrossRef.
- X. Guo and R. Waser, Electrical properties of the grain boundaries of oxygen ion conductors: Acceptor-doped zirconia and ceria, Prog. Mater. Sci., 2006, 51(2), 151–210 CrossRef CAS.
- Z. Cheng, B. J. Sherman and C. S. Lo, Carbon dioxide activation and dissociation on ceria (110): A density functional theory study, J. Chem. Phys., 2013, 138(1), 014702 CrossRef.
- S. Galmarini, U. Aschauer, P. Bowen and S. C. Parker, Atomistic Simulation of Y-Doped α-Alumina Interfaces, J. Am. Ceram. Soc., 2008, 91(11), 3643–3651 CrossRef CAS.
- G. W. Watson, E. T. Kelsey, N. H. de Leeuw, D. J. Harris and S. C. Parker, Atomistic simulation of dislocations, surfaces and interfaces in MgO, J. Chem. Soc., Faraday Trans., 1996, 92(3), 433–438 RSC.
- S. von Alfthan, N. A. Benedek, L. Chen, A. Chua, D. Cockayne, K. J. Dudeck, C. Elsässer, M. W. Finnis, C. T. Koch, B. Rahmati, M. Rühle, S.-J. Shih and A. P. Sutton, The Structure of Grain Boundaries in Strontium Titanate: Theory, Simulation, and Electron Microscopy, Annu. Rev. Mater. Res., 2010, 40(1), 557–599 CrossRef CAS.
- O. Kienzle, M. Exner and F. Ernst, Atomistic Structure of Σ = 3, (111) Grain Boundaries in Strontium Titanate, Phys. Status Solidi A, 1998, 166(1), 57–71 CrossRef CAS.
- D. Srivastava, F. Azough, R. Freer, E. Combe, R. Funahashi, D. M. Kepaptsoglou, Q. M. Ramasse, M. Molinari, S. R. Yeandel, J. D. Baran and S. C. Parker, Crystal structure and thermoelectric properties of Sr–Mo substituted CaMnO3: a combined experimental and computational study, J. Mater. Chem. C, 2015, 3(47), 12245–12259 RSC.
- S. R. Yeandel, M. Molinari and S. C. Parker, The impact of tilt grain boundaries on the thermal transport in perovskite SrTiO3 layered nanostructures. A computational study, Nanoscale, 2018, 10(31), 15010–15022 RSC.
- S. Sasano, R. Ishikawa, K. Kawahara, T. Kimura, Y. H. Ikuhara, N. Shibata and Y. Ikuhara, Grain boundary Li-ion conductivity in (Li0.33La0.56)TiO3 polycrystal, Appl. Phys. Lett., 2020, 116(4), 043901 CrossRef CAS.
- T. Smith, R. S. Rana, P. Missiaen, K. D. Rose, A. Sahni, H. Singh and L. Singh, High bat (Chiroptera) diversity in the Early Eocene of India, Naturwissenschaften, 2007, 94, 1003–1009 CrossRef CAS.
- S. Nosé, A unified formulation of the constant temperature molecular dynamics methods, J. Chem. Phys., 1984, 81(1), 511–519 CrossRef.
- W. G. Hoover, Canonical dynamics: Equilibrium phase-space distributions, Phys. Rev. A: At., Mol., Opt. Phys., 1985, 31(3), 1695–1697 CrossRef.
- A. Pedone, G. Malavasi, M. C. Menziani, A. N. Cormack and U. Segre, A New Self-Consistent Empirical Interatomic Potential Model for Oxides, Silicates, and Silica-Based Glasses, J. Phys. Chem. B, 2006, 110(24), 11780–11795 CrossRef CAS.
- Y. Deng, C. Eames, J.-N. Chotard, F. Lalère, V. Seznec, S. Emge, O. Pecher, C. P. Grey, C. Masquelier and M. S. Islam, Structural and Mechanistic Insights into Fast Lithium-Ion Conduction in Li4SiO4–Li3PO4 Solid Electrolytes, J. Am. Chem. Soc., 2015, 137(28), 9136–9145 CrossRef CAS.
- S. M. Wood, C. Eames, E. Kendrick and M. S. Islam, Sodium Ion Diffusion and Voltage Trends in Phosphates Na4M3(PO4)2P2O7 (M = Fe, Mn, Co, Ni) for Possible High-Rate Cathodes, J. Phys. Chem. C, 2015, 119(28), 15935–15941 CrossRef CAS.
- Y. Deng, C. Eames, B. Fleutot, R. David, J.-N. Chotard, E. Suard, C. Masquelier and M. S. Islam, Enhancing the Lithium Ion Conductivity in Lithium Superionic Conductor (LISICON) Solid Electrolytes through a Mixed Polyanion Effect, ACS Appl. Mater. Interfaces, 2017, 9(8), 7050–7058 CrossRef CAS.
- Y. Deng, C. Eames, L. H. B. Nguyen, O. Pecher, K. J. Griffith, M. Courty, B. Fleutot, J.-N. Chotard, C. P. Grey, M. S. Islam and C. Masquelier, Crystal Structures, Local Atomic Environments, and Ion Diffusion Mechanisms of Scandium-Substituted Sodium Superionic Conductor (NASICON) Solid Electrolytes, Chem. Mater., 2018, 30(8), 2618–2630 CrossRef CAS.
- J. A. Dawson, P. Canepa, T. Famprikis, C. Masquelier and M. S. Islam, Atomic-Scale Influence of Grain Boundaries on Li-Ion Conduction in Solid Electrolytes for All-Solid-State Batteries, J. Am. Chem. Soc., 2018, 140(1), 362–368 CrossRef CAS.
- N. R. Williams, M. Molinari, S. C. Parker and M. T. Storr, Atomistic investigation of the structure and transport properties of tilt grain boundaries of UO2, J. Nucl. Mater., 2015, 458, 45–55 CrossRef CAS.
- M. L. Martínez-Sarrión, L. Mestres, M. Morales and M. Herraiz, Crystal Chemistry and Conductivity Studies in the System La0.5+x+yLi0.5−3xTi1−3yCr3yO3, J. Solid State Chem., 2000, 155(2), 280–285 CrossRef.
- A. I. Ruiz, M. L. López, M. L. Veiga and C. Pico, Electrical properties of La1.33−xLi3xTi2O6 (0.1 < x < 0.3), Solid State Ionics, 1998, 112(3), 291–297 CrossRef CAS.
- A. I. Ruiz, M. L. López, M. L. Veiga and C. Pico, Structural Refinement by Neutron Diffraction of La1.12Li0.62Ti2O6, J. Solid State Chem., 1999, 148(2), 329–332 CrossRef CAS.
- J. A. Dawson and I. Tanaka, Local Structure and Energetics of Pr- and La-Doped SrTiO3 Grain Boundaries and the Influence on Core–Shell Structure Formation, J. Phys. Chem. C, 2014, 118(44), 25765–25778 CrossRef CAS.
- T. Oyama, N. Wada, H. Takagi and M. Yoshiya, Trapping of oxygen vacancy at grain boundary and its correlation with local atomic configuration and resultant excess energy in barium titanate: A systematic computational analysis, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 82(13), 134107 CrossRef.
- B. Joakim Nyman, E. E. Helgee and G. Wahnström, Oxygen vacancy segregation and space-charge effects in grain boundaries of dry and hydrated BaZrO3, Appl. Phys. Lett., 2012, 100(6), 061903 CrossRef.
- Y. Harada, T. Ishigaki, H. Kawai and J. Kuwano, Lithium ion conductivity of polycrystalline perovskite La0.67−xLi3xTiO3 with ordered and disordered arrangements of the A-site ions, Solid State Ionics, 1998, 108(1), 407–413 CrossRef CAS.
- C.-h. Chen and J. Du, Lithium Ion Diffusion Mechanism in Lithium Lanthanum Titanate Solid-State Electrolytes from Atomistic Simulations, J. Am. Ceram. Soc., 2015, 98(2), 534–542 CrossRef CAS.
- J. A. Dawson, P. Canepa, M. J. Clarke, T. Famprikis, D. Ghosh and M. S. Islam, Toward Understanding the Different Influences of Grain Boundaries on Ion Transport in Sulfide and Oxide Solid Electrolytes, Chem. Mater., 2019, 31(14), 5296–5304 CrossRef CAS.
- S. Yu and D. J. Siegel, Grain Boundary Contributions to Li-Ion Transport in the Solid Electrolyte Li7La3Zr2O12 (LLZO), Chem. Mater., 2017, 29(22), 9639–9647 CrossRef CAS.
- M. Lachal, R. Bouchet, A. Boulineau, S. Surblé, C. Rossignol, F. Alloin and S. Obbade, Remarkable impact of grains boundaries on the chemical delithiation kinetics of LiFePO4, Solid State Ionics, 2017, 300, 187–194 CrossRef CAS.
- B. Feng, N. R. Lugg, A. Kumamoto, Y. Ikuhara and N. Shibata, Direct Observation of Oxygen Vacancy Distribution across Yttria-Stabilized Zirconia Grain Boundaries, ACS Nano, 2017, 11(11), 11376–11382 CrossRef CAS.
- H. Khassaf, S. K. Yadavalli, Y. Zhou, N. P. Padture and A. I. Kingon, Effect of Grain Boundaries on Charge Transport in Methylammonium Lead Iodide Perovskite Thin Films, J. Phys. Chem. C, 2019, 123(9), 5321–5325 CrossRef CAS.
- S. Kim, J. Fleig and J. Maier, Space charge conduction: Simple analytical solutions for ionic and mixed conductors and application to nanocrystalline ceria, Phys. Chem. Chem. Phys., 2003, 5(11), 2268–2273 RSC.
- J. Maier, Nanoionics: ion transport and electrochemical storage in confined systems, Nat. Mater., 2005, 4(11), 805–815 CrossRef CAS.
- Y. Inaguma, J. Yu, T. Katsumata and M. Itoh, Lithium Ion Conductivity in a Perovskite Lanthanum Lithium Titanate Single Crystal, J. Ceram. Soc. Jpn., 1997, 105(1222), 548–550 CrossRef CAS.
- S. Stramare, V. Thangadurai and W. Weppner, Lithium Lanthanum Titanates:
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) A Review, Chem. Mater., 2003, 15(21), 3974–3990 CrossRef CAS.
A Review, Chem. Mater., 2003, 15(21), 3974–3990 CrossRef CAS. - H. Geng, A. Mei, Y. Lin and C. Nan, Effect of sintering atmosphere on ionic conduction and structure of Li0.5La0.5TiO3 solid electrolytes, Mater. Sci. Eng. C, 2009, 164(2), 91–95 CrossRef CAS.
- K. Ohara, Y. Kawakita, L. Pusztai, L. Temleitner, S. Kohara, N. Inoue and S. Takeda, Structural disorder in lithium lanthanum titanate: the basis of superionic conduction, J. Phys.: Condens. Matter, 2010, 22(40), 404203 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/d0ta11539h |
| This journal is © The Royal Society of Chemistry 2021 |