A pressure induced reversal to the 9R perovskite in Ba₃MoNbO_8.5

Abstract

Ba₃MoNbO_8.5 is an oxide ion conductor with an unconventional hybrid crystal structure that is intermediate between the 9R-perovskite (A₃B₃O₉) and the palmierite (A₃B₂O₈). The crystal structure is highly disordered with vacancies distributed across two cation (M(1) and M(2)) and oxygen sites (O(2) and O(3)), with Mo and Nb in variable coordinate environments. M(1)–O(1)–O(2) and M(2)–O(1) sites are associated with the formation of (Mo,Nb)O₆ octahedra, whilst tetrahedral units are composed of M(1)–O(1)–O(3) atoms. Upon increasing the temperature, the structure undergoes a change in occupancy in favour of the O(3) site, which results in a change in metal co-ordination as the tetrahedral to octahedral ratio increases. We demonstrate that the structure can also be tuned using externally applied pressure. Variable pressure studies ≤4.8 GPa indicate that densification of the unit cell induces the reverse effect, as the occupancy of the O(2) site increases and the palmierite contribution is suppressed. Our results strongly suggest that by 5.2 GPa the O(3) position will be completely empty as the 9R unit cell stabilises with a network of octahedral MO₆ units. Pressure induces a flattening of M(1)O₄ tetrahedra in the palmierite layers, as M(1)O₆ octahedra become more regular in geometry. Bond valence site energy calculations show that pressure increases the height of all energy barriers to migration along the three-dimensional diffusion pathways, increasing the energy of the dominant pathway from 0.35 to 0.95 eV. The relaxation energy, E₂, disappears above 2.8 GPa, when the average polyhedral distortion (σ(R)) falls below 0.07 Å, indicating the existence of a critical minimum. The bulk modulus of Ba₃MoNbO_8.5 is exceptionally low (50(2) GPa) for a layered oxide material and is closer to that of the halide perovskites. These results demonstrate a high degree of flexibility, in terms of the softness of the lattice and variable metal coordination, emphasising the potential for these materials in multi sensory and thin film applications.

---

Introduction

Solid-state oxide ion conducting materials are an essential component of many modern technologies, such as solid oxide fuel cells (SOFCs), solid oxide electrolyser cells (SOECs) and sensors.^1,2 Therefore, much research is aimed at discovering novel electrolyte materials which demonstrate competitive oxide ion conductivity at intermediate temperatures (300–600 °C). One such material is Ba₃MoNbO_8.5, which exhibits a significant bulk oxide ion conductivity of 2.2 × 10⁻³ S cm⁻¹ at 600 °C and good stability over a wide range of oxygen partial pressures.³ Neutron diffraction data shows that the average structure is a disordered hybrid of the 9R hexagonal perovskite (A₃B₃O₉) and palmierite (A₃B₂O₈) structures shown in Fig. 1. The 9R hexagonal structure consists of nine AO₃ layers stacked along the c-axis in the order (hhc)₃, with trimers of face-sharing BO₆ octahedra connected through corner-sharing. The cation and anion deficient palmierite structure (A₃B₂O₈) arises from the replacement of the cubic-AO₃ layer with an oxygen deficient AO₂ layer. This interrupts the connected trimers of BO₆ octahedra, resulting in layers of isolated BO₄ tetrahedra separated by layers of vacant octahedra. The cation vacancies introduced by the palmierite structure are distributed across two partially occupied metal sites, M(1) and M(2). Incorporation of Mo⁶⁺ and Nb⁵⁺ in a 1 : 1 ratio creates mixed coordination environments due to the competitive occupation of the partially occupied O(2) and O(3) sites within the palmierite-like layers (of average composition [BaO_2.5]). The variable coordination environment of the M(1) site is a key feature for achieving high levels of ionic transport, as the conductivity is heavily influenced by the tetrahedral to octahedral ratio. The ratio increases with temperature and lowers the energy barriers for ionic migration by increasing the number of available migration pathways.⁴ Subsequent pair distribution function (PDF) analysis suggested the alternation of M(1) octahedra and tetrahedra within every set of three polyhedra; in addition to the existence of an intermediate five-fold MO₅ unit.⁵ The temperature dependent inhomogeneous distribution of octahedral and tetrahedral nanodomains was also confirmed at the local level.⁶ This uncorrelated disordered randomisation of occupied and vacant oxygen sites is induced by the fast oxide ion migration at high temperature. A structural rearrangement is observed above 300 °C, resulting in an increase in the occupancy of the M(1) and O(3) sites, and a simultaneous decrease in the occupancy of the M(2) and O(2) sites.⁵ Therefore, the ratio of M(1)O_x tetrahedra : octahedra increases with temperature, coinciding with a decrease in activation energy and enhancement of the ionic conductivity. PDF analysis confirms this trend, showing a higher proportion of local M(1)O₄ tetrahedra at high temperatures compared to M(1)O₆ octahedra. The number of 5-fold coordination sites remained relatively constant throughout the temperature range.⁶ Both Mo⁶⁺ and Nb⁵⁺ are d⁰ cations and are therefore capable of second order Jahn–Teller distortions, thereby inducing out-of-centre displacement and polyhedral distortion effects, which are known to aid oxide ion conductivity.⁷ Furthermore, displacement of the M(1) cation away from the mobile O(2)/O(3) sites, whether by second-order Jahn–Teller distortions or structural change accompanying oxygen/vacancy rearrangement, is also shown to favour oxide ion conductivity.⁸ These structural effects, in addition to the tetrahedral : octahedral ratio, increase with temperature and are mutually supportive in enhancing the ionic transport.

Fig. 1 The change in structure of Ba₃MoNbO_8.5 when tuned by pressure (left) and temperature (right). (a) The change in population of O(2) and O(3) sites with pressure, which favours stabilisation of the 9R-perovskite derivative (shown in (b)). (c) The unit cell of the palmierite structure, which may be tuned with temperature by the increase in fractional occupancy of the O(3) site as shown in (d).⁵ For (b) and (c) Ba atoms (green spheres); Nb1/Mo1 (purple polyhedra); Nb2/Mo2 (grey polyhedra, vacant in the palmierite structure); oxygen (pink spheres).

Here, we report the effect of pressure on the structure of Ba₃MoNbO_8.5 and its influence on the key structural motifs that are known to affect conductivity. The results show that the disordered structure can be tuned by pressure, as densification of the cell promotes a re-distribution of the oxygen population in favour of the O(2) site, increasing the occurrence of 9R-type regions. We demonstrate that the hybridity of the structure can be moved away from the palmierite phase by controlling the distribution across O(2) and O(3) sites. The results strongly suggest that by 5.2 GPa all palmierite character will be completely suppressed and the 9R unit cell will be fully stabilised.

Experimental

Ba₃MoNbO_8.5 samples were prepared by solid-state reaction of stoichiometric amounts of BaCO₃ (99.999%, Sigma-Aldrich), MoO₃ (99.98%, Sigma-Aldrich) and Nb₂O₅ (99.98%, Sigma-Aldrich). The starting materials were ground using a mortar and pestle until homogenous. The resulting powder was pressed into a pellet and calcined in an alumina crucible at 900 °C for 10 hours to decarbonate. The pellet was then reground, pelleted and heated at 1100 °C for 48 hours before being cooled to room temperature at a rate of 5 °C min⁻¹. The latter grinding and heating step was repeated until a phase pure product was obtained. Room-temperature X-ray powder diffraction patterns were collected on a PANalytical X'Pert powder diffractometer equipped with a Cu Kα tube. Data were recorded in the range 20° < 2θ < 65°, with a step size of 0.013°. High pressure time-of-flight (TOF) neutron powder diffraction experiments were performed on the PEARL diffractometer at the ISIS Neutron and Muon Facility (Rutherford Appleton Laboratory, Harwell, Oxford, UK) at room temperature and pressures of 0.1 MPa, 0.9 GPa, 1.7 GPa, 2.8 GPa, 4.3 GPa and 4.8 GPa.⁹ Ba₃MoNbO_8.5 powder was sealed in a titanium–zirconium alloy gasket. Highly transparent zirconia-toughened alumina (ZTA) anvils were used, along with a Pb pressure marker and 4 : 1 perdeuterated methanol:ethanol as a pressure medium. Data were acquired in the TOF range 1500–19 900 μs using the 90 degree detector banks with a total collection time of between 3–6 h at each pressure. The lead equation of state (EOS) used to calculate the pressure was a Birch–Murnaghan equation of the form:where V₀ is the unit cell volume at zero pressure, V the unit cell volume at pressure P, B₀ the zero pressure bulk modulus and B′ is the pressure derivative of the ambient bulk modulus. For Pb, the values were taken to be, B₀ = 42 GPa, B′ = 5.¹⁰ A wavelength-dependent attenuation correction was applied to account for the different sample environment materials before the data were analysed. The relationship between the normalised volume and pressure was fitted with a Birch–Murnaghan function using the EosFit7-GUI software.¹¹

Rietveld analysis was performed using the GSAS/EXPGUI and GSAS-II packages.^12,13 The hybrid 9R polytype-palmierite model was used as a starting model for the low pressure data.^3–5 Difference Fourier maps were created using GSAS/EXPGUI and visualised using VESTA.¹⁴

Bond valence site energy (BVSE) calculations were performed using the softBV program.^15,16 Using the structural models from Rietveld refinement as the input, BVSE landscapes for the interaction of a test O²⁻ ion were calculated for a dense grid of points with a resolution of 0.1 Å. BVSE models of migration barriers were plotted from the calculated energy profiles of the pathway segments.

Analysis of minimum bonding ellipsoids using the PIEFACE software was employed to evaluate the effect of pressure on the relaxation of the average metal coordination polyhedra.¹⁷ Polyhedral distortion was quantified by the standard deviation, σ(R), of the three principal ellipsoid's radii (R_x, R_y, and R_z).

Results and discussion

Crystal structure

Laboratory XRD on the samples prepared for the neutron diffraction study showed peaks corresponding to single-phase 9-layered Ba₃MoNbO_9.5. The pattern could be indexed on the trigonal R3̄m H space group with unit cell parameters of a = 5.931(2) Å and c = 21.110(7) Å. The material obtained was an off-white colour which could be stored at room temperature in air with no decomposition observed. Fig. 2 shows the neutron diffraction data and Rietveld refinement fit obtained for Ba₃MoNbO_8.5 at ∼0 and 4.8 GPa. The model previously reported for Ba₃MoNbO_8.5 was used as a basis for the variable pressure Rietveld analysis⁵ with the addition of the split M(2) 6c site from ref. 5. The highly disordered structure is intermediate between the 9R perovskite and palmierite (Fig. 2b and c respectively), with vacancies distributed across two cation (M1 and M2) and two oxygen sites (O2 and O3). The intermediate structure arises as the O(2) and O(3) positions (depicted in Table S1†) cannot be simultaneously occupied. An excellent fit to this model was obtained at all pressures. There is no evidence of a phase transition over the pressure range measured, there was no evidence of additional peaks or peak splitting. The complex sample environment contained phases of Pb, Al₂O₃ and ZrO₂, which were incorporated into the fit and are represented by the additional reflection markers in Fig. 2.

Fig. 2 The Rietveld refinement of Ba₃MoNbO_8.5 at 0.1 MPa (top) and 4.8 GPa (bottom). Black dots indicate the observed data, the red line the Rietveld fit and background function, the purple line is the difference between the observed and the calculated patterns. The bars are the reflection positions of the sample environment and sample; from top to bottom – ZrO₂ (blue), Ba₃MoNbO_8.5 (black), Pb (green) and Al₂O₃ (orange).

Nb⁵⁺ and Mo⁶⁺ possess similar relative scattering powers for neutrons therefore it is not possible to resolve their independent contributions. It is assumed that the cations are disordered over the 6c sites and will be referred to as M(1) and M(2). Atomic displacement parameters, U_jj, were refined anisotropically for all positions with the exception of the O(3) 36i split site, which required a U_iso parameter as previously reported.^3,4 Constraints were applied to the U_jj values on the Ba, Nb/Mo and O(1)/O(2) sites. The refined atomic displacement values for the low pressure data within the gasket were in good agreement with previous reports.^3,4 The in-plane atomic displacement values, U₁₁ : U₂₂, for each M and O site decreased with pressure, with a concurrent increase in U₃₃. The constrained values for M(1) and M(2) sites show U₃₃ > U₁₁ : U_22, as they are positioned directly above (and below) the active O(2) and O(3) sites. Displacement of O(1) and O(2) atoms is clearly larger in the ab plane than along c, indicating mainly two-dimensional motion. As previously reported, the O(3) site has a large U_iso value (∼0.03–0.05 Ų) due to the presence of positional disorder. This disorder is modelled using a split 36i site. The corresponding fit parameters, refined lattice constants, bond lengths and angles at each pressure are given in Tables S1–S3.† The unit cell parameters, a = b ≠ c, decrease upon increasing pressure with no discontinuities observed. The axial compressibility, k, of the cell parameters was calculated from the linear fit of normalised plots of a/a₀ and c/c₀, where for example, k_a = −1a(da/dP) (Fig. S1†). Values of k = 5.6 × 10⁻³ GPa⁻¹ were obtained for both a and c, revealing that the compression is isotropic and that the structure displays an equal degree of elasticity in all directions. While the majority of perovskites exhibit some degree of axial anisotropy under pressure, elastically isotropic and quasi-isotropic structures do exist, for example SrZrO₃.¹⁸ A second order Birch–Murnaghan fit to the normalised volume data, V/V₀, is shown in Fig. S2.† Analysis using the EOSFit7 (ref. 11) software revealed a bulk modulus (K₀) of 50(1) GPa for the refined V₀ value of 644.8(6) ų, when the pressure derivative (K′) was fixed at 4. The bulk modulus at ambient pressure signifies a material's susceptibility to pressure; and is an indicator of its inherent flexibility. The bulk modulus is noticeably lower than for most layered oxide materials which exhibit K₀ > 150 GPa.^19–21 In contrast, halide perovskites are well known for their remarkably soft lattices and typically low K₀ values (<30 GPa).^22–24 Such a low bulk modulus enhances their photophysical properties under pressure and allows halides to be easily developed into thin films, which is useful during solar cell production. The relatively low bulk modulus of Ba₃MoNbO_8.5 suggests that it is comparably much softer than the majority of oxide materials and an excellent candidate for thin film devices. Such a high degree of lattice compressibility allows for the systematic structural tuning of Ba₃MoNbO_8.5 without adjusting the composition; and explains why such facile structural transformations are enabled with both pressure and temperature.

Ba₃MoNbO_8.5 is known to be highly disordered with respect to its variable cation and anion environment, therefore, vacancies were included in the initial model for Rietveld analysis according to the distribution reported elsewhere.³ The Ba(1), Ba(2) and O(1) positions refined to within ±1% of their full occupancy and were therefore fixed at 1.0. The fractional occupancies of M(1), M(2), O(2) and O(3) sites were refined and the results for the 0.1 MPa data are in good agreement with other reports for this compound at ambient conditions. The change in the occupancy of the two oxygen sites with increasing pressure is in stark contrast to that which is observed with temperature, as a reverse structural modification occurs (Fig. 1d). As pressure is applied, the occupancy of the O(3) position decreases with a concurrent increase in the population of the O(2) site as depicted in Fig. 1a. The occupancy of these positions defines the hybridity of Ba₃MoNbO_8.5, as the O(3) position is specific to the palmierite unit cell. The observed pressure response represents a continuous decrease in the average number of (Mo,Nb)O₄ tetrahedra, from 58% at 0.1 MPa to just 6% at 4.8 GPa (Fig. 3). Moreover, extrapolation of the data in Fig. 2a indicates that a small increase in pressure (of just 0.4 GPa) to 5.2 GPa would render the O(3) site completely empty; allowing full stabilisation of the 9R perovskite phase and complete suppression of the palmierite. Upon decompression, the oxygen positions redistribute back to their ambient positions, giving O(2) and O(3) refined fractional occupation values of 0.473(3) and 0.09(1) respectively (χ² = 1.1, wR_p = 3.10%). Therefore, the effects of pressure are reversible, and one can shift the phase back towards equilibrium with no lasting change in crystal structure. The re-distribution of vacancies within the cubic layers is supported by comparing the difference Fourier maps at 0.1 MPa and 4.8 GPa (shown in the insets of Fig. 3). The maps were produced from the Rietveld fit with the O(3) site occupancy fixed at zero. The resultant images are viewed along the [001] direction at z = 0. The ambient pressure data presents significant scattering density at the O(3) position (0, 0, z), with a clear decrease in scattering density at this site for the data at 4.8 GPa. This confirms the depopulation of oxygen ions from the 36i position, as they redistribute onto the O(2) site. In addition to oxygen vacancies, there is also considerable disorder present on the cation sites. The cation vacancies undergo a continuous redistribution with temperature, as the M(1) site increases in occupancy and the M(2) sites decreases. However, the cation lattice is much more robust to applied pressure and no discernible change in fractional occupancy occurs across these sites ≤3.8 GPa (Fig. S4†). Pressure is therefore inducing a switching of the average co-ordination environment of M(1) cations from CN 4 to CN 6, rather than the formation of additional M(2)O₆ octahedra. These results emphasise the inherent flexibility of the hybrid structure of Ba₃MoNbO_8.5, as its complex polymorphism can be subtly tuned with both pressure and temperature.

Fig. 3 The decrease in the number of average tetrahedral environments expressed as a percentage of total polyhedra. Insets show the difference Fourier maps, at ambient pressure and high pressure, as seen along the [001] direction at z = 0.

All bond lengths show a general decrease upon compression with a non-linear variation. A comparison with other oxides can be made when interpreting the changes in A–O bond lengths with pressure, as a relationship exists between the bulk modulus (B₀), cation formal charge (Z_A) and the mean cation–O distance (d_A) according to the equation:²⁵

For Ba₃MoNbO_8.5,Z_A = 2 and d_Ba–O ∼ 2.84 Å, giving a bulk modulus of ∼53 GPa. This is in excellent agreement with our observed value of 50(2) GPa from the Birch–Murnaghan fit in Fig. S3,† therefore, we conclude that the compressibility of the structure is primarily due to the larger and softer Ba–O bonds rather than M–O bonds.

Polyhedral distortion

It is well known that polyhedral distortion plays an important role in the ionic conductivity of Ba₃MoNbO_8.5.⁶ For example, replacing Mo with the weaker distorter, W, results in a significant reduction in the oxide ion conductivity at low temperature. In Ba₃WNbO_8.5 and Ba₃W_1.2Nb_0.8O_8.6 the second order Jahn–Teller distortion is supressed which, along with the increase in the octahedral to tetrahedral ratio, raises the activation energy for migration.^26,27 All MO₆ octahedra tend towards more ideal geometry (90°) over the pressure range measured. O(1)–M(2)–O(1) angles show two values which increase from 84.939(9)° to 85.94(4)° and decrease from 95.061(9)° to 94.06(4)°. The M(1) octahedral environment is defined by the O(1)–M(1)–O(2) and O(2)–M(1)–O(2) angles (γ and δ respectively) which are shown in Fig. S5.† The M(1) atoms also occupy the centre of the tetrahedra; coordinated with 1 × axial M(1)–O(3) and 3 × intra-planar M(1)–O(1) bonds. The tetrahedra are defined by the angle β-O(1)–M(1)–O(3) which is the average of the three angles presented in Table S3.† The already distorted β-O(1)–M(1)–O(3) angle increases from 114.551(5)° to 117.5(2)° (Fig. 4) as an opening of the tetrahedra occurs. Moreover, the α-O(1)–M(1)–O(1) environment which represents the prism formed by three O(1) atoms within the plane, tend towards more square planar geometry. One can observe that the pressure dependence of the β, γ and δ angles changes rapidly above 2.8 GPa, indicating that this pressure represents a threshold during the compression of the polyhedra. With increasing pressure, O(1) atoms gradually move in an upwards trajectory, parallel to the c axis, as the M(1) atom navigates downwards. These synonymous movements are represented by the evolving change in z co-ordinates given in Table S1,† and along with the trends in bond angles, correspond to a flattening of the tetrahedra within the cubic layers. This was supported by fitting the smallest volume ellipsoid around the polyhedra and defining the distortion in terms of the three-principle axis, and its orientation in space. This was carried out using EllipsoidGUI within the PIEFACE software package.¹⁷ The results are expressed by the standard deviation, σ(R), of the ellipsoid radii R_x, R_y and R_z. The average polyhedral distortion decreases with pressure from 0.072 Å to 0.067 Å indicating that overall, the second order Jahn–Teller distortion is being suppressed. However, examination of the individual environments indicates that M(1)O₄ tetrahedra become increasingly distorted with pressure, as σ(R) increases from 0.061 Å to 0.067 Å. Conversely, the M(1)O₆ octahedra undergo a significant decrease in distortion, as σ(R) falls from 0.083 Å to 0.067 Å. For d⁰ transition metal complexes, the crystal field stabilisation energy (CFSE) for tetrahedral and octahedral coordination with oxygen is zero for both environments, yet, an increase in pressure for variable coordinate metals generally leads to complexes with a higher number of metal–oxygen bonds as the unit cell becomes increasingly densified. The generation of octahedra is facilitated by the increased distortion and flattening of the co-existing tetrahedra, as a consequence of this densification. It is possible that the tetrahedral distortion is key to the compression mechanism, as the distortion resulting from the relatively strong cation–anion bonding acts to lower the kinetic energy barriers for octahedrally coordinated cations, similar to that seen in quartz and quartz-like structures such as α-GeO₂.²⁸ The shape of the variable coordinate M(1) polyhedra can be described using the ellipsoid shape parameter, S. As previously reported the octahedra form more oblate shaped environments, while the tetrahedra are axially stretched. S increases with pressure, indicating that both polyhedral environments become more axially stretched parallel to the c axis, and increasingly prolate in shape as the unit cell is compressed. This explains the change in thermal displacement parameters of the metal atoms in Table S1.†U₁₁ : U₂₂ decrease with pressure, as motion is restricted within the plane, and motion in the z direction increases (corresponding to U₃₃) as the MO_x polyhedra become more axially stretched.

Fig. 4 The change in β-O(1)–M(1)–O(3) angle with pressure. Inset shows the evolving tetrahedral environment as β and α increase and decrease, respectively. The geometry distorts away from the regular tetrahedron shape, tending towards increasingly square planar geometry. The movement of the O atoms indicates a flattening of the tetrahedra.

Bond valence analysis and the effect of pressure on migration pathways

Bond-valence site energy (BVSE) calculations were carried out in order to assess the impact of pressure on the energy landscape of Ba₃MoNbO_8.5 and available migration pathways. The softBV programme was used to analyse the refined structural models at all pressures. Three possible conduction pathways persist over the pressure range measured, with sizeable connectivity between and O(2)–O(3), O(1)–O(2) and O(1)–O(1) positions represented by E₁, E₃ and E₄ respectively. The dominant conduction pathway (E₁) is located within the ab plane and carries the lowest associated BVSE barrier to conduction. The two-dimensional pathway can be viewed along the c axis in Fig. S7.† This is in accordance with previous reports and confirms that the main conduction pathway in Ba₃MoNbO_8.5 is two-dimensional within the palmierite-like layers. Previous BVSE and maximum entropy studies indicate diffusion occurs over the partially occupied face of M(1)O₆ octahedra resulting in the formation of newly coordinated M(1)O_4–5 units.^29,30 The saddle point associated with E₁ corresponds to oxide ion exchange along the connected distribution of O(2)/O(3) oxygen sites, therefore, the magnitude of E₁ will be influenced by the average distribution of oxygen atoms across these positions. The conductivity of Ba₃MoNbO_8.5 is known to increase as the ratio of tetrahedra increases. An increase in the number of lower coordination geometries is known to provide more favourable and dynamic environments for oxygen exchange between metal units. In corroboration, as the concentration of tetrahedra within the structure reaches a maximum at ∼500 °C, there is a reduction in the activation energy from 1.21 eV to 0.73 eV.³ Pressure induces an opposite response, as the ratio of tetrahedra to octahedra decreases, and the change in relative bond valence energy barriers for O(2)–O(3) diffusion increases, as shown by the increase in height of E₁ in Fig. 5. The number of tetrahedra within the structure falls from 58% at 0.1 MPa to 6% under 4.8 GPa of applied pressure, as the fractional occupancy of the O(2) position rises, and there is an associated increase in E₁ from 0.35 eV to 0.95 eV. The 2-dimensional migration pathway becomes blocked as the network of tetrahedra is disrupted and there is reduced exchange between O(2)/O(3) sites. When P = 4.2 GPa the E₁ energy barrier is 0.82 eV, with an associated tetrahedral percentage of 18%. This is synonymous with Ba₃WNbO_8.5 at ambient pressure (E₁ = 0.82 eV with 14% tetrahedra²⁶) indicating that the energy barrier for 2-dimensional migration within these systems is directly proportional to the average O(2)/O(3) population and the resulting tetrahedral percentage. Furthermore, a second energy barrier (E₂) can be observed up to 2.8 GPa. The evolution of E₂ is shown in Fig. 6. E₂ is associated with the relaxation of metal polyhedra during oxygen diffusion, and its height is linked to the average distortion of M(1)O_x units and hence, σ(R).³⁰E₂ decreases with pressure as the increased concentration of octahedra become more regular in geometry. Above 2.8 GPa, E₂ disappears as the distortion drops below a critical minimum (∼0.07 Å), and E₂ is no longer relevant within the energy landscape of Ba₃MoNbO_8.5. The suppression of E₂ has a clear influence on the dominant 2D conduction pathway, as a crossover can be seen at this critical pressure (2.8 GPa) in the variation of E₁ (Fig. 7). The energy barrier for diffusion across O(2) and O(3) sites increases steeply above this point suggesting that the absence of the relaxation energy drives up the energy barriers to migration as the motional enthalpy of ions is increased. The analogous compound, Ba₃WNbO_8.5,^26,30 has a low value of σ(R) ∼ 0.047 Å and no sizeable E₂ barrier, therefore, it can be ascertained that the E₂ barrier is likely absent for members of the Ba₃MNbO_8.5 system with σ(R) values below 0.07 Å. It is also worth noting that there is a steep change in bond angle variances >2.8 GPa. Above this pressure, the E₂ energy barrier disappears and the distortion represented by σ(R) falls below the critical minimum, indicating that this pressure represents a threshold for polyhedral distortion effects.

Fig. 5 The evolving energy landscape of Ba₃MoNbO_8.5 with pressure. E₁ is the dominant conduction pathway within the 2-dimensional palmierite layers. E₃ and E₄ are higher energy pathways parallel to the c axis representing conductivity between O1/O1 and O1/O2 sites.

Fig. 6 The energy profile of E₁ and E₂ at 0.1 MPa and 2.8 GPa. The elimination of E₂ at 2.8 GPa is shown in the inset.

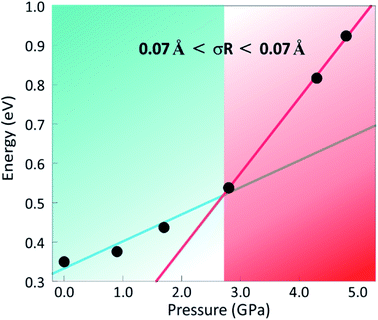Fig. 7 The change in E₁ (eV) with pressure indicating a crossover at 2.8 GPa, above which a steep increase in E₁ occurs upon elimination of the E₂ relaxation energy as σ(R) falls below 0.07 Å.

The overall conductivity of the Ba₃M′M′′O_8.5 family is also dependent on O(1)–O(1) and O(1)–O(2) migratory pathways. Both pathways represent migration parallel to the c axis, facilitating transport across a three-dimensional network which is preserved upon compression of the unit cell. Two Ba and one M cation form a bottleneck window through which oxygen ions migrate, similar to LSGM-electrolytes.³² As the O(1) site remains fully occupied over the pressure range measured, it is likely that any diffusion between the apical oxygen sites occurs via an intra-polyhedral route. The height of the energy barriers associated with O(1)–O(1) and O(1)–O(2) diffusion both increase with P, as shown in Fig. 5. It has been suggested that shorter M–O bonds can increase the number of trapped ions migrating along these pathways, which drives up the associated trapping enthalpy (ΔH_t).³¹ It is clear from Table S2,† that all metal–oxygen bonds contract under compression of the unit cell, therefore, it is possible that ΔH_t becomes larger; restricting transport and adding to the associated energy barriers along all three-axis.

In addition to the polyhedral ratio and distortion effects, the displacement (D) of metal cations in relation to the mobile oxygen ions is also a factor to consider within the energy landscape of Ba₃MNbO_8.5 materials. For Ba₃MoNbO_8.5, above 300 °C the M(1) cations are displaced away from the mobile ions towards the [O(1)–O(1)–O(1)] face of the M(1)–O(1)₃ unit.⁴ This lowers the motional enthalpy required for migration, as seen in other ionic conductors, and is believed to facilitate rapid transport. The variation of M(1)–O distances and angles with pressure indicates that a similar displacement occurs (Fig. S8†) with a maximum value of D = −0.08 Å achieved at 4.8 GPa. The enhanced displacement from the equilibrium position in Ba₃MoNbO_8.5 is likely due to the flattening of the tetrahedra that is observed upon compression of the unit cell. As the energy barriers to migration increase exponentially over the pressure range measured, we can infer that displacement away from mobile ions is not favourable for the conductivity in the absence of a high tetrahedral:octahedral ratio and substantial polyhedral distortion.

Conclusions

We have reported the pressure response of Ba₃MoNbO_8.5 between 0.1 MPa and 4.8 GPa. In contrast with temperature, the hybrid structure undergoes a re-distribution in the population of disordered O(2) and O(3) sites, favouring the occupancy of the former and therefore decreasing the tetrahedral: octahedral ratio. Our estimations indicate that all palmierite character, and associated tetrahedral environments, will be eradicated by 5.2 GPa. The change in structure is reversible, as data obtained upon decompression reveals that the oxygen site occupancies revert to their original equilibrium values. This variable pressure study highlights the inherent flexibility of this disordered material and the ability to subtly tune its hybrid structure using both pressure and temperature.

The anionic lattice undergoes a smooth and continuous change in occupancy with P, while the metal cation lattice is more robust to pressure showing no discernible change at pressures < 3.8 GPa. The highly distorted structure of Ba₃MoNbO_8.5 at ambient pressure becomes less distorted with P, as the average σ(R) value falls and the second order Jahn–Teller distortion is suppressed. Examination of individual polyhedral environments indicates that more regular octahedra are generated within the unit cell at the expense of increasingly distorted and flattened tetrahedra. These combined factors act to increase the energy barriers for migration along all available pathways, changing the energy landscape of Ba₃MoNbO_8.5. Moreover, we show that there is likely a critical value of σR, and Ba₃MNbO_8.5 materials with values below 0.07 Å will lack the E₂ relaxation energy associated with the distortion of MO_x polyhedra. The crossover in E₁ energy demonstrates that the absence of this relaxation energy has a significant effect on the two-dimensional transport. This is a key feature within the energy landscape of the Ba₃M′M′′O_8.5 family and will be an important consideration for the future synthesis of materials. The combination of an unfavourable polyhedral ratio, the overall reduction in distorted environments and the compression of the unit cell volume all act to drive up the energy barriers to migration of the oxide ions within the plane and along c. These findings indicate that pressure will most likely suppress ionic transport within the Ba₃M′M′′O_8.5 family. Previous studies indicate considerable water uptake within the Ba–O(2)–O(3) layers which effects the disordered distribution of oxygen and, therefore, the conductivity response.³³ Therefore, variable pressure physical property measurements are warranted in order to investigate the use of these materials for multiparameter (P–T–H) triple sensors based on their conductivity response to pressure, temperature and humidity stimuli.³⁴ We also show that the compressibility is largely due to soft Ba–O bonds and that the exceptionally low bulk modulus of Ba₃MoNbO_8.5 (K₀ = 50(2) GPa) is closer in magnitude to that of the halide perovskites, which makes it a promising material for thin film applications. The low bulk modulus also explains why such facile structural transformations are enabled with both pressure and temperature.

Conflicts of interest

There are no conflicts of interest to declare.

Acknowledgements

This research was supported by the University of Aberdeen. We also acknowledge the Science and Technology Facilities Council (STFC).

References

1. R. M. Ormerod, Chem. Soc. Rev., 2003, 32, 17–28.
2. M. Ni, M. K. Leung and D. Y. Leung, Int. J. Hydrogen Energy, 2008, 33, 2337–2354.
3. S. Fop, J. M. Skakle, A. C. McLaughlin, P. A. Connor, J. T. Irvine, R. I. Smith and E. J. Wildman, J. Am. Chem. Soc., 2016, 138, 16764–16769.
4. S. Fop, E. J. Wildman, J. T. Irvine, P. A. Connor, J. M. Skakle, C. Ritter and A. C. Mclaughlin, Chem. Mater., 2017, 29, 4146–4152.
5. M. S. Chambers, K. S. McCombie, J. E. Auckett, A. C. McLaughlin, J. T. Irvine, P. A. Chater, J. S. Evans and I. R. Evans, J. Mater. Chem. A, 2019, 7, 25503–25510.
6. M. Coduri, A. Bernasconi, H. E Fischer and L. Malavasi, J. Mater. Chem. A, 2020, 8(40), 21227–21240.
7. J. B. Goodenough, A. Manthiram, M. Paranthaman and Y. S. Zhen, Mater. Sci. Eng., B, 1992, 12(4), 357–364.
8. S. Fop, K. S. McCombie, E. J. Wildman, J. M. Skakle and A. C. Mclaughlin, Chem. Commun., 2019, 55(15), 2127–2137.
9. C. L. Bull, N. P. Funnell, M. G. Tucker, S. Hull, D. J. Francis and W. G. Marshall, High Pressure Res., 2016, 36(4), 493–511.
10. A. D. Fortes, RAL Technical Report, RAL-TR-2019-002, 2019.
11. J. Gonzalez-Platas, M. Alvaro, F. Nestola and R. Angel, J. Appl. Crystallogr., 2016, 49(4), 1377–1382.
12. B. H. Toby, J. Appl. Crystallogr., 2001, 34, 210–213.
13. B. H. Toby and R. B. von Dreele, J. Appl. Crystallogr., 2013, 46, 544–549.
14. K. Momma and F. Izumi, J. Appl. Crystallogr., 2011, 44, 1272–1276.
15. H. Chen, L. L. Wong and S. Adams, Acta Crystallogr., Sect. B: Struct. Sci., Cryst. Eng. Mater., 2019, 75, 18–33.
16. H. Chen and S. Adams, IUCrJ, 2017, 4, 614–625.
17. J. Cumby and J. P. Attfield, Nat. Commun., 2017, 8, 1–8.
18. K. S. Knight and C. L. Bull, Solid State Sci., 2016, 62, 90–104.
19. I. R. Shein, V. L. Kozhevnikov and A. L. Ivanovskii, Solid State Sci., 2008, 10, 217–225.
20. R. D. King-Smith and D. Vanderbilt, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 49, 5828.
21. E. Mattern, J. M. Y. Ricard and J. Bass, Geophys. J. Int., 2005, 160, 973–990.
22. A. Jaffe, Y. Lin and H. I. Karunadasa, ACS Energy Lett., 2017, 2, 1549–1555.
23. X. Lü, Y. Wang, C. C. Stoumpos, Q. Hu, X. Guo, H. Chen, L. Yang, J. S. Smith, W. Yang, Y. Zhao and H. Xu, Adv. Mater., 2016, 28, 8663–8668.
24. L. Wang, K. Wang and B. Zou, J. Phys. Chem. Lett., 2016, 7, 2556–2562.
25. D. Errandonea, J. Pellicer-Porres, F. J. Manjón, A. Segura, C. Ferrer-Roca, R. S. Kumar, O. Tschauner, P. Rodríguez-Hernández, J. López-Solano, S. Radescu and A. Mujica, Phys. Rev. B: Condens. Matter Mater. Phys., 2005, 72, 174106.
26. K. S. McCombie, E. J. Wildman, S. Fop, R. I. Smith, J. M. Skakle and A. C. Mclaughlin, J. Mater. Chem. A, 2018, 6, 5290–5295.
27. K. S. McCombie, E. J. Wildman, C. Ritter, R. I. Smith, J. M. Skakle and A. C. Mclaughlin, Inorg. Chem., 2018, 57, 11942–11947.
28. J. Dong, X. Zhang, Q. Zhang, Y. Wu, X. Wu, Z. Wu and D. Chen, New J. Phys., 2014, 16, 023022.
29. M. Yashima, T. Tsujiguchi, K. Fujii, E. Niwa, S. Nishioka, J. R. Hester and K. Maeda, J. Mater. Chem. A, 2019, 7, 13910–13916.
30. A. Gilane, S. Fop, F. Sher, R. I. Smith and A. C. Mclaughlin, J. Mater. Chem. A, 2020, 8, 16506–16514.
31. S. Fop, K. McCombie, R. I. Smith and A. C. McLaughlin, Chem. Mater., 2020, 32, 4724–4733.
32. K. Huang, R. S. Tichy and J. B. Goodenough, J. Am. Ceram. Soc., 1998, 81, 2565–2575.
33. S. Fop, K. S. McCombie, E. J. Wildman, J. M. Skakle, J. T. Irvine, P. A. Connor, C. Savaniu, C. Ritter and A. C. Mclaughlin, Nat. Mater., 2020, 6, 752–757.
34. S. Han, N. U. H. Alvi, L. Granlöf, H. Granberg, M. Berggren, S. Fabiano and X. Crispin, Adv. Sci., 2019, 6, 1802128.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: 10.1039/d0ta11270d

---