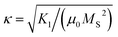Designing of magnetic MAB phases for energy applications

Abstract

Based on high-throughput density functional theory calculations, we performed screening for stable magnetic MAB compounds and predicted potential strong magnets for permanent magnet and magnetocaloric applications. The thermodynamical, mechanical, and dynamical stabilities are systematically evaluated, resulting in 21 unreported compounds on the convex hull, and 434 materials being metastable considering convex hull tolerance to be 100 meV per atom. Analysis based on the Hume-Rothery rules revealed that the valence electron concentration and size factor difference are of significant importance in determining the stability, with good correspondence with the local atomic bonding. We found 71 compounds with the absolute value of magneto-crystalline anisotropy energy above 1.0 MJ m⁻³ and 23 compounds with a uniaxial anisotropy greater than 0.4 MJ m⁻³, which are potential gap magnets. Based on the magnetic deformation proxy, 99 compounds were identified as potential materials with interesting magnetocaloric performance.

---

1 Introduction

The modern industrial and societal demands for advanced functional magnetic materials are growing faster as we are witnessing the global expansion of hybrid-electric vehicles, robotics, wind turbines, and automation, leading to a strong incentive on the green energy revolution.^1,2 Particularly, the efficient harvesting of renewable energy (such as wind energy) and endeavor to reduce the greenhouse effect (mainly through the development of e-mobility and magnetic refrigeration) have intensified the impetus to design resource-efficient magnetic materials with optimal performance, such as permanent magnets and magnetocaloric materials. For instance, one interesting question is to identify the so-called gap magnets,³i.e., permanent magnets with their energy density (BH)max⁴ lying between the widely applied AlNiCo and ferrites⁵ and the high-performance Sm–Co⁶ and Nd–Fe–B-based⁷ permanent magnets. Potential candidates can be characterized using the dimensionless figure of merit ,⁸ providing an effective descriptor for high-throughput screening. Moreover, following the discovery of Gd₅Si₂Ge₂ (ref. 9) and LaFeSi₁₃ (ref. 10) with giant magnetocaloric effect (MCE) around room temperature, magnetic refrigeration technology is assumed to be capable of competing with and hopefully surpassing conventional refrigeration in terms of energy efficiency, environmentally friendly and ecological impact in the near future.^11–13 However, most permanent magnets and potential magnetocaloric materials with high performance are based on the intermetallic compounds containing rare-earths (RE), which are resource critical.¹⁴ Therefore, rare-earth-free permanent magnets and MCE materials with enhanced efficiency over a broad temperature range and useful secondary properties, such as mechanical stability, corrosion resistance, shapeability, sustainability, and recyclability, are still desirable.^1,15,16

The MAB phases with nanolaminated crystal structures exhibit intriguing magnetic properties and mechanical deformation behavior, which have attracted considerable attention recently.¹⁷ Such materials are ternary borides comprising stacked M–B layers (M = transition metal, B = boron) interleaved by monolayers of A atoms. In this regard, the crystal structures are quite similar to those of the well-known MAX phases M_n+1AX_n (X = C and N, A denotes a main group element), which host a unique combination of metallic and ceramic properties.¹⁸ The novel magnetic nanolaminates recently discovered in the MAX phases,¹⁹ are also expected in the MAB phases. Moreover, Fe₂AlB₂ was found to be a promising magnetocaloric material exhibiting an interesting MCE,²⁰ with the ordering temperature around 300 K confirmed by experimental^21,22 and theoretical studies.^23–25 Ke et al.²⁶ investigated the intrinsic properties of Fe₂AlB₂, and found a MAE as large as −1.34 MJ cm⁻³, in good agreement with the experiments.²² Recently, Cr₄AlB₄ with a novel structure of MAB phase has been synthesized consistent with the theoretical calculations.²⁷ Khazaei et al.²⁸ carried out high-throughput (HTP) calculations on Al-containing non-magnetic MAB phases and predicted 9 stable compounds. More recently, Miao et al.²⁹ reported another HTP screening for Ti–A–B, Zr–A–B, and Hf–A–B and predicted 7 thermodynamically stable compounds. Therefore, an interesting question is whether there exist more stable MAB compounds beyond the above-mentioned cases and whether are they good candidates as potential functional magnetic materials.

In this work, based on HTP density functional theory (DFT) calculations, we systematically studied the stabilities and the magnetic properties of the MAB compounds to identify possible candidates for permanent magnets and magnetocaloric materials. Six experimentally synthesized MAB phases and three non-MAB phases (as competitive phases) are considered (Fig. 1), including MAB³⁰ (space group Cmcm), M₂AB₂ (ref. 31) (space group Cmcm), M₃A₂B₂ (ref. 32) (space group Cmcm), M₃AB₄ (ref. 33) (space group Immm), M₄AB₄ (ref. 27) (space group Immm) and M₄AB₆ (ref. 34) (space group Cmcm); non-MAB phases are M₅AB₂ (ref. 35) (space group I4/mcm), M₃A₂B₂ (ref. 36) (space group P2/m) and M₄A₃B₂ (ref. 36) (space group P4/mmm). Three non-MAB phases are considered as competitive phases in order to make the prediction of MAB compounds more reliable. Such compounds are flexible in the chemical compositions and have tunable magnetic properties. For example, Fe₅SiB₂ has a T_C higher than 760 K, a M_S larger than 1 MA m⁻¹, and a MAE more than 0.30 MJ m⁻³ at room temperature.^37–41 After validating all the experimentally known phases, we identified stable and metastable ternary borides based on the systematic evaluation of the thermodynamical, mechanical, and dynamical stabilities. Taking the M₂AB₂-type compounds as an example, we investigated the effect of magnetic ordering on the thermodynamic stability, followed by a comprehensive analysis of the stability trend following the Hume-Rothery rules and local atomic bonding. The MAE and magnetic deformation proxy are evaluated explicitly, which help to screen for potential permanent magnets and magnetocaloric materials. Our work expands the materials library of rare-earth free permanent magnets and magnetic refrigeration, and thus provides valuable guidance to further theoretical and experimental studies to design advanced magnetic materials in transition metal-based ternary borides for energy applications.^13,16

Fig. 1 Crystal structures of considered MAB phases (a–f) and non-MAB phases (g and h): (a) 222-type [Cmcm], (b) 212-type [Cmcm], (c) 314-type [Pmmm], (d) 416-type [Cmmm], (e) 322-type [Cmcm], (f) 414-type [Immm], (g) 512-type [I4/mcm], (h) 322-type [P2/m] and (i) 432-type [P4/mmm].

2 Computational details

The DFT calculations are performed using an in-house developed HTP environment^42,43 to determine the thermodynamical stability for the above mentioned six MAB and three non-MAB phases, as demonstrated in recent studies.^44–46 It is noted that the non-MAB phases are regarded as competitive phases for the MAB phase to obtain the reliable convex hull, which is also applied in designing MAX phases by considering antiperovskites as a competitive phase.⁴⁵ Thermodynamical stability is evaluated by considering the formation energy (E_f) and the distance to the convex hull with respect to all the relevant competing phases available in the OQMD database.⁴⁷ All the calculations are carried out using the Vienna ab initio simulation package (VASP) code.^48,49 The MAE of the predicted stable phases is obtained using the full-potential local-orbital (FPLO)⁵⁰ code in the force theorem regime, and the recently proposed magnetic deformation proxy⁵¹ is used to evaluate the MCE. More details of the computational processes can be found in the ESI.†

3 Results and discussion

3.1 Stabilities of phases

3.1.1 Thermodynamical stability. The thermodynamical stability of the MAB and non-MAB phases (shown in Fig. 1) are obtained based on the formation energy ΔE_f and distance to the convex hull ΔE_h, where ΔE_f < 0 and ΔE_h = 0 are required for the stable phases. In general, ΔE_f < 0 ensures that the target compounds are energetically stable against decomposing into the constituent elements following the reaction M_xA_yB_z → xM + yA + zB, whereas ΔE_h = 0 denotes the stability upon the decomposition into any binary and ternary phases according to the reaction ΔE_h = E_tot (predicted phase) − E_tot (competing phases). In our calculations, the competing phases include all the relevant compounds found in the OQMD database.^47,52 As summarized in Table 1, there are 21 compounds satisfying the thermodynamic stability criteria, 17 of them are with one of the MAB structures. According to the literature, 15 ternary borides with one of the considered structures have been experimentally synthesized, as listed in Table 1. All such compounds exhibit ΔE_f < 0 and ΔE_h < 80 meV per atom (due to the possible numerical errors in DFT, competing phases, and finite-temperature effects), validating our methodology and hence the validity of the newly predicted phases. The resulting lattice parameters are in good agreement with the existing measurements and other theoretical calculations, as listed in Table 1. A special case is Co₅PB₂, where the lattice constants are underestimated (overestimated) along [100] ([001]) directions. This is also observed in previous DFT calculations,⁵³ which may be driven by the missing spin fluctuations as confirmed in (Fe_1−xCo_x)₂B.⁵⁴

Table 1 List of MAB and non-MAB phases that we found stable based on relative stability analysis. The present considered phases experimentally synthesized are indicated by asterisks (*). Lattice parameters (Å), formation energy (eV per atom), distance to the convex hull (eV per atom), competing phases, magnetism (Mag.) and magnetic moment (M and the unit as μ_B per magnetic atom) in considered phases are shown

Phases	Space group	Lattice			ΔEf	ΔEh	Competing phases	Mag.	M
		a	b	c
FeBeB	63	2.648	12.164	2.925	−0.326	0	FeB, Be2Fe, B	FM	0.422
MnBeB	63	2.811	12.252	2.809	−0.378	0	MnB, Be	NM	0.002
Fe2AlB^*2	65	2.916	11.019	2.851	−0.401	0	FeAl6, AlB2, FeB	FM	1.330
Ref. Exp.^20		2.928	11.033	2.868
Ref. Cal.^26		2.915	11.017	2.851
Fe2BeB2	65	2.904	9.947	2.749	−0.344	0	Be2Fe, B, FeB	AFM	0.760
Cr2AlB^*2	65	2.923	11.051	2.932	−0.466	0	Cr3AlB4, Cr7Al45, CrB	NM	0.010
Ref. Exp.^34		2.937	11.051	2.968
Ref. Cal.^26		2.921	11.034	2.929
Mn2AlB^*2	65	2.894	11.080	2.831	−0.471	0	Mn4Al11, MnB, MnB4	AFM	0.765
Ref. Exp.^24		2.923	11.070	2.899				AFM
Ref. Cal.^26		2.887	11.109	2.830				AFM
Mn2BeB2	65	2.846	9.969	2.815	−0.435	0	MnB, Be	NM	0.011
Cr3AlB^*4	47	2.939	2.939	8.091	−0.445	0	Cr2AlB2, CrB4, CrB	NM	0.049
Ref. Exp.^34		2.956	2.978	8.054
Ref. Cal.^56		2.938	2.943	8.090
Cr4AlB^*6	65	2.947	21.328	2.943	−0.422	0.012	CrB4, Cr3AlB4, CrB	NM	0.003
Ref. Exp.^34		2.952	21.280	3.013
Ref. Cal.^57		2.972	21.389	2.961
Fe4AlB4	71	2.927	18.565	2.870	−0.417	0	AlFe2B2, FeB	FM	1.271
Fe4BeB4	71	2.918	17.513	2.821	−0.377	0	FeB, Be2Fe, B	FM	1.017
Fe4GaB4	71	2.939	18.557	2.883	−0.343	0	FeB, Ga3Fe, B	FM	1.288
Fe4MgB4	71	2.932	19.626	2.875	−0.354	0	FeB, Mg	FM	1.391
Fe4ZnB4	71	2.931	18.726	2.872	−0.348	0	FeB, Zn	FM	1.326
Cr4AlB^*4	71	2.920	18.856	2.939	−0.510	0	AlCr2B2, CrB	NM	0
Ref. Exp.^27		2.934	18.891	2.973
Ref. Cal.^27		2.932	18.912	2.957
Mn4BeB4	71	2.899	17.591	2.878	−0.467	0	MnB, Be	FM	0.878
Mn4AlB4	71	2.929	18.591	2.889	−0.499	0	MnB, Mn2AlB2	FM	1.014
Mn4IrB4	71	2.959	18.716	2.966	−0.450	0	MnB, Ir	FM	2.003
Ni4AuB4	71	3.012	18.793	2.950	−0.224	0	Au, Ni4B3,	NM	0
Ni4CuB4	71	2.992	18.125	2.875	−0.227	0	B, Cu, Ni4B3	NM	0
Ni4PdB4	71	2.996	18.453	2.931	−0.265	0	Ni4B3, BPd2, B	NM	0
Ni4PtB4	71	2.995	18.351	2.960	−0.267	0	BPt2, Ni4B3, B	NM	0
Ni4ZnB4	71	2.992	18.517	2.880	−0.261	0	Ni4B3, B, ZnNi3B2	NM	0
Fe3Al2B^*2	10	5.685	2.833	8.593	−0.426	0	FeAl6, AlB2, FeB	FM	0.784
Ref. Exp.^36		5.723	2.857	2.857
Fe4Al3B2	123	8.083	8.083	2.791	−0.411	0	AlFe, AlFe2B2	NM	0.002
Co4Be3B2	123	7.586	7.586	2.586	−0.395	0	Be3Co, BeCo, CoB	NM	0
Ni4Li3B2	123	8.049	8.049	2.734	−0.252	0	Li, Ni2B	NM	0.0002
Fe5BeB2	140	5.455	5.455	9.914	−0.292	0	Be2Fe, Fe2B, Fe	FM	1.932
Fe5PB^*2	140	5.570	5.570	10.436	−0.392	0.033	Fe2B, FeB, Fe2P	FM	1.705
Ref. Exp.^35		5.548	5.548	10.332				FM	1.730
Ref. Exp.^40		5.485	5.485	10.348				FM	1.720
Ref. Exp.^58		5.492	5.492	10.365				FM	1.658
Ref. Cal.^53		5.456	5.456	10.296				FM	1.770
Fe5SiB2	140	5.509	5.509	10.299	−0.359	0.003	Fe2B, FeSi	FM	1.731
Ref. Exp.^38		5.551	5.551	10.336				FM	1.808
Ref. Exp.^37		5.554	5.554	10.343				FM	1.750
Ref. Cal.^39		5.546	5.546	10.341				FM	1.840
Co5PB^*2	140	5.279	5.279	10.477	−0.357	0.079	Co2P, CoB, Co	FM	0.409
Ref. Exp.^59		5.420	5.420	10.200
Ref. Cal.^53		5.284	5.284	10.541				FM	0.440
Co5SiB^*2	140	5.484	5.484	9.942	−0.337	0.042	CoB, Co2Si, Co	FM	0.394
Ref. Exp.^60
Ref. Cal.^39		5.511	5.511	9.953				FM	0.484
Cr5PB^*2	140	5.537	5.537	10.317	−0.474	0.032	Cr3P, CrB	NM	0.022
Ref. Exp.^61		5.593	5.593	10.370
Cr5B^*3	140	5.431	5.431	9.923	−0.418	0	CrB, Cr2B	NM	0
Ref. Exp.^62		5.460	5.460	10.460
Mn5PB^*2	140	5.509	5.509	10.287	−0.480	0.033	Mn2B, MnB, Mn2P	FM	1.665
Ref. Exp.^59		5.540	5.540	10.490
Ref. Exp.^63		5.540	5.540	10.490
Mn5SiB^*2	140	5.559	5.559	10.293	−0.415	0.003	MnSi, Mn2B	FM	1.583
Ref. Exp.^63		5.540	5.540	10.490

---

Furthermore, not all the compounds are magnetic, e.g., with finite magnetization larger than 0.05 μ_B per magnetic atom (Table 1). It is observed that the nonmagnetic compounds occur mostly for the Cr-, Mn-, and Ni-based cases, whereas Fe₄Al₃B₂ and Co₄Be₃B₂ are nonmagnetic as well. This can be understood based on the Stoner criteria, where Iν(E_F) > 1 indicate possible itinerant magnetic ordering, with I being the Stoner parameter and ν(E_F) the density of states (DOS) at the Fermi energy E_F of the nonmagnetic state. For instance, the Stoner parameters of magnetic atoms range between 0.6 and 0.75 from Cr to Ni,⁵⁵ thus those compounds with marginal ν(E_F) smaller than 1.4 states per eV per magnetic atom end up as nonmagnetic (Fig. S3†) because Iν(E_F) < 1. Moreover, the predicted results agree well with previous experimental and theoretical reports, e.g., Fe₅PB₂ with average magnetization 1.71 μ_B/Fe⁴⁰ and Cr₄AlB_4/6 being nonmagnetic.^27,34 Furthermore, it is observed that there exist nonzero induced magnetic moments on the nonmagnetic atoms which are antiparallel to the magnetic moments of the 3d atoms. For instance, Mn₄BeB₄ has the smallest ratio M_tot/M_3d of about 0.94, where the magnetic moments of non-metal B atoms are about −0.05 μ_B per B atom and those of metal Be atoms are smaller than −0.01 μ_B per Be atom.

Interestingly, the distance to the convex hull for the experimentally synthesized compounds are finite (Table 1), e.g., Cr₄AlB₆, Fe₅PB₂ and Co₅PB₂ with distances to the convex hull of 12, 33 and 79 meV per atom, respectively. Co₅PB₅ with a distance to the convex hull being 79 meV per atom is a special case, where there is also a 3% deviation in the theoretical and experimental lattice constants. In fact, the calculated lattice constants of this compound agree well with previously reported calculations.⁵³ Nevertheless, this suggests that a loose tolerance ΔE_h < 100 meV per atom is reasonable, though it is not deliberately chosen to cover the Co₅PB₅ phase.

Critical tolerance with comparable values for the convex hull has also been adopted in other HTP studies.^43,46,64 This leads to 434 (335 are MAB phases) stable compounds, as listed in Table S1 in the ESI.† As a consequence, our predictions become consistent with another HTP study²⁸ focusing on Al-containing MAB phases with early transition metals on the M-sites. For instance, 8 novel MAB phases they found, i.e., CrAlB, MnAlB, Cr₃Al₂B₂, Mn₃Al₂B₂, Ni₃Al₂B₂, Mn₃AlB₄, and Fe₃AlB₄, are also predicted to be stable using the loose tolerance on the convex hull, as listed in the Table S10.† It is noted that even if such compounds are metastable, they can still be synthesized using non-equilibrium methods such as MBE and ball milling. Hereafter we will consider the stability trend and magnetic properties for all those compounds. Last but not least, it is essential to consider the non-MAB phases as competing phases beyond those in the OQMD database. It is observed that the 322-MAB Fe₃Al₂B₂ is stable with ΔE_h = 0 compared with competing phases in OQMD, whereas it becomes metastable with ΔE_h = 33 meV per atom after considering the non-MAB Fe₃Al₂B₂. Certainly there are other competing phases and even novel crystal structures beyond those considered in this work, which will be saved for future investigation after experimental validations.

Another interesting question for predicting stable magnetic materials is whether the magnetic configurations would influence the thermodynamic stability, since most HTP calculations are done assuming the ferromagnetic (FM) state as in the OQMD and the Materials Project.⁶⁵ This applies particularly to Mn-based compounds, as revealed by a recent work that the energy landscape of the convex hull is drastically changed after considering the magnetic ground state.⁶⁶ According to the literature, the 212-type Mn₂AlB₂ is observed to display an AFM magnetic ground state with Néel temperature about 390 K,^26,67,68 thus we performed extensive calculations on the predicted 212-type MAB compounds. As summarized in Table S2,† 15 out of 54 magnetic compounds prefer AFM magnetic configurations, including not only Mn-based but also Fe- and Co-based compounds. The magnetic ground states are consistent with those obtained from our Monte Carlo modeling based on the Heisenberg model taking exchange parameters from DFT calculations (not shown), which will be discussed in detail elsewhere. Nevertheless, the energy difference between the FM and AFM states is less than 20 meV per atom, hence the magnetic ground state has no strong impact on the thermodynamic stability for such compounds. This can be attributed to the nano-laminated crystal structure, where the magnetic interaction between the local Mn-moments is relatively weak, in comparison to the strongly frustrated fcc-lattice from the Cu₃Au lattice considered in ref. 66. It is noted that systematic evaluation of the magnetic ground states is a challenge, hereafter we will focus on the physical properties of the FM states, which should be valid for most of the other compounds.

After the thermodynamic stability, mechanical and dynamical stabilities should be addressed as well in order to make systematic predictions. It is observed that mechanical stability plays a marginal role as explicitly demonstrated for 21 stable compounds on the convex hull. This is consistent with our previous studies on the antiperovskite compounds.⁴⁶ For the orthorhombic MAB phases, there are nine independent elastic constants C₁₁, C₂₂, C₃₃, C₄₄, C₅₅, C₆₆, C₁₂, C₁₃, and C₂₃. For the tetragonal non-MAB phases, there are six independent elastic constants C₁₁, C₃₃, C₄₄, C₆₆, C₁₂, and C₁₃. According to the mechanical stability defined in the ref. 69, none of the novel compounds predicted to be thermodynamically stable is found to be mechanically unstable. In addition, the dynamical stability is verified by examining the phonon spectra as compiled in Fig. S2† for 21 predicted and 15 known cases. Obviously, there is no imaginary modes observed for 35 compounds, indicating that those compounds are stable against local atomic displacements. The resulting phonon spectra for Cr₂AlB₂ and Cr₃AlB₄ are in good agreement with previous reported results.⁷⁰ The mechanical (not shown) and dynamical (as indicated by phonon spectra in Fig. S2†) stabilities seem to be of marginal importance for the newly predicted compounds on the convex hull (cf.Table 1), which is consistent with our previous studies on the antiperovskite compounds.⁴⁶ Due to the expensive computational cost, we have not performed such detailed evaluations for the other predicted compounds with the distance to the convex hull smaller than 100 meV per atom.

Nevertheless, for Ni₄Li₃B₂ there exists an imaginary mode at the M point. This suggests that the compound may end up with other crystal structures or synthesized on certain substrates using molecular beam epitaxy.

3.1.2 Trends in the stability. To understand the trend of stabilities for the MAB and non-MAB phases, the number of stable compounds (ΔE_h < 100 meV per atom) with respect to the A element are shown in Fig. S4.† It is obvious that most elements in the periodic table act as a constituent element stabilizing at least one of the considered crystal structures, whereas nine out of 59 elements (i.e., K, Rb, Cs, Sr, Ba, Zr, N, Sb, and Bi) do not form any stable phases. Particularly, each of the five elements like Be, Al, Pt, Zn, and Ir support more than 22 stable phases. Moreover, among all the structure types considered in this work, 136 compounds are stable with the 414-type structure, albeit the first compound Cr₄AlB₄ was reported in 2019.²⁷

Taking the 212-type MAB structure as an example, the stability trend with respect to the chemical composition can be understood based on the Hume-Rothery rules.⁷¹ Such rules are formulated based on the difference of size, electronegativity factors and the valence electron concentration (VEC). It is observed that the electronegativity difference between the M and A elements has no strong correlation with the stability (Fig. S5†), same as the MAX compounds.⁷² On the other hand, as shown in Fig. 2, both the atomic radius difference of the M and A elements 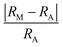and VEC have significant influence on the stability. Clearly, most stable compounds are within the region and VEC < 5.5. The newly reported novel phases in ref. 28 also prove the practicality of the current expression factors. Similar behavior is also observed for the 414-type MAB compounds with a slightly smaller tolerance for VEC < 6, as shown in Fig. S6.† The reason might be due to the fact that the M-site and boron-site contributing less valence electrons because of the extended M–B block (Fig. 1).

Fig. 2 The stability map of 212-MAB phases (circle symbols represent unstable phases in the present work; triangle symbols represent possible stable phases with convex hull distance below 100 meV per atom in the present work; square symbols represent newly reported novel phases in ref. 28).

The general trend in the stability can be elucidated based on the chemical orbital Hamilton population (COHP) obtained using the LOBSTER code,⁷³ which provides an atomic picture about the bonding. As an example which is representative for all the compounds we considered, the bond-resolved COHP is shown for M₂AlB₂ (where M are Cr, Mn, Fe, Co and Ni) and Fe₂AB₂ (where A are Be, Mg, Ca, Sr and Ba) in Fig. S8.† Focusing on varying the M elements, the number of valence electron on the M-sites increases from 6 in Cr₂AlB₂, to 8 in Fe₂AlB₂, and finally to 10 in Ni₂AlB₂. For Cr₂AlB₂, it is obvious that the values of –COHP are all positive below the Fermi energy, indicating only boning states are occupied in the corresponding bonds, which leads to a high overall stability (Fig. S8†) Increasing the number of valence electron to 10 in Ni₂AlB₂, the negative energies –COHP appeared below the Fermi energy in the Ni–B, Ni–Al, and Ni–Ni bonds. The occupation of such anti-bonding states weakens the bonds and therefore destabilizes the Ni₂AlB₂ compound. Therefore, the ICOHP of M–Al and M–B are increasing within the number of valence electron increasing, which indicates the corresponding bond strength weakens. Similar behaviour is also observed in the COPH os Fe₂AB₂ compounds with varying A elements being Be, Ca, and Ba (Fig. S8†). As the atomic size changes from 0.99 Å (Be), 1.74 Å (Ca) and 2.06 Å (Ba), the bond strength of those compounds becomes weaker, which are confirmed by the COHP values of Fe–Fe, Fe–B, Fe–A and A–B.

Hence, with respect to varying both M and A elements with increasing number of valence electrons and atomic size, the Fermi energy is shifted into the anti-bonding states, leading to instability. This helps to understand the trend observed in Fig. 2, which provide valuable guidance to guide the synthesis of MAB phases by substituting the M/A sites or via forming solid solutions.

3.2 Magnetic properties

3.2.1 MAE. Turning now to the magnetic properties, we focus on the magnetocrystalline anisotropy energy (MAE) and magnetocaloric effect (MCE), in order to identify potential candidates for permanent magnet and magnetocaloric applications. The MAE is caused by the broken continuous symmetry of magnetization directions due to the spin–orbit coupling (SOC),⁷⁴ which is defined (denoted as K) in terms of

K_n̂1−n̂2 = E_n̂1 − E_n̂2, (1)

where E_n̂ denotes the total energy with the magnetization direction parallel to n̂. In the present work, we consider n̂ along three crystalline directions, namely, [100], [010] and [001], as MAB compounds have orthorhombic structures (Fig. 1). This leads to three MAEs, i.e., K_001–010, K_001–100 and K_010–100. Fig. 3 shows the MAE with respect to the saturation magnetization (M_S), in comparison with the experimentally known permanent magnets. There are in total 71 cases (cf. Table S6 in the ESI†) with the absolute value of at least one MAE greater than 1.0 MJ m⁻³. For instance, the MAE of Fe₂AlB₂ has been evaluated by different groups,^21,22,26 and our result of −1.14 MJ m⁻³ is in good agreement with the experimental measurements of −0.9 MJ m⁻³ at 50 K by Barua²² and theoretical calculation −1.34 MJ m⁻³ by Ke.²⁶ In the newly predicted compounds, the MAB phase Mn₄PtB₄ has the largest MAE as 13.498, 11.948 and −1.550 MJ m⁻³ for K_001–010, K_001–100 and K_010–100. Additionally, the 111-type FePtB shows the largest MAE in non-Mn-containing compounds as −10.646, 7.225 and −3.421 MJ m⁻³ for K_010–100, K_001–010 and K_001–100, suggesting the b-direction (c-direction) is easy (hard) axis. Based on the dimensionless figure of merit ,⁸ there exist quite a few compounds which can be classified as hard magnets. Particularly, the MAE of such ternary TM borides fill the gap between the widely used low performance magnets (such as AlNiCo and ferrite) and high performance magnets (such as Sm–Co and Nd–Fe–B).

Fig. 3 The MAE vs. magnetization of the promising candidates of targeted phases. The dashed lines correspond to magnetic hardness parameter for values κ = 1 and 0.1. Hard magnetic materials (κ > 1) can be used to make efficient permanent magnets of any shape.

However, not only the absolute values of the MAE but also the sign matters, e.g., the easy axis (direction with the lowest energy) is ideally aligned along a special crystalline axis. For all the MAB compounds, the [001] direction along the stacking direction of the M–B layers (Fig. 1) is chosen, corresponding to the most-probably exposed surfaces for such nano-laminated structures. For the non-MAB phases of the tetragonal space groups, the special axis is chosen to be the axis of 4-fold rotational symmetry, i.e., the [001] direction in Fig. 1(g and i). The MAE for the 322-type compounds (Fig. 1(h)) is overall small thus we do not consider them. Correspondingly, we found 16 MAB and 7 non-MAB phases with a significant out-of-plane MAE (>0.4 MJ m⁻³), as well as 33 (18) MAB (non-MAB) compounds with a reasonable in-plane MAE (absolute value larger than 0.4 MJ m⁻³), as listed in Table S7.† Among them, the 322-type MAB compound Mn₃Ir₂B₂ has the largest out-of-plane MAE of 10.17 MJ m⁻³ for K_010–001, and Fe₂ReB₂ with a large MAE of 9.00 MJ m⁻³ in K_010–001. Interestingly, the MAE value of Fe₃Zn₂B₂ is as large as 3.00 MJ m⁻³ in K_100–001 while its M_S is comparable to that of MnAl. It contains no expensive, toxic or critical element, which is a good candidate permanent magnet material. Moreover, Fe₇B₂ has a sizable MAE 0.681 MJ m⁻³, which is quite comparable to that of hcp Co. Such a phase is beyond the known binary Fe–B phase diagram,⁷⁵ which might be synthesizable under non-equilibrium conditions. Last but not least, our results (Fig. 3 and Table S6†) provides reasonable matrix compounds whose MAE can be further enhanced by proper doping to engineer permanent magnets. For instance, our calculations reveal that Fe₅PB₂ has an MAE of 0.63 MJ m⁻³ consistent with the experimental measured value of 0.65 MJ m⁻³,⁴¹ whereas a recent work demonstrated that its MAE can be enhanced by substitutionally doping tungsten.⁷⁶

As discussed above, most compounds with significant MAE contain 5d elements, such as Pt, Ir, and Re. This suggests that the MAE is originated from the enhanced atomic SOC strength for the 5d-shell of such elements. Following Ref. 77, the atomic resolved SOC energy changes are listed in Table S8† for the 111-type FeXB with X = Ni, Pd, and Pt. As the atomic SOC strength increases from 98 meV for Ni, 185 meV for Pd, to 533 meV for Pt,⁷⁸ the contribution from the X element to the MAE is becoming more significant, as given by the change of atom-resolved SOC energy ΔE_SOC = E_SOC(n̂₁) − E_SOC(n̂₂). For FeNiB, ΔE_SOC(Fe) (−0.492 meV per atom in [100]–[010] direction) dominants the total ΔE_SOC (−0.586 meV per f.u. in [100]–[010] direction) of the compound, as the SOC strength is comparable for Fe (55 meV) and Ni. Furthermore, for FeXB with X = Ni, Pd, and Pt, the ΔE_SOC of Ni, Pd, and Pt are −0.093, 0.702, and 2.603 meV per atom between two magnetization directions [100] and [010], corresponding to the changes in the total MAE of −0.128, 0.181, and 2.106 meV per atom, respectively. That is, ΔE_SOC of X has a more dominant contribution to the total ΔE_SOC and hence the MAE, when moving down the group from 3d to 5d elements. In the FePtB, the contribution of ΔE_SOC of Pt is 84% in total ΔE_SOC. Therefore, like FePt,⁷⁹ the 5d elements have a more significant contribution to the MAE because of enhanced atomic SOC strength, though the magnetic moments on such elements are induced by those of the 3d atoms.

3.2.2 MCE. As introduced above, it is postulated that ternary TM borides are promising candidates for MCE applications, such as Fe₅SiB₂ (ref. 37) and Fe₂AlB₂.^20–22,25 To search for more candidates in the predicted MAB and non-MAB compounds, we performed screening based on the magnetic deformation proxy.⁵¹ It is demonstrated that the magnetic entropy change ΔS_M upon magneto-structural transitions has a strong correlation with the magnetic deformation and where P = A_nonmag⁻¹·A_mag with A_nonmag and A_mag being the lattice constants of the nonmagnetic and magnetic unit cells. Although there is no direct scaling between ΔS and Σ_M, it is suggested that Σ_M > 1.5% is a reasonable cutoff to select the promising compounds.⁵¹

Fig. 4 shows the 99 potential MCMs with Σ_M > 1.5% from 434 compounds with convex hull ΔE < 100 meV per atom. Among them, the reported⁵¹Σ_M of Fe₅SiB₂ (2.14%) and Fe₂AlB₂ (2.05%) are confirmed in our calculations, with the resulting Σ_M of 2.03% and 1.96%, respectively. Interestingly, there is positive correlation between the magnetization density and the magnitude of magnetic deformation, i.e., as the magnetic deformation increases, the magnetization of compounds also increase (Fig. 4). It is noted that 82 out of 99 potential MCMs locating at Σ_M < 3.5%, and the magnetization concentrating between 500 to 1000 emu cm⁻³. Particularly, there are four compounds, e.g., Fe₅B₂ (322-MAB), Fe₃Co₂B₂ (322-MAB), Mn₃Co₂B₂ (322-MAB), and Fe₂B (111-MAB), at the upper-right corner, which perform on both large magnetization and magnetic deformation. We suspect such compounds can exhibit significant ΔS_M upon second order phase transition at the corresponding Curie temperature, which will be saved for detailed investigation in the future. Additionally, isostructural doping can be applied to improve the magnetocaloric performance⁸⁰ or to fine tune the magnetostructural or metamagnetic transitions,⁸¹ which enables further design of magnetocaloric materials with optimal performance.

Fig. 4 The 99 potential MCMs with magnetic deformation Σ_M > 1.5%. The color bar marks the distance to the convex hull. The dash line indicates a positive correlation between the magnetization density and the magnitude of magnetic deformation.

Several important aspects on possible MCE in such materials are noteworthy, based on the distributing map with respect to the M and A sites as shown in Fig. S9.† For instance, compounds with Fe and Mn occupying the M-site show a high possibility to posses a large MCE based on the magnetic deformation, which have been confirmed in several reported compounds.^63,82,83 Based on the correlations observed in known MCMs in ref. 51, such materials are likely to show a strong magnetocaloric effect and are therefore excellent candidates for experimental study. Moreover, compounds with Mn/Fe/Co, Ru/Rh/Pd and Os/Ir/Pt occupying the A-site also show a high potential to host remarkable magnetocaloric properties. Furthermore, it is noted the fact that Fe₂AlB₂ is composed entirely of earth-abundant elements. This provides a major advantage at least from a cost and resource point of view, over the competing MCMs that contain expensive critical elements (e.g., Gd, Gd₅Si₂Ge₂, FeRh). Therefore, such economic material without critical elements appears especially appealing to us, and the present system M_xA_yB_z, when A = Al, Zn, Si and Fe should be attracted more attention, such as Fe₄AlB₄ (2.33%), Fe₃AlB₄ (2.11%), Fe₄SiB₄ (2.73%), Fe₃ZnB₄ (2.42%) and Fe₅B₂ (Cmmm, 6.56%) (Fig. S9†).

4 Conclusion

In summary, our high-throughput screening on 6 types of MAB phases and 3 types of competing non-MAB phases predict 434 magnetic ternary transition metal borides which are potential candidates for permanent magnets and magnetocaloric materials. After validating the 15 reported compounds, 21 novel compounds are identified to be stable based on the systematic evaluation of thermodynamic, mechanical, and dynamical stabilities, and the number of stable compounds is increased to 434 taking the tolerance of convex hull being 100 meV per atom. It is observed that the magnetic ground state for such compounds with layered structures does not have a strong influence on the thermodynamic stability. The trend of stability for the MAB phase can be understood based on the Hume-Rothery rules, where the size factor difference and the valence electron concentration play a critical role. Such a trend can be further attributed to the bond-resolved COHP, providing intuitive guidance for experimental synthesis. The detailed evaluation of the magnetocrystalline anisotropy energy and the magnetic deformations leads to 23 compounds with significant uniaxial anisotropy (>0.4 MJ m⁻³) and 99 systems with reasonable magnetic deformation (Σ_M > 1.5%). For those compounds containing no expensive, toxic, or critical elements, it is observed that Fe₃Zn₂B₂ is a reasonable candidate as gap permanent magnet, and Fe₄AlB₄, Fe₃AlB₄, Fe₃ZnB₄, and Fe₅B₂ as potential magnetocaloric materials. This work paves the way for designing more magnetic materials for energy applications. In particular, it also provides a good starting point to search for novel two-dimensional magnetic materials, i.e., MBene, based on detailed evaluation of the exfoliation energy and follow-up experiments.⁸⁴ At last, the realistic assessment of the predicted potential MAB phases are conducting and will add to our library^13,16 soon. All the raw data are freely available in the Novel Materials Discovery (NOMAD) Laboratory.⁸⁵

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

The authors gratefully thank Manuel Richter for providing the SOC strength data and helpful discussions. This work was also supported by the Deutsche Forschungsgemeinschaft – Project-ID 405553726 – TRR 270. Part of this work was supported by the European Research Council (ERC) under the European Union's Horizon 2020 Research and Innovation Program (Grant No. 743116-project Cool Innov). The Lichtenberg high performance computer of the TU Darmstadt is gratefully acknowledged for the computational resources where the calculations were conducted for this project.

References

1. O. Gutfleisch, M. A. Willard, E. Brück, C. H. Chen, S. Sankar and J. P. Liu, Adv. Mater., 2011, 23, 821–842.
2. K. Skokov and O. Gutfleisch, Scr. Mater., 2018, 154, 289–294.
3. J. Coey, Scr. Mater., 2012, 67, 524–529.
4. O. Gutfleisch, J. Phys. D: Appl. Phys., 2000, 33, 157.
5. S. Sugimoto, J. Phys. D: Appl. Phys., 2011, 44, 064001.
6. K. J. Strnat and R. M. Strnat, J. Magn. Magn. Mater., 1991, 100, 38–56.
7. J. Herbst and J. Croat, J. Magn. Magn. Mater., 1991, 100, 57–78.
8. J. Coey, J. Condens. Matter Phys., 2014, 26, 064211.
9. V. K. Pecharsky and K. A. Gschneidner Jr, Phys. Rev. Lett., 1997, 78, 4494.
10. O. Gutfleisch, A. Yan and K.-H. Müller, J. Appl. Phys., 2005, 97, 10M305.
11. O. Gutfleisch, T. Gottschall, M. Fries, D. Benke, I. Radulov, K. P. Skokov, H. Wende, M. Gruner, M. Acet and P. Entel, et al. , Philos. Trans. R. Soc., A, 2016, 374, 20150308.
12. F. Scheibel, T. Gottschall, A. Taubel, M. Fries, K. P. Skokov, A. Terwey, W. Keune, K. Ollefs, H. Wende and M. Farle, et al. , Energy Technol., 2018, 6, 1397–1428.
13. T. Gottschall, K. P. Skokov, M. Fries, A. Taubel, I. Radulov, F. Scheibel, D. Benke, S. Riegg and O. Gutfleisch, Adv. Energy Mater., 2019, 9, 1901322.
14. D. Sander, S. O. Valenzuela, D. Makarov, C. Marrows, E. Fullerton, P. Fischer, J. McCord, P. Vavassori, S. Mangin and P. Pirro, et al. , J. Phys. D: Appl. Phys., 2017, 50, 363001.
15. J. Mohapatra and J. P. Liu, Handbook of Magnetic Materials, Elsevier, 2018, vol. 27, pp. 1–57.
16. M. KuzâMin, K. Skokov, H. Jian, I. Radulov and O. Gutfleisch, J. Condens. Matter Phys., 2014, 26, 064205.
17. S. Kota, M. Sokol and M. W. Barsoum, Int. Mater. Rev., 2019, 1–30.
18. M. W. Barsoum, Prog. Solid State Chem., 2000, 28, 201–281.
19. A. S. Ingason, M. Dahlqvist and J. Rosén, J. Condens. Matter Phys., 2016, 28, 433003.
20. X. Tan, P. Chai, C. M. Thompson and M. Shatruk, J. Am. Chem. Soc., 2013, 135, 9553–9557.
21. J. Cedervall, M. S. Andersson, T. Sarkar, E. K. Delczeg-Czirjak, L. Bergqvist, T. C. Hansen, P. Beran, P. Nordblad and M. Sahlberg, J. Alloys Compd., 2016, 664, 784–791.
22. R. Barua, B. Lejeune, L. Ke, G. Hadjipanayis, E. M. Levin, R. McCallum, M. Kramer and L. Lewis, J. Alloys Compd., 2018, 745, 505–512.
23. P. Chai, S. A. Stoian, X. Tan, P. A. Dube and M. Shatruk, J. Solid State Chem., 2015, 224, 52–61.
24. K. Kádas, D. Iuşan, J. Hellsvik, J. Cedervall, P. Berastegui, M. Sahlberg, U. Jansson and O. Eriksson, J. Condens. Matter Phys., 2017, 29, 155402.
25. A. El Boukili, N. Tahiri, E. Salmani, H. Ez-Zahraouy, M. Hamedoun, A. Benyoussef, M. Balli and O. Mounkachi, Intermetallics, 2019, 104, 84–89.
26. L. Ke, B. N. Harmon and M. J. Kramer, Phys. Rev. B, 2017, 95, 104427.
27. H. Zhang, F. Dai, H. Xiang, Z. Zhang and Y. Zhou, J. Mater. Sci. Technol., 2019, 35, 530–534.
28. M. Khazaei, J. Wang, M. Estili, A. Ranjbar, S. Suehara, M. Arai, K. Esfarjani and S. Yunoki, Nanoscale, 2019, 11, 11305–11314.
29. N. Miao, J. Wang, Y. Gong, J. Wu, H. Niu, S. Wang, K. Li, A. R. Oganov, T. Tada and H. Hosono, Chem. Mater., 2020, 32, 6947–6957.
30. W. Jeitschko, Monatsh. Chem., 1966, 97, 1472–1476.
31. W. Jeitschko, Acta Crystallogr., Sect. B: Struct. Crystallogr. Cryst. Chem., 1969, 25, 163–165.
32. W. Jung, K. Schweitzer and Z. Kristallogr, Cryst. Mater., 1986, 174, 109–110.
33. N. Chaban and I. Kuz'ma, Izvestiya Akademii Nauk SSSR, Neorganicheskie Materialy, 1973, 9, 1908–1911.
34. M. Ade and H. Hillebrecht, Inorg. Chem., 2015, 54, 6122–6135.
35. L. Häggström, R. Wäppling, T. Ericsson, Y. Andersson and S. Rundqvist, J. Solid State Chem., 1975, 13, 84–91.
36. S. Hirt, F. Hilfinger and H. Hillebrecht, Z. Kristallogr. - Cryst. Mater., 2018, 233, 295–307.
37. J. Cedervall, S. Kontos, T. C. Hansen, O. Balmes, F. J. Martinez-Casado, Z. Matej, P. Beran, P. Svedlindh, K. Gunnarsson and M. Sahlberg, J. Solid State Chem., 2016, 235, 113–118.
38. M. A. McGuire and D. S. Parker, J. Appl. Phys., 2015, 118, 163903.
39. M. Werwiński, S. Kontos, K. Gunnarsson, P. Svedlindh, J. Cedervall, V. Höglin, M. Sahlberg, A. Edström, O. Eriksson and J. Rusz, Phys. Rev. B, 2016, 93, 174412.
40. T. N. Lamichhane, V. Taufour, S. Thimmaiah, D. S. Parker, S. L. Bud’ko and P. C. Canfield, J. Magn. Magn. Mater., 2016, 401, 525–531.
41. D. Hedlund, J. Cedervall, A. Edström, M. Werwiński, S. Kontos, O. Eriksson, J. Rusz, P. Svedlindh, M. Sahlberg and K. Gunnarsson, Phys. Rev. B, 2017, 96, 094433.
42. I. Opahle, G. K. Madsen and R. Drautz, Phys. Chem. Chem. Phys., 2012, 14, 16197–16202.
43. I. Opahle, A. Parma, E. J. McEniry, R. Drautz and G. K. H. Madsen, New J. Phys., 2013, 15, 105010.
44. Q. Gao, I. Opahle, O. Gutfleisch and H. Zhang, Acta Mater., 2020, 186, 355–362.
45. D. Ohmer, G. Qiang, I. Opahle, H. K. Singh and H. Zhang, Phys. Rev. Mater., 2019, 3, 053803.
46. H. K. Singh, Z. Zhang, I. Opahle, D. Ohmer, Y. Yao and H. Zhang, Chem. Mater., 2018, 30, 6983–6991.
47. J. E. Saal, S. Kirklin, M. Aykol, B. Meredig and C. Wolverton, JOM, 2013, 65, 1501–1509.
48. G. Kresse and J. Furthmüller, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 11169.
49. G. Kresse and D. Joubert, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 1758.
50. K. Koepernik and H. Eschrig, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 1743.
51. J. D. Bocarsly, E. E. Levin, C. A. Garcia, K. Schwennicke, S. D. Wilson and R. Seshadri, Chem. Mater., 2017, 29, 1613–1622.
52. S. Kirklin, J. E. Saal, B. Meredig, A. Thompson, J. W. Doak, M. Aykol, S. Rühl and C. Wolverton, npj Comput. Mater., 2015, 1, 15010.
53. M. Werwiński, A. Edström, J. Rusz, D. Hedlund, K. Gunnarsson, P. Svedlindh, J. Cedervall and M. Sahlberg, Phys. Rev. B, 2018, 98, 214431.
54. I. A. Zhuravlev, V. P. Antropov and K. D. Belashchenko, Phys. Rev. Lett., 2015, 115, 217201.
55. P. Oppeneer, Handbook of Magnetic Materials, Elsevier, Amsterdam, 2001, vol. 13.
56. X.-H. Li, C.-H. Xing, H.-L. Cui and R.-Z. Zhang, J. Phys. Chem. Solids, 2019, 126, 65–71.
57. Y. Zhou, H. Xiang, F. Dai and Z. Feng, Mater. Res. Lett., 2017, 5, 440–448.
58. J. Cedervall, E. Nonnet, D. Hedlund, L. HaÌggstroÌm, T. Ericsson, M. WerwinÌski, A. EdstroÌm, J. Rusz, P. Svedlindh and K. Gunnarsson, et al. , Inorg. Chem., 2018, 57, 777–784.
59. S. Rundqvist, et al. , Acta Chem. Scand., 1962, 16, 1–19.
60. C. Bormio-Nunes, C. A. Nunes, A. A. Coelho, M. I. S. T. Faria, P. A. Suzuki and G. C. Coelho, J. Alloys Compd., 2010, 508, 5–8.
61. H. Baurecht, H. Boller and H. Nowotny, Monatsh. Chem., 1971, 102, 373–384.
62. C. Guy and A. Uraz, J. Less-Common Met., 1976, 48, 199–203.
63. Z. Xie, D. Geng and Z. Zhang, Appl. Phys. Lett., 2010, 97, 202504.
64. X. Wang, R. Xiao, H. Li and L. Chen, Phys. Rev. Lett., 2017, 118, 195901.
65. A. Jain, S. P. Ong, G. Hautier, W. Chen, W. D. Richards, S. Dacek, S. Cholia, D. Gunter, D. Skinner, G. Ceder and K. a. Persson, APL Mater., 2013, 1, 011002.
66. I. Opahle, H. K. Singh, J. Zemen, O. Gutfleisch and H. Zhang, 2020, arXiv preprint arXiv:2001.00959.
67. D. Potashnikov, E. Caspi, A. Pesach, A. Hoser, S. Kota, L. Verger, M. Barsoum, I. Felner, A. Keren and O. Rivin, J. Magn. Magn. Mater., 2019, 471, 468–474.
68. J. Cedervall, M. S. Andersson, D. Iuşan, E. K. Delczeg-Czirjak, U. Jansson, P. Nordblad and M. Sahlberg, J. Magn. Magn. Mater., 2019, 482, 54–60.
69. F. Mouhat and F.-X. Coudert, Phys. Rev. B: Condens. Matter Mater. Phys., 2014, 90, 224104.
70. Y. Bai, X. Qi, X. He, D. Sun, F. Kong, Y. Zheng, R. Wang and A. I. Duff, J. Am. Chem. Soc., 2019, 102, 3715–3727.
71. U. Mizutani, MRS Bull., 2012, 37, 169.
72. Y. Zhang, Z. Mao, Q. Han, Y. Li, M. Li, S. Du, Z. Chai and Q. Huang, Materialia, 2020, 12, 100810.
73. S. Maintz, V. L. Deringer, A. L. Tchougréeff and R. Dronskowski, J. Comput. Chem., 2016, 37, 1030–1035.
74. P. Bruno, Phys. Rev. B: Condens. Matter Mater. Phys., 1989, 39, 865.
75. B. Hallemans, P. Wollants and J. Roos, Z. Metallkd., 1994, 85, 676–682.
76. J. Thakur, P. Rani, M. Tomar, V. Gupta and M. K. Kashyap, AIP Conf. Proc., 2019, p. 020012.
77. V. Antropov, L. Ke and D. Åberg, Solid State Commun., 2014, 194, 35–38.
78. M. Richter, J. Phys. D: Appl. Phys., 1998, 31, 1017.
79. G. Daalderop, P. Kelly and M. Schuurmans, Phys. Rev. B: Condens. Matter Mater. Phys., 1991, 44, 12054.
80. C. A. Garcia, J. D. Bocarsly and R. Seshadri, Phys. Rev. Mater., 2020, 4, 024402.
81. J. A. Arregi, M. Horkỳ, K. Fabianová, R. Tolley, E. E. Fullerton and V. Uhlíř, J. Phys. D: Appl. Phys., 2018, 51, 105001.
82. P. Arora, M. Chattopadhyay and S. Roy, Appl. Phys. Lett., 2007, 91, 062508.
83. M. Yu, L. Lewis and A. Moodenbaugh, J. Appl. Phys., 2003, 93, 10128–10130.
84. L. T. Alameda, P. Moradifar, Z. P. Metzger, N. Alem and R. E. Schaak, J. Am. Chem. Soc., 2018, 140, 8833–8840.
85. N. N. M. Discovery, (please search for the data using the author name “Chen Shen”), https://repository.nomad-coe.eu.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: 10.1039/d0ta11026d

---