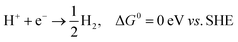Design of phosphorus-functionalized MXenes for highly efficient hydrogen evolution reaction

Abstract

As an important family of 2D materials, MXenes show great potential in various applications due to their specific physical and chemical properties, such as high conductivity and surface activity. Here, we investigate 54 phosphorus-functionalized MXenes (P-MXenes) and screen out 10 stable structures by analyzing their dynamical, thermal, and mechanical stabilities based on first-principles calculations. We find that these stable P-MXenes remain metallic and show weak magnetism. We show that they are effective as electrocatalysts for the hydrogen evolution reaction (HER) with near-zero Gibbs free energies of hydrogen adsorption, which are comparable to that of Pt. To understand the microkinetic process in the HER, an explicit water model is used to examine the Volmer–Heyrovsky (V–H) and Volmer–Tafel (V–T) pathways. We find that P-MXenes show a high HER performance along the V–H process due to the low activation barrier. Our systematic study confirms the possibility for the phosphorus-functionalization of MXenes, guides the design of novel electrocatalysts for the HER via surface-modification, and provides deep understanding on the HER mechanism.

---

1 Introduction

Two-dimensional (2D) materials have been intensively studied from theoretical and experimental perspectives due to their excellent physical and chemical properties, such as semiconductivity, strong spin-orbital coupling, high conductivity, and chemical activity.^1,2 2D materials, such as graphene, black phosphorus, transition metal dichalcogenides, and hexagonal boron nitride, have shown wide-range applications spanning from devices, optoelectronics, sensors, and catalysts, to medical science and technology.^3–5 As a fast-growing family of 2D materials, MXenes have recently attracted increasing attention because of their unique combination of various properties, such as electrical conductivity, mechanical property, and chemical activity, which result especially in application for energy storage and harvesting, such as Li batteries, supercapacitors, and catalysis.^6,7 MXenes are 2D transition metal carbides or nitrides with a general formula of M_n+1X_n (n = 1–3), where the metal atoms are exposed on their surfaces. MXenes have strong interaction with small molecules, such as O₂ and H₂O, and show high activity in the oxygen reduction reaction (ORR) and water splitting.^8–10

Normally, MXenes could be obtained by chemically etching their precursors, leading to a functionalized surface with various functional groups, such as O, F, Cl, OH, and N.^11–16 Surface-functionalized MXenes exhibit different physical and chemical properties from their pristine counterparts. For example, Ti₂CO₂ is semiconducting, while Ti₂C is metallic.¹⁷ Most importantly, surface functionalization benefits the catalytic performance of MXenes. For example, oxygen-functionalized Ti₃C₂ (Ti₃C₂O₂) presented the best HER activity with a nearly perfect Gibbs free energy (∼0 eV) at a H coverage of 4/8, much better than that of bare Ti₃C₂ (∼−1.4 eV).¹⁸ Therefore, novel properties, such as improved catalytic activity and long-term stability, could be developed in MXenes by modifying their surface chemistry.^19–21

Recently, phosphorized MoCT_x was obtained by a simple phosphorization, and showed improved HER activity, indicating the potentially excellent properties of MXenes in combination with the P element.²² Moreover, as an earth-abundant element (∼0.1%), phosphorus plays a vital role in modern society; then how to fully use it is also a hot issue in scientific research.²³ To the best of our knowledge, however, there is no systematic investigation of phosphorus-functionalized MXenes (P-MXenes) and their application in catalysis. In this work, we present a comprehensive study on 54 P-functionalized M₂C (M = transition metals) monolayers in different symmetries (2H-CC, 2H-CH, 2H-HH, 1T-CC, 1T-CH, and 1T-HH) and evaluate their structural, mechanical, magnetic, electronic and catalytic properties based on density-functional theory (DFT) calculations. We find that 10 structures are dynamically, mechanically, and thermodynamically stable. We show that M₂CP₂ remains metallic and some of the monolayers exhibit weak or no magnetism due to the anti-magnetic moment of P or the hybridization between TM-d (TM-transition metal) and P-p orbitals. We further show that their phases could be transferred between 2H-CH and 2H-HH/-CC with a low energy barrier. P-MXenes demonstrate excellent HER performance because the Gibbs free energy of hydrogen adsorption is near zero at certain H coverages. Based on an explicit water model, we find that the H* reduction on P-MXenes via the V–H process experiences a relatively low energy barrier at the equilibrium electrode potential.

2 Computational methods

All the computations were performed based on density-functional theory (DFT), as implemented in the Vienna Ab initio Simulation Package (VASP).^24,25 The Perdew–Burke–Ernzerhof (PBE) functional within the generalized gradient approximation was used for the exchange–correlation energy.²⁶ The cutoff energy for the plane-wave basis was 500 eV. The coverage tolerances for energy and force were set to 10⁻⁵ eV and −0.02 eV Å⁻¹, respectively. The Brillouin zone was sampled with a K-point of 4 × 4 × 1 for the supercell 3 × 3 × 1 in reciprocal space during geometry optimization.²⁷ To avoid interaction between neighboring images, a vacuum space of >15 Å was adopted in the z direction. The standard hydrogen electrode (U_SHE) was theoretically defined in solution (pH = 0, p(H₂) = 1 bar). The DFT-D3 method was adopted to include dispersion correction for the hydrogen bonding between water molecules.²⁸ The climbing-image nudged elastic band (CI-NEB) method²⁹ implemented in VASP was used to determine the diffusion energy barrier and the minimum energy pathways for H₂ evolution on the P-MXene surface. The transition states were obtained by relaxing the force below 0.05 eV Å⁻¹. Only one imaginary frequency exists in the transition state.

In an acid solution, the overall HER pathway can be described as:³⁰

Upon setting the reference potential to be that of the standard hydrogen electrode (SHE), the chemical potential (chemical potential per H) for the initial (H⁺ + e⁻) and final (1/2H₂) states is equal.³¹ Hence, the Gibbs free energy of an intermediate adsorbed hydrogen (H*) is an important descriptor for the HER activity of the electrocatalyst, and the HER performance can be quantified using the reaction Gibbs free energy of hydrogen adsorption (ΔG_H),

ΔG_H = ΔE_H + E_ZPE − TΔS

where, ΔE_H is the energy difference directly obtained by DFT calculations and is defined as:

ΔE_H = E[nH] − E[(n − 1)H] − 1/2E[H₂]

where E[nH] and E[(n − 1)H] represent the total energies of the catalyst adsorbing n and (n − 1)H atoms, respectively. E[H₂] is the energy of H₂. ΔE_ZPE and TΔS are zero-point energy and the entropy between adsorbed hydrogen and hydrogen in the gas phase, respectively, where ΔE_ZPE − TΔS is obtained using the Vaspkit code.³²

3 Results and discussion

In this work, we focus on searching for new stable P-functionalized MXenes (M₂CP₂), which have a five-atom-thick layer in a sequence of P–M–C–M–P. Considering that there are two possible phases (2H and 1T) and three alignments (CC, CH, and HH) of the P atom on the surfaces of M₂C, there are six structures for each M₂CP₂ (Fig. 1). Specifically, there are two possible sites for P to stay, top carbon (C) and the center of the honeycomb (H). If the P atoms at both sides occupy the C or H sites, these structures are named M₂CP₂-2H(1T)-CC or M₂CP₂-2H(1T)-HH. Otherwise, the structure is denoted as M₂CP₂-2H(1T)-CH, in which the P atoms align asymmetrically on both sides. In the family of 2D M₂CP₂, M is the transition metal (TM), including 3d (Ti, V, and Cr), 4d (Zr, Nb, and Mo), and 5d (Hf, Ta, and W) elements. To evaluate the structural stability and possible experimental realization, a series of calculations are carried out, including structure optimization, formation energy, phonon dispersion, mechanical property, and ab initio molecular dynamics (AIMD) simulation.³³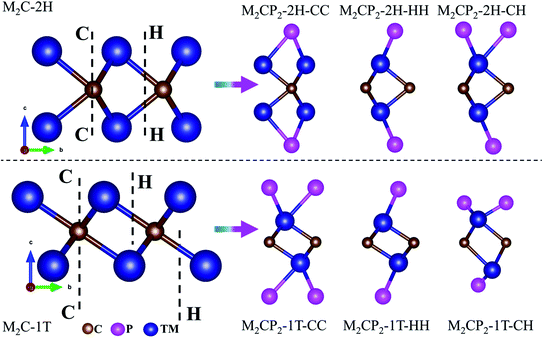

Fig. 1 Side views of optimized 2D M₂C and P-functionalized M₂C (M₂CP₂) with different symmetries. Blue, brown and purple denote transition metals, carbon and phosphorus, respectively.

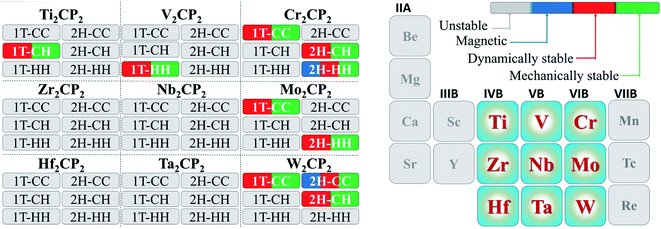
3.1 Structure optimization and stability

We first carried out calculations to confirm the dynamical stabilities of the designed structures. Our computations indicate that all structures of M₂CP₂ for M = Zr, Nb, Hf, and Ta are dynamically unstable because of the large imaginary frequencies in the Brillouin zone (Fig. S1–S6†). For M = Ti, V, Cr, Mo, and W, some M₂CP₂ structures show the perfect phonon dispersion spectra (Fig. S7†). Specifically, Cr₂CP₂ (W₂CP₂) is stable in 1T-CC, 2H-CH (2H-CC), and 2H-CH phases (Fig. S8†). Mo₂CP₂ has two possible stable structures, Mo₂CP₂-1T-CC/2H-HH (Fig. S9†). Ti₂CP₂ and V₂CP₂ exhibit only one stable structure, that is, Ti₂CP₂-1T-CH and V₂CP₂-1T-HH (Fig. S9†). We further screen out the stable structures by AIMD at 300 K for 2 ps with a time step of 1 fs. The results show that all the above predicted structures are stable at room temperature (Fig. S10†).

Additionally, the mechanical stability is calculated. For 2D materials, the criteria for evaluating mechanical stability are based on the Born principle,³⁴ by calculating four nonzero elastic constants c₁₁, c₂₂, c₁₂, and c₆₆ using the standard Voigt notation.³⁵ Moreover, the hexagonal structure further reduces the complexity, since c₁₁ = c₂₂ and c₆₆ = (c₁₁ − c₁₂)/2 according to the symmetry.³⁴ Then the 2D membrane is stable if the in-plane planar Young's (Y_x, Y_y) and shear moduli (G_xy) are positive, which are calculated below:

Y_x = (c₁₁c₂₂ − c₁₂c₂₁)/c₂₂

Y_y = (c₁₁c₂₂ − c₁₂c₂₁)/c₁₁

G_xy = c₆₆

The strain–stress method is adopted to calculate Y_x and G_xy,³⁶ and graphene is taken as a reference. The calculated Young's and shear moduli of graphene are 341.42 and 144.82 N m⁻¹ (Table 1), respectively, which are in good agreement with the previous study.³⁵ Although the mechanical strengths of P-MXenes could not be compatible with that of graphene due to the much smaller values of Young's and shear moduli, their mechanical stabilities are promising because of the positive Y_x and G_xy (Table 1).

Table 1 In-plane planar elastic constants c₁₁, Young's moduli Y_x and Y_y, and shear moduli G_xy of M₂CP₂

	c 11 (N m^−1)	Y x (N m^−1)	Y y (N m^−1)	G xy (N m^−1)
Graphene	352.68	341.42	341.42	144.82
W2CP2-1T-CC	174.12	128.64	128.64	42.57
W2CP2-2H-CC	214.19	95.38	95.38	27.33
W2CP2-2H-CH	202.15	136.09	136.09	43.30
Cr2CP2-1T-CC	152.31	131.15	131.15	47.77
Cr2CP2-2H-HH	219.16	144.30	144.30	45.54
Cr2CP2-2H-CH	208.98	131.04	131.04	40.68
Mo2CP2-2H-HH	199.15	132.12	132.12	41.81
Mo2CP2-1T-CC	158.05	125.28	125.28	43.04
Ti2CP2-1T-CH	171.13	144.43	144.43	51.77
V2CP2-1T-CH	147.36	63.06	63.06	17.95
V2CP2-1T-HH	181.33	110.95	110.95	34.18

---

We further calculated the formation energy (E_f) to evaluate the possibility for the experimental realization of stable 2D P-MXenes using E_f = E(M₂CP₂) − E(M₂C) − 2E(P), where E(M₂CP₂) and E(M₂C) are the total energies of 2D M₂CP₂ and M₂C, respectively, and E(P) is the chemical potential of the P atom obtained from the total energy of its unit cell divided by the number of atoms in the cell. The results show that most of the processes are exothermic due to the negative formation energy (Table S1†), indicating that they could be fabricated in experiments. However, Ti₂CP₂-1T-CH exhibits a large positive E_f of 11.64 eV, leading to less possibility for its experimental realization (endothermic process).

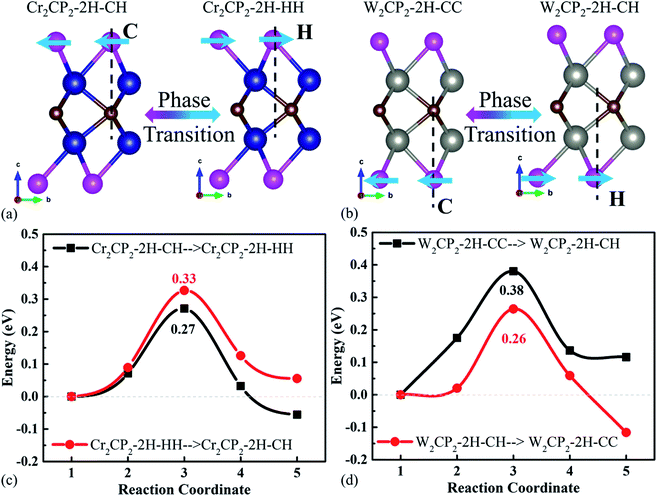
It was recently reported that the phase transition of MXenes could be resulting from oxygen coverage.³⁷ Meanwhile, we see that the energies of the designed structures with the same formula are close to each other (Table S2†). For example, the energy difference between Cr₂CP₂-2H-CH (W₂CP₂-2H-CC) and Cr₂CP₂-2H-HH (W₂CP₂-2H-CH) is merely 0.05 (0.12) eV, indicating that the phase transition would happen between these two phases. To confirm this point, the CI-NEB method was adopted to investigate the kinetic transition barrier using Cr₂CP₂ and W₂CP₂ as examples (Fig. 2). The P atoms aligned to the C atoms move to the center of the honeycomb, leading to the phase transition from 2H-CC (2H-CH) to 2H-CH (2H-HH) (Fig. 2a and b). We find that the transition barriers are quite small, 0.27 and 0.26 eV for 2H-CH to 2H-HH and 2H-CH to 2H-CC, respectively (Fig. 2c and d). Reversely, the barriers are slightly higher, 0.33 and 0.38 eV for the transitions, respectively. Additionally, 1T-CC is believed to be the ground states of Cr₂CP₂ , Mo₂CP₂, and W₂CP₂, due to the more negative system energies (Table S2†). It is believed that the stable stacking of P-MXenes is important to their physical and chemical properties.³⁷ Moreover, the low energy barrier for a phase transition is beneficial to volume stability when external ions or molecules are adsorbed on the surface of P-MXenes, leading to potential application in ion-batteries³⁸ and catalysis.³⁹

Fig. 2 Phase transitions between similar structures of M₂CP₂. The schematic representation of phase transition for (a) Cr₂CP₂ and (b) W₂CP₂. The corresponding reaction energy for (c) Cr₂CP₂ and (d) W₂CP₂.

3.2 Electronic and magnetic properties

The above analysis shows that ten 2D M₂CP₂ structures are dynamically, thermally, and mechanically stable. Based on the optimized structures, we investigated their electronic and magnetic properties. We find that all the stable 2D M₂CP₂ structures are metallic, as indicated by their gapless band structures near the Fermi level (Fig. S11 and S12†). Herein, the surface covered with the P atoms cannot change its highly conductive properties, which should be beneficial to its catalytic applications.

Different from the electronic properties, the magnetism of 2D M₂CP₂ becomes weak or even disappears compared with the magnetic M₂C. The calculated results show that only Cr₂CP₂-2H-HH and W₂CP₂-2H-CC have non-zero magnetic moments, which are mainly contributed to Cr (0.28 μ_B) and W atoms (0.09 μ_B) (Fig. S12†). Specifically, a large magnetic moment in Cr₂C is quenched by the P atom after the surface functionalization. To understand the change, the spin-polarized partial densities of states (PDOSs) of Cr and P were calculated for Cr₂C and Cr₂CP₂-1T-CC. The 2D and 3D charge density differences were also calculated to find the charge transfer between P and Cr. We can see that the strong magnetism in Cr₂C is contributed to the high asymmetry of spin-up and spin-down Cr-d states, especially the localized Cr-d orbitals near the Fermi level (dashed line at 0 eV, Fig. 3). However, the electrons between Cr and C redistribute and accumulate between Cr and P when the surfaces of Cr₂C are covered with the P atoms, leading to a symmetric distribution of spin-up and spin-down PDOSs. Then, the system magnetic moment of Cr₂CP₂ disappears. The results confirm that the magnetic properties of MXenes depend on their terminal groups.⁴⁰

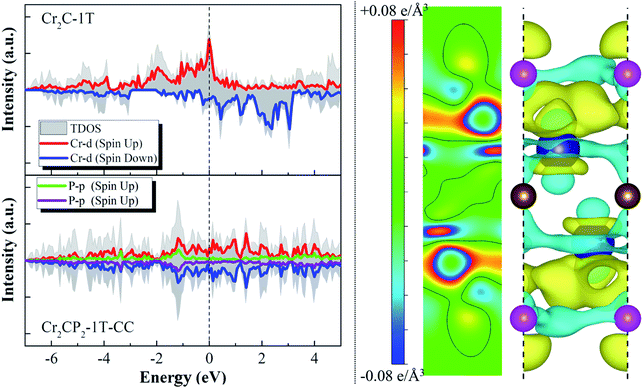Fig. 3 Spin-polarized densities of states (DOSs) of Cr₂C-1T and Cr₂CP₂-1T-CC (left column); 2D and 3D charge density differences of Cr₂CP₂-1T-CC (right column). The isosurface is set to 0.06e Å⁻³.

Based on the above analysis, the physical properties of the 54 designed M₂CP₂ monolayers are summarized (Fig. 4).

Fig. 4 Summary of structural, dynamical, mechanical and magnetic properties of 2D M₂CP₂.

3.3 ΔG_H on M₂CP₂ and the optimal coverage

Pure M₂C with transition metals exposed on the surfaces has been proved to effectively split water molecules. However, the strong M–H bonding impedes the reaction rate, as indicated by the large Gibbs free energy (ΔG_H) of *H (<−1.0 eV).⁴¹ The moderate strength of the P–H bond has been proved to facilitate the HER activity in phosphorus-based materials.^31,42 Metallic M₂CP₂ also has high conductivity, which is a prerequisite for electrocatalysis (Fig. S11 and S12†). Hence, it is meaningful to study the HER performance of stable M₂CP₂ with high intrinsic conductivity and rich-P surfaces.

In thermal equilibrium, ΔG_H qualitatively evaluates the HER performance in an acid situation. ΔG_H is more close to 0 eV, so the reaction is faster.³⁰ We consider all possible adsorption sites of *H on one surface of M₂CP₂ (H₁–H₃, Fig. S13a†). The results indicate that H prefers the H₁ site (top of the P atom), due to the lowest adsorption energy (Table S3†). It is noted that some predicted stable M₂CP₂ shows large surface distortion at a certain H coverage due to the relatively small Young's moduli (Table 1). For example, V₂CP₂ shows large surface distortion when only one H adsorbs on it because its Y_x (63.06 N m⁻¹) is the smallest among the 10 stable structures (Fig. S14†). W₂CP₂-2H-CC and Mo₂CP₂-2H-HH could remain stable until the second and third H atom anchors, due to the relatively large Y_x (Fig. S14† and Table 1). The large surface distortion means that these M₂CP₂ structures may be unstable in the HER process, which will not be considered in the following discussion.

Then, we calculated ΔG_H as a function of H coverage in the absence of a water layer (Fig. 5). The results suggest that a P-MXene is catalytically active for the HER, due to the overall low values for the adsorption energy (<|0.5 eV|). Compared with P-MXenes with M = 3d elements (e.g. Cr), 4d and 5d element (e.g. Mo and W) based P-MXenes have stronger H adsorption at low coverage, as indicated by the Barge charge analysis (Fig. S17†). For example, ΔG_H is around −0.1 eV for Cr₂CP₂-2H-CH at a hydrogen coverage of 1/9 (Fig. 5a), while that of W₂CP₂-2H-CH is about −0.42 eV (Fig. 5b). We can see that free energy close to 0 eV happens at a hydrogen coverage from 1/9 to 3/9 for Cr₂CP₂, while 3/9–5/9 for Mo₂CP₂ and W₂CP₂. Hence, the HER is optimal at a H coverage of 2/9 for Cr₂CP₂ and 4/9 for W- or Mo-based P-MXenes, respectively.

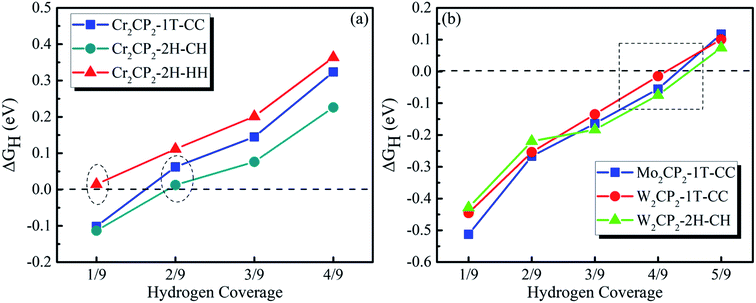Fig. 5 Calculated ΔG_H as a function of hydrogen coverage on (a) Cr₂CP₂ and (b) Mo₂/W₂CP₂, respectively.

As reported, ΔG_H is related not only to the binding energy between H and the slab, but also to the coverages (numbers and arrangement) of H atoms on the active surface.⁴³ Therefore, we analyze the effect of these two factors on the HER in detail (ESI†). We find that the value of charge transfer in the previous step dramatically affects the HER performance in the next step and nearly all M₂CP₂ structures prefer the pathway of R4 (P1 → P13 → P124 → P1234) (Fig. S16 and S17†). Our result shows that the HER performance is sensitive to the H coverage and arrangement on the surface, which provides a guidance for the HER improvement by controlling the active sites and the distance between adsorbed H through space confinement.⁴⁴

3.4 Water–catalyst interface

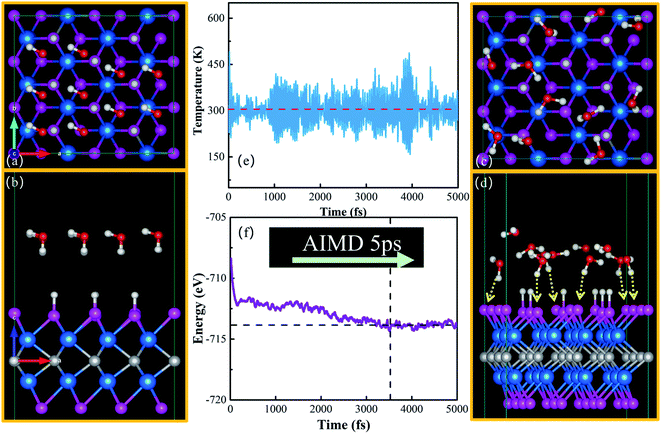
The above evaluation of the HER performance on M₂CP₂ is based on the thermoneutral electrode potential (ΔG_H → 0 eV). Although most materials have a ΔG_H quite close to that of Pt(111) (0.08 eV), their HER performances cannot be comparable to that of Pt(111), that is, the principle of G ∼ 0 eV for hydrogen evolution cannot explain the observed kinetics only.⁴⁵ Recently, an explicit water model was proposed to evaluate the Volmer, Tafel, and Heyrovsky steps from microkinetic perspectives (Fig. S19†).

Then, we examine the HER microkinetic activity around the H coverage for optimal HER (Fig. 6) using W₂CP₂-2H-CH (WCH) as an example. The water–catalyst interface is a crucial part in this simulation. We adopted the approach proposed by Lindgren et al., which was initially used to study the HER on Pt(111).⁴⁵ The Helmholtz layer is often set to a 3 Å electrical double layer, which can be represented by one water layer. By tuning the number of H atoms, the electrostatic potential of the interface can be adjusted, which is deduced from the calculation of the work function.⁴⁵

Fig. 6 Top (a) and side (b) views of the initial configuration of the water–catalyst system; top (c) and side (d) views of the stable water–solid interface after the AIMD simulation. Variations of temperature (e) and energy (f) for the water–WCH interface in the AIMD simulations.

Here, we put one layer of water molecules on the surface of H-adsorbed WCH. A supercell with a size of 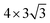units and a H coverage of 6/12 was used. The initial setup of the water layer is that the H atoms of each H₂O molecule point down toward the surface, as proposed by Tang Qi et al.⁴⁶ (Fig. 6a and b). A stable water layer with 10H₂O molecules is achieved by AIMD simulation at 300 K for 5 ps. The tiny variation of energy indicates that the water layer is stable after 3.5 ps (dashed line, Fig. 6f). We find that there has a weak bonding between P and H₂O, as highlighted by the yellow dashed arrow (Fig. 6d). Since there is no experimental study on the exact structure of the water overlayer on WCH, we calculated the electrode potential corresponding to the model system at −0.28 V, in comparison with a NHE (4.4 V, Fig. S12†), which agrees well with a previous study.⁴⁷

Then, a proton (H⁺) is added onto the water molecule to introduce a hydronium ion (H₃O⁺),⁴⁶ which is further optimized to obtain a stable structure (Fig. S20†). The possible pathways for HER include the Volmer–Heyrovsky (V–H) and Volmer–Tafel (V–T) reactions in acid media (Fig. S19†). It is believed that the Volmer process is very fast, in which initial adsorption of a proton from the acid solution takes place to form an adsorbed H*. Then, if a dissolved proton from the water layer reacts with H* on the surface of the catalyst, H₂ is generated, which is called the V–H reaction (Fig. S20†). If two H*s evolve into one H₂, the process is called the V–T mechanism (Fig. S20†). Since there are proton–electron transfers in a supercell with a periodic boundary, we will use the extrapolation method to counterbalance the changed electrode potential along this pathway.⁴⁶ That is, the reaction energy (ΔE = E(FS) − E(IS)) and activation energy (E_a) at balanced electrode potential (ΔU = 0, work function difference between the IS (initial step) and FS (final step)) will be achieved by extrapolating the results to the balanced electrode potential (Fig. S21†).

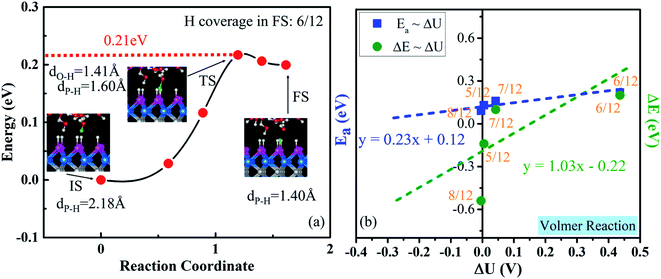
3.5 First step of the HER process: Volmer reaction

Now, we consider the very first step: the Volmer step, which is indicated by the minimum-energy path for the transfer of one proton to the WCH surface (Fig. 7a). It exhibits quite a small activation energy of 0.21 eV and a reaction energy of 0.20 eV. In the transition state, the transferred H is in the middle between O and P, d_O–H = 1.41 Å and d_P–H = 1.60 Å. To obtain the reaction energy (ΔE) and activation energy (E_a) at the balanced electrode potential, we extrapolate our results by studying the Volmer reaction around the optimal H coverage (Fig. 7b and S22†) and the change of ΔU between the IS and FS (Table S4†). The extrapolated E_a and ΔE are 0.12 and −0.22 eV, respectively, indicating that the Volmer step is exothermic (ΔE < 0) and has a small energy barrier at an electrode potential around −0.28 V vs. NHE on the WCH monolayer.

Fig. 7 (a) Minimum-energy pathway for the Volmer reaction on the WCH surface at a H coverage of 6/12 in the final state. Insets show the side views of the IS, TS and FS, where the transferred H is presented in a green color. (b) Reaction energy (ΔE) and activation energy (E_a) for the Volmer reaction as a function of the change in electrode potential ΔU.

3.6 Second step of the HER process: V–H reaction

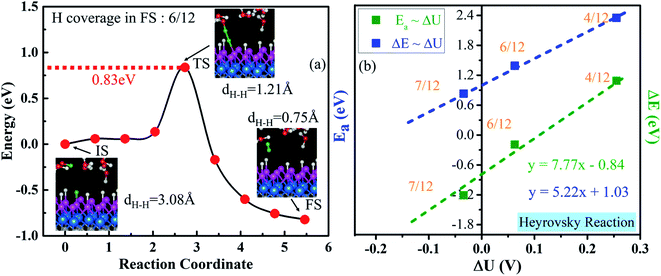
As illustrated in Section 3.4, the V–H reaction needs a proton–electron pair in the water layer to attack one surface H* (Heyrovsky step), where one H* is approached by a hydrogen ion of H₃O⁺ in the water layer and breaks to form H₂ (Fig. 8a). We find that a surface H* and a proton start to approach from a distance of 3.08 Å and break from the catalyst's surface and H₃O⁺ when they are close to 1.21 Å. Then, they climb a barrier of 0.83 eV to overcome the transition step (TS). Lastly, they evolve into one weakly adsorbed H₂ molecule with a d_H–H of 0.75 Å above the catalyst. The corresponding activation energy and reaction energy are 0.83 eV and −0.82 eV at a H coverage of 6/12 (final state), respectively. We also calculate E_a and ΔE at different H coverages (Fig. S23†). Similar to those for the Volmer step, the extrapolated E_a and ΔE for the Heyrovsky reaction are 1.03 and −0.84 eV, respectively (Fig. 8b). Therefore, the H desorption is the rate-determining step in the V–H pathway, due to the much larger activation barrier, compared with that of the Volmer step (0.12 eV, Fig. 7).

Fig. 8 (a) Minimum-energy pathway of the Heyrovsky reaction on the WCH surface at a H coverage of 6/12 in the final state. Insets show the side views of the IS, TS and FS, where the transferred H is presented in a green color. (b) Reaction energy (ΔE) and activation energy (E_a) for the Heyrovsky reaction as a function of the change in electrode potential ΔU.

3.7 Second step of the HER process: V–T reaction

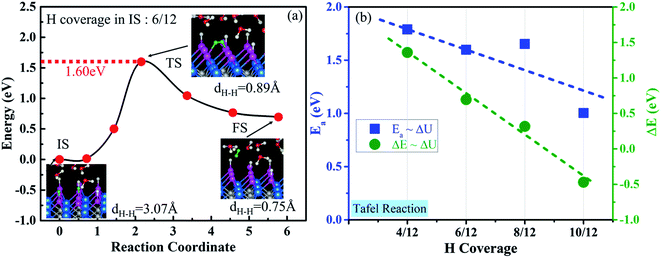
Two surface H atoms evolve into one H₂ in the Tafel process, where there is no extra charge transfer between the water layer and catalyst (Fig. S20†). Therefore, the work function remains unchanged from the initial state to the final state, leading to an uncharged surface potential during the reaction (Fig. S21d†). To evaluate the formation of H₂ from two H*s, the activation and reaction energies were calculated (Fig. S19†) on the WCH surface with a H coverage of 6/12. We find that two adjacent H atoms have a distance (H*–H*) of 3.07 Å in the IS. They approach each other and form a TS with a d_H–H of 0.89 Å. In the final state, the evolved H₂ molecule desorbs from the WCH surface with a H–H bond length of 0.75 Å. The activation energy (E_a) for this Tafel process is calculated to be 1.60 eV, and the reaction energy (ΔE) to be 0.69 eV (Fig. 9a). We also calculate E_a and ΔE at different H coverages (Fig. S24†). Both activation and reaction energies are sensitive to the H coverage (Fig. 9b), and decrease as the H coverage increases. But, we notice that the Tafel reaction is still sluggish even though E_a is down to 1.0 eV at a H coverage of 10/12, which is much larger than the E_a in the Heyrovsky reaction (≤1.0 eV) around an optimal coverage of 4/9.

Fig. 9 (a) Minimum-energy pathway of the Tafel reaction on the WCH surface at a H coverage of 4/9 in the initial state. Insets show the side views of the IS, TS and FS, where the energetic H* is presented in a green color. (b) Activation energy for the Tafel reaction as a function of hydrogen coverage in the IS.

Overall, we study the Volmer, Heyrovsky, and Tafel reactions based on the 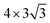WCH supercell at an electrode potential of −0.28 V around a H coverage of 4/9 (∼44%). We find that both activation energies of Heyrovsky and Tafel processes decrease as the H coverage increases, due to the weak binding of P–H at high H coverage (Fig. S16†). By comparing the energy barriers of Heyrovsky and Tafel reactions, we see that E_a for the Heyrovsky pathway goes down faster than that of the Tafel one, and an intersection is observed at a H coverage of 14%. Hence, we conclude that the HER process on P-MXenes follows the V–T pathway with a considerably low reaction barrier at a low H coverage (Fig. 10). As the coverage increased (>14%), it turns to the V–H pathway, due to the low reaction barrier of the Heyrovsky step (Fig. 10). We believe that the V–H process is dominant at the mainly driven coverage (green band, Fig. 10). Besides, we also compare our work with other typical 2D catalyst studies on the HER performance (Table S5†). We find that P-functionalized MXenes show great potential as HER catalysts, due to the relatively low activation barrier and small reaction energy.

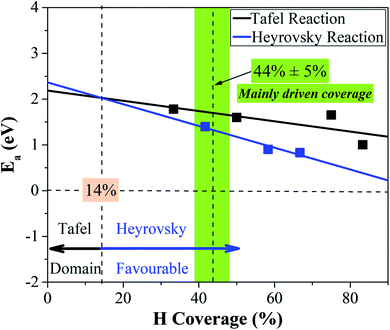Fig. 10 Competition between the Tafel and Heyrovsky reactions as a function of hydrogen coverage in the IS.

4 Conculsions

In summary, we design a new family of MXenes by P-functionalization and systematically investigate their stability, electronic and magnetic properties, and HER performance based on DFT calculations. We find 10 stable structures out of 54 predefined structures. The band structures indicate that the stable structures are metallic with high conductivity, suggesting their potential applications in electrocatalysis. The magnetic moments of MXenes are reduced or disappear after their surfaces are covered with phosphorus atoms due to the hybridization between TM-d and P-p orbitals. Importantly, these stable P-MXenes demonstrate excellent HER performance, due to the Gibbs free energy of hydrogen adsorption near zero at a certain H coverage. We further show that P-MXenes show a potential high HER performance via the Volmer–Heyrovsky mechanism with a relatively low reaction barrier. We expect that our findings will provide insightful guidance on the design of functionalized MXenes and other 2D catalysts for the promotion of water splitting.

Conflicts of interest

There are no conflicts of interest to declare.

Acknowledgements

This work was supported by the Science and Technology Development Fund from Macau SAR (FDCT-0102/2019/A2, FDCT-0035/2019/AGJ, FDCT-0154/2019/A3, FDCT-0081/2019/AMJ, FDCT-199/2017/A3, and FDCT-0125/2018/A3) and Multi-Year Research Grants (MYRG2017-00027-FST, MYRG2018-00003-IAPME, and MYRG2017-00149-FST) from the University of Macau. The DFT calculations were performed at High Performance Computing Cluster (HPCC) of Information and Communication Technology Office (ICTO) at University of Macau.

References

1. E. Skúlason, G. S. Karlberg, J. Rossmeisl, T. Bligaard, J. Greeley, H. Jónsson and J. K. Nørskov, Phys. Chem. Chem. Phys., 2007, 9, 3241–3250.
2. J. R. Schaibley, H. Yu, G. Clark, P. Rivera, J. S. Ross, K. L. Seyler, W. Yao and X. Xu, Nat. Rev. Mater., 2016, 1, 1–15.
3. A. F. Khan, D. A. Brownson, E. P. Randviir, G. C. Smith and C. E. Banks, Anal. Chem., 2016, 88, 9729–9737.
4. K. Novoselov, A. Mishchenko, A. Carvalho and A. C. Neto, Science, 2016, 353, aac9439.
5. Y. Kong, H. Ai, W. Wang, X. Xie, K. H. Lo, S. Wang and H. Pan, ACS Appl. Nano Mater., 2020, 3, 2804–2812.
6. Z. W. Seh, K. D. Fredrickson, B. Anasori, J. Kibsgaard, A. L. Strickler, M. R. Lukatskaya, Y. Gogotsi, T. F. Jaramillo and A. Vojvodic, ACS Energy Lett., 2016, 1, 589–594.
7. X. Liang, A. Garsuch and L. F. Nazar, Angew. Chem., 2015, 127, 3979–3983.
8. Z. Li, Z. Zhuang, F. Lv, H. Zhu, L. Zhou, M. Luo, J. Zhu, Z. Lang, S. Feng and W. Chen, Adv. Mater., 2018, 30, 1803220.
9. C. F. Du, K. N. Dinh, Q. Liang, Y. Zheng, Y. Luo, J. Zhang and Q. Yan, Adv. Energy Mater., 2018, 8, 1801127.
10. C. Ling, L. Shi, Y. Ouyang, Q. Chen and J. Wang, Adv. Sci., 2016, 3, 1600180.
11. C. Ling, L. Shi, Y. Ouyang and J. Wang, Chem. Mater., 2016, 28, 9026–9032.
12. A. C. Rajan, A. Mishra, S. Satsangi, R. Vaish, H. Mizuseki, K.-R. Lee and A. K. Singh, Chem. Mater., 2018, 30, 4031–4038.
13. H. Weng, A. Ranjbar, Y. Liang, Z. Song, M. Khazaei, S. Yunoki, M. Arai, Y. Kawazoe, Z. Fang and X. Dai, Phys. Rev. B: Condens. Matter Mater. Phys., 2015, 92, 075436.
14. S. Li, P. Tuo, J. Xie, X. Zhang, J. Xu, J. Bao, B. Pan and Y. Xie, Nano Energy, 2018, 47, 512–518.
15. D. Wang, Y. Gao, Y. Liu, Y. Gogotsi, X. Meng, G. Chen and Y. Wei, J. Mater. Chem. A, 2017, 5, 24720–24727.
16. M. Khazaei, M. Arai, T. Sasaki, A. Ranjbar, Y. Liang and S. Yunoki, Phys. Rev. B: Condens. Matter Mater. Phys., 2015, 92, 075411.
17. Y. Zhang, X.-H. Zha, K. Luo, N. Qiu, Y. Zhou, J. He, Z. Chai, Z. Huang, Q. Huang and Y. Liang, J. Phys. Chem. C, 2019, 123, 6802–6811.
18. J. Liu, W. Peng, Y. Li, F. Zhang and X. Fan, Trans. Tianjin Univ., 2020, 1–23.
19. Y. Li, X. Deng, J. Tian, Z. Liang and H. Cui, Appl. Mater. Today, 2018, 13, 217–227.
20. H. Yu, Y. Wang, Y. Jing, J. Ma, C. F. Du and Q. Yan, Small, 2019, 15, 1901503.
21. Z. Fu, C. Ling and J. Wang, J. Mater. Chem. A, 2020, 8, 7801–7807.
22. G. Qu, Y. Zhou, T. Wu, G. Zhao, F. Li, Y. Kang and C. Xu, ACS Appl. Energy Mater., 2018, 1, 7206–7212.
23. K. Ruttenberg, TrGeo, 2003, vol. 8, p. 682.
24. G. Kresse and J. Furthmüller, Comput. Mater. Sci., 1996, 6, 15–50.
25. G. Kresse and J. Furthmüller, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 11169.
26. J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865.
27. H. J. Monkhorst and J. D. Pack, Phys. Rev. B: Solid State, 1976, 13, 5188.
28. E. Skúlason, V. Tripkovic, M. E. Björketun, S. Gudmundsdottir, G. Karlberg, J. Rossmeisl, T. Bligaard, H. Jónsson and J. K. Nørskov, J. Phys. Chem. C, 2010, 114, 18182–18197.
29. G. Henkelman, B. P. Uberuaga and H. Jónsson, J. Chem. Phys., 2000, 113, 9901–9904.
30. J. K. Nørskov, T. Bligaard, A. Logadottir, J. Kitchin, J. G. Chen, S. Pandelov and U. Stimming, J. Electrochem. Soc., 2005, 152, J23.
31. J. K. Nørskov, J. Rossmeisl, A. Logadottir, L. Lindqvist, J. R. Kitchin, T. Bligaard and H. Jonsson, J. Phys. Chem. B, 2004, 108, 17886–17892.
32. V. Wang, N. Xu, J. Liu, G. Tang and W. Geng, 2019, arXiv preprint arXiv:1908.08269.
33. R. N. Barnett and U. Landman, Phys. Rev. B: Condens. Matter Mater. Phys., 1993, 48, 2081.
34. Y. Ding and Y. Wang, J. Phys. Chem. C, 2013, 117, 18266–18278.
35. R. C. Andrew, R. E. Mapasha, A. M. Ukpong and N. Chetty, Phys. Rev. B: Condens. Matter Mater. Phys., 2012, 85, 125428.
36. A. Politano and G. Chiarello, Nano Res., 2015, 8, 1847–1856.
37. J. D. Gouveia, F. Viñes, F. Illas and J. R. Gomes, Phys. Rev. Mater., 2020, 4, 054003.
38. X. Li, M. Li, Q. Yang, H. Li, H. Xu, Z. Chai, K. Chen, Z. Liu, Z. Tang and L. Ma, ACS Nano, 2020, 14, 541–551.
39. H. Pan, Sci. Rep., 2016, 6, 32531.
40. N. C. Frey, A. Bandyopadhyay, H. Kumar, B. Anasori, Y. Gogotsi and V. B. Shenoy, ACS Nano, 2019, 13, 2831–2839.
41. L. R. Johnson, S. Sridhar, L. Zhang, K. D. Fredrickson, A. S. Raman, J. Jang, C. Leach, A. Padmanabhan, C. C. Price and N. C. Frey, ACS Catal., 2019, 10, 253–264.
42. S. Lin, Y. Li, J. Qian and S. P. Lau, Mater. Today Energy, 2019, 12, 1–25.
43. B. Conway and L. Bai, Electrochim. Acta, 1986, 31, 1013–1024.
44. Z. Chen, K. Leng, X. Zhao, S. Malkhandi, W. Tang, B. Tian, L. Dong, L. Zheng, M. Lin and B. S. Yeo, Nat. Commun., 2017, 8, 1–9.
45. P. Lindgren, G. Kastlunger and A. A. Peterson, ACS Catal., 2019, 10, 121–128.
46. Q. Tang and D.-e. Jiang, ACS Catal., 2016, 6, 4953–4961.
47. J. Rossmeisl, E. Skúlason, M. E. Björketun, V. Tripkovic and J. K. Nørskov, Chem. Phys. Lett., 2008, 466, 68–71.

---

Footnotes

† Electronic supplementary information (ESI) available. See DOI: 10.1039/d0ta10136b

‡ These authors contributed equally to this work.

---