Open Access Article
Open Access ArticleUnravelling thermal stress due to thermal expansion mismatch in metal–organic frameworks for methane storage†
Jelle
Wieme
 and
Veronique
Van Speybroeck
and
Veronique
Van Speybroeck
 *
*
Center for Molecular Modeling, Ghent University, Tech Lane Ghent Science Park Campus A, Technologiepark 46, 9052 Zwijnaarde, Belgium. E-mail: veronique.vanspeybroeck@ugent.be
First published on 1st February 2021
Abstract
Thermal stress is present in all systems undergoing temperature changes during their operation. Metal–organic frameworks (MOFs) are a class of porous, crystalline materials ideally suited for a wide range of adsorption-based technologies. The release and consumption of the heat of adsorption instigate temperature fluctuations and thermal stress in these materials that could induce disruptive volume changes. To bring these materials to engineering applications, it is of utmost importance to understand their thermal expansion behavior and the overall induced thermal stress due to thermal expansion mismatch with other components. In this work, we focus on a large group of MOFs known to have promising methane adsorption properties and predict their thermal expansion coefficients based on force field molecular dynamics simulations. Negative thermal expansion (NTE) behavior is predicted for all studied MOFs, and the magnitude of the NTE coefficients is found to be positively correlated with the degree of porosity of the frameworks. Finally, as a proxy for the thermal stress, the thermal pressure coefficient is calculated, which is found to be in the range between polymers and ceramics. Variations within the operating temperature range of MOFs are therefore expected to result in a relatively low thermal stress.
1. Introduction
Temperature fluctuations inducing thermal stress impact the operation of many technological applications. This particularly applies to systems composed of various material constituents in close contact with each other. For example, internal stress arises when the volume response upon varying temperature differs between two components. This so-called thermal expansion mismatch may lead to system failures due to cracks or plastic deformation,1,2 but was recently also exploited to stabilize otherwise inaccessible material phases.3In this study, we focus on metal–organic frameworks (MOFs). This promising class of porous, crystalline materials has mainly been investigated for adsorption-based technologies,4–6 and distinguishes itself from other candidate materials by its chemical and physical versatility.4 These applications where adsorption and desorption processes lie at the basis of their operation might especially be prone to thermal stress as the exchange of guest molecules with the porous framework could lead to large temperature changes without a proper heat management strategy.7–9 Moreover, the temperature is sometimes also used as control parameter for adsorption or desorption of guest molecules in some setups, i.e. temperature swing adsorption (TSA).10
Up to now, there has been limited interest in exploring the thermal properties of these frameworks, despite their relevance for practical adoption of MOFs as adsorbents. It is known that MOFs have a moderate thermal stability,11,12 a small heat capacity range11,13 and are considered to be poor conductors of heat,13,14 but most studies on thermal characteristics focus on a narrow set of well-known materials. The property that has received most attention is their thermal expansion behavior (e.g. ref. 15–18). Many frameworks display negative thermal expansion (NTE), i.e. the volume decreases when the temperature is increased.13,19 While this anomalous behavior could be beneficial for the development of zero-expansion composites for highly-specialized applications,20 it poses some additional design constraints when in contact with conventional materials. Various practical ways of controlling the thermal expansion behavior of MOFs have already experimentally been demonstrated: retrofitting,21 adsorption of guest molecules,17,22,23 changing the organic linkers or metal ions,17,24,25 adding functional groups,16 incorporating defects,26etc. Computational studies corroborate these findings.15,18,27,28
Thermal stress due to thermal expansion mismatch has received even less attention,29 but it was mentioned in the context of MOF thin film applications.30,31 However, it could also be imagined to play a role when MOFs are used in confined environments such as volume-limited storage tank applications for natural gas and hydrogen storage. How thermal stress will impact the durability of the MOF crystals has not yet been investigated. Of course, the tolerable change of thermal expansion mismatch will also depend on the mechanical properties of the framework. It is already known that MOFs are mechanically not very stable, and much research into this is currently being performed.32–34
As a first step towards a better understanding of thermal stress effects, we provide in this work an estimate of the hypothetical thermal stress in closed storage systems by investigating the pressure necessary to keep the MOF from expanding or contracting when the temperature changes (Fig. 1(a)). In other words, we assume that the magnitude of thermal expansion of the MOF is much larger than the relative volume change of its surroundings. In practice, this will also depend on the contact material, but microscopic insight into solid/solid interfaces with MOFs is still in its infancy, except a number of studies on MOF/polymer interfaces for mixed matrix membranes.35 Therefore, we focus on the intrinsic characteristics of a pure MOF crystal and start our investigation by computing the thermal expansion coefficient of a selection of 52 rigid MOFs containing Zn, Cu, Al or Zr inorganic building blocks using force field molecular dynamics (Fig. 1(b)). These MOFs were all experimentally reported to possess good methane storage properties,36 which is necessary for several envisioned application areas of MOFs as efficient adsorbent.37,38 Subsequently, we compute the thermal pressure coefficient γ as the product of the thermal expansion coefficient α0 and the bulk modulus β0 (Fig. 1(c)). This quantity has mainly been considered in the context of thermal effects on the equation of state of solids,39,40 and we introduce it here as an intuitive indicator of the magnitude of isotropic thermal stress. We compare the thermal pressure coefficient with other materials, and with reported amorphization pressures of MOFs to get an intuitive understanding of its magnitude. This comparison suggests that variations within the operating temperature range of MOFs are expected to result in relatively low thermal stress. Finally, our results enable to identify some trends in terms of general MOF characteristics such as porosity and density.
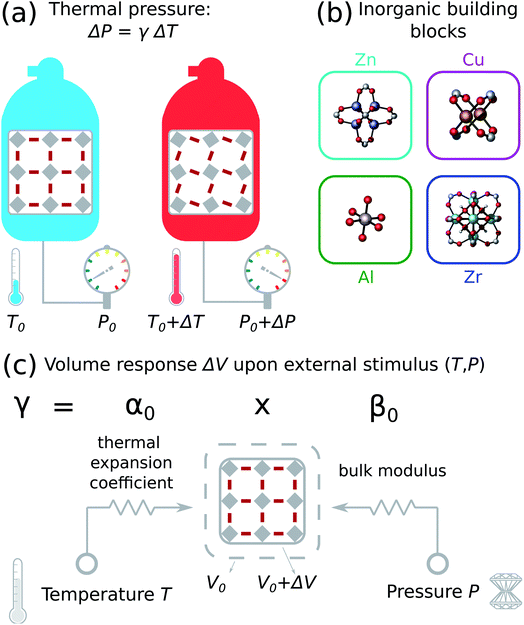 | ||
| Fig. 1 (a) Thermal stress in a storage system subject to a temperature rise approximated with an isotropic thermal pressure. (b) MOFs containing zinc, copper, aluminum and zirconium inorganic building blocks were considered in this study. A full overview is given in Tables S1–S4 in the ESI.† (c) The thermal pressure coefficient γ is an important parameter to quantify the isotropic thermal pressure, which is determined by the resistance to change volume upon temperature (thermal expansion coefficient α0) and pressure (bulk modulus β0) stimuli. | ||
2. Methods
2.1 Materials
The 52 MOFs and their original references are listed in Tables S1–S4 in the ESI.†2.2 Force field derivation
The large unit cells of the MOFs under study make sufficiently long first-principles simulations impossible, and therefore we resorted to a more approximate technique, i.e. force fields.41 The potential energy surface (PES) is then modelled by an analytical force field energy expression relying on a combination of covalent and noncovalent terms.The covalent terms mimic the chemically bonded network, and the required covalent force field parameters were derived with our in-house developed QuickFF protocol.42,43 First, an accurate quantum mechanical PES is obtained using first-principles calculations on cluster models of the inorganic and organic building blocks of the MOFs. The required input data for the QuickFF protocol (equilibrium positions, and forces and Hessian calculated on this structure) are generated using the B3LYP exchange–correlation functional44 as implemented in Gaussian 16.45 Subsequently, using a fitting procedure, the unknown force constants are derived such that the force field PES approximates the quantum mechanical PES in the neighbourhood of the equilibrium structure. The force field expressions used for the approximation of the PES depend on the internal coordinates (bonds, bends, out-of-plane distances, dihedrals), and both anharmonic and cross terms are included in the force field.43
The noncovalent terms include the electrostatic and van der Waals interactions. Minimal Basis Iterative Stockholder (MBIS) charges are used to describe the Coulomb force between Gaussian charge distributions centered on the nuclei.46 These charges were derived from an all-electron density of the respective cluster model. Finally, the van der Waals interactions were modeled by the MM3-Buckingham model47 up to a finite cutoff of 12 Å and were supplemented with tail corrections.48
2.3 Molecular dynamics simulations
Molecular dynamics (MD) simulations were performed in the isothermal–isobaric (NPT) ensemble. They were conducted at 1 bar and for temperatures in between 200 K and 400 K in steps of 50 K.The MD simulations were carried out with LAMMPS49 using a Verlet time step of 0.5 fs. The temperature is controlled by a Nosé–Hoover chain thermostat50 containing three beads with a relaxation time of 0.1 ps, while the pressure is controlled by a Martyna–Tuckerman–Tobias–Klein barostat51 using a relaxation time of 1 ps. For most structures, 5 ns of data were obtained, while for the largest systems, 3 ns were used because of the larger computational cost. An equilibration time of 500 ps was taken into account before extracting the properties from these MD simulations.
 | (1) |
We obtain α0 from the NPT MD simulations by fitting a linear polynomial to the ensemble averaged (indicated as 〈⋅〉) natural logarithm of the volumes according to eqn (1):
〈ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) V〉 ≈ α0T + V0, V〉 ≈ α0T + V0, | (2) |
| MOF | α 0 (MK−1) | α 0 (MK−1) | α 0 (MK−1) | β 0 (GPa) | β 0 (GPa) | β 0 (GPa) |
|---|---|---|---|---|---|---|
| This work | Experiment | Simulations | This work | Experiment | Simulations | |
| Al-soc-MOF-1 | −13 | — | −19![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 13 13 |
9 | — | — |
| HKUST-1 | −10 | [−15, −12]21,55,56 | [−36, −9]13,41,57–59 | 21 | 30![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 60 60 |
[25–35]57–59,61 |
| IRMOF-8 | −40 | — | [−32, −21]15,62 | 5 | — | [2, 11]15,62,63 |
| IRMOF-10 | −48 | — | [−55, −16]13,41,59,62 | 5 | — | [3, 9]59,62–64 |
| MOF-5 | −37 | [−48, −39]65,66 | [−79, −9]13,15,27,41,52,59,62,67,68 | 11 | — | [4, 22]15,41,59,62–64,67,69–75 |
| MOF-177 | −30 | — | [−39, −28]13,62 | 6 | — | 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 74 74 |
| MOF-205 | −29 | — | −33![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 18 18 |
7 | — | 11![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 74 74 |
| MOF-210 | −97 | — | −55![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 18 18 |
2 | — | — |
| MOF-505 | −11 | — | −17![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 13 13 |
20 | — | — |
| PCN-68 | −42 | — | −54![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 18 18 |
7 | — | — |
| UMCM-1 | −41 | — | −47![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 13 13 |
6 | — | — |
The normal modes and corresponding frequencies to investigate the origin of the thermal expansion were derived using the harmonic approximation at 0 K. The force field Hessian was computed with Yaff.54
| γ = α0β0. | (3) |
In other words, γ is the product of the thermal expansion coefficient α0 and the bulk modulus β0. To compute this quantity, we extracted the bulk modulus from the NPT MD simulations at 300 K using a fluctuation formula:
 | (4) |
2.4 Structural properties
The structural properties (density ρ, accessible surface area (ASA), probe-occupiable void fraction, and largest cavity diameter (LCD)) were derived from the optimal structure at 0 K using Zeo++![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 76 (N2 probe molecule with kinetic diameter 3.64 Å).
76 (N2 probe molecule with kinetic diameter 3.64 Å).
3. Results
3.1 Thermal expansion
Experimentally, thermal expansion behavior is typically studied using variable-temperature diffraction measurements.17,55,66 By collecting patterns at different temperatures, it becomes possible to fit the equilibrium volume as a function of temperature. In this work, we have used computational methods to extract the same information. Molecular dynamics simulations were employed in the isothermal–isobaric (NPT) ensemble. We determined the equilibrium volume V at a mechanical pressure P of 1 bar and for temperatures T in a range from 200 K to 400 K in steps of 50 K, and fitted them to determine the well-known thermal expansion coefficient α0 (see eqn (1)).This procedure was applied to a set of diverse MOFs known for their methane storage properties.36 All 52 materials are listed in Tables S1–S4 in the ESI.† To the best of our knowledge, this is the most comprehensive set to date for the topic under study. It does not cover the whole class of MOFs as it is merely a selection from experimentally reported structures, but contains different metal nodes (Zn4O, Cu2COO4, Zr, Al) (Fig. 1(b)) and topological families.
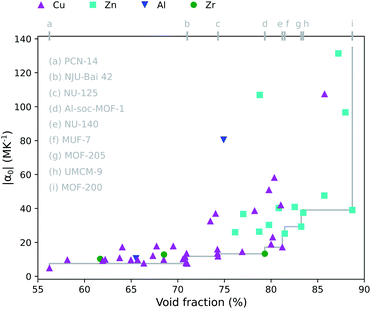
A positive correlation between the magnitude of the thermal expansion coefficient and the pore size has already been demonstrated in other studies focusing on a particular topology15,27 or on a limited set of frameworks.17,18 Not surprisingly, we find for our materials a similar result in Fig. 2 where the absolute value of the thermal expansion coefficient as a function of the void fraction is displayed. Consistent with our more diverse set of MOFs, a larger spread is observed, but the general trend remains preserved. Analogous relations are shown for the largest cavity diameter (Fig. S1†) and the accessible surface area (Fig. S2†) in the ESI.† Although Fig. 2 and S3† seem to suggest that MOFs with a Zn4O inorganic building block tend to have a larger thermal expansion, this picture might be misleading as the investigated materials certainly do not cover the whole chemical space in terms of e.g. the void fraction.77 To investigate the effect of the chemical building blocks on the thermal expansion, the other building blocks and topology should ideally be kept fixed.17
All 52 frameworks in our set display NTE behavior in the temperature range from 200 K to 400 K. We find thermal expansion coefficients in a wide range from −5 MK−1 to −131 MK−1 with an average of −30 MK−1 in Table 2. The individual thermal expansion coefficients are tabulated for every MOF in Tables S1–S4 in the ESI.† These results again corroborate the widespread existence of NTE in network materials.19 Furthermore, we find three MOFs (MOF-180,78 MOF-905![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 79 and PCN-610/NU-100
79 and PCN-610/NU-100![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 80,81) exhibiting so-called colossal NTE behavior (|α0| > 100 MK−1)82 that might be worth exploring experimentally for specific applications. On the one hand, MOF-180 and PCN-610 contain among the largest tritopic and hexatopic organic linkers in our set, respectively, while MOF-905 has relatively short ditopic and tritopic organic linkers (Fig. S4 and Tables S6, S8†). On the other hand, other MOFs with a similar large linker length possess a relatively low coefficient (MOF-200
80,81) exhibiting so-called colossal NTE behavior (|α0| > 100 MK−1)82 that might be worth exploring experimentally for specific applications. On the one hand, MOF-180 and PCN-610 contain among the largest tritopic and hexatopic organic linkers in our set, respectively, while MOF-905 has relatively short ditopic and tritopic organic linkers (Fig. S4 and Tables S6, S8†). On the other hand, other MOFs with a similar large linker length possess a relatively low coefficient (MOF-200![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 78). This suggests that having a very long organic linker is neither a sufficient nor a necessary condition for large thermal expansion. Furthermore, there are MOFs in our set with higher largest cavity diameters and void fractions, but still have much lower thermal expansion coefficients. It only illustrates the difficult relationship between the extent of negative thermal expansion and factors such as the length and type of the organic linker, and the topology.
78). This suggests that having a very long organic linker is neither a sufficient nor a necessary condition for large thermal expansion. Furthermore, there are MOFs in our set with higher largest cavity diameters and void fractions, but still have much lower thermal expansion coefficients. It only illustrates the difficult relationship between the extent of negative thermal expansion and factors such as the length and type of the organic linker, and the topology.
| X | μ X | m X | σ X | minX | maxX |
|---|---|---|---|---|---|
| ρ (kg m−3) | 551 | 553 | 182 | 204 | 894 |
| ASA (m2 g−1) | 3934 | 3970 | 1129 | 1163 | 6358 |
| Void fraction (%) | 73 | 74 | 10 | 32 | 89 |
| LCD (Å) | 16 | 15 | 6 | 9 | 32 |
| α 0 (MK−1) | −30 | −17 | 28 | −131 | −5 |
| β 0 (GPa) | 9 | 8 | 5 | 1 | 21 |
| γ (MPa K−1) | −0.18 | −0.16 | 0.09 | −0.42 | −0.03 |
Generally speaking, the magnitude of thermal expansion of MOFs is larger than most typical materials because of their large free voids.13 This does not pose a problem as long as the crystal can freely expand or contract in every direction. However, depending on the type of application, the material will be restricted to adapt in one or more directions with lower expansion coefficients as MOFs will be integrated in miniaturised devices connected to other materials and components.30,83–86 This restriction imposes thermal stress due to the thermal expansion mismatch. Only a limited number of experimental studies have actually monitored thermal expansion mismatch in MOFs. For instance, Wöll and co-workers demonstrated that a HKUST-1 thin film was stable under repeated heating–cooling cycles although the thermal expansion behavior of the MOF layer and substrate differ strongly.29 The same was observed in a different setup by the group of Weckhuysen.87
From a practical point of view, if several candidate MOFs perform similarly in terms of e.g. gas uptake, it will in many cases be beneficial to select the one with the lowest thermal expansion coefficient. One way of doing this is by constructing the Pareto front within a set of materials to optimize multiple objectives.88,89 This is demonstrated for the thermal expansion and empty pore space in Fig. 2. It is not possible to find a MOF within the group of materials under study that has a lower thermal expansion and a higher void fraction than the MOFs on the Pareto front, which are listed in Fig. 2. For instance, this shows that it is possible to have a crystal with almost 90% empty space, while still having a moderate thermal expansion coefficient of −40 MK−1 (MOF-200).
The origin of the large NTE of MOFs has been ascribed to low-energy transverse motions.19,90,91 To establish the link between the presence of collective motions with low frequencies and the relative thermal expansion, we computed the normal mode spectrum with the harmonic approximation. Fig. 3 illustrates that the relative number of low frequency modes is coupled with the thermal expansion behaviour, as MOFs displaying the largest thermal expansion coefficients possess the highest degree of low frequencies in their spectrum and vice versa. The indicated quadrants serve as a guide to the eye for this qualitative trend. The underlying mechanisms for NTE are framework dependent, and to elucidate them in-depth case studies are necessary as previously was demonstrated for MOF-5,65,66 HKUST-1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 55 and MIL-53(Al),91 for example. Further methodological developments in (computational) spectroscopy are required to systematically unravel the character of these important low-frequency vibrations.92,93
55 and MIL-53(Al),91 for example. Further methodological developments in (computational) spectroscopy are required to systematically unravel the character of these important low-frequency vibrations.92,93
In summary, our diverse set of MOFs again shows that the magnitude of thermal expansion is positively correlated with the porosity of the framework. The same holds to some extent for the presence of low vibrational modes. In other words, these findings thus indicate that in order to limit the thermal expansion mismatch with other materials (possessing much lower expansion coefficients), one should prefer the densest MOF structure in case various candidates display similar adsorption characteristics.
3.2 Thermal pressure
Thermal stress is intimately linked with the mechanical rigidity and stability of the material.94 As many MOFs are prone to mechanical failure and a reduction in porosity during post-synthetic processing steps, it is essential to develop a good understanding of their mechanical properties.12,32,33 Thermal stress is a directional dependent quantity that can be calculated by multiplying the thermal expansion coefficient, the Young modulus and the temperature change. As MOFs can behave very anisotropically,95 we focus instead on the coefficient of the isotropic thermal pressure in this work (see eqn (3)).The thermal pressure coefficient γ provides information on the mechanical pressure rise in a closed, restricted system subjected to a uniform temperature rise as ΔP = γΔT. The product in eqn (3) combines the engineering parameters that describe how the volume of the material responds to pressure with its equivalent in terms of the temperature (Fig. 1(c)). Both properties are of primary importance when considering devices where MOFs will come in contact with other materials.
They are not independent of each other. While the degree of thermal expansion is positively correlated with increasing porosity, the opposite is true for the bulk modulus. The latter was clearly illustrated by a large-scale computational screening of MOFs by Moghadam et al.34 As a result, the bulk modulus and the thermal expansion coefficient are roughly inversely correlated, which is obvious from the results shown in Fig. 4. Here, the bulk modulus is plotted versus the magnitude of the thermal expansion coefficient. On the one hand, relatively high bulk moduli of approximately 20 GPa are found for copper-paddle wheel MOFs with limited NTE coefficients such as MOF-505/NOTT-10096,97 and HKUST-1.98 For the latter material, experiment estimates a value of about 30 GPa.60 On the other hand, MOFs that display colossal NTE all have bulk moduli below 5 GPa.
 | ||
| Fig. 4 Bulk modulus β0versus the magnitude of the thermal expansion coefficient |α0|. A Pareto front where |α0| is minimized and β0 is maximised is shown. | ||
The inverse relation between both α0 and β0 results in a thermal pressure coefficient γ that shows no correlation with typical framework characteristics such as void fraction, density or internal surface area. This is illustrated in Fig. 5, where γ is plotted against the density. On average γ is found to be −0.18 MPa K−1 (Table 2), which corresponds with pulling the framework isotropically when the temperature increases. Of course, the minus sign – and thus tension instead of compression – comes from the NTE behavior.
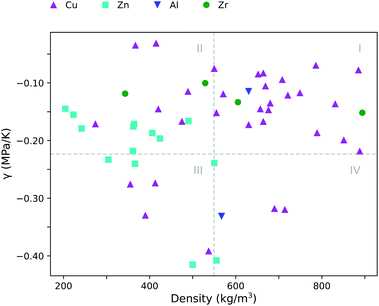 | ||
| Fig. 5 Thermal pressure coefficient γ as a function of the density ρ. The indicated quadrants serve as a guide to the eye. | ||
The thermal pressure rise can finally be found by multiplying γ with a temperature change ΔT (Fig. 1(a)). Of course, this depends on the application involving MOFs, and is only a rough estimate as both the bulk modulus and the thermal expansion coefficient are also influenced by guests and temperature.99 For example, consider the case of methane adsorption at room temperature. While only a few experimental studies have reported dynamical temperature changes due to the heat of adsorption,7,8 it can be expected that even at very high gas pressures this will not go beyond 100 K.13 For a hypothetical setup with MOFs confined and restricted in a closed system, this would maximally result in a thermal pressure rise between −42 MPa and −5 MPa for the materials under study (Table 2). This is relatively small compared to amorphization pressures that lead to pore collapse during compression (from 50 MPa to pressures beyond 1 GPa).34,100
4. Discussion
Finally, we compare our simulated data with other conventional materials in Fig. 6 to better understand the magnitude of the thermal pressure coefficients. Mechanical and thermal properties of MOFs have been situated at the border of polymers and ceramics in the past.13,32 The same can now be said for γ, which is a quantity combining both thermal and mechanical properties. On the one hand, polymers tend to have higher thermal expansion coefficients, but they are also mechanically weaker. Ceramics, on the other hand, have typically lower thermal expansion coefficients than MOFs, but have a wide range of bulk moduli. It is clear, however, that the thermal pressure coefficients of metals are an order of magnitude larger.From Fig. 6, it is obvious that there is a link between the thermal pressure coefficient and the density of a material on a larger scale. The simulated results for the MOFs under study fit in this trend. This relation can intuitively be understood as γ can also be written using the Maxwell relations as:
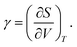 | (5) |
A dense material will typically require a smaller volume change to instigate the same entropy change as a less dense material.
5. Conclusions
In summary, this work investigated the thermal expansion behavior and its link with thermal stress. On a set consisting of more than fifty MOFs reported for methane storage, we demonstrate that the magnitude of the thermal expansion coefficient is positively correlated with the porosity of the framework. We predict for all materials NTE with three frameworks displaying a colossal volume change around room temperature. Although in-depth studies will be required to understand the link between specific collective motions and thermal expansion, we show that a relatively high percentage of low vibrational modes in the normal mode spectrum is an indicator for potentially large temperature-induced volume changes.As a first measure for thermal stress, we introduce the thermal pressure coefficient γ, which is the product of the thermal expansion coefficient and the bulk modulus. As both properties are roughly inversely correlated, we do not find a clear link between framework characteristics and γ. The simulated thermal pressure coefficients γ of the investigated MOFs were found to be relatively low, in between the range of polymers and ceramics. Systems working near thermal equilibrium conditions where MOF crystals are restricted in volume change (e.g. due to thermal expansion mismatch) are predicted to produce thermal pressure rises of only a couple of megapascals. The materials are then subjected to an isotropic pulling force much lower than typical amorphization pressures, and are therefore not expected to easily fail.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work is supported by the Fund for Scientific Research Flanders (FWO). V. V. S. acknowledges funding from the European Union’s Horizon 2020 research and innovation program (consolidator ERC grant agreement no. 647755 – DYNPOR (2015–2020)). The work is furthermore supported by the Research Board of Ghent University (BOF). The computational resources and services used in this work were provided by VSC (Flemish Supercomputer Center), funded by Ghent University, FWO and the Flemish Government department EWI.Notes and references
- K. Chen, J. Cole, C. Conger, J. Draskovic, M. Lohr, K. Klein, T. Scheidemantel and P. Schiffer, Nature, 2006, 442, 257 CrossRef CAS PubMed.
- G. Abadias, J. Vac. Sci. Technol., 2018, 36, 020801 CrossRef.
- J. D. Steele, J. Handong, I. Dovgaliuk, R. F. Berger, T. Braeckevelt, H. Yuan, C. Martin, E. Solano, K. Lejaeghere, S. M. J. Rogge, C. Notebaert, W. Vandezande, K. P. F. Janssen, B. Goderis, E. Debroye, Y.-K. Wang, Y. Dong, D. Ma, M. Saidaminov, H. Tan, Z. Lu, V. Dyadkin, D. Chernyshov, V. Van Speybroeck, E. H. Sargent, J. Hofkens and M. B. Roeffaers, Science, 2019, 365, 679–684 CrossRef CAS PubMed.
- H. Furukawa, K. E. Cordova, M. O'Keeffe and O. M. Yaghi, Science, 2013, 341, 1230444 CrossRef PubMed.
- P. Silva, S. M. F. Vilela and F. A. Almeida Paz, Chem. Soc. Rev., 2015, 44, 6774–6803 RSC.
- C. A. Trickett, A. Helal, B. A. Al-Maythalony, Z. H. Zamani, K. E. Cordova and O. M. Yaghi, Nat. Rev. Mater., 2017, 2, 17045 CrossRef CAS.
- V. Bon, N. Kavoosi, I. Senkovska and S. Kaskel, ACS Appl. Mater. Interfaces, 2015, 7, 222292–222300 CrossRef PubMed.
- M. Beckner and A. Dailly, Appl. Energy, 2016, 162, 506–514 CrossRef CAS.
- J. Xiao, M. Hu, P. Bénard and R. Chahine, Int. J. Hydrogen Energy, 2013, 38, 13000–13010 CrossRef CAS.
- J. A. Mason, K. Sumida, Z. R. Herm, R. Krishna and J. R. Long, Chem. Sci., 2011, 4, 3030–3040 CAS.
- B. Mu and K. S. Walton, J. Phys. Chem. C, 2011, 115, 22748–22754 CrossRef CAS.
- A. J. Howarth, Y. Liu, P. Li, Z. Li, T. C. Wang, J. T. Hupp and O. K. Farha, Nat. Rev. Mater., 2016, 1, 15018 CrossRef CAS.
- J. Wieme, S. Vandenbrande, A. Lamaire, V. Kapil, L. Vanduyfhuys and V. Van Speybroeck, ACS Appl. Mater. Interfaces, 2019, 11, 38697–38707 CrossRef CAS PubMed.
- H. Babaei, A. J. H. McGaughey and C. E. Wilmer, Chem. Sci., 2017, 8, 583–589 RSC.
- S. S. Han and W. A. Goddard, J. Phys. Chem. C, 2007, 111, 15185–15191 CrossRef CAS.
- S. Henke, A. Schneemann and R. A. Fischer, Adv. Funct. Mater., 2013, 23, 5990–5996 CrossRef CAS.
- N. C. Burtch, S. J. Baxter, J. Heinen, A. Bird, A. Schneemann, D. Dubbeldam and A. P. Wilkinson, Adv. Funct. Mater., 2019, 1904669 CrossRef CAS.
- J. D. Evans, J. P. Dürholt, S. Kaskel and R. Schmid, J. Mater. Chem. A, 2019, 7, 24019–24026 RSC.
- C. S. Coates and A. L. Goodwin, Mater. Horiz., 2019, 6, 211–218 RSC.
- G. D. Barrera, J. A. O. Bruno, T. H. K. Barron and N. L. Allan, J. Phys.: Condens. Matter, 2005, 17, 4 CrossRef.
- C. Schneider, D. Bodesheim, M. G. Ehrenreich, V. Crocellà, J. Mink, R. A. Fischer, K. T. Butler and G. Kieslich, J. Am. Chem. Soc., 2019, 141, 10504 CrossRef CAS PubMed.
- I. Grobler, V. J. Smith, P. M. Bhatt, S. A. Herbert and L. J. Barbour, J. Am. Chem. Soc., 2013, 135, 6411–6414 CrossRef CAS.
- J. E. Auckett, A. A. Barkhordarian, S. H. Ogilvie, S. G. Duyker, H. Chevreau, V. K. Peterson and C. J. Kepert, Nat. Commun., 2018, 9, 4873 CrossRef.
- C. Nanthamathee, S. Ling, B. Slater and M. P. Attfield, Chem. Mater., 2015, 27, 85–95 CrossRef CAS.
- S. J. Baxter, A. Scheemann, A. D. Ready, P. Wijeratne, A. P. Wilkinson and N. C. Burtch, J. Am. Chem. Soc., 2019, 141, 12849–12854 CrossRef CAS PubMed.
- M. J. Cliffe, J. A. Hill, C. A. Murray, F.-X. Coudert and A. L. Goodwin, Phys. Chem. Chem. Phys., 2015, 17, 11586–11592 RSC.
- D. Dubbeldam, K. S. Walton, D. E. Ellis and R. Q. Snurr, Angew. Chem., Int. Ed., 2007, 46, 4496–4499 CrossRef CAS PubMed.
- S. R. G. Balestra, R. Bueno-Perez, S. Hamad, D. Dubbeldam, R. A. Ruiz-Salvador and S. Calero, Chem. Mater., 2016, 28, 8296–8304 CrossRef CAS PubMed.
- Z. Wang, P. G. Weidler, C. Azucena, L. Heinke and C. Wöll, Microporous Mesoporous Mater., 2016, 222, 241–246 CrossRef CAS.
- I. Stassen, N. Burtch, A. Talin, P. Falcaro, M. Allendorf and R. Ameloot, Chem. Soc. Rev., 2017, 46, 3185 RSC.
- N. C. Burtch, J. Heinen, T. D. Bennett, D. Dubbeldam and M. D. Allendorf, Adv. Mater., 2018, 30, 1704124 CrossRef PubMed.
- J. C. Tan and A. K. Cheetham, Chem. Soc. Rev., 2011, 40, 1059–1080 RSC.
- L. R. Redfern and O. K. Farha, Chem. Sci., 2019, 10, 10666–10679 RSC.
- P. Z. Moghadam, S. M. J. Rogge, A. Li, C.-M. Chow, J. Wieme, N. Moharrami, M. Aragones-Anglada, G. Conduit, D. A. Gomez-Gualdron, V. Van Speybroeck and D. Fairen-Jimenez, Matter, 2019, 1, 219–234 CrossRef.
- R. Semino, N. A. Ramsahye, A. Ghoufi and G. Maurin, J. Phys. Chem. C, 2016, 8, 809–819 CAS.
- Y. He, F. Chen, B. Li, G. Qian, W. Zhou and B. Chen, Coord. Chem. Rev., 2017, 373, 167–198 CrossRef.
- C. M. Simon, J. Kim, D. A. Gomez-Gualdron, J. S. Camp, Y. G. Chung, R. L. Martin, R. Mercado, M. W. Deem, D. Gunter, M. Haranczyk, D. S. Sholl, R. Q. Snurr and B. Smit, Energy Environ. Sci., 2015, 8, 1190–1199 RSC.
- J. A. Mason, J. Oktawiec, M. K. Taylor, M. R. Hudson, J. Rodriguez, J. E. Bachman, M. I. Gonzalez, A. Cervellino, A. Guagliardi, C. M. Brown, P. L. Llewellyn, N. Masciocchi and J. R. Long, Nature, 2015, 527, 357–361 CrossRef CAS PubMed.
- O. L. Anderson, J. Phys. Chem. Solids, 1997, 58, 335–343 CrossRef CAS.
- T. J. B. Holland and R. Powell, J. Struct. Geol., 2011, 29, 333–383 CAS.
- P. G. Boyd, S. M. Moosavi, M. Witman and B. Smit, J. Phys. Chem. Lett., 2017, 8, 357–363 CrossRef CAS PubMed.
- L. Vanduyfhuys, S. Vandenbrande, T. Verstraelen, R. Schmid, M. Waroquier and V. Van Speybroeck, J. Comput. Chem., 2015, 36, 1015–1027 CrossRef CAS PubMed.
- L. Vanduyfhuys, S. Vandenbrande, J. Wieme, M. Waroquier, T. Verstraelen and V. Van Speybroeck, J. Comput. Chem., 2018, 39, 999–1011 CrossRef CAS PubMed.
- A. D. Becke, J. Chem. Phys., 1993, 98, 5648–5652 CrossRef CAS.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, G. A. Petersson, H. Nakatsuji, X. Li, M. Caricato, A. V. Marenich, J. Bloino, B. G. Janesko, R. Gomperts, B. Mennucci, H. P. Hratchian, J. V. Ortiz, A. F. Izmaylov, J. L. Sonnenberg, D. Williams-Young, F. Ding, F. Lipparini, F. Egidi, J. Goings, B. Peng, A. Petrone, T. Henderson, D. Ranasinghe, V. G. Zakrzewski, J. Gao, N. Rega, G. Zheng, W. Liang, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, K. Throssell, J. A. Montgomery, Jr, J. E. Peralta, F. Ogliaro, M. J. Bearpark, J. J. Heyd, E. N. Brothers, K. N. Kudin, V. N. Staroverov, T. A. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. P. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, J. M. Millam, M. Klene, C. Adamo, R. Cammi, J. W. Ochterski, R. L. Martin, K. Morokuma, O. Farkas, J. B. Foresman and D. J. Fox, Gaussian 16 Revision E.01, Gaussian Inc., Wallingford CT, 2016 Search PubMed.
- T. Verstraelen, S. Vandenbrande, F. Heidar-Zadeh, L. Vanduyfhuys, V. Van Speybroeck, M. Waroquier and P. W. Ayers, J. Chem. Theory Comput., 2016, 12, 3894–3912 CrossRef CAS PubMed.
- J. H. Lii and N. L. Allinger, J. Am. Chem. Soc., 1989, 111, 8576–8582 CrossRef CAS.
- H. Sun, J. Phys. Chem. B, 1998, 102, 7338–7364 CrossRef CAS.
- S. Plimpton, J. Comput. Phys., 1995, 117, 1–19 CrossRef CAS.
- G. J. Martyna, M. L. Klein and M. Tuckerman, J. Chem. Phys., 1992, 97, 2635–2643 CrossRef.
- G. J. Martyna, M. E. Tuckerman, D. J. Tobias and M. L. Klein, Mol. Phys., 1996, 87, 1117–1157 CrossRef CAS.
- A. Lamaire, J. Wieme, S. M. J. Rogge, M. Waroquier and V. Van Speybroeck, J. Chem. Phys., 2019, 150, 094503 CrossRef PubMed.
- V. Kapil, J. Wieme, S. Vandenbrande, A. Lamaire, V. Van Speybroeck and M. Ceriotti, J. Chem. Theory Comput., 2019, 15, 3237–3249 CrossRef CAS PubMed.
- T. Verstraelen, L. Vanduyfhuys, S. Vandenbrande and S. M. J. Rogge, Yaff 1.5.0, 2019, http://molmod.github.io/yaff/index.html Search PubMed.
- Y. Wu, A. Kobayashi, G. J. Halder, V. K. Peterson, K. W. Chapman, N. Lock, P. D. Southon and C. J. Kepert, Angew. Chem., Int. Ed., 2008, 47, 8929–8932 CrossRef CAS PubMed.
- V. K. Peterson, G. J. Kearley, Y. Wu, A. J. Ramirez-Cuesta, E. Kemner and C. J. Kepert, Angew. Chem., Int. Ed., 2010, 49, 585–588 CrossRef CAS PubMed.
- L. Zhao, Q. Yang, Q. Ma, C. Zhong, J. Mi and D. Liu, J. Mol. Model., 2011, 17, 227–234 CrossRef CAS.
- M. Tafipolsky, S. Amirjalayer and R. Schmid, J. Phys. Chem. C, 2010, 114, 14402–14409 CrossRef CAS.
- J. K. Bristow, D. Tiana and A. Walsh, J. Chem. Theory Comput., 2014, 10, 4644–4652 CrossRef CAS.
- K. W. Chapman, G. J. Halder and P. J. Chupas, J. Am. Chem. Soc., 2008, 10524–10526 CrossRef CAS PubMed.
- H. Wu, T. Yildirim and W. Zhou, J. Phys. Chem. Lett., 2013, 4, 925–930 CrossRef CAS PubMed.
- Y. Sun and H. Sun, J. Mol. Model., 2014, 20, 2146 CrossRef PubMed.
- A. Kuc, A. Enyashin and G. Seifert, J. Phys. Chem. B, 2007, 111, 8179–8186 CrossRef CAS PubMed.
- K. Banlusan and A. Strachan, J. Chem. Phys., 2017, 146, 184705 CrossRef.
- W. Zhou, H. Wu, T. Yildirim, J. R. Simpson and A. R. Hight Walker, Phys. Rev. B: Condens. Matter Mater. Phys., 2008, 78, 054114 CrossRef.
- N. Lock, Y. Wu, M. Christensen, L. J. Cameron, V. K. Peterson, A. J. Bridgeman, C. J. Kepert and B. B. Iversen, J. Phys. Chem. C, 2010, 114, 16181–16186 CrossRef CAS.
- J. A. Greathouse and M. D. Allendorf, J. Phys. Chem. C, 2008, 112, 5795–5802 CrossRef CAS.
- M. R. Ryder, J. Maul, B. Civalleri and A. Erba, Adv. Theory Simul., 2019, 2, 1900093 CrossRef CAS.
- W. Zhou and T. Yildirim, Phys. Rev. B: Condens. Matter Mater. Phys., 2006, 74, 180301 CrossRef.
- A. Samanta, T. Furuta and J. Li, J. Chem. Phys., 2006, 125, 084714 CrossRef PubMed.
- M. Tafipolsky and R. Schmid, J. Phys. Chem. B, 2009, 113, 1341–1352 CrossRef CAS PubMed.
- D. F. Bahr, J. A. Reid, W. M. Mook, C. A. Bauer, R. Stumpf, A. J. Skulan, N. R. Moody, B. A. Simmons, M. M. Shindel and M. D. Allendorf, Phys. Rev. B: Condens. Matter Mater. Phys., 2008, 76, 059902 CrossRef.
- S. M. J. Rogge, L. Vanduyfhuys, A. Ghysels, M. Waroquier, T. Verstraelen, G. Maurin and V. Van Speybroeck, J. Chem. Theory Comput., 2015, 11, 12 CrossRef PubMed.
- B. Lukose, B. Supronowicz, P. S. Petkov, J. Frenzel, A. B. Kuc, G. Seifert, G. N. Vayssilov and T. Heine, Phys. Status Solidi B, 2012, 249, 335–342 CrossRef CAS.
- M. Mattesini, J. M. Soler and F. Ynduráin, Phys. Rev. B: Condens. Matter Mater. Phys., 2006, 73, 094111 CrossRef.
- T. F. Willems, C. H. Rycroft, M. Kazi, J. C. Meza and M. Haranczyk, Microporous Mesoporous Mater., 2012, 149, 134–141 CrossRef CAS.
- S. M. Moosavi, A. Nandy, K. M. Jablonka, D. Ongari, J. P. Janet, P. G. Boyd, Y. Lee, B. Smit and H. J. Kulik, Nat. Commun., 2020, 11, 4068 CrossRef CAS.
- H. Furukawa, N. Ko, Y. B. Go, N. Aratani, S. B. Choi, E. Choi, O. A. Yazaydin, R. Q. Snurr, M. O'Keeffe, J. Kim and O. M. Yaghi, Science, 2010, 329, 424–428 CrossRef CAS PubMed.
- J. Jiang, H. Furukawa, Y.-B. Zhang and O. M. Yaghi, J. Am. Chem. Soc., 2016, 138, 10244–10251 CrossRef CAS PubMed.
- D. Yuan, D. Zhao, D. Sun and H.-C. Zhou, Angew. Chem., Int. Ed., 2010, 49, 5357–5361 CrossRef CAS PubMed.
- O. K. Farha, O. A. Yazaydin, I. Eryazici, C. D. Malliakas, B. G. Hauser, M. G. Kanatzidis, S. T. Nguyen, R. Q. Snurr and J. T. Hupp, Nat. Chem., 2010, 2, 944–948 CrossRef CAS PubMed.
- A. L. Goodwin, D. A. Keen, M. G. Tucker, M. T. Dove, L. Peters and J. S. O. Evans, J. Am. Chem. Soc., 2008, 130, 9660–9661 CrossRef CAS PubMed.
- A. Bétard and R. A. Fischer, Chem. Rev., 2012, 112, 1055–1083 CrossRef PubMed.
- Q.-L. Zhu and Q. Xu, Chem. Soc. Rev., 2014, 43, 5468–5512 RSC.
- P. Falcaro, R. Ricco, C. M. Doherty, K. Liang, A. J. Hill and M. J. Styles, Chem. Soc. Rev., 2014, 43, 5513–5560 RSC.
- J. Liu and C. Wöll, Chem. Soc. Rev., 2017, 46, 5730–5770 RSC.
- R. P. Brand, L. D. B. Mandemaker, G. Delen, N. Rijnveld and B. M. Weckhuysen, Chem.–Eur. J., 2018, 19, 2397–2404 CAS.
- J. Greeley, T. F. Jaramillo, J. Bonde, I. Chorkendorff and J. Nørskov, Nat. Mater., 2006, 5, 909–913 CrossRef CAS PubMed.
- K. Lejaeghere, S. Cottenier and V. Van Speybroeck, Phys. Rev. Lett., 2013, 111, 075501 CrossRef PubMed.
- M. R. Ryder, B. Van de Voorde, B. Civalleri, T. D. Bennett, S. Mukhopadhyay, G. Cinque, F. Fernandez-Alonso, D. De Vos, S. Rudić and J.-C. Tan, Phys. Rev. Lett., 2017, 118, 255502 CrossRef.
- A. E. J. Hoffman, J. Wieme, S. M. J. Rogge, L. Vanduyfhuys and V. Van Speybroeck, Z. Kristallogr. - Cryst. Mater., 2019, 234, 529–545 CrossRef CAS.
- P. U. Jepsen and S. J. Clark, Chem. Phys. Lett., 2007, 442, 275–280 CrossRef CAS.
- C. R. Jacob and M. Reiher, J. Chem. Phys., 2009, 130, 084106 CrossRef PubMed.
- A. M. Evans, M. R. Ryder, N. C. Flanders, E. Vitaku, L. X. Chen and W. R. Dichtel, Ind. Eng. Chem. Res., 2019, 58, 9883–9887 CrossRef CAS.
- A. U. Ortiz, A. Boutin, A. H. Fuchs and F.-X. Coudert, Phys. Rev. Lett., 2012, 109, 195502 CrossRef PubMed.
- B. Chen, N. W. Ockwig, A. R. Millward, D. S. Contreras and O. M. Yaghi, Angew. Chem., Int. Ed., 2005, 44, 4745–4749 CrossRef CAS.
- X. Lin, J. Jia, X. Zhao, M. Thomas, A. J. Blake, G. S. Walker, N. R. Champness, P. Hubberstey and M. Schröder, Angew. Chem., Int. Ed., 2006, 45, 7358–7364 CrossRef CAS PubMed.
- S. S.-Y. Chui, S. M.-F. Lo, J. P. H. Charmant, G. A. Orpen and I. D. Williams, Science, 1999, 283, 1148–1150 CrossRef CAS PubMed.
- J. Heinen, A. D. Ready, T. D. Bennett, D. Dubbeldam, R. W. Friddle and N. C. Burtch, ACS Appl. Mater. Interfaces, 2018, 10, 21079–21083 CrossRef CAS PubMed.
- T. D. Bennett and A. K. Cheetham, Acc. Chem. Res., 2014, 47, 1555–1562 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/d0ta09462e |
| This journal is © The Royal Society of Chemistry 2021 |