Open Access Article
Open Access ArticleDefect chemistry and transport properties of perovskite-type oxides La1−xCaxFeO3−δ†
Jia
Song‡
 a,
Shaochen
Zhu
a,
Shaochen
Zhu
 a,
De
Ning§
b and
Henny J. M.
Bouwmeester
a,
De
Ning§
b and
Henny J. M.
Bouwmeester
 *acd
*acd
aElectrochemistry Research Group, Membrane Science and Technology, MESA+ Institute for Nanotechnology, University of Twente, P.O. Box 217, 7500 AE, Enschede, The Netherlands. E-mail: h.j.m.bouwmeester@utwente.nl
bHelmholtz-Zentrum Berlin für Materialien und Energie, Hahn-Meitner-Platz 1, 14109 Berlin, Germany
cCAS Key Laboratory of Materials for Energy Conversion, Department of Materials Science and Engineering, University of Science and Technology of China, Hefei, 230026, P. R. China
dForschungszentrum Jülich GmbH, Institute of Energy and Climate Research-IEK-1, Leo-Brandt-Str. 1, D-52425, Jülich, Germany
First published on 10th December 2020
Abstract
Structural evolution, electrical conductivity, oxygen nonstoichiometry and oxygen transport properties of perovskite-type oxides La1−xCaxFeO3−δ (x = 0.05, 0.10, 0.15, 0.20, 0.30 and 0.40) are investigated. All investigated compositions exhibit, under ambient air, a phase transition from room-temperature orthorhombic (space group Pbnm) to rhombohedral (space group R![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) c) at elevated temperature. The transition temperature is found to decrease gradually from 900 °C for x = 0.05 to 625 °C for x = 0.40. Analysis of the data of oxygen nonstoichiometry obtained by thermogravimetry shows that under the given experimental conditions the Ca dopant is predominantly compensated by formation of electron holes rather than by oxygen vacancies. Maximum electrical conductivity under air is found for the composition with x = 0.30 (123 S cm−1 at 650 °C). Analysis of the temperature dependence of the mobility of the electron holes in terms of Emin–Holstein's theory indicates that small polaron theory fails for the compositions with high Ca contents x = 0.30 and x = 0.40. This is tentatively explained by the increased delocalization of charge carriers with increasing Ca dopant concentration. The oxygen transport properties of La1−xCaxFeO3−δ in the range 650–900 °C are evaluated using the electrical conductivity relaxation (ECR) technique. Combined with data of oxygen non-stoichiometry, the obtained results enable calculation of the oxygen vacancy diffusion coefficient and associated ionic conductivity. Both parameters increase with increasing Ca content in La1−xCaxFeO3−δ, while it is found that the effective migration barrier for oxygen diffusion decreases with decreasing oxygen vacancy formation enthalpy.
c) at elevated temperature. The transition temperature is found to decrease gradually from 900 °C for x = 0.05 to 625 °C for x = 0.40. Analysis of the data of oxygen nonstoichiometry obtained by thermogravimetry shows that under the given experimental conditions the Ca dopant is predominantly compensated by formation of electron holes rather than by oxygen vacancies. Maximum electrical conductivity under air is found for the composition with x = 0.30 (123 S cm−1 at 650 °C). Analysis of the temperature dependence of the mobility of the electron holes in terms of Emin–Holstein's theory indicates that small polaron theory fails for the compositions with high Ca contents x = 0.30 and x = 0.40. This is tentatively explained by the increased delocalization of charge carriers with increasing Ca dopant concentration. The oxygen transport properties of La1−xCaxFeO3−δ in the range 650–900 °C are evaluated using the electrical conductivity relaxation (ECR) technique. Combined with data of oxygen non-stoichiometry, the obtained results enable calculation of the oxygen vacancy diffusion coefficient and associated ionic conductivity. Both parameters increase with increasing Ca content in La1−xCaxFeO3−δ, while it is found that the effective migration barrier for oxygen diffusion decreases with decreasing oxygen vacancy formation enthalpy.
1. Introduction
Mixed ionic–electronic conducting oxides are extensively investigated for potential application as air electrode in reversible solid oxide cells (RSOCs) that can be operated either as a solid oxide fuel cell (SOFC) or as a solid electrolyte electrolysis cell (SOEC).1–3 The most popular electrodes considered to date are the perovskite-structured oxides La0.6Sr0.4CoO3−δ (LSC) and La0.6Sr0.4Co0.2Fe0.8O3−δ (LSCF), though many other compositions and structure types are currently being investigated.4 Oxygen ion transport in these oxides is mediated via a vacancy mechanism. A-site substitution of trivalent lanthanum with divalent strontium in the ABO3 perovskite oxides serves to create oxygen vacancies and, hence, to enhance oxygen ionic conductivity. A drawback in the case of above compositions is the clear mismatch between the ionic radii of host and dopant ions, La3+ (XII) = 1.36 Å and Sr2+ (XII) = 1.44 Å, which is believed to be the cause of segregation of Sr2+ ions to the grain boundaries and to the surface. The latter has a detrimental effect on the surface oxygen exchange kinetics.5–8 Apart from this, the long-term thermodynamic stability of materials under actual operating conditions is an issue. The poor stability of cobalt-containing perovskites under reducing atmospheres, reactivity towards commonly used electrolytes and – last but not least – the high price of cobalt have urged researchers to explore cobalt-free mixed conducting electrodes with high electrocatalytic activity.9–11In recent studies by Berger et al.,12,13 La0.8Ca0.2FeO3−δ (LCF82) has been put forward as a promising electrode for RSOCs. The choice for calcium (Ca2+ (XII) = 1.34 Å) rather than strontium not only reduces the mismatch between host and dopant ions, but also the lower basicity of Ca2+ compared to that of Sr2+ ions reduces vulnerability towards carbonation and, hence, surface degradation upon contact with CO2. The thermal expansion coefficient of LCF82 is found in perfect match with that of state-of-the-art electrolytes,12 whereas the material shows electrical conductivities in usual ranges of temperature and oxygen partial pressure (pO2) in excess of 100 S cm−1, which is often regarded as the threshold value for use as electrode.14 It is further found that LCF82 exhibits high surface exchange and chemical diffusion coefficients with values exceeding those of state-of-the-art materials like LSC and LSCF.12
In our preceding work, investigating the influence of the earth–alkaline–metal dopant on structure, electrical and oxygen transport of La0.6A0.4FeO3−δ (A = Ca, Sr, Ba), we found that the kinetic parameters for La0.6Ca0.4FeO3−δ (LCF64) resemble those of La0.6Sr0.4FeO3−δ (LSF64).15 Compared to extensive reports in literature on structure, electrical conductivity and oxygen transport properties of La1−xSrxFeO3−δ (LSF),16–21 only a few reports are available on selected compositions in the series La1−xCaxFeO3−δ.12,22,23 This prompted us to conduct a more systematic study. In this study, the electrical conductivity and oxygen transport properties of La1−xCaxFeO3−δ (x = 0.05, 0.10, 0.15, 0.20, 0.30 and 0.40) are investigated by means of electrical conductivity relaxation (ECR). Thermal evolution of the crystal structure and oxygen nonstoichiometry of the materials are investigated by high-temperature X-ray diffraction (HT-XRD) and thermogravimetric analysis (TGA).
2. Experimental
2.1 Sample preparation
Powders of La1−xCaxFeO3−δ (x = 0.05, 0.10, 0.15, 0.20, 0.30 and 0.40) were prepared via a modified Pechini method, as described elsewhere.24 Stoichiometric amounts of La(NO3)3·6H2O (Alfa Aesar, 99.9%), Ca(NO3)2·4H2O (Sigma-Aldrich, 99%) and Fe(NO3)3·9H2O (Sigma-Aldrich, ≥98%) were dissolved in water followed by the addition of C10H16N2O8 (EDTA, Sigma-Aldrich, >99%) and C6H8O7 (citric acid, Alfa Aesar, >99.5%) as chelating agents. The pH of the solution was adjusted to 7 using concentrated NH4OH (Sigma-Aldrich, 30 w/v%). After evaporation of the water, the foam-like gel reached self-ignition at around 350 °C. The obtained raw ashes were calcined at 900 °C for 5 h, using heating/cooling rates of 5 °C min−1. The chemical composition of the powders was checked by X-ray fluorescence (XRF) using a Philips PW1480 apparatus. The obtained powders were pelletized by uniaxial pressing at 25 MPa followed by isostatic pressing at 400 MPa for 2 min. Subsequently, the pellets were sintered at 1120 °C for 5 h in air with heating/cooling rates of 2 °C min−1. The relative density of the pellets was above 94% of their theoretical value as measured by Archimedes' method.2.2 Characterization
The calcined powders were studied by room-temperature X-ray diffraction (XRD, D2 PHASER, Bruker) with Cu Kα1 radiation (λ = 1.54060 Å) in air. Data were collected in a step-scan mode over the 2θ range 20–90 °C with a step size of 0.01° and a counting time of 8 s. The thermal evolution of the structures was investigated using high-temperature X-ray diffraction (HT-XRD, D8 Advance, Bruker) in air from 600 °C to 1000 °C with 25 °C intervals. The sample was heated to the desired temperature with a heating rate of 25 °C min−1, followed by a dwell of 15 min to ensure equilibration. XRD patterns were recorded in the 2θ range of 20–90° with a step size of 0.015° and a counting time of 1.3 s. The FullProf software package was used for Rietveld refinements of the patterns.25The oxygen nonstoichiometry of the samples was determined by thermogravimetric analysis (TGA, Netsch STA F3 Jupiter). Data were collected during cooling from 900 °C to 650 °C, with intervals of 25 °C and a dwell time of 30 min at each temperature before data acquisition. The measurements were conducted in oxygen–nitrogen mixtures containing either 4.5%, 10%, 21%, 42% or 90% of O2, corresponding to the pO2 values maintained during ECR experiments (see below). Prior to data collection, the powder was heated under 4.5% O2 to 900 °C, with a heating rate of 20 °C min−1 and a dwell time of at least 2.5 h, in order to remove impurities like adsorbed water and CO2. Following prior studies on La1−xSrxFeO3−δ (0 ≤ x ≤ 0.6),17 all compositions in the present study were considered to be stoichiometric (δ = 0) at a pO2 of 0.21 atm below 150 °C.
Samples for electrical conductivity relaxation (ECR) measurements were prepared by grinding and cutting dense sintered pellets to planar-sheet shaped samples with approximate dimensions 12 × 5 × 0.5 mm3. The sample surface was polished using diamond polishing discs (JZ Primo, Xinhui China) down to 0.5 μm. A four-probe DC method was used to collect data of electrical conductivity. Two gold wires (Alfa Aesar, 99.999%, Ø = 0.25 mm) were wrapped around both ends of the sample for current supply. Two additional gold wires were wrapped 1 mm remote from the current electrodes to act as voltage probes. To ensure good contact between the gold wires and the sample, sulphur-free gold paste (home-made) was applied on the sample surface directly underneath the gold wires. Finally, the sample was annealed at 950 °C in air for 1 h to sinter the gold paste and thermally cure the polished sample surface. Data of the transient electrical conductivity was collected following oxidation and reduction step changes in pO2 between 0.100 and 0.210 bar. Measurements were conducted following stepwise cooling from 900 °C to 650 °C with intervals of 25 °C, heating/cooling rates of 10 °C min−1 and a dwell time of 60 min at each temperature before data acquisition. The chemical diffusion coefficient Dchem and the surface exchange coefficient kchem were determined by fitting the transient conductivity to the appropriate solution of Fick's second law using a non-linear least-squares program based on the Levenberg–Marquardt algorithm. Detailed descriptions of the ECR technique and the model used for data fitting are given elsewhere.19,26
3. Results and discussion
3.1 Crystal structure
Fig. 1 shows the room temperature XRD patterns of La1−xCaxFeO3−δ (x = 0.05, 0.10, 0.15, 0.20, 0.30 and 0.40). All patterns could be fitted using orthorhombic space group Pbnm. Corresponding lattice parameters and reliability factors from Rietveld refinements are listed in Table 1. Other structural parameters obtained from the refinements are listed in Table S1.† No impurity peaks are found in the patterns, suggesting that all compositions are single phase. The chemical composition of the powders appeared to be in good agreement with the intended nominal composition as was checked by XRF (see Fig. S1†). | ||
| Fig. 1 Measured (red symbols) and calculated (black lines) of XRD powder patterns of La1−xCaxFeO3−δ for (a) x = 0.05, (b) x = 0.10, (c) x = 0.15, (d) x = 0.20, (e) x = 0.30 and (f) x = 0.40. Data were recorded at room temperature in ambient air. The calculated positions of Bragg peaks and the residual plots are given under the patterns. Data for x = 0.40 were taken from our previous study.15 | ||
| x = 0.05 | x = 0.10 | x = 0.15 | x = 0.20 | x = 0.30 | x = 0.40 | |
|---|---|---|---|---|---|---|
| a/Å | 5.54765(4) | 5.54089(11) | 5.52984(11) | 5.52167(15) | 5.50262(10) | 5.48822(12) |
| b/Å | 5.55664(3) | 5.54966(8) | 5.54068(9) | 5.53475(13) | 5.52552(9) | 5.51710(15) |
| c/Å | 7.84294(5) | 7.83187(13) | 7.81634(14) | 7.80452(19) | 7.77789(13) | 7.75721(17) |
| V/Å3 | 241.769(2) | 240.831(4) | 239.485(4) | 238.514(5) | 236.486(4) | 234.881(4) |
| R wp/% | 4.96 | 6.33 | 7.33 | 7.19 | 5.72 | 6.29 |
| R exp/% | 1.99 | 4.55 | 4.89 | 4.06 | 2.41 | 2.52 |
| R Bragg/% | 1.275 | 1.769 | 1.868 | 2.050 | 1.875 | 2.237 |
| χ 2 | 6.22 | 1.93 | 2.25 | 3.14 | 5.65 | 6.23 |
As is shown in Fig. 2, the lattice parameters show a clear negative dependence on Ca content, which suggests at first glance formation of Fe4+ (0.585 Å (XI)) as the primary compensating defect, noting that the Fe4+ ion has a smaller radius than Fe3+ (0.645 Å (XI) – high spin). The degree of electronic versus ionic compensation of the Ca dopant in La1−xCaxFeO3−δ is further discussed below. The quoted ionic radii are taken from Shannon's compilation.27 In general, a good agreement is found between the lattice parameters from this study and those of similar compositions reported by Price et al.22
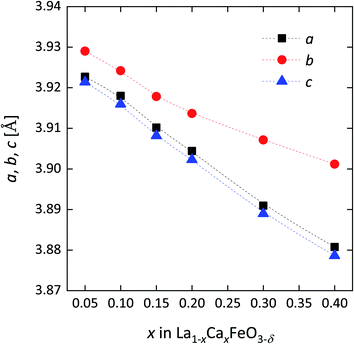 | ||
Fig. 2 Lattice parameters of La1−xCaxFeO3−δ as a function of x from Rietveld refinements of room temperature XRD powder patterns (cf.Fig. 1). Orthorhombic (Pbnm) lattice parameters for LCF phases are presented as pseudo-cubic lattice parameters, calculated using  , ,  and and  . . | ||
The temperature dependences of the pseudo-cubic lattice parameters obtained from Rietveld refinements of the HT-XRD patterns of samples La1−xCaxFeO3−δ are listed in Fig. 3. These give evidence of a structural phase transition from orthorhombic to rhombohedral (space group R![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) c), i.e., a slightly distorted cubic structure, occurring in all of the investigated compositions. The degree of distortion is found to decrease with temperature and Ca content. For example, at 1000 °C, the rhombohedral angle decreases in the order x = 0.05 (60.31°) > x = 0.10 (60.28°) > x = 0.15 (60.24°) > x = 0.20 (60.19°) > x = 0.30 (60.11°) > x = 0.40 (60.09°), noting that the value of 60° corresponds to ideal cubic symmetry. The observed transition temperatures are listed in Table 2 and compared, as far as available, with those found using differential scanning calorimetry (DSC) by Price et al.22 The lowering of the transition temperature with Ca content can be explained by the concomitant decrease of the deformation of the perovskite structure.
c), i.e., a slightly distorted cubic structure, occurring in all of the investigated compositions. The degree of distortion is found to decrease with temperature and Ca content. For example, at 1000 °C, the rhombohedral angle decreases in the order x = 0.05 (60.31°) > x = 0.10 (60.28°) > x = 0.15 (60.24°) > x = 0.20 (60.19°) > x = 0.30 (60.11°) > x = 0.40 (60.09°), noting that the value of 60° corresponds to ideal cubic symmetry. The observed transition temperatures are listed in Table 2 and compared, as far as available, with those found using differential scanning calorimetry (DSC) by Price et al.22 The lowering of the transition temperature with Ca content can be explained by the concomitant decrease of the deformation of the perovskite structure.
 | ||
Fig. 3 Lattice parameters of La1−xCaxFeO3−δ for (a) x = 0.05, (b) x = 0.10, (c) x = 0.15, (d) x = 0.20, (e) x = 0.30 and (f) x = 0.40 as a function of temperature from Rietveld refinements of HT-XRD patterns recorded in ambient air. For the orthorhombic (Pbnm) structure pseudo-cubic lattice parameters are given, calculated using  , ,  and and  . For the rhombohedral (R . For the rhombohedral (R![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) c) structure, a = b = c ≡ a. Data for x = 0.40 were taken from our previous study.15 c) structure, a = b = c ≡ a. Data for x = 0.40 were taken from our previous study.15 | ||
| x = 0.05 | x = 0.10 | x = 0.15 | x = 0.20 | x= 0.30 | x = 0.40 | |
|---|---|---|---|---|---|---|
| This work | 900 °C | 825 °C | 775 °C | 775 °C | 725 °C | 625 °C |
| Price et al.22 | — | 834 °C | — | 738 °C | 688 °C | 602 °C |
3.2 Oxygen nonstoichiometry
The oxygen nonstoichiometry (δ) of La1−xCaxFeO3−δ was investigated as a function of temperature and pO2 by thermogravimetric analysis. A typical measurement scheme is shown in Fig. S2.† Corresponding data plotted as a function of pO2, at different temperatures, for each of the compositions are shown in Fig. 4. As can be inferred from these figures, δ, at a given temperature and pO2, increases with increasing Ca mole fraction. | ||
| Fig. 4 Oxygen stoichiometry (3 − δ) of La1−xCaxFeO3−δ for (a) x = 0.05, (b) x = 0.10, (c) x = 0.15, (d) x = 0.20, (e) x = 0.30 and (f) x = 0.40 as a function of log(pO2) at different temperatures. Dashed lines are drawn to guide the eye. Data for x = 0.40 were taken from our previous study.15 | ||
Starting point in our discussion of the defect chemistry of La1−xCaxFeO3−δ is the model developed by Mizusaki et al.16–18 for La1−xSrxFeO3−δ. Assuming localized and non-interacting defects, the oxidation reaction is described, in Kröger–Vink notation, as
 | (1) |
with equilibrium constant in the ideal solution approximation
 | (2) |
Under oxidizing conditions,  coexists with
coexists with  , which is reflected in the reduced charge neutrality equation corresponding to this region, which reads
, which is reflected in the reduced charge neutrality equation corresponding to this region, which reads
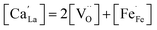 | (3) |
showing that the partial substitution of La3+ ions by Ca2+ is charge compensated by the formation of localized electron holes 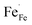 (Fe4+) and oxygen vacancies
(Fe4+) and oxygen vacancies  . Eqn (3) ignores the presence of localized electrons
. Eqn (3) ignores the presence of localized electrons  (Fe2+), arising from disproportionation of two Fe3+ ions in Fe2+ and Fe4+,
(Fe2+), arising from disproportionation of two Fe3+ ions in Fe2+ and Fe4+,
 | (4) |
which electronic defects become predominant under reducing conditions, and that of structural vacancies on lanthanum  and iron
and iron  sites. Using eqn (3), the concentration of
sites. Using eqn (3), the concentration of  in La1−xCaxFeO3−δ at a given temperature and pO2 can be calculated from corresponding data of oxygen nonstoichiometry (Fig. 4). Fig. 5 shows the results of such calculations for pO2 = 0.1 atm and pO2 = 1 atm, at 800 °C, from which figure it can be inferred that under the given experimental conditions in each of the compositions electronic compensation of the Ca dopant dominates over ionic compensation.
in La1−xCaxFeO3−δ at a given temperature and pO2 can be calculated from corresponding data of oxygen nonstoichiometry (Fig. 4). Fig. 5 shows the results of such calculations for pO2 = 0.1 atm and pO2 = 1 atm, at 800 °C, from which figure it can be inferred that under the given experimental conditions in each of the compositions electronic compensation of the Ca dopant dominates over ionic compensation.
The use of eqn (2) to describe the equilibrium between oxygen in the gas phase and oxygen in the oxide relies on the assumption that the oxygen incorporation energetics is independent of the concentration of involved point defects, which are further taken to be randomly distributed among available lattice sites. The validity of this assumption in the experimental range of the measurements can be checked by estimating the standard enthalpy change (ΔH0ox) involved in the oxidation reaction (reaction (1)). The relationship between the standard free Gibbs energy change (ΔG0ox) and the equilibrium constant (Kox) is
ΔG0ox = ΔH0ox − TΔS0ox = −RT![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln(Kox) ln(Kox) | (5) |
 | (6) |
which is known as the van 't Hoff equation, while ΔS0ox is calculated from the intercept. ln(Kox) vs. 1/T plots, at constant pO2, for La0.7Ca0.3FeO3−δ are shown in Fig. 6a. The observed non-linearity and the observation that different plots are obtained at different pO2 values indicate that Kox is a non-ideal equilibrium constant. Fig. 6b shows ln(Kox) vs. 1/T plots, at constant δ, for La0.7Ca0.3FeO3−δ. Distinct from those presented in Fig. 6a, linear plots are obtained, with slopes that are a function of δ. Similar results were obtained for the other compositions investigated in this work. Values of ΔH0ox and ΔS0ox extracted from ln(Kox) vs. 1/T plots, at constant δ, for the different compositions La1−xCaxFeO3−δ are shown in Fig. 6c and d, respectively. Fig. 6c shows that for a given Ca dopant concentration x in the series La1−xCaxFeO3−δ, ΔH0ox becomes more exothermic with increasing δ, while at a fixed value of δ, ΔH0ox becomes more endothermic (less exothermic) with increasing x.
 | ||
| Fig. 6 van 't Hoff plots of Kox for La0.7Ca0.3FeO3−δ at (a) constant pO2 and (b) constant δ. (c) Enthalpy (ΔH0ox) and (d) entropy (ΔS0ox) of oxidation (reaction (1)) at given values of x in La1−xCaxFeO3−δ as a function of δ. Data in (c) and (d) were extracted from ln(Kox) vs. 1/T plots, at constant δ. | ||
The isotherms in Fig. 4 allow evaluation of the chemical potential of oxygen relative to that in equilibrium with gaseous O2 at 1 atm,
 | (7) |
The partial molar enthalpy of oxygen, ΔhO, and the partial molar entropy of oxygen, ΔsO, can be deduced from ln(pO2) vs. 1/T (or equivalent) plots, at constant δ, according to
 | (8) |
Typical plots and resultant values of ΔhO and ΔsO for compositions La1−xCaxFeO3−δ are shown in Fig. S3.† In view of eqn (3), i.e., ignoring charge disproportionation (reaction (4)), the slopes of ln(Kox) vs. 1/T at constant δ relate to those derived from ln(pO2) vs. 1/T plots. It follows
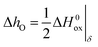 | (9) |
The partial molar entropy can be represented as
| ΔsO = Δs0O − sconf | (10) |
Regarded in terms of the reverse of reaction (1), i.e., the oxygen reduction reaction, the present results show that the energetic cost of formation of oxygen vacancies in La1−xCaxFeO3−δ is higher at higher oxygen nonstoichiometry, while smaller, at fixed δ, if La is partly substituted by Ca. These observations may be related, e.g., to an increase in the oxygen bond strength with increasing oxygen nonstoichiometry (due to the concomitant increase in the average oxidation state of the transition metal cation), a decrease in the oxygen bond strength with Ca content (Ca–O bonds are weaker than La–O bonds) and/or changes in the electronic structure. First principle calculations indeed confirm that the oxygen vacancy formation energy, ΔhV(= −ΔhO = −1/2ΔH0ox) is significantly lowered with alkaline–earth metal dopant concentrations in La1−xSrxFeO3−δ (ref. 28) and La1−xCaxFeO3−δ (ref. 29) which is in line with the results shown in Fig. 6c. Both cited studies show that the electron holes induced by Sr or Ca substitution have significant O 2p character as has been confirmed by experimental studies using X-ray absorption spectroscopy.30 These findings suggest that the electron holes in both series of oxides are (at least, to some extent) delocalized due to which the mass action law is expected to break down.31 Nonideal thermodynamic behavior of the defects as observed for La1−xCaxFeO3−δ in this study has also been reported for a number of related perovskite oxides, including Ba1−xSrxFeO3−δ (x = 0, 0.5),32,33 (Ba0.5Sr0.5)1.04Co0.8Fe0.2O3−δ,32 Ba0.5Sr0.5Co0.4Fe0.6O3−δ,32 La0.4Sr0.6Co1−yFeyO3−δ (y = 0.2, 0.4),34 SrCo0.8Fe0.2O3−δ,35 and La1−xSrxCoO3−δ (0.1 ≤ x ≤ 0.7).31,36 These and present findings are, however, in contrast with data of high-temperature drop calorimetry and thermogravimetry on La1−xSrxFeO3−δ.17,18,37 In these studies, ΔH0ox for La1−xSrxFeO3−δ is found virtually independent of the oxygen nonstoichiometry at an average value of −200 ± 50 kJ mol−1 for 0 ≤ x ≤ 0.5 and at −140 ± 30 kJ mol−1 for 0.5 ≤ x ≤ 1.0. Corresponding changes with x within the specified ranges are found to be within experimental error. Further work is required to understand the nonideal energetics of the defect species in La1−xCaxFeO3−δ.
3.3 Electrical conductivity
Fig. 7a shows Arrhenius plots of the total electrical conductivity in air of the different compositions La1−xCaxFeO3−δ. The conductivity includes both ionic and electronic contributions. Since under the given experimental conditions electron holes are the predominant charge carriers (Fig. 5) and their mobility will be much higher than that of oxygen vacancies, it can safely be assumed that the contribution of ionic conductivity to the total electrical conductivity is negligible.Previous studies have suggested that electrical conduction in La1−xAxFeO3 (A = Ca, Sr) at elevated temperatures occurs by p-type small polaron hopping,16,20,38 and can be expressed as
 | (11) |
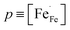 and μh are the concentration (mole fraction) and mobility of electron holes, respectively, is Avogadro's number, Vm is the molar volume, and e is the electronic charge. The charge carrier concentration p as a function of temperature for each composition La1−xCaxFeO3−δ was determined from corresponding data of oxygen nonstoichiometry, while the mobility μh was calculated with the help of eqn (11). Arrhenius plots of both parameters for the different compositions La1−xCaxFeO3−δ are shown in Fig. 7b and c, respectively. Fig. 7a shows that the electrical conductivity of La1−xCaxFeO3−δ, at 650 °C, increases with Ca mole fraction up to a value of 123 S cm−1 for x = 0.3. The results displayed in Fig. 7b make clear that this increase can be attributed to the concomitant increase in the charge carrier concentration. The lowering of electrical conductivity on going from composition x = 0.3 to x = 0.4 (Fig. 7a) is caused by the decreasing mobility, which is found much lower for x = 0.40 than for x = 0.30. The observed decrease of the electrical conductivity with temperature for both compositions x = 0.30 and x = 0.40 (Fig. 7a) can be attributed to a lowering of both the concentration and mobility of the charge carriers with increasing temperature.
and μh are the concentration (mole fraction) and mobility of electron holes, respectively, is Avogadro's number, Vm is the molar volume, and e is the electronic charge. The charge carrier concentration p as a function of temperature for each composition La1−xCaxFeO3−δ was determined from corresponding data of oxygen nonstoichiometry, while the mobility μh was calculated with the help of eqn (11). Arrhenius plots of both parameters for the different compositions La1−xCaxFeO3−δ are shown in Fig. 7b and c, respectively. Fig. 7a shows that the electrical conductivity of La1−xCaxFeO3−δ, at 650 °C, increases with Ca mole fraction up to a value of 123 S cm−1 for x = 0.3. The results displayed in Fig. 7b make clear that this increase can be attributed to the concomitant increase in the charge carrier concentration. The lowering of electrical conductivity on going from composition x = 0.3 to x = 0.4 (Fig. 7a) is caused by the decreasing mobility, which is found much lower for x = 0.40 than for x = 0.30. The observed decrease of the electrical conductivity with temperature for both compositions x = 0.30 and x = 0.40 (Fig. 7a) can be attributed to a lowering of both the concentration and mobility of the charge carriers with increasing temperature.
To discriminate between adiabatic and non-adiabatic regimes of small polaron hopping, we have analyzed the electrical mobility in terms of Emin–Holstein's theory.39–41 In the event of coincidence of local distortions of initial and final states, the temperature-dependent mobility in this theory is given by
 | (12) |
 takes into account the probability that the adjacent site to which the polaron hops may already be occupied.42 Accordingly, the plot of
takes into account the probability that the adjacent site to which the polaron hops may already be occupied.42 Accordingly, the plot of 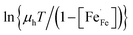 vs. 1000/T should give a straight line with activation energy
vs. 1000/T should give a straight line with activation energy  in the adiabatic regime. In the non-adiabatic regime,39 the charge carrier moves too slowly to adjust to rapid lattice fluctuations and, hence, misses such ‘coincidence events’, lowering the net hopping rate. The mobility of electron holes is then given by
in the adiabatic regime. In the non-adiabatic regime,39 the charge carrier moves too slowly to adjust to rapid lattice fluctuations and, hence, misses such ‘coincidence events’, lowering the net hopping rate. The mobility of electron holes is then given by | (13) |
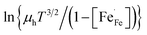 vs. 1000/T should give a straight line with activation energy
vs. 1000/T should give a straight line with activation energy  . Fig. 8a and b show corresponding data fitted to each model. The equations for the linear relationships along with the coefficients of determination (R2) are presented in Table 3. Both models fit the data for compositions x = 0.05, 0.10, 0.15 and 0.20 reasonably well. Based on the results, however, it is difficult to substantiate either model. Comparison of the obtained R2 values indicates a slight favor for the non-adiabatic model. Clear departures from linear relationships are, however, obtained for compositions x = 0.30 and 0.40.
. Fig. 8a and b show corresponding data fitted to each model. The equations for the linear relationships along with the coefficients of determination (R2) are presented in Table 3. Both models fit the data for compositions x = 0.05, 0.10, 0.15 and 0.20 reasonably well. Based on the results, however, it is difficult to substantiate either model. Comparison of the obtained R2 values indicates a slight favor for the non-adiabatic model. Clear departures from linear relationships are, however, obtained for compositions x = 0.30 and 0.40.
 | ||
Fig. 8 Plots of (a)  vs. 1000/T (adiabatic regime) and (b) vs. 1000/T (adiabatic regime) and (b)  vs. 1000/T (non-adiabatic regime) for La1−xCaxFeO3−δ at pO2 = 0.21 atm. The dashed lines are drawn to guide the eye. vs. 1000/T (non-adiabatic regime) for La1−xCaxFeO3−δ at pO2 = 0.21 atm. The dashed lines are drawn to guide the eye. | ||
 vs. 1000/T (adiabatic regime) and
vs. 1000/T (adiabatic regime) and  vs. 1000/T (non-adiabatic regime) plots as shown in Fig. 8a and b, respectively, along with the coefficients of determination (R2)
vs. 1000/T (non-adiabatic regime) plots as shown in Fig. 8a and b, respectively, along with the coefficients of determination (R2)
Fig. S4a† shows the pO2 dependence of the electrical conductivity of La1−xCaxFeO3−δ, at 800 °C. For all compositions, it is found that the calculated electron hole mobility is suppressed by decreasing pO2, suggesting that the presence of oxygen vacancies highly influences the apparent mobility, e.g., by disruption of Fe4+–O–Fe3+ migration pathways, oxygen vacancies acting as traps or as scattering centres for the electrons (Fig. S4b and S5†).
Above, we have analyzed the apparent hole mobility in La1−xCaxFeO3−δ in terms of hopping of small polarons, which is a thermally activated process. As seen from Fig. 7c, the apparent hole mobility in the compositions with x = 0.30 and 0.40 is rather found to decrease with increasing temperature. As alluded to before, several studies based on density functional theory and X-ray adsorption spectroscopy have revealed that the Fe 3d and O 2p states in La1−xAxFeO3−δ (A = Ca, Sr) and related perovskites are hybridized to some degree. The extent of hybridisation is proposed to increase with the oxidation state of the transition metal ion,43 causing increased delocalisation of the charge carriers. Clearly, more research is warranted to clarify the nature of the charge carriers in these solids.
3.4 Electrical conductivity relaxation
The oxygen transport properties of phases La1−xCaxFeO3−δ were evaluated using the ECR technique. It is recalled that measurements were conducted using small pO2 steps, i.e., between 0.100 and 0.215 atm, ensuring conditions close to equilibrium. Fig. 9 shows normalized conductivity relaxation curves for a given sample obtained for oxidation steps at different temperatures along with the respective fits to the theoretical model. It can be seen that the time needed to reach equilibrium is longer as the temperature is reduced. Curve fitting allows simultaneous determination of the chemical diffusion coefficient, Dchem, and the surface exchange coefficient, kchem, provided that fitting is sensitive to both parameters. Both parameters can be most reliably assessed from fitting if the sample length is close to Dchem/kchem, as parameterized by the Biot number (Bi).44 This number represents the ratio between the characteristic times for diffusion, τdiff = lz2/Dchem, and that for surface exchange, τexch = lz/kchem, lz being the half-thickness of the sample,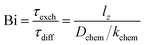 | (14) |
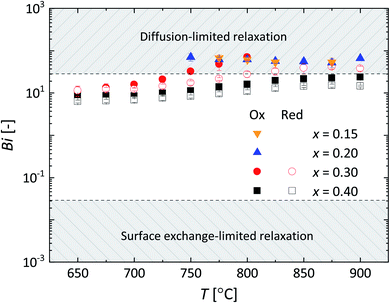 | ||
| Fig. 10 Temperature dependence of the Biot number (Bi) for La1−xCaxFeO3−δ. Error bars are within the size of the symbols. Following Den Otter et al.25 the mixed-controlled region is found for 0.03 ≤ Bi ≤ 30. | ||
Arrhenius plots of Dchem and kchem for the different La1−xCaxFeO3−δ compositions are shown in Fig. 11a and b, respectively. There is no significant difference between the results from oxidation and reductions runs. Obtained values of Dchem for x = 0.10 and x = 0.20 are in good agreement with corresponding values reported by Berger et al.12,23 (Fig. 11a). The agreement is less good comparing values of kchem for x = 0.20 with those reported by Berger et al.12 (Fig. 11b). This may at least partly be due to the difficulty in determining kchem as the materials exhibit exceptionally high surface exchange rates, as was noted before by Berger et al.23 In the present study, values of kchem could only be accurately assessed from the relaxation curves for compositions x = 0.15, x = 0.20, x = 0.30 and x = 0.40. Note from Fig. 11b that all these compositions show higher surface exchange rates than state-of-the-art La0.58Sr0.4Co0.2Fe0.8O3−δ (LSCF).45 Recent research has learned that the surface exchange rate on oxide surfaces may be highly influenced by, e.g., surface enrichment due to segregation, surface impurities and grain size.5,6,45 The high exchange rates found for La1−xCaxFeO3−δ deserve more focused research, but this is considered beyond the scope of this work.
 | ||
| Fig. 11 Arrhenius plots of the (a) chemical diffusion coefficient (Dchem) and (b) surface exchange coefficient (kchem) for La1−xCaxFeO3−δ (0.100 ↔ 0.215 atm). Filled and open symbols represent data of oxidation and reduction step changes, respectively (for data from this study only). Error bars are within the size of the symbols. The dashed lines are from linear fitting of the data. Data for La0.9Ca0.1FeO3−δ (0.10 ↔ 0.15 atm),22 La0.8Ca0.2FeO3−δ (0.10 ↔ 0.15 atm),12 and La0.58Sr0.4Co0.2Fe0.8O3−δ (LSCF6428; 0.20 ↔ 0.40 atm)43 from the cited literature are shown for comparison. The pressure range between brackets denotes the step change in pO2 used in the ECR measurements. | ||
Apart from x = 0.05, the temperature dependences of Dchem of compositions La1−xCaxFeO3−δ exhibit non-Arrhenius behavior (Fig. 11a). The variation in slope with temperature is linked with the existence regions of the orthorhombic (space group Pbnm) and rhombohedral (space group R![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) c) phases as may be inferred by comparing the data in Fig. 11a with the structural data shown in Fig. 3. Apparent activation energies of Dchem in both temperature regions deduced from the data in Fig. 11a are listed in Table S2.† Note from this table that significantly higher activation energies are found in the temperature region of the orthorhombic phase. As Dchem is a lumped parameter, the different activation energies in both temperature regions may either have a kinetic or a thermodynamic origin.
c) phases as may be inferred by comparing the data in Fig. 11a with the structural data shown in Fig. 3. Apparent activation energies of Dchem in both temperature regions deduced from the data in Fig. 11a are listed in Table S2.† Note from this table that significantly higher activation energies are found in the temperature region of the orthorhombic phase. As Dchem is a lumped parameter, the different activation energies in both temperature regions may either have a kinetic or a thermodynamic origin.
3.5 Ionic conductivity and oxygen diffusivity
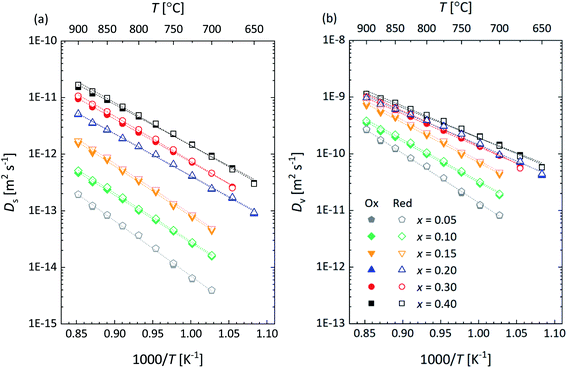
To further analyze the influence of Ca substitution on the oxygen transport properties of La1−xCaxFeO3−δ, the oxygen self-diffusion coefficient, Ds, and vacancy diffusion coefficient, Dv, of the different compositions were calculated. Ds was calculated, using the relationship19| Dchem = γODs | (15) |
 | (16) |
| cO × Ds = cv × Dv | (17) |
Fig. 13 shows Arrhenius plots of the ionic conductivity, σion, of La1−xCaxFeO3−δ calculated using the Nernst–Einstein equation,
 | (18) |
The obtained results clearly reveal that the isothermal value of σion increases with the mole fraction x of the Ca dopant. This is due to the increase in the concentration of oxygen vacancies with x in La1−xCaxFeO3−δ as can be inferred from the data presented in Fig. 4, but at least in part due to the concomitant increase in Dv as is shown in Fig. 14a. The results in the latter figure demonstrate that Dv at fixed temperature increases with Ca content to reach an almost constant value at x ≥ 0.20. The observed behavior is consistent with the concomitant decrease in the oxygen migration barrier, Em, with increasing x in La1−xCaxFeO3−δ as shown in Fig. 14b. Em is found to decrease from 1.72 ± 0.02 eV for x = 0.05 to an average value of 1.08 ± 0.03 eV for x = 0.40 (Table S4†). The observed migration barriers at small values of x are distinctly larger than those reported for single crystals of La1−xSrxCoO3−δ (77 ± 21 kJ mol−1 (x = 0), 79 ± 25 kJ mol−1 (x = 0.1))47 and La1−xSrxFeO3−δ (74 ± 24 kJ mol−1 (x = 0), 79 ± 25 kJ mol−1 (x = 0.1), 114 ± 23 kJ mol−1 (x = 0.25) by Ishigaki et al.47
 | ||
| Fig. 14 (a) Oxygen vacancy diffusion coefficient (Dv) and (b) migration energy (Em) as a function of x in La1−xCaxFeO3−δ as derived from data presented in Fig. 12b. | ||
The motion of oxygen ions through the oxide lattice is described by an activated hopping process and involves the breaking of cations bonds with oxygen and partial charge transfer from oxygen to the adjacent transition metal or the Fermi level (i.e., resembling the process of oxygen vacancy formation) and migration along the minimum energy pathway to the next nearest-neighbor site, thereby migrating through a critical A2B triangle (formed by two A cations and one B cation). Many researchers have attempted to correlate the experimentally observed migration barriers with various descriptors, like the free lattice volume, oxygen bond strength, lattice distortion, critical radius, etc.53–56 Using ab initio methods, Mayeshiba and Morgan57 found that descriptors like the O p-band center energy and oxygen vacancy formation energy correlate well with the oxygen migration barrier for a group of over 40 perovskite oxides. Both descriptors are related to the metal–oxygen bond strength, which obviously raises the question whether one of the used descriptors is redundant. The O p-band center energy (which is defined as the centroid of the projected density of states (PDOS) relative to the Fermi level) is found to correlate well with the oxygen vacancy formation enthalpy, which suggests that electronic contributions are highly important to oxygen vacancy formation in perovskite oxides.57–60
Assuming that all oxygen sites are equivalent, random walk theory of diffusion predicts that the vacancy diffusivity Dv is directly proportional to the fraction of occupied sites and, hence, to the oxygen concentration cO which, for small values of the oxygen vacancy concentration cv, is virtually constant.61 For this reason, measured activation energies of Dv are commonly interpreted as the migration energy (Em), assuming that all other atomistic parameters, including the characteristic lattice frequency and hopping distance, remain constant with changes in cv. Fig. 15 shows the migration barriers thus obtained for La1−xCaxFeO3−δ (Table S4†) plotted against the oxygen vacancy formation energies, ΔhV, at two different values of δ, as evaluated from corresponding van 't Hoff plots (Fig. 6b). Both curves exhibit a trend similar to that observed for the group of perovskite oxides by Mayeshiba and Morgan57 in the sense that the migration barrier in La1−xCaxFeO3−δ is found to decrease with decreasing ΔhV. As discussed in Section 3.2, values of ΔhV for La1−xCaxFeO3−δ depend both on x and δ. A more detailed analysis of the correlation between Em and ΔhV in La1−xCaxFeO3−δ must therefore await evaluation of the migration barriers in compositions La1−xCaxFeO3−δ as a function of both x and δ.
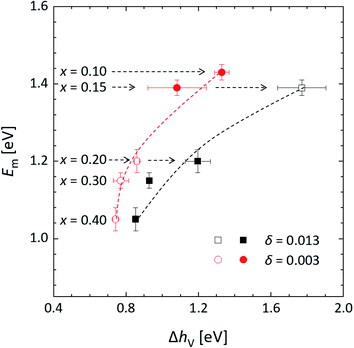 | ||
| Fig. 15 Migration energy (Em) vs. oxygen vacancy formation energy (ΔhV). Em was evaluated at constant pO2 (extracted from data presented in Fig. 12b), while ΔhV = −1/2ΔH0ox was evaluated at constant oxygen nonstoichiometry (extracted from data presented in Fig. 6c), at δ = 0.003 and at δ = 0.013. Data presented by open symbols were obtained by extrapolation. | ||
4. Conclusions
In this work, we have shown that:(i) Perovskite-type oxides La1−xCaxFeO3−δ (x = 0.05, 0.10, 0.15, 0.20, 0.30 and 0.40) exhibit a phase transition, under ambient air, from room-temperature orthorhombic (space group Pbnm) to a rhombohedral (space group R![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) c), i.e., a slightly distorted cubic, structure at elevated temperature. The transition temperature decreases gradually from 900 °C for x = 0.05 to 625 °C for x = 0.40.
c), i.e., a slightly distorted cubic, structure at elevated temperature. The transition temperature decreases gradually from 900 °C for x = 0.05 to 625 °C for x = 0.40.
The combined data of thermogravimetry, electrical conductivity and electrical conductivity relaxation measurements on La1−xCaxFeO3−δ reveal that:
(ii) the Ca dopant is predominantly compensated by the formation of electron holes (electronic compensation) rather than by oxygen vacancies (ionic compensation). The enthalpy of oxidation is found to decrease with increasing oxygen nonstoichiometry δ, while it becomes more endothermic (less exothermic), at constant δ, with increasing x.
(iii) Maximum electrical conductivity of value 123 S cm−1 at 650 °C is found, under air, for x = 0.30. The temperature dependence of the calculated mobility of electron holes x = 0.10, 0.15, 0.15 and 0.20 is found to be in accordance with Emin–Holstein's theory (adiabatic and non-adiabatic regimes), but fails for the compositions with high Ca contents x = 0.30 and x = 0.40. This is tentatively explained by the increased delocalization of charge carriers with increasing the Ca dopant concentration.
(iv) The effective migration barrier for oxygen diffusion in La1−xCaxFeO3−δ decreases with decreasing oxygen vacancy formation enthalpy (less negative enthalpy of oxidation). The latter is found to depend both on Ca content and the level of oxygen nonstoichiometry. The ionic conductivity increases with increasing Ca content in La1−xCaxFeO3−δ due to the resultant increases in oxygen nonstoichiometry and vacancy diffusivity.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
Financial support from the Dutch Technology Foundation (STW, now part of NWO; Project Nr. 15325) and the Chinese Scholarship Council (CSC 201406340102) are gratefully acknowledged.References
- S. Y. Gómez and D. Hotza, Renewable Sustainable Energy Rev., 2016, 61, 155–174 CrossRef.
- J. C. Ruiz-Morales, D. Marrero-López, J. Canales-Vázquez and J. T. S. Irvine, RSC Adv., 2011, 1, 1403–1414 RSC.
- C. Sun, R. Hui and J. Roller, J. Solid State Electrochem., 2010, 14, 1125–1144 CrossRef CAS.
- M. B. Mogensen, M. Chen, H. L. Frandsen, C. Graves, J. B. Hansen, K. V. Hansen, A. Hauch, T. Jacobsen, S. H. Jensen, T. L. Skafte and X. Sun, Clean Energy, 2019, 3, 175–201 CrossRef.
- J. Druce, H. Téllez, M. Burriel, M. D. Sharp, L. J. Fawcett, S. N. Cook, D. S. McPhail, T. Ishihara, H. H. Brongersma and J. a. Kilner, Energy Environ. Sci., 2014, 7, 3593–3599 RSC.
- Đ. Tripković, R. Küngas, M. B. Mogensen and P. V. Hendriksen, J. Mater. Chem. A, 2019, 7, 11782–11791 RSC.
- W. Jung and H. L. Tuller, Energy Environ. Sci., 2012, 5, 5370–5378 RSC.
- D. Oh, D. Gostovic and E. D. Wachsman, J. Mater. Res., 2012, 27, 1992–1999 CrossRef CAS.
- F. Morin, G. Trudel and Y. Denos, Solid State Ionics, 1997, 96, 129–139 CrossRef CAS.
- J. Ovenstone, J. S. White and S. T. Misture, J. Power Sources, 2008, 181, 56–61 CrossRef CAS.
- J. M. Ralph, C. Rossignol and R. Kumar, J. Electrochem. Soc., 2003, 150, 1518–1522 CrossRef.
- C. Berger, E. Bucher, A. Windischbacher, A. D. Boese and W. Sitte, J. Solid State Chem., 2018, 259, 57–66 CrossRef CAS.
- C. Berger, E. Bucher, C. Gspan, A. Menzel and W. Sitte, J. Electrochem. Soc., 2017, 164, F3008–F3018 CrossRef CAS.
- B. C. H. Steele, K. M. Hori and S. Uchino, Solid State Ionics, 2000, 135, 445–450 CrossRef CAS.
- J. Song, D. Ning and H. J. M. Bouwmeester, Phys. Chem. Chem. Phys., 2020, 22, 11984–11995 RSC.
- J. Mizusaki, T. Sasamoto, W. R. Cannon and H. K. Bowen, J. Am. Ceram. Soc., 1983, 66, 247–252 CrossRef CAS.
- J. Mizusaki, M. Yoshihiro, S. Yamauchi and K. Fueki, J. Solid State Chem., 1985, 58, 257–266 CrossRef CAS.
- J. Mizusaki, M. Yoshihiro, S. Yamauchi and K. Fueki, J. Solid State Chem., 1987, 67, 1–8 CrossRef CAS.
- J. E. Ten Elshof, M. H. R. Lankhorst and H. J. M. Bouwmeester, J. Electrochem. Soc., 1997, 144, 1060–1067 CrossRef.
- M. V. Patrakeev, I. A. Leonidov, V. L. Kozhevnikov and K. R. Poeppelmeier, J. Solid State Chem., 2005, 178, 921–927 CrossRef CAS.
- A. Fossdal, M. Menon, I. Waernhus, K. Wiik, M.-A. Einarsrud and T. Grande, J. Am. Ceram. Soc., 2010, 87, 1952–1958 CrossRef.
- P. M. Price, E. Rabenberg, D. Thomsen, S. T. Misture and D. P. Butt, J. Am. Ceram. Soc., 2014, 97, 2241–2248 CrossRef CAS.
- C. Berger, E. Bucher and W. Sitte, Solid State Ionics, 2017, 299, 46–54 CrossRef CAS.
- L. Winnubst, S. A. Veldhuis, R. Ruhl, S. F. P. ten Donkelaar, H. J. M. Bouwmeester and A. Nijmeijer, Ceram. Int., 2015, 41, 13709–13715 CrossRef.
- J. Rodríguez-carvajal, Phys. Rev. B: Condens. Matter Mater. Phys., 1993, 15, 49–55 Search PubMed.
- M. W. den Otter, H. J. M. Bouwmeester, B. A. Boukamp and H. Verweij, J. Electrochem. Soc., 2001, 148, J1–J6 CrossRef CAS.
- R. D. Shannon, Acta Crystallogr., Sect. A: Cryst. Phys., Diffr., Theor. Gen. Crystallogr., 1976, 32, 751–767 CrossRef.
- A. M. Ritzmann, A. B. Muñoz-García, M. Pavone, J. A. Keith and E. A. Carter, Chem. Mater., 2013, 25, 3011–3019 CrossRef CAS.
- R. Pushpa, D. Daniel and D. P. Butt, Solid State Ionics, 2013, 249–250, 184–190 CrossRef CAS.
- M. Abbate, F. M. F. de Groot, J. C. Fuggle, A. Fujimori, O. Strebel, F. Lopez, M. Domke, G. Kaindl, G. A. Sawatzky, M. Takano, Y. Takeda, H. Eisaki and S. Uchida, Phys. Rev. B: Condens. Matter Mater. Phys., 1992, 46, 4511–4519 CrossRef CAS.
- M. H. R. Lankhorst, H. J. M. Bouwmeester and H. Verweij, Phys. Rev. Lett., 1996, 77, 2989–2992 CrossRef CAS.
- L. Wang, BSCF SOFC cathode materials: Bulk properties, kinetics and mechanism of oxygen reduction, PhD thesis, University of Stuttgart, Stuttgart, Germany, 2009.
- M. F. Hoedl, D. Gryaznov, R. Merkle, E. A. Kotomin and J. Maier, J. Phys. Chem. C, 2020, 124, 11780–11789 CrossRef CAS.
- E. Bucher, W. Sitte, G. B. Caraman, V. A. Cherepanov, T. V. Aksenova and M. V. Ananyev, Solid State Ionics, 2006, 177, 3109–3115 CrossRef CAS.
- N. Grunbaum, L. Mogni, F. Prado and A. Caneiro, J. Solid State Chem., 2004, 177, 2350–2357 CrossRef CAS.
- J. Mizusaki, Y. Mima, S. Yamauchi, K. Fueki and H. Tagawa, J. Solid State Chem., 1989, 80, 102–111 CrossRef CAS.
- J. Cheng, A. Navrotsky, X. D. Zhou and H. U. Anderson, Chem. Mater., 2005, 17, 2197–2207 CrossRef CAS.
- C. Shi, H. Qin, M. Zhao, X. Wang, L. Li and J. Hu, Sens. Actuators, B, 2014, 190, 25–31 CrossRef CAS.
- T. Holstein, Ann. Phys., 1959, 8, 343–389 CAS.
- L. Friedman and T. Holstein, Ann. Phys., 1963, 21, 494–549 CAS.
- D. Emin and T. Holstein, Ann. Phys., 1969, 53, 439–520 Search PubMed.
- K. J. Yoon, P. a. Zink, S. Gopalan, U. B. Pal and L. R. Pederson, J. Electrochem. Soc., 2009, 156, B795–B800 CrossRef CAS.
- J. Suntivich, W. T. Hong, Y. Lee, J. M. Rondinelli, W. Yang, J. B. Goodenough, B. Dabrowski, J. W. Freeland and Y. Shao-Horn, J. Phys. Chem. C, 2014, 118, 1856–1863 CrossRef CAS.
- R. Ruhl, J. Song, V. Thore, S. P. Singh, K. Wiik, Y. Larring and H. J. M. Bouwmeester, Phys. Chem. Chem. Phys., 2019, 21, 21824–21835 RSC.
- S. Saher, S. Naqash, B. A. Boukamp, B. Hu, C. Xia and H. J. M. Bouwmeester, J. Mater. Chem. A, 2017, 5, 4991–4999 RSC.
- H. J. M. Bouwmeester and A. J. Burggraaf, in The CRC Handbook of Solid State Electrochemistry, ed. P. J. Gellings and H. J. M. Bouwmeester, CRC, New York, 1997, p. 481 Search PubMed.
- T. Ishigaki, S. Yamauchi, K. Kishio, J. Mizusaki and K. Fueki, J. Solid State Chem., 1988, 73, 179–187 CrossRef CAS.
- J. Yoo, A. Verma, S. Wang and A. J. Jacobson, J. Electrochem. Soc., 2005, 152, A497–A505 CrossRef CAS.
- R. De Souza and J. A. Kilner, Solid State Ionics, 1998, 106, 175–187 CrossRef CAS.
- A. Esquirol, J. Kilner and N. Brandon, Solid State Ionics, 2004, 175, 63–67 CrossRef CAS.
- J. Mizusaki, Solid State Ionics, 1992, 52, 79–91 CrossRef CAS.
- J. A. Kilner, Solid State Ionics, 2000, 129, 13–23 CrossRef CAS.
- J. A. Kilner and R. J. Brook, Solid State Ionics, 1982, 6, 237–252 CrossRef CAS.
- M. Mogensen, D. Lybye, N. Bonanos, P. V. Hendriksen and F. W. Poulsen, Solid State Ionics, 2004, 174, 279–286 CrossRef CAS.
- Z. Ogumi, K. Amezawa, M. Oishi, Y. Uchimoto, H. Arai, T. Nakao, Y. Orikasa, A. Mineshige and T. Ina, J. Mater. Chem., 2011, 21, 14013 RSC.
- Y. A. Mastrikov, R. Merkle, E. A. Kotomin, M. M. Kuklja and J. Maier, Phys. Chem. Chem. Phys., 2013, 15, 911–918 RSC.
- T. T. Mayeshiba and D. D. Morgan, Solid State Ionics, 2016, 296, 71–77 CrossRef CAS.
- Y. L. Lee, J. Kleis, J. Rossmeisl, Y. Shao-Horn and D. Morgan, Energy Environ. Sci., 2011, 4, 3966–3970 RSC.
- J. Hwang, Z. Feng, N. Charles, X. R. Wang, D. Lee, K. A. Stoerzinger, S. Muy, R. R. Rao, D. Lee, R. Jacobs, D. Morgan and Y. Shao-Horn, Mater. Today, 2019, 31, 100–118 CrossRef CAS.
- A. M. Deml, V. Stevanović, A. M. Holder, M. Sanders, R. Ohayre and C. B. Musgrave, Chem. Mater., 2014, 26, 6595–6602 CrossRef CAS.
- J. A. Kilner, R. A. De Souza and I. C. Fullarton, Solid State Ionics, 1996, 86–88, 703–709 CrossRef CAS.
Footnotes |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/d0ta07508f |
| ‡ Separation and Conversion Technology, Flemish Institute for Technological Research (VITO), Boeretang 200, Mol 2400, Belgium |
| § Center for Information Photonics and Energy Materials, Shenzhen Institutes of Advanced Technology (SIAT), Chinese Academy of Sciences, Shenzhen 518055, P. R. China |
| This journal is © The Royal Society of Chemistry 2021 |