Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Laser fabrication of hybrid electrodes composed of nanocarbons mixed with cerium and manganese oxides for supercapacitive energy storage†
Pablo
García Lebière
 *a,
Ángel
Pérez del Pino
*a,
Ángel
Pérez del Pino
 a,
Guillem Domènech
Domingo
a,
Constantin
Logofatu
a,
Guillem Domènech
Domingo
a,
Constantin
Logofatu
 bd,
Immaculada
Martínez-Rovira
bd,
Immaculada
Martínez-Rovira
 c,
Ibraheem
Yousef
c,
Ibraheem
Yousef
 c and
Enikö
György
c and
Enikö
György
 abd
abd
aInstitute of Materials Science of Barcelona, ICMAB-CSIC, Campus UAB, 08193 Bellaterra, Spain. E-mail: pgarcia2@icmab.es; Tel: +34 935801853
bNational Institute for Materials Physics, PO Box MG 7, 77125 Bucharest, Romania
cALBA Synchrotron, Carrer de la Llum, 2-26, 08290 Cerdanyola del Vallès, Spain
dNational Institute for Lasers, Plasma and Radiation Physics, PO Box MG 36, 77125 Bucharest, Romania
First published on 14th December 2020
Abstract
Novel composite materials are being investigated for improving the energy storage performance of electrochemical capacitors. For this goal, synergistic effects via the combination of diverse types of materials are crucial. In this work, electrodes composed of reduced graphene oxide, multiwall carbon nanotubes, as well as cerium and manganese oxides were fabricated through reactive inverse matrix-assisted pulsed laser evaporation (RIMAPLE). UV-pulsed laser irradiation of frozen aqueous dispersions containing graphene oxide sheets, carbon nanotubes, and ceria nanoentities, besides manganese acetate precursor, led to the simultaneous chemical transformation and co-deposition of hybrid electrodes onto flexible metallic substrates via photothermal and photochemical processes. Thorough morphological and compositional studies of the electrodes demonstrated the laser-induced reduction of graphene oxide, besides the crystallization of a mixture of cerium and manganese oxide nanostructures decorating the carbon nanoentities during the deposition process. Electrochemical analyses revealed a remarkable improvement of performance with the combination of electrochemical double layer in the porous nanocarbon framework with pseudocapacitance from the oxide nanostructures, obtaining excellent volumetric capacitances of up to 140 F cm−3 at 10 mV s−1 with the combination of all four materials. The attained results are the best ones yet published regarding RIMAPLE of hybrid nanocarbon-based electrodes with micrometric thickness. Finally, symmetric electrochemical capacitors were fabricated using aqueous electrolyte, revealing excellent stability upon tens of thousands of charge–discharge cycles.
1. Introduction
The technological advance of portable consumer electronics, wearable medical devices, electric vehicles, smart electric grids and the emerging Internet of Things requires innovation in energy storage technologies.1 Without doubts, electrochemical energy storage technologies play a major role in this subject. In particular, supercapacitors are important for their fast and reversible use of energy, high power density, long cycle life, low maintenance cost, and environment-friendly nature.2,3 The storage mechanism of supercapacitors consists in two contributions: (i) the electrostatic accumulation of ionic charges from the electrolyte on the electrode's surface (electric double layer, EDL); and (ii) through surface reversible faradaic redox reactions at the surface of the active materials (pseudocapacitance).4 Carbon-based materials are widely investigated for supercapacitor electrodes using EDL mechanism (i.e. activated carbon, reduced graphene oxide, rGO; carbon nanotubes, CNT).5–8 Many transition metal oxides (TMO) have been reported as either intrinsic or extrinsic pseudocapacitive materials, i.e. RuO2, MnO2, Fe3O4, NiO or V2O5.4,8,9 Combining materials with both energy storage mechanisms can lead to synergistic effects, in which the electrochemical performance is enhanced, avoiding the low conductivity, poor stability and durability during charge/discharge processes common in metal oxides and preserving the advantages of rGO and CNT like high thermal conductivity, high electron mobility, mechanical stability and large surface area.8,10 Cerium dioxide (CeO2) is an important rare earth metal oxide, abundant and inexpensive, which outstanding supercapacitive performance has been recently reported as nanostructures,11–13 in combination with carbon-based materials14,15 or other TMO.16,17 Despite its good redox characteristics, it suffers from poor conductivity and structure stability as stated before. Consequently, it is worth the study of this material in combination with carbon materials and TMO. In recent years, it has been proven that the electrical conductivity can be enhanced with the combination of two or more metal oxide materials. Hence, increasing charge transport improves their charge storage performance.18 These combinations of metal oxides possess different oxidation states enabling multiple redox reactions, enhancing rapid faradaic reactions from the metal species with synergistic effects.19 Transition metal oxides based on manganese (MnOx) are promising materials with good electrochemical performance, low price, abundance, environmentally friendly and structural diversity. Although MnO2 is the most performant of the oxides,20 MnO and Mn3O4 are also used for supercapacitor electrodes with good performance.21–24 Recently, many studies were focused on the study of supercapacitive behaviour of mixtures composed of two or more metal oxides. Regarding CeO2, enhanced performance has been reported in combination with cobalt16 and ZnO,25 and for manganese oxides, in combination with Co3O4,26 ZnO,27 Fe2O3,28 Cu2O,29 and different metal ions as cobalt, copper, nickel or chromium.30,31 Moreover, many reports combined MnO2 and CeO2 with outstanding performance32–36 but a limited number of reports deal with Mn3O4.37 In summary, the synergistic effect obtained from the combination of cerium and manganese oxide materials might point to a promising composite for supercapacitive devices.The synthesis of carbon-based materials decorated with metal-oxide nanostructures can be achieved by laser-based techniques. These fabrication methods have a high potential for fast and versatile production of flexible supercapacitor electrodes and devices avoiding lasting high-temperature conditions and toxic chemicals.38,39 Importantly, laser methods produce very fast photolysis and heating of the irradiated material leading to the development of chemical reactions and phase changes out of the thermodynamic equilibrium that cannot be developed through conventional techniques. Additionally, laser heating can change the thermo-optical properties of the medium introducing non-linearities in the interaction process. Therefore, unusual chemical pathways and reaction products, novel material microstructures and phases, and new morphologies can be obtained.40 Considering these advantages, reactive inverse matrix-assisted pulsed laser evaporation (RIMAPLE) stands up as a promising method for the fabrication of composite films formed by carbon nanomaterials coated with transition metal oxide nanostructures for supercapacitor electrodes.41–46 In this approach, the coating of the carbon nanomaterials is provided by the melting and recrystallization of TMO nanoparticles (NPs) present in the target. Remarkably, Steiner et al. proved that MAPLE technique also allows the deposition of metal oxides nanoparticles using aqueous solutions of metal organic precursors (acetates) in the frozen targets.47 Thus, the UV photon energy and developed temperature rise are high enough for the laser-induced decomposition of the acetate precursors, allowing the free metal ions to crystallize nanostructures within the target before the ejection of material. To the best of our knowledge, the combined deposition of nanoentities by using metal organic precursors has not been addressed so far.
In this work, we present a novel RIMAPLE method for the synthesis of micrometric-thick hybrid electrodes composed of rGO and multiwall carbon nanotubes (MWCNTs) decorated with cerium and manganese oxides by combination of CeO2 NPs and Mn-based metal organic precursors in the target. Laser-induced photothermal/photochemical mechanisms led to the formation of CeO2 and Ce2O3 besides MnO and Mn3O4 nanostructures on the surface of rGO sheets and MWCNTs. The morphological, structural and electrochemical properties of the obtained electrodes were investigated. The contribution of the different components to the electrochemical performance was also studied. It is noted a significant increase of the volumetric capacitance in the final composite due to the insertion of CNTs that prevents re-stacking of rGO sheets and increases the porosity,48 as well as the increase of pseudocapacitance provided by cerium and manganese oxides. As a proof of concept a symmetric electrochemical capacitor was assembled to test the fabricated electrodes in practical use, exhibiting outstanding stability performance upon cycling.
2. Experimental
2.1 Samples fabrication
RIMAPLE targets were prepared by mixing different aqueous dispersions composed of graphene oxide (GO) powder (NanoInnova Technologies), multiwall carbon nanotubes (Sigma-Aldrich), cerium(IV) oxide nanoparticles (Sigma-Aldrich) and manganese(II) acetate (Sigma-Aldrich). GO powder was composed of 1–15 layers thick flakes around 1 μm2 in lateral size. Carbon nanotubes were about 10 nm in diameter and up to 1.5 μm in length, doped with carboxylic groups for enhancing their dispersibility. CeO2 nanoparticles were about 25 nm in diameter. The concentration of GO and CeO2 nanoparticles were chosen as 5 wt% for preventing precipitation and excessively high viscosity of the dispersions, and for obtaining high rate deposition process. The concentration of the rest of the precursors was varied to investigate their influence in the electrodes' performance. Table 1 shows the relative concentration of the precursors present in the dispersions. Once synthesized, the dispersions were stirred and sonicated at room temperature. MAPLE targets were prepared by filling 3 mL aluminium holder and immediately flash frozen submerging it in liquid-N2. Finally, the holders with the frozen dispersions were placed inside the deposition chamber and remained frozen during the deposition process by using a liquid N2-cooled holder. This flash-freezing method ensures the homogeneity of the target dispersion and allows a congruent deposition of the material.| Dispersion | Composition |
|---|---|
| GO-Ce | GO (5 wt%) + CeO2 NPs (5 wt%) |
| CNT-Ce | MWCNT (2 wt%) + CeO2 NPs (5 wt%) |
| GO-CNT-Ce-515 | GO (5 wt%) + MWCNT (1 wt%) + CeO2 NPs (5 wt%) |
| GO-CNT-Ce-525 | GO (5 wt%) + MWCNT (2 wt%) + CeO2 NPs (5 wt%) |
| GO-CNT-Ce-Mn-5151 | GO (5 wt%) + MWCNT (1 wt%) + CeO2 NPs (5 wt%) + Mn(CH3CO2)2 (1 wt%) |
| GO-CNT-Ce-Mn-5152 | GO (5 wt%) + MWCNT (1 wt%) + CeO2 NPs (5 wt%) + Mn(CH3CO2)2 (2 wt%) |
| GO-CNT-Ce-Mn-5155 | GO (5 wt%) + MWCNT (1 wt%) + CeO2 NPs (5 wt%) + Mn(CH3CO2)2 (5 wt%) |
The films were deposited by accumulation of 6000 UV laser pulses (266 nm wavelength, ≈4 ns pulse duration, 10 Hz repetition rate) with 0.4 J cm−2 laser fluence submitted to the frozen target using a Quantel Brilliant B Nd:YAG laser system. During the deposition, the laser beam scanned the target surface at an incident angle of 45°. Flexible and conducting 1 × 1 cm2 substrates made of (i) 0.5 mm-thick copper and (ii) 0.1 mm-thick stainless steel AISI 316L, were positioned in front of the target at a separation distance of 4 cm. The deposition process was performed at room temperature, in a 20 Pa N2 background gas environment after evacuation to a residual pressure of 0.1 Pa.
A symmetric electrochemical capacitor was assembled with the best performant electrode by using stainless steel AISI 316L substrate (1 cm2 area, 0.1 mm thickness) as current collector. The electrodes were separated by glass microfiber filter paper (Prat Dumas) impregnated with 1 M Na2SO4 aqueous electrolyte. A few cm long copper contacts were attached to the steel current collector and the system was sealed with plastic film using an impulse heat sealer type IS300C.
2.2 Characterization techniques
Thermal simulations of the GO, CNT and CeO2 nanoparticles within the water ice matrix were performed by solving the transient heat equation using the finite element method with COMSOL 5.5 software. The thickness and the morphology of the composite films were studied by field emission scanning electron microscopy (SEM) using QUANTA 200 FEG-ESEM and extreme high resolution (XHRSEM) Magellan 400 L microscopes (FEI). The study of their structural properties was performed through high resolution transmission electron microscopy (HRTEM) and high-angle annular dark field (HAADF) imaging in high resolution scanning transmission electron microscopy (STEM) through a Tecnai F20 equipment (FEI). The chemical composition of the fabricated films was investigated by X-ray photoelectron spectroscopy (XPS) using a SPECS XPS spectrometer based on a Phoibos 150 electron energy analyser operated in a constant energy mode. The system used the aluminium anode (Al Kα 1486.74 eV) as a monochromatic X-ray source. Wide range spectra over 1500 eV binding energies were recorded using a 50 eV analyser pass energy. High resolution spectra were also acquired over 20 eV ranges at 10 eV pass energy with an energy resolution of 0.7 eV. All the XPS measurements were performed in ultra-high vacuum (≈10−7 Pa). Synchrotron-based Fourier Transform Infrared Microspectroscopy (SR-FTIRM) was also used to study the chemical composition of the composite materials. This analysis was carried out at the infrared beamline MIRAS of ALBA synchrotron light source using a Hyperion 3000 microscope coupled to a Vertex 70 spectrometer (Bruker, Germany). The microscope is equipped with a liquid N2-cooled mercury cadmium telluride 50 μm MCT detector. A 36× Schwarzschild objective (NA = 0.52) was used and all the spectra were collected in the trans-reflection mode using a single masking aperture size of 10 × 10 μm2. A collection of 9 spectra for each sample was obtained in the 4000–600 cm−1 mid-infrared spectral range at 4 cm−1 spectral resolution with 1024 co-added scans per spectrum. For the correct identification of bands, baselines were subtracted.The electrochemical performance of the fabricated electrodes was investigated through cyclic voltammetry (CV) in the voltage range [0, 0.8] V using a Keithley 2450-EC Electrochemistry Lab System. The samples deposited on stainless steel were used as working electrodes in a three-electrode configuration. The analyses were performed in a 0.5 cm2 samples area using a plate material electrochemical cell (Bio-logic), and Ag/AgCl reference electrode (3 M KCl internal solution), a Pt wire counter electrode and 1 M Na2SO4 aqueous solution as electrolyte at room temperature. Galvanostatic charge–discharge (GCD) analyses were performed with the same cell configuration as CV studies changing the current density. Electrochemical impedance spectroscopy (EIS) measurements were also fulfilled through a Hioki IM3590 chemical impedance analyser. Impedance values were acquired in the frequency range of 1 Hz to 200 kHz at open circuit potential with an amplitude perturbation of 5 mV. An average of 5 measurements per data point was obtained to minimize the experimental error. Regression of EIS data to equivalent circuit models was performed using EIS Spectrum Analyser software.
3. Results and discussion
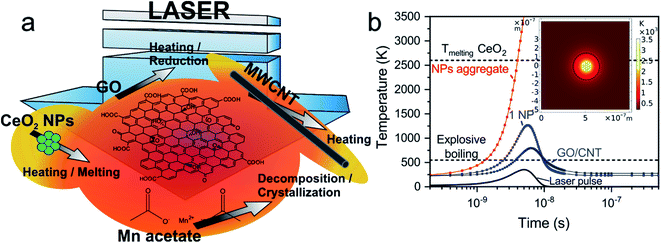
The targets submitted to laser radiation are composed of a mixture of GO sheets, MWCNTs and CeO2 NPs homogeneously dispersed in a frozen matrix of water at a measured temperature of about −30 °C. Due to the low temperature of the matrix, the targets having Mn precursor are considered to mainly contain aggregated Mn(CH3COO)2 molecules. Fig. 1a displays a scheme of the proposed mechanisms occurring during laser irradiation of the target. Photochemical processes involve the direct breaking of chemical bonds and photothermal interactions are caused by the thermalization of the excited electrons having interaction times longer than photochemical processes ones.49 Preceding studies proved the photochemical reduction of GO solutions by UV light.50 Using the laser radiation with 266 nm wavelength, which corresponds to ca. 4.7 eV photon energy, there is enough energy for the reduction taking into account that the threshold was determined to be 3.2 eV.50 Therefore, the photochemical processes are considered to be the dominating ones for GO reduction51 even though photothermal processes also take place. Regarding graphitic domains of GO and MWCNTs, the main process is considered to be photothermal due to the lack of enough photonic energy to break C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C sp2 bonds (6.4 eV).52 The UV radiation excites both σ and π-bonded electrons constituent of graphene and CNT structures, leading to their fast heating.53 Considering the absorption of CeO2 nanoparticles (bandgap of ca. 3.2 eV
C sp2 bonds (6.4 eV).52 The UV radiation excites both σ and π-bonded electrons constituent of graphene and CNT structures, leading to their fast heating.53 Considering the absorption of CeO2 nanoparticles (bandgap of ca. 3.2 eV![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 54), the excited electrons would also lead to significant heating by electron-phonon scattering. It is noteworthy that they would not be energetic enough for the CeO2 reduction to form Ce2O3
54), the excited electrons would also lead to significant heating by electron-phonon scattering. It is noteworthy that they would not be energetic enough for the CeO2 reduction to form Ce2O3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 55 despite that photochemical processes drive the exothermal reduction of GO producing a large amount of heat.56 Nevertheless, the presence of intrinsic oxygen vacancies from the nanoparticle lattice or laser-induced defects may generate a reversible transition between the cerium oxidation states Ce4+ and Ce3+.57 Lastly, the laser radiation absorbed by manganese acetate molecules has enough energy to break the Mn–O bond from the acetate (photodissociation process).55 However, Steiner et al. established that in reactive MAPLE process the decomposition of acetates is dominated by photothermal pathways and their deposition can be limited by a water explosive boiling temperature lower than the decomposition one.47 In the present work, the main contribution of thermal energy required to reach the decomposition temperature of the Mn acetate is due to GO, CNTs and CeO2 NPs, which rapidly heat the matrix surrounding them beyond the acetate decomposition temperature (over 600 K).58,59 Additionally, photochemical processes can occur producing diverse species of manganese oxide.60
55 despite that photochemical processes drive the exothermal reduction of GO producing a large amount of heat.56 Nevertheless, the presence of intrinsic oxygen vacancies from the nanoparticle lattice or laser-induced defects may generate a reversible transition between the cerium oxidation states Ce4+ and Ce3+.57 Lastly, the laser radiation absorbed by manganese acetate molecules has enough energy to break the Mn–O bond from the acetate (photodissociation process).55 However, Steiner et al. established that in reactive MAPLE process the decomposition of acetates is dominated by photothermal pathways and their deposition can be limited by a water explosive boiling temperature lower than the decomposition one.47 In the present work, the main contribution of thermal energy required to reach the decomposition temperature of the Mn acetate is due to GO, CNTs and CeO2 NPs, which rapidly heat the matrix surrounding them beyond the acetate decomposition temperature (over 600 K).58,59 Additionally, photochemical processes can occur producing diverse species of manganese oxide.60
Previous works studied UV laser irradiation of GO, MWCNT and different types NPs immersed in a water-ice target during RIMAPLE deposition process.61,62 In this work, CeO2 NPs were used for the first time in RIMAPLE experiments. Considering the thermophysical63 and optical properties64 of CeO2 NPs, the temperature evolution was simulated upon one laser pulse irradiation. As previously reported, water ice is transparent to the used UV radiation though the nanocarbon materials and the oxide NPs absorb it, being rapidly heated. As observed in Fig. 1b, the sudden heat released by a single NP or a carbon nanoentity (GO, CNT) leads to an explosive boiling of the surrounding water ice resulting in the deposition of material onto the facing substrate.45,47 The laser-induced chemical reactions cause the reduction of GO, resulting in a material similar to pristine graphene, called reduced graphene oxide (rGO)62 and the thermally-driven recrystallization of the metal oxide nanostructures, which rise over 1000 °C during several ns. The photothermal simulations indicate that the individual heating of a CeO2 NP is far from reaching its melting temperature. Nonetheless, it is well known the tendency of NPs to aggregate. Laser irradiation of small NPs aggregates with at least double the radius of a single one is enough to induce the CeO2 phase change as it is demonstrated in Fig. 1b. Moreover, the reached matrix temperature in a radius of ca. 200 nm around CeO2 NPs, GO and CNTs would be enough for the decomposition of manganese acetate molecules, producing the crystallization of its oxides, as previously mentioned. Seven different samples were prepared (Table 1): four of them to optimize the concentration of GO-CNT-CeO2 and three with different concentration of manganese acetate. The electrodes will be referred onwards as their corresponding dispersion. The fabricated films are adhered to the flexible substrate and show homogeneous black colour. As seen in Table S1,† film thickness is similar in all of them, varying in the range of 1.1–1.7 μm.
3.1 Morphological characterization
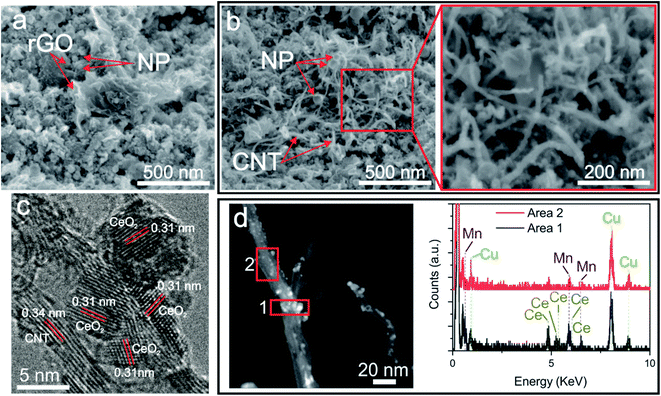
Morphological XHRSEM analyses reveal that all the fabricated samples present a homogeneous structure without visible differences at low magnification with the addition of the different compounds (Fig. S1†). At higher magnification, the homogeneity and evenly distribution of compounds of the GO-Ce (Fig. S2a†) and CNT-Ce (Fig. S2b†) electrodes are clear. Both carbon-based materials present neither visible structural damage nor wrinkles. The combination of GO, CNT and CeO2 NPs (Fig. S2c†), produces a similar structure than in the previous cases but with a visible variation of porosity. However, the addition of manganese acetate does not reflect significant differences. At even higher magnification, there is no obvious difference in the samples with the increasing amount of manganese acetate (Fig. S3†). Focusing on CNTs amount, Fig. S4† illustrates influence in morphology by the addition of a higher concentration. The addition of 2 wt% of CNTs causes their agglomeration (Fig. S4b†), not noticeable in lower concentration where the CNTs are evenly distributed. Fig. 2a and b show various XHRSEM images where it can be differentiated the presence of rGO sheets and CNTs randomly distributed and decorated with nanostructures. Interestingly, it can also be witnessed the formation of nanostructures along the CNTs (zoomed region of Fig. 2b). Focusing on the size of nanoparticles, average diameters in the range of 5–75 nm were measured, though highest resolution images demonstrate sizes as small as 1.5 nm. This size range, different from that of raw CeO2 NPs (25 nm) is due to laser-induced structural-chemical transformation during the deposition process. Molten CeO2 NPs would suffer dewetting, forming smaller particles, besides coalescence, forming larger ones. In the samples obtained with targets containing Mn acetate, the formation of manganese oxide crystallites is expected from Mn ions dissolved in boiling water, generating nanostructures with different sizes in the fabricated electrode. In Fig. 2c, a CNT (0.34 nm interplanar distance) covered by nanocrystals is shown by HRTEM. The crystal structures observed on the surface show interplanar distance of 0.31 nm corresponding to (111) CeO2 (JCPDS 00-004-0593). These structures, about 5 nm in size, are located at the surface of the CNTs and do not appear highly aggregated. It is worth noting that this crystal distribution is suitable for energy storage because the CNT works both as scaffold and as current collector for the insulating metal oxides, which store energy through pseudocapacitance. Moreover, the small size of the oxide crystals allows maintaining their electric resistance low. Additional HRTEM image of electrodes containing rGO, CNT and ceria NPs show different crystalline domains compatible with (101) Ce2O3 (JCPDs 00-023-1048) besides (111) CeO2, with varying size domains from 5 to 35 nm (Fig. S5†). The change in the oxidation state of Ce ions proves that ceria suffers reduction processes during deposition. The HRTEM image shown in Fig. 3 reveals different crystal structures identified in GO-CNT-Ce-Mn-5155, a sample where Mn component is present. Both CeO2 and Ce2O3 were observed, being the same crystal structures found in samples without Mn. At the same time, the Mn oxide species are MnO (JCPDS 04-005-4310) and Mn3O4 (JCPDS 01-075-0765). This corroborates the decomposition of the original acetate and the crystallization mechanism forming oxides. In this case, the Mn ions suffer oxidation during laser irradiation since Mn3O4 has two different states of oxidation (Mn2+, Mn3+) that were not present in the original compound (only Mn2+ in the acetate). Both Ce- and Mn-based nanostructures can be found on rGO (Fig. 3) and CNT, as seen in HAADF-STEM analysis shown in Fig. 2d. Importantly, it can be determined that both Mn and Ce oxides can be found in the same CNT but without sharing position. Hence, there is no indication of the formation of mixed oxides during the deposition process. The average size of NPs in the Ce region (1) is 2.8 nm and in the Mn region (2) is 1.7 nm, being slightly smaller Mn structures than Ce ones in general.3.2 Compositional characterization
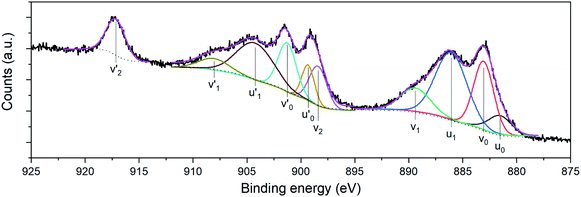
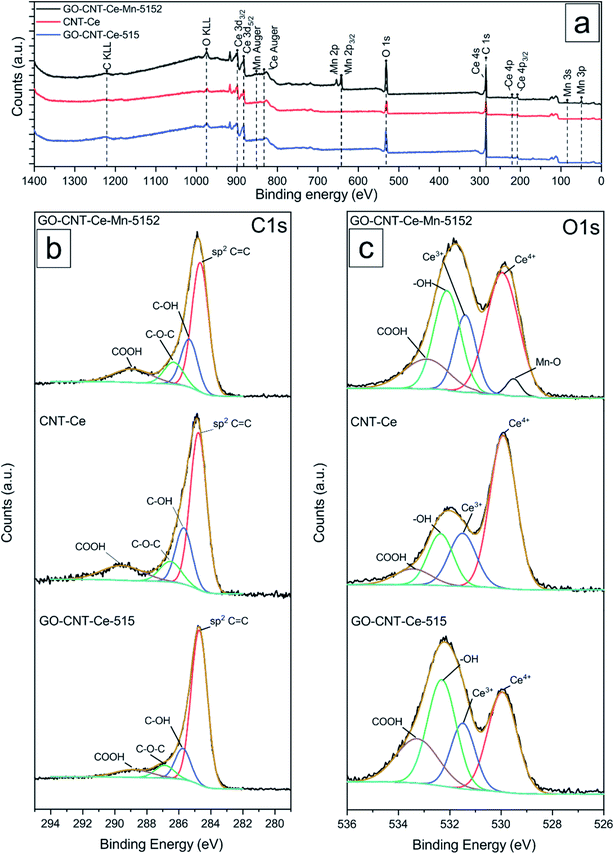
Compositional analyses of the fabricated electrodes were performed using XPS and SR-FTIRM. Fig. 4a shows a wide XPS spectrum identifying C, O, Ce and Mn XPS peaks besides some other Auger peaks of characteristic samples (CNT-Ce, GO-CNT-Ce-515 and GO-CNT-Ce-Mn-5152). All three spectra contain equivalent peaks at wide XPS, with the presence of Mn related peaks on the GO-CNT-Ce-Mn-5152 spectrum. No signal of nitrogen is recorded, revealing a negligible incorporation of N from background gas during the deposition process. In Fig. 4b and c the C 1s and O 1s high-resolution spectra of characteristic electrodes are presented, respectively. C 1s peak is deconvoluted into sp2-bonded carbon (284.8 eV) probably containing some contribution of sp3 bonds, and carbon-oxygen hydroxyl (285.7 eV), epoxide (286.5 eV) and carboxylic (289.5 eV) groups.61 Note the absence of carbonyl groups, generally present in RIMAPLE samples containing NiO, TiO2 and Fe3O4 NPs.41,61,65 Analysing the percentage of each peak, similar results are obtained between the three electrodes (Fig. S6a†). Regarding the GO-CNT-Ce-515 sample, the sp2-bonded C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C contribution is higher than in the others, indicating a greater graphitic structure restitution, even though this signal is the main contribution in all of them. Furthermore, O 1s signal is deconvoluted in Ce4+ (529.95 eV), Ce3+ (531.4 eV) also related to oxygen vacancies O2− in the lattice of metal oxide, hydroxyl (532.15 eV) and carboxyl (532.91 eV) bond contributions.66–68 In the samples including manganese acetate in the dispersion, the deconvolutions also include the O−2 structural peak, related to Mn–O–Mn bond (529.64 eV).69,70 This peak is the most intense in the O 1s spectra of Mn oxides (ca. 80%). Therefore, the contribution of hydroxyl and water peaks is negligible. Using the Ce4+ and Ce3+ peaks, the relative content of each is calculated with the relative integrated area of the constituent peaks, revealing similar percentage of Ce4+ in CNT-Ce, GO-CNT-Ce-515 and GO-CNT-Ce-Mn-5152 (73%, 61% and 71%, respectively) (Fig. S6b†). For a better enquiry of the study of Ce states, Fig. 5 shows the deconvolution of the Ce 3d3/2 and 3d5/2 signals. The six peaks labelled as v0, v1, v2 (3d5/2) and
C contribution is higher than in the others, indicating a greater graphitic structure restitution, even though this signal is the main contribution in all of them. Furthermore, O 1s signal is deconvoluted in Ce4+ (529.95 eV), Ce3+ (531.4 eV) also related to oxygen vacancies O2− in the lattice of metal oxide, hydroxyl (532.15 eV) and carboxyl (532.91 eV) bond contributions.66–68 In the samples including manganese acetate in the dispersion, the deconvolutions also include the O−2 structural peak, related to Mn–O–Mn bond (529.64 eV).69,70 This peak is the most intense in the O 1s spectra of Mn oxides (ca. 80%). Therefore, the contribution of hydroxyl and water peaks is negligible. Using the Ce4+ and Ce3+ peaks, the relative content of each is calculated with the relative integrated area of the constituent peaks, revealing similar percentage of Ce4+ in CNT-Ce, GO-CNT-Ce-515 and GO-CNT-Ce-Mn-5152 (73%, 61% and 71%, respectively) (Fig. S6b†). For a better enquiry of the study of Ce states, Fig. 5 shows the deconvolution of the Ce 3d3/2 and 3d5/2 signals. The six peaks labelled as v0, v1, v2 (3d5/2) and  ,
,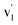 and
and  (3d3/2) refer to the three pairs of spin–orbit doublets characteristic of Ce4+ 3d final states. Another two pairs of spin–orbit doublets
(3d3/2) refer to the three pairs of spin–orbit doublets characteristic of Ce4+ 3d final states. Another two pairs of spin–orbit doublets  and
and 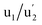 correspond to Ce3+.71 It is worth noting that these doublets are not present in the XPS spectrum of raw-CeO2 nanoparticles, as seen in Fig. S7.† As for samples containing Mn, the Ce 3d3/2 line overlaps with the Auger Mn line LMM (900 eV). Since in this case a reasonable deconvolution cannot be performed for the calculation of Ce4+, we use the relation
correspond to Ce3+.71 It is worth noting that these doublets are not present in the XPS spectrum of raw-CeO2 nanoparticles, as seen in Fig. S7.† As for samples containing Mn, the Ce 3d3/2 line overlaps with the Auger Mn line LMM (900 eV). Since in this case a reasonable deconvolution cannot be performed for the calculation of Ce4+, we use the relation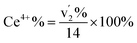 | (1) |
 is the percentage of
is the percentage of  peak area respect to the total Ce 3d area, with the relative error in the range of 10%.72 Using this relation, the percentage of Ce4+ for raw-CeO2 nanoparticles is 100%, for GO-CNT-Ce-Mn-5152 is 78%, for CNT-Ce of Ce4+ is 69% and 70% for GO-CNT-Ce-515. The three last values are similar to the ones obtained from the study of O 1s band. All three spectra from the fabricated electrodes present similar percentage of Ce3+ and Ce4+. The coexistence of both states leads to the presence of Ce2O3 and CeO2 as determined with HRTEM analyses. Moreover, there is a possibility of the existence of intermediate states of CeO2−x with partially reduced CeO2. Therefore, some of the original NPs suffer reduction during the deposition process, changing from Ce4+ to Ce3+ state. Taking into account that stoichiometric CeO2 is an insulator, this reduction is important for enhancing the capability to store and mobilize oxygen within the ceria matrix and for increasing the electronic conduction attributed to the formation of small polarons which follow a hopping mechanism to diffuse.68,73
peak area respect to the total Ce 3d area, with the relative error in the range of 10%.72 Using this relation, the percentage of Ce4+ for raw-CeO2 nanoparticles is 100%, for GO-CNT-Ce-Mn-5152 is 78%, for CNT-Ce of Ce4+ is 69% and 70% for GO-CNT-Ce-515. The three last values are similar to the ones obtained from the study of O 1s band. All three spectra from the fabricated electrodes present similar percentage of Ce3+ and Ce4+. The coexistence of both states leads to the presence of Ce2O3 and CeO2 as determined with HRTEM analyses. Moreover, there is a possibility of the existence of intermediate states of CeO2−x with partially reduced CeO2. Therefore, some of the original NPs suffer reduction during the deposition process, changing from Ce4+ to Ce3+ state. Taking into account that stoichiometric CeO2 is an insulator, this reduction is important for enhancing the capability to store and mobilize oxygen within the ceria matrix and for increasing the electronic conduction attributed to the formation of small polarons which follow a hopping mechanism to diffuse.68,73
 | ||
| Fig. 4 (a) Wide XPS spectra and fitting curves of high-resolution (b) C 1s and (c) O 1s spectra of samples GO-CNT-Ce-Mn-5152, CNT-Ce and GO-CNT-Ce-515. | ||
XPS spectra of the Mn 2p line (Fig. 6a) is complex because of the presence of a multiplet structure.74 The Mn 2p3/2 spectra is characteristic of the Mn3O4 and MnO compounds, having peaks at ca. 641.5 eV, 642.9 eV and 646.1 eV.31,74 The doublet separation of the Mn 2p1/2 and Mn 2p3/2 spin orbit (12 eV) is also in agreement with these phases. The similar binding energies of Mn 2p3/2 peaks hinders the obtainment of the compositional percentages of the compounds. Fortunately, there is a characteristic satellite of Mn2+ and splitting of the Mn 3s line (Fig. 6b) that depends on the oxidation state.75 This splitting in the measured spectra corroborates the presence of MnO and Mn3O4 phases75 which is consistent with HRTEM analyses revealing interplanar distances compatible with both oxide phases. From the Mn 3s XPS spectrum it can be determined that the sample contains a mixture of Mn2+ (62%) and Mn3+ (38%) states, therefore, having a mixture of MnO (43% Mn2+) with Mn3O4 (19% Mn2+ and 38% Mn3+). It is worth noticing that neither peaks related to Ce–Mn bonds nor mixed phases have been recorded, pointing out to the main formation of separated cerium and manganese oxides, and a negligible incorporation of Mn ions into the CeO2 structure even during its molten state. This fact is in concordance with TEM-EDX results (Fig. 2d).
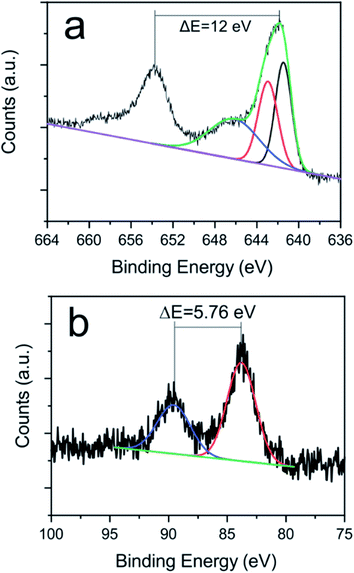 | ||
| Fig. 6 High resolution (a) Mn 2p and (b) Mn 3s XPS spectra and its fitting curves of sample GO-CNT-Ce-Mn-5152. | ||
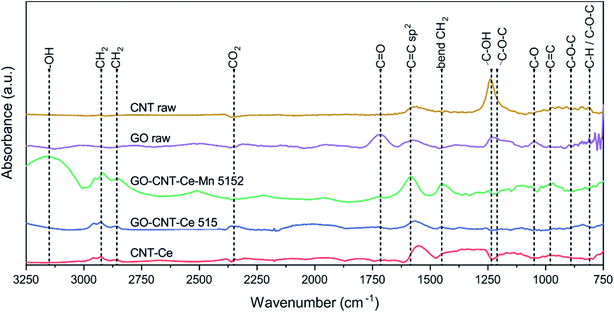
To continue with a deeper study of compositional analysis, synchrotron-based FTIRM studies were performed. Despite the low quantity of material contained in the films, intense synchrotron light source allowed to identify various characteristic bands in the trans-reflection operation mode. Fig. 7 shows the SR-FTIRM of representative samples. GO-raw spectrum has peaks at 810 cm−1 (attributed to C–H and/or C–O–C groups), 890 cm−1 (C–O–C), 1050 cm−1 (C–O alkoxy), 1210 cm−1 (C–O–C), 1235 cm−1 (C–OH) and at 1715 cm−1 (C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O), all of them oxygen-containing groups. The spectrum also reveals a flatten band at 1600 cm−1 (C
O), all of them oxygen-containing groups. The spectrum also reveals a flatten band at 1600 cm−1 (C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C sp2).76,77 All of the oxygen-containing bands are reduced or disappear in the characteristic spectra of the deposited samples containing GO, proving its reduction during deposition process. CNT-raw spectrum mainly reveals C–OH band from the carboxylic functionalization, though C
C sp2).76,77 All of the oxygen-containing bands are reduced or disappear in the characteristic spectra of the deposited samples containing GO, proving its reduction during deposition process. CNT-raw spectrum mainly reveals C–OH band from the carboxylic functionalization, though C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O band is not witnessed, and the C
O band is not witnessed, and the C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C sp2 bond from the carbon structure appears slightly shifted to lower wavenumbers.78 The bands originated from carboxylic groups disappear in the spectra of GO-CNT-Ce-Mn-5152, GO-CNT-Ce-515 and CNT-Ce.
C sp2 bond from the carbon structure appears slightly shifted to lower wavenumbers.78 The bands originated from carboxylic groups disappear in the spectra of GO-CNT-Ce-Mn-5152, GO-CNT-Ce-515 and CNT-Ce.
The spectra of the deposited samples reveal a band at 980 cm−1 (C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C). The C
C). The C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C sp2 groups are notable in the spectra of all the deposited samples, showing a broadband in the range 1560–1600 cm−1. The doublet peaks at 2857 cm−1 and 2925 cm−1 are assigned to symmetric and antisymmetric stretching vibrations of –CH2 and the peak at 1450 cm−1 correspond to –CH2 bending.79,80 These groups are constituents of alkyl chains, probably formed during reconfiguration of GO to rGO and have been reported to contribute to the electrochemical performance.81 The small bands located at 2350 cm−1 are assigned to CO2. The bands above 3150 cm−1 are assigned to –OH groups.
C sp2 groups are notable in the spectra of all the deposited samples, showing a broadband in the range 1560–1600 cm−1. The doublet peaks at 2857 cm−1 and 2925 cm−1 are assigned to symmetric and antisymmetric stretching vibrations of –CH2 and the peak at 1450 cm−1 correspond to –CH2 bending.79,80 These groups are constituents of alkyl chains, probably formed during reconfiguration of GO to rGO and have been reported to contribute to the electrochemical performance.81 The small bands located at 2350 cm−1 are assigned to CO2. The bands above 3150 cm−1 are assigned to –OH groups.
3.3 Electrochemical characterization
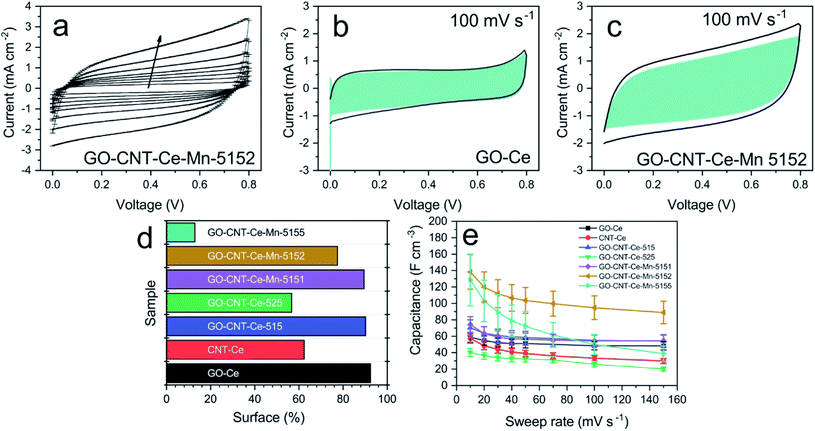
Electrochemical analyses were performed to study the energy storage of the electrodes fabricated through cyclic voltammetry (CV) in the 0–0.8 V voltage window and 10–150 mV s−1 sweep rate ranges. Fig. 8a shows typical voltammograms for the different sweep rates. The peak present at ca. 0.8 V is due to the oxygen-evolution reaction in the aqueous electrolyte. The recorded voltammograms show quasi-rectangular shape and no presence of prominent peaks, attributed to redox reactions. This behaviour points to capacitive (surface) processes as main charge storage mechanisms in the electrodes.82,83 To obtain more proves of the surface dominance mechanism, the capacitance contribution of surface and diffusion-controlled charge storage processes are differentiated. In surface-dominant reactions, response current varies linearly with the sweep rate (s). By contrast, processes controlled by semi-infinite diffusion (bulk) are proportional to the square root of the sweep rate.9 Therefore, the current can be expressed as| i(s,V) = icap + idiff = k1s + k2s1/2 | (2) |
Taking this into account, k1 and k2 constants can be determined from the fitting of i(s,V)/s1/2versus s1/2, hence differentiating the capacitive current contribution from that of diffusion-controlled processes. Fig. 8b and c present the voltammograms of the electrodes GO-Ce and GO-CNT-Ce-Mn-5152, respectively, for 100 mV s−1 sweep rate with highlighted region of the capacitive contribution from the total current measured. Accordingly, Fig. 8d shows the percentage of the capacitive contribution for all the samples. Regarding GO-CNT-Ce-Mn-5155, k1 and k2 terms might not be correctly calculated due to lack of linearity of eqn (2) in most of voltage values. Thus, no simple mechanism for the origin of the sweep-rate dependence can be determined. A reported explanation of this behaviour is called the “porous-electrode” effect. The signal may become attenuated in pores having finite resistance leading to a progressively increase of iR-drop in them. Therefore, local response current will become attenuated and cannot be expressed as a simple relation between current and s or s1/2.84,85 Thus, the surface percentage could be underestimated. Despite the behaviour of this specific sample, in the majority of cases, the main contributions are surface processes. Interestingly, the addition of Mn oxides and CNT increases the diffusive component despite their pseudocapacitive behaviour4 and porosity increase,46 respectively. Considering the major contribution of surface process and the quasi-rectangular shape of the voltammograms, the volumetric capacitance (Cv) of the electrodes can be calculated from CV data at different sweep rates following the equation
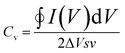 | (3) |
Galvanostatic charge–discharge (GCD) measurements were performed to the electrodes in a current density range of 0.2–2 mA cm−2. A typical charge–discharge curve is presented in Fig. 9a, showing the quasi-linear voltage response with time that generates the characteristic triangular shape of capacitive materials. It can be also observed that with the increasing current, the charge/discharge time decreases. The coulombic efficiency (discharge/charge time relation) is around 98%, hence no charge is practically lost during operation. The volumetric capacitance can be calculated from the GCD data using
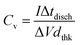 | (4) |
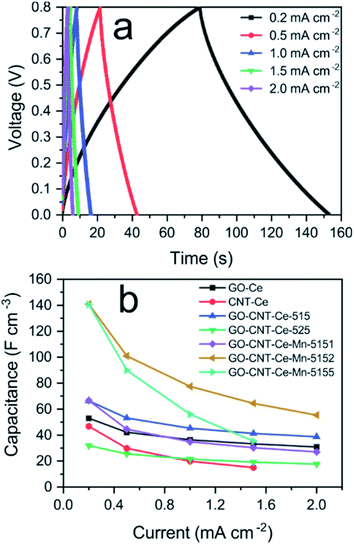 | ||
| Fig. 9 (a) Volumetric capacitance vs. applied current density of all the fabricated samples; (b) galvanostatic charge–discharge data of GO-CNT-Ce-Mn-5152 for different applied currents. | ||
The best values of volumetric capacitance acquired with either CV or GCD, are comparable to the ones reported in the literature6,87 and almost one order of magnitude higher than GO-CNT-NiO electrodes also obtained with RIMAPLE.46
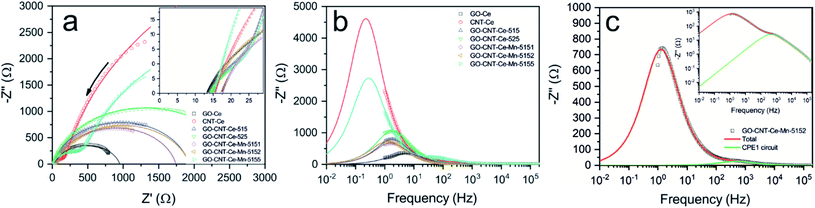
Additional studies of the electrodes were performed with electrochemical impedance spectroscopy (EIS) measurements. Fig. 10a presents the Nyquist plot for all the samples, where the expected behaviour of carbon-based porous electrodes can be observed. At high and middle frequencies, EDL and charge transfer reactions take place, producing a partial semicircle loop. At low frequency, diffusion processes are predominant, generating the quasi-linear straight line in some cases and partial semicircle of finite diffusion in the rest.88 All the curves were fitted using the equivalent circuit represented in Fig. S9† (modified Randles cell), and its plot is presented as continuous lines in Fig. 10a. The equivalent circuit is composed of three resistances: R1 as equivalent series resistance (ESR), R2 as charge-transfer resistance and R3 accounting for leakages. The two other components are constant phase elements (CPE). The impedance of these elements is described as
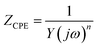 | (5) |
In this case, Y represents the capacitance and n index has a value between 0 and 1. A CPE with n value of 1 indicates an ideal capacitor, whereas lower values account for material inhomogeneity. CPE1 represents the double layer charge storage processes and CPE2 adds the pseudocapacitive contribution generated by redox mechanisms.45 Table S2† summarizes the values of the elements for the equivalent circuit fitting of the EIS data. The ESR or R1, that can also be determined in the cut of the horizontal axis in the inset of Fig. 10a, is similar in all the electrodes (about 15 Ω). This resistance is the sum of the intrinsic resistance of electrodes and that of the electrolyte. The R2 (charge-transfer resistance) values are similar in all the electrodes except in CNT-Ce and GO-CNT-Ce-Mn-5155, which show about one order of magnitude higher values. Those electrodes presented higher decay of capacitance at higher sweep rates (Fig. 8e). This higher resistance accounts for a slower storage of energy, decreasing the performance in fast sweep rates. Warburg impedance elements were negligible in the fitted model, pointing to R2 element as the one including the contribution of electrolyte diffusion in the studied frequency range. R3 (leakage resistance) values are in the order of kΩ revealing low charge leakage. Regarding CPE, all n values are higher than 0.82 confirming almost ideal capacitors. It is important to notice the significant increase of capacitance values for CPE2 (pseudocapacitance) in the samples including Mn oxides, proving the high pseudocapacitance incorporated to the electrodes through these compounds.
For a deeper study of the impedance spectra, a key parameter is the relaxation time constant, τ, that acts as a factor of merit and it is characteristic of each sample. The frequently used method to determine τ is with the phase Bode plot, with the corresponding time on the cut at 45°. However, this method of determination is not applicable when the series resistance to the parallel R|CPE circuit has a similar order of magnitude in resistance values.89 In these cases, the difficulties can be overcome with the representation of the impedance imaginary part as function of the frequency. The resistance components have purely real impedance component, and they do not intervene in this plot. Therefore, the contribution comes merely from the capacitive components, where the relaxation time constant can be obtained through the inverse of frequency at local maximum. Fig. 10b presents the plot of the impedance imaginary component of all the measured data (points) and simulation with the equivalent circuit transfer function (lines). The low frequency maximum, which corresponds to pseudocapacitive relaxation time (CPE2), is clearly determined. It is important to take into account that two samples (CNT-Ce and GO-CNT-Ce-Mn-5155) have this maximum below 1 Hz, which is the minimum experimentally measured frequency and its values are calculated. Because of the high signal of the low frequency maximum, the relaxation time constant related to faster processes found at higher frequency values, cannot be directly determined. However, a capacitor behaves as a short circuit when excited at frequencies much higher than their characteristic one. Therefore, the impedance contribution of the rest of the elements can be calculated using the obtained equivalent circuit parameters and considering a circuit without neither CPE2 nor R3, obtaining the relaxation time constant related to CPE1. Fig. 10c presents the deconvolution of one specific case (GO-CNT-Ce-Mn-5152) to show the different contributions. A bulge can be differentiated, specially using logarithmic scale on the imaginary impedance axis (inset of Fig. 10c). Table 2 shows the obtained relaxation time constants related to the two different processes involved (EDL and pseudocapacitance). Relaxation time constants related to CPE1 are similar in all the cases, in the order of the millisecond, except for CNT-Ce and GO-CNT-Ce-Mn-5155, which have slightly higher times. On the other hand, relaxation times related to CPE2 exhibit significant variations. The addition of CNT to GO-Ce increases the characteristic time, and the addition of Mn oxides induces an even higher increase of characteristic times, accounting for the remarkable increase of the pseudocapacitance and diffusion processes. The characteristic time of CNT-Ce is also higher than the GO-Ce due to the increase of porosity between CNTs, which produces aggregated oxide structures that lead to slower charge transport mechanisms.
| Relaxation time constant from CPE1 (ms) | Relaxation time constant from CPE2 (ms) | |
|---|---|---|
| GO-Ce | 2 | 200 |
| CNT-Ce | 7 | 4500 |
| GO-CNT-Ce-515 | 2 | 550 |
| GO-CNT-Ce-525 | 1 | 550 |
| GO-CNT-Ce-Mn-5151 | 2 | 600 |
| GO-CNT-Ce-Mn-5152 | 2 | 800 |
| GO-CNT-Ce-Mn-5155 | 18 | 3600 |
3.4 Device fabrication and performance study
The working performance of the best volumetric capacitance electrode was investigated by assembling a symmetric electrochemical capacitor with two GO-CNT-Ce-Mn-5152 electrodes. Fig. 11a shows the typical voltammograms for various sweep rates, presenting similar shape to the single electrode (Fig. 8a). The volumetric capacitance at different sweep rates (CV) and different applied current (GCD) can be found in Fig. 11b and c, respectively, reaching ca. 25 F cm−3 in both cases. As expected, the values are lower than with a single electrode due to the fact that both capacitors are in series. The Ragone plot (volumetric energy vs. power densities), shown in Fig. 11d, allows the evaluation of the global performance of the device. For the calculation, the total volume of the active material has been used. A comparison of different energy storage devices is also presented.45,90,91 It is important to emphasize the increase in both energy and power densities as compared to previous RIMAPLE symmetric N-doped rGO-NiO device, obtained with the same fabrication technique. As witnessed, the fabricated CeOx-MnOx-rGO-CNT capacitor exhibits higher power and energy densities, up to 5.4 W cm−3 and 2.2 mW h cm−3, respectively. Despite that submicrometric thickness electrodes obtained by RIMAPLE method are reported having comparable or higher storage capabilities,45,61,92 it has to be taken into account that the performance of such thin electrodes will not be scalable without losses due to microstructural rearrangements that hinders the electrolyte diffusion and interaction with active material.93 The stability of the device was also studied by galvanostatic charge–discharge cycling at ca. 2 mA cm−2 current density (Fig. 11e). The capacitance retention and the coulombic efficiency decay ca. 10% after 20![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 cycles, maintaining the triangular charge–discharge shape practically unaltered (Fig. 11e, inset). The decay is presumably related to electrolyte drying process as previously suggested for poorly sealed devices. Further work will be focused on both the enhancement of the EC sealing and post-mortem analyses of the electrodes. Even though, the stability has been proved, doubling the number of cycles from previous experiments.45
000 cycles, maintaining the triangular charge–discharge shape practically unaltered (Fig. 11e, inset). The decay is presumably related to electrolyte drying process as previously suggested for poorly sealed devices. Further work will be focused on both the enhancement of the EC sealing and post-mortem analyses of the electrodes. Even though, the stability has been proved, doubling the number of cycles from previous experiments.45
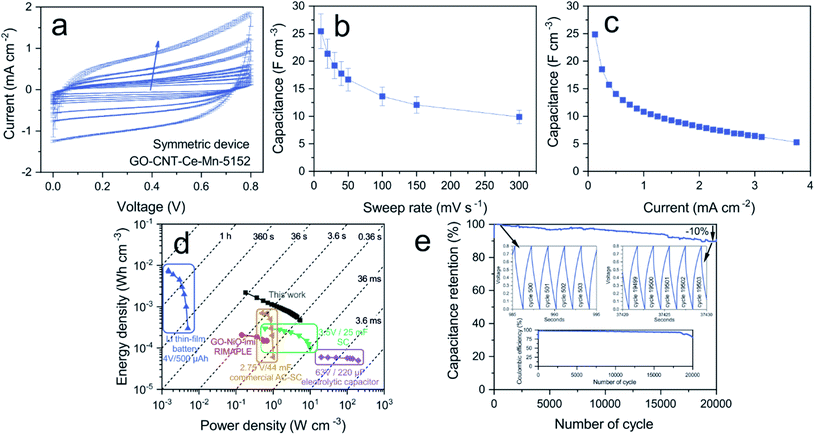 | ||
| Fig. 11 (a) CV curves of symmetric device GO-CNT-Ce-Mn-5152 (arrow indicates the increasing sweep rate), (b) volumetric capacitance vs. sweep rate, (c) volumetric capacitance vs. applied current, (d) Energy and power densities of the fabricated SC compared with commercially available energy storage systems. Data for the lithium battery, 3.5 V/25 mF supercapacitor (SC) and 6.3 V/220 μF electrolytic capacitor,90 data for the 2.75 V/44 mV activated carbon supercapacitor (AC-SC)91 and GO-NiO-imi symmetric device.45 (e) Capacitance retention with charge–discharge zoomed regions (superior insets) and coulombic efficiency (inferior inset). | ||
Conclusions
The presented hybrid electrodes developed by RIMAPLE laser technique show excellent performance for electrochemical supercapacitors. Through UV laser radiation, a myriad of photochemical and photothermal processes occur inducing the reduction of GO and the crystallization of metal oxides on the surface of carbon nanomaterials. The decomposition of manganese acetate through laser processing is demonstrated with the formation of different oxides, MnO and Mn3O4, besides chemical modification of ceria nanoparticles, submitted to melting-coalescence-dewetting mechanisms, changing their crystallographic phase to Ce2O3. The thorough morphological, compositional and electrochemical analyses of the electrodes provide proper understanding of the composite fabricated and the mechanisms involved in charge storage. The electrodes fabricated with rGO, MWCNT, Ce and Mn oxides combine EDL and pseudocapacitance storage mechanisms. The maximum volumetric capacitance of 140 F cm−3 obtained is significantly higher than in previous works using RIMAPLE technique with NiO NPs. Finally, the assembly of a symmetric electrochemical capacitor proves the practical use of the developed hybrid electrodes standing out their remarkable high stability upon cycling. These outstanding results open the door to innovative and versatile development of supercapacitors using laser deposition techniques, with combinations of different metal oxides either in nanoparticles or in ionic forms (dissolved metal organic precursors), allowing the formation of binary metal oxides systems with new properties besides the use of different combinations of carbon nanomaterials.Conflicts of interest
There are no conflicts to declare.Acknowledgements
The authors thank the financial support of the Spanish Ministry of Economy, Industry and Competitiveness under the project ENE2017-89210-C2-1-R and support from AGAUR of Generalitat de Catalunya through projects 2017 SGR 1086 and 2017 SGR 1771. PGL thanks the financial support of the Spanish Ministry of Economy, Industry and Competitiveness through the grant BES-2017-081652 for the formation of scientific researchers. ICMAB acknowledges financial support from the Spanish Ministry of Economy and Competitiveness, through Severo Ochoa FUNFUTURE (CEX2019-000917-S). The FTIRM experiments were performed at MIRAS beamline at ALBA Synchrotron with the collaboration of ALBA staff. We acknowledge support of the publication fee by the CSIC Open Access Publication Support Initiative through its Unit of Information Resources for Research (URICI).References
- E. Pomerantseva, F. Bonaccorso, X. Feng, Y. Cui and Y. Gogotsi, Science, 2019, 366, 1–12 CrossRef.
- Poonam, K. Sharma, A. Arora and S. K. Tripathi, Journal of Energy Storage, 2019, 21, 801–825 CrossRef.
- J. Yan, Q. Wang, T. Wei and Z. Fan, Adv. Energy Mater., 2014, 4, 1–43 Search PubMed.
- A. González, E. Goikolea, J. A. Barrena and R. Mysyk, Renewable Sustainable Energy Rev., 2016, 58, 1189–1206 CrossRef.
- L. Li, J. Zhang, Z. Peng, Y. Li, C. Gao, Y. Ji, R. Ye, N. D. Kim, Q. Zhong, Y. Yang, H. Fei, G. Ruan and J. M. Tour, Adv. Mater., 2016, 28, 838–845 CrossRef CAS.
- M. Wuttke, Z. Liu, H. Lu, A. Narita and K. Müllen, Batteries Supercaps, 2019, 2, 929–933 CrossRef CAS.
- X. Huang, X. Qi, F. Boey and H. Zhang, Chem. Soc. Rev., 2012, 41, 666–686 RSC.
- A. Borenstein, O. Hanna, R. Attias, S. Luski, T. Brousse and D. Aurbach, J. Mater. Chem. A, 2017, 5, 12653–12672 RSC.
- V. Augustyn, P. Simon and B. Dunn, Energy Environ. Sci., 2014, 7, 1597–1614 RSC.
- M. Zhi, C. Xiang, J. Li, M. Li and N. Wu, Nanoscale, 2013, 5, 72–88 RSC.
- N. Padmanathan and S. Selladurai, RSC Adv., 2014, 4, 6527–6534 RSC.
- N. Maheswari and G. Muralidharan, Energy and Fuels, 2015, 29, 8246–8253 CrossRef CAS.
- K. Prasanna, P. Santhoshkumar, Y. N. Jo, I. N. Sivagami, S. H. Kang, Y. C. Joe and C. W. Lee, Appl. Surf. Sci., 2018, 449, 454–460 CrossRef CAS.
- Y. Luo, T. Yang, Q. Zhao and M. Zhang, J. Alloys Compd., 2017, 729, 64–70 CrossRef CAS.
- D. Deng, N. Chen, X. Xiao, S. Du and Y. Wang, Ionics, 2017, 23, 121–129 CrossRef CAS.
- R. Murugan, G. Ravi, R. Yuvakkumar, S. Rajendran, N. Maheswari, G. Muralidharan and Y. Hayakawa, Ceram. Int., 2017, 43, 10494–10501 CrossRef CAS.
- S. J. Zhu, J. Q. Jia, T. Wang, D. Zhao, J. Yang, F. Dong, Z. G. Shang and Y. X. Zhang, Chem. Commun., 2015, 51, 14840–14843 RSC.
- A. K. Singh, D. Sarkar, K. Karmakar, K. Mandal and G. G. Khan, ACS Appl. Mater. Interfaces, 2016, 8, 20786–20792 CrossRef CAS.
- Y. Wang, H. Wei, H. Lv, Z. Chen, J. Zhang, X. Yan, L. Lee, Z. M. Wang and Y. L. Chueh, ACS Nano, 2019, 13, 11235–11248 CrossRef CAS.
- H. Jia, Y. Cai, X. Zheng, J. Lin, H. Liang, J. Qi, J. Cao, J. Feng and W. Fei, ACS Appl. Mater. Interfaces, 2018, 10, 38963–38969 CrossRef CAS.
- S. Nagamuthu, S. Vijayakumar and G. Muralidharan, Energy and Fuels, 2013, 27, 3508–3515 CrossRef CAS.
- G. Lee, D. Kim, J. Yun, Y. Ko, J. Cho and J. S. Ha, Nanoscale, 2014, 6, 9655–9664 RSC.
- S. Chen, L. Wang, M. Huang, L. Kang, Z. Lei, H. Xu, F. Shi and Z. H. Liu, Electrochim. Acta, 2017, 242, 10–18 CrossRef CAS.
- T. Xiong, W. S. V. Lee, X. Huang and J. M. Xue, J. Mater. Chem. A, 2017, 5, 12762–12768 RSC.
- G. He, H. Fan, L. Ma, K. Wang, C. Liu, D. Ding and L. Chen, Appl. Surf. Sci., 2016, 366, 129–138 CrossRef CAS.
- J. Liu, J. Jiang, C. Cheng, H. Li, J. Zhang, H. Gong and H. J. Fan, Adv. Mater., 2011, 23, 2076–2081 CrossRef CAS.
- X. Sun, Q. Li, Y. Lü and Y. Mao, Chem. Commun., 2013, 49, 4456–4458 RSC.
- D. Sarkar, G. G. Khan, A. K. Singh and K. Mandal, J. Phys. Chem. C, 2013, 117, 15523–15531 CrossRef CAS.
- Y. Gu, J. Cai, M. He, L. Kang, Z. Lei and Z. H. Liu, J. Power Sources, 2013, 239, 347–355 CrossRef CAS.
- F. Li, G. Li, H. Chen, J. Q. Jia, F. Dong, Y. B. Hu, Z. G. Shang and Y. X. Zhang, J. Power Sources, 2015, 296, 86–91 CrossRef CAS.
- R. Dong, Q. Ye, L. Kuang, X. Lu, Y. Zhang, X. Zhang, G. Tan, Y. Wen and F. Wang, ACS Appl. Mater. Interfaces, 2013, 5, 9508–9516 CrossRef CAS.
- G. Wang, Z. Ma, G. Zhang, C. Li and G. Shao, Electrochim. Acta, 2015, 182, 1070–1077 CrossRef CAS.
- H. Zhang, J. Gu, J. Tong, Y. Hu, B. Guan, B. Hu, J. Zhao and C. Wang, Chem. Eng. J., 2016, 286, 139–149 CrossRef CAS.
- G. P. Ojha, B. Pant, S. J. Park, M. Park and H. Y. Kim, J. Colloid Interface Sci., 2017, 494, 338–344 CrossRef CAS.
- R. Rajagopal and K. S. Ryu, ChemElectroChem, 2018, 5, 2218–2227 CrossRef CAS.
- R. Peng, H. Zhang, L. Gui, Y. Zheng, Z. Wu, Y. Luo and P. Yu, Electrochim. Acta, 2019, 319, 95–100 CrossRef CAS.
- C. Liu, H. Sun, J. Qian, Z. Chen, F. Chen, S. Liu, Y. Lv, X. Lu and A. Chen, J. Alloys Compd., 2017, 722, 54–59 CrossRef CAS.
- R. You, Y. Liu, Y. Hao, D. Han, Y. Zhang and Z. You, Adv. Mater., 2019, 1901981, 1–22 Search PubMed.
- X. Y. Fu, Z. Di Chen, Y. L. Zhang, D. D. Han, J. N. Ma, W. Wang, Z. R. Zhang, H. Xia and H. B. Sun, Nanoscale, 2019, 11, 9133–9140 RSC.
- D. Bäuerle, Laser Processing and Chemistry, 2011, vol. 208 Search PubMed.
- S. M. O'Malley, J. Tomko, Á. Pérez del Pino, C. Logofatu and E. György, J. Phys. Chem. C, 2014, 118, 27911–27919 CrossRef.
- E. György, C. Logofatu, Á. Pérez del Pino, A. Datcu, O. Pascu and R. Ivan, Ceram. Int., 2018, 44, 1826–1835 CrossRef.
- R. Ivan, C. Popescu, A. P. del Pino, I. Yousef, C. Logofatu and E. György, J. Mater. Sci., 2019, 54, 3927–3941 CrossRef CAS.
- A. Queraltó, Á. Pérez del Pino, C. Logofatu, A. Datcu, R. Amade, I. Alshaikh, E. Bertrán, I. Urzica and E. György, J. Alloys Compd., 2017, 726, 1003–1013 CrossRef.
- Á. Pérez del Pino, M. A. Ramadan, P. García Lebière, R. Ivan, C. Logofatu, I. Yousef and E. György, Appl. Surf. Sci., 2019, 484, 245–256 CrossRef.
- Á. Pérez Del Pino, M. Rodríguez López, M. A. Ramadan, P. García Lebière, C. Logofatu, I. Martínez-Rovira, I. Yousef and E. György, Phys. Chem. Chem. Phys., 2019, 21, 25175–25186 RSC.
- M. A. Steiner and J. M. Fitz-Gerald, Appl. Phys. A: Mater. Sci. Process., 2015, 119, 629–638 CrossRef CAS.
- X. Cui, R. Lv, R. U. R. Sagar, C. Liu and Z. Zhang, Electrochim. Acta, 2015, 169, 342–350 CrossRef CAS.
- A. Queraltó, Á. Pérez del Pino, M. De La Mata, J. Arbiol, M. Tristany, X. Obradors and T. Puig, Chem. Mater., 2016, 28, 6136–6145 CrossRef.
- V. A. Smirnov, A. A. Arbuzov, Y. M. Shul'ga, S. A. Baskakov, V. M. Martynenko, V. E. Muradyan and E. I. Kresova, High Energy Chem., 2011, 45, 57–61 CrossRef CAS.
- Z. Wan, E. W. Streed, M. Lobino, S. Wang, R. T. Sang, I. S. Cole, D. V. Thiel and Q. Li, Adv. Mater. Technol., 2018, 3, 1–19 Search PubMed.
- A. Vogel and V. Venugopalan, Chem. Rev., 2003, 103, 577–644 CrossRef CAS.
- Á. Pérez del Pino, E. György, L. Cabana, B. Ballesteros and G. Tobias, J. Appl. Phys., 2014, 115, 093501 CrossRef.
- E. K. Goharshadi, S. Samiee and P. Nancarrow, J. Colloid Interface Sci., 2011, 356, 473–480 CrossRef CAS.
- J. A. Dean and N. A. Lange, Lange's handbook of chemistry, McGraw-Hill, New York, 1999 Search PubMed.
- J. Y. Hwang, M. F. El-Kady, Y. Wang, L. Wang, Y. Shao, K. Marsh, J. M. Ko and R. B. Kaner, Nano Energy, 2015, 18, 57–70 CrossRef CAS.
- A. Younis, D. Chu and S. Li, in Functionalized Nanomaterials, ed. M. Akhyar Farrukh, IntechOpen, 2016, pp. 53–68 Search PubMed.
- D. A. Edwards and R. N. Hayward, Can. J. Chem., 1968, 46, 3443–3446 CrossRef CAS.
- M. A. Mohamed and S. A. Halawy, Thermochim. Acta, 1994, 242, 173–186 CrossRef CAS.
- N. A. M. Barakat, K. Do Woo, S. G. Ansari, J. A. Ko, M. A. Kanjwal and H. Y. Kim, Appl. Phys. A: Mater. Sci. Process., 2009, 95, 769–776 CrossRef CAS.
- Á. Pérez del Pino, A. Martínez Villarroya, A. Chuquitarqui, C. Logofatu, D. Tonti and E. György, J. Mater. Chem. A, 2018, 6, 16074–16086 RSC.
- Á. Pérez del Pino, E. György, C. Logofatu and A. Duta, J. Phys. D: Appl. Phys., 2013, 46, 1–8 Search PubMed.
- A. T. Nelson, D. R. Rittman, J. T. White, J. T. Dunwoody, M. Kato and K. J. McClellan, J. Am. Ceram. Soc., 2014, 97, 3652–3659 CrossRef CAS.
- S. Debnath, M. R. Islam and M. S. R. Khan, Bull. Mater. Sci., 2007, 30, 315–319 CrossRef CAS.
- Á. Pérez del Pino, E. György, C. Logofatu, J. Puigmartí-Luis and W. Gao, Carbon, 2015, 93, 373–383 CrossRef.
- C. Barth, C. Laffon, R. Olbrich, A. Ranguis, P. Parent and M. Reichling, Sci. Rep., 2016, 6, 2–7 CrossRef.
- Á. Pérez del Pino, A. González-Campo, S. Giraldo, J. Peral, E. György, C. Logofatu, A. J. DeMello and J. Puigmartí-Luis, Carbon, 2018, 130, 48–58 CrossRef.
- Y. Wu, R. Shu, J. Zhang, Z. Wan, J. Shi, Y. Liu, G. Zhao and M. Zheng, J. Alloys Compd., 2020, 819, 152944 CrossRef CAS.
- D. Banerjee and H. W. Nesbitt, Geochim. Cosmochim. Acta, 1999, 63, 3025–3038 CrossRef CAS.
- Z. Zeng, X. Long, H. Zhou, E. Guo, X. Wang and Z. Hu, Electrochim. Acta, 2015, 163, 107–115 CrossRef CAS.
- L. Qiu, F. Liu, L. Zhao, Y. Ma and J. Yao, Appl. Surf. Sci., 2006, 252, 4931–4935 CrossRef CAS.
- X. Yu and G. Li, J. Alloys Compd., 2004, 364, 193–198 CrossRef CAS.
- J. J. Plata, A. M. Márquez and J. F. Sanz, J. Phys. Chem. C, 2013, 117, 14502–14509 CrossRef CAS.
- M. C. Biesinger, B. P. Payne, A. P. Grosvenor, L. W. M. Lau, A. R. Gerson and R. S. C. Smart, Appl. Surf. Sci., 2011, 257, 2717–2730 CrossRef CAS.
- F. Müller, R. De Masi, D. Reinicke, P. Steiner, S. Hüfner and K. Stöwe, Surf. Sci., 2002, 520, 158–172 CrossRef.
- R. Trusovas, G. Račiukaitis, G. Niaura, J. Barkauskas, G. Valušis and R. Pauliukaite, Adv. Opt. Mater., 2016, 4, 37–65 CrossRef CAS.
- X. Mao, J. Xu, X. He, W. Yang, Y. Yang, L. Xu, Y. Zhao and Y. Zhou, Appl. Surf. Sci., 2018, 435, 1228–1236 CrossRef CAS.
- C. S. Chen, X. H. Chen, L. S. Xu, Z. Yang and W. H. Li, Carbon, 2005, 43, 1660–1666 CrossRef CAS.
- M. Shateri-Khalilabad and M. E. Yazdanshenas, Cellulose, 2013, 20, 963–972 CrossRef CAS.
- A. Kaniyoor, T. T. Baby and S. Ramaprabhu, J. Mater. Chem., 2010, 20, 8467–8469 RSC.
- G. Zhao, F. G. Zhao, J. Sun, W. Wang, Y. Lu, W. S. Li and Q. Y. Chen, Carbon, 2015, 94, 114–119 CrossRef CAS.
- Y. Gogotsi and R. M. Penner, ACS Nano, 2018, 12, 2081–2083 CrossRef CAS.
- J. Liu, J. Wang, C. Xu, H. Jiang, C. Li, L. Zhang, J. Lin and Z. X. Shen, Adv. Sci., 2018, 5, 1–19 Search PubMed.
- T. C. Liu, W. G. Pell, B. E. Conway and S. L. Roberson, J. Electrochem. Soc., 1998, 145, 1882–1888 CrossRef CAS.
- E. Barsoukov and J. R. Macdonald, Impedance Spectroscopy Theory, Experiment, and Applications, John Wiley & Sons, Inc., Hoboken, New Jersey, 2005, vol. 125 Search PubMed.
- R. Ivan, C. Popescu, Á. Pérez del Pino, C. Logofatu and E. György, Appl. Surf. Sci., 2020, 509, 145359 CrossRef CAS.
- H. Jin, J. Li, Y. Yuan, J. Wang, J. Lu and S. Wang, Adv. Energy Mater., 2018, 8, 1–12 Search PubMed.
- F. Bardé, P. L. Taberna, J. M. Tarascon and M. R. Palacín, J. Power Sources, 2008, 179, 830–836 CrossRef.
- V. F. Lvovich, Impedance Spectroscopy: Applications to Electrochemical and Dielectric Phenomena, John Wiley & Sons, 2012 Search PubMed.
- D. Pech, M. Brunet, H. Durou, P. Huang, V. Mochalin, Y. Gogotsi, P. L. Taberna and P. Simon, Nat. Nanotechnol., 2010, 5, 651–654 CrossRef CAS.
- M. F. El-Kady and R. B. Kaner, Nat. Commun., 2013, 4, 1–9 Search PubMed.
- A. Queraltó, A. P. del Pino, C. Logofatu, A. Datcu, R. Amade, E. Bertran-Serra and E. György, Ceram. Int., 2018, 44, 20409–20416 CrossRef.
- J. Chmiola, P. L. T. Celine Largeot, P. Simon and Y. Gogotsi, Science, 2010, 328, 480–483 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/d0ta06756c |
| This journal is © The Royal Society of Chemistry 2021 |