Correction: Characterizing surface wetting and interfacial properties using enhanced sampling (SWIPES)

Abstract

Correction for ‘Characterizing surface wetting and interfacial properties using enhanced sampling (SWIPES)’ by Hao Jiang et al., Soft Matter, 2019, 15, 860–869, DOI: 10.1039/C8SM02317D.

---

The authors regret their use of the average fluid center of mass, 〈x_COM〉_κ,N*, as a proxy for the vapor–liquid interface location, H. Although both 〈x_COM〉_κ,N* ≈ H and h_COM ≡ d〈x_COM〉_κ,N*/dN* ≈ h are excellent approximations for thin surfaces, these assumptions can lead to systematic error in h for thicker surfaces. In particular, in the ESI for this correction notice,† we use simple geometric arguments to show:where α is the fraction of the simulation box taken up by the surface along the z-axis, and λ is the fraction of water molecules that are outside the observation volume, v. Thus, when either the surfaces are thin relative to the liquid slab (α → 0), or most of the water molecules in the system are in v (λ → 0), h_COM → h.

An alternative, more robust approach for obtaining h is to approximate the location of the vapor–liquid interface, H, using the half-density isosurface, , for each biased simulation. This isosurface is implicitly defined by 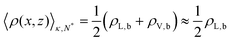, where ρ_L,b and ρ_V,b are the bulk liquid and vapor densities, respectively. In practice, we obtain 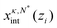at each value z_i by fitting 〈ρ(x,z_i)〉_κ,N* to the sigmoidal function: 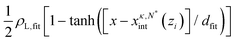, where ρ_L,fit, d_fit, and are fit parameters. We then average over the z-axis to obtain 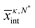, and compute h_int as the slope of vs. N*. 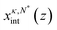In averaging over z, the region near the surface (within 1.5 nm of the outermost layer of solid atoms) was excluded because the fluid density in this region tends to be dominated by packing effects rather than interfacial physics.

Fig. 2b and 3b show vs. N* for the surfaces with ε_SW = 1.94 and 0.001 kJ mol⁻¹, respectively. The results for all the surfaces considered are summarized in Table 1, and highlight that in agreement with eqn (1), h_COM is 13–17% smaller than h. Our use of h_COM thus led to γ_VL(∝1/h) being overestimated (γ^COM_VL = 62(2) mJ m⁻²); using h_int instead results in an estimate of γ^int_VL = 56(2) mJ m⁻², which is consistent with the values reported in the literature, once differences in the cutoff distances for the Lennard-Jones potential are accounted for. Note that our previous comparison to the literature did not account for such differences. Our use of h_COM also led to kγ_VL being overestimated by roughly 15%; however, our use of γ^COM_VL to compute the corresponding wetting coefficients, k_COM, resulted in a fortuitous cancellation of errors, such that approximating h by h_COM did not lead to substantive errors in k; see Fig. 4a. In particular, this error cancellation resulted from the fact that h_COM/h_int depends primarily on the system setup geometry (eqn (1)), and is more or less independent of ε_SW (Table 1).

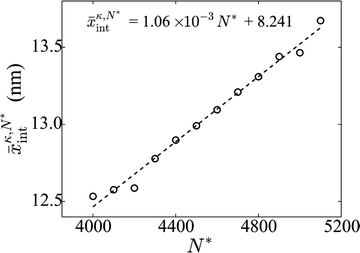Fig. 2 (b) The variation of 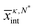with N* (symbols) is shown for the LJ surface with ε_SW = 1.94 kJ mol⁻¹. The dashed line is a linear fit to the simulation data.

Fig. 3 (b) The variation of 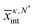with N* (symbols) is shown for the LJ surface with ε_SW = 0.001 kJ mol⁻¹. The dashed line is a linear fit to the simulation data.

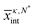Table 1 For surfaces with different surface–water attractions, ε_SW, the slope, h_int, obtained by fitting vs. N* to a straight line is shown, and is compared against h_COM. The values of h_COM/h_int are roughly independent of ε_SW, and in good agreement with eqn (1); for our simulation setup, α = 0.23, and λ ≈ 0.63 (for the typical 〈Ñ_v〉_κ,N* ≈ 4500), resulting in

ε SW (kJ mol^−1)	h int × 10^3 (nm)	h COM/hint
0.001	1.05(2)	0.87(3)
0.5	1.02(3)	0.87(3)
1	1.05(2)	0.85(2)
1.5	1.05(2)	0.85(2)
1.94	1.06(3)	0.83(3)
2.4	1.14(4)	0.83(3)

---

Fig. 4 (a) Wetting coefficients, k, estimated from SWIPES using h_int. Due to a cancellation of errors, the estimates of k agree well with those originally reported (as k_F). Also shown for comparison are k_D and k_I, which are computed as before.

In conclusion, our use of x_COM as a proxy for interface location, H: (i) led to an error of roughly 15% in our estimate of γ_VL; (ii) did not affect our estimates of k (within error); and (iii) did not change the main conclusions of this work. The authors would like to acknowledge Sean M. Marks for his role in identifying and correcting the issue discussed in this Correction notice.

The Royal Society of Chemistry apologises for these errors and any consequent inconvenience to authors and readers.

---

Footnote

† Electronic supplementary information (ESI) for this correction notice showing the derivation of eqn (1) is available alongside the original article, DOI: 10.1039/c8sm02317d

---