Microbial Brazil nut effect

Abstract

The Brazil nut effect (BNE) is a counter-intuitive process of segregation of a large object inside a vibrated granular medium (GM), which has been studied widely by subjecting GMs to various kinds of shears and vibrations. In this article, we report a new kind of BNE which occurs as a consequence of granular fluctuations induced by microbe-generated gas bubbles. We call it the ‘microbial Brazil nut effect’. The paper demonstrates microbial BNE for a bidisperse granular mixture as well as for intruder segregation. Furthermore, using X-ray μCT and a simple scaling argument for segregation velocity, the paper clarifies the transport mechanics of an intruder inside a bubbly granular bed. We think the reported phenomenon should be ubiquitous in the microbe-populated wet sandy floors of waterbodies and may have some implication on the distribution of material near the floors.

---

1. Introduction

The Brazil nut effect or BNE is a seemingly counterintuitive phenomenon, whereby, when a granular mixture is shaken vigorously through some external mechanism, eventually, the larger constituents of the mixture segregate to the top, whereas the smaller particles end up at the bottom.¹ Because of its industrial relevance and exciting physics involved behind it, BNE has attracted a considerable research from scientific and engineering communities in recent decades. To list a few far-reaching implications, the concept of BNE has been used to elucidate astrophysical phenomena like the distributions of boulders on the surfaces of asteroids,² the geological processes such as the formation of stone armors on riverbeds,³ and the pattern formation in early mammalian embryos.⁴ Furthermore, the knowledge of BNE is important to various industries including that of pharmaceutical manufacturing, foodstuff processing and powder metallurgy.⁵

Traditionally, for a dry cohesionless granular medium, two competing theories exist to explain the BNE. The first one is the Rosato's theory of ‘ratcheting’ or ‘void filling’, where smaller grains can fall underneath a void created by a larger grains when it is shaken vertically by an external agency.^6–8 The second mechanism, fundamentally different from granular ratcheting, is the theory of ‘granular convection’ where entire granular bed moves with thin downward moving regions near the wall of the flask and a large upward moving region near the center.^9–11 Both these theories, on an average, tend to segregate the larger object to the top of the granular medium.

In nature, however, the granular mixtures are not always dry. Broadly speaking, they can be classified into three major categories: (i) a dry granular mixture with no liquid content (say, desert sand) (ii) an unsaturated granular mixture with small amount of liquid (say, moist soil), and (iii) a completely immersed granular mixture (say, ocean floor). The corresponding BNE phenomena gets quirkier, when liquid phase is introduced to a dry granular medium. It has been reported that the granular segregation is drastically affected by the volume fraction of the liquid.¹² Even for a miniscule small amount of liquid, there is a sharp increase in the segregation time-scale due to intergranular cohesion stemming from the formation of liquid bridges between the grains.^13,14 These capillary bridges make a granular bed more resistant to deformation.¹⁵ At higher liquid volume fractions (between 2.5% to 15%), the bridges begin to coalesce leading to formation of granular clusters, however, the granular cohesivity is not affected and it remains constant, independent of the liquid content (as the projected grain area where pressure acts via capillary bridges is unchanged).^16,17 If the liquid volume fraction is increased even more, such that all interstitial spaces are completely filled with liquid, the capillary bridges disappear and the medium again becomes cohesionless like a dry granular medium. That being said, a completely immersed (or saturated) granular medium flows much more easily as compared to its dry counterpart due to intergranular lubrication, which in effect provides an enhanced BNE as reported by some scientists.^18,19

The researches in the field of granular segregation, extensively studied the phenomenon by subjecting the granular medium to external (horizontal or vertical) vibrations,^20–23 by driving the granular medium along an inclined slope^24,25 or by shearing it inside a shear boxes and annular cells.^26,27 In this study, we explore the granular segregation in a completely different setting, that is, inside a saturated bubbly granular bed. The motivation originates from waterbodies, whereby, their wet sandy floors are bustling with bubbles that generated by benthic microorganisms (like cyanobacteria, yeasts, etc.) via ambient nutrient metabolism. The perennial growth, rupture and release of these bubbles inside sandy sediments can create granular disturbances which are analogous to external vibrations in traditional BNE, and hence, have a potential to propel a buried intruder or cause granular segregation. We call this phenomenon as ‘microbial Brazil nut effect’ and to the best of authors’ knowledge, this is the first study which reports the granular segregation which is induced by bubbles.

In the next section, we will firstly demonstrate the granular segregation inside a bi-disperse granular mixture and characterize the length and time-scale of bubble-induced granular fluctuations. In Section 3, we show the transport of a cuboidal intruder inside a bubbly granular bed and investigate various parameters (bubbling rate, bed height, intruder size, surface cavities and grain diameter) that affects its segregation. Next, in Section 4, using X-ray μCT, we clarify the transport mechanics of microbial BNE and propose a simple scaling argument to estimate the intruder velocity, which showed reasonable agreement with the experiments. Finally, we present our concluding remarks in Section 5. Our experimental techniques, methods and protocols can be found in Section 6.

2. The bubble-induced Brazil nut effect

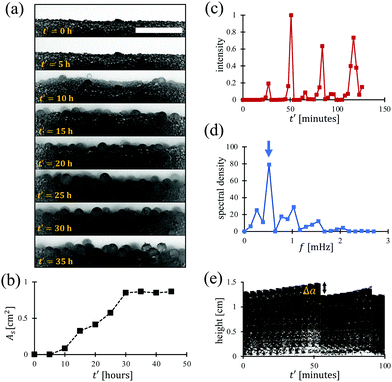
In this section, we are going to illustrate that the size-based segregation can be achieved inside a completely immersed granular mixture which is subjected to bubble-induced vibrations. Throughout this research, the naturally and industrially ubiquitous process of yeast fermentation is exploited as a source of bubbles. To start the experiment, the bottom of a prototypical fermenting flask is filled with a bi-disperse mixture of glass beads which are immersed completely in a liquid culture medium (with density ρ_M = 1.00 g cm⁻³) along with yeast cells. The bi-disperse mixture is made up of glass beads of two different sizes (with diameters d₁ = 0.5 mm and d₂ = 2 mm) of same mass densities (ρ_G = 2.40 g cm⁻³) such that the mass fraction ϕ₁ of smaller beads is equal to the mass fraction ϕ₂ of larger beads i.e., ϕ₁ ≈ ϕ₂.

As yeasts begin to metabolize sugar, the gas generation commences. Since, all yeast cells have percolated (being denser than the culture medium) to the bottom of the granular bed, the bubble production is primarily from the floor of the flask. These bubbles rise slowly through interstitial spaces between grains, eventually escaping into the liquid regime. During their lifetime in the granular medium, bubbles can grow, rise and collapse. When many such bubbles, reside simultaneously inside the granular medium, the ambient grains experience chaotic disturbances, which gives rise to a bubble-induced BNE, and it is demonstrated through an observation of a region near the interface of the granular bed and the aqueous medium as Fig. 1(a). Observe how the larger glass beads end up on the top of the granular bed over the course of fermentation. This is the phenomenon of microbial BNE (please watch ‘ESI,† Movie S1’). A time change of such segregation phenomenon is shown in Fig. 1(b) through an area parameter A_s, which represents the evolution of area occupied by the larger beads near the interface on the observation plane. The time-scale for complete segregation is about 30 hours.

Fig. 1 Bubble-induced Brazil nut effect. (a) The demonstration of size segregation in a bidisperse granular medium. The scale is 1 cm. (b) The time change in area A_s occupied by larger beads near the interface. (c) The fluctuation in spatially averaged image intensity of a monodisperse granular bed as a representative of bubble-induced granular fluctuation. (d) The spectral density of granular fluctuations to obtain dominant fluctuation frequency f_d. (e) The height fluctuation of the fluid–granular medium interface to characterize the length scale of fluctuations. Δa is the sudden displacement of the interface and is the length scale of granular fluctuations.

Now, to characterize bubble-induced granular fluctuations, we measured the time-change in the spatially-averaged image intensity of entire granular bed in the observation plane. As bubbles bustle through the granular medium, this image intensity fluctuates, which we take as a representative of the mean bubble-induced effects in the bed. A sudden change in such average image intensity implies that either a large bubble has collapsed or has escaped out into the liquid regime. A graphical illustration of the same inside a bubbly monodisperse granular bed (diameter d_G = 0.5 mm, density ρ_G = 2.40 g cm⁻³, the solid volume fraction ϕ_G ≈ 0.66) is shown along with its spectral density in Fig. 1(c) and (d), respectively. The inverse of the dominant frequency f_d (≈ 4.1 × 10⁻⁴ Hz, shown by the arrow) can characterize the dominant time-scale of granular fluctuations as about 2.4 × 10³ s. On the other hand, to get the length-scale of granular fluctuations, we measured the sudden displacement of the interface through intensity spike events, near the center of the flask, as Fig. 1(e). Note that even though the upward movement of the interface is smooth, the fall initiated by spike events is sharp and the magnitude of this fall Δa can represent the maximum length scale of granular fluctuations. Experimentally, for the given setting, it was observed that the fall Δa ≈ 1.9 mm was very close to the mean bubble diameter d_B ≈ 2.1 ± 0.3 mm inside the granular medium. We will build upon this length and time scaling in upcoming sections to explain our further experimental observations. Please find the details of our experimental techniques in Section 6.

The reported segregation phenomenon can be regarded as ‘quasi-static’, because the time taken for total segregation is about 30 hours and the total vertical distance traversed by large grains is less than 1 cm (cf.Fig. 1(a) and (b)). Quantitatively speaking, the viscous number I_v is usually used to quantify the relative significance of external disturbances and the granular rearrangement in an immersed granular medium.^28,29 In our case, I_v can be estimated as the ratio of the timescale τ₁ of granular rearrangement under overburden pressure P_p to the timescale of bubble-induced effects. The scale τ₂ can be taken as the inverse of the dominant frequency f_d of granular fluctuations (cf.Fig. 1(d)) such that τ₂ ∼ 1/f_d ≈ 2.4 × 10³ s. Also, the rearrangement scale τ₁ can be obtained through the scaling τ₁ ∼ η_M/P_p where, η_M (≈ 10⁻³ Pa s) is the viscosity of the aqueous medium. For a typical length equivalent to the length scale Δa (≈ 1.9 mm) of granular fluctuations, P_p = (ρ_G − ρ_M)gΔa, yielding τ₁ ≈ 3.84 μs, which is negligibly small as compared to τ₂, indicating that the demonstrated phenomenon falls within the quasi-static limit as I_v → 0.

Having reported the microbial BNE within a completely immersed granular mixture along with relevant scaling arguments, next we will probe the transport of a single intruder and investigate various governing parameters behind its bubble-induced segregation.

3. Single intruder transport

3.1. Demonstration

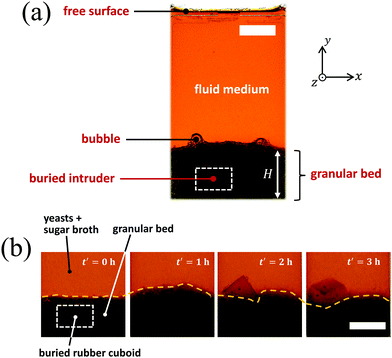
To study single intruder transport via microbial BNE, we employ a physical model of a waterbody as shown in Fig. 2(a). The floor of a typical waterbody is composed of wet sandy sediments that are populated with microbes which continuously generate bubbles through various metabolic processes.³⁰ Due to the sheer enormity of the amount of wastes that are dumped into waterbodies,³¹ these sediments must have various man-made objects buried inside them, majority of which should be larger than the length scale of a sand grain. This, therefore, makes the floors of waterbodies ripe for microbial BNE. As previously mentioned, in our setting, we use yeasts as model microorganisms because of their ubiquity and their capability to perform fermentation and produce gas bubbles. The aqueous medium is nutrient-rich water (YPD medium) which is the source of food for yeasts. The bottom of the experimental flask is filled up to height H with glass beads (ρ_G = 2.40 g cm⁻³) of diameter d_G = 0.5 mm, that acts as the model benthic granular layer having a solid volume fraction ϕ_G ≈ 0.66. Also, a cuboidal intruder made up of silicone rubber (ρ_I = 1.10 g cm⁻³) is buried inside this layer of glass beads as a representative non-biodegradable waste. Note from Fig. 2(b), that this intruder manages to traverse out of the granular medium with the help of yeast-generated bubbles. Please also watch ‘ESI,† Movie S2’.

Fig. 2 Single intruder transport. (a) The experimental setting for demonstrating single-intruder transport through bubbles produced via yeast fermentation. The mass density of the aqueous medium is ρ_M = 1.0 g cm⁻³. The diameter d_G of glass beads is 0.5 mm and have a mass density of ρ_G = 2.4 g cm⁻³. The silicone intruder has a mass density of ρ_I = 1.2 g cm⁻³ with dimensions {[small script l]_x, [small script l]_y, [small script l]_z} = {1, 0.6, 1} cm. The z-direction is out of the plane of the paper/screen and the scale is 1 cm. (b) The upward transport of the cuboidal intruder through bubble-induced granular effects. The scale is 1 cm.

Before moving on to describe the transport mechanics in Section 4, we investigate various parameters that might influence bubble-induced intruder transport within the granular medium in the next sub-section.

3.2. Parametric study

(i) Bubble generation. Since the reported phenomenon is bubble-induced, our initial interest is to study the effect of the amount of bubble generation. From Srivastava et al.,³² we know that the total bubble volume generation rate f_G (m³ s⁻¹) in yeast fermentation follows a dynamic curve as shown in the inset of Fig. 3(a). As the bubble production is not uniform in time, we picked three different time regimes with different bubble generation rates and investigated intruder transport in each case. The chosen time periods were (a) t = 20–25 h (weak bubbling), (b) t = 30–35 h (strong bubbling) and, (c) t > 45 h (very weak bubbling), post-initial yeast inoculation. Firstly, we measured the time-averaged vertical velocity 〈v〉 of the intruder inside the granular medium as shown in Fig. 3(a). The graph reveals that if the bubbling is strong the intruder ascension is fast. To understand this, we plotted the spectral densities for bubble-induced granular fluctuations as illustrated in Fig. 3(b). One observes that the dominant granular fluctuation frequency f_d (shown by arrows) is small when the bubbling is weak (f_d ≈ 5.2 × 10⁻⁴ Hz, t = 20–25 h) and is large when the bubbling is strong (f_d ≈ 2.45 × 10⁻³ Hz, t = 30–35 h). This means a stronger bubble generation increases the frequency of granular fluctuations. It should also be mentioned here that the fluctuation length scale Δa in different regimes of bubble generation did not vary significantly (cf. inset of Fig. 3(b)) and remained within 4.7% of 1.89 mm for all our observations, implying that a change in bubbling rate affects the time scale but not the length scale of granular fluctuations. Hence, the faster intruder ascension during strong bubbling can be attributed to an increase in granular fluctuation frequencies.

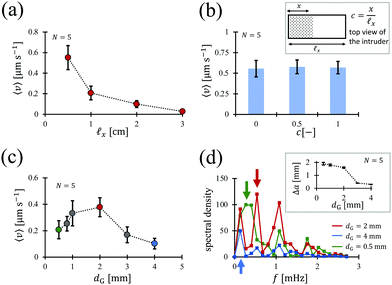
Fig. 3 Effect of bubbling and bed height. (a) The average intruder ascension velocity 〈v〉 in three different regimes of bubble generation (d_G = 0.5 mm, H = 1.0 cm, [small script l]_x = 1 cm). Error bars denote standard deviation. The inset shows the gas generation rate by S. cerevisiae yeasts (adapted from ref. 32). (b) The spectral densities of bubble-induced granular fluctuations in different bubbling regimes. The arrows indicate the dominant frequency f_d (d_G = 0.5 mm, H = 1.0 cm, [small script l]_x = 1 cm). The inset shows the fluctuation amplitude is not affected by the bubble generation rate. Error bars denote standard deviation. (c) The decrement in average intruder ascension velocity 〈v〉 with an increase in bed height (d_G = 0.5 mm, t = 20–25 h, [small script l]_x = 1 cm). Error bars denote standard deviation. (d) The spectral densities of bubble-induced granular fluctuations with different bed heights. The arrows indicate the dominant frequency f_d (d_G = 0.5 mm, t = 20–25 h, [small script l]_x = 1 cm). The inset shows the fluctuation amplitude is not affected by the bed height. Error bars denote standard deviation.

(ii) Granular bed height. The filling height H of the granular bed is another important parameter that influences the transport of an intruder which is initially placed at the bottom of the granular bed. To assess its effect, we measured the average intruder ascension velocity 〈v〉 in granular beds with different H (0.6 cm, 1 cm, 1.25 cm, 1.5 cm), while keeping all other parameters unchanged. The results plotted as Fig. 3(c) illustrate that the intruder rise is slowed down when the granular bed is made thicker. Moreover, from Fig. 3(d), it can be noticed that the dominant granular fluctuation frequency f_d decreases as the bed height is increased. As far as the length scale Δa is concerned, we did not observe a significant variation (cf. inset of Fig. 3(d)) and it was within 2% of 1.91 mm for all H. This implies that a change in bed height, like bubbling rate, only influences the time scale of granular fluctuations. Therefore, the intruder impediment due to an increase in bed height stems from a corresponding reduction in granular fluctuation frequencies.

(iii) Intruder size. The next parameter we look into is the size of the intruder. In our experiments, we varied the length [small script l]_x (0.6 cm, 1 cm, 2 cm, 3 cm) of the cuboid without changing its width [small script l]_y (1 cm) and its thickness [small script l]_z (0.6 cm) and measured the average intruder ascension velocity 〈v〉. The results are plotted as Fig. 4(a) and they show that the intruder rise is slowed down with an increase in length [small script l]_x of the cuboid. This an important finding regarding bubble-induced microbial BNE, and is unlike the observations made in classical BNE, whereby, a larger intruder segregates much faster as compared to a smaller one.³³ The distinction stems from a difference in the void creation mechanisms between the two phenomena, which we will discuss in Section 4.

Fig. 4 Effect of intruder size, surface cavities and grain size. (a) The decrement in average intruder ascension 〈v〉 with an increase in its length [small script l]_x (d_G = 0.5 mm, H = 1.0 cm, t = 20–25 h). Error bars denote standard deviation. (b) The effect of cavity distribution ratio c on average intruder velocity 〈v〉 (d_G = 0.5 mm, H = 1.0 cm, t = 20–25 h, [small script l]_x = 1 cm). Error bars denote standard deviation. (c) The demonstration of a maximum in average intruder velocity 〈v〉 with grain diameter d_G (H = 1.25 cm, t = 20–25 h, [small script l]_x = 1 cm). Error bars denote standard deviation. (d) The spectral densities of bubble-induced granular fluctuations with different grain diameters. The arrows indicate the dominant frequency f_d (H = 1.25 cm, t = 20–25 h, [small script l]_x = 1 cm). Inset shows the decrement in the fluctuation amplitude with an increase in grain diameter. Error bars denote standard deviation.

(iv) Surface cavities. The adhesion of bubbles on the surface of a hydrophobic object, such as a silicone rubber, can play a crucial role in its transport. If there are large number of bubbles adhering to the object, its effective density is reduced which affects the buoyant force it experiences. Now, the bubble residence on a hydrophobic surface can be elongated by introducing artificial surface cavities.³⁴ In our experiments, we added artificial cavities (of length scale of 100 μm with a mean distance of 500 μm between them) on the top surface of the cuboid and defined a parameter called the ‘cavity distribution ratio’ c, which is given as the ratio of the area of the surface that has artificial cavities to the total surface area, as shown in the inset of Fig. 4(b). If this cuboid is kept in a liquid, the presence of cavities would influence the bubble nucleation and bubble residence on its surface (also, see ‘ESI,† text’). However, the effect of surface cavities is unknown if the same cuboid is kept inside a granular medium. When we measured the average intruder ascension velocity 〈v〉 for cavity distribution ratios c = 0, 0.5 and 1.0 (cf.Fig. 4(b)), it was found that intruder velocity 〈v〉 remains unchanged, suggesting that the effect of cavities is negligible for an intruder inside the granular medium and the adhesion of bubbles to the surface does not have a significant contribution in intruder transport.

(v) Grain diameter. The last parameter that we study is the grain diameter d_G. We observed, from our experiments, that if the grain diameter is below 2 mm, the grains can be held on the surface of the bubbles and bubbles can grow to much larger sizes inside the granular medium. This is intuitive because if the granular bed is made up of smaller grains, bubbles remain trapped in interstitial spaces and continue to accumulate gas unless the buoyant force on them becomes large enough to overcome the surface tension. However, if the grain size is greater than 2 mm, the bubbles can simply percolate upwards through interstitial liquid,^35,36 such that the bubble size becomes independent of the grain size. It is important to mention here that the theoretical prediction³⁷ for threshold grain size d_T for bubble size transition into saturation is , where γ is the surface tension and ρ_M is the mass density of the YPD medium.

The grain diameter dependent bubble behavior should have some implications on the intruder transport phenomenon. To assess this, we measured the average intruder ascension velocity 〈v〉 for various grain diameters d_G from 0.5 mm to 4 mm and the corresponding results are plotted as Fig. 4(c). Interestingly enough, the intruder velocity 〈v〉 displays a maximum at d_G = 2 mm, which as previously mentioned, is also the threshold grain size for bubble size saturation. The explanation behind this could be, when the grain size is decreased below d_T, trapped bubbles grow for a longer time, and as a consequence the granular fluctuation frequency induced by bubble collapse and bubble release from the granular medium are slowed down, thereby, impeding the intruder transport. On the other hand, if the grain size is increased beyond d_T, the bubble-induced fluctuations experienced by larger grains become weaker than that which are experienced by smaller grains, which again slows down the rise of the intruder. To concretize our reasoning a bit more, we also plotted the spectral densities for granular fluctuations for grain diameters d_G = 0.5 mm, 2 mm and 4 mm as Fig. 4(d). It can be observed that the dominant fluctuation frequency (shown by arrows) is the largest of the three for the grain size d_G = 2 mm. Furthermore, the granular fluctuation length scale Δa, as illustrated in the inset of Fig. 4(d), is seen to decrease with an increase in the grain diameter.

4. Transport mechanics

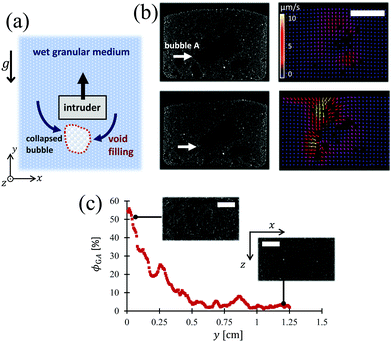
Till now, we have demonstrated the phenomenon of bubble-induced microbial BNE for a bi-disperse granular mixture and for a single intruder granular system. We have also highlighted the influence of various parameters on single intruder transport, including that of bubble generation, granular bed height, intruder size, intruder surface cavities and grain diameter.

To understand the mechanism behind the reported phenomenon, it is imperative to look inside the granular medium. In order to do this, we used X-rays and coupled it with particle image velocimetry (PIV) technique to observe granular and intruder movement. Consequently, we discovered an interesting process of void-filling which is initiated when a bubble leaves the granular medium or when a bubble suddenly collapses, a schematic of which is shown in Fig. 5(a). From X-ray μCT images of the granular medium in Fig. 5(b), observe that when ‘bubble A’, denoted by white arrow, disappears, the ambient granular vectors turn towards the void and fill it, preventing the intruder from falling back. The phenomenon is somewhat similar to Rosato's void filling theory¹ which we will revisit shortly. Also, please note that, since granular disturbances near the walls of the flask were negligible, it rules out Knight's theory of large-scale granular convection in our case.⁹

Fig. 5 Transport mechanics. (a) A schematic of void-filling mechanism. (b) The demonstration of void filling mechanism through X-ray and particle image velocimetry color bar shows velocity magnitude. The black patches represent bubbles. (c) The demonstration of inhomogeneity of bubble distribution in the granular medium. ϕ_GA is the area fraction of gas bubbles at a particular y. The insets show the X-ray images, where scales are 1 cm. (d_G = 0.5 mm, H = 1.25 cm, t = 20–25 h, [small script l]_x = 1 cm).

Moving on, the physics of granular flows is nuanced. The rapid granular flows are usually described through kinetic theories for grain collisions, whereas extremely slow granular flows (also called the quasi-static flows) are characterized by frictional rheology under a Mohr–Coulomb framework. Classically, the quasi-static flows (QSFs), have been reported to possess a yield criterion and to display shear rate independence, implying that for QSFs, the drag an intruder experiences is independent of its velocity.³⁸ However, interestingly, when the granular medium is weakly vibrated through some mechanism, it ‘fluidizes’ the medium, such that the yield behavior disappears and drag forces scale linearly with intruder velocities^39,40 very similar to a Stokes’ fluid.

In our case, assuming that the granular medium is sufficiently fluidized through bubble-induced effects, the equation of motion for an intruder can be given through a stochastic differential equation,

mv̇ = F_ext − cηL_Iv, (1)

where, m is the mass of the intruder, v is the velocity of the intruder, c is a dimensionless constant and F_ext is an external force. Second term on the right is the drag exerted on the intruder (of characteristic length L_I) due to its motion through a granular medium of apparent viscosity η.

The external force F_ext has two primary ingredients in our setting. Firstly, there is a buoyant force acting on the intruder due to the density offset Δρ between the object and the granular medium, and secondly, there is a random force that an intruder experiences from bubble-induced granular fluctuations. Let us write this external force term as, F_ext = ΔρgV_I + F_rand(t), where V_I is the volume of the intruder, g is the acceleration due to Earth's gravity and F_rand(t) is a random force which is responsible for bubble-induced microbial BNE. The average direction of F_rand(t) depends upon the distribution of bubbles in the granular medium, such that, if the bubbles are homogenously distributed, by symmetry, the average intruder's velocity will not be affected by this random force. However, we experimentally observed that, there are predominantly more bubbles near the bottom than near the top of the granular medium (as yeast cells are present at the floor), such that the gas volume fraction ϕ_GV(y) is a decreasing function of y, where y is measured from the bottom of the flask (cf.Fig. 5(c)). This breaks the symmetry of F_rand(t), so that its effect becomes non-zero mean and a time-averaged directional bias appears. The concept is reminiscent of the ‘void-filling theory’ by Rosato,¹ according to which when a granular medium is shook vertically, the intruder jumps, creating a void in its wake which is immediately filled up by the smaller grains, eventually propelling the intruder upwards. However, in an overdamped quasi-static case, such as ours, the voids are created either when there is a sudden bubble collapse or when a bubble leaves the granular medium. The important thing to note here is that in classical BNE, the intruder size determines the void size. However, in bubble-induced microbial BNE, the trapped bubble size governs the void size and the corresponding upward displacement of the intruder. Also, the time scale for intruder transport by bubble-induced microbial BNE can be determined by the dominant frequency f_d of such bubble collapsing/bubble leaving events, unlike by an external forcing frequency as in classical BNE.

Neglecting the inertial term, the expression for the time-averaged velocity of the intruder can be obtained from eqn (1) as,

where, 〈·〉 denotes the time-average and U_BNE is the time-averaged intruder drift velocity due to bubble-induced microbial BNE which is written like, . Since the intruder transport is governed through the mean bubble diameter d_B and the dominant frequency f_d of bubble collapsing/bubble leaving events, the drift velocity can be scaled as 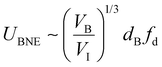, where V_B is the average volume of a bubble. It should be restated here from the previous section that the frequency f_d is a function of bubble generation rate f_G, bed height H and the grain size d_G, whereas, the trapped bubble size d_B (and hence the fluctuation length scale Δa) is dependent only upon the grain size d_G. The relative volume dependence is assumed because, for example, if the same volume of bubble collapses below intruders of two different sizes made up of same material, the collapse would displace an equal grain volume and an equal intruder volume, implying that the smaller intruder would travel a comparatively larger distance by this collapse event.

The eqn (2) clearly illustrates that there are two contributors to single intruder transport in a bubbly and sufficiently fluidized wet granular medium, namely, (a) buoyancy due to density offset, and (b) a non-zero mean bubble-induced granular fluctuations. If the second term in eqn (2) is dominant, it will explain why in our experiments, the intruder velocity decreases as we increase the size of the intruder (cf. Section 3.2(iii)), which is where the bubble-induced microbial BNE is distinct from the classical BNE. To clarify this, let us take the instance of a cuboidal intruder of size [small script l]_x = 1 cm, buried in a granular bed of thickness H = 1 cm, with grains of size d_G = 0.5 mm and a packing fraction ϕ_G ≈ 0.66. Since, for these settings, the mean trapped bubble diameter d_B ≈ 2.1 mm and a dominant granular fluctuation frequency f_d ≈ 4.1 × 10⁻⁴ Hz (weak bubbling regime), it yields U_BNE ≈ 0.17 μm s⁻¹, constituting the majority of average intruder velocity 〈v〉, which we experimentally measured to be 0.21 ± 0.08 μm s⁻¹. This, therefore, indicates that, in the given setup, the drift caused by the bubble-induced microbial BNE is the dominant transport mechanism in segregating the intruder out of the granular medium.

We would, however, like to comment that the exact prediction of the intruder velocity would require a much-detailed study of the rheo-physics of a fluidized bubbly granular medium and its apparent viscosity, which still is an open problem.

As an aside, we would also like to compare the reported segregation phenomenon with the bubble-induced segregation in dry, gas-fluidized beds. The formation of bubbles in a gas-fluidized bed is a common occurrence in chemical industries. The envelopes of these so called ‘bubbles’ are porous and are made up of granular particles, which is unlike gas bubbles inside a liquid with continuous fluid envelopes. The behavior of these bubbles in a gas-fluidized bed is similar to a rising gas bubble in a highly viscous fluid. That being said, a significant difference exists in the corresponding bubble-induced segregation phenomena in a granular mixture. Inside a gas-fluidized bed, given the all particles have same density, the larger ingredient of the granular mixture sinks to the bottom (i.e., jetsam), while the smaller one reaches the top (i.e., flotsam).⁴¹ This is the opposite of what happens in classical BNE and in reported bubble-induced BNE inside a wet granular bed, whereby, larger ingredients end up at the top of the mixture through void formation. At slow gas velocities, this difference occurs because as a bubble (in a gas-fluidized bed) with small particles on its envelope traverses up and encounters a larger particle, it creates an instability which leads to the collapse of that large particle into the bubble due to gravity.⁴² This mechanism, therefore, preferentially transports the larger particle to the bottom of the granular mixture.

5. Conclusions

In this article, using a laboratory-scale physical model of a waterbody, we reported the novel phenomenon of bubble-induced microbial Brazil nut effect through bubbles that are produced by the metabolism of nutrients by microbes in an aqueous medium. The phenomenon was seen both for a completely immersed bi-disperse granular mixture and for a large single intruder buried at the bottom of a granular bed. We noticed that such segregation was extremely slow and fell within the non-inertial quasi-static regime. The intruder segregation velocity was observed to increase with bubble generation rate and decrease with bed height and intruder size. The segregation displayed a maximum with granular diameter and remained unaffected by the distribution of artificial surface cavities on intruder. The parametric studies also revealed that the time-scale of bubble-induced granular fluctuations depends upon the bubble generation rate, granular bed height and the grain diameter, whereas, the fluctuation length-scale was found to vary with the grain size.

We clarified the transport mechanics of bubble-induced microbial BNE using X-rays and discovered the process of ‘void-filling’ which is the primary driver behind the reported phenomenon. This was further supported through a simple scaling argument which showed reasonable agreement with our observations and implied the relative dominance of void filling over buoyancy effects in our setting.

In the end, we would like to speculate that this phenomenon of bubble-induced microbial BNE should be ubiquitous in the benthic granular layers of waterbodies and should have an impact on distribution of material (wastes, nutrients, etc.) inside (and near) the completely immersed granular floors. Also, this work can be extended in the future to make more accurate predictions of intruder velocities by incorporating the physics of granular viscosity into the proposed equation.

6. Materials and methods

6.1. Cell culture protocol

We used a fermenting strain of yeasts (Saccharomyces cerevisiae) of top-fermenting (Fermentis, SAFALE S-04) kind throughout this research. The yeast culture was done in three steps, involving dry yeast hydration, a solid YPDA (Yeast Extract, Peptone, D-glucose, Agar) culture and a liquid YPD culture. The cells obtained after this process were called ‘freshly cultured yeasts’ Further details of the cell culture protocols can be found in Srivastava.³²

6.2. Visualization technique

Our experimental technique for observing the bubble-induced BNE is as follows: the experimental flask was back illuminated with a white light source which is an L.E.D. and was observed horizontally with the help of a DSLR (D5200, NIKKOR 18–55 mm, Nikon) inside a dark chamber. In general, the observation durations last for five hours with each image being three minutes apart. The sequence of images is used to obtain time-lapse movies and is analyzed for intensity fluctuations using an open-source software ImageJ.

6.3. Spectral density

To characterize granular fluctuations, we utilized the fluctuations in image intensities of the granular medium arising due to bubble induced effects. To do this, a sequence of images was taken using a DSLR (D5200, NIKKOR 18–55 mm, Nikon) camera for two hours with a time step of 3 minutes. The time-variation in mean image intensity in entire granular bed was measured using an open-source software ImageJ. Whenever a bubble leaves or collapses, this image intensity fluctuates sharply and we use this fluctuation as a representative of bubble-induced effects in granular medium. This time-series was then used to obtain the spectral density through Fast Fourier Transform (FFT), which helped us to obtain the dominant frequency f_d of granular fluctuations. This technique is utilized to get Fig. 1(c), (d), 3(b), (d) and 4(d).

6.4. Amplitude fluctuations

To get the amplitude Δa of granular fluctuations, we tracked the interface of the aqueous medium and granular bed using ImageJ and measured the sudden displacement of the interface, which is initiated by the bubble collapse or bubble leaving events. This was used to get Fig. 1(e) and insets of Fig. 3(b), (d) and 4(d). Please be noted that all the experiments for estimation of spectral densities and measurement of amplitude of granular fluctuations were done for a monodisperse granular mixture without an intruder.

6.5. Average intruder ascension

In order to estimate the average intruder ascension velocity 〈v〉, we measured the total vertical distance traversed by the intruder inside the granular medium, during the period of observation as Δy, and this is then divided by the total time taken Δt by the intruder to move this distance. This acts as the time averaged intruder ascension velocity in granular medium and is behind Fig. 3(a), (c) and 4(a)–(c).

6.6. X-Ray visualization

We used an X-ray μCT device (Yamato Scientific, TDM1000-IS/S) for X-ray visualization of the granular medium (as in for Fig. 5(b) and (c)). The irradiated X-rays had specifications of 80 kV and 45 μA. Which are individually adjusted for X-ray absorptions of the interposition materials.⁴³ The images were taken by rotating the flask, so that for one rotation we had 720 images with 0.5 degrees rotational step size. The average number of images per projection was six and the total scan time was approximately five minutes. The xy, yz and xz slices were obtained such that the each of them had 512 × 512 pixels, which yielded a spatial resolution of 56.8 μm along x, y and z directions. Velocity vectors for granular flow fields was obtained using 2D-PIV (Particle Image Velocimetry; Flownizer2D, DITECT) by measuring the cross-correlation between consecutive pairs of xz slices.^44,45 The sampling time for the PIV was 20 minutes with and the interrogation window size is 25 × 25 pixels (2.8 μm × 2.8 μm) and the post-PIV spatial filtering was done using a 3 × 3 median filter. Any temporal smoothing for the PIV data was not performed.

6.7. Bubble distribution

To get the variation in bubble distribution inside granular medium, we used X-ray μCT images as obtained in the previous sub-section. The x–z slices were segmented using intensity thresholding (using ImageJ) to extract the black patches which represent bubbles, and then the area percent ϕ_GA of these patches were calculated. The spatial step size δy between these slices was 56.8 μm. Also, the bubble area fraction ϕ_GA tends towards the bubble volume fraction ϕ_GV if the step size δy → 0.

6.8. Trapped bubble size

We used X-ray μCT images to estimate the length scale of bubbles inside the granular medium which usually have eccentric shapes. The mean bubble volume V_B was obtained as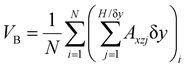 , where N is the total number of bubbles, H is the total height of the granular bed, δy is the spatial step increment between x–z slices, A_xzj is the area of a single bubble in jth slice and i is the marker for bubbles. Using this, the equivalent spherical diameter (ESD) d_B of trapped bubbles was estimated as d_B = (6V_B/π)^1/3.

Author contributions

T. I., K. K., and A. S. formulated and designed the research, A. S. performed experiments with inputs from T. I. and K. K. All authors were involved in data interpretations, theoretical modelling and manuscript preparation.

Conflicts of interest

Authors declare no competing interests.

Acknowledgements

The authors acknowledge the support of Japanese Society for the Promotion of Science KAKENHI (grants no. 21H04999, 17H00853, 19H02059, 21H05306 and 21H05308) and JST FOREST grant no. JPMJFR2024.

References

1. A. Rosato, K. J. Strandburg, F. Prinz and R. H. Swendsen, Why the Brazil nuts are on top: Size segregation of particulate matter by shaking, Phys. Rev. Lett., 1987, 58, 1038.
2. S. Matsumura, D. C. Richardson, P. Michel, S. R. Schwartz and R.-L. Ballouz, The Brazil nut effect and its application to asteroids, Mon. Not. R. Astron. Soc., 2014, 443, 3368–3380.
3. B. Ferdowsi, C. P. Ortiz, M. Houssais and D. J. Jerolmack, River-bed armouring as a granular segregation phenomenon, Nat. Commun., 2017, 8, 1–10.
4. Z. Guo, et al., Brazil Nut Effect Drives Pattern Formation in Early Mammalian Embryos, bioRxiv, 2021 DOI:10.1101/2021.02.26.433068.
5. C.-C. Liao and S.-S. Hsiau, Transport properties and segregation phenomena in vibrating granular beds, KONA Powder Part. J., 2016, 33, 109–126.
6. J. Bridgwater, N. W. Sharpe and D. C. Stocker, Particle mixing by percolation, Trans. Inst. Chem. Eng., 1969, 47, T114–T119.
7. A. Rosato, F. Prinz, K. J. Standburg and R. Swendsen, Monte Carlo simulation of particulate matter segregation, Powder Technol., 1986, 49, 59–69,  DOI:10.1016/0032-5910(86)85005-7.
8. L. Vanel, A. D. Rosato and R. N. Dave, Rise-time regimes of a large sphere in vibrated bulk solids, Phys. Rev. Lett., 1997, 78, 1255.
9. J. B. Knight, H. M. Jaeger and S. R. Nagel, Vibration-induced size separation in granular media: The convection connection, Phys. Rev. Lett., 1993, 70, 3728.
10. W. Cooke, S. Warr, J. M. Huntley and R. C. Ball, Particle size segregation in a two-dimensional bed undergoing vertical vibration, Phys. Rev. E: Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top., 1996, 53, 2812.
11. T. Pöschel and H. J. Herrmann, Size segregation and convection, EPL, 1995, 29, 123.
12. S. S. Hsiau, C. C. Liao, C. H. Tai and C. Y. Wang, The dynamics of wet granular matter under a vertical vibration bed, Granular Matter, 2013, 15, 437–446,  DOI:10.1007/s10035-013-0412-1.
13. N. Fraysse, H. Thomé and L. Petit, Humidity effects on the stability of a sandpile, Eur. Phys. J. B, 1999, 11, 615–619.
14. D. J. Hornbaker, R. Albert, I. Albert, A.-L. Barabási and P. Schiffer, What keeps sandcastles standing?, Nature, 1997, 387, 765.
15. S. Nowak, A. Samadani and A. Kudrolli, Maximum angle of stability of a wet granular pile, Nat. Phys., 2005, 1, 50–52.
16. A. Kudrolli, Sticky sand, Nat. Mater., 2008, 7, 174–175.
17. A. Samadani and A. Kudrolli, Segregation transitions in wet granular matter, Phys. Rev. Lett., 2000, 85, 5102.
18. M. C. Leaper, A. J. Smith, M. R. Swift, P. J. King, H. E. Webster, N. J. Miles and S. W. Kingman, The behaviour of water-immersed glass-bronze particulate systems under vertical vibration, Granular Matter, 2005, 7, 57–67,  DOI:10.1007/s10035-004-0185-7.
19. C. P. Clement, H. A. Pacheco-Martinez, M. R. Swift and P. J. King, The water-enhanced Brazil nut effect, EPL, 2010, 91, 54001,  DOI:10.1209/0295-5075/91/54001.
20. D. A. Huerta and J. C. Ruiz-Suárez, Vibration-induced granular segregation: a phenomenon driven by three mechanisms, Phys. Rev. Lett., 2004, 92, 114301.
21. X. Yuan, N. Zheng, Q. Shi, G. Sun and L. Li, Segregation in mixtures of granular chains and spherical grains under vertical vibration, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2013, 87, 42203.
22. T. Mullin, Coarsening of self-organized clusters in binary mixtures of particles, Phys. Rev. Lett., 2000, 84, 4741.
23. P. M. Reis, G. Ehrhardt, A. Stephenson and T. Mullin, Gases, liquids and crystals in granular segregation, EPL, 2004, 66, 357.
24. J. W. Vallance and S. B. Savage, Particle Segregation in Granular Flows Down Chutes, in IUTAM Symposium on Segregation in Granular flows, Springer, 2000, pp. 31–51 DOI:10.1007/978-94-015-9498-1_3.
25. S. Wiederseiner, N. Andreini, G. Épely-Chauvin, G. Moser, M. Monnereau, J. M. N. T. Gray and C. Ancey, Experimental investigation into segregating granular flows down chutes, Phys. Fluids, 2011, 23, 13301,  DOI:10.1063/1.3536658.
26. L. A. Golick and K. E. Daniels, Mixing and segregation rates in sheared granular materials, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2009, 80, 42301.
27. A. M. Scott and J. Bridgwater, Interparticle percolation: a fundamental solids mixing mechanism, Ind. Eng. Chem. Fundam., 1975, 14, 22–27.
28. O. Pouliquen and Y. Forterre, A non-local rheology for dense granular flows, Philos. Trans. R. Soc., A, 2009, 367, 5091–5107.
29. F. Boyer, É. Guazzelli and O. Pouliquen, Unifying suspension and granular rheology, Phys. Rev. Lett., 2011, 107, 188301.
30. G. Gerdes, What are Microbial Mats?, Microbial Mats, Springer, 2010, pp. 3–25 DOI:10.1007/978-90-481-3799-2_1.
31. WWAP UN. 2003 The world water development report 1: Water for people, water for life. United Nations World Water Assessment Programme. Executive summary.
32. A. Srivastava, K. Kikuchi and T. Ishikawa, The bubble-induced population dynamics of fermenting yeasts, J. R. Soc., Interface, 2020, 17, 20200735,  DOI:10.1098/rsif.2020.0735.
33. K. Liffman, K. Muniandy, M. Rhodes, D. Gutteridge and G. Metcalfe, A segregation mechanism in a vertically shaken bed, Granular Matter, 2001, 3, 205–214.
34. F. J. Lesage and F. Marois, Experimental and numerical analysis of quasi-static bubble size and shape characteristics at detachment, Int. J. Heat Mass Transfer, 2013, 64, 53–69.
35. B. G. Pokusaev, D. A. Kazenin and S. P. Karlov, Immersion tomographic study of the motion of bubbles in a flooded granular bed, Theor. Found. Chem. Eng., 2004, 38, 561–568,  DOI:10.1007/s11236-005-0017-4.
36. M. C. Brooks, W. R. Wise and M. D. Annable, Fundamental changes in in situ air sparging how patterns, Groundwater Monit. Rem., 1999, 19, 105–113.
37. J. A. Meier, J. S. Jewell, C. E. Brennen and J. Imberger, Bubbles emerging from a submerged granular bed, J. Fluid Mech., 2011, 666, 189–203.
38. R. Albert, M. A. Pfeifer, A.-L. Barabási and P. Schiffer, Slow drag in a granular medium, Phys. Rev. Lett., 1999, 82, 205.
39. P. Das, S. Puri and M. Schwartz, Intruder dynamics in a frictional granular fluid: A molecular dynamics study, Phys. Rev. E, 2020, 102, 42905.
40. K. Nichol, A. Zanin, R. Bastien, E. Wandersman and M. van Hecke, Flow-induced agitations create a granular fluid, Phys. Rev. Lett., 2010, 104, 78302.
41. M. A. Gilbertson and I. Eames, Segregation patterns in gas-fluidized systems, J. Fluid Mech., 2001, 433, 347–356.
42. P. N. Rowe and A. W. Nienow, Particle mixing and segregation in gas fluidised beds. A review, Powder Technol., 1976, 15, 141–147.
43. K. Kikuchi, M. A. Stremler, S. Chatterjee, W.-K. Lee, O. Mochizuki and J. J. Socha, Burst mode pumping: A new mechanism of drinking in mosquitoes, Sci. Rep., 2018, 8, 1–15.
44. Y. Nonaka, K. Kikuchi, K. Numayama-Tsuruta, A. Kage, H. Ueno and T. Ishikawa, Inhomogeneous distribution of Chlamydomonas in a cylindrical container with a bubble plume, Biol. Open, 2016, 5, 154–160,  DOI:10.1242/bio.015669.
45. K. Kikuchi and O. Mochizuki, Micro-PIV (micro particle image velocimetry) visualization of red blood cells (RBCs) sucked by a female mosquito, Meas. Sci. Technol., 2011, 22, 64002,  DOI:10.1088/0957-0233/22/6/064002.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: 10.1039/d1sm01327k

---