The energy landscapes of bidisperse particle assemblies on a sphere

Abstract

The interplay between crystalline ordering, curvature, and size dispersity make the packing of bidisperse mixtures of particles on a sphere a varied and complex phenomenon. These structures have functional significance in a broad range of systems, such as cellular organisation in spherical epithelia, catalytic activity in binary colloidosomes, and chemical activity in heterofullerenes. In this contribution, we elucidate the potential energy landscapes for systems of repulsive, bidisperse particles confined to the surface of a sphere. It is commonly asserted that particle size dispersity destroys ordered arrangements, leading to glassy landscapes. Surprisingly, across a range of compositions, we find highly ordered global minima. Moreover, a minority of small particles is able to passivate defects, stabilising bidisperse global minima relative to monodisperse systems. However, our landscape analysis also reveals that bidispersity introduces numerous defective, low-lying states that are expected to cause broken ergodicity in corresponding experimental and computational systems. Probing the global minimum structures further, particle segregation is energetically preferred at intermediate compositions, contrasting with the approximate icosahedral global packing at either end of the composition range. Finally, changing the composition has a dramatic effect on the heat capacity: systems with low-symmetry global minima have melting temperatures an order of magnitude lower than monodisperse or high-symmetry systems. This observation may provide a further example of the principle of maximum symmetry: higher symmetry global minima exhibit a larger energy separation from the minima that define the high-entropy phase-like region of configuration space, raising the transition temperature.

---

Introduction

Attempting to wrap a 2D planar hexagonal lattice around the surface of a sphere necessitates the introduction of topological defects.¹ In physical systems, such as arrangements of repulsive particles, the competition between regular packing, curvature, and strain energy minimisation^2,3 has been found to produce a broad range of defect structures^4–7 and frequent examples of metastability.^8,9 Separately, introducing size dispersity into the packing of particles is known to introduce severe frustration, leading to irregularly structured, glassy landscapes.^4,10–12 The combined interactions of regular packing, spherical curvature, and bidispersity have recently begun to be investigated, exhibiting extraordinarily diverse packing arrangements with multifunnel energy landscapes corresponding to alternative low-lying structures separated by high barriers.^13–15

Examples of size-disperse packings associated with spherical topology can be found in a wealth of natural and synthetic systems. Furthermore, putative functions have been attributed to the packing arrangements and defect motifs. A biological example of this phenomenon arises for non-proliferative spherical epithelial monolayers (SphEMs) that surround Ascidian eggs.¹⁶ The highly defective arrangements have been attributed to cell size dispersity, and it has been suggested that the cell patterning may regulate the induction of downstream biological processes, such as cell death.¹⁷ Another important biological example is the calcium carbonate plating of coccolithophores (see for example ref. 18), a key regulator of marine CO₂.¹⁹

In colloid science, colloidal capsules show a remarkable range of functionalities.²⁰ For example, capsules formed from two species of different size and chemical functionality have recently been shown to enable robust enzymatic catalysis in pickering emulsions,²¹ bifunctional magnetic/fluorescent nanoparticle assemblies for theranostics in medicine,²² and enhanced electrocatalysis.²³ In the latter application, it was suggested that the highly defective packing of Au and Pd nanoparticles is responsible for improved catalytic performance.

Finally, in synthetic chemistry, the binary arrangements of atoms in heteroatom-doped fullerenes are important for stability and chemical reactivity. For example, boron-doped fullerenes have applications ranging from photonics to hydrogen storage,^24–26 nitrogen-doped fullerenes have suggested applications in fuel cells,²⁷ and silicon-doped fullerenes in catalysis.²⁸

In the present work, we survey and analyse the potential energy landscapes for the bidisperse arrangement of repulsive particles on a sphere. To begin with, we analyse the structure and energy of the predicted global minima relative to the monodisperse case. We find that the complexity of the landscapes make it relatively challenging to locate the global minima. This problem is tackled using generalised basin-hopping global optimisation to define biminima, which are minima in both configurational and permutational space.²⁹ Interestingly, we find that a minority of small particles are able to passivate the topological defects necessary for spherical packings. Rather than destroying the global ordering,¹⁴ we find that bidispersity is capable of stabilising high-symmetry structures relative to the monodisperse case. In contrast, a majority of small particles destabilises the global minima. Probing the global minima structures further, we find a general trade-off between high symmetry and particle size segregation, with segregation the energetically favoured strategy to lower the energy at intermediate proportions of small particles.

We then examine the potential energy landscapes to compare systems with widely different degrees of ordering in the global energy minimum. Despite the diversity in the ground state structures, all the landscapes exhibit very numerous defective states, many of which are deeper than the global minimum. The principal effect of bidispersity is therefore not necessarily to disrupt low-energy regular packings, but rather to create broken ergodicity in terms of low-lying minima separated by high barriers. This organisation explains the large range of highly defective structures observed in experimental and simulated systems, which may not be able to sample the lowest-energy structures on feasible time scales.^13–15 Probing these landscapes further, we study how the icosahedral order parameter and particle segregation change through the energy range of local minima. Of particular interest is that, for the systems tested, the degree of segregation is not strongly correlated with the energy, and is instead controlled by the number of small particles. Finally, by studying the calculated heat capacities, we find that melting transitions in systems with low-symmetry global minima occur at temperatures an order of magnitude lower than for both monodisperse systems and binary systems with high-symmetry global minima.

Methods

The spherical systems we consider consist of N repulsive particles of two types, A and B, with populations N_A and N_B, respectively. Throughout, we fix N = 72 and vary N_A for this initial survey. We choose N = 72 to allow a broad range of point groups to be investigated, ranging from low, C₁ symmetry, to particularly high I-symmetry, as observed in monodisperse systems.³⁰ 72 is sufficiently small that we can robustly locate global minimum energy structures and explore the energy landscapes extensively for benchmarking. N = 72 also has physical relevance, for example being representative of small SphEMs.¹⁶ Hence we investigate this relatively small but non-trivial system in detail to lay the foundations for larger systems in the future.

Varying N_A and N_B = N − N_A allows us to investigate binary systems with a wide range of structural order. The spherical surface on which the particles are confined has fixed radius R = 5. The particles are modelled as repulsive Lennard-Jones centres, where the pair interaction energy E_ij between particles i and j is defined as

Here, r_ij is the 3D Cartesian particle separation, with S_i and S_j describing the effective interaction length scales of each particle. In this work, we fix S_A = 0.9 and S_B = 1.1 to explore the effect of modestly perturbing a monodisperse system. 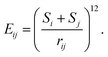This size disparity is also representative of physical systems, for example the cell size distribution in SphEMs¹⁶ and the bond length differences in boron-doped fullerenes.^25,26 No cutoff was applied when evaluating the pair energies in eqn (1).

The total energy E of the system is the sum of E_ij over all particle pairs. To scale the total energy for comparison of different systems, we normalise the interaction range S_i + S_j by [small sigma, Greek, macron], where [small sigma, Greek, macron] is the average range: [small sigma, Greek, macron] = 2(N_AS_A + N_BS_B)/N. To highlight the relative stabilisation of a system of energy E, compared to the monodisperse global energy minimum of energy E_ref, we normalise E_ij by E_ref. This treatment ensures that the reduced energy E′ of any global minimum of N = 72 identical particles is 1, regardless of the interaction range or sphere radius.

To find the global potential energy minima, we initially employed a basic basin-hopping (BH) global optimization approach.^31–33 Here, one iteration consists of a trial displacement to the particle positions followed by energy minimisation to yield a candidate minimum. This candidate is accepted or rejected as input into the next iteration based on the energy change from the previous iteration. However, except for extreme values of N_A, candidate global minima were not located reliably from initial configurations within 10⁶ BH iterations. From previous analysis of binary Lennard-Jones clusters, this problem is known to be caused by the combinatorially large number of arrangements of particles A and B within any specified configuration.³⁴ We therefore employed a generalised basin-hopping approach, the Quench-Assisted Local Combinatorial Search algorithm (QALCS)^29,34 to locate biminima, structures that are potential energy minima in both configurational and permutational space. Here, starting from an initial random quenched configuration, a series of optimal A–B swaps were made, each followed by configurational minimisation, until there remained no swaps that produced further reduction in the potential energy. This procedure was repeated from a range of random initial configurations. For all N_A, approximately 100 such repeats proved sufficient to find a global minimum candidate that could not be improved further with 500 repeats.

The energy landscapes were constructed by harvesting databases of minima and the transition states that connect them, defined geometrically, as index one stationary points.³⁵ Transition states were approximately located between pairs of minima using the Doubly-Nudged^36,37 Elastic Band^38,39 algorithm (DNEB), and refined using Hybrid Eigenvector-Following (HEF).^38,40,41 BH, QALCS, DNEB, HEF, and stationary point database construction were carried out using the programs GMIN, OPTIM and PATHSAMPLE.⁴²

To calculate the heat capacities at constant volume, C_v, we used the harmonic superposition approximation to the vibrational density of states for each minimum.^43,44 This formulation can be expressed as

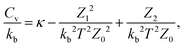where k_b is the Boltzmann constant, T is the temperature, and κ is the number of vibrational degrees of freedom in the system. Here, the N particles are confined to the surface of a sphere, so that κ = 2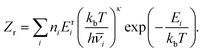N − 3. The Z_r are the moments of the potential energy E, defined as,The summation is over all minima, h is the Planck constant, [small nu, Greek, macron] is the geometric mean vibrational frequency of the normal modes, and n is the combinatorial weighting factor: n_i = 2N_A!N_B!/O_i, where O_i is the point group order for minimum i.

Two order parameters are used throughout to evaluate the particle arrangements. The first is the icosahedral order parameter Q₆,⁴⁵ which is calculated for the arrangement of all pentagonal sites. Q₆ is a bond-orientational order parameter, where here the ‘bonds’ connect each pentagonal site to the centre of the sphere. Perfect icosahedral packing yields Q₆ ≈ 0.66. The second index we call the clustering parameter, C_AB, which measures the degree of segregation between the particle types. C_A is defined as the average fraction of nearest neighbours to a type-A particle that are also of type A. C_B is defined similarly for B-type particles. We define C_AB as the product C_AB = C_AC_B. C_AB is large if all A-type particles are clustered together and all B-type particles are clustered together, achieving species separation.

Throughout, we use Voronoi constructions to visualise the particle packing arrangements and highlight the local packing arrangements. In all images, pentagonal sites are coloured red, hexagonal sites are green, and heptagonal sites are blue. Sites occupied by type B particles are shaded darker.

Results and discussions

The monodisperse potential energy landscape

It is helpful to begin by analysing the potential energy landscape for packing 72 identical repulsive particles on a sphere, illustrated as a disconnectivity graph^46,47 in Fig. 1. A disconnectivity graph is a one-dimensional representation of the landscape, where the vertical scale here represents the potential energy and minima are located at the ends of the branches. The points where two branches join indicate the minimum energy transition state that must be overcome to interconvert the corresponding minima. Here, the global minimum has icosahedral symmetry (point group I), with the fewest number of disclinations possible, identical to the packing of repulsive point charges.⁴⁸ The energy of this state defines the reference, against which we normalise all subsequent reported energies, as detailed in the Methods. We also find two higher energy states: one featuring tetrapentagon defects, with point group O, and a higher energy state with point group D₂.

Fig. 1 Disconnectivity graph for a system of 72 monodisperse repulsive particles arranged on a sphere. The global minimum energy state defines the E′ = 1 level. The three minima are illustrated using Voronoi constructions.

This landscape possesses two key features that contrast significantly with the binary systems studied below. Firstly, the monodisperse minima are simply connected, with only two minimum energy pathways existing between the I and O, and I and D₂ states. Secondly, the landscape is strongly funnelled:⁴⁹ the minimum energy barriers from the two high energy states are significantly smaller than both the range of energies spanned by all minima, and the barrier out of the global minimum.

Bidisperse global minima

We now examine the properties of the binary global minima as N_A varies, summarised in Fig. 2 and Table 1. In Fig. 2a, the reduced energy of each global minimum E′ is plotted against N_A. By reducing the total energy with respect to the average interaction range [small sigma, Greek, macron], we effectively eliminate the average repulsion energy due simply to the average particle size changing, highlighting instead the energetic contributions arising from packing.

Fig. 2 (a) Variation in the scaled energy of the global minima as the number of A particles N_A increases. Particularly stable states with respect to particle substitution are highlighted in red, and illustrated. Subscripts indicate N_A. (b and c) The global minimum states at extreme values of N_A preserve the approximate icosahedral arrangements of five-coordinate sites. (d) Variation of the icosahedral order parameter for five-coordinate sites Q₆ and clustering parameter C_AB with N_A. The dashed blue line indicates ideal icosahedral packing. (e) Examples of states with: high Q₆ and low C_AB, low Q₆ and high C_AB, high Q₆ and high C_AB, and low Q₆ and low C_AB, from top to bottom, respectively.

Table 1 Point groups for the putative global minima of 72 particles with variable numbers of the small, A-type particles N_A

N A	Point group	N A	Point group	N A	Point group
0	I	24	O	48	C 1
1	C 5	25	C 1	49	C 1
2	C 2	26	C 1	50	C 1
3	C 3	27	C 1	51	C 1
4	C 2	28	C 1	52	C 1
5	C 1	29	C 1	53	C 1
6	C 5	30	C 3	54	C 2
7	C 1	31	C 1	55	C 1
8	C 2	32	C 1	56	C 1
9	C 3	33	C 1	57	C 3
10	C 2	34	C 1	58	C 1
11	C 5	35	C 1	59	C 1
12	I	36	C 1	60	C 1
13	C 1	37	C 1	61	C 1
14	C 1	38	C 1	62	C 1
15	C 1	39	C 1	63	C 1
16	C 1	40	C 2	64	C 4
17	C 1	41	C 1	65	C 1
18	C 1	42	C 1	66	C 1
19	C 1	43	C 1	67	C 5
20	C 2	44	C 1	68	C 1
21	C 1	45	C 1	69	C 1
22	C 2	46	C 1	70	C 1
23	C 1	47	C 1	71	C 1

---

Starting from an initial monodisperse system, increasing N_A results in a monotonic decrease in E′ up to N_A = 12. In Fig. 2b, this trend is shown to be due to A-type particles successively occupying the pentagonal sites in the approximately icosahedral configuration. It is energetically favourable for the small particles to occupy these sites, as the pentagonal sites in the monodisperse global minimum occupy approximately 0.93 the area of the hexagonal sites. The N_A = 12 system, point group I, represents the overall minimum E′ system with respect to substitution of A-type and B-type particles.

Increasing N_A further, the global minima tend to depart from icosahedral or other high-symmetry packings, with E′ generally increasing up to N_A = 49. A notable exception to both of these trends occurs at N_A = 24, where we observe a state of point group O that closely corresponds to the 2nd-lowest energy state in the monodisperse system. The presence of 24 small particles occupying the 24 pentagonal sites is sufficiently stabilising that the O state becomes the global minimum. The tetrapentagon patches exhibited in these O states have been shown to arise in packings of repulsive monodisperse point charges,⁹ and interestingly, similar structures also occur in biological SphEMs¹⁶ and colloidosomes.⁵⁰

For N_A > 49, the global minima are destabilised relative to the monodisperse system. We can view these arrangements as monodisperse systems of small particles (A), doped with a minority of large particles (B). It is well established that lattice defects inducing a local area increase also induce negative curvature in otherwise 2D sheets (see for example ref. 51 and 52). Hence it is particularly unfavourable to confine negative-curvature-inducing defects to a positively curved surface. In this region, however, there also exist locally low-energy states with high symmetry. The most notable of these states is at N_A = 64 with point group C₄. From this result we conclude that a few small particles can effectively passivate the topological defects in the spherical packing, while a few large particles exacerbate these defects.

Finally, as N_A approaches 72, the approximate icosahedral particle arrangement returns in the predicted global minima. As shown in Fig. 2c, the minority large particles pack successively around a pentagonal site. This trend arises because in the distorted lattice, the largest sites are always found around the same pentagonal defect.

How closely the global minima conform to icosahedral arrangements is quantified in Fig. 2d through the Q₆ order parameter. As described above, conformations close to icosahedral symmetry are observed for N_A ≤ 18 and N_A ≥ 66, with mostly low values of Q₆ for intermediate N_A. Also in Fig. 2d we plot the order parameter C_AB, describing the segregation of the A and B particles. C_AB is particularly large at intermediate N_A, suggesting that when the ratio of A and B particles is not commensurate with icosahedral packing, a successful strategy to reduce the energy is to separate the system into A-rich and B-rich regions. Examples of configurations that adhere to this trade-off between Q₆ and C_AB are illustrated in Fig. 2e. At N_A = 12, Q₆ is large, whereas C_AB is small, as all A particles are separated. At N_A = 43, Q₆ is small, whereas C_AB is large. However, there are exceptions to this general trade-off. N_A = 55 exhibits a large Q₆, as all pentagonal sites are occupied by A atoms, but also a large C_AB as all hexagonal sites are separated into A-only and B-only regions. Conversely, for N_A = 64, both Q₆ and C_AB are small, as the high-symmetry (non-icosahedral) structure distributes the large particles individually over the sphere.

Bidisperse potential energy landscapes

We now examine the potential energy landscapes for three systems: N_A = 12, featuring the highest symmetry, lowest E′ global minimum; N_A = 30, exhibiting an intermediate symmetry (C₃) global minimum with E′ < 1; and N_A = 60, exhibiting a low symmetry (C₁) global minimum with E′ > 1. In Fig. 3, the three disconnectivity graphs are plotted on the same scale. The potential energy density of minima is too high to include them all in a disconnectivity graph, since an inexhaustive search produces in excess of 10⁵ minima. Instead, random samples of 150 connected minima are shown for each example, which are representative of more comprehensive disconnectivity graphs. The first key difference between the monodisperse and binary landscapes is that the number of minima in the binary systems vastly exceed the three in the monodisperse case. This difference can be explained and quantified by taking a combinatorial approach. We treat the N_A particles as a small perturbation to an otherwise monodisperse system. For example, by distinguishing N_A particles in the monodisperse I-minimum this state splits into multiple distinguishable minima. We use the Redfield–Pólya enumeration theorem to count these unique combinations, which has successfully been applied before to count atomic arrangements in heterofullerenes.⁵³ Here, for N_A = 12 and 60, we expect approximately 3 × 10¹¹ states, whereas for N_A = 30, we expect 3 × 10¹⁸. However, this analysis assumes that the A-type particles have no effect on the spatial arrangement or stability of the monodisperse state, and does not consider new stable states that differ in structure from the monodisperse cases. It remains an interesting open question to establish whether increasing the size ratio between A and B particles increases or reduces the total number of minima, compared to when A and B are treated as infinitesimal perturbations of the monodisperse system.

Fig. 3 (a–c) Disconnectivity graphs for N_A = 12, 30, and 60 respectively, shown plotted on the same scale with the E′ = 1 level indicated. For visual clarity, only a representative sample of 150 connected minima are shown. The global minimum energy structures are also indicated, with front and back views for N_A = 30 and 60.

The second key difference between the monodisperse and binary landscapes is that the binary landscapes are weakly funnelled with numerous deep minima, reminiscent of binary clusters.⁴ This structure explains the diversity of stable states observed in experiments when prepared from a high temperature quench,¹⁴ in simulations when relaxing to a local minimum from a random starting configuration,¹³ and perhaps also the diverse packing arrangements of polydisperse epithelial cells in SphEMs.¹⁶

From previous analysis of the landscapes for Lennard-Jones clusters,⁵⁴ we might have expected particularly high-symmetry, low-energy global minima to be associated with strongly funnelled landscapes. Surprisingly, however, this trend is not reflected in Fig. 3, in which all three landscapes appear qualitatively similar. For N_A = 12, the high-symmetry I-global minimum is distinguished as the lowest energy state by a modest margin, but is not the deepest minimum located. The N_A = 12 and N_A = 30 landscapes are both modestly funnelled, with the N_A = 60 landscape marginally shallower.

We now examine the structural differences in the minima both within and between the landscapes, summarised in Fig. 4. Across the energy range of each landscape, we randomly sample 100 minima lying within E′ intervals of 0.01. For intervals containing fewer than 100 minima, all of them are included. From these samples, we compute the average and standard deviation of the order parameters Q₆ and C_AB.

Fig. 4 (a–c) Variation of the icosahedral order parameter for five-coordinate sites Q₆ and clustering parameter C_AB with E′ for N_A = 12, 30, and 60, respectively. Error bars indicate the standard deviation in the samples. The grey histogram illustrates the population density in the libraries of local minima. Representative minima from the extreme ends of the stability ranges are illustrated beneath.

For N_A = 12, shown in Fig. 4a, we see that at low energies, the icosahedral symmetry is well-preserved. As with the example minimum shown, these systems are indeed defective variants of the global minimum. At higher energies, this ordering is lost, and we observe highly defective states. However, there is little change in the clustering across the energy range. At N_A = 30, shown in Fig. 4b, the low energy states are again defective variants of the global minimum, with relatively high C_AB and low Q₆. C_AB exhibits a modest decrease as E′ increases. Interestingly, the majority of defects in the hexagonal lattice occur within A-regions: it is relatively rare for the necessary pentagonal defects to be populated by the larger B particles, even in high-energy systems. At N_A = 60, illustrated in Fig. 4c, we see a partial recovery of icosahedral packing for the pentagonal sites at low energy, as shown in the structure illustrated. However, this order disappears at high energy. C_AB also changes relatively little, suggesting overall that the degree of segregation of the particles depends almost exclusively on N_A and not E′. This critical dependence on N_A is particularly pertinent to binary pattern formation on spheres, in which the degree of clustering plays a functional role.

Heat capacities

Finally, we examine the heat capacities at constant volume, C_v, for the binary and monodisperse systems considered, shown in Fig. 5. Throughout, we have scaled all reported potential energies by the normalisation factor E_ref/[small sigma, Greek, macron]¹². We also employ this construction in Fig. 5 to scale the thermal energy, allowing for a direct comparison of C_v between the different systems.

Fig. 5 Constant volume heat capacities for the monodisperse system (N_A = 0) and three binary systems (N_A = 12, 30, 60) on a normalised thermal energy scale.

Although the disconnectivity graphs appear qualitatively similar in Fig. 3, striking thermodynamic differences are revealed in the C_v profiles. As a reference, the monodisperse system exhibits a single, low-amplitude peak, consistent with a significant occupation probability change from the global minimum to the two higher energy states. For N_A = 12, the peak in C_v is associated with the occupation probability increase in a substantial proportion of the database of minima, so we may view this feature as a melting transition.⁴⁴ The substantial stabilisation of the global minimum relative to all excited states shifts the melting peak to higher temperatures than for the monodisperse system. The multiplicity of excited states increases the peak amplitude. For N_A = 30, two peaks are observed. The lower temperature peak corresponds to a solid–solid transition, in which the population of a small number of minima, which are close in energy to the global minimum, becomes significant. The higher temperature peak corresponds to a melting transition. For N_A = 60, the separation of energy scales within the low energy minima, and between the low and higher energy minima, is not so distinct, producing a shouldered peak rather than two distinct peaks. Compared to N_A = 12, the reduced stability of the global minimum relative to the excited states for both the N_A = 30 and N_A = 60 systems, shifts the peaks to temperatures an order of magnitude lower.

It is interesting to note that the different heat capacity profiles provide further evidence for the principle of maximum symmetry.⁵⁵ Stated briefly, the principle suggests that although the mean energy of high-symmetry and low-symmetry structures is not expected to differ substantially, high-symmetry systems exhibit a wider variance of energies, and hence are more likely to be found as global minima. Hence the N_A = 12, I-global minimum has a larger energy separation from the numerous low-symmetry excited states than for the N_A = 30 or N_A = 60 systems. This result suggests that the N_A = 12 system shows a higher melting temperature precisely because of the high symmetry of the global minimum.

The melting transitions of Lennard-Jones clusters are mostly driven by the landscape entropy, associated with the relatively large number of higher potential energy minima, as opposed to the well entropy, which corresponds to the vibrational entropy contributions of each individual minimum.^44,56 The vibrational entropy usually increases for higher-lying minima. Employing harmonic vibrational densities of states then causes a systematic shift in the melting point to higher temperature, because the entropy underestimate is greater for the liquid-like phase. Within the harmonic approximation, we may evaluate the difference in Helmholtz free energy F between state j and the global potential energy minimum (denoted state ‘o’), as

F_j − F_o = −k_BT(log O_o − log O_j + κ log [small nu, Greek, macron]_o − κ log [small nu, Greek, macron]_j) + E_j − E_o. (4)

In these binary systems we find that the major contribution to entropic stabilisation arises from the differences in mean vibrational frequencies, log [small nu, Greek, macron]. For N_A = 12, the relatively soft normal modes of the global potential energy minimum mean that the ground state is entropically stabilised, which is an unusual situation. In contrast, for N_A = 30, the ground state is entropically destabilised relative to nearly all the other states. For N_A = 60, a mixture of entropic stabilisation and destabilisation occurs for all states relative to the global potential energy minimum configuration.

An interesting extension to the present investigation would be to study the kinetics of bidisperse spherical systems to analyse how the underlying potential energy landscape encodes the glassy dynamics observed recently in experiment.¹⁴

Conclusions

We have analysed the structures and potential energy landscapes of bidisperse systems of repulsive particles confined to a spherical surface. By varying the number of small particles at fixed total particle number, we identified a range of high-symmetry binary packings. Moreover, small particles were able to passivate topological defects, so that, surprisingly, certain bidisperse systems were stabilised relative to the monodisperse case. Importantly, however, for all the landscapes we surveyed, an overwhelming number of defective, low-lying minima were located, which we expect to destroy ergodicity in many experimental and computational systems. A consequence of this effect is that, in order to find global minima, more specialised techniques were required to locate biminima, corresponding to minima in both configurational and permutational space.

For the global minima, an interesting competition was identified between local ordering, favouring particle segregation, and global ordering, favouring high-symmetry structures. In the corresponding energy landscapes, low energy structures are largely defective global minima, while high energy structures tend to exhibit substantially reduced global ordering. Interestingly, the degree of segregation between the particle types only depends on the composition, not the energy, and this is a key conclusion for applications where function depends on particle clustering.

Finally, we found that the melting temperature for systems with low-symmetry ground states is an order of magnitude lower than for monodisperse, or high-symmetry binary systems. Although highly ordered global minima exist for many binary systems, broken ergodicity and low melting temperatures are responsible for the significant variety of structures observed in nature, experiments, and simulations.

Recent work is beginning to explore the rich array of structures and organisation arising from polydispersity (see for example ref. 15, 57 and 58). Going forward it will be interesting to investigate how curvature, the interaction potential, and polydispersity interact to affect the energy landscape, and how these parameters might be exploited in designing functionality.

Author contributions

AFB and JRP contributed equally to the preparation of this manuscript, including formal analysis, investigation, visualization, and writing the original draft. JRP also contributed to the methodology and software developed by DJW. DJW supervised the project, with JRP as co-supervisor. DJW led the project conceptualization, funding acquisition, project administration, and writing, reviewing and editing.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

The authors would like to acknowledge the encouragement and experimental work of Daria S. Roshal, Marianne Martin, Kirill Fedorenko, Virginie Molle, Stephen Baghdiguian, and Sergey B. Rochal, which promoted the development of this research. The authors also acknowledge Halim Kusumaatmaja for the original software development of the binary spherical systems used here. DJW gratefully acknowledges the EPSRC for financial support.

References

1. M. J. Bowick and L. Giomi, Adv. Phys., 2009, 58, 449–563.
2. M. Dodgson and M. Moore, Phys. Rev. B: Condens. Matter Mater. Phys., 1997, 55, 3816–3831.
3. C. R. Li, W. J. Dong, L. Gao and Z. X. Cao, Appl. Phys. Lett., 2008, 93, 34108.
4. V. K. de Souza and D. J. Wales, J. Chem. Phys., 2009, 130, 194508.
5. A. R. Bausch, M. J. Bowick, A. Cacciuto, A. D. Dinsmore, M. F. Hsu, D. R. Nelson, M. G. Nikolaides, A. Travesset and D. A. Weitz, Science, 2003, 299, 1716–1718.
6. M. Bowick, A. Cacciuto, D. R. Nelson and A. Travesset, Phys. Rev. Lett., 2002, 89, 185502.
7. A. Pérez-Garrido and M. A. Moore, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 60, 15628–15631.
8. T. Erber and G. M. Hockney, J. Phys. A: Gen. Phys., 1991, 24, L1369–L1377.
9. D. J. Wales and S. Ulker, Phys. Rev. B: Condens. Matter Mater. Phys., 2006, 74, 212101.
10. T. S. Ingebrigtsen and H. Tanaka, J. Phys. Chem. B, 2015, 119, 11052–11062.
11. M. D. Ediger and P. Harrowell, J. Chem. Phys., 2012, 137, 080901.
12. T. Hamanaka and A. Onuki, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2007, 75, 41503.
13. A. M. Mascioli, C. J. Burke, M. Q. Giso and T. J. Atherton, Soft Matter, 2017, 13, 7090–7097.
14. N. Singh, A. K. Sood and R. Ganapathy, Nat. Commun., 2020, 11, 4967.
15. S. Fortuna and D. L. Cheung, Colloids Interface Sci. Commun., 2017, 17, 10–13.
16. D. S. Roshal, K. Azzag, E. Le Goff, S. B. Rochal and S. Baghdiguian, Sci. Rep., 2020, 10, 7652.
17. C. Martinand-Mari, B. Maury, F. Rousset, A. Sahuquet, G. Mennessier, S. Rochal, V. Lorman, P. Mangeat and S. Baghdiguian, PLoS One, 2009, 4, e4202.
18. K.-H. Baumann and B. Boeckel, J. Micropalaeontology, 2013, 32, 123–133.
19. U. Riebesell, I. Zondervan, B. Rost, P. D. Tortell, R. E. Zeebe and F. M. Morel, Nature, 2000, 407, 364–366.
20. T. Bollhorst, K. Rezwan and M. Maas, Chem. Soc. Rev., 2017, 46, 2091–2126.
21. H. Jiang, L. Liu, Y. Li, S. Yin and T. Ngai, ACS Appl. Mater. Interfaces, 2020, 12, 4989–4997.
22. T. Bollhorst, S. Shahabi, K. Wçrz, C. Petters, R. Dringen, M. Maas and K. Rezwan, Angew. Chem., Int. Ed., 2015, 54, 118–123.
23. L. Zhang, Q. Fan, X. Sha, P. Zhong, J. Zhang, Y. Yin and C. Gao, Chem. Sci., 2017, 8, 6103–6110.
24. Z. Chen, X. Zhao and A. Tang, J. Phys. Chem. A, 1999, 103, 10961–10968.
25. R. H. Xie, L. Jensen, G. W. Bryant, J. Zhao and V. H. Smith, Chem. Phys. Lett., 2003, 375, 445–451.
26. I. Garg, H. Sharma, K. Dharamvir and V. K. Jindal, J. Comput. Theor. Nanosci., 2011, 8, 642–655.
27. S. H. Noh, C. Kwon, J. Hwang, T. Ohsaka, B. J. Kim, T. Y. Kim, Y. G. Yoon, Z. Chen, M. H. Seo and B. Han, Nanoscale, 2017, 9, 7373–7379.
28. F. G. Bernal Texca, E. Chigo-Anota, L. Tepech Carrillo and M. Castro, Int. J. Comput. Mater. Sci. Eng., 2017, 1103, 1–10.
29. D. Schebarchov and D. J. Wales, Phys. Rev. Lett., 2014, 113, 156102.
30. R. Zandi, D. Reguera, R. F. Bruinsma, W. M. Gelbart and J. Rudnick, Proc. Natl. Acad. Sci. U. S. A., 2004, 101, 15556–15560.
31. Z. Li and H. A. Scheraga, Proc. Natl. Acad. Sci. U. S. A., 1987, 84, 6611–6615.
32. D. J. Wales and J. P. K. Doye, J. Phys. Chem. A, 1997, 101, 5111–5116.
33. D. J. Wales and H. A. Scheraga, Science, 1999, 285, 1368–1372.
34. D. Schebarchov and D. J. Wales, J. Chem. Phys., 2013, 139, 221101.
35. J. N. Murrell and K. J. Laidler, Trans. Faraday Soc., 1968, 64, 371–377.
36. S. A. Trygubenko and D. J. Wales, J. Chem. Phys., 2004, 120, 2082–2094.
37. S. A. Trygubenko and D. J. Wales, J. Chem. Phys., 2004, 121, 6689–6697.
38. G. Henkelman, B. P. Uberuaga and H. Jónsson, J. Chem. Phys., 2000, 113, 9901–9904.
39. G. Henkelman and H. Jónsson, J. Chem. Phys., 2000, 113, 9978–9985.
40. L. J. Munro and D. J. Wales, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 3969–3980.
41. Y. Zeng, P. Xiao and G. Henkelman, J. Chem. Phys., 2014, 140, 044115.
42. http://www-wales.ch.cam.ac.uk/software.html .
43. D. J. Wales, Mol. Phys., 1993, 78, 151–171.
44. D. J. Wales, Phys. Rev. E, 2017, 95, 030105(R).
45. P. J. Steinhardt, D. R. Nelson and M. Ronchetti, Phys. Rev. B: Condens. Matter Mater. Phys., 1983, 28, 784.
46. O. M. Becker and M. Karplus, J. Chem. Phys., 1997, 106, 1495–1517.
47. D. J. Wales, M. A. Miller and T. R. Walsh, Nature, 1998, 394, 758–760.
48. D. J. Wales, J. P. K. Doye, A. Dullweber, M. P. Hodges, F. Y. Naumkin, F. Calvo, J. Hernández-Rojas and T. F. Middleton, The Cambridge Cluster Database, 2001, http://www-wales.ch.cam.ac.uk/CCD.html.
49. N. D. Socci, J. N. Onuchic and P. G. Wolynes, Proteins: Struct., Funct., Genet., 1998, 32, 136–158.
50. D. S. Roshal, Phys. Solid State, 2013, 55, 2128–2131.
51. N. A. García, A. D. Pezzutti, R. A. Register, D. A. Vega and L. R. Gómez, Soft Matter, 2015, 11, 898–907.
52. H. S. Seung and D. R. Nelson, Phys. Rev. A: At., Mol., Opt. Phys., 1988, 38, 1005–1018.
53. M. Ghorbani and M. Songhori, Fullerenes, Nanotubes, Carbon Nanostruct., 2013, 21, 460–471.
54. J. P. K. Doye, M. A. Miller and D. J. Wales, J. Chem. Phys., 1999, 111, 8417–8428.
55. D. J. Wales, Chem. Phys. Lett., 1998, 285, 330–336.
56. D. J. Wales, Energy Landscapes: Frequently Asked Questions, https://www.ch.cam.ac.uk/group/wales.
57. I. Azizi and Y. Rabin, Entropy, 2020, 22, 570.
58. T. S. Ingebrigtsen and H. Tanaka, J. Phys. Chem. B, 2016, 120, 7704–7713.

---

Footnote

† These authors contributed equally to this work.

---