Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Deformation profiles and microscopic dynamics of complex fluids during oscillatory shear experiments†
Paolo
Edera
 a,
Matteo
Brizioli
a,
Matteo
Brizioli
 a,
Giuliano
Zanchetta
a,
Giuliano
Zanchetta
 a,
George
Petekidis
a,
George
Petekidis
 b,
Fabio
Giavazzi
b,
Fabio
Giavazzi
 a and
Roberto
Cerbino
a and
Roberto
Cerbino
 *ac
*ac
aDipartimento di Biotecnologie Mediche e Medicina Traslazionale, Università degli Studi di Milano, via F.lli Cervi 93, 20090 Segrate, Italy. E-mail: roberto.cerbino@univie.ac.at
bFORTH/IESL and Department of Materials Science and Technology, University of Crete, 71110 Heraklion, Greece
cUniversity of Vienna, Faculty of Physics, Boltzmanngasse 5, 1090 Vienna, Austria
First published on 6th September 2021
Abstract
Oscillatory shear tests are widely used in rheology to characterize the linear and non-linear mechanical response of complex fluids, including the yielding transition. There is an increasing urge to acquire detailed knowledge of the deformation field that is effectively present across the sample during these tests; at the same time, there is mounting evidence that the macroscopic rheological response depends on the elusive microscopic behavior of the material constituents. Here we employ a strain-controlled shear-cell with transparent walls to visualize and quantify the dynamics of tracers embedded in various cyclically sheared complex fluids, ranging from almost-ideal elastic to yield stress fluids. For each sample, we use image correlation processing to measure the macroscopic deformation field, and echo-differential dynamic microscopy to probe the microscopic irreversible sample dynamics in reciprocal space; finally, we devise a simple scheme to spatially map the rearrangements in the sheared sample, once again without tracking the tracers. For the yield stress sample, we obtain a wave-vector dependent characterization of shear-induced diffusion across the yielding transition, which is accompanied by a three-order-of-magnitude speed-up of the dynamics and by a transition from localized, intermittent rearrangements to a more spatially homogeneous and temporally uniform activity. Our tracking free approach is intrinsically multi-scale, can successfully discriminate between different types of dynamics, and can be automated to minimize user intervention. Applications are many, as it can be translated to other imaging modes, including fluorescence, and can be used with sub-resolution tracers and even without tracers, for samples that provide intrinsic optical contrast.
1 Introduction
As compared with molecular hard solids – such as steel, wood or bones – soft materials made of micron-sized constituents promptly deform with relatively small mechanical loads: we easily spread butter on a slice of bread, mindlessly distribute toothpaste on our teeth, effortlessly rub our faces with cream, smoothly tickle our palate with a chocolate mousse, and readily pull our cheeks with a little pinch. Beyond having practically ubiquitous consequences in our lives, this softness opens up unique possibilities when doing experimental research on soft matter. A paradigmatic example is passive microrheology, in which the linear moduli of a soft material are probed by embedded microscopic tracer particles that operate as micro-scale rheometers powered by tiny thermal fluctuations.1,2 Despite being a technique that has had enormous success, passive microrheology is unable to provide complete rheological information in all cases of interest. For instance, if the storage modulus of the material is too large or if one is interested in the non-linear rheological properties, it is often preferred to recur to active microrheology, in which at least one of the embedded particles is driven by an external force obtained, for instance, via optical or magnetic trapping.1,3–5 Passive and active microrheology techniques are very powerful tools for the characterization of soft materials, as they can access high frequencies and enable a space-resolved study of the rheological properties of complex, heterogeneous systems.3 However, the fact that the energy is injected at a local, particle scale makes them unsuitable to study and predict the complex failure modes observed in soft materials when they are mechanically perturbed at the macroscopic scale.More insightful information on the microscopic mechanisms underlying plasticity in soft materials can be obtained by imposing a controlled macroscopic deformation to the sample – for instance by displacing one or more of the confining surfaces of a shear rheometer – while monitoring over time the structural rearrangements occurring at the microscale. Rearrangements are typically monitored by accurate tracking of embedded tracer particles, performed in direct (rheo-microscopy or rheo-imaging) or in reciprocal space (rheo-scattering), very often but not necessarily by optical means.6–9 These rearrangements may be partly or entirely reversible, with the irreversible component becoming dominant for increasing shear strain across the transition to non-linearity.10–14 This kind of experiments thus provides very useful insights on how the microscopic structure and dynamics determine the material rheology, which can be used to design enhanced materials, e.g. with a longer lifetime, controlled relaxation, improved ductility or emerging memory.15
A variety of shear rheology tests is compatible with the simultaneous characterization of the tracer particles' motion. The latter can be generally split into the sum of affine and non-affine displacements16; the relative importance of these two contributions depends on the type of test, and on the scheme used to sample the particles' configuration in space and time. For instance, during Small/Medium/Large Amplitude Oscillatory Shear (SAOS/MAOS/LAOS) rheology experiments, the so-called echo protocol enables one sampling the microscopic configuration at each deformation cycle, by obtaining a stroboscopic movie of the particles configurations either in direct or in reciprocal space. In this way, the affine contribution is suppressed and one can focus on the non-affine irreversible particle rearrangements.
Most of the initial experiments with the echo protocol were performed with Diffusing Wave Spectroscopy (DWS),10 and Dynamic Light Scattering (DLS).17 Being based on the collection of multiply scattered light, DWS is very sensitive to a single, small length scale, whereas DLS is intrinsically a multi-scale technique, at the expense of an increased experimental complexity.18 More recently, microscopy has also been employed to track particle motion in oscillatory shear experiments with the echo protocol.12
If one is interested in going beyond the study of irreversible non-affine particle displacements typically obtained with the echo protocol, imaging and microscopy offer an important advantage over scattering experiments: the affine particle motion that characterizes the intra-cycle particle dynamics can be readily removed from the particle trajectories, whereas more caution is needed in scattering experiments.19 However, the information extracted from scattering experiments is characterized by an enviable statistical robustness. For these reasons, it would be interesting to have both techniques available during oscillatory shear experiments.
A possible compromise is represented by Digital Fourier Microscopy (DFM),20 a family of techniques based on collecting in direct space temporal sequences of images of the sample, which are subsequently spatially Fourier transformed to obtain scattering information in the reciprocal space as a function of the wave-vector q. The most popular DFM technique is Differential Dynamic Microscopy (DDM),21–24 which relies on subtracting images acquired at different times, a feature that appears well suited to echo experiments: when two images acquired at an integer multiple of the shear oscillation period are subtracted, only the irreversible particle displacements are captured and contribute to the final result. At the same time, one can take advantage of the availability of the direct space movies to remove the rigid translations associated to the affine intra-cycle particle dynamics,25 a step that may benefit from the large amount of image registration algorithms available.26
The potential of DDM in combination with shear rheology experiments was recently suggested in two companion articles by Aime and Cipelletti,6,19 in which the authors performed a critical comparison with DLS for probing shear-induced rearrangements in Fourier space. In both cases, the intermediate scattering functions for q parallel to the direction of the applied shear (shear direction) are mostly dominated by the relaxation due to the affine particle displacements, whereas in the perpendicular direction (vorticity direction) only the non-affine particle rearrangements are probed. The main advantage of DDM over DLS is that the limited spatial coherence of illumination typical of bright-field DDM experiments results in a finite, q-dependent depth-of-focus, which can be used to probe slices of the sample perpendicular to the optical axis.22 This capability is surely appealing for those cases where the deformation field deviates from a simple homogeneous profile, such as in the presence of wall slip, shear banding, or edge fracture.27 All these different phenomena have the common effect of making the actual deformation field inhomogeneous and difficult to predict, causing problems in the interpretation of the results of both rheological and DLS experiments. Indeed, while in a rheological experiment, the characterization of the material constitutive equation for the shear stress σ(γ), requires the accurate knowledge of the actual shear strain γ of the sample, in DLS experiments, where the signal is the result of an average over the entire scattering volume, it is almost impossible to discern the contributions coming from different portions of a macroscopically inhomogeneous sample. Aime and Cipelletti have clearly and convincingly showed that a proper DDM characterization of the affine displacements is possible, providing that an instrument calibration of the q-dependent depth-of-focus is performed.19 However, the full potential of combining DDM analysis with an echo protocol, where the effect of affine displacements is minimized, remains yet unexplored.
In this work, we perform oscillatory shear experiments with a strain-controlled cell, characterized by a parallel-sliding-plates geometry. During the sample oscillation, we monitor the dynamics of tracer particles by using bright-field DDM in conjunction with the echo protocol (echo-DDM). The depth-of-focus is tuned and optimized by varying the numerical aperture of the microscope condenser so that, even if the deformation field is not homogeneous across the whole gap, it is possible to selectively image narrow “slices” of the sample, where the shear can be assumed to be approximately constant (see Fig. 1). We apply this optimization procedure to the imaging of various samples, some of which presenting heterogeneity of the deformation field in the direction of the velocity gradient (gradient direction). We perform a preliminary accurate characterization of the deformation field across the whole gap in standard samples with pure elastic solid or pure viscous liquid response, retrieving the expected linear deformation profile. By applying the same protocol to more complex soft matter samples (a viscoelastic fluid and a yield stress material), we demonstrate that our approach can also effectively probe deviations from such ideal profile, due for example to wall slip or shear banding. Quantification of these effects is key to correctly relate the microscopic irreversible dynamics to the local macroscopic deformation in echo experiments.
Once obtained a reliable characterization of the local strain for all our samples, we use echo-DDM to probe the presence of a shear-induced non-affine rearrangements. The elastic solid, characterized by the absence of a true irreversible non-affine dynamics, serves as a reference to estimate the instrumental limits; as expected, Newtonian and Maxwell liquids do not exhibit any appreciable variation in non-affine activity as a function of the shear amplitude; by contrast, in the yield stress sample, we find intermittent, small scale displacements of the tracers for small strain amplitudes, and shear-induced diffusion28–31 for amplitudes larger than the one corresponding to the crossover point of the viscoelastic moduli. All the results obtained with echo-DDM are compared and found in agreement with particle tracking (PT) analysis of the tracer motion. Finally, we propose a simple yet robust scheme to draw activity maps highlighting the rearrangements that occur in the sheared sample.
The manuscript is organized as follows: in the Materials and methods section we describe the tested samples (Section 2.1), the experimental setup (Section 2.2), and the experimental protocols enabling the characterization of the macroscopic deformation field (Section 2.3) and of the irreversible non-affine dynamics (Section 2.4). The results obtained in the characterization of the deformation profile and of the shear-induced rearrangements are presented and discussed in Sections 3.1 and 3.2, respectively, before presenting some concluding comments in Section 4.
2 Materials and methods
2.1 Samples
We test our experimental approach on samples that are representative of different classes of materials: an elastomer (Sylgard), a Newtonian fluid (silicon oil), a Maxwell fluid (worm-like micelles, WLM), and a simple yield stress fluid (Carbopol). All the samples in our study are fairly transparent and are thus seeded with tracer particles of known size. However, seeding is not needed if the sample already provides a sufficient optical contrast, because DDM can capture the dynamics of a variety of samples including molecular mixtures32,33 and liquid crystals.34Sylgard 184 (Dow Corning) is as a two-component system made of a silicon oil and a curing agent. A small fraction (ϕ ∼ 0.1%) of sterically stabilized PMMA particles of diameter 260 nm are dispersed in the silicon oil base before adding the curing agent. The sample is then mixed thoroughly, centrifuged to get rid of bubbles, and finally loaded in the shear-cell before the completion of the curing process, which takes about 48 h at room temperature. The so-obtained sample is expected to behave like a perfectly homogeneous elastic material over a wide range of shear strains.35 The silicon oil that we use is the viscous component described above in the preparation of Sylgard. This sample behaves as a Newtonian viscous fluid with a shear viscosity η ≃ 5 Pa s.36 Worm-like micelles are obtained by dispersing Hexadecylpyridinium chloride monohydrate (CpyCl) surfactant in water with Sodium Salicylate (NaSal) as a counter-ion.37,38 Both components have been purchased from Sigma-Aldrich as powders. CpyCl is dispersed in Milliq water at a concentration 200 mM and taken to 40 °C for 30 minutes, until it turns to a clear solution. NaSal is dispersed in Milliq water at a concentration of 120 mM. The two dispersions are slowly mixed in a 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 ratio and left on a rotating mixer overnight. The final molarities are 100 mM and 60 mM for CpyCl and NaSal, respectively. Polystyrene particles of 2 μm diameter (PS2, Microparticles GmbH) are dispersed at a volume fraction ϕ = 0.05%. The dispersion is initially mixed manually with a spatula and left on a rotating mixer for one night. Carbopol 971 P NF has been purchased from Lubrizol as a single component powder. The powder is dispersed in MilliQ water to obtain a concentrated starting solution with concentration c = 5 wt% The obtained dispersion has an acidic pH, that is neutralized by adding few drops of NaOH 10 M to 10 ml of concentrated dispersion, while gently stirring for several days by keeping the pH controlled. At the end of the mixing phase, the neutralized dispersion is then diluted to obtain the sample at the desired concentration c = 0.5 wt%. We found that this preparation procedure ensures the reproducibility of the rheological properties of the Carbopol samples. Eventually, PS2 tracer particles are dispersed at a volume concentration ϕ = 0.05%. Before the experiment, all samples are centrifuged to get rid of the air bubbles. We note that the choice of the tracer particle size for the Carbopol sample was guided by preparatory experiments in which we investigated the tracer dynamics in Carbopol at rest for different particle diameters: 0.5, 0.8, 2, and 5 microns. For the 0.5 and 0.8 micron particles, we found that roughly half of the particles appeared stuck and the other half underwent caged dynamics. By contrast, for the 2 and 5 micron tracers, all the particles were substantially trapped. These observations, in agreement with seminal microrheological studies of Carbopol EDT 2050,39 point to the existence of a characteristic microstructural length scale, which in our Carpobol sample is smaller than 2 micron.
1 ratio and left on a rotating mixer overnight. The final molarities are 100 mM and 60 mM for CpyCl and NaSal, respectively. Polystyrene particles of 2 μm diameter (PS2, Microparticles GmbH) are dispersed at a volume fraction ϕ = 0.05%. The dispersion is initially mixed manually with a spatula and left on a rotating mixer for one night. Carbopol 971 P NF has been purchased from Lubrizol as a single component powder. The powder is dispersed in MilliQ water to obtain a concentrated starting solution with concentration c = 5 wt% The obtained dispersion has an acidic pH, that is neutralized by adding few drops of NaOH 10 M to 10 ml of concentrated dispersion, while gently stirring for several days by keeping the pH controlled. At the end of the mixing phase, the neutralized dispersion is then diluted to obtain the sample at the desired concentration c = 0.5 wt%. We found that this preparation procedure ensures the reproducibility of the rheological properties of the Carbopol samples. Eventually, PS2 tracer particles are dispersed at a volume concentration ϕ = 0.05%. Before the experiment, all samples are centrifuged to get rid of the air bubbles. We note that the choice of the tracer particle size for the Carbopol sample was guided by preparatory experiments in which we investigated the tracer dynamics in Carbopol at rest for different particle diameters: 0.5, 0.8, 2, and 5 microns. For the 0.5 and 0.8 micron particles, we found that roughly half of the particles appeared stuck and the other half underwent caged dynamics. By contrast, for the 2 and 5 micron tracers, all the particles were substantially trapped. These observations, in agreement with seminal microrheological studies of Carbopol EDT 2050,39 point to the existence of a characteristic microstructural length scale, which in our Carpobol sample is smaller than 2 micron.
2.2 Experimental setup
ΔX0(t) = A0![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sin(2πft)ûx, while we keep the bottom plate fixed sin(2πft)ûx, while we keep the bottom plate fixed | (1) |
Due to a memory buffer register limitation, with the current version of the shear-cell control software the length of an oscillatory experiment is limited to 500 cycles. Moreover, the shear-cell does not provide a real-time output signal proportional to the position of the moving plate, which could have been used to trigger a synchronized camera acquisition. Synchronization is a crucial issue in our setup and it will be discussed in detail in Section 2.4.3.
2.3 Deformation field
It is known that in several conditions of interest, the deformation field within a sheared sample may be non-homogeneous even when a uniform stress is applied.41 Two examples of deviation from homogeneity are shear banding and wall slip. These phenomena affect a wide variety of samples42–44 and while they have an indisputable effect on the mechanical response and thus on the interpretation of rheological data, it is not easy to pinpoint their presence from purely mechanical measurements. In the following, we provide a simplified description of these effects in the case of the parallel sliding plates geometry, which is the one used in our experiments and is schematically represented in Fig. 1. A key advantage of this geometry, compared to other common configurations like rotating plate-plate or rotating cone-plate, is that it allows imposing a uniform strain at the confining surfaces while ensuring easy optical access to the sample.6,12,13Ideally, when a uniform displacement ΔX0 = A0ûx is imposed on the top plate, while the bottom one is fixed, an affine displacement field is produced in the sample
| ΔX(z) = zγ0ûx, | (2) |
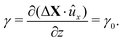 | (3) |
Deviations from this ideal case occur for example in case of wall slip, when the adhesion between the sample and the confining plates is not sufficient to prevent their relative motion. When wall slip occurs, in the absence of other effects, like shear-banding, eqn (2) modifies to
| ΔX(z) = (z − z0)γ0cûx, | (4) |
Another important example of deviation from homogeneity of the deformation field is shear banding, corresponding to the separation of the sample into macroscopic regions (bands) with different local shear strains.44,45 As an example, one can consider the simplistic case of a system separated in two bands, in the absence of wall slip, which is described by the displacement profile
 | (5) |
In our bright-field microscopy experiments, we exploit the optical sectioning capability resulting from the partial coherence of illumination to obtain an accurate characterization of the displacement ΔX(z) at different heights z, and thus a faithful reconstruction of the actual shear strain profile γ(z) within the sample.
We calculate the spatial cross-correlation function c(r,t) of each pair of consecutive frames collected at a given height
| c(r,t) = ΣxI(x,t + δt)·I(x + r,t). | (6) |
![[r with combining macron]](https://www.rsc.org/images/entities/b_char_0072_0304.gif) (t) of the peak of c(r,t) provides an estimate for the rigid displacement occurred between the two images, taken at times t and t + δt, respectively. By summing up all contributions from consecutive image pairs, we reconstruct the full displacement profile
(t) of the peak of c(r,t) provides an estimate for the rigid displacement occurred between the two images, taken at times t and t + δt, respectively. By summing up all contributions from consecutive image pairs, we reconstruct the full displacement profile 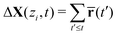 at the considered vertical position, as schematically shown in Fig. 2(a). Fitting of this profile to a sinusoidal function enables extracting the corresponding amplitude A(zi) (see Fig. 2(b)). We then estimate the local shear strain by numerically evaluating the partial derivative of the displacement field along the vertical direction γ(z) = ∂A0(z)/∂z. During an oscillatory shear experiment, we perform repeated scans at different times to monitor a possible time evolution of the deformation profile (further details in the ESI†).
at the considered vertical position, as schematically shown in Fig. 2(a). Fitting of this profile to a sinusoidal function enables extracting the corresponding amplitude A(zi) (see Fig. 2(b)). We then estimate the local shear strain by numerically evaluating the partial derivative of the displacement field along the vertical direction γ(z) = ∂A0(z)/∂z. During an oscillatory shear experiment, we perform repeated scans at different times to monitor a possible time evolution of the deformation profile (further details in the ESI†).
2.4 Microscopic non-affine displacements
The emergence of both reversible and irreversible microscopic non-affine displacements has been reported in simulations and experiments on sheared soft solids, and it has been related to the transition from linear to non-linear mechanical response, as well as to their yielding or flow behavior.17,31,48,49 In such cases, even if the macroscopic displacement field ΔX remains homogeneous (see eqn (2)), the actual displacement field:| Δx(x,y,z,t) = ΔX(z,t) + ΔxN.A.(x,y,z,t). | (7) |
| D(q,Δt) = 〈|Î(q,t + Δt) − Î(q,t)|2〉, | (8) |
| D(q,Δt) = a(q)[1 − f(q,Δt)] + b(q). | (9) |
Once a(q) and b(q) are known, eqn (9) can be inverted to obtain the ISF. The sample dynamics can be then extracted, for example, by assuming a specific model for the statistics of the particle displacements and fitting it to the ISF. For a dispersion of identical, non-interacting Brownian particles in a Newtonian fluid, the ISF is azimuthally symmetric and is given by f(q,Δt) = e−D0q2Δt, where D0 is the diffusion coefficient of the particles. In this case, D0 can be estimated as a coefficient of the q-dependent relaxation rate Γ(q) = D0q2, obtained by fitting an exponential function e−Γ(q)Δt to the ISF for different wavevectors (see Fig. 3(e) and (f)). More generally, at least in the case of identical, non-interacting particles, the IFS can be expressed in terms of the Fourier transform of the probability distribution function of particle displacements P(r,Δt), i.e. the self part of the van Hove function52
 | (10) |
 | (11) |
Characterization of the oscillation frequency. In our setup, the shear-cell and the camera are controlled by two different computers. The first step is to characterize the frequency of the shear-cell in terms of the clock of the camera's computer. We observed that the actual frequency of oscillation is systematically different from the nominal one in an amplitude-dependent fashion, so that the actual frequency f turns out to be a function of the two input parameters f(f0,A0). This function for f0 = 1 Hz, A0 ∈ (10 μm, 1 mm) is reported in ESI† (Fig. S2). The relative difference between the nominal and actual oscillation frequency (f − f0)/f0 is typically or the order of 0.1%. This difference turns out to be significant, especially for long experiments lasting some hundreds of oscillations. The experiment-to-experiment variability is estimated with the root mean square deviation measured for fixed input parameters (f0,A0),
![[small delta, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0c5.gif) f ∼ 1 × 10−5 Hz (details of the frequency characterization are given in ESI†).
f ∼ 1 × 10−5 Hz (details of the frequency characterization are given in ESI†).
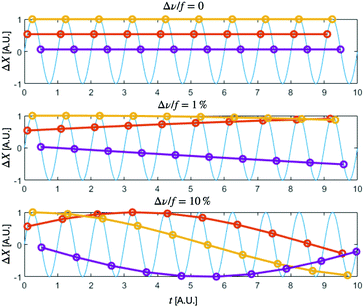
Frequency matching. To increase the statistics while keeping the duration of the experiments fixed, it is convenient to acquire more than one image per period. Thus the acquisition frequency ν has to meet the condition ν = mφf. The frequency ν is set indirectly by setting the delay time between two consecutive images Δt0, that can be determined with a precision of 0.01 ms. This introduces a rounding error δνround/f ∼ 10−5 of the same order of magnitude as the intrinsic shear frequency variability (see ESI† for details). The parameter mφ has been chosen in order to minimize the rounding error. Since different shear amplitudes lead to a different actual frequency, the number of images per period may vary between experiments at different amplitude, taking values in the interval mφ ∈ [4,8].
Residual drift and registration. The residual frequency mismatch results in a phase-dependent apparent drift (Fig. 4) that is quite evident in long acquisitions. By means of the same image cross-correlation algorithm used for the determination of the displacement field (see Section 2.3.1), we characterize the residual drift, and we remove its effect with a custom sub-pixel registration algorithm implemented in the Fourier space and described in detail in ESI.† In the case of fluid samples, actual drifts, corresponding to macroscopic flows, could also occur as a consequence of the loose lateral confinement. With the aforementioned registration algorithm, we can effectively remove these global contributions as well.
| In(x|φm) = I(x,(n + φm/2π)T). | (12) |
| Ps(Δx,Δt) = 〈δ[Δx − (x(i)(t + Δt) − x(i)(t))]〉, |
| Pv(Δy,Δt) = 〈δ[Δy − (y(i)(t + Δt) − y(i)(t))]〉. |
| MSDs(Δt) = 〈|x(i)(t + Δt) − x(i)(t)|2〉, |
| MSDv(Δt) = 〈|y(i)(t + Δt) − y(i)(t)|2〉. |
3 Results
3.1 Measurement of the deformation profiles
For each of the four samples, we perform a detailed characterization of the deformation profile which is produced when an oscillatory shear deformation of different amplitude is imposed. | ||
| Fig. 5 Direct measurement of the deformation field. (a) Displacement profile A(z) in the Carbopol sample along the velocity gradient (z) direction for different applied strain amplitudes γ0 ∈ [10,100]% (blue corresponds to 10% and yellow to 100%). Symbols of different colors represent experimental data obtained at a different imposed shear amplitude, while lines are best fitting curves with the model of eqn (4). For each amplitude, two independent, steady-state measurements are performed. In (b) the same profiles are rescaled with the amplitude A0 of the imposed displacement. (c) Deformation-loss-factor for different samples as a function of the imposed shear strain γ0. Symbols correspond to Carbopol data. The color code is the same of panels (a and b). | ||
3.2 Echo-DDM
Once a detailed characterization of the sample deformation field is available, we proceed to quantify the shear-induced irreversible dynamics with the echo-DDM approach introduced in Section 2.4.2. As pointed out in Section 2.4.3, a key requirement for the accurate determination of the non-affine, irreversible tracer displacements in the sample is the absence of spurious contributions (such as drifts or external vibrations) that could mask the genuine signal. Small imperfections or asymmetries in the setup may lead to a stress unbalance which, in the absence of an effective lateral confinement, can induce a net, albeit typically very small, sample flow. The relevance of this effect is found to crucially depend on the rheological properties of the material and it is particularly severe for low or no yield stress samples (see ESI† for more details). As shear-induced flows are often not perfectly homogeneous, they cannot be completely removed with the registration procedure described in Section 2.4.3. As a matter of fact, for both the silicon oil and the WLM samples, the residual effect of shear-induced flows are found be large enough to dominate the microscopic dynamics (see ESI†), suggesting that our shear geometry is not optimal to measure irreversible tracer displacements in fluid-like samples. We stress that the effect under discussion has no impact on the results for the deformation profiles reported in Section 3.1, as the displacement per period associated with shear-induced flows is typically at least two orders of magnitude smaller than the amplitude of the affine displacement (see Fig. S5, ESI†).We thus focus on the two samples that display a solid-like behavior at rest: Sylgard and Carbopol. For these samples, all the echo acquisitions are performed at the center of the cell: z = h/2. This allows to neglect boundary effects (including the small wall slip) since the distance between the focal plane and the sample edges is way larger than the depth-of-focus h/2 ≫ Lf. In principle, it would be also possible to perform measurements in the vicinity of the moving wall to study in more detail the plastic activity triggered by the interaction of the sample with the boundaries and, more generally, the role of surface boundary conditions for the flow of soft materials.57
As expected, the dynamics, along both the shear and the vorticity direction, is extremely slow and only the very first part of the decay of the ISFs can be observed. Nevertheless, when the ISFs are plotted as function of the rescaled delay time qΔt, a nice collapse of all the curves is observed (insets of Fig. 6), suggesting the presence of a ballistic-like relaxation mechanism.20 Assuming an exponential-like decay f(q,Δt) ≃ e−vqΔt, we can get a rough, order-of-magnitude estimate of the characteristic associated velocity along the shear direction vs ∼ 3 × 10−4 μm s−1.
We attribute this ultra-slow dynamics to the presence of an apparent relative motion of the different planes contributing to the image, which is due to the combination of imperfect synchronization and axial velocity gradient (see ESI† for details). Consistently with this interpretation, we found that vb compares fairly well with the characteristic velocity spread 2πδνγ0Lf ∼ 5 × 10−4 expected in the presence of a synchronization error δν ∼ 10−5 Hz (see Section 2.4.3) and a finite depth-of-focus Lf ∼ 10 μm. Moreover, we observe that the characteristic velocity related with the ballistic decay of the ISF along the vorticity direction is markedly slower (by about a factor of three, see inset of Fig. 6(b)) compared to vs. This is consistent with the presence in the echo images of an apparent ballistic motion mainly directed along the shear direction and marginally contributing to the dynamics in the perpendicular direction due to the finite angular aperture of the bow-tie regions used to calculate fv(q,Δt) (see Section 2.4.1).
These results show that the residual effects of imperfect synchronization of the echo dynamics are rather small, corresponding to characteristic displacements of less than 1 nm per cycle. As it will be explicitly demonstrated in the next subsection, as soon as a genuine contribution to the dynamics, due to structural rearrangements, is present, the ballistic term discussed in this subsection can be safely neglected.
Below the crossover point. When the imposed amplitude is small (γ0 = 20%), visual inspection of the echo image sequences reveals that most of the tracers do not move appreciably, while a few of them undergo rare, intermittent displacements (see ESI† Movie M1). The occurrence of these isolated rearrangement events can be highlighted by considering instantaneous (Fig. 7b) or integrated echo activity maps (Fig. 7c). Instantaneous echo activity maps are obtained as the square modulus of the difference between two consecutive images within an echo sequence |In(x) − In+1(x)|2, while the integrated map corresponds to the time average of all the instantaneous maps in the sequence, and is a proxy of the cumulative rearrangements occurred in the sample during the whole experiment.
To be more quantitative, we apply echo-DDM by considering separately the dynamics along the shear and the vorticity direction. As it can be seen from Fig. 8(a) and (b), for this amplitude we cannot capture the full relaxation of the ISFs within our observation window. Nevertheless, as shown in the inset of panels (a,b), all the ISFs obtained for q ∈ [0.15–2.2] μm−1 nicely collapse onto a single master curve when plotted as a function of the rescaled time delay q2Δt. This indicates that even below yielding the system undergoes an (extremely slow) diffusive-like relaxation, which results from irreversible rearrangements. This is in agreement with the seminal observations made with DWS in ref. 10. Here, we have the advantage that we can characterize this irreversible dynamics as a function of the wave-vector q on a well-defined plane in the sample, while being able to simultaneously measure the local strain. In order to measure the q-dependent relaxation rates, we thus fitted the phenomenological model f(q,Δt) = [1 + ΔtΓ(q)]−1, to the experimental ISFs. According to eqn (11), this model provides the Fickean scaling 〈Δx2(Δt)〉 = 2D0Δt for the 1D MSD when the DDM relaxation rates exhibit a quadratic dependence Γ(q) = D0q2 on the wavevector. This is exactly the scaling that we observe in both directions, with a moderate deviation only for the smallest values of q (Fig. 8(c)). By fitting the relaxation rates we obtain the estimates Ds = (2.2 ± 0.2) × 10−4 μm2 s−1 and Dv = (2.6 ± 0.2) × 10−4 μm2 s−1 for the diffusion coefficient associated with the shear-induced effective dynamics of the tracers along the shear and the vorticity direction, respectively. Within the experimental error, the shear-induced dynamics is isotropic Ds ≃ Dv with values for the diffusion coefficients about one order of magnitude larger than the one associated with the thermal motion of the same tracers in Carbopol under stationary conditions (see ESI† for details). Beyond being slower, the tracer dynamics in the sample at rest is also non-intermittent, which contrasts with the rare, intermittent rearrangements that can be spotted in the sample sheared below the yield strain. Interestingly, this small number of intermittently rearranging particles coexist with a larger number of slowly, yet persistently rearranging ones, with the result that the overall tracer dynamics remains diffusive. In these conditions, the determination of the diffusion coefficient is sensitive to the choice of the field of view, and it would be interesting to study the spatial correlation between rearrangements. A detailed study of these effects goes beyond the scope of the present study.
The results obtained with DDM on the echo image sequences are confirmed by PT analysis of the same sequences. The estimated PDF of the tracer displacements along the shear and the vorticity direction, is shown in Fig. 9(a) and (b), respectively. In agreement with DDM analysis, we do not find any statistically significant difference between the shear and the vorticity direction, confirming that the dynamics is substantially isotropic. Interestingly, for all investigated time delays, the PDFs is not Gaussian, as one would expect for ordinary diffusion, but displays exponential-like tails. Nevertheless, the MSDs in the shear and vorticity directions, reported in panel (c), display a clean linear dependence on the delay time, MSDs(Δt) ≃ 2DPT,vΔt, MSDv(Δt) ≃ 2DPT,vΔt, indicating Fickean diffusion. The value of the associated diffusion coefficient is found to be DPT,s = (1.14 ± 0.08) × 10−4 μm2 s−1 and DPT,v = (1.24 ± 0.1) × 10−4 μm2 s−1 respectively. The discrepancy (about a factor of 2) between the estimates for the diffusion coefficient obtained from DDM and PT can be probably attributed to differences in the populations whose dynamics is captured by the two techniques (DDM sees all the particles and PT only a user-dependent selection).
Above the crossover point. When the sample is subjected to a large amplitude shear deformation γ0 = 80%, exceeding the crossover threshold γC, a dramatic change in the echo dynamics is observed. The amplitude of tracer displacements increases by orders of magnitude and the shear-induced activity shows a much larger degree of spatial homogeneity and temporal uniformity (see ESI† Movie M2). This can be also appreciated by inspecting the echo activity maps reported in Fig. 7(e) and (f), outlining the presence of plastic, irreversible rearrangements distributed across the whole field of view. The speed-up of the dynamics is well captured by echo-DDM analysis. In contrast with the small deformation case, the obtained ISFs display an almost complete temporal relaxation for all the investigated q-values, in both the shear and the vorticity direction (see Fig. 8(d) and (e)). By plotting the ISFs as a function of the rescaled time delay q2Δt, an excellent collapse of the ISFs on a single master curve is observed, highlighting once again a diffusive-like dynamics (inset of panels (d and e)). As it can be appreciated from Fig. 8(d) and (e), over the whole considered q-range, the decay of ISFs is very well captured by the same one-parameter fitting model f(q,Δt) = [1 + ΔtΓ(q)]−1 used for the small deformation case. The obtained q-dependent relaxation rates show a quadratic scaling with q along both directions (Fig. 8f). Remarkably, in this case the dynamics is no longer isotropic, displaying a faster relaxation along the shear direction. Indeed, fitting the experimental relaxation rates to Γv(q) = Dvq2 and Γs(q) = Dsq2 provides Dv = (1.9 ± 0.3) × 10−1 μm2 s−1 and Ds = (2.9 ± 0.3) × 10−1 μm2 s−1, respectively. Comparing the diffusion coefficients for γ0 = 20% and γ0 = 80%, we observe a ∼1000-fold speed-up of the dynamics for large amplitude deformation, which is a strong signature of shear-induced diffusion. PT-based analysis of the same data fully corroborates the results obtained with echo-DDM, and in this case the agreement with DDM is even better than for small deformation. In particular, they exhibit a linear dependence on Δt. From a linear fit MSD = 2DΔt of the MSDs along both the investigated directions (Fig. 9f) we obtain DPT,v = (1.7 ± 0.2) × 10−1 μm2 s−1 and DPT,s = (2.8 ± 0.2) × 10−1 μm2 s−1, respectively, in fairly good agreement with the results obtained from echo-DDM.
4 Conclusion
In this paper, we combined oscillatory deformation in a simple shear geometry with bright-field optical microscopy. For four different samples, we characterized the deformation field, finding stationary and homogeneous deformation fields. We observed the presence of partial slip, and we measured the actual local deformation. In echo measurements, we observed drifts of different origin: “apparent” drifts due to an imperfect synchronization between the shear and the acquisition frequencies, and “real” drifts due to unavoidable instrumental imperfections and the lack of horizontal confinement. The effect of drift on the microscopic dynamics is corrected with a custom sub-pixel registration algorithm. Eventually, the DDM algorithm is applied to echo movies. In the case of an “ideal” elastic solid, the applied procedure shows, as expected, the absence of shear-induced-dynamics. In the fluid-like samples, the dynamics is dominated by flows generated by small asymmetry in the setup and by the lack of lateral confinement of the samples. Although our registration algorithm can significantly reduce the impact of these drifts, their residual effect is still large enough to prevent the observation of any additional shear-induced dynamics.With Carbopol, we perform experiments by using two different strain amplitudes, below and above the yield strain. The smaller amplitude causes a spatially heterogeneous, temporally intermittent activity of the tracer particles, which results in extremely slow, substantially isotropic shear-induced diffusion. Above the yield strain, the shear-induced diffusive relaxation becomes anisotropic and very fast, with an observed speed-up of about 103 compared to the previous case. Our results with Carbopol represent the first clear observation of a truly diffusive dispersion relation Γ(q) ∼ q2 in fluids that are yielding during oscillatory experiments. Of note, this behavior contrasts with recent results obtained with X-ray photon correlation spectroscopy13,59 in which a faster-than-diffusive relaxation (closer to the behavior observed in colloidal polycrystals60) was found for a nanoemulsion and a colloidal gel; at the same time, our results agree with the original interpretation provided for dense emulsions10 and colloidal glasses,11,17 in both cases lacking an experimental determination of the dispersion relation.
Beyond providing reliable and quantitative information about the shear-induced microscopic rearrangements, our approach also enables characterizing the deformation profiles across the sample and, in turn, spotting slippage, shear bands or other unwanted effects. This is made possible by the partial coherence of the illuminating light, which not only helps in identifying the presence of the above-mentioned phenomena, but also allows imaging a selected slice of the sample. In this work, we imaged its central part, where the deformation is homogeneous, by excluding the sample boundaries where deviations from homogeneity (mainly due to wall slip) possibly occur. In case of shear-banding, the z-selectivity of the microscope can be exploited to select zones where the macroscopic deformation field is approximately homogeneous, an important advantage over traditional single and multiple light scattering approaches. For this reason, our technique appears promising for the study of the plastic dynamics in the presence of shear banding, the interplay between non-affine displacements and shear banding representing a very interesting, yet not much explored topic. Another advantage of our approach is that it makes it possible to combine real-space pre-processing (drift correction) and Fourier-space analysis (Echo-DDM), which leads to a considerable simplification of the data interpretation.
Extensions of our approach to other imaging modes (e.g. confocal fluorescence microscopy) are easily within reach, as well as combination with a commercial rheometer provided that the sample remains optically accessible. Finally, the usual advantages (and disadvantages) of DDM over PT hold, including the capability of DDM to probe the dynamics of sub-resolution particles.2
Conflicts of interest
There are no conflicts to declare.Acknowledgements
We acknowledge useful discussions with Manuel Escobedo, Stefan Egelhaaf, and Veronique Trappe. The work benefited from support from the European Soft Matter Infrastructure (EUSMI).Notes and references
- T. A. Waigh, Rep. Prog. Phys., 2016, 79, 074601 CrossRef PubMed.
- P. Edera, D. Bergamini, V. Trappe, F. Giavazzi and R. Cerbino, Phys. Rev. Mater., 2017, 1, 073804 CrossRef.
- R. M. Robertson-Anderson, Optical tweezers microrheology: from the basics to advanced techniques and applications, 2018 Search PubMed.
- J. Lin and M. T. Valentine, Appl. Phys. Lett., 2012, 100, 201902 CrossRef.
- V. Vitali, G. Nava, A. Corno, M. Pezzotti, F. Bragheri, P. Paiè, R. Osellame, M. A. Ortenzi, I. Cristiani and P. Minzioni, et al. , Soft Matter, 2021, 17, 3105–3112 RSC.
- S. Aime and L. Cipelletti, Soft Matter, 2019, 15, 200–212 RSC.
- A. P. Eberle and L. Porcar, Curr. Opin. Colloid Interface Sci., 2012, 17, 33–43 CrossRef CAS.
- G. Zanchetta and R. Cerbino, J. Phys.: Condens. Matter, 2010, 22, 323102 CrossRef PubMed.
- B. Saint-Michel, H. Bodiguel, S. Meeker and S. Manneville, Phys. Rev. Appl., 2017, 8, 014023 CrossRef.
- P. Hébraud, F. Lequeux, J. Munch and D. Pine, Phys. Rev. Lett., 1997, 78, 4657 CrossRef.
- G. Petekidis, D. Vlassopoulos and P. N. Pusey, Faraday Discuss., 2003, 123, 287–302 RSC.
- E. D. Knowlton, D. J. Pine and L. Cipelletti, Soft Matter, 2014, 10, 6931–6940 RSC.
- M. C. Rogers, K. Chen, L. Andrzejewski, S. Narayanan, S. Ramakrishnan, R. L. Leheny and J. L. Harden, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2014, 90, 062310 CrossRef PubMed.
- S. Aime, L. Ramos and L. Cipelletti, Proc. Natl. Acad. Sci. U. S. A., 2018, 115, 3587–3592 CrossRef CAS PubMed.
- A. Z. Nelson and R. H. Ewoldt, Soft Matter, 2017, 33, 7578 RSC.
- D. T. Chen, Q. Wen, P. A. Janmey, J. C. Crocker and A. G. Yodh, Annu. Rev. Condens. Matter Phys., 2010, 1, 301–322 CrossRef CAS.
- G. Petekidis, A. Moussaid and P. Pusey, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2002, 66, 051402 CrossRef CAS PubMed.
- F. Scheffold and R. Cerbino, Curr. Opin. Colloid Interface Sci., 2007, 12, 50–57 CrossRef CAS.
- S. Aime and L. Cipelletti, Soft Matter, 2019, 15, 213–226 RSC.
- F. Giavazzi and R. Cerbino, J. Opt., 2014, 16, 083001 CrossRef.
- R. Cerbino and V. Trappe, Phys. Rev. Lett., 2008, 100, 188102 CrossRef PubMed.
- F. Giavazzi, D. Brogioli, V. Trappe, T. Bellini and R. Cerbino, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2009, 80, 031403 CrossRef PubMed.
- R. Cerbino and P. Cicuta, J. Chem. Phys., 2017, 147, 110901 CrossRef PubMed.
- R. Cerbino, F. Giavazzi and M. E. Helgeson, J. Polym. Sci., 2021 DOI:10.1002/pol.20210217.
- R. Cerbino, S. Villa, A. Palamidessi, E. Frittoli, G. Scita and F. Giavazzi, Soft Matter, 2021, 17, 3550–3559 RSC.
- A. A. Goshtasby, 2-D and 3-D image registration: for medical, remote sensing, and industrial applications, John Wiley & Sons, 2005 Search PubMed.
- T. Divoux, M. A. Fardin, S. Manneville and S. Lerouge, Annu. Rev. Fluid Mech., 2016, 48, 81–103 CrossRef.
- K. Miyazaki, D. R. Reichman and R. Yamamoto, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2004, 70, 011501 CrossRef PubMed.
- R. Evans, M. Cates and P. Sollich, Eur. Phys. J. B, 1999, 10, 705–718 CrossRef CAS.
- F. Khabaz and R. T. Bonnecaze, Phys. Fluids, 2021, 33, 013315 CrossRef CAS.
- L. Mohan, C. Pellet, M. Cloitre and R. Bonnecaze, J. Rheol., 2013, 57, 1023–1046 CrossRef CAS.
- S. Buzzaccaro, E. Secchi and R. Piazza, Phys. Rev. Lett., 2013, 111, 048101 CrossRef PubMed.
- F. Giavazzi, A. Fornasieri, A. Vailati and R. Cerbino, Eur. Phys. J. E: Soft Matter Biol. Phys., 2016, 39, 1–11 CrossRef CAS PubMed.
- F. Giavazzi, S. Crotti, A. Speciale, F. Serra, G. Zanchetta, V. Trappe, M. Buscaglia, T. Bellini and R. Cerbino, Soft Matter, 2014, 10, 3938–3949 RSC.
- S. Aime, L. Ramos, J.-M. Fromental, G. Prevot, R. Jelinek and L. Cipelletti, Rev. Sci. Instrum., 2016, 87, 123907 CrossRef CAS PubMed.
- http://www.farnell.com/datasheets/3154500.pdf .
- C. A. Dreiss, Soft Matter, 2007, 3, 956–970 RSC.
- V. Vitali, G. Nava, G. Zanchetta, F. Bragheri, A. Crespi, R. Osellame, T. Bellini, I. Cristiani and P. Minzioni, Sci. Rep., 2020, 10, 1–11 CrossRef PubMed.
- F. K. Oppong, L. Rubatat, B. J. Frisken, A. E. Bailey and J. R. De Bruyn, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2006, 73, 041405 CrossRef PubMed.
- J.-B. Boitte, C. Vizcano, L. Benyahia, J.-M. Herry, C. Michon and M. Hayert, Rev. Sci. Instrum., 2013, 84, 013709 CrossRef PubMed.
- M. Dinkgreve, M. Fazilati, M. Denn and D. Bonn, J. Rheol., 2018, 62, 773–780 CrossRef CAS.
- V. V. Vasisht and E. Del Gado, Phys. Rev. E, 2020, 102, 012603 CrossRef CAS PubMed.
- H. J. Barlow, J. O. Cochran and S. M. Fielding, Phys. Rev. Lett., 2020, 125, 168003 CrossRef CAS PubMed.
- T. Divoux, D. Tamarii, C. Barentin and S. Manneville, Phys. Rev. Lett., 2010, 104, 208301 CrossRef PubMed.
- G. Ovarlez, S. Rodts, X. Chateau and P. Coussot, Rheol. Acta, 2009, 48, 831–844 CrossRef CAS.
- J. R. Seth, C. Locatelli-Champagne, F. Monti, R. T. Bonnecaze and M. Cloitre, Soft Matter, 2012, 8, 140–148 RSC.
- T. Divoux, V. Lapeyre, V. Ravaine and S. Manneville, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2015, 92, 060301 CrossRef PubMed.
- C. Goldenberg, A. Tanguy and J.-L. Barrat, EPL, 2007, 80, 16003 CrossRef.
- J. Colombo and E. Del Gado, J. Rheol., 2014, 58, 1089–1116 CrossRef CAS.
- F. Giavazzi, P. Edera, P. J. Lu and R. Cerbino, Eur. Phys. J. E: Soft Matter Biol. Phys., 2017, 40, 1–9 CrossRef CAS PubMed.
- R. Cerbino, D. Piotti, M. Buscaglia and F. Giavazzi, J. Phys.: Condens. Matter, 2017, 30, 025901 CrossRef PubMed.
- J.-P. Hansen and I. R. McDonald, Theory of simple liquids: with applications to soft matter, Academic Press, 2013 Search PubMed.
- R. Höhler, S. Cohen-Addad and H. Hoballah, Phys. Rev. Lett., 1997, 79, 1154–1157 CrossRef.
- T. Gibaud, D. Frelat and S. Manneville, Soft Matter, 2010, 6, 3482–3488 RSC.
- V. Pelletier, N. Gal, P. Fournier and M. L. Kilfoil, Phys. Rev. Lett., 2009, 102, 188303 CrossRef PubMed.
- Y. M. Joshi and G. Petekidis, Rheol. Acta, 2018, 57, 521–549 CrossRef CAS.
- V. Mansard, L. Bocquet and A. Colin, Soft Matter, 2014, 10, 6984–6989 RSC.
- M. Dinkgreve, J. Paredes, M. M. Denn and D. Bonn, J. Non-Newtonian Fluid Mech., 2016, 238, 233–241 CrossRef CAS.
- M. C. Rogers, K. Chen, M. J. Pagenkopp, T. G. Mason, S. Narayanan, J. L. Harden and R. L. Leheny, Phys. Rev. Mater., 2018, 2, 095601 CrossRef CAS.
- E. Tamborini, L. Cipelletti and L. Ramos, Phys. Rev. Lett., 2014, 113, 078301 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/d1sm01068a |
| This journal is © The Royal Society of Chemistry 2021 |