Controlled viscoelastic particle encapsulation in microfluidic devices

Abstract

The encapsulation of particles in droplets using microfluidic devices finds application across several fields ranging from biomedical engineering to materials science. The encapsulation process, however, is often affected by poor single encapsulation efficiency, quantified by the Poisson statistics, with droplets containing more than one particle or with several empty droplets. We here demonstrate that viscoelastic aqueous solutions of xanthan gum enable controlled single particle encapsulation in microfluidic devices with a single encapsulation efficiency up to 2-fold larger than the one predicted by the Poisson statistics. We achieved such a result by identifying viscoelastic xanthan gum aqueous solutions that could drive particle ordering before approaching the encapsulation area and simultaneously form uniform droplets. This is the first experimental evidence of viscoelastic encapsulation in microfluidic devices, the existing literature on the subject being focused on Newtonian suspending liquids. We first studied the process of viscoelastic droplet formation, and found that the droplet length normalised by the channel diameter scaled as predicted for Newtonian solutions. At variance with Newtonian solutions, we observed that the droplet formation mechanism became unstable above critical values of the Weissenberg number, which quantifies the elasticity of the xanthan gum solutions carrying the particles. In terms of controlled encapsulation, we discovered that the single encapsulation efficiency was larger than the Poisson values in a specific range of xanthan gum mass concentrations. Finally, we introduced an empirical formula that can help the design of controlled viscoelastic encapsulation systems.

---

1 Introduction

The encapsulation of objects such as particles and cells in nanoliter droplets confined within microfluidic devices is a flourishing field of research¹ that has led to significant advancements in single-cell analysis,² multiple emulsion synthesis,^3–6 and production of biomaterials.⁷ In a standard microfluidic particle encapsulation configuration, there are two relevant liquid streams: the first one, called the dispersed phase, contains the particles to be encapsulated; the other one, called the continuous phase, is employed to form droplets at a constant frequency f_drop when the two liquid streams meet at a junction.^8,9 One of the main limitations affecting several encapsulation applications is the encapsulation of multiple particles in the same droplet or, conversely, the case of empty droplets.^10,11 To reduce the probability of multiple particle encapsulation in a single droplet, one approach is to dilute significantly the dispersed phase containing the suspended particles. However, this approach has negative impact on the throughput in the case of single-cell analysis, and it also promotes a substantial increase in the number of empty droplets. Under such uncontrolled conditions, the efficiency of single particle encapsulation is governed by the Poisson statistics.^10,11

The problem of uncontrolled encapsulation was initially addressed by Edd et al.¹⁰, who employed the phenomenon of inertial ordering, where inertial forces¹² were used to equally space, i.e., order, particles at specific equilibrium positions along the channel cross-section, to form a train^13,14 of particles approaching the encapsulation area of the microfluidic device at a constant frequency f_p. By synchronising the frequency f_p with the constant frequency of droplet formation f_drop, they achieved an encapsulation efficiency significantly larger than the one predicted by the Poisson statistics, introducing the concept of controlled encapsulation. Hereafter, controlled encapsulation refers to an encapsulation process with efficiency significantly larger than the one predicted by the Poisson statistics. The pioneering work by Edd et al.¹⁰ was followed up by Kemna et al.,¹¹ who designed a spiral microfluidic channel to order particles on a single streamline near the channel wall: this stream of particles was then encapsulated in droplets using a flow-focusing geometry. Lagus et al.¹⁵ employed inertial microfluidics to control the simultaneous encapsulation of two particles in the same droplet, a process that is extremely important in single-cell analysis applications, such as the Drop-seq technology, where a barcoded bead is encapsulated together with a cell in order to extract the cell m-RNA.¹⁶ More recently, the same principle of controlled encapsulation has been applied to significantly improve the efficiency of the Drop-seq process.^17,18

The controlled encapsulation technique has, so far, been demonstrated for Newtonian fluids only, while no experimental (or numerical) evidence of this phenomenon in non-Newtonian viscoelastic liquids has been reported. The reason for that is related to the challenge of identifying a non-Newtonian liquid which can simultaneously enable particle ordering and droplet formation. Droplet formation in viscoelastic liquids has often been limited by the problem of long filament thread that prevents the droplet breakup,^19–21 while experimental evidence of viscoelastic ordering has only been introduced recently.²² In their work, Del Giudice et al.²² demonstrated that a viscoelastic shear-thinning solution of hyaluronic acid drove the formation of an equally spaced particle train on the centreline of a straight microfluidic channel. However, the zero-shear viscosity of the solution was very high, thus somehow making the idea of generating droplets in a simple microfluidic flow challenging. Very recently, we discovered that viscoelastic aqueous solutions of xanthan gum with zero-shear viscosity up to five times smaller than the one used by Del Giudice et al.²² could be used to form a particle train on the centreline of a commercial hydrophilic serpentine microchannel.²³ This discovery opened the way to investigate the possibility of achieving a controlled encapsulation in viscoelastic solutions, as the formation of xanthan gum droplets in microfluidic geometries has recently been demonstrated.^24–26 Such an achievement is expected to open new research directions in the field of single-cell analysis where non-Newtonian liquids have successfully been employed for cell separation and manipulation,²⁷ as well as in materials science where viscoelastic fluids may be used for the synthesis of novel materials.^1,28

In this work, we reported the first experimental evidence of controlled viscoelastic encapsulation in microfluidic devices. We used aqueous xanthan gum (XG) solutions as the dispersed phase and mineral oil as the continuous phase, both flowing in a commercial T-junction microfluidic device with hydrophobic coating. We first characterised the phenomenon of droplet formation for several aqueous XG solutions, and then proceeded to demonstrate the controlled encapsulation phenomenon. The aqueous XG solutions drove particle ordering at the centreline of the microfluidic device; when reaching the encapsulation area, particles were subsequently encapsulated. Our methodology resulted in a significant increase of the encapsulation efficiency compared to the value predicted by the Poisson statistics.

2 Experimental

2.1 XG preparation and characterisation

Aqueous solutions of xanthan gum (XG) in the range of 0.05 to 0.6 wt% were prepared by dissolving Xanthomonas campestris (Sigma Aldrich, UK) in deionised water; the resulting solutions were stirred using a magnetic stirrer for 12 hours to allow full dissolution of the polymer. Rheological properties of XG solutions were measured using a stress-controlled rheometer (AR-G2, TA Instruments) with a double-gap geometry at a constant temperature of T = 22 °C. All of the XG solutions exhibited strong shear-thinning behaviour across the range of applied shear rate values 10⁻¹ < [small gamma, Greek, dot above] < 10³ s⁻¹ and for all the concentrations investigated (Fig. 1a). At shear rate values [small gamma, Greek, dot above] < 10⁻¹ s⁻¹, XG solutions began to display a zero-shear plateau. As the concentration of XG was increased, the zero-shear viscosity plateau increased and the transition to power-law region started at lower shear rate values. Small Amplitude Oscillatory Shear (SAOS) measurements were performed to characterise the viscoelastic properties of the XG solutions (Fig. 1b). Despite observing a distinct and pronounced viscoelastic behaviour for all the XG solutions investigated (Fig. 1b), we were unable to observe the terminal region at low frequencies where the storage and the loss modulus are proportional to ω² and ω, respectively.²⁹ Hence, we were not able to determine the longest relaxation time using standard SAOS measurements. The values of the longest relaxation time λ for all the XG solutions were estimated using the same methodology employed by Boris et al.³⁰ on polystyrene sulphonate solutions and by Wyatt and Liberatore³¹ on aqueous xanthan gum solutions. Specifically, we evaluated λ from the viscosity curve of Fig. 1a as λ = 1/[small gamma, Greek, dot above]_c, where [small gamma, Greek, dot above]_c is the critical shear rate value marking the onset of the shear-thinning. The exact value of [small gamma, Greek, dot above]_c was determined as the intersection between the power-law fit applied in the shear-thinning regime and the straight line indicating the zero-shear plateau (Fig. 1a). Longest relaxation time values of 7.7, 10.36, 14, 16 and 22.5 s were obtained for the XG concentrations of 0.05, 0.1, 0.2, 0.3 and 0.6 wt%, respectively. Our estimated values of relaxation time showed a good agreement with values reported in the literature for XG solutions.³¹

Fig. 1 Rheological characterisation of xanthan gum (XG) solutions at mass concentrations of 0.05, 0.1, 0.2, 0.3 and 0.6 wt%. (a) Shear viscosity of aqueous solutions of xanthan gum as function of the shear rate [small gamma, Greek, dot above]: All the solutions display a clear shear-thinning behaviour above a critical value of the shear rate [small gamma, Greek, dot above]_c evaluated as the intersection between the power-law fit applied in the shear-thinning regime and the straight line indicating the zero-shear-rate plateau. The inverse of [small gamma, Greek, dot above] was employed to estimate the longest relaxation time of each solution, i.e., λ = 1/[small gamma, Greek, dot above]_c. (b) Storage and loss modulus obtained via small amplitude oscillatory shear tests with an imposed deformation of 5%. The two slopes represent the scaling for the storage (∝ω²) and loss modulus (∝ω) in the terminal region.²⁹ All the solutions display significant elastic properties.

Mineral oil (Sigma Aldrich, UK) was used as the continuous phase in both droplet generation and encapsulation experiments. Span 80 (Sigma Aldrich, UK), a non-ionic surfactant, at 1 wt% concentration was added to the oil phase to stabilize the interface between XG and mineral oil. The viscosity of the mineral oil was found to be constant (Newtonian liquid) and equal to 29 mPa s. The interfacial tension values between all the XG solutions and the mineral oil were measured using a force tensiometer (Sigma 702, Biolin Scientific) equipped with a du Noüy ring. In this methodology, the du Noüy ring is first submerged in the XG solution and then the mineral oil is poured on the top. The ring is brought into contact with the interface using a microbalance and the interfacial tension is obtained by measuring the force required to separate the ring from the interface. The measured values of interfacial tension were independent of the XG concentration, being equal to 3.4 ± 0.1 mN m⁻¹ with the addition of Span 80 to the mineral oil (the interfacial tension was 19 ± 0.1 mN m⁻¹ in the absence of Span 80).

Polystyrene particles (Polysciences Inc.) with diameter d = 20 ± 2 μm at a constant bulk concentration of ϕ = 0.3 wt% were added to the XG solutions. PS particles were originally suspended in water at a mass concentration of 2.56 wt%. The required amount to form the suspension at ϕ = 0.3 wt% was added to the XG solutions directly, causing a negligible dilution of the original XG concentration of no more than 10%. The resulting suspension was mixed using a vortex mixer (Fisherbrand ZX3) to fully disperse the polystyrene particles in the XG solutions. The suspension was further put in an ultrasonic bath for 2 minutes to remove potential aggregates prior to performing experiments.

2.2 Experimental setup

A commercial glass T-junction chip with hydrophobic surface coating (Dolomite Microfluidics) having a nearly circular cross-section of diameter D = 100 μm was employed for all the experiments (schematics in Fig. 2a). Videos of both droplet generation and particle encapsulation were captured at a frame rate of 2000–4000 fps using a high speed camera (Photron, fastcam Mini UX50) mounted on an inverted microscope (Zeiss Axiovert 135). For the droplet generation experiments, both continuous (mineral oil) and dispersed phase (XG solutions) liquids were pumped into the microchip using a syringe pump (KD Scientific) in the range of 0.1 < Q < 10 μL min⁻¹. The captured videos were analysed using a home-made code written in Matlab to determine size and frequency of droplet generation. For the particle encapsulation experiments, the continuous phase was pumped in the microfluidic device using a syringe pump (KD Scientific) while the dispersed phase (XG solutions) containing particles was pumped using a pressure pump (Dolomite Microfluidics), in agreement with our recent work.²³ A particle tracking algorithm was employed to measure inter-particle spacing, size, and velocity of the flowing particles before the T-junction encapsulation region. Droplets were detected automatically using a Matlab home-made image analysis code, while the number of particles per each droplet was counted manually.

Fig. 2 Xanthan gum droplet generation in a hydrophobic T-junction. (a) Schematic representation of the T-junction device and of the inlets for the two liquids. (b) Normalised droplet size L/D, where L is the droplet length and D is the channel diameter (see experimental snapshot), as a function of the ratio Q_XG/Q_Oil, where Q_XG is the flow rate of the xanthan gum solutions (dispersed phase) and Q_Oil is the flow rate of the oil (continuous phase). Data are described by the scaling L/D = 1 + 2Q_XG/Q_Oil derived for Newtonian droplets (Fig. S1, ESI†). (c) Frequency of droplet generation f_drop for different concentrations of xanthan gum as a function of the product Q_XGQ_Oil. Data points collapse on the master curve f_drop = A(Q_XGQ_Oil)^B with A = 9.22 and B = 2/3, with the units of both flow rates being μL min⁻¹. (d) Onset of flow instability during droplet generation. Above the critical dispersed phase flow rate 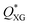a transition to parallel flow is observed and droplet formation becomes unstable. Data collapsed on a single master curve when plotted as critical Weissenberg number Wi* versus capillary number of the continuous phase (oil) Ca. Longest relaxation times λ are estimated from intersection of power-law region and zero-shear viscosity in Fig. 1a. (see the main text for more details).

2.3 Dimensionless parameters

Generally speaking, the properties of two immiscible fluids that determine the droplet size are the interfacial tension γ, the dynamic viscosity of both dispersed and continuous phases μ_d and μ_c, and the flow rate of the two phases³²Q_d and Q_c. Subscript d and c refer to dispersed and continuous phase, respectively. Data were analysed in terms of the normalised parameter Q_d/Q_c, in agreement with the literature.^33,34 We also used the capillary number Ca for the continuous phase, defined as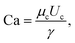where U_c = 4Q_c/(πD²) is the average velocity of continuous phase fluid with D being the channel diameter. The resulting capillary number values spanned the range of Ca ∈ [0.001 − 0.1].

To quantify the viscoelastic effects, we employed the Weissenberg number Wi defined as³⁵

where the characteristic time scale of dispersed phase was estimated by the apparent wall shear rate for a Newtonian fluid [small gamma, Greek, dot above] = 32Q_d/(πD³).

For this range of control parameters, the largest Reynolds number value for the continuous phase was Re = ρ_cU_cD/μ_c = 6.4 × 10⁻², and hence, inertial effects were negligible.

3 Results and discussion

3.1 Generation of uniform viscoelastic droplets

The ultimate goal of this manuscript is to demonstrate the controlled encapsulation of particles using XG solutions. The first step in this direction is to study the droplet formation in the T-junction device using XG solutions as the dispersed phase. We investigated the mechanism of break-up, and the scaling characteristics of XG droplet generation over a wide range of XG concentrations and imposed flow rate ratios. In the T-junction, two immiscible liquids flow into separate inlet channels that intersect at a 90° angle (Fig. 2a). Regardless of the XG concentration, we observed the formation of a XG liquid thread that first elongated along the main channel and then quickly thinned to form a primary droplet connected to a thin filament, which then pinched off to form satellite droplets (Video S1 and S2, ESI†). The formation of satellite droplets in microfluidic channels have been previously reported for polymeric solutions in both T-junctions³⁶ and flow focusing geometries.^19,20,24,37 Carrier et al.³⁸ have also observed satellite droplets for Newtonian liquids in a T-junction microchannel. We carried out experiments using water as the dispersed phase and oil as the continuous phase (Fig. S1, ESI†); however, we did not notice any satellite droplet formation, in agreement with the previous experiments by Li et al.³⁶ We can then conclude that the formation of satellite droplets in our experiments was related to the viscoelasticity of the xanthan gum solutions.

Previous studies on Newtonian droplets^32,33 reported that the normalised droplet length L/D, where L is the droplet length and D is the channel diameter, scales as L/D = 1 +αQ_d/Q_c, where α is a constant dependent upon the geometry employed. Our results on the Newtonian droplets (Fig. S1, ESI†) collapsed on the master curve L/D = 1 + 2Q_w/Q_Oil, where Q_w is the water flow rate and Q_Oil is the oil flow rate, also reported as a solid line in Fig. 2b. We noticed that our data for the non-Newtonian XG droplets also collapsed on the same Newtonian master curve regardless of the XG concentration (Fig. 2b), in agreement with the results by Rostami and Morini,²⁴ thus suggesting that the viscoelasticity of the solution affects the dynamics of droplet formation compared to the Newtonian case (e.g., the presence of a filament), rather than the droplet size. We also found that the XG concentration was not affecting the droplet size, in agreement with recent experiments²⁴ and numerical simulations^26,39 featuring shear-thinning droplet formation.

In the context of controlled particle and cell encapsulation, it is important to derive a clear relation between the frequency of droplet generated f_drop and the flow rate values of both the continuous (Q_oil) and the dispersed (Q_XG) phase. Indeed, the frequency f_drop needs to be then synchronised to the frequency f_p of particles or cells approaching the encapsulation area in order to achieve a controlled encapsulation.^10,11,15 We evaluated the frequency of droplet formation by measuring the time period between the formation of two consecutive droplets and by then averaging over the total number of detected droplets. Interestingly, our data collapsed on a single master curve (Fig. 2c) described by the following expression:

f_drop = A(Q_XGQ_Oil)^B, (3)

where A = 9.22 and B = 2/3 obtained by fitting the data in the flow rate range of 0.3–9 μL min⁻¹, with the units of both flow rates being μL min⁻¹. A qualitative argument to justify the scaling of eqn (3) is reported in the following. As the oil phase flow rate increased (larger Ca) stronger viscous shear and drag was exerted on the XG thread that pinched off the fluid faster, leading to larger frequency values. An increase of Q_XG accelerated the squeezing and the necking of the thread resulting in larger frequency values. Our qualitative observation is also in good agreement with previous works on Newtonian droplets formed in flow-focusing geometries.⁴⁰ Clearly, changes in the values of both Q_XG and Q_Oil will affect the droplet size as well as the frequency, and the droplet size can be derived via L/D = 1 + 2Q_XG/Q_Oil (Fig. 2b).

Although we observed continuous generation of viscoelastic XG drops, there was an upper limit to the dispersed phase flow rate for stable droplet generation at each Ca number (Fig. 2d, Fig. S2 and Video S3, ESI†). For each flow rate of the oil continuous phase Q_Oil, we identified a critical value of the dispersed phase flow rate , above which the flow became unstable (Fig. S2, ESI†). The value of 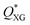for each Q_Oil value was found to decrease with the increase of the XG concentration, meaning that solutions at larger XG concentrations led to unstable flow at lower flow rate values (Fig. S2, ESI†). Notably, the instability data collapsed on a single master curve when plotted as a critical Weissenberg number Wi* versus the capillary number Ca (Fig. 2d), suggesting that the viscoelasticity of the XG solutions was responsible for the observed instability. The droplet formation mechanism for Wi < Wi* was stable over several hours, meaning that no time-dependent instability was observed.

In summary, we demonstrated the continuous formation of XG droplets in a T-junction hydrophobic device. We observed that the normalised droplet length scaled as L/D = 1 + 2Q_XG/Q_oil, similar to the Newtonian droplet case. The frequency of droplet formation could be described as f_drop = A(Q_XGQ_Oil)^B, where A = 9.22 and B = 2/3 obtained by fitting the data in the flow rate range of 0.3–9 μL min⁻¹, with the units of both flow rates being μL min⁻¹. Finally, we observed a clear flow instability during droplet formation at values of the Weissenberg number Wi above the critical value Wi*, suggesting an elasticity-driven instability. These results lay the foundation to study the controlled encapsulation of particles, as described in the following paragraph.

3.2 Controlled encapsulation of particles

After investigating the droplet generation phenomenon, it is now time to see whether XG can trigger a controlled particle encapsulation. In general, the encapsulation of particles is governed by the Poisson statistics,¹¹ where the probability P(k,n) of finding a drop containing n particles, when the process of loading particles into drops is purely random is P(k,n) = kⁿexp(−k)/(n!), here k is the average number of particles per drop.^11,15 For instance, if the average number of particles is k = 1, the probability of encapsulating n = 1 particles per droplet is 37%. A way to increase the encapsulation efficiency above the Poisson limit is to equally space flowing particles before approaching the encapsulation area.^10,11,15 When particles are equally spaced (i.e., ordered), the frequency of particles approaching the encapsulation area f_p is constant and can be synchronised to the frequency of droplet formation f_drop: in this way, a theoretically deterministic encapsulation (100% encapsulation efficiency) can be achieved. We recently demonstrated that an aqueous XG 0.1 wt% solution promoted viscoelastic ordering on the channel centreline in a hydrophilic channel.²³ We then employed the same configuration reported in Fig. 2a to see whether we could overcome the Poisson limit (Fig. S2, ESI†). We observed that particles arrived at the encapsulation region focused on the centreline, but were not ordered, with a few aggregates of particles in the form of doublets and triplets that were subsequently encapsulated. Despite this being the first experimental evidence of particle encapsulation in viscoelastic liquids, the lack of particle ordering was caused by the fact that the inlet channel was only 2 cm long, thus making the encapsulation process entirely governed by the Poisson statistics, without clear advantages over the existing methodologies (Fig. S3, ESI†). This was expected because we previously demonstrated that long channels with L_channel/D ≈ 2500 are required to order particles suspended in XG solutions.²³ We then swapped the inlet for xanthan gum with the inlet of the mineral oil, as depicted in Fig. 3a, in order to increase the channel length available for the particles to self-order before reaching the encapsulation area. We first quantified the normalised inter-particle spacing S* = s/d, where s is the distance between consecutive particles and d is the particle diameter, of particles approaching the encapsulation area for different XG concentrations (Fig. 3 and Fig. S4, ESI†). At the lowest XG concentration of 0.05 wt%, particles did not focus nor self-order at the channel centreline (Fig. S5, ESI†). When increasing the concentration to XG 0.1 wt%, ordering improved (Fig. S4, ESI†); however, we surprisingly observed the presence of large particle aggregates which affected the overall inter-particle distribution (Video S4, ESI†). The number of aggregates reduced when increasing the XG concentration (Fig. 3b and Fig. S4, ESI†), where a clear peak for S* was observed. After achieving centreline particle ordering in XG solutions, we employed the same device configuration of Fig. 3a to produce XG droplets with encapsulated particles. For XG 0.2 wt% and for XG 0.3 wt%, we successfully demonstrated an increase of the single encapsulation efficiency far above the Poisson limit (Fig. 3c, Fig. S4 and Video S5, ESI†), leading to a controlled encapsulation. Specifically, for XG 0.2 wt%, the encapsulation efficiency improved from ≈37% (uncontrolled, Poisson) to ≈50% (controlled), while for XG 0.3 wt%, the encapsulation efficiency improved from ≈37% (uncontrolled, Poisson) to ≈60% (controlled), with a maximum relative increase of almost 40%, comparable with the results on controlled inertial encapsulation.^10,11 Larger values of encapsulation efficiency could be obtained by reducing the fluctuations in the particle concentration experienced in microfluidic devices, which affects the relative distance between consecutive particles.^23,41 The controlled encapsulation principle is based on the fact that f_drop = f_p; however, when the number of particles observed in a frame fluctuates, the resulting frequency f_p is not constant and affects the controlled encapsulation process; this is also discussed in the next section. For XG 0.6 wt%, we observed a dual scenario that prevented controlled encapsulation. At low imposed pressure drops, particles were focused near the channel wall (Video S6, ESI†) and they did not display any type of ordering, in agreement with previous experiments on other shear-thinning liquids.⁴² Better ordering was obtained for XG 0.6 wt% at higher flow rate values manifesting itself by exhibiting a clear peak in inter particle-spacing distribution (Fig S6 and Video S7, ESI†). However, at such larger flow rate values, we fell above the critical Weissenberg number Wi* for the onset of unstable droplet formation, thus preventing any type of encapsulation. The efficiency of the encapsulation process was found to be stable for 15 minutes, but we did not investigate the encapsulation efficiency over a longer time frame. The encapsulation efficiency is expected to decrease over a long period of time (i.e., hours) because of the particle sedimentation in the stock solution, which causes a dilution of the particle system flowing in the microfluidic channel, with consequent changes in the particle spacing,^22,23 resulting in the modification of the optimised conditions for controlled encapsulation.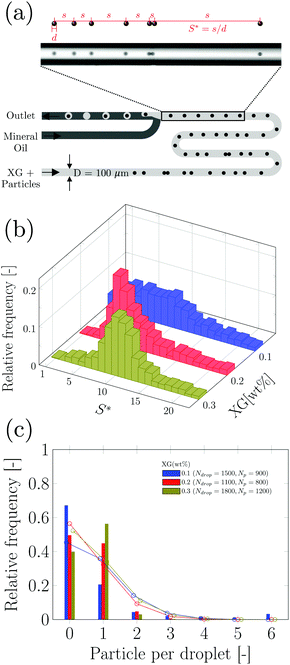

Fig. 3 Controlled encapsulation of particles in xanthan gum solutions. (a) Schematic representation of the T-junction device and of the fluid inlets: note that the inlets are swapped compared to Fig. 2a. The experimental snapshot explains the definition of the normalised inter-particle distance S* = s/d. where s is the distance between consecutive particles and d is the particle diameter. (b) Histograms of normalised inter-particle spacing S* = s/d before reaching encapsulation area as a function of the xanthan gum concentration for an imposed pressure drop of 1100 mbar (Q_XG ≈ 4.75 μL min⁻¹, Q_Oil = 9 μL min⁻¹, [small gamma, Greek, dot above]_wall,XG ≈ 800 s⁻¹), 1300 mbar (Q_XG ≈ 2.25 μL min⁻¹, Q_Oil = 12 μL min⁻¹, [small gamma, Greek, dot above]_wall,XG ≈ 380 s⁻¹) and 1500 mbar (Q_XG ≈ 3.0 μL min⁻¹, Q_Oil = 9 μL min⁻¹, [small gamma, Greek, dot above]_wall,XG ≈ 500 s⁻¹) for 0.1 wt%, 0.2 wt% and 0.3 wt%, respectively. These represent the best conditions for controlled encapsulation: the results for other imposed pressure drop values are in Fig. S4 (ESI†). (c) Histograms of relative frequency of encapsulated particles as function of the particles per droplets for different xanthan gum concentrations. The relative frequency is defined as the number of times we observed a given number of particles in each droplet divided by the overall number of droplets. The probability of single particle encapsulation increases with the xanthan gum concentration. Experimental data are reported as bars colour coded as in (b), while the Poisson statistics values are reported as open circles over the bars. Additional encapsulation results for other imposed xanthan gum pressure drop values are reported in Fig. S4 (ESI†).

Before concluding this section, it is worth mentioning that the particle aggregates found at XG 0.1 wt% were not observed in our previous work using the hydrophilic microchannel, despite spanning the same flow conditions and using the same channel geometry,²³ suggesting that surface properties may have an effect on the hydrodynamic interactions among flowing particles suspended in viscoelastic liquids. Numerical simulations carried out by Trofa et al.⁴³ found that changes in the slip length (signifying changes of the surface properties) affected the focusing dynamics of the particles; however, the paper did not feature results on particle ordering. Recent numerical simulations regarding the attraction and repulsion dynamics of pairs of particles suspended in a viscoelastic liquid and flowing in a cylindrical channel⁴⁴ suggested that the τ_zz component of the viscoelastic stress, where z is the flow direction, is responsible for the observed attraction/repulsion dynamics. It is reasonable to believe that when changing the surface properties from hydrophilic to hydrophobic, the shape of the τ_zz profile changes, thus altering the attraction/repulsion dynamics. The aggregates would disappear at larger XG concentrations as an increase of the shear-thinning properties has been demonstrated to enhance particle repulsion over attraction⁴⁴, in agreement with our observations. This means that the aggregates we observed in XG 0.1 wt% could be due to an increase of the attraction dynamics between consecutive particles compared to the hydrophilic case. Future studies will need to clarify this aspect as, to the best of our knowledge, we are not aware of any available study featuring the effect of surface properties on particle ordering in viscoelastic liquids.

In summary, we provided the first experimental evidence of controlled encapsulation using a viscoelastic polymer solution. We discovered that the optimal XG concentration range for controlled encapsulation was between 0.2 wt% and 0.3 wt%. For XG 0.05 wt%, despite droplets being formed, particles were not ordered (nor focused), and for XG 0.6 wt%, particles were ordered at the channel centreline, however, at flow rate values for which droplet formation was unstable.

3.3 Local particle concentration and predictive expression to obtain a controlled encapsulation

The controlled encapsulation phenomenon reported above is based on the synergy between the controlled formation of viscoelastic droplets with frequency f_drop and the viscoelastic ordering of particles approaching the encapsulation area. Since the XG viscoelasticity drives the formation of a train of equally distanced particles with spacing S_eq on a single line (the channel centreline) ahead of the encapsulation area, it is possible to derive an expression for the frequency of particles approaching the encapsulation area f_p. By then imposing f_drop = f_p, it is possible to obtain a predictive relation for the flow rate values required to achieve controlled encapsulation. While in principle this may seem an easy task, the frequency of particles approaching the encapsulation area is rarely constant during the experiments because of the well-known problem of fluctuations of the number of particles in each frame^23,41 which, in turn, affect the value of f_p. We recently introduced the concept of local concentration ϕ_l to account for particle concentration fluctuations²³, defined aswhere N and L are the number of particles per frame and the length of observation frame, respectively. Since for the XG concentrations in the range 0.1 wt% to 0.3 wt%, particles were ordered at the centreline, the local concentration changed in the range of 0 ≤ ϕ_l ≤ 1. The lower limit indicated empty frames, while the upper limit represented a string of particles in contact with each other along the full frame length. For a microchannel with a circular cross section, where particles are all aligned on the centreline, the local concentration is related to the bulk concentration via²² where β = d/D is the ratio between the particle diameter d and the channel diameter D. For each of the cases reported in Fig. 3, we first identified all the independent frames having the same number of particles (i.e., the same local concentration ϕ_l) approaching the encapsulation area. For each local concentration value, we subsequently evaluated the encapsulation efficiency for a fixed flow rate of the oil phase and for a fixed pressure drop of the xanthan gum phase (Fig. 4). In doing so, we were able to study the encapsulation phenomenon as if there were no concentration fluctuations. Regardless of the XG concentration, single encapsulation efficiency outperformed the Poisson statistic value, with an increase of encapsulation efficiency up to 80% for XG 0.3 wt% compared with the ≈37% predicted by the Poisson statistics. In practical terms, if there would be a strategy to nullify particle concentration fluctuations in microchannels, the combination of particle ordering and droplet formation could potentially lead to a deterministic (100% efficiency) encapsulation. For each XG concentration, we also observed an expected non-monotonic behaviour for encapsulation efficiency, with an optimal local concentration ϕ_l,opt at which the single encapsulation efficiency was the highest possible. Note that, there can only be one optimal local concentration ϕ_l for which the frequency of particles arriving at the encapsulation area is locally synchronised with the droplet generation at a frequency f_drop. At ϕ_l < ϕ_l,opt, the number of empty droplets (i.e., 0 particles per droplet) was larger because the f_p < f_drop; conversely, at ϕ_l > ϕ_l,opt the number of droplets with more than one encapsulated particle was larger because f_p > f_drop. We observed the largest value of the single encapsulation efficiency for XG 0.3 wt% at local concentration ϕ_l = 0.1, with an overall efficiency of 80%, more than 2-fold the Poisson limit. The value of the optimal concentration depends upon the values of the flow rate for both the continuous and the dispersed phase, thus justifying the need for introducing a predictive expression aimed at identifying operational parameters to achieve controlled encapsulation.

Fig. 4 Data of Fig. 3 plotted in terms of local particle concentration ϕ_l for XG 0.1 wt% (a), XG 0.2 wt% (b) and XG 0.3 wt% (c). We observe an optimal value of single encapsulation efficiency corresponding to a value of the local concentration ϕ_l,opt. Experimental snapshots are colour coded with the bar representing the experimental results. The Poisson statistics value is reported as a circle on the bars.

The local concentration is a more robust parameter than the bulk concentration to derive the expression for the frequency of particles approaching the encapsulation area f_p. In an ideal particle train, for a fixed local concentration ϕ_l, particles are equally spaced with inter-particle distance S = S_eq, and the relation between these two parameters was found to be²²ϕ_l = d/S_eq. The frequency of equally spaced particles with inter-particle spacing S_eq arriving at the encapsulation area with velocity u can be expressed as

The optimal encapsulation condition is obtained when f_drop = f_p. By rearranging eqn (5) and (3), we obtain

where A = 9.22, B = 2/3, Q_XG and Q_Oil are expressed in μL min⁻¹, d is expressed in metres and u is expressed in m s⁻¹. Eqn (6) can be used to calculate the flow rate of oil required to encapsulate particles with diameter d at concentration ϕ_l suspended in xanthan gum and flowing with volumetric flow rate Q_XG; the velocity of the particles flowing at the channel centreline, u, can be determined experimentally. Eqn (6) can also be used to derive the value of ϕ_l,opt given the other parameters. We tested the validity of eqn (6) on the data of Fig. 4: the optimal values of concentration for single encapsulation ϕ_l,opt were ϕ_l,opt = 0.116, ϕ_l,opt = 0.133 and ϕ_l,opt = 0.097 for XG 0.1 wt%, XG 0.2 wt% and XG 0.3 wt%, respectively, in excellent agreement with the experimentally observed values.

4 Conclusions

In this work, we presented the first experimental evidence of controlled particle encapsulation using the synergy between viscoelastic ordering and viscoelastic droplet formation in a T-junction microfluidic device with hydrophobic coating.

We first studied the continuous formation of XG droplets, and we observed that the normalised droplet length scaled as L/D = 1 + 2Q_XG/Q_oil, similarly to the Newtonian droplet case. The frequency of droplet formation could be described as f_drop = A(Q_XGQ_Oil)^B, where A = 9.22 and B = 2/3 obtained by fitting the data in the flow rate range of 0.3–9 μL min⁻¹, with the units of both flow rates being μL min⁻¹. Finally, we observed a clear flow instability during droplet formation at values of the Weissenberg number Wi above the critical value Wi*, suggesting an elasticity-driven instability.

In terms of particle encapsulation, we discovered that the optimal XG concentration range for controlled encapsulation was between 0.2 wt% and 0.3 wt%. For XG 0.05 wt%, despite droplets being formed, particles were not ordered (nor focused). For XG 0.6 wt%, particles did order at the channel centreline, however, at flow rate values for which droplet formation was unstable. Finally, we introduced a predictive expression that can help the design of controlled viscoelastic encapsulation systems.

Future works will need to identify additional viscoelastic liquids that can enable controlled encapsulation. Other microfluidic geometries will also need to be investigated: we believe that microfluidic devices having channel inlets such as the one designed by Liu et al.⁴⁵ can substantially reduce the fluctuations of particle concentrations, thus leading to a nearly deterministic encapsulation. The addition of an electric field²⁵ at the T-junction could simplify the formation of XG droplets thus enlarging the range of XG concentrations for which controlled encapsulation is possible. Experiments and numerical simulations aimed at clarifying the effect of microchannel surface properties on the mechanism of particle ordering are required to better design new microfluidic devices employing viscoelastic ordering. Future studies should also target both viscoelastic ordering and controlled encapsulation of cells. This is not a straightforward step, as cells generally require the addition of phosphate buffer saline (PBS) in order to survive during the experiment.⁴² However, the addition of PBS alters the ionic strength in XG,⁴⁶ causing a potential variation of the cell–cell interactions during train formation. Our results also lay the foundation for future works featuring important biological applications for encapsulated particles and cells, namely, droplet splitting, dilution and merging.^47–51 Specifically, the splitting of droplets containing either electric or magnetic particles could be achieved using either magnetic or electric external fields:^47,52 the presence of a viscoelastic fluid in the droplet is not expected to lead to any drawback, as also previously demonstrated for micrometer-sized magnetic particles flowing in a viscoelastic liquid and separated deterministically using a simple magnet.⁵³ Droplet dilution and merging may present some drawbacks caused by the additional resistance caused by the viscoelastic fluid in the droplet; in such conditions, active electric or acoustic fields together with hydrodynamic traps may be investigated to address arising issues.^48,49 Finally, our results can contribute to open new research direction in the formation of colloidal crystals⁹ and synthesis of colloidal structures in microfluidics.²⁸

Author contributions

FDG designed the research. K. S. carried out the experiments, wrote the Matlab codes and analysed the data. All the authors critically discussed the results. All the authors wrote the manuscript and approved the final submission.

Conflicts of interest

The results presented in this manuscript have been submitted as part of a patent application.

Acknowledgements

We thank Prof. Amy Shen and Prof. Gaetano D'Avino for useful comments on the manuscript. We acknowledge support from EPSRC New investigator Award (grant ref. EP/S036490/1).

Notes and references

1. F. Del Giudice, G. D'Avino and P. L. Maffettone, Lab Chip, 2021, 21, 2069–2094.
2. Y. Ding, P. D. Howes and A. J. deMello, Anal. Chem., 2019, 92, 132–149.
3. A. Sattari, P. Hanafizadeh and M. Hoorfar, Adv. Colloid Interface Sci., 2020, 102208.
4. V. A. Turek, Y. Francescato, P. Cadinu, C. R. Crick, L. Elliott, Y. Chen, V. Urland, A. P. Ivanov, L. Velleman and M. Hong, et al. , ACS Photonics, 2016, 3, 35–42.
5. X. Xu, F. Tian, X. Liu, R. M. Parker, Y. Lan, Y. Wu, Z. Yu, O. A. Scherman and C. Abell, Chem. – Eur. J., 2015, 21, 15516–15519.
6. S. Sajjadi, M. Alroaithi, A. S. Chaurasia and F. Jahanzad, Langmuir, 2019, 35, 12731–12743.
7. F. Fontana, J. P. Martins, G. Torrieri and H. A. Santos, Adv. Mater. Technol., 2019, 4, 1800611.
8. J. Nunes, S. Tsai, J. Wan and H. A. Stone, J. Phys. D: Appl. Phys., 2013, 46, 114002.
9. P. Parthiban, P. S. Doyle and M. Hashimoto, Soft Matter, 2019, 15, 4244–4254.
10. J. F. Edd, D. Di Carlo, K. J. Humphry, S. Köster, D. Irimia, D. A. Weitz and M. Toner, Lab Chip, 2008, 8, 1262–1264.
11. E. W. Kemna, R. M. Schoeman, F. Wolbers, I. Vermes, D. A. Weitz and A. Van Den Berg, Lab Chip, 2012, 12, 2881–2887.
12. M. Masaeli, E. Sollier, H. Amini, W. Mao, K. Camacho, N. Doshi, S. Mitragotri, A. Alexeev and D. Di Carlo, Phys. Rev. X, 2012, 2, 031017.
13. G. Segre and A. Silberberg, et al. , J. Fluid Mech., 1962, 14, 136–157.
14. J.-P. Matas, V. Glezer, É. Guazzelli and J. F. Morris, Phys. Fluids, 2004, 16, 4192–4195.
15. T. P. Lagus and J. F. Edd, RSC Adv., 2013, 3, 20512–20522.
16. E. Z. Macosko, A. Basu, R. Satija, J. Nemesh, K. Shekhar, M. Goldman, I. Tirosh, A. R. Bialas, N. Kamitaki and E. M. Martersteck, et al. , Cell, 2015, 161, 1202–1214.
17. H.-S. Moon, K. Je, J.-W. Min, D. Park, K.-Y. Han, S.-H. Shin, W.-Y. Park, C. E. Yoo and S.-H. Kim, Lab Chip, 2018, 18, 775–784.
18. L. Li, P. Wu, Z. Luo, L. Wang, W. Ding, T. Wu, J. Chen, J. He, Y. He and H. Wang, et al. , ACS Sens., 2019, 4, 1299–1305.
19. Y. Ren, Z. Liu and H. C. Shum, Lab Chip, 2015, 15, 121–134.
20. P. E. Arratia, J. P. Gollub and D. J. Durian, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2008, 77, 036309.
21. F. Ingremeau and H. Kellay, Phys. Rev. X, 2013, 3, 041002.
22. F. Del Giudice, G. D'Avino, F. Greco, P. L. Maffettone and A. Q. Shen, Phys. Rev. Appl., 2018, 10, 064058.
23. A. Jeyasountharan, K. Shahrivar, G. D’Avino and F. Del Giudice, Anal. Chem., 2021, 93(13), 5503–5512.
24. B. Rostami and G. L. Morini, Int. J. Multiphase Flow, 2018, 105, 202–216.
25. M. Shojaeian and S. Hardt, Appl. Phys. Lett., 2018, 112, 194102.
26. M. Fatehifar, A. Revell and M. Jabbari, Polymers, 2021, 13, 1915.
27. J. Zhou and I. Papautsky, Microsyst. Nanoeng., 2020, 6, 1–24.
28. Z. Ge, O. Tammisola and L. Brandt, Soft Matter, 2019, 15, 3451–3460.
29. C. W. Macosko, Rheology: principles, measurements, and applications, VCH Publishes, 1994.
30. D. C. Boris and R. H. Colby, Macromolecules, 1998, 31, 5746–5755.
31. N. B. Wyatt and M. W. Liberatore, J. Appl. Polym. Sci., 2009, 114, 4076–4084.
32. P. Garstecki, M. J. Fuerstman, H. A. Stone and G. M. Whitesides, Lab Chip, 2006, 6, 437–446.
33. G. F. Christopher, N. N. Noharuddin, J. A. Taylor and S. L. Anna, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2008, 78, 036317.
34. I. Chakraborty, J. Ricouvier, P. Yazhgur, P. Tabeling and A. Leshansky, Phys. Fluids, 2019, 31, 022010.
35. J. Dealy, Rheol. Bull, 2010, 79, 14–18.
36. X.-B. Li, F.-C. Li, H. Kinoshita, M. Oishi and M. Oshima, Microfluid. Nanofluid., 2015, 18, 1007–1021.
37. W. Du, T. Fu, Q. Zhang, C. Zhu, Y. Ma and H. Z. Li, Chem. Eng. Sci., 2016, 153, 255–269.
38. O. Carrier, D. Funfschilling and H. Z. Li, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2014, 89, 013003.
39. V.-L. Wong, K. Loizou, P.-L. Lau, R. S. Graham and B. N. Hewakandamby, Chem. Eng. Sci., 2017, 174, 157–173.
40. W. Yu, X. Liu, Y. Zhao and Y. Chen, Chem. Eng. Sci., 2019, 203, 259–284.
41. S. Kahkeshani, H. Haddadi and D. Di Carlo, J. Fluid Mech., 2016, 786, R3.
42. F. Del Giudice, S. Sathish, G. D'Avino and A. Q. Shen, Anal. Chem., 2017, 89, 13146–13159.
43. M. Trofa, G. D'Avino, M. A. Hulsen and P. L. Maffettone, J. Non-Newtonian Fluid Mech., 2016, 236, 123–131.
44. G. D'Avino and P. L. Maffettone, Microfluid. Nanofluid., 2019, 23, 1–14.
45. L. Liu, H. Xu, H. Xiu, N. Xiang and Z. Ni, Analyst, 2020, 145, 5128–5133.
46. M. Cho, S. O. Hong, S. H. Lee, K. Hyun and J. M. Kim, Micromachines, 2019, 10, 535.
47. M. Tenje, A. Fornell, M. Ohlin and J. Nilsson, Particle manipulation methods in droplet microfluidics, 2018.
48. H. Gu, M. H. Duits and F. Mugele, Int. J. Mol. Sci., 2011, 12, 2572–2597.
49. C. N. Baroud, F. Gallaire and R. Dangla, Lab Chip, 2010, 10, 2032–2045.
50. H. S. Rho, Y. Yang, L. W. Terstappen, H. Gardeniers, S. Le Gac and P. Habibovic, J. Ind. Eng. Chem., 2020, 91, 231–239.
51. W. Postek, T. Kaminski and P. Garstecki, Analyst, 2017, 142, 2901–2911.
52. M. A. Bijarchi, M. Dizani, M. Honarmand and M. B. Shafii, Soft Matter, 2021, 17, 1317–1329.
53. F. Del Giudice, H. Madadi, M. M. Villone, G. D'Avino, A. M. Cusano, R. Vecchione, M. Ventre, P. L. Maffettone and P. A. Netti, Lab Chip, 2015, 15, 1912–1922.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: 10.1039/d1sm00941a

---