Electrokinetic sweeping of colloids at a reactive magnesium oxide interface

Abstract

Investigating the electrokinetic (EK) response in the vicinity of interfaces has regained interest due to the development of new membrane based processes for energy harvesting or soil depollution. However, the case of reactive interfaces, ubiquitous in these processes, remains scarcely explored. Here we experimentally investigate the EK response of a model interface between an aqueous electrolyte and a bulk MgO crystal surface (100), for different pH. For that purpose, we use a lab-scale non invasive method to monitor the zeta potential of the interface versus time, by confocal fluorescent particle tracking. An unexpected motion of the particles, repelled and then attracted again by the interface is observed. We attributed this motion to the surface reactivity, inducing ion concentration gradients perpendicular to the interface and subsequent diffusiophoresis of the charged particle. Accordingly, we could describe at a semi-quantitative level the particle dynamics by solving numerically the Poisson–Nernst–Planck equations to establish concentration profile in the system and subsequent diffusiophoretic motion. These experiments open the way to the characterization of both the EK response and the reaction rate in the vicinity of reactive interfaces.

---

1 Introduction

The development of new green processes for energy conversion is now crucial for the society. Towards the reach of the so-called “energetic mix”, electrokinetic energy conversion (EKEC), evoked for the first time by Osterle in 1964,¹ has regained interest recently, in particular in the context of blue energy² and waste heat³ harvesting. EKEC is based on EK effects, which cover all possible couplings between different types of transport (i.e. when a thermodynamic gradient of one kind induces a flux of another kind) occurring at interfaces. The most studied two reciprocal EK effects consist of electro-osmotic flows and streaming current,⁴ the first one being the flow generated by an electrical field whereas the second one is the current induced by a pressure gradient. Both effects take their origin in the so-called electric double layer,⁴ where ions reorganize to screen the surface charge. The amplitude of these EK effects is quantified by the so-called zeta potential, denoted ζ. The latter is directly linked to the surface charge, which can depend on the local ion concentration due to charge regulation, ion binding or specific adsorption effects.⁴

Recently, the quest to design more efficient materials is very active, focusing mainly on monolayered materials^5–9 with unprecedented properties. As a less explored alternative, reactive interfaces, that locally produce or consume ions, could provide a versatile platform to control and enhance EKEC. In particular, theoretical simulations have recently focused on metal oxide surfaces, such as magnesium oxide (MgO) or zinc oxide (ZnO),^10,11 and demonstrated a specific behavior of the first layer of water near the interface, which has strong consequences on interfacial transport properties. It is then crucial to probe experimentally the EK response of such materials to support these numerical observations.

The EK response near reactive interfaces has also been extensively but indirectly investigated in the process of EK remediation. This process, widely used for depollution, consists of applying an electric field to a liquid saturated soil in order to remove organic and inorganic compounds or heavy metals.^12,13 Competition between electrophoresis of the impurities and electroosmosis generated near the clay particle interfaces takes place, rendering crucial the understanding of EK response near such reactive interfaces. However, due to the complexity of the processes,^14,15 model experiments near well-defined reactive interfaces are still lacking while vital.

What is the EK response of interfaces of reactive materials and does this response evolve with time are the questions we would like to address. As a first step, we investigate the EK response near a MgO substrate, which will dissolve in water at low pH to release magnesium cations. The reaction kinetics is moderate,¹⁶ allowing us to probe experimentally the effect of this reactivity. For that, we used a specific set-up,^17,18 using confocal microscopy and colloidal tracking, to probe the zeta potential of a plain substrate as a function of time, and for different pH. We show that the reactions occurring at the interface indeed modify the value of the zeta potential, but also impact the colloid concentration profile near the interfaces. This unexpected motion of the colloids is attributed to the ionic concentration gradients that establish due to interfacial reaction, as reported previously with Nafion.^19–21 Finally, we describe semi-quantitatively this behavior and we show that it can be used as an indirect but simple way to quantify MgO-water interfacial reactivity.

2 Methods

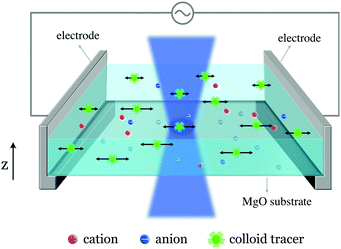
The EK transport investigation at the aqueous electrolyte–MgO interface was realized using the experimental setup shown in Fig. 1. This approach was proposed and validated at liquid–solid or liquid–gas interfaces.^17,18 We briefly recall here the main features. The system comprises an experimental tank made from PDMS (polydimethylsiloxane), whose bottom consists in a MgO(100) substrate (Goodfellow), as shown in Fig. 1. The tank has a dimension of 1 × 1 × 0.5 cm³. For zeta potential measurements, two Ag/AgCl plates (0.15 mm thick, Goodfellow) serve as electrodes and are placed perpendicularly to the MgO surface. The tank is filled with a KCl solution (10⁻⁴ M). The electrodes are connected to an AC voltage generator, which delivers a sinusoidal signal (f = 2 Hz, peak-to-peak amplitude ranging from 5 to 15 V throughout the present study). Consequently, an electric field, parallel to the interface, is established. A commercial solution of amine-modified fluorescent polystyrene spheres of diameter 200 nm (yellow-green‚ fluorescent [505/515 nm], 2% solids [volume/volume], Thermofisher) is diluted in our liquid tanks, with a dilution volume ratio of 1/1000. The colloid displacements and amplitude under the AC field are recorded in a horizontal plane, parallel to the substrate–liquid interface, with a high-speed confocal microscope (Leica TCS SP5 DMI6000) and analyzed with a homemade Python code embedding the Trackpy package.²² We apply a digital band-pass filter (between 1.5 and 3 Hz) on the displacements’ temporal signal to isolate the linear response from noises, using the Scipy signal processing toolbox.²³ This procedure is repeated for different altitudes, noted z, from the MgO substrate. To determine the magnitude of the electro-osmotic velocity generated at the interface, one needs to determine the different origins of the particle motion.

Fig. 1 Illustration of the experimental set-up. The tank has a dimension of 1 × 1 × 0.5 cm³, and is filled of a KCl solution with fluorescent polystyrene spheres as tracers. An external AC electric field can be applied on the system and the motion of the tracers is recorded by a high speed confocal microscope. The blue shade corresponds to the LASER beam of the microscope.

3 Colloid motion

3.1 Longitudinal motion: zeta-potential measurements

The motion perpendicular to the electrodes results from two mechanisms. First, the tangential sinusoidal applied electric field E induces an oscillatory electroosmotic velocity of the liquid at the interface. The tracers are then advected by this electroosmotic flow, whose velocity reads u_eo(z) = −U_eo exp(− z/z₀)cos(ωt − z/z₀), where U_eo = ζεE/η is the magnitude of the electroosmotic velocity in the vicinity of the liquid–solid interface – with ζ the zeta potential of the solid, and z₀ = 416 μm is the viscous momentum diffusion length scale for water,¹⁸ with f = ω/2π = 2 Hz and η = 1.09 mPa s at T = 16.5 °C (we worked at this temperature due to a laser generator cooling concern). Second, the positively charged tracers move by electrophoresis u_ep = U_ep cos(ωt − ϕ), where U_ep = ζ_cεE/η is the magnitude of the electrophoretic velocity of the colloid tracers – with their own zeta potential ζ_c, and ϕ is a phase shift between these two contributions, which has been discussed previously.¹⁸ The tangential displacement amplitude of the tracers can then be expressed as:¹⁸where the three fitting parameters are U_eo, U_ep and ϕ. Fig. 2 presents a typical measurement. The red line corresponds to the best fit of the experimental data using eqn (1). The zeta potentials of the MgO surface and the tracers can be measured at the same time from U_eo and U_ep.

Fig. 2 Typical measurement of the amplitude of the colloid tracers displacement during each period as a function of the distance to the solid surface z. Operating frequency is 2 Hz. Blue circle: experimental data recorded with the high-speed confocal microscope and treated by the homemade Python code. For each point, the error is estimated to be 0.09 μm for the amplitude (corresponding to the pixel size), and 16 μm for the z position (depth of field of the confocal microscope). Red line: fit of the experimental data using eqn (1), with U_eo = 69.9 μm s⁻¹, U_ep = 44.0 μm s⁻¹ and ϕ_t = 0.01 for this specific case. Inset: Typical signal of tracers’ average position as a function of time (maroon line) under the AC field (green line).

We performed measurements in different pH media, from pH ∼ 3 to pH ∼ 14. For acidic conditions, HCl was added in the solution to reach the target pH, whereas for the basic ones, KOH was added. The initial pH was measured by a pH meter (Hanna instrument). For each experiment, between two consecutive measurements, we withdrew a few drops of liquid from the tank and used a pH paper to evaluate the pH evolution. The pH variations did not exceed 1 during ∼4 hours.

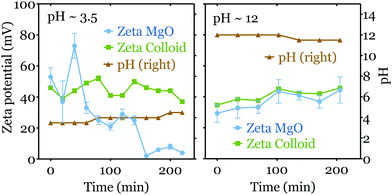
In acidic media (pH < 6), due to chemical reactions at the interface, the zeta potential of the MgO surface decreases with time. Here we first consider the initial zeta potential measurements as a function of pH. In Fig. 3, we averaged the results of the first three measurements of each experiment for pH < 6 (corresponding to a timelapse of one hour), while for pH ≥ 6 we considered all the data obtained, as no time variations were observed (see Fig. 4).

Fig. 3 Zeta potential for MgO surface and colloid tracers versus the average pH during the experiment. For pH < 6, where ζ varied with time, the measurement was averaged over the first hour of multiple experiments; for pH ≥ 6, where ζ remained constant, the measurement was averaged over ∼4 hours of multiple experiments.

Fig. 4 Evolution of the zeta potential of MgO surface and colloid tracers (left axis), and of the pH (right axis) as a function of time. Several measurements were performed during ∼4 hours for the same sample. Left: Acidic medium with initial pH ∼ 3.5. Right: Basic medium with initial pH ∼ 12. The error bars were estimated from the non linear fitting error of U_eo and U_ep. Those for colloid tracers are generally smaller than the symbol size.

The initial zeta potential of the MgO surface decreases slightly for increasing pH, but it does not show a point of zero charge (PZC), i.e. a pH at which the net charge on the colloid is equal to zero. This result differs from zeta potential measurements for MgO realized with powders or nano-particles in colloid suspension systems using electrophoresis.^24–26 They indeed usually show a moderate value (ζ < 20 mV) in neutral pH condition and present a PZC around pH = 12. However, in suspensions, the crystallinity and moreover the crystalline planes exposed to water are less controlled and can differ from our bulk monocrystalline MgO(100) surface.

One can note also that the colloid tracers have a relatively constant zeta potential ζ_c ∼ 40 mV. The evolution of ζ_c depends on the colloid's acid dissociation constant (pKa) and its molecular details such as functionalized groups. As we measure simultaneously ζ_c and ζ for each experiments, these variations do not modify the accuracy of our measurements of ζ. One can note that the values obtained are close to the ones obtained with a zeta-meter in different conditions.¹⁸

We now turn to the time evolution of the zeta potential. As mentioned above and shown in Fig. 4 (left), the zeta potential of the MgO surface decreases dramatically from ∼50 mV to ∼5 mV during 4 hours in the acidic mediums (initial pH = 3.5), while that of colloids ζ_c stays relatively constant. Meanwhile the pH value increases to ∼4.5. In contrast, in the basic media both ζ and ζ_c do not display a strong variation over the same period (see Fig. 4 right). The value of pH decreases slightly from 12 to ∼11.5 in the tank.

3.2 Motion of colloids perpendicular to the surface

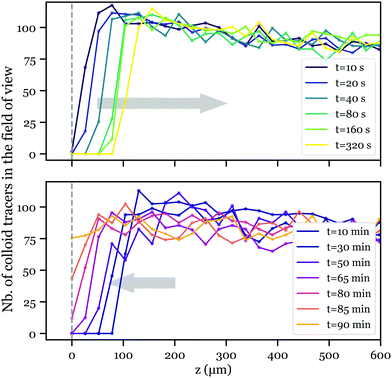
Strikingly, when performing the zeta potential measurement in low pH conditions (pH < 5), we observed a tracer depletion close to the liquid–solid interface at the beginning of each measurement, while after ca. 90 minutes, tracers were observed again. As fewer colloid tracers are present in the vicinity of the interface, the determination of the velocity profile in this region is less accurate, so are the ζ potential measurements at short times and low pH. This results in an increase of the error bars, as observed in Fig. 4. The variations of ζ versus time remains nevertheless larger than the error bars.

To investigate this depletion phenomenon, we performed this experiment without the AC electric field, and recovered the same behavior. To quantify this, once the solution (pH < 5) was injected in the tank, we started to record the number of tracers against the distance z to the MgO surface, using the fast z-scan mode of the confocal microscope. Fig. 5 shows the number of tracers in the field of view as a function of z at different times. In the first three hundred seconds, tracers seem to be “pushed” away from the wall (Fig. 5 top, OUT trip), and after about 10 minutes, they move back again with much slower kinetics (Fig. 5 bottom, BACK trip).

Fig. 5 Number of colloid tracers in the field of view of the microscope as a function of the distance to the solid surface in an independent experiment (without external electric field E) with initial pH = 3.5. Top: Curves recorded immediately after the deposition of electrolyte solution in the tank (OUT trip). Bottom: Curves recorded after ∼10 minutes (BACK trip). The captions indicate the time from the deposition. Between t = 320 s and t = 10 min, the evolution is very slow and the curves are almost superimposed, which are not shown for clarity. The error on the number of counted particles is ±1.

The distinguishable kinetics in the OUT and BACK trips reveal different origins for colloid motion. To characterize these kinetics, we define the front of the depleted zone z_f as the position where the number of tracers in the field of view reaches a threshold value N₀ = 60, approximately equal to 75% of the bulk value far from the interface. Fig. 6 presents the evolution of z_f² with time for both OUT (left) and BACK (right) trips. We first focus on the BACK trip. Data from different experiments were regrouped together and show a linear behavior of z_f²versus time, characteristic of a diffusive motion. The corresponding 1-D diffusion coefficient, given by half the slope of the linear fit, reads (1.3 ± 0.2) × 10⁻¹² m² s⁻¹. Meanwhile, a theoretical diffusion coefficient of the tracers can be evaluated through the Stokes–Einstein relation, with D_th = k_BT/(6πηr) = 1.94 × 10⁻¹² m² s⁻¹, where η = 1.09 × 10⁻³ Pa s is the water viscosity at ∼16.5 °C, and r = 100 nm is the radius of the tracers. The theoretical value matches our observations, indicating that tracers self-diffusion governs the colloid BACK trip. The origin of the colloid motion in the OUT trip is less straightforward. A diffusive-like behavior is also observed, but the corresponding diffusion coefficient, (0.8 ± 0.1) × 10⁻¹⁰ m², is much larger than that of the colloids. We now try to model this motion and to elucidate its origin.

Fig. 6 Evolution of the squared depletion front position z_f²versus time for the OUT (left) and BACK (right) trip. Both trips show a diffusive-like behavior, where z_f²(t) can be fitted linearly. The corresponding diffusion coefficient, given by half the slope of the fit, is (0.8 ± 0.1) × 10⁻¹⁰ m² for the OUT trip, and (1.3 ± 0.2) × 10⁻¹² m² s⁻¹ for the BACK trip. The error on the front position is given by the sampling in the z direction by the confocal microscope, 26.9 μm.

4 Modeling: surface reaction and salt concentration gradients

The mechanism that can explain our observations is the following: reactivity of the MgO substrate with water induces source and sink of ions in the vicinity of the surface. These ions diffuse and this creates some gradients of ion concentration and composition perpendicular to the wall ; additionally, an electric field will be induced in the solution to avoid charge separation. The concentration gradients and the electric field will induce a diffusiophoretic and an electrophoretic motion of the colloids, respectively (Fig. 7). After a while, the reactions near the surface stop and the gradients vanish (i.e. the source is over or the ions have filled the entire space), and the colloids diffuse back. We will now try to predict the dynamics of the colloids with these simple ingredients. In both cases, we expect a diffusive-like behavior corresponding to solute diffusion for gradients establishment in the OUT regime, and then simple colloid diffusion in the BACK one. We assume also that the velocity of colloids adapts instantaneously to the gradient of salt.

Fig. 7 Illustration of the different sources of motion for the colloid tracers in the direction normal to the interface: gradients of ions concentration generated by the surface reactivity induce a diffusiophoretic motion of the colloids; an electric field also appears to avoid charge separation, which induces an electrophoretic motion of the colloids.

To describe the chemical reactions at the interface, we follow the model and experimental data of Fruhwirth et al.¹⁶ In our acidic conditions, the reaction that takes place at the MgO solid surface is the following:

MgO_solid + 2H⁺ → MgO·H_solid⁺ + H⁺ → Mg²⁺ + H₂O

We note v the speed of dissolution, i.e. the number of moles of MgO dissolved per unit time and area. In ref. 16, experimental measurements were performed for MgO(100) and MgO(111) surfaces. Values presented below are for MgO(100) at 25 °C, slightly different from our working conditions (T = 16.5 °C). For a pH < 5, the kinetics of dissociation depends on the concentration of Mg²⁺ and H⁺ ions at the interface and their relative values, noting pMg and pH the quantities −log[c_Mg²⁺,surf] and −log[c_H⁺,surf] respectively, with the concentrations expressed in mol L⁻¹:

• if c_H⁺,surf ≥ c_Mg²⁺,surf: the speed of dissolution reads v = v₀ − kpH, with v₀ = 2.389 × 10⁻⁹ mol cm⁻² s⁻¹ and k = 0.4875 × 10⁻⁹ mol cm⁻² s⁻¹;

• if c_H⁺,surf < c_Mg2⁺,surf: the speed reads , with and .

Accordingly, we consider hereafter four species i in solution, the background salt ions K⁺ and Cl⁻, and the released and consumed ions at the surface H⁺ and Mg²⁺. Note that in this acidic regime, OH⁻ is negligible and hereafter omitted. With each species having different mobilities, concentration heterogeneities induce an electric field E(t, z) = −∂_zV in the solution to avoid charge separation. Overall bulk conservation equations for each ion species i write:

where c_i(t, z) is the concentration, j_i(t, z) the total (diffusive and electrophoretic) flux of i along the z direction, D_i the diffusion coefficient, z_i the ion valency, e the elementary charge, k_B the Boltzmann constant and T the temperature.

These mass transport equations are completed by electrical consideration. With the considered scales much larger than the Debye screening length, the system is locally electroneutral. This yields the condition together with the Poisson equation for the electrical potential ∂_zzV = 0. In addition, in the absence of charge injection in the system, the charge conservation imposes that the electrical current along the z direction vanishes .

These bulk equations are complemented by boundary conditions. Far from the MgO surface (z → ∞), electric field and potential vanish at all time t, while ion species reach their reference bulk concentration: c_K⁺(t, ∞) = c_bkg, c_H⁺(t, ∞) = 10^−pH_bkg, c_Cl⁻(t, ∞) = c_K⁺(t, ∞) + c_H⁺(t, ∞) and c_Mg²⁺(t, ∞) = 0. Note that accordingly, these concentrations also correspond to the initial condition: c_i(0, z) = c_i(t, ∞). Finally, the surface reactivity imposes the ion fluxes j_i(t,z = 0): j_K⁺ = j_Cl⁻ = 0, and j_H⁺ = −2j_Mg²⁺ = −2v.

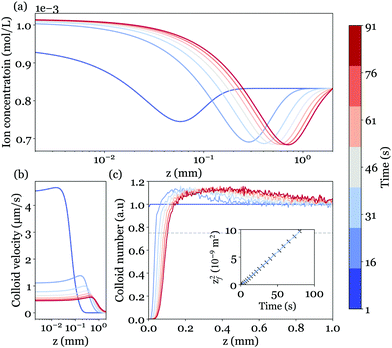
To solve these equations to obtain the ion concentration profiles and the electric field in the system, we performed 1-D finite-element simulations with the COMSOL Multiphysics software on a system with 5 cm in length. Parameters were chosen in accordance with experimental values: c_bkg = 10⁻⁴ M, pH_bkg = 3.5. Fig. 8(a) shows the total ion concentration profile at different times.

Fig. 8 (a) Computed total ion concentration (Mg²⁺, H⁺, K⁺, Cl⁻) profile as a function of time. (b) Computed colloid velocity profiles v_c(z, t) as a function of time. The colloids move from the solid surface to the bulk of the liquid, with a decreasing velocity. (c) Colloid concentration profiles computed from diffusive and advective transport at v_c(z, t) of an initially homogeneous profile. Colloids diffusion coefficient is set to their theoretical Stokes–Einstein value D_c = 2 × 10⁻¹² m² s⁻¹. The front position z_f corresponds to 75% of the far-field reference concentration of colloids. Inset: Linear regression of z_f² against time, with a corresponding diffusion coefficient of 0.6 × 10⁻¹⁰ m² s⁻¹. Profiles are computed for time from 1 to 92 s after the beginning of the reaction, at pH = 3.5.

With ion concentration and electric potentials independently determined as a function of time, it is now possible to consider the transport of our colloidal particles in suspension. Indeed, beside their (weak) self-diffusion, particles will exhibit phoretic drifts due to the gradients of concentration and potential generated at the MgO surface. While the colloid response to gradients of a single univalent salt has been extensively addressed,^27–30 multivalent and asymmetric species have received less attention.^31–33 Although a general formulation was recently obtained,³³ a simple formula can be derived in the regime of moderate surface potential³¹ to yield a phoretic velocity of the form:

The first term corresponds to the osmotic contribution to the colloid drift, while the second is a more classical electrophoretic response, but with an electric field that emerges from the ions' concentration profiles. In the present situation, the osmotic response retains the colloids while electrophoresis pushes them away. Note that in this model, variations of ζ_c as a function of the local concentration are neglected, in agreement with linear response theory.²⁷

Fig. 8(b) displays the colloid velocity profiles at different instants after the reaction begins. Consistently with the early depletion of colloids observed experimentally, we find from the calculated ions concentration that the electrophoretic contribution dominates over the diffusiophoretic one. The colloids are indeed expelled from the solid surface, with a velocity decreasing over time.

To go beyond and determine the colloid tracers concentration profile, we adopt a Lagrangian approach and consider an assembly of discrete particles, initially homogeneously distributed in the liquid. Each of the particle trajectories is obtained by integration of an overdamped Langevin equation to account for the weak Brownian diffusivity. The colloid position at time t + Δt is computed as , with N(t) a random variable from a normal distribution of unit variance and zero mean.³⁴ The colloid concentration profiles are eventually obtained from an histogram of all instantaneous positions; the computed profiles are shown in Fig. 8(c). The overall behavior closely matches the experimental observations, with a growing depleted region nearby the MgO surface, delimited by a sharp front followed by a small accumulation pike smoothing over time.

More quantitatively, the front position z_f is defined accordingly to the experimental procedure (Fig. 5) and corresponds to a 75% threshold based on the far-field reference concentration of colloids. The front dynamics is shown in the inset of Fig. 8(c), and also follows the diffusive-like behavior evidenced in experiments. The corresponding diffusion coefficient (half the slope of z_f²(t)) reads D_eff = 0.6 × 10⁻¹⁰ m⁻² s⁻¹, and is almost in quantitative agreement with the experimental value 0.8 ± 0.1 × 10⁻¹⁰ m² s⁻¹ (see Fig. 6 left), without any adjustable parameters. Several factors could explain the small remaining difference since both diffusiophoresis and electrophoresis are controlled by ion concentration gradients, and depend on the dissolution velocity. For example, one should note that the surface dissolution dynamics considered here is a simplified linear model.¹⁶ Actual dynamics could be more complex due to the local variations of pH and geometry. To illustrate this, an AFM image of the MgO surface after seven experiments at low pH is reported in Fig. 9. AFM imaging was performed in tapping mode in air using an MFP-3D AFM (Asylum Research). We observed randomly distributed holes in the substrate with a typical diameter of 2 μm and a typical depth of hundreds nm, showing the complex geometry of the reactive substrate.

Fig. 9 AFM image of the MgO surface after seven experiments at low pH. The roughness of the original surface is ∼0.2 nm, measured with AFM.

The two dynamics (OUT-BACK) are separated by one order of magnitude in timescale. The transition between the two regimes is attributed to the fading of salt gradient so that colloidal diffusio-phoretic motion drops and diffusion becomes dominant. This fading will depend on the details of the surface reaction kinetics and should be investigated beyond scaling laws. Moreover, the extent of the depleted zone can also be set by diffusion boundary layers associated to advection.

5 Conclusions

Using confocal particle tracking near a substrate, we investigated the EK response, and in particular the zeta potential, of a reactive MgO crystal surface as a function of the environment and time. At large pH (pH = 12), we did not observe the commonly accepted zero point charge but rather a constant zeta potential around 50 mV, which does not evolve with time. In this regime, the surface appears chemically inert. On the contrary, in acidic conditions, the zeta potential decreases continuously with time to reach a value close to zero. In these particular conditions, we observed that the tracked particles are expelled from the surface of the substrate. We attributed this behavior to diffusiophoresis of the charged particles, due to salt concentration gradient induced by the MgO chemical dissolution at the surface. The particle dynamics can be modeled by solving numerically the Poisson–Nernst–Planck equations to establish concentration profiles in the system and subsequent diffusiophoretic motion. These new findings offer many perspectives. In particular, from the determination of the colloid concentration profile versus time in the vicinity of the surface, one can indirectly, but within a lab and in real time, monitor the reaction dynamics at the interface, together with its EK response. The proper link between these two measurements would help to elucidate the modeling of EK response near reactive interfaces at both the chemical and physical scales. In terms of applications, reactive MgO substrates do not evidence a giant EK response. However, their slow dissolution with time can be a simple way to generate controlled salt gradients, with associated applications in energy conversion. Concerning soil depollution, this first approach shows that even in a model system (a millimetric pure flat interface), complex behaviors have to be considered. Real systems, spanning over tens of meters, constituted of mixtures of reactive interfaces with non regular shapes and on which DC fields are applied for days, bring their own complexity and require to be investigated step by step.

Conflicts of interest

There are no conflict to declare.

Acknowledgements

The authors thank Baptiste Blanc and Marie Le Merrer for fruitful discussions, Agnes Piednoir for AFM images and Gilles Simon for set-up conception and realization. This work is supported by the ANR, Project ANR-16-CE06-0004-01 NECtAR. LJ is supported by the Institut Universitaire de France.

Notes and references

1. J. F. Osterle, J. Appl. Mech., 1964, 31, 161–164.
2. A. Siria, M.-L. Bocquet and L. Bocquet, Nat. Rev. Chem., 2017, 1, 0091.
3. L. Fu, L. Joly and S. Merabia, Phys. Rev. Lett., 2019, 123, 138001.
4. R. J. Hunter, Foundations of colloid science, Oxford University Press, 2001.
5. A. Siria, P. Poncharal, A.-L. Biance, R. Fulcrand, X. Blase, S. T. Purcell and L. Bocquet, Nature, 2013, 494, 455–458.
6. J. Feng, M. Graf, K. Liu, D. Ovchinnikov, D. Dumcenco, M. Heiranian, V. Nandigana, N. R. Aluru, A. Kis and A. Radenovic, Nature, 2016, 536, 197–200.
7. T. Mouterde, A. Keerthi, A. Poggioli, S. A. Dar, A. Siria, A. K. Geim, L. Bocquet and B. Radha, Nature, 2019, 567, 87–90.
8. L. Bocquet and E. Charlaix, Chem. Soc. Rev., 2010, 39, 1073–1095.
9. Z. Zhang, X. Li, J. Yin, Y. Xu, W. Fei, M. Xue, Q. Wang, J. Zhou and W. Guo, Nat. Nanotechnol., 2018, 13, 1109–1119.
10. G. Tocci and A. Michaelides, J. Phys. Chem. Lett., 2014, 5, 474–480.
11. S. Laporte, F. Finocchi, L. Paulatto, M. Blanchard, E. Balan, F. Guyot and A. M. Saitta, Phys. Chem. Chem. Phys., 2015, 17, 20382–20390.
12. Y. B. Acar and A. N. Alshawabkeh, Environ. Sci. Technol., 1993, 27, 2638–2647.
13. R. F. Probstein and R. E. Hicks, Science, 1993, 260, 498–503.
14. C. Peng, J. O. Almeira and A. Abou-Shady, Sep. Purif. Technol., 2013, 118, 591–597.
15. S. Hasan, I. Ahmed, A. Housani and A. Giwa, Sci. Rep., 2016, 6, 1–14.
16. O. Fruhwirth, G. Herzog, I. Hollerer and A. Rachetti, Surf. Technol., 1985, 24, 301–317.
17. J. C. Corbett, F. McNeil-Watson, R. O. Jack and M. Howarth, Colloids Surf., A, 2012, 396, 169–176.
18. B. Blanc, O. Bonhomme, P.-F. Brevet, E. Benichou, C. Ybert and A.-L. Biance, Soft Matter, 2018, 14, 2604–2609.
19. D. Florea, S. Musa, J. M. Huyghe and H. M. Wyss, Proc. Natl. Acad. Sci. U. S. A., 2014, 111, 6554–6559.
20. M. J. Esplandiu, D. Reguera and J. Fraxedas, Soft Matter, 2020, 16, 3717–3726.
21. S. Musa, D. Florea, H. M. Wyss and J. M. Huyghe, Soft Matter, 2016, 12, 1127–1132.
22. D. B. Allan, T. Caswell, N. C. Keim and C. M. van der Wel, Soft-matter/trackpy: Trackpy v0.4.2, 2019 DOI:10.5281/zenodo.3492186.
23. C. R. Harris, K. J. Millman, S. J. van der Walt, R. Gommers, P. Virtanen, D. Cournapeau, E. Wieser, J. Taylor, S. Berg, N. J. Smith, R. Kern, M. Picus, S. Hoyer, M. H. van Kerkwijk, M. Brett, A. Haldane, J. Fernández del Río, M. Wiebe, P. Peterson, P. Gérard-Marchant, K. Sheppard, T. Reddy, W. Weckesser, H. Abbasi, C. Gohlke and T. E. Oliphant, Nature, 2020, 585, 357–362.
24. L. Ai, H. Yue and J. Jiang, Nanoscale, 2012, 4, 5401–5408.
25. P.-Y. Wu, Y.-P. Jiang, Q.-Y. Zhang, Y. Jia, D.-Y. Peng and W. Xu, New J. Chem., 2016, 40, 2878–2885.
26. B. Wang, X. Xiong, H. Ren and Z. Huang, RSC Adv., 2017, 7, 43464–43473.
27. J. L. Anderson, Annu. Rev. Fluid Mech., 1989, 21, 61–99.
28. B. Abecassis, C. Cottin-Bizonne, C. Ybert, A. Ajdari and L. Bocquet, Nat. Mater., 2008, 7, 785–789.
29. J. T. Ault, P. B. Warren, S. Shin and H. A. Stone, Soft Matter, 2017, 13, 9015–9023.
30. A. Banerjee, I. Williams, R. N. Azevedo, M. E. Helgeson and T. M. Squires, Proc. Natl. Acad. Sci. U. S. A., 2016, 113, 8612–8617.
31. T.-Y. Chiang and D. Velegol, J. Colloid Interface Sci., 2014, 424, 120–123.
32. N. Shi, R. Nery-Azevedo, A. I. Abdel-Fattah and T. M. Squires, Phys. Rev. Lett., 2016, 117, 258001.
33. A. Gupta, B. Rallabandi and H. A. Stone, Phys. Rev. Fluids, 2019, 4, 1–15.
34. C. W. Gardiner, Handbook of Stochastic Methods, Springer Berlin Heidelberg, Berlin, Heidelberg, 2004, vol. 13.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: 10.1039/d1sm00908g

---