Polymer ligand binding to surface-immobilized gold nanoparticles: a fluorescence-based study on the adsorption kinetics

Abstract

We report on a simple, fluorescence-based method for the investigation of the binding kinetics of polystyrene ligands, dispersed in an organic solvent, to substrate supported gold nanoparticles. For this purpose, we develop a protocol for the immobilization of gold nanoparticles on glass substrates, that yields sub-monolayers of randomly distributed particles with excellent homogeneity and reproducibility. Using fluorescently labeled polystyrene, we monitor the ligand concentration in bulk dispersion in real time and follow the binding to the particle-decorated substrates. The influence of the ligand molecular weight on the binding kinetics is investigated. We correlate the reaction rates with the diffusion coefficients of the different ligands and are able to describe the molecular weight dependency with a simple kinetic model. Both the diffusion and the activation step appear to contribute to the effective reaction rates.

---

Introduction

Surface functionalized gold nanoparticles (AuNPs) are a widely used tool in research and diagnostics.^1–3 Thanks to their versatile surface functionalization and intense coloration, AuNPs provide an excellent platform for antibody assays with an intrinsic optical read-out, which also is the basis of SARS-CoV-2 rapid test kits.^4,5 Common types of surface functionalization include short chain alkyl thiols and amines,^6–8 linear and branched polymers (e.g. PEG),^9–12 polypeptides and proteins, as well as nucleic acids.^13–15 Such ligands are typically introduced in order to enhance colloidal stability in various environments and to introduce new functionalities to the nanoparticle surface. Many ligands address both aspects to a certain degree. Whereas small molecules tend to aid only in stabilization, larger, more specialized molecules, i.e. proteins and nucleic acids, can provide extended functionality. Modified synthetic polymers on the other hand can be tailored to combine both outstanding stabilization and functionality.^16,17 We have previously investigated the structure and stabilization of polystyrene (PS) functionalized AuNPs dispersed in various organic solvents.¹⁸ Despite the promising characteristics of polymer functionalized AuNPs, the mechanism and kinetics of the ligand binding and brush formation have not yet been studied in detail – for several reasons. Firstly, while there has been extensive theoretical work on polymer brushes, pioneered by Alexander and de Gennes,^19,20 the models for curved surfaces and charged polymers tend to be complex and are limited to static brushes.^21–23 The continuous increase in computing power and the advent of large molecular dynamics simulations now allow more detailed computational studies of brush properties.^24–28 However, there are only few models addressing the dynamics of polymer adsorption and brush formation. Whereas earlier research has been focused on non-specific polymer adsorption,^29,30 a comprehensive model for the thermodynamics and kinetics of end-grafted brush formation on flat surfaces has been developed by Ligoure and Leibler in 1990.³¹ Their model predicts that the brush formation kinetics are governed by the reptation-like diffusion of polymer chains through the layer of already adsorbed ligands. In addition to the complexity of theoretical models, the kinetics of brush formation on nanoparticles are also difficult to investigate by lab experiments. Although established methods, such as attenuated total reflection (ATR) IR spectroscopy,²⁹ surface plasmon spectroscopy (SPS),³² and quartz crystal microbalance (QCM),³³ can be used to monitor adsorption processes on flat gold surfaces in real time, these techniques use specialized and expensive substrates. Moreover, adsorption processes on particles and rough surfaces cannot be investigated with ease. The investigation of adsorption processes on dispersed AuNPs is even more challenging, as there are few experimental techniques that can resolve potentially fast processes at the nanometer scale. Spectroscopic methods have been used successfully to investigate the adsorption of small molecules and biomacromolecules on AuNPs in dispersion and on surfaces.^34–39 To the best of our knowledge, the adsorption and brush formation of linear polymers to AuNP surfaces have not been examined to date.

Here, we report on a simple fluorescence spectroscopy-based approach that allows for the investigation of the adsorption kinetics and brush formation of linear PS homopolymer ligands on small AuNPs. By using substrate-supported AuNPs, the particles are contained outside the bulk sample volume, allowing us to detect fluorophores in solution with greater fidelity, while maintaining the chemical nature of the particles.

Experimental section

Materials

2,2′-Azobisisobutyronitrile (AIBN, 98%, Sigma-Aldrich) was recrystallized from methanol. Styrene (99%, Acros Organics) was passed over basic alumina before use. 2-(Dodecylthiocarbonothioylthio)-2-methylpropanoic acid 3-azido-1-propanol ester (CTA, 98%, Sigma-Aldrich), gold(III) chloride hydrate (HAuCl₄, 99.995%, Sigma-Aldrich), trisodium citrate dihydrate (Na₃Cit·2H₂O, ≥99%, Sigma-Aldrich), citric acid monohydrate (H₃Cit·H₂O, ≥99.5%, AppliChem), ethylenediaminetetraacetic acid tetrasodium salt dihydrate (Na₄EDTA, ≥99%, Sigma-Aldrich), sodium azide (99%, Acros Organics), tetrabutylammonium azide (>95%, TCI), ATTO 488-NHS (ATTO-TEC), dibenzylcyclooctyne-amine (DBCO-amine, >95%, Jena Bioscience), 3-(aminopropyl)-trimethoxysilane (APTMS, 97%, Sigma-Aldrich), N,N-dimethylformamide (p.a., Honeywell), and Sephadex LH-20 (GE Healthcare) were used as received. Ultrapure water with a resistivity of 18 MΩ cm was used for syntheses and purification.

Synthesis

Synthesis of gold nanoparticles. Spherical gold nanoparticles were prepared using an improved inverse Turkevich protocol adapted from the work by Schulz et al.⁴⁰ 500 mL of Milli-Q water were heated to the boil in an Erlenmeyer flask. 0.15 mL of an aqueous solution of Na₄EDTA (0.1 M) and a solution of 245 mg (0.83 mmol) of Na₃Cit·2H₂O and 58.3 mg (0.28 mmol) of H₃Cit·H₂O in 10 mL of Milli-Q water were added. This solution was stirred for 15 min. It should be noted that the duration of this step is crucial for the high reproducibility of the synthesis. Then, 3.3 mL of HAuCl₄ (25 mM aqueous solution) were added under vigorous stirring. The characteristic color change from colorless to grey, purple, and finally wine red was observed within the first minute after the addition of the gold salt. The reaction was kept stirring for 20 min at boil before letting it cool down to room temperature. The concentration of the particle dispersion was estimated from the extinction at a wavelength of 400 nm in the UV/vis spectrum.⁴¹

Synthesis of α,ω-functionalized polystyrene ligands. PS ligands were synthesized by reversible addition–fragmentation chain transfer (RAFT) polymerization in bulk (Scheme 1). The CTA chosen for the synthesis introduces a trithiocarbonate group at one chain end and an azide at the other chain end. The sulfur-containing trithiocarbonate terminus can bind to the AuNP surface, whereas the azide group will be used for dye labeling. As a general procedure, the CTA was weighed-in first, then adding AIBN from a stock solution in styrene and filling up with styrene to reach the desired monomer/CTA ratio. The flask was then sealed and the solution was purged with argon for 20 min before placing it in an oil bath that was pre-heated to 70 °C. The reaction was kept stirring until the desired monomer conversion was reached. The monomer conversion was monitored by ¹H-NMR spectroscopy. All polymers were purified by precipitating three times from methanol. The details for each batch and the analysis results are summarized in Table 1.

Scheme 1 Synthesis of α,ω-functionalized PS and cleavage of the trithiocarbonate group.

Table 1 Summary of quantities and reaction conditions for all batches of polystyrene ligands used in this work. The table contains the molar quantities n of the used chemicals, the reaction temperatures T, the reaction times t_r, the number average molecular weights M_n, and dispersity M_w/M_n determined by size exclusion chromatography

Batch	n(CTA) [mmol]	n(AIBN) [mmol]	n(styrene) [mmol]	T [°C]	t r [h]	M n,SEC [g mol^−1]	M w/Mn
PS6.5	0.54	0.054	70	70	15	6500	1.10
PS21	0.22	0.044	211	70	17	21 400	1.16
PS33	0.22	0.044	211	70	89	33 200	1.15

---

The trithiocarbonate terminus was cleaved in order to obtain more reactive thiol end groups using a modified version of a protocol published by Y. Wu et al.⁴² Although the trithiocarbonate group has been found to bind to gold surfaces,^43–45 the bulky C₁₂ sidechain may reduce the binding strength and increase the ligand footprint compared to a truly end-on grafted chain. In order to prevent loss of the azide terminus due to nucleophilic substitution by primary amines or alcoholamines that are frequently used for trithiocarbonate cleavage, this protocol uses sodium azide as nucleophile.⁴² Briefly, 50 μmol of polymer were dissolved in 20 mL DMF and 60 mg of sodium azide were added. In order to overcome the low solubility of sodium azide in DMF, a solution of 10 mg of tetrabutylammonium azide in 0.5 mL of DMF was added as a phase transfer catalyst. The mixture was then stirred at room temperature for 96 h to achieve quantitative conversion of trithiocarbonate groups. Polymers were purified by triple precipitation from methanol. Successful cleavage was confirmed by the lack of the strong π → π* absorption band at approximately λ = 315 nm of the trithiocarbonate group in the UV/vis spectrum.⁴⁶

Fluorescent labeling of PS ligands. 1 mg (1 μmol) of ATTO 488-NHS and 4 mg (15 mmol) of DBCO-amine were dissolved in 1 mL of anhydrous DMF and stirred at room temperature for 4 days. The raw product was passed over a column of Sephadex LH-20. The strongly fluorescent main fraction was passed over the column again and stored as a 0.5 mM solution in DMF (Scheme 2).

Scheme 2 Coupling of ATTO 488-NHS to DBCO-amine.

ESI-MS: m/z = 886.2 [ATTO 488-DBCO + K], 870.3 [ATTO 488-DBCO + Na], 848.1 [ATTO 488-DBCO].

1 μmol of the PS ligands were dissolved in 0.5 mL of DMF. 0.2 mL of ATTO-DBCO (0.5 mM in DMF) were added, corresponding to a maximum degree of labeling of 10%. The solution was stirred at room temperature for 5 days to ensure quantitative turnover. The polymer was precipitated by addition of 1 mL of methanol and centrifugation at 10 000g relative centrifugal force (rcf.) for 90 min. It was re-dissolved in DMF and precipitated again. The labeled polymers were dried in vacuo and stored as 1 mM solutions in DMF (Scheme 3).

Scheme 3 Coupling of ATTO 488-DBCO to α,ω-functionalized PS.

Amine-functionalization of glass slides and AuNP deposition. Standard size glass slides were cleaned with RCA-1 solution for 30 min, rinsed with Milli-Q water and ethanol and dried at 60 °C.⁴⁷ The slides were immersed in a solution containing 0.5 vol% of APTMS and 0.2 vol% glacial acetic acid in methanol and incubated at room temperature for 3 h. The slides were sonicated in ethanol for 10 min to remove physisorbed silane, dried with N₂ and incubated at 60 °C for 1 h to improve silane binding. The slides were sonicated twice in ethanol and once in Milli-Q water for 10 min each and dried at 60 °C. For particle immobilization the slides were placed in Petri dishes and 2 mL of AuNP dispersion (c = 1 nM) were dispensed on each of the slides. The Petri dishes were covered and the slides were incubated overnight. The now colorless solution was removed with a pipette, the slides were rinsed with Milli-Q water and ethanol and dried with N₂. For the kinetics measurements, the substrates were cut into smaller pieces (∼8 × 26 mm²) and exposed to O₂ plasma (0.2 mbar, 200 W, 5 min) using a PlasmaFlecto10 (plasma technology GmbH, Germany). The samples were incubated in pH 7 buffer solution for 2 h to remove oxidation products and to equilibrate the surface charge. Finally, the substrates were rinsed with Milli-Q water followed by ethanol.

Methods

Dynamic light scattering (DLS). Angle-dependent DLS was used to investigate the diffusion characteristics and hydrodynamic dimensions of the PS ligands. All measurements were performed on a 3D LS Spectrometer (LS Instruments, Switzerland) operated in 2D pseudo-cross correlation mode. The setup was equipped with a HeNe laser (λ = 632.8 nm) and a decalin bath for temperature control and refractive index matching. Solutions of 5 g L⁻¹ PS in DMF were prepared and passed through a 0.45 μm PTFE syringe filter directly into borosilicate cuvettes. Samples were equilibrated in the decalin bath at 20 °C for 15 min before the measurements. Three measurements per angle were performed at angles between 30° and 140° in 10° increments. Measurement times were between 90 and 120 s, depending on the molecular weight of the polymer. The obtained correlation functions were analyzed using cumulant analysis following the method reported by Frisken.⁴⁸

Transmission electron microscopy (TEM). TEM investigations were performed on a JEM-2100Plus (JEOL, Japan) operating in bright-field mode at 80 kV acceleration voltage. Samples of aqueous dispersions were prepared by dispensing 7 μL of dilute particle dispersion on carbon-coated copper grids (200 mesh, Science Services, Germany) and drying in air. ImageJ (v.1.50, NIH, USA) was used for image processing and analysis.

Atomic force microscopy (AFM). We used AFM to investigate the surface density of AuNPs immobilized on amine-functionalized glass substrates and the morphology of the particles before and after ligand binding. Measurements were performed on a NanoWizard 4 (JPK Instruments, Germany). For the investigation of packing density, the AFM was operated in intermittent contact (AC) mode using OTESPA-R3 (Bruker, USA, f = 300 kHz, k = 26 N m⁻¹, r_tip = 7 nm) probes. 1 μm × 1 μm scans were measured at a line rate of 1 Hz. For the investigation of particle morphology, the AFM was operated in quantitative imaging (QI) mode, a high-resolution force mapping technique, using SNL-B (Bruker, USA, f = 23 kHz, k = 0.12 N m⁻¹, r_tip = 2 nm) probes. In this mode, a force curve is measured for each pixel and the force curves are analyzed using batch processing in order to obtain information on height, stiffness, and adhesion for each pixel, from which an image is then constructed. The tip velocity for approach and withdrawal was 20 μm s⁻¹ and the setpoint force was 1 nN.

Fluorescence spectroscopy. We used fluorescence spectroscopy as a main technique to investigate the kinetics of polymer ligand binding to substrate supported AuNPs. Measurements were performed on a FLS 980 (Edinburgh Instruments, UK) equipped with a Xe lamp as light source and PMT detector in a 90° setup. For kinetics measurements, 2.5 mL of 10 nM dye-labeled PS in DMF were filled into quartz cuvettes (Hellma, Germany) with a stirring bar and seated in the temperature-controlled cuvette holder set to 20 °C. The stirring bar was actuated by a small magnetic stirrer placed on top of the cuvette. The samples were equilibrated for 30 min. Synchronous spectra were measured for excitation wavelengths, λ_ex, from 480 to 550 nm and an emission offset of 20 nm. Both excitation and emission bandwidths were set to 5 nm. The step width and integration time were 1 nm and 0.2 s, respectively. Two runs per measurement were performed and the intensities from both runs were added. The spectra were corrected for fluctuations of source intensity using a photodiode reference detector. A spectrum was recorded every 10 min. After 10 measurements (90 min), the substrate supported gold nanoparticles were added, fixing the substrate to the cuvette wall opposite of the emission arm of the spectrometer. A sketch of the measurement setup is show in Fig. S1 in the ESI.† The spectra were analyzed using a Gaussian fit with a linear background.

Results & discussion

The strong absorbance of AuNPs in dispersion represents an inherent challenge for their use in fluorescence spectroscopy methods. Unless there is little or no spectral overlap between the excitation and emission of the dye and the absorbance of the AuNPs, the particles will absorb a large portion of the excitation beam and the light emitted from the fluorophores. For typical particle concentrations, this can result in a significant decrease of the detected emission intensity and changes the shape of the recorded spectrum.⁴⁹ It also gives rise to a dilemma, whenever AuNPs and fluorophores are used in concentrations of similar orders of magnitude: Similar to a strong inner filter effect, the overall sample concentration strongly affects emission intensity and spectral shape in a non-linear fashion.⁵⁰ The effect can be minimized, for instance by reducing the path length of the light through the sample, but can never be avoided completely. In this work we follow a different approach by using substrate-supported AuNPs as a model system for the investigation of polymer ligand binding kinetics. To do so, we prepared monodisperse, spherical AuNPs according to an improved inverse Turkevich method.⁴⁰ The particles obtained by this method are polycrystalline without strong faceting. As organothiols have been shown to adsorb differently to the various crystal facets and edges of gold surfaces, the morphology and crystallinity of gold particles is expected to affect the ligand binding kinetics and grafting density.^26,51Fig. 1A shows a representative TEM micrograph of the as-prepared AuNPs. Aggregates shown in the image are a result of the drying process during sample preparation and are absent in dilute aqueous dispersion. The average particle diameter was determined as 12.2 ± 0.8 nm. The size histogram and corresponding Gaussian fit to the distribution are shown in Fig. 1B.

Fig. 1 (A) Representative TEM image of as-prepared AuNPs used in this work. (B) Histogram and corresponding Gaussian fit of particle diameters obtained from several TEM images. (C) SEC curves of the PS ligands obtained from RAFT synthesis. (D) Normalized excitation, emission, and synchronous spectra of PS₂₁-ATTO.

For the ligand exchange experiments, we synthesized α,ω-functionalized PS homopolymer ligands with three different molecular weights by RAFT polymerization. One chain end carries the thiol group binding to the AuNP surface, whereas the other terminus carries the dye label or otherwise the residual azide group. Fig. 1C shows the molecular weight distribution curves obtained from SEC in THF. All three polymers exhibit a single peak and a small shoulder, which corresponds to the chain–chain termination product. Due to the nature of the RAFT mechanism, these longer chains do not carry a thiol group and are therefore not relevant in our kinetics investigation. As shown in Table 1, the polymers have dispersities between 1.10 and 1.16. The polymers were partly functionalized with fluorescent ATTO 488, a Rhodamine 110 derivative, using strain-promoted azide–alkyne cycloaddition (SPAAC) coupling. For this purpose, ATTO 488-NHS was first functionalized with DBCO-amine and then coupled to the polymers. As only 0.1 equivalents of dye were used, most of the polymer chains are not functionalized. The exact degree of functionalization is not easily accessible. However, a relatively low fraction of functionalized chains is preferable in order to avoid alteration of the binding kinetics by ionic dye–dye interactions between adsorbed polymer chains. Fig. 1D shows normalized fluorescence spectra measured of PS₃₃-ATTO. The excitation and emission spectrum exhibit the typical mirror symmetry commonly observed for Rhodamine derivatives. The synchronous spectrum is obtained by scanning through the excitation and emission wavelengths simultaneously with a fixed offset between the two. Synchronous scans are particularly helpful for systems, in which the exact excitation and emission maxima are unknown or change over time, while the Stokes shift remains constant. Consequently, the intensities measured in synchronous mode should not be affected as strongly by spectral shifts of excitation or emission maxima as, for instance, single wavelength kinetic measurements. Another advantage in this particular case is the high symmetry of the peak in the synchronous spectrum, which can be fitted by a Gaussian function. This increases the precision in the determination of fluorescence intensities, especially for poor signal-to-noise ratios. Since the effective dye concentrations during measurements are very small (∼1 nM), the inner filter effect of the dye itself can be neglected. These characteristics allow us to assume a proportionality between the measured fluorescence intensity and the concentration of dye-labeled polymer in solution.

In order to immobilize AuNPs, we functionalized the surface of soda-lime glass substrates with APTMS, which introduces primary amine groups on the surface. AuNPs are then deposited by covering the amine-functionalized glass slides with an aqueous particle dispersion. The particles are fixed to the surface by a combination of amine coordination and van der Waals forces. Fig. 2A shows a representative AFM image of a substrate after AuNP deposition and rinsing. The particles are randomly distributed and do not form clusters during deposition. The concentric rings in the FFT in the inset of Fig. 2A underlines the random distribution of the AuNPs on the substrate. The periodicity of the rings is caused by the correlation of particle size and minimum allowed distance, whereas the particle positions are fully uncorrelated. The deposition process is highly reproducible. Fig. 2B shows the particle number density from two AFM measurement series, each on five individual samples. All AFM images and further discussion of the particle arrangement can be found in Fig. S2–S7 in the ESI.† The average particle number density is 684 ± 40 μm⁻², as indicated by the dashed, horizontal line and the grey area.

Fig. 2 (A) Representative AFM height image for AuNPs immobilized on amine-functionalized glass slides. The inset shows the corresponding FFT. (B) AuNP number densities measured from multiple samples. The dashed, horizontal line and the grey area represent the average particle number density and its standard deviation, respectively.

After the AuNP deposition, the residual amine groups have to be deactivated in order to prevent non-specific adsorption of dye-labeled polymer to the glass surface. We achieved this by plasma oxidation.

The principle of our fluorescence based kinetic investigation is depicted in Scheme 4. Initially, all polymer (partially dye labeled) is in the bulk phase and the substrate carrying the AuNPs is placed at one side of the reaction volume, i.e. in the cuvette. The polymer ligands gradually diffuse to the AuNP surface, adsorb, and form a brush. Thus, the concentration of dye-labeled and unlabeled polymer in the bulk phase decreases over time, which is tracked in situ by fluorescence measurements in the bulk phase.

Scheme 4 Representation of the ligand binding process to substrate-supported AuNPs (red spheres). The fluorescence intensity of the bulk phase, resembled by the green coloration of the background, decreases during the reaction time Δt, due to the binding of dye-labeled polymer to the AuNP surface.

We performed measurements in triplicate for ligands with molecular weights of 6.5, 21, and 33 kg mol⁻¹ with a starting concentration of c₀ = 10 nM in DMF. The development of the fluorescence intensities over time is shown in Fig. 3A–C. All intensity profiles exhibit a single exponential decrease with time. Eqn (1) is used for fitting, where I_∞ is the plateau intensity for t → ∞, I₀ is the starting intensity, k_eff is the effective rate constant and t₀ is the starting time.

I(t) = I_∞ + (I₀ − I_∞)exp[−k_eff(t − t₀)] (1)

In order to prove the single exponential nature of our binding kinetics, the intensity differences I(t) − I_∞ for t ≤ 500 min, are shown as a semi-logarithmic plots in Fig. 3D–F. Within this timeframe, all measurements show a linear change of the logarithmic fluorescence intensity.

Fig. 3 (A–C) Peak fluorescence intensities as a function of time measured in the bulk phase during the ligand binding to surface-immobilized AuNPs. The separate curves for each molecular weight represent repeated measurements and are deliberately offset for clarity. (D–F) Semi-logarithmic plots of the fluorescence intensities in relation to the plateau intensity I_∞. (G–I) Corresponding plots of temporal evolution of the calculated number of polymer chains, N_PS, per particle.

The effective rate constants, k_eff, obtained from fits to the experimental data using eqn (1) are summarized in Table 2. There is a clear trend for decreasing effective rate constants with increasing molecular weight. However, we expect a more complex dependency of k_eff on various other parameters, including the polymer concentration, the total available gold surface area, the size and curvature of the AuNPs, and the spacing between the particles. Thus, the exact dimensionality of k_eff is unknown and depends on the reaction parameters that contribute to the full kinetic model.

Table 2 Fitted effective rate constants, average effective rate constants, and average number of polymer chains per particle for each molecular weight

Ligand	k eff × 10^−5 [s^−1]	k̄ eff × 10^−5 [s^−1]	f̄ ∞
a Error is standard deviation from fit. b Error is standard deviation of individual fit values.
PS6.5	16.8 ± 0.4^a	15 ± 1^b	45 ± 3^b
	13.7 ± 0.3^a
	14.4 ± 0.3^a
PS21	9.5 ± 0.5^a	9.1 ± 0.4^b	28 ± 4^b
	9.1 ± 0.2^a
	8.7 ± 0.2^a
PS33	8.5 ± 0.2^a	7.8 ± 0.6^b	29 ± 2^b
	7.0 ± 0.1^a
	8.0 ± 0.1^a

---

Another interesting aspect of the ligand binding is the surface coverage or grafting density that is achieved in equilibrium. As the exact surface area of substrate supported AuNPs that is accessible by the ligands is unknown, we express the surface coverage as the average number of adsorbed chains per particle, f. We calculate f from the intensity–time curves according to eqn (2), where c_PS and V_PS are the concentration and volume of the ligand solution respectively, A_s is the surface area of the substrate, and σ_AuNP is the particle number density of AuNPs on the substrate.

The corresponding plots of f as a function of time are shown in Fig. 3G–I. We observe a slight dependency of f on the molecular weight of the ligand, with the highest value being achieved for the shortest ligand. The difference between ligands with molecular weights of 21 and 33 kg mol⁻¹ is negligible. Values for the average number of chains per particle at the end of the process, f̄_∞, are given in Table 2. The equilibrium concentration, i.e. the concentration of chains remaining in solution decreases with increasing f̄_∞ and is therefore lowest for the 6.5 kg mol⁻¹ ligand. The equilibrium state appears to be determined by the free energy change due to chain stretching, which we discuss in detail in the ESI.† We find a strikingly similar degree of stretching of chains within the polymer brushes formed by the three different ligands.

We now want to further investigate the influence of molecular weight and diffusion characteristics of the polymer ligands on the binding kinetics. For this purpose, we employ multi-angle DLS to directly measure the polymer diffusion coefficients in dilute solution. Fig. 4A shows plots of the average decay constants, Γ, as a function of the squared magnitude of the scattering vector, q². The magnitude of the scattering vector is calculated using eqn (3), where n is the refractive index of the medium, λ is the wavelength of the laser used for the experiment and θ is the scattering angle.

Decay constants were obtained from cumulant fits of the recorded intensity–time autocorrelation functions.⁴⁸ For Brownian diffusion, Γ and q are related by:

Γ = D_tq² (4)

Here D_t is the translational diffusion coefficient. Hence, the slopes of the linear fits in Fig. 4A correspond to the diffusion coefficients.

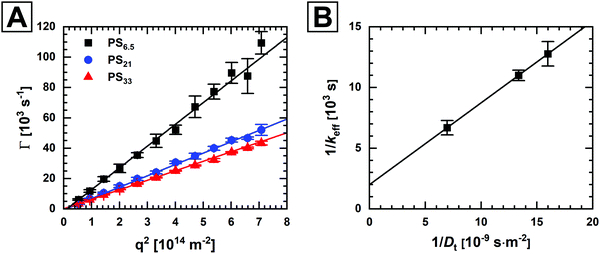Fig. 4 (A) Decay constants from angle-dependent DLS measurements. The solid lines are linear fits to the data according to eqn (4). The slope of the fit yields the diffusion coefficients. (B) Reciprocal plot of the effective rate constant against the polymer diffusion coefficient.

As our kinetics appear much simpler than the one predicted by Ligoure and Leibler,³¹ we attempt to linearize the relationship between k_eff and D_t using a general approach for diffusion-controlled reactions. For reactions, in which the rate constant of the transport process, k_d, and the rate constant of the activation-governed reaction step, k_a, are of a similar order of magnitude, k_eff can be approximated following eqn (5).

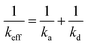In the classic Smoluchowski model, the rate constant of diffusion is defined as k_d = 4πrD, where r is the interaction radius and D the diffusion coefficient. However, this simple form was derived for reactions of isotropic reactants in solution. Thus, we restrict ourselves to the assumption that k_d ∝ D_t with a proportionality factor β and re-write eqn (5) as:

Plotting 1/k_effversus 1/D_t in Fig. 4B, we find excellent agreement with the postulated linearity.

From the linear fit we determined the reaction rates k_a and k_d,M, which are summarized in Table 3. The values indicate that both principal steps of the ligand binding process are indeed similarly slow. Furthermore, we can determine a crossover molecular weight, M_c, at k_a = k_d, for which the kinetics change from predominantly diffusion-limited to predominantly activation-limited. In our case, we find M_c ≈ 1.2 kg mol⁻¹, corresponding to chain dimensions on the order of the Kuhn length, l_K, for PS. This finding bears significance, as chains do not form random coils and cannot entangle at length scales below l_K. Therefore, such a short chain will behave like a small, rod-like molecule. Moreover, it also complies with the model developed by Ligoure and Leibler, in which the repulsive interaction between an approaching chain and the brush vanishes for distances d < l_K from the surface. In reverse, their theory also suggests that the diffusion of chains that are significantly larger than l_K is strongly hindered by the forming brush,³¹ which is also supported by our data.

Table 3 Summary of reaction rates of the diffusion and the activation steps of the ligand binding process

k a × 10^−5 [s^−1]	k d,6.5 × 10^−5 [s^−1]	k d,21 × 10^−5 [s^−1]	k d,33 × 10^−5 [s^−1]
50.1 ± 0.3	21.3 ± 0.4	11.1 ± 0.2	9.3 ± 0.1

---

Finally, we used AFM to characterize the samples after the ligand binding experiments. The AuNP number density on the substrate remained unchanged with an average of 666 ± 17 μm⁻² from three scans. The AFM images are shown in Fig. S8–S10 in the ESI.† This confirms the strong adhesion of the particles to the glass substrate. In addition, we investigated the specificity of the ligand binding. We measured high resolution force maps on substrates with immobilized AuNPs before and after the ligand binding reaction. Please refer to the ESI† for details on these AFM measurements, including a step-by-step explanation of raw data analysis in Fig. S11–S15 (ESI†). Height profiles for samples prior to and after ligand binding with PS₃₃ are shown in Fig. 5A and B respectively. The reference force, i.e. the point on the force curve from which the height information was obtained, was 50 pN. There are distinct differences between the images with and without polymer. Firstly, the height profile for the sample without polymer shows a rather abrupt height step along the edges of the particle footprint. The much smoother height profile for the sample with PS₃₃ could be a result of softness from the ligand shell. Secondly, the sample after ligand binding shows shallow bridges between adjacent particles, which are not present for the sample without polymer. The apparent softness and the bridging between particles are both indications for the presence of polymer on the particles. Fig. 5C and D shows the corresponding adhesion plots obtained from the same force maps. The adhesion force is the minimum of the force curve during probe withdrawal. For both samples the strongest adhesion force is measured on the flat substrate, whereas the adhesion on the AuNPs appears to be weaker. This can be attributed to the high curvature of the AuNPs surface and therefore smaller effective contact area between probe and particle. Moreover, the glass substrate is prone to condensation of water, which results in capillary forces. Similar to the height image, the particles on the sample without polymer are more distinctly contrasted against the substrate. We observe much more diffuse outlines of the particles for the sample after ligand binding. The aforementioned bridges between individual particles are nearly indistinguishable from the particles themselves. The features described here can be observed for all three molecular weights (AFM images in Fig. S16–S19 in the ESI†) but are most pronounced for PS₃₃. We therefore conclude that the polymer ligands can in fact be visualized. The accumulation of material around the AuNPs confirms that the polymer is specifically adsorbed to the gold surface rather than non-specifically to the entire sample surface. We observed non-specific adsorption on glass slides functionalized with APTMS that were not treated with plasma, as shown by the fluorescence intensity curves in Fig. S20 in the ESI.†

Fig. 5 (A and B) AFM height images of AuNPs immobilized on glass before and after the ligand binding reaction with PS₃₃ ligand respectively for a reference force of 50 pN. (C and D) Corresponding adhesion force maps measured in air. The apparent elongation of particles for the sample without polymer is a result of thermal sample creep.

Conclusion

We used a simple fluorescence spectroscopy method for the investigation of the binding kinetics of PS ligands to AuNPs that were immobilized on glass substrates. Using PS ligands with different molecular weights, we found a strong dependence of the adsorption rate on the size and diffusion coefficient of the polymer chains. Based on a standard kinetic model for diffusion-limited reactions, we found similar contributions of activation- and diffusion-limited steps to the effective reaction rate. From the low diffusive rate constants we deduced a strong hindrance of chain diffusion to the AuNP surface by polymer already attached to the particle surface. The concentration–time profiles were successfully described by single exponential functions, which is in agreement with theory for a system close to equilibrium.³¹ Such an approximation could be justified by the relatively low starting concentration of ligands, where the chemical potential of the dissolved chains is sufficiently small. Different kinetics may be observed for larger molecular weights or higher polymer concentrations. We used AFM to visualize the polymer chains on the particles in dry state and were able to confirm the specific adsorption of PS on the AuNP surface.

The substrate supported approach can be used for kinetic investigation of ligand binding kinetics by other methods, such as spectroscopic dark field microscopy. Given sufficient instrument sensitivity, the refractive index dependency of the localized surface plasmon resonance could be used to directly measure the polymer grafting in real time. Furthermore, we want to highlight that our approach can be easily extended to other polymers including more complex architectures as for example in block copolymers.

Conflicts of interest

There are no conflicts of interest to declare.

Acknowledgements

MK would like to thank the DFG for funding under grant KA3880/6-1. The authors acknowledge the DFG and the state of NRW for funding the cryo-TEM (INST 208/749-1 FUGG). The authors also would like to thank Marius Otten for TEM measurements and Stephanie Scheelen from Macromolecular Chemistry for SEC measurements.

References

1. E. Boisselier and D. Astruc, Gold Nanoparticles in Nanomedicine: Preparations, Imaging, Diagnostics, Therapies and Toxicity, Chem. Soc. Rev., 2009, 38(6), 1759–1782.
2. K. Saha, S. S. Agasti, C. Kim, X. Li and V. M. Rotello, Gold Nanoparticles in Chemical and Biological Sensing, Chem. Rev., 2012, 112(5), 2739–2779.
3. P. M. Tiwari, K. Vig, V. A. Dennis and S. R. Singh, Functionalized Gold Nanoparticles and Their Biomedical Applications, Nanomaterials, 2011, 1(1), 31–63.
4. H. N. Abdelhamid and G. Badr, Nanobiotechnology as a Platform for the Diagnosis of COVID-19: A Review, Nanotechnol. Environ. Eng., 2021, 6(1), 19.
5. C. Huang, T. Wen, F.-J. Shi, X.-Y. Zeng and Y.-J. Jiao, Rapid Detection of IgM Antibodies Against the SARS-CoV-2 Virus via Colloidal Gold Nanoparticle-Based Lateral-Flow Assay, ACS Omega, 2020, 5(21), 12550–12556.
6. K. S. Mayya and F. Caruso, Phase Transfer of Surface-Modified Gold Nanoparticles by Hydrophobization with Alkylamines, Langmuir, 2003, 19(17), 6987–6993.
7. M. Karg, N. Schelero, C. Oppel, M. Gradzielski, T. Hellweg and R. von Klitzing, Versatile Phase Transfer of Gold Nanoparticles from Aqueous Media to Different Organic Media, Chem. – Eur. J., 2011, 17(16), 4648–4654.
8. S. Ehlert, S. M. Taheri, D. Pirner, M. Drechsler, H.-W. Schmidt and S. Förster, Polymer Ligand Exchange to Control Stabilization and Compatibilization of Nanocrystals, ACS Nano, 2014, 8(6), 6114–6122.
9. W. P. Wuelfing, S. M. Gross, D. T. Miles and R. W. Murray, Nanometer Gold Clusters Protected by Surface-Bound Monolayers of Thiolated Poly(ethylene glycol) Polymer Electrolyte, J. Am. Chem. Soc., 1998, 120(48), 12696–12697.
10. K. Rahme, L. Chen, R. G. Hobbs, M. A. Morris, C. O'Driscoll and J. D. Holmes, PEGylated Gold Nanoparticles: Polymer Quantification as a Function of PEG Lengths and Nanoparticle Dimensions, RSC Adv., 2013, 3(17), 6085–6094.
11. M. K. Corbierre, N. S. Cameron and R. B. Lennox, Polymer-Stabilized Gold Nanoparticles with High Grafting Densities, Langmuir, 2004, 20(7), 2867–2873.
12. G. Prencipe, S. M. Tabakman, K. Welsher, Z. Liu, A. P. Goodwin, L. Zhang, J. Henry and H. Dai, PEG Branched Polymer for Functionalization of Nanomaterials with Ultralong Blood Circulation, J. Am. Chem. Soc., 2009, 131(13), 4783–4787.
13. S. J. Hurst, A. K. R. Lytton-Jean and C. A. Mirkin, Maximizing DNA Loading on a Range of Gold Nanoparticle Sizes, Anal. Chem., 2006, 78(24), 8313–8318.
14. C. M. Niemeyer and B. Ceyhan, DNA-Directed Functionalization of Colloidal Gold with Proteins, Angew. Chem., Int. Ed., 2001, 40(19), 3685–3688.
15. J. M. Abad, S. F. L. Mertens, M. Pita, V. M. Fernández and D. J. Schiffrin, Functionalization of Thioctic Acid-Capped Gold Nanoparticles for Specific Immobilization of Histidine-Tagged Proteins, J. Am. Chem. Soc., 2005, 127(15), 5689–5694.
16. S. O. Pereira, A. Barros-Timmons and T. Trindade, Polymer@gold Nanoparticles Prepared via RAFT Polymerization for Opto-Biodetection, Polymers, 2018, 10(2), 189.
17. J. Shan and H. Tenhu, Recent Advances in Polymer Protected Gold Nanoparticles: Synthesis, Properties and Applications, Chem. Commun., 2007,(44), 4580–4598.
18. J. Sindram, M. Krüsmann, M. Otten, T. Pauly, L. Nagel-Steger and M. Karg, Versatile Route toward Hydrophobically Polymer-Grafted Gold Nanoparticles from Aqueous Dispersions, J. Phys. Chem. B, 2021 DOI:10.1021/acs.jpcb.1c03772.
19. S. Alexander, Adsorption of Chain Molecules With a Polar Head a Scaling Description, J. Phys., 1977, 38(8), 983–987.
20. P. G. de Gennes, Conformations of Polymers Attached to an Interface, Macromolecules, 1980, 13(5), 1069–1075.
21. M. Daoud and J. P. Cotton, Star Shaped Polymers: A Model for the Conformation and its Concentration Dependence, J. Phys., 1982, 43(3), 531–538.
22. C. M. Wijmans and E. B. Zhulina, Polymer Brushes at Curved Surfaces, Macromolecules, 1993, 26(26), 7214–7224.
23. E. B. Zhulina, T. M. Birshtein and O. V. Borisov, Curved Polymer and Polyelectrolyte Brushes Beyond the Daoud-Cotton Model, Eur. Phys. J. E: Soft Matter Biol. Phys., 2006, 20(3), 243–256.
24. K. Binder, Scaling concepts for polymer brushes and their test with computer simulation, Eur. Phys. J. E: Soft Matter Biol. Phys., 2002, 9(3), 293–298.
25. D. Dimitrov, A. Milchev and K. Binder, Polymer Brushes on Flat and Curved Substrates: Scaling Concepts and Computer Simulations, Macromol. Symp., 2007, 252(1), 47–57.
26. T. Djebaili, J. Richardi, S. Abel and M. Marchi, Atomistic Simulations of the Surface Coverage of Large Gold Nanocrystals, J. Phys. Chem. C, 2013, 117(34), 17791–17800.
27. R. C. Hayward and W. W. Graessley, Excluded Volume Effects in Polymer Solutions. 1. Dilute Solution Properties of Linear Chains in Good and ϑ Solvents, Macromolecules, 1999, 32(10), 3502–3509.
28. F. L. Verso, L. Yelash, S. A. Egorov and K. Binder, Interactions Between Polymer Brush-Coated Spherical Nanoparticles: The Good Solvent Case, J. Chem. Phys., 2011, 135(21), 214902.
29. P. Frantz and S. Granick, Kinetics of Polymer Adsorption and Desorption, Phys. Rev. Lett., 1991, 66(7), 899–902.
30. J. F. Douglas, H. E. Johnson and S. Granick, A Simple Kinetic Model of Polymer Adsorption and Desorption, Science, 1993, 262(5142), 2010–2012.
31. C. Ligoure and L. Leibler, Thermodynamics and Kinetics of Grafting End-Functionalized Polymers to an Interface, J. Phys., 1990, 51(12), 1313–1328.
32. K. A. Peterlinz and R. Georgiadis, In Situ Kinetics of Self-Assembly by Surface Plasmon Resonance Spectroscopy, Langmuir, 1996, 12(20), 4731–4740.
33. H. Xu and J. B. Schlenoff, Kinetics, Isotherms, and Competition in Polymer Adsorption Using the Quartz Crystal Microbalance, Langmuir, 1994, 10(1), 241–245.
34. E. M. Nelson and L. J. Rothberg, Kinetics and Mechanism of Single-Stranded DNA Adsorption onto Citrate-Stabilized Gold Nanoparticles in Colloidal Solution, Langmuir, 2011, 27(5), 1770–1777.
35. H. Li and L. J. Rothberg, Label-Free Colorimetric Detection of Specific Sequences in Genomic DNA Amplified by the Polymerase Chain Reaction, J. Am. Chem. Soc., 2004, 126(35), 10958–10961.
36. K. Siriwardana, A. Wang, K. Vangala, N. Fitzkee and D. Zhang, Probing the Effects of Cysteine Residues on Protein Adsorption onto Gold Nanoparticles Using Wild-Type and Mutated GB3 Proteins, Langmuir, 2013, 29(35), 10990–10996.
37. B. Jin, W.-J. Bao, Z.-Q. Wu and X.-H. Xia, In Situ Monitoring of Protein Adsorption on a Nanoparticulated Gold Film by Attenuated Total Reflection Surface-Enhanced Infrared Absorption Spectroscopy, Langmuir, 2012, 28(25), 9460–9465.
38. R. Dinkel, B. Braunschweig and W. Peukert, Fast and Slow Ligand Exchange at the Surface of Colloidal Gold Nanoparticles, J. Phys. Chem. C, 2016, 120(3), 1673–1682.
39. S. Perumal, A. Hofmann, N. Scholz, E. Rühl and C. Graf, Kinetics Study of the Binding of Multivalent Ligands on Size-Selected Gold Nanoparticles, Langmuir, 2011, 27(8), 4456–4464.
40. F. Schulz, T. Homolka, N. G. Bast, V. Puntes, H. Weller and T. Vossmeyer, Little Adjustments Significantly Improve the Turkevich Synthesis of Gold Nanoparticles, Langmuir, 2014, 30(35), 10779–10784.
41. T. Honold, D. Skrybeck, K. G. Wagner and M. Karg, Fully Reversible Quantitative Phase Transfer of Gold Nanoparticles Using Bifunctional PNIPAM Ligands, Langmuir, 2017, 33(1), 253–261.
42. Y. Wu, Y. Zhou, J. Zhu, W. Zhang, X. Pan, Z. Zhang and X. Zhu, Fast Conversion of Terminal Thiocarbonylthio Groups of RAFT Polymers to “Clickable” Thiol Groups via Versatile Sodium Azide, Polym. Chem., 2014, 5(19), 5546–5550.
43. A.-S. Duwez, P. Guillet, C. Colard, J.-F. Gohy and C.-A. Fustin, Dithioesters and Trithiocarbonates as Anchoring Groups for the “Grafting-To” Approach, Macromolecules, 2006, 39(8), 2729–2731.
44. B. Ebeling and P. Vana, RAFT-Polymers with Single and Multiple Trithiocarbonate Groups as Uniform Gold-Nanoparticle Coatings, Macromolecules, 2013, 46(12), 4862–4871.
45. C.-A. Fustin and A.-S. Duwez, Dithioesters and Trithiocarbonates Monolayers on Gold, J. Electron Spectrosc. Relat. Phenom., 2009, 172(1), 104–106.
46. K. Skrabania, A. Miasnikova, A. M. Bivigou-Koumba, D. Zehm and A. Laschewsky, Examining the UV-vis Absorption of RAFT Chain Transfer Agents and Their Use for Polymer Analysis, Polym. Chem., 2011, 2(9), 2074–2083.
47. W. P. Kern and A. David, Cleaning Solutions Based on Hydrogen Peroxide for use in Silicon Semiconductor Technology, RCA Rev., 1970, 31(2), 187–206.
48. B. J. Frisken, Revisiting the Method of Cumulants for the Analysis of Dynamic Light-Scattering Data, Appl. Opt., 2001, 40(24), 4087–4091.
49. L. Xu, B. Li and Y. Jin, Inner Filter Effect of Gold Nanoparticles on the Fluorescence of Quantum Dots and its Application to Biological Aminothiols Detection, Talanta, 2011, 84(2), 558–564.
50. M. Kubista, R. Sjöback, S. Eriksson and B. Albinsson, Experimental Correction for the Inner-Filter Effect in Fluorescence Spectra, Analyst, 1994, 119(3), 417–419.
51. L. Strong and G. M. Whitesides, Structures of Self-Assembled Monolayer Films of Organosulfur Compounds Adsorbed on Gold Single Crystals: Electron Diffraction Studies, Langmuir, 1988, 4(3), 546–558.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: 10.1039/d1sm00892g

---