Open Access Article
Open Access ArticleActive binary switching of soft colloids: stability and structural properties
Michael
Bley
a,
Joachim
Dzubiella
*ab and
Arturo
Moncho-Jordá
 *cd
*cd
aPhysikalisches Institut, Albert-Ludwigs-Universität Freiburg, Hermann-Herder Straße 3, D-79104 Freiburg, Germany. E-mail: joachim.dzubiella@physik.uni-freiburg.de
bResearch Group for Simulations of Energy Materials, Helmholtz-Zentrum Berlin für Materialien und Energie, D-14109 Berlin, Germany. E-mail: moncho@ugr.es
cDepartamento de Física Aplicada, Universidad de Granada, Campus Fuentenueva S/N, 18071 Granada, Spain
dCarlos I Institute of Theoretical and Computational Physics, Facultad de Ciencias, Universidad de Granada, Campus Fuentenueva S/N, 18071 Granada, Spain
First published on 29th July 2021
Abstract
We employ reactive dynamical density functional theory (R-DDFT) and reactive Brownian dynamics (R-BD) simulations to study the non-equilibrium structure and phase behavior of an active dispersion of soft Gaussian colloids with binary interaction switching, i.e., we consider a one-component colloidal system in which every particle can individually switch stochastically between two interaction states (here, sizes ‘big’ and ‘small’) at predefined rates. We consider the influence of switching activity on the inhomogeneous density profiles of the colloids confined by various external potentials, as well as on their pair structure and phase behavior in bulk solutions. For the latter, we extend the R-DDFT method to incorporate the Percus test-particle route. Our results demonstrate that switching activity strongly modifies the steady-state density profiles and structural (pair) correlations. In particular, the switching rate interpolates from a near-equilibrium binary colloidal mixture of two states at very low rates to a non-equilibrium, ‘one-state liquid’ at very high rates characterized by one, average interaction size. The latter limit can be described by an equivalent effective one-component (EOC) equilibrium system, for which the exact analytical expression for the effective pair potential is a diffusion-weighted superposition of the active systems' pair potentials. This leads to the interesting fact that under certain conditions an interacting switching system can behave like a non-interacting (ideal) gas in the limit of high switching rates. Moreover, for colloids that are unstable (i.e., demix) near equilibrium, we demonstrate that phase separation and micro-clustering in both confinement and bulk can be dynamically controlled by the switching rate, and vanish for high rates. All R-DDFT results are in excellent agreement with our R-BD simulations.
1 Introduction
Active matter systems are usually defined as collections of particles containing internal degrees of freedom with the ability to take in and dissipate energy and, in the process, execute systematic movement. Examples of active soft matter systems are self-propelled nanoparticles,1,2 active Brownian particles,3–6 active contractile biopolymers such as myosin II motors acting on actin filaments inside the cytoskeleton of living cells,7,8 or biological systems such as bacteria.9 These non-equilibrium systems have drawn the attention of the soft matter scientific community in the recent years due to the very rich dynamic and phase behavior.10 By continually consuming energy, they circumvent the laws of equilibrium thermodynamics, leading to steady states that depend on kinetic parameters.11Biological activity, in particular mediated through fuel-driven changes of molecular properties and conformations, has been made responsible for liquid–liquid phase separation and condensation in cells, with large implications for physiology and disease.12,13 Living cells contain distinct sub-compartments to facilitate spatiotemporal regulation of biochemical reactions where transient microstructuring is key for function. Recently, novel systems have been designed to achieve programmable transient conformational states fueled by chemical signals with a controlled lifetime.14–16 All these applications can be included in a more ambitious project of discovering supramolecular systems with non-equilibrium transient morphologies for designing future active, adaptive and autonomous materials.17 The microscopic origins and features of non-equilibrium structuring, however, are not well understood. Theoretical frameworks for interacting reaction-diffusion systems have been linked so far only to microstructuring dynamics of non-active systems driven by chemical reactions18–21 or virus infections.22,23
In this work, in contrast to the well-studied motile activity,11,24 we focus on a different kind of active system formed by colloids in which each individual particle can actively switch between two different states at some specific kinetic rate. These states, for example, can differ in the particle conformations and thus have a different interaction size. Such a system may represent a good model for mimicking the behavior of soft active hydrogels or vesicles switching (or ‘breathing’) between two states14,25–27 or responsive, conformationally switching biopolymers.12,28,29 Recent developments have provided also the opportunity to create soft micromachines with programmable morphology.30
We note that such a system could also be viewed as a binary mixture of two different colloidal types, where each species switches into the other at some specific kinetic rate. Regarding the experimental realization, however, this would involve mass transfer and reversible chemical reactions between the colloidal particles or from some reservoir. Here, we have in mind autonomous soft particles, like hydrogels, vesicles, or artificial cells, etc., which are internally fueled and thus can actively change size or shape individually. For vanishing switching rates, such a system is in equilibrium, and a two-component colloidal mixture of two different species A and B represents the same system. These binary systems can also be unstable, i.e., demix in equilibrium, if particle types or states, A and B, are incompatible, as well known for colloidal mixtures.31 For infinite rates we will demonstrate that our actively switching system can be mapped to an effective one-component equilibrium system with equivalent structure.
In our paper we consider in particular soft colloids interacting through Gaussian pair potentials with binary switching between two sizes (referred as ‘big’ (b) and ‘small’ (s) from now on). These Gaussian pair potentials represent a generic model for polymers and soft colloidal hydrogels32–34 and cells.35 To investigate structural features of such an active colloidal dispersion, we make use of a reactive dynamical density functional theory (R-DDFT) previously used in similar problems18–23,36 and solve it in the non-equilibrium steady-state. To check for the quality of the R-DDFT, which makes mean-field assumptions for spatiotemporal correlations, we complement our study with reactive Brownian dynamics (R-BD) computer simulations. These methods allows us to investigate the effects of active switching on the inhomogeneous density profiles of mixtures confined in various external potentials, such as slab geometry and inside an spherical cavity. To study the phase behavior and structure also of bulk systems, we generalize the R-DDFT to incorporate the Percus test-particle route.31 We also consider binary systems which are unstable and demix in equilibrium and investigate how they respond to switching interactions.
We demonstrate in our work that the switching rate has drastic effects on colloidal structure and phase behavior. In particular, we show that the rate interpolates between a system comparable to the corresponding equilibrium binary mixture at low rates and a non-equilibrium effective 'one-state' liquid for large rates, strongly affecting the structure and stability in bulk and confinement. Importantly, we show that sufficiently fast switching impedes the phase separation of an (in equilibrium) unstable fluid, allowing the control of the degree of demixing and local microstructuring by tuning the activity rate. The system also demonstrates a high degree of versatility, as the interaction parameters can be chosen to obtain, for instance, a purely ideal effective system in the limit of fast switching rates, even though particle interactions are non-negligible. The results are in excellent agreement with the reactive BD computer simulations, which further support all our data and the high quality of the R-DDFT approach. Hence, our work describes how active systems of switching particles modify the inhomogeneous properties in comparison to non-active systems, and how this may be exploited to control the structure and phase behavior.
2 Theory
We investigate an active system formed by colloids in binary states, i.e., a colloid has either a big (b) or a small (s) size. Particles of state b have the ability to spontaneously convert into state s at some fixed rate kbs (units of time−1), and similarly particles of state s switch into particles of state b at rate ksb, . This kind of switching binary mixtures offers the possibility to study the role played by the switching activity on the non-equilibrium properties.
. This kind of switching binary mixtures offers the possibility to study the role played by the switching activity on the non-equilibrium properties.
With the purpose of characterizing the effect of the activity on all these properties, we make use of a well-known model system formed by a binary mixture of soft Gaussian colloids, defined by the following pair interaction potentials37
| βuij = εije−r2/σij2 with i,j = s,b, | (1) |
2.1 Stationary compositions of switching particles
Let first consider the time evolution of the particle concentrations for a homogeneous system (bulk) in which states b and s switch one into each other, b ⇌ s. We consider the binary system formed by Nb particles of state b and Ns particles of state s contained within a volume V, at fixed temperature T. The bulk number densities of species of each state are given by ρi = Ni/V (i = b,s). We denote the total number density by ρT = ρb + ρs, and the molar fractions by xs = ρs/ρT and xb = 1 − xs. The first-order differential equations that rule the switching kinetics can be written as | (2) |
In each case, the first term of the right hand represents the production, whereas the second one the disappearance of this component. These coupled differential equations are analytically solvable, starting from the initial conditions ρb(t = 0) = ρb0 and ρs(t = 0) = ρs0, leading to the following time dependent concentrations
 | (3) |
2.2 Reactive dynamical density functional theory (R-DDFT)
 | (4) |
| Ji = −Di[∇ρi(r,t) + ρi(r,t)β∇(uexti(r) + μexi(r,t))], | (5) |
 . Fex[{ρi(r,t)}] is the equilibrium excess free energy functional with the equilibrium density profiles replaced by the non-equilibrium ones ρi(r,t).
. Fex[{ρi(r,t)}] is the equilibrium excess free energy functional with the equilibrium density profiles replaced by the non-equilibrium ones ρi(r,t).
The equilibrium and non-equilibrium properties of soft Gaussian particles described by eqn (1) are well represented by a weakly correlated mean-field fluid over a surprisingly wide density and temperature range, being more accurate by increasing particle densities.33 The mean-field free energy functional for colloidal mixtures of two states, i = b,s, reads as:
 | (6) |
Using eqn (6) we find the mean-field non-equilibrium excess chemical potential
 | (7) |
Starting from a non-equilibrium initial state, the time-dependent density profiles, {ρi(r,t)}, evolve towards the final equilibrium distribution, {ρeqi(r)}, in which the diffusive fluxes of both species become zero at any point of the space, Ji = 0.
However, the DDFT method described before is restricted to the case of non-active systems. The question that naturally arises at this point is how the DDFT formulation can be generalized to active systems, in which each particle switches between two states b and s at some predefined rates. In this case, the time evolution of the particle concentrations is not only caused by the diffusive fluxes {Ji}, as they do not account for the production and disappearance of each component due to the switching activity, provided by eqn (2). This process occurs locally, so the conversion rate of big colloids into small ones and vice versa only depends on the local concentrations of both species. Therefore, the classical DDFT framework has to be extended to consider this new effect. This can be achieved by including into the continuity equation (eqn (4)) new terms to account for the production and disappearance of particles due to active switching, which follow the kinetic equations (eqn (2)). The resulting theoretical framework, called reactive dynamical density functional theory (R-DDFT), has been successfully applied to similar problems.18–21,36 According to R-DDFT, the time evolution of the density profiles of big and small soft colloids is given by the following set of differential equations:
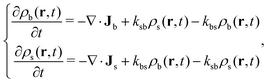 | (8) |
If the external potentials uexti(r) are time independent, then the system evolves in time until a steady state is eventually reached. However, this final (activity-present) state does not imply that the net fluxes are zero any more. Instead, the steady-state density profiles (∂ρi/∂t = 0) in the presence of switching activity are the solution to
 | (9) |
 | (10) |
Therefore, the bulk properties (and so the composition of the mixture of states) will remain constant, even though the inhomogeneous properties induced by the presence of external potentials, confining walls or by phase separation will still be affected by the switching activity. As eqn (10) interconnects both kinetic rate constants, we can use only one of them, for instance kbs, to characterize the switching rate. It can be written as the inverse of the characteristic big-to-small conversion time, kbs = 1/τ. We can compare τ with the typical diffusion time for small particles, τ0 = σs2/Ds. We therefore conveniently define the switching activity as
 | (11) |
For a ≪ 1, the b ⇌ s conversion rate is so slow that the time evolution of the density profiles is dominated by the diffusion. In this case, any switching event at some specific location is rapidly compensated by diffusive fluxes of particles that balance the effect of the activity. In the limit a → 0 the classical (equilibrium) DFT of a true binary mixture is recovered. In this particular case, the density profiles converge to the equilibrium distribution for t → ∞. For a ≫ 1 the exchange rate is so large that the diffusion is not fast enough to compensate its effects, so switching events dominate over diffusion. Thus, in the final steady-state the particle states b and s can not be distinguished anymore because they do not have enough time to diffuse and reorganize according to the applied external potentials. Consequently, in every point of the space we have that both steady-state density profiles share the same shape. We elaborate on this in the next subsection.
 | (12) |
Similarly, the effective interparticle particle pair potential takes the following analytical form
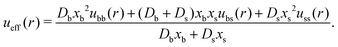 | (13) |
These arguments show that the microstructure in the limit a → ∞ actually corresponds to the one of an effective one-component system (EOC) in equilibrium.
It is important to emphasize here some important points. First, eqn (12) and (13) for the effective external and interparticle interactions of the EOC equilibrium fluid are only correctly defined in the limit of very fast activity rates, a ≫ 1. If we are not in this limit, the non-equilibrium system cannot be mapped onto an non-active effective one-component fluid. Second, ueff(r) depends on the assumptions made for the excess free energy in the DFT. The analytical form provided by eqn (13) represents a particular result for the binary mean-field fluid. Different prescriptions for Fex will lead to different expressions for the effective pair potential. Finally, uexteff(r) and ueff(r) depend on the dynamic properties of the system. If we change the diffusion coefficients, the effective pair potential will be different too, and so the steady-state density profiles. Consequently, properties such as the bulk pressure of the fluid, obtained via integration of the compressibility equation, will depend on the particle diffusivities, which is a clear signature that the active system is not in equilibrium for a ≠ 0, even though it reaches the steady-state for t → ∞.
2.3 R-DDFT for Percus' test particle route
For a binary mixture of big and small colloids interacting with pair potentials that only depend on interparticle distance, r, the microstructure is fully determined by the big–big, big–small and small–small time-dependent radial distribution functions gbb(r,t), gbs(r,t) and gss(r,t) of the homogeneous bulk suspension (without confining external potential).In order to calculate gij(r), we need to generalize the R-DDFT framework. For this purpose, we first make use of the Percus test particle route.42,43 Within this method, in principle one should solve the R-DDFT equations in the presence of a test particle of state i located at the origin r = 0 that acts as an external potential for the mixture. The density profiles of particle of state j around this central particle, ρij(r,t), normalized by the corresponding bulk density ρbulkj, provide the radial distribution function, gij(r,t) = ρij(r,t)/ρbulkj. However, this procedure still lacks a very important feature of the real active switching mixture: the external potential exerted by the central particle is not fixed, but it fluctuates due to the switching of the central colloid.
To introduce the switching of the external potential, the two-state R-DDFT framework must be extended to a four-state R-DDFT that also takes the transition probability between the two possible states of the fluctuating central particle into account. We denote ρpij(r,t) as the probability density of finding a particle of state j located at a distance r from a central particle of state i at time t, and define the the vector ρp(r,t) as
| ρp(r,t) = (ρpbb(r,t),ρpbs(r,t),ρpsb(r,t),ρpss(r,t)). | (14) |
Analogously, we can define the vector including the four currents
| J = (Jbb,Jbs,Jsb,Jss). | (15) |
In the context of the mean-field approximation, the diffusive currents are given by
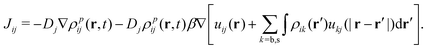 | (16) |
The time evolution of the probability densities ρpij(r,t) obeys the following set of four coupled Fokker–Planck equations, which include particle interactions (modeled through the mean-field approach)44–46
 | (17) |
The transition rate matrix  takes into account not only the switching between both kind of colloids (b and s) distributed around the central potential, but also the switching of the fluctuating external potential in itself. It is given by
takes into account not only the switching between both kind of colloids (b and s) distributed around the central potential, but also the switching of the fluctuating external potential in itself. It is given by
 | (18) |
 satisfies the required properties of any transition matrix, namely
satisfies the required properties of any transition matrix, namely 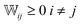 and
and  .47
.47
2.4 Boundary conditions and numerical details
To solve the R-DDFT (eqn (8)), three boundary conditions are required. First, the initial density profiles (for t = 0) have to be specified: ρi(r,t = 0) = ρi0(r). The second and third condition involve the knowledge of the number densities in two different locations. For binary active mixtures confined between two planar walls separated by a distance L, these conditions impose zero diffusive fluxes at both confining walls: Ji(z = 0,t) = Ji(z = L,t) = 0. For mixtures confined inside a spherical cavity of radius R, we get Ji(r = 0,t) = 0 due to spherical symmetry at the center of the cavity and Ji(r = R,t) = 0 (closed confining spherical wall). Finally, to integrate the four-state R-DDFT (eqn (17)), we also have the condition Jij(r = 0,t) = 0 (spherical symmetry), whereas the third condition imposes fixed probability densities far away from the central particle r → ∞, given by ρpbb(∞,t) = ksb2/(kbs + ksb)2, ρpss(∞,t) = kbs2/(kbs + ksb)2 and ρpbs(∞,t) = ρpsb(∞,t) = kbsksb/(kbs + ksb)2. In this way, the composition of the mixture in the bulk is preserved.In order to numerically integrate the R-DDFT and the stochastic R-DDFT equations, we use a spatial grid of Δz = Δr = 0.01σs. The time step has been fixed to Δt = 10−5τ0, which is small enough to avoid the appearance of numerical instabilities (Δt < Δz2/(2Ds)). For the case of the calculation of the radial distribution functions, the integration extends over a distance larger that rmax = 80σs to avoid finite-size effects, using Fast Fourier Transforms to evaluate the convolution integrals appearing in eqn (16).
3 Reactive Brownian dynamics (R-BD) computer simulations
Complementary to the R-DDFT, all systems have been simulated using a reactive Brownian dynamics (R-BD) algorithm, which includes active switching between the two different states of colloids, b and s. The overdamped Langevin equation of motion for a particle i writes| ξiṙi = −∇U(ri) + r(t), | (19) |
 | (20) |
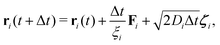 | (21) |
| System | ε bb | ε ss | ε bs | σ b/σs | σ bs/σs | ρ T σ s 3 | x s | D s/Db |
|---|---|---|---|---|---|---|---|---|
| M1 | 2.0 | 2.0 | 2.0 | 2.0 | 1.5 | 0.191 | 0.5 | 2.0 |
| M2 | 2.0 | 2.0 | −2.0 | 1.0 | 1.0 | 0.76 | 0.5 | 1.0 |
| M3 | 2.0 | 2.0 | 1.0 | 1.504 | 1.277 | 2.4 | 0.75 | 1.504 |
| M4 | 2.0 | 2.0 | 1.888 | 1.504 | 1.277 | 2.4 | 0.75 | 1.504 |
The possibility of active switching between the particle states is checked after every integration step, and the probabilities of switching are defined as
| pbs = 1 − e−kbsΔt, psb = 1 − e−ksbΔt | (22) |
These R-BD simulations for up to 8100 switching particles have been conducted using an own code for production times up to 25τB and the parameters presented in Table 1. The box sizes have been varied for the bulk simulations at the given densities to reduce finite size effects. For the cubic and spherical system, cut-off distances for the pairwise interactions have been set to values close to half of the respective box size ranging from 5.9 to 7.4σs for cubic box dimensions with edge lengths 12 and 15σs, respectively. For the bulk simulations of the systems M3 and M4, periodic boundary conditions (pbc) have been applied on the cubic simulation cells. In the simulations of the mixtures M1 and M2 confined between two walls, the pbc have been maintained in the two dimensions perpendicular to the separation vector of the walls with box sizes lx = ly = 10σs at a separation distance lz = 2.5σs, using a cut-off distance of 3.5σs. The spherical cavity has radius 6.0σs (same for the potential cut-off).
4 Results and discussion
We explore two different conditions of confinement (i.e., between two parallel planar walls and inside a spherical compartment) as well as bulk solutions (without external potentials). Starting from an initial non-equilibrium configuration, the particle densities ρi(r,t) evolve in time until a final steady-state regime is reached. This final state depends on the switching activity rate, a. We use our mean-field R-DDFT to determine the inhomogeneous steady-state density profiles of confined colloids, ρi(r), and the four-state R-DDFT to calculate the steady-state radial distribution functions of the bulk suspension, gij(r). In all cases, theoretical results are compared with the R-BD simulations. We cover activities ranging from a = 0 (non-active equilibrium state) to a = 1000 (fast switching rate regime), which yields results comparable to a → ∞.Table 1 shows the interaction parameters, number densities and state compositions of four different active systems of Gaussian colloids (systems M1 to M4) that will be matter of investigation. Systems M1 to M3 correspond to stable mixtures (they do not phase separate in equilibrium), whereas system M4 is located inside the unstable region of the phase diagram, so it undergoes fluid-fluid demixing.49 In all cases, the kinetic rate constants have been chosen to fulfill the condition given by eqn (10) to preserve the composition of the mixture of states. The particle diffusivities are in all cases assumed to follow the Einstein relation, Di = kBT/(3πησi), so Db = (σs/σb)Ds.
In addition to the active systems, we also explore the effective one-component (EOC) in equilibrium, which is equivalent to the active system in the limit a → ∞ where all external potentials and all particle–particle pair interactions converge to the same effective potentials, given by eqn (12) and by eqn (13), respectively.
4.1 Inhomogeneous properties and microstructure of stable mixtures
| βuextb(z) =βuexts(z) = 10(e−50z/σs + e−50(L−z)/σs) | (23) |
The theoretical density profiles are obtained starting at time t = 0 from the equilibrium profiles of the non-active system (a = 0), and then turning on the activity at t > 0. The local densities evolve rapidly at short times and finally converge to the final steady state, in which the effect of the activity is exactly balanced by the diffusive currents. Black solid and red dashed lines in Fig. 1 show the steady-state profiles of big and small colloids for a = 0, 10, and 1000. As observed, activity modifies the density profiles near each wall, even though the average concentrations of each component remain unaltered. The adsorption peak of big particles decreases whereas the concentration peak of small particles close to the wall shows an increase coupled with a reduction of the depletion region.
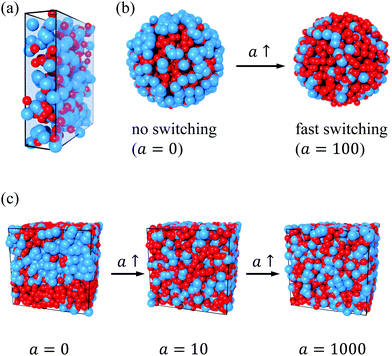
In addition to the theoretical calculations, we performed R-BD simulations in the same conditions to estimate the reliability of our mean-field R-DDFT method. Fig. 2(a) depicts a representative snapshot of system M1 confined betweeen two planar walls for a = 0. The nearly quantitative agreement between the R-DDFT theoretical predictions and the R-BD simulation data obtained in the steady-state regime (depicted as hollow symbols in Fig. 1) indicates that the reactive mean-field DDFT is able to capture the non-equilibrium structure of the active mixture of states of the soft colloids for any activity rate a. It should be remarked that the mean-field approach used in our theoretical model (eqn (6)) compares very well to the simulation data, even for the small values of the particle number densities of system M1.
For very large activities, the system finally tends to a steady-state in which the density profiles of big and small particles converge to each other. This fact can be clearly observed in Fig. 1(c) where the density profiles for a = 1000 are shown. As the activity rate increases, particle switching enforces a decrease of the concentration of big colloids and an increase of small ones close to the walls. For a = 1000, both profiles converge to a common form, thus indicating that the binary system behaves as an effective one-component system (EOC) in the limit of large switching activity.
This result can be rationalized as follows: the switching activity introduces in the system a delocalization of the particle states (big and small), in the sense that a colloid of state b in certain location is suddenly converted into a particle of state s. If a ≪ 1 the switching events are rare and the diffusive currents are still able to preserve the distinction between both states. However, for a ≫ 1 many switching effects occur during the diffusive time τ0, so particles do not move fast enough to rearrange their location by diffusion. Consequently, they tend to experience the same average interparticle effective interaction (uij(r) → ueff(r) for a → ∞). In order to confirm this, we include in plot Fig. 1(c) the corresponding prediction from the equilibrium EOC, where the colloids are interacting through an average external and particle–particle pair potentials given by eqn (12) and (13), respectively (blue lines for theory and blue symbols for R-BD simulations). The agreement between the density profiles obtained for a = 1000 and the EOC confirms that the active system indeed converges to the EOC model in the limit of large switching rates.
It is important to emphasize again that the active system in the limit a → ∞ cannot be confound with a truly equilibrium system. Indeed, the effective potentials ueff(r) and uexteff(r) in contrast to the conventional ones, include the diffusion constants, which is a signature of the non-equilibrium nature of the underlying mixture. In fact, the component with a larger diffusivity contributes more to the average.
 | (24) |
Fig. 3 depicts the steady-state density profiles of the active M2 system for a = 0 (equilibrium), 10 and 1000. The accordance between theory and simulation is very good in all cases. Differences are only observed around the adsorption peak close to the attractive wall for each component, where the theory overestimates the local density. This discrepancy can be attributed to the limitation of the mean-field approach when predicting the structure in regions with strong density variations.
Again, the steady-state density profiles in the regime of very fast switching rates converge to the ones obtained for the corresponding EOC. For the particular choice of interaction parameters of system M2, the resulting effective pair interaction potential and external potential are given by ueff(r) = 0 and uexteff(z) = 0 (excluding the auxiliary short-range potential that prevents wall penetration). In other words, in the limit of fast switching activities, a ≫ 1, particle interactions are dynamically neutralized leading to a system that effectively behaves as an ideal system. This can clearly appreciated in Fig. 3(c), in which the density profiles of both components tend to a flat distribution typical of a non-interacting system. It is well known that ideal systems do not exist in nature; they are an idealization limit for diluted and weakly interacting systems. Consequently, these result points out a surprising property of potential practical interest of active switching systems: they can be designed to fully reproduce the behavior of a real ideal system, even though particle interactions are non-negligible.
To explore the role of the switching activity on the microstructure, we employed our four-state R-DDFT and R-BD simulations to determine gij(r) for increasing activity rates. We selected the system M3 of repulsive Gaussian colloids shown in Table 1. The interaction range of this system represents fairly well the simulation data for mixtures of linear flexible polymers with a number of monomers Nm = 200 (big) and 100 (small), immersed in a good solvent.33 Since εbs < εbb = εss, there is a decrease of energy penalty by placing unlike species as neighbors, which in turn favors mixing between both components. In fact, mixture M3 is a stable system that does not exhibit fluid-fluid demixing.
Lines in plots (a)–(d) of Fig. 4 show the steady-state radial distribution functions (gbb(r), gss(r) and gss(r)) obtained from our theory for four different values of the switching activity rate, namely a = 0 (equilibrium), 1, 10 and 1000. The corresponding simulated radial distribution functions in the steady-state regime are shown as hollow symbols in Fig. 4. Excellent agreement is found between simulations and theoretical predictions, thus confirming that incorporating the test-particle route to the four-states R-DDFT represents a reliable method to predict the microstructure of non-equilibrium active switching mixtures. Since the mean-field approach involved in our model (see eqn (6)) becomes exact in the high density limit, this agreement is expected to improve even more by increasing the bulk total number density of the system, ρT.
All pair interactions in system M3 are purely repulsive, and thus the resulting gij(r) have a soft correlation hole at small interparticle distances, typically observed in this kind of soft repulsive potentials. The hole is smaller for gbs(r) due to the weaker repulsion between big and small colloids. This soft correlation hole is gradually reduced as ρT increases, a behavior typical of finite core potentials, approaching the ideal-gas-like behavior in the high density limit. For a = 0, the three partial radial distribution functions are very different from each other, but increasing the switching activity leads to a progressive approach of the three distribution functions. In the limit of large a, the three functions converge to the same common profile, which in turn matches the corresponding g(r) for the EOC (ueff(r) given by eqn (13)).
Fig. 4(e) depicts the theoretical and simulated number–number static structure factor for system M3 with a = 0, a = 1000 and the EOC. It is defined as SNN(q) = 1 + ρTĥave(q), where ĥave(q) is the Fourier transform of the average distribution function,  . For a = 0, the correlation wells of gbb(r) and gss(r) close to r = 0 are deeper than the one for gbs(r), whereas for a = 1000 the three distribution functions have converged to the same functional form, leaving the average almost unaffected. In contrast to this behavior, we will show in the following section that SNN(q) shows important changes with a for a system that phase-separates in equilibrium, so it becomes an excellent indicator of the onset of fluid–fluid demixing.
. For a = 0, the correlation wells of gbb(r) and gss(r) close to r = 0 are deeper than the one for gbs(r), whereas for a = 1000 the three distribution functions have converged to the same functional form, leaving the average almost unaffected. In contrast to this behavior, we will show in the following section that SNN(q) shows important changes with a for a system that phase-separates in equilibrium, so it becomes an excellent indicator of the onset of fluid–fluid demixing.
4.2 Phase separation dynamically controlled by interaction switching
The conditions for stability and the phase diagrams of repulsive Gaussian mixtures have been extensively studied under the mean-field approach.33,49 We select a particular mixture with the same interaction parameters than system M3, but shifting the big-small interaction to εbs = 1.888. Although this change seems to be small, it has a very relevant impact of the phase behavior since the system now phase separates into two solutions of different composition above the critical point, located at 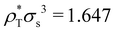 and
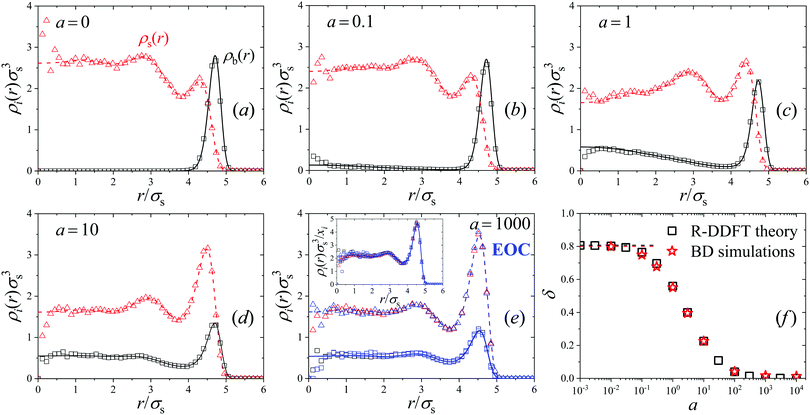
and 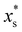 = 0.7.33,49 In order to ensure the phase separation of our Gaussian mixture of states, we chose a total number density given by ρTσs3 = 2.4 and composition xs = 0.75 (system M4 in Table 1). This binary mixture demixes spontaneously for a = 0, as shown in the R-BD simulation snapshot in Fig. 2(c).
= 0.7.33,49 In order to ensure the phase separation of our Gaussian mixture of states, we chose a total number density given by ρTσs3 = 2.4 and composition xs = 0.75 (system M4 in Table 1). This binary mixture demixes spontaneously for a = 0, as shown in the R-BD simulation snapshot in Fig. 2(c).
To investigate the effect of the activity on the phase coexistence, we apply the method described by Archer,40,50i.e. we confine the system inside a spherical cavity of radius Rcav = 6σs by means of repulsive spherically symmetric external potentials
 | (25) |
The degree of separation between both components can be quantified by means of the demixing order parameter δ, defined as
 | (26) |
The new steady-state profiles with a non-zero activity are depicted as solid and dashed lines in plots Fig. 5(b)–(e) for a = 0.1 to 1, 10 and a = 1000, respectively. These plots show that increasing activity a enhances the density of big colloids in the center and the concentration of small particles at the outer layer, indicating activity-driven mixing. For small values of a the conversion of particles of state s inside the phase with larger concentration of particles of state b (and vice versa) is so slow compared to the characteristic diffusion time that the diffusive fluxes are able to restore both coexistent phases. However, for activities above a = 1, both density profiles approach to each other, so demixing becomes significantly suppressed. In addition, for a = 1000 both profiles adopt the same form, which means that the states in system are the same everywhere on average, which occurs as a mixed microstate. This can be appreciated by plotting the normalized density profiles ρi(r)/xi (see inset in Fig. 5(e)), which converge to exactly the same common profile, described by the EOC. It should be noted that the normalized density profiles for a = 0 and a = 1000/EOC differ. Higher activities lead to an accumulation of the now rapidly switching particles at the outer layer at r ≈ 5.0σs, since the frequent switching between the two sizes leads to effectively bigger average particles sizes.
The dynamic transition from a phase-separated system to activity-enforced mixed microstates is clearly visible in the simulation snapshot of Fig. 2(b), obtained for system M4 in the steady state. For a = 0, big (blue) colloids are mainly located close to the external wall of the spherical compartment, whereas an even distribution is observed for a = 100. The corresponding simulated density profiles are shown as hollow symbols in plots (a)–(e) of Fig. 5. Also here we find excellent agreement between theoretical predictions and R-BD computer simulations. Fig. 5(f) shows the demixing parameter δ (eqn (26)) as a function of the activity. As observed, the transition is gradual and centered close to a = 1, which represents the inflection point separating mixed and demixed states. In the limit a → ∞, δ tends to zero, indicating that the binary system is totally mixed. These results indicate that switching the activity can be used as a tool to dynamically control the demixing state of mixtures.
The R-BD simulation snapshots in Fig. 2(c) indicate a transition from a phase separated system for a = 0 to a completely homogenous mixed microstate for a = 1000. Evidences of mixing can be also seen in Fig. 6(e) and (f), where SNN(q) is plotted using linear and log scale from a = 0.048 to a = 1000 for the R-DDFT theory. It is well know that SNN(q) tends to diverge at small q-vectors when approaching the fluid–fluid spinodal, e.g., by changing temperature or density. In our case we are not moving a thermodynamic equilibrium state variable, instead we are decreasing the activity, but we do observe a similar behavior. For a ≥ 10, the activity rate is large enough to prevent the phase separation of the mixture. Indeed, in this regime the static structure factor shows the typical smooth behavior of stable mixtures of Gaussian colloids. However, as we decrease a below this value, a peak develops in the region of small q-vectors. The height of this peak shows a significant increase as we decrease the activity below a = 1. For a = 0.048, we get large stable peaks at low q, which clearly indicates that the switching activity cannot stabilize the system, so it undergoes micro-phase separation. The peaks are roughly at q ≃ 0.5–1σs, indicating clusters of size of multiple colloidal sizes 2π/q ≃ 6–12σs. These sizes are one order of magnitude smaller that the size of the spherical cell size used to integrate the R-DDFT equations (of about lmax ≈ 80σs), so these predictions are not a consequence of finite size effects.
The agreement between theory and simulations is very good for a ≥ 10, but it worsens by decreasing a due to the limitation of the mean-field approximation in conditions where the system is affected by large density fluctuations due to phase separation. As observed, the R-BD simulation results also exhibit the appearance of a structure factor peak for small switching activities. Although we can not conclude from the simulation data the formation of finite-sized micro-clusters because the correlation length of the clusters is close to half of the simulation box size, simulation snapshots (see Fig. 2(c)) indicate that macroscopic phase separation is only recovered in the limit of (almost) total absence of switching. In addition, the peaks are located at a similar location than the R-DDFT predictions, which are not affected by finite size effects, which strongly supports the formation of micro-clusters as the switching activity decreases.
What is the physical origin of the activity-induced mixing? From a dynamical/mechanical perspective, one can argue that the non-additive forces that lead to demixing are only acting temporarily for the transient small-big pairs and, if switching is sufficiently fast, are counterbalanced by diffusive mixing of like pairs. That is the reason for micro-clustering and related to a typical finite diffusive length 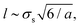 that is roughly the length a particle can travel before it changes its identity. Only during this time a demixed region of size l can be generated, before, on average, diffusive mixing sets in. In the range of a = 0.1 to 1, the length is about 3 to 8σs and thus indeed close to the correlation length calculated by R-DDFT.
that is roughly the length a particle can travel before it changes its identity. Only during this time a demixed region of size l can be generated, before, on average, diffusive mixing sets in. In the range of a = 0.1 to 1, the length is about 3 to 8σs and thus indeed close to the correlation length calculated by R-DDFT.
From a thermodynamic perspective, it seems the power generated by the switching propagates into the system and produces useful entropy in terms of helping the system to mix again. However, a detailed study of this is out of scope of this work and is postponed to future work.
5 Conclusions
We used reactive mean-field dynamical density functional theory (R-DDFT) and Brownian dynamics (R-BD) simulations to investigate the structural properties and phase behavior of active, binary switching Gaussian colloids in the steady-state regime. Our results underline that switching activity has a important effect on the inhomogeneous density profiles of the binary mixture of states confined between planar walls with external potentials.While average structures, e.g., mass density profiles, are surprisingly little affected by switching, the appearance of the distinct colloidal states can be localized and spatially controlled by the rate. This interesting finding may be important for controlling functionality of switching systems, such as in soft biorobotics.30 For very large switching rates, we show that the active mixture of states can be mapped onto an equivalent effective one-component fluid in equilibrium because the diffusive fluxes are not fast enough to restore the particle positions during two consecutive switching events. The effective pair interaction of this EOC system depends on the dynamical properties of the active mixture such as the particle diffusion coefficient, so the latter also corresponds to a non-equilibrium system in the limit of infinitely fast switching. We expect also interesting physics for the diffusive behavior, where the long time diffusion constant (also accessible by DDFT43) might interpolate between a mean diffusion for small a and the diffusion of a mean size for large activities.52 This limit also offers an additional property of potential practical interest, since the interaction parameters can be chosen to obtain, in the limit of fast switching activities, a purely ideal effective system, even though partial particle interactions are non-negligible.
The switching activity also has important effects on the phase behavior of the system. We show that increasing the activity suppresses the phase separation of an (in equilibrium) demixed system confined inside a spherical cavity, inducing a gradual spatial mixing of the two states. The same behavior is also observed in the microstructure of a bulk suspension, where the big-big radial distribution function gbb(r) shows a progressive decrease in the region of small interparticle distances by increasing the switching activity, indicating the dissolution of aggregates of colloids in the big state. This peak disappears for large enough switching rates, showing that the switching rate can be exploited to dynamically control the degree of demixing, i.e., (in)homogenization of spatial state distributions by tuning the activity rate. Moreover, we note that the number–number static structure factor of the bulk system shows that the mean structure of the dispersion (averaged over both states) is only slightly affected from active switching, implying that activity can be used for spatial separation of properties and possibly connected to colloidal functionality, while mass distributions remain essentially conserved. This could be interesting in smart material design, e.g., for dispersions of ‘soft bioroboters’.30
In all cases, R-DDFT predictions are in excellent agreement with R-BD computer simulations, thus confirming that R-DDFT constitutes a powerful tool to access the microstructure and phase behavior of active switching binary mixtures. We only find semi-quantitative agreement in the limit of small a, since the mean-field approach is not able to fully capture the density fluctuations induced by the phase separation.
In future investigations we are planning to study how interaction switching can be used to tune depletion forces between colloidal objects immersed in a mixture of soft active switching particles. Other possible direction is to investigate the coupling between the switching rates to local properties of the environment, such as colloidal density, for example, in bacterial quorum sensing.53 Theoretically, this could benefit from the recently introduced models for responsive colloids.52,54 Moreover, it will be interesting to investigate the non-equilibrium thermodynamics of actively switching colloids. Obviously, internal switching can perform useful work, e.g., mixing an in equilibrium demixed system. Future studies shall address the relations between power transfer, entropy production, and structure of the system, as in related active matter systems.55,56 Activity-structure relationships should be useful for non-equilibrium-based material design. Finally, another interesting future study could be the inclusion of inertia, leading to Langevin (underdamped Brownian) dynamics of actively switching colloids. Here, it can be expected that inclusion of inertia will pump more kinetic energy into the system and a higher temperature steady-state will be reached, modifying distributions and the strength of demixing. In addition, inertia could affect the short- and intermediate time dynamics of the system. In particular, for less soft pair potentials, a sudden switch of interactions creates large forces and extended ‘memory’ in the short-time ballistic motions. Typical correlation lengths may be significantly affected by this, perhaps even the long-time dynamics as in Active Brownian Particles (ABPs),57,58 and future studies will hopefully analyze and quantify these effects.
Conflicts of interest
There are no conflicts to declare.Appendix
Determination of ueff(r) and uexteff(r)
In this Appendix we show that in the limit of very fast switching rates, a ≫ 1, the active mixture behaves as an effective one-component system (EOC), so particle–particle interactions are all given by lima→∞uij(r) = ueff(r) (i,j = b,s). For the same reason, the external potential acting on both species also converges to the same effective potential lima→∞uexti(r) = uexteff(r). In our demonstration we are also able to deduce the explicit expressions for uexteff(r) and ueff(r). For this purpose, we need to make use of the condition given by eqn (10) relating the kinetic rate constants and the composition, which can be written as ksb/(kbs + ksb) = xb and kbs/(kbs + ksb) = xs. We remind that this condition guarantees that the relative compositions xi (i = b,s) are preserved even through the local density profiles change due to the switching activity.In the limit of very fast switching rates, a ≫ 1, switching events occur much faster that the rate of diffusion, kbs ≫ Ds/σs2, so there is a large separation between the typical time scales of switching and diffusion. For very short times, t ≪ σs2/Ds, the R-DDFT differential equations (eqn (8)) are dominated by switching events, so
 | (27) |
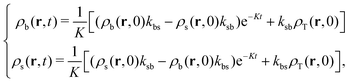 | (28) |
| ρs(r,t) = xsρT(r,t), ρb(r,t) = xbρT(r,t) ∀t ≫ kbs−1. | (29) |
These results can be physically interpreted in the following way: For a ≫ 1 and t ≫ kbs−1, the switching events are so fast that both particle states cannot be distinguished because colloids do not have enough time to diffuse and reorganize according to the applied external potentials. Consequently, both steady-state density profiles share the same shape.
If we evaluate the non-equilibrium production and disappearance of particles for t ≫ kbs−1 and employ the condition provided by eqn (10), we find that
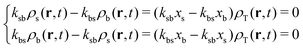 | (30) |
Therefore, the R-DDFT equations for a ≫ 1 and t ≫ kbs−1 can be written as
 | (31) |
Expanding the terms in eqn (31) we find
 | (32) |
On the one hand, a closed equation for ρ(r,t) can be obtained by simply adding both expressions and using eqn (29), so  . After some reorganization of terms, we obtain
. After some reorganization of terms, we obtain
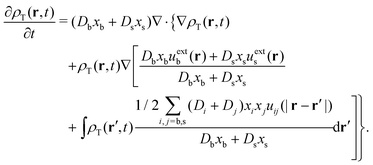 | (33) |
On the other hand, the continuity equation for the effective (non-active) one-component mean-field fluid of density ρT(r,t) is
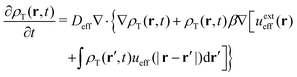 | (34) |
From the last two equations, we show that the time evolution of an active switching system with a ≫ 1 and t ≫ kbs−1 can be completely mapped to an effective non-active one-component system (EOC), for which lima→∞uij(r) = ueff(r) and lima→∞uexti(r) = uexteff(r). Comparing both expressions, we deduce the effective diffusion coefficient of the one-component fluid as the mean diffusion, given by
| Deff = Dbxb + Dsxs. | (35) |
In addition, the effective external potential is
 | (36) |
Finally, the effective interparticle particle pair potential is
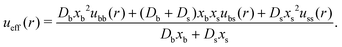 | (37) |
Acknowledgements
The authors acknowledge support by the state of Baden-Württemberg through bwHPC and the German Research Foundation (DFG) through grant no INST 39/963-1 FUGG (bwForCluster NEMO). A. M.-J. thanks the program Visiting Scholars of the University of Granada (Project PPVS2018-08) and the Plan Andaluz de Investigación, Desarrollo e Innovación of the Junta de Andalucía (Project PY20_00241) for financial support.Notes and references
- A. Leeth Holterhoff, V. Girgis and J. G. Gibbs, Chem. Commun., 2020, 56, 4082–4085 RSC.
- G. Gompper, R. G. Winkler, T. Speck, A. Solon, C. Nardini, F. Peruani, H. Löwen, R. Golestanian, U. B. Kaupp, L. Alvarez, T. Kiørboe, E. Lauga, W. C. K. Poon, A. DeSimone, S. Muiños-Landin, A. Fischer, N. A. Söker, F. Cichos, R. Kapral, P. Gaspard, M. Ripoll, F. Sagues, A. Doostmohammadi, J. M. Yeomans, I. S. Aranson, C. Bechinger, H. Stark, C. K. Hemelrijk, F. J. Nedelec, T. Sarkar, T. Aryaksama, M. Lacroix, G. Duclos, V. Yashunsky, P. Silberzan, M. Arroyo and S. Kale, J. Phys.: Condens. Matter, 2020, 32, 193001 CrossRef CAS PubMed.
- S. Ebbens, Curr. Opin. Colloid Interface Sci., 2016, 21, 14–23 CrossRef CAS.
- J. T. Siebert, F. Dittrich, F. Schmid, K. Binder, T. Speck and P. Virnau, Phys. Rev. E, 2018, 98, 030601 CrossRef CAS.
- J. Bickmann and R. Wittkowski, Phys. Rev. Res., 2020, 2, 033241 CrossRef CAS.
- F. Turci and N. B. Wilding, Phys. Rev. Lett., 2021, 126, 038002 CrossRef CAS PubMed.
- M. Guo, A. Ehrlicher, M. Jensen, M. Renz, J. Moore, R. Goldman, J. Lippincott-Schwartz, F. Mackintosh and D. Weitz, Cell, 2014, 158, 822–832 CrossRef CAS PubMed.
- É. Fodor, M. Guo, N. S. Gov, P. Visco, D. A. Weitz and F. van Wijland, Europhys. Lett., 2015, 110, 48005 CrossRef.
- M. C. Marchetti, J. F. Joanny, S. Ramaswamy, T. B. Liverpool, J. Prost, M. Rao and R. A. Simha, Rev. Mod. Phys., 2013, 85, 1143–1189 CrossRef CAS.
- J. Stenhammar, R. Wittkowski, D. Marenduzzo and M. E. Cates, Phys. Rev. Lett., 2015, 114, 018301 CrossRef CAS PubMed.
- M. E. Cates and J. Tailleur, Annu. Rev. Condens. Matter Phys., 2015, 6, 219–244 CrossRef CAS.
- Y. Shin and C. P. Brangwynne, Science, 2017, 357, 1253 CrossRef CAS PubMed.
- J. Berry, C. P. Brangwynne and M. Haataja, Rep. Prog. Phys., 2018, 81, 046601 CrossRef PubMed.
- T. Heuser, E. Weyandt and A. Walther, Angew. Chem., Int. Ed., 2015, 54, 13258–13262 CrossRef CAS PubMed.
- L. Heinen and A. Walther, Chem. Sci., 2017, 8, 4100–4107 RSC.
- K. Jalani, S. Dhiman, A. Jain and S. J. George, Chem. Sci., 2017, 8, 6030–6036 RSC.
- A. Walther, Adv. Mater., 2019, n/a, 1905111 Search PubMed.
- S. C. Glotzer, E. A. Di Marzio and M. Muthukumar, Phys. Rev. Lett., 1995, 74, 2034–2037 CrossRef CAS PubMed.
- J. F. Lutsko and G. Nicolis, Soft Matter, 2016, 12, 93–98 RSC.
- H. M. Al-Saedi, A. J. Archer and J. Ward, Phys. Rev. E, 2018, 98, 022407 CrossRef CAS.
- Y. Liu and H. Liu, AIChE J., 2020, 66, e16824 CAS.
- M. te Vrugt, J. Bickmann and R. Wittkowski, Nat. Commun., 2020, 11, 5576 CrossRef CAS PubMed.
- M. te Vrugt, J. Bickmann and R. Wittkowski, J. Phys. Commun., 2021, 5, 055008 CrossRef.
- C. Bechinger, R. Di Leonardo, H. Löwen, C. Reichhardt, G. Volpe and G. Volpe, Rev. Mod. Phys., 2016, 88, 045006 CrossRef.
- R. Yoshida, T. Takahashi, T. Yamaguchi and H. Ichijo, J. Am. Chem. Soc., 1996, 118, 5134–5135 CrossRef CAS.
- L. Heinen, T. Heuser, A. Steinschulte and A. Walther, Nano Lett., 2017, 17, 4989–4995 CrossRef CAS.
- H. Che, S. Cao and J. C. M. van Hest, J. Am. Chem. Soc., 2018, 140, 5356–5359 CrossRef CAS.
- U. B. Choi, J. J. McCann, K. R. Weninger and M. E. Bowen, Structure, 2011, 19, 566–576 CrossRef CAS PubMed.
- S. Dhiman, A. Jain and S. J. George, Angew. Chem., Int. Ed., 2017, 56, 1329–1333 CrossRef CAS PubMed.
- H.-W. Huang, M. S. Sakar, A. J. Petruska, S. Pané and B. J. Nelson, Nat. Commun., 2016, 7, 12263 CrossRef CAS PubMed.
- J.-P. Hansen and I. McDonald, Theory of Simple Liquids, Academic Press, 4th edn, 2013 Search PubMed.
- A. A. Louis, P. G. Bolhuis, J. P. Hansen and E. J. Meijer, Phys. Rev. Lett., 2000, 85, 2522–2525 CrossRef CAS PubMed.
- A. A. Louis, P. G. Bolhuis and J. P. Hansen, Phys. Rev. E: Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top., 2000, 62, 7961–7972 CrossRef CAS PubMed.
- A. Scotti, S. Bochenek, M. Brugnoni, M. A. Fernandez-Rodriguez, M. F. Schulte, J. E. Houston, A. P. H. Gelissen, I. I. Potemkin, L. Isa and W. Richtering, Nat. Commun., 2019, 10, 1418 CrossRef CAS PubMed.
- R. G. Winkler, D. A. Fedosov and G. Gompper, Curr. Opin. Colloid Interface Sci., 2014, 19, 594–610 CrossRef CAS.
- A. Moncho-Jordá and J. Dzubiella, Phys. Rev. Lett., 2020, 125, 078001 CrossRef PubMed.
- F. H. Stillinger, J. Chem. Phys., 1976, 65, 3968–3974 CrossRef CAS.
- U. M. B. Marconi and P. Tarazona, J. Chem. Phys., 1999, 110, 8032–8044 CrossRef CAS.
- A. J. Archer and R. Evans, J. Chem. Phys., 2004, 121, 4246–4254 CrossRef CAS PubMed.
- A. J. Archer, J. Phys.: Condens. Matter, 2005, 17, 1405–1427 CrossRef CAS.
- M. te Vrugt, H. Löwen and R. Wittkowski, Adv. Phys., 2020, 69, 121–247 CrossRef.
- J. K. Percus, Phys. Rev. Lett., 1962, 8, 462–463 CrossRef.
- A. J. Archer, P. Hopkins and M. Schmidt, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2007, 75, 040501 CrossRef PubMed.
- C. R. Doering and J. C. Gadoua, Phys. Rev. Lett., 1992, 69, 2318–2321 CrossRef PubMed.
- U. Zürcher and C. R. Doering, Phys. Rev. E: Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top., 1993, 47, 3862–3869 CrossRef PubMed.
- J. J. Kolb, S. Angioletti-Uberti and J. Dzubiella, J. Chem. Phys., 2016, 144, 081102 CrossRef PubMed.
- N. G. van Kampen, Stochastic Processes in Physics and Chemistry, 3rd Edn, North-Holland, 2007 Search PubMed.
- D. L. Ermak and J. A. McCammon, J. Chem. Phys., 1978, 69, 1352–1360 CrossRef CAS.
- A. J. Archer and R. Evans, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2001, 64, 041501 CrossRef CAS PubMed.
- A. J. Archer, J. Phys.: Condens. Matter, 2005, 17, S3253–S3258 CrossRef CAS.
- A. J. Archer and R. Evans, J. Phys.: Condens. Matter, 2002, 14, 1131–1141 CrossRef CAS.
- U. Baul and J. Dzubiella, J. Phys.: Condens. Matter, 2021, 33, 174002 CrossRef CAS PubMed.
- T. Bäuerle, A. Fischer, T. Speck and C. Bechinger, Nat. Commun., 2018, 9, 3232 CrossRef PubMed.
- Y.-C. Lin, B. Rotenberg and J. Dzubiella, Phys. Rev. E, 2020, 102, 042602 CrossRef CAS PubMed.
- E. Fodor, C. Nardini, M. E. Cates, J. Tailleur, P. Visco and F. van Wijland, Phys. Rev. Lett., 2016, 117, 038103 CrossRef PubMed.
- D. Mandal, K. Klymko and M. R. DeWeese, Phys. Rev. Lett., 2017, 119, 258001 CrossRef PubMed.
- C. Scholz, S. Jahanshahi, A. Ldov and H. Löwen, Nat. Commun., 2018, 9, 5156 CrossRef PubMed.
- H. Löwen, J. Chem. Phys., 2020, 152, 040901 CrossRef PubMed.
| This journal is © The Royal Society of Chemistry 2021 |