Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Energy dependent XPS measurements on thin films of a poly(vinyl methyl ether)/polystyrene blend concentration profile on a nanometer resolution to understand the behavior of nanofilms†
Marcel
Gawek‡
,
Sherif
Madkour‡§
,
Paulina
Szymoniak
 ,
Jörg
Radnik
,
Jörg
Radnik
 and
Andreas
Schönhals
and
Andreas
Schönhals
 *
*
Bundesanstalt für Materialforschung und – prüfung (BAM) (Fachbereich 6.6), Unter den Eichen 87, 12205 Berlin, Germany. E-mail: Andreas.Schoenhals@bam.de; Fax: +49 30/8104-1617; Tel: +49 30/8104-3384
First published on 17th June 2021
Abstract
The composition of the surface layer in dependence from the distance of the polymer/air interface in thin films with thicknesses below 100 nm of miscible polymer blends in a spatial region of a few nanometers is not investigated completely. Here, thin films of the blend poly(vinyl methyl ether) (PVME)/polystyrene (PS) with a composition of 25/75 wt% are investigated by Energy Resolved X-ray Photoelectron Spectroscopy (ER-XPS) at a synchrotron storage ring using excitation energies lower than 1 keV. By changing the energy of the photons the information depth is varied in the range from ca. 1 nm to 10 nm. Therefore, the PVME concentration could be estimated in dependence from the distance of the polymer/air interface for film thicknesses below 100 nm. Firstly, as expected for increasing information depth the PVME concentration decreases. Secondly, it was found that the PVME concentration at the surface has a complicated dependence on the film thickness. It increases with decreasing film thickness until 30 nm where a maximum is reached. For smaller film thicknesses the PVME concentration decreases. A simplified layer model is used to calculate the effective PVME concentration in the different spatial regions of the surface layer.
1. Introduction
For decades, polymer blends have been an integral part of materials science due to their numerous applications. However, as the thermodynamics of blending polymers seldom allows polymers to be miscible, most polymer blends employed are immiscible. Nevertheless, thermodynamically miscible polymers could have multiple advantages for industrial applications. At the very least, miscible blends will be homogeneous at some spatial length scale, which could improve the final properties and the targeted quality.Furthermore, the emergence of new advanced applications in functional coatings, batteries, innovative organic electronics, and hybrid materials depends strongly on organic and/or polymeric materials, often blends, confined in thin films or at interfaces.1,2 However, capturing the true potential of these materials requires a strong fundamental understanding upon which, tailor-made properties for the corresponding applications could be achieved. Consequently, research on blends of miscible polymers has received increased interest in recent years.3–11 This includes studies on bulk miscible polymer blends, and polymer blends nanoconfined in thin films as well as thin films of polymer films with embedded nanoparticles.12
In general, blending of miscible polymers leads to a distribution of spatial compositions on the nanoscale, which are deviated from that of the bulk averaged concentration.13–15 This not only influences properties like glassy dynamics,9–11,15,16 glass transition and fragility (see for instance ref. 13, 15 and 17), but also wettability and adhesion18 depending on the molecular weight used. This is also true for thin films. However, additional effects become more pronounced at the nanoscale. For instance, the surface tension of the components of the blend,19 with respect to air and to the substrate, plays a key role. This is due to the surface enrichment and the preferential adsorption phenomena of one of the components relative to the other. This could further alter the compositional heterogeneities. Nevertheless, the latter phenomena and their effect on the overall molecular miscibility are still not well understood.
It has been known for some time that the thermal glass transition temperature Tthermg of thin polymer films depends on the film thickness where an increase as well as a decrease of Tthermg, compared to the bulk value, was observed depending on the polymer and the substrate.20–28 A three-layer model has been introduced to discuss the thickness dependence of Tthermg of thin polymer films.2 It consists firstly of an adsorbed layer with a reduced segmental mobility, secondly a bulk-like layer in the middle of the film, and thirdly a surface layer with a higher molecular mobility. A more detailed discussion can be found in the ESI.† The measured thermal glass transition temperature of the whole film is a complicated average of all of these effects of the different layers.
Differently from the thickness dependence of Tthermg, measured at the transition from an equilibrium melt to a nonequilibrium glassy state, the dynamic glass transition temperature Tdyng is measured in equilibrium at a given frequency, for instance by dielectric (BDS) or specific heat spectroscopy (SHS). Interestingly, Tdyng shows mostly no thickness dependence for the homopolymers studied.29,30 In contrast, experiments on thin films of poly(vinyl methyl ether) (PVME)/polystyrene (PS) blends carried out by BDS and SHS showed a unique thickness dependence of Tdyng31–34 while the Tdyng values for PS and PVME are independent of film thickness.28,35,36 For instance, for the sample composition of 25 wt% PVME and 75 wt% PS, a complicated dependence of Tdyng on the film thickness has been found by SHS (see Fig. 1).30
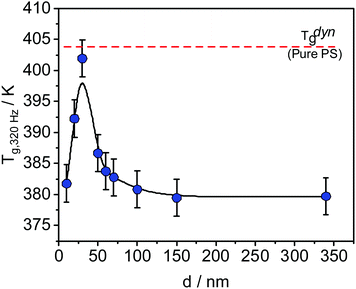 | ||
| Fig. 1 Dynamic glass transition temperature as a function of the sample thickness measured with SHS at 320 Hz for thin films of the blend PVME/PS with the composition 25 wt%/75 wt%. The line is a guide for the eye. The data were taken from ref. 29. | ||
T dyng increases with decreasing film thickness until a maximum at ca. 30 nm, where the value of Tdyng is approximately equal to that of PS, indicated by the dashed red line in Fig. 1. With a further decrease of the film thickness, Tdyng decreases. Madkour et al. hypothesized that this behavior is a counterbalance effect of a PVME-rich surface layer at the polymer/air interface and an adsorbed layer at the substrate.30
Furthermore, for the exact same polymer blend, the molecular dynamics of the PVME within thin supported films was investigated by broadband dielectric spectroscopy (BDS) utilizing crossed electrode capacitors (CEC, film prepared between two Al electrodes) and also nanostructure capacitors (NSC, one free air/polymer interface).32 It was shown that for bulk-like films (down to film thickness >110 nm), three different relaxation processes were observed depending on film thickness denoted as α2-, α1- and α′-relaxation. A generalized relaxation map showing the temperature dependence of the relaxation rates of all processes in Arrhenius coordinates is given in Fig. 2. The α2- and α1-relaxation are observed at temperatures above Tthermg, whereas the α′-process is found below Tthermg. For thicker samples, the relaxation rates of the α′-relaxation agree with that of the bulk, whereas for the thinner samples (<107 nm) the process becomes too weak to be detected. The relaxation rates of the α1-relaxation were found to be thickness dependent, becoming faster compared to that of the bulk with decreasing film thickness. Furthermore, the apparent activation energy of this process decreases with decreasing film thickness (see inset Fig. 2). This result is explained by an increased localization of PVME segments compared with that of PS, resulting from different local compositions. In other words, even the bulk samples have three different local compositions resulting in a distribution of modes.
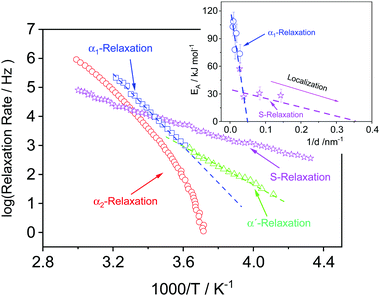 | ||
| Fig. 2 Generalized relaxation map for thin PVME/PS films with the composition of 25 wt%/75 wt%: red – α2-relaxation for the 107 nm film measured by CEC, blue – α1-relaxation for the 107 nm film measured by CEC, green – α′-relaxation for the 107 nm film measured by CEC. Please note that the α′-relaxation is only observed for film thicknesses above 30 nm. Violet – S-relaxation for a 7 nm film measured by NSC. Lines are a guide for the eye. This process is observed only for thin films with film thickness of 30 nm and below. Inset: Activation energy versus inverse film thickness: blue – α1-relaxation, violet – S-relaxation. Lines are a guide for the eye. The data were taken from ref. 32. | ||
However, the dielectric spectra of supported films, with thicknesses of 37, 26, 12 and 7 nm showed a slightly different behavior. For the 37 nm thick film, the α1-relaxation is the dominant process in the spectra. The relaxation rates of this process are shifted to higher frequencies, compared to the α1-relaxation obtained for the 37 nm film capped between two aluminum electrodes. This speeding-up of the molecular mobility was discussed in terms of a PVME-rich layer at the polymer/air interface.
Moreover, for the thinnest films (ca. <30 nm) an additional relaxation process was detected, which is called process S. It was assigned to fluctuations or adsorption/desorption processes of PVME segments within the loosely bound part of the adsorbed layer, proving that an PVME enrichment also takes place at the polymer/substrate interface. The apparent activation energy of the S-process has a different thickness dependence than that of the α1-relaxation, providing further evidence that the molecular origins of the two processes are different (see inset Fig. 2). Despite the strong proof and direct probing of the relaxation process assigned to the different compositional modes, the fundamental understanding of why the S process appears specifically around 30 nm, is still a mystery.
Until now, the concentration of PVME in the surface layer and the resulting compositional gradient within the film were investigated in dependence on the film thickness only for thick films with thicknesses larger than 100 nm and in the bulk state.37,38 This work is concentrated on film thicknesses below 100 nm. An understanding and elucidation of the compositional gradient in thin films with thickness below 100 nm is required to understand the results obtained by BDS and SHS discussed above.
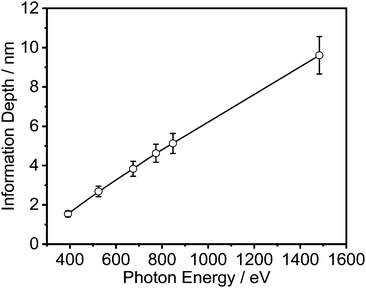
To further quantify and understand the compositional heterogeneities appearing at the air/polymer interface, the surface composition of PVME/PS blends was investigated using X-ray Photoelectron Spectroscopy (XPS).39,40 In the conventional approach, one photon energy (Al Kα radiation with an energy of 1486.6 eV) is used. For the relevant C1s photoelectrons, the information depth is about 10 nm for this photon energy. In this near-surface region, conclusions about local heterogeneities are not possible to draw. Moreover, for thin films with thicknesses of about 10 nm, the photoelectrons will originate from the entire film. Therefore, the obtained results would not deliver a description of the free surface layer, but approximately that of the entire film.
Besides XPS, Static Secondary Ion Mass Spectroscopy (SSIMS) was previously employed to investigate the surface composition of PVME/PS blends at the polymer/air interface.41,42 This method is extremely surface-sensitive with an information depth of about 1 nm, but the quantification is difficult. Moreover, for the PVME/PS blend system, in some investigations one component has to be deuterated which has some influence on the miscibility.32 In addition, ellipsometry43,44 and attenuated total reflectance Fourier transform infrared spectroscopy45 were also utilized. The latter method has a sampling depth of 3 μm, which is also not suitable for studying thin films. Finally, neutron reflectivity can be employed to investigate the surface of thin films.37,46 The investigations require one component to be deuterated to establish the necessary contrast. It is known that the deuteration changes the miscibility and so the phase diagram.32 Therefore, the results obtained for a deuterated system might be not comparable to those of a non deuterated one.
In principle, angle-dependent (conventional) XPS could be used to estimate the composition of a surface layer of a sample.36,47 In this work, an alternative approach is introduced to study the compositional heterogeneities in thin films of polymer blends as a function of their film thickness, where a range of different photon energies is considered. This approach leads to different information depth and consequently to detailed information about the compositional heterogeneities in the respective ranges without sample destruction. Energy resolved XPS measurements have some advantages over angle dependent XPS experiments. The latter require a very flat surface. Moreover, the angle must be adjusted quite accurately to obtain reliable quantitative results especially when a larger series of samples are compared. Also, energy resolved measurements are a bit more surface sensitive. For angle dependent measurements, with increasing angle the intensity decreases and herewith the signal/noise ratio. This approach employed here gives a first overview about the vertical composition of the near-surface region of thin films with thicknesses below 100 nm, and detailed calculations, and simulations of the gradient structure of the thin polymer films are beyond the scope of this study.
The PVME concentration near the polymer/air interface of thin films of PVME/PS blends, with a nominal composition of 25/75 wt%, was measured using energy resolved XPS. These measurements were compared to conventional XPS measurements with a photon energy of 1486.6 eV. By analysis of the C1s peak, the concentration of PVME can be estimated in dependence on the information depth by keeping in mind that PVME consists of C–O and C–H bonds, whereas PS has only C–H bonds. Further concentration ratios will be considered in future work.
2. Experimental
Materials
Polymers were purchased from Aldrich Inc. The polymers were used as received from the producer which ensured high purity. PVME was obtained as an aqueous solution (50 wt%, molecular weight Mw = 91 kg mol−1, polydispersity PDI = 2.1). PS has a molecular weight of 524 kg mol−1 and a PDI of 1.04. Tthermg for the bulk state were determined by DSC (10 K min−1, second heating run) to be 246 K, 376 K and 293 K for dried PVME, PS, and PVME/PS 25/75 wt%, respectively. For details regarding film preparation, see ref. 32 and the ESI.† The samples were annealed at Tg,bulk + 50 K for 72 h in an oil-free vacuum to remove residual solvent and stresses induced by spin coating.48 The thickness of the film and its topography was determined by atomic force microscopy. No sign of dewetting was observed.XPS
Conventional XPS measurements were performed using a Kratos AXIS Ultra DLD with monochromatic Al Kα radiation with an energy of 1486.6 eV. The samples were placed on a stainless-steel sample holder and fixed with double adhesive carbon tape. The angle between the detector and the sample surface was 90 degrees (normal emission), and the angle between the X-ray source and the sample was 60 degrees. All spectra were processed using the program Unifit (version 2018). A sum of Lorentzian and Gaussian (L–G mixing of 0.2) was used as the fit function in combination with a Tougaard background. After fitting of the C1s spectra, all spectra were calibrated to the reference energy of the C1s component at 285.0 eV.BESSY
Energy resolved XPS measurements were carried out at the synchrotron BESSY II at Helmholtz Zentrum Berlin (HZB). The spectra were acquired at the HE-SGM monochromator dipole magnet CRG beamline at the photon energies given in Table S1 (ESI†) and Fig. 3. Like for the conventional measurements, the spectra were measured in normal emission. Here, the angle between the source and the sample was 45°. For the detection of the spectra a Scienta R3000 analyzer was used. All spectra were processed in the same way as the ones measured conventionally.The effective attenuation lengths of the photoelectrons were determined using the NIST standard reference database (version 1.3, SRD 82).49 For this estimation a band gap of 10 eV and a density for both polymers of 1.05 g cm−3 was used. The uncertainty in the estimated mean free path length was 10%.50
3. Results and discussion
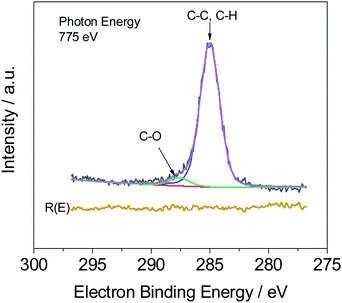
Fig. 4 illustrates, as expected, that two peaks occur in the measured C1s spectra, which are assigned to C–C (C–H) and C–O bonds. The weight fraction of PVME wPVME is estimated from the areas under the peaks (IC–H and IC–O, see Fig. 4) using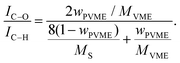 | (1) |
However, the calculations are only correct for perfectly clean samples. In general, a thin layer of carbonaceous material is found on the surface of air-exposed materials (adventitious carbon). This adventitious carbon comprises hydrocarbon species with a small amount of oxygen functionalities,51 which leads to additional contributions to the C–H peak. Such adventitious carbon is obtained on most air-exposed samples and has nothing to do with the employed polymers or its purity. Furthermore, a slight oxidation can be expected. The latter effect is considered in the uncertainty budget. The adventitious carbon is due to hydrocarbons adsorbed from the air atmosphere. However, due to the hydrocarbon contamination of the surface, the calculation of the weight fraction of PVME must be corrected. In particular, for the very surface-sensitive measurements with low excitation energies, a significant influence of this contamination layer can be expected. One possibility is to consider the surface contamination in the calculations of the effective attenuation length or in the simulations of the spectra of the films (see ref. 50 and references cited there). Here we have chosen an experimental approach and compared the composition of a pure PVME sample with a thickness of 15 nm which was kept in a vacuum, from preparation until the measurement at the theoretical IC–O/IC–H ratio of 2. (A C1s XPS spectrum of PVME is given in the ESI,† see Fig. S1.) By handling in vacuo, the surface contamination can be minimized. In this approach, a correction factor (1 + x) is introduced, which corrects the influence of the hydrocarbon contamination on the IC–O/IC–H ratio. This assumption of hydrocarbons as the main components in the surface contamination is well justified.51 Following these considerations, a correction factor can be calculated according to
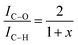 | (2) |
| E/eV | 1 + x |
|---|---|
| 392 | 11.9 |
| 525 | 7.21 |
| 677 | 5.18 |
| 775 | 3.85 |
| 848 | 4.24 |
| 1486.6 | 1.48 |
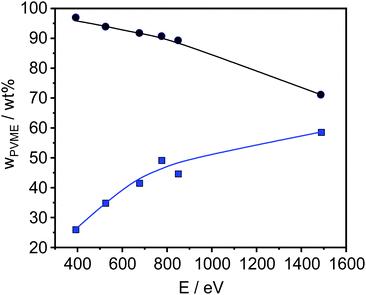 | ||
| Fig. 5 PVME concentration versus photon energy of a 45 nm sample before (blue points) and after correction (black points). The lines are a guide for the eye. | ||
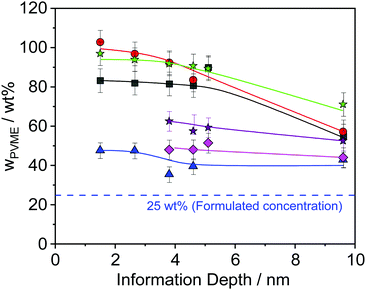
The obtained results are depicted in Fig. 6 and 7. For all film thicknesses and information depths, the concentration of PVME is increased compared to the bulk (formulated) concentration of 25 wt% (see Fig. 4). This result is already known from the literature. The surface enrichment of PVME at the polymer/air interface is due to the difference in the surface energies of the polymers with respect to air, which is γPVME = 36 mJ m−2 for PVME and γPS = 40.2 mJ m−2 for PS.38 Therefore, the enrichment of PVME at the surface is energetically preferred. As is also known from the literature, the highest used X-ray energy of 1486.6 eV is not high enough to reach an information depth with the formulated concentration of PVME. In further work it is planned that hard X-rays will be employed to reach deeper regions. It must be noted that for all film thicknesses an enrichment of PVME in the near-surface region was observed, which conforms to the well-known findings from the literature.37,38 Interestingly, the dependence of wPVME at the information depth of 10 nm, which is typical for an XPS lab experiment is less pronounced than for the lower information depths, which could only be investigated with the low excitation energies used at the synchrotron. This observation stressed the importance of such experiments for the structural elucidation of such films with thicknesses below 100 nm. It should be noted that the thinnest investigated film had a thickness of 15 nm. Therefore, the contributions from oxygen containing groups of the substrate should be quite small.
Theoretical approaches for the concentration profile based on a Flory–Huggins model predict an exponential decay.52 These theoretical results were confirmed for a mixture of PVME blended with end-functionalized PS (symmetrical composition 50 wt%) with a film thickness larger than 100 nm.35 A closer inspection of Fig. 6 reveals that the PVME concentration profile also decays exponentially for film thicknesses larger than 30 nm (see Fig. S2 in the ESI†) where the decay length depends on the film thickness. For a smaller film thickness the concentration does not decay exponentially. To discuss this in the framework of the theoretical approach given above one has to consider that this model consists of an air/polymer interface and an infinitely thick polymer film with no second interface. This means that this model cannot be appropriately applied for the thin films discussed here, especially for those with low film thickness where the influence of polymer/substrate interface also becomes more and more dominant. For a discussion of thin films, the model has to be extended by a second interface which is not in the scope of this work. Moreover, because no thickness of the polymer film is included in the mean field Flory–Huggins approach, the model cannot predict any thickness dependence.
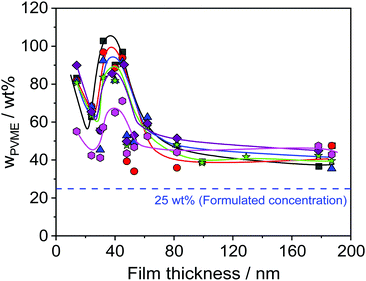
Furthermore, Fig. 6 reveals that the concentration of PVME has a complicated dependence on the film thickness. Therefore, the concentration of PVME is plotted versus the film thickness in Fig. 7, for all photon energies.
Despite the scattering of the data (which reflects the measurement uncertainty within), Fig. 7 shows three features. Firstly, a minimum of wPVME at 25 nm is observed. Secondly, a maximum between 30 nm and 40 nm is observed. For the maximum, the PVME concentration is about 100 wt% for the lowest photon energy. This means that a part of the surface layer with a thickness defined by the lowest photon energy consists only of PVME. The third feature is the saturation of wPVME for film thicknesses higher than 50 nm. This means that for all photon energies, i.e. all information depths, wPVME is about 40 wt% for film thicknesses above 50 nm. In other words, the composition of the film is relatively homogeneous in the outermost 10 nm. The almost constant level of the PVME concentration observed for film thicknesses higher than 50 nm is further called the saturation level.
The dependence of the PVME concentration on the film thickness observed in Fig. 7 shows a remarkable resemblance to the dependence of Tdyng on the film thickness depicted in Fig. 1. This is further supported by the fact that for films with a thickness of 30 nm, Tdyng is close to that of pure PS films as discussed in ref. 29 and 30. This could also be interpreted as a form of nanophase separation. To elucidate that, a simplified model is assumed. For the 30 nm film, the thickness of the near surface region close to the air/polymer can be estimated assuming an exponential decay of the outgoing photoelectrons, originating from the deeper parts of the film. Such an analysis will lead to a length scale where the number of photo electrons originating from PVME is decayed to 1/e. The calculated PVME concentration in this near surface region decreases from 3.3 nm, for an excitation energy of 525 eV, to 2.7 nm for an excitation energy of 1486.6 eV, continuously. For sharp phase boundaries this value should be constant for all excitation energies. Therefore, this behavior can be explained as a near surface region of PVME with a slight intermixing between PVME and PS, resulting in a gradient of the PVME concentration. For film thicknesses smaller than 30 nm, the thickness of the bulk-like layer further decreases. Consequently, polystyrene should be introduced into the surface layer, which leads to a lower amount of PVME in the outermost surface layer for all information depths (see Fig. 7). This also means that the PVME concentration in the bulk-like layer in the middle of the film increases. This result agrees with the decrease of Tdyng for film thicknesses smaller than 30 nm. This agreement provides further evidence that the correction for adventitious carbon is effective.
As discussed above for ca. 25 nm a local minimum is observed in the dependence of the PVME concentration on the film thickness (see Fig. 7). For film thicknesses smaller than 25 nm the PVME concentration increases again with a further decrease in film thickness. This increase in the PVME concentration might be assigned to the adsorbed layer. Therefore, hard X-ray photoelectron spectroscopy (HAXPES) investigations are necessary which are planned in the near future. Previously it was evidenced by solvent leaching experiments that the adsorbed layers in thin films of PVME/PS consist of PVME.31 Nevertheless, differently from the adsorbed layer of leached films for the adsorbed layer within thin films it could not be excluded that some PS is also incorporated in the adsorbed layer especially for low film thicknesses. On the other hand, contributions from the topmost surface layer may also occur.
It is interesting to note that it was found by ellipsometry investigations that 30 nm is the film thickness where information from the adsorbed layer percolates to the bulk-like layer of the film.53 Several further studies have also shown that at a threshold thickness of ca. 30 nm the thickness dependence of segmental dynamics and glass transition could change. This was shown for thin films of poly(2-vinyl pyridine) P2VP,54 star-shaped PS,17 and PVME/PS blends.29,31,32 The reason behind this behavior is still not understood. For completeness it should be mentioned that there are also theoretical models for surface segregations including also further experimental data.55,56
Glor et al. showed for P2VP that with decreasing film thickness from 217 nm to 16 nm, the onset (T+) and offset (T−) temperatures of the glass transition shift to higher and lower temperatures, with respect to the bulk behavior, respectively. This behavior was discussed in terms of a gradient of the molecular mobility within the films. For thick films (∼217 nm), the dynamics is homogeneous, and no influence of both interfaces could be observed. However, at 33 nm they proposed that the length scale of the gradient of the molecular mobility could reach at least 33 nm thus resulting in a sharp increase in the glass transition breadth. For thinner films than 16 nm two distinct transitions were observed, which were assigned both to two separate a glass transition related to both coexisting layers. This result might indicate that the gradient is not relevant anymore, where the difference in the molecular dynamics of the free surface and that of the irreversible adsorbed layer becomes too large to maintain a gradient in a 16 nm or thinner film. It should be noted that the temperature range measured in ref. 29 was broad enough to detect in principle the upper and the lower glass transitions. Nevertheless, only one glass transition was observed for the system discussed here.
Thin films of the PVME/PS blend could serve as a model system to shed some light on what happens to the molecular dynamics of the different layers within the thin films, utilizing the surface segregation phenomena, where differences in the molecular dynamics would be enhanced due to local compositional heterogeneities, induced by the asymmetry in the segmental dynamics of PVME and PS. To further understand the behavior seen at 30 nm film thickness, the gradient in the composition, which defines the compositional heterogeneities within the surface layer must be further quantified. In an attempt to do so, a very simplified approach is introduced. The calculation in this approach assumes that all photoelectrons from a depths does not exponential decay within the information depth. Therefore, this approach is semiquantitative and gives an idea about the compositional gradient within the different film thicknesses.
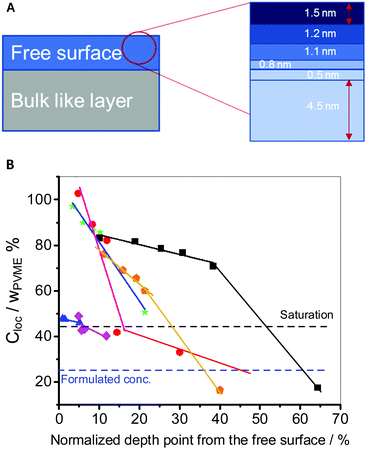
Here, the film down to an information depth of 9.6 nm from the air/polymer interface is approximated by sublayers having thicknesses corresponding to the different information depths of two neighboring photon energies Yi = Xi+n − Xi where Xi and Xi+n are the information depths at a given photon energy i (see Fig. 8A). To avoid an overlap with the meaning of the layers discussed above these sublayers Yi of the surface layer are further called information levels. n is the corresponding difference in the photon energies. The Xi, Yi and n values are given in Table 2. A local PVME concentration Cloc is considered for each information level, which can be iteratively estimated by
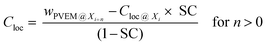 | (3) |
| Photon energy (i)/eV | n/eV | Information depth (Xi)/nm | Distance from the information level above (Yi)/nm | SC | C loc/wPVME (%) |
|---|---|---|---|---|---|
| 392 | 0 | 1.5 | 1.5 | 1 | 97.0 |
| 525 | 133 | 2.7 | 1.2 | 0.44 | 90.1 |
| 676 | 151 | 3.8 | 1.1 | 0.29 | 86.6 |
| 775 | 99 | 4.6 | 0.8 | 0.17 | 85.6 |
| 849 | 74 | 5.1 | 0.5 | 0.10 | 76.3 |
| 1486.6 | 637.6 | 9.6 | 4.5 | 0.47 | 50.5 |
Fig. 8A depicts a schematic representation of this concept. Fig. S3 in the ESI† gives an example of the local PVME concentrations for different information levels Yiversus the film thicknesses. However, to compare the compositional gradient of different film thicknesses, the distance over which this gradient is taking place must be factored in. This is due to the fact that the miscibility of both compounds is not only due to the properties of the polymers but is also influenced by the presence of the interfaces. The relative influence of the interfaces on the miscibility will change with the film thickness. Therefore, the information depth point is normalized by the film thickness (Xi/film thickness). The local PVME Cloc concentrations are plotted versus Xi/film thickness × 100% in Fig. 8B. The slope of this function represents the concentration gradient in the first 9.6 nm for each film thickness. The higher the slope, the stronger is the compositional gradient.
Fig. 8B reveals new insights into the compositional gradient and thus the dynamic heterogeneities of the surface layer as a function of the film thickness. First, as discussed above there is a kind of saturation level of the PVME concentration in the surface layer (minimum of surface enrichment of PVME), with 42 wt% PVME (observed for thick films: 200 nm to 80 nm). This probably means that at this level of confinement, the compositional heterogeneity gradient within the film is not too high and would reach the formulated concentration (25 wt% PVME) within the bulk-like layer. However, the low gradient translates to small incremental composition changes taking place over larger length scales. This results in a thick part of the surface layer with a different average compositional gradient as compared to the bulk like layer. The dynamics of both layers are heterogeneous, and no direct influence of either interface could be observed. Consequently, Tthermg,film (>100 nm) = Tthermg,bulk and Tdyng,film (>100 nm) = Tdyng,bulk.29 This is also in line with the results obtained by BDS showing two cooperative segmental dynamic relaxations; the α1- and α2-relaxation similar to the bulk (see also Fig. 2).32
Due to mass conservation, a further decease in the film thickness will take place at the cost of the thickness of the bulk-like layer. This results in a slight increase of Tdyng,film in the thickness range from 80 nm to 50 nm, as the effect of both PVME enriched interfaces influences the composition of the bulk-like layer, resulting in a higher PS concentration.
As discussed above, below 50 nm, the surface layer seems to form a nanophase separated layered structure. This takes place as the compositional gradient becomes higher within the film, due to the decrease of the thickness of the bulk-like layer over which the gradient could reach the saturation level and then the formulated concentration (Fig. 8B). At this length, the surface layer constitutes ca. 10–20% of the total film thickness, consisting of two sublayers: (I) an enriched PVME surface sublayer followed by (II) a PVME-rich sublayer (with a lower PVME concentration) starting from the saturation level concentration, which is higher than the formulated concentration. Additionally, the thickness of the adsorbed layer decreases slightly, as was recently shown in ref. 53, for identically prepared PVME films to the ones used here. This yields the observed increase in Tdyng, compared to the bulk value measured for thick films.
It is worth noting that it was shown in ref. 47 that thin films with thickness below 35 nm, could not form a stable leachable adsorbed layer. This was explained by the “loosely” bound part of the adsorbed layer starting to disappear, leaving only the strongly bound layer, which is susceptible to dewetting during the leaching experiments.
At ca. 30 nm, a threshold thickness is reached, where also due to mass conservation, the thickness of the adsorbed layer starts to decrease and so does its PVME concentration. This was confirmed by BDS,32 where an additional localized relaxation process called “S-relaxation” was observed only for films with thicknesses of 30 nm and below (see Fig. 2). The activation energy of this process decreases with decreasing film thickness, pointing to further restriction of the PVME segments. This is probably due to higher PS concentration within the adsorbed layer, which induces the extra localization of the PVME segments (see inset Fig. 2).
Remarkably, the total thickness of the surface layer is not significantly changed, as depicted in Fig. 8B. Whereas the bulk-like layer is still constituting the largest portion of the film. This results in further compositional frustration, which results in a drastic increase in the PVME concentration of the outermost part of the surface layer.
This is also in agreement with BDS results for the exact same system.32 In principle, the aforementioned PS-rich layer would have negligible signal in the dielectric spectra, due to the weak dipole moment of PS. This explains the observed disappearance of the α1-relaxation process for films with thicknesses below 26 nm.32
A further decrease in the film thickness (<30 nm) underlines the discussed influences of both interfaces at the substrate and at the air/polymer interface. Consequently, the properties of the films are determined mainly by the surface and the interface. At this thickness, the formulated concentration level (equilibrium level) could probably not be reached within a significant part of the film. This explains the yielded broadening in glass transition,30 further decrease in Tdyng,29 (see Fig. 1), and the disappearance of α1-relaxation (only a more pronounced S-relaxation process).32
4. Conclusions
Here, energy resolved XPS measurements were presented for the thin films of the miscible blend PVME/PS with a composition of 25 wt%/75 wt%. This technique will provide information about the spatial distribution of PVME up to an attenuation length of ca. 10 nm depending on the photon energy. Firstly, it was found that the estimated concentration of PVME decreases with increasing photon energy. Secondly, the PVME concentration versus the film thickness shows a complex behavior. With decreasing film thickness wPVME increases until a maximum at 30 nm where for the outermost nanometer ca. 100 wt% PVME was found. With a further decrease of the film thickness the concentration of PVME decreases indicating that the surface layer contains more polystyrene. At the lowest film thicknesses of 15 nm, wPVMES increases again which can be explained by the influence of the layer adsorbed on the substrate consisting mainly of PVME.The data obtained here by energy resolved XPS agree with previous investigations on the same system by specific heat spectroscopy where a corresponding behavior was observed for the dynamic glass transition temperature. The results given here help to understand the thermal data better from a microscopic point of view.
Author contributions
AS initiated and guided the project, MG prepared the samples and analyzed all the XPS measurements, and JR carried out the XPS measurements. SM and PS contributed significantly to the interpretation of the data. The manuscript was written by MG, SM and AS with contributions from JR and PS.Conflicts of interest
There are no conflicts to declare.Acknowledgements
The German Science Foundation DFG (Project number 124846229) is acknowledged for financial support. The authors thank the BESSY II synchrotron radiation source (Helmholtz Center, Berlin) for the allocation of beamtime at the HE-SGM beamline.References
- S. Delcambre, R. Riggleman, J. de Pablo and P. Nealey, Mechanical Properties of Antiplasticized Polymer Nanostructures, Soft Matter, 2010, 6, 2475–2483 RSC.
- M. Ediger and J. A. Forrest, Dynamics near Free Surfaces and the Glass Transition in Thin Polymer Films: A View to the Future, Macromolecules, 2014, 47, 471–478 CrossRef CAS.
- A. Alegria, J. Colmenero, K. L. Ngai and C. M. Roland, Observation of the Component Dynamics in a Miscible Polymer Blend by Dielectric and Mechanical Spectroscopies, Macromolecules, 1994, 27, 4486–4492 CrossRef CAS.
- I. Cendoya, A. Alegria, J. M. Alberdi, J. Colmenero, H. Grimm, D. Richter and B. Frick, Effect of Blending on the PVME Dynamics. A Dielectric, NMR, and QENS Investigation, Macromolecules, 1999, 32, 4065–4078 CrossRef CAS.
- H. Takeno, M. Kobayashi and T. Aikawa, Localized Cooperative Molecular Motion in Miscible Polymer Mixtures with Large Difference in Glass-Transition Temperatures, Macromolecules, 2006, 39, 2183–2190 CrossRef CAS.
- R. H. Colby and J. E. G. Lipson, Modeling the Segmental Relaxation Time Distribution of Miscible Polymer Blends: Polyisoprene/Poly(vinylethylene), Macromolecules, 2005, 38, 4919–4928 CrossRef CAS.
- F. Alvarez, A. Alegria and J. Colmenero, Study of the Two-Component Segmental Dynamics of Poly(vinylethylene)/Polyisoprene Miscible Blends, Macromolecules, 1997, 30, 597–604 CrossRef CAS.
- A. Arbe, A. Alegria, J. Colmenero, S. Hoffmann, L. Willner and D. Richter, Segmental Dynamics in Poly(vinylethylene)/Polyisoprene Miscible Blends Revisited. A Neutron Scattering and Broadband Dielectric Spectroscopy Investigation, Macromolecules, 1999, 32, 7572–7581 CrossRef CAS.
- D. Cangialosi, G. A. Schwartz, A. Alegria and J. Colmenero, Combining configurational entropy and self-concentration to describe the component dynamics in miscible polymer blends, J. Chem. Phys., 2005, 123, 144908 CrossRef CAS PubMed.
- K. L. Ngai and S. Capaccioli, Unified explanation of the anomalous dynamic properties of highly asymmetric polymer blends, J. Chem. Phys., 2013, 138, 054903 CrossRef CAS PubMed.
- Y. He, T. R. Lutz and M. D. Ediger, Segmental and terminal dynamics in miscible polymer mixtures: Tests of the Lodge-McLeish model, J. Chem. Phys., 2003, 119, 9956 CrossRef CAS.
- A. Das, A. B. Dey, S. Chattpadhyay, G. De, M. K. Sanyal and R. Mukherjee, Nanpparticle induced morphology modulation in spin coated PS/PMMA blend thin films, Langmuir, 2020, 36, 15270–15282 CrossRef CAS PubMed.
- T. P. Lodge and T. C. B. McLeish, Self-Concentrations and Effective Glass Transition Temperatures in Polymer Blends, Macromolecules, 2000, 33(14), 5278–5284 CrossRef CAS.
- G. Katana, E. W. Fischer, Th. Hack, V. Abetz and F. Kremer, Influence of concentration fluctuations on dielectric α-relaxation of homogeneous polymer mixtures, Macromolecules, 1995, 8, 2714–2722 CrossRef.
- J. Colmenero and A. Arbe, Segmental dynamics in miscible polymer blends: recent results and open questions, Soft Matter, 2007, 3, 1474–1484 RSC.
- E. C. Glor, R. J. Composto and Z. Fakhraai, Glass Transition Dynamics and Fragility of Ultrathin Miscible Polymer Blend Films, Macromolecules, 2015, 48, 6682–6689 CrossRef CAS.
- S. Napolitano, E. Glynos and N. B. Tito, Glass transition of polymers in bulk, confined geometries, and near interfaces, Rep. Prog. Phys., 2017, 80, 036602 CrossRef PubMed.
- H. Nakanishi and P. Pincus, Surface spinodals and extended wetting in fluids and polymer solutions, J. Chem. Phys., 1983, 79, 997 CrossRef CAS.
- G. Dee and B. B. Sauer, The Surface Tension of Polymer Blends: Theory and Experiment, Macromolecules, 1993, 26, 2771–2778 CrossRef CAS.
- J. L. Keddie, R. A. L. Jones and R. A. Cory, Interface and Surface Effects on the Glass-Transition Temperature in Thin Polymer Films, Faraday Discuss., 1994, 98, 219–230 RSC.
- J. L. Keddie, R. A. L. Jones and R. A. Cory, Size-Dependent Depression of the Glass Transition Temperature in Polymer Films, Europhys. Lett., 1994, 27(1), 59–64 CrossRef CAS.
- J. A. Forrest and K. Dalnoki-Veress, The glass transition in thin polymer films, Adv. Colloid Interface Sci., 2001, 94, 167–196 CrossRef CAS.
- C. J. Ellison, R. L. Ruszowski, N. J. Fredin and J. M. Torkelson, Dramatic Reduction of the Effect of Nanoconfinement on the Glass Transition of Polymer Films via Addition of Small-Molecule Diluent, Phys. Rev. Lett., 2004, 92(9), 095702 CrossRef PubMed.
- R. A. Riggleman, K. Yoshimoto, J. F. Douglas and J. J. de Pablo, Influence of Confinement on the Fragility of Antiplasticized and Pure Polymer Films, Phys. Rev. Lett., 2006, 97, 045502 CrossRef PubMed.
- Z. Fakhraai and J. A. Forrest, Probing Slow Dynamics in Supported Thin Polymer Films, Phys. Rev. Lett., 2005, 95, 025701 CrossRef PubMed.
- V. Lupascu, S. J. Picken and M. Wübbenhorst, Cooperative and non-cooperative dynamics in ultra-thin films of polystyrene studied by dielectric spectroscopy and capacitive dilatometry, J. Non-Cryst. Solids, 2006, 352, 5594–5600 CrossRef CAS.
- H. Yoon and G. B. McKenna, Substrate Effects on Glass Transition and Free Surface Viscoelasticity of Ultrathin Polystyrene Films, Macromolecules, 2014, 47, 8808–8818 CrossRef CAS.
- V. M. Boucher, D. Cangialosi, H. Yin, A. Schönhals, A. Alegra and J. Colmenero, Tg depression and invariant segmental dynamics in polystyrene thin films, Soft Matter, 2012, 8, 5119 RSC.
- K. Paeng, S. F. Swallen and M. D. Ediger, Direct Measurement of Molecular Motion in Freestanding Polystyrene Thin Films, J. Am. Chem. Soc., 2011, 133, 8444–8447 CrossRef CAS PubMed.
- H. Yin, S. Madkour and A. Schönhals, Unambiguous Evidence for a Highly Mobile Surface Layer in Ultrathin Polymer Films by Specific Heat Spectroscopy on Blends, Macromolecules, 2015, 48, 4836–4941 Search PubMed.
- S. Madkour, P. Szymoniak, C. Schick and A. Schönhals, Unexpected behavior of ultra-thin films of blends of polystyrene/poly(vinyl methyl ether) studied by specific heat spectroscopy, J. Chem. Phys., 2017, 146, 203321 CrossRef PubMed.
- S. Madkour, P. Szymoniak, A. Hertwig, M. Heidari, R. von Klitzing, S. Napolitano, M. Sferraza and A. Schönhals, Decoupling of Dynamic and Thermal Glass Transition in Thin Films of a PVME/PS Blend, ACS Macro Lett., 2017, 6, 1156–1161 CrossRef CAS.
- S. Madkour, P. Szymoniak, J. Radnik and A. Schönhals, Unraveling the Dynamics of Nanoscopically Confined PVME in Thin Films of a Miscible PVME/PS Blend, ACS Appl. Mater. Interfaces, 2017, 9, 37289–37299 CrossRef CAS PubMed.
- P. Szymoniak, M. Gawek, S. Madkour and A. Schönhals, Confinement and localization effects revealed for thin films of the miscible blend Poly(vinyl methyl ether)/Polystyrene with a composition of 25/75 wt%, Eur. Phys. J. E: Soft Matter Biol. Phys., 2019, 42, 101 CrossRef PubMed.
- S. Madkour, P. Szymoniak, M. Heidari, R. von Klitzing and A. Schönhals, Unveiling the dynamics of self-assembled layers of thin films of poly(vinyl methyl ether) (PVME) by nanosized relaxation spectroscopy, ACS Appl. Mater. Interfaces, 2017, 9, 7535–7546 CrossRef CAS PubMed.
- H. Yin and A. Schönhals, Calorimetric glass transition of ultrathin poly(vinyl methyl ether) films, Polymer, 2013, 54, 2067–2070 CrossRef CAS.
- D. Kawaguchi, K. Tanaka and T. Kajiyama, Surface composition control via chain end segregation in blend films of polystyrene and poly(vinyl methyl ether), Macromolecules, 2003, 36, 6824–6830 CrossRef CAS.
- Q. S. Bhatia, D. H. Pan and J. T. Koberstein, Preferential surface adsorption in miscible blends of polystyrene and poly(vinyl methyl ether), Macromolecules, 1988, 21, 2166–2175 CrossRef CAS.
- D. H.-K. Pan and W. M. Prest, Surfaces of polymer blends: X-ray photoelectron spectroscopy studies of polystyrene/poly(vinyl methyl ether) blends, J. Appl. Phys., 1985, 58, 2861–2870 CrossRef CAS.
- K. Tanaka, J.-S. Yoon, A. Takaharam and T. Kajiyama, Ultrathinning-Induced Surface Phase Separation of Polystyrene/Poly(vinyl methyl ether) Blend Film, Macromolecules, 1995, 28, 934–938 CrossRef CAS.
- Q. Bhatia and M. Burrel, Static SIMS Study of Miscible Blends of Polystyrene and Poly(vinyl methyl ether), Surf. Interface Anal., 1990, 15, 388–391 CrossRef CAS.
- H. Yang and P. F. Green, Role of Spatial Compositional Heterogeneity on Component Dynamics in Miscible Bulk and Thin Film Polymer/Polymer Blends, Macromolecules, 2013, 46, 9390–9395 CrossRef CAS.
- K. R. Thomas, N. Clarke, R. Poetes, M. Morarin and U. Steiner, Wetting induced instabilities in miscible polymer blends, Soft Matter, 2010, 6, 3517–3523 RSC.
- T. Xia, Y.-P. Qin and T. Huang, Phase Separation, Wetting and Dewetting in PS/PVME Blend Thin Films: Dependence on Film Thickness and Composition ratio. Chinese, J. Polym. Sci., 2018, 1–9 Search PubMed.
- J. M. G. Cowie, B. G. Devlin and I. J. McEwen, A study of surface enrichment in polystyrene/poly(vinyl methyl ether) blends using attenuated total reflectance infra-red spectroscopy, Polymer, 1993, 34, 501–504 CrossRef CAS.
- H. Ogawa, T. Kanaya, K. Nishida, C. Matsuba, J. P. Majewski and E. Watkins, Time-resolved specular and off-specular neutron reflectivity measurements on deuterated polystyrene and poly(vinyl methyl ether) blend thin films during dewetting, J. Chem. Phys., 2009, 131, 104907 CrossRef.
- Surface and Interfacial Aspects of Biomedical Polymers, ed. J. D. Andrade, Springer, 1985 Search PubMed.
- G. Reiter, M. Hamieh, P. Damman, S. Sclavons, S. Gabrielle, T. Vilmin and E. Raphael, Residual stresses in thin polymer films cause rupture and dominate early stages of dewetting, Nat. Mater., 2005, 9, 754–758 CrossRef PubMed.
- C. J. Powell and A. Jablonski, NIST electron effective attenuation length database, Version 1.3, SRD 82, National Institute of Standards and Technology, Gaithersburg, MD, 2011 Search PubMed.
- A. Jabloski and C. J. Powel, Effective attenuation lengths for different quantitative applications of X-ray photoelectron spectroscopy, J. Phys. Chem. Ref. Data, 2020, 46, 033102 CrossRef.
- T. L. Barr and S. Seal, Nature of the use of adventitious carbon as binding energy standard, J. Vac. Sci. Technol., A, 1995, 13, 1239 CrossRef CAS.
- I. Schmidt and K. Binder, Model calculations for wetting transition in polymer mixtures, J. Phys., 1985, 46, 1631–1644 CrossRef CAS.
- S. Madkour, M. Gawek, A. Hertwig and A. Schönhals, Do Interfacial Layers in Thin Films Act as an Independent Layer Within Thin Films?, Macromolecules, 2021, 54, 509–519 CrossRef CAS.
- E. C. Glor, G. V. Angrand and Z. Fakhraai, Exploring the broadening and the existence of two glass transitions due to competing interfacial effects in thin, supported polymer films, J. Chem. Phys., 2017, 146, 203330 CrossRef PubMed.
- A. Hariharan, S. K. Kumar, M. H. Rafailovich, J. Sokolov, X. Zheng, D. Duong, S. Schwarz and T. P. Russel, The effect of finite film thickness on the surface segregation in symmetric binary polymer mixtures, J. Chem. Phys., 1993, 99, 656 CrossRef CAS.
- H. Nakanishi and P. Pincus, Surface spinodals and extended wetting in fluids and polymer solutions, J. Chem. Phys., 1983, 79, 997 CrossRef CAS.
Footnotes |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/d1sm00656h |
| ‡ MG and SM contributed equivalently to the presented research. Therefore, both researchers should be considered simultaneously as first authors. |
| § Current address: BASF SE, Carl-Bosch-Str. 38, 67056 Ludwigshafen, Germany. |
| This journal is © The Royal Society of Chemistry 2021 |