Molecular mobility and crystallization of renewable poly(ethylene furanoate) in situ filled with carbon nanotubes and graphene nanoparticles

Abstract

We investigate the thermal transitions and molecular mobility in new nanocomposites of biobased poly(ethylene furanoate) (PEF), by calorimetry and dielectric spectroscopy, supplemented by X-ray diffraction, Fourier transform infra-red spectroscopy and polarized light microscopy. The emphasis is placed on the facilitation of the crystallization of PEF, which is in general low and slow due to structural limitations that result in poor nucleation. Tuning of the crystalline fraction (CF) and semicrystalline morphology are important for optimization of the mechanical performance and manipulation of the permeation of small molecules (e.g., in packaging applications). The nucleation and CF are successfully improved here by the in situ filling of PEF with 0.5–2.5 wt% of carbon nanotubes (CNTs) and graphene nanoplatelets (GNPs). The improvements are discussed in connection with weak or absent interfacial polymer–filler interactions. CNTs were found to be more effective in facilitating crystallization, as compared with GNPs, possibly due to their larger aspect ratio. The segmental dynamics of PEF are both accelerated and decelerated by the addition of GNP and CNT, respectively, with complex phenomena contributing to the effects, namely, nucleation, changes in molar mass and changes in the free volume. The molecular mobility of PEF is moderately affected ‘directly’ by the particles, whereas stronger effects are induced by crystallization (an indirect effect) and, furthermore, by the increase in the length of alkylene sequences on the chain. Local dynamics exhibit time scale disturbances when the temperature approaches that of the glass transition, which is proposed here to be a common characteristic in the case of mobilities originating from the polymer backbone for these as well as different polyesters. Despite the weak effects on molecular mobility, the role of the fillers as nucleating agents seems to be further exploitable in the frame of envisaged applications, as the use of such fillers in combination with thermal treatment offer possibilities for manipulating the semicrystalline morphology, ion transport and, subsequently, permeation of small molecules.

---

1. Introduction

During the past decade, humanity has faced globally increasing interest in environmental concerns, involving, among others, the use of materials (e.g., polymers) in our everyday life. Along with the need for better materials performance, the needs of specialized and new applications are also growing continuously. Regarding polymeric materials, this issue is being addressed by the scientific community via the development of biobased and renewable polymers.^1–3

Poly(n-alkylene furanoate)s (PnAF)s, also called poly(alkylene furandicarboxylate)s, belong to a modern class of polymers that are based on 2,5-furandicarboxylic acid, a renewable building block derived from 5-hydroxymethylfurfural sources, known as poly(alkylene-2,5-furan-dicarboxylate)s.^4–7 Moreover, 2,5-furandicarboxylic acid is the bio-derived homologue of terephthalic acid,^8–10i.e., a monomer widely employed for the production of commodity plastics applied today. PnAFs are biodegradable polyesters developed in today's frame of a green and circular economy,^2,11 aimed at replacing the fossil-based homologue polymers in a wide range of applications, from industry and bio-medicine to everyday life. PnAFs have already been employed within packaging applications, owing to their exceptional gas barrier performance^12,13 in addition to their relatively good mechanical behavior. PnAFs are generally synthesized by two-stage polycondensation methods, where, up to this point, the most common PnAFs are those with a number of n-alkylene units of 2–6.

Since these polyesters are semicrystalline, their performance is strongly connected with their crystallinity, namely, the crystalline fraction (CF) and the semicrystalline morphology,^14,15 in general called their ‘crystallizability’. Due to structural limitations originating from the existence of the ‘heavy’ furan ring¹⁶ and the relatively small chain lengths (low M_n values), PnAFs are characterized by a quite rigid chain backbone and, thus, exhibit a difficulty to crystallize.^4,5,16 Crystallization is facilitated, in general, upon increasing of the n-alkylene sequence length, for example when changing from n = 2 and 3 [poly(ethylene furanoate) (PEF)^5,17 and poly(propylene furanoate) (PPF), respectively] to n = 4 and 6 [poly(butylene furanoate) (PBF) and poly(hexylene furanoate) (PHF)].^4,16,18 In principle the polycondensation methods result in low molar mass PnAFs, which is the reason why in many cases PnAFs do not easily crystallize during cooling from the melt state, whereas they demonstrate quite strong cold crystallization during heating.^5,19 This suggests that for the crystallization of PnAFs strong supercooling is necessary²⁰ as, most probably, the main difficulty of these polyesters arises from nucleation disability. As in many other cases of polymers, including either renewable or non-renewable polymers,^21–25 the solution to these issues has been found via the preparation of polymer nanocomposites (PNCs). Via the introduction of nanoparticles, nucleation is indeed facilitated,^{21,22,26–28} moreover, the CF increases. As expected, the CF also depends on the thermal treatment employed for crystallization, namely, non-isothermal or isothermal, as well as the choice of the overall temperature treatment.^20,29 Alternations in the CF and semicrystalline morphology (the size, number, and distribution of crystallites) have direct impacts on a variety of macroscopic properties (the performance) of the polymeric materials, such as the mechanical properties,^13,30,31 small molecule permeation,^13,32,33 and electrical^30,34,35 and thermal conductivity.^36,37

In our recent works,^18,31,38,39 we have demonstrated the potential for tuning the crystallizability of three furan based polyesters, namely, PPF, PBF and PHF, by reinforcing the polymer via the in situ introduction of low amounts of various types nanoparticles, which act as nucleating agents, to the PnAF matrix. The nanoparticles consisted of montmorillonite clays,^40,41 graphene nanoplatelets (GNPs) and graphene oxide (GO),⁴² carbon nanotubes (CNTs),⁴³ and halloysite nanotubes or spherical nanosilicas.⁴⁴ It has been shown that the reinforcing/nucleating action of these nanoparticles correlates well with the provided sites. These latter sites can be represented by the nanofiller's specific surface area and the aspect ratio.^18,19,31,39 In this frame, two of the most successful nucleating agents for PnAFs have been found to be CNTs and GNPs. Secondly, interfacial interactions, related to surface chemistry/filler modifications,^10,45,46 seem to play an important role on nucleation and crystallization. For example, in a recent work,¹⁹ we have studied PPF filled in situ with low amounts (only 1 wt%) of CNTs and GO, both surface-modified and unmodified. We revealed that while the modifications enhance the polymer–particles adhesion, strikingly, the strong interfacial interaction resulted in the retardation of crystallization.¹⁹ These effects seem to exist not only for PnAFs, but also for polymers characterized by more flexible chains, such as polylactides^35,47 and, furthermore, rubbers.^48,49

As expected, the segmental mobility of the chains is connected with both stages of crystallization, nucleation and crystal formation. Segmental mobility can be followed by the effects on the glass transition, e.g., by calorimetry, whereas rich information on molecular dynamics can be supplied by the advanced technique of broadband dielectric spectroscopy (BDS).⁵⁰ The latter is a technique characterized by high resolving power and, thus, has proved quite illuminating on the polymer dynamics of complex systems,^51–57 including the involvement of crystallization.^58–60 Both techniques are employed as main investigation tools here. Regarding PnAFs, there is still a quite small number of published studies on their molecular mobility.^{19,31,39,61–66} Up to this point and to the best of our knowledge, the main factor that seems to govern the dynamics of PnAFs chains seems to be the polymer chain length, namely, the length of the alkylene sequences on the backbone⁶⁴ and the overall chain in terms of molar mass (M_n),^19,39 as PnAFs are mainly of low M_n (some tens of kg mol⁻¹). Secondly, when changing from the amorphous to the semicrystalline state, segmental dynamics moderately decelerates due to constraints imposed by the crystals,^39,66 whereas in the case of quite tight semicrystalline morphologies, segmental dynamics may accelerate and decrease in cooperativity, as a result of spatial confinement.¹⁸ The latter is in general an indirect effect of nanoparticle introduction. Finally, there have been reported cases of filler-induced dynamics (a direct effect), alongside the main mobility, that have been proposed to arise from the mobility of modified chains in the vicinity of the filler interface.^31,38,39

Motivated by the previously shown systematic effects and the small number of published reports on this new class of materials, herein, we prepare and investigate, for the first time, the structure–property relationships in two series of PEF-based PNCs, loaded in situ with 0.5–2.5 wt% CNTs and GNPs and compare them with the unfilled PEF. It should be reported that the said nanoparticles seem at first thought incompatible with the ‘green’ character of PnAFs; nevertheless, the same or similar carbon-based fillers have been successfully incorporated in the past within different biobased polymeric matrices.^67–70 The present study involves as main the investigation tools differential scanning calorimetry (DSC) for crystallization and glass transition and BDS for assessing the local and segmental mobility. To supplement these techniques and illuminate specific points regarding the structure (interfacial interactions), crystal structuring (lamellae thickness, etc.) and semicrystalline morphology, we have respectively employed Fourier-transform infrared spectroscopy (FTIR), X-ray diffraction (XRD) and polarized light microscopy (PLM). The samples are studied initially in the amorphous state to record any direct filler effects and, secondly, in the semicrystalline state (upon cold crystallization) to detect the indirect effects (via crystallization).

2. Materials and methods

2.1. Materials

PEF was synthesized via a two-stage transesterification/polycondensation method^5,38 described schematically in Scheme 1. 2,5-Dimethylfuran-dicarboxylate (DMFD) and ethylene glycol (EG), were introduced in the polyesterification apparatus, in a molar ratio of diester/diol of 1 : 2.2, along with 400 ppm of tetra-butyl orthotitanate (TBT) catalyst. For the first stage (transesterification), the mixture was heated at 160 °C for 1.5 h under argon flow, at 170 °C for 1.5 h and at 180 °C for 1 h. This step is considered complete after all the theoretical amount of CH₃OH (Scheme 1) has been distillated and collected in a graduated cylinder. For the polycondensation step, a vacuum (5 Pa) was applied to remove the excess diol over a 30 min period, in order to avoid excessive foaming and sublimation of the oligomers. We note, from the methodological point of view, that the latter are unwanted regarding the melt polycondensation. Afterwards, the temperature was increased to 210 °C for 1.5 h along with the stirring speed being increased to 450 rpm. Subsequently, the temperature was increased to 225 °C, kept there for 1.5 hours and, finally, elevated to 240 °C and kept there for another 1 hour.

Scheme 1 Schematic representation of the transesterification and polycondensation stages during the synthesis of poly(ethylene furanoate).

All chemicals were of analytical grade and had been supplied by Sigma-Aldrich Co. (Taufkirchen, Germany).

As fillers for the PNCs, we selected two of the most efficient heterogeneous nucleation agents based on previous studies on PnAFs and other polyesters, namely, multiwalled carbon nanotubes, CNTs, and graphene nanoplatelets, GNPs. CNTs were supplied by Timesnano Chengdu Organic Chemicals Co. (China), and had been synthesized via chemical vapor deposition. CNTs exhibit average diameters of 10–20 nm, a length of ∼10 μm, and a specific surface area of ∼110 m² g⁻¹. GNPs were purchased from XG Sciences (under the code name ‘xGnP-Grade M’) and were of 2.2 g cm⁻³ mass density, 5 μm diameter, 6–8 nm thickness and ∼120–150 m² g⁻¹ specific surface area.

Two series of totally six PEF-based PNCs, namely, PEF/CNTs and PEF/GNPs, were synthesized containing 0.5, 1.0 and 2.5 wt% nanoparticles. The synthesis took place in situ with the two-stage polycondensation method, namely, esterification and polycondensation.³⁸ Prior to the reaction, a dispersion of the nanofillers in the EG was prepared. This was achieved by subjecting the mixture to sonication for 20 min. This way a homogenous dispersion of the fillers is achieved in the monomers, which results in a homogenous dispersion of the nanoparticles in the final polymers, as shown from our previous work.^19,38

2.2. Characterization methods

2.2.1. Fourier transform infra-red spectroscopy (FTIR). The FTIR measurements were performed employing a SPECTRUM 1000 PerkinElmer FTIR spectrometer (MA, USA) using KBr tablets, in the wavenumber range 4000–500 cm⁻¹, with a resolution for each spectrum of 2 cm⁻¹. The number of co-added scans was 16.

2.2.2. Differential scanning calorimetry (DSC). DSC was employed to assess the thermal transition, with the main focus on crystallization and the glass transition. To that aim, we employed TA Q200 DSC apparatus (TA, USA), and the measurements were performed in a high purity nitrogen atmosphere, on samples of 6–8 mg in closed aluminium pans. The DSC apparatus had been previously calibrated with sapphires and indium, for the heat capacity and temperature, respectively. A first heating run was performed to erase any thermal history, at 10 K min⁻¹ up to 260 °C. Subsequently, two main thermal scans were performed. Scan 1: in order to produce amorphous samples, initially melted samples were cooled to −10 °C at the fastest possible rate, namely ∼110 K min⁻¹, in the temperature range of the expected crystallization (‘jump’ command of the TA software), held there for a period of 5 min and, finally, heated to 240 °C at 10 K min⁻¹. Scan 2: the melted samples were cooled at 10 K min⁻¹ to 0 °C, held there for a period of 1 min and, subsequently, heated to 240 °C at 10 K min⁻¹.

Following previous work,^47,71,72 from the evaluation of the physical properties, namely the enthalpy of crystallization, ΔH_c, and the heat capacity change during the glass transition, Δc_p, we may further estimate the various fractions existing in the semicrystalline polymers and PNCs. First, the crystalline fraction, CF, is obtained using the following equation

CF = ΔH_c,n/ΔH_100% (1)

where, ΔH_c,n is ΔH_c upon normalization to the polymer fraction, w_polym, and ΔH_100% is the enthalpy of fusion of the fully crystallized polymer, which is mainly taken as 137 J g⁻¹ from the literature.⁵ Then from the measured Δc_p of the glass transition, which is the measure of the mobile polymer fraction that contributes to the glass transition, we estimate the mobile amorphous fraction, MAF, and, upon assumption, the rigid amorphous fraction, RAF,^71,72 using the following equations,

Δc_p,n = Δc_p/[w_polym(1 − CF)] (2)

MAF = Δc_p,n(1 − CF)/Δc^amorphous_p,PEF (3)

1 = CF + MAF + RAF (4)

wherein Δc^amorphous_p,PEF is the heat capacity change during the glass transition of the amorphous unfilled PEF matrix. Eqn (4) describes the so-called ‘3-phase model’ (RAF, MAF, CF) of polymer systems.^71,72

2.2.3. X-Ray diffraction (XRD). XRD measurements were performed by means of a MiniFlex II XRD system (Rigaku Co., Japan) with Cu Kα radiation (λ = 0.154 nm) over the 2θ range from 5 to 50°, at steps of 0.05°, at a scanning speed 1 deg min⁻¹. The samples were measured in the semicrystalline state, in particular, upon melting, quenching at room temperature (RT) and, subsequently, annealed at 180 °C for 30 min.

2.2.4. Polarized light microscopy (PLM). PLM images were recorded using a Nikon Optiphot-1 polarizing microscope equipped with a Linkam THMS 600 heated stage, a Linkam TP91 control unit and a Jenoptic ProgRes C10Plus camera, during non-isothermal crystallization of initially melted samples, first, during cooling (hot or melt crystallization) and, subsequently, during heating (cold crystallization).

2.2.5. Broadband dielectric spectroscopy (BDS). To assess the molecular mobility, the BDS technique⁵⁰ was employed. Measurements were employed by means of a Novocontrol BDS setup (Novocontrol GmbH, Germany) on samples in the form of cylindrical disks of ∼1.5 mm in height and 20 mm in diameter, placed between finely polished brass electrodes (capacitor). An alternating voltage was applied and the complex dielectric permittivity, ε* = ε′ − i·ε′′, was recorded isothermally as a function of the frequency in the range from 10⁻¹ to 10⁶ Hz and in the temperature range between −150 and 130 °C at steps of 5 or 10 K. For the first BDS scan, the samples were initially amorphous. Up to the highest temperature (130 °C), the samples suffered isothermal cold crystallization annealing. Immediately after that, BDS scans were performed from 40 and 130 °C (scan 2).

Regarding the molecular mobility, the conventional exploitable parameter is the imaginary part of the dielectric permittivity, ε′′, which is related to the dielectric losses.⁵⁰ To extract the wanted information for a relaxation process, i.e. on the time scale (f_max or τ_max), the dielectric strength (Δε) and relaxation time distribution, proper mathematical models are used to fit the ε′′(f,T) spectra. One of the models usually adopted for the data is the Havriliak–Negami (HN)⁵⁰ model (eqn (5)),

where, ε_∞ describes the value of the real part of the dielectric permittivity, ε′, for f ≫ f₀, f₀ is a characteristic frequency related to the frequency of the maximum dielectric loss (ε′′) and α_HN and β_HN are the shape parameters of the relaxation, determining the width and symmetry or asymmetry, respectively. A sum of HN terms, one for each of the relaxations present in the frequency window at the temperature of measurement, are critically fitted to the experimental data and the fitting parameters are determined. The data by this analysis are generally shown in the form of the so called ‘Arrhenius plots’ or ‘activation diagrams’ in terms of the reciprocal temperature (1000/T) dependence of the frequency of the ε′′ peak maximum, f_max. Such a type of representation is adopted for this work.

For local (secondary) relaxations, the time scale of the response is analyzed in terms of the Arrhenius equation,⁵⁰

whereas the co-operative segmental (primary) α relaxation, i.e., the dielectric analogue of the glass transition, is analyzed in terms of the Vogel–Fulcher–Tammann (VFT) equation.⁵⁰In eqn (6), f_0,VFT is a frequency constant and E_act is the activation energy of the relaxation. In eqn (7), f_0,VFT is a frequency constant (in the range between 10⁻¹² and 10⁻¹⁴ Hz), B is a material constant (= DT₀, where D is the so-called fragility strength parameter), and T₀ is the Vogel temperature, all aforementioned parameters being material dependent.

3. Results and discussion

3.1. Thermal transitions

FTIR spectra were recorded for all samples and are comparatively presented here in Fig. 1a. The various FTIR peaks recorded and described therein provide confirmation of the successful synthesis of the polymers, and the results for PNCs are in accordance with similar work based on the said type of nano-additives.^10,19,38,73

Fig. 1 (a) FTIR spectra of PEF and all PEF-based PNCs in the overall wavenumber range. (b) Shows a focus on FTIR peaks related to the vibration of the furan ring double bonds, where the inset presents similar data for poly(propylene furanoate) (PPF) and PNCs based on PPF in situ filled with surface modified CNTs and graphene oxide (GO) from a previous study.¹⁹

In particular, the FTIR peaks located at ∼3160 and ∼3120 cm⁻¹ originate from the expected C_sp²–H bonds, while those located at ∼3000, ∼2920 and ∼2780 cm⁻¹ arise from the C_sp³–H bonds of ethylene glycol.

The findings by FTIR of our main interest here refer to the ester bonds, namely the peaks at ∼1715 cm⁻¹, and those arising from the double bond of the PEF furan ring, located at ∼1575 cm⁻¹ and at ∼1530 cm⁻¹. The said bonds have been found in the past to be involved within the polymer–fillers interactions, as being the most active sites. For example, we have recorded in PPF and PBF serious disturbances (migrations toward lower wavenumbers, see the inset to Fig. 1b) of these peaks when strong interfacial interactions were formed between the polymers and the surface modified CNTs and GO.¹⁹ Similar disturbances have been recorded in the past with other polymers in the form of PNCs.^53,74 In our case here, such noteworthy changes are not recorded in the PNCs (e.g., in Fig. 1b), thus, we extract a first indication for weak or absent particle–PEF interactions. This point is important as, based on numerous reports^{19,27,35,49,75} (and references therein), strong interfacial interactions seem to preclude the role of nanofillers as nucleating agents for crystallization.

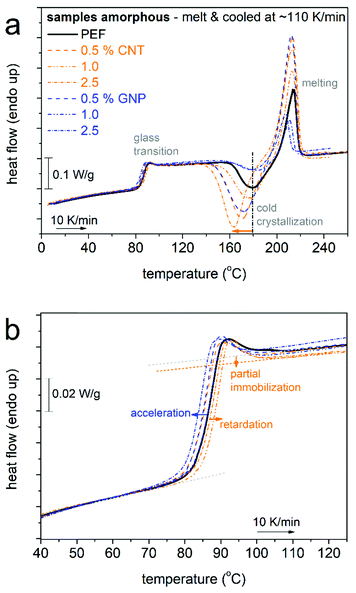
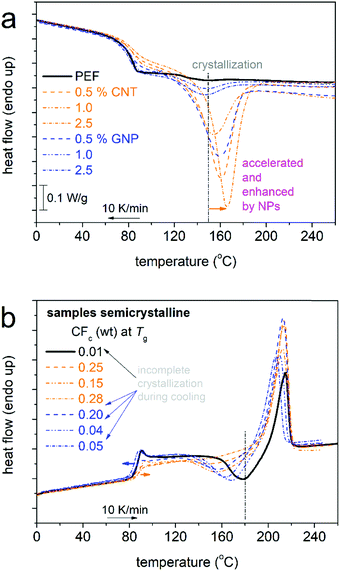
We proceed with results from DSC on the thermal transitions. In Fig. 2 and 3, we show the results of scan 1 and scan 2, respectively. The results from both scans have been evaluated, and the extracted data are listed in Table 1 and the main outcomes are comparatively shown in Fig. 4.

Fig. 2 DSC heating curves of scan 1 for all samples in the amorphous state (melted and fast cooled) in (a) the overall temperature range and (b) focusing on the glass transition. The heat flow has been normalized to the sample mass. Indicated are the main thermal transitions. The added arrows mark the filler effects on cold crystallization and the glass transition.

Fig. 3 (a and b) DSC heating curves of scan 2 for all samples (a) during cooling at 10 K min⁻¹ from the melt and (b) during the subsequent heating. The added arrows mark the filler effects on (a) the melt crystallization and (b) the glass transition. The heat flow has been normalized to the sample mass.

Table 1 Values of interest by DSC for both measurement protocols. The glass transition temperature (T_g), heat capacity change during the glass transition upon normalization to the amorphous polymer fraction (Δc_p,n), cold crystallization temperature (T_cc), melting temperature (T_m), melt crystallization temperature (T_c), mobile amorphous fraction (MAF), rigid amorphous fraction (RAF), and crystalline fraction (CF). Included are values on the average molar mass (M_n), as obtained by intrinsic viscosity measurements⁷⁶

		Scan 1 – amorphous (cooled at ∼110 K min^−1)						Scan 2 – semicrystalline (cooled at 10 K min^−1)
	M n (g mol^−1)	T g (°C)	Δcp,n (J g^−1 K^−1)	MAF (±0.02)	RAF (±0.02)	T cc (°C)	T m (°C)	T c (°C)	CF (wt)	MAF	RAF	T g (°C)	T m (°C)
PEF	12k	86	0.49	1.00	0.00	180	213	149	0.01	0.88	0.11	86	215
0.5% CNT	8k	85	0.44	0.90	0.10	171	213	160	0.25	0.55	0.20	86	214
1.0% CNT	15k	88	0.43	0.88	0.12	177	213	154	0.15	0.64	0.21	88	212
2.5% CNT	8k	87	0.43	0.88	0.12	164	213	165	0.28	0.48	0.24	88	213
0.5% GNP	7k	85	0.47	0.96	0.04	172	212	158	0.20	0.63	0.17	85	213
1.0% GNP	11k	85	0.43	0.88	0.12	184	211	147	0.04	0.84	0.12	86	210
2.5% GNP	7k	84	0.47	0.96	0.04	179	208	146	0.05	0.86	0.09	83	207

---

Fig. 4 Filler NP loading dependence of variables referring to (a) crystallization in terms of nucleation and fraction, (b) the glass transition temperature and (c) the mobile and rigid amorphous fraction, for both DSC measurement protocols, namely in the amorphous (am., solid symbols) and semicrystalline (sc., semi-open symbols) states.

We recall that for scan 1 (Fig. 2), initially amorphous samples have been subjected to fast cooling from the melt state and subsequent heating at 10 K min⁻¹. At about 80 °C in Fig. 2, the glass transition step is recorded for all samples. Neat PEF demonstrates the characteristic temperature, T_g, estimated by the half Δc_p method, to equal 86 °C, whereas the corresponding Δc_p equals 0.49 (±0.01) J g⁻¹ K⁻¹. The glass transition is shown in more detail in Fig. 2b. CNTs tend to increase the T_g (85–88 °C in Table 1 and Fig. 4b) and suppress the Δc_p, which upon normalization to the polymer mass (Δc_p,n) equals 0.43–0.44 J g⁻¹ K⁻¹. The addition of GNPs, on the other hand, resulted in the lowering of T_g by 1–2 K and a more moderate suppression of Δc_p,n (0.43–0.47 J g⁻¹ K⁻¹) as compared with the CNTs.

The suppression of T_g in the PNCs seems to correlate with the lowering of M_n, whereas its elevation would in general suggest the existence of constraints on the mobility of the bulk-like (mobile) chains. In particular for PEF + 1.0 wt% CNT, T_g is elevated by 2 K as compared with neat PEF and this coincides with the corresponding elevation of M_n; therefore, both the constraints and the chain length contribute to its molecular mobility. Independently of the filler type, the suppression of Δc_p,n can be rationalized by the concept of the RAF.⁷⁷Viaeqn (3) and (4), the RAF for scan 1 is estimated as 0.04–0.12 for PEF/GNPs and slightly larger, at 0.10–0.12, for PEF/CNTs (Fig. 4c). It should be noted that for scan 1, i.e., for amorphous polymers, this RAF is linked to the presence of nanoparticles. The difference in RAF in Fig. 4c could be due to the quite large specific surface area of the CNTs as compared with the GNPs, in combination with the expected good quality of the filler dispersion due to the in situ PNC synthesis.^10,38 For the time being, we conclude that the presence of CNTs imposes more constraints on the mobility of PEF as compared with the GNPs. We should mark, however, that the samples have suffered strong supercooling, thus, we would expect that at T around T_g there may exist significant numbers of crystallization nuclei, i.e., of PEF itself and those related to the presence of impurities and the nanoparticles. Since the interfacial interactions are expected to be weak, which is supported by the relatively low values of the RAF, both cases of PNCs fit well with a recently proposed model, which considers that the RAF in the amorphous state of PNCs filled with nucleating acting fillers represents ordered polymer structures^26,78 around crystallization nuclei (including fillers) and not the interfacial ‘bound’ polymer.^27,47,49,79 So, in our case the RAF produced during scan 1 should not consist of conventional bound polymer chains, but of ‘ordered-like’ chains around the nanoparticles at the nucleation stage.^26,27,47,78 Upon the formation of crystallites, this RAF is expected to be merged within the crystals, as was found to happen in previous reports on PNCs based on nucleating-acting fillers^{27,34,39,47,49,74,79} (and references therein).

Subsequently, when heating above T_g, strong and fast cold crystallization are recorded in the PNCs as compared with PEF (Fig. 2a). Similarly, in scan 2, during cooling from the melt in Fig. 3a, the PNCs exhibit stronger and faster melt-crystallization. Both results provide strong support for the nucleating role of these nanoparticles and the scenario mentioned above.

It is also interesting to comment on the overshoot at the high temperature side of the glass transition in Fig. 2b. The overshoot has been connected to the high degree of freedom of a polymer⁸⁰ and, additionally, to the structural relaxation.⁸¹ In the case of PNCs with strong attractive interfacial interactions, this overshoot is suppressed or even vanishes⁸² (and references therein), indicating partial loss of motional freedom for the bulk-like polymer chains. This is not recorded here, as the overshoot is preserved in our PNCs. The results support the findings on the weak interfacial interactions.

The lower T_g values in PEF/GNPs could be connected with the effects of the confinement of PEF chains between the nanoplatelets. This cannot be firmly supported by the small fraction of GNPs, nor by the findings from XRD. Therefore, one way to understand the lower T_g values in the PNCs, next to the lowering of M_n, is the increasing of free polymer volume⁸³ away from the particles, most probably due to the concentration of polymer chains around the nucleating-acting GNPs.⁸⁴ The same situation could stand also for PEF/CNTs, within which the effect of the constraints (tendency to increase T_g) is more pronounced.

The situation on segmental mobility is obviously complex, leaving little room for definite interpretations. Results from BDS with respect to the dynamics are expected to be richer and, thus, more illuminating.

Coming back to crystallization, from only a glance at the data of both scans (Fig. 2a and 3a), it becomes clear that the nanoparticles facilitate crystallization in both the rate, namely by lowering the cold crystallization temperature T_cc and increasing the melt crystallization temperature T_c, and the amount (CF), since a strong increase in the crystallization enthalpies is observed (Fig. 4a). The CF during melt crystallization (scan 2, Table 1) equals 0.01 for neat PEF, and increases to between 0.15 and 0.28 in the PEF/CNTs and between 0.04 and 0.20 in the PEF/GNPs. These results are comparatively shown also in Fig. 4a, wherein the improvement in properties is optimized for 0.5 wt% filler, and partly for 2.5 wt% filler, whereas it is moderate for 1.0 wt% filler.

For PEF + 1.0 wt% CNTs and GNPs, the parameters related to crystallization (T_c, T_cc, and CF in Fig. 4a) seem to not follow the general filler loading trends and suggest the precluded nucleating effects of the CNTs. This may correlate with a somewhat worse distribution of CNTs, besides the in situ PNC preparation synthesis. Such an effect could be checked by direct microscopy measurements (SEM, TEM) in the future. The effects may also correlate with the differences in chain lengths, as the disturbed trends coincide with the PNCs exhibiting the highest M_n values among the other compositions (Table 1).

The ‘3-phase model’ (eqn (4)) was employed for the semicrystalline state and the produced results on the MAF and RAF are shown in Fig. 4c. Therein, compared with the amorphous state, for PEF/CNTs, the involvement of the CF resulted in significant reduction of the MAF and elevation of the RAF. The increase in the RAF by ∼10% is clearly due to rigid chains located (half-immersed) around the crystals.⁷⁷ For the cases of filler facilitating crystallization, almost all of the RAF is expected to correlate with crystals, whereas the RAF of the amorphous state was due to initial crystallization stages, whereas, upon completion of crystallization, that RAF is merged within the crystallites.^27,47,49 The effects of GNPs on the CF were weaker; thus, the corresponding effects on the MAF and RAF are moderate in Fig. 4c.

In Fig. 3b, upon the formation of crystals, the overshoot on the glass transition (strong in the amorphous state in all samples, Fig. 2b) tends to be reduced with the increase in the CF. The result suggests the major role of crystals on reducing the freedom of motion for the mobile amorphous PEF chains, as compared with the minor role of the nanoparticles themselves accompanied by weak or absent polymer–filler interactions.

Clearly the CNTs have a stronger impact on all thermal transitions and polymer fractions in the PNCs.

A final comment with respect to DSC refers to melting. The melting temperature, T_m, is, independently, from the thermal treatment, slightly lower in the PNCs, suggesting a somehow lower quality of the crystallites. This may be relevant to the T_m being systematically lower for the lower M_n values (Table 1). We will comment further on this point in light of the data from XRD and PLM.

3.2. Semicrystalline morphology and crystal structure

To draw a more complete picture on the crystallization, structure and semicrystalline morphology, we performed PLM measurements during non-isothermal cooling from the melt to RT, subsequent heating at 180 °C and, additionally, isothermal annealing at 180 °C. By this route, on the one hand, we imitated the DSC scan 2 and, on the other hand, we subjected the sample to both large supercooling and, finally, maximized chains diffusion (180 °C), which was aimed at maximizing crystallization. The results by PLM as described are shown in Fig. 5 for all samples in terms of representative snapshots. PEF crystals are quite small, namely, compared with the given scale the sizes of the crystals are of some μm. The striking difference between neat PEF and PNCs is that in the latter the crystals seem to be larger in size. Please note that for the PNCs with 1 wt% filler the crystals are comparable in size to those on neat PEF and this, interestingly, coincides with the comparable M_n values.

Fig. 5 PLM micrographs for all samples upon non-isothermal crystallization (left images) during cooling from the melt at the noted temperatures as representatives of crystallization completion and (right images) during the subsequent heating up to 180 °C.

The samples were studied by XRD, employing the same thermal protocol as in PLM with the final step again being annealing at 180 °C. The results are shown comparatively for all compositions in Fig. 6, and are in accordance with previous findings on PEF.^5,85 The data revealed that although the diffraction peak number is the same between the unfilled and filled PEF, the positions of peaks in the PNCs are migrated toward slightly lower 2θ. This migration is generally considered as in indication of altered crystal structure.

Fig. 6 XRD curves for PEF and all PNCs, described on the plot, upon crystallization annealing at 180 °C.

The altered chain packing in the crystals (XRD) along with the larger spherulites (PLM) in the PNCs could suggest a better crystal quality of the PNCs. This is opposite to our conclusion regarding the lowering of T_m in DSC; thus, the origins of this recording may be not straightforward. For the moment, we have no further comments on that.

3.3. Molecular dynamics

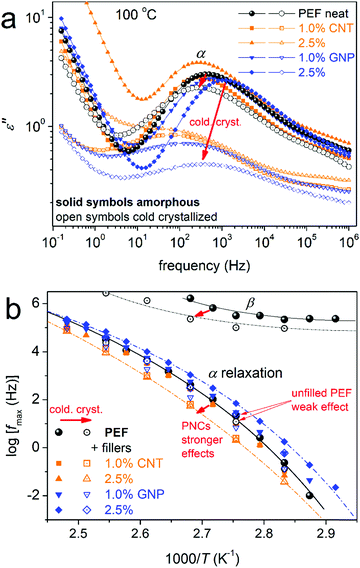
The data by BDS are discussed here in terms of the imaginary part of the dielectric permittivity, ε′′, related to the dielectric loss.⁵⁰

Fig. 7a shows via a representative example of the measurement, the full temperature evolution of ε′′(f) (isothermal curves) for initially amorphous neat PEF. For temperatures below T_g, local molecular (dipolar) mobilities dominate the ε′′(f) signal. The individual relaxation processes are observed as peaks of ε′′(f), which, here, are mainly complex. For example, at −10 °C in Fig. 7b, based on the performed critical analysis, the ε′′(f) signal is found to actually be the superposition of two distinct relaxation processes, named β (f_max ≈ 10³ Hz) and β₂ (f_max ≈ 10⁰ Hz). At temperatures closely above T_g, ε′′(f) is elevated by 1–2 orders of magnitude, due to the activation of the segmental α relaxation, which is the dielectric analogue of the glass transition.⁵⁰ At T ≥ 110 °C, the peak of α relaxation exhibits a sudden suppression in strength (Fig. 7a), which is a result of cold crystallization. Compared with calorimetry (please see Fig. 2a), cold crystallization in BDS takes place at a lower temperature, which is expected due to somewhat slower equivalent heating rate, as the samples stay at each temperature for a period of 8–9 minutes (isothermal recordings) prior to heating to the next required temperature. With the further temperature increase and following the low frequency side of our measurement window, a sharp increase of the signal is recorded. The latter originates on the involvement of complex ionic conductivity phenomena, such as charge transport, interfacial polarizations, etc.^50,86

Fig. 7 (a) BDS raw data of neat amorphous PEF in the form of the imaginary part of the dielectric permittivity, ε′′, against frequency. The temperature evolution of the recorded mobilities is indicated by the added arrows. (b) Examples of the analysis of the complex spectra at 105 and −10 °C in terms of Havriliak–Negami (HN) model functions.

The molecular mobility is discussed in the following text on the basis of the dielectric–calorimetric map (Arrhenius plots) of Fig. 8, as constructed by the overall analysis results.

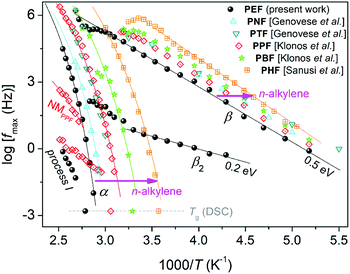Fig. 8 Arrhenius plot, or activation diagram, for neat PEF from the present study. The results are compared with neat PnAFs from the literature on PPF (∼20 kg mol⁻¹, CF ≈ 0 wt),¹⁹ PBF (∼20 kg mol⁻¹, CF ≈ 0 wt),³⁹ PHF (CF ≈ 0.45 wt),¹⁸ poly(neopentyl 2,5-furanoate) (PNF, 34 kg mol⁻¹, CF ≠ 0)⁶³ and poly(trimethylene 2,5-furanoate) (PTF, 34.2 kg mol⁻¹, CF ≠ 0).⁶³ The added lines connecting the experimental points are fittings of the VFT and Arrhenius equations.

The local β relaxation, fitted with a symmetric HN term (eqn (5)) of α_HN ≈ 0.3 and β_HN = 1 (on average over temperature), has been proposed in previous works on PnAFs by Soccio, Ezquerra and coworkers to originate from ‘crankshaft motions of the molecular group of the polymer related to the chemical link between the aromatic ring and the ester carbon aromatic ring’.^63,87 Moreover, β has been proposed to be activated in the amorphous polymer regions.^31,88,89 Due to its local character, the time scale of β is, as expected, described well by the Arrhenius equation (eqn (6)), with a temperature-independent activation energy E_act of 0.5 eV (or ∼50 kJ mol⁻¹). The process exhibits a disturbance in its time scale when T increases and approaches T_g. Such changes in local mobilities arising from the early stages of matrix thermal transitions have been recorded in the past for PnAFs, including PEF.^{18,19,31,62,63} Qualitatively similar disturbances on local processes have been recorded for other polyester families, such as polylactides^90,91 and polycaprolactone.⁷⁹ Interestingly, this behavior suggests secondary processes that arise from molecular units (dipolar) located at the backbone of the chains and seems to be a common characteristic of polyesters. Finally, comparing the data for PEF here with the different PnAFs of n = 3–6 in Fig. 8, we record a ‘coupling’ between local and segmental dynamics, as the migration of the main α process is accompanied by a similar one of β toward the same direction (almost vertical in the activation diagram).

The additional local relaxation β₂ is, as compared to β, a weaker and slower process as it is recorded at lower frequencies/higher temperatures. β₂ was necessary for the fitting, for all samples here. The peak was fitted with a symmetric HN term (β_HN = 1 in eqn (5)) of α_HN ≈ 0.5, which makes it quite a narrow relaxation, in other words, a narrower range of relaxation times.⁵⁰ Based on the fitting of the Arrhenius equation, at T < T_g the E_act of β₂ is low (∼0.2 eV). The relaxation as described does not resemble other processes discussed on PnAFs in the past, although in some cases there may be a record, e.g., in ref. 64. For the time being, we have no further comments on the possible origins of β₂, as there are no similar data available in the literature for comparison.

Coming to segmental mobility in neat PEF, α relaxation can be clearly seen from the raw data. In the amorphous case, the α value of PEF is fitted by an asymmetric HN term with α_HN ≈ 0.7 and β_HN ≈ 0.6, on average over temperature. However, upon cold crystallization, this tends to become symmetric and wider. The time scale of α is in accordance with previous findings.⁶⁴ In Fig. 8, segmental dynamics are clearly dominated by the n-alkylene number, rather than the molecular weight or the amount of CF. In particular, α accelerates systematically with increasing n. This can be understood, in parallel to the previously discussed mobilization of the PnAF chain,^5,16 when increasing the length of the alkylene sequences that lay next to the ‘quite heavy’ furan ring. We should note that this effect was demonstrated for the first time by Papamokos et al.⁶⁴ on a series of PnAFs with n changing from 2 to 12. In recent studies, we have reported that the weaker effects of molecular weight, as compared with that of n, are common for PnAFs with n = 3, 4 and 6, even in the cases of M_n changing from 8 to 20 kg mol⁻¹, a range that should include an M_n threshold for chain entanglements.⁹² Subsequently, based on the aforementioned effects on local mobility, β dynamics should be also be governed by n-alkylene number (indirectly).

Process I at the highest temperature side of the activation diagram was fitted by a HN term of α_HN ≈ 0.9 and β_HN = 1. Despite the small number of experimental points, process I seems in Fig. 8 to exhibit an Arrhenius-type time scale or a VFT one with very low fragility. Process I could be the so-called ‘σ’ process (or else the ‘conductivity relaxation process’), which, however, would be expected to be stronger.⁸⁶ In our case, the Δε of process I is smaller than that of α by about one order of magnitude. The process I peak could also originate from interfacial polarization.⁵⁰

The attention is turned to the PNCs. The raw BDS data can be summarized in the comparative isochronal ε′′ plots of Fig. 9, created by replotting the isothermally recorded data, at the selected frequency of 10³ Hz. Overall, the same number and type of relaxation processes as those of neat PEF are recorded in the PNCs. Any filler effects are discussed on the basis of the time scale and dielectric strength of the recorded relaxations. Therefore, we constructed Fig. 10, which demonstrates the comparative activation map in terms of time scale (Fig. 10a) and the reciprocal temperature dependence of Δε (Fig. 10b).

Fig. 9 Comparative isochronal plots of ε′′(T) at f = 3 kHz for all samples. Indicated are the relaxation processes recorded. For comparison of BDS with calorimetry with respect to segmental mobility, the calorimetric glass transition of neat PEF has been added (which corresponds to the right vertical scale).

Fig. 10 Comparative (a) Arrhenius plots and (b) dielectric strength for all compositions, indicated by the relaxation processes recorded. The symbols are described in (b). The calorimetric T_g points have been included in (a) at the corresponding equivalent frequency (log f_eq ≈ −2.8), whereas the added lines connecting the experimental data are fittings of the Arrhenius and VFT equations. The inset to (a) presents a focus on α relaxation.

In Fig. 10a, local dynamics show insignificant changes in time scale; however, there seems to be systematically weak suppression of Δε in Fig. 10b, especially in the case of β₂. An exception to the systematic behavior is the case of PEF + 2.5 wt% CNTs, within which an overall increase in the dielectric signal is observed (Fig. 9 and 10b). The effect may arise from the formation of an internal field due to the highly conductive fillers at the higher loading, as has been found in other cases of PNCs.⁹³

Moderate although clear alterations are recorded on the segmental α relaxation in the PNCs. The time scale of α exhibits both accelerations and decelerations (Fig. 10a) and, in general, suppression in Δε (Fig. 10b). The changes can be followed by the formalism of the estimated dielectric (T_g,diel)^50,82 and calorimetric (T_g) glass transition temperature shown in Fig. 11. For neat PEF, T_g,diel equals 72 °C, for PEF/CNTs equals 68–72 °C and for PEF/GNPs equals 66–70 °C. Besides the expected discrepancy between the two in principle different techniques, which do not seem to monitor the same relaxation modes, there are qualitative similarities in the acceleration/deceleration of segmental dynamics between the two series of PNCs. As in DSC, complex phenomena seem to contribute here, namely the changes in M_n,¹⁹ the involvement of filler–polymer and/or chain–chain associations (PEF is nucleated in all cases prior to the recording of α)⁸⁴ and, possibly, changes in the free volume (more clear in PEF/GNPs).⁸³ Next to that and following previous work,^19,50 we have estimated the fragility (cooperativity) index, m, for α relaxation. The data have been included in Fig. 11 and show an overall suppression of cooperativity in the PNCs (m ≈ 92–99) as compared with neat PEF (m ≈ 101). T_g,diel and m systematically increase/decrease with filler loading in the CNT-/GNP-based PNCs, respectively. These two distinct effects could suggest a decrease/decrease of free volume of the polymer away from the particles when the fractions of the particles increase. From the methodological point of view, BDS seems to be more sensitive in delicate alterations as compared to calorimetry. Regarding Δε in Fig. 10b, α is slightly weaker in the PNCs, which is in accordance with effects on the calorimetric strength, Δc_p (Fig. 2a and Table 1).

Fig. 11 Column diagrams of T_g, calorimetric against dielectric (left scale), and m, fragility index of α relaxation (right scale), in the amorphous state.

Coming to process I for the PNCs, two effects are revealed in Fig. 10. Process I is faster and weaker in PEF/GNPs whereas it is slower and significantly stronger PEF/CNTs. We note that during the fitting of process I in the PNCs, HN terms of similar parameters to those of neat PEF were obtained. For the time being we have no solid interpretation on the origins of the said process.

In the final section of this work, we comment on the effects on the mobility of chains and ions upon cold crystallization. In the amorphous state, the presence of the fillers imposed moderate facilitation of ion transport (Fig. 12a, i.e., at temperatures above T_g) and this is an indirect filler effect, via the facilitation of polymer chain diffusion. Upon the formation of crystals, conductivity is suppressed in PEF; moreover, it is strongly blocked in the PNCs (Fig. 12a), which is interesting from the point of view of future applications. Please compare this with the different quality in the semicrystalline morphology in Fig. 5 (PLM) upon cold crystallization between the neat matrix and the PNCs. The different strength of crystallization on conductivity is, as expected, also similar on the segmental dynamics. Upon cold crystallization, α relaxation in Fig. 12 exhibits a slight deceleration and strength suppression in PEF, whereas it is more strongly retarded and suppressed in all PNCs, as the crystals introduce serious constraints on molecular mobility.^58,94 The effect is obviously due to the role of the fillers in nucleating crystallization.

Fig. 12 Effects of cold crystallization (arrows) on α relaxation on PEF and selected PNCs, shown in terms of (a) raw ε′′(f) data at the selected temperature of 100 °C and (b) time scale – Arrhenius plots upon analysis.

Last but not least, it is worth-noting that the deceleration of α has also driven β relaxation to decelerate (Fig. 12b), an effect that provides additional support for the proposed dependence between this local and segmental mobilities.

4. Conclusions

In this article, we attempted to improve the weak and slow crystallizability of PEF, which arises from its inability to nucleate due to the presence of the heavy furan ring in combination with the short alkylene sequences on the polymer backbone. CNTs and GNPs were, for the first time, introduced in situ into PEF at low fractions and this resulted, according to DSC, in the facilitation of crystallization by enhancing nucleation (a direct filler effect) and, secondly, by altering the polymer free volume (an indirect effect). The results on nucleation were found be compatible with recently proposed scenarios of fillers facilitating crystallization in the case of weak or absent interfacial polymer–filler interactions, such as in our case (FTIR). Under identical thermal treatments, the filler-induced crystals are larger (PLM) and exhibit changed lamellar structuring (XRD) as compared with those of unfilled PEF. Between these two types of filler, the impact on facilitating crystallization was found to be larger for CNTs than for GNPs, possibly due to the larger specific surface area or aspect ratio of the CNTs. Coming to molecular mobility, the combination of DSC with BDS proved once again quite fruitful. It was revealed, in agreement between the two techniques, that segmental mobility (the glass transition and α relaxation) in the amorphous state decelerates in PEF/CNTs and accelerates in PEF/GNPs. The effects of strong nucleation (existing in the amorphous state) and an increase in the free volume⁸³ are proposed to be the main factors governing the amorphous mobility in the cases of CNTs and GNPs, respectively. The effect of M_n, exhibiting minor and moderate changes in the PNCs, was found to be of secondary importance here. Subsequently, the presence of crystals led to the deceleration of chain dynamics and, under identical thermal histories, the effect was demonstrated to be stronger in the PNCs as compared with PEF. In a comparison with previous studies and other parameters referring to the polymer structure, the n-alkylene number seems to be the most effective factor that dominates mobility of the PnAF. At sub-glass transition temperatures, the local β (with known origins) and the new β₂ relaxations were recorded. β exhibits time scale disturbances when the temperature approaches T_g, which resembles previous cases of PnAFs and other polyesters, as marked here for the first time. Despite the yet unknown origins of β₂ relaxation, there seems to be a connection with the filler presence, as its strength decreases in PNCs. The discussed effects relating to the presence of the fillers or/and polymer crystals, namely, on ion transport enhancement or blocking a variety of extents, in connection with the different semicrystalline morphologies, are quite interesting and useful for such materials. As PnAFs are intended for use in packaging applications, wherein the manipulation of properties, such as crystallization and permeability, is wanted, here, this manipulation has proved achievable via both the material preparation and the thermal treatment.

Author contributions

Dimitra Kourtidou: investigation, formal analysis, validation, writing – review and editing. Panagiotis A. Klonos: conceptualization, methodology, investigation, formal analysis, visualization, writing – original draft. Lazaros Papadopoulos: investigation, formal analysis, validation, writing – review and editing. Apostolos Kyritsis: resources, validation, writing – review and editing. Dimitrios N. Bikiaris: supervision, resources, conceptualization, writing – review and editing. Konstantinos Chrissafis: supervision, validation, conceptualization, writing – review and editing.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

The research work was supported by the Hellenic Foundation for Research and Innovation (HFRI) under the HFRI PhD Fellowship grant (Fellowship Number 1123).

References

1. R. A. Sheldon, Green Chem., 2017, 19, 18–43.
2. M. Hong and E. Y. X. Chen, Green Chem., 2017, 19, 3692–3706.
3. N. Kasmi, C. Pinel, D. Da Silva Perez, R. Dieden and Y. Habibi, Green Chem., 2021, 12, 991–1001.
4. G. Z. Papageorgiou, D. G. Papageorgiou, Z. Terzopoulou and D. N. Bikiaris, Eur. Polym. J., 2016, 83, 202–229.
5. G. Z. Papageorgiou, V. Tsanaktsis and D. N. Bikiaris, Phys. Chem. Chem. Phys., 2014, 16, 7946–7958.
6. A. F. Sousa, C. Vilela, A. C. Fonseca, M. Matos, C. S. R. Freire, G. J. M. Gruter, J. F. J. Coelho and A. J. D. Silvestre, Polym. Chem., 2015, 6, 5961–5983.
7. Z. Terzopoulou, L. Papadopoulos, A. Zamboulis, D. G. Papageorgiou, G. Z. Papageorgiou and D. N. Bikiaris, Polymers, 2020, 12, 1209.
8. T. Pan, J. Deng, Q. Xu, Y. Zuo, Q. Guo and Y. Fu, ChemSusChem, 2013, 6, 47–50.
9. A. Gandini, A. J. D. Silvestre, C. P. Neto, A. F. Sousa and M. Gomes, J. Polym. Sci., Part A: Polym. Chem., 2009, 47, 295–298.
10. H. Xie, H. Meng, L. Wu, B. G. Li and P. Dubois, Eur. Polym. J., 2019, 121, 109266.
11. W. Post, A. Susa, R. Blaauw, K. Molenveld and R. J. I. Knoop, Polym. Rev., 2020, 60, 359–388.
12. F. Nederberg, R. L. Bell and J. M. Torradas, US20160311208A1, 2016.
13. H. Xie, L. Wu, B. G. Li and P. Dubois, Biomacromolecules, 2019, 20, 353–364.
14. R. Androsch, R. Zhang and C. Schick, Polymer, 2019, 176, 227–235.
15. J. Leng, N. Kang, D. Y. Wang, A. Wurm, C. Schick and A. Schönhals, Polymer, 2017, 103, 257–264.
16. G. Z. Papageorgiou, D. G. Papageorgiou, V. Tsanaktsis and D. N. Bikiaris, Polymer, 2015, 62, 28–38.
17. E. Forestier, N. Guigo, C. Combeaud, N. Billon and N. Sbirrazzuoli, Macromolecules, 2020, 53, 8693–8703.
18. O. M. Sanusi, L. Papadopoulos, P. A. Klonos, Z. Terzopoulou, N. Aït Hocina, A. Benelfellah, G. Z. Papageorgiou, A. Kyritsis and D. N. Bikiaris, Polymers, 2020, 12, 1239.
19. P. A. Klonos, L. Papadopoulos, G. Z. Papageorgiou, A. Kyritsis, P. Pissis and D. N. Bikiaris, J. Phys. Chem. C, 2020, 124, 10220–10234.
20. C. Schick, Anal. Bioanal. Chem., 2009, 395, 1589–1611.
21. J. M. Raquez, Y. Habibi, M. Murariu and P. Dubois, Prog. Polym. Sci., 2013, 38, 1504–1542.
22. S. Saeidlou, M. A. Huneault, H. Li and C. B. Park, Prog. Polym. Sci., 2012, 37, 1657–1677.
23. T. P. Gumede, A. S. Luyt and A. J. Müller, eXPRESS Polym. Lett., 2018, 12, 505–529.
24. D. R. Paul and L. M. Robeson, Polymer, 2008, 49, 3187–3204.
25. S. K. Kumar and R. Krishnamoorti, Annu. Rev. Chem. Biomol. Eng., 2010, 1, 37–58.
26. M. Hedge, E. T. Samulski, M. Rubinstein and T. J. Dingemans, Compos. Sci. Technol., 2015, 110, 176–187.
27. P. Klonos, Z. Terzopoulou, S. Koutsoumpis, S. Zidropoulos, S. Kripotou, G. Z. Papageorgiou, D. Bikiaris, A. Kyritsis and P. Pissis, Eur. Polym. J., 2016, 82, 16–34.
28. A. S. Altorbaq, A. M. Jimenez, J. Pribyl, B. Benicewicz, A. J. Müller and S. K. Kumar, Macromolecules, 2021, 54, 1063–1072.
29. A. Toda, R. Androsch and C. Schick, Polymer, 2016, 91, 239–263.
30. E. Logakis, C. Pandis, V. Peoglos, P. Pissis, C. Stergiou, J. Pionteck, P. Pötschke, M. Mičušík and M. Omastová, J. Polym. Sci., Part B: Polym. Phys., 2009, 47, 764–774.
31. P. A. Klonos, L. Papadopoulos, D. Tzetzis, A. Kyritsis, G. Z. Papageorgiou and D. N. Bikiaris, Mater. Today Commun., 2019, 20, 100585.
32. J. Lin, S. Shenogin and S. Nazarenko, Polymer, 2002, 43, 4733–4743.
33. C. R. Bilchak, et al. , ACS Nano, 2020, 14, 17174–17183.
34. P. A. Klonos, V. Peoglos, D. N. Bikiaris and A. Kyritsis, J. Phys. Chem. C, 2020, 124, 5469–5479.
35. L. Papadopoulos, et al. , Polymer, 2021, 217, 23457.
36. A. Tessema, D. Zhao, J. Moll, S. Xu, R. Yang, C. Li, S. K. Kumar and A. Kidane, Polym. Test., 2017, 57, 101–106.
37. P. A. Klonos, S. N. Tegopoulos, C. S. Koutsiara, E. Kontou, P. Pissis and A. Kyritsis, Soft Matter, 2019, 18, 1813–1824.
38. L. Papadopoulos, P. A. Klonos, D. Tzetzis, G. Z. Papageorgiou, A. Kyritsis and D. N. Bikiaris, Polymer, 2020, 189, 122172.
39. P. A. Klonos, L. Papadopoulos, Z. Terzopoulou, G. Z. Papageorgiou, A. Kyritsis and D. N. Bikiaris, J. Phys. Chem. B, 2020, 124, 7306–7317.
40. J. R. Potts, D. R. Dreyer, C. W. Bielawski and R. S. Ruoff, Polymer, 2011, 52, 2–25.
41. K. Chrissopoulou and S. H. Anastasiadis, Soft Matter, 2015, 11, 3746–3766.
42. S. S. Ray and M. Okamoto, Prog. Polym. Sci., 2003, 28, 1539–1641.
43. M. Moniruzzaman and K. I. Winey, Macromolecules, 2006, 39, 5194–5205.
44. H. Zou, S. Wu and J. Shen, Chem. Rev., 2008, 108, 3893–3957.
45. N. Bachhar, Y. Jiao, M. Asai, P. Akcora, R. Bandyopadhyaya and S. K. Kumar, Macromolecules, 2017, 50, 7730–7738.
46. Y. Lin, L. Liu, G. Xu, D. Zhang, A. Guan and G. Wu, J. Phys. Chem. C, 2015, 119, 12956–12966.
47. P. Klonos and P. Pissis, Polymer, 2017, 112, 228–243.
48. P. Klonos, A. Panagopoulou, L. Bokobza, A. Kyritsis, V. Peoglos and P. Pissis, Polymer, 2010, 51, 5490–5499.
49. P. Klonos, I. Y. Sulym, D. Sternik, P. Konstantinou, O. V. Goncharuk, A. Deryło-Marczewska, V. M. Gun’ko, A. Kyritsis and P. Pissis, Polymer, 2018, 139, 130–144.
50. F. Kremer and F. Schönhals, Broadband dielectric spectroscopy, Springer, New York, 2003.
51. A. Schönhals, H. Goering, C. Schick, M. Frick, M. Mayorova and R. Zorn, Eur. Phys. J.: Spec. Top., 2007, 141, 255–259.
52. D. Fragiadakis, P. Pissis and L. Bokobza, Polymer, 2005, 46, 6001–6008.
53. M. Füllbrandt, P. J. Purohit and A. Schönhals, Macromolecules, 2013, 46, 4626–4632.
54. S. Cerveny, G. A. Schwartz, J. Otegui, J. Colmenero, J. Loichen and S. Westermann, J. Phys. Chem. C, 2012, 116, 24340–24349.
55. S. Madkour, P. Szymoniak, M. Heidari, R. Von Klitzing and A. Schönhals, ACS Appl. Mater. Interfaces, 2017, 9, 7535–7546.
56. P. A. Klonos, N. Patelis, E. Glynos, G. Sakellariou and A. Kyritsis, Macromolecules, 2019, 52, 9334–9340.
57. P. Szymoniak, B. R. Pauw, X. Qu and A. Schönhals, Soft Matter, 2020, 16, 5406–5421.
58. T. Ezquerra and A. Nogales, Crystallization as studied by broadband dielectric spectroscopy, Springer Nature, Switzerland, 2020.
59. D. E. Martínez-Tong, B. Vanroy, M. Wübbenhorst, A. Nogales and S. Napolitano, Macromolecules, 2014, 47, 2354–2360.
60. Y. Suzuki, H. Duran, W. Akram, M. Steinhart, G. Floudas and H. J. Butt, Soft Matter, 2013, 9, 9189–9198.
61. S. K. Burgess, J. E. Leisen, B. E. Kraftschik, C. R. Mubarak, R. M. Kriegel and W. J. Koros, Macromolecules, 2014, 47, 1383–1391.
62. T. Dimitriadis, D. N. Bikiaris, G. Z. Papageorgiou and G. Floudas, Macromol. Chem. Phys., 2016, 217, 2056–2062.
63. L. Genovese, M. Soccio, N. Lotti, A. Munari, A. Szymczyk, S. Paszkiewicz, A. Linares, A. Nogales and T. A. Ezquerra, Phys. Chem. Chem. Phys., 2018, 20, 15696–15706.
64. G. Papamokos, T. Dimitriadis, D. N. Bikiaris, G. Z. Papageorgiou and G. Floudas, Macromolecules, 2019, 52, 6533–6546.
65. A. Bourder, S. Araujo, S. Thiyagarajan, L. Delbreilh, A. Esposito and E. Dargent, Polymer, 2021, 213, 123225.
66. C. F. Araujo, M. M. Nolasco, P. J. A. Ribeiro-Claro, S. Rudic, A. J. D. Silvestre, P. D. Vaz and A. F. Sousa, Macromolecules, 2018, 51, 3515–3526.
67. T. P. Gumede, A. S. Luyt and A. J. Müller, eXPRESS Polym. Lett., 2018, 12, 505–529.
68. H. Norazlina and Y. Kamal, Polym. Bull., 2015, 72, 931–961.
69. C. R. Arza, P. Jannasch and F. H. J. Maurer, Eur. Polym. J., 2014, 59, 262–269.
70. S. Evlashin, et al. , Materials, 2019, 12, 2991.
71. A. Sargsyan, A. Tonoyan, S. Davtyan and C. Schick, Eur. Polym. J., 2007, 43, 3113.
72. A. Wurm, M. Ismail, B. Kretzschmar, D. Pospiech and C. Schick, Macromolecules, 2010, 43, 1480–1487.
73. L. Papadopoulos, Z. Terzopoulou, D. N. Bikiaris, D. Patsiaoura, K. Chrissafis, D. G. Papageorgiou and G. Z. Papageorgiou, Polymers, 2018, 10, 937.
74. Z. Terzopoulou, P. A. Klonos, A. Kyritsis, A. Tziolas, A. Avgeropoulos, G. Z. Papageorgiou and D. N. Bikiaris, Polymer, 2019, 166, 1–12.
75. P. Klonos, Y. Bolbukh, C. S. Koutsiara, K. Zagfeiris, O. D. Kalogeri, D. Sternik, A. Derylo-Marczewska, V. Tertykh and P. Pissis, Polymer, 2018, 148, 1–13.
76. L. Papadopoulos, E. Xanthopoulou, G. N. Nikolaidis, A. Zamboulis, D. S. Achilias, G. Z. Papageorgiou and D. N. Bikiaris, Materials, 2020, 13, 4880.
77. R. Androsch, M. L. Di Lorenzo, C. Schick and B. Wunderlich, Polymer, 2010, 51, 4639–4662.
78. J. N. Coleman, M. Cadek, K. P. Ryan, A. Fonseca, J. B. Nagy, W. J. Blau and M. S. Ferreira, Polymer, 2006, 47, 8556.
79. S. Koutsoumpis, A. Poulakis, P. Klonos, S. Kripotou, V. Tsanaktsis, D. N. Bikiaris, A. Kyritsis and P. Pissis, Thermochim. Acta, 2018, 666, 229–240.
80. S. Montserrat, J. L. Gomez Ribelles and J. M. Meseguer, Polymer, 1998, 39, 3801–3807.
81. X. Monnier and D. Cangialosi, Thermochim. Acta, 2019, 677, 60–66.
82. P. Klonos, K. Kulyk, M. V. Borysenko, V. M. Gun’ko, A. Kyritsis and P. Pissis, Macromolecules, 2016, 49, 9457–9473.
83. V. M. Boucher, D. Cangialosi, A. Alegría, J. Colmenero, I. Pastoriza-Santos and L. M. Liz-Marzan, Soft Matter, 2011, 7, 3607–3620.
84. K. Pusnik Cresnar, L. Fras Zemljic, L. Papadopoulos, Z. Terzopoulou, A. Zamboulis, P. A. Klonos, D. N. Bikiaris, A. Kyritsis and P. Pissis, Mater. Today Commun., 2021, 27, 102192.
85. E. Forestier, C. Combeaud, N. Guigo, G. Monge, J. M. Haudin, N. Sbirrazzuoli and N. Billon, Polymer, 2020, 187, 122126.
86. R. Richert, A. Agapov and A. P. Sokolov, J. Chem. Phys., 2011, 134, 104508.
87. M. Soccio, D. E. Martinez-Tong, G. Guidotti, B. Robles-Hernandez, A. Munari, N. Lotti and A. Alegria, Polymers, 2020, 12, 1355.
88. A. Nogales, Z. Denchev and T. A. Ezquerra, Macromolecules, 2000, 33, 9367–9375.
89. C. Alvarez, I. Šics, A. Nogales, Z. Denchev, S. S. Funari and T. A. Ezquerra, Polymer, 2004, 45, 3953–3959.
90. J. Leng, P. J. Purohit, N. Kang, D. Y. Wang, J. Falkenhagen, F. Emmerling, A. F. Thünemann and A. Schöhhals, Eur. Polym. J., 2015, 68, 338–354.
91. A. R. Brás, M. T. Viciosa, Y. Wang, M. Dionisio and J. F. Mano, Macromolecules, 2006, 39, 6513–6520.
92. A. L. Agapov and A. P. Sokolov, Macromolecules, 2009, 42, 2877–2878.
93. K. A. Page and K. Adachi, Polymer, 2006, 47, 6406–6413.
94. R. Lund, A. Alegría, L. Goitandia, J. Colmenero, M. A. Gonzalez and P. Lindner, Macromolecules, 2008, 41, 1364–1376.

---