Self-assembly of millimeter-scale magnetic particles in suspension

Abstract

Self-assembly is ubiquitous at all scales in nature. Most studies have focused on the self-assembly of micron-scale and nano-scale components. In this study, we explore the self-assembly of millimeter-scale magnetic particles in a bubble-column reactor to form 9 different structures. Two component systems (N–N and S–S particles) assemble faster than one-component systems (all particles have N–S poles) because they have more numerous bonding pathways. In addition, two-components add control to process initiation and evolution, and enable the formation of complex structures such as squares, tetrahedra and cubes. Self-assembly is collision-limited, thus, the formation time increases with the total number of bonds required to form the structure and the injected power. The dimensionless Mason number captures the interplay between hydrodynamic forces and magnetic interactions: self-assembly is most efficient at intermediate Mason numbers (the system is quasi-static at low Mason numbers with limited chances for particle interaction; on the other hand, hydrodynamic forces prevail over dipole–dipole interactions and hinder bonding at high Mason numbers). Two strategies to improve yield involve (1) the inclusion of pre-assembled nucleation templates to prevent the formation of incorrect initial structures that lead to kinetic traps, and (2) the presence of boundaries to geometrically filter unwanted configurations and to overcome kinetic traps through particle–wall collisions. Yield maximization involves system operation at an optimal Mason number, the inclusion of nucleation templates and the use of engineered boundaries (size and shape).

---

1 Introduction

Self-assembly can attain static or dynamic equilibrium states. Static self-assembly refers to the spontaneous organization of discrete particles into ordered structures without external intervention.^1–3 The assembly process continues until the available particles form a stable structure that minimizes the system free energy either globally or locally.⁴ Static self-assembly is ubiquitous at all scales in nature. Examples include the arrangement of atoms into crystals,⁵ the aggregation of amphiphilic molecules into micelles or lipids,⁶ the assembly of proteins into viral capsids^7–10 and the association of functional nanoparticles.¹¹ On the other hand, dynamic self-assembly defines systems where particles continuously dissipate energy to sustain the ordered state;^2,12 examples include the self-organization of ants, birds and microrobots into swarms.^13–15

All self-assembly systems involve: (1) elemental particles (e.g. molecules, DNA tiles, PDMS plates, 3D-printed tiles), (2) their interactions (e.g. electrical bonds, capillarity, magnetic), (3) a gas or liquid medium, (4) boundaries including interfaces, and (5) an energy source to sustain relative displacements that can lead to self-assembly e.g. mechanical vibration, heat, external field.^12,16–27

Kinetic traps are intermediate states with local energy minima that hinder the evolution towards the most stable target configuration.^28,29 Reversible bonds may help to overcome kinetic traps and correct errors during assembly.^2,10,12 Nucleation templates – as in heterogenous nucleation – and geometrical constraints can guide self-assembly and improve yield;^11,30,31 in fact, boundaries aid the self-assembly of lipid vesicles at the molecular scale³² and of 3D printed particles at the macroscale.^27,29

Multi-component building blocks can form more complex structures than single-component systems and exhibit a wider range of properties;^33,34 furthermore, multi-component systems allow for precise process initiation control. Salient examples include the self-assembly of DNA from thousands of distinct elements^23,24 and the self-assembly of proteins and peptides to form supramolecular functional structures.³³

Most of the work on self-assembly has focused on micron-scale and nano-scale particles controlled by electrical bonds and Brownian motion. Very few studies investigate the self-assembly of millimeter-size particles, where gravity, inertia and hydrodynamic interactions prevail. Yet, self-assembly can become a manufacturing technique for millimeter-scale objects that are inconvenient for robotic manipulation,^18,29,35,36 especially when formation times are not a limiting factor.¹ Furthermore, millimeter-scale self-assembly can provide valuable insight relevant to micron and nano-scale processes.

This study focuses on the self-assembly of millimeter-scale magnetic particles and seeks to understand concepts that apply to self-assembly at all scales, including assembly kinetics and the role of boundaries.

2 Experimental study – materials and methods

Experiments use plastic particles of different shapes: rods, tripods, circular quadrants and elbows (Fig. 1). All particles are 3D-printed with an acrylonitrile butadiene styrene filament (ABS; filament density = 1.04 g cm⁻³; the particle bulk densities are rod: ρ_p = 1.03 g cm⁻³, tripod: ρ_p = 1.00 g cm⁻³; printer: Ultimaker 2+). We fix small disc-shaped Ni–Cu plated Neodymium magnets (diameter = 1.6 mm, thickness = 0.8 mm, pull = 379 grams) at both ends of each particle with a preassigned exposed magnetic pole, either North N or South S (Fig. 2A).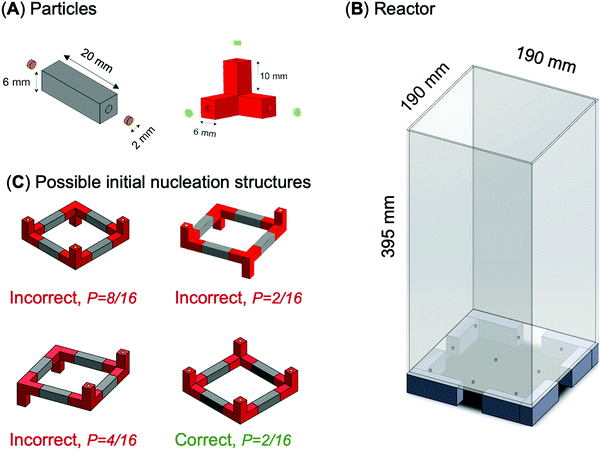

Fig. 1 Target structures tested in this study. N_t is the total number of bonds in the structure.

Fig. 2 Experimental study. (A) Rod and tripod particles. Small disc-shaped magnets are fixed at the ends of each particle. The magnetic pole facing the particle is the hidden pole; brown and green magnets have exposed poles with opposite polarities. (B) Large bubble column reactor. (C) Possible initial nucleation structures for tripods and rods with probability of formation P (refer to Table S1, ESI†).

These particle shapes and end-polarity allow us to explore 9 different structures (Fig. 1). One-component circular quadrants involve particles with N–S poles (Fig. 1A). On the other hand, two-component systems involve particles with the same end polarity, either N–N or S–S (Fig. 1B–G). The two-component three-dimensional tetrahedra and cubes combine tripods with three exposed S-poles and rods with two exposed N-poles (Fig. 1H and I).

Particles are suspended in a glycerol–water mixture (26% by volume glycerol, density ρ_f = 1.04 g ml⁻¹, viscosity = 2 cP) inside a bubble-column reactor (length = width = 190 mm, height = 395 mm, Fig. 2B). Compressed air enters the bottom of the column through nine evenly-spaced needles (needle internal diameter = 0.66 mm, length = 14 mm). A high-resolution flow-meter (Brooks Instruments 1250-55) continuously monitors the air flow rate while a video camera (Sony) records the assembly process.

The test protocol used for all two-component tests conducted in this study consists of four steps: (1) fill the column with the viscous fluid, (2) start air injection, (3) release the first group of particles into the fluid and (4) add the second group. Particle image velocimetry measurements show that the average particle velocity increases with increasing air injection rate (see Fig. S1 for details, ESI†).³⁷ We use a similar but smaller bubble column reactor (cylinder diameter = 94 mm) to study self-assembly in confined environments. The self-assembly of two-component systems can only start after the two components are mixed in the suspension. There is a weak interaction between the exposed S-pole in one rod and the hidden N-pole in the other, however, these incidental bonds readily break.

3 Results

One-component versus two-component self-assembly

Four identical particles with N–S binding terminals can build a one-component circle (Fig. 1A), while two N–N particles and two S–S particles are needed for a two-component circle (Fig. 1B). We compare their self-assembly in the small bubble-column reactor using an air injection rate that favors bond formation and structure assembly over disassembly (air injection rate = 3.7 l min⁻¹). Fig. 3 shows the formation times for the one- and two-component circles; cumulative trends follow log-normal distribution functions. Experimental results show that the two-component system (average time 〈t〉 = 10 min) assembles faster than the one-component system (〈t〉 = 17 min – based on 14 trials each).

Fig. 3 Assembly of one-component (blue) and two-component (red) circles. Cumulative distribution function for the time required to form the circles. The one-component circle is made of 4 identical N–S particles; the two-component circle is made of two N–N particles and two S–S particles (refer to Fig. 1A and B). Points: experimental data. Dashed lines: log-normal distribution. Mean ± standard deviation – one component: 16.8 ± 12.1 min. Two components: 10.2 ± 12.6 min. Air injection rate = 3.7 l min⁻¹.

Let's consider the assembly pathways for the four particles involved in one- and two-component circles. In the one-component system, the N-pole in one particle can bind to the S-poles in any of the three other particles. However, the N-pole in two-component N–N particles can bind to four S-poles in S–S particles. The complete “bonding graphs” for both systems show that the two-component system has a total of 128 possible assembly pathways, while the one-component circle has only 48 possible pathways (Fig. S2, ESI†). Hence, the two-component circle experiences more efficient self-assembly (Fig. 3).

Degree of structural complexity (two components)

We tested the self-assembly of all two-component systems shown in Fig. 1, repeating tests multiple times. The number of bonds in the various target structures N_t is a measure of their complexity (Fig. 1). The movies S1 through S4 (ESI†) show the self-assembly of a two-component circle, square, tetrahedral and cube. Fig. 4 illustrates snapshots taken during the self-assembly of 8 tripods and 12 rods to form a cube. In some cases, particles can form multiple structures with improved efficiency (for example the two circles and triangles in Fig. 1E and F).

Fig. 4 Self-assembly of 8 tripods and 12 rods to form a cube.

Formation times ranged from 40 seconds to more than 10 hours. Fig. 5A shows that the formation time increases with the total number of bonds N_t; in fact, the higher the number of bonds N_t, the higher the number of intermediate structures and kinetic traps the system encounters during self-assembly. We repeat the experiments for each target structure ten times and define the product yield as the ratio of the number of trials that result in successful error-free structures within 10 hours to the total number of 10 trials attempted. The yield is 100% for the 2D shapes (circles N_t = 4, triangles N_t = 6 and squares N_t = 8) but significantly lower for the 3D shapes (tetrahedra N_t = 12 and cubes N_t = 24, Fig. 5B).

Fig. 5 Formation time and yield as a function of structural complexity in terms of number of bonds N_t for the circles, triangles, squares, tetrahedra and cubes. Experiments are repeated a minimum of 10 times for each shape. The maximum duration for each test is 10 hours. (A) Formation time: the large dark markers represent the average formation time; asterisk * means that the structure did not form within 10 hours; the arrow ↑ indicates that the average time based on formed structures is a lower bound. (B) Product yield. All tests conducted in the small reactor with an air injection rate of 3.7 l min⁻¹.

The initial “nucleation structure” plays a critical role in the formation time and yield of complex structures. In fact, incorrect initial nucleation structures are responsible for the low yield in tetrahedra and cubes. Fig. 2C shows four equally stable nucleation structures formed by tripod and rod particles during cube assembly. We can conclude that (1) the nucleation of the correct initial structure has a low probability P = 12.5% – Table S1 (ESI†), and (2) alternative initial structures are equally stable and particles remain bonded in a kinetic trap that would require a high input energy transient to overcome.

We perform additional experiments where we introduce a pre-assembled nucleation template made of four tripods and four rods into the reactor (structure 4 in Fig. 2C), in addition to the remaining four tripods and eight rods. In this case, the yield improves significantly from 0.2 to 0.8 (10 trials each; air injection rate = 2.0 l min⁻¹ for trials with and without template).

Some experiments involve the particles needed to generate one structure only; this initial condition minimizes kinetic traps. In fact, the outcome is not unique when experiments involve the particles needed to form two structures (Fig. 1E–G). For example, the 6 vertices and 6 rods can either assemble into two separate triangles or conjoined triangles.

4 Analysis and discussion

Assembly kinetics

Self-assembly in a bubble-column reactor is a collision-limited reaction: particles can only bond when they approach each other.²⁸ The self-assembly of millimeter-scale magnetic particles suspended in a viscous fluid involves hydrodynamic drag, magnetic dipole–dipole interactions, buoyancy and inertia. The dimensionless Mason number captures the interplay between drag and dipole interactions:^38,39The system is quasi-static at low Mason numbers, there are limited chances for particle interaction and self-assembly progresses slowly. On the other hand, hydrodynamic drag forces prevail over dipole–dipole interactions at high Mason numbers, they hinder self-assembly and might even break previously formed bonds. As product yield depends on assembly and disassembly rates,³ there must be an optimal Mason number for self-assembly.

We explore the assembly kinetics of 8 tripods and 12 rods in the large bubble column reactor (note: the asymptotic structure is the cube – Fig. 1I). We subject the system to five different air injection rates and repeat each experiment three times (Movies S5 and S6, ESI†). Results in Fig. 6 show that the number of bonds increases asymptotically with time, in agreement with previous studies.⁴⁰ A hyperbolic saturation curve adequately describes the data:

where n_bt is the asymptotic number of bonds, t is time and t* is the characteristic time to form n_bt/2 bonds (note: we adopt n_bt = 19 < N_t for all cases). The minimum characteristic time t* (or maximum assembly rate) is observed for 3.7 l min⁻¹ air injection rate. This agitation energy defines the optimal Mason number (Mn ≈ 1.4) for the given system. Fig. S1 (ESI†) shows the average Mason numbers at various air injection rates.

Fig. 6 The effect of kinetic energy on bond creation. Target structure: cube made of 8 tripods and 12 rods (large bubble-column reactor). The air injection rate varies from 2.6 l min⁻¹ to 9.7 l min⁻¹. A hyperbolic saturation curve fits the data, where t* is the characteristic time to form n_bt/2 of the bonds. We repeat experiments three times at each air injection rate. Inset: The inverse of the characteristic time (1/t*) as a function of the air injection rate. Points: experimental data. Dashed lines: upper and lower bound fits using eqn (4).

These results resemble the effect of heat on crystal nucleation and growth rate.^41,42 The classical nucleation theory estimates the nucleation rate J [# events m⁻³ s⁻¹] as a function of the number of molecules near the nucleation site and the probability that molecules have enough energy to overcome the formation barrier:^43,44

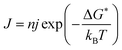where ΔG* [J] is the nucleation formation energy at the critical nucleation size, T [K] is temperature, k_B [J K⁻¹] is Boltzmann constant, n [# particles per m³] particle concentration and j [# events per s] the rate at which molecules approach the nucleation site.⁴⁴

An analogous analysis applies to millimeter-scale magnetic particles. There are two competing trends. At low flow rates, the assembly rate J_a [# events m⁻³ s⁻¹] depends on the particle collision rate j_c [# events m⁻³ s⁻¹] which is proportional to the air injection rate q [m³ s⁻¹] and particle concentration n [# particles m⁻³]; let's adopt an asymptotically linear relation j_c = α·n·q. At high flow rates, the j_c-collisions will not render stable bonds if the kinetic energy resulting from the hydrodynamic force K [J] exceeds the binding energy arising from magnetic dipole interactions U [J]. If we assume that particle velocities follow a Maxwell–Boltzmann distribution,⁴⁵ then the probability that K > U is β exp(−U/K) where the β-factor from the Maxwell–Boltzmann distribution has a weak dependence on K and U, and the kinetic energy K = 1/2·m·v_p² depends on the air injection rate q. The two trends combine and anticipate an optimal air injection rate (Fig. 6, inset):

The effect of confinement: boundaries as geometric filters

The more complex structures in Fig. 1 formed in the small reactor only, whereas long open chains self-assembled in the large reactor. Let's compare the evolution of unmatched open ends (free terminal bonding sites, monitored manually from the videos of the experiments) between 8 tripods and 12 rods in the small and large reactors to explore the effect of confinement (Fig. 7). The number of open ends in the large reactor decreases monotonically towards an asymptotic value corresponding to a kinetic trap (Fig. 7A shows an example of an assembled structure in a kinetic trap). In the small reactor, the particles build different intermediate structures often with local minima (Fig. 7B inset) but continuously recover from kinetic traps to eventually form the most stable target structure (Fig. 7B). Clearly, confinement acts as a geometric filter that prevents the formation of long open structures and thus plays an important role in self-assembly.

Fig. 7 The effect of confinement on structure formation: Unmatched open ends (free terminal bonding sites) as a function of time. Target structure: a cube made of 8 tripods and 12 rods. (A) Large reactor. (B) Small reactor. CF is the confinement factor defined as the ratio between the side length of the cube and the reactor size. The inset shows the recovery from a kinetic trap during the final stages of assembly in the small reactor.

We test the effect of confinement by varying the confinement factor CF defined as the ratio of the target structure's characteristic size to the diameter of the reactor (experiments: we varied the triangle side length and used the small reactor in all tests). Fig. 8 shows that the formation time and yield for the self-assembly of triangles have an optimum value at an intermediate confinement factor CF. An under-confined system (low CF) results in unrestricted structural geometries, as well as low particle volumetric concentration and low particle collision rate (eqn (4)). Assembly time and yield improve as the confinement factor increases. Particle–wall collision frequency increases with increasing confinement factor, and causes more frequent breakage of partial structures. While disassembly allows recovery from kinetic traps, frequent structure-wall collisions in an over-confined reactor cause continuous fragmentation and delay structure formation. Clearly, an optimum confinement factor minimizes formation time and maximizes yield. (Note: air injection favors particle movement in the vertical direction and adds an additional constrain or bias – see Fig. S1 and Movies S1 through S6, ESI†).

Fig. 8 The effect of confinement on structure formation time and yield. Target structure: triangle made of 3 elbows and 3 rods. The confinement factor is defined as the ratio between the side length of the triangle (variable) and the diameter of the reactor (fixed: 94 mm). Yield and formation times are calculated from 10 trials in each case; the maximum duration for each trial is 10 hours. The large blue markers represent the average formation time. Asterisk * indicates that the triangle did not form within 10 hours. Arrow ↑ indicates that the average based on formed triangles is a lower bound to the true average time. All tests conducted in the small reactor with an air injection rate of 3.7 l min⁻¹.

We can anticipate that the reactor shape also affects the evolving morphology of the assembled structure. In fact, cubic nanoparticles self-assemble into cubic superlattices in under-confined systems⁴⁶ and into spherical structures in confining emulsion droplets.⁴⁷ Similarly, copolymers assemble into thin films when confined between parallel plates, into cylinders when confined in pores with square and triangular cross-sections, and bend into helices and stacked toroids in cylindrical pores with circular cross-sections.⁴⁸ Furthermore, different structures emerge under moving rather than static boundary conditions.⁴⁹ This suggests the possibility of feedback-controlled boundary conditions to optimize self-assembly.

5 Conclusions

This study explored the self-assembly of millimeter-scale magnetic particles in one and two-component systems. Two-components enable the formation of complex structures and add control to process initiation and evolution. The self-assembly of two component systems benefits from more numerous bonding pathways and results in more efficient assembly than one-component systems.

The self-assembly of millimeter-scale particles is collision-limited. The optimal kinetic energy for self-assembly is a trade-off between collision rate, bonding probability and debonding out of energy traps. Self-assembly is most efficient at intermediate Mason numbers.

Formation time increases and yield decreases with structural complexity. We explored two possible strategies to improve yield. Pre-assembled initial nucleation templates prevent the formation of incorrect initial structures that lead to kinetic traps; therefore, nucleation templates result in significant yield improvements. Equally important is the role of boundaries, including interfaces: boundaries act as geometric filters that exclude unwanted configurations, constrain assembly pathways and help overcome kinetic traps through particle–wall collisions. Geometric boundaries can be engineered (size and shape) to optimize self-assembly.

List of notations

J [# events m^−3 s^−1]	Nucleation rate
j [# events per s]	Attachment rate
J a [# events m^−3 s^−1]	Assembly rate
j c [# events per s]	Collision rate
K [J]	Kinetic energy of a particle
k B [J K^−1]	Boltzmann constant
Mn [ ]	Mason number = hydrodynamic drag/magnetic dipole–dipole interaction
n [1 m^−3]	Particle concentration
n b [ ]	Number of bonds formed at time t during self-assembly
n bt [ ]	Asymptotic number of bonds the particles form during self-assembly
q [m^3 s^−1]	Air injection flow rate
T [K]	Temperature
t* [s]	Characteristic time to form nbt/2 bonds
〈t〉 [min]	Average formation time
U [J]	Magnetic potential energy for dipole–dipole interaction
v p [m s^−1]	Average particle velocity
α [1 m^−3]	Proportionality factor between collision rate and injection flow rate
β [ ]	Factor in the Maxwell–Boltzmann distribution
ΔG* [J]	Formation Gibbs free energy for nucleation
ρ f [kg m^−3]	Fluid density
ρ p [kg m^−3]	Particle bulk density

Author contributions

All authors have contributed substantially to the manuscript and approved the final submission.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

Support for this research was provided by the KAUST endowment. G. Abelskamp edited the manuscript.

References

1. S. Whitelam, Physics, 2014, 7, 62.
2. G. M. Whitesides and M. Boncheva, Proc. Natl. Acad. Sci. U. S. A., 2002, 99, 4769–4774.
3. M. Mastrangeli, S. Abbasi, C. Varel, C. Van Hoof, J. P. Celis and K. F. Böhringer, J. Micromech. Microeng., 2009, 19, 083001.
4. C. O'Mahony, R. Farell, T. Goshal, J. Holmes and M. Morris, in Thermodynamics – Systems in equilibrium and non-equilibrium, ed. J. C. Moreno-Pirajan, Intechopen, 2011.
5. P. G. Vekilov, Prog. Cryst. Growth Charact. Mater., 2002, 45, 175–199.
6. M. Bergstrom, in Application of thermodynamics to biological and materials science, ed. M. Tadashi, IntechOpen, 2011.
7. J. D. Perlmutter and M. F. Hagan, Annu. Rev. Phys. Chem., 2015, 66, 217–239.
8. R. F. Garmann, A. M. Goldfain and V. N. Manoharan, Proc. Natl. Acad. Sci. U. S. A., 2019, 116, 22485–22490.
9. A. J. Olson, Y. H. E. Hu and E. Keinan, Proc. Natl. Acad. Sci. U. S. A., 2007, 104, 20731–20736.
10. A. J. Olson, Nat. Nanotechnol., 2015, 10, 728.
11. M. Grzelczak, J. Vermant, E. M. Furst and L. M. Liz-Marzán, ACS Nano, 2010, 4, 3591–3605.
12. G. M. Whitesides and B. Grzybowski, Science, 2002, 295, 2418–2421.
13. B. Yigit, Y. Alapan and M. Sitti, Soft Matter, 2020, 16, 1996–2004.
14. R. F. Ismagilov, A. Schwartz, N. Bowden and G. M. Whitesides, Angew. Chem., Int. Ed., 2002, 41, 652–654.
15. O. Feinerman, I. Pinkoviezky, A. Gelblum, E. Fonio and N. S. Gov, Nat. Phys., 2018, 14, 683–693.
16. I. S. Choi, N. B. Bowden and G. M. Whitesides, Angew. Chem., Int. Ed., 1999, 38, 3078–3081.
17. M. Golosovsky, Y. Saado and D. Davidov, Appl. Phys. Lett., 1999, 75, 4168–4170.
18. D. H. Gracias, J. Tien, T. L. Breen, C. Hsu and G. M. Whitesides, Science, 2000, 289, 1170–1172.
19. N. B. Bowden, M. Weck, I. S. Choi and G. M. Whitesides, Acc. Chem. Res., 2001, 34, 231–238.
20. J. C. Love, A. R. Urbach, M. G. Prentiss and G. M. Whitesides, J. Am. Chem. Soc., 2003, 125, 12696–12697.
21. S. Zhang, Nat. Biotechnol., 2003, 21, 1171–1178.
22. F. Ilievski, M. Mani, G. M. Whitesides and M. P. Brenner, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2011, 83, 017301.
23. W. M. Jacobs, A. Reinhardt and D. Frenkel, J. Chem. Phys., 2015, 142, 021101.
24. W. M. Jacobs, A. Reinhardt and D. Frenkel, Proc. Natl. Acad. Sci. U. S. A., 2015, 112, 6313–6318.
25. T. A. G. Hageman, P. A. Löthman, M. Dirnberger, M. C. Elwenspoek, A. Manz and L. Abelmann, J. Appl. Phys., 2018, 123, 024901.
26. P. A. Löthman, T. A. G. Hageman, M. C. Elwenspoek, G. J. M. Krijnen, M. Mastrangeli, A. Manz and L. Abelmann, Adv. Mater. Interfaces, 2019, 0, 1900963.
27. L. Abelmann, T. A. G. Hageman, P. A. Löthman, M. Mastrangeli and M. C. Elwenspoek, Sci. Adv., 2020, 6, eaba2007.
28. D. Ipparthi, A. Winslow, M. Sitti, M. Dorigo and M. Mastrangeli, Soft Matter, 2017, 13, 7595–7608.
29. A. Hacohen, I. Hanniel, Y. Nikulshin, S. Wolfus, A. Abu-Horowitz and I. Bachelet, Sci. Rep., 2015, 5, 12257.
30. P. Skovborg, H. J. Ng, P. Rasmussen and U. Mohn, Chem. Eng. Sci., 1993, 48, 445–453.
31. S. Dai, J. Y. Lee and J. C. Santamarina, Fluid Phase Equilib., 2014, 378, 107–112.
32. E. Lopez-Fontal, A. Grochmal, T. Foran, L. Milanesi and S. Tomas, Chem. Sci., 2018, 9, 1760–1768.
33. B. O. Okesola and A. Mata, Chem. Soc. Rev., 2018, 47, 3721–3736.
34. E. R. Draper, E. G. B. Eden, T. O. McDonald and D. J. Adams, Nat. Chem., 2015, 7, 848.
35. M. Boncheva, S. A. Andreev, L. Mahadevan, A. Winkleman, D. R. Reichman, M. G. Prentiss, S. Whitesides and G. M. Whitesides, Proc. Natl. Acad. Sci. U. S. A., 2005, 102, 3924–3929.
36. A. Ekblaw, E. Shuter and J. Paradiso, presented in part at the AIAA Scitech 2019 forum, smart adaptable deployable structures, 2019.
37. D. H. Kelley and N. T. Ouellette, Am. J. Phys., 2011, 79, 267–273.
38. J. de Vicente, D. J. Klingenberg and R. Hidalgo-Alvarez, Soft Matter, 2011, 7, 3701–3710.
39. G. Bossis, S. Lacis, A. Meunier and O. Volkova, J. Magn. Magn. Mater., 2002, 252, 224–228.
40. W. Zheng and H. O. Jacobs, Adv. Funct. Mater., 2005, 15, 732–738.
41. J. W. Mullin and K. D. Raven, Nature, 1962, 195, 35–38.
42. V. Nappo, R. Sullivan, R. Davey, S. Kuhn, A. Gavriilidis and L. Mazzei, Chem. Eng. Res. Des., 2018, 136, 48–56.
43. J. H. t. Horst and D. Kashchiev, J. Chem. Phys., 2005, 123, 114507.
44. R. P. Sear, J. Phys.: Condens. Matter, 2007, 19, 033101.
45. D. Camuffo, in Microclimate for Cultural Heritage, ed. D. Camuffo, Elsevier, Boston, 2nd edn, 2014, pp. 347–366 DOI:10.1016/B978-0-444-63296-8.00010-X.
46. Y. Nagaoka, K. Hills-Kimball, R. Tan, R. Li, Z. Wang and O. Chen, Adv. Mater., 2017, 29, 1606666.
47. D. Wang, M. Hermes, R. Kotni, Y. Wu, N. Tasios, Y. Liu, B. de Nijs, E. B. van der Wee, C. B. Murray, M. Dijkstra and A. van Blaaderen, Nat. Commun., 2018, 9, 2228.
48. A.-C. Shi and B. Li, Soft Matter, 2013, 9, 1398–1413.
49. U. Culha, Z. S. Davidson, M. Mastrangeli and M. Sitti, Proc. Natl. Acad. Sci. U. S. A., 2020, 117, 11306–11313.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: 10.1039/d1sm00588j

---