Open Access Article
Open Access ArticleModuli and modes in the Mikado model
Karsten
Baumgarten
and
Brian P.
Tighe

Delft University of Technology, Process & Energy Laboratory, Leeghwaterstraat 39, 2628 CB Delft, The Netherlands. E-mail: b.p.tighe@tudelft.nl
First published on 16th June 2021
Abstract
We determine how low frequency vibrational modes control the elastic shear modulus of Mikado networks, a minimal mechanical model for semi-flexible fiber networks. From prior work it is known that when the fiber bending modulus is sufficiently small, (i) the shear modulus of 2D Mikado networks scales as a power law in the fiber line density, G ∼ ρα+1, and (ii) the networks also possess an anomalous abundance of soft (low-frequency) vibrational modes with a characteristic frequency ωκ ∼ ρβ/2. While it has been suggested that α and β are identical, the preponderance of evidence indicates that α is larger than theoretical predictions for β. We resolve this inconsistency by measuring the vibrational density of states in Mikado networks for the first time. Supported by these results, we then demonstrate analytically that α = β + 1. In so doing, we uncover new insights into the coupling between soft modes and shear, as well as the origin of the crossover from bending- to stretching-dominated response.
Mikado networks1 are a widely studied off-lattice model for the mechanics of semiflexible fiber networks.2–9 Two-dimensional Mikado networks consist of slender rods with stretching modulus μ and bending modulus κ, which are randomly deposited in a box and crosslinked at each intersection point. At a phenomenological level, the model successfully reproduces important features of real fiber networks, including the affine to non-affine crossover in linear response (discussed below) and the onset of strain stiffening at a critical strain scale.10–13 The model also serves as a bridge to other soft matter systems where floppiness and non-affinity play an important role, such as solid foams and confluent tissues,14–16 soft sphere packings,17–22 and random spring networks.23–28
The goal of this article is to determine how low frequency (“soft”) vibrational modes control the shear modulus G in 2D Mikado networks. It is natural to expect the displacements of crosslinks during shear deformation to project strongly on soft modes, which implies a relationship to the modulus. This relationship has the potential to explain the strong non-affine fluctuations that are known to emerge in fiber networks, by connecting them to the floppy (zero frequency) vibrational modes of freely bending (κ = 0) networks, which are inherently non-affine. However, precisely how soft modes set the modulus remains unclear, as there is an apparent contradiction between existing results in the literature. While both G1,3,4,7 and the typical soft mode frequency ωκ5,6 display anomalous power law scaling with the fiber line density ρ (defined below), the best estimates of their respective exponents do not appear to be compatible. In order to describe this discrepancy more precisely, we must first summarize what is known about moduli and modes separately.
Shear modulus. We begin with the shear modulus of bi-periodic networks of N fibers in an area A, as depicted in Fig. 1a. There are three independent, microscopic length scales that characterize such a network. The first is the fiber length ![[small script l]](https://www.rsc.org/images/entities/i_char_e146.gif) f. The second is the mean length of a fiber segment between two crosslinkers. A Poissonian fiber deposition process results in a mean segment length
f. The second is the mean length of a fiber segment between two crosslinkers. A Poissonian fiber deposition process results in a mean segment length ![[small script l]](https://www.rsc.org/images/entities/i_char_e146.gif) s = π/(2ρ), where the fiber line density ρ ≡ N
s = π/(2ρ), where the fiber line density ρ ≡ N![[small script l]](https://www.rsc.org/images/entities/i_char_e146.gif) f/A is the total length of fiber per unit area. The third length
f/A is the total length of fiber per unit area. The third length ![[small script l]](https://www.rsc.org/images/entities/i_char_e146.gif) b ≡ (κ/μ)1/2 is mechanical; it represents the natural length over which a free fiber bends. When mechanical properties of networks are expressed in dimensionless form, they must be functions of two dimensionless ratios constructed from these three length scales. We choose
b ≡ (κ/μ)1/2 is mechanical; it represents the natural length over which a free fiber bends. When mechanical properties of networks are expressed in dimensionless form, they must be functions of two dimensionless ratios constructed from these three length scales. We choose ![[small script l]](https://www.rsc.org/images/entities/i_char_e146.gif) b/
b/![[small script l]](https://www.rsc.org/images/entities/i_char_e146.gif) f and ρ
f and ρ![[small script l]](https://www.rsc.org/images/entities/i_char_e146.gif) f.
f.
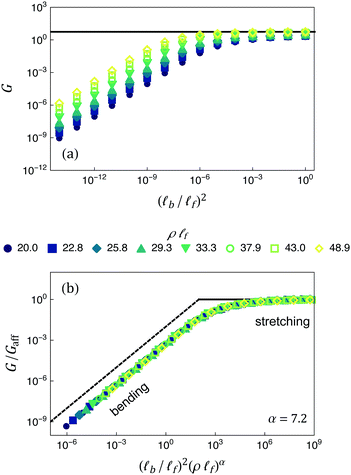
The most relevant features of G can be illustrated by varying the bending modulus κ while holding all other model parameters fixed (i.e., varying ![[small script l]](https://www.rsc.org/images/entities/i_char_e146.gif) b/
b/![[small script l]](https://www.rsc.org/images/entities/i_char_e146.gif) f at fixed ρ
f at fixed ρ![[small script l]](https://www.rsc.org/images/entities/i_char_e146.gif) f), as shown using our own data in Fig. 2a (details below). If we look first at larger values of κ, then eventually the energetic penalty for bending will be so large that the fibers essentially do not bend. Numerics indicate that when deformation is stretching-dominated, the displacements of crosslinks follow the global deformation affinely.1,3 The shear modulus is therefore given by its affine value G ≃ Gaff, which can be calculated exactly4 and scales as Gaff ∼ μρ/
f), as shown using our own data in Fig. 2a (details below). If we look first at larger values of κ, then eventually the energetic penalty for bending will be so large that the fibers essentially do not bend. Numerics indicate that when deformation is stretching-dominated, the displacements of crosslinks follow the global deformation affinely.1,3 The shear modulus is therefore given by its affine value G ≃ Gaff, which can be calculated exactly4 and scales as Gaff ∼ μρ/![[small script l]](https://www.rsc.org/images/entities/i_char_e146.gif) f in densely crosslinked networks. If instead we look at small κ, bending eventually becomes energetically favorable to stretching, the response becomes strongly non-affine, and G becomes much smaller than Gaff. Hence the shear modulus displays a crossover between stretching- and bending-dominated deformation, which correlate with affine and non-affine response, respectively. The bending-dominated regime is of particular interest, both because affine deformation is comparatively simple to model, and because non-affinity represents strong deviations from the mean response.
f in densely crosslinked networks. If instead we look at small κ, bending eventually becomes energetically favorable to stretching, the response becomes strongly non-affine, and G becomes much smaller than Gaff. Hence the shear modulus displays a crossover between stretching- and bending-dominated deformation, which correlate with affine and non-affine response, respectively. The bending-dominated regime is of particular interest, both because affine deformation is comparatively simple to model, and because non-affinity represents strong deviations from the mean response.
It is evident from Fig. 2a that the value (![[small script l]](https://www.rsc.org/images/entities/i_char_e146.gif) b/
b/![[small script l]](https://www.rsc.org/images/entities/i_char_e146.gif) f)* where the bending- to stretching-dominated crossover occurs depends itself on ρ
f)* where the bending- to stretching-dominated crossover occurs depends itself on ρ![[small script l]](https://www.rsc.org/images/entities/i_char_e146.gif) f. If we assume power law scaling (
f. If we assume power law scaling (![[small script l]](https://www.rsc.org/images/entities/i_char_e146.gif) b/
b/![[small script l]](https://www.rsc.org/images/entities/i_char_e146.gif) f)* ∼ (ρ
f)* ∼ (ρ![[small script l]](https://www.rsc.org/images/entities/i_char_e146.gif) f)−α/2 for some undetermined exponent α, it is then natural to expect that the dimensionless shear modulus
f)−α/2 for some undetermined exponent α, it is then natural to expect that the dimensionless shear modulus ![[capital G, script]](https://www.rsc.org/images/entities/char_e112.gif) ≡ G/Gaff can be written as a function of the variable z = (
≡ G/Gaff can be written as a function of the variable z = (![[small script l]](https://www.rsc.org/images/entities/i_char_e146.gif) b/
b/![[small script l]](https://www.rsc.org/images/entities/i_char_e146.gif) f)2(ρ
f)2(ρ![[small script l]](https://www.rsc.org/images/entities/i_char_e146.gif) f)α. The scaling function has the form
f)α. The scaling function has the form
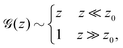 | (1) |
![[capital G, script]](https://www.rsc.org/images/entities/char_e112.gif) ≃ 1 for large z ensures that G ≃ Gaff is recovered, while the form
≃ 1 for large z ensures that G ≃ Gaff is recovered, while the form ![[capital G, script]](https://www.rsc.org/images/entities/char_e112.gif) ∼ z for small z is necessary so that G is proportional to κ and independent of μ in the bending-dominated regime. The value of α has been estimated numerically by several groups.† Wilhelm and Frey found α ≈ 5.7.1 Head et al.3,4 estimated α ≈ 8 for networks with ρ
∼ z for small z is necessary so that G is proportional to κ and independent of μ in the bending-dominated regime. The value of α has been estimated numerically by several groups.† Wilhelm and Frey found α ≈ 5.7.1 Head et al.3,4 estimated α ≈ 8 for networks with ρ![[small script l]](https://www.rsc.org/images/entities/i_char_e146.gif) f as large as 120 (comparable to Wilhelm and Frey), but suggested that α will approach a value of 7 when larger values of ρ
f as large as 120 (comparable to Wilhelm and Frey), but suggested that α will approach a value of 7 when larger values of ρ![[small script l]](https://www.rsc.org/images/entities/i_char_e146.gif) f are accessed. Shahsavari and Picu7 simulated ρ
f are accessed. Shahsavari and Picu7 simulated ρ![[small script l]](https://www.rsc.org/images/entities/i_char_e146.gif) f as large as 300 and found α ≈ 7. Head et al.4 also presented a mean field scaling argument that predicts α = 7; however, it does not invoke modes and so does not clarify their relationship to the modulus. As shown in Fig. 2b and described in greater detail below, we obtain good data collapse with our own numerical results for α ≈ 7.2.‡
f as large as 300 and found α ≈ 7. Head et al.4 also presented a mean field scaling argument that predicts α = 7; however, it does not invoke modes and so does not clarify their relationship to the modulus. As shown in Fig. 2b and described in greater detail below, we obtain good data collapse with our own numerical results for α ≈ 7.2.‡
For completeness, we note that Mikado networks undergo a rigidity percolation transition at a critical fiber line density ρc ≈ 5.7.1,2 Like the prior studies discussed above, we estimate α using data well above ρc. G crosses over to a qualitatively different scaling regime as ρ → ρc from above. This regime is not the focus of the present study.
Soft modes. Let us now turn to soft vibrational modes in Mikado networks. If fibers are allowed to bend freely (κ = 0), then Mikado networks always possess so-called floppy modes.2,5,8 These are non-rigid body motions that can be performed without doing work, and therefore correspond to vibrational modes with zero frequency. A finite bending stiffness stabilizes floppy motions, lifting them to finite frequency. As floppy motions are intrinsically non-affine, the number and vibrational frequencies of soft modes must be fundamentally related to non-affine fluctuations in mechanical response.
In two seminal papers, Heussinger and Frey (HF) developed what has come to be known as floppy mode theory (FMT).5,6 The theory (i) explicitly constructs the floppy modes in freely bending Mikado networks, and (ii) uses these modes to build a set of trial modes, and thereby predict the characteristic soft mode frequency ωκ at small but finite bending modulus using the variational method. Each trial mode is constructed by displacing one of the N fibers a distance δx along its axis. This motion is opposed by the rest of the network, and therefore carries an energetic cost W(δx) = (1/2)Kκδx2. The average effective “spring constant” Kκ sets the characteristic frequency, ωκ ∼ Kκ1/2. By using the crosslink displacements from a floppy mode and the known distribution of segment sizes, HF found
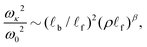 | (2) |
![[small script l]](https://www.rsc.org/images/entities/i_char_e146.gif) f)1/2. Depending on the specific approximations that are made, FMT predicts β = 6 or β ≈ 5.75.
f)1/2. Depending on the specific approximations that are made, FMT predicts β = 6 or β ≈ 5.75.
Rather than directly measuring the frequency ωκ, HF tested their theory indirectly by measuring the shear modulus. To predict G, they equated the energy of the shear deformation, GAγ2, with the energy NW(δx) stored by the soft modes under shear. However, it is not apparent what the typical axial displacement δx should be. In order to close this gap, they further assumed that the center of mass of each fiber displaces affinely. We shall refer to this as the affine fiber approximation (AFA). It implies that each fiber undergoes an axial displacement δx ∼ ![[small script l]](https://www.rsc.org/images/entities/i_char_e146.gif) fγ relative to its environment. The shear modulus is then
fγ relative to its environment. The shear modulus is then
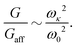 | (3) |
Taken together, eqn (1)–(3) imply α = β. Based on this relation, Heussinger and Frey concluded that the numerical result α = 5.7 from Wilhelm and Frey1 validates their theoretical predictions for β. However, as noted above, independent studies3,4,7 conclude instead that α ≈ 7. In our opinion, the preponderance of evidence indicates that α is not equal to the FMT prediction for β.
Hence we have a puzzle. The discrepancy between α and the theoretically predicted value of β indicates that there is a gap in our understanding of non-affine response in the Mikado model – and, by extension, in fiber networks in general. Where is the missing physics? The persistence of this gap is due, at least in part, to the paucity of data for the vibrational density of states (and hence ωκ) in Mikado networks and related models.29 Since ωκ has not been measured directly, one possibility is that β is larger than the HF theory predicts. We test this by presenting the first direct measurement of ωκ in the Mikado model, as shown in Fig. 3a (details below). We obtain the best collapse of the data for β = 6.1, with reasonable collapse in the range 5.8 ≤ β ≤ 6.5. This result for β is in reasonable agreement with FMT, and also too small to account for the discrepancy between α and β.
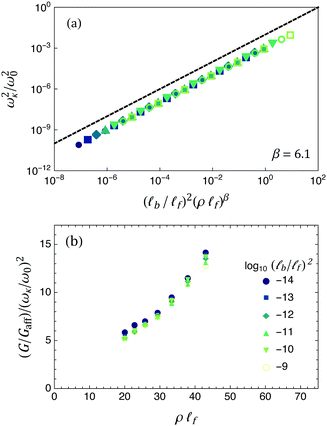 | ||
Fig. 3 (a) The characteristic frequency ωκ of soft vibrational modes in a Mikado network plotted versus (![[small script l]](https://www.rsc.org/images/entities/i_char_e146.gif) b/ b/![[small script l]](https://www.rsc.org/images/entities/i_char_e146.gif) f)2(ρ f)2(ρ![[small script l]](https://www.rsc.org/images/entities/i_char_e146.gif) f)β with β = 6.1. See Fig. 2 for legend. The dashed line has a slope of 1. (b) The ratio of the dimensionless shear modulus shear modulus G/Gaff to the characteristic frequency ωκ is not constant when plotted versus fiber line density, which implies α ≠ β. f)β with β = 6.1. See Fig. 2 for legend. The dashed line has a slope of 1. (b) The ratio of the dimensionless shear modulus shear modulus G/Gaff to the characteristic frequency ωκ is not constant when plotted versus fiber line density, which implies α ≠ β. | ||
The second possible explanation for the discrepancy, which we favor, is that the affine fiber approximation is incorrect, and hence that the relation α = β is unjustified. This view is supported by Fig. 3b, which plots the ratio (G/Gaff)/(ωκ2/ω02). eqn (3) predicts this ratio to be independent of the fiber line density, but instead we find a roughly linear trend. In the following sections, we will present evidence that in fact
| α = β + 1. | (4) |
1 Shear response in the Mikado model
We now define the Mikado model in greater detail, and demonstrate how to calculate the shear modulus from the crosslink displacements in response to an imposed shear stress.Mikado networks consist of N filaments of equal length ![[small script l]](https://www.rsc.org/images/entities/i_char_e146.gif) f, which are deposited randomly in a biperiodic square system of linear size L and area A = L2. Their positions and orientations are drawn from uniform probability distributions. If, during the deposition process, two filaments intersect, they form a crosslink around which the filaments can freely rotate. The crosslinks cannot be broken. In the initial condition, i.e. after deposition and prior to shear, the fibers are straight lines subdivided into co-linear segments by the crosslinks. We trim so-called “dangling ends,” i.e. segments at the end of a fiber that are attached via a single crosslink, because they neither stretch nor bend. We choose units of length and energy such that
f, which are deposited randomly in a biperiodic square system of linear size L and area A = L2. Their positions and orientations are drawn from uniform probability distributions. If, during the deposition process, two filaments intersect, they form a crosslink around which the filaments can freely rotate. The crosslinks cannot be broken. In the initial condition, i.e. after deposition and prior to shear, the fibers are straight lines subdivided into co-linear segments by the crosslinks. We trim so-called “dangling ends,” i.e. segments at the end of a fiber that are attached via a single crosslink, because they neither stretch nor bend. We choose units of length and energy such that ![[small script l]](https://www.rsc.org/images/entities/i_char_e146.gif) f = 1 and μ = 1 and fix A = 9
f = 1 and μ = 1 and fix A = 9![[small script l]](https://www.rsc.org/images/entities/i_char_e146.gif) f2. Nevertheless, we continue to write
f2. Nevertheless, we continue to write ![[small script l]](https://www.rsc.org/images/entities/i_char_e146.gif) f and κ in scaling relations for transparency.
f and κ in scaling relations for transparency.
The energy of a network configuation is given by
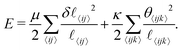 | (5) |
Here 〈ij〉 denotes the segment connecting crosslinks i and j, and 〈ijk〉 labels two consecutive segments 〈ij〉 and 〈jk〉 on the same fiber. The quantity δ![[small script l]](https://www.rsc.org/images/entities/i_char_e146.gif) 〈ij〉 is the change in the length of segment 〈ij〉 from its value in the initial condition. The angle θ〈ijk〉 measures the deviation from co-linearity of adjacent segments 〈ij〉 and 〈jk〉, and
〈ij〉 is the change in the length of segment 〈ij〉 from its value in the initial condition. The angle θ〈ijk〉 measures the deviation from co-linearity of adjacent segments 〈ij〉 and 〈jk〉, and ![[small script l]](https://www.rsc.org/images/entities/i_char_e146.gif) 〈ijk〉 is the average of
〈ijk〉 is the average of ![[small script l]](https://www.rsc.org/images/entities/i_char_e146.gif) 〈ij〉 and
〈ij〉 and ![[small script l]](https://www.rsc.org/images/entities/i_char_e146.gif) 〈jk〉.
〈jk〉.
By construction, the network is initially in a stress-free state. When subjected to a shear stress σ, the box undergoes a shear strain γ and the crosslinks displace from their initial positions. We consider a simple shear in which the lattice vectors of the initially square unit cell become
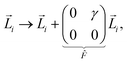 | (6) |
![[F with combining circumflex]](https://www.rsc.org/images/entities/i_char_0046_0302.gif) is the deformation gradient. The crosslink displacements can be expressed as a sum of affine and non-affine terms. Denoting the position of crosslink i as
is the deformation gradient. The crosslink displacements can be expressed as a sum of affine and non-affine terms. Denoting the position of crosslink i as ![[X with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0058_20d1.gif) i, its affine displacement is
i, its affine displacement is ![[A with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0041_20d1.gif) i =
i = ![[F with combining circumflex]](https://www.rsc.org/images/entities/i_char_0046_0302.gif)
![[X with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0058_20d1.gif) i. Collecting the 2N× Cartesian components of the crosslink positions in a vector |X〉 (and similarly for other quantities), the crosslink positions after shearing are |X〉 + |A〉 + |U〉, where |U〉 represents the non-affine part of the displacements. While each element of |U〉 is an independent degree of freedom, specifying the shear strain selects the value of |A〉 on each crosslink. Hence a shear displacement of the network is described by 2N× + 1 degrees of freedom in total.
i. Collecting the 2N× Cartesian components of the crosslink positions in a vector |X〉 (and similarly for other quantities), the crosslink positions after shearing are |X〉 + |A〉 + |U〉, where |U〉 represents the non-affine part of the displacements. While each element of |U〉 is an independent degree of freedom, specifying the shear strain selects the value of |A〉 on each crosslink. Hence a shear displacement of the network is described by 2N× + 1 degrees of freedom in total.
The response to shear can be determined by expanding the energy (5) in the components of |U〉 and γ. In the harmonic approximation, the result is
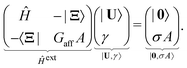 | (7) |
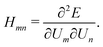 | (8) |
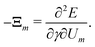 | (9) |
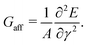 | (10) |
The shear modulus can be determined numerically by selecting a value of the shear stress σ and inverting eqn (7) numerically to find |U,γ〉. The modulus can then be read off from G = σ/γ. The results of this procedure, which were already discussed in the Introduction, are plotted in Fig. 2 after averaging over 100 samples per condition. To estimate the exponent α, we introduce a trial value αtrial and select the n data points (zi,![[capital G, script]](https://www.rsc.org/images/entities/char_e112.gif) i) satisfying z(αtrial) < 0.1. According to eqn (1), the variable gi =
i) satisfying z(αtrial) < 0.1. According to eqn (1), the variable gi = ![[capital G, script]](https://www.rsc.org/images/entities/char_e112.gif) i/zi should approach a constant value, independent of zi. Deviations from this expectation are quantified by the cost function
i/zi should approach a constant value, independent of zi. Deviations from this expectation are quantified by the cost function 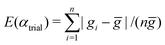 , which quantifies the relative amplitude of fluctuations about the mean ḡ. At αtrial = 7.2, the function obtains its minimum value Emin = 8.2 × 10−3, meaning data collapse to within less than 1% of the average. E remains within 50% of its minimum for 6.9 ≤ αtrial ≤ 7.6.
, which quantifies the relative amplitude of fluctuations about the mean ḡ. At αtrial = 7.2, the function obtains its minimum value Emin = 8.2 × 10−3, meaning data collapse to within less than 1% of the average. E remains within 50% of its minimum for 6.9 ≤ αtrial ≤ 7.6.
2 Density of states and soft modes
To make further progress, we now follow the approach developed in ref. 20,27,30, and consider the eigenmodes of Ĥext. These serve as a convenient eigenbasis in which to express the quasistatic displacements of a network's nodes. Eigenmodes of the Hessian are also eigenmodes of the dynamical matrix for the case where each crosslink is assigned unit mass, which motivates our choice to describe them as (undamped) “vibrational modes.” Nevertheless, eigenvalues of the Hessian have units of stiffness (force/length), rather than (frequency)2. The same Hessian can be used to model, e.g., overdamped relaxations in the presence of a solute, see ref. 20,27.Each mode |Un,Λn〉 satisfies the eigenvalue equation
| Ĥext|Un,Λn〉 = ωn2|Un,Λn〉, | (11) |
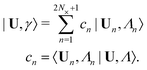 | (12) |
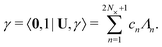 | (13) |
We now solve for G = σ/γ by inserting eqn (12) in (7) and exploiting the orthonormality of modes to find
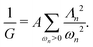 | (14) |
It is useful to rewrite eqn (14) in the continuum limit. To do this we assume that Λn2N2 is independent of N (which will be justified below) and define Λ(ω)/N2 to be the average of Λn2 in the interval [ω,ω + dω]). Similarly, we introduce the density of states D(ω), which is the probability density of ω in the same interval. We then have
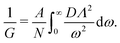 | (15) |
The Mikado density of states D(ω) is plotted in Fig. 4 for one value of ρ and varying κ. It features two distinct bands. The lower band shifts with varying κ, while the upper band remains unchanged. We conclude that the lower band contains bending-dominated modes, and the upper band contains stretching-dominated modes.
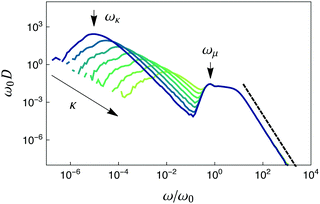 | ||
Fig. 4 The Mikado density of states for ρ![[small script l]](https://www.rsc.org/images/entities/i_char_e146.gif) f = 20.0 and κ = 10−14…10−8 in decade steps. The frequencies ωκ and ωμ are indicated with arrows for the lowest value of κ. The dashed line has slope − 3. f = 20.0 and κ = 10−14…10−8 in decade steps. The frequencies ωκ and ωμ are indicated with arrows for the lowest value of κ. The dashed line has slope − 3. | ||
The bending-dominated band is characterized by its peak frequency ωκ, which we identify with the frequency scale studied by HF. We have estimated ωκ by fitting log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) D to a parabola in log
D to a parabola in log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ω in the vicinity of the peak. These data are plotted in Fig. 3a. As noted in the Introduction, we find that ωκ2 scales with (
ω in the vicinity of the peak. These data are plotted in Fig. 3a. As noted in the Introduction, we find that ωκ2 scales with (![[small script l]](https://www.rsc.org/images/entities/i_char_e146.gif) b
b![[small script l]](https://www.rsc.org/images/entities/i_char_e146.gif) f)2(ρ
f)2(ρ![[small script l]](https://www.rsc.org/images/entities/i_char_e146.gif) f)β. Estimating β in the same way as α above, we find the best collapse for βtrial = 6.1, with Emin = 0.01. The cost function remains within 50% of its minimum for 5.8 ≤ βtrial ≤ 6.5.
f)β. Estimating β in the same way as α above, we find the best collapse for βtrial = 6.1, with Emin = 0.01. The cost function remains within 50% of its minimum for 5.8 ≤ βtrial ≤ 6.5.
The stretching-dominated band is characterized by a low frequency shoulder at a frequency ωμ. While ωμ is independent of κ, it shifts to lower frequencies when the fiber line density is increased, as shown in Fig. 5a. We discuss ωμ further in the following section. The large-ω tail of the stretching-dominated band is due to longitudinal vibrations ω‖ ∼ (μ/![[small script l]](https://www.rsc.org/images/entities/i_char_e146.gif) )1/2 of individual fiber segments with length
)1/2 of individual fiber segments with length ![[small script l]](https://www.rsc.org/images/entities/i_char_e146.gif) . These frequencies are spread out by the distribution of segment lengths P(
. These frequencies are spread out by the distribution of segment lengths P(![[small script l]](https://www.rsc.org/images/entities/i_char_e146.gif) ), which is exponential due to the Poissonian deposition process. The tail is then D ∼ P[
), which is exponential due to the Poissonian deposition process. The tail is then D ∼ P[![[small script l]](https://www.rsc.org/images/entities/i_char_e146.gif) (ω‖)]|d
(ω‖)]|d![[small script l]](https://www.rsc.org/images/entities/i_char_e146.gif) /dω‖| ∼ ω−3 (Fig. 4, dashed line).
/dω‖| ∼ ω−3 (Fig. 4, dashed line).
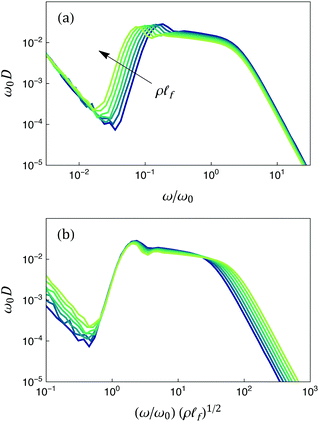 | ||
| Fig. 5 (a) Density of states for κ = 10−14 and varying fiber line density. (b) The same data, now with ω rescaled by the prediction of eqn (18) for ωμ. | ||
3 Two types of soft modes
We will demonstrate that α = β + 1 in two separate ways, neither of which invoke the AFA. In the following section, we will directly calculate G in terms of the peak frequency ωκ in the bending-dominated regime. But first, we present a scaling analysis of the characteristic frequencies in the density of states. The main question will be determining when the bending- and stretching-dominated bands merge, i.e. when ωκ becomes comparable to ωμ. Therefore we must first determine how ωμ scales with fiber line density.The stretching-dominated band is independent of the bending modulus κ, and therefore persists in freely-bending networks with κ = 0. The vibrational modes of central force networks have been studied extensively,23–25,27,28,31–33 and we will now adapt these results to Mikado networks to determine the scaling of ωμ.
The mean coordination Z of a Mikado network obeys an upper bound Z ≤ Zc = 4, where Zc is known as the central force isostatic point.§ It represents the lowest coordination where there are enough springs to constrain all possible non-rigid body motions of the network. It is straightforward to show that ΔZ ≡ Zc − Z ∼ 1/(ρ![[small script l]](https://www.rsc.org/images/entities/i_char_e146.gif) f) in Mikado networks. Therefore densely crosslinked, freely bending Mikado networks are central force networks close to, but below, their rigidity transition.2,8,29
f) in Mikado networks. Therefore densely crosslinked, freely bending Mikado networks are central force networks close to, but below, their rigidity transition.2,8,29
Central force networks on either side of Zc display an abundance of soft modes whose spatial character strongly resembles floppy motions,24,33i.e. the relative motion of each pair of nodes i and j connected by a spring is predominantly transverse to the unit vector ![[n with combining circumflex]](https://www.rsc.org/images/entities/i_char_006e_0302.gif) ij pointing from i to j. We shall refer to these as stretching-dominated soft modes, to distinguish them from the soft modes of FMT. The softest stretching-dominated soft modes have frequency ωμ. When Z < Zc, the density of states below ωμ is gapped, i.e. there are no modes between ωμ and the floppy modes at ω = 0.24 The dependence of ωμ on ΔZ can be calculated with variational arguments reminiscent of FMT,33 or with effective medium theory.24 The result is
ij pointing from i to j. We shall refer to these as stretching-dominated soft modes, to distinguish them from the soft modes of FMT. The softest stretching-dominated soft modes have frequency ωμ. When Z < Zc, the density of states below ωμ is gapped, i.e. there are no modes between ωμ and the floppy modes at ω = 0.24 The dependence of ωμ on ΔZ can be calculated with variational arguments reminiscent of FMT,33 or with effective medium theory.24 The result is
| ωμ ∼ keff1/2|ΔZ|, | (16) |
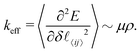 | (17) |
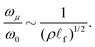 | (18) |
![[small script l]](https://www.rsc.org/images/entities/i_char_e146.gif) f by rescaling the frequency ω with the prediction of eqn (18).
f by rescaling the frequency ω with the prediction of eqn (18).
Having determined the scaling of ωμ, we can now motivate the crossover between bending- and stretching-dominated shear response. We expect network response to project strongly on the softest modes. Therefore the response to shear will be dominated by fiber bending when the density of states has a well-defined bending-dominated band. This condition is satisfied so long as ωκ ≪ ωμ. The crossover from bending- to stretching-dominated response will occur when ωκ and ωμ become comparable,
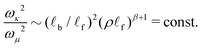 | (19) |
![[small script l]](https://www.rsc.org/images/entities/i_char_e146.gif) b/
b/![[small script l]](https://www.rsc.org/images/entities/i_char_e146.gif) f)2(ρ
f)2(ρ![[small script l]](https://www.rsc.org/images/entities/i_char_e146.gif) f)α = z0. As these two conditions must be equivalent, we conclude that α = β + 1. This is our first main result.
f)α = z0. As these two conditions must be equivalent, we conclude that α = β + 1. This is our first main result.
4 Directly relating the shear modulus to soft modes
We now derive the relation α = β + 1 by a different but compatible route. Namely, we calculate G in the bending-dominated regime directly from the sum rule (14).We begin by rewriting the sum rule as a bound on G, by restricting the sum to the O(N) soft modes,
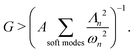 | (20) |
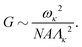 | (21) |
In order to evaluate G, we must determine Λκ2. Acting on eqn (11) from the left with 〈0,1|, solving for Λn2, and taking the thermodynamic limit gives
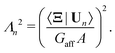 | (22) |
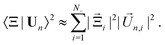 | (23) |
![[U with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0055_20d1.gif) n,i|2 is O(1/N×).¶
n,i|2 is O(1/N×).¶
The quantity 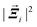 requires closer consideration. Recall that |Ξ〉 represents the force imbalance on each crosslink after an affine deformation of the network.|| Affine displacements do not bend fibers, so the forces they generate are only due to stretching. Let us consider a single fiber. Affine shear changes the length
requires closer consideration. Recall that |Ξ〉 represents the force imbalance on each crosslink after an affine deformation of the network.|| Affine displacements do not bend fibers, so the forces they generate are only due to stretching. Let us consider a single fiber. Affine shear changes the length ![[small script l]](https://www.rsc.org/images/entities/i_char_e146.gif) α of each segment by an amount δ
α of each segment by an amount δ![[small script l]](https://www.rsc.org/images/entities/i_char_e146.gif) 〈ij〉 = A(θ)γ
〈ij〉 = A(θ)γ![[small script l]](https://www.rsc.org/images/entities/i_char_e146.gif) α, where A(θ) is a prefactor that depends only on the orientation of the fiber and is therefore the same for all segments on the same fiber. The force in segment α is f〈ij〉 = μδ
α, where A(θ) is a prefactor that depends only on the orientation of the fiber and is therefore the same for all segments on the same fiber. The force in segment α is f〈ij〉 = μδ![[small script l]](https://www.rsc.org/images/entities/i_char_e146.gif) 〈ij〉/
〈ij〉/![[small script l]](https://www.rsc.org/images/entities/i_char_e146.gif) 〈ij〉 = μA(θ)γ. Note that the force is independent of the segment length
〈ij〉 = μA(θ)γ. Note that the force is independent of the segment length ![[small script l]](https://www.rsc.org/images/entities/i_char_e146.gif) 〈ij〉. As a result, affine shear induces an identical force in each segment of a fiber. The segments are co-linear prior to shearing, and therefore the net force on a crosslink vanishes unless the crosslink is at one of the two ends of a fiber (or is attached to a dangling end, if they have not been trimmed). In other words,
〈ij〉. As a result, affine shear induces an identical force in each segment of a fiber. The segments are co-linear prior to shearing, and therefore the net force on a crosslink vanishes unless the crosslink is at one of the two ends of a fiber (or is attached to a dangling end, if they have not been trimmed). In other words, 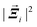 is zero on interior crosslinks and O(μ2) on terminal crosslinks. As there are O(N) terminal crosslinks, rather than O(N×), the sum in eqn (23) can be rewritten
is zero on interior crosslinks and O(μ2) on terminal crosslinks. As there are O(N) terminal crosslinks, rather than O(N×), the sum in eqn (23) can be rewritten
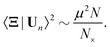 | (24) |
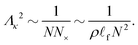 | (25) |
![[small script l]](https://www.rsc.org/images/entities/i_char_e146.gif) f. Inserting (25) in (21), we find
f. Inserting (25) in (21), we find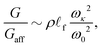 | (26) |
5 Discussion
We have demonstrated how soft modes determine the shear modulus of densely crosslinked Mikado networks in the bending-dominated regime. In so doing, we have resolved an apparent discrepancy in the literature between the predictions of floppy mode theory and independent measurements of the shear modulus. We find no reason to question the predictions of FMT regarding the scaling of the characteristic frequency ωκ in eqn (2). However, eqn (3) and the prediction that α = β, are not correct. As these relationships rely on the affine fiber approximation, the natural conclusion is that the AFA does not hold. Our results imply that the typical fiber displacement during shear is δx ∼ (ρ![[small script l]](https://www.rsc.org/images/entities/i_char_e146.gif) f)(α−β)/2
f)(α−β)/2![[small script l]](https://www.rsc.org/images/entities/i_char_e146.gif) fγ = (ρ
fγ = (ρ![[small script l]](https://www.rsc.org/images/entities/i_char_e146.gif) f)1/2
f)1/2![[small script l]](https://www.rsc.org/images/entities/i_char_e146.gif) fγ, which is much larger than the value
fγ, which is much larger than the value ![[small script l]](https://www.rsc.org/images/entities/i_char_e146.gif) fγ predicted by the AFA. We have been unable to find an intuitive explanation for this scaling relation.
fγ predicted by the AFA. We have been unable to find an intuitive explanation for this scaling relation.
It is natural to ask why the early work of Wilhelm and Frey yielded an estimate α ≈ 5.7 that is significantly smaller than subsequent estimates. In our opinion, this is because they fitted data for ρ > 15 to the form G/Gaff ∼ Δρα, where Δρ = ρ − ρc (recall ρc ≈ 5.7). While the difference between using ρ and Δρ in the scaling relation becomes negligible sufficiently far above the percolation threshold, fitting to a power law in Δρ gives systematically lower estimates of α. We have shown that FMT predicts that G scales as a power of ρ in the bending-dominated regime.
Our work has generated two additional insights into Mikado network mechanics. First, bending-dominated response correlates with the existence of a well-separated band of bending-dominated soft modes. We have shown that Mikado networks also possess stretching-dominated soft modes. The bending-dominated regime ends, and the gap between bending- and stretching-dominated modes closes, when the characteristic frequency of stretching-dominated soft modes, ωμ, becomes comparable to the bending-dominated soft mode frequency ωκ. The frequency ωμ is set by the network's proximity to the central-force isostatic state. Our results therefore indicate that the isostatic point plays a governing role in the bending- to stretching-dominated crossover in 2D Mikado networks. This is distinct from fiber networks in 3D, which can undergo a similar crossover while remaining well below the central force isostatic point.34
A second insight is that bending-dominated soft modes couple to shear in a non-trivial way. This coupling is encoded in the system-size dependence of Λκ2. Simple dimensional analysis reveals that Λκ2 must be inversely proportional to the square of an extensive quantity. We have shown that this squared extensive quantity is an admixture of the number of fibers and the number of crosslinks, Λκ2 ∼ 1/(NN×). This is a consequence of the co-linearity of crosslinks along a fiber. This prediction is corroborated by numerical studies in which the crosslink positions in the initial condition are gradually perturbed, which qualitatively changes the scaling of G with fiber line density.6
Our results suggest several directions for future work. In addition to elastic moduli, the density of states can be used to calculate linear response properties such as the storage and loss moduli,20 sound transmission,35 and thermal expansion coefficients.26 It can also predict the onset of nonlinear properties such as strain stiffening and shocks.27,36,37 Finally, a detailed understanding of structure–property relationships can facilitate the design of network architectures with tunable properties, such as moduli and failure onset.13,38–42
Conflicts of interest
There are no conflicts of interest to declare.Acknowledgements
It is a pleasure to acknowledge helpful discussions with Claus Heussinger. This work was supported financially by the Nederlandse Organisatie voor Wetenschappelijk Onderzoek (Netherlands Organization for Scientific Research, NWO), as well as by NWO Exacte Wetenschappen (Physical Sciences) through the use of supercomputer facilities.References
- J. Wilhelm and E. Frey, Phys. Rev. Lett., 2003, 91, 108103 Search PubMed.
- M. Latva-Kokko, J. Mäkinen and J. Timonen, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2001, 63, 046113 Search PubMed.
- D. A. Head, A. J. Levine and F. MacKintosh, Phys. Rev. Lett., 2003, 91, 108102 Search PubMed.
- D. Head, A. Levine and F. MacKintosh, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2003, 68, 061907 Search PubMed.
- C. Heussinger and E. Frey, Phys. Rev. Lett., 2006, 97, 105501 Search PubMed.
- C. Heussinger, B. Schaefer and E. Frey, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2007, 76, 031906 Search PubMed.
- A. Shahsavari and R. Picu, Int. J. Solids Struct., 2013, 50, 3332–3338 Search PubMed.
- M. F. Vermeulen, A. Bose, C. Storm and W. G. Ellenbroek, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2017, 96, 053003 Search PubMed.
- D. Zhou, L. Zhang and X. Mao, Phys. Rev. Lett., 2018, 120, 068003 Search PubMed.
- M. L. Gardel, F. Nakamura, J. H. Hartwig, J. C. Crocker, T. P. Stossel and D. A. Weitz, Proc. Natl. Acad. Sci. U. S. A., 2006, 103, 1762–1767 Search PubMed.
- G. Koenderink, M. Atakhorrami, F. MacKintosh and C. F. Schmidt, Phys. Rev. Lett., 2006, 96, 138307 Search PubMed.
- R. Tharmann, M. M. Claessens and A. R. Bausch, Phys. Rev. Lett., 2007, 98, 088103 Search PubMed.
- P. H. Kouwer, M. Koepf, V. A. Le Sage, M. Jaspers, A. M. Van Buul, Z. H. Eksteen-Akeroyd, T. Woltinge, E. Schwartz, H. J. Kitto and R. Hoogenboom, et al. , Nature, 2013, 493, 651–655 Search PubMed.
- C. Heussinger and E. Frey, Phys. Rev. Lett., 2006, 96, 017802 Search PubMed.
- D. Bi, J. Lopez, J. M. Schwarz and M. L. Manning, Nat. Phys., 2015, 11, 1074–1079 Search PubMed.
- D. M. Sussman and M. Merkel, Soft Matter, 2018, 14, 3397–3403 Search PubMed.
- D. J. Durian, Phys. Rev. Lett., 1995, 75, 4780–4783 Search PubMed.
- C. S. O'Hern, L. E. Silbert, A. J. Liu and S. R. Nagel, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2003, 68, 011306 Search PubMed.
- C. Heussinger and J.-L. Barrat, Phys. Rev. Lett., 2009, 102, 218303 Search PubMed.
- B. P. Tighe, Phys. Rev. Lett., 2011, 107, 158303 Search PubMed.
- K. Baumgarten and B. P. Tighe, Soft Matter, 2017, 13, 8368–8378 Search PubMed.
- D. J. Koeze, L. Hong, A. Kumar and B. P. Tighe, Phys. Rev. Res., 2020, 2, 032047 Search PubMed.
- B. P. Tighe, Phys. Rev. Lett., 2012, 109, 168303 Search PubMed.
- G. Düring, E. Lerner and M. Wyart, Soft Matter, 2013, 9, 146–154 Search PubMed.
- M. Yucht, M. Sheinman and C. Broedersz, Soft Matter, 2013, 9, 7000–7006 Search PubMed.
- C. Buss, C. Heussinger and O. Hallatschek, Soft Matter, 2016, 12, 7682–7687 Search PubMed.
- K. Baumgarten and B. P. Tighe, Phys. Rev. Lett., 2018, 120, 148004 Search PubMed.
- M. Merkel, K. Baumgarten, B. P. Tighe and M. L. Manning, Proc. Natl. Acad. Sci. U. S. A., 2019, 116, 6560–6568 Search PubMed.
- E. Huisman and T. C. Lubensky, Phys. Rev. Lett., 2011, 106, 088301 Search PubMed.
- S. Dagois-Bohy, B. P. Tighe, J. Simon, S. Henkes and M. van Hecke, Phys. Rev. Lett., 2012, 109, 095703 Search PubMed.
- M. Wyart, L. E. Silbert, S. R. Nagel and T. A. Witten, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2005, 72, 051306 Search PubMed.
- W. G. Ellenbroek, Z. Zeravcic, W. van Saarloos and M. van Hecke, EPL, 2009, 87, 34004 Search PubMed.
- L. Yan, E. DeGiuli and M. Wyart, Europhys. Lett., 2016, 114, 26003 Search PubMed.
- C. Broedersz, M. Sheinman and F. MacKintosh, Phys. Rev. Lett., 2012, 108, 078102 Search PubMed.
- K. Saitoh and H. Mizuno, 2020, arXiv: 2008.09760.
- S. Ulrich, N. Upadhyaya, B. van Opheusden and V. Vitelli, Proc. Natl. Acad. Sci. U. S. A., 2013, 110, 20929–20934 Search PubMed.
- R. Rens, C. Villarroel, G. Düring and E. Lerner, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2018, 98, 062411 Search PubMed.
- M. M. Driscoll, B. G.-g. Chen, T. H. Beuman, S. Ulrich, S. R. Nagel and V. Vitelli, Proc. Natl. Acad. Sci. U. S. A., 2016, 113, 10813–10817 Search PubMed.
- L. Zhang, D. Z. Rocklin, L. M. Sander and X. Mao, Phys. Rev. Mater., 2017, 1, 052602 Search PubMed.
- B. E. Vos, L. C. Liebrand, M. Vahabi, A. Biebricher, G. J. Wuite, E. J. Peterman, N. A. Kurniawan, F. C. MacKintosh and G. H. Koenderink, Soft Matter, 2017, 13, 8886–8893 Search PubMed.
- D. R. Reid, N. Pashine, J. M. Wozniak, H. M. Jaeger, A. J. Liu, S. R. Nagel and J. J. de Pablo, Proc. Natl. Acad. Sci. U. S. A., 2018, 201717442 Search PubMed.
- R. Rens and E. Lerner, Eur. Phys. J. E: Soft Matter Biol. Phys., 2019, 42, 1–11 Search PubMed.
Footnotes |
| † The scaling function (1) follows the discussion by Shahsavari and Picu.7 Other authors rescale their data differently, but still determine exponents that can be compared to α directly. Namely, α is equal to μ − 1 from ref. 1, and 2 + 2/z from ref. 3,4. |
‡ Our simulations access a narrower range in ρ![[small script l]](https://www.rsc.org/images/entities/i_char_e146.gif) f because, unlike prior work, we determine each network's eigenfrequencies, which is significantly more computationally expensive than calculating their shear moduli. f because, unlike prior work, we determine each network's eigenfrequencies, which is significantly more computationally expensive than calculating their shear moduli. |
| § The value Zc = 4 is the prediction of a mean field counting argument due to Maxwell. While not all random networks obey mean field counting, Mikado networks do. |
¶ Normalization guarantees |![[U with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0055_20d1.gif) n,i|2 ∼ O(1/N×), provided the mode is extended. As the floppy modes in freely bending Mikado networks are localized (motion is restricted to a central fiber and the secondary fibers with which it is crosslinked), one might worry that the soft modes are localized, as well. However, this is not the case. When the bending modulus is small but finite, the secondary fibers trigger motion in ternary fibers, and so forth. HF demonstrated that the axial displacements of the non-central fibers are of the same order of magnitude as the central fiber. n,i|2 ∼ O(1/N×), provided the mode is extended. As the floppy modes in freely bending Mikado networks are localized (motion is restricted to a central fiber and the secondary fibers with which it is crosslinked), one might worry that the soft modes are localized, as well. However, this is not the case. When the bending modulus is small but finite, the secondary fibers trigger motion in ternary fibers, and so forth. HF demonstrated that the axial displacements of the non-central fibers are of the same order of magnitude as the central fiber. |
| || It may seem odd that the force imbalance due to an affine shear plays a role in determining G in the bending regime, where deformations are strongly non-affine. This can be understood by thinking of shear as a two-step process. In the first step, the system is deformed affinely, which, due to disorder, generates force imbalances on nodes. In the second step, the nodes displace non-affinely to relieve these force imbalances. |
| This journal is © The Royal Society of Chemistry 2021 |