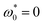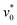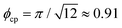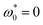Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Emergent vortices and phase separation in systems of chiral active particles with dipolar interactions
Guo-Jun
Liao
 * and
Sabine H. L.
Klapp
*
* and
Sabine H. L.
Klapp
*
Institut für Theoretische Physik, Technische Universität Berlin, Hardenbergstr. 36, D-10623 Berlin, Germany. E-mail: guo-jun.liao@campus.tu-berlin.de; klapp@physik.tu-berlin.de
First published on 25th June 2021
Abstract
Using Brownian dynamics (BD) simulations we investigate the self-organization of a monolayer of chiral active particles with dipolar interactions. Each particle is driven by both, translational and rotational self-propulsion, and carries a permanent point dipole moment at its center. The direction of the translational propulsion for each particle is chosen to be parallel to its dipole moment. Simulations are performed at high dipolar coupling strength and a density below that related to motility-induced phase separation in simple active Brownian particles. Despite this restriction, we observe a wealth of phenomena including formation of two types of vortices, phase separation, and flocking transitions. To understand the appearance and disappearance of vortices in the many-particle system, we further investigate the dynamics of simple ring structures under the impact of self-propulsion.
1 Introduction
Systems of self-propelled particles consist of a large number of motile constituents, each of which is capable of continuously converting energy from an internal source or the surroundings into mechanical motion.1,2 Examples of biological self-propelled particles can be found over a wide range of length and time scales, from bird flocks, fish schools, mammalian herds, and pedestrian crowds in our daily life, to bacteria, sperm cells, and microtubules at the microscale.3,4 Self-propelled particles can also be synthesized in the laboratory, famous examples including bimetallic nanorods,5,6 spherical Janus particles,7,8 and magnetic rollers.9–11 It is now well established that already relatively simple systems of self-propelled particles can display complex collective behavior, giving rise to a still increasing scientific interest.12 A prominent example of such complex behavior is motility-induced phase separation (MIPS), which occurs in systems of disk-shaped, active Brownian particles above a critical density Φcrit.13–17 Another “classical” example is the flocking transition in the Vicsek model,18 a system of self-propelled point-like particles with ferromagnetic interactions.The majority of theoretical and numerical studies on active particles assumes that each particle tends to “swim” along a straight line due to the translational self-propulsion. However, this assumption clearly becomes invalid once the chiral symmetry along the propelling direction is broken. Such broken symmetry often introduces a rotational self-propulsion, which, together with a translational self-propulsion, causes a single swimmer to move along a perfect circular path in the absence of thermal noise.19 Hence, active particles simultaneously subject to the rotational and translational self-propulsion are generally referred to as “chiral active particles,”4 or “circle swimmers.”20 Famous examples include E. coli cells close to a surface,21,22 FtsZ proteins,23–25 and synthetic L-shaped particle.26
Recent research has shown that chiral motion (i.e., circle swimming) can indeed significantly change the self-assembly dynamics in active systems. Already for the simplest models of chiral active particles, it has been shown analytically and numerically that circle swimming generally suppresses MIPS,27 induces clockwise vortices,28 and yields hyperuniform structures with vanishing long-wavelength (but large local) density fluctuations.29 Recent studies of circle swimmers with short-range anisotropic interactions have revealed even more intriguing features. For example, simulations have demonstrated that chiral active particles with an asymmetric24,30,31 or elongated32 shape display vortex structures. Chiral active particles with chemotactic alignment can form a global traveling wave.33 Further, chiral active particles with polar (i.e., ferromagnetic Heisenberg-like) interactions exhibit rotating macrodroplets,34,35 chimera states,36–38 chiral self-recognition,39 dynamical frustration,40 or a surface-population reversal effect in ring-shaped confinement.41 Additional effects can arise in the presence of a rotating magnetic field, where disk-shaped chiral active particles without anisotropic interactions can display chiral separation and polar ordering.42
In the present study, we go one step further and consider chiral active particles with dipole–dipole interactions. These interactions differ from the previously considered anisotropic ones by the longer range and by a more complicated angular dependency. That is, the pair interaction depends not only on the angle between the two involved dipole moments, but also on their spatial configuration which eventually promotes chain formation. To explore the role of these factors for the resulting collective behavior is interesting not only from an academic point of view. Rather, many microswimmers have embedded (permanent or induced) magnetic or electric dipole moments giving rise to dipole–dipole interactions, examples being metallodielectric Janus spheres,7,43 magnetotactic bacteria,44,45 and magnetic rollers.9–11 Therefore, the overall aim of this study is to enhance the understanding of the active matter systems involving circle swimming and dipole–dipole interactions.
To this end, we consider a two-dimensional system of chiral active particles with dipolar interactions, each of which moves at a self-propulsion speed (characterized by the particle motility) and rotates at an “active” angular speed. The (permanent) dipole moment embedded in each particle is assumed to be directed along the direction of translational self-propulsion. Our model combines features of non-dipolar, disk-shaped circle swimmers28 and dipolar active Brownian particles.46 Therefore, we refer to our model as dipolar circle swimmers in the rest of this paper. Based on Brownian dynamics simulations, we explore a wide range of the particle motility and the active angular speed at a large dipolar coupling strength and a low density.
As a unique feature of dipolar circle swimmers, we observe two types of vortices, which we refer to as Type I and Type II vortices. Type I vortices consist of forward-moving particles whose dipole moments display counterclockwise patterns, while Type II vortices are backward-moving particles whose dipole moments show clockwise structures. As the motility increases from zero, Type II vortices vanish, and the system exhibits significant phase separation with the dense domain characterized by giant Type I vortices. We show that some aspects of the vortex formation can be explained by considering the dynamics of simple ring structures. At even higher motilities, the system displays flocking patterns, in which dipolar circle swimmers self-assemble into polar clusters and show a significant global orientational order.
The rest of this paper is organized as follows. In Section 2 we describe our methods of investigation, including the model, the simulation setup, and the target quantities. An overview of the system behavior (at a fixed density) is given in Section 3.1. In Sections 3.2–3.5, we discuss specific aspects such as chain formation, clustering and phase separation, emergence of vortices, and orientational ordering. Finally, we summarize our findings and provide an outlook in Section 4.
2 Model and methods of investigation
Our model system of dipolar circle swimmers combines the previously investigated model of the dipolar active Brownian particles46 and the model of spherical circle swimmers.19,28,29,47–49 Therefore, various methods of investigation can be transferred from previous works. In the following, we summarize the main points and refer the reader for details to ref. 28 and 46.2.1 Model
We consider N disk-shaped Brownian particles with diameter σ dispersed in a monolayer in the xy-plane. Each of the particles carries a permanent point dipole moment μi located at its center. In addition, each particle is subject to a self-propulsion force F0êi (i = 1,…,N) and torque M0ẑ. The particle orientation êi denotes the direction of self-propulsion force and is assumed to be directed along the unit dipole moment![[small mu, Greek, circumflex]](https://www.rsc.org/images/entities/b_i_char_e0b3.gif) i at each instant of time, i.e., êi =
i at each instant of time, i.e., êi = ![[small mu, Greek, circumflex]](https://www.rsc.org/images/entities/b_i_char_e0b3.gif) i. The pairwise interaction potential for two swimmers i and j is given by
i. The pairwise interaction potential for two swimmers i and j is given by| upair(rij, μi, μj) = usr(rij) + udd(rij, μi, μj), | (1) |
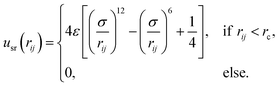 | (2) |
The second term on the right-hand side of eqn (1) represents the (long-range) dipole–dipole (dd) interaction, given by
 | (3) |
2.2 Equations of motion
To investigate the dynamical self-assembly of dipolar circle swimmers, we perform extensive Brownian dynamics (BD) simulations involving N particles in a squared box with side length L. The motion of the ith particle is described by the coupled Langevin equations in the overdamped limit,19| ṙi = βDt[F0êi −∇riUi + ξi(t)], | (4) |
![[small psi, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a5.gif) i = βDr[M0 − ∂ψiUi + Γi(t)], i = βDr[M0 − ∂ψiUi + Γi(t)], | (5) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ψi, sin
ψi, sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ψi). Focusing on ψi as the relevant angle, we implicitly assume that the dipole moment μi are oriented along in-plane directions (for justification, see Section 2.3). The dots above ri and ψi on the left-hand side of eqn (4) and (5) indicate time derivatives, and the potential energy for the ith particle Ui is the sum over all the pairwise potentials between particle i and all the other particles j, i.e.,
ψi). Focusing on ψi as the relevant angle, we implicitly assume that the dipole moment μi are oriented along in-plane directions (for justification, see Section 2.3). The dots above ri and ψi on the left-hand side of eqn (4) and (5) indicate time derivatives, and the potential energy for the ith particle Ui is the sum over all the pairwise potentials between particle i and all the other particles j, i.e.,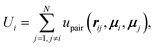 | (6) |
In eqn (4), Dt denotes the translational diffusion constant (we do not use the tensorial quantity due to the disk-like shape of the particles). Correspondingly, for the rotational motion, Dr describes the rotational diffusion constant. To account for the Brownian motion, the random force ξi(t) and torque Γi(t) are Gaussian white noises, which have zero means and are delta correlated, 〈ξi(t)〉 = 0, 〈Γi(t)〉 = 0,  , and
, and  . Here, the angle brackets 〈⋯〉 stand for ensemble average, and ⊗ denotes dyadic product. Finally, it is worth recalling the behavior of a single circle swimmer (without interacting with other swimmers). In the absence of thermal fluctuations and at M0 > 0, the swimmer moves along a closed circular path of radius R = DtF0/(DrM0) and rotates counterclockwise at a self-propulsion speed v0 = βDtF0 and angular speed ω0 = βDrM0.19
. Here, the angle brackets 〈⋯〉 stand for ensemble average, and ⊗ denotes dyadic product. Finally, it is worth recalling the behavior of a single circle swimmer (without interacting with other swimmers). In the absence of thermal fluctuations and at M0 > 0, the swimmer moves along a closed circular path of radius R = DtF0/(DrM0) and rotates counterclockwise at a self-propulsion speed v0 = βDtF0 and angular speed ω0 = βDrM0.19
2.3 Parameter choice
Following ref. 46, we choose the strength of steric repulsion as ε* = 10 and Dr = 2.57914Dt/σ2. The dipolar coupling strength is set to λ = 10, such that the dipolar pair energy of two particles at contact is ten times the thermal energy. To model chain formation and orientational ordering in dipolar colloids, one typically considers dipolar coupling strengths between λ ≈ 1 and λ ≈ 10.51–53 However, test simulations of the present model with λ varying from 0 to 10 show that vortices (which will be discussed in Section 3.4) only appear once λ ≈ 10. A further increase of λ > 10 requires even smaller time steps δt, which, together with the long-range feature of dipole–dipole interactions, makes the simulations even more computationally expensive. Therefore, in the present work the dipolar coupling strength is fixed to λ = 10. For passive monolayers of such strongly coupled dipolar particles, it is well known that there is a pronounced tendency to orient along in-plane directions; specifically, one observes self-assembly into chains and rings,54–58 or dense planar ordered states.54,59–61 Therefore, we here assume beforehand that the dipole moment μi lies in the xy-plane, i.e., the z-component is neglected. Based on this assumption, a two-dimensional Ewald summation is employed to deal with the long-range feature of dipole–dipole interactions, as outlined in the Appendix of ref. 46.
Eqn (4) and (5) are solved numerically via the Euler–Maruyama method62 with a discrete time step δt = 2 × 10−5τ, where τ = σ2/Dt denotes the Brownian diffusive time. We define the particle diameter σ, the thermal energy kBT, and the Brownian diffusive time τ as the units of length, energy, and time, respectively. All physical quantities in the system are then expressed in the units based on the dimensional combination of these three basic units. Consistent with our earlier work,28 the impact of the translational and rotational self-propulsion with respect to the thermal noise is represented by the dimensionless motility  and the active angular speed
and the active angular speed 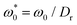 . Moreover, we set the particle number to N = 1156, unless otherwise stated. The sizes of the present simulations are limited to the order of 103 particles, due to the expensive computational cost resulting from the long-range feature of dipole–dipole interactions and the necessity of using small time step δt = 2 × 10−5τ for simulating active particles with strong steric repulsion (ε* = 10).
. Moreover, we set the particle number to N = 1156, unless otherwise stated. The sizes of the present simulations are limited to the order of 103 particles, due to the expensive computational cost resulting from the long-range feature of dipole–dipole interactions and the necessity of using small time step δt = 2 × 10−5τ for simulating active particles with strong steric repulsion (ε* = 10).
As the initial configuration for all simulations, we distribute particles on a square lattice and assign a random orientation to each of them. For reaching a steady state, we typically wait at least 5 × 105 steps. Then, we start to measure the statistical properties (see Section 2.4) every 500 steps and collect at least 1000 samples for each realization.
Our main focus of this study is on the pattern formation of dipolar circle swimmers in the regime of low densities. Specifically, the mean area fraction is chosen to be Φ = Nπσeff2/(4L2) = 0.23, where the effective hard disk diameter is given by σeff ≈ 1.07851σ (see ref. 46 for details). We note that the density considered here is below the critical density of motility-induced phase separation (MIPS), Φcrit, in purely repulsive systems, which is in the range 0.28 ≲ Φcrit ≲ 0.4.63,64 In other words, at Φ = 0.23 and in the absence of dipole–dipole interactions, MIPS does not occur even at extremely high motilities  .
.
2.4 Observables
In this section we discuss the relevant observables and their numerical analysis (more details can be found in ref. 28 and 46). ,
,  , and λ = 0) at Φ = 0.23. Further, for the present system of dipolar circle swimmers, the location of the first peak and the first valley do not vary too much upon variation of
, and λ = 0) at Φ = 0.23. Further, for the present system of dipolar circle swimmers, the location of the first peak and the first valley do not vary too much upon variation of 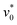 and
and  . Therefore, we fix rL = 1.2σ throughout this work for simplicity.
. Therefore, we fix rL = 1.2σ throughout this work for simplicity.
The percolated dipolar networks may break, e.g., upon an increase of temperature.68 In this case, the system may display a “string” fluid state with many “polymerized” chains, which are composed of dipolar spheres connecting with their neighbors in a head-to-tail fashion. In self-assembly studies of dipolar systems, these chain structures are commonly quantified by the degree of “polymerization,”46,64,68,76
| ϕp = 〈Np〉/N. | (7) |
We note that the above definition of a chain cannot distinguish between an elongated chain and a compact disk-shaped cluster with local head-to-tail ordering. This problem cannot be solved by adding more complex criteria to the definition of clusters (as ref. 46 does), i.e., μi·μj > 0 and (μi·rij)(μj·rij) > 0, since head-to-tail ordering is present in all types of aggregates. The degree of polymerization ϕp defined in eqn (7) approaches unity if all particles self-assemble into string-like chains or disk-shaped clusters, and is zero if there is no chain structure. We consider the system to display a state with polymerized string fluids if ϕp > 0.5, and no giant disk-shaped clusters (to be discussed later) are present.
| ϕc = 〈n1c〉/N, | (8) |
Finally, to identify phase separation, we employ a Voronoi tessellation to obtain the probability distribution function P(ϕ) of the local area fraction ϕ without a short-time average (see ref. 46 for details). The system is regarded to display phase separation if the density profile P(ϕ) shows a double-peak structure. Subsequently, the coexisting densities are the density values corresponding to the peaks.
![[small mu, Greek, circumflex]](https://www.rsc.org/images/entities/b_i_char_e0b3.gif) i = êi),
i = êi),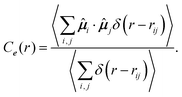 | (9) |
![[small mu, Greek, circumflex]](https://www.rsc.org/images/entities/b_i_char_e0b3.gif) i·
i·![[small mu, Greek, circumflex]](https://www.rsc.org/images/entities/b_i_char_e0b3.gif) j =
j = ![[small mu, Greek, circumflex]](https://www.rsc.org/images/entities/b_i_char_e0b3.gif) i·
i·![[small mu, Greek, circumflex]](https://www.rsc.org/images/entities/b_i_char_e0b3.gif) i = 1. Since particles do not overlap, we have rij > 0 for i ≠ j. Thus, we obtain Ce(r = 0) = 1. If particle i and j are infinitely far apart (rij → +∞), we assume that their average orientational correlation is very weak and is thus approximately zero at the given low density. Since Ce(0) = 1 and limr→+∞Ce(r) ≈ 0, a negative correlation at a finite distance r represents that particle orientations (i.e., propulsion directions) on average point in the opposite directions when separated by the distance r. Hence, the system is regarded to self-assemble into vortex structures if Ce(r) shows negative values at finite distances. The distance corresponding to the minimum of Ce(r) can be used to characterize the average diameter of vortices de, defined by
i = 1. Since particles do not overlap, we have rij > 0 for i ≠ j. Thus, we obtain Ce(r = 0) = 1. If particle i and j are infinitely far apart (rij → +∞), we assume that their average orientational correlation is very weak and is thus approximately zero at the given low density. Since Ce(0) = 1 and limr→+∞Ce(r) ≈ 0, a negative correlation at a finite distance r represents that particle orientations (i.e., propulsion directions) on average point in the opposite directions when separated by the distance r. Hence, the system is regarded to self-assemble into vortex structures if Ce(r) shows negative values at finite distances. The distance corresponding to the minimum of Ce(r) can be used to characterize the average diameter of vortices de, defined by | (10) |
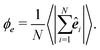 | (11) |
Depending on the length scale of polar clusters with respect to the particle number N, the flocking states can be further classified into micro- and macro-flocking states. To this end, we follow the treatment in ref. 46 and measure the distribution function of the cluster size P(n), which is the probability that a randomly selected cluster is composed of n particles. In the case of macro-flocking, the system is usually composed of several large polar clusters with many small polar clusters, such that P(n) is extremely small at large n. To solve this problem, we consider the weighted distribution function nP(n), whose value is proportional to the probability that a randomly selected particle belongs to a chain with a size n. We identify the swimmers are in a micro-flocking state if ϕe > 0.5 and the characteristic cluster size in the weighted distribution function nP(n) does not scale with the particle number N. In contrast, the dipolar circle swimmers display a macro-flocking state if ϕe > 0.5 and the size of the giant clusters corresponding to the peak structure in nP(n) scales with N.
3 Results and discussion
In this section we present results from extensive BD simulations for a wide range of motilities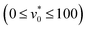 and angular speeds
and angular speeds  at a fixed area fraction Φ = 0.23 and dipolar coupling strength λ = 10. In the subsequent Section 3.1, we first give an overview of the observed states, and then discuss in Sections 3.3–3.5 various aspects in detail.
at a fixed area fraction Φ = 0.23 and dipolar coupling strength λ = 10. In the subsequent Section 3.1, we first give an overview of the observed states, and then discuss in Sections 3.3–3.5 various aspects in detail.
3.1 Non-equilibrium state diagram
Based on the targeted quantities described in Section 2.4, we have identified six states whose characteristics are summarized in Table 1. The resulting non-equilibrium state diagram spanned in the plane is shown in Fig. 1, and representative simulation snapshots are given in Fig. 2.
plane is shown in Fig. 1, and representative simulation snapshots are given in Fig. 2.
| State | Chain formation | Clustering, phase separation and emergent vortices | Orientational ordering |
|---|---|---|---|
| Percolated networks | Π > 0.5, ϕp > 0.5 | d e < 3 | ϕ e ≤ 0.5 |
| Chain-like structures | Π ≤ 0.5, ϕp > 0.5 | d e < 3 | ϕ e ≤ 0.5 |
| Finite-size vortices | — | d e ≥ 3, single peak in P(ϕ) | ϕ e ≤ 0.5 |
| Vortices with phase separation | — | d e ≥ 3, double peaks in P(ϕ) | ϕ e ≤ 0.5 |
| Micro-flocking | — | Monotonic decay of nP(n) | ϕ e > 0.5 |
| Macro-flocking | — | Broad shoulder or a peak in nP(n) at large n | ϕ e > 0.5 |
 | ||
Fig. 1 State diagram in the plane spanned by the motility  and angular speed and angular speed  at Φ = 0.23. The position of the symbols on the diagram indicates the parameter combinations used in simulations. We have observed percolated networks (PN, black circles), string fluids (SF, blue crosses), finite-size vortices (FV, red open squares), vortices with phase separation (VPS, red filled squares), micro-flocking (mF, green triangles), and macro-flocking (MF, orange diamonds), for details of this classification see Table 1. Overlapping symbols denote bistable states. The region surrounded by the dashed lines indicates a parameter regime where the system is percolated. at Φ = 0.23. The position of the symbols on the diagram indicates the parameter combinations used in simulations. We have observed percolated networks (PN, black circles), string fluids (SF, blue crosses), finite-size vortices (FV, red open squares), vortices with phase separation (VPS, red filled squares), micro-flocking (mF, green triangles), and macro-flocking (MF, orange diamonds), for details of this classification see Table 1. Overlapping symbols denote bistable states. The region surrounded by the dashed lines indicates a parameter regime where the system is percolated. | ||
In the passive limit  , the system displays percolated networks [see Fig. 2(g)], which is in agreement with simulation studies for a monolayer of passive dipolar spheres.55,56 For a finite motility
, the system displays percolated networks [see Fig. 2(g)], which is in agreement with simulation studies for a monolayer of passive dipolar spheres.55,56 For a finite motility  and in the limit of linear swimmers
and in the limit of linear swimmers  , our model reduces to the model of dipolar active Brownian particles.46 Upon increasing
, our model reduces to the model of dipolar active Brownian particles.46 Upon increasing  this system undergoes a transition from a string fluid state characterized by chain-like structures [see Fig. 2(d)] into a micro-flocking state with finite-size polar clusters [see Fig. 2(a)].
this system undergoes a transition from a string fluid state characterized by chain-like structures [see Fig. 2(d)] into a micro-flocking state with finite-size polar clusters [see Fig. 2(a)].
Novel behavior emerges as the angular speed 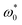 becomes non-zero. At vanishing motility
becomes non-zero. At vanishing motility  , a slight increase in
, a slight increase in  from zero leads to the emergence of two types of vortex patterns, which will be discussed in detail in Section 3.4. As a “side effect” of the vortex formation, phase separation occurs at angular speeds
from zero leads to the emergence of two types of vortex patterns, which will be discussed in detail in Section 3.4. As a “side effect” of the vortex formation, phase separation occurs at angular speeds  [see Fig. 2(h)]. A further increase in
[see Fig. 2(h)]. A further increase in  renders the vortex patterns less pronounced, suppresses the phase separation, and breaks the percolated structures, as shown in Fig. 2(i).
renders the vortex patterns less pronounced, suppresses the phase separation, and breaks the percolated structures, as shown in Fig. 2(i).
Considering a finite motility of  , the swimmers exhibit a string fluid state at small angular speeds
, the swimmers exhibit a string fluid state at small angular speeds  , while intermediate and fast rotation
, while intermediate and fast rotation  induce the formation of vortices combined with phase separation, whose sizes decrease with increasing
induce the formation of vortices combined with phase separation, whose sizes decrease with increasing  [see Fig. 2(e and f)].
[see Fig. 2(e and f)].
Finally, at high motilities  and slow rotation
and slow rotation  , the chain-like structures observed at low motilities break; instead, the system displays a micro-flocking state [see Fig. 2(a and b)]. At intermediate angular speeds
, the chain-like structures observed at low motilities break; instead, the system displays a micro-flocking state [see Fig. 2(a and b)]. At intermediate angular speeds  , the dipolar circle swimmers self-assemble into vortices with accompanying phase separation. Here we note that the parameter window of the angular speed
, the dipolar circle swimmers self-assemble into vortices with accompanying phase separation. Here we note that the parameter window of the angular speed  for the vortex formation is narrower than the low motility case
for the vortex formation is narrower than the low motility case  . For fast rotation such as
. For fast rotation such as  , the system exhibits a macro-flocking state, where the sizes of flocking patterns are comparable to the simulation box [see Fig. 2(c)]. Interestingly, we also observe bistable states involving vortices and macro-flocking at
, the system exhibits a macro-flocking state, where the sizes of flocking patterns are comparable to the simulation box [see Fig. 2(c)]. Interestingly, we also observe bistable states involving vortices and macro-flocking at 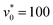 and
and  . This bistability will be further discussed in Section 3.3.
. This bistability will be further discussed in Section 3.3.
3.2 Chain formation
We start our detailed discussion of the system's behavior by focusing on the bottom left part of the state diagram in Fig. 1, where the key phenomenon is chain formation. We begin by investigating the percolation probability Π and the degree of polymerization ϕp defined in Section 2.4.1. Fig. 3(a) shows the percolation probability Π as a function of the motility for various angular speeds
for various angular speeds  . At
. At  and
and  , Π approaches unity, which corresponds to the percolated networks well known for the passive case.65 Upon an increase of
, Π approaches unity, which corresponds to the percolated networks well known for the passive case.65 Upon an increase of 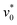 from zero at zero angular speed
from zero at zero angular speed  , Π quickly decays and reaches a value close to zero when
, Π quickly decays and reaches a value close to zero when  . The corresponding snapshot is shown in Fig. 2(d).† For finite (fixed) values of
. The corresponding snapshot is shown in Fig. 2(d).† For finite (fixed) values of  , Π decreases more drastically with
, Π decreases more drastically with 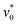 , and this decrease becomes the more pronounced the larger
, and this decrease becomes the more pronounced the larger  is. This suggests that both, the motility and the active rotation, tend to suppress the percolation behavior (relative to the passive case).
is. This suggests that both, the motility and the active rotation, tend to suppress the percolation behavior (relative to the passive case).
 | ||
Fig. 3 (a) Percolation probability Π and (b) degree of polymerization ϕp as a function of the motility  for angular speed for angular speed  (black circles), 1 (red squares), 2 (green diamonds), 4 (blue triangles up), and 10 (orange triangles down). The dashed horizontal line in each figure marks the values Π = 0.5 (a) and ϕp = 0.5 (b). Above this line, the system is percolated or polymerized, respectively (see Table 1). The solid lines are guides to the eye. (black circles), 1 (red squares), 2 (green diamonds), 4 (blue triangles up), and 10 (orange triangles down). The dashed horizontal line in each figure marks the values Π = 0.5 (a) and ϕp = 0.5 (b). Above this line, the system is percolated or polymerized, respectively (see Table 1). The solid lines are guides to the eye. | ||
Once Π has dropped to values below 0.5, the percolated networks have dissolved, yielding a fluid state with chains that do not span over the simulation box. To quantify these chain structures, we calculate the degree of “polymerization” ϕp defined in eqn (7). We recall that ϕp alone cannot distinguish long string-like chains and compact disk-shaped clusters. To avoid possible confusion, in the following we only present the results for ϕp when indeed chain structures are formed. Results plotted in Fig. 3(b) show that, indeed, the polymerization ϕp is close to unity at zero motility and gradually decreases as  increases. Once
increases. Once  , the chain structures essentially disappear. We also find that the degree of polymerization ϕp is essentially unaffected by rotation for the small values of
, the chain structures essentially disappear. We also find that the degree of polymerization ϕp is essentially unaffected by rotation for the small values of  considered here
considered here 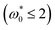 . The observed decrease of ϕp at small
. The observed decrease of ϕp at small  (and Φ = 0.23) is, qualitatively, in a good agreement with earlier studies of dipolar active particles, where
(and Φ = 0.23) is, qualitatively, in a good agreement with earlier studies of dipolar active particles, where  .46 Once
.46 Once  , the dipolar circle swimmers may self-assemble into patterns distinct from chain structures, such as compact clusters, which we will discuss in the following sections.
, the dipolar circle swimmers may self-assemble into patterns distinct from chain structures, such as compact clusters, which we will discuss in the following sections.
3.3 Clustering and phase separation
It is well established that non-dipolar active Brownian particles can exhibit clustering and even phase separation at sufficiently large motilities (and appropriate densities).14,16,28,74,78 In the absence of active rotation or alignment interactions,14–16,78 the clustering behavior is purely induced by the interplay between the particle motility and the steric repulsion.To quantify the clustering behavior in the present system, we first calculate the fraction of the largest cluster ϕc, see eqn (8) and Fig. 4. In the passive limit ( and
and  ), one finds ϕc ≈ 1. This is due to the large value of λ, which leads to strong head–tail-alignment and thus, to the formation of percolated networks, with percolation probability Π ≈ 1 [see Fig. 2(g) and 3(a)]. Upon an increase of
), one finds ϕc ≈ 1. This is due to the large value of λ, which leads to strong head–tail-alignment and thus, to the formation of percolated networks, with percolation probability Π ≈ 1 [see Fig. 2(g) and 3(a)]. Upon an increase of  from zero at
from zero at  , the order parameter ϕc decreases (as does Π), indicating that the percolated networks are suppressed by the active rotation. This seems plausible, since the active rotation tends to destroy the head-to-tail alignment. This leads to a breaking of percolated chains and, hence, a decrease of ϕc.
, the order parameter ϕc decreases (as does Π), indicating that the percolated networks are suppressed by the active rotation. This seems plausible, since the active rotation tends to destroy the head-to-tail alignment. This leads to a breaking of percolated chains and, hence, a decrease of ϕc.
At finite  the situation changes. Inspecting Fig. 3(a) again, we see that at
the situation changes. Inspecting Fig. 3(a) again, we see that at 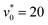 , the system is only partially percolated (with
, the system is only partially percolated (with  ) for
) for  , and if
, and if 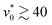 , the system is not percolated at all (with Π ≈ 0) for all explored
, the system is not percolated at all (with Π ≈ 0) for all explored  . We infer from the data that for
. We infer from the data that for 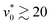 , the values of ϕc > 0.5 seen in Fig. 4 truly indicate the formation of giant compact clusters, rather than that of percolated networks. We also find from Fig. 4 that for
, the values of ϕc > 0.5 seen in Fig. 4 truly indicate the formation of giant compact clusters, rather than that of percolated networks. We also find from Fig. 4 that for  , ϕc varies non-monotonically with
, ϕc varies non-monotonically with  . We interpret this interesting observation such that giant clusters only appear at intermediate angular speeds
. We interpret this interesting observation such that giant clusters only appear at intermediate angular speeds 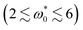 , whereas the system is rather homogeneous (ϕc ≤ 0.5) for slow and fast rotation. Further, with increasing motilities
, whereas the system is rather homogeneous (ϕc ≤ 0.5) for slow and fast rotation. Further, with increasing motilities 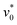 , the window of
, the window of  values corresponding to giant clusters is shifted toward larger
values corresponding to giant clusters is shifted toward larger  . We conclude that at finite
. We conclude that at finite  , the motility tends to suppress (rather than enhance) the formation of giant clusters.
, the motility tends to suppress (rather than enhance) the formation of giant clusters.
A particularly complex situation occurs at very high motilities. For example, at  we observed that the system of dipolar circle swimmers can change within a single simulation from one state with ϕc ≈ 1 (indicating giant clusters) to another state with ϕc ≲ 0.5, or the other way around (snapshots not shown here). To check whether both of these states are steady states, we created multiple long-time realizations at
we observed that the system of dipolar circle swimmers can change within a single simulation from one state with ϕc ≈ 1 (indicating giant clusters) to another state with ϕc ≲ 0.5, or the other way around (snapshots not shown here). To check whether both of these states are steady states, we created multiple long-time realizations at  and various
and various 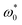 . Indeed, two different steady-state results were found from independent simulation realizations in the range
. Indeed, two different steady-state results were found from independent simulation realizations in the range  , indicating a bistability. Specifically, the realizations with ϕc ≈ 1 are characterized by giant clusters, while those with ϕc ≲ 0.5 correspond to a macro-flocking state, where macroscopic swarming is observed. The flocking behavior of dipolar circle swimmers will be discussed later in detail in Section 3.5.
, indicating a bistability. Specifically, the realizations with ϕc ≈ 1 are characterized by giant clusters, while those with ϕc ≲ 0.5 correspond to a macro-flocking state, where macroscopic swarming is observed. The flocking behavior of dipolar circle swimmers will be discussed later in detail in Section 3.5.
Given the formation of giant clusters at suitable combinations of  and
and  , it is interesting to explore whether this leads to phase separation. To this end, we plot in Fig. 5 the probability distribution function P(ϕ) of the local area fraction ϕ for various angular speeds
, it is interesting to explore whether this leads to phase separation. To this end, we plot in Fig. 5 the probability distribution function P(ϕ) of the local area fraction ϕ for various angular speeds  , taking the motility
, taking the motility  as an example. Phase separation is indicated by a double-peak structure of P(ϕ), where the coexisting densities are the density values corresponding to the peaks. From Fig. 5 we see that at zero and small angular speeds
as an example. Phase separation is indicated by a double-peak structure of P(ϕ), where the coexisting densities are the density values corresponding to the peaks. From Fig. 5 we see that at zero and small angular speeds 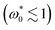 , the distribution function displays only a single peak located at ϕ ≈ 0.1, indicating that the system is essentially homogeneous. It is noted that at
, the distribution function displays only a single peak located at ϕ ≈ 0.1, indicating that the system is essentially homogeneous. It is noted that at  and
and  , the system exhibits a state with string fluids (see Fig. 1), i.e., particles tend to form short linear chains. As a result, the distribution function is not symmetric and shows a pronounced tail at high densities. In contrast, at intermediate angular speeds
, the system exhibits a state with string fluids (see Fig. 1), i.e., particles tend to form short linear chains. As a result, the distribution function is not symmetric and shows a pronounced tail at high densities. In contrast, at intermediate angular speeds 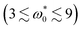 , we observe that P(ϕ) exhibits two well-defined peaks, showing that the dipolar circle swimmers phase-separate into dilute and dense domains. Finally, at a large angular speed
, we observe that P(ϕ) exhibits two well-defined peaks, showing that the dipolar circle swimmers phase-separate into dilute and dense domains. Finally, at a large angular speed 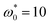 , the second maximum at high densities is only weakly pronounced, indicating that the dense domains almost disappear. Therefore, we expect that phase separation will eventually vanish upon further increase of
, the second maximum at high densities is only weakly pronounced, indicating that the dense domains almost disappear. Therefore, we expect that phase separation will eventually vanish upon further increase of  .
.
Finally, we plot in Fig. 6 the coexistence densities in the ( , ϕ) plane for various angular speeds
, ϕ) plane for various angular speeds  . At an intermediate angular speed
. At an intermediate angular speed  , the system displays phase separation for a broad range of the motility,
, the system displays phase separation for a broad range of the motility, 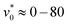 . Further, the density difference, Δϕ = ϕd − ϕg, between the dense and the gas-like region first increases with
. Further, the density difference, Δϕ = ϕd − ϕg, between the dense and the gas-like region first increases with  from zero to 20, and then decreases upon further increasing
from zero to 20, and then decreases upon further increasing 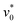 from 20 to 80. This non-monotonic behavior of Δϕ may be attributed to the fact that the parameter regime for
from 20 to 80. This non-monotonic behavior of Δϕ may be attributed to the fact that the parameter regime for  and
and 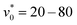 is very close to the state boundary between string fluids and vortices with phase separation (see Fig. 1). As
is very close to the state boundary between string fluids and vortices with phase separation (see Fig. 1). As  increases from 3 to 5, the motility range where phase separation occurs is shifted toward larger motilities
increases from 3 to 5, the motility range where phase separation occurs is shifted toward larger motilities  with Δϕ increasing monotonically with
with Δϕ increasing monotonically with 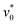 . At large angular speeds such as
. At large angular speeds such as 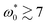 , the range of the motility shrinks to
, the range of the motility shrinks to  . Moreover, the area enclosed by the curves of coexisting densities decreases with
. Moreover, the area enclosed by the curves of coexisting densities decreases with  , suggesting that phase separation is in general suppressed by
, suggesting that phase separation is in general suppressed by  . The suppression of phase separation is also consistent with the vanishing peak of P(ϕ) at high densities for ω0 = 10 in Fig. 5. Indeed, at extremely large
. The suppression of phase separation is also consistent with the vanishing peak of P(ϕ) at high densities for ω0 = 10 in Fig. 5. Indeed, at extremely large  each of the particles tends to swim along a small circular path. Thus, it quickly alters its propulsion direction, causing the large dense domain to “melt” and break into small pieces. Similar observations regarding the impact of
each of the particles tends to swim along a small circular path. Thus, it quickly alters its propulsion direction, causing the large dense domain to “melt” and break into small pieces. Similar observations regarding the impact of  on phase separation have been made for systems of non-dipolar circle swimmers.28
on phase separation have been made for systems of non-dipolar circle swimmers.28
3.4 Emergent vortices
In this section we explore in detail an intriguing “byproduct” of the phase separation discussed in Section 3.3, namely, the formation vortices occupying the dense domain [for an illustration, see Fig. 2(e)].![[small mu, Greek, circumflex]](https://www.rsc.org/images/entities/b_i_char_e0b3.gif) i by a parameter gi(t), defined as
i by a parameter gi(t), defined as| gi(t) = vi,s(t)·êi(t), | (12) |
 | (13) |
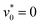 and Δts = 0.01τ for
and Δts = 0.01τ for  .
.
 | ||
Fig. 7 Representative simulation snapshots at  and three values of the motility. Each of the disk-shaped particles is represented by an arrow indicating the particle orientation êi. For better visual quality, all arrows are scaled by a factor of 3 and are formatted with red (blue) color if the particle moves against (along) its own orientation [see eqn (12)]. The blue arrows display type I vortices (a–c), and the red arrows exhibit type II vortices (a). and three values of the motility. Each of the disk-shaped particles is represented by an arrow indicating the particle orientation êi. For better visual quality, all arrows are scaled by a factor of 3 and are formatted with red (blue) color if the particle moves against (along) its own orientation [see eqn (12)]. The blue arrows display type I vortices (a–c), and the red arrows exhibit type II vortices (a). | ||
All color-coded snapshots in Fig. 7 refer to  . At zero motility
. At zero motility  , the particles have no tendency to move along their orientation. Therefore, the numbers of particles moving forward (blue) and backward (red) are on average equal, consistent with Fig. 7(a). A surprising result, however, is that forward- and backward-moving particles aggregate with particles displaying the same kind of motion, yielding vortices. In each instant of time, the chirality of the vortex structure formed by the forward-moving particles is counterclockwise, which we refer to as Type I vortices. In contrast, the chiral structure of the backward-moving particles is clockwise (Type II vortex). We note, however, that since the intrinsic active rotation drives each of the particles to rotate counterclockwise (see Section 2.2), the direction of overall rotation for both, Type I and Type II vortices, is counterclockwise. The detailed discussion about the physical origin of the emergent Type I and Type II vortices is postponed to Section 3.4.2.
, the particles have no tendency to move along their orientation. Therefore, the numbers of particles moving forward (blue) and backward (red) are on average equal, consistent with Fig. 7(a). A surprising result, however, is that forward- and backward-moving particles aggregate with particles displaying the same kind of motion, yielding vortices. In each instant of time, the chirality of the vortex structure formed by the forward-moving particles is counterclockwise, which we refer to as Type I vortices. In contrast, the chiral structure of the backward-moving particles is clockwise (Type II vortex). We note, however, that since the intrinsic active rotation drives each of the particles to rotate counterclockwise (see Section 2.2), the direction of overall rotation for both, Type I and Type II vortices, is counterclockwise. The detailed discussion about the physical origin of the emergent Type I and Type II vortices is postponed to Section 3.4.2.
Once the motility becomes non-zero, the particles tend to self-propel along their orientation (instantaneous) orientation. We thus expect that values of gi > 0 become more and more relevant. Indeed, as seen from Fig. 7(b), we only observe forward-moving swimmers which are represented by blue arrows as  increases from zero to 40. Comparing Fig. 7(a and b), we further see that the vortex size significantly increases with
increases from zero to 40. Comparing Fig. 7(a and b), we further see that the vortex size significantly increases with  .
.
At an even higher motility [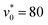 , see Fig. 7(c)], the disk-shaped vortex structures seen at lower motilities are slightly distorted and have a hole in the vortex center. To understand this, we recall that an isolated circle swimmer moves along a circular path with a radius R = v0/ω0.19 Thus, R increases with v0. This ideal motion, however, is disturbed by the presence of other swimmers, which makes it increasingly difficult to stay in the center of a giant vortex when R becomes larger. This eventually leads to a hole in the vortex center.
, see Fig. 7(c)], the disk-shaped vortex structures seen at lower motilities are slightly distorted and have a hole in the vortex center. To understand this, we recall that an isolated circle swimmer moves along a circular path with a radius R = v0/ω0.19 Thus, R increases with v0. This ideal motion, however, is disturbed by the presence of other swimmers, which makes it increasingly difficult to stay in the center of a giant vortex when R becomes larger. This eventually leads to a hole in the vortex center.
Further information on the vortex structure and size is provided by the orientational correlation function Ce(r), whose detailed analysis is presented in Appendix A. Here, we focus on the vortex diameter de, which is obtained from the minimum of Ce(r) (see Section 2.4.3). Fig. 8 shows de as a function of the angular speed  for various motilities
for various motilities  . Upon an increase of
. Upon an increase of  , the range of
, the range of  where vortices appear is narrowed. For all explored motilities, de generally decreases with the angular speed
where vortices appear is narrowed. For all explored motilities, de generally decreases with the angular speed  , and the curves are shifted toward a larger de as
, and the curves are shifted toward a larger de as  increases. Specifically, we observe a power law decay with an exponent ν ≈ −2 for
increases. Specifically, we observe a power law decay with an exponent ν ≈ −2 for  . This exponent is different from that observed in studies of the rotating Vicsek model (and variants) where ν = −1.34,35
. This exponent is different from that observed in studies of the rotating Vicsek model (and variants) where ν = −1.34,35
Finally, at a fixed motility such as  and upon an increase of the angular speed from
and upon an increase of the angular speed from  to
to  , the system undergoes a transition from a state with short linear chains (i.e., string fluids) to a state with giant vortices, as shown in Fig. 2(d and e). Here we identify the transition by a drastic increase of ϕc (see Fig. 4), and by the appearance of negative orientational correlations [see Fig. 12(b)]. Clearly, it would be very interesting to see whether this non-equilibrium transition is/resembles a first-order or continuous transition. However, such a study would require more extensive simulations and a full analysis of the order parameters, which is out of scope for the present paper.
, the system undergoes a transition from a state with short linear chains (i.e., string fluids) to a state with giant vortices, as shown in Fig. 2(d and e). Here we identify the transition by a drastic increase of ϕc (see Fig. 4), and by the appearance of negative orientational correlations [see Fig. 12(b)]. Clearly, it would be very interesting to see whether this non-equilibrium transition is/resembles a first-order or continuous transition. However, such a study would require more extensive simulations and a full analysis of the order parameters, which is out of scope for the present paper.
 , test simulations of a simplified double-chain structure to investigate the impact of the motility
, test simulations of a simplified double-chain structure to investigate the impact of the motility  . As an initial configuration, Nt dipolar particles are arranged into two anti-parallel chains lying side by side, see Fig. 9(a and c). Within each chain, the dipole moments are oriented head-to-tail. As illustrated in Fig. 9(a and c), we consider two different arrangements of these double-chain configurations, which are the mirror image of each other, meaning that they have opposite “chirality.” The center-to-center distance between the two chains is chosen to be 2σ. Each of the chains is composed of Nt/2 = 7 dipolar particles, such that the resulting chain length corresponds to the vortex diameter de/σ ≈ 7 observed at
. As an initial configuration, Nt dipolar particles are arranged into two anti-parallel chains lying side by side, see Fig. 9(a and c). Within each chain, the dipole moments are oriented head-to-tail. As illustrated in Fig. 9(a and c), we consider two different arrangements of these double-chain configurations, which are the mirror image of each other, meaning that they have opposite “chirality.” The center-to-center distance between the two chains is chosen to be 2σ. Each of the chains is composed of Nt/2 = 7 dipolar particles, such that the resulting chain length corresponds to the vortex diameter de/σ ≈ 7 observed at  and
and  (see Fig. 8). For simplicity, the thermal fluctuations are neglected.
(see Fig. 8). For simplicity, the thermal fluctuations are neglected.
 | ||
Fig. 9 (a and c) Sketches of two initial chain configurations composed of Nt = 14 dipolar circle swimmers. The black arrows indicate the particle orientation at t/τ = 0. (b and d) The inverse of maximum gyration radius, Rg,M−1, between 30 ≤ t/τ ≤ 40 as a function of the motility 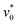 for initial configuration (a) (black circles) and (c) (red squares) at the angular speed for initial configuration (a) (black circles) and (c) (red squares) at the angular speed 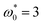 . Sketches show respective configurations characterized by Rg,M−1, where the red (blue) arrow indicates that the particle's velocity points against (along) its orientation [see eqn (12) with Δts = 0.01τ] and the dashed arrows indicate the particle motion. The rectangles with curved angles relate data with corresponding sketches. . Sketches show respective configurations characterized by Rg,M−1, where the red (blue) arrow indicates that the particle's velocity points against (along) its orientation [see eqn (12) with Δts = 0.01τ] and the dashed arrows indicate the particle motion. The rectangles with curved angles relate data with corresponding sketches. | ||
Upon starting the simulations with  and
and  we observe, for both initial configurations, that the swimmers rearrange themselves into a stable ring structure. The difference, however, is that the particles in the ring move forward (like in a Type I vortex) when starting from configuration (a), while the particles move backward when starting from the other initial configuration. This difference is due to the competition between the ring chirality favored by the initial configuration and the counterclockwise rotation supported by the active rotation. To further characterize the ring structure, we consider the gyration radius, given by
we observe, for both initial configurations, that the swimmers rearrange themselves into a stable ring structure. The difference, however, is that the particles in the ring move forward (like in a Type I vortex) when starting from configuration (a), while the particles move backward when starting from the other initial configuration. This difference is due to the competition between the ring chirality favored by the initial configuration and the counterclockwise rotation supported by the active rotation. To further characterize the ring structure, we consider the gyration radius, given by
 | (14) |
 for the initial configuration sketched in Fig. 9(a and c), respectively. The choice of this time interval is based on the fact that no transient structure is observed at t/τ > 20. The quantity Rg,M−1/σ−1 is about 0.4 for a stable ring structure and reaches a value smaller than 0.1 if two chains do not form a ring. As
for the initial configuration sketched in Fig. 9(a and c), respectively. The choice of this time interval is based on the fact that no transient structure is observed at t/τ > 20. The quantity Rg,M−1/σ−1 is about 0.4 for a stable ring structure and reaches a value smaller than 0.1 if two chains do not form a ring. As  , both Type I and Type II rings are stable, which conforms with the emergence of Type I and Type II vortices at
, both Type I and Type II rings are stable, which conforms with the emergence of Type I and Type II vortices at  and
and  [see Fig. 2(h) and 7(a)]. We also see that two chains no longer form a ring once
[see Fig. 2(h) and 7(a)]. We also see that two chains no longer form a ring once  is greater than a “critical” motility
is greater than a “critical” motility  . In this latter case, each chain swims along a circular path and does not collide with the other chain within the simulation time, see the sketches on the right side of Fig. 9(b and d). Importantly,
. In this latter case, each chain swims along a circular path and does not collide with the other chain within the simulation time, see the sketches on the right side of Fig. 9(b and d). Importantly,  for the Type II ring is much smaller
for the Type II ring is much smaller  than that for the Type I ring
than that for the Type I ring  . This explains why the system is dominated by the Type I vortices at intermediate motilities [see Fig. 2(e) and 7(b)]. Further increasing
. This explains why the system is dominated by the Type I vortices at intermediate motilities [see Fig. 2(e) and 7(b)]. Further increasing  leads to the breaking of both Type I and Type II rings [see Fig. 2(b)], suggesting that vortices will eventually vanish for large
leads to the breaking of both Type I and Type II rings [see Fig. 2(b)], suggesting that vortices will eventually vanish for large  . Indeed, for
. Indeed, for 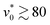 the system can display flocking behavior, which we will further address in the following Section 3.5.
the system can display flocking behavior, which we will further address in the following Section 3.5.
To check whether the vortex emergence is sensitive to the system size of the simulations, we performed various test simulations at  and
and  with the particle number ranging from N = 100 to N = 2500. We observed that giant vortex structures already emerge at N ≈ 400 and persist up to N = 2500 (results not shown here).
with the particle number ranging from N = 100 to N = 2500. We observed that giant vortex structures already emerge at N ≈ 400 and persist up to N = 2500 (results not shown here).
The vortex formation in the present work is of fundamental difference from the emergence of the clockwise vortices in systems of simple (non-dipolar, disk-shaped) circle swimmers,28 and the macroscopic droplets reported in studies of the rotating Vicsek model34 and its variant.35 For simple circle swimmers, the clockwise vortices do not appear at a density lower than the critical density of MIPS, Φcrit ≈ 0.3.28 Further, their formation relies on the steric collision of particles in the dilute region with the boundary of giant clusters. In contrast, for dipolar circle swimmers, the vortex patterns appear already at densities lower than Φcrit. For circle swimmers with polar alignment, such as the rotating Vicsek model34 and its variant,35 macroscopic droplets emerge at small angular speed  . Inside the droplets, particles align themselves with their neighbors and are directed along a single direction. This direction rotates in response to the active rotation exerted on each of the particles. These macroscopic droplets are significantly different from the giant vortices observed in dipolar circle swimmers, suggesting that the type of alignment interactions is crucial for the pattern formation of circle swimmers.
. Inside the droplets, particles align themselves with their neighbors and are directed along a single direction. This direction rotates in response to the active rotation exerted on each of the particles. These macroscopic droplets are significantly different from the giant vortices observed in dipolar circle swimmers, suggesting that the type of alignment interactions is crucial for the pattern formation of circle swimmers.
3.5 Orientational ordering
In this last section, we switch our focus onto motility-induced orientational ordering appearing at large (see the top part of the state diagram in Fig. 1). We note that in the present model, the orientational order of dipole moments μi implies coherent motion, i.e., flocking. The orientational order can be characterized by the global polar order parameter ϕe, defined in eqn (11). Fig. 10 shows ϕe as a function of the angular speed
(see the top part of the state diagram in Fig. 1). We note that in the present model, the orientational order of dipole moments μi implies coherent motion, i.e., flocking. The orientational order can be characterized by the global polar order parameter ϕe, defined in eqn (11). Fig. 10 shows ϕe as a function of the angular speed  for various motilities
for various motilities 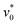 . At low motilities
. At low motilities  , ϕe decreases monotonically with
, ϕe decreases monotonically with  , and there is no significant ordering behavior. In contrast, strong translational self-propulsion
, and there is no significant ordering behavior. In contrast, strong translational self-propulsion 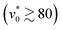 induces significant global polarization at small and large angular speeds (
induces significant global polarization at small and large angular speeds ( and
and  ) [see Fig. 2(a–c)], while at intermediate angular speeds
) [see Fig. 2(a–c)], while at intermediate angular speeds 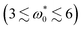 we find that ϕe ≤ 0.2. Here, the system forms vortex patterns [see Fig. 8 and Table 1]. Further, Fig. 10 reveals that the system reaches bistable states at
we find that ϕe ≤ 0.2. Here, the system forms vortex patterns [see Fig. 8 and Table 1]. Further, Fig. 10 reveals that the system reaches bistable states at  and
and  , consistent with earlier discussion of Fig. 4.
, consistent with earlier discussion of Fig. 4.
 | ||
Fig. 10 Global polarization ϕe as a function of the angular speed  for the motility for the motility  (black circles), 20 (red squares), 40 (green diamonds), 60 (blue triangles up), 80 (orange triangles down), and 100 (violet crosses). At (black circles), 20 (red squares), 40 (green diamonds), 60 (blue triangles up), 80 (orange triangles down), and 100 (violet crosses). At  and and  , the two values of ϕe reflect the bistability already indicated in Fig. 4. The dashed line marks where ϕe = 0.5. The results that lie above this line indicate that the system is in a flocking state. , the two values of ϕe reflect the bistability already indicated in Fig. 4. The dashed line marks where ϕe = 0.5. The results that lie above this line indicate that the system is in a flocking state. | ||
Taking a closer look at Fig. 2(a–c), we find that the size of the ordered (“flocking”) structures formed at large  significantly depends on
significantly depends on 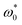 . To further characterize this behavior we consider the (weighted) distribution of the cluster size, nP(n), and their dependence on the overall particle number N. Results for
. To further characterize this behavior we consider the (weighted) distribution of the cluster size, nP(n), and their dependence on the overall particle number N. Results for  are shown in Fig. 11. As can bee seen in Fig. 11(a), for zero rotation
are shown in Fig. 11. As can bee seen in Fig. 11(a), for zero rotation 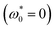 the distributions decrease monotonically with the cluster size n and collapse onto one curve for
the distributions decrease monotonically with the cluster size n and collapse onto one curve for  . This indicates that these are only small clusters whose size does not scale with the particle number N. According to Table 1, we classify such a situation as a “micro-flocking” state. In contrast, the weighted distribution function for fast rotation decays at small cluster sizes n, but exhibits a broad peak at large n [see Fig. 11(b)]. This peak corresponds to the large swarms shown in Fig. 2(c). On increasing the particle numbers N, the decay of nP(n) at small n becomes faster, while the peak at large n is shifted toward a larger n. In other words, the size of the formed structure scales with the particle number N, indicating the emergence of macroscopic swarming patterns. Based on Table 1, we identify this as a “macro-flocking” state.
. This indicates that these are only small clusters whose size does not scale with the particle number N. According to Table 1, we classify such a situation as a “micro-flocking” state. In contrast, the weighted distribution function for fast rotation decays at small cluster sizes n, but exhibits a broad peak at large n [see Fig. 11(b)]. This peak corresponds to the large swarms shown in Fig. 2(c). On increasing the particle numbers N, the decay of nP(n) at small n becomes faster, while the peak at large n is shifted toward a larger n. In other words, the size of the formed structure scales with the particle number N, indicating the emergence of macroscopic swarming patterns. Based on Table 1, we identify this as a “macro-flocking” state.
The mechanism underlying the flocking behavior of dipolar active systems is quite complex already in the absence of circle swimming (that is, at  , see ref. 46): Short linear chains formed by dipolar active particles with head–tail orientation tend to align their velocities upon collisions (see Fig. 8 of ref. 46). In ref. 46, it is found that macro-flocking appears once the density increases from Φ = 0.23 to Φ = 0.58. This suggests that the transition from micro- to macro-flocking may be attributed to a density-induced enhancement of particle collisions. For the present system of chiral dipolar active particles, a similar effect may take place: we suspect that the circle swimming of each particle leads again to an enhancement of collisions, similar to an increase of density. This might explain why the present, chiral system exhibits macro-flocking already at smaller densities than the corresponding non-chiral system
, see ref. 46): Short linear chains formed by dipolar active particles with head–tail orientation tend to align their velocities upon collisions (see Fig. 8 of ref. 46). In ref. 46, it is found that macro-flocking appears once the density increases from Φ = 0.23 to Φ = 0.58. This suggests that the transition from micro- to macro-flocking may be attributed to a density-induced enhancement of particle collisions. For the present system of chiral dipolar active particles, a similar effect may take place: we suspect that the circle swimming of each particle leads again to an enhancement of collisions, similar to an increase of density. This might explain why the present, chiral system exhibits macro-flocking already at smaller densities than the corresponding non-chiral system  .
.
We note that our observation concerning the size of the flocking pattern contrasts the behavior previously observed in systems of chiral active particles with polar interaction. There, the size of flocking patterns is inversely proportional to the angular speed.34,35 This suggests that different types of alignment interactions between active particles may significantly change the fundamental properties of flocking behavior.
4 Conclusions
In this work, we performed extensive Brownian dynamics (BD) simulations to investigate the pattern formation of dipolar circle swimmers dispersed on a monolayer. To this end, we explored a wide range of active angular speeds and motilities at a fixed density below that related to MIPS in simple systems and large dipolar coupling strength.At a sufficiently large angular speed 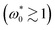 and zero motility
and zero motility  , the system undergoes a transition from a state with percolated networks into a state with Type I and Type II vortices. Upon an increase of
, the system undergoes a transition from a state with percolated networks into a state with Type I and Type II vortices. Upon an increase of  from zero, the Type II vortices vanish, and the system displays phase separation with the dense domain characterized by giant Type I vortices. Based on test simulations of two anti-parallel chains composed of strongly coupled dipolar particles, we proposed a “ring” argument to unveil the underlying mechanism of the vortex formation and the disappearance of Type II vortices. In contrast with our model, the vortex structures are not observed in systems of circle swimmers with ferromagnetic Heisenberg-like interactions.34,35 Instead, these systems display macroscopic polar droplets, in which swimmers move coherently along a certain direction and the direction rotates in accordance with the active rotation exerting on each circle swimmer. To further unravel the differences, we performed Brownian dynamics simulations of circle swimmers with ferromagnetic interactions decaying with a Yukawa potential (as a function of separation),87,88 and, thus, decay with the particle distance. Our preliminary results (not shown here) do not show any vortex structures, either.
from zero, the Type II vortices vanish, and the system displays phase separation with the dense domain characterized by giant Type I vortices. Based on test simulations of two anti-parallel chains composed of strongly coupled dipolar particles, we proposed a “ring” argument to unveil the underlying mechanism of the vortex formation and the disappearance of Type II vortices. In contrast with our model, the vortex structures are not observed in systems of circle swimmers with ferromagnetic Heisenberg-like interactions.34,35 Instead, these systems display macroscopic polar droplets, in which swimmers move coherently along a certain direction and the direction rotates in accordance with the active rotation exerting on each circle swimmer. To further unravel the differences, we performed Brownian dynamics simulations of circle swimmers with ferromagnetic interactions decaying with a Yukawa potential (as a function of separation),87,88 and, thus, decay with the particle distance. Our preliminary results (not shown here) do not show any vortex structures, either.
A further increase of the motility  leads to two distinct flocking states, which can be distinguished by the cluster size distribution. Consistent with the behavior of dipolar active Brownian particles,46 dipolar circle swimmers at zero and slow rotation display a micro-flocking state
leads to two distinct flocking states, which can be distinguished by the cluster size distribution. Consistent with the behavior of dipolar active Brownian particles,46 dipolar circle swimmers at zero and slow rotation display a micro-flocking state  . In contrast, dipolar swimmers with fast rotation
. In contrast, dipolar swimmers with fast rotation  exhibit a macro-flocking state. This is again distinctly different from circle swimmers with short-range ferromagnetic interactions, in which the size of polar clusters decreases upon an increase of the active angular speed.34,35 Hence, the type of anisotropic interactions that align particle velocities plays a vital role in determining the fundamental self-organization process for systems of circle swimmers.
exhibit a macro-flocking state. This is again distinctly different from circle swimmers with short-range ferromagnetic interactions, in which the size of polar clusters decreases upon an increase of the active angular speed.34,35 Hence, the type of anisotropic interactions that align particle velocities plays a vital role in determining the fundamental self-organization process for systems of circle swimmers.
For completeness, we also performed simulations for circle swimmers with truncated dipole–dipole interactions (results not shown here). Here, the Ewald summation was not employed, and the dipole–dipole interactions were truncated at r = 3σ. In this case, the flocking transition is shifted to a much larger motility  . More importantly, we did not observe any vortex patterns throughout the explored parameter regime. This suggests that not only the angle dependency, but also the long-range character of dipole–dipole interactions is crucial for the collective behavior of dipolar active systems and, thus, should be not be neglected.
. More importantly, we did not observe any vortex patterns throughout the explored parameter regime. This suggests that not only the angle dependency, but also the long-range character of dipole–dipole interactions is crucial for the collective behavior of dipolar active systems and, thus, should be not be neglected.
The model studied in the present paper does not account for hydrodynamic interactions between particles. However, hydrodynamic interactions can have a profound impact on the dynamical self-assembly of active colloidal systems, such as the suppression of MIPS89–92 and the emergence of global polar ordering.93–97 In systems of rotating particles, it is found that hydrodynamic interactions can induce cluster rotation, such that the overall cluster and the individual particles rotate in the same direction.98 In the present work, we have seen that the giant Type I vortices and circle swimmers rotate in the same direction. Hence, we expect that hydrodynamics can further promote the formation of giant Type I vortices. Nevertheless, the detailed influence of hydrodynamics on dipolar circle swimmers remains to be unveiled by future works.
Furthermore, it is well established that mixtures of active and passive colloidal particles display fascinating collective behavior that is distinctly different from that of the corresponding one-component systems.64,76,99–101 Therefore, one future direction could be to consider mixtures of circle swimmers and passive dipolar particles, whose self-assembly process can be further controlled by the proportion of species.
Finally, the majority of the research works on systems of active particles focus on their collective behavior in two dimensions (2D), whereas the real-world suspensions of self-propelled colloids are often in three dimensions (3D). The dimensionality may play an important role in the motility-induced phenomena, such as the critical motility for MIPS102 and the critical exponents for flocking transition.86 In the present 2D model of dipolar circle swimmers, we assume that the particles are confined to a flat surface, and the rotation axis for each particle is restricted to be normal to the surface. It will be interesting to discover the similarities and differences in our model system when moving from 2D to 3D.
Conflicts of interest
There are no conflicts to declare.Appendix A: orientational correlation function
To characterize the vortex structure, we calculate the orientational correlation function Ce(r) defined in eqn (9). Results are shown in Fig. 12. For passive dipolar particles ( and
and  ), Ce(r) decays with r and reaches zero at r/σ ≈ 10 [see Fig. 12(a)]. Upon an increase of
), Ce(r) decays with r and reaches zero at r/σ ≈ 10 [see Fig. 12(a)]. Upon an increase of 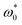 from zero to 1, Ce(r) decays faster than the case where
from zero to 1, Ce(r) decays faster than the case where  and displays a negative correlation with a minimum Ce(r) ≈ −0.15 at r/σ ≈ 10. As have been discussed in Section 2.4.3, the negative correlation indicates the emergence of vortex structures. Further, the distance corresponding to the minimum of Ce(r) determines the average vortex diameter [see eqn (10)], and the minimum value of the correlation function Ce(de) ≈ −0.15 represents the prominence of the vortex structures. As the angular speed increases from 1 to 10, both the vortex diameter de and the significance of the vortex structures decrease, indicating that the vortex structures occur at a sufficiently large angular speed
and displays a negative correlation with a minimum Ce(r) ≈ −0.15 at r/σ ≈ 10. As have been discussed in Section 2.4.3, the negative correlation indicates the emergence of vortex structures. Further, the distance corresponding to the minimum of Ce(r) determines the average vortex diameter [see eqn (10)], and the minimum value of the correlation function Ce(de) ≈ −0.15 represents the prominence of the vortex structures. As the angular speed increases from 1 to 10, both the vortex diameter de and the significance of the vortex structures decrease, indicating that the vortex structures occur at a sufficiently large angular speed  and are inhibited by further increasing
and are inhibited by further increasing  .
.
Comparing the results for 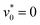 and
and  , the vortex structures emerge at
, the vortex structures emerge at 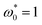 for
for  , whereas for
, whereas for  the vortices appears at a larger angular speed
the vortices appears at a larger angular speed 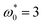 [see Fig. 12(b)]. In particular, the vortex size de becomes much larger and is close to the half of the side length of the simulation box (L/2 ≈ 33.69σ), suggesting that there might be finite-size effect for de. In other words, de may scale with the total number of particles N, which requires further investigation. Nevertheless, since the long-range character of dipole–dipole interactions requires expensive computational resources, the present simulations are limited to the order of 103 particles. A further increase of
[see Fig. 12(b)]. In particular, the vortex size de becomes much larger and is close to the half of the side length of the simulation box (L/2 ≈ 33.69σ), suggesting that there might be finite-size effect for de. In other words, de may scale with the total number of particles N, which requires further investigation. Nevertheless, since the long-range character of dipole–dipole interactions requires expensive computational resources, the present simulations are limited to the order of 103 particles. A further increase of  from 3 to 10 causes the giant vortices to break into smaller vortices.
from 3 to 10 causes the giant vortices to break into smaller vortices.
At high motilities such as  , Ce(r) drastically decays at short distances r/σ ≤ 3 and gradually reaches a value close to 0.3 at r = L/2 for zero, small and large angular speeds
, Ce(r) drastically decays at short distances r/σ ≤ 3 and gradually reaches a value close to 0.3 at r = L/2 for zero, small and large angular speeds  . The non-vanishing, positive correlation function indicates the emergence of global orientational order, which is discussed in detail in Section 3.5. At the intermediate angular speeds (ω = 3 and 5), the minimum of Ce(r) appear at r ≲ L/2.
. The non-vanishing, positive correlation function indicates the emergence of global orientational order, which is discussed in detail in Section 3.5. At the intermediate angular speeds (ω = 3 and 5), the minimum of Ce(r) appear at r ≲ L/2.
Acknowledgements
This work was financially supported by the Deutsche Forschungsgemeinschaft under GRK 1524 (DFG No. 599982).References
- P. Romanczuk, M. Bär, W. Ebeling, B. Lindner and L. Schimansky-Geier, Eur. Phys. J. Spec. Top., 2012, 202, 1 CrossRef CAS.
- A. Zöttl and H. Stark, J. Phys.: Condens. Matter, 2016, 28, 253001 CrossRef.
- S. Ramaswamy, Annu. Rev. Condens. Matter Phys., 2010, 1, 323 CrossRef.
- C. Bechinger, R. Di Leonardo, H. Löwen, C. Reichhardt, G. Volpe and G. Volpe, Rev. Mod. Phys., 2016, 88, 045006 CrossRef.
- W. F. Paxton, K. C. Kistler, C. C. Olmeda, A. Sen, S. K. St. Angelo, Y. Cao, T. E. Mallouk, P. E. Lammert and V. H. Crespi, J. Am. Chem. Soc., 2004, 126, 13424 CrossRef CAS PubMed.
- W. F. Paxton, P. T. Baker, T. R. Kline, Y. Wang, T. E. Mallouk and A. Sen, J. Am. Chem. Soc., 2006, 128, 14881 CrossRef CAS PubMed.
- S. Gangwal, O. J. Cayre, M. Z. Bazant and O. D. Velev, Phys. Rev. Lett., 2008, 100, 058302 CrossRef PubMed.
- I. Buttinoni, G. Volpe, F. Kümmel, G. Volpe and C. Bechinger, J. Phys.: Condens. Matter, 2012, 24, 284129 CrossRef PubMed.
- A. Kaiser, A. Snezhko and I. S. Aranson, Sci. Adv., 2017, 3, e1601469 CrossRef PubMed.
- G. Kokot and A. Snezhko, Nat. Commun., 2018, 9, 2344 CrossRef PubMed.
- K. Han, G. Kokot, O. Tovkach, A. Glatz, I. S. Aranson and A. Snezhko, Proc. Natl. Acad. Sci. U. S. A., 2020, 117, 9706 CrossRef CAS PubMed.
- G. Gompper, R. G. Winkler, T. Speck, A. Solon, C. Nardini, F. Peruani, H. Löwen, R. Golestanian, U. B. Kaupp, L. Alvarez, T. Kiørboe, E. Lauga, W. C. K. Poon, A. DeSimone, S. Muiños-Landin, A. Fischer, N. A. Söker, F. Cichos, R. Kapral, P. Gaspard, M. Ripoll, F. Sagues, A. Doostmohammadi, J. M. Yeomans, I. S. Aranson, C. Bechinger, H. Stark, C. K. Hemelrijk, F. J. Nedelec, T. Sarkar, T. Aryaksama, M. Lacroix, G. Duclos, V. Yashunsky, P. Silberzan, M. Arroyo and S. Kale, J. Phys.: Condens. Matter, 2020, 32, 193001 CrossRef CAS PubMed.
- J. Tailleur and M. E. Cates, Phys. Rev. Lett., 2008, 100, 218103 CrossRef CAS PubMed.
- I. Buttinoni, J. Bialké, F. Kümmel, H. Löwen, C. Bechinger and T. Speck, Phys. Rev. Lett., 2013, 110, 238301 CrossRef PubMed.
- M. E. Cates and J. Tailleur, Annu. Rev. Condens. Matter Phys., 2015, 6, 219 CrossRef CAS.
- T. Speck, A. M. Menzel, J. Bialké and H. Löwen, J. Chem. Phys., 2015, 142, 224109 CrossRef PubMed.
- P. Digregorio, D. Levis, A. Suma, L. F. Cugliandolo, G. Gonnella and I. Pagonabarraga, Phys. Rev. Lett., 2018, 121, 098003 CrossRef CAS PubMed.
- T. Vicsek, A. Czirók, E. Ben-Jacob, I. Cohen and O. Shochet, Phys. Rev. Lett., 1995, 75, 1226 CrossRef CAS PubMed.
- S. van Teeffelen and H. Löwen, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2008, 78, 020101 CrossRef PubMed.
- H. Löwen, Eur. Phys. J. Spec. Top., 2016, 225, 2319 CrossRef.
- W. R. DiLuzio, L. Turner, M. Mayer, P. Garstecki, D. B. Weibel, H. C. Berg and G. M. Whitesides, Nature, 2005, 435, 1271 CrossRef CAS PubMed.
- E. Lauga, W. R. DiLuzio, G. M. Whitesides and H. A. Stone, Biophys. J., 2006, 90, 400 CrossRef CAS PubMed.
- M. Loose and T. J. Mitchison, Nat. Cell Biol., 2014, 16, 38 CrossRef CAS PubMed.
- J. Denk, L. Huber, E. Reithmann and E. Frey, Phys. Rev. Lett., 2016, 116, 178301 CrossRef PubMed.
- D. A. Ramirez-Diaz, D. A. García-Soriano, A. Raso, J. Mücksch, M. Feingold, G. Rivas and P. Schwille, PLoS Biol., 2018, 16, e2004845 CrossRef PubMed.
- F. Kümmel, B. ten Hagen, R. Wittkowski, I. Buttinoni, R. Eichhorn, G. Volpe, H. Löwen and C. Bechinger, Phys. Rev. Lett., 2013, 110, 198302 CrossRef PubMed.
- J. Bickmann, S. Bröker, J. Jeggle and R. Wittkowski, 2020, arXiv: 2010.05262v1 [cond-mat.soft].
- G.-J. Liao and S. H. L. Klapp, Soft Matter, 2018, 14, 7873 RSC.
- Q.-L. Lei, M. P. Ciamarra and R. Ni, Sci. Adv., 2019, 5, eaau7423 CrossRef PubMed.
- Y. Yang, F. Qiu and G. Gompper, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2014, 89, 012720 CrossRef PubMed.
- B. Zhang, A. Sokolov and A. Snezhko, Nat. Commun., 2020, 11, 1 Search PubMed.
- A. Kaiser and H. Löwen, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2013, 87, 032712 CrossRef.
- B. Liebchen, M. E. Cates and D. Marenduzzo, Soft Matter, 2016, 12, 7259 RSC.
- B. Liebchen and D. Levis, Phys. Rev. Lett., 2017, 119, 058002 CrossRef PubMed.
- D. Levis and B. Liebchen, J. Phys.: Condens. Matter, 2018, 30, 084001 CrossRef PubMed.
- N. Kruk, Y. Maistrenko and H. Koeppl, Phys. Rev. E, 2018, 98, 032219 CrossRef CAS.
- N. Kruk, J. A. Carrillo and H. Koeppl, Phys. Rev. E, 2020, 102, 022604 CrossRef CAS PubMed.
- N. Kruk, J. A. Carrillo and H. Koeppl, 2020, arXiv: 2008.08493v2 [math.NA].
- P. Arora, A. K. Sood and R. Ganapathy, Sci. Adv., 2021, 7, 331 Search PubMed.
- Z. F. Huang, A. M. Menzel and H. Löwen, Phys. Rev. Lett., 2020, 125, 218002 CrossRef CAS PubMed.
- Z. Fazli and A. Naji, Phys. Rev. E, 2021, 103, 022601 CrossRef CAS PubMed.
- F. J. Lin, J. J. Liao and B. Q. Ai, J. Chem. Phys., 2020, 152, 224903 CrossRef CAS PubMed.
- F. Kogler and S. H. L. Klapp, EPL, 2015, 110, 10004 CrossRef.
- F. Meng, D. Matsunaga and R. Golestanian, Phys. Rev. Lett., 2018, 120, 188101 CrossRef CAS PubMed.
- S. Klumpp, C. T. Lefèvre, M. Bennet and D. Faivre, Phys. Rep., 2018, 789, 1 CrossRef.
- G.-J. Liao, C. K. Hall and S. H. L. Klapp, Soft Matter, 2020, 16, 2208 RSC.
- M. Mijalkov and G. Volpe, Soft Matter, 2013, 9, 6376 RSC.
- X. Ao, P. K. Ghosh, Y. Li, G. Schmid, P. Hänggi and F. Marchesoni, EPL, 2015, 109, 10003 CrossRef.
- S. Jahanshahi, H. Löwen and B. ten Hagen, Phys. Rev. E, 2017, 95, 022606 CrossRef PubMed.
- J. D. Weeks, D. Chandler and H. C. Andersen, J. Chem. Phys., 1971, 54, 5237 CrossRef CAS.
- J.-J. Weis and D. Levesque, Advanced computer simulation approaches for soft matter sciences II, Springer, Berlin, Heidelberg, 2005, pp. 163–225 Search PubMed.
- H. Schmidle and S. H. L. Klapp, J. Chem. Phys., 2011, 134, 114903 CrossRef PubMed.
- S. Jäger, H. Schmidle and S. H. L. Klapp, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2012, 86, 011402 CrossRef PubMed.
- J. M. Tavares, J. J. Weis and M. M. Telo da Gama, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2002, 65, 061201 CrossRef CAS PubMed.
- P. D. Duncan and P. J. Camp, J. Chem. Phys., 2004, 121, 11322 CrossRef CAS PubMed.
- P. D. Duncan and P. J. Camp, Phys. Rev. Lett., 2006, 97, 107202 CrossRef PubMed.
- S. Kantorovich, J. J. Cerdà and C. Holm, Phys. Chem. Chem. Phys., 2008, 10, 1883 RSC.
- J. J. Cerdà, S. Kantorovich and C. Holm, J. Phys.: Condens. Matter, 2008, 20, 204125 CrossRef PubMed.
- S. H. L. Klapp and M. Schoen, J. Chem. Phys., 2002, 117, 8050 CrossRef CAS.
- W.-Z. Ouyang, S.-H. Xu and Z.-W. Sun, J. Chem. Phys., 2011, 134, 014901 CrossRef PubMed.
- R. Geiger and S. H. L. Klapp, J. Mod. Phys., 2013, 04, 401 CrossRef.
- P. E. Kloeden and E. Platen, Numerical solution of stochastic differential equations, Springer, Berlin, Heidelberg, 1992 Search PubMed.
- I. R. Bruss and S. C. Glotzer, Phys. Rev. E, 2018, 97, 042609 CrossRef CAS PubMed.
- R. C. Maloney, G.-J. Liao, S. H. Klapp and C. K. Hall, Soft Matter, 2020, 16, 3779 RSC.
- D. Laría and F. Vericat, Phys. Rev. A: At., Mol., Opt. Phys., 1991, 43, 1932 CrossRef PubMed.
- J. J. Weis and D. Levesque, Phys. Rev. Lett., 1993, 71, 2729 CrossRef CAS PubMed.
- L. Rovigatti, J. Russo and F. Sciortino, Phys. Rev. Lett., 2011, 107, 237801 CrossRef PubMed.
- L. Rovigatti, J. Russo and F. Sciortino, Soft Matter, 2012, 8, 6310 RSC.
- L. Rovigatti, S. Kantorovich, A. O. Ivanov, J. M. Tavares and F. Sciortino, J. Chem. Phys., 2013, 139, 134901 CrossRef PubMed.
- S. Kantorovich, A. O. Ivanov, L. Rovigatti, J. M. Tavares and F. Sciortino, Phys. Rev. Lett., 2013, 110, 148306 CrossRef PubMed.
- S. S. Kantorovich and A. O. Ivanov, in Soft matter self-assembly, ed. C. N. Likos, F. Sciortino, P. Ziherl and E. Zaccarelli, IOS Press, 2016, pp. 137–163 Search PubMed.
- M. Ronti, L. Rovigatti, J. M. Tavares, A. O. Ivanov, S. S. Kantorovich and F. Sciortino, Soft Matter, 2017, 13, 7870 RSC.
- P. J. Camp, in Modern problems of molecular Physics, ed. L. A. Bulavin and A. V. Chalyi, Springer, Cham, 2018, pp. 185–204 Search PubMed.
- E. Sesé-Sansa, I. Pagonabarraga and D. Levis, EPL, 2018, 124, 30004 CrossRef.
- M. N. Van Der Linden, L. C. Alexander, D. G. Aarts and O. Dauchot, Phys. Rev. Lett., 2019, 123, 098001 CrossRef CAS PubMed.
- R. C. Maloney and C. K. Hall, Langmuir, 2020, 36, 6378 CrossRef CAS PubMed.
- M. Pu, H. Jiang and Z. Hou, Soft Matter, 2017, 13, 4112 RSC.
- T. Speck, J. Bialké, A. M. Menzel and H. Löwen, Phys. Rev. Lett., 2014, 112, 218304 CrossRef.
- Y. Sumino, K. H. Nagai, Y. Shitaka, D. Tanaka, K. Yoshikawa, H. Chaté and K. Oiwa, Nature, 2012, 483, 448 CrossRef CAS PubMed.
- H. H. Wensink, J. Dunkel, S. Heidenreich, K. Drescher, R. E. Goldstein, H. Löwen and J. M. Yeomans, Proc. Natl. Acad. Sci. U. S. A., 2012, 109, 14308 CrossRef CAS PubMed.
- H. Wioland, F. G. Woodhouse, J. Dunkel, J. O. Kessler and R. E. Goldstein, Phys. Rev. Lett., 2013, 110, 268102 CrossRef PubMed.
- H. Reinken, D. Nishiguchi, S. Heidenreich, A. Sokolov, M. Bär, S. H. Klapp and I. S. Aranson, Commun. Phys., 2020, 3, 1 CrossRef.
- D. A. Ramirez-Diaz, D. A. Garcia-Soriano, A. Raso, M. Feingold, G. Rivas and P. Schwille, Biophys. J., 2017, 112, 133a CrossRef.
- I. H. Riedel, K. Kruse and J. Howard, Science, 2005, 309, 300 CrossRef CAS.
- A. Martín-Gómez, D. Levis, A. Díaz-Guilera and I. Pagonabarraga, Soft Matter, 2018, 14, 2610 RSC.
- F. Ginelli, Eur. Phys. J.: Spec. Top., 2016, 225, 2099 Search PubMed.
- K. Lichtner, A. J. Archer and S. H. L. Klapp, J. Chem. Phys., 2012, 136, 024502 CrossRef CAS PubMed.
- K. Lichtner and S. H. L. Klapp, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2013, 88, 032301 CrossRef CAS PubMed.
- R. Matas Navarro, R. Golestanian, T. B. Liverpool and S. M. Fielding, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2014, 90, 032304 CrossRef PubMed.
- R. Matas Navarro and S. M. Fielding, Soft Matter, 2015, 11, 7525 RSC.
- M. Theers, E. Westphal, K. Qi, R. G. Winkler and G. Gompper, Soft Matter, 2018, 14, 8590 RSC.
- F. J. Schwarzendahl and M. G. Mazza, J. Chem. Phys., 2019, 150, 184902 CrossRef PubMed.
- F. Alarcón and I. Pagonabarraga, J. Mol. Liq., 2013, 185, 56 CrossRef.
- B. Delmotte, E. E. Keaveny, F. Plouraboué and E. Climent, J. Comput. Phys., 2015, 302, 524 CrossRef.
- N. Yoshinaga and T. B. Liverpool, Phys. Rev. E, 2017, 96, 020603 CrossRef PubMed.
- N. Yoshinaga and T. B. Liverpool, Eur. Phys. J. E: Soft Matter Biol. Phys., 2018, 41, 76 CrossRef.
- C. Hoell, H. Löwen and A. M. Menzel, J. Chem. Phys., 2018, 149, 144902 CrossRef PubMed.
- S. Jäger, H. Stark and S. H. L. Klapp, J. Phys.: Condens. Matter, 2013, 25, 195104 CrossRef.
- J. Stenhammar, R. Wittkowski, D. Marenduzzo and M. E. Cates, Phys. Rev. Lett., 2015, 114, 018301 CrossRef CAS.
- A. Wysocki, R. G. Winkler and G. Gompper, New J. Phys., 2016, 18, 123030 CrossRef.
- R. Wittkowski, J. Stenhammar and M. E. Cates, New J. Phys., 2017, 19, 105003 CrossRef.
- J. Stenhammar, D. Marenduzzo, R. J. Allen and M. E. Cates, Soft Matter, 2014, 10, 1489 RSC.
Footnote |
† The arrows in Fig. 2(d) are chosen to be three times as large as the diameter of a disk-shaped swimmer for better visualization. However, this choice may create an unrealistic visual effect that some neighboring chains in Fig. 2(d) seem to be connected and span over the simulation cell. In fact, it is not the case, since the percolation probability Π approaches zero at 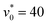 and and  [see Fig. 3(a)]. [see Fig. 3(a)]. |
| This journal is © The Royal Society of Chemistry 2021 |