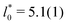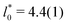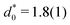Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Formation and internal ordering of periodic microphases in colloidal models with competing interactions†
Horacio
Serna
 a,
Antonio Díaz
Pozuelo
a,
Antonio Díaz
Pozuelo
 b,
Eva G.
Noya
b,
Eva G.
Noya
 *b and
Wojciech T.
Góźdź
*b and
Wojciech T.
Góźdź
 a
a
aInstitute of Physical Chemistry Polish Academy of Sciences, Kasprzaka 44/52, 01-224 Warsaw, Poland. E-mail: wtg@ichf.edu.pl
bInstituto de Química Física Rocasolano, CSIC, C/Serrano 119, 28006 Madrid, Spain. E-mail: eva.noya@gmail.com
First published on 30th April 2021
Abstract
Theory and simulations predict that colloidal particles with short-range attractive and long-range repulsive interactions form periodic microphases if there is a proper balance between the attractive and repulsive contributions. However, the experimental identification of such structures has remained elusive to date. Using molecular dynamics simulations, we investigate the phase behaviour of a model system that stabilizes a cluster-crystal, a cylindrical and a lamellar phase at low temperatures. Besides the transition from the fluid to the periodic microphases, we also observe the internal freezing of the clusters at a lower temperature. Finally, our study indicates that, for the chosen model parameters, the three periodic microphases are kinetically accessible from the fluid phase.
1 Introduction
Theoretical and simulation studies have shown that systems with competing short-range attractive and long-range repulsive (SALR) interactions may exhibit a complex phase diagram in which several periodic microphases are thermodynamically stable, including cluster-crystals, cylindrical, and lamellar phases.1–5 This phase behaviour should be universal regardless of the physical origin of the attractive and repulsive contributions.1 It is thus somewhat bewildering that ordered microphases have not yet been observed in experimental colloidal systems, where, in principle, competing interactions can be easily controlled by tuning the electrostatic and depletion interactions.6,7 The reason why this is so is not clear, and different hypotheses have been put forward, that point to the slow kinetics of these systems,6,8,9 to the experimental colloidal polydispersity,10 or even to subtle effects in the colloidal suspension that are not properly accounted for in a simple SALR effective potential.11Given this controversy, we find it surprising that simulation studies of model SALR systems are mostly focused on equilibrium properties, with dynamic aspects being comparatively much less studied. Besides, most simulation and experimental efforts have been devoted so far to understanding the dynamical behaviour of some globular proteins, such as lysozyme, that undergoes a glass transition at intermediate densities that can be explained by the formation of stable clusters in solution.7,12,13 However, the kinetic accessibility of the periodic phases has been hardly investigated. One exception is the recent work by Zhuang and Charbonneau that found several dynamic transitions in the fluid phase, and that revealed that the lamellar phase should be kinetically accessible.14
In this work, we perform Molecular Dynamics (MD) simulations of a model system of colloidal particles with competing interactions at the microphase-forming region to investigate the structural and dynamical changes that the system undergoes when it is gradually quenched from the fluid phase to well beyond the fluid-microphase transition. For that purpose, we use a model consisting of a Lennard-Jones term with a screened electrostatic interaction expressed as a Yukawa contribution (LJY), whose model parameters are chosen inspired by the square-well-linear (SWL) model potential for which the thermodynamic stability of the cluster-crystal, the cylindrical and the lamellar phases was rigorously proven.5 We found that those phases are also obtained for the LJY model and, differently from the SWL system, a freezing transition within the clusters is also observed at somewhat lower temperatures. The analysis of the dynamic behaviour along three isochores stabilizing each of these periodic microphases indicates that all three should be accessible from the fluid phase.
2 Model and methods
The interaction between colloidal particles was modelled with an effective SALR potential that results from the addition of a generalized Lennard-Jones (LJ) 2α–α term plus a screened electrostatic interaction represented by a Yukawa potential: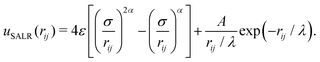 | (1) |
 | ||
| Fig. 1 Comparison between the SWL potential from ref. 4 and the LJY potential used in this paper. | ||
The phase behaviour of the system was explored by performing MD simulations in the isobaric-isothermal (NpT) ensemble. By allowing the box side to change, we enable the relaxation of the strain associated with the incommensurability of the assembled periodic modulated phases with the simulation box.
MD simulations were performed with the open source MD package LAMMPS,21 in which the truncated and shifted LJY model described above was implemented in an external subroutine coded by us. The simulation box contains N = 1991 particles. The simulations were run for 10 × 106 MD steps for equilibration and 2 × 106 steps for averaging with a time step  . Temperature and pressure were controlled using the Nose–Hoover thermostat and barostat with the relaxation times 100dt and 1000dt, respectively. Simulations were performed over a range of pressures (p* = pσ3/ε) between 0.01 and 0.55 and temperatures (T* = kBT/ε) between 0.15 and 1.0.
. Temperature and pressure were controlled using the Nose–Hoover thermostat and barostat with the relaxation times 100dt and 1000dt, respectively. Simulations were performed over a range of pressures (p* = pσ3/ε) between 0.01 and 0.55 and temperatures (T* = kBT/ε) between 0.15 and 1.0.
The structure formed at each thermodynamic state was identified from local density plots. These plots were built by dividing the simulation box into a grid of cubic cells of side length approximately equal to σ, and averaging the density in these cells over 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 independent configurations. The graphical representation of density isosurfaces allows a clear visualization of the clusters shape and position. We used the OpenDX software for visualizing the isosurfaces of the density plots. Clusters were also identified by performing a cluster analysis,22 in which two particles are considered to be nearest neighbours if the distance between them is lower than the distance to the first minimum in the radial distribution function. Specifically, we took rcut = 1.6σ for the cluster and cylindrical phases and rcut = 1.4σ for the lamellar phase. In order to assess if the fluid is percolating, we used the algorithm described in ref. 23, which allows us to determine if at least one of the clusters spans along any of the dimensions of the simulation box. The fluid is considered to be percolating when all the configurations analyzed for a given state point have at least one percolating cluster.
000 independent configurations. The graphical representation of density isosurfaces allows a clear visualization of the clusters shape and position. We used the OpenDX software for visualizing the isosurfaces of the density plots. Clusters were also identified by performing a cluster analysis,22 in which two particles are considered to be nearest neighbours if the distance between them is lower than the distance to the first minimum in the radial distribution function. Specifically, we took rcut = 1.6σ for the cluster and cylindrical phases and rcut = 1.4σ for the lamellar phase. In order to assess if the fluid is percolating, we used the algorithm described in ref. 23, which allows us to determine if at least one of the clusters spans along any of the dimensions of the simulation box. The fluid is considered to be percolating when all the configurations analyzed for a given state point have at least one percolating cluster.
With the aim of determining the lattice structure of the cluster-crystal, we computed the cluster–cluster pair distribution function (CC-PDF) using the centers of mass of the clusters. Bond-orientational order diagrams (BOOD) are another useful tool for crystal identification.24 These diagrams are calculated by projecting the bonds formed by a central cluster and its first coordination shell on a unit sphere. As for the CC-PDF, the BOOD was evaluated using the center of mass of the clusters, and the first coordination shell is defined as those clusters that are at shorter distances than the first minimum of the CC-PDF. The unit sphere was then plotted in a two-dimensional plane by using Lambert projection to help its visualization.
The dynamic properties, i.e. the mean squared displacement (MSD) and the coherent and incoherent scattering functions, are obtained from canonical ensemble (NVT) simulations. Typically these NVT simulations consist of 106 MD steps, once the system has reached equilibrium.
3 Results
3.1 Thermodynamic properties
 , and cluster size,
, and cluster size,  , in the periodic microphases. d0 corresponds to the diameter of the spherical and cylindrical clusters in the cluster-crystal and cylindrical phases, respectively, and to the width of the lamellae in the lamellar phase
, in the periodic microphases. d0 corresponds to the diameter of the spherical and cylindrical clusters in the cluster-crystal and cylindrical phases, respectively, and to the width of the lamellae in the lamellar phase
Regarding the lattice structure of the cluster-crystal, the CC-PDF and BOOD calculated from a simulation of a system with N = 1991 (corresponding to a box edge size L/σ = 23.42) exhibit a behaviour intermediate between that expected for the face-centred-cubic (FCC) and the body-centred-cubic (BCC) lattices. Our hypothesis is that this intermediate behaviour might be caused by finite size effects that persist up to very large system sizes due to the commensurability of the lattices with only certain box sizes. Thus, we performed additional NpT MD simulations (at T* = 0.20 and p* = 0.05) using numbers of particles compatible with the formation of the FCC or the BCC lattices in a cubic box. We found that the fluid readily assembles into the BCC cluster-crystal when the system size is chosen compatible with this lattice, whereas system sizes compatible with the FCC lattice always lead to the formation of crystals with defects. The cluster–cluster pair distribution function (CC-PDF) and BOOD obtained from a simulation with N = 1200 are shown in Fig. 3. The CC-PDF and specially the BOOD exhibits the typical pattern of the BCC lattice.24 Even though a more rigorous study is needed to unambiguously determine the structure of the cluster-crystal, the present results indicate that, for our model potential, the BCC is likely more stable than the FCC crystal. In studies on the hard spheres plus double Yukawa (HSDY) potential, theoretical approaches predict the stability of the BCC cluster crystal.1,25 However, the hexagonal-close packed (HCP) cluster-crystal, almost degenerate with the FCC crystal, can also be stable at low temperature3 for the HSDY potential. Curiously, for the SWL model considered in ref. 4, the FCC cluster-crystal was found to be the stable phase. These differences in the symmetry of the cluster-crystal phase might be related to the differences in the steepness of the effective repulsion in SALR models.
Even though the LJY considered in this work and the SWL model studied in ref. 4 cannot be directly compared, another worth mentioning difference between both models is that the cluster-crystal forms more easily from the fluid phase for the LJY than for the SWL model. In particular, for the LJY model, the cluster-crystal is quickly obtained from NpT MD simulations at the appropriate thermodynamic conditions, but also from grand canonical Monte Carlo (GCMC) simulations performed with a bespoke code. However, using the same GCMC code we have never observed that the fluid assembled in a cluster-crystal in the SWL model. We performed numerous simulations for the SWL model (using the same systems sizes and simulation lengths as for the LJY model) at different thermodynamic conditions at which the cluster-crystal is stable for this model, as reported in ref. 4. However, the cluster-crystal never formed spontaneously in these simulations.
The only phase that is often predicted by theory and simulations for systems with competing interactions but that was not observed in our simulations is a bi-continuous gyroid phase.4,25 A preliminary sweep of temperatures and densities in the ranges T* = 0.30–0.20 at ΔT* = 0.01 increments and ρ* = 0.290–0.370 at Δρ* = 0.001 increments allowed us to identify partially ordered structures reminiscent of the gyroid phase at ρ* ≈ 0.325–0.335 and T* ≈ 0.25–0.30. These results indicate that this phase might also be stable for the LJY model. However, this question is beyond the scope of this work and a more thorough study on the assembly of the gyroid phase is left for future research.
 | (2) |
 | ||
| Fig. 4 Pair distribution function, g(r), and static structure factor, S(q), as a function of temperature along three isochores at which the periodic cluster (ρ* = 0.155), cylindrical (ρ* = 0.252) and lamellar (ρ* = 0.407) phases spontaneously form at sufficiently low temperatures. The cut-off radii used in the local environment analyses were chosen from the location of the first minimum in the PDF. Specifically, we chose rcut = 1.6σ for the cluster and cylindrical phases and rcut = 1.4σ for the lamellar phase. The wave-vectors corresponding to the first and second peaks in S(q) emerging from correlations between nearest clusters (qm) and between nearest particles (qp) are marked in the figures. The coherent and incoherent intermediate scattering functions were evaluated at these wave-vectors (see Fig. 10). | ||
The presence of a low-q peak in the SSF up to T* = 0.5 reveals the tendency of the particles to aggregate. This peak becomes particularly sharp for T* ≤ 0.4. It is located at approximately the same value of q, within the uncertainty of our calculations, for the three considered densities. The second peak in the SSF, corresponding to nearest neighbour particles, shifts to somewhat higher values of q as temperature decreases at the three considered densities. This is simply reflecting that nearest neighbour particles achieve a better packing at lower temperatures.
Lamellar phase. At high pressure (p* = 0.5), for which the lamellar phase forms at low temperature, the enthalpy exhibits two discontinuities with their corresponding hysteresis loops (see Fig. 5). This means that the system undergoes two first-order phase transitions: one at T* = 0.37–0.41 from the percolating fluid to a liquid lamellar phase (particles in the lamellae behave like liquid), and the other at T* = 0.28–0.34 from liquid to crystalline lamellae (particles in the lamellae behave like in solid). Both density and energy are discontinuous in the two transitions. Note that the nature of the transition from the fluid to the lamellar phase is often predicted as first-order (or weak first-order) by theories aimed to explain the behaviour of asymmetric block copolymers26 and most generally of modulated phases.27 Visual inspection of configurations at temperatures above (T* = 0.32) and below (T* = 0.20) the latter transition reveals that in both cases colloidal particles organize in lamellae, the difference being that lamellae become crystalline at the lower temperature (see Fig. 6).
 | ||
| Fig. 6 Top row: Representative configurations of liquid (T* = 0.32, left) and crystalline (T* = 0.20, right) lamellar phases at p* = 0.50. Particles with solid local environments are colored in yellow and particles with liquid local environments in green. Bottom panel: average fraction of solid particles (Ps) as obtained using the Lechner and Dellago local order parameter.28 | ||
To further confirm that this first-order transition corresponds to the internal freezing of the lamellae (at the particle scale), we analyzed the local order of the particles using the Lechner and Dellago bond order parameter ![[q with combining macron]](https://www.rsc.org/images/entities/i_char_0071_0304.gif) 6.28 In bulk systems, this order parameter is able to distinguish particles in a liquid environment from particles in compact solid environments (both FCC and HCP). As can be seen in Fig. 6, in our particular case, lamellae consist of a stack of two hexagonally-packed layers with a few small groups of particles on each surface of the lamellae. Even in this situation, the order parameter
6.28 In bulk systems, this order parameter is able to distinguish particles in a liquid environment from particles in compact solid environments (both FCC and HCP). As can be seen in Fig. 6, in our particular case, lamellae consist of a stack of two hexagonally-packed layers with a few small groups of particles on each surface of the lamellae. Even in this situation, the order parameter ![[q with combining macron]](https://www.rsc.org/images/entities/i_char_0071_0304.gif) 6 is able to distinguish particles with liquid-like environments from particles with solid-like environments. We use rcut = 1.40σ (first minimum of the PDF at low temperature, see left-bottom panel of Fig. 4) to define the first coordination shell and
6 is able to distinguish particles with liquid-like environments from particles with solid-like environments. We use rcut = 1.40σ (first minimum of the PDF at low temperature, see left-bottom panel of Fig. 4) to define the first coordination shell and ![[q with combining macron]](https://www.rsc.org/images/entities/i_char_0071_0304.gif) 6,limit = 0.43 as the threshold value to discriminate liquid-like from solid-like environments (a motivation to choose that value is provided in Section S1 in the ESI†). The probability of finding particles in solid-like local environments (Ps) as a function of temperature along the p* = 0.50 isobar is shown in Fig. 6. The curves of the fraction of solid-like particles in the lamellae exhibit a hysteresis loop, as those observed in the density and energy. In the heating run, this function adopts values close to one at very low temperature, decreases slowly as the temperature increases, until that at T* = 0.315 it undergoes a sudden drop to values close to zero, proving that lamellae are solid-like below this temperature and liquid-like above it.
6,limit = 0.43 as the threshold value to discriminate liquid-like from solid-like environments (a motivation to choose that value is provided in Section S1 in the ESI†). The probability of finding particles in solid-like local environments (Ps) as a function of temperature along the p* = 0.50 isobar is shown in Fig. 6. The curves of the fraction of solid-like particles in the lamellae exhibit a hysteresis loop, as those observed in the density and energy. In the heating run, this function adopts values close to one at very low temperature, decreases slowly as the temperature increases, until that at T* = 0.315 it undergoes a sudden drop to values close to zero, proving that lamellae are solid-like below this temperature and liquid-like above it.
Cylindrical phase. Moving now to the cylindrical phase, the enthalpy exhibits a discontinuity with an associated hysteresis loop at 0.33 < T* < 0.37, followed by a subtle change of slope at T* ≈ 0.28 (see Fig. 5). In this case, the discontinuity in the enthalpy comes mainly from a discontinuity in the energy, as density only exhibits a small jump along this transition. Our hypothesis is that the discontinuity is caused by the transition from the percolating fluid to the cylindrical phase, and the change of slope at lower temperatures is related to the internal freezing of the cylindrical clusters.
The ordering at the cluster and particles scales is readily visible from instantaneous configurations. Representative snapshots of the cylindrical phase at temperatures above (T* = 0.33) below (T* = 0.20) the change of slope are shown in the top row of Fig. 7. At both temperatures cylinders are arranged in a hexagonal lattice. However, whereas cylinders are internally ordered at T* = 0.20, they adopt more disordered configurations at T* = 0.33. In particular, the structure of the cylinders at low temperatures can be described as pentagonal tubes formed by interpenetration of icosahedra sharing a five-fold axis. The internal ordering of the cylindrical clusters with temperature was monitored by performing a common neighbour analysis (CNA),29 taking a fixed cut-off radius of 1.6σ (first minimum in the pair distribution function of the cylindrical and cluster-crystal, see Fig. 4) to consider that two particles are nearest neighbours. This analysis allows us to distinguish nearly perfect local icosahedral from disordered environments. The CNA was performed with the OVITO visualization tool.30 For each temperature along the p* = 0.20 isobar, the fraction of particles with icosahedral environment Pico was estimated by averaging the CNA results for twenty independent configurations. As can be seen in the lower panel of Fig. 7, at low temperature about 15% of the particles have an icosahedral environment. Note that in a perfect pentagonal tube of interpenetrated icosahedra only 20% of the particles (those at the center of the interpenetrated icosahedra) have an icosahedral environment, since those that are on the surface are not identified as icosahedral with the CNA due to the missing bonds. Based on this analysis, it can be concluded that, at the lowest temperature, about 75% of the particles have ordered local environments in the cylindrical clusters. As temperature increases, the average fraction of particles with icosahedral environment decreases gradually and adopts values close to zero at high temperature (i.e, above the transition from the cylindrical phase to the percolating fluid, at T* = 0.36). Interestingly, the faster change of slope of Pico occurs at exactly the same temperature (T* = 0.28) at which a small change of slope is observed in the enthalpy (Fig. 5).
Cluster-crystal phase. Finally, at low pressure (p* = 0.05), for which the cluster-crystal spontaneously forms at low temperature, the enthalpy does not exhibit any discontinuity, neither in heating nor in cooling runs. Only a small change of slope is observed at T* ≈ 0.27. A more detailed look reveals that whereas the average energy remains continuous, the density undergoes a mild discontinuity with an associated hysteresis loop in the neighbourhood of the change of slope in the entalphy (0.27 < T* < 0.30). However, as the pressure is rather low, the energy is the dominant contribution to the enthalpy and the hysteresis loop is not visible in the enthalpy.
Motivated by the finding that both the cylindrical and lamellar phases freeze at the particle scale at temperatures below the transition from the fluid to the periodic modulated phases, we also analysed the internal ordering of the clusters along the p* = 0.05 isobar. As for the cylindrical case, a CNA analysis was used to detect the onset of icosahedral ordering at the particle scale. The average fraction of particles with icosahedral symmetry, Pico, and the cluster size distribution, P(n), at different temperatures are shown in Fig. 8, together with two representative configurations of the cluster-crystal at T* = 0.2 (at which Pico ≈ 0.1) and at T* = 0.33 (at which Pico ≈ 0.02). Similarly to the cylindrical phase, at low temperature, particles at the center of the clusters exhibit local icosahedral environments (shown in yellow in Fig. 8). The cluster size distribution at T* = 0.25 takes the maximum values for sizes between n = 19 and n = 25. These clusters often adopt non-spherical configurations, and their shapes can be generally described as interpenetrated icosahedra (see Fig. 8). In particular, for n = 19 the structure consists of two interpenetrated icosahedra sharing a five-fold axis, so that the two internal particles have icosahedral environments. Covering the surface of the n = 19 cluster with additional particles allows to have up to three (n = 23) or even four (n = 26) particles with icosahedral local environments. Interestingly, these geometries correspond to putative global minima of clusters in which interactions between particles are described by Lennard-Jones and other simple models,31–33 suggesting that the enhanced probability found for these sizes might be related to their higher energetic stability. The average fraction of particles with icosahedral local environments adopts values slightly above 0.1 at low temperature, which means that nearly all the particles belong to ordered clusters (about 10%, 13% and 15% of particles with n = 19, n = 23 and n = 26 have icosahedral local environments, respectively). As temperature increases Pico decays smoothly reaching a value close to zero at T* ≥ 0.35, at which the cluster-crystal has already melted into a cluster-fluid. In this case, the structural reorganization of the cluster-fluid into the cluster-crystal occurs at similar temperatures as the internal freezing of the clusters.
The internal freezing of the modulated phases formed by colloids with competing interactions has already been reported in previous experimental10 and simulation studies.34–37 However, simulations of the SWL model at temperatures well below the temperature at which the periodic microphases become thermodynamically stable did not show evidence of such ordering at the particle scale,4 although the authors speculate that microphases probably also order internally at low temperature. In the future, it would be interesting to study whether this transition occurs at lower temperatures in potentials with a flat minimum, such as the SWL model, than in potentials with a sharp attractive minimum as the one considered in this work.
3.2 Dynamic properties
 | (3) |
The evolution of the MSD with temperature along the three chosen isochores is shown in Fig. 9. In the three cases, at high temperatures the fluid reaches the diffusive regime at long times and, as temperature decreases, the movement of the particles slows down. However, the temperature at which this slowing down occurs depends on the density.
At low densities (ρ* = 0.155) corresponding to the cluster-crystal, the MSD reaches the diffusive regime at long times for T* ≳ 0.3, and becomes sub-diffusive below T* = 0.275 (Fig. 9, left panel). This temperature coincides roughly with that at which the enthalpy (T* ≈ 0.27) exhibits a small discontinuity that signals the structural reorganization from a fluid of clusters to the cluster-crystal. At T* = 0.20 the MSD remains low for the whole duration of the simulation, with a behaviour that is reminiscent of a solid. At this low temperature, the particle movement occurs mainly via vibrational and rotational moves of the clusters about the lattice positions of the cluster-crystal, and to a lesser extent to exchange of particles between the clusters and to intra-cluster particle movements. Large translational moves of the clusters are severely hindered (see Fig. S3 and S4 and movie in the ESI†).
At this low density, the MSD exhibits three clearly distinguishable regimes at short, intermediate and long times. After the initial ballistic movement at short times, the movement of the particles moderately slows down at distances of the order of the typical bond length, dmin/σ = 21/6 − 1 = 0.12, followed by another deceleration at intermediate time and distances comparable to the cluster size dclust/σ = d0/σ − 1 ≈ 2.5 (taking the value of d0/σ at T* = 0.2 provided in Section 3.1). Beyond this distance, the movement of the particles enters the diffusive or sub-diffusive regimes depending on the temperature, as explained above. This picture is compatible with a scenario in which particles first rattle around their positions (short times), then move within the clusters by single particle displacements or by vibrations and rotations of the clusters (intermediate times), and finally travel long distances by jumping to neighbour clusters and by translations of the clusters as a whole (long times). This behaviour is very similar to that reported by Fernandez Toledano et al.8 in a study of the LJY model but with a different set of parameters so that the attraction range is much shorter than that of the model studied here (the maximum of the potential at intermediate distances is located at 1.07σ, as compared to 2.10σ in our case). In this model with a shorter range attraction, the second change of slope occurs at the maximum bond distance dmax, but in our system it correlates better with the size of the clusters (see Fig. 9).
Moving now to intermediate density (ρ* = 0.252) corresponding to the cylindrical phase (Fig. 9, central panel), the MSD reaches the diffusive regime at long times at T* ≥ 0.325 and gradually becomes sub-diffusive below this temperature. This threshold temperature is below the transition from the percolating fluid to the cylindrical phase (that occurs at 0.33 < T* < 0.37 as revealed by the hysteresis loop in the enthalpy curve). This suggests that the particles diffusion mechanisms are probably not so different in the percolating fluid and in the cylindrical phase at temperatures just below the transition. This behaviour is completely different from that observed in the cluster-crystal, in which the movement of the particles at long times starts to be sub-diffusive exactly at the transition from the cluster-fluid to the cluster-crystal. We speculate that this different behaviour might arise from the fact that particles in the cluster-crystal can only travel long distances either by migrating to other clusters or by large translational moves of the clusters as a whole. These two types of movements are largely impeded at low temperature in the cluster-crystal (see Fig. S4 in the ESI†). However, in the cylindrical phase, particles might still move long distances without the need to resort to those two types of movements, simply by displacements along the axial direction of the cylinders. Note that the long-time MSD exhibits large departures from the diffusive behaviour at temperatures starting at T* = 0.30 and specially below T* = 0.275, indicating that the particle movement is further impeded below this temperature, coincident with the onset of structural intra-cylinder ordering at T* = 0.28.
At short and intermediate times, three clearly different regions are again observed in the MSD at ρ* = 0.252. There is an initial slowing down of the movement of the particles at distances similar to the average bond length dmin/σ, followed by a second slowing down at distances comparable to the cylinder diameter dclust/σ = d0/σ − 1 = 2.3 (taking the value of d0/σ = 3.3 reported at T* = 0.2 in Section 3.1). Displacements larger than the diameter of the cylinder can only be achieved either by particle displacements along the axial direction of the cylinders or by particle jumps between neighbouring clusters.
Finally, at high density (ρ* = 0.407), at which the lamellar phase forms at low temperature (Fig. 9, right panel), the movement of the particles at long times is diffusive at T* ≳ 0.30 and sub-diffusive below this temperature. This change in the dynamic behaviour occurs roughly at the same temperature at which the freezing of the lamellae takes place (0.28 ≲ T* ≲ 0.34). Note that the MSD at T* = 0.30 was obtained in a simulation from the cooling branch of the hysteresis loop. At lower temperatures, the diffusion of the particles is significantly reduced, consistently with the fact that the bond correlation function adopts values close to one even after long simulation times (see Fig. S3 in the ESI†). Regarding the behaviour at short and intermediate times, the MSD exhibits only one slowing down at the typical bond distance (dmin/σ). The second slowing down observed at distances compatible with the cluster size for the cluster-crystal and the cylindrical phase is not significant for the lamellar phase. We speculate that as lamellae are infinite in two dimensions of space, the width of the lamellae does not pose a strong constraint on the particles displacements.
Note that the MSD of the lamellar phase was measured in simulations in which the lamellae are oriented along the diagonal of the cubic simulation box. Curiously, when the lamellae are oriented parallel to one of the sides, solid-like lamellae exhibit flat surfaces and can slide with respect to the adjacent lamellae just by collective movement, giving rise to large MSD. However, it is difficult to quantify the magnitude of the drift as it is very likely affected by finite size effects, the simplifications introduced in our effective potential and the neglect of hydrodynamic interactions. As our aim is to investigate the single particle displacement, we performed the dynamic study using a configuration in which the lamellae are oriented along the diagonal of the box, so that the sliding of the layers is prevented by the periodicity of the simulation box. Similarly, there are many examples in the literature in which floating or sliding non-interacting sheets and cylindrical phases have been reported, such as S-layer proteins,38 CdTe nanocrystals,39 nanosheets of diblock copolymers,40 the columnar phase formed by DNA-cationic-lipid complexes,41 or inverse patchy colloids.42
 | (4) |
 | (5) |
These functions are often used to characterize the structural relaxation of colloidal systems with competing interactions.14,16,36,43 Here, we evaluated F(q,t) and Fs(q,t) at wave-vectors close to the first (qm) and second peaks (qp) that emerge in the structure factor at intermediate and low temperature (see Fig. 4), the first coming from correlations between nearest neighbour clusters and the second one resulting from nearest neighbour particles, respectively.
The evolution with temperature of the correlations at the microphase scale (corresponding to the pre-peak at  , see Fig. 4) is shown in the left panels of Fig. 10. The first observation is that at T* ≳ 0.4 both the coherent and incoherent functions exhibit a seemly one-step decay at the three densities considered, going to zero in the timescale of our simulations with similar relaxation times. In this temperature range, the decay of the correlations becomes somewhat slower as density increases. The scattering functions at T* ≳ 0.4 can often be fitted reasonably well to a stretched exponential, although the observed deviations might reveal a complex relaxation process in which several mechanisms occur at different timescales (see Fig. S5 and S6 in the ESI†).
, see Fig. 4) is shown in the left panels of Fig. 10. The first observation is that at T* ≳ 0.4 both the coherent and incoherent functions exhibit a seemly one-step decay at the three densities considered, going to zero in the timescale of our simulations with similar relaxation times. In this temperature range, the decay of the correlations becomes somewhat slower as density increases. The scattering functions at T* ≳ 0.4 can often be fitted reasonably well to a stretched exponential, although the observed deviations might reveal a complex relaxation process in which several mechanisms occur at different timescales (see Fig. S5 and S6 in the ESI†).
At T* ≲ 0.3, the behaviour is markedly different depending on the density. At the lower density (ρ* = 0.155), both the coherent and incoherent correlations decay to zero at T* = 0.3, at which the fluid of clusters is the stable phase. Specially in the incoherent correlation function two decay steps can be clearly identified, which indicates that at least two mechanisms with different relaxation times are involved. At T* = 0.2, both the coherent and the incoherent scattering functions experience a first decay followed by a plateau that survives over the timescale of our simulations. At this low temperature, large translational movements of the clusters are largely impeded, but they experience vibrational and rotational moves about the lattice positions of the cluster-crystal (see the movie provided in the ESI†). Note that cluster rotational moves had already been reported in a previous study by Toledano et al.8 We speculate that the first decay is associated to these vibrational and orientational moves of the clusters. This is consistent with the fact that the plateau value is significantly higher for the coherent than for the incoherent scattering functions.
At intermediate density (ρ* = 0.252) and at T* ≤ 0.3 neither the coherent nor the incoherent correlation functions at the microphase scale decay to zero in the timescale of our simulations, indicating that much longer times are needed to achieve a good sampling at these conditions. At T* = 0.2 the difference between the collective and single particle correlations is lower than that observed in the cluster phase. Our hypothesis is that equivalent rotations of the cylinders as those observed in the cluster-crystal are largely impeded in the cylindrical phase due to the periodic boundary conditions. On the contrary, at high density (ρ* = 0.407), the incoherent correlations decay to zero at T* = 0.3, but the collective correlations do not. At T* = 0.2 large correlations are observed either in the coherent and incoherent correlation functions at the microphase scale, indicating the solid-like character of the lamellae. This is further confirmed by measurements of the bond correlation function, that show that most of the particles remain bonded to the same neighbour particles over the timescale of our simulations (see Fig. S3 ESI†).
The evolution with temperature of the correlations at the particle scale, measured at the second peak in S(q) (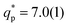 for the cluster-crystal,
for the cluster-crystal,  for the cylindrical, and
for the cylindrical, and  for the lamellar) is shown in the right panels of Fig. 10. In this case, the correlations decay to zero quite rapidly at all temperatures and at all densities, except for the lamellar phase at T* = 0.2. As shown in Fig. S3 in the ESI,† at this low temperature, in the lamellar phase most of the particles remain surrounded by the same neighbour particles for at least 10 million MD steps. However, in the cluster-crystal and the cylindrical hexagonal phase, although slowly, a moderately large number of particles is able to exchange neighbours in the course of our simulations. Correlations at the particle scale also increase with density at constant temperature.
for the lamellar) is shown in the right panels of Fig. 10. In this case, the correlations decay to zero quite rapidly at all temperatures and at all densities, except for the lamellar phase at T* = 0.2. As shown in Fig. S3 in the ESI,† at this low temperature, in the lamellar phase most of the particles remain surrounded by the same neighbour particles for at least 10 million MD steps. However, in the cluster-crystal and the cylindrical hexagonal phase, although slowly, a moderately large number of particles is able to exchange neighbours in the course of our simulations. Correlations at the particle scale also increase with density at constant temperature.
4 Summary and conclusions
In this article we have performed a thermodynamic, structural and dynamic study of a colloidal system with competing interactions. We have found that, for the model potential considered, the cluster-crystal and the cylindrical and lamellar phases freeze at low temperature. Although the freezing of the lamellar phase has already been documented in former studies,34,35 in this work we show that similar freezing transformations can also occur in the cluster-crystal and cylindrical phases, but discontinuities in the energy, the density or the order parameter coincident with the freezing of the microphases were only observed in the lamellar phase. Note that as thermodynamic phase transitions are not possible in one-dimensional systems and as cylindrical clusters can be considered as systems whose dimension is intermediate between one- and two-, the cylindrical phases formed in SALR systems could be used to investigate the nature of the internal order–disorder transition as the radius of the cylinders increases (which might be achieved by increasing the attraction interaction range).In the dynamical analysis we did not find any signal of dynamic arrest at temperatures just above those at which periodic microphases emerge and that could kinetically prevent their formation in experiments. Besides that, the three periodic microphases formed readily in our unbiased simulations, which indicates that the free energy barriers for the nucleation of the periodic modulated phases from the fluid phase are not very high. We speculate that, although the strength of the attractive and repulsive contributions can be modified in experiments with colloids, these phases have not yet been observed in the laboratory due to the difficulty of finely tuning the appropriate length scales of the effective interactions.11 On the other hand, the thermodynamic phase space has not been sufficiently explored in experimental colloidal systems so far.14
In previous work, it has been shown that colloidal systems with competing interactions may be tuned by confinement to form exotic structures that are not present in bulk or to help the nucleation of periodic microphases that are stable in bulk according to theory and simulations but that remain experimentally elusive.44–47 Thus, in the future, it would be also interesting to study the dynamics under confinement. We wonder if periodic microphases can be also made kinetically favoured (and not only thermodynamically) under the appropriate confinement conditions.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
This publication is part of a project that has received funding from the European Unions Horizon 2020 research and innovation programme under the Marie Skłodowska-Curie grant agreement No. 711859. Scientific work funded from the financial resources for science in the years 2017–2021 awarded by the Polish Ministry of Science and Higher Education for the implementation of an international co-financed project. We would also like to acknowledge the support from NCN, Grant No 2018/30/Q/ST3/00434 and from the Agencia Estatal de Investigación and the Fondo Europeo de Desarrollo Regional (FEDER), Grant No FIS2017-89361-C3-2-P.References
- A. Ciach, J. Pekalski and W. Góźdź, Soft Matter, 2013, 9, 6301–6308 RSC.
- A. Ciach and W. Góźdź, Condens. Matter Phys., 2010, 13, 23603 CrossRef.
- D. Pini and A. Parola, Soft Matter, 2017, 13, 9259–9272 RSC.
- Y. Zhuang, K. Zhang and P. Charbonneau, Phys. Rev. Lett., 2016, 116, 098301 CrossRef PubMed.
- Y. Zhuang and P. Charbonneau, J. Phys. Chem. B, 2016, 120, 6178–6188 CrossRef CAS PubMed.
- A. I. Campbell, V. J. Anderson, J. S. van Duijneveldt and P. Bartlett, Phys. Rev. Lett., 2005, 94, 208301 CrossRef PubMed.
- J. Ruiz-Franco and E. Zaccarelli, Annu. Rev. Condens. Matter Phys., 2021, 12, 51–70 CrossRef CAS.
- J. C. F. Toledano, F. Sciortino and E. Zaccarelli, Soft Matter, 2009, 5, 2390–2398 RSC.
- C. L. Klix, C. P. Royall and H. Tanaka, Phys. Rev. Lett., 2010, 104, 165702 CrossRef PubMed.
- T. H. Zhang, B. W. M. Kuipers, W. de Tian, J. Groenewold and W. K. Kegel, Soft Matter, 2015, 11, 297–302 RSC.
- C. P. Royall, Soft Matter, 2018, 14, 4020–4028 RSC.
- F. Cardinaux, E. Zaccarelli, A. Stradner, S. Bucciarelli, B. Farago, S. U. Egelhaaf, F. Sciortino and P. Schurtenberger, J. Phys. Chem. B, 2011, 115, 7227–7237 CrossRef CAS PubMed.
- P. D. Godfrin, S. D. Hudson, K. Hong, L. Porcar, P. Falus, N. J. Wagner and Y. Liu, Phys. Rev. Lett., 2015, 115, 228302 CrossRef PubMed.
- Y. Zhuang and P. Charbonneau, J. Chem. Phys., 2017, 147, 091102 CrossRef PubMed.
- F. Sciortino, S. Mossa, E. Zaccarelli and P. Tartaglia, Phys. Rev. Lett., 2004, 93, 055701 CrossRef PubMed.
- F. Sciortino, P. Tartaglia and E. Zaccarelli, J. Phys. Chem. B, 2005, 109, 21942–21953 CrossRef CAS PubMed.
- E. Mani, W. Lechner, W. K. Kegel and P. G. Bolhuis, Soft Matter, 2014, 10, 4479–4486 RSC.
- A. P. Santos, J. Pekalski and A. Z. Panagiotopoulos, Soft Matter, 2017, 13, 8055–8063 RSC.
- M. G. Noro and D. Frenkel, J. Chem. Phys., 2000, 113, 2941 CrossRef CAS.
- P. D. Godfrin, N. E. Valadez-Pérez, R. Castañeda-Priego, N. J. Wagner and Y. Liu, Soft Matter, 2014, 10, 5061–5071 RSC.
- S. Plimpton, J. Comput. Phys., 1995, 117, 1–19 CrossRef CAS.
- M. P. Allen and D. J. Tildesley, Computer Simulation of Liquids, Oxford university press, 2017 Search PubMed.
- J. Škvor and I. Nezbeda, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2009, 79, 041141 CrossRef PubMed.
- M. Spellings and S. C. Glotzer, AIChE J., 2018, 64, 2198–2206 CrossRef CAS.
- A. Ciach, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2008, 78, 061505 CrossRef CAS PubMed.
- F. S. Bates and G. H. Fredrickson, Annu. Rev. Phys. Chem., 1990, 41, 525–557 CrossRef CAS PubMed.
- M. Seul and D. Andelman, Science, 1995, 267, 476–483 CrossRef CAS PubMed.
- W. Lechner and C. Dellago, J. Chem. Phys., 2008, 129, 114707 CrossRef PubMed.
- D. Faken and H. Jónsson, Comput. Mater. Sci., 1994, 2, 279–286 CrossRef CAS.
- A. Stukowski, Model. Simul. Mater. Sci. Eng., 2010, 18, 015012 CrossRef.
- J. P. K. Doye, D. J. Wales, F. H. Zetterling and D. Dzugutov, J. Chem. Phys., 2003, 118, 2792 CrossRef CAS.
- J. P. K. Doye and D. J. Wales, J. Chem. Soc., Faraday Trans., 1997, 4233 RSC.
- D. J. Wales and J. P. K. Doye, J. Phys. Chem. A, 1997, 101, 5111 CrossRef CAS.
- A. De Candia, E. Del Gado, A. Fierro, N. Sator, M. Tarzia and A. Coniglio, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2006, 74, 010403 CrossRef CAS PubMed.
- A. Coniglio, A. de Candia and A. Fierro, Mol. Phys., 2011, 109, 2981–2987 CrossRef CAS.
- D. F. Schwanzer, D. Coslovich and G. Kahl, J. Phys.: Condens. Matter, 2016, 28, 414015 CrossRef PubMed.
- J. Pekalski, W. Rzadkowski and A. Z. Panagiotopoulos, J. Chem. Phys., 2020, 152, 204905 CrossRef CAS PubMed.
- U. B. Sleytr, C. Huber, N. Ilk, D. Pum, B. Schuster and E. M. Egelseer, FEMS Microbiol. Lett., 2007, 267, 131–144 CrossRef CAS PubMed.
- Z. Tang, Z. Zhangm, Y. Wang, S. C. Glotzer and N. A. Kotov, Science, 2006, 314, 274–278 CrossRef CAS PubMed.
- Z. Shi, Y. Wei, C. Zhu, J. Sun and Z. Li, Macromolecules, 2018, 51, 6344 CrossRef CAS.
- C. S. O'Hern and T. C. Lubensky, Phys. Rev. Lett., 1998, 80, 4345 CrossRef.
- E. G. Noya, I. Kolovos, G. Doppelbauer, G. Kahl and E. Bianchi, Soft Matter, 2014, 10, 8464 RSC.
- Z. Varga and J. Swan, Soft Matter, 2016, 12, 7670–7681 RSC.
- N. G. Almarza, J. Pekalski and A. Ciach, Soft Matter, 2016, 12, 7551 RSC.
- H. Serna, E. G. Noya and W. T. Góźdź, Langmuir, 2018, 35, 702–708 CrossRef PubMed.
- H. Serna, E. G. Noya and W. T. Góźdź, Soft Matter, 2020, 16, 718–727 RSC.
- H. Serna, E. G. Noya and W. T. Góźdź, J. Phys. Chem. B, 2020, 124, 10567–10577 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/d1sm00445j |
| This journal is © The Royal Society of Chemistry 2021 |