Temperature and salt controlled tuning of protein clusters

Abstract

The formation of molecular assemblies in protein solutions is of strong interest both from a fundamental viewpoint and for biomedical applications. While ordered and desired protein assemblies are indispensable for some biological functions, undesired protein condensation can induce serious diseases. As a common cofactor, the presence of salt ions is essential for some biological processes involving proteins, and in aqueous suspensions of proteins can also give rise to complex phase diagrams including homogeneous solutions, large aggregates, and dissolution regimes. Here, we systematically study the cluster formation approaching the phase separation in aqueous solutions of the globular protein BSA as a function of temperature (T), the protein concentration (c_p) and the concentrations of the trivalent salts YCl₃ and LaCl₃ (c_s). As an important complement to structural, i.e. time-averaged, techniques we employ a dynamical technique that can detect clusters even when they are transient on the order of a few nanoseconds. By employing incoherent neutron spectroscopy, we unambiguously determine the short-time self-diffusion of the protein clusters depending on c_p, c_s and T. We determine the cluster size in terms of effective hydrodynamic radii as manifested by the cluster center-of-mass diffusion coefficients D. For both salts, we find a simple functional form D(c_p, c_s, T) in the parameter range explored. The calculated inter-particle attraction strength, determined from the microscopic and short-time diffusive properties of the samples, increases with salt concentration and temperature in the regime investigated and can be linked to the macroscopic behavior of the samples.

---

1 Introduction

The quantitative understanding and the rational control of the formation of protein clusters in liquid suspensions is of interest for applications in the biomedical field since protein aggregation plays a role in diseases,¹ such as cataracts² or Alzheimer's disease.³ Moreover, drug delivery can be affected by protein clusters in several ways: for instance, therapeutic proteins can be concentrated in solutions of transient clusters, whilst still maintaining their functionality⁴ and a triggered disassembly of reversible clusters of therapeutic proteins can be used e.g. for drug delivery purposes.^5,6 The rational control of clusters is particularly important at high protein concentrations⁷ relevant for drug formulations.⁸ Moreover, the sensitivity of such formulations to temperature changes from refrigerated storage to up to physiological conditions is important. Studies at high protein concentrations are also relevant for the understanding of diffusive processes of proteins in their highly crowded natural environments.⁹ At the same time, the resulting viscosity of the therapeutic may become an issue.^10–13 An understanding of the cluster formation might help to prevent the formation of medically problematic irreversible protein clusters.¹⁴ This motivates the pursuit of a quantitative physical modeling of protein aggregation and dissolution.

For instance, cluster formation in aqueous solutions of lysozyme^15–17 and of monoclonal antibodies^18–20 has been investigated using different techniques such as small-angle scattering,¹⁵ neutron-spin echo spectroscopy,^16,19,21 nuclear magnetic resonance,¹⁷ and rheology.²⁰ More recently, theoretical descriptions of transient protein cluster formation, coarse-grained, as well as fully atomistic molecular dynamics simulations^22–24 have been presented.

One of the central points of such studies was that a purely structural characterization of amorphous clusters can often be ambiguous^16,25 since similar signatures are expected for both long-living and transient clusters. In this situation, dynamic signatures are of utmost importance, as they provide information about clusters which are not only closely arranged, but also move as a whole on a certain time scale.^16,21

In this study, we address the effect of cations and temperature on cluster formation in aqueous solutions of the protein bovine serum albumin (BSA) by monitoring its self-diffusion. BSA solutions in the presence of various cations constitute a well-explored and robust model system in terms of its macroscopic phase behavior as well as in terms of its structure and protein–protein interactions accessible by small angle scattering.^26,27 The cations binding to the protein surface induce charge compensation and, ultimately, charge inversion for increasing concentrations c_s of trivalent salts in aqueous solutions of negatively charged globular proteins, which results in complex phase diagrams (Fig. 1a).^26,27 Nevertheless, a clear understanding of the cluster formation upon approaching phase transitions is still missing.

Fig. 1 (a) Schematic view of the phase diagram of the protein solutions investigated, depending on the temperature T, protein concentration c_p, and salt concentration c_s. Blue dots represent the systematic measurements presented. (b) Artistic rendering of the cluster formation, according to the findings in this work, based on the actual master curves for the normalized diffusion D versus the normalized YCl₃ salt concentration and temperature (Fig. 3), illustrating growing clusters with rising temperature and salt concentration.

The various phases comprise regimes that manifest themselves visually as transparent solution regimes and as turbid regimes, respectively. In most of the systems studied, a transparent solution regime can be observed at low salt concentrations c_s ≪ c* (Regime I) as well as at very high salt concentrations c_s ≫ c** (Regime III), where c* and c** denote the respective phase boundaries that depend on c_p. Within the range c* < c_s < c** (Regime II), protein condensation and formation of large clusters can be observed. In this study, we investigate samples in Regime I systematically approaching c*, i.e., c_s → c* with c_s < c*, at different temperatures (Fig. 1b).

As the underlying theoretical picture, ion binding and bridging, i.e. a cation-activated attraction, have been used to explain the experimental phase diagram,²⁸ which predicts cluster formation when approaching c*. This picture of ion binding was experimentally investigated by isothermal titration calorimetry (ITC) and ζ-potential measurements.^29,30

Previous work using both dynamic light scattering (DLS)³¹ and quasi-elastic neutron scattering (QENS)³² indeed found signatures of clusters. While the interpretation of DLS results is challenging due to the attractive interactions influencing the observed gradient diffusion, incoherent QENS directly provides the apparent center-of-mass self-diffusion D of the protein monomers and clusters.^32,33 Here, the term “apparent” accounts for the simultaneous observation of the rotational and translational contributions to the center-of-mass diffusion at large momentum transfers. Due to the high q investigated, corresponding to length scales much smaller than the protein–protein distance, and due to the dominant incoherent scattering from the proteins in the heavy water (D₂O) solvent, the observation of protein center-of-mass self-dynamics is an intrinsic property of our experiment and not a model-based approximation. Therefore, the observable center-of-mass diffusion directly reflects the hydrodynamic radius and therefore the cluster size without requiring any assumption on the monomer–monomer or cluster–cluster correlation lengths. Moreover, QENS can access solutions with very high protein concentrations, including opaque solutions, that are difficult or impossible to access by DLS due to multiple scattering effects. As opposed to DLS, QENS in the setting used in the present study probes the short-time diffusion in terms of colloid physics. On this time scale on the order of one nanosecond, hydrodynamic interactions dominate over direct interactions such as protein–protein collisions, and the root mean square displacement of the proteins amounts to only a small fraction of their radius. While a distribution of monomers and dimers of BSA in solution has been observed at low protein concentrations in the absence of salt,^34,35 at the high protein concentrations investigated here, the salt-free solutions agree with the picture of an effectively monomeric system.^36–38

Previously,³² cluster formation of BSA in D₂O was observed upon approaching c* for YCl₃ at constant temperature (295 K), using incoherent QENS. A master curve for D depending only on the ratio c_s/c_p was found for these conditions. Here, we present a study of the influence of temperature as the crucial control parameter on the system. Moreover, we compare two different salts, namely YCl₃ and LaCl₃, which differ by their cation radii and hydration number in solution and have previously been found to induce qualitatively similar but quantitatively different phase behaviors of BSA.^39,40 A fundamental understanding of such differences can be highly relevant for instance for enzymatic activity studies, as previously reported specifically for Y³⁺ and La³⁺ cations.⁴¹ Importantly, we find a temperature dependence of the cluster formation which can be described by simple heuristic models, and we use a more advanced model based on patchy-particle colloid physics to determine thermodynamic parameters driving the cluster formation. Although even this advanced colloid picture may still be overly simplistic due to assumptions made regarding the non-fractality of clusters and a fixed number of binding sites, this picture paves the way for further investigations.

2 Experiment and methods

BSA was obtained from Sigma Aldrich as lyophilized powder (catalog number A3059, 98% purity) and used without additional purification. YCl₃ (18 682, 99.9% purity), LaCl₃ (87 911, anhydrous, 99.9% purity) and D₂O (14 764, 99.8% purity) were obtained from Alfa Aesar. The samples were prepared following the protocols established in earlier studies^32,42 using 100 mM salt stock solutions.

The experiments were carried out on the cold neutron backscattering silicon spectrometer (BASIS) at the Spallation Neutron Source (SNS), Oak Ridge, Tennessee, using its Si(111) analyzers (experiment numbers IPTS 15974.1 and 18578.1). BASIS provides an energy resolution of approx. 3.5 μeV FWHM and an energy range −100 μeV ≤ ħω ≤ +100 μeV at a scattering vector range 0.4 Å⁻¹ ≤ q ≤ 1.9 Å⁻¹.⁴³ The samples were kept in indium-sealed double-walled cylindrical aluminum containers (distance between the walls Δr = 0.15 mm, outer diameter 23 mm) and inserted into a closed-cycle cryostat for the measurements. Raw data were reduced using Mantid⁴⁴ and subsequently corrected for self-shielding⁴⁵ and analyzed using own routines in Matlab 2019a (The MathWorks, Inc.) employing the Optimization and Curve Fitting Toolboxes.

The BSA solutions were measured at three different protein concentrations c_p = 100, 200, 300 mg ml⁻¹ prepared by adding the given protein mass to D₂O, such that the total effective hydrodynamic volume fractions in these sample series were defined by φ_h = c_pξ/(1 + c_pξ)·(R_h/R)³, ξ = 0.74 ml g⁻¹ being the protein specific volume, R_h and R the hydrodynamic and dry protein radius, respectively. Thus, we measured the salt series at φ_h = 0.18, 0.33, and 0.46. While a distribution of monomers and dimers of BSA in solution has been observed at low protein concentrations in the absence of salt,^34,35 at the high protein concentrations investigated here, the solutions free from tri-valent salts agree with the picture of an effectively monomeric system,³⁶ corroborated by the onset of self-buffering.

3 Theoretical description of the scattering function of a solution containing clusters

3.1 Quasi-elastic neutron scattering (QENS)

Being a function of the energy transfer ħω and the momentum transfer ħq, the incoherent quasi-elastic scattering signal S(q, ω) of protein solutions can be described by a sum of the contributions of the solvent S_D2O(q, ω) and the protein S_Prot(q, ω) convoluted with the instrumental resolution function [scr R, script letter R]:

S(q, ω) = [scr R, script letter R] ⊗ {β_D2OS_D2O(q, ω) + βS_Prot(q, ω)} (1)

with the q-dependent scalars β(q) and β_D2O(q). To compare the solvent (D₂O) contribution in a concentrated protein solution to a pure solvent measurement, the signal has to be rescaled by a factor β_D2O accounting for the protein volume fraction.³³ Since proteins are not rigid bodies, their scattering signal in the case of monodisperse solutions contains the scattering signals from their global, i.e. center-of-mass, and internal diffusive dynamics, respectively, which we separate according to:^33,46–48with the Dirac delta function δ(ω) and the elastic incoherent structure factor (EISF) A₀ accounting for confined motions in the protein.^32,33,49,50 The EISF is well-described by the superposition of diffusive motion confined in a sphere, approximately accounting for protein backbone motions, and jumps between three sites, accounting for molecular reorientations, notably those of methyl groups.^42,50

Depending on the nature of the protein studied, several models have been used to describe its internal dynamics, such as jump diffusion models,^33,51 descriptions based on energy landscapes,⁵² and models of switching diffusive states.^42,53 The latter one, described in detail in the ESI,† is used here in the global fits to describe the internal dynamics, by accounting for the superposition of the separate contributions from the protein backbone and side chains, respectively. Importantly, by ‘global fits’ we denote fits in which not only the solvent water contribution but also the dependencies of all components of the model on the momentum transfer are fixed, such that the number of free fit parameters results in a well-posed optimization. For the center-of-mass dynamics, numerous QENS studies confirm a Brownian self-diffusion of the proteins in solution in the short-time limit.³³ The scattering function S_Prot,global(q, ω) can be described by one apparent global center-of-mass diffusion coefficient D_app, which contains contributions from rotational and translational diffusion.^33,54,55 In the presence of clusters, D_app represents their averaged diffusion coefficient given by eqn (10).^32,33,56 This scattering function can be expressed by a Lorentzian function with the width γ = D_appq²:

S_Prot,global(q, ω) = [script L]_γ(ω) (3)

The previously described expressions can be used to describe the experimentally measured scattering function.

Given the limited range and resolution of the spectrometer in energy and momentum transfer, as well as in view of our already complex but still simplified model, it is evident that not all types of motion in the sample can be fully captured or described. Types of motion that may be missed for instance include motions of large protein subdomains or relative motions of proteins within clusters.^35,57

3.2 Cluster statistics

We now present a framework for the further analysis of the results. In a system containing scatterers with N different sizes, which diffuse independently, the scattering function can be written as a sum of the individual contributionswith the relative weight w_j of particles of type j. In a cluster-forming system with patch attraction, these relative weights w_j can be replaced using the cluster size distribution, ρ_n, which can be described by the Flory–Stockmeyer theory as a function of the binding probability p_b, and the number of patches per particle m:^32,58with ρ being the total number density of particles. The rotational and translational diffusion coefficients of a n-cluster can be calculated with the Stokes–Einstein relations for the dilute limit, and can then be rescaled to the corresponding volume fraction φ by the scalar functions f_t(φ) (ref. 59, eqn (11) and (12)) and f_r(φ) (ref. 60 and eqn (21)):with the temperature-dependent viscosity of D₂O η(T)⁶¹ and the radius . The relation 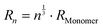does not imply compact clusters, but the absence of fractality. The central assumption is that each monomer adds the volume corresponding to the effective hydrodynamic radius R₁ to the cluster volume. Since the hydrodynamic radius R₁ of a monomer is larger than the bare volume for nonspherical proteins such as BSA, this effective volume accounts roughly for effects of nonspherical shape and intra-cluster water. These assumptions may be exceedingly simplistic, but only relate to the scaling of the short-time diffusive properties. A similar volume fraction scaling was assumed for all particles in the solution.

The apparent diffusion coefficient, combining the contributions of rotational and translational diffusion, for each n-cluster by assuming a homogeneous hydrogen distribution of a sphere with radius R_n and minimizing the [Doublestruck L]² norm:³³

with the scalar a(n, q) depending on q and γ = D_app·q². The scattering function for the center-of-mass diffusion, which can be described with one single Lorentzian [script L]_γ(ω) for a monodisperse solution, therefore results in³²In first order, the scattering function can be approximated by a Lorentzian function [script L]_γglobal(ω) with the width γ_global = D_globalq². We use this relation to obtain the model parameter p_b from the experimental global diffusion coefficient D_global ≤ D_Mono, where D_Mono denotes the diffusion coefficient of monomers. Practically, we generate a calibration curve assuming an equidistant list of diffusion coefficients D_global, generate a scattering function for each coefficient and fit each with eqn (10). It is, thus, possible to determine the dependence of the diffusion coefficient on p_b. Normalizing this dependence by the diffusion coefficient of the monomer (Fig. S7, ESI†) results in a calibration curve, which can then be used to transform the experimentally obtained normalized diffusion coefficients shown in Fig. 3 into binding probabilities p_b (Fig. 4).

From p_b, a semiquantitative understanding of the underlying binding energies can be found using Wertheim theory for patchy particles with m bonding sites. The binding energy p_b can therefore be described as a function of the attraction strength ε_AB between two particles A and B:^28,62,63

Δ_AB = 4πg_HS(d)K_ABF_AB (12)

with K_AB defined by Chapman et al.⁶³ as an integral measuring the volume associated with the binding sites A and B and the Carnahan–Starling contact value for the pair correlation function g_HS(d) of the hard sphere reference system with the particle diameter d.²⁸

4 Results and discussion

Data reduction followed previously published protocols.^33,64 Taking into account the resolution function [scr R, script letter R](q, ω) with five fixed non-centered Gaussian functions for each q, it is possible to model the scattering signal using eqn (1) and (2). In all fits performed, the scattering signal contribution of D₂O was rescaled to take into account the specific volume of BSA and modeled with one Lorentzian based on data from neutron time-of-flight spectroscopy.³³

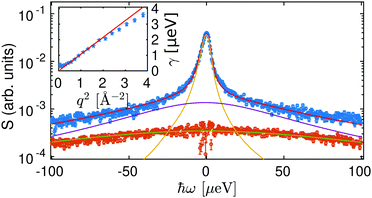
In a first approach, the scattering functions describing the contribution of the center-of-mass and internal diffusive dynamics were modeled by two Lorentzians.^32,33,56,64 An example spectrum with a corresponding fit is displayed in Fig. 2. The width γ of the Lorentzian [script L]_γ(ω), accounting for the center-of-mass diffusion, can be described with the diffusion coefficient D = γ/q² (inset of Fig. 2 and Fig. S1, ESI†) revealing a simple Fickian diffusion.

Fig. 2 Example spectrum (blue circles) from a BSA-YCl₃ solution with c_p = 200 mg ml⁻¹, c_s = 15.1 mM, T = 280 K at q = 1.15 Å⁻¹ fitted with two free Lorentzians describing the protein diffusion and a third fixed Lorentzian accounting for the D₂O contribution (brown circles) that is rescaled to account for the excluded volume by the proteins. Red, yellow, violet and green lines represent the fit result, the center-of-mass and internal diffusion as well as the water contribution (D₂O), respectively. Inset: HWHM γ of the narrower Lorentzian (symbols) versus q² and associated fit (line) yielding the apparent center-of-mass short-time self-diffusion D.

Second, this q-dependence was fixed in a subsequent fit to obtain a more robust procedure describing the energy transfer as well as the q-dependence simultaneously. The internal dynamics are described using the switching model reported in eqn (S1) of the ESI.† Representative fits are shown in the ESI† (Fig. S2). Fig. 3 shows the normalized diffusion coefficients obtained from these fits for both salts investigated (YCl₃ and LaCl₃) for different temperatures and for different ratios of the salt concentration (c_s) and protein concentration (c_p) c_s/c_p. To compare this slowing down with the previous studies,³² the data at a given temperature and protein concentration were fitted for both salts individually by

with a₂, a₄ and D⁰ = D(c_s = 0, c_p) being fit parameters. D(c_s = 0, c_p) was used for the normalization of the corresponding diffusion coefficients of the salt series. The fits are shown in Fig. 3. The temperature dependence of the fit parameters a₂ and a₄ is depicted in Fig. S5 (ESI†). In this representation, the significant differences between the two salts become apparent.

Fig. 3 Normalized observable center-of-mass diffusion coefficients D(c_s/c_p)/D(c_s = 0, c_p) as a function of c_s/c_p for different temperatures. Diffusion coefficients of samples with c_p = 200 mg ml⁻¹ and c_p = 300 mg ml⁻¹ are denoted by stars and squares, respectively. Red filled and blue open symbols represent samples with YCl₃ and LaCl₃, respectively. The dotted lines represent fits according to eqn (14).

The normalization of the diffusion coefficient to D⁰ = D(c_s = 0, c_p) eliminates both the slowing-down of the scattering particles due to crowding⁶⁴ and the Stokes–Einstein temperature dependencies of the salt-free protein solution.³² Changes in the normalized diffusion coefficients can therefore be related to changes in the average hydrodynamic radii of the particles studied. For each temperature and type of salt, normalized diffusion coefficients at different protein concentrations decrease by the same amount as a function of the number of salt ions per protein.

As can be seen in Fig. 3, the normalized diffusion coefficients obtained from the sample series containing LaCl₃ decay more slowly than the normalized diffusion coefficients of the samples with YCl₃. At the same c_s/c_p and at the nanosecond time and nanometer length scales given by the experimental set-up, YCl₃ induces a cluster size distribution with a larger average cluster size than LaCl₃. In other words, at a given salt and protein concentration, the protein clusters are bigger in the case of YCl₃ than in the case of LaCl₃. On the macroscopic level, this results in a broader second regime in which clusters render the solution turbid, which is consistent with previous studies of the phase diagram.³⁹

From the normalized diffusion coefficients, the stickiness parameter can be calculated.⁶⁵ Its dependence on temperature and salt concentration is shown in Fig. S6 (ESI†).

The internal dynamics described by eqn (S1) do not change with an increasing number of salt ions per protein within the accuracy of our experiment (see Fig. S3 and S4, ESI†). While in the salt-free solution, the model describes the diffusive dynamics of the backbones and the side chains,⁴² in the presence of clusters it also averages over the internal diffusion of the proteins within the clusters. The fact that the fit parameters for the internal dynamics do not change with increasing salt concentration, i.e. during cluster formation, indicates that the internal dynamics on the time scales investigated are not influenced by the presence of the salt ions and verifies a posteriori the simplified fit approach.

Having established the experimental results, we now turn to the determination of the cluster distribution. To determine the binding probability p_b, the experimental normalized diffusion coefficients D/D₀ and its errors can be used to calculate the protein–protein binding probabilities³² using calibration curves (Fig. S7, ESI†) based on eqn (6)–(10) with m = 4 patches. The resulting p_b are depicted in Fig. 4. The cluster radii were calculated based on the assumption that the clusters scale with an effective volume thus . As shown in Fig. S8 (ESI†), the choice of m = 4 patches (e.g. compared with m = 6) does change the quantitative but not the qualitative trend of the calculated p_b. The resulting p_b can be compared by normalizing it to the percolation limit p^max_b = (m − 1)⁻¹.⁶⁶ We therefore assume m = 4 independent from c_p and c_s for the further analysis.

Fig. 4 Salt-induced protein–protein binding probability p_b, calculated as described in the text, as a function of the number of salt cations per protein molecule for different temperatures. Stars and circles represent values of c_p = 200 mg ml⁻¹ and c_p = 300 mg ml⁻¹, respectively. Blue, cyan, green and red symbols represent values for T = 280 K, T = 295 K, T = 310 K and T = 325 K, respectively. In the right subplot, the different cluster size distributions are displayed for YCl₃ at T = 280 K and c_p = 200 mg ml⁻¹ for the different salt concentrations.

For both salts investigated, the calculated salt-induced protein–protein binding probabilities (Fig. 4) increase with increasing temperature and with increasing amount of salt cations per protein. Similarly to the normalized diffusion coefficients, they appear to only depend on the number of salt cations per protein.

Based on eqn (11)–(13), we determine the attraction strengths ε_AB (Fig. 5) and its errors including the error propagation. For both systems studied, ε_AB increases with temperature and salt concentration, which is consistent with the LCST-LLPS phase behavior observed for these systems³⁹ and with SANS data, which show the change from a system dominated by a screened Coulomb potential towards an attractive system for both salts investigated (see Fig. S10, ESI†).

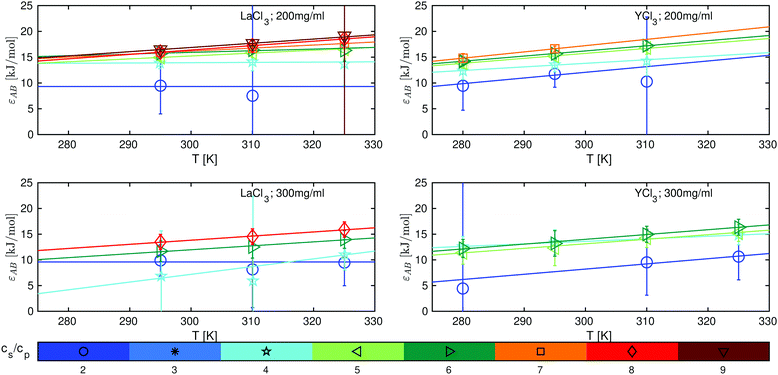Fig. 5 Protein–protein attraction strength ε_AB as a function of temperature for LaCl₃ (left panels) and YCl₃ (right panels) at BSA protein concentrations c_p = 200 mg ml⁻¹ (top) and c_p = 300 mg ml⁻¹ (bottom). The different c_s/c_p ratios are color-coded as shown in the legend. The lines represent linear fits of eqn (15).

The attraction strength ε_AB is determined by the chemical potential μ_s(c_s) which depends on the free binding energy ε_b between a protein and a salt ion and on the free bridging energy ε_uo between an unoccupied and an occupied patch of two different proteins.²⁸ The two free energies can be expressed by entropic and enthalpic contributions.³⁰ However, given the different sample composition as well as the significantly higher protein concentration, it should be emphasized that the present study, performed at high protein concentrations and in D₂O, is not expected to yield the same results as previous studies.³⁰ The dependence of the chemical potential μ_s on the salt concentration can only be described with respect to calibration measurements. We therefore limit the analysis to the temperature dependence of the potential depth −ε_AB and report the salt dependencies of the entropy ΔS and the value of the free energy at 20 °C:

−ε_AB(T) = −ε_AB(T = 20 °C) − ΔS·(T − 20 °C). (15)

A linear fit allows to extract the free energy ε_AB at T = 20 °C and the entropy ΔS for the different conditions as given by eqn (15). The dependence of these two quantities on the salt concentration is shown in Fig. 6. For both salts, the free energy at 20 °C increases with increasing salt concentration. The smaller number of different temperatures in the case of LaCl₃ leads to increased uncertainties in the values for the entropy and the free energy at 20 °C, but trends similar to those of BSA–YCl₃ samples can be observed. The values depend only slightly on the choice of the number of binding sites m (see Fig. S9, ESI†).

Fig. 6 Fit results from eqn (15): free energy ε_AB at T = 20 °C and entropy ΔS of the protein solution versus number of cations per protein c_s/c_p. The subplots on the left and on the right represent samples with LaCl₃ and with YCl₃, respectively. Blue squares and red stars represent samples with c_p = 200 mg ml⁻¹ and c_p = 300 mg ml⁻¹, respectively. For filled symbols, errors are smaller than the symbols if they are not visible. For open symbols, the determined errors are bigger than the range shown. Dotted lines represent guides to the eye.

Although the available data set is still small, the results in Fig. 6 corroborate a significant positive entropy change. Averaging the fitted slopes ΔS(c_s/c_p) (Fig. 6) suggests that the entropic contribution of YCl₃ is larger than LaCl₃. The significant positive entropic change supports the notion that entropy plays an important role for the clustering, consistent with the earlier findings on the entropic role for the overall phase behavior with a lower-critical solution temperature.³⁰ Moreover, the free energy at 20 °C shows a significant increase for the cases studied. The dependence on the salt concentration is more pronounced in the case of YCl₃. In our analysis we have obviously neglected the effect of impurities in the sample such as residual other proteins as well as the effect of possible residual monovalent salts. For this reason, absolute values may be subject to systematic errors, but the relative trends are robust due to the normalization of the diffusion coefficients. Moreover, we stress again that our model is obviously simplistic and based on various assumptions on the system that may require further verification.

5 Conclusion

We investigated the short-time self-diffusion of BSA solutions in the presence of different trivalent salts, approaching c* at different temperatures. We found master curves describing the salt-induced slowing down of the short-time self-diffusion depending on the temperature and the salt used, confirming the one observed for YCl₃ at 295 K.³² At higher temperatures, the master curve decays faster than at lower temperatures and salt-dependent effects become more pronounced. This faster decay at higher temperatures implies that the cluster size increases with rising temperature. From the normalized master curve describing the protein diffusion coefficients, the salt-induced protein–protein binding probability was calculated. Consistent with the observation of decreasing normalized diffusion coefficients with rising c_s/c_p, the binding probability increases with increasing number of salt ions per protein and with raising temperature. Based on the binding probabilities, the salt-induced protein–protein attraction strength is derived. Investigating the temperature dependence of the sample enabled us to separate the entropic and enthalpic contributions characterizing the system. The dependence of the attraction strength on the salt concentration, temperature and type of cation is consistent with the macroscopic phase behavior described previously. Especially at high temperatures, the attraction strength induced by the YCl₃ was stronger than the one induced by LaCl₃. For both salts, the free energy at the 20 °C increases with increasing number of salt ions per protein.

In this study, we successfully linked the microscopic quantities obtained from the short-time self-diffusion with the macroscopic time-averaged phase behavior of the samples. The overall experimental approach to understand structural and thermodynamic properties via energy-resolved scattering data provides an interesting tool for future investigations of assembly e.g. in complex biological systems. Importantly, our study illustrates that temperature can be used to assemble and dissociate clusters and that essential thermodynamic parameters involved in this process can be quantitatively understood.

Overall we present a highly simplistic system both in terms of the sample preparation and in terms of the modeling. Given this simplicity, our results are remarkably robust and consistent. Due to its access to highly dense and opaque protein solutions, our framework can in the future be employed, for instance, to study medically relevant monoclonal antibody (mAb) solutions, where the cluster formation at high concentrations poses a serious obstacle to create mAb formulations suitable for subcutaneous injection and where temperature changes from, e.g., the refrigerator temperature up to the physiological temperature can have a strong impact on the mAb cluster phase, and where the specific type of mAb as well as additives such as salts are assumed to have a significant impact on the cluster formation.^67,68 The unique coherence time of our backscattering experiment on the order of one nanosecond, corresponding to the short-time diffusion regime, renders it highly specific to hydrodynamic interactions while effects from direct interactions such as protein–protein collisions can be neglected. For this reason, concepts from colloid physics can be applied in a more straight-forward manner than in the long-time diffusion regime.

Author contributions

C. B., M. G., F. Z., F. R.-R., F. S., and T. S. designed research. C. B., M. G., M. K. B., L. B., N. H. J., and T. S. performed experiments at ORNL. C. B. and O. M. performed the D33 measurements. C. B., M. G., F. R.-R., and T. S. analyzed data. All authors contributed to interpreting the results and writing the manuscript.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

This research used resources at the Spallation Neutron Source, a DOE Office of Science User Facility operated by the Oak Ridge National Laboratory. We thank the SNS, the Department of Energy (DOE) and the JCNS partner user program for allocation of beamtime on BASIS. C. B. thanks the ILL for a PhD studentship. L. B. acknowledges an ILL studentship to fund the research for her diploma thesis carried out in the ILL spectroscopy group. The authors thank the ILL-ESRF Partnership for Soft and Condensed Matter (PSCM, Grenoble) for sharing lab resources. We thank R. Moody, R. Goyette and E. Mamontov for support during the experiments and for fruitful discussions. C. B., M. K. B. and L. B. gratefully acknowledge the financial support provided by JCNS to perform the neutron scattering measurements at the Spallation Neutron Source (SNS), Oak Ridge, USA. Financial support from BMBF (05K19VTB), ANR (ANR-16-CE92-0009, ImmunoglobulinCrowding), DFG and the Royal Physiographic Society of Lund is gratefully acknowledged.

References

1. M. Ziaunys, T. Sneideris and V. Smirnovas, Formation of distinct prion protein amyloid fibrils under identical experimental conditions, Sci. Rep., 2020, 10, 4572.
2. G. B. Benedek, Cataract as a protein condensation disease: The proctor lecture, Invest. Ophthalmol. Vis. Sci., 1997, 38(10), 1911–1921.
3. J. D. Gunton, A. Shiryayev and D. L. Pagan, Protein Condensation Kinetic Pathways to Crystallization and Disease, Cambridge, New York, 2008.
4. K. P. Johnston, J. A. Maynard, T. M. Truskett, A. U. Borwankar, M. A. Miller, B. K. Wilson, A. K. Dinin, T. A. Khan and K. J. Kaczorowski, Concentrated dispersions of equilibrium protein nanoclusters that reversibly dissociate into active monomers, ACS Nano, 2012, 6(2), 1357–1369.
5. A. R. Yadav and S. K. Mohite, Recent advances in protein and peptide drug delivery, Res. J. Pharm. Dosage Forms Technol., 2020, 12(3), 205.
6. C. Allen, D. Maysinger and A. Eisenberg, Nano-engineering block copolymer aggregates for drug delivery, Colloids Surf., B, 1999, 16(1), 3–27.
7. A. U. Borwankar, A. K. Dinin, J. R. Laber, A. Twu, B. K. Wilson, J. A. Maynard, T. M. Truskett and K. P. Johnston, Tunable equilibrium nanocluster dispersions at high protein concentrations, Soft Matter, 2013, 9(6), 1766–1771.
8. S. J. Shire, Z. Shahrokh and J. Liu, Challenges in the development of high protein concentration formulations, J. Pharm. Sci., 2004, 93(6), 1390–1402.
9. R. J. Ellis, Macromolecular crowding: an important but neglected aspect of the intracellular environment, Curr. Opin. Struct. Biol., 2001, 11(1), 114–119.
10. A. Vedadghavami, C. Zhang and A. G. Bajpayee, Overcoming negatively charged tissue barriers: Drug delivery using cationic peptides and proteins, Nano Today, 2020, 34, 100898.
11. P. D. Godfrin, I. E. Zarraga, J. Zarzar, L. Porcar, P. Falus, N. J. Wagner and Y. Liu, Effect of hierarchical cluster formation on the viscosity of concentrated monoclonal antibody formulations studied by neutron scattering, J. Phys. Chem. B, 2016, 120(2), 278–291.
12. Z. Zhang and Y. Liu, Recent progresses of understanding the viscosity of concentrated protein solutions, Curr. Opin. Chem. Eng., 2017, 16, 48–55.
13. M. Shah, D. Corbett, A. Lanzaro, A. Roche, N. Sibanda, P. Davis, S. Uddin, C. F. van der Walle, R. Curtis and A. Pluen, Micro- and macro-viscosity relations in high concentration antibody solutions, Eur. J. Pharm. Biopharm., 2020, 153, 211–221.
14. K. D. Ratanji, J. P. Derrick, R. J. Dearman and I. Kimber, Immunogenicity of therapeutic proteins: Influence of aggregation, J. Immunotoxicol., 2013, 11(2), 99–109.
15. A. Stradner, H. Sedgwick, F. Cardinaux, W. C. K. Poon, S. U. Egelhaaf and P. Schurtenberger, Equilibrium cluster formation in concentrated protein solutions and colloids, Nature, 2004, 432(7016), 492–495.
16. L. Porcar, P. Falus, W.-R. Chen, A. Faraone, E. Fratini, K. Hong, P. Baglioni and Y. Liu, Formation of the dynamic clusters in concentrated lysozyme protein solutions, J. Phys. Chem. Lett., 2009, 1(1), 126–129.
17. Y. Liu, L. Porcar, J. Chen, W.-R. Chen, P. Falus, A. Faraone, E. Fratini, K. Hong and P. Baglioni, Lysozyme protein solution with an intermediate range order structure, J. Phys. Chem. B, 2010, 115(22), 7238–7247.
18. E. J. Yearley, P. D. Godfrin, T. Perevozchikova, H. Zhang, P. Falus, L. Porcar, M. Nagao, J. E. Curtis, P. Gawande, R. Taing, I. E. Zarraga, N. J. Wagner and Y. Liu, Observation of small cluster formation in concentrated monoclonal antibody solutions and its implications to solution viscosity, Biophys. J., 2014, 106(8), 1763–1770.
19. P. D. Godfrin, S. D. Hudson, K. Hong, L. Porcar, P. Falus, N. J. Wagner and Y. Liu, Short-time glassy dynamics in viscous protein solutions with competing interactions, Phys. Rev. Lett., 2015, 115(22), 228302.
20. V. L. Dharmaraj, P. D. Godfrin, Y. Liu and S. D. Hudson, Rheology of clustering protein solutions, Biomicrofluidics, 2016, 10(4), 043509.
21. F. Cardinaux, E. Zaccarelli, A. Stradner, S. Bucciarelli, B. Farago, S. U. Egelhaaf, F. Sciortino and P. Schurtenberger, Cluster-driven dynamical arrest in concentrated lysozyme solutions, J. Phys. Chem. B, 2011, 115(22), 7227–7237.
22. S. Bucciarelli, J. S. Myung, B. Farago, S. Das, G. A. Vliegenthart, O. Holderer, R. G. Winkler, P. Schurtenberger, G. Gompper and A. Stradner, Dramatic influence of patchy attractions on short-time protein diffusion under crowded conditions, Sci. Adv., 2016, 2(12), e1601432.
23. J. Riest, G. Nägele, Y. Liu, N. J. Wagner and P. D. Godfrin, Short-time dynamics of lysozyme solutions with competing short-range attraction and long-range repulsion: Experiment and theory, J. Chem. Phys., 2018, 148(6), 065101.
24. S. von Bülow, M. Siggel, M. Linke and G. Hummer, Dynamic cluster formation determines viscosity and diffusion in dense protein solutions, Proc. Natl. Acad. Sci. U. S. A., 2019, 116(20), 9843–9852.
25. A. Shukla, E. Mylonas, E. Di Cola, S. Finet, P. Timmins, T. Narayanan and D. I. Svergun, Absence of equilibrium cluster phase in concentrated lysozyme solutions, Proc. Natl. Acad. Sci. U. S. A., 2008, 105(13), 5075–5080.
26. F. Zhang, F. Roosen-Runge, A. Sauter, M. Wolf, R. M. J. Jacobs and F. Schreiber, Reentrant condensation, liquid-liquid phase separation and crystallization in protein solutions induced by multivalent metal ions, Pure Appl. Chem., 2014, 86(2), 191–202.
27. O. Matsarskaia, F. Roosen-Runge and F. Schreiber, Multivalent ions and biomolecules: Attempting a comprehensive perspective, ChemPhysChem, 2020, 21(16), 1742–1767.
28. F. Roosen-Runge, F. Zhang, F. Schreiber and R. Roth, Ion-activated attractive patches as a mechanism for controlled protein interactions, Sci. Rep., 2014, 4, 7016.
29. F. Roosen-Runge, B. S. Heck, F. Zhang, O. Kohlbacher and F. Schreiber, Interplay of pH and binding of multivalent metal ions: Charge inversion and reentrant condensation in protein solutions, J. Phys. Chem. B, 2013, 117(18), 5777–5787.
30. O. Matsarskaia, M. K. Braun, F. Roosen-Runge, M. Wolf, F. Zhang, R. Roth and F. Schreiber, Cation-induced hydration effects cause lower critical solution temperature behavior in protein solutions, J. Phys. Chem. B, 2016, 120(31), 7731–7736.
31. D. Soraruf, F. Roosen-Runge, M. Grimaldo, F. Zanini, R. Schweins, T. Seydel, F. Zhang, R. Roth, M. Oettel and F. Schreiber, Protein cluster formation in aqueous solution in the presence of multivalent metal ions – a light scattering study, Soft Matter, 2014, 10, 894–902.
32. M. Grimaldo, F. Roosen-Runge, M. Hennig, F. Zanini, F. Zhang, M. Zamponi, N. Jalarvo, F. Schreiber and T. Seydel, Salt-induced universal slowing down of the short-time self-diffusion of a globular protein in aqueous solution, J. Phys. Chem. Lett., 2015, 6(13), 2577–2582.
33. M. Grimaldo, F. Roosen-Runge, F. Zhang, F. Schreiber and T. Seydel, Dynamics of Proteins in Solution, Q. Rev. Biophys., 2019, 52, e7.
34. V. Levi and F. L. González Flecha, Reversible fast-dimerization of bovine serum albumin detected by fluorescence resonance energy transfer, Biochim. Biophys. Acta, Proteins Proteomics, 2002, 1599(1), 141–148.
35. F. Ameseder, R. Biehl, O. Holderer, D. Richter and A. M. Stadler, Localised contacts lead to nanosecond hinge motions in dimeric bovine serum albumin, Phys. Chem. Chem. Phys., 2019, 21(34), 18477–18485.
36. F. Roosen-Runge, M. Hennig, F. Zhang, R. M. J. Jacobs, M. Sztucki, H. Schober, T. Seydel and F. Schreiber, Protein self-diffusion in crowded solutions, Proc. Natl. Acad. Sci. U. S. A., 2011, 108(29), 11815–11820.
37. Y. R. Gokarn, E. Kras, C. Nodgaard, V. Dharmavaram, R. M. Fesinmeyer, H. Hultgen, S. Brych, R. L. Remmele Jr., D. N. Brems and S. Hershenson, Self-buffering antibody formulations, J. Pharm. Sci., 2008, 97(8), 3051–3066,  DOI:10.1002/jps.21232.
38. D. Molodenskiy, E. Shirshin, T. Tikhonova, A. Gruzinov, G. Peters and F. Spinozzi, Thermally induced conformational changes and protein–protein interactions of bovine serum albumin in aqueous solution under different pH and ionic strengths as revealed by SAXS measurements, Phys. Chem. Chem. Phys., 2017, 19(26), 17143–17155,  10.1039/c6cp08809k.
39. O. Matsarskaia, F. Roosen-Runge, G. Lotze, J. Möller, A. Mariani, F. Zhang and F. Schreiber, Tuning phase transitions of aqueous protein solutions by multivalent cations, Phys. Chem. Chem. Phys., 2018, 20(42), 27214–27225.
40. O. Matsarskaia, S. Da Vela, A. Mariani, Z. Fu, F. Zhang and F. Schreiber, Phase-separation kinetics in protein–salt mixtures with compositionally tuned interactions, J. Phys. Chem. B, 2019, 123(9), 1913–1919.
41. G. E. Smolka, E. R. Birnbaum and D. W. Darnall, Rare earth metal ions as substitutes for the calcium ion in Bacillus subtilis. alpha.-amylase, Biochemistry, 1971, 10(24), 4556–4561.
42. M. Grimaldo, F. Roosen-Runge, M. Hennig, F. Zanini, F. Zhang, N. Jalarvo, M. Zamponi, F. Schreiber and T. Seydel, Hierarchical molecular dynamics of bovine serum albumin in concentrated aqueous solution below and above thermal denaturation, Phys. Chem. Chem. Phys., 2015, 17(6), 4645–4655.
43. E. Mamontov and K. W. Herwig, A time-of-flight backscattering spectrometer at the spallation neutron source, BASIS, Rev. Sci. Instrum., 2011, 82(8), 085109.
44. O. Arnold, J. C. Bilheux, J. M. Borreguero, A. Buts, S. I. Campbell, L. Chapon, M. Doucet, N. Draper, R. Ferraz Leal, M. A. Gigg, V. E. Lynch, A. Markvardsen, D. J. Mikkelson, R. L. Mikkelson, R. Miller, K. Palmen, P. Parker, G. Passos, T. G. Perring, P. F. Peterson, S. Ren, M. A. Reuter, A. T. Savici, J. W. Taylor, R. J. Taylor, R. Tolchenov, W. Zhou and J. Zikovsky, Mantid—Data analysis and visualization package for neutron scattering and μSR experiments, Nucl. Instrum. Methods Phys. Res., Sect. A, 2014, 764, 156–166.
45. H. Paalman and C. Pings, Numerical evaluation of X-ray absorption factors for cylindrical samples and annular sample cells, J. Appl. Phys., 1962, 33(8), 2635–2639.
46. K. Shou, M. Sarter, N. R. de Souza, L. de Campo, A. E. Whitten, P. W. Kuchel, C. J. Garvey and A. M. Stadler, Effect of red blood cell shape changes on haemoglobin interactions and dynamics: A neutron scattering study, R. Soc. Open Sci., 2020, 7(10), 201507.
47. M.-S. Appavou, S. Busch, W. Doster, A. Gaspar and T. Unruh, The influence of 2 kbar pressure on the global and internal dynamics of human hemoglobin observed by quasielastic neutron scattering, Eur. Biophys. J., 2011, 40(6), 705–714.
48. A. M. Stadler, J. Schneidewind, M. Zamponi, E. Knieps-Grünhagen, S. Gholami, U. Schwaneberg, I. Rivalta, M. Garavelli, M. D. Davari, K.-E. Jaeger and U. Krauss, Ternary complex formation and photoactivation of a photoenzyme results in altered protein dynamics, J. Phys. Chem. B, 2019, 123(34), 7372–7384.
49. K. Wood, C. Caronna, P. Fouquet, W. Haussler, F. Natali, J. Ollivier, A. Orecchini, M. Plazanet and G. Zaccai, A benchmark for protein dynamics: Ribonuclease A measured by neutron scattering in a large wavevector-energy transfer range, Chem. Phys., 2008, 345(2), 305–314.
50. M. Bée, Quasielastic neutron scattering: principles and applications in solid state chemistry, biology, and materials science, Adam Hilger, 1988.
51. A. M. Stadler, E. Knieps-Grünhagen, M. Bocola, W. Lohstroh, M. Zamponi and U. Krauss, Photoactivation reduces side-chain dynamics of a LOV photoreceptor, Biophys. J., 2016, 110(5), 1064–1074.
52. H. Frauenfelder, R. D. Young and P. W. Fenimore, Dynamics and the free-energy landscape of proteins, explored with the Mössbauer effect and quasi-elastic neutron scattering, J. Phys. Chem. B, 2013, 117(42), 13301–13307.
53. F. Roosen-Runge, D. J. Bicout and J.-L. Barrat, Analytical correlation functions for motion through diffusivity landscapes, J. Chem. Phys., 2016, 144(20), 204109.
54. A. M. Stadler, I. Digel, G. M. Artmann, J. P. Embs, G. Zaccai and G. Büldt, Hemoglobin dynamics in red blood cells: Correlation to body temperature, Biophys. J., 2008, 95(11), 5449–5461.
55. J. Pérez, J.-M. Zanotti and D. Durand, Evolution of the internal dynamics of two globular proteins from dry powder to solution, Biophys. J., 1999, 77(1), 454–469.
56. M. K. Braun, M. Grimaldo, F. Roosen-Runge, I. Hoffmann, O. Czakkel, M. Sztucki, F. Zhang, F. Schreiber and T. Seydel, Crowding-controlled cluster size in concentrated aqueous protein solutions: Structure, self-and collective diffusion, J. Phys. Chem. Lett., 2017, 8, 2590–2596.
57. L. Hong, N. Jain, X. Cheng, A. Bernal, M. Tyagi and J. C. Smith, Determination of functional collective motions in a protein at atomic resolution using coherent neutron scattering, Sci. Adv., 2016, 2, 10.
58. P. J. Flory, Molecular size distribution in three dimensional polymers. I. Gelation, J. Am. Chem. Soc., 1941, 63(11), 3083–3090.
59. M. Tokuyama and I. Oppenheim, Dynamics of hard-sphere suspensions, Phys. Rev. E: Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top., 1994, 50(1), R16–R19.
60. A. J. Banchio and G. Nägele, Short-time transport properties in dense suspensions: From neutral to charge-stabilized colloidal spheres, J. Chem. Phys., 2008, 128(10), 104903.
61. C. H. Cho, J. Urquidi, S. Singh and G. Wilse Robinson, Thermal Offset Viscosities of Liquid H2O, D2O, and T2O, J. Phys. Chem. B, 1999, 103(11), 1991–1994.
62. M. S. Wertheim, Fluids with highly directional attractive forces. I. Statistical thermodynamics. English, J. Stat. Phys., 1984, 35(1–2), 19–34.
63. W. G. Chapman, G. Jackson and K. E. Gubbins, Phase equilibria of associating fluids, Mol. Phys., 1988, 65(5), 1057–1079.
64. M. Grimaldo, F. Roosen-Runge, F. Zhang, T. Seydel and F. Schreiber, Diffusion and dynamics of γ-globulin in crowded aqueous solutions, J. Phys. Chem. B, 2014, 118, 7203–7209.
65. B. Cichocki and B. U. Felderhof, Diffusion coefficients and effective viscosity of suspensions of sticky hard spheres with hydrodynamic interactions, J. Chem. Phys., 1990, 93(6), 4427–4432.
66. F. Sciortino and E. Zaccarelli, Reversible gels of patchy particles, Curr. Opin. Solid State Mater. Sci., 2011, 15(6), 246–253.
67. D. Leveque, Subcutaneous administration of anticancer agents, Anticancer Res., 2014, 34(4), 1579–1586.
68. S. Jolles and J. W. Sleasman, Subcutaneous immunoglobulin replacement therapy with Hizentra®, the first 20% SCIG preparation: A practical approach, Adv. Ther., 2011, 28(7), 521–533.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: 10.1039/d1sm00418b

---