Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Effect of sticker clustering on the dynamics of associative networks†
Irina
Mahmad Rasid
a,
Changwoo
Do
 b,
Niels
Holten-Andersen
*a and
Bradley D.
Olsen
b,
Niels
Holten-Andersen
*a and
Bradley D.
Olsen
 *c
*c
aDepartment of Materials Science and Engineering, Massachusetts Institute of Technology, 77 Massachusetts Avenue, Cambridge, Massachusetts 02139, USA. E-mail: nielsholtenandersen@gmail.com
bNeutron Scattering Division, Oak Ridge National Laboratory, Oak Ridge, Tennessee 37830, USA
cDepartment of Chemical Engineering, Massachusetts Institute of Technology, 77 Massachusetts Avenue, Cambridge, Massachusetts 02139, USA. E-mail: bdolsen@mit.edu
First published on 23rd September 2021
Abstract
Recent experimental and theoretical work has shown that sticker clustering can be used to enhance properties such as toughness and creep resistance of polymer networks. While it is clear that the changes in properties are related to a change in network topology, the mechanistic relationship is still not well understood. In this work, the effect of sticker clustering was investigated by comparing the dynamics of random copolymers with those where the stickers are clustered at the ends of the chain in the unentangled regime using both linear mechanics and diffusion measurements. Copolymers of N,N-dimethyl acrylamide (DMA) and pendant histidine groups were synthesized using reversible addition–fragmentation chain transfer (RAFT) polymerization. The clustered polymers were synthesized using a bifunctional RAFT agent, such that the midblock consisted of PDMA and the two end blocks were random copolymers of DMA and the histidine-functionalized monomer. Upon addition of Ni ions, transient metal-coordinate crosslinks are formed as histidine–Ni complexes. Combined studies of rheology, neutron scattering and self-diffusion measurements using forced Rayleigh scattering revealed changes to the network topology and stress relaxation modes. The network topology is proposed to consist of aggregates of the histidine–Ni complexes bridged by the non-associative midblock. Therefore, stress relaxation requires the cooperative dissociation of multiple bonds, resulting in increased relaxation times. The increased relaxation times, however, were accompanied by faster diffusion. This is attributed to the presence of defects such as elastically inactive chain loops. This study demonstrates that the effects of cooperative sticker dissociation can be observed even in the presence of a significant fraction of loop defects which are known to alter the nonlinear properties of conventional telechelic polymers.
Introduction
Associative networks are ubiquitous both in natural and synthetic materials, and the dynamics within these networks dictate many of their desirable properties such as self-healing and stress relaxation.1,2 The versatility of these materials is the result of the wide array of design options, ranging from different chain architectures (linear vs. star)3,4 to binding chemistry5,6 to solvent environments7 to junction functionality.8,9 One strategy that has garnered interest of late is the clustering of stickers such that they are concentrated at the chain ends.10–12 This results in the chain ends participating in multivalent interactions due to the proximity of the stickers to one another. In biological systems, the presence of multiple binding sites in the form of multivalent ligands can enhance the strength and specificity of interactions compared to weak binding affinities of monovalent ligands.13,14 For example, protein–carbohydrate recognition events mediate processes such as pathogen–cell adhesion and inflammatory response, and carbohydrate epitopes are often present as multivalent arrays at the cell membrane to serve as highly efficient ligands. In synthetic systems, sticker clustering has been demonstrated to be a promising approach for designing networks with improved toughness, dissipation and creep resistance.10,15 However, the molecular mechanism for these improvements is not fully understood.As an accessible model of clustered systems, several studies have now been performed on networks formed by chains with a triblock architecture of a soluble midblock with two end blocks that are random copolymers of the stickers and diluent monomer. In comparison to random copolymers of the same molecular weight and number of stickers per chain, a delay in the terminal relaxation time was reported, accompanied by a higher activation energy for the onset of flow for the clustered copolymers.10,11,16 This delay has been attributed to the need for cooperative dissociation of multiple bonds before the chains are able to relax.15,17 The higher activation energy indicates that these networks have a stronger temperature dependence, and this has been suggested to originate from the difference in the formation of bonds as the temperature is reduced.17 While lowering the temperature should drive the system to favor bond association in both random and clustered sticker configurations, the proximity of the stickers in the clustered polymers enhances this effect. In some systems, the triblock chain architecture leads to microphase separation and results in the formation of structures such as cylinders16 and lamellae.18 However, changes in the viscoelastic properties were observed even for networks that did not undergo microphase separation,10 which indicates that the physics behind these changes in mechanical properties are not solely the result of microphase separation.
Self-diffusion measurements using forced Rayleigh scattering (FRS) provide an orthogonal probe to mechanical property measurements that can provide insight into the dynamics of associative polymer networks. Studies of several unentangled networks3,5,6 have revealed further details of the dynamics of these gels over length scales of several time the radius of gyration, Rg of the polymer. The previously investigated systems include a protein gel with pentavalent coiled–coiled associations,5 a four-arm star polymer end-functionalized with terpyridine and crosslinked with Zn2+ in DMF6 and linear random copolymers with pendant histidine groups crosslinked with Ni2+ in water.3 In all these systems, superdiffusive scaling was observed at the smaller range of length scales that is experimentally accessible, prior to transitioning to a regime with Fickian scaling. The observation of superdiffusive scaling in these networks was attributed to the presence of two diffusive modes with distinct diffusivities, which are walking and hopping, in the molecular model developed by Ramirez et al.19 Walking refers to diffusive modes where motion of the chains require sequential dissociations and reassociations of the stickers while hopping refers to diffusive modes where the chains dissociate all of its stickers to diffuse over several times the Rg. These dynamics were not detectable from studies of the polymers’ viscoelastic properties and provide further insights into the dynamics of associative networks.
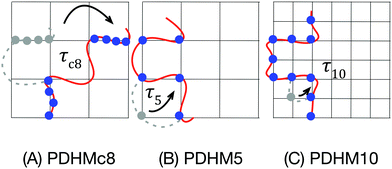
In this work, the dynamics and mechanics of a model associative network was investigated using rheology, small-angle neutron scattering (SANS) and FRS to provide a more detailed picture of the effect of sticker clustering. The model polymer system consists of random copolymers of N,N-dimethyl acrylamide (DMA) and a histidine-functionalized monomer, synthesized using RAFT polymerization. The clustered polymer was synthesized using a bifunctional RAFT agent, such that the midblock consists of only PDMA while the end blocks are random copolymers of DMA and the histidine-functionalized monomer (Fig. 1(A)). On addition of Ni2+, the crosslinks are formed as histidine–Ni complexes. The histidine–Ni complex was chosen because its kinetics have been thoroughly characterized,20 making it particularly suited to elucidate the effect of sticker clustering. This publication compares this new data on clustered polymers to those with randomly distributed stickers, published in a previous work.3 The effect of sticker clustering on the network structure was probed through SANS experiments, while network stiffness and terminal relaxation were characterized using rheology. To complement these measurements, self-diffusion within the network was probed using FRS, a technique which has not been applied in earlier studies investigating the effect of sticker clustering.10,11 Comparisons of the results to existing theories provide insights into the molecular mechanism behind the observed behaviors.
Methods
Materials
Fluorescein-5-maleimide was purchased from ThermoFisher Scientific. N-(3-N-Boc-Nim-trityl-N-3-methacrylamidopropyl-L-histidinamide (HisMA)20 and 2-(ethylthio-carbonothioylthio)-2-methylpropionic acid (EMP)21 were synthesized following published procedures. N,N-Dimethyl-acrylamide (DMA) was purified through a basic alumina column to remove inhibitor before polymerization. All other chemical reagents were purchased from Sigma-Aldrich or VWR and used as received. Polymers PDHM5 and PDHM10 were synthesized for a previous publication,3 and the same polymers were used in this study. All data for PDHM10 was taken from the previous study, while some additional data was collected on PDHM5 for this study.Characterizations
Gel permeation chromatography (GPC) measurements were performed on an Agilent 1260 LC system with two ResiPore columns (300 × 7.5 mm, Agilent Technologies, Santa Clara, CA) in series at a flow rate of 1 mL min−1 at 70 °C, where DMF with 0.02 M LiBr was used as the mobile phase. The molecular weights were determined using a Wyatt miniDAWN TREOS multiangle light scattering detector and a Wyatt Optilab T-rEX differential refractive index detector. Liquid chromatrography-mass spectrometry (LC-MS) analysis was performed using an Agilent 1260 Infinity LC system coupled with a 6130 quadrupole mass spectrometer. A mixture of 0.1% formic acid in water and MeCN was used as the mobile phase. NMR spectra were recorded on a Varian 400 MHz spectrometer. The residual undeuterated solvent peaks were used as references (7.27 ppm for CDCl3 and 4.79 ppm for D2O).Synthesis of EMP dimer
In a Schlenk flask, EMP (0.763 g, 3.4 mmol) was dissolved in 10 mL of anhydrous DMF. Hexafluorophosphate azabenzotriazole tetramethyl uronium (HATU) (1.29 g, 3.4 mmol) and 4-methylmorpholine (0.5 g, 5.0 mmol) were added, and the solution was stirred, under nitrogen atmosphere, for 30 minutes. Ethylene diamine (0.11 mL, 1.7 mmol) was added slowly, and the reaction was stirred overnight (Scheme 1). Then, the solvent was removed under vacuum, and the crude product was dissolved in 50 mL of DCM. The organic solution was washed with deionized water (3 × 50 mL), washed with brine (3 × 50 mL), and dried over Na2SO4, The product was then filtered and concentrated under vacuum. The crude product was purified via column chromatography with silica gel as the stationary phase and hexanes and ethyl acetate (70![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 30 to 40
30 to 40![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 60) as eluents. The product was obtained as a yellow solid in 89% yield. 1H NMR (400 MHz, CDCl3) δ 6.79 (s, 1H), 3.33 (s, 2H), 3.32 (q, J = 7.4, 6.1 Hz, 2H), 1.66 (s, 6H), 1.36 (t, J = 7.5 Hz, 3H). LRMS (ESI) m/z calculated for C16H28N2O2S6 [M + H]+ 473.1, found 473.1.
60) as eluents. The product was obtained as a yellow solid in 89% yield. 1H NMR (400 MHz, CDCl3) δ 6.79 (s, 1H), 3.33 (s, 2H), 3.32 (q, J = 7.4, 6.1 Hz, 2H), 1.66 (s, 6H), 1.36 (t, J = 7.5 Hz, 3H). LRMS (ESI) m/z calculated for C16H28N2O2S6 [M + H]+ 473.1, found 473.1.
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 8
8![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1
1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.2. This monomer pair was chosen because the reactivity ratios for acrylamide and methacrylamide have been shown to be close to unity.22,23 Therefore, the two monomers are expected to copolymerize in a nearly statistical manner, with HisMA distributed evenly in the end blocks. The polymerization was performed in MeCN at 60 °C for 7 h. In the first stage of the synthesis, DMA was polymerized until a molar mass of 15.9 kg mol−1 was achieved, as determined by DMF GPC. Then HisMA, dissolved in MeCN, was cannulated into the reaction vial. Once the desired conversion was achieved, the reaction was quenched by exposure to air and cooling to room temperature. The polymer was purified by precipitation into diethyl ether once and dried under vacuum. The mole fraction of HisMA in the polymer was determined to be 2.9 mol% by 1H NMR (Fig. S1, ESI†), close to the feed composition of 2.7 mol%. The molar mass of polymer was characterized by DMF GPC prior to the deprotection step and was determined to be 29.5 kg mol−1 (Fig. S2, ESI†). To remove the Boc and Trt protecting groups, the resulting polymers (700 mg) were dissolved in DCM (11.7 mL). Water (291.7 μL), triisopropylsilane (TIPS, 291.7 μL), and trifluoracetic acid (TFA, 11.7 mL) were sequentially added to the solution. The mixture was stirred at room temperature for 2 h. The volatiles were then removed under vacuum, and the residue was dissolved in MeOH. The polymers were recovered by precipitation into diethyl ether twice. The polymers were then dissolved in water, transferred to a centrifugal filter (3 kDa MWCO), and spun at 4000 × g for 1 h. More water was then added, and the filtration was repeated four times. The polymers were then filtered through a 0.45 μm filter and lyophilized to yield 550.6 mg of product. Complete removal of the Boc and Trt groups was evidenced by 1H NMR (Fig. S3, ESI†).
0.2. This monomer pair was chosen because the reactivity ratios for acrylamide and methacrylamide have been shown to be close to unity.22,23 Therefore, the two monomers are expected to copolymerize in a nearly statistical manner, with HisMA distributed evenly in the end blocks. The polymerization was performed in MeCN at 60 °C for 7 h. In the first stage of the synthesis, DMA was polymerized until a molar mass of 15.9 kg mol−1 was achieved, as determined by DMF GPC. Then HisMA, dissolved in MeCN, was cannulated into the reaction vial. Once the desired conversion was achieved, the reaction was quenched by exposure to air and cooling to room temperature. The polymer was purified by precipitation into diethyl ether once and dried under vacuum. The mole fraction of HisMA in the polymer was determined to be 2.9 mol% by 1H NMR (Fig. S1, ESI†), close to the feed composition of 2.7 mol%. The molar mass of polymer was characterized by DMF GPC prior to the deprotection step and was determined to be 29.5 kg mol−1 (Fig. S2, ESI†). To remove the Boc and Trt protecting groups, the resulting polymers (700 mg) were dissolved in DCM (11.7 mL). Water (291.7 μL), triisopropylsilane (TIPS, 291.7 μL), and trifluoracetic acid (TFA, 11.7 mL) were sequentially added to the solution. The mixture was stirred at room temperature for 2 h. The volatiles were then removed under vacuum, and the residue was dissolved in MeOH. The polymers were recovered by precipitation into diethyl ether twice. The polymers were then dissolved in water, transferred to a centrifugal filter (3 kDa MWCO), and spun at 4000 × g for 1 h. More water was then added, and the filtration was repeated four times. The polymers were then filtered through a 0.45 μm filter and lyophilized to yield 550.6 mg of product. Complete removal of the Boc and Trt groups was evidenced by 1H NMR (Fig. S3, ESI†).
Synthesis of fluorescein-labeled PDHMc8 polymers
The deprotected polymers (25 mg, 0.9 μmol) were first dissolved in 1.25 mL DMF, and then hexylamine (4.79 μL, 36 μmol) was added. The reaction was stirred under a nitrogen atmosphere overnight to minimize undesirable cysteine oxidation and to ensure complete aminolysis. Then tris(2-carboxyethyl)phosphine hydrochloride (TCEP·HCl, 5.2 mg, 18 μmol) and maleimide-functionalized fluorescein (7.74 mg in 180 μL of DMSO, 18 μmol) were added to the reaction mixture. After the reaction was stirred overnight in the dark, the solution was diluted with 30 mL 5% DMSO in water. The mixture was transferred to a centrifugal filter (3 kDa MWCO), spun at 4000 × g for 1 h at 4 °C, and further diluted 30 mL with 5% DMSO in water. This process was repeated several times until the spin-through fraction was colorless. A final spin with water then removed the DMSO. Polymers were filtered through a 0.45 μm filter and lyophilized to yield 13.9 mg of final product.Gel preparation
The gels of the PDMA polymers with pendant histidine groups were prepared following previously published procedures.3,20 The polymers were first dissolved in a Bis–Tris buffer (100 mM, pH 7.0), and complete dissolution was confirmed when the solution appeared clear. The appropriate volume of a stock solution containing 200 mM NiCl2 and 100 mM Bis–Tris was then added, and the mixture was vortexed for 15 s. The volume of NiCl2 stock solution required to prepare the gels at 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 of histidine
1 of histidine![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Ni was determined by calculating the concentration of histidine in the polymer using 1H NMR (Fig. S1, ESI†). Once mixed, the appropriate volume of a stock solution of 1 M NaOH with 100 mM Bis–Tris buffer was then added to adjust the pH to 7.0. The volume of NaOH stock solution required to adjust the pH to 7.0 was determined by titration experiments in dilute solution (Fig. S4, ESI†). The gels were then mixed with a micro spatula until a macroscopically homogenous gel was obtained, and the gels were centrifuged at 21
Ni was determined by calculating the concentration of histidine in the polymer using 1H NMR (Fig. S1, ESI†). Once mixed, the appropriate volume of a stock solution of 1 M NaOH with 100 mM Bis–Tris buffer was then added to adjust the pH to 7.0. The volume of NaOH stock solution required to adjust the pH to 7.0 was determined by titration experiments in dilute solution (Fig. S4, ESI†). The gels were then mixed with a micro spatula until a macroscopically homogenous gel was obtained, and the gels were centrifuged at 21![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 100 × g to remove air bubbles introduced during mixing.
100 × g to remove air bubbles introduced during mixing.
Small-angle neutron scattering (SANS)
SANS experiments were conducted at the Oak Ridge National Laboratory Spallation Neutron Source (ORNL SNS) Extended Q-Range SANS Diffractometer. The beam aperture was 8 mm. To facilitate neutron scattering contrast in SANS experiments, Bis–Tris buffered D2O (75 mM Bis–Tris and 25 mM HCl in D2O) was prepared by gravimetric measurements of the buffer components to reach pD 7.0. Additionally, the 200 mM stock solution of NiCl2 was prepared by dissolving 252.9 mg of NiCl2 in 10 mL of the Bis–Tris buffered D2O with pD 7.0. The 1 M NaOD stock solution was prepared by diluting 30% (w/w) solution of NaOD in D2O with the Bis–Tris buffer with pD 7.0. All stock solutions were filtered using 0.2 μm Acrodisc syringe filters (PALL Corporation). The gels were prepared as previously described and pressed between two quartz disks with a Teflon spacer (1 mm thickness, 13 mm inner diameter, 17 mm outer diamater). The quartz sample sandwich was then loaded in a titanium cell. Scattering patterns were measured using sample-to-detector distances of 2.5, 4.0 and 9.0 m, with neutron wavelength bands of 2.0–6.0 Å, 4.0–7.5 Å and 15.0–17.5 Å, respectively. This corresponds to a Q-range of 0.02–10 nm−1. All experiments were performed at 25 °C. The raw scattering intensity was reduced using the Mantid reduction package24 and corrected for the background by subtracting the scattering from an empty sample cell and a sample cell containing buffered D2O. The absolute intensity was calibrated using a porous silica standard sample. The reduced SANS curves were fit using non-linear least squares regression to a correlation length model.25–28Rheology
Frequency sweep experiments were performed on an Anton Paar 301 Physica rheometer, using a stainless-steel cone–plate upper geometry (25 mm in diameter, 1° angle). Inertial calibration and motor adjustment were performed before each measurement. All hydrogel samples were centrifuged at 21![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 100 × g for 10 min at 4 °C to remove bubbles before loading onto the rheometer. Dehydration was minimized by adding mineral oil to the sample edge. Experiments were performed at four temperatures: 5, 15, 25, and 35 °C. The temperature was controlled by a Peltier plate. Time-temperature superposition was used to construct master curves, and the procedure is described in Section D (p. 8) of the ESI.† Experiments were performed at 1% strain, which was within the linear viscoelastic (LVE) region as determined by strain sweep experiments.
100 × g for 10 min at 4 °C to remove bubbles before loading onto the rheometer. Dehydration was minimized by adding mineral oil to the sample edge. Experiments were performed at four temperatures: 5, 15, 25, and 35 °C. The temperature was controlled by a Peltier plate. Time-temperature superposition was used to construct master curves, and the procedure is described in Section D (p. 8) of the ESI.† Experiments were performed at 1% strain, which was within the linear viscoelastic (LVE) region as determined by strain sweep experiments.
Forced Rayleigh scattering
For self-diffusion measurements, 80 μM of the fluorescein-labelled polymers was added before the addition of NiCl2 stock solution during the gel preparation. This allows for thorough mixing of the fluorescein-labelled polymers into the solution before the formation of the gel. All samples were sealed between two quartz disks (17 mm in diameter) separated by a 0.2 mm thick Teflon spacer. To eliminate shear history from loading, all samples were left overnight at room temperature. Samples were equilibrated at the desired temperature for 1 h before further experiments were performed. The self-diffusion measurements were performed using forced Rayleigh scattering (FRS), as previously described.5,29,30 Briefly, a 100 mW continuous wave laser with λ = 488 nm was split into two beams which were individually refocused and crossed at an angle of θ onto the sample. This generated a holographic grating of characteristic spacing d that is defined by the following equation | (1) |
 | (2) |
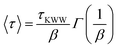 | (3) |
 | (4) |
Results and discussion
Effect of HisMA distribution on critical concentration regimes
When categorizing the dynamic regime of associative polymers, the important concentration regimes to consider are the chain overlap, ϕoverlap, strand (between stickers) overlap, ϕs, and entanglement concentration, ϕe (see ESI† for calculation).31,32 Since the degree of polymerization, N is approximately ∼250 for all the polymers investigated, ϕoverlap and ϕe (which depends on N) are similar for the three polymers (Table 1). In contrast, ϕs is proportional to the spacing between the stickers, l. Since l = N/S, ϕs is inversely proportional to the average number of stickers per chain, S, for the random copolymers. For the clustered polymer, there are two spacings that must be considered, which are the midblock separating the two chains ends, lmid = 160, and the average spacing between stickers in the two end blocks, lend = 14, such that two ϕs can be calculated (Table 1). The gels investigated in this work were prepared at 25% and 30% (w/v), which is well above ϕoverlap and well below ϕe, such that an unentangled, percolated network is formed. Additionally, ϕs defines the limit above which most stickers should be in interchain bonds, such that gels prepared below this concentration are predicted to have a significant fraction of intrachain bonds. For the random copolymers, ϕ = 25% (w/v) is above ϕs. For the clustered polymer, it is above ϕs for the midblock but below ϕs for the end blocks. Thus, for the clustered polymer, the chains are overlapping enough to form interchain bonds between different chains, but these bonds likely exist as aggregates bridged by the midblocks. Since the same trends were observed for the gels at 30% (w/v) (see Fig. S6–S8 in Section E of ESI†) the following analysis will focus on the gels prepared at 25% (w/v).| Polymer | M w (kg mol−1) [Đ] | Mol% HisMAb | S | N | l | ϕ overlap (w/v) | ϕ e (w/v) | ϕ s (w/v) |
|---|---|---|---|---|---|---|---|---|
| a M w is the weight average molar mass, Đ is the dispersity, S is the average number of stickers per chain, N is the average degree of polymerization, l is the average spacing between stickers, ϕoverlap is the chain overlap concentration, ϕe is the entanglement concentration and ϕs is the overlap of strand between stickers. b Calculated from 1H NMR. c Calculated based on l = 160. d Calculated based on l = 14, which is the average spacing between stickers in the end blocks. | ||||||||
| PDHM5 | 26.6 [1.03] | 2.09 | 4.98 | 238 | 48 | 3.1% | 49.4% | 11.6% |
| PDHM10 | 30.7 [1.04] | 3.74 | 9.58 | 256 | 27 | 3.0% | 46.1% | 19.0% |
| PDHMc8 | 29.5 [1.03] | 2.88 | 7.57 | 263 | l mid = 160 (midblock) | 2.9% | 44.7% | 4.2%c |
| l end = 14 (end blocks) | — | — | 35.4%d | |||||
Effect of clustering on linear viscoelastic properties and network topology
The linear viscoelastic response of the gels indicates that the network topology and mode of stress relaxation is altered by sticker clustering. The frequency sweeps for all the gels at a concentration of 25% (w/v) show a single plateau, Gp, in the storage modulus, G′ at high angular frequencies which crosses over with the loss modulus, G′′ with crossover angular frequency, ωc (Fig. 2(A–C)). While the relaxation times, τ = 2π/ωc, show an increase with the number of stickers per chain (τ5 < τc8 < τ10), the modulus does not show this trend. Rather, the plateau modulus of the clustered sticker polymer is lower than either of the two polymers with randomly distributed stickers: Gp,c8 < Gp,5 < Gp,10. | ||
| Fig. 2 Plot of bTG′ (filled symbols) and bTG′′ (unfilled symbols) vs. aTω for (A) PDHMc8, (B) PDHM5 and (C) PDHM10 at 25% (w/v), measured at 5–35 °C. All data sets are master curves constructed by time-temperature superposition referenced to 35 °C. Data for PDHM5 and PDHM10 at 35 °C previously reported in ref. 3. | ||
The plateau modulus, Gp is a measure of the concentration of elastically active strands, and the trend observed for Gp can be explained by considering the relation between Gp and the average spacing between crosslinks, l under the affine network assumption. For gels prepared at a concentration of ϕ (volume fraction),
 | (5) |
Further evidence of the proposed changes in network topology is provided by small angle neutron scattering (SANS) experiments. The appearance of an upturn at low q (onset shown by black single arrows in Fig. 4) is a feature often observed in disordered hydrogels,25 as expected for hydrogels formed from polymers with associative groups along their backbone. This upturn begins at a larger q for the PDHMc8 gel which indicates the presence of inhomogeneity at smaller length scales than expected for networks made with random copolymers with the same average composition. To quantify this effect, the SANS data was fit to an empirical correlation length model developed by Hammouda et al.,35 that has been used to analyze scattering from other hydrogels.25–28 The scattering intensity in the correlation length model is given by
 | (6) |
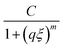 captures the high-q scattering and is the Lorentzian function which characterizes local network structure. The correlation length ξ represents a weighted average of the polymer blob size in the network, and given that the gel concentration was kept constant, it is expected to be similar for all three gels.25 The Porod and Lorentzian scale (A and C) and the Porod and Lorentzian exponents (n and m) along with ξ were obtained by a nonlinear least-squares fit of the data. The m exponent of all the gels are approximately 2 (Table S1, ESI†), which indicates that the polymers are behaving as though in a good solvent consistent with the assumption of good solvents conditions used to calculate the overlap concentration.
captures the high-q scattering and is the Lorentzian function which characterizes local network structure. The correlation length ξ represents a weighted average of the polymer blob size in the network, and given that the gel concentration was kept constant, it is expected to be similar for all three gels.25 The Porod and Lorentzian scale (A and C) and the Porod and Lorentzian exponents (n and m) along with ξ were obtained by a nonlinear least-squares fit of the data. The m exponent of all the gels are approximately 2 (Table S1, ESI†), which indicates that the polymers are behaving as though in a good solvent consistent with the assumption of good solvents conditions used to calculate the overlap concentration.
 | ||
Fig. 4 Scattered intensity from SANS experiments for PDHMc8, PDHM5 and PDHM10 at 25% (w/v), measured at 25 °C. The solid lines are fits to a correlation length model. The dashed lines are fits to the first term (A/qn) and the dotted lines are fits to the second term 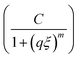 in eqn (5). The clustering strength is defined as the first term in eqn (5) with q = 0.04 nm−1 (shown by double arrow for PDHMc8). The black single arrows indicate the onset of the upturn with decreasing q in each curve. The spectra have been shifted vertically for clarity. in eqn (5). The clustering strength is defined as the first term in eqn (5) with q = 0.04 nm−1 (shown by double arrow for PDHMc8). The black single arrows indicate the onset of the upturn with decreasing q in each curve. The spectra have been shifted vertically for clarity. | ||
The main difference between the three polymers is captured by the first term, A/qn which defines the clustering strength from a large network structure and has been used as a method to evaluate the clustering strength of random polymer networks.25,27,35,36 Note that while no quantitative relation can be inferred from this factor, a high clustering strength is associated with networks while low clustering strength corresponds to dissolved chains.25,27,35,36 The clustering strength is significantly higher for PDHMc8 compared to PDHM5 and PDHM10 (Fig. 5). The value of q was chosen to be 0.04 nm−1 because it is low enough to be well within the Porod scattering regime.25,27,35,36 As shown in Fig. 5, the clustering strength increases with decreasing average spacing between the stickers, l, for the random copolymers. For the clustered stickers gel, the high clustering strength is consistent with the scattering response being dominated by a network of average sticker spacing corresponding to lend. Thus, this result provides further evidence that the end blocks in the clustered polymer network have formed aggregates of the histidine-Ni complexes. Within these aggregates, the network structure shows similarity to the structure formed by random copolymers with average sticker spacing of lend. From Fig. 4 (and the fit parameters in Table S1, ESI†) the second term from fitting to the correlation length model is very similar for all three gels, which confirms that the gels are a disordered one-phase system.25 As such, the SANS data indicates that the sticker clustering in the PDHMc8 polymers leads to the formation of aggregates of the histidine–Ni complexes, without inducing phase separation in the gels. As indicated by the lower plateau modulus (Fig. 3), these aggregates are connected by the midblock, which acts as the elastically active chains under linear deformation.
 | ||
| Fig. 5 Clustering strength (from the low-q feature in SANS data) as function of the average spacing between stickers, l. For the clustered copolymer, lmid = 160 is the average number of repeat units in the midblock and lend = 14 is the average spacing between stickers in the end blocks. The clustering strength is defined as the first term in eqn (5) with q = 0.04 nm−1. | ||
Effect of sticker clustering on mode of stress relaxation
Along with changes in the network topology, sticker clustering alters the mode of stress relaxation. In the PDHMc8 gels, network stress relaxation requires cooperative dissociation of multiple bonds, while the random copolymer gel networks relax stress when single bonds dissociate and bind to a new partner. This difference in stress relaxation mechanism is reflected by the increased temperature dependence of the relaxation time for the PDHMc8 gel compared to the random copolymers (Fig. 6). As shown in Fig. 6, the relaxation times of the gels increase in the order of τ5 < τc8 < τ10. Additionally, the relaxation times of the gels are all longer than τd, which is the histidine–Ni2+ complex dissociation time as measured in dilute solution reported by Tang et al.20 These observations can be explained by considering the molecular mechanism for stress relaxation in the random and clustered copolymers as summarized in Fig. 7.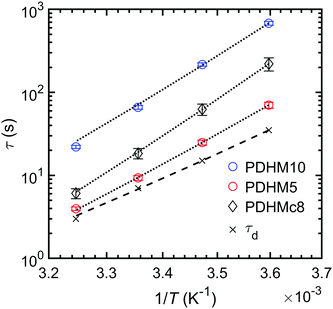 | ||
| Fig. 6 Network relaxation time τ obtained from frequency sweeps at varying temperatures for gels at 25% (w/v). The black dotted lines are fits to an Arrhenius law. The histidine–Ni complex dissociation time, τd, (measured in dilute solution)20 is included for comparison. | ||
For the random copolymers, the stress relaxation time scale order of τd < τ5 < τ10 is consistent with the concept of bond renormalization put forth in the sticky Rouse model for linear polymers with stickers distributed evenly along the chain.32 In the sticky Rouse model, the stress relaxation times measured in frequency sweeps correspond to the bond exchange times. For networks where the equilibrium constant, Keq ≫ 1 (Keq = ka/kd where ka and kd are the rate constants for association and dissociation respectively), as is the case for the gels studied in this work most of the stickers are in the associated state.20 As such, once a sticker dissociates there are very few exchange partners that are available. Thus, the newly dissociated stickers would have to explore the surrounding volume to find a new partner that is in the dissociated state. In the presence of neighboring stickers, the volume a sticker can explore is reduced such that the stickers have a lower probability of finding a new partner that is in a dissociated state32 (compare panel B and C in Fig. 7). As a result, the dissociated sticker will have to return to the same partner multiple times before successfully exchanging partners. The sticky Rouse model additionally predicts that the need for multiple bond dissociations results in the apparent activation energy for chain stress relaxation to be approximately 1.3 times higher than for single bond dissociation, but that activation energy should be independent of the number of stickers along the chain (S).32 These predictions are consistent with our data as the activation energies for the random copolymers obtained from the Arrhenius fits (Fig. 6) are relatively similar (Ea,5 = 69 ± 1 kJ mol−1 and Ea,10 = 78 ± 6 kJ mol−1), but significantly higher than Ea,d = 56 ± 4 kJ mol−1 (reported in ref. 20).
For the clustered copolymer, the increased relaxation time compared to the bond dissociation time (τd < τc8) has a different origin, as indicated by the higher activation energy of Ea,c8 = 84 ± 1 kJ mol−1 for the PDHMc8 gel. The higher activation energy can be explained by the model proposed by Sing et al.15 for telechelic polymers with multipart stickers at the chain ends. In this model, stress relaxation requires the cooperative dissociation of the stickers for pull-out of the chain ends. The model predicts that as the number of stickers at each chain end increases, the relaxation time, τ, and activation energy, Ea, will both increase because multiple stickers must be released prior to stress relaxation. The number of stickers that must be cooperatively dissociated for stress relaxation to occur can be estimated as
| x = Ea,x/Ed | (7) |
Effect of sticker clustering on self-diffusion
Self-diffusion measurements of the gels showed that diffusion was faster for the PDHMc8 gels compared to PDHM5 and PDHM10 gels despite the fact that PDHMc8 has more stickers than PDHM5 (Fig. 8). As previously reported for the PDHM5 and PDHM10 gels,3 phenomenological superdiffusive scaling was observed for the PDHMc8 gel at smaller length scales prior to transitioning to Fickian scaling at d2 ∼ 200 μm2. Therefore, while sticker clustering has increased the diffusivity of the polymers compared to the random copolymers, it did not affect the length scales over which the apparent superdiffusive scaling occurs. New self-diffusion measurements for PDHM5 and PDHMc8 at lower temperatures of 25, 20 and 15 °C, showed that the same trends were observed across all the temperatures. Note that self-diffusion measurements for PDHM10 at temperatures below 35 °C were not experimentally accessible.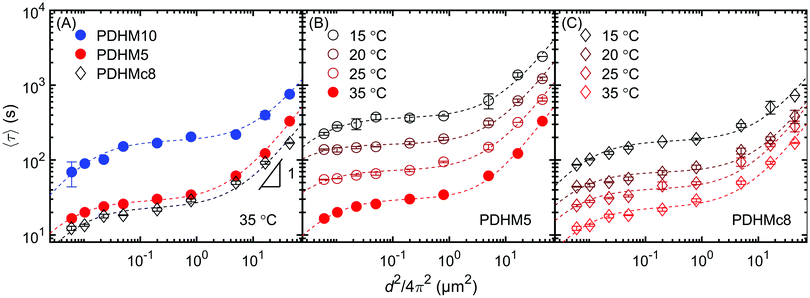 | ||
| Fig. 8 Plot of 〈τ〉 vs. d2 for PDHMc8, PDHM5 and PDHM10 measured at 35 °C. (B) PDHM5 and (C) PDHMc8 measured at 15–35 °C. All gels prepared at a concentration of 25% (w/v). The dashed lines are fits to the two-state model5. Error bars represent one standard deviation of measurements performed in triplicate. Note that the data shown for PDHM5 and PDHM10 at 35 °C (filled symbols) was reported in an earlier publication,3 while remaining data for PDHM5 was newly measured on the same polymers that were previously synthesized in ref. 3. | ||
Superdiffusive scaling that transitions to Fickian diffusion at length scales larger than the Rg has been previously reported in other unentangled associative networks as well.3,5,6,38 A previously proposed two-state model5 demonstrated that the presence of two diffusive modes, with distinct diffusivities can lead to the appearance of superdiffusive scaling at length scales larger than Rg. This has been confirmed through simulations performed by Ramirez et al.19 The two-state model5 was able to capture self-diffusion data for such studies of unentangled associative networks showing superdiffusive scaling and is likewise able to capture the self-diffusion data for gels in this work (dashed lines in Fig. 8). As discussed in detail in an earlier publication,3 the two modes of diffusion in the random copolymers PDHM5 and PDHM10 were proposed to be walking and hopping, based on the molecular model of Ramirez et al.19 However, the molecular model does not consider the effect of sticker clustering. Thus, the analysis in this work will focus on fits to the two-state model which quantitively fits the data, but without assigning a molecular mechanism to the two diffusion modes.5
The two-state model5 hypothesizes that the polymers in an associative network exist in two states, the associated and mobile states, with distinct diffusivities, DA and DM (units: μm s−1), where DA ≪ DM. The polymers can interconvert between the two states with interconversion rates, kon and koff (units: s−1), with pseudo-first order kinetics. Since the physical details of the two diffusive states are not specified in the model, the model can be applied for the PDHMc8 gels without modification; however, kon and koff should not be taken as physical rate constants. While the individual model parameters DA, DM, kon and koff cannot be independently determined, as discussed by Tang et al.,5 the parameters of interest are the effective diffusivity in the large length-scale Fickian regime, given by DM,eff = DM/(1 + Keq) and the anomaly index, γKeq = DA/DM·kon/koff. Note that γKeq is inversely proportional to the extent of the superdiffusive regime and can take any value between 0 and 1.
The observation of faster diffusion in the PDHMc8 gels compared to the PDHM5 and PDHM10 gels across all temperatures was not expected based on the trend observed with the stress relaxation times (τ5 < τc8 < τ10 in Fig. 6). The faster diffusion is seen in Fig. 9(A) as a higher effective diffusivity in the large-length-scale Fickian regime, DM,eff. Following the approach of de Gennes, the diffusivity is related to the relaxation time through the relation D ≈ Rg2/τ,39 such that D ∼ τ−1. Based on this relation, the effective diffusivity in the Fickian regime, DM,eff is expected to show the inverse of the trend with the relaxation times, such that DM,eff,5 > DM,eff,c8 > DM,eff,10. Thus, while the trends observed for the random copolymers are consistent with the predictions of the sticky Rouse model, as discussed in ref. 3, the diffusing species measured for the PDHMc8 gels are not governed by the same time scales for mechanical relaxation as measured in the frequency sweeps.
This discordant result can be further understood by considering the temperature dependence of the DM,eff along with the temperature dependence of the relaxation times. From the Arrhenius fits in Fig. 9(A), the activation energies for diffusion are ED,5 = 100 ± 10 kJ mol−1 and ED,c8 = 44 ± 20 kJ mol−1. For PDHM5, the higher activation energy for diffusion compared to the activation energy for stress relaxation (Ea,5 = 69 ± 1 kJ mol−1) indicates that more interchain bonds must be dissociated for the chain to diffuse several times its radius of gyration, Rg. For the PDHMc8, not only is the activation energy for diffusion lower than the activation energy for stress relaxation (Ea,c8 = 84 ± 1 kJ mol−1), the average value is lower than the activation energy for bond dissociation that was measured in dilute solution, Ea,d = 56 ± 4 kJ mol−1 (reported in ref. 20). This suggests that self-diffusion in the PDHMc8 gels is mostly governed by single bond dissociations, which contrasts with the need for cooperative dissociation of multiple bonds for stress relaxation. The need for cooperative dissociation indicates that the elastically active chains are bound to the network through multiple interchain bonds. Thus, dissociation of a single bond in the elastically active chains will mean that several other interchain bonds are still in the associated state, and the chains will be unable to diffuse over length scales spanning several times its Rg. This result implies that self-diffusion measurement for the clustered polymer is dominated by defects such as chain loops or even “superloops” where just a few bond dissociations can result in a cluster of multiple chains diffusing a significant distance (Fig. 10(A)).40 Similar results have been reported for diffusion measurements using fluorescence recovery after photobleaching (FRAP) on telechelic hydrophobically modified ethoxylated urethane (HEUR), where the defects were found to dominate self-diffusion measurements.41 It should be noted that due to the statistical nature of the random copolymerization used to prepare the polymers in this work, the number of stickers per chain end will show a distribution. The distribution of the number of stickers per chain end can be approximated by a Poisson distribution42 and as shown in Fig. 10(B), a small fraction of the chains (estimated to be 0.018) will exist as dangling chains (Fig. 10(A)). Defects such as chain loops and dangling chains can contribute to self-diffusion measurements but are elastically inactive since they cannot bridge two aggregates. This demonstrates that cooperative effects as indicated in the stress relaxation measurements can be seen even in the presence of a significant fraction of loop defects and dangling chains in the network. While the loop defects are elastically inactive, their presence in the telechelic hydrophobically modified ethoxylated urethane (HEUR) networks have been associated with the observation of shear thickening under nonlinear deformation.43 This indicates that sticker clustering likely affects the nonlinear deformation behavior of these networks as well.
 | ||
| Fig. 10 (A) Schematic showing the additional types of defects that can be present in the clustered polymer network. The restriction imposed by the proximity of the stickers to its neighbor can also create more defects such as intrachain bonds and dissociated bonds than found in the random copolymers. (B) The distribution of number of stickers/chain end estimated by a Poisson distribution.42 | ||
Sticker clustering and temperature have minimal effects on the extent of the superdiffusive scaling as seen in the very similar values of γKeq in Fig. 9(B). Since γKeq can be recast as γKeq = DA/DM,eff, γKeq can be interpreted as the ratio of apparent mobilities of molecules in the associative and mobile states.5 Thus, the slightly larger values of γKeq for PDHMc8 suggests that changes in the mobility of molecules upon association are more pronounced for the clustered polymers. This is consistent with the results presented in this work, where the presence of the stickers in close proximity at the chain ends appears to drive the formation of multiple bonds for each chain end. While γKeq is larger for PDHMc8 compared to the random copolymers across all the temperatures investigated, this difference is small especially in comparison to the other unentangled associative networks previously investigated, which showed γKeq in the range of 0.06–0.001.5,6 These other studies were performed on very different model systems, including hydrogels formed by linear proteins with four associating coiled-coil domains5 and four-arm star-shaped polymers end-functionalized with terpyridine moieties that are complexed with Zn2+ in DMF.6 Thus, these results suggest that γKeq is strongly influenced by the features of the gels that were kept constant between the random and clustered copolymers, including the binding chemistry and molecular weight of the polymers, compared to the relatively weak effect of sticker clustering and temperature.
Effect of temperature on the network topology
The opposite trends observed with the temperature dependence of the stress relaxation times and self-diffusion measurements indicates that temperature does not alter the network structure significantly. Decreasing the temperature should drive the system to favor bond association in both random and clustered sticker configurations.15,31,32 In the clustered polymer, the close proximity of the stickers to one another enhances this effect, resulting in the stronger temperature dependence in the stress relaxation measurements.17 However, the weaker dependence shown by the self-diffusion measurements indicates that the formation of more associations occurs within the loops and superloops themselves, such that the distribution of the interchain bonds is not altered between the elastically active and inactive parts of the network. This result was also reported by Feldman et al. who compared random and clustered copolymers using hydrogen-bonding polymer melts.10 Their study reported that small angle X-ray scattering (SAXS) experiments performed over varying temperatures showed minimal change, indicating that temperature does not alter the network topology.Comparison to other studies
Beyond the effect of sticker clustering, the bond chemistry is also an important factor in the final properties of the network. In addition to the study reported by Feldman et al. which compared random and clustered copolymers of hydrogen-bonding polymer melts,10 a second study was reported by Wu et al. which compared random and clustered copolymers of ionomers.11 Both studies found that the stress relaxation times were increased with clustering; however, this effect was much stronger in the ionomers where the terminal relaxation times were not experimentally accessible. This is likely due to the propensity for the ionic groups to form large aggregates with high junction functionality11 compared to the binary associations of the histidine–Ni complexes studies in this work. While the results reported by Wu et al. showed that the plateau in the storage modulus is lowered by clustering, as seen in this work, Feldman et al. found that clustering had no effect on the plateau in the storage modulus. The origin of this discrepancy is unknown, but it highlights the effect of the binding chemistry. It should be noted that the two studies focused on linear rheology experiments combined with SAXS and did not include self-diffusion measurements.Conclusions
In this work, the effect of sticker clustering was investigated by comparing the properties of the model associative network to random copolymers with the same chemical composition. Sticker clustering was found to alter the network topology and stress relaxation mechanism, as indicated by frequency sweeps, small angle neutron scattering and self-diffusion studies using forced Rayleigh scattering. The network prepared from the clustered polymers consists of aggregates of the histidine–Ni complexes that are bridged by the non-associative midblocks. The presence of multiple stickers at the chain ends results in an increase in the stress relaxation times due to the need for cooperative dissociation of multiple bonds for chain pull-out to occur. The weak effect of temperature on the self-diffusion measurements for the clustered polymer further revealed that the diffusion measurements were dominated by defects, such as superloops, that have been reported for other telechelic polymers (with a single associative group at the chain ends). This weak temperature dependence was not observed for the random copolymer, indicating that the clustering of the stickers drives the formation of these loop defects which are known to affect nonlinear rheology properties of associative networks. Additionally, the observation of phenomenological superdiffusive scaling here shows strong similarities to those observed in the random copolymer, which provide further insights for the development of the molecular model for diffusion.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was supported in part by the MRSEC Program of the National Science Foundation under award number DMR – 1419807, the National Science Foundation under Award DMR-1709315, the U.S. Army Research Office through the Institute for Soldier Nanotechnologies under Contract W911NF-07-D-0004 and the Office of Naval Research (ONR) under the Young Investigators Program Grant ONR.N00014-15-1-2763. A portion of this research used resources at the Spallation Neutron Source, a DOE Office of Science User Facility operated by the Oak Ridge National Laboratory.Notes and references
- S. Zechel, M. D. Hager, T. Priemel and M. J. Harrington, Biomimetics, 2019, 4, 20 CrossRef CAS PubMed.
- C.-H. Li, C. Wang, C. Keplinger, J.-L. Zuo, L. Jin, Y. Sun, P. Zheng, Y. Cao, F. Lissel and C. Linder, Nat. Chem., 2016, 8, 618–624 CrossRef CAS PubMed.
- I. Mahmad Rasid, N. Holten-Andersen and B. D. Olsen, Macromolecules, 2021, 54, 1354–1365 CrossRef CAS.
- S. C. Grindy, R. Learsch, D. Mozhdehi, J. Cheng, D. G. Barrett, Z. Guan, P. B. Messersmith and N. Holten-Andersen, Nat. Mater., 2015, 14, 1210–1216 CrossRef CAS PubMed.
- S. Tang, M. Wang and B. D. Olsen, J. Am. Chem. Soc., 2015, 137, 3946–3957 CrossRef CAS PubMed.
- S. Tang, A. Habicht, S. Li, S. Seiffert and B. D. Olsen, Macromolecules, 2016, 49, 5599–5608 CrossRef CAS.
- T. Rossow, A. Habicht and S. Seiffert, Macromolecules, 2014, 47, 6473–6482 CrossRef CAS.
- Q. Li, D. G. Barrett, P. B. Messersmith and N. Holten-Andersen, ACS Nano, 2016, 10, 1317–1324 CrossRef CAS PubMed.
- S. C. Grindy, M. Lenz and N. Holten-Andersen, Macromolecules, 2016, 49, 8306–8312 CrossRef CAS.
- K. E. Feldman, M. J. Kade, E. W. Meijer, C. J. Hawker and E. J. Kramer, Macromolecules, 2009, 42, 9072–9081 CrossRef CAS.
- S. Wu, S. Liu, Z. Zhang and Q. Chen, Macromolecules, 2019, 52, 2265–2276 CrossRef CAS.
- Y. Lei and T. P. Lodge, Soft Matter, 2012, 8, 2110 RSC.
- L. L. Kiessling and J. C. Grim, Chem. Soc. Rev., 2013, 42, 4476–4491 RSC.
- E. Zumbro, J. Witten and A. Alexander-Katz, Biophys. J., 2019, 117, 892–902 CrossRef CAS PubMed.
- M. K. Sing, J. Ramirez and B. D. Olsen, J. Chem. Phys., 2017, 147, 194902 CrossRef PubMed.
- T. P. Lodge, M. A. Blazey, Z. Liu and I. W. Hamley, Macromol. Chem. Phys., 1997, 198, 983–995 CrossRef CAS.
- A. Noro, Y. Matsushita and T. P. Lodge, Macromolecules, 2008, 41, 5839–5844 CrossRef CAS.
- D. Ehlich, M. Takenaka, S. Okamoto and T. Hashimoto, Macromolecules, 1993, 26, 189–197 CrossRef CAS.
- J. Ramirez, T. J. Dursch and B. D. Olsen, Macromolecules, 2018, 51, 2517–2525 CrossRef CAS.
- S. Tang and B. D. Olsen, Macromolecules, 2016, 49, 9163–9175 CrossRef CAS.
- B. V. K. J. Schmidt, M. Hetzer, H. Ritter and C. Barner-Kowollik, Macromolecules, 2011, 44, 7220–7232 CrossRef CAS.
- F. Dainton and W. Sisley, Trans. Faraday Soc., 1963, 59, 1385–1389 RSC.
- S. Durmaz and O. Okay, Polymer, 2000, 41, 3693–3704 CrossRef CAS.
- Mantid (2013): Manipulation and Analysis Toolkit for Instrument Data, DOI: 10.5286/software/mantidX.Y.Z.
- E. M. Saffer, M. A. Lackey, D. M. Griffin, S. Kishore, G. N. Tew and S. R. Bhatia, Soft Matter, 2014, 10, 1905–1916 RSC.
- Y. J. Yang, D. J. Mai, T. J. Dursch and B. D. Olsen, Biomacromolecules, 2018, 19, 3905–3916 CrossRef CAS PubMed.
- B. Hammouda, F. Horkay and M. L. Becker, Macromolecules, 2005, 38, 2019–2021 CrossRef CAS.
- R. A. Hule, R. P. Nagarkar, B. Hammouda, J. P. Schneider and D. J. Pochan, Macromolecules, 2009, 42, 7137–7145 CrossRef CAS PubMed.
- M. Wang, K. Timachova and B. D. Olsen, Macromolecules, 2013, 46, 5694–5701 CrossRef CAS.
- M. Wang, K. Timachova and B. D. Olsen, Macromolecules, 2013, 46, 1651–1658 CrossRef CAS PubMed.
- M. Rubinstein and A. N. Semenov, Macromolecules, 2001, 34, 1058–1068 CrossRef CAS.
- M. Rubinstein and A. N. Semenov, Macromolecules, 1998, 31, 1386–1397 CrossRef CAS.
- X. Zhang, C. Liu and Z. Wang, Polymer, 2008, 49, 3353–3361 CrossRef CAS.
- C. Wang, W. Shi, W. Zhang, X. Zhang, Y. Katsumoto and Y. Ozaki, Nano Lett., 2002, 2, 1169–1172 CrossRef CAS.
- B. Hammouda, D. L. Ho and S. Kline, Macromolecules, 2004, 37, 6932–6937 CrossRef CAS.
- B. Wu, M. Siglreitmeier, C. Debus, D. Schwahn, H. Colfen and V. Pipich, Macromol. Biosci., 2018, 18, e1800018 CrossRef PubMed.
- J. Wang, R. Wang, Y. Gu, A. Sourakov, B. D. Olsen and J. A. Johnson, Chem. Sci., 2019, 10, 5332–5337 RSC.
- P. B. Rapp, A. K. Omar, B. R. Silverman, Z. G. Wang and D. A. Tirrell, J. Am. Chem. Soc., 2018, 140, 14185–14194 CrossRef CAS PubMed.
- P. De Gennes, Macromolecules, 1976, 9, 594–598 CrossRef CAS.
- P. I. Hurtado, L. Berthier and W. Kob, Phys. Rev. Lett., 2007, 98, 135503 CrossRef PubMed.
- S. Suzuki, T. Uneyama and H. Watanabe, Macromolecules, 2013, 46, 3497–3504 CrossRef CAS.
- W. H. Stockmayer, J. Chem. Phys., 1945, 13, 199–207 CrossRef CAS.
- T. Uneyama, S. Suzuki and H. Watanabe, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2012, 86, 031802 CrossRef PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/d1sm00392e |
| This journal is © The Royal Society of Chemistry 2021 |