Dynamics and extensional rheology of polymer–surfactant association complexes
Carina D. V.
Martínez Narváez
,
Thomas
Mazur
and
Vivek
Sharma
 *
*
Chemical Engineering, University of Illinois at Chicago, 929 W. Taylor St, IL 60608, USA. E-mail: viveks@uic.edu
First published on 21st May 2021
Abstract
Understanding and characterizing the influence of polymers and surfactants on rheology, application, and processing is critical for designing complex fluid formulations for enhanced oil recovery, pharmaceuticals, cosmetics, foods, inks, agricultural sprays, and coatings. It is well-established that the addition of anionic surfactant like sodium dodecyl sulfate (SDS) to an aqueous solution of an oppositely-charged or uncharged polymer like poly(ethylene oxide) (PEO) can result in the formation of the polymer–surfactant association complexes (P0S−ACs) and a non-monotonic concentration-dependent variation in zero shear viscosity. However, the extensional rheology response of polymer–surfactant mixtures remains relatively poorly understood, partially due to characterization challenges that arise for low viscosity, low elasticity fluids, even though the response to strong extensional flows impacts drop formation and many processing operations. In this article, we use the recently developed dripping-onto-substrate (DoS) rheometry protocols to characterize the pinching dynamics and extensional rheology response of aqueous P0S− solutions formulated with PEO (P0) and SDS (S−), respectively. We find the PEO–SDS mixtures display a significantly weaker concentration-dependent variation in the extensional relaxation time, filament lifespan, and extensional viscosity values than anticipated by the measured shear viscosity.
Introduction
Macromolecular engineering of formulations requires understanding and characterization of the influence of macromolecular (polymers, proteins), condensed (particles, drops, bubbles), or self-associated (micelles and vesicles) dispersants on the interfacial and rheological properties.1 Nearly a century of experimental and theoretical efforts have enabled us to elucidate how macroscopic shear rheology response of polymer solutions and melts depends on macromolecular properties, including the molecular weight, concentration, charge fraction as well as matrix/solvent properties.1–5 However, the interaction and, often, the pairwise complexation of a polymer with another polymer, particle, surfactant, or micelle present significant challenges in formulation engineering, as the physicochemical hydrodynamics of various components, as well as the complexes, must be characterized and understood.6–11 For example, in aqueous solutions, the interaction between polymers and surfactants can lead to spontaneous cooperative binding and complexation above a critical aggregation concentration (CAC), especially when one or both species are charged.10,11 In this contribution, we characterize and elucidate the influence of an uncharged polymer (P0), an anionic surfactant (S−), and their association complexes (PSACs or P0S−ACs) on the interfacial, rheological and processing behavior of model two-ingredient formulations. In previous studies,8–14 for a fixed polymer concentration, an increase in shear viscosity as a function of surfactant concentration occurs beyond CAC, and a peak value manifests at the polymer saturation point (PSP), followed by a marginal decrease. However, it is unknown if similar non-monotonic trends arise for pinching dynamics and extensional rheology of P0S− systems, including P0 = PEO (poly(ethylene oxide) and S− = SDS (sodium dodecyl sulfate), motivating this study.Polymer–surfactant mixtures and complexes influence the stability, rheology, and applications of paints and coatings, printing inks, cosmetics, foams, nanoemulsions, enhanced-oil recovery, agrochemical sprays, food, and biological fluids, such as saliva, and tracheal mucus.8,10,15–21 Polymers perform the role of film or fiber formers, shear rheology modifiers, processing aids to change drop size distribution (in spraying and coating applications), or stickiness, and as stabilizers, flocculants, or compatibilizers. Surfactants change surface tension, alter wetting and spreading behavior, abet in foam and emulsion formation, solubilize drugs or dirt in micelles to facilitate drug delivery or detergency, and act as processing aids in free-surface flows. Spontaneous self-assembly of amphiphilic surfactants in aqueous solutions leads to the formation of micelles above a critical micelle concentration (CMC),22 whereas in the presence of polymer, surfactants self-aggregate above CAC.9,10,12,23 In addition to shear viscosity, tensiometry, conductometry, NMR, and steady-state fluorescence quenching aid in identifying CMC and CAC.9,12–14,24,25 Several recent simulation papers attempt to provide a molecular picture of self-assembly and interactions.26,27 Though CAC < CMC, the CAC is lower by one order of magnitude or more if both species are oppositely charged leading to a strong electrostatic driving force. However, the values of CMC and CAC are comparable for P0S− systems like PEO–SDS, investigated here.
Dispensing and liquid transfer to substrates by dripping, jetting, or spraying involve capillarity-driven pinching of liquid necks.28–30 As streamwise velocity gradients associated with extensional flows arise in pinching necks, jettability, sprayability, spinnability, and stringiness depend on extensional rheology response and pinching dynamics.28–30 Likewise, making foams and emulsions, gravure printing, and dispersal of drops by coughing, sneezing, and speaking, the underlying spread of viral flu involves pinching dynamics of multi-component fluids.31–33 Addition of even a dilute amount of polymer with high molecular weight causes significant changes in the formation, size, and size distribution of drops.17,34–39 For Newtonian fluids, an interplay of viscous, inertial, and capillary stresses results in inertiocapillary, and viscocapillary dynamics respectively observed for low (Oh < 1) and high viscosity Newtonian fluids (Oh > 1). Here, the Ohnesorge number, 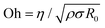 provides a dimensionless measure of viscosity, (ratio of viscocapillary to inertiocapillary timescales), and scales the shear viscosity, with the square-root of the product of density, ρ surface tension, σ, and a length-scale, R0.28,29 Polymer stretching and alignment in response to strong extensional flow fields within pinching necks contribute extra viscoelastic stresses that alter pinching rate and timespan.34–41 Analysis of pinching dynamics allows characterization of the extensional relaxation time, λE and extensional viscosity, ηE. In solutions of flexible polymers like PEO,42–48λE can be much higher than the shear relaxation time, λs and ηE can be several orders of magnitude higher than shear viscosity, ηs, though Newtonian fluids exhibit a Trouton ratio, Tr = ηE/ηs = 3 (and thus, one parameter captures their flow behavior).
provides a dimensionless measure of viscosity, (ratio of viscocapillary to inertiocapillary timescales), and scales the shear viscosity, with the square-root of the product of density, ρ surface tension, σ, and a length-scale, R0.28,29 Polymer stretching and alignment in response to strong extensional flow fields within pinching necks contribute extra viscoelastic stresses that alter pinching rate and timespan.34–41 Analysis of pinching dynamics allows characterization of the extensional relaxation time, λE and extensional viscosity, ηE. In solutions of flexible polymers like PEO,42–48λE can be much higher than the shear relaxation time, λs and ηE can be several orders of magnitude higher than shear viscosity, ηs, though Newtonian fluids exhibit a Trouton ratio, Tr = ηE/ηs = 3 (and thus, one parameter captures their flow behavior).
However, characterizing extensional rheology response is rather challenging as measurements require bespoke instrumentation, display high sensitivity to deformation history, and can be influenced by elastic or inertial flow instabilities that can arise in microfluidic and stagnation flow devices.29,37,49–54 Furthermore, most techniques are better suited for fluids with relatively high viscosity, and typically the range of accessible strain or strain rates is rather limited.37,44,47,50,51,55Table 1 summarizes the published datasets56–63 on P0S− systems acquired with two commercially-available techniques: RFX opposed jet and CaBER (capillary breakup extensional rheometer). The measurements rely on a flexible, relatively high molecular weight (Mw) polymer, and the few data points included show that the critical extensional rate, ![[small epsi, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a1.gif) c for the onset of strain hardening, decreases on surfactant addition. The range (and number) of surfactant concentrations explored at a fixed polymer concentration is limited, and it is not apparent if the extensional rheology response exhibits a non-monotonic concentration-dependent variation. Furthermore, Dontula et al. showed that strong inertial effects and shear within the nozzle render the opposed jets technique unsuitable for quantitative or accurate measurements of ηE.60,64 Likewise, characterization with standard capillary breakup extensional rheometer (CaBER) protocols is limited to liquids with λs, λE > 1 ms and ηs > 50 mPa s, as a finite time (nearly 50 ms) is needed for applying step-strain to a liquid bridge formed between two plates.29,51,65 Indeed, Miller and Copper-White62 note: “These solutions are at the very threshold of the operational space for the CaBER technique.” The motivations underlying the current contribution are three-fold: (i) address the characterization challenges using dripping-onto-substrate (DoS) rheometry protocols we developed recently,44–48,53,66–69 (ii) obtain comprehensive datasets to examine that non-monotonic concentration-dependence is observed in processes influenced by pinching dynamics and extensional rheology response, and (iii) seek an understanding of the role played by a combination of electrostatic and hydrodynamic stretching for uncharged polymer (P0), an anionic surfactant (S−), and their association complexes (PSACs or P0S−ACs).
c for the onset of strain hardening, decreases on surfactant addition. The range (and number) of surfactant concentrations explored at a fixed polymer concentration is limited, and it is not apparent if the extensional rheology response exhibits a non-monotonic concentration-dependent variation. Furthermore, Dontula et al. showed that strong inertial effects and shear within the nozzle render the opposed jets technique unsuitable for quantitative or accurate measurements of ηE.60,64 Likewise, characterization with standard capillary breakup extensional rheometer (CaBER) protocols is limited to liquids with λs, λE > 1 ms and ηs > 50 mPa s, as a finite time (nearly 50 ms) is needed for applying step-strain to a liquid bridge formed between two plates.29,51,65 Indeed, Miller and Copper-White62 note: “These solutions are at the very threshold of the operational space for the CaBER technique.” The motivations underlying the current contribution are three-fold: (i) address the characterization challenges using dripping-onto-substrate (DoS) rheometry protocols we developed recently,44–48,53,66–69 (ii) obtain comprehensive datasets to examine that non-monotonic concentration-dependence is observed in processes influenced by pinching dynamics and extensional rheology response, and (iii) seek an understanding of the role played by a combination of electrostatic and hydrodynamic stretching for uncharged polymer (P0), an anionic surfactant (S−), and their association complexes (PSACs or P0S−ACs).
| Authors, reference (year) | Polymer–surfactant (Mw g mol−1), solvent | c polymer (wt%), csurfactant (mM) | Technique | Remarks |
|---|---|---|---|---|
| Eastman, Goodwin & Howe56 (2000) | PVP–SDS (0.7 × 106), water | c > c*, 27–500 mM | RFX Opposed-jet | Strain hardening observed |
| Smitter…Saez57–59 (2001–2002) | PEO–SDS (4 × 106 & 8 × 106), water | 0.01 < c/c* < 2, c < CMC | RFX Opposed-jet | ΔP vs. ![[small epsi, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a1.gif) plots show strain hardening, plots show strain hardening, ![[small epsi, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a1.gif) c decreases on adding SDS c decreases on adding SDS |
| Cooper-White, et al.60 (2002) | PEO–SDS (1 × 106), 50 wt% glycerol | c/c* ∼ 1, 8–32 mM | RFX Opposed-jet | Tr < 120, strain hardening, ![[small epsi, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a1.gif) c decreases on adding SDS c decreases on adding SDS |
| Torres…Saez61 (2008) | PEO–SDS or SDBS (4 × 106), water | 500 ppm, c < c* = 550 ppm | RFX Opposed-jet | Extensional thickening. ![[small epsi, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a1.gif) c decreases above CAC c decreases above CAC |
| E. Miller & Cooper-White62 (2009) | PEO–SDS (2 × 106), water | 0.75 wt%, 5, 8, 16, 32 mM | CaBER | λ E and apparent ηE reported for four SDS concentrations |
| Wang…Cooper-White63 (2016) | PEO-Tween20 or SDS (2 × 106), water | 0.75 wt%, c/c* < 1 | CaBER | λ E reported. DST measurements included |
Experimental methods and materials
We characterize the pinching dynamics and extensional rheology response using dripping-onto-substrate (DoS) rheometry protocols.44–48,53,66,67 Several studies, including our own, describe the characterization of the extensional rheology and pinching dynamics using (DoS) rheometry for solutions of neutral and charged polymers,44–47,53,66,67,70–78 inks and particle suspensions,46,79,80 wormlike micellar solutions,46,81–84 hydrocolloids and food materials (cellulose gum solutions, ketchup, mayo),46,67 and cosmetics (nail lacquer formulations, hand-cream, shampoo, and conditioners).46,68,69 The DoS rheometry involve visualization and analysis of pinching necks created by dripping a finite volume of a liquid from a fixed nozzle onto a partially wetting substrate. Briefly, the fluid is pumped at a low and fixed flowrate, Q = 0.02 mL min−1 through a nozzle with an outer and inner diameter of D0 = 2R0 = 1.27 mm and Di = 0.838 mm, respectively. A finite volume of the liquid is released onto a substrate placed at distance H, such that the aspect ratio of H/D0 ≈ 3. The DoS videos are further analyzed with specially written MATLAB codes for determining radius evolution over time. We measure the surface tension values using the maximum bubble pressure tensiometry (MBPT) set-up we built. MBPT relies on the measurement of maximum bubble pressure as a function of bubbling rate and facilitates the measurement of time-dependent variation in surface tension correlated with the rate of mass transfer of surface-active agents to a freshly formed interface.85–87 We checked that the pseudo-equilibrium values obtained using MBPT are comparable to equilibrium surface tension values obtained using pendant drop tensiometry and identified CMC and CAC values. We report steady shear viscosity measurements made using a torsional rheometer, using a concentric cylinder (double gap) Couette cell on an Anton Paar MCR 302 rheometer at 25 °C.The polymer PEO with an average molecular weight Mw = 1.0 × 106 g mol−1 and the surfactant SDS purchased from Sigma-Aldrich were used without further purification. Aqueous PEO solutions were prepared by slowly adding dry polymer powder to deionized water. The PEO solutions were left on a roller for a minimum of five days to ensure homogeneous and slow mixing, as high shear mixing flows can lead to chain scission.88,89 Subsequently, SDS was added and left overnight on a roller for complete mixing. The polymer concentrations used in this study lie below the overlap concentration (c* = 0.17%) of the surfactant-free polymer solutions. The stretching of PEO chains by electrostatics on complexation with charged surfactant and micelles, and by hydrodynamics in extensional flows lower threshold for overlap and interchain interactions.2,4,42,47,48,66,90
Results and discussion
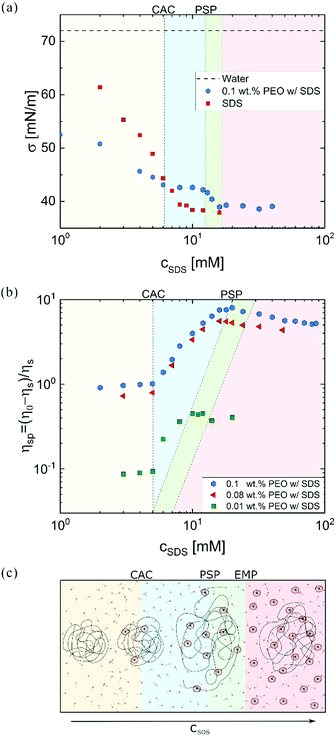
Critical aggregation concentration (CAC) and polymer saturation point (PSP)
Fig. 1a shows that the surface tension of the polymer-free solutions progressively decreases with cSDS but attains a relatively constant value above a CMC. For a fixed PEO concentration, SDS addition lowers the surface tension up to CAC that signals the onset of the polymer–surfactant complexation. Beyond polymer saturation point (PSP), surface tension decreases towards the values for polymer-free SDS solutions. The plot of specific viscosity ηsp = (η0 − ηs)/ηs as a function of cSDS (see Fig. 1b) displays a plateau region at low surfactant concentration, and an increase in viscosity above the critical aggregate concentration (CAC), with the peak value at PSP. At excess micelle point (EMP), the unimer concentration equals the CMC value, and free micelles form. Here, viscosity of water defines solvent viscosity, ηs, such that ηsp values capture the solute contribution to η0. Specific viscosity measured at lower polymer concentrations (0.08 and 0.01 wt%) exhibits the same CAC value of 5 mM. However, the PSP values depend on polymer concentration, in agreement with the previous reports on P0S− systems including PEO–SDS, PEO–SBDS, and PVP–SDS.61,91 The changes in surface tension and steady shear viscosity are influenced by the surfactant-like and the polymer-like behavior of the polymer–surfactant complex, respectively.25Fig. 1c schematically illustrates the evolution of uncharged polymer–anionic surfactant (P0S−) interactions and complexation under equilibrium conditions as a function of surfactant concentration. The picture, inspired by previous experimental and theoretical work, is sketched for a dilute polymer concentration.8–14,24,92–95 The onset of P0S− complexation occurs at CAC as self-assembly drives the formation of surfactant clusters or “beads” (bound micelles) on stringlike polymer chains, forming a “beaded-necklace.”9,10,96 The colored background in Fig. 2 visually aids in identifying the four regimes: I: Below CAC; both polymer and surfactant unimers coexist in equilibrium: no bound or free micelles, no necklace. II: CAC-PSP, the formation of partially beaded-necklace, and coil expansion. III PSP-EMP, the size and number of beads increases with cSDS. IV: EMP – beyond, beaded necklace, free micelles, and unimers coexist. The increase in cSDS beyond PSP leads to increased electrostatic screening and coil contraction. As free micelles form above EMP, it is also referred to as CMCp. The size of beads or the aggregation number, Nagg (20–50) for SDS clusters bound to PEO at cSDS ≪ PSP is lower than the Nagg = 60–80 for free micelles in the polymer-free SDS solutions (cSDS < 100 mM).97,98 The Nagg increases with cSDS in both cases, and above PSP, beads have Nagg similar to free micelles.92,98 The beaded-necklace chain in the presence of excess unimers is hydrodynamically similar to a polyelectrolyte chain in the presence of added ions.25
Characterization of pinching dynamics
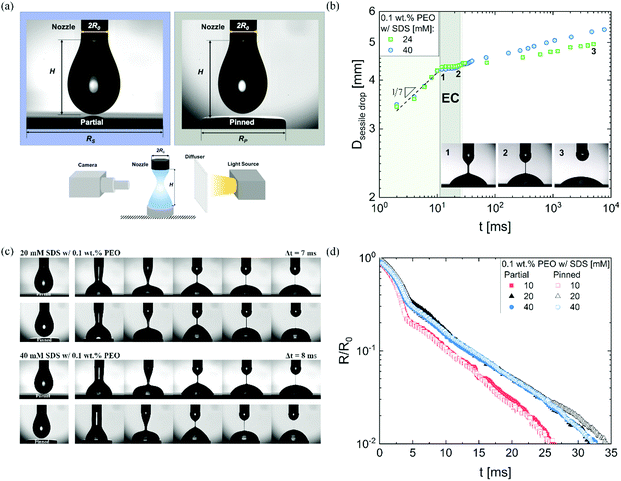
We use DoS rheometry protocols to investigate the influence of change in conformation of beaded-necklace chains on pinching dynamics and extensional rheology response. In a typical DoS rheometry experiment, drops are released onto an unbounded, partial wetting substrate at distance H from the nozzle of diameter 2R0. However, as surfactants can influence wettability,99,100 here we evaluate the influence of partial vs. pinned wetting, before discussing the extensional rheology response. Fig. 2a shows the pendant drops visualized before touching and spreading for both partial and pinned wetting, and includes a schematic illustrating how a disc-shaped substrate provides a pinned contact line. Fig. 2b shows the sessile drop diameter expansion for 24 and 40 mM SDS with 0.1 wt% PEO over the partially wetting substrate. An initial scaling of t1/7 associated with spreading involving dissipation near the contact line,100 observed for both concentrations followed by a plateau regime that nearly coincides with the elastocapillary region (EC), relevant for extensional rheology characterization (discussed next). The apparent contact angle and the diameter of the sessile drop are nearly unchanged between the instants 1 and 2 (see snapshots), and further spreading occurs long after the pinch-off event (image at instant 3 is at t = O(1000 ms), whereas the pinch-off occurs before t <50 ms).The neck shape evolution for pinned and partial wetting conditions are included in Fig. 2c for 20 and 40 mM SDS with 0.1 wt% PEO, and visually, the neck shape and pinching rate appear comparable. The corresponding radius evolution data included in Fig. 2d shows that partial and pinned wetting display quantitatively similar behavior. We include an additional dataset for 10 mM SDS to highlight the similarity in the neck thinning dynamics. In our studies with DoS rheometry protocols, we use the pinching laws that were derived for self-thinning dynamics by assuming that spreading and pinching dynamics are decoupled.44–48,53 Though in Dinic et al.46 we discussed the use of a pinned contact line on a disk to emulate a pinned lower drop in CaBER experiments, we found that the partial wetting substrates provide pragmatic and quantitative measurements. Our choice was also guided by our experimental observations using different substrates consonant with the extensive literature on the influence of moving contact lines on the capillary breakup, and transfer ratio (TR: the fraction of liquid transferred to a lower plate) that find an enhancement in pinching rates and TR on wetting substrates (relatively small contact angles, and high surface energy).101–106 Previously, Zhang and Muller81 utilized the pinned wetting for DoS rheometry of surfactant solutions. More recently, Wu et al.84 dripped wormlike micellar solutions on high surface energy metal surfaces, and found that the moving contact lines impact pinching dynamics only for Capillary number, Ca > 0.1, where 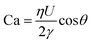 is defined using mean spreading velocity, U and apparent contact angle, θ. We find Ca ≪ 0.1 for partial wetting substrates (larger θ, leads to smaller Ca). In practice, the wetting behavior of substrate must be evaluated for each liquid used in DoS rheometry experiments.
is defined using mean spreading velocity, U and apparent contact angle, θ. We find Ca ≪ 0.1 for partial wetting substrates (larger θ, leads to smaller Ca). In practice, the wetting behavior of substrate must be evaluated for each liquid used in DoS rheometry experiments.
Fig. 3a shows the neck shape evolution of PEO/SDS mixtures with a matched starting point of R/R0 ∼ 0.5. A single conical neck forms for pure water as shown in the image sequence in the top row with a timestep, Δt = 0.5 ms. In contrast, slender cylindrical necks form for the polymer–surfactant solutions and exhibit delayed pinch-off (Δt = 5 ms). An increase in SDS concentration leads to a non-monotonic change in filament lifespan, tf thus requiring more snapshots for 16 mM SDS than for 8 mM as well as 32 mM SDS. Interaction of PEO with the ionic surfactant, SDS leading to the formation of an electrostatically stretched beaded-necklace increases tf and η0(cSDS), and shifts the onset of shear thinning response for cSDS >8 mM to the measurable range, as seen in Fig. 3b (the Carreau model fits are included as a dotted line).
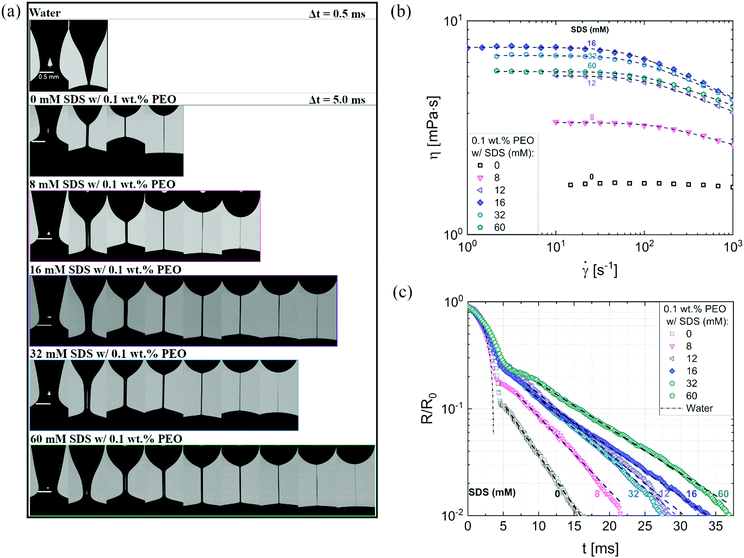 | ||
| Fig. 3 Contrasting the concentration dependence on radius evolution data obtained using DoS rheometry and shear viscosity data obtained with torsional rheometry. (a) Representative snapshots exhibit a comparison of different neck shapes for water, polymer (PEO), and polymer–surfactant solutions (PEO/SDS). (a) The shear rheology response of polyethylene oxide (PEO) and sodium dodecyl sulfate (SDS) aqueous solutions were characterized using a concentric cylinder (double gap) Couette cell on an Anton Paar MCR 302 rheometer at 25 °C. A matched flow curve is observed for 12 and 60 mM SDS. The Carreau model fits are included as a dotted line. (c) Radius evolution of PEO/SDS solutions. The addition of SDS to polymer solutions (PEO) delays pinch-off event compared to the polymer solution with no SDS added. 60 mM SDS do not overlap with 12 mM, as seen in shear viscosity data. Dashed lines show EC fits obtained using eqn (2). | ||
Though the addition of 12 mM and 60 mM SDS to the PEO solutions results in a nearly matched shear viscosity, the pinching dynamics are remarkably dissimilar, with a longer pinching time manifested for 60 mM. The radius evolution data in Fig. 3c also displays a longer tf for 16 mM than for 32 mM, and though tf for 60 mM is larger than for 32 mM. As the shear viscosity of the P0S− systems used in the study is relatively low, leading to Oh < 1, the initial radius evolution shows an inertiocapillary response for all mixtures, described by the following expression:
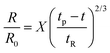 | (1) |
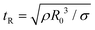 represents the characteristic inertiocapillary time and tp represents the pinch-off time or filament lifespan for a Newtonian fluid and is used a parameter for fitting the IC regime for polymeric fluids. The experimentally measured values of X as well as the values obtained using volume-of-fluid based numerical simulations vary between 0.4–0.6, as detailed elsewhere.28,29,107 Even though the interplay of gravity and capillarity influences the shape of the pendant drop, gravity exercises a negligible impact on the pinching dynamics. The value of the dimensionless group, Bond number, Bo = ΔρgR2/σ becomes rather small as pinching proceeds for it ranges between Bo = 0.06–0.1 if nozzle size R = R0, is used for estimation, and Bo ≪ 1 within the pinching neck.
represents the characteristic inertiocapillary time and tp represents the pinch-off time or filament lifespan for a Newtonian fluid and is used a parameter for fitting the IC regime for polymeric fluids. The experimentally measured values of X as well as the values obtained using volume-of-fluid based numerical simulations vary between 0.4–0.6, as detailed elsewhere.28,29,107 Even though the interplay of gravity and capillarity influences the shape of the pendant drop, gravity exercises a negligible impact on the pinching dynamics. The value of the dimensionless group, Bond number, Bo = ΔρgR2/σ becomes rather small as pinching proceeds for it ranges between Bo = 0.06–0.1 if nozzle size R = R0, is used for estimation, and Bo ≪ 1 within the pinching neck.
In contrast, the elastocapillary regime displays an exponentially slow decay in the radius that can be described by the following expression:
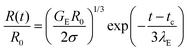 | (2) |
In some cases, finite extensibility effects,47,48,53,117,118 (not included in the Oldroyd-B model) manifest as a terminal viscoelastocapillary (TVEC) regime, with a linear decrease in radius R(t)/R0 = (tf − t)/tTVEC. Here tTVEC = 2OhTr∞ with Tr∞ = η∞E/η defined as the ratio of a strain-rate and strain independent steady, terminal extensional viscosity, η∞E and the rate-independent zero shear viscosity. The fits to the TVEC regime allow the computation of η∞E and the filament lifespan, tf (or the overall pinch-off time). Table 2 lists the parameters extracted by analyzing the radius evolution data and also includes the values of the zero shear viscosity and surface tension measured using torsional shear rheometry and maximum bubble pressure tensiometry, respectively.
| c SDS (mM) | η 0 (mPa s) | λ s (ms) | σ (mN m−1) | t c (ms) | R c/R0 (−) | t f (ms) | λ E (ms) |
|---|---|---|---|---|---|---|---|
| 0 | 1.7 | — | 62.1 | 4.6 ± 0.1 | 0.112 | 13.9 ± 0.3 | 1.5 ± 0.05 |
| 2 | 1.7 | — | 48.2 | 4.7 ± 0.2 | 0.101 | 19.5 ± 0.2 | 2.1 ± 0.04 |
| 4 | 1.8 | — | 45.4 | 4.5 ± 0.1 | 0.136 | 17.7 ± 0.3 | 2.0 ± 0.01 |
| 5 | 1.8 | — | 44.6 | 5.1 ± 0.2 | 0.143 | 19.0 ± 0.7 | 1.9 ± 0.06 |
| 8 | 3.4 | 7.3 | 43.3 | 4.7 ± 0.4 | 0.167 | 20.0 ± 0.6 | 2.1 ± 0.01 |
| 10 | 4.4 | 8.0 | 43.0 | 4.5 ± 0.4 | 0.205 | 20.4 ± 1.6 | 2.2 ± 0.04 |
| 12 | 5.6 | 10.8 | 42.2 | 4.2 ± 0.5 | 0.302 | 26.5 ± 0.8 | 2.6 ± 0.03 |
| 14 | 6.5 | 11.8 | 40.3 | 5.0 ± 0.2 | 0.227 | 28.1 ± 1.4 | 3.4 ± 0.04 |
| 20 | 8.0 | 14.1 | 39.8 | 5.1 ± 0.2 | 0.270 | 29.2 ± 0.9 | 2.9 ± 0.07 |
| 24 | 7.3 | 12.6 | 39.1 | 4.7 ± 0.2 | 0.281 | 26.1 ± 0.5 | 2.5 ± 0.04 |
| 32 | 6.9 | 13.4 | 38.6 | 4.9 ± 0.5 | 0.246 | 25.2 ± 0.7 | 2.6 ± 0.01 |
| 40 | 6.4 | 12.0 | 39.0 | 5.9 ± 0.5 | 0.246 | 29.5 ± 1.4 | 3.4 ± 0.13 |
Extensional relaxation time and extensional viscosity
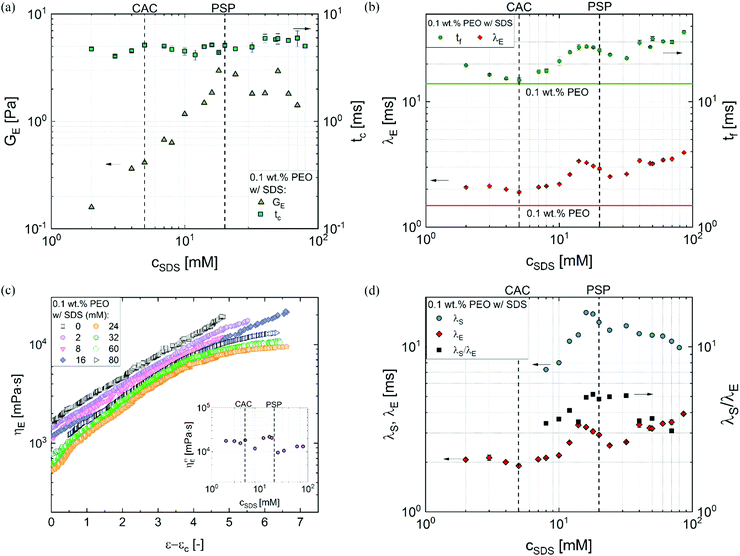
Fig. 4a shows the plot of GE and tcvs. cSDS and even though the value of tc shows slight variation, GE increases linearly up to PSP (error bars are similar to the size of symbols). Fig. 4b shows that the extensional relaxation time, λE obtained by fitting the radius evolution profiles included in Fig. 3c (and the data for a few extra concentrations) for a fixed PEO (0.1 wt%) concentration, exhibits a non-monotonic variation with cSDS. The peak observed at 14 mM exhibits λE value that is 2.3 times the value obtained for the surfactant-free PEO solution (included as a horizontal line). As the cSDS increases, λE remains nearly constant even as CAC is exceeded, and λE increases with concentration once cSDS exceeds 10 mM (∼2 times CAC), rising to a peak value at 14 mM even though PSP = 20 mM is computed from the specific viscosity curve. We observe that the filament lifespan, tf also exhibits a non-monotonic concentration dependence distinct from the response expected using shear rheology response. On increasing surfactant concentration further, λE value dips and then increases again beyond cSDS = 24 mM. In addition to extensional relaxation time, the analysis of radius evolution data using the expression ηE![[small epsi, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a1.gif) (t) = σ/R(t) facilitates the computation of an apparent extensional viscosity ηE = ηtE(ε,
(t) = σ/R(t) facilitates the computation of an apparent extensional viscosity ηE = ηtE(ε,![[small epsi, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a1.gif) ,t). The balance between extensional and capillary stresses is carried out assuming inertial and viscous terms are negligible. Here, capillary stress depends on the ratio of surface tension, σ to the transient neck radius. Though the effect of dynamic adsorption is not considered here (a detailed investigation is ongoing), previous studies indicate that soluble surfactants with fast adsorption kinetics and concentrations above CMC show significant surface coverage,119–122 unlike insoluble surfactants that provide contributions by Marangoni stresses and are entirely swept away from the pinch-off zone in the late stage.123,124 The extension rate,
,t). The balance between extensional and capillary stresses is carried out assuming inertial and viscous terms are negligible. Here, capillary stress depends on the ratio of surface tension, σ to the transient neck radius. Though the effect of dynamic adsorption is not considered here (a detailed investigation is ongoing), previous studies indicate that soluble surfactants with fast adsorption kinetics and concentrations above CMC show significant surface coverage,119–122 unlike insoluble surfactants that provide contributions by Marangoni stresses and are entirely swept away from the pinch-off zone in the late stage.123,124 The extension rate, ![[small epsi, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a1.gif) = −2Ṙ(t)/R(t) determined from the radius evolution profiles, exhibits a constant value in the EC regime. However, in IC and TVEC regimes, the value diverges as
= −2Ṙ(t)/R(t) determined from the radius evolution profiles, exhibits a constant value in the EC regime. However, in IC and TVEC regimes, the value diverges as ![[small epsi, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a1.gif) = 2n/(tp − t) with n = 2/3 and 1 respectively.
= 2n/(tp − t) with n = 2/3 and 1 respectively.
The apparent extensional viscosity plotted as a function of Hencky strain, ε = 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln(R0/R(t)) in Fig. 4c exhibits strain hardening for all systems and the TVEC regime is manifested for the solutions with cSDS > 24 mM. The extensional viscosity value and Tr for the surfactant-free PEO solution are higher than the PEO–SDS solutions with cSDS < 16 mM. The measured value of maximum extensional viscosity that correspond to the steady, terminal extensional viscosity values for cSDS > 24 mM, shown in the inset of Fig. 4c, show relatively weak concentration-dependent variation in comparison to the shear viscosity response. The Tr ratio estimated using the ratio of these plotted values to the corresponding zero shear viscosity values are nearly three times lower than the value measured for the SDS-free PEO solution, correlated with the higher extensibility (ratio of stretched chain to unperturbed coil size) in comparison to electrostatically stretched, beaded-necklace chains. The Trouton ratios measured for PEO–SDS solutions are in the range of Tr ∼ O(103–104), that is up to two orders of magnitude greater than the values calculated using the opposed-jet technique and reported by Cooper-White et al.60 for similar PEO–SDS solutions (made with glycerol-water mixtures and 0.15 wt% PEO). However, Tr ∼ O(103–104) agree with the more recent extensional viscosity values measured using CaBER (for SDS < 32 mM) by the same co-authors.62,63 As the opposed-jet technique presents challenges for quantitative characterization,60,64 and both capillarity-based methods show comparable Tr values, we conclude that even though the maximum extensional viscosity is 103–104 fold higher, the nearly-matched stretched chain size provides comparable values for the PEO–SDS solutions as shown in the inset of Fig. 4c.
ln(R0/R(t)) in Fig. 4c exhibits strain hardening for all systems and the TVEC regime is manifested for the solutions with cSDS > 24 mM. The extensional viscosity value and Tr for the surfactant-free PEO solution are higher than the PEO–SDS solutions with cSDS < 16 mM. The measured value of maximum extensional viscosity that correspond to the steady, terminal extensional viscosity values for cSDS > 24 mM, shown in the inset of Fig. 4c, show relatively weak concentration-dependent variation in comparison to the shear viscosity response. The Tr ratio estimated using the ratio of these plotted values to the corresponding zero shear viscosity values are nearly three times lower than the value measured for the SDS-free PEO solution, correlated with the higher extensibility (ratio of stretched chain to unperturbed coil size) in comparison to electrostatically stretched, beaded-necklace chains. The Trouton ratios measured for PEO–SDS solutions are in the range of Tr ∼ O(103–104), that is up to two orders of magnitude greater than the values calculated using the opposed-jet technique and reported by Cooper-White et al.60 for similar PEO–SDS solutions (made with glycerol-water mixtures and 0.15 wt% PEO). However, Tr ∼ O(103–104) agree with the more recent extensional viscosity values measured using CaBER (for SDS < 32 mM) by the same co-authors.62,63 As the opposed-jet technique presents challenges for quantitative characterization,60,64 and both capillarity-based methods show comparable Tr values, we conclude that even though the maximum extensional viscosity is 103–104 fold higher, the nearly-matched stretched chain size provides comparable values for the PEO–SDS solutions as shown in the inset of Fig. 4c.
A comparison of the shear and extensional relaxation times is shown in Fig. 4d. Remarkably, the λs values estimated using the Carreau model fits for 12–60 mM are an order of magnitude larger than the λE values, implying that the conformations, strain, degree of chain overlap, and relaxation dynamics are quite different in shear and extensional flow fields. Though extensional relaxation time is longer than λs for neutral polymers as well as polyelectrolytes,37,38,42,45,47,48,66,67,71,90 the rather large values for λs observed in the polymer–surfactant mixtures compared to extensional relaxation time are consistent with three scenarios. Previous studies that show λs > λE arises due to the role played by transient junctions created by entanglements for neutral polymers,43,125 and by stickers for associative polymer solutions.126 The observation of λs > λE in wormlike micellar fluids127–130 is often attributed to different dynamics of micelle creation and destruction for the stretched states in response to shear and extensional flow. Here, the PEO concentration is relatively low compared to entanglement concentration and SDS concentrations are well below the range where wormlike micelles form. Even though complexation expands coils and alters the size of self-assembled structures, the formation of entanglements or wormlike micelles is unlikely. Therefore, the observation of λs > λE suggests that some beads are acting as transient junctions, and the creation and destruction rate of such junctions change in the presence of strong extensional flows.
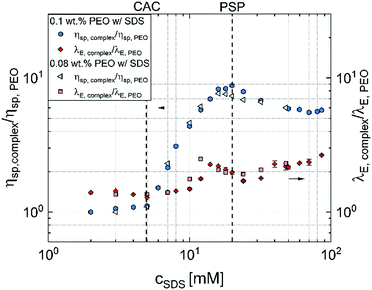
Fig. 5 summarizes the key findings of this contribution and presents the contrasting shear and extensional rheology response using zero shear viscosity and extensional relaxation time values obtained for the aqueous PEO–SDS mixtures normalized by the corresponding values obtained for SDS-free PEO solutions with 0.08 wt% and 0.1 wt% PEO. Though shear viscosity increases by nearly an order of magnitude, the extensional relaxation time increases only by a factor of two, and the peak values for the latter are not obtained at the PSP or the peak observed in shear viscosity measurements. The increase in concentration-dependent zero shear rate viscosity η0 values at low cSDS, up to a peak at PSP, followed by a dip is often attributed to the influence of surfactant unimers and bound/free micelles on the conformation of “beaded-necklace” polymer chains. The range and extent of electrostatic interactions affect polymer conformation and influence inter- and intrachain interactions that lead to nearly an order of magnitude higher peak viscosity. A ten-fold increase in viscosity implies the beaded necklace chains are either in semi-dilute regime (as the overlap concentration for polyelectrolytes is lower, and semi-dilute regime that arises for c* > 1 shows ηsp > 1) or the beads effectively behave like transient junctions (complexes behave like associative polymers).
The solution viscosity is relatively low and hence the viscoelastic response is below the resolution in the oscillatory shear measurements, thus preventing us from making direct comparisons with transient network models. However, the onset of shear thinning and the decay constant obtained from elastocapillary pinching provide us with two distinct measurements of relaxation time, contrasted in Fig. 4d. The enhanced values of η0 and λs, and limited or complete disassociation of such transient junctions in strong flows,126 leads to shear thinning response as well as manifestation of extensional relaxation time, λE values comparable to the stretched neutral chains. Extensional rheology characterization of multi-sticker associative polysaccharides with flow birefringence and excess pressure drop across a stagnation point in cross-slot extensional rheometer37 and of hydrophobically modified alkali-soluble emulsion (HASE) polymers using opposed jets131 suggest that associative polymer solutions show a pronounced degree of extensional thinning as the response is dictated by destruction of the transient network. In contrast, the aqueous solutions of PEO–SDS mixtures show strain hardening in Fig. 4c, with nearly matched maximum extensional viscosity values. However, the studies on associative polysaccharides were carried out at much higher polymer volume fractions and as polysaccharides show lower flexibility and extensibility than PEO, the relative enhancements in Tr ratio, even for bare polysaccharides, are quite low at comparable molecular weights.47,48,53
Conclusions
In summary, the addition of a charged surfactant like SDS to an uncharged polymer like PEO increases the pervaded volume, leading to a lower overlap concentration, lower critical shear rate for the onset of shear thinning, and higher measured specific viscosity values (almost an order of magnitude higher). However, the extensional relaxation time and extensional viscosity exhibit a weaker concentration-dependence as the relaxation dynamics and drag of the hydrodynamically-stretched chains are comparable even if surfactant changes the equilibrium coil size. The relatively weak variation in filament lifespan and extensional relaxation time cannot be anticipated with shear rheology characterization. We rationalize the observations by treating P0S−ACs as stretched, charged, beaded-necklace chains with electrostatic-stretching determined by surfactant concentration and hydrodynamic-stretching sensitive to flow type. As macromolecules can undergo relatively large stretch, even coil-stretch transition, under the effect of an extensional flow, the extent of stretching determines the value of Tr especially in the finite extensibility regime. We find that Tr values for the P0S− systems are nearly a factor of 3 lower, implying the extensibility itself is 1.7 times lower, consistent with the previous determination of conformational changes in an uncharged polymer that interacts with an ionic surfactant. We anticipate that protocols and findings described herein will help in a better understanding of the rheological and processing behavior of formulations containing flexible uncharged polymers and ionic surfactants, especially during processing operations involving strong extensional flows.Author contributions
CM primarily carried out all the experiments described in the study. TM, under CM's mentorship, carried out the tensiometry experiments. CM and VS analyzed the data and wrote the manuscript.Conflicts of interest
There are no conflicts to declare.Acknowledgements
CM and VS would like to acknowledge funding support by NSF CBET 1806011, PPG industries, and the 3M nontenured faculty award (NTFA). CM also wishes to acknowledge a Teaching Assistantship by the Department of Chemistry at UIC. TM is currently employed at Abbott (Gurnee, IL) and carried out research as an undergraduate student at UIC. The authors acknowledge Dr Naveen Reddy (U. Hasselt), Dr Hari Katepalli (Dow), and Dr Karthika Suresh and the students from the ODES-lab for a close reading of the manuscript. Lastly, the authors wish to acknowledge discussions with Dr Jelena Dinic (UChicago) on the influence of the underlying substrate for JD had carried out an evaluation of the influence of different substrates first at UIC and later at KU Leuven in collaboration with Dr Naveen Reddy, Dr Susanna Formenti, and Prof. Christian Clasen.References
- R. G. Larson, The Structure and Rheology of Complex Fluids, Oxford University Press, New York, 1999 Search PubMed.
- M. Rubinstein and R. H. Colby, Polymer Physics, Oxford University Press, New York, 2003 Search PubMed.
- Z.-G. Wang, Macromolecules, 2017, 50, 9073–9114 CrossRef CAS.
- M. Muthukumar, Macromolecules, 2017, 50(24), 9528–9560 CrossRef CAS PubMed.
- J. R. Prakash, Curr. Opin. Colloid Interface Sci., 2019, 43, 63–79 CrossRef CAS.
- S. Srivastava and M. V. Tirrell, Adv. Chem. Phys., 2016, 161, 499–544 CrossRef CAS.
- E. S. G. Shaqfeh, AlChE J., 2019, 65, e16575 CrossRef.
- E. Guzmán, S. Llamas, A. Maestro, L. Fernández-Peña, A. Akanno, R. Miller, F. Ortega and R. G. Rubio, Adv. Colloid Interface Sci., 2016, 233, 38–64 CrossRef PubMed.
- E. D. Goddard, J. Colloid Interface Sci., 2002, 256, 228–235 CrossRef CAS.
- Interactions of Surfactants with Polymers and Proteins, ed. E. D. Goddard and K. P. Ananthapadmanabhan, CRC Press, 1993 Search PubMed.
- L. Piculell and B. Lindman, Adv. Colloid Interface Sci., 1992, 41, 149–178 CrossRef CAS.
- E. D. Goddard, J. Am. Oil Chem. Soc., 1994, 71, 1–16 CrossRef CAS.
- R. Nagarajan, J. Chem. Phys., 1989, 90, 1980–1994 CrossRef CAS.
- R. Nagarajan, In Polymer–surfactant interactions, New Horizons: Detergents for the New Millennium Conference Invited Paper, American Oil Chemists Society and Consumer Specialty Products Association, 2001.
- T. L. Carlson, J. Y. Lock and R. L. Carrier, Annu. Rev. Biomed. Eng., 2018, 20, 197–220 CrossRef CAS PubMed.
- E. Hilz and A. W. P. Vermeer, Crop Protection, 2013, 44, 75–83 CrossRef.
- E. Villermaux, J. Fluid Mech., 2020, 898, P1 CrossRef CAS.
- J. Kim, Y. Gao, C. Hebebrand, E. Peirtsegaele and M. E. Helgeson, Soft Matter, 2013, 9, 6897–6910 RSC.
- A. Jaishankar, V. Sharma and G. H. McKinley, Soft Matter, 2011, 7, 7623–7634 RSC.
- N. Kristen and R. von Klitzing, Soft Matter, 2010, 6, 849–861 RSC.
- A. Gupta, H. B. Eral, T. A. Hatton and P. S. Doyle, Soft Matter, 2016, 12, 2826–2841 RSC.
- J. N. Israelachvili, Intermolecular and Surface Forces, Academic Press, 3rd edn, 2011 Search PubMed.
- E. D. Goddard, Colloids Surf., 1986, 19, 255–300 CrossRef CAS.
- B. Z. Shang, Z. Wang and R. G. Larson, J. Phys. Chem. B, 2008, 112, 2888–2900 CrossRef CAS PubMed.
- J. Francois, J. Dayantis and J. Sabbadin, Eur. Polym. J., 1985, 21, 165–174 CrossRef CAS.
- S. Banerjee, C. Cazeneuve, N. Baghdadli, S. Ringeissen, F. A. M. Leermakers and G. S. Luengo, Soft Matter, 2015, 11, 2504–2511 RSC.
- L. Kunche and U. Natarajan, Soft Matter, 2021, 17, 670–687 RSC.
- J. Eggers and M. A. Fontelos, Singularities: Formation, Structure, and Propagation, Cambridge University Press, Cambridge, UK, 2015 Search PubMed.
- G. H. McKinley, Rheol. Rev., 2005, 1–48 CAS.
- O. A. Basaran, H. Gao and P. P. Bhat, Annu. Rev. Fluid Mech., 2013, 45, 85–113 CrossRef.
- M. Abkarian and H. A. Stone, Phys. Rev. Fluids, 2020, 5, 102301 CrossRef.
- R. Hamed, D. M. Schenck and J. Fiegel, Soft Matter, 2020, 16, 7823–7834 RSC.
- B. E. Scharfman, A. H. Techet, J. W. M. Bush and L. Bourouiba, Exp. Fluids, 2016, 57, 24 CrossRef CAS PubMed.
- Y. Christanti and L. M. Walker, J. Non-Newtonian Fluid Mech., 2001, 100, 9–26 CrossRef CAS.
- Y. Christanti and L. M. Walker, J. Rheol., 2002, 46, 733–748 CrossRef CAS.
- Y. Christanti and L. M. Walker, Atomization Sprays, 2006, 16, 777–790 Search PubMed.
- V. Sharma, S. J. Haward, J. Serdy, B. Keshavarz, A. Soderlund, P. Threlfall-Holmes and G. H. McKinley, Soft Matter, 2015, 11, 3251–3270 RSC.
- B. Keshavarz, V. Sharma, E. C. Houze, M. R. Koerner, J. R. Moore, P. M. Cotts, P. Threlfall-Holmes and G. H. McKinley, J. Non-Newtonian Fluid Mech., 2015, 222, 171–189 CrossRef CAS.
- B. Keshavarz, E. C. Houze, J. R. Moore, M. R. Koerner and G. H. McKinley, Phys. Rev. Lett., 2016, 117, 154502 CrossRef PubMed.
- V. M. Entov and E. J. Hinch, J. Non-Newtonian Fluid Mech., 1997, 72, 31–54 CrossRef CAS.
- V. M. Entov and A. L. Yarin, Fluid Dyn., 1984, 19, 21–29 CrossRef.
- V. Tirtaatmadja, G. H. McKinley and J. J. Cooper-White, Phys. Fluids, 2006, 18, 043101 CrossRef.
- O. Arnolds, H. Buggisch, D. Sachsenheimer and N. Willenbacher, Rheol. Acta, 2010, 49, 1207–1217 CrossRef CAS.
- J. Dinic, Y. Zhang, L. N. Jimenez and V. Sharma, ACS Macro Lett., 2015, 4, 804–808 CrossRef CAS.
- J. Dinic, M. Biagioli and V. Sharma, J. Polym. Sci., Part B: Polym. Phys., 2017, 55, 1692–1704 CrossRef CAS.
- J. Dinic, L. N. Jimenez and V. Sharma, Lab Chip, 2017, 17, 460–473 RSC.
- J. Dinic and V. Sharma, Proc. Natl. Acad. Sci. U. S. A., 2019, 116, 8766–8774 CrossRef CAS PubMed.
- J. Dinic and V. Sharma, Macromolecules, 2020, 53, 4821–4835 CrossRef CAS.
- T. Q. Nguyen and H. H. Kausch, Flexible Polymer Chains in Elongational Flow: Theory and Experiment, Springer-Verlag, Berlin, 1999 Search PubMed.
- D. F. James and K. Walters, in Techniques of Rheological Measurement, ed. A. A. Collyer, Elsevier, New York, 1994, ch. 2, pp. 33–53 Search PubMed.
- L. E. Rodd, T. P. Scott, J. J. Cooper-White and G. H. McKinley, Appl. Rheol., 2005, 15, 12–27 CAS.
- C. J. S. Petrie, J. Non-Newtonian Fluid Mech., 2006, 137, 1–14 CrossRef CAS.
- J. Dinic and V. Sharma, Macromolecules, 2020, 53, 3424–3437 CrossRef CAS.
- P. Fischer and E. J. Windhab, Curr. Opin. Colloid Interface Sci., 2011, 16, 36–40 CrossRef CAS.
- C. W. Macosko, Rheology: Principles, Measurements and Applications, VCH Publishers Inc, New York, 1994 Search PubMed.
- J. R. Eastman, J. W. Goodwin and A. M. Howe, Colloids Surf., A, 2000, 161, 329–338 CrossRef CAS.
- L. M. Smitter, J. F. Guedez, A. J. Müller and A. E. Saez, J. Colloid Interface Sci., 2001, 236, 343–353 CrossRef CAS PubMed.
- L. M. Smitter, J. C. Ruiz, M. E. Torres, A. J. Müller and A. E. Saez, J. Colloid Interface Sci., 2002, 251, 388–397 CrossRef CAS PubMed.
- L. M. Smitter, M. E. Torres, A. J. Müller and A. E. Saez, J. Colloid Interface Sci., 2001, 244, 164–172 CrossRef CAS.
- J. J. Cooper-White, R. C. Crooks, K. Chockalingam and D. V. Boger, Ind. Eng. Chem. Res., 2002, 41, 6443–6459 CrossRef CAS.
- M. F. Torres, A. J. Muller, M. A. Szidarovszky and A. E. Saez, J. Colloid Interface Sci., 2008, 326, 254–260 CrossRef CAS PubMed.
- E. Miller and J. Cooper-White, J. Non-Newtonian Fluid Mech., 2009, 160, 22–30 CrossRef CAS.
- R. Wang, G. Dorr, A. Hewitt and J. Cooper-White, Colloids Surf., A, 2016, 500, 88–97 CrossRef CAS.
- P. Dontula, M. Pasquali, L. Scriven and C. W. Macosko, Rheol. Acta, 1997, 36, 429–448 CrossRef CAS.
- L. Campo-Deano and C. Clasen, J. Non-Newtonian Fluid Mech., 2010, 165, 1688–1699 CrossRef CAS.
- L. N. Jimenez, J. Dinic, N. Parsi and V. Sharma, Macromolecules, 2018, 51, 5191–5208 CrossRef CAS.
- L. N. Jimenez, C. D. V. Martínez Narváez and V. Sharma, Phys. Fluids, 2020, 32, 012113 CrossRef CAS.
- L. N. Jimenez, C. D. Martínez Narváez, C. Xu, S. Bacchi and V. Sharma, Soft Matter, 2021, 17, 5197–5213 RSC.
- L. N. Jimenez, C. D. V. Martínez Narváez, C. Xu, S. Bacchi and V. Sharma, Surface Science and Adhesion in Cosmetics, 2021, pp. 109–150 Search PubMed.
- K. W. Hsiao, J. Dinic, Y. Ren, V. Sharma and C. M. Schroeder, Phys. Fluids, 2017, 29, 121603 CrossRef.
- A. V. Walter, L. N. Jimenez, J. Dinic, V. Sharma and K. A. Erk, Rheol. Acta, 2019, 58, 145–157 CrossRef CAS.
- K. A. Marshall, A. M. Liedtke, A. H. Todt and T. W. Walker, Exp. Fluids, 2017, 58(69), 9 Search PubMed.
- N. S. Suteria, S. Gupta, R. Potineni, S. K. Baier and S. A. Vanapalli, Rheol. Acta, 2019, 58, 403–417 CrossRef CAS.
- K. A. Marshall and T. W. Walker, Rheol. Acta, 2019, 58, 573–590 CrossRef CAS.
- T. J. Murdoch, E. Pashkovski, R. Patterson, R. W. Carpick and D. Lee, ACS Appl. Polym. Mater., 2020, 2, 4062–4070 CrossRef.
- Y. Su, B. Palacios and R. Zenit, Phys. Rev. Fluids, 2021, 6, 033303 CrossRef.
- A. Franco-Gómez, H. Onuki, Y. Yokoyama, Y. Nagatsu and Y. Tagawa, Exp. Fluids, 2021, 62, 1–15 CrossRef.
- S. Gupta and S. A. Vanapalli, Phys. Fluids, 2020, 32, 012006 CrossRef CAS.
- M. Rosello, S. Sur, B. Barbet and J. P. Rothstein, J. Non-Newtonian Fluid Mech., 2019, 266, 160–170 CrossRef CAS.
- S. Khandavalli, N. Sharma-Nene, S. Kabir, S. Sur, J. P. Rothstein, K. C. Neyerlin, S. A. Mauger and M. Ulsh, ACS Appl. Polym. Mater., 2021, 3(5), 2374–2384 CrossRef CAS.
- Y. Zhang and S. J. Muller, Phys. Rev. Fluids, 2018, 3 CAS.
- S. J. Wu and H. Mohammadigoushki, J. Rheol., 2018, 62, 1061–1069 CrossRef CAS.
- R. Omidvar, S. Wu and H. Mohammadigoushki, J. Rheol., 2019, 63, 33–44 CrossRef CAS.
- S. Wu and H. Mohammadigoushki, Phys. Rev. Fluids, 2020, 5, 053303 CrossRef.
- N. C. Christov, K. D. Danov, P. A. Kralchevsky, K. P. Ananthapadmanabhan and A. Lips, Langmuir, 2006, 22, 7528–7542 CrossRef CAS PubMed.
- V. B. Fainerman, R. Miller and P. Joos, Colloid Polym. Sci., 1994, 272, 731–739 CrossRef CAS.
- E. I. Franses, O. A. Basaran and C. H. Chang, Curr. Opin. Colloid Interface Sci., 1996, 1, 296–303 CrossRef CAS.
- J. A. Odell, A. Keller and Y. Rabin, J. Chem. Phys., 1988, 88, 4022–4028 CrossRef CAS.
- S. Garrepally, S. Jouenne, P. D. Olmsted and F. Lequeux, J. Rheol., 2020, 64, 601–614 CrossRef CAS.
- C. Clasen, J. P. Plog, W. M. Kulicke, M. Owens, C. Macosko, L. E. Scriven, M. Verani and G. H. McKinley, J. Rheol., 2006, 50, 849–881 CrossRef CAS.
- A. J. Müller, Y. Garcés, M. Torres, B. Scharifker and A. E. Sáez, Aqueous Polymer—Cosolute Systems, Springer, 2003, pp. 73–81 Search PubMed.
- B. Cabane, J. Phys. Chem., 1977, 81, 1639–1645 CrossRef CAS.
- B. Cabane and R. Duplessix, J. Phys., 1982, 43, 1529–1542 CrossRef CAS.
- B. Cabane and R. Duplessix, Colloids Surf., 1985, 13, 19–33 CrossRef CAS.
- B. Cabane and R. Duplessix, J. Phys., 1987, 48, 651–662 CrossRef CAS.
- K. Shirahama, K. Tsujii and T. Takagi, J. Biochem., 1974, 75, 309–319 CrossRef CAS PubMed.
- F. H. Quina, P. M. Nassar, J. B. S. Bonilha and B. L. Bales, J. Phys. Chem., 1995, 99, 17028–17031 CrossRef CAS.
- B. Cabane, R. Duplessix and T. Zemb, J. Phys., 1985, 46, 2161–2178 CrossRef CAS.
- P. G. de Gennes, F. Brochard-Wyart and D. Quéré, Capillarity and Wetting Phenomena: Drops, Bubbles, Pearls, Waves, Springer-Verlag, New York, 2004 Search PubMed.
- D. Bonn, J. Eggers, J. Indekeu, J. Meunier and E. Rolley, Rev. Mod. Phys., 2009, 81, 739–805 CrossRef CAS.
- S. Kumar, Annu. Rev. Fluid Mech., 2014, 47, 67–94 CrossRef.
- H. W. Kang, H. J. Sung, T.-M. Lee, D.-S. Kim and C.-J. Kim, J. Micromechanics Microeng., 2008, 19, 015025 CrossRef.
- S. Dodds, M. Carvalho and S. Kumar, Phys. Fluids, 2011, 23, 092101 CrossRef.
- H. Chen, A. Amirfazli and T. Tang, Langmuir, 2013, 29, 3310–3319 CrossRef CAS PubMed.
- A. K. Sankaran and J. P. Rothstein, J. Non-Newtonian Fluid Mech., 2012, 175, 64–75 CrossRef.
- B. Qian and K. S. Breuer, J. Fluid Mech., 2011, 666, 554–572 CrossRef.
- J. Dinic and V. Sharma, Phys. Fluids, 2019, 31, 021211 CrossRef.
- J. Zhou and M. Doi, Phys. Rev. Fluids, 2018, 3, 084004 CrossRef.
- A. Ardekani, V. Sharma and G. H. McKinley, J. Fluid Mech., 2010, 665, 46–56 CrossRef.
- C. Wagner, L. Bourouiba and G. H. McKinley, J. Non-Newtonian Fluid Mech., 2015, 218, 53–61 CrossRef CAS.
- J. Eggers, M. A. Herrada and J. H. Snoeijer, J. Fluid Mech., 2020, 887 DOI:10.1017/jfm.2020.18.
- A. Deblais, M. A. Herrada, J. Eggers and D. Bonn, J. Fluid Mech., 2020, 904 DOI:10.1017/jfm.2020.765.
- P. P. Bhat, S. Appathurai, M. T. Harris, M. Pasquali, G. H. McKinley and O. A. Basaran, Nat. Phys., 2010, 6, 625–631 Search PubMed.
- R. Prabhakar, S. Gadkari, T. Gopesh and M. J. Shaw, J. Rheol., 2016, 60, 345–366 CrossRef CAS.
- R. Prabhakar, C. Sasmal, D. A. Nguyen, T. Sridhar and J. R. Prakash, Phys. Rev. Fluids, 2017, 2, 011301 CrossRef.
- M. Renardy, Rheol. Rev., 2004, 2, 171–196 Search PubMed.
- M. Stelter, G. Brenn, A. L. Yarin, R. P. Singh and F. Durst, J. Rheol., 2000, 44, 595–616 CrossRef CAS.
- M. Stelter, G. Brenn, A. L. Yarin, R. P. Singh and F. Durst, J. Rheol., 2002, 46, 507–527 CrossRef CAS.
- F. Jin, N. R. Gupta and K. J. Stebe, Phys. Fluids, 2006, 18, 022103 CrossRef.
- M. R. de Saint Vincent, J. Petit, M. Aytouna, J.-P. Delville, D. Bonn and H. Kellay, J. Fluid Mech., 2012, 692, 499–510 CrossRef.
- M. Roché, M. Aytouna, D. Bonn and H. Kellay, Phys. Rev. Lett., 2009, 103, 264501 CrossRef PubMed.
- W. Lee, L. M. Walker and S. L. Anna, Macromol. Mater. Eng., 2011, 296, 203–213 CrossRef CAS.
- M.-L. E. Timmermans and J. R. Lister, J. Fluid Mech., 2002, 459, 289–306 CrossRef CAS.
- P. M. Kamat, B. W. Wagoner, S. S. Thete and O. A. Basaran, Phys. Rev. Fluids, 2018, 3, 043602 CrossRef.
- D. Sachsenheimer, B. Hochstein and N. Willenbacher, Rheol. Acta, 2014, 53, 725–739 CrossRef CAS.
- N. Willenbacher, Y. Matter, I. Gubaydullin and V. Schaedler, Korea-Australia Rheol. J., 2008, 20, 109–116 Search PubMed.
- B. Yesilata, C. Clasen and G. H. McKinley, J. Non-Newtonian Fluid Mech., 2006, 133, 73–90 CrossRef CAS.
- A. Bhardwaj, E. Miller and J. P. Rothstein, J. Rheol., 2007, 51, 693–719 CrossRef CAS.
- D. Sachsenheimer, C. Oelschlaeger, S. Müller, J. Küstner, S. Bindgen and N. Willenbacher, J. Rheol., 2014, 58, 2017–2042 CrossRef CAS.
- R. Omidvar, A. Dalili, A. Mir and H. Mohammadigoushki, J. Non-Newtonian Fluid Mech., 2018, 252, 48–56 CrossRef CAS.
- H. Tan, K. C. Tam, V. Tirtaatmadja, R. D. Jenkins and D. R. Bassett, J. Non-Newtonian Fluid Mech., 2000, 92, 167–185 CrossRef CAS.
| This journal is © The Royal Society of Chemistry 2021 |