Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Isomorphs in nanoconfined liquids†
Benjamin M. G. D.
Carter
 ab,
C. Patrick
Royall
ab,
C. Patrick
Royall
 acd,
Jeppe C.
Dyre
acd,
Jeppe C.
Dyre
 e and
Trond S.
Ingebrigtsen
e and
Trond S.
Ingebrigtsen
 *e
*e
aH.H. Wills Physics Laboratory, Tyndall Avenue, Bristol, BS8 1TL, UK
bBristol Centre for Functional Nanomaterials, Tyndall Avenue, Bristol, BS8 1TL, UK
cSchool of Chemistry, University of Bristol, Cantock's Close, Bristol, BS8 1TS, UK
dCentre for Nanoscience and Quantum Information, Tyndall Avenue, Bristol, BS8 1FD, UK
eDepartment of Science and Environment, Roskilde University, Postbox 260, DK-4000 Roskilde, Denmark. E-mail: trond@ruc.dk
First published on 13th September 2021
Abstract
We study in this paper the possible existence of Roskilde-simple liquids and their isomorphs in a rough-wall nanoconfinement. Isomorphs are curves in the thermodynamic phase diagram along which structure and dynamics are invariant in suitable nondimensionalized units. Two model liquids using molecular dynamics computer simulations are considered: the single-component Lennard-Jones (LJ) liquid and the Kob–Andersen binary LJ mixture, both of which in the bulk phases are known to have good isomorphs. Nanoconfinement is implemented by adopting a slit-pore geometry with fcc crystalline walls; this implies inhomogenous density profiles both parallel and perpendicular to the confining walls. Despite this fact and consistent with an earlier study [Ingebrigtsen et al., Phys. Rev. Lett., 2013, 111, 235901] we find that these two nanoconfined liquids have isomorphs to a good approximation. More specifically, we show good invariance along the isomorphs of inhomogenous density profiles, mean-square displacements, and higher-order structures probed using the topological cluster classification algorithm. Our study thus provides an alternative framework for understanding nanoconfined liquids.
I. Introduction
An important simplification in the study of liquids via computer simulations is to apply so-called periodic boundary conditions. The liquid is thereby free from any confining surfaces which affect its structure and dynamics by imposing an external force field on the liquid.1,2 This simplification is, however, hard to achieve in experiments, and most liquids in nature are in contact with, or confined by, one or several surfaces.3–14 Recent experiments on levitation of metallic liquids using electrostatic or magnetic fields,15–18 ionic solution droplets in optical tweezers,19 and especially colloids20 come closer to the simplification of standard computer simulations,15–18 but still have “free surfaces” that may affect the probed quantities. Significantly, the added complexity induced by the walls has made fundamental theories of nanoconfined liquids slower to develop, in particular for the dynamics.21–26Roskilde-simple liquids (also called R-simple liquids) are liquids with strong correlations between equilibrium fluctuations of the virial W and the potential energy U in the NVT ensemble.27–34 Van der Waals and metallic liquids have been shown to belong to this class of liquids whereas, e.g., hydrogen-bonding liquids are not R-simple. R-simple liquids have isomorphs in the thermodynamic phase diagram which are curves along which structure and dynamics are invariant in reduced units. This fact makes R-simple liquids simpler than other types of liquids. As an example, Rosenfeld's excess entropy scaling can be explained using the concept of isomorphs.35,36 In Rosenfeld's excess-entropy scaling reduced transport coefficients ![[X with combining tilde]](https://www.rsc.org/images/entities/i_char_0058_0303.gif) are functions of the entropy minus the ideal contribution at the same density and temperature, i.e.,
are functions of the entropy minus the ideal contribution at the same density and temperature, i.e., ![[X with combining tilde]](https://www.rsc.org/images/entities/i_char_0058_0303.gif) = f(Sex), where Sex(ρ,T) = S(ρ,T) − Sid(ρ,T). Since both the reduced dynamics and the excess entropy are invariant along the same curves (isomorphs), this fact explains Rosenfeld's excess entropy scaling. This scaling law is, however, only one of many consequences of having isomorphs (see, e.g., ref. 32).
= f(Sex), where Sex(ρ,T) = S(ρ,T) − Sid(ρ,T). Since both the reduced dynamics and the excess entropy are invariant along the same curves (isomorphs), this fact explains Rosenfeld's excess entropy scaling. This scaling law is, however, only one of many consequences of having isomorphs (see, e.g., ref. 32).
Extending the isomorph theory to nanoconfined fluids is therefore of paramount importance as this would offer an alternative framework in which confined fluids could be understood and analyzed. An earlier computer simulation study investigated R-simple liquids in confinement using an idealized slit-pore geometry.37 It was found that even heavily nanoconfined liquids have isomorphs to a good approximation, except for confinements around one or two particle diameters. Idealized slit-pore confinement implies that only the density profile perpendicular to the walls is inhomogenous.
To model more realistic confinement conditions, we study in this paper two model liquids confined to a slit-pore geometry with fcc crystalline walls. The structure and dynamics of liquids confined by fcc walls have been studied before and shown to exhibit density profiles that are highly inhomogenous, both parallel and perpendicular to the confining walls.3–5 Our aim here is to investigate whether isomorphs survive under such strong inhomogeneities. This is a first step in the direction of studying more realistic confinement conditions relevant, e.g., for industrial applications and biological systems.
We find that, despite the appearance of strong inhomogenous density profiles in the liquid, isomorphs do survive down to a few particle-diameters confinements enabling the applicability of results from the isomorph theory to more complex confined liquids. We conjecture from this study that R-simple liquids and isomorphs are relevant for a much larger class of confinements consistent with previous studies of excess-entropy scaling in nanoconfinement.38
At lower temperatures than what we consider here, higher-order structures have been shown to exhibit differences between isomorphic states.39 Here therefore, we also probe measures of higher-order structures and investigate minimum energy clusters in the liquid of interest.40 We find that little difference is seen in higher-order structure along isomorphs of the confined liquids.
The paper is organised as follows. Section II introduces the models and methods we apply in this study, and Section III gives a short introduction to R-simple liquids and their isomorphs. Section IV presents results for the single-component Lennard-Jones (LJ) liquid where we, amongst other things, study isomorphs. Section V presents similar results for the Kob–Andersen binary LJ mixture. Section VI summaries and presents a brief outlook.
II. Simulation methods
We use standard Nosé–Hoover molecular dynamics computer simulations in the NVT ensemble (as implemented in the RUMD package41) to study two model liquids in confinement: the single-component Lennard-Jones (SCLJ) liquid and the Kob–Andersen binary LJ mixture (KABLJ).42,43 In both models, the pair interaction between the liquid particle i of type α and the liquid particle j of type β is described by the LJ pair potential given by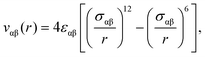 | (1) |
For most state points we simulate around one million time steps with a time step of Δt = 0.0025 after obtaining equilibrium. Equilibrium is ascertained from the decay of the intermediate scattering function and by running the simulations back-to-back at least twice.
A. Simulation units
Throughout the study, we use two different sets of nondimensionalized units: one set is based on the microscopic parameters of the LJ potential with length scale σAA and energy scale εAA of the larger (A) particle, which is standard in computer simulations, and another set of nondimensionalized units using macroscopic quantities with length given in units of ρ−1/3, energy in units of kBT, and time in units of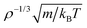 as applied in isomorph scaling.30 We refer to macroscopic nondimensionalized units as reduced units and use a tilde above the variable name to indicate a reduced quantity; otherwise LJ units are implicitly assumed.
as applied in isomorph scaling.30 We refer to macroscopic nondimensionalized units as reduced units and use a tilde above the variable name to indicate a reduced quantity; otherwise LJ units are implicitly assumed.
B. Nanoconfinement
Nanoconfinement is modelled using a slit-pore geometry in which the 100 surface of a fcc crystal is exposed to the liquid. The two crystal planes are placed in registry (i.e., the two crystal planes do not match). The distance between the two walls is denoted by H, measured from the centers of the confining fcc particles (see Fig. 1). | ||
| Fig. 1 The simulated slit-pore geometry confinement for the KABLJ mixture.44 Dark purple is the larger A-particle, pink is the smaller B-particle, and blue is the crystalline wall particles. The distance between the two walls is H, here H = 8. The two crystal planes are in registry. | ||
The slit pore is created as follows. First a fcc crystal with the correct density (using four crystal layers) is created and then replicated and translated a large distance away. Another fcc lattice is then created with the correct number of liquid particles in between the two walls for the chosen liquid density and wall spacing. The system is then compressed very slowly while the liquid particles are allowed to melt. In doing so, standard periodic boundary conditions are applied in the z-direction but since the liquid particles cannot penetrate through the walls, and the walls are frozen in place (see below) the simulations mimic infinite confinement.
The liquid–wall pair interactions are described by the LJ potential in eqn (1). For the SCLJ liquid we use the parameters σAW = 1 and εAW = 1, in which W denotes a wall particle. For the KABLJ mixture we derived the interaction parameters from Lorentz–Berthelot mixing rules with σAW = 0.97, εAW = 1, σBW = 0.91, and εBW = 0.707, where we used σWW = 0.94 and εWW = 1 to calculate these numbers. The cutoff of the liquid–wall pair interaction is rc = 2.50σαW.
For the SCLJ liquid we use the liquid density ρ = 0.85 as a reference and vary the temperature T = [0.50; 6] in steps of ΔT = 0.2 with H = [2, 4, 6, 8, 10] and N = [274, 1233, 822, 1024, 1370] liquid particles and N = [1024, 2304, 1024, 1096, 1024] wall particles. The same values are used to vary εAW in steps of ΔεAW = 0.2 at T = 2. The density of the fcc walls is for the majority of the simulations (except for the isomorph generation) kept fixed at ρW = 1, but we also study the effect of varying this parameter at H = 6 and T = 2 for SCLJ. For ρW = 0.4, 0.6, 0.8, 1.2, 1.4 we used N = [3408, 2601, 2147, 1638, 1478] liquid particles and for the wall N = 2304.
For the KABLJ mixture we focus on the liquid density ρ = 1.20 with T = [0.5; 6] in steps of ΔT = 0.2 with H = [4, 6, 8, 10] and N = [2477, 2090, 2787, 3484] liquid A particles and N = [4096, 2304, 2304, 2304] wall particles. The same values are used to vary εαW in steps of ΔεαW = 0.2 at T = 2.5. The density of the wall is ρW = 1, and we use a single-component crystal.
The simulations use a Nosé–Hoover NVT thermostat on the liquid particles whereas, for simplicity, the wall particles are frozen in place, i.e., T = 0 for the walls. Thermostatting the walls and the nature of the exposed surface may have observable effects on the structure and dynamics of confined liquids.45,46 This issue we ignore in this investigation.
The phase behavior of confined liquids is rather complex and has been studied extensively in the literature.3–5,13,47–50 For confined systems the solid–liquid transition is sensitive to the spacing between the walls H, e.g., how many crystal layers the pore can accommodate, the registry of the two walls, and the strength of the wall–liquid interaction. This transition has also been shown to occur as several transitions in a cascade-like way depending on H.49 Furthermore, precrystallization in the layer closest to the walls is common in confinement; in our case where the walls are fcc this phenomenon appears already at high temperatures for both liquids.
C. Topological cluster classification
We identify higher-order structures of the confined liquid using the topological cluster classification (TCC) algorithm which carries out a Voronoi decomposition and seeks structures topologically identical to geometric motifs of particular interest.40 In Sections IV and V, we also compare results of the TCC for the confined system with the bulk system at the same density and temperature. For these bulk simulations we use standard Monte-Carlo NVT simulation with N = 4000 particles.III. Roskilde-simple liquids
We provide here a brief introduction to Roskile-simple (R-simple) liquids and their isomorphs; a review is given in ref. 32. R-simple liquids are characterized by strong correlations between the equilibrium fluctuations of the potential energy U and virial W in the NVT ensemble.27–34 This correlation is quantified by the Pearson correlation coefficient R defined by27 | (2) |
Van der Waals and metallic liquids are usually R-simple whereas, e.g., hydrogen-bonding, covalent-bonding and strongly ionic liquids are not. More specifically, in simulations the SCLJ liquid, the KABLJ mixture, the Wahnström OTP model, bead-spring polymer models, and many more are R-simple. Strong UW correlation has also been verified in experiments on weakly dipolar organic molecules.51–53
Initially, the bulk liquid phase was studied, but the concept of R-simple liquids was later extended to crystals,54 nanoconfined liquids,37 nonlinear sheared liquids,55 polydisperse liquids,34,56 quantum-mechanical ab inito liquid metals,57 and more.58
R-simple liquids are characterized by the following ordering of potential energy values for most configurations33
| U(Ra) < U(Rb) ⇒ U(λRa) < U(λRb), | (3) |
R-simple liquids exhibit a number of simple properties,59 most of which are consequences of the existence of isomorphs. Isomorphs are curves in the thermodynamic phase diagram of R-simple liquids along which structure and dynamics to a good approximation are invariant in reduced units (see the previous section). Isomorphs are defined as curves of constant excess entropy and can be generated via the following relation
 | (4) |
In this article, however, we generate isomorphs using a different procedure. A first-order approximation to eqn (3) implies that the Boltzmann factors of two isomorphic state points are proportional (also the old definition of isomorphs30), i.e.,
exp(−U(R(1))/kBT1) = C12![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(−U(R(2))/kBT2), exp(−U(R(2))/kBT2), | (5) |
For confined systems the wall distance H is an independent variable, similar to density and temperature in bulk liquids. We choose here to let H (and the crystal density) follow the overall scaling in liquid density, i.e. H scales with (ρ1/ρ2)1/3. This choice is consistent with the definition in a previous study of isomorphs in nanoconfinement.37 This study37,63 also indicated that it might be possible to keep the wall distance fixed, but we do not consider this in more detail here. It is important to note that the state points we identify as being isomorphic under confinement in general are not isomorphic in the bulk.
As mentioned in Section II, precrystallization near the walls is well known for nanoconfined liquids. Previous works49,50 on confined liquids have shown that it can be advantageous to exclude these particles in the free energy analysis as they effectively become part of the walls. This might lead to the question of whether or not this should be taken into account in the generation of isomorphs. We found in a previous study63 that this crystallization scales perfectly along the isomorphs and hence one does not need to exclude them.
IV. Single-component Lennard-Jones liquid
We commence the study by probing the correlation coefficient R and density-scaling exponent γ for the SCLJ liquid in confinement. The next section considers the same quantities for the KABLJ mixture.A. Variation in the correlation coefficient R and density-scaling exponent γ
This subsection studies how the above mentioned quantities are affected by changing the following parameters related to the confinement: the distance between the two walls H, the strength of the liquid–wall interaction εLW, and the crystal density ρW.Fig. 2 shows how R and γ (eqn (2) and (4)) vary with temperature for several slit-pore widths in the range H = [2; 10]. The confinement thus ranges from almost a single layer of liquid particles to more bulk-like conditions. The densities of the liquid and wall are kept constant with ρL = 0.85 and ρW = 1, respectively. For simplicity, we here and henceforth define the liquid density as ρL ≡ N/AH, where A is the exposed surface area of the crystal. We thus do not take into account any excluded volume near the walls when calculating the confined liquid density.38 As a reference, the bulk liquid has R ≈ 0.96 at the chosen liquid density and temperatures around unity.
The correlation coefficient R increases with temperature, and for temperatures above unity we find only a very weak dependence on H as close encounters start to play a big role. For low temperatures we find that the slit-pore is fully crystallized but depending on H negative pressures are also encountered. Negative pressure tends to break any strong correlation as the system wants to phase separate. In the previous smooth slit-pore study,37 a decrease in R was observed with smaller H. There were two effects in play for this breakdown: crystallization and the wall potential. Typically, two-phase coexistence lowers the correlation coefficient. In the bulk, for a SCLJ liquid the explanation for Roskilde simplicity is given in terms of an inverse power-law and linear potential, the latter of which adds to a constant when summing over the nearest neighbours. This linear potential will not match perfectly with the walls, compared to the liquid particles, and therefore also lowers the correlation coefficient. As H is lowered this effect becomes stronger as more particles feel the full effect of the walls. Here, we do not observe this strong effect for fcc walls.
The density-scaling exponent γ displays the opposite trend in Fig. 2(b) showing a monotonic decrease with temperature for all H (except for the negative pressure state points). γ is noted to increase with slit-pore width, but no theory currently exists for γ's dependence on H.28,64 We find a possible slit-pore-width dependent plateau for γ between 4 and 5 which signifies that γ is also dependent on H in confined liquids. More investigations are nevertheless needed to determine if this H-dependent plateau truly exists and if it has a physical significance.
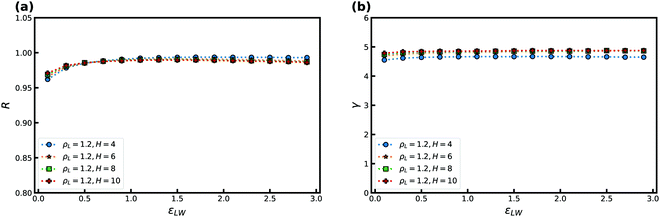
We now consider the effect of varying the attraction between the wall and the confined liquid particles. In doing so, we keep the wall–liquid cutoff fixed at rc = 2.5σAW which should not affect our results much, given that the range of interaction of the wall is short for R-simple liquids in nanoconfinement.65 This was also confirmed by probing a cutoff at rc = 5.0σAW. Fig. 3 shows R and γ as a function of εLW at T = 2 and ρL = 0.85, again for several H. As the simulations use εAA = 1, for εLW > 1 we have an “attractive” wall, and when εLW < 1 it becomes a “repulsive” wall with respect to the interactions between the liquid particles.
Fig. 3(a) shows that R depends significantly on εLW. For the larger H, a decrease in the correlation coefficient is found with increasing attraction as the wall potential plays a bigger role. This trend is also observed with decreasing strength as the system becomes more gas like. For H = 2, the correlation coefficient R increases with εLW as the slit-pore crystallizes fully (the solid, in general, has higher R than the liquid phase28). The density-scaling exponent in Fig. 3(b) displays a behavior that mimics that of the correlation coefficient, but the maximum is displaced to lower values of εLW.
The highest value of R, and therefore the maximum, is expected to appear when the wall particles are most similar to the liquid particles, which here means around εLW = 1. We observe that the maximum occurs slightly to the left for R and is consistent with this expectation but for much lower values for γ. We currently have no explanation for this observation.
Another means to probe the coupling between the confined liquid and the walls is to change the density of the fcc walls ρW. In Fig. 4 we show the correlation coefficient and density-scaling exponent as a function of the density of the crystal. The liquid density is kept constant at ρL = 0.85 and H = 6. We note that changing the crystal density does not keep a constant energy density, and hence particles will automatically interact more strongly with the walls as a whole for higher densities and the opposite for lower densities.
We observe for low ρW that R decreases when the density of the wall is reduced, though it remains well above 0.90. This effect can be attributed to particles penetrating into the walls (not shown). For high ρW the correlation coefficient remains virtually constant. Almost no effect on γ is noted in Fig. 4(b) for both low and high ρW.
B. Isomorph invariance of reduced density profiles and dynamics
We now turn to isomorphs in the nanoconfined system. To this end, we consider the behaviour along an isomorph and contrast it with an isochore at a density ρL = 0.85. Isomorphs in the SCLJ liquid were generated by the direct-isomorph-check method (see Section III). We consider two different slit-pore widths, one with H ≈ 6 and one with H ≈ 10; recall that H is adjusted with the liquid density along the isomorphs. These two distances span a strong and medium confined liquid.Density profiles perpendicular to the walls along an isomorph with H ≈ 10 are shown in Fig. 5(a). For comparison, results for an isochore with the same temperature variation are given in Fig. 5(b). From this point forward a yellow figure background denotes data obtained along an isomorph, and a pink figure background denotes data obtained along an isochore.
We find that the density profiles to a good approximation are invariant along the isomorph with a 24% density increase, whereas this is not the case along the isochore in Fig. 5(b). For the isochore, significant changes in all peak heights with temperature are observed, in particular for the layer closest to the wall indicating pre-crystallisation even at H = 10. This pre-crystallization is, however, nicely preserved on the isomorph.
Fig. 6 displays the in-plane density profiles in the layer closest to the walls, i.e., for the layer around |![[z with combining tilde]](https://www.rsc.org/images/entities/i_char_007a_0303.gif) | ≈ 4, for the first and the last state points of Fig. 5. The density profile is shown for one unit cell of the crystalline walls. The isomorph (a) shows excellent scaling with the liquid particles situated in between the wall particles and exhibits very little change in the density profile whereas the isochore (b) displays a density field that is increasingly smeared out as T is increased, confirming the pre-crystallisation. Similar behavior is observed for the remaining layers (not shown).
| ≈ 4, for the first and the last state points of Fig. 5. The density profile is shown for one unit cell of the crystalline walls. The isomorph (a) shows excellent scaling with the liquid particles situated in between the wall particles and exhibits very little change in the density profile whereas the isochore (b) displays a density field that is increasingly smeared out as T is increased, confirming the pre-crystallisation. Similar behavior is observed for the remaining layers (not shown).
 | ||
Fig. 6 Reduced in-plane density profiles of the liquid particles in the layer closest to the walls, i.e. |![[z with combining tilde]](https://www.rsc.org/images/entities/i_char_007a_0303.gif) | ≈ 4, for the first (left) and last (right) state points of the (a) isomorph and (b) isochore of Fig. 5. One unit cell of the crystalline walls is shown; the yellow circles indicate fcc wall particles. | ≈ 4, for the first (left) and last (right) state points of the (a) isomorph and (b) isochore of Fig. 5. One unit cell of the crystalline walls is shown; the yellow circles indicate fcc wall particles. | ||
Dynamical properties such as the mean-squared displacement (MSD) or the intermediate scattering function are also invariant along an isomorph, and we now examine how well this behaviour holds in nanoconfinement. To do so, we consider the reduced MSD parallel and normal to the walls as a function of reduced time in Fig. 7 along the same isomorph and isochore as before. The MSD is averaged over the entire slit-pore. We find excellent invariance along the isomorph and visible variation for the isochore. For the bulk liquid, at these high temperatures, one would see a similar scaling in comparison to the isochore; the differences becoming more pronounced with the degree of supercooling.32
 | ||
| Fig. 7 Reduced average mean-square displacements parallel and normal to the walls along the isomorph and isochore of Fig. 5. (a) Isomorph, parallel dynamics. (b) Isochore, parallel dynamics. (c) Isomorph, normal dynamics. (d) Isochore, normal dynamics. | ||
C. Isomorph invariance of higher-order structures
Two-point spatial correlation functions, such as the radial distribution function, have been shown to a good approximation to be invariant along isomorphs in simulations of both bulk and smooth-wall confined systems.30,34,37,66 Higher-order structural correlations have until very recently67 been investigated to a lesser extent and could well be less invariant than the two-body correlation functions as the isomorph theory is approximate. In particular, geometric motifs, so-called locally favoured structures (LFS) such as the bicapped square antiprism68,69 have been seen to vary significantly along isomorphs in supercooled KABLJ.39As a final probe of isomorphs for the confined SCLJ liquid we investigate in Fig. 8 and 9 invariance of higher-order structures. The liquids here are not supercooled much, and thus rather than a locally favoured structure we instead consider minimum energy clusters of 5 ≤ m ≤ 13 particles for these systems.69,70 These minimum energy clusters typically include the LFS, although the latter often exhibit a specific symmetry71 while the minimum energy clusters for each system exhibit a range of symmetries. In addition, we consider populations of the hcp and fcc crystalline structures. The minimum energy structures are identified by the topological cluster classification.40 The eight structures of the SCLJ system are depicted in the figures (top left in each panel).40,70,72
We find that the distribution of clusters is, to an excellent approximation, invariant along the isomorph but not along the isochore. For all structures on the isochore the variation is around a factor of two with hardly any visible variation along the isomorph. Very minor deviations are, however, noted for the 9B and 11C structures along the isomorph. We emphasize that the probing of these structures does not imply relevance of these structures for the dynamics of the liquid but merely used for testing invariance of higher-order structures along an isomorph which are predicted to be invariant.
While the structures considered exhibit very little change along the isomorph, the changes between the behaviour of the different clusters is notable in itself. We can identify three regimes: small amorphous clusters, larger amorphous clusters and crystalline structures. As shown in Fig. 8(a) and (c), the smaller amorphous clusters, the triangular bipyramid 5A and octahedron 6A, largely follow the density profiles illustrated in Fig. 5. Larger amorphous clusters, beginning with the pentagonal bipyramid 7A, have a degree of fivefold symmetry and their population is suppressed close to the wall (see Fig. 8(e), (g) and 9(a), (c)). Interestingly, this is not observed in the case of a free interface where the cluster population is rather slaved to the density profile.73 A rather different behaviour is found for the crystalline structures, where the layer by the wall has a high population of particles in a crystalline environment, but the population in the middle of the slit is very small (Fig. 9(e) and (g)).
We compare these results with bulk populations of the corresponding clusters for the same temperature and density as shown by the colored data points in Fig. 8 and 9. The data points are plotted for the isochore data but may be taken to be representative of the isomorph data on the left hand side of the figure. Even in the centre of the slit, the results show a strong enhancement of cluster population with respect to the bulk in all cases except for the hcp and fcc crystals, whose population in the centre of the slit is negligible. This is remarkable, given that for a free liquid–vapour interface, cluster populations reach their bulk value around a diameter from the interface.73 Further work is called for to understand this unexpected increase in higher-order structure in confinement.
In the ESI† we present results for an isomorph with H ≈ 6. We find excellent scaling of density profiles and mean-square displacements. To conclude on the SCLJ liquid, we find that isomorphs survive into heavily confined systems with fcc crystalline walls and have excellent scaling also for higher-order structures.
V. Kob–Andersen binary Lennard-Jones mixture
We now turn to investigate similar quantities for the KABLJ mixture. Although being a binary mixture prized for its glassforming ability, the KABLJ mixture is prone to crystallization in the bulk.74 The mechanism for crystallization in the bulk occurs through the formation of fcc (and hcp) nuclei of the majority A species.74 We find that the KABLJ mixture like the SCLJ liquid in confinement also (pre)crystallizes and suggests that heterogeneous nucleation at the walls (which are patterned as an fcc structure) is a powerful mechanism for the KABLJ mixture, as also seen for other simple liquids.3,4,50A. Variation in the correlation coefficient R and density-scaling exponent γ
Fig. 10 displays R and γ as a function of temperature for several slit-pore widths H for the KABLJ mixture at ρL = 1.2 and ρW = 1 with εAW = 1, and εBW = 0.707. The bulk correlation coefficient at this density is R ≈ 0.96. As for the SCLJ liquid we find an increase in R and a decrease in γ with temperature. For the KABLJ mixture, however, at low temperatures we do not find full crystallization as one expects for a reasonable glassformer. We find that the precrystallization consists only of A-particles.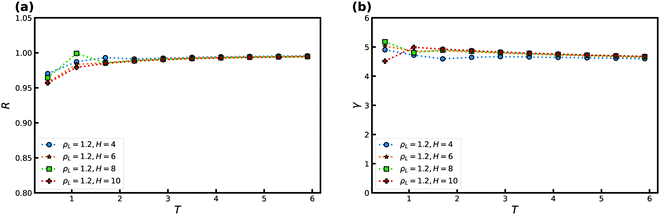 | ||
| Fig. 10 R and γ as a function of temperature T for several slit-pore widths H for the KABLJ mixture at ρL = 1.2 and ρW = 1. (a) R as a function of temperature. (b) γ as a function of temperature. | ||
Next, we consider the effect of changing the liquid–wall interaction strength εLW in Fig. 11. A weak maximum is noted for both R and γ and is displaced slightly away from the value of εAW = 1. Good correlation is noted for the entire range of attractions. For the KABLJ mixture the effect of the crystal density ρW was not investigated.
B. Isomorph invariance of reduced density profiles and dynamics
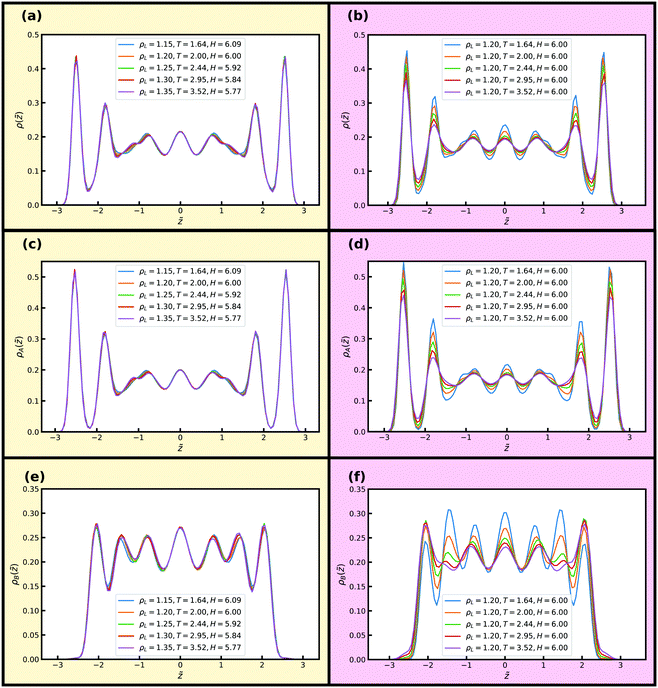
For the KABLJ mixture we also investigate two isomorphs with H ≈ 6 and H ≈ 10 to facilitate comparison with the SCLJ liquid in the previous section. Fig. 12(a), (c) and (e) show reduced normal density profiles for the total and partial densities along an isomorph with 17% density increase and H ≈ 6. Fig. 12(b), (d) and (f) show the corresponding quantities along an isochore. Good invariance is noted along the isomorph but not along the isochore where again significant changes in the peak heights are noted for all density profiles, in particular for the B-particle density profiles (Fig. 12(f)).
Fig. 13 shows reduced in-plane total density profiles for the layer closest to the wall, i.e. |![[z with combining tilde]](https://www.rsc.org/images/entities/i_char_007a_0303.gif) | ≈ 2.7, for the first and last state points of the same isomorph and isochore. For the KABLJ mixture the in-plane density profile does not seem to show a strong deterioration along the isochore as found for the SCLJ liquid, which could be anticipated from the height variation of the first peak in Fig. 12(b). Nevertheless the invariance is still visually worse than that of the isomorph.
| ≈ 2.7, for the first and last state points of the same isomorph and isochore. For the KABLJ mixture the in-plane density profile does not seem to show a strong deterioration along the isochore as found for the SCLJ liquid, which could be anticipated from the height variation of the first peak in Fig. 12(b). Nevertheless the invariance is still visually worse than that of the isomorph.
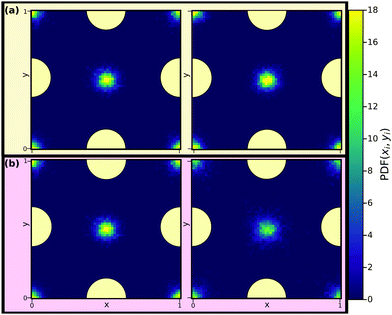 | ||
Fig. 13 Reduced in-plane total density profiles of the liquid particles in the layer closest to the walls, i.e. |![[z with combining tilde]](https://www.rsc.org/images/entities/i_char_007a_0303.gif) | ≈ 2.7, for the first (left) and last (right) state points along the isomorph (a) and the isochore (b) of Fig. 12. One unit cell of the crystalline walls is shown; the yellow circles indicating fcc wall particles. | ≈ 2.7, for the first (left) and last (right) state points along the isomorph (a) and the isochore (b) of Fig. 12. One unit cell of the crystalline walls is shown; the yellow circles indicating fcc wall particles. | ||
For the reduced normal and parallel A-particle MSDs in Fig. 14 almost perfect scaling is observed along the isomorph while approximately a decade deviation in diffusion coefficient is observed for the isochore. These deviations in MSD are similar to what is seen for supercooled bulk liquids.30,34 We find for the B-particles a very similar scaling behaviour (not shown).
C. Isomorph invariance of higher-order structures
Finally, we consider invariance of selected minimum energy clusters for the KABLJ mixture40,69 in Fig. 15 and 16, reaching a similar conclusion as for the SCLJ liquid with excellent invariance along the isomorph but not along the isochore, the latter showing around a factor of two variation in almost all structures. Although, the bicapped square antiprism (11A) structure has been shown to correlate reasonably to the dynamics of the KABLJ system69,75–77 we find very few bicapped square antiprisms at the higher temperatures considered here (the onset temperature for glassy dynamics, at which the bicapped square antiprism becomes popular, is around T ≈ 1.0), and 11A is therefore not included in the figures.It is quite remarkable that the minimum energy clusters of the KABLJ system40,69 show such a good invariance, even for higher-order correlations, given that previous work showed a significant discrepancy in precisely the same system,39 although at the lower temperature T = 1.0. The results presented here are at a higher temperature (T > 2.0), the magnitude of the discrepancy and its rather weak temperature dependence leads one to speculate whether the confinement may somehow influence the agreement.
In comparing with the bulk values (data points in Fig. 15 and 16 right hand side), we see similar to the SCLJ system (Fig. 8 and 9) that in many cases the cluster population even at the centre of the slit is markedly higher than the bulk liquid at the same state point. However, this is not universally the case here, as the m = 7 polytetrahedron (7K) in fact seems to sit right on the confined data for some state points, while at higher temperature the bulk population seems higher than the confined system. The reasons for the change in behaviour of this structure and, as noted above, why the minimum energy clusters typically have a reduced population with respect to the bulk is an interesting topic for future work. In the ESI,† we compare bulk KABLJ data with the smooth wall simulations of ref. 37. We find here that the agreement is better and hence the templating of the walls plays a role.
We provide in ESI† figures for an isomorph with H ≈ 10. Similar conclusions are reached, showing again good invariance along the isomorph.
VI. Summary and outlook
Isomorphs are curves in the thermodynamic phase diagram of R-simple liquids along which structure and dynamics in reduced units to a good approximation are invariant. However, nanoconfined liquids show strikingly different behavior from bulk liquids in terms of their structure and dynamics.4 It is therefore not obvious that concepts demonstrated in the bulk apply also to confined liquids. Extending the isomorph framework to nanoconfined liquids is important as theories for nanoconfined liquids have been slower to develop due to the added complexity.A previous study37 explored the existence of isomorphs in nanoconfined liquids using a smooth slit-pore geometry and found that isomorphs do survive under confinement. Here, we have studied the effect of introducing highly inhomogenous density profiles both parallel and perpendicular to the walls by applying more realistic crystalline fcc walls. The effect of the wall-to-wall distance H, the strength of liquid–wall interactions εLW, and the crystal density ρW were explored on two bulk R-simple liquids: the SCLJ liquid and the KABLJ mixture.
Although strong inhomogeneities occur in this type of confinement, we found that R-simple liquids and isomorphs survive down to a few particle diameters confinement. More specifically, along isomorphs we probed density profiles, normal and parallel mean-squared displacements, as well as higher-order structures using the topological cluster classification algorithm. Even for higher-order correlations of populations of minimum energy clusters up to 13 particles, we found excellent invariance along the isomorphs. This is notable, as in the bulk, albeit at lower temperatures, considerable deviation was found for higher-order structures even when the two-point structure scaled well.39 Curiously, in many (but not all) of these clusters, the population in the confined system, even at the centre, is markedly higher than that in the bulk for the same state point. This is remarkable, given that in the case of a free liquid–vapour interface, the cluster population reaches its bulk value within around a diameter of the interface;73 we found that this is likely connected to the templating of the walls. This curiosity should be investigated in future work.
We conjecture from the current study that even very complicated confinements, e.g., carbon nanotubes, can exhibit Roskilde simplicity and thus also their associated scaling laws, such as Rosenfeld excess-entropy scaling. This provides an important simplification of the phase diagram and valuable insights into the structures and dynamics of confined liquids. In this connection, an intriguing path for further research is the development of equations of state for confined liquids using the isomorph theory.31 Furthermore, it is known that thermostatting the walls can affect the structure of the confined liquid to a great extent45,46 and hence might also affect Roskilde simplicity. This would have to be studied in more detail in the future.
Conflicts of interest
There are no conflicts of interest to declare.Acknowledgements
B. M. G. D. C., J. C. D., and T. S. I. are supported by the VILLUM Foundation's Matter Grant (No. 16515). B. M. G. D. C. acknowledges funding from EPSRC with grant code EP/L016648/1. C. P. R. acknowledges the Royal Society and European Research Council (ERC consolidator grant NANOPRS, project number 617266) for financial support.References
- M. P. Allen and D. J. Tildesley, Computer Simulation of Liquids, Oxford University Press, New York, 1987 Search PubMed.
- D. Frenkel and B. Smit, Understanding Molecular Simulation, Academic Press, San Diego, 2nd edn, 2002 Search PubMed.
- S. Toxvaerd, J. Chem. Phys., 1981, 74, 1998 CrossRef CAS.
- M. Schoen, D. J. Diestler and J. H. Cushman, J. Chem. Phys., 1987, 87, 5464 CrossRef CAS.
- M. Schoen, J. H. Cushman, D. J. Diestler and C. L. Rhykerd, J. Chem. Phys., 1988, 88, 1394 CrossRef CAS.
- J. M. Drake and J. Klafter, Phys. Today, 1990, 43, 46 CrossRef CAS.
- S. Granick, Science, 1991, 253, 1374 CrossRef CAS PubMed.
- C. L. Jackson and G. B. McKenna, J. Non-Cryst. Solids, 1991, 131–133, 221 CrossRef CAS.
- J. L. Keddie, R. A. L. Jones and R. A. Cory, Europhys. Lett., 1994, 27, 59 CrossRef CAS.
- B. Bhushan, J. N. Israelachvili and U. Landman, Nature, 1995, 374, 607 CrossRef CAS.
- P. Scheidler, W. Kob and K. Binder, J. Phys. IV, 2000, 10, 33 Search PubMed.
- F. W. Starr, T. B. Schrøder and S. C. Glotzer, Macromolecules, 2002, 35, 4481 CrossRef CAS.
- C. Alba-Simionesco, B. Coasne, G. Dosseh, G. Dudziak, K. E. Gubbins, R. Radhakrishnan and M. Sliwinska-Bartkowiak, J. Phys.: Condens. Matter, 2006, 18, R15 CrossRef CAS PubMed.
- R. Richert, Annu. Rev. Phys. Chem., 2011, 62, 65 CrossRef CAS PubMed.
- T. Voigtmann, A. Meyer, D. Holland-Moritz, S. Stüber, T. Hansen and T. Unruh, EPL, 2008, 82, 66001 CrossRef.
- A. Bartsch, K. Rätzke, A. Meyer and F. Faupel, Phys. Rev. Lett., 2010, 104, 195901 CrossRef PubMed.
- J. Brillo, A. I. Pommrich and A. Meyer, Phys. Rev. Lett., 2011, 107, 165902 CrossRef CAS PubMed.
- F. Yang, T. Unruh and A. Meyer, EPL, 2014, 107, 26001 CrossRef.
- J. F. Robinson, F. K. A. Gregson, R. E. H. Miles, R. P. Reid and C. P. Royall, J. Chem. Phys., 2020, 152, 074503 CrossRef CAS PubMed.
- I. Williams, E. C. Oğuz, P. Bartlett, H. Lowen and C. P. Royall, J. Chem. Phys., 2015, 142, 024505 CrossRef PubMed.
- R. Evans, Adv. Phys., 1979, 28, 143 CrossRef CAS.
- V. Krakoviack, Phys. Rev. Lett., 2005, 94, 065703 CrossRef CAS PubMed.
- S. Lang, V. Botan, M. Oettel, D. Hajnal, T. Franosch and R. Schilling, Phys. Rev. Lett., 2010, 105, 125701 CrossRef PubMed.
- S. Lang, R. Schilling, V. Krakoviack and T. Franosch, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2012, 86, 021502 CrossRef PubMed.
- J. S. Hansen, P. J. Daivis, J. C. Dyre, B. D. Todd and H. Bruus, J. Chem. Phys., 2013, 138, 034503 CrossRef CAS PubMed.
- J. S. Hansen, J. C. Dyre, P. Daivis, B. D. Todd and H. Bruus, Langmuir, 2015, 31, 13275 CrossRef CAS PubMed.
- N. P. Bailey, U. R. Pedersen, N. Gnan, T. B. Schrøder and J. C. Dyre, J. Chem. Phys., 2008, 129, 184507 CrossRef PubMed.
- N. P. Bailey, U. R. Pedersen, N. Gnan, T. B. Schrøder and J. C. Dyre, J. Chem. Phys., 2008, 129, 184508 CrossRef PubMed.
- T. B. Schrøder, N. P. Bailey, U. R. Pedersen, N. Gnan and J. C. Dyre, J. Chem. Phys., 2009, 131, 234503 CrossRef PubMed.
- N. Gnan, T. B. Schrøder, U. R. Pedersen, N. P. Bailey and J. C. Dyre, J. Chem. Phys., 2009, 131, 234504 CrossRef PubMed.
- T. B. Schrøder, N. Gnan, U. R. Pedersen, N. P. Bailey and J. C. Dyre, J. Chem. Phys., 2011, 134, 164505 CrossRef PubMed.
- J. C. Dyre, J. Phys. Chem. B, 2014, 118, 10007 CrossRef CAS PubMed.
- T. B. Schrøder and J. C. Dyre, J. Chem. Phys., 2014, 141, 204502 CrossRef PubMed.
- T. S. Ingebrigtsen and H. Tanaka, J. Phys. Chem. B, 2015, 119, 11052 CrossRef CAS PubMed.
- Y. Rosenfeld, Phys. Rev. A: At., Mol., Opt. Phys., 1977, 15, 2545 CrossRef.
- Y. Rosenfeld, J. Phys.: Condens. Matter, 1999, 11, 5415 CrossRef CAS.
- T. S. Ingebrigtsen, J. R. Errington, T. M. Truskett and J. C. Dyre, Phys. Rev. Lett., 2013, 111, 235901 CrossRef PubMed.
- R. Chopra, T. M. Truskett and J. R. Errington, J. Chem. Phys., 2010, 133, 104506 CrossRef PubMed.
- A. Malins, J. Eggers and C. P. Royall, J. Chem. Phys., 2013, 139, 234505 CrossRef PubMed.
- A. Malins, S. R. Williams, J. Eggers and C. P. Royall, J. Chem. Phys., 2013, 139, 234506 CrossRef PubMed.
- N. P. Bailey, T. S. Ingebrigtsen, J. S. Hansen, A. A. Veldhorst, L. Bøhling, C. A. Lemarchand, A. E. Olsen, A. K. Bacher, H. Larsen, J. C. Dyre and T. B. Schrøder, SciPost Phys., 2017, 3, 038 CrossRef.
- W. Kob and H. C. Andersen, Phys. Rev. E: Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top., 1995, 51, 4626 CrossRef CAS PubMed.
- W. Kob and H. C. Andersen, Phys. Rev. E: Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top., 1995, 52, 4134 CrossRef CAS PubMed.
- A. Stukowski, Modell. Simul. Mater. Sci. Eng., 2010, 18, 015012 CrossRef.
- D. J. Diestler and M. Schoen, J. Chem. Phys., 1996, 104, 6784 CrossRef CAS.
- S. Bernardi, B. D. Todd and D. J. Searles, J. Chem. Phys., 2010, 132, 244706 CrossRef PubMed.
- R. Radhakrishnan, K. E. Gubbins and M. Sliwinska-Bartkowiak, J. Chem. Phys., 2000, 112, 11048 CrossRef CAS.
- H. Dominguez, A. Patrykiejew and S. Sokotowski, Mol. Phys., 2003, 101, 1867 CrossRef CAS.
- L. Wan, C. R. Iacovella, T. D. Nguyen, H. Docherty and P. T. Cummings, Phys. Rev. B: Condens. Matter Mater. Phys., 2012, 86, 214105 CrossRef.
- L. Gai, C. R. Iacovella, L. Wan, C. McCabe and P. T. Cummings, J. Chem. Phys., 2015, 143, 054504 CrossRef PubMed.
- D. Gundermann, U. R. Pedersen, T. Hecksher, N. P. Bailey, B. Jakobsen, T. Christensen, N. B. Olsen, T. B. Schrøder, D. Fragiadakis, R. Casalini, C. M. Roland, J. C. Dyre and K. Niss, Nat. Phys., 2011, 7, 816 Search PubMed.
- L. A. Roed, D. Gundermann, J. C. Dyre and K. Niss, J. Chem. Phys., 2013, 139, 101101 CrossRef PubMed.
- W. Xiao, J. Tofteskov, T. V. Christensen, J. C. Dyre and K. Niss, J. Non-Cryst. Solids, 2015, 407, 190 CrossRef CAS.
- D. E. Albrechtsen, A. E. Olsen, U. R. Pedersen, T. B. Schrøder and J. C. Dyre, Phys. Rev. B: Condens. Matter Mater. Phys., 2014, 90, 094106 CrossRef CAS.
- L. Separdar, N. P. Bailey, T. B. Schrøder, S. Davatolhagh and J. C. Dyre, J. Chem. Phys., 2013, 138, 154505 CrossRef PubMed.
- T. S. Ingebrigtsen and H. Tanaka, J. Phys. Chem. B, 2016, 120, 7704 CrossRef CAS PubMed.
- F. Hummel, G. Kresse, J. C. Dyre and U. R. Pedersen, Phys. Rev. B: Condens. Matter Mater. Phys., 2015, 92, 174116 CrossRef.
- U. R. Pedersen, L. Costigliola, N. P. Bailey, T. B. Schrøder and J. C. Dyre, Nat. Commun., 2016, 7, 12386 CrossRef CAS PubMed.
- T. S. Ingebrigtsen, T. B. Schrøder and J. C. Dyre, Phys. Rev. X, 2012, 2, 011011 Search PubMed.
- J. C. Dyre, J. Chem. Phys., 2018, 149, 210901 CrossRef PubMed.
- A. Tölle, Rep. Prog. Phys., 2001, 64, 1473 CrossRef.
- C. Dreyfus, A. Aouadi, J. Gapinski, M. Matos-Lopes, W. Steffen, A. Patkowski and R. M. Pick, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2003, 68, 011204 CrossRef CAS PubMed.
- T. S. Ingebrigtsen, PhD thesis, Roskilde University, 2013.
- T. S. Ingebrigtsen, L. Bøhling, T. B. Schrøder and J. C. Dyre, J. Chem. Phys., 2012, 136, 061102 CrossRef PubMed.
- T. S. Ingebrigtsen and J. C. Dyre, Soft Matter, 2014, 10, 4324 RSC.
- A. K. Bacher, T. B. Schrøder and J. C. Dyre, J. Chem. Phys., 2018, 149, 114501 CrossRef PubMed.
- M. Rahman, B. M. G. D. Carter, S. Saw, I. M. Douglass, L. Costigliola, T. S. Ingebrigtsen, T. B. Schrøder, U. R. Pedersen and J. C. Dyre, Molecules, 2021, 26, 1746 CrossRef CAS PubMed.
- D. Coslovich and G. Pastore, J. Chem. Phys., 2007, 127, 124504 CrossRef CAS PubMed.
- A. Malins, J. Eggers, H. Tanaka and C. P. Royall, Faraday Discuss., 2013, 167, 405 RSC.
- J. Taffs, A. Malins, S. R. Williams and C. P. Royall, J. Chem. Phys., 2010, 133, 244901 CrossRef PubMed.
- A. J. Dunleavy, K. Wiesner, R. Yamamoto and C. P. Royall, Nat. Commun., 2015, 6, 6089 CrossRef CAS PubMed.
- B. M. G. D. Carter, F. Turci, P. Ronceray and C. P. Royall, J. Chem. Phys., 2018, 148, 204511 CrossRef PubMed.
- M. Godonoga, A. Malins, J. Eggers and C. P. Royall, Mol. Phys., 2011, 109, 1393 CrossRef CAS.
- T. S. Ingebrigtsen, J. C. Dyre, T. B. Schrøder and C. P. Royall, Phys. Rev. X, 2019, 9, 031016 CAS.
- P. Crowther, F. Turci and C. P. Royall, J. Chem. Phys., 2015, 143, 044503 CrossRef PubMed.
- T. Speck, A. Malins and C. P. Royall, Phys. Rev. Lett., 2012, 109, 195703 CrossRef PubMed.
- F. Turci, C. P. Royall and T. Speck, Phys. Rev. X, 2017, 7, 031028 Search PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/d1sm00233c |
| This journal is © The Royal Society of Chemistry 2021 |