Open Access Article
Open Access ArticleEfficacy of simple continuum models for diverse granular intrusions†
Shashank
Agarwal
 a,
Andras
Karsai
a,
Andras
Karsai
 b,
Daniel I.
Goldman
b and
Ken
Kamrin
b,
Daniel I.
Goldman
b and
Ken
Kamrin
 *a
*a
aDepartment of Mechanical Engineering, MIT, Cambridge, USA. E-mail: kkamrin@mit.edu
bDepartment of Physics, Georgia Tech, Atlanta, USA
First published on 29th June 2021
Abstract
Granular intrusion is commonly observed in natural and human-made settings. Unlike typical solids and fluids, granular media can simultaneously display fluid-like and solid-like characteristics in a variety of intrusion scenarios. This multi-phase behavior increases the difficulty of accurately modeling these and other yielding (or flowable) materials. Micro-scale modeling methods, such as DEM (Discrete Element Method), capture this behavior by modeling the media at the grain scale, but there is often interest in the macro-scale characterizations of such systems. We examine the efficacy of a macro-scale continuum approach in modeling and understanding the physics of various macroscopic phenomena in a variety of granular intrusion cases using two basic frictional yielding constitutive models. We compare predicted granular force response and material flow to experimental data in four quasi-2D intrusion cases: (1) depth-dependent force response in horizontal submerged-intruder motion; (2) separation-dependent drag variation in parallel-plate vertical-intrusion; (3) initial-density-dependent drag fluctuations in free surface plowing, and (4) flow zone development during vertical plate intrusions in under-compacted granular media. Our continuum modeling approach captures the flow process and drag forces while providing key meso- and macro-scopic insights. The modeling results are then compared to experimental data. Our study highlights how continuum modeling approaches provide an alternative for efficient modeling as well as a conceptual understanding of various granular intrusion phenomena.
1 Introduction
Granular intrusion is common in various natural and human-made situations.1–3 In many cases, the flow response to intrusion leads to a multi-phase behavior of the granular media, where the media shifts among solid-like, fluid-like, and gas-like states.4,5 This behavior depends on material properties and local variables such as pressure and granular packing fraction.6 The space and time dependence of these fields, as well as the multi-phase behavior of the media, makes granular flow response challenging and computationally expensive to model.Discrete Element Methods (DEM) are reliable and established methods for modeling granular media.7,8 In DEM, the granular medium is modeled at the particle level, with the frictional, elastic contact forces between adjacent and interacting particles obtained using standard contact models like Hertzian and Hookean contacts,9,10 generally with an assumption of no plastic yielding of the individual grains. The elastic and external forces are integrated via Newton's laws of motion to calculate particle velocities and positions. In the past few decades, DEM has played a major role in the advancement of the field of granular media.11,12 However, the precision of DEM comes at a computational cost. As an example, a 0.1 mm particle diameter granular system with a 0.5 m per side cubic domain would require evaluating ∼9 × 1011 DOF per time step (at a packing fraction of 0.64 with 6 degrees of freedom, DOF per particle). While current large-scale granular DEM studies remain in the range of ∼107 particles (∼108 DOF),13,14 efforts are being made to extend this range. Most recently, some have reached the ∼109 DOF range with the use of supercomputers and GPUs.15
In recent years, there has been a growing interest in modeling increasingly large granular systems, such as those relevant in ballistic impacts, wheeled locomotion, and agricultural plowing.1–3,16,17 This has led to a push for computationally faster alternatives to DEM, such as using continuum descriptions of granular media and further reduced models such as Resistive Force Theory.18–20 At the fundamental level, cohesionless granular media can be described as a plastic material with a frictional yield criterion and no cohesion strength (hence no ability to support tension). But, a comprehensive continuum model for fully describing a granular material requires incorporating a variety of behaviors shown by the media arising from the constituent grain shape, size, stiffness, distribution, and inter-particle interaction properties,5 as well as effects due to the surrounding air (pressure and flow-drag) on the granular media.21 Thus, often scenario-specific simplifications are made during constitutive model development. Conversely, even for a simple granular material, a constitutive framework encapsulating all granular phenomena would have to merge many different pieces together, e.g. dissipative kinetic theory22,23 in dilute regimes; strengthening based on packing fraction24 and internal state variables (like fabric and hysteresis) evolution;25 rate-dependence of the strength (such as μ(I) rheology26); non-trivial yield surface shapes in stress space;27 and particle size effects28,29 in the dense flow regime.
A variety of computational methods have been developed and utilized recently to aid in simulating continuum models for large deformation processes, such as the Material Point Method (MPM),18,30–32 the Particle Finite Element Method (PFEM),33 and Smoothed Particle Hydrodynamics (SPH).34 In this regard, a recent study on high-speed locomotion of wheels20 in grains, a process which involves complex trans-phase characteristics of the soil and non-trivial grain motions, revealed that a continuum treatment implemented with MPM captures the essential behaviors and agrees well with experimental data. In the present work, we highlight the capability of the continuum approach in modeling and explaining diverse granular intrusion phenomena using a very minimal set of constitutive ingredients. The phenomena we focus on herein have been independently studied in the literature, and our goal is to demonstrate that they can be quantitatively modeled and unified under a family of basic constitutive assumptions. We first introduce two constitutive representations of non-cohesive granular media: a non-dilatant plasticity model (NDPM), and a dilatant plasticity model (DPM). The DPM model permits dilatancy during dense flow while the NDPM model assumes dense flow is a constant-volume process. Thus, the NDPM is suitable for modeling steady-state granular behaviors, while the DPM is a more suitable model for transient flow processes. The latter is also a more elaborate model that converges to the former model under certain limits. Both of these models have their respective advantages depending on the scenarios they simulate. We do not include micro-inertial μ(I) effects25 (effects of grain-level inertia on material properties) in these models; thus both of these constitutive models are rate-insensitive.
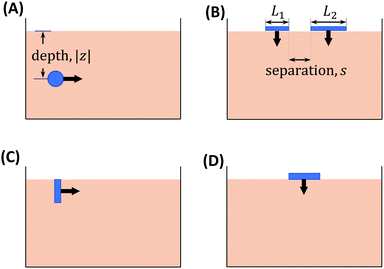
We demonstrate the utility of each model by considering granular flow and force response in four fundamental intrusion cases which have been studied in the literature: (1) depth-dependent force response in horizontal submerged intruder motion; (2) separation-dependent drag variation in parallel plate vertical intrusion; (3) initial density-dependent drag fluctuations in free surface plowing; and (4) flow zone development during vertical plate intrusions in under-compacted granular media (Fig. 1). We use NDPM in the first two cases (which focus on a steady response), and DPM in the latter two cases (where transient effects are the focus). Our continuum modeling approach captures the dynamics of such granular flows and gives a deeper macroscopic insight into each of these cases. Thus, our study highlights the efficacy of continuum modeling for predictive purposes, as well as in developing macroscopic conceptual understanding of diverse granular intrusion phenomena.
2 Material and methodology
We use two constitutive models to represent granular volumes in this study, namely: a non-dilatant plasticity model (NDPM), and a dilatant plasticity model (DPM). We first explain the two models in detail and then explain the numerical method we use to implement the schemes.Non-dilatant plasticity model (NDPM)
This model is taken from Dunatunga and Kamrin.30,35 The model assumes a rate-insensitive, Drucker–Prager yield criterion, incompressible plastic shear flow (with no dilatancy), and cohesionless response in extension whereby the material becomes stress-free below a ‘critical density’, ρd. The constitutive flow equations representing the above behaviors are shown below. These simultaneous constraints describe the material's separation behavior, shear yield condition, and tensorial co-directionality, respectively:| (ρ − ρd)P = 0 and P ≥ 0 and ρ ≤ ρd, | (1) |
![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) (τ − μsP) = 0 and (τ − μsP) = 0 and ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) ≥ 0 and τ ≤ μsP, ≥ 0 and τ ≤ μsP, | (2) |
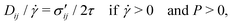 | (3) |
 is the equivalent shear rate.
is the equivalent shear rate. 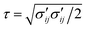 is the equivalent shear stress,
is the equivalent shear stress,  is the deviatoric part of Cauchy stress tensor, Dij = (∂ivj + ∂jvi)/2 is the flow rate tensor.
is the deviatoric part of Cauchy stress tensor, Dij = (∂ivj + ∂jvi)/2 is the flow rate tensor.
For simplicity, the equations above are expressed in rigid-plastic form, where the flow rate is approximately all due to plastic flow. However, we also include a small elastic component which ensures that below the yield criterion the grains have a well-defined solid constitutive behavior. The model evolves the flow by solving the momentum balance equations, ∂jσij + ρgi = ρ![[v with combining dot above]](https://www.rsc.org/images/entities/i_char_0076_0307.gif) i. We also assume a constant friction coefficient μf between the granular continuum and solid-body surfaces. The internal friction value μs is often measured from the tangent of the angle of repose for the granular media or from a direct shear test.36 We refer to this model as the ‘Non-Dilatant Plasticity Model’ (NDPM). We provide the input material properties used in various cases in the relevant sections. A basic implementation of this continuum modeling approach can be downloaded for Matlab.37
i. We also assume a constant friction coefficient μf between the granular continuum and solid-body surfaces. The internal friction value μs is often measured from the tangent of the angle of repose for the granular media or from a direct shear test.36 We refer to this model as the ‘Non-Dilatant Plasticity Model’ (NDPM). We provide the input material properties used in various cases in the relevant sections. A basic implementation of this continuum modeling approach can be downloaded for Matlab.37
Dilatant plasticity model (DPM)
While NDPM assumes a single critical granular density cutoff for the entire granular volume in the system, this is often not the case in real granular systems. Granular media can support stress in a range of densities including close and loose packings.5 The second model we present addresses this limitation of the NDPM model and allows for density evolution in the media.6 This model takes inspiration from the family of critical state models.6,24 We use a simple rigid-particle version of the Critical State model in which grains are not modeled to crush under hydrostatic loads; rather, they only have a hydrostatic elastic response in this case. When pressure is non-zero, the material is deemed to be in a ‘dense state’ and the density evolution occurs through shearing-based Reynolds dilation/contraction,38 representing particle rearrangements at the granular level. In a dense state, the packing fraction ϕ is equal to an evolving state variable ϕd. Every shearing action in dense media drives the local value of ϕd towards a limiting steady-state critical packing fraction, ϕc. Furthermore, when the packing fraction varies, the material's friction coefficient also changes; material with low packing fraction has low consolidation and thus has less strength than more consolidated media.Thus, in terms of constitutive relations, the simultaneous constraints describing the material's separation behavior and shear yield condition (eqn (1) and (2), respectively) remain the same with the two exceptions that the close-packed density, ρd, and internal friction value, μs, are non-constant local state variables (which vary with time and space), as follows:
| ρd = ρgϕd, μs = μc + (ϕd − ϕc)χ | (4) |
 | (5) |
In addition to the material's separation behavior and shear yield condition (eqn (1) and (2)), the material flow rule has a deviatoric dependence as before (eqn (3)) but due to dilation now also has a corresponding volumetric component. The volumetric strain-rate is given by the dilatancy variable, β. The plastic flow rate tensor, thus, has the form:
 | (6) |
While DPM is a more elaborate representation of granular media compared to NDPM, NDPM is easier to implement and is computationally more efficient to solve. In this study, we aim to highlight the advantages and sufficiency of using each of these constitutive forms on a case-by-case basis.
For the numerical implementation, we use a continuum simulation approach based on the Material Point Method (MPM),39 a derivative of the fluid-implicit-particle (FLIP) method for implementing a continuum description of granular media. The MPM implementation uses a combination of Lagrangian material points, which contain the state of the continuum, and a background computational mesh that is used to solve the equations of motion. Since the state is saved on the material points, the mesh is reset at the beginning of each computational step without any information loss, and thus the method allows for large deformations in the media without the error associated with large mesh deformations. A schematic representation of an explicit time-integration MPM-step is shown in Fig. 2. We use the MPM implementation described in Dunatunga and Kamrin30 to implement the different constitutive equations representing granular volumes assuming 2D plane-strain motion. We choose the spatial grid resolution (Δx) in each system on a case-by-case basis, such that all the geometric features are well represented and all system outputs converge. Also, to ensure numerical stability, we choose a time step (Δt) that satisfies the CFL condition based on minimum element size, maximum Young's modulus, and minimum medium density.
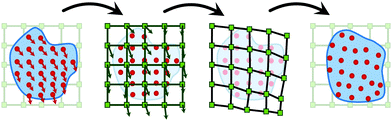 | ||
| Fig. 2 Sample explicit time integration step in MPM: a sample explicit time-integration step used in an MPM implementation. The Lagrangian tracers representing material points (solid red circles) carry the state of material over time and space. The background grid (green squares) assists in integrating the motion on the simulation domain and is reset each step. More details can be found in Dunatunga and Kamrin.30 | ||
3 Results and discussion
3.1 Drag and lift on submerged cylinder dragging
Drag and lift forces on submerged objects in granular media are relevant in processes such as mixing, mining, soil-buried pipelines, and animal locomotion.40–42 Over the past two decades, several studies43–46 have explored the mechanisms and the variation of these forces by considering the horizontal dragging of submerged, rigid cylinders (at different depths) as a test case. We specifically consider the work of Guillard et al.,44 who observed that the horizontal drag force on cylindrical objects moving horizontally increases with increasing depth while the vertical lift force plateaus in such motions for depths greater than a O(1) factor of the cylindrical diameter. The observations consider a depth range deep enough so that the cylinders are completely immersed in the granular bed even at the minimum depth. At very low depths near the free surface, the dragging motion of the cylinders results in an accumulation of the media in front of the intruders. This accumulation can augment the depth-dependence of drag forces and thus can change the force trends mentioned above. Thus, we do not consider such a near free-surface depth range in this study (as in Ding et al.46) and focus on depths ≥2.5D.The experimental drag and lift results in Guillard et al.44 were obtained by evaluating torques and vertical lifts on horizontal cylinders inside large granular beds rotated about the vertical axis. After a half rotation or so about the vertical axis, the authors observed a reduction in the force response as the cylinder begins re-interacting with the disturbed material as it is rotated multiple times. Here, we use the quasi-steady data obtained from the first half rotation of the cylinder, before it interacts with the disturbed media. Presumably, density variations play a smaller role in this portion, and we choose to compare the behavior observed with that of the NDPM model.
A schematic representation of the cylinder drag case is provided in Fig. 1A. For the NDPM implementation, we use a grain density ρg of 2520 kg m−3, and a critical packing fraction of 0.60. We calibrate the internal friction value (μs) for glass beads to 0.48 to accurately model the initial slope of depth vs drag graph from the experiments. This is in line with the expected range of μs for the glass beads which lies in the 0.39–0.55 range (corresponding to an angle of repose range ∼22–29°, depending on the surface roughness).47 The calibration absorbs possible inconsistencies between our 2D simulations with 3D experiments and also incorporates the variations due to indirect measurements of experimental drag and lift from rotating cylinder experiments.44
The cylinder is modeled as an elastic body with a high elastic modulus, thereby acting as an approximate rigid body. The media-cylinder interface friction coefficient (μf) is set to 0.35. The cylinder diameter, D is 4 mm, and the presumed out-of-plane length, w is 1 m (as the simulations are 2D plane-strain). We use a 0.20 m × 0.16 m granular bed, and a 5 × 10−4 m spatial resolution (Δx) for simulating these cases.
Fig. 3A and B show the comparison of Guillard's experimental data to our continuum results. The linearly increasing nature of drag vs. depth graphs, along with the plateauing of lift vs. depth graphs are well captured. The visualizations of plastic strains and strain rates (Fig. 3C and D) qualitatively agree with those reported in previous numerical and experimental studies.43,44 Notably, the variation of the equivalent plastic strain shows a strong semblance with the work of Wu et al.45 Additionally, we also plot the variation of the local hydrostatic pressure at four different depths in Fig. 3E. The pressure distribution shows an asymmetry about the intruder, consistent with the existence of both drag and lift forces, and as the intruder's depth increases the vertical asymmetry diminishes, which is consistent with the plateauing of the lift force and continued growth of drag force.
 | ||
| Fig. 3 Case 1: experiments vs. simulations for drag and lift on submerged cylinders (using NDPM model): comparison of experimental data44 (in blue) and the continuum simulation results (in red) for variation of (A) drag, and (B) lift on a submerged cylinder moving in granular media at depth |z|. The drag and lift forces are non-dimensionalized with characteristic force π(D/2)2ρdgw where D is the cylinder diameter, ρd is the effective medium density, g is the gravity, and w is out-of-plane cylinder width. Both experiments and continuum results use D = 4 mm, ρd = 1512 kg m−3, and g = 9.8 m s−2. Similarly, the depth is non-dimensionalized with cylinder diameter, D. Variation of macroscopic state variables: (C) equivalent plastic strain, (D) equivalent plastic strain rate, and (E) local hydrostatic pressure at four different depths, |z| = [10,30,51,71] mm. The gray circle indicates the cylinder position and the drag direction is from left to right. See Movie S1 (ESI†) for visualizing material flow over time for cylinder drag cases considered in (C) and (D). | ||
Similar to past DEM studies by Guillard et al.44 and experimental studies by Wu et al.,45Fig. 3C and D show high localization of the flow field for the depths greater than the lift turnover depth. A further increase in depth after this point results in a minimal-to-no change in the material flow profile. The drag and lift force behaviors are also related to this flow localization behavior. While the drag forces continue to increase linearly with depth, the lift forces become saturated near the depth the flow localizes, indicating a possible correlation between the flow and force. Fig. 3E indicates a reducing asymmetry of the pressure variation around the cylinder as depth increases, consistent with the notion that drag forces continue to increase but lift forces plateau. A deeper analysis of this variation (i.e. the distribution and the relative magnitude of pressure) to understand the mechanics of the force distributions on different faces of the intruders is reserved for future study.
Thus, the case of dragging submerged cylinders provides an example where NDPM captures the observed intrusion behavior.
3.2 Vertical drag in two-plate granular intrusions
Multi-body intrusions offer another commonly encountered scenario in real-life situations. Several researchers48–50 have examined the dynamics of granular intrusions involving multiple intruding bodies. The case we study specifically takes inspiration from the work of Swapnil et al.50 who examined the variation of vertical drag forces on a pair of parallel rigid plates during vertical downward intrusions as a function of the separation between them. They observed a peak in the average vertical drag (measured as work per unit depth) as the separation between the plates was increased. A similar ‘cooperative effect’ was observed by Merceron et al.49 during the upward motion of parallel intruders in the granular media. When the separation between the intruders was below a critical value, jammed media between the intruders was observed. We use NDPM to investigate the phenomena observed by Swapnil et al.50 and focus on the regime where intruders and separations are large enough that the role of particle size effects is minimal. We also conduct experiments to verify claims that follow from theoretical analysis of the NDPM model.A schematic representation of the case is given in Fig. 1B. The case is studied in two parts. In the first part, we use generic material properties (provided next) to determine the behavior of the continuum model in the single-plate intrusion case. And in the second part, a direct quantitative comparison of simulation results with the experiments is done in the two-plate intrusion case (details later). We use a set of generic NDPM fitting properties from the earlier case, i.e. a grain density, ρg of 2520 kg m−3, a critical packing fraction of 0.6, but choose the internal friction coefficient to be μs = 0.4, which is more common for glass beads.47 The plates were modeled as stiff elastic bodies with vertical displacement of control points assigned; thus, the plates act as quasi-rigid objects with a common fixed downward velocity. The intrusion velocity was set to 0.1 m s−1 in all simulations, and the media-plate surface friction was set to 0.35. We use a 1.2 m × 0.6 m granular bed, and a 1.25 × 10−3 m spatial resolution (Δx) for simulating these cases.
 , and mass as ρdL3, we obtain:
, and mass as ρdL3, we obtain: | (7) |
![[f with combining circumflex]](https://www.rsc.org/images/entities/i_char_0066_0302.gif) represents some unknown function. Recall that we are scaling based on NDPM, so certain properties such as the particle diameter do not appear in the above relation.
represents some unknown function. Recall that we are scaling based on NDPM, so certain properties such as the particle diameter do not appear in the above relation.
The dependence of FD on z can be divided into two regimes. (1) At low depths z ≪ L, the variable z/L is negligible and can be ignored. And (2), at larger depths, the drag forces FD are known to show a linear dependence on depth (after an initial jump in the vertical drag near free surfaces52–55). In both of these regimes, we set the dependence of FD on w to be linear assuming the plane-strain nature of the intrusions. We also focus on intrusions that are sufficiently slow such that FD is independent of velocity v (low-velocity regimes) as seen in the work of Swapnil et al.50
With the above assumptions, in the z ≪ L regime, we obtain:
 | (8) |
 | (9) |
Using the simulation's force output, in Fig. 4B and C we plot the observed relationships between F and L at, respectively, a smaller depth (where initial peaks occur) and in a deeper regime, where linear force variations are predicted. The forces in Fig. 4C are averaged over a depth window (zi − zf), i.e. . The expected trends from the dimensional analysis are apparent. Besides our own simulation results, the linear dependence of drag force on intruder area, once deep enough, is a well studied relation.52–54 We reiterate that our simulations are all in the quasistatic regime. Thus, the velocity contributions are negligible in comparison to static force contributions in our study. Thus, the initial peak in the force response is not related to inertial drag as seen in faster intrusions.53,56
. The expected trends from the dimensional analysis are apparent. Besides our own simulation results, the linear dependence of drag force on intruder area, once deep enough, is a well studied relation.52–54 We reiterate that our simulations are all in the quasistatic regime. Thus, the velocity contributions are negligible in comparison to static force contributions in our study. Thus, the initial peak in the force response is not related to inertial drag as seen in faster intrusions.53,56
Physically, the initial force maxima (Fpeak) in the force vs. displacement graphs of Fig. 4A correspond to the force requirements for initiating media flow in the system. The Fpeak force contributions enable the beginning of flow by initiating the shearing of the media, which exists at some finite strength due to finite pressure under the plate. From slip-line theory for granular intrusions,57 the flow develops a wedge-shaped no-shear-zone below the intruder, which has an acute angle of π/2 − tan−1(μ) (where μ represents the material internal friction). Thus, the requirement of shearing media of a finite strength along the wedge-shaped shear zone is responsible for these force contributions. We can also obtain an intuition for the initial L2 dependence of force by considering the conventional limit analysis for indentation of materials with yield stress Y, common in manufacturing processes such as drawing and blanking.58 In such cases, indenter force per unit out-of-plane width, F, varies as F ∝ Y × L for L the indenter plate length. In frictional media, the strength is pressure-sensitive. With Y = μ × P and supposing P grows linearly along the edge of the no-shear-zone wedge, the mean strength along the edge grows ∝ L. Substitution of Y ∝ L in the limit analysis formula then gives the observed quadratic dependence of the drag force on L. We do not further investigate these forces but identify that the existence of small regions of under-compacted granular media near free surfaces is expected to suppress the growth of such forces in many cases (see Fig. 8D). Our simulations indicate that the drag forces’ dependence of F on L enter linear regimes at depths z ∼ O(10−1)L. These forces are unique from the ‘added mass’ effects59 and other macro-inertial effects52,53 in granular impacts that are common in high-speed intrusion (and vary ∝ v2) since our intrusion velocities are small.
Fig. 5A and D show the variation of force for different combinations of plate widths and plate separations. Continuum modeling shows the existence of force peaks for both equal plate cases (Fig. 5A) and unequal plate cases (Fig. 5D). Our observations are in accord with similar experiments and DEM simulations by Swapnil et al.'s50 for equal plates. As the continuum modeling successfully captures the behavior, the detailed material states in these simulations can help identify the macro-mechanical origins of the phenomena. We visualize the material flow by plotting snapshots of the plastic strain in a few of these cases. The plastic strain fields before, at, and after the force peak in Fig. 5B and E, suggest a macro-mechanical picture. We observe higher granular flow interaction between the two plates as the separation between the plates is decreased. For a single plate intruder, any neighboring flow restriction is expected to make it more difficult to push material during the intrusion. Thus, decreasing plate separation results in increasing drag on each plate. Once the plates are sufficiently close, a large wedge-shaped rigid zone forms spanning the plates, causing the two plates to act as a large single plate. Thus, any further reduction in the separation does not result in additional flow restriction. Instead, it leads to a reduction in the effective area of the merged plate systems, and thereby the drag forces decrease upon a further decrease in separation. It is interesting to note that the material flow profiles when the two plates are together or far-separated are similar to the classical plasticity solution of Prandtl60 for yielding of metals upon indentation under a plate, characterized by a single rigid wedge of media under the indenter and flow emanating from both edges of the wedge. However, when the plates are separated but very close, the flow profile looks similar to the indentation plasticity solution of Hill,61 characterized by two smaller wedges under the plate and flow emanating only from the two outermost edges. We also plot the variation of local hydrostatic pressure in the media for the two cases in Fig. 5C and F. The ratio of local pressure magnitudes with equivalent hydrostatic pressure, ρdgz, is large (∼40) in accord with the observations of Brezinski et al.54 To understand the behavior of the flow solutions, we re-derive the scaling relations for combinations of plates of different lengths L1 and L2 (L1 ≤ L2) assuming NDPM, similar to the single plate case. Using base units of length as Lavg = 1/2(L1 + L2), time as  , and mass as ρdLavg3, we obtain:
, and mass as ρdLavg3, we obtain:
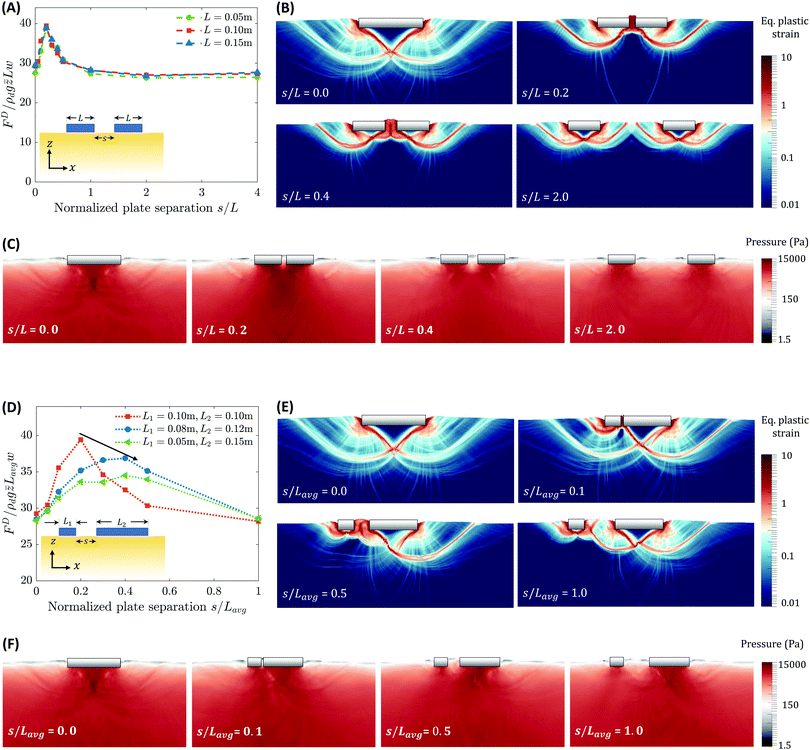 | ||
Fig. 5
Case 2: vertical intrusion of two parallel plates (using NDPM model): (A) variation of vertical drag (normalized) with plate separation, s (normalised to plate width L) for equally sized plates (L = 0.10 m each). (B) The corresponding equivalent plastic strain fields and (C) local hydrostatic pressure fields at different separations. (D) Variation of vertical drag with plate separation, s (normalised with average plate width Lavg = (L1 + L2)/2) for unequally sized plates (L1 = 0.05 m and L2 = 0.15 m). (E) The corresponding equivalent plastic strain fields and (F) local hydrostatic pressure fields at different separations. The forces FD in (A) and (D) are averaged over a depth range (zi − zf) of 0.04–0.08 m for all the cases and an average depth, ![[z with combining macron]](https://www.rsc.org/images/entities/i_char_007a_0304.gif) = 0.06 m, w = 1 m, g = 9.8 m s−2, ρd = 1512 kg m−3 (= ρg × ϕ) is used. The simulations are plane-strain and glass bead properties are used for simulating granular media (ρg = 2520 kg m−3, ϕ = 0.6, μs = 0.4). See Movie S2 (ESI†) for visualizing material flow over time for the two cases considered in (B) and (E). = 0.06 m, w = 1 m, g = 9.8 m s−2, ρd = 1512 kg m−3 (= ρg × ϕ) is used. The simulations are plane-strain and glass bead properties are used for simulating granular media (ρg = 2520 kg m−3, ϕ = 0.6, μs = 0.4). See Movie S2 (ESI†) for visualizing material flow over time for the two cases considered in (B) and (E). | ||
With similar assumptions as before in the moderate-depth regime (F ∝ z),
FD = ρdgzLavgw![[f with combining circumflex]](https://www.rsc.org/images/entities/i_char_0066_0302.gif) (μs,μf,s/Lavg,L1/L2). (μs,μf,s/Lavg,L1/L2). |
![[F with combining tilde]](https://www.rsc.org/images/entities/i_char_0046_0303.gif) = FD/ρdgzLavgw, we get
= FD/ρdgzLavgw, we get![[F with combining tilde]](https://www.rsc.org/images/entities/i_char_0046_0303.gif) = = ![[f with combining circumflex]](https://www.rsc.org/images/entities/i_char_0066_0302.gif) (μs,μf,s/Lavg,L1/L2) (μs,μf,s/Lavg,L1/L2) | (10) |
![[F with combining tilde]](https://www.rsc.org/images/entities/i_char_0046_0303.gif) = = ![[f with combining circumflex]](https://www.rsc.org/images/entities/i_char_0066_0302.gif) (μs,μf,s/L). (μs,μf,s/L). | (11) |
Based on eqn (10), for F ∝ z, we obtain following relations for peak separation (sp) and corresponding peak force (Fp) values:
sp = Lavg![[f with combining circumflex]](https://www.rsc.org/images/entities/i_char_0066_0302.gif) 1(L1/L2,μs,μf), 1(L1/L2,μs,μf), | (12) |
Fp = ρdgzLavg![[f with combining circumflex]](https://www.rsc.org/images/entities/i_char_0066_0302.gif) 2(L1/L2,μs,μf). 2(L1/L2,μs,μf). | (13) |
For equal plates (L1 = L2 = L = Lavg) we obtain
sp = L![[f with combining circumflex]](https://www.rsc.org/images/entities/i_char_0066_0302.gif) 1(μs,μf), 1(μs,μf), | (14) |
Fp = ρdgzwL![[f with combining circumflex]](https://www.rsc.org/images/entities/i_char_0066_0302.gif) 2(μs,μf). 2(μs,μf). | (15) |
We also verify these drag force variations and the peak separation scaling relation with new vertical intrusion experiments and compare them to calibrated continuum simulations (see Fig. 6 for the details). A DENSO VS087 robot arm intruded an apparatus that held pairs of steel plates at various separations into a bed of loosely consolidated Quikrete Pool Filter Sand with grain density ρg = 2520 kg m−3, and effective close-packed density ρd = 1512 kg m−3. The internal friction value of this medium was μs = 0.72 based on angle of repose measurements from experimental tilting tests, with the media globally fluidized for 15 seconds to an initial packing fraction of ϕ ≈ 0.58 for all trials. All intrusions were performed at 11 mm s−1, where speed dependence of the force response is negligible. Over 128 trials, the net resistive forces on the pair of intruding plates were measured using an ATI Mini40 force transducer. We observed a satisfactory match between the experiments and the simulations. The fact that the experimental data for different values of L collapse onto a single dimensionless master curve supports the robustness of the scaling relation implied by NDPM in eqn (11). Additionally, we observe that although both the Fig. 5(A) and 6 show peaks in normalised force responses of the media at low separations, the shapes of the graphs are not ‘identical’. This variation is expected because eqn (11) indicates that the graph between normalized drag (![[F with combining tilde]](https://www.rsc.org/images/entities/i_char_0046_0303.gif) ) and normalized separation (s/L) depends on material friction properties (μs and μf) and the two cases use different internal friction (μs) values.
) and normalized separation (s/L) depends on material friction properties (μs and μf) and the two cases use different internal friction (μs) values.
We also briefly explore, in our simulations, the effect of changing plate width ratios on the peak separation distance (sp), and the peak separation force (Fp) in our study (see Fig. 5D). We find that Fp monotonically decreases from a maximum value to F∞ as the plate ratio decreases from 1 to 0 (note that plate-ratio L1/L2 is always ≤1 as L1 ≤ L2 by definition). The normalized peak separation distance (sp/Lavg) increases with decreasing plate-ratios (L1/L2). The peak separation relations are also expected to be a function of μs from scaling analysis (eqn (13)). Thus, an in-depth shape and material property dependence characterization of this phenomenon is relegated to future study. Similarly, a more comprehensive amalgamation of the macroscopic insight we develop in this study with the microscopic observations made by Swapnil et al.49 for grain-scale plate lengths can be attempted in the future studies.
3.3 Drag variations in the plowing of granular media
This case takes inspiration from the work of Gravish et al.62 who studied drag force fluctuations in the plowing of granular beds at different initial packing fractions. A Discrete Element Method (DEM) based study of the case was also performed by Kobayakawa et al.63 Both of these studies observed increasing drag force fluctuations with an increasing initial packing fraction of the granular beds. Similar force fluctuations were observed by Kashizadeh and Hambleton64 on reduced-order modeling of the plowing processes in sands and by Jin et al.65 in the development of a new single-gravity (1-g) small scale testing methodology. As this phenomenon directly relates to the changing density of the media, we use the more detailed DPM model for this case.A schematic representation of this case is given in Fig. 1C. Both of the reported studies were performed in 3D while our simulations are 2D plane-strain. Characterizing the effects of this difference in our studies is difficult, so we do not attempt an exact match. Nevertheless, we do expect the 2D simulations to capture the phenomena qualitatively and the drag forces to be similar in their magnitudes. We once again use the glass bead material properties used in the previous case. We use a grain density ρg of 2520 kg m−3, a critical packing fraction ϕc of 0.6, a steady-state critical internal friction μc of 0.4, and a scaling coefficient χ of 2.5. Similar to previous cases, the plates are modeled as elastic bodies with high elastic modulus to approximate rigid bodies. The media/plate interface friction (μf) was set to 0.35. We use a 2.4 m × 0.4 m granular bed, and a 4 × 10−3 m spatial resolution (Δx) for simulating these cases. The plowing plate dimensions are 0.03 × 0.08 m2.
Fig. 7 shows the variation of horizontal drag forces from the Gravish et al.62 experiments alongside our continuum simulations. The continuum results are scaled proportionally to the out-of-plane width in Gravish et al.62 The mean drag force and force fluctuations from continuum modeling are plotted in Fig. 7D and E, showing smooth forces transition to larger, fluctuating forces as the initial packing fraction rises above ϕc. The same trends can be seen in experiments, cf.Fig. 7A and B. A visual free surface comparison between experiments and the simulations also shows the similarity of flows as ϕi varies, cf.Fig. 7C and F. In the over-compacted case, the continuum results show a stepped pattern forming on the surface but it is not as persistent as the wavy patterns observed in the experiments. This is due to the 2D nature of our simulations. The 2D nature restricts the material from flowing in an out-of-plane direction, which causes the material to flow over the existing waves and overrun the wavy patterns. Such patterns are otherwise not overrun in 3D experiments and are more visible in over-compacted cases.
 | ||
| Fig. 7 Case 3: force fluctuations during plowing (using DPM model): variation of drag forces at various initial packing fractions in Gravish et al.'s62 experiments: (A) time variation of drag forces, and (B) average drag forces. The average values of forces for three initial packing fractions in (A) are shown with corresponding colored arrows in (B). Corresponding continuum simulations: (D) time variation of drag forces (force plots for consecutive ϕi are shifted vertically by 0, 40, 80, and 120 N respectively for improved visualization), and (E) averaged drag forces. Visualisation of the free surface in under/over compacted granular media: top view from Gravish et al.'s62 experiments (C), and side view in continuum simulations (F). (G) Variation of material packing fraction from continuum simulations in initially under-compacted (ϕi = 0.57) and over-compacted (ϕi = 0.63) media cases considered in (F). The simulations are plane-strain and glass bead properties are used for simulating granular media (ρg = 2520 kg m−3, ϕc = 0.6, μc = 0.4, χ = 5.0, ϕmin = 0.45). See Movie S3 (ESI†) for visualizing time evolution of material front during plowing of under- and over-compacted media from experiments and simulations. Figure (A)–(C) are modified from Gravish et al.62 [Photo credits: (C) N. Gravish, P. B. Umbanhowar and D. I. Goldman, Georgia Institute of Technology]. | ||
The observed shear patterns, free-surface profiles, and force fluctuations shown in Fig. 7A–C are in accord with the shear-softening (shear-strengthening) of over-compacted (under-compacted) granular media that is built-in to the DPM model. In a sample initially under-compacted (ϕi < ϕc), shear deformations cause compaction, resulting in higher densities along the sheared regions than in the bulk (see eqn (5)). This density increase results in higher shear strength along the shear zone (see eqn (4)). Thus, further loading in such systems induces shear to occur in the weaker material adjacent to the shear band, which effectively spreads the shearing in such systems. On the other hand, in the over-compacted case, shear deformations dilate the material, resulting in lower density in the sheared region than in the bulk, which results in lower shear strength there. Hence, continued loading causes shear to accumulate along the thin zone of initial failure causing the appearance of a strong shear band. This process continues until the total force requirement for shearing along the existing band exceeds that for creating a new shear band in the bulk (after which the same process repeats itself). Thus, in over-compacted media, a visually separable shear band formation pattern occurs (Fig. 7F). In initially over-compacted cases (ϕi > ϕc), increasing the initial packing fraction of the media results in an increased plate motion requirement between successive shear band formations (due to increased strength of the media in the bulk) and thus the force fluctuation magnitudes increase (and their spatial frequency decreases) with increasing packing fraction (observed also by Gravish et al.62). We also plot the variation of the packing fraction in the media from continuum modeling in Fig. 7G. The figure provides a visualization of changing packing fraction ahead of the plate in accordance with the smooth versus banded mechanism explained above.
3.4 Development of a shear deformation zone in plate intrusions
This last case takes inspiration from the work of Aguilar and Goldman59 and highlights the capability of the basic DPM model in capturing the development of the flow profile during vertical intrusion of single plates. A schematic representation of the case is given in Fig. 1D. Aguilar and Goldman59 postulated that the formation of a rigid No Shear Zone (NSZ) ahead of a flat plate during vertical intrusion is an incremental growth process. In three dimensions, this growth takes the form of a rigid frustum shape which grows from a low height frustum with a fixed base (matching the shape of the intruder) to a fully developed cone/pyramid at the completion of the mechanism. For a circular base, the final shape is a cone. In two dimensions, like our case, this would translate to successive isosceles trapezoids (with larger parallel edges matching the intruder's intruding edge) leading to a wedge shape with the base as the intruder's leading edge.Fig. 8 shows the variation of intrusion forces and successive velocity profiles in under-compacted granular intrusion experiments compared to our continuum simulations. We model the granular media, poppy seeds, with the DPM to incorporate the effect of density transitions. We use material properties for poppy seeds with a grain density ρg = 1100 kg m−3, a critical packing fraction ϕc = 0.60, a steady-state critical internal friction μc = 0.53, and a scaling coefficient χ = 5.0. The media/plate interface friction (μf) was set to 0.35. We use a 0.5 m × 0.2 m granular bed, and a 5 × 10−4 m spatial resolution (Δx) for simulating these cases. The intruding plate dimensions are 0.04 m × 0.02 m.
 | ||
Fig. 8
Case 4: material front development during vertical intrusion (using DPM model): (A) experimental data from Aguilar and Goldman.59 The experiments intruded a circular plate of 0.051 m diameter into poppy seeds (ρg = 1100 kg m−3) at various initial packing fractions (ϕi). (B) Schematic of Aguilar and Goldman's cone growth model.59 (C) Continuum modelling force data from 2D plane strain simulations. We intrude 0.04 m wide flat plates into material with properties ρg = 1100 kg m−3, μc = 0.53, ϕc = 0.60, and χ = 5.0 as calibrated to poppy seeds. (D) Mechanism of solid zone development apparent from continuum modeling. (E) PIV analysis of constant speed plate intrusions: new set of experiments were conducted by intruding L = 40 mm wide rectangular flat plates next to a clear plexiglass wall at a constant low speed, v = 150 mm s−1, in loosely packed poppy seeds. The initial three frames represent the cone growth phase and the last frame (![[t with combining tilde]](https://www.rsc.org/images/entities/i_char_0074_0303.gif) ∼ 0.30) shows the stability of the cone at later stages of the intrusion. Time is non-dimensionalized ( ∼ 0.30) shows the stability of the cone at later stages of the intrusion. Time is non-dimensionalized (![[t with combining tilde]](https://www.rsc.org/images/entities/i_char_0074_0303.gif) = t/t0) by t0 ≡ L/v. The velocity is normalized by intrusion speed, v, and strain rates by = t/t0) by t0 ≡ L/v. The velocity is normalized by intrusion speed, v, and strain rates by ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/char_e0a2.gif) 0 ≡ 1/t0. We plot these results in the intruder's frame of reference. (F) Continuum simulation results: vertical velocity and equivalent plastic strain rate fields during vertical intrusion in initially under-compacted media (ϕi = 0.55) for material properties discussed in (C). We also show the evolution of packing fraction (ϕ) from continuum modeling in (G). See Movie S4 (ESI†) for visualizing material flow over time for various initial packing fractions (ϕi) including the one considered in (F). 0 ≡ 1/t0. We plot these results in the intruder's frame of reference. (F) Continuum simulation results: vertical velocity and equivalent plastic strain rate fields during vertical intrusion in initially under-compacted media (ϕi = 0.55) for material properties discussed in (C). We also show the evolution of packing fraction (ϕ) from continuum modeling in (G). See Movie S4 (ESI†) for visualizing material flow over time for various initial packing fractions (ϕi) including the one considered in (F). | ||
The force trends from simulation qualitatively match the trends from Aguilar's experiments (compare Fig. 8A–C), keeping in mind that Aguilar uses a 3D circular plate while our simulations are in 2D plane-strain. In a set of separate experiments using a rectangular plate intruder and PIV (Fig. 8E) we observed the flow zone development appears similar to continuum results (Fig. 8F). These trends also agree with general observations from a 3D DEM study done by Feng et al.66 The Aguilar and Goldman59 study presents a model whereby the rigid cone emerges from a growing rigid frustum of constant base angle that gets progressively longer until converging to the final cone shape (Fig. 8B). However, in our simulations, the zone actually starts as a ‘short’ wedge coincident with the plate bottom, having a larger apex angle (expected by slip-line theory to be approximately π/2 − tan−1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) μi for μi the friction at the initial density) due to the low initial packing fraction of the media. The rigid front then grows by ‘fanning out’ from the diagonal edges (see Fig. 8D), as the edges represent the zone experiencing maximum shear-compaction and hence the most strengthening. This growth can be observed as well from density variations, shown in Fig. 8G. The growing density of the region results in an increasing internal friction value in the zone below the intruder and results in the development of a progressively sharpening, quasi-rigid trapezoid-like shape under the plate. As the intruder moves deeper, the process converges to a final wedge shape (with a sharper half-angle equal to ‘π/2 − tan−1
μi for μi the friction at the initial density) due to the low initial packing fraction of the media. The rigid front then grows by ‘fanning out’ from the diagonal edges (see Fig. 8D), as the edges represent the zone experiencing maximum shear-compaction and hence the most strengthening. This growth can be observed as well from density variations, shown in Fig. 8G. The growing density of the region results in an increasing internal friction value in the zone below the intruder and results in the development of a progressively sharpening, quasi-rigid trapezoid-like shape under the plate. As the intruder moves deeper, the process converges to a final wedge shape (with a sharper half-angle equal to ‘π/2 − tan−1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) μc’). Thus the DPM model provides an apt description of the observed behavior in under compacted granular intrusion.
μc’). Thus the DPM model provides an apt description of the observed behavior in under compacted granular intrusion.
4 Approach limitations and their implications
While the continuum modeling and the numerical implementation used in this study are able to represent the considered cases to a sufficient degree, both the model and the method have their limitations. Clearly, as emphasized in the introduction, the phenomena incorporated in a constitutive model limits the behavior the model can capture, and the constitutive relations we use here intentionally exclude certain effects for the benefit of simplicity. Similarly, MPM has known accuracy limitations given by the choice of the grid resolution, material point density, shape functions, and the means of representing contact between domains. For instance, MPM inherently captures a locally volume averaged material response everywhere. If during the flow an element has a low number of interior material points, the accuracy of the integration is also diminished. But these issues can be overcome with an appropriate choice of shape functions and refined discretization. Specifically for these issues, use of more advanced methods such as the hybrid DEM-MPM approach (such as Yue et al.67 and Chen et al.68) or dynamic particle enrichment (such as Zhu et al.69) could be used at the expense of computation time. The use of smoother and wider shape functions could also help decrease numerical fluctuations often observed in MPM.705 Conclusions
In this work we demonstrated the efficacy of continuum modeling in four intrusion cases using two continuum descriptions of granular media—(1) depth-dependent force response in horizontal submerged intruder motion; (2) separation-dependent drag variation in parallel plate vertical intrusion; (3) initial density-dependent drag fluctuations in free-surface plowing; and (4) flow zone development in vertical plate intrusions in under compacted granular media (see Fig. 1). The study shows that relatively simple, friction-based plasticity models capture a large variety of granular intrusion phenomena. Moreover, the models provide a useful macroscopic understanding of granular intrusion processes, which are often primary interests in engineering applications, and remove the additional complexity of trying to determine large-scale physics from grain-scale observations. The simplicity of these continuum models also streamlines this understanding, both by exclusion – i.e. if such a model works, it implies that mechanisms or effects lying outside the model's formulation are not crucial to the outcome – and by admitting simple scaling analyses as we have utilized throughout. Such simplifications will certainly limit the accuracy of these models in a variety of cases, but an incremental approach of adding physical augmentations (such as micro-inertial effects, particle size effects, or evolving fabric variables) provides a systematic approach for exploring the underlying physics in diverse cases. For instance, we do not use μ(I) rheology in either of the models in this study; the fact that our modeling still captures the observed behaviors indicates micro-inertial effects are not a key mechanism in the observed behaviors. We also emphasize that the continuum approach is useful for determining further-reduced models of intrusion, due to the simplicity of its large-scale characterization of systems. One such study was done in Agarwal et al.,20 which develops a generalized, rate-dependent, dynamic resistive force theory (DRFT) for rapid intrusion of generic intruders. In the future, the work could be extended to three dimensions to extensively compare the computational advantage of using such methods. Furthermore, the continuum treatment could help reconcile granular behavior with similar behaviors observed in other, more standard continua. For example, Minetti et al.71 reported that during swimming in water, slight separation between fingers increases propulsive thrust, similar to our observation for slightly separated granular intruders.71,72 Comparing and analyzing continuum forms could provide insights into the rationale behind such similarities, as was done in other flow resistance studies.73Conflicts of interest
There are no conflicts to declare.Acknowledgements
SA and KK acknowledge support from Army Research Office (ARO) grants W911NF1510196, W911NF1810118, and W911NF1910431. AK and DG acknowledge support from ARO grant W911NF-18-1-0120. We also acknowledge support from the U.S. Army's Tank Automotive Research, Development, and Engineering Center (TARDEC) and thank Dr Christian Hubicki for his support in conducting vertical intrusion experiments.Notes and references
- A. Soliman, S. Reid and W. Johnson, Int. J. Mech. Sci., 1976, 18, 279–284 CrossRef.
- M. Omidvar, M. Iskander and S. Bless, Int. J. Impact Eng., 2014, 66, 60–82 CrossRef.
- D. Ortiz, N. Gravish and M. T. Tolley, IEEE Robot. Autom. Lett., 2019, 4, 2630–2636 Search PubMed.
- D. Van Der Meer, Annu. Rev. Fluid Mech., 2017, 49, 463 CrossRef.
- B. Andreotti, Y. Forterre and O. Pouliquen, Granular media: between fluid and solid, Cambridge University Press, 2013 Search PubMed.
- D. M. Wood, Soil behaviour and critical state soil mechanics, Cambridge University Press, 1990 Search PubMed.
- R. P. Jensen, P. J. Bosscher, M. E. Plesha and T. B. Edil, Int. J. Numer. Anal. Methods Geomech., 1999, 23, 531–547 CrossRef.
- R. P. Jensen, M. E. Plesha, T. B. Edil, P. J. Bosscher and N. B. Kahla, Int. J. Geomech., 2001, 1, 21–39 CrossRef.
- N. V. Brilliantov, F. Spahn, J.-M. Hertzsch and T. Pöschel, Phys. Rev. E: Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top., 1996, 53, 5382 CrossRef CAS PubMed.
- L. E. Silbert, D. Ertas, G. S. Grest, T. C. Halsey, D. Levine and S. J. Plimpton, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2001, 64, 051302 CrossRef CAS PubMed.
- K. Kamrin and G. Koval, Phys. Rev. Lett., 2012, 108, 178301 CrossRef PubMed.
- S. Kim and K. Kamrin, Phys. Rev. Lett., 2020, 125(8), 088002 CrossRef CAS PubMed.
- D. Jajcevic, E. Siegmann, C. Radeke and J. G. Khinast, Chem. Eng. Sci., 2013, 98, 298–310 CrossRef CAS.
- W. Zhong, A. Yu, X. Liu, Z. Tong and H. Zhang, Powder Technol., 2016, 302, 108–152 CrossRef CAS.
- C. Kelly, N. Olsen and D. Negrut, Multibody Syst. Dyn., 2020, 5, 355–379 CrossRef.
- N. Vriend, J. McElwaine, B. Sovilla, C. Keylock, M. Ash and P. Brennan, Geophys. Res. Lett., 2013, 40, 727–731 CrossRef.
- K. E. Daniels and N. W. Hayman, J. Geophys. Res.: Solid Earth, 2008, 113, B11 Search PubMed.
- S. Agarwal, C. Senatore, T. Zhang, M. Kingsbury, K. Iagnemma, D. I. Goldman and K. Kamrin, J. Terramechanics, 2019, 85, 1–14 CrossRef.
- C. Li, T. Zhang and D. I. Goldman, Science, 2013, 339, 1408–1412 CrossRef CAS PubMed.
- S. Agarwal, A. Karsai, D. I. Goldman and K. Kamrin, Sci. Adv., 2021, 7, eabe0631 CrossRef PubMed.
- N. Mahabadi and J. Jang, Appl. Phys. Lett., 2017, 110, 041907 CrossRef.
- N. V. Brilliantov and T. Pöschel, Kinetic theory of granular gases, Oxford University Press, 2010 Search PubMed.
- J. T. Jenkins and M. Richman, Phys. Fluids, 1985, 28, 3485–3494 CrossRef CAS.
- A. Schofield and P. Wroth, Critical state soil mechanics, McGraw-hill, 1968 Search PubMed.
- H.-S. Yu, Keynote lecture. Proc. 12th Int. Conf. IACMAG, Goa, India, 2008, pp. 361–378.
- P. Jop, Y. Forterre and O. Pouliquen, Nature, 2006, 441, 727–730 CrossRef CAS PubMed.
- J. Wiacek, M. Molenda, J. Horabik, et al., Mechanical properties of granular agro-materials. Continuum and discrete approach, Polska Akademia Nauk, 2011 Search PubMed.
- D. L. Henann and K. Kamrin, Proc. Natl. Acad. Sci. U. S. A., 2013, 110, 6730–6735 CrossRef CAS PubMed.
- K. Kamrin, Front. Phys., 2019, 7, 116 CrossRef.
- S. Dunatunga and K. Kamrin, J. Fluid Mech., 2015, 779, 483–513 CrossRef CAS.
- G. Daviet and F. Bertails-Descoubes, ACM Trans. Graph., 2016, 35, 1–13 CrossRef.
- G. Daviet and F. Bertails-Descoubes, J. Non-Newtonian Fluid Mech., 2016, 234, 15–35 CrossRef CAS.
- C. Dávalos, J. Cante, J. Hernández and J. Oliver, Int. J. Solids Struct., 2015, 71, 99–125 CrossRef.
- C. Peng, X. Guo, W. Wu and Y. Wang, Acta Geotech., 2016, 11, 1231–1247 CrossRef.
- S. Dunatunga and K. Kamrin, J. Mech. Phys. Solids, 2017, 100, 45–60 CrossRef CAS.
- D. W. Taylor, Fundamentals of soil mechanics, LWW, 1948, vol. 66 Search PubMed.
- S. Agarwal, Continuum Modeling of Granular Flows and Intrusions, 2020, MATLAB Central File Exchange.
- Osborne Reynolds, Philos. Mag., 1885, 20(127), 469–481 Search PubMed.
- D. Sulsky, Z. Chen and H. L. Schreyer, Comput. Methods Appl. Mech. Eng., 1994, 118, 179–196 CrossRef.
- A. Jarray, H. Shi, B. J. Scheper, M. Habibi and S. Luding, Sci. Rep., 2019, 9, 1–12 CAS.
- J. Aguilar, T. Zhang, F. Qian, M. Kingsbury, B. McInroe, N. Mazouchova, C. Li, R. Maladen, C. Gong and M. Travers, et al. , Rep. Prog. Phys., 2016, 79, 110001 CrossRef PubMed.
- H. Li, Y. Lai, L. Wang, X. Yang, N. Jiang, L. Li, C. Wang and B. Yang, Cold Reg. Sci. Technol., 2019, 157, 171–186 CrossRef.
- X. Zhang, D. Sheng, G. P. Kouretzis, K. Krabbenhoft and S. W. Sloan, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2015, 91, 022204 CrossRef PubMed.
- F. Guillard, Y. Forterre and O. Pouliquen, Phys. Fluids, 2014, 26, 043301 CrossRef.
- J. Wu, G. Kouretzis, L. Suwal, Y. Ansari and S. W. Sloan, Can. Geotech. J., 2020, 57, 1472–1483 CrossRef.
- Y. Ding, N. Gravish and D. I. Goldman, Phys. Rev. Lett., 2011, 106, 028001 CrossRef PubMed.
- M. Klinkmüller, G. Schreurs, M. Rosenau and H. Kemnitz, Tectonophysics, 2016, 684, 23–38 CrossRef.
- R. L. De La Cruz and G. Caballero-Robledo, J. Fluid Mech., 2016, 800, 248–263 CrossRef.
- A. Merceron, A. Sauret and P. Jop, EPL, 2018, 121, 34005 CrossRef.
- S. Pravin, B. Chang, E. Han, L. London, D. I. Goldman, H. M. Jaeger and S. T. Hsieh, 2020, arXiv preprint arXiv:2010.15172.
- A. H. Clark and R. P. Behringer, EPL, 2013, 101, 64001 CrossRef CAS.
- L. K. Roth, E. Han and H. M. Jaeger, Phys. Rev. Lett., 2021, 126, 218001 CrossRef CAS PubMed.
- H. Katsuragi and D. J. Durian, Nat. Phys., 2007, 3, 420–423 Search PubMed.
- T. A. Brzinski III, P. Mayor and D. J. Durian, Phys. Rev. Lett., 2013, 111, 168002 CrossRef PubMed.
- W. Kang, Y. Feng, C. Liu and R. Blumenfeld, Nat. Commun., 2018, 9, 1–9 CrossRef PubMed.
- C. S. Bester and R. P. Behringer, Phys. Rev. E, 2017, 95, 032906 CrossRef PubMed.
- V. V. Sokolovski, Statics of soil media, Butterworths Scientific Publications, 1960 Search PubMed.
- A. F. Bower, Chapter 6, Applied mechanics of Solids, CRC Press, 2009 Search PubMed.
- J. Aguilar and D. I. Goldman, Nat. Phys., 2016, 12, 278–283 Search PubMed.
- L. Prandtl, Nachr. Ges. Wiss. Gottingen, 1920, 74–85 Search PubMed.
- R. Hill, Q. J. Mech. Appl. Math., 1949, 2, 40–52 CrossRef.
- N. Gravish, P. B. Umbanhowar and D. I. Goldman, Phys. Rev. Lett., 2010, 105, 128301 CrossRef PubMed.
- M. Kobayakawa, S. Miyai, T. Tsuji and T. Tanaka, J. Terramechanics, 2020, 90, 3–10 CrossRef.
- E. Kashizadeh, J. Hambleton and S. Stanier, Proc. 14th Int. Conf. IACMAG, Kyoto, Japan, 2015, pp. 159–164.
- Z. Jin, Z. Shi and J. Hambleton, Spree Internal Report, 2020, 20-7/495S.
- Y. Feng, R. Blumenfeld and C. Liu, Soft Matter, 2019, 15, 3008–3017 RSC.
- Y. Yue, B. Smith, P. Y. Chen, M. Chantharayukhonthorn, K. Kamrin and E. Grinspun, ACM Trans. Graph., 2018, 37, 1–19 CrossRef.
- P. Y. Chen, M. Chantharayukhonthorn, Y. Yue, E. Grinspun and K. Kamrin, J. Mech. Phys. Solids, 2021, 104404 CrossRef.
- F. Zhu, J. Zhao, S. Li, Y. Tang and G. Wang, Computer Graphics Forum, 2017, pp. 381–392 Search PubMed.
- M. Steffen, R. M. Kirby and M. Berzins, Int. J. Numer. Meth. Eng., 2008, 76, 922–948 CrossRef.
- A. E. Minetti, G. Machtsiras and J. C. Masters, J. Biomech., 2009, 42, 2188–2190 CrossRef PubMed.
- N. Sidelnik and B. Young, Sports Eng., 2006, 9, 129–135 CrossRef.
- H. Askari and K. Kamrin, Nat. Mater., 2016, 15, 1274–1279 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/d1sm00130b |
| This journal is © The Royal Society of Chemistry 2021 |