Open Access Article
Open Access ArticleInterface-induced hysteretic volume phase transition of microgels: simulation and experiment†
Jannis
Kolker
 *a,
Johannes
Harrer
*a,
Johannes
Harrer
 *b,
Simone
Ciarella
*b,
Simone
Ciarella
 c,
Marcel
Rey
c,
Marcel
Rey
 b,
Maret
Ickler
b,
Liesbeth M. C.
Janssen
c,
Nicolas
Vogel
b,
Maret
Ickler
b,
Liesbeth M. C.
Janssen
c,
Nicolas
Vogel
 b and
Hartmut
Löwen
b and
Hartmut
Löwen
 a
a
aInstitut für Theoretische Physik II, Heinrich-Heine-Universität Düsseldorf, Universitätsstrasse 1, D-40225 Düsseldorf, Germany. E-mail: kolker@thphy.uni-duesseldorf.de
bInstitute of Particle Technology, Friedrich-Alexander University Erlangen-Nürnberg, Cauerstrasse 4, 91058 Erlangen, Germany. E-mail: johannes.harrer@fau.de
cSoft Matter and Biological Physics, Department of Applied Physics, Eindhoven University of Technology, P. O. Box 513, 5600MB Eindhoven, The Netherlands
First published on 5th May 2021
Abstract
Thermo-responsive microgel particles can exhibit a drastic volume shrinkage upon increasing the solvent temperature. Recently we found that the spreading of poly(N-isopropylacrylamide) (PNiPAm) microgels at a liquid interface under the influence of surface tension hinders the temperature-induced volume phase transition. In addition, we observed a hysteresis behavior upon temperature cycling, i.e. a different evolution in microgel size and shape depending on whether the microgel was initially adsorbed to the interface in expanded or collapsed state. Here, we model the volume phase transition of such microgels at an air/water interface by monomer-resolved Brownian dynamics simulations and compare the observed behavior with experiments. We reproduce the experimentally observed hysteresis in the microgel dimensions upon temperature variation. Our simulations did not observe any hysteresis for microgels dispersed in the bulk liquid, suggesting that it results from the distinct interfacial morphology of the microgel adsorbed at the liquid interface. An initially collapsed microgel brought to the interface and subjected to subsequent swelling and collapsing (resp. cooling and heating) will end up in a larger size than it had in the original collapsed state. Further temperature cycling, however, only shows a much reduced hysteresis, in agreement with our experimental observations. We attribute the hysteretic behavior to a kinetically trapped initial collapsed configuration, which relaxes upon expanding in the swollen state. We find a similar behavior for linear PNiPAm chains adsorbed to an interface. Our combined experimental – simulation investigation provides new insights into the volume phase transition of PNiPAm materials adsorbed to liquid interfaces.
1 Introduction
Soft microgels consisting of a swollen polymer network possess fascinating properties. Their soft nature allows them to undergo significant deformations, for example when adsorbed to an interface.1,2 In addition, stimuli-responsive properties can be encoded in their molecular structure, allowing microgels to undergo sharp transitions between swollen and collapsed states upon an external stimulus.3–5 This dynamic behavior has important consequences. From an applied side, stimuli-responsive microgels serve as dynamic and reversible emulsion stabilizers6–10 or vehicles for drug-delivery, due to their ability to take up and release molecules on demand.4,11 From a fundamental side, soft microgels serve as model systems for classical many-body systems to model atomistic physical phenomena such as melting of crystal lattices,12,13 solid–solid phase transitions,14 or complex self-assembly.15–17Among the most prominent microgel systems are crosslinked poly(N-isopropylacrylamide) (PNiPAm)-based microgels, which exhibit a drastic volume shrinkage in aqueous dispersion above 32 °C.18–20 During this volume phase transition, nonpolar groups of the PNiPAm microgel aggregate and bound water is expelled from the macromolecule to increase the entropy of the system.3,19,20 This volume phase transition has been extensively explored through experimental studies,5,20–22 computer simulations5,23–35 and statistical theory.36–44
However, in many actual applications such as emulsion stabilization6–8 or surface patterning15,45,46 microgel particles are exposed and attracted to a liquid interface, where the spatial isotropy of the microgel is broken and a more complex behavior results. Therefore it is important to understand their structural and dynamical properties when confined to a liquid interface. In fact, it was shown that at liquid interfaces, microgels deform into a fried-egg-like structure1,2,47–49 where the core possesses a disk-like shape and the surrounding dangling polymer chains form a quasi two-dimensional layer close to the interface, termed the corona. Correspondingly, the volume phase transition is strongly modified due to the presence of the interface. Recent experiments50–52 have analyzed the volume phase transition at the interface and showed that the volume phase transition in the lateral direction is strongly hindered by the presence of the liquid interface. In addition, a hysteresis behaviour upon swelling and deswelling of microgels dependent on whether the microgels were deposited in the swollen or collapsed state was found.50,53 Though monomer-resolved computer simulations have considered the microgel structure at an interface,50,54,55 the hysteretic behaviour was not yet reproduced in computer simulations.
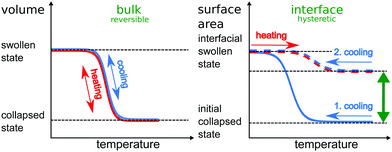
Here we present extensive Brownian dynamics simulations to confirm and investigate the hysteresis on a monomer-resolved scale. The microgel particle is modelled by a coarse-grained polymer network with effective beads.23,24 The interface is described by an external effective potential attractive for the beads. Within our simulations we are able to reproduce and quantify the hysteresis behavior and the corresponding structural change of the microgel particle. In our protocol the microgel particle is first equilibrated in the bulk either in the collapsed (high temperature) or in the swollen (low temperature) state and then brought to the interface and “equilibrated” there again. Fig. 1 schematically outlines the temperature cycling experiments used for this investigation. A swollen particle adsorbed to the interface responds reversibly to further collapsing and swelling (resp. heating and cooling) cycles. An initially collapsed particle adsorbed to the interface, however, experiences structural changes upon temperature cycling. Instead of reversible regaining its initial size, the microgel remains significantly more expanded after undergoing a temperature cycle. We attribute this hysteretic behaviour to an initial kinetically trapped collapsed state. This behavior is purely induced by the interface, as a similar temperature cycling of a bulk microgel does not show any hysteresis. We investigate these interfacial volume phase transitions as a function of crosslinker density. In both experiments and simulations, we find that less crosslinked microgels exhibit a larger hysteresis. In addition, we show that even linear PNiPAm chains adsorbed to an interface undergo a hysteretic behavior upon temperature cycling, indicating that the hysteresis does not only depend on the architecture of the microgel, but originates from the molecular nature of the polymer itself.
2 Materials and methods
We adopt the modelling proposed in ref. 25 and 55–57 describing a microgel particle on a monomer-resolved level with no explicit solvent. In detail, the microgel particle consists of two types of beads, monomers and crosslinkers, which define its internal architecture. A monomer is covalently linked to either a neighbouring other monomer or to a crosslinker by springs and the maximum number of these bonds is two. A crosslinking bead, on the other hand, has four of such bonds. In terms of all other interactions (next nearest neighbour interactions, etc.) monomers and crosslinkers do not differ. The covalent bonds are described by a finite-extensible-nonlinear-elastic (FENE) potential25,55 (see ESI†) with a characteristic energy scale ε, a maximal bond expansion![[R with combining tilde]](https://www.rsc.org/images/entities/i_char_0052_0303.gif) 0 = 1.5σ and an effective spring constant
0 = 1.5σ and an effective spring constant ![[k with combining tilde]](https://www.rsc.org/images/entities/i_char_006b_0303.gif) f = 15ε/σ2. The remaining bead–bead interactions are modelled by a repulsive Week–Chandler–Andersen (WCA) potential25,55 given explicitly in the ESI† which contains the size σ of the repulsive monomers as a length and the repulsion strength ε, as the same energy scale as for the FENE potential. Henceforth we choose σ and ε as units of length and energy.
f = 15ε/σ2. The remaining bead–bead interactions are modelled by a repulsive Week–Chandler–Andersen (WCA) potential25,55 given explicitly in the ESI† which contains the size σ of the repulsive monomers as a length and the repulsion strength ε, as the same energy scale as for the FENE potential. Henceforth we choose σ and ε as units of length and energy.
To incorporate the thermoresponsivity of the microgel particle effectively, a further attractive bead–bead pair potential25 is added given by
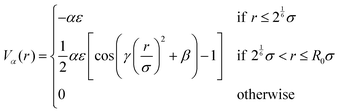 | (1) |
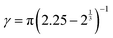 and β = 2π − 2.25γ.58 Importantly, the effective attraction strength is controlled by the parameter α, which mimics the quality of the solvent in an implicit manner. The value α = 1.55 describes a strong attraction (relative to the bead repulsions) imitating poor solvent conditions25,58 and therefore mimicking the collapsed state of the microgel. For good solvent conditions the value α = 0 is used such that there is no attraction at all,25,58 reflecting the swollen state. In our simulations, we varied the effective attraction strength α between the two extreme cases in the range 0 ≤ α ≤ 1.55 and refer to the α = 0 case as the “fully swollen state” and the α = 1.55 case as the “fully collapsed state”. As the solvent quality is controlled by temperature in the experiments, α = 0 corresponds to a low temperature, below the volume phase transition of the PNiPAm microgels, and α = 1.55 to a high temperature situation above the volume phase transition. For the connection between the effective attraction strength α and the temperature dependence on PNiPAm microgels we refer to ref. 25. The internal architecture of the microgel particle is as in ref. 23, 25 and 55 and depends on the crosslinker density. In our simulations we represent each microgel particle by a total number of N = 5500 beads, which includes a fraction of homogeneously distributed crosslinkers. The percentage of crosslinkers is an important parameter in our simulations and will be systematically varied between 0 and 4.5%.
and β = 2π − 2.25γ.58 Importantly, the effective attraction strength is controlled by the parameter α, which mimics the quality of the solvent in an implicit manner. The value α = 1.55 describes a strong attraction (relative to the bead repulsions) imitating poor solvent conditions25,58 and therefore mimicking the collapsed state of the microgel. For good solvent conditions the value α = 0 is used such that there is no attraction at all,25,58 reflecting the swollen state. In our simulations, we varied the effective attraction strength α between the two extreme cases in the range 0 ≤ α ≤ 1.55 and refer to the α = 0 case as the “fully swollen state” and the α = 1.55 case as the “fully collapsed state”. As the solvent quality is controlled by temperature in the experiments, α = 0 corresponds to a low temperature, below the volume phase transition of the PNiPAm microgels, and α = 1.55 to a high temperature situation above the volume phase transition. For the connection between the effective attraction strength α and the temperature dependence on PNiPAm microgels we refer to ref. 25. The internal architecture of the microgel particle is as in ref. 23, 25 and 55 and depends on the crosslinker density. In our simulations we represent each microgel particle by a total number of N = 5500 beads, which includes a fraction of homogeneously distributed crosslinkers. The percentage of crosslinkers is an important parameter in our simulations and will be systematically varied between 0 and 4.5%.
To mimic the effect of an air–water interface, we follow ref. 50 and add an external potential; the potential is defined such that the interface normal is along the z direction. Explicitly, for each bead, the external potential is a combination of an effective Lennard-Jones potential on the water side and a steep linear potential on the air side. We introduce a typical range σext for the effective bead–interface interaction and a shifted z-coordinate ![[z with combining tilde]](https://www.rsc.org/images/entities/i_char_007a_0303.gif) by
by 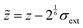 ; the derivative of the potential (i.e. the force) is defined to be continuous at a matching point
; the derivative of the potential (i.e. the force) is defined to be continuous at a matching point ![[z with combining tilde]](https://www.rsc.org/images/entities/i_char_007a_0303.gif) a < 0. In detail,
a < 0. In detail,
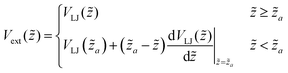 | (2) |
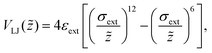 | (3) |
![[z with combining tilde]](https://www.rsc.org/images/entities/i_char_007a_0303.gif) = 0 where the potential is minimal. Physically this attraction towards the interface results from surface tension reduction by reducing the bare air–water interfacial area when a bead is adsorbed at the interface. The large difference in the bead chemical potential between the air and the water phase is reflected by the steep increase of Vext(
= 0 where the potential is minimal. Physically this attraction towards the interface results from surface tension reduction by reducing the bare air–water interfacial area when a bead is adsorbed at the interface. The large difference in the bead chemical potential between the air and the water phase is reflected by the steep increase of Vext(![[z with combining tilde]](https://www.rsc.org/images/entities/i_char_007a_0303.gif) ) for
) for ![[z with combining tilde]](https://www.rsc.org/images/entities/i_char_007a_0303.gif) <
< ![[z with combining tilde]](https://www.rsc.org/images/entities/i_char_007a_0303.gif) a. In the following we have chosen εext = 5.5ε, to ensure a sufficiently strong adsorption strength towards the interface (a calculation for comparison with the experiment can be found in the ESI†), and σext = 0.5σ corresponding to a relatively deep and stiff minimum around
a. In the following we have chosen εext = 5.5ε, to ensure a sufficiently strong adsorption strength towards the interface (a calculation for comparison with the experiment can be found in the ESI†), and σext = 0.5σ corresponding to a relatively deep and stiff minimum around ![[z with combining tilde]](https://www.rsc.org/images/entities/i_char_007a_0303.gif) = 0. A harmonic expansion around the origin
= 0. A harmonic expansion around the origin ![[z with combining tilde]](https://www.rsc.org/images/entities/i_char_007a_0303.gif) = 0 yields a large spring constant of 22ε/σ2 which is enforcing a bead monolayer as observed by the very thin corona formed by polymer chains expanding at the liquid interface. Finally we have chosen the matching position za, i.e. the point where the Lennard-Jones behavior changes to a constant force, as
= 0 yields a large spring constant of 22ε/σ2 which is enforcing a bead monolayer as observed by the very thin corona formed by polymer chains expanding at the liquid interface. Finally we have chosen the matching position za, i.e. the point where the Lennard-Jones behavior changes to a constant force, as ![[z with combining tilde]](https://www.rsc.org/images/entities/i_char_007a_0303.gif) a = −0.01σ.
a = −0.01σ.
We simulate the bead dynamics as Brownian dynamics with an implicit solvent, whereby the short-time bead self-diffusion coefficient D0 sets a characteristic Brownian time scale τB = D0/σ2. The latter defines our unit of time in the following. A finite time step of Δt = 0.00005τB is used to integrate the equations of motion with an Euler forward scheme. All of the Brownian dynamics simulations are performed with the HOOMD-Blue package59 and are visualized by OVITO.60
In our modelling it is important to distinguish between a solvent bath temperature T* – which sets the Brownian fluctuations – and the implicit temperature influence on the effective bead–bead attraction strength α. Since the temperature change is small compared to the absolute room temperature, we have fixed the solvent bath temperature to kBT* = ε throughout all of our simulations but changed solely the effective attraction strength α, in agreement with typical protocols in the literature.23,25 For simplicity, there is no distinction between the interactions of the beads in the interface and in the bulk.
Our simulation protocol is as follows: first we equilibrate the microgel particle in the bulk (i.e. in the absence of the interface external potential (2)) and thus gain an equilibrated initial bead configuration. This is done separately for the “fully swollen state” with α = 0 and for the “fully collapsed state” with α = 1.55. We then instantaneously expose the initial bead configuration to the potential (2) such that the z-coordinate of the center of mass of the particle is a distance of 10σ apart from the interface position at ![[z with combining tilde]](https://www.rsc.org/images/entities/i_char_007a_0303.gif) = 0. We then relax the system for a long waiting time tw of typically 5 × 103τB. The relaxed configuration is – in the presence of the interface – subject to a sudden change in the attraction parameter α from 0 to 1.55 or, respectively from 1.55 to 0. Physically this means that the solvent quality temperature is abruptly changed from high to low (or vice versa). We then allow the system to undergo relaxation for another waiting time; this relaxation process is referred to as “collapsing” (if α has been suddenly increased), or as “swelling” (if α has been suddenly decreased). Finally we reverse α to its initial value, thus establishing one “cycle”. After a third waiting time the resulting configuration is compared to the first configuration at the same α relaxed at the interface from its initial bulk state. If there is a significant difference in the extent of the configuration, the system is called hysteretic. The protocol is repeated several times leading to a “cycling process” which is composed of alternating “swelling” and “collapsing” processes. Appropriate averages are taken to ensure that the behavior does not suffer from peculiarities of the initial configuration.
= 0. We then relax the system for a long waiting time tw of typically 5 × 103τB. The relaxed configuration is – in the presence of the interface – subject to a sudden change in the attraction parameter α from 0 to 1.55 or, respectively from 1.55 to 0. Physically this means that the solvent quality temperature is abruptly changed from high to low (or vice versa). We then allow the system to undergo relaxation for another waiting time; this relaxation process is referred to as “collapsing” (if α has been suddenly increased), or as “swelling” (if α has been suddenly decreased). Finally we reverse α to its initial value, thus establishing one “cycle”. After a third waiting time the resulting configuration is compared to the first configuration at the same α relaxed at the interface from its initial bulk state. If there is a significant difference in the extent of the configuration, the system is called hysteretic. The protocol is repeated several times leading to a “cycling process” which is composed of alternating “swelling” and “collapsing” processes. Appropriate averages are taken to ensure that the behavior does not suffer from peculiarities of the initial configuration.
The diagnostics to identify hysteresis is done via monitoring the lateral radius of gyration, Rlat(t), as a function of time t. The lateral (or projected) radius of gyration is defined as
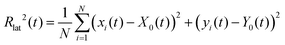 | (4) |
![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) i(t) = (x(t)),y(t),z(t)) as the location of the bead i, and
i(t) = (x(t)),y(t),z(t)) as the location of the bead i, and 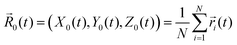 is the instantaneous center of the microgel particle. Finally, we can also infer the lateral osmotic pressure from the fraction of beads in the interfacial region. Here, by definition, a bead is in the interfacial region if its
is the instantaneous center of the microgel particle. Finally, we can also infer the lateral osmotic pressure from the fraction of beads in the interfacial region. Here, by definition, a bead is in the interfacial region if its ![[z with combining tilde]](https://www.rsc.org/images/entities/i_char_007a_0303.gif) -coordinate lies between −0.5σ and 0.5σ. We also analyze the internal core–corona structure in more detail by using a “hull parameter” Δ(r), which brings us also into a position to extract a core radius Rc and an outer corona radius. Details of the procedure are described in the ESI.†
-coordinate lies between −0.5σ and 0.5σ. We also analyze the internal core–corona structure in more detail by using a “hull parameter” Δ(r), which brings us also into a position to extract a core radius Rc and an outer corona radius. Details of the procedure are described in the ESI.†
2.1 Experiments
PNiPAm microgels crosslinked by N,N′-methylenebis(acrylamide) with different crosslinking densities are synthesized by precipitation polymerisation according to a previously published protocol.61 The cycling experiments involving the differently crosslinked microgels are conducted in a similar fashion as developed in an earlier publication.50 When starting from the collapsed state, 0.05 w% microgels dispersed in an ethanol/water mixture (1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1) with a temperature of 70 °C are spread at the air/water interface on a Langmuir–Blodgett trough (KSV Nima), which is preheated to the initial temperature of 60 °C. Similarly, when starting from the swollen state, the microgel dispersion is spread at room temperature. The trough is heated using a thermostat by increasing the temperature by 10 °C every 10 minutes. Conversely, the trough is passively cooled by switching off the thermostat. The interfacial arrangement as a function of temperature is then deposited onto a silicon wafer (0.5 × 10 cm2) lifted at 0.1 mm min−1 through the interface, while the corresponding surface pressure is measured using the Wilhelmy plate method. The microgels are characterized ex situ by image analysis of scanning electron microscopy (Zeiss Gemini 500) images of the transferred interfacial layer. From these images, the size of the microgel core is quantified by a custom-written Matlab software.50
1) with a temperature of 70 °C are spread at the air/water interface on a Langmuir–Blodgett trough (KSV Nima), which is preheated to the initial temperature of 60 °C. Similarly, when starting from the swollen state, the microgel dispersion is spread at room temperature. The trough is heated using a thermostat by increasing the temperature by 10 °C every 10 minutes. Conversely, the trough is passively cooled by switching off the thermostat. The interfacial arrangement as a function of temperature is then deposited onto a silicon wafer (0.5 × 10 cm2) lifted at 0.1 mm min−1 through the interface, while the corresponding surface pressure is measured using the Wilhelmy plate method. The microgels are characterized ex situ by image analysis of scanning electron microscopy (Zeiss Gemini 500) images of the transferred interfacial layer. From these images, the size of the microgel core is quantified by a custom-written Matlab software.50
3 Results and discussion
3.1 Non-hysteretic microgel swelling in the bulk
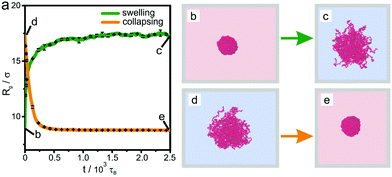
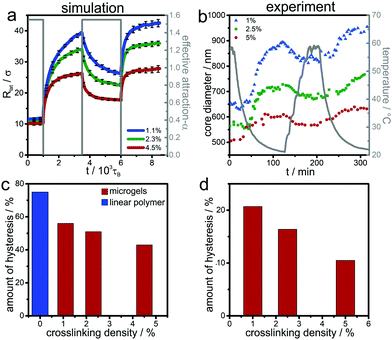
First, as a reference, we simulate the bulk behavior of a microgel. Fig. 2 shows the time evolution of the radius of gyration during swelling and collapsing together with typical initial and final simulation snapshots before and after the swelling and collapsing processes. The initial configurations (marked with (b) and (d)) are equilibrated for a long relaxation time of typically 5000τB, and are therefore practically fully relaxed. After a sudden increase (or decrease) of effective attraction α (mimicking an increase or decrease the temperature, respectively) the radius saturates quickly (i.e. within a relaxation time of roughly 1000τB) indicating equilibration. After a long relaxation for a simulation time of about 2500τB two final configurations marked with (c) and (e) in Fig. 2 are reached. These two final configurations (c) and (e) are similar to the initial conditions (d) and (b) in Fig. 2, i.e. both swollen and both collapsed configurations exhibit a similar radius of gyration. Importantly, this implies that swelling and subsequent collapsing are completely reversible in this bulk experiment on the accessible time scale of the simulation, or in other terms, there is no hysteresis. This non-hysteretic bulk behavior in size is in agreement with experiments.22 Once the reversible behavior of the volume phase transition is established, one can trivially add a cycle of subsequent swelling and collapsing processes, which always results in an equilibrated state. Likewise, one can perform a multi-cycle process by adding many subsequent swelling and collapsing processes. Again one finds reversible behavior such that after each cycling process the system is in the same equilibrated state. The latter feature will change significantly at interfaces which we shall show next.3.2 Liquid interface-induced hysteresis of microgel morphology
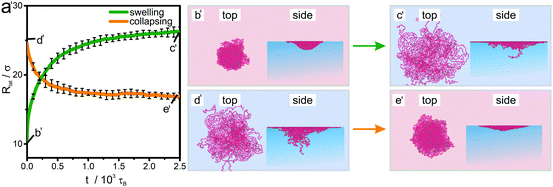
The hysteretic behavior found for the volume phase transition at the interface in the collapsing process is in contrast to the swelling process where the swollen end state (c′) practically exhibits the same lateral radius of gyration as the initial state (d′) of a microgel adsorbed to the interface from a swollen bulk conformation. The clue to understand this difference lies in the nature of the starting state (b′). In the collapsed state at the interface, the equilibration is kinetically hindered by the strong attractive interactions between the beads. Therefore we hypothesize that they are kinetically trapped since they cannot escape quickly to relax all constraints. If a swelling process is induced by improving the solvent quality, these constraints are released and the microgel relaxes faster to its equilibrium state. Again we emphasize that the allotted relaxation time at the interface for the collapsed state is long as compared to the typical time for swelling and collapsing in the simulation but not enough to achieve full equilibration. This “explosion” in relaxation time scales for interfacially collapsed states is in accordance with the experimental findings in literature.50,52,63 Since the bead interactions are not affected by the interface, some parts of the polymer chains move back into the bulk as the attraction decreases which is probably due to the simplified assumption that the bead–bead interactions is the same in the interface and in the bulk. In the experiments typically a more complex relationship is encountered.50
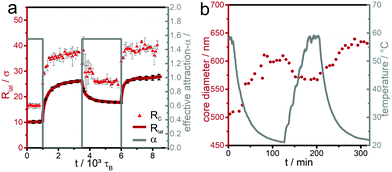
The hysteretic behavior is reflected in the two length scales characterizing the microgel particle, namely the lateral radius of gyration Rlat and the core radius Rc as documented in Fig. 4a. Indeed our analysis of the morphology by the hull parameter Δ(r) (Fig. S2, ESI†) reveals a clear distinction between core and corona for the different states in the cycling process and documents that our simulation scheme reproduces the fried-egg structure of a microgel at the interface.1,2,47–49 The core region is much more compressed due to the interfacial attraction to the beads. Therefore the effect of kinetic arrest in the core is much more amplified when the particle is brought to the interface as compared to the bulk situation. This gives a clue to understand the underlying reason for the hysteretic behavior at the interface.
We compare the hysteresis observed in simulation with experimental data, obtained for an interfacial assembly of microgels on the air/water interface of a Langmuir trough exposed to changes in the temperature of the water subphase. The diameter of the microgel cores are quantified by image analysis of scanning electron microscopy images after transfer to a solid substrate. Interestingly, the experimental data shows a similar hysteretic behavior, evidenced by a change in core diameter between the initial adsorption in collapsed state and the first temperature cycling as seen in Fig. 4b. However, in the experiments the change of solvent quality (temperature) is not stepwise but smoothened due to experimental constraints (compare the gray line in Fig. 4b to the sharp jump of the effective attraction α shown along with the simulation data in Fig. 4a). Simulations with a multiple stepwise change in effective attraction α have also been performed and are compared with the sudden stepwise change for a crosslinking density of 2.3%, see Fig. S1 ESI.† In this comparison, no significant difference in hysteresis was found for the two different forms of change.
3.3 Impact of the degree of crosslinking
![[scr R, script letter R]](https://www.rsc.org/images/entities/char_e531.gif) , where
, where ![[scr R, script letter R]](https://www.rsc.org/images/entities/char_e531.gif) is the ratio between the two microgel radii before and after the first cycling process. For the simulations, the ratio
is the ratio between the two microgel radii before and after the first cycling process. For the simulations, the ratio ![[scr R, script letter R]](https://www.rsc.org/images/entities/char_e531.gif) is taken as Rlat (t = 1000τB)/Rlat (t = 6000τB), see Fig. 5a, and for the experiments we take for
is taken as Rlat (t = 1000τB)/Rlat (t = 6000τB), see Fig. 5a, and for the experiments we take for ![[scr R, script letter R]](https://www.rsc.org/images/entities/char_e531.gif) the ratio of the two radii at times 210 min and 0 min, see Fig. 5b. In the absence of hysteresis, the two radii coincide such that
the ratio of the two radii at times 210 min and 0 min, see Fig. 5b. In the absence of hysteresis, the two radii coincide such that ![[scr R, script letter R]](https://www.rsc.org/images/entities/char_e531.gif) is one and the amount of hysteresis vanishes.
is one and the amount of hysteresis vanishes.
Both experimental and simulation data show that the relative amount of hysteresis decreases with increasing crosslinking density (Fig. 5c and d). We rationalize this behavior based on an intuitive argument stemming from the kinetics of the initially trapped state. For a more connected polymer network the microgel is more resistant against the stretching effect of the interface and therefore it is stretched out less. This explains why the hysteresis is smaller for higher crosslinking density. Conversely, if the degree of crosslinking is small, long dangling chains can be much more entangled and therefore contribute much more to the amount of hysteresis. Indeed in the extreme case of a single linear chain, additional simulation and experimental data indicate that the relative amount of hysteresis is even higher than the values found for the lowest crosslinking density of one percent; for simulation data see again Fig. 5c. The number of beads in the simulation of the linear chain is identical to that contained in the microgel particle, namely 5500 beads.
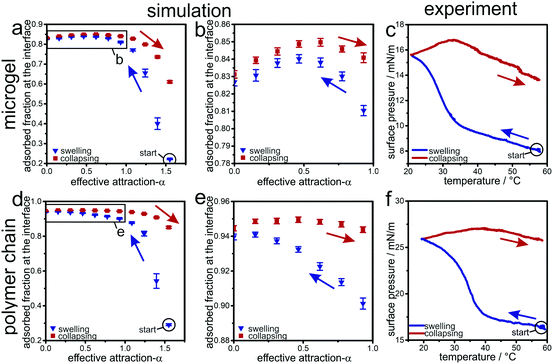
In the experimental system, the decrease in surface tension in the presence of microgels (or, the increase in surface pressure) relates to the surface density of PNiPAm chains adsorbed to the air/water interface. In simulations, the corresponding quantity is the surface density of adsorbed beads, which is directly accessible. Fig. 6a and c compares the evolution of the adsorbed microgel fraction determined in simulation with the surface pressure measured in experiment as a function of the effective attraction α or the temperature, respectively. The data are obtained by starting with an interfacially adsorbed microgel with high effective attractions α resp. high temperature T (solid points). This initially collapsed microgel is then slowly swollen at the interface by a decrease the attraction (resp. temperature), as shown by blue points/blue line. The swelling increases the area occupied by the microgel (see above), and thus decreases the surface tension – or increases the surface pressure in experiment (Fig. 6c). Concomitantly, the swelling causes more beads to adsorb to the interface as the system passes through the volume phase transition (Fig. 6a and b).
Notably, the maximal number of adsorbed beads occurs closely at α ≈ 0.6 where the bulk collapse transition happens23,25 and is thus correlated to the bulk volume transition. Interestingly, in the simulation data, a slight decrease of the adsorbed beads is absorbed when the attraction vanishes. This is due to the fact that parts of the chains go back into the bulk due to entropic reasons. The swollen microgels are subsequently collapsed (or heated) again. The red data points/red line in Fig. 6a–c show the associated evolution of the adsorbed fraction of microgel beads (simulations) and surface pressure (experiments), respectively. In both experiment and simulation, a hysteresis is observed, in agreement with the data shown before. The fraction of adsorbed beads and the surface pressure increases for this increase in α or temperature, compared to the initial values at low temperature culminating in a maximum at a temperature which roughly coincides with the bulk volume transition. We interpret this maximum as a joint effect of the interfacial attraction to the beads and the effective attraction between the beads. When the bulk volume transition temperature is reached from below, the bulk attraction wins and drags beads from the interface into the bulk. We remark that upon cooling a similar maximum is found in the simulations but not in the experiments; the reason for this slight discrepancy remains unclear.
Finally, as a reference, we also show data for a linear polymer chain in Fig. 6d–f. The linear chain shows similar trends in the surface pressure and the fraction of the adsorbed monomers as the microgel, but there is no maximum in the adsorbed bead fraction during the swelling process. Thus the curves coincide nicely.
4 Conclusions
We used monomer-resolved computer simulations and air/water-interfacial experiments to investigate the volume phase transition of PNiPAm microgels in bulk and adsorbed to an interface. Our results underline that the presence of an interface significantly changes the volume phase transition. Particularly, we found a significant hysteretic behavior for microgels undergoing the phase transition at the interface. A microgel adsorbed in the collapsed state to the interface does not return to its initial configuration when subjected to a temperature cycle. Instead, it relaxes into a more stretched configuration. An initially swollen microgel, however, undergoes reversible transitions between collapsed and swollen states upon temperature cycling. We therefore attribute the hysteresis effect of the collapsed microgel at the interface to a kinetically trapped initial state which can be released by swelling the microgel. Essentially the same results can also be observed for an oil–water interface.50,52 We find that the hysteresis is more pronounced for weaker degree of crosslinking and is even observed for linear PNiPAm chains.Our results demonstrate that it is possible to model complex polymer-interface phenomena via a comparably simple model that balances internal and interfacial attractions. This modelling approach may therefore also be transferred to other stimuli-responsive polymer systems, curved interfaces, or more crowded systems formed by multiple, overlapping interfacial microgels.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
N. V., H. L. and L. M. C. J. acknowledge funding from the Deutsche Forschungsgemeinschaft (DFG) under grant numbers VO 1824/8-1 and LO 418/22-1, respectively. N. V. also acknowledges support by the Interdisciplinary Center for Functional Particle Systems (FPS). J. K. thanks Jens Grauer for helpful discussions.Notes and references
- K. Geisel, L. Isa and W. Richtering, Langmuir, 2012, 28, 15770–15776 CrossRef CAS PubMed.
- M. Rey, M. A. Fernandez-Rodriguez, M. Karg, L. Isa and N. Vogel, Acc. Chem. Res., 2020, 53, 414–424, DOI:10.1021/acs.accounts.9b00528.
- R. Pelton, Adv. Colloid Interface Sci., 2000, 85, 1–33, DOI:10.1016/S0001-8686(99)00023-8.
- M. Karg, A. Pich, T. Hellweg, T. Hoare, L. A. Lyon, J. J. Crassous, D. Suzuki, R. A. Gumerov, S. Schneider, I. I. Potemkin and W. Richtering, Langmuir, 2019, 35, 6231–6255 CrossRef CAS PubMed.
- R. Keidel, A. Ghavami, D. M. Lugo, G. Lotze, O. Virtanen, P. Beumers, J. S. Pedersen, A. Bardow, R. G. Winkler and W. Richtering, Sci. Adv., 2018, 4, eaao7086, DOI:10.1126/sciadv.aao7086.
- Z. Li and T. Ngai, Nanoscale, 2013, 5, 1399–1410 RSC.
- T. Ngai, S. H. Behrens and H. Auweter, Chem. Commun., 2005, 331–333, 10.1039/B412330A.
- V. Schmitt and V. Ravaine, Curr. Opin. Colloid Interface Sci., 2013, 18, 532–541 CrossRef CAS.
- M. A. Fernandez-Rodriguez, A. Martín-Molina and J. Maldonado-Valderrama, Adv. Colloid Interface Sci., 2021, 288, 102350, DOI:10.1016/j.cis.2020.102350.
- M.-C. Tatry, P. Galanopoulo, L. Waldmann, V. Lapeyre, P. Garrigue, V. Schmitt and V. Ravaine, J. Colloid Interface Sci., 2021, 589, 96–109 CrossRef CAS PubMed.
- D. Klinger and K. Landfester, Polymer, 2012, 53, 5209–5231 CrossRef CAS.
- F. Wang, Z. Zheng, Y. Peng, Y. Han and Z. Wang, Science, 2012, 338, 87–90 CrossRef PubMed.
- A. M. Alsayed, M. F. Islam, J. Zhang, P. J. Collings and A. G. Yodh, Science, 2005, 309, 1207–1210 CrossRef CAS PubMed.
- Y. Peng, F. Wang, Z. Wang, A. M. Alsayed, Z. Zhang, A. G. Yodh and Y. Han, Nat. Mater., 2015, 14, 101–108 CrossRef CAS PubMed.
- F. Grillo, M. A. Fernandez-Rodriguez, M. N. Antonopoulou, D. Gerber and L. Isa, Nature, 2020, 582, 219–224 CrossRef CAS PubMed.
- S. Ciarella, M. Rey, J. Harrer, N. Holstein, M. Ickler, H. Löwen, N. Vogel and L. M. C. Janssen, 2020, arXiv preprint arXiv:2008.13695.
- K. Volk, F. Deißenbeck, S. Mandal, H. Löwen and M. Karg, Phys. Chem. Chem. Phys., 2019, 21, 19153–19162 RSC.
- L. T. Lee, B. Jean and A. Menelle, Langmuir, 1999, 15, 3267–3272 CrossRef CAS.
- H. Senff and W. Richtering, J. Chem. Phys., 1999, 111, 1705–1711 CrossRef CAS.
- K. Shiraga, H. Naito, T. Suzuki, N. Kondo and Y. Ogawa, J. Phys. Chem. B, 2015, 119, 5576–5587 CrossRef CAS PubMed.
- G. M. Conley, S. Nöjd, M. Braibanti, P. Schurtenberger and F. Scheffold, Colloids Surf., A, 2016, 499, 18–23 CrossRef CAS.
- K. Kratz, T. Hellweg and W. Eimer, Polymer, 2001, 42, 6631–6639 CrossRef CAS.
- L. Rovigatti, N. Gnan and E. Zaccarelli, J. Phys.: Condens. Matter, 2017, 30, 044001 CrossRef PubMed.
- F. Camerin, N. Gnan, L. Rovigatti and E. Zaccarelli, Sci. Rep., 2018, 8, 14426–14438, DOI:10.1038/s41598-018-32642-5.
- N. Gnan, L. Rovigatti, M. Bergman and E. Zaccarelli, Macromolecules, 2017, 50, 8777–8786 CrossRef CAS PubMed.
- G. Del Monte, A. Ninarello, F. Camerin, L. Rovigatti, N. Gnan and E. Zaccarelli, Soft Matter, 2019, 15, 8113–8128 RSC.
- A. J. Moreno and F. L. Verso, Soft Matter, 2018, 14, 7083–7096 RSC.
- T. J. Weyer and A. R. Denton, Soft Matter, 2018, 14, 4530–4540 RSC.
- M. Quesada-Pérez, J. Ramos, J. Forcada and A. Martn-Molina, J. Chem. Phys., 2012, 136, 244903 CrossRef PubMed.
- M. Brugnoni, A. Scotti, A. A. Rudov, A. P. Gelissen, T. Caumanns, A. Radulescu, T. Eckert, A. Pich, I. I. Potemkin and W. Richtering, Macromolecules, 2018, 51, 2662–2671 CrossRef CAS.
- A. Scotti, A. R. Denton, M. Brugnoni, J. E. Houston, R. Schweins, I. I. Potemkin and W. Richtering, Macromolecules, 2019, 52, 3995–4007 CrossRef CAS.
- S. Nikolov, A. Fernandez-Nieves and A. Alexeev, Appl. Math. Mech., 2018, 39, 47–62 CrossRef.
- A. R. Denton and Q. Tang, J. Chem. Phys., 2016, 145, 164901 CrossRef PubMed.
- M. M. Hedrick, J. K. Chung and A. R. Denton, J. Chem. Phys., 2015, 142, 034904 CrossRef PubMed.
- G. Giupponi, D. M. A. Buzza and D. B. Adolf, Macromolecules, 2007, 40, 5959–5965 CrossRef CAS.
- Y. Hertle, M. Zeiser, C. Hasenöhrl, P. Busch and T. Hellweg, Colloid Polym. Sci., 2010, 288, 1047–1059 CrossRef CAS.
- C. G. Lopez and W. Richtering, Soft Matter, 2017, 13, 8271–8280 RSC.
- D. Zhi, Y. Huang, X. Han, H. Liu and Y. Hu, Chem. Eng. Sci., 2010, 65, 3223–3230 CrossRef CAS.
- W. Toh, T. Y. Ng, J. Hu and Z. Liu, Int. J. Solids Struct., 2014, 51, 4440–4451 CrossRef CAS.
- U. Baul and J. Dzubiella, 2020, arXiv preprint arXiv:2011.03398.
- Y. C. Lin, B. Rotenberg and J. Dzubiella, Phys. Rev. E, 2020, 102, 42602 CrossRef CAS PubMed.
- A. Moncho-Jordá and J. Dzubiella, Phys. Chem. Chem. Phys., 2016, 18, 5372–5385 RSC.
- G. Giupponi and D. Buzza, J. Chem. Phys., 2004, 120, 10290–10298 CrossRef CAS PubMed.
- Surface Tension of Water from Dortmund Data Bank, http://www.ddbst.com/en/EED/PCP/SFT{_}C174.php.
- E. S. A. Goerlitzer, R. Mohammadi, S. Nechayev, K. Volk, M. Rey, P. Banzer, M. Karg and N. Vogel, Adv. Mater., 2020, 32, 2070173, DOI:10.1002/adma.202070173.
- B. M. Rey, R. Elnathan, R. Ditcovski, K. Geisel, M. Zanini, M. A. Fernandez-Rodriguez, V. V. Naik, A. Frutiger, W. Richtering, T. Ellenbogen, N. H. Voelcker and L. Isa, Nano Lett., 2016, 16, 157–163, DOI:10.1021/acs.nanolett.5b03414.
- R. W. Style, L. Isa and E. R. Dufresne, Soft Matter, 2015, 11, 7412–7419 RSC.
- H. Mehrabian, J. Harting and J. H. Snoeijer, Soft Matter, 2016, 12, 1062–1073 RSC.
- K. Zielińska, H. Sun, R. A. Campbell, A. Zarbakhsh and M. Resmini, Nanoscale, 2016, 8, 4951–4960 RSC.
- J. Harrer, M. Rey, S. Ciarella, H. Löwen, L. M. Janssen and N. Vogel, Langmuir, 2019, 35, 10512–10521 CrossRef CAS PubMed.
- S. Bochenek, A. Scotti, W. Ogieglo, M. Á. Fernández-Rodríguez, M. F. Schulte, R. A. Gumerov, N. V. Bushuev, I. I. Potemkin, M. Wessling, L. Isa and W. Richtering, Langmuir, 2019, 35, 16780–16792 CrossRef CAS PubMed.
- S. Bochenek, A. Scotti and W. Richtering, Soft Matter, 2021, 17, 976–988, 10.1039/D0SM01774D.
- Z. Li, W. Richtering and T. Ngai, Soft Matter, 2014, 10, 6182–6191 RSC.
- F. Camerin, N. Gnan, J. Ruiz-Franco, A. Ninarello, L. Rovigatti and E. Zaccarelli, Phys. Rev. X, 2020, 10, 031012 CAS.
- F. Camerin, M. A. Fernandez-Rodrguez, L. Rovigatti, M.-N. Antonopoulou, N. Gnan, A. Ninarello, L. Isa and E. Zaccarelli, ACS Nano, 2019, 13, 4548–4559 CrossRef CAS.
- M. J. Bergman, N. Gnan, M. Obiols-Rabasa, J.-M. Meijer, L. Rovigatti, E. Zaccarelli and P. Schurtenberger, Nat. Commun., 2018, 9, 5039–5050, DOI:10.1038/s41467-018-07332-5.
- L. Rovigatti, N. Gnan, A. Ninarello and E. Zaccarelli, Macromolecules, 2019, 52, 4895–4906 CrossRef CAS.
- T. Soddemann, B. Dünweg and K. Kremer, Eur. Phys. J. E: Soft Matter Biol. Phys., 2001, 6, 409–419 CrossRef CAS.
- J. A. Anderson, J. Glaser and S. C. Glotzer, Comput. Mater. Sci., 2020, 173, 109363 CrossRef CAS.
- A. Stukowski, Modell. Simul. Mater. Sci. Eng., 2009, 18, 015012 CrossRef.
- M. Rey, X. Hou, J. S. J. Tang and N. Vogel, Soft Matter, 2017, 13, 8717–8727 RSC.
- K. Geisel, L. Isa and W. Richtering, Langmuir, 2012, 28, 15770–15776 CrossRef CAS PubMed.
- M. F. Schulte, A. Scotti, M. Brugnoni, S. Bochenek, A. Mourran and W. Richtering, Langmuir, 2019, 35, 14769–14781 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/d1sm00111f |
| This journal is © The Royal Society of Chemistry 2021 |