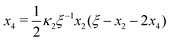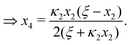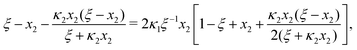DOI:
10.1039/D1SM00070E
(Paper)
Soft Matter, 2021,
17, 5375-5383
Divalent ligand-monovalent molecule binding
Received
14th January 2021
, Accepted 23rd April 2021
First published on 26th April 2021
Abstract
Simultaneous binding of a divalent ligand to two identical monovalent molecules is a widespread phenomenon in biology and chemistry. Here, we describe how two such monovalent molecules B bind to a divalent ligand AA to form the intermediate and final complexes AA·B and AA·B2. Cases wherein the total concentration [AA]T is either much larger or much smaller than the total concentration [B]T have been studied earlier, but a systematic description of comparable concentrations [AA]T and [B]T is missing. Here, we present numerical and analytical results for the concentrations [AA·B] and [AA·B2] for the entire range 0 < [B]T/[AA]T < ∞. Specifically, we theoretically study three types of experimental procedures: dilution of AA and B at fixed [B]T/[AA]T, addition of AA at fixed [B]T, and addition of B at fixed [AA]T. When [AA]T and [B]T are comparable, the concentrations of free ligands and molecules both decrease upon binding. Such depletion is expected to be important in cellular contexts, e.g., in antigen detection and in coincidence detection of proteins or lipids.
1 Introduction
Chemical binding is at the heart of many processes in biology, including oxygen binding to haemoglobin, self assembly, antibodies binding to antigens, and growth factors binding to their transmembrane receptors.1–7 In many cases, binding interactions should be specific and strong, yet reversible.8–11 One way to accomplish such a “molecular velcro” is through ligands containing many ligating units per molecule: Multivalent ligands are known to bind some transmembrane receptors more readily than their monovalent counterparts (with one binding site per ligand).8 This makes multivalent ligands interesting in clinical applications, where less therapeutic cargo is needed for the same response. The intuitive explanation why multivalent ligands can bind more readily to some receptors on a plasma membrane or a viral envelope goes as follows. After the binding of a first ligating unit with association constant K1, other ligating units of a multivalent ligand are close to other membrane-bound receptors as well. Around a first bound unit, a second ligating unit is thought to sweep out a semi circle with a radius set by the (fixed) distance between ligating units.12–15 As this distance is a few nanometers at most, the effective concentration of ligating units belonging to a partly-bound multivalent ligand is much higher than the concentration of unbound ligands nearby. More generally, for flexible rather than stiff linkers between ligating units,16,17 effective concentrations can be determined rigorously within statistical mechanics.18,19
In turn, high effective concentrations are reflected in a high association constant K2 for binding a second ligating unit of a multivalent ligand, and the same for further binding steps. Systems for which K2/K1 > 1 are called cooperative.20–23 In the above example of large effective concentrations, one speaks of apparent cooperativity. This is to distinguish it from true cooperativity based on allostery,24 which refers to binding pockets whose binding affinity changes when nearby pockets are occupied, as happens for the binding of oxygen to haemoglobin.25 In either way, the hallmark of cooperativity is the switching from mostly-unbound to mostly-bound ligands over a narrow concentration range.20
Equations for the concentrations of molecules involved in binding reactions are typically nonlinear and with a high polynomial order. In two simple cases—the binding of a monovalent ligand to a monovalent receptor1,3 and the binding of two different monovalent ligands to one type of monovalent protein26—the concentrations of all involved species can be expressed analytically nonetheless. For more complicated reactions, analytical progress is often only possible if one molecular species is assumed to be in excess as compared to other species.20,27 This limit is only appropriate to certain systems and experiments. If no molecular species is in excess as compared to the other present in the system, the full reaction-rate equations should be solved, and binding will deplete the unbound species.
In this article we explore the interplay between multivalency, cooperativity, and depletion. We do so by discussing the reversible binding of a divalent ligand AA to two identical monovalent molecules B [Fig. 1(a)],
| | | AA + 2B ⇌ AA·B + B ⇌ AA·B2, | (1) |
as it is the simplest binding reaction that can display nontrivial effects of multivalency and cooperativity.
20,21,23Eqn (1) also has value in its own right: It captures hormone action,
28 the binding of divalent antibodies to antigens on pathogens,
12,13,27,29–32 and it was realised in synthetic systems.
16 In many biological systems to which
eqn (1) may be relevant, B may represent a protein or a cell membrane receptor. Yet, to keep our discussion completely general, we refer to B simply by “molecule”. We denote the total volumetric concentration of ligands AA and molecules B—both bound and unbound—by [AA]
T and [B]
T. Most prior works studied the reaction in
eqn (1) assuming either [AA]
T ≪ [B]
T or [AA]
T ≫ [B]
T [
Fig. 1(b)]. For instance, Hunter and Anderson
20 asserted that the concentration of monovalent molecules is hardly affected ([B] ≈ [B]
T) by the reaction in
eqn (1) if it happens at [AA]
T ≪ [B]
T; Perelson and DeLisi
27 asserted that the concentration of divalent ligands is hardly affected ([AA] ≈ [AA]
T) by the reaction in
eqn (1) if it happens at [AA]
T ≫ [B]
T. As we move away from these limits, neither [AA] ≈ [AA]
T nor [B] ≈ [B]
T can hold as the reaction in
eqn (1) will deplete both the free ligands AA and the molecules B. Here, we study the binding of divalent ligands AA to monovalent molecules B over the complete range 0 < [B]
T/[AA]
T < ∞.
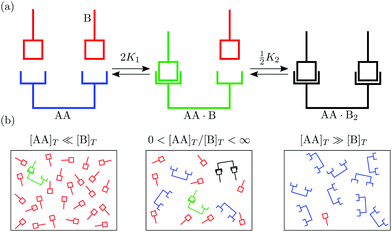 |
| | Fig. 1 (a) Binding of two monovalent molecules B to a divalent ligand AA, to form the complexes AA·B and AA·B2. (b) Different relative concentrations of [AA]T and [B]T. | |
2 Model
The reaction in eqn (1) does not affect the total number of AA and B molecules, which gives the following particle-conservation constraints| | | [AA]T = [AA] + [AA·B] + [AA·B2], | (2a) |
| | | [B]T = [B] + [AA·B] + 2[AA·B2]. | (2b) |
In Appendix A we show how the reaction-rate equations associated with eqn (1) reduce at steady state to| | 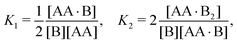 | (3) |
where K1 and K2 are the association constants, and where factors of 1/2 and 2 account for the degeneracy of the intermediate complex AA·B. While ref. 13, 20, 21 and 30 used the same convention, ref. 27 absorbed the factor 1/2 into K1, and ref. 29 and 32 absorbed the factors 1/2 and 2 into K1 and K2.
To model divalent antibody binding to monovalent surface-bound antigens, ref. 12 and 13 expressed concentrations of antigens and (partly) bound complexes in numbers per unit area.13,29 Yet, the governing equations of ref. 13 and 29 could also be cast into the form of eqn (2) and (3), that is, with volumetric concentrations only, and the effect of reduced positional freedom of surface-bound molecules absorbed into the constants K1 and K2. Hence, though volumetric concentrations appear in our eqn (2) and (3), this set of equations can just as well describe a binding process wherein either AA or B is confined to a thin (membrane) surface (see also page 13 of ref. 1). Still, an assumption underlying the derivation of eqn (3) in terms of concentrations is that all species are well mixed. This assumption may be violated for certain types of B molecules, for instance, receptors that cluster at the plasma membrane.33,34
From the four expressions in eqn (2) and (3) we can determine the four unknown concentrations [AA], [B], [AA·B], and [AA·B2] in terms of the four physical parameters K1, K2, [AA]T, and [B]T. First, we eliminate [AA] and [B] from eqn (3) with eqn (2),
| | | [AA·B] = 2K1([B]T − [AA·B] − 2[AA·B2]) × ([AA]T − [AA·B] − [AA·B2]), | (4a) |
| | 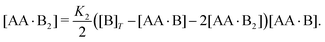 | (4b) |
Next, we rewrite
eqn (4b) to
| | 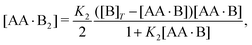 | (5) |
with which we eliminate [AA·B
2] from
eqn (4a),
| a[AA·B]3 + b[AA·B]2 + c[AA·B] + d = 0, |
| b ≡ 2(K1 − K2 − [AA]TK1K2), |
| c ≡ 2K1[AA]T(K2[B]T − 1) − 2K1[B]T − K1K2[B]T2− 1, |
The cubic
eqn (6) for [AA·B] can be solved analytically with Cardano's formula. Unfortunately, its solution for general
K1,
K2, [AA]
T, and [B]
T, presented in Appendix B, is too cumbersome to be of use. We therefore also present analytical solutions to
eqn (5) and (6) for specific (limiting) values of
K1,
K2, [AA]
T, and [B]
T in Appendices C–E. First, Appendix C covers the case
K2 =
K1. The cubic term in
eqn (6) then vanishes, leaving behind a quadratic equation that can be easily solved analytically for [AA·B] [see
eqn (C2a)]. Also [AA·B
2] and the “occupancy”
20θ ≡ ([AA·B]/2 + [AA·B
2])/[AA]
T are governed by simple expressions [see eqn (C4)]. Intuitively, for
K2 =
K1, each divalent ligand AA acts as two independent monovalent ligands A binding to two molecules B:
θ coincides with a literature expression
3 for the concentration of bound A·B at a molecule-to-ligand ratio [B]
T/(2[A]
T). Second, Appendix D covers the case [AA]
T ≪ [B]
T. We rederive Hunter and Anderson's results
20 for [AA·B] and [AA·B
2] and show that they contain errors of order
![[scr O, script letter O]](https://www.rsc.org/images/entities/char_e52e.gif)
([AA]
T/[B]
T). Last, Appendix E covers the case [AA]
T ≫ [B]
T. For this case, we solve
eqn (6) with a power series approximation to [AA·B]. Our solutions to [AA·B] and [AA·B
2] differ from Perelson and DeLisi's results
27 from
![[scr O, script letter O]](https://www.rsc.org/images/entities/char_e52e.gif)
([B]
T3/[AA]
T3) onwards.
While in eqn (6) we isolated [AA·B] from eqn (2) and (3), we could have also chosen to isolate [B] instead. Indeed, cubic equations for [B] were reported in eqn (S) of ref. 13 and eqn (25) of ref. 29 [which we rederive in Appendix F]. However, neither of those articles discussed the dependence of [AA·B] and [AA·B2] on K1, K2, [AA]T, and [B]T in as much detail as we do below.
3 Results
We present numerical results for [AA·B] and [AA·B2] from eqn (5) and (6) for different choices of fixed and varied K1, K2, [AA]T, and [B]T. Specifically, we mimic a dilution experiment, wherein we vary [AA]T and [B]T at fixed [B]T/[AA]T; a titration-like experiment, wherein we vary [AA]T at fixed [B]T; and another titration-like experiment, wherein we vary [B]T at fixed [AA]T. While the concentrations [AA]T and [B]T can be experimentally varied over decades, K1 and K2 are set by fixed molecular properties.18,19 Accordingly, we mostly consider different but fixed values of the “cooperativity parameter” α = K2/K1. α is related to the free energy of interaction between sites, see eqn (10) of ref. 20. We reinforce our numerical solutions of eqn (5) and (6) by the aforementioned analytical expressions for specific parameter values [see Appendices C–E].
3.1 Diluting a solution of AA and B at fixed [B]T/[AA]T
We consider a solution with initial concentrations [AA]T and [B]T to which solvent is added. In such a dilution experiment, [AA]T and [B]T decrease at fixed [B]T/[AA]T, K1, and K2. Fig. 2 shows numerical results for [AA·B]/[AA]T (a) and [AA·B2]/[AA]T (b) as a function of K1[B]T, for several [B]T/[AA]T and K2 = K1. First, we see that the numerical solutions for [B]T/[AA]T = 100 (yellow triangles and lines) are close to Hunter and Anderson's predictions [eqn (D1) and (D2)], indicated by thick grey solid lines. For [B]T/[AA]T = 100 and K1[B]T = 103, we evaluated that [B] = 0.98[B]T; hence, the assumption [B] = [B]T of ref. 20 is satisfied to a high degree at this [B]T/[AA]T value. Second, the numerical results for [B]T/[AA]T = 0.2 (purple diamonds) are close to Perelson and DeLisi's predictions eqn (E4) and (E5) (purple dashed lines). Yet, we observe tiny differences between the numerical predictions and eqn (E4) around K1[B]T = 1 in panel (a). This observation reinforces our analytical insight of Appendix E, namely, that eqn (E4) and (E5) contain errors of ![[scr O, script letter O]](https://www.rsc.org/images/entities/char_e52e.gif) ([B]T3/[AA]T3). For [B]T/[AA]T = 0.2 and K1[B]T = 103, we evaluated that [AA] = 0.81[AA]T; hence, the assumption [AA] = [AA]T of ref. 27 is satisfied to some extend at this [B]T/[AA]T value. Comparing to our earlier evaluation of [B] at [B]T/[AA]T = 100, we see that, as anticipated in the introduction, the closer [B]T/[AA]T is to unity, the stronger the unbound species are depleted. Third, a salient feature of the curves in Fig. 2(a) are the plateaus for K1[B]T ≫ 1 and [B]T ≈ [AA]T. As we derive in Appendix C [specifically, eqn (C3)], their height is set by
([B]T3/[AA]T3). For [B]T/[AA]T = 0.2 and K1[B]T = 103, we evaluated that [AA] = 0.81[AA]T; hence, the assumption [AA] = [AA]T of ref. 27 is satisfied to some extend at this [B]T/[AA]T value. Comparing to our earlier evaluation of [B] at [B]T/[AA]T = 100, we see that, as anticipated in the introduction, the closer [B]T/[AA]T is to unity, the stronger the unbound species are depleted. Third, a salient feature of the curves in Fig. 2(a) are the plateaus for K1[B]T ≫ 1 and [B]T ≈ [AA]T. As we derive in Appendix C [specifically, eqn (C3)], their height is set by| | 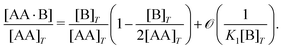 | (7) |
We indicate the predictions from eqn (7) with crosses in Fig. 2(a). The plateau height in Fig. 2(a) is maximal for [B]T = [AA]T, as also follows from eqn (7). Fourth, note that [AA·B] cannot exceed the total concentrations of its constituents [AA]T and [B]T; hence, 0 < [AA·B]/[AA]T < min(1,[B]T/[AA]T). Likewise, for [AA·B2], we find that 0 < [AA·B2]/[AA]T < min(1,[B]T/(2[AA]T)). The data in Fig. 2 satisfies these constraints.
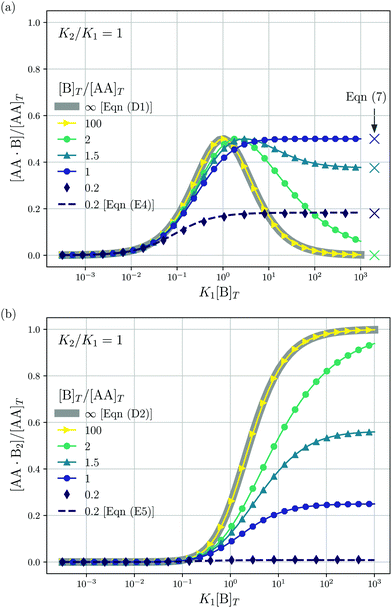 |
| | Fig. 2 Theoretical predictions for a dilution experiment, wherein [AA]T and [B]T vary at fixed [B]T/[AA]T, K1, and K2. We show [AA·B]/[AA]T (a), [AA·B2]/[AA]T (b) as a function of K1[B]T for K2/K1 = 1 and [B]T/[AA]T = 0.2,1,1.5,2.0 and 100. Also shown are approximations to [AA·B]/[AA]T and [AA·B2]/[AA]T for [B]T ≫ [AA]T [eqn (D1) and (D2)] and for [B]T ≪ [AA]T [eqn (E4) and (E5)]. Panel (a) shows the analytical predictions from eqn (7) for K1[B]T ≫ 1 with crosses. | |
Fig. 3 shows the occupancy θ for K2/K1 = 1 (a) and K2/K1 = 100 (b) and other parameters as in Fig. 2. For [B]T/[AA]T = 100, we again observe good agreement between Hunter and Anderson's expression [eqn (D3)] and the numerical data for θ, both for K2/K1 = 1 and K2/K1 = 100. Next, we see that increasing the cooperativity parameter K2/K1 shifts θ curves to smaller K1[B]T values and that θ switches from θ ≈ 0 to θ ≈ 1 over a narrower K1[B]T range—the hallmark of cooperativity. To characterise the slope of θ, we numerically determined the Hill coefficient
| | 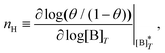 | (8) |
where
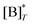
is the molecular concentration at half occupancy,
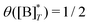
.
Fig. 3(c) shows the
K2/
K1 dependence of
nH for several [B]
T/[AA]
T. As such,
Fig. 3(c) generalises Fig. 6 of
ref. 20, where [B]
T ≫ [AA]
T was considered. In that case,
nH is given by
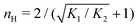
[
cf.eqn (D4)], indicated in
Fig. 3(c) with a thick grey solid line. We see that, for [B]
T/[AA]
T = 100, the numerically determined
nH is close to predictions from
eqn (D4). Conversely, we see that
nH → 0 for [B]
T/[AA]
T → 1.
Fig. 4(a) and (b) show that half occupancy (
θ = 1/2) is not reached if [B]
T/[AA]
T < 1; hence,
nH is undetermined for [B]
T/[AA]
T < 1. The symbols in
Fig. 3(c) for
K2 =
K1 represent the analytical expression
eqn (C8). These symbols match perfectly to the numerical
nH predictions.
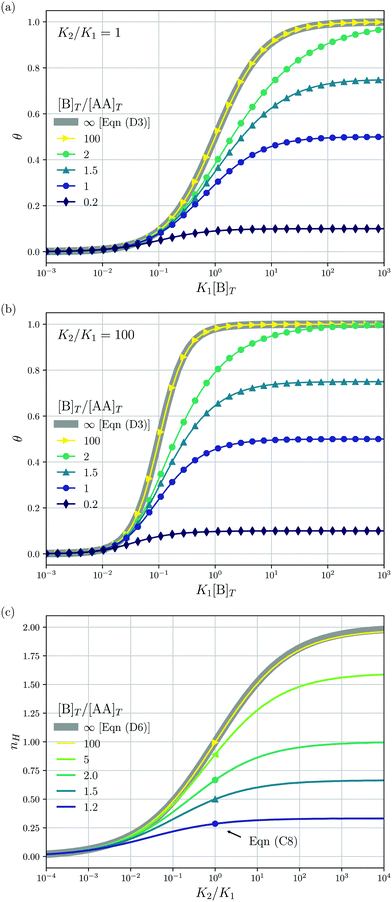 |
| | Fig. 3 The occupancy θ for K2/K1 = 1 (a) and K2/K1 = 100 (b) and other parameters as in Fig. 2. Panel (c) shows the Hill coefficient nH [eqn (8)] for several [B]T/[AA]T > 1 (lines) and predictions for K2 = K1 of the analytical expression eqn (C8) (symbols). The thick grey lines represent eqn (D3) [(a and b)] and eqn (D4) (c), corresponding to [B]T/[AA]T → ∞. | |
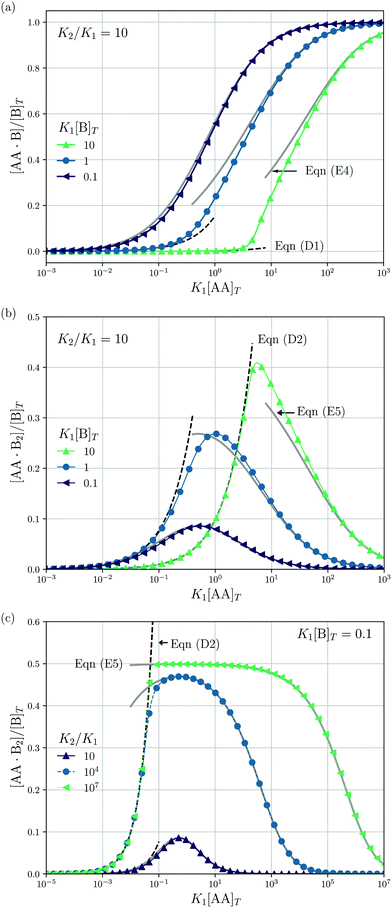 |
| | Fig. 4 Theoretical predictions for a titration-like experiment wherein [AA]T increases at fixed K1, K2, and [B]T. We show [AA·B]/[B]T (a) and [AA·B2]/[B]T [(b and c)] as a function of K1[AA]T for K2/K1 = 10 and several K1[B]T [(a and b)] and for K1[B]T = 0.1 and several K2/K1 (c). Panel (a) also shows eqn (E4) (grey lines) and eqn (D1) (grey dashed lines); panels (b and c) also show eqn (E5) (grey solid lines) and eqn (D2) (black dashed lines). | |
3.2 Adding AA to a solution of B
Next, we study a case wherein [AA]T is varied at fixed [B]T, K1, and K2. These conditions hold approximately in a titration experiment wherein a concentrated solution of AA is added to a dilute solution of B—provided that the “titrant” AA barely affects the volume of the B-containing solution; hence, neither affects [B]T. While eqn (6) could just as well be solved for a case wherein [B]T decreases as [AA]T increases, for clarity, we prefer to keep [B]T fixed here. Clearly, starting from [AA]T = 0 and adding much AA, we can span the complete range of 0 < [B]T/[AA]T < ∞. The expressions derived in Appendices D and E for [B]T ≫ [AA]T and [B]T ≪ [AA]T can thus be expected to hold either at the start or the end of this titration-like experiment. Fig. 4 shows numerical results for [AA·B]/[B]T (a) and [AA·B2]/[B]T [(b) and (c)] as a function of K1[AA]T for K2/K1 = 10 and several K1[B]T [(a) and (b)] and for K1[B]T = 0.1 and several K2/K1 (c). These panels display a well-documented effect: given a limited amount of B molecules, saturating a solution with AA will make the doubly-bound complex AA·B2 rare compared to its singly-bound counterpart AA·B, which is reflected in bell-shaped [AA·B2]/[B]T curves.1,27 Intuitively, when the B molecules have many AA ligands to choose from, it is unlikely that two Bs will bind the same divalent ligand. However, for a very large cooperativity parameter K2/K1, one would expect the doubly bound complex AA·B2 to become more probable at a given K1[AA]T. This is indeed observed in Fig. 4(c) for K2/K1 = 107. There, once [AA]T > [B]T, the AA ligands bind every available B molecule, and overwhelmingly so in doubly-bound AA·B2 complexes. This means that there are half as many AA·B2 complexes as B molecules, which explains the plateau value 0.5 in Fig. 4(c). Yet, even for large K2/K1, saturating by AA will again drive [AA·B2] down, for the same above-given reason. If, in a practical application, the objective is to bind as many B as possible (for instance to prevent a virus from attaching to a cell surface, see Fig. 2 of ref. 8), using a divalent ligand with K2/K1 ≫ 1 may be successful. Beyond [AA]T ≈ [B]T, there is no point in further increasing [AA]T, as all B will be bound from thereon.
An analytical expression [eqn (E5)] for bell-shaped [AA·B2]/[B]T curves was found in ref. 27 under the assumption that [B]T ≪ [AA]T. From their expression followed that [AA·B2]/[B]T reaches a maximal value 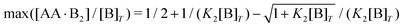 at K1[AA]T = 1/2 and that [AA·B2]/[B]T should be symmetric around this maximum when plotted against log(K1[AA]T).27 For K2/K1 = 10 and K2[B]T = [0.1,1,10] as used in Fig. 4(b), we find max([AA·B2]/[B]T) = [0.0857,0.268,0.410], which are close to the peak values observed there. For K1[B]T = 0.1, we see that eqn (E5) (grey lines) actually closely follows the numerical data for all K1[AA]T considered. Conversely, for K1[B]T = [1,10], the bell shape of [AA·B2]/[B]T becomes skewed and shifts away from K1[AA]T = 1/2 to larger K1[AA]T. For these K1[B]T values, the assumption [B]T ≪ [AA]T is incorrect for small K1[AA]T. For K1[AA]T = 1 and K1[B]T = 10, for example, one has that [B]T/[AA]T = 10, so the assumption [B]T ≪ [AA]T underlying eqn (E5) is not justified. For these K1[AA]T and K1[B]T values, it makes more sense to compare the numerical data to eqn (D2), which was derived under the opposite assumption [B]T ≫ [AA]T. Indeed, in the regime of small K1[AA]T, the numerical data in Fig. 4(b) is accurately described by eqn (D2) (black dashed lines). Hence, as the ratio [B]T/[AA]T varies during a titration experiment, the analytical expressions for [AA·B]/[B]T and [AA·B2]/[B]T for different [B]T/[AA]T limits hold in different K1[AA]T-regimes. Similar observations can be made in Fig. 4(a) and (c). For instance, we see that [AA·B]/[B]T is decently described by eqn (E4) for K1[B]T = 0.1 and all considered K1[AA]T. Conversely, for K1[B]T = [1,10], we see that [AA·B]/[B]T is described by eqn (D1) for small K1[AA]T and by eqn (E4) for large K1[AA]T. Similar to [AA·B2]/[AA]T, also [AA·B]/[AA]T shifts towards larger K1[AA]T for larger K1[B]T.
at K1[AA]T = 1/2 and that [AA·B2]/[B]T should be symmetric around this maximum when plotted against log(K1[AA]T).27 For K2/K1 = 10 and K2[B]T = [0.1,1,10] as used in Fig. 4(b), we find max([AA·B2]/[B]T) = [0.0857,0.268,0.410], which are close to the peak values observed there. For K1[B]T = 0.1, we see that eqn (E5) (grey lines) actually closely follows the numerical data for all K1[AA]T considered. Conversely, for K1[B]T = [1,10], the bell shape of [AA·B2]/[B]T becomes skewed and shifts away from K1[AA]T = 1/2 to larger K1[AA]T. For these K1[B]T values, the assumption [B]T ≪ [AA]T is incorrect for small K1[AA]T. For K1[AA]T = 1 and K1[B]T = 10, for example, one has that [B]T/[AA]T = 10, so the assumption [B]T ≪ [AA]T underlying eqn (E5) is not justified. For these K1[AA]T and K1[B]T values, it makes more sense to compare the numerical data to eqn (D2), which was derived under the opposite assumption [B]T ≫ [AA]T. Indeed, in the regime of small K1[AA]T, the numerical data in Fig. 4(b) is accurately described by eqn (D2) (black dashed lines). Hence, as the ratio [B]T/[AA]T varies during a titration experiment, the analytical expressions for [AA·B]/[B]T and [AA·B2]/[B]T for different [B]T/[AA]T limits hold in different K1[AA]T-regimes. Similar observations can be made in Fig. 4(a) and (c). For instance, we see that [AA·B]/[B]T is decently described by eqn (E4) for K1[B]T = 0.1 and all considered K1[AA]T. Conversely, for K1[B]T = [1,10], we see that [AA·B]/[B]T is described by eqn (D1) for small K1[AA]T and by eqn (E4) for large K1[AA]T. Similar to [AA·B2]/[AA]T, also [AA·B]/[AA]T shifts towards larger K1[AA]T for larger K1[B]T.
3.3 Adding B to a solution of AA
Lastly, we mimic a titration experiment wherein [B]T is varied at fixed [AA]T, K1, and K2. As our governing eqn (2) and (3) are not invariant under swapping AA and B—unlike, for example, A and B in the reaction A + B ⇌ AB, see ref. 3—we can expect results different from the previous subsection, wherein [AA]T was varied at fixed [B]T, K1, and K2. Fig. 5 shows [AA·B]/[AA]T (a) and [AA·B2]/[AA]T (b) as a function of K1[B]T for K2/K1 = 10 and various K1[AA]T. Compared to adding AA to a solution of B discussed before, we see that qualitative features of [AA·B] and [AA·B2]—sigmoidal and bell shapes—have interchanged. Intuitively, in a solution saturated with B molecules, AA ligands are likely to find two binding partners, yielding high [AA·B2]. Both [AA·B]/[AA]T and [AA·B2]/[AA]T shift towards larger K1[B]T for larger K1[AA]T. As in Fig. 4, in Fig. 5 we also show predictions from eqn (D1) and (D2) (black dashed lines) and eqn (E4) and (E5) (grey solid lines). These analytical expressions are again seen to agree fairly well with the numerical results for [AA·B]/[AA]T and [AA·B2]/[AA]T, in this case either for large or small K1[B]T. Unlike Fig. 4, where eqn (D1) and (D2) depend on K1[B]T, eqn (D1) and (D2) in Fig. 5 are independent of K1[AA]T.
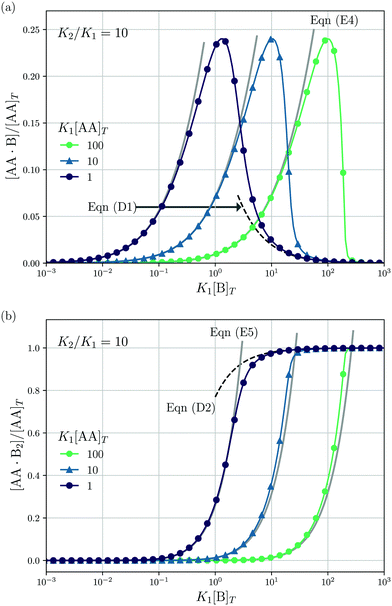 |
| | Fig. 5 Theoretical predictions for a titration-like experiment wherein [B]T increases at fixed K1, K2, and [AA]T. We show [AA·B]/[AA]T (a) and [AA·B2]/[AA]T (b) as a function of K1[B]T for K2/K1 = 10 and several K1[AA]T. Panel (a) also shows eqn (E4) (grey solid lines) and eqn (D1) (black dashed line); panel (b) also shows eqn (E5) (grey solid lines) and eqn (D2) (black dashed line). | |
4 Conclusion
We have described the reversible binding of two identical monovalent molecules B to a divalent ligand AA. The same process has been studied before, but only in concentration limits of either many more divalent ligands than monovalent molecules or vice versa. We considered any ratio of concentrations of divalent ligands and monovalent molecules instead. Our theoretical work is rooted in the classical reaction-rate equations for the above reaction. At steady state, these reduce to four coupled equations for the concentrations [AA], [B], [AA·B], and [AA·B2] of unbound, partly bound, and fully bound molecule-ligand complexes, with dependence on the four parameters K1, K2, [AA]T, and [B]T. We have highlighted the role played by the different parameters by mimicking three different experiments wherein we either varied [AA]T and [B]T at fixed [B]T/[AA]T, varied [AA]T at fixed [B]T, or varied [B]T at fixed [AA]T. In these different scenarios, the concentrations [AA·B] and [AA·B2] exhibit a rich and nontrivial dependence on K1[B]T (or K1[AA]T), K2/K1, and [B]T/[AA]T. Specifically, curves for [AA·B] and [AA·B2] as a function of K1[AA]T or K1[B]T are either sigmoidal or (roughly) bell shaped. Which of these two shapes appears depends on the varied parameters and on the values of the fixed parameters. In one case [Fig. 2(a)], we observed a transition from a sigmoidal to a bell shape with increasing [B]T/[AA]T. Only in the limits [B]T/[AA]T → ∞ and [B]T/[AA]T → 0 do we recover the results of [Hunter and Anderson, Angewandte Chemie International Edition, 2009, 48, 7488] and of [Perelson and DeLisi, Mathematical Biosciences, 1980, 48, 71]; at finite [B]T/[AA]T, their results contain errors of ![[scr O, script letter O]](https://www.rsc.org/images/entities/char_e52e.gif) ([AA]T/[B]T) and
([AA]T/[B]T) and ![[scr O, script letter O]](https://www.rsc.org/images/entities/char_e52e.gif) ([B]T3/[AA]T3), respectively.
([B]T3/[AA]T3), respectively.
Comparable concentrations of reacting species can occur both in in vivo and in synthetic biological systems. The constraint of particle conservation in homodivalent ligand-monovalent molecule binding—described in this article—can be especially relevant in cellular contexts, where few molecules of either species may be present. However, for tiny systems with small numbers of particles, the reaction rate equation-type modelling that underlies our results breaks down. Our results could then be used as a benchmark in more accurate stochastic models for the same reaction35 or in models that account for molecular crowding.36 Our work can also be a stepping stone to study how different protein-to-ligand ratios affect heterodivalent interactions15,37–39 and the competition between monovalent and divalent receptors for divalent ligands.31,40
Conflicts of interest
There are no conflicts to declare.
A Derivation of eqn (3) from reaction-rate equations
We repeat eqn (1)| | 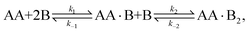 | (A1) |
where now k1 and k2 and k−1 and k−2 are forward and backward reaction rates, respectively. From the law of mass action follow the reaction-rate equations,| | 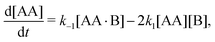 | (A2a) |
| | 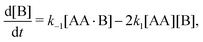 | (A2b) |
| | 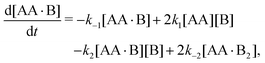 | (A2c) |
| | 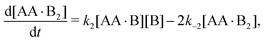 | (A2d) |
which need to be supplement with initial concentrations of the four species, which we choose as| | | [AA](t = 0) ≡ [AA]T, | (A3a) |
Time-dependent concentrations were studied in ref. 14. Here, we study the steady state, for which eqn (A2a) and (A2b) are identical and eqn (A2c) is the sum of eqn (A2a) and (A2d). Writing K1 = k1/k−1 and K2 = k2/k−2, we arrive at eqn (3) of the main text.
B General solution to eqn (6)
From hereon, we use the following dimensionless parameters: dimensionless concentrations x1 = [AA]/[AA]T, x2 = [B]/[AA]T, x3 = [AA·B]/[AA]T and x4 = [AA·B2]/[AA]T; dimensionless association constants (or, equivalently, “normalized concentration” scales20) κ1 = K1[B]T and κ2 = K2[B]T; the ligand-to-molecule ratio ξ = [B]T/[AA]T, and the “cooperativity parameter” α = K2/K1. Using these definitions, we rewrite eqn (2) and (3) to| | 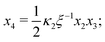 | (B1d) |
Eqn (4) to| | | x3 = 2κ1ξ−1(ξ − x3 − 2x4)(1 − x3 − x4), | (B2a) |
| | 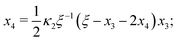 | (B2b) |
Eqn (5) to| | 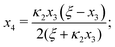 | (B3) |
and eqn (6) to
| ax33 + bx32 + cx3 + d = 0, |
| c ≡ 2ξκ1(κ2 − 1) − ξ2(2κ1 + κ1κ2+ 1), |
Substituting x3 = u − a/3 into eqn (B4) yields| | 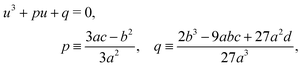 | (B5) |
whose solution, with Viète's formula, reads| | 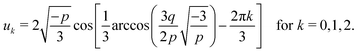 | (B6) |
Depending on the values of κ1,κ2, and ξ, the determinant Δ = −(4p3 + 27q2) can be both positive and negative. Hence, for different parameter settings, eqn (6) has either three real roots or one real and two complex roots.
C No cooperativity, α = K2/K1 = 1
In absence of cooperativity (K1 = K2) we have that κ1 = κ2 ≡ κ and eqn (B4) simplifies to| | | −2κ2x32 + ξ[2κ(κ − 1) − ξ(κ + 1)2]x3 + 2κξ2 = 0. | (C1) |
The positive solution to the quadratic eqn (C1) reads| | 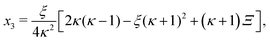 | (C2a) |
with| | 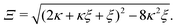 | (C2b) |
For the interpretation of the plateaus at κ ≫ 1 in Fig. 3(a), we note that, for κ ≫ 1 and ξ ≈ 1,| | x3 = ξ(1 − ξ/2) + ![[scr O, script letter O]](https://www.rsc.org/images/entities/char_e52e.gif) (κ−1). (κ−1). | (C3) |
Eqn (C3) breaks down for ξ > 2, as x3 < 0 corresponds to [AA·B] < 0, which is nonphysical.
Inserting eqn (C2) into x4 [eqn (B3)] and θ ≡ x3/2 + x4 yields
| | 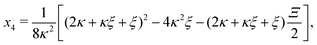 | (C4a) |
| | 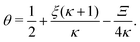 | (C4b) |
We note that the case of
K2/
K1 = 1 considered here is related to the simpler reaction A + B ⇌ A·B. Comparing two solutions with equal concentrations of [AA] and [A], the number of ligating units in the former solution is twice as high. Replacing
ξ → 2
ξ in
eqn (C4b) accordingly, this expression reduces to eqn (4.38) of
ref. 3 for the scaled concentration [A·B]/[A]
T at a ligand-to-molecule ratio
ξ = [B]
T/[A]
T.
In terms of the dimensionless parameters, the Hill coefficient of eqn (8) can be expressed as
| | 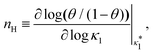 | (C5) |
where
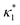
is such that
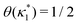
; hence,
| | 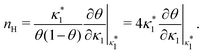 | (C6) |
Inserting
eqn (C4b), we find
| | 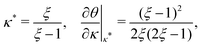 | (C7) |
and
| | 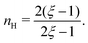 | (C8) |
We find that
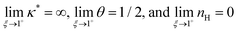
. For smaller
ξ, the condition of half occupancy in the definition of the Hill coefficient is never fulfilled, leaving
nH undefined for
ξ ≤ 1.
D Few divalent ligands [AA]T ≪ [B]T (ξ ≫ 1)
For ξ ≫ 1, eqn (B4) reduces to| | 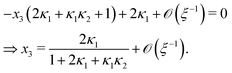 | (D1) |
Inserting eqn (D1) into eqn (B3) and again taking ξ ≫ 1, we find| | 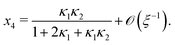 | (D2) |
The occupancy θ is found as| | 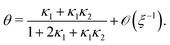 | (D3) |
Eqn (D1)–(D3) coincide with eqn (S20)–(S22) of ref. 20, which were used to draw Fig. 4 therein.
For the case ξ ≫ 1, we find nH in terms of the cooperativity parameter α by inserting eqn (D3) into eqn (C6),
| | 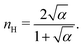 | (D4) |
E Many divalent ligands [AA]T ≫ [B]T (ξ ≪ 1)
Next, we seek approximate solutions to eqn (B4) for ξ ≪ 1. We insert the power series 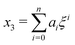 into eqn (B4), collect terms of equal order in ξ, and demand the coefficient of each successive order in ξ to be zero. For n = 3, we find
into eqn (B4), collect terms of equal order in ξ, and demand the coefficient of each successive order in ξ to be zero. For n = 3, we find| | 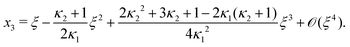 | (E1) |
We insert eqn (E1) into eqn (B3) and find| | 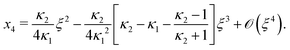 | (E2) |
Ref. 27 attacked the same problem differently. They stated that [AA] = [AA]T holds approximately if [AA]T ≫ [B]T. Then, the term (1 − x3 − x4) in eqn (B2a), which stems from [AA] should be replaced by 1, yielding| | | x3 = 2κ1ξ−1(ξ − x3 − 2x4), | (E3) |
instead. Inserting x4 [eqn (B3)] as before now yields| | 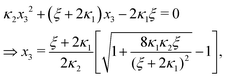 | (E4) |
equivalent to eqn (19) of ref. 27.
We insert eqn (E4) into eqn (B3) and find
| | 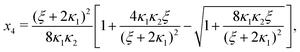 | (E5) |
equivalent to eqn (20) of
ref. 27.
As eqn (E4) and (E5) were derived setting x1 = 1, argued on the basis of ξ ≪ 1, the ξ-range of validity of these expression is not obvious. Expanding eqn (E4) for small ξ,
| | 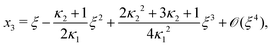 | (E6) |
we see that
eqn (E1) and (E6) differ at
![[scr O, script letter O]](https://www.rsc.org/images/entities/char_e52e.gif)
(
ξ3). Practically, setting
κ1 =
κ2 = 10
2, the two approximations
eqn (E1) and (E6) differ from the numerically found root by 0.0001% and 0.52% at
ξ = 0.1 and 0.5% and 50% at
ξ = 1, respectively. As expected: for small
ξ, both approximations are decent and for
ξ = 1,
eqn (E1) performs better.
Likewise, expanding eqn (E5) for small ξ yields
| | 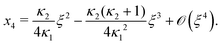 | (E7) |
Again, differences between
eqn (E2) and (E7) appear at
![[scr O, script letter O]](https://www.rsc.org/images/entities/char_e52e.gif)
(
ξ3). Concluding, eqn (19) and (20) of
ref. 27, contain errors of
![[scr O, script letter O]](https://www.rsc.org/images/entities/char_e52e.gif)
(
ξ3).
F Cubic equation for x2
In Section 2 and Appendix B, we reduced the original four coupled equations in eqn (2) and (3) to a single cubic equation for [AA·B] (or x3). This was a convenient choice for us as we focused our discussion on [AA·B] and [AA·B2]. Yet, as we show next, we may have also derived a cubic equation for [B] instead. From eqn (B1a) and (B1b) we findFrom eqn (F1a) and (B1d) we find| | 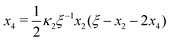 | (F2) |
| | 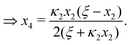 | (F3) |
Inserting eqn (F1a) and (F1b) into eqn (B1c) we find| | | ξ − x2 − 2x4 = 2κ1ξ−1x2(1 − x3 − x4) = 2κ1ξ−1x2(1 − ξ + x2 + x4). | (F4) |
Inserting eqn (F3) gives| | 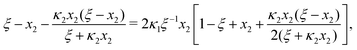 | (F5) |
which yields| | | 0 = x23κ1κ2 + x22(2κ1κ2+ 2κ1ξ − κ2κ1ξ) + x2(ξ2 + 2κ1ξ − 2κ1ξ2) − ξ3, | (F6) |
or, in our original notation,| | | 0 = [B]3K1K2 + [B]2(2K1 − K2K1[B]0 + 2K1K2[AA]T) + [B](1 + 2K1[AA]T − 2K1[B]T) − [B]T. | (F7) |
Eqn (F7) is equivalent to eqn (25) of ref. 29—up to factor 2 discrepancies in a few places, which we trace back to her eqn (15), the counterpart of our eqn (B1c) and (B1d), which does not include prefactors 2 and 1/2. Redefining our K1 → K1/2 and K2 → 2K2 lifts these discrepancies. Moreover, eqn (F7) is equivalent to eqn (S) of ref. 13 in the case that their “nonreactive fraction parameter” nr is set to nr = 0.
Acknowledgements
We thank Susanne Liese and Kay Schink for stimulating discussions. MJ and HS were supported by an Advanced Grant from the European Research Council (no. 788954). The research leading to these results has received funding from the European Union's Horizon 2020 research and innovation programme under the Marie Skłodowska-Curie grant agreement No 801133.
References
-
D. A. Lauffenburger and J. J. Linderman, Receptors: models for binding, trafficking, and signaling, Oxford University Press, 1996 Search PubMed.
-
J. P. Keener and J. Sneyd, Mathematical physiology, Springer, 1998, vol. 1 Search PubMed.
-
R. A. Copeland, Protein-ligand binding equilibria, Wiley, New York, 2000, pp. 76–108 Search PubMed.
- O. Wolkenhauer, P. Wellstead, K.-H. Cho, R. Grima and S. Schnell, Essays Biochem., 2008, 45, 41–56 CrossRef PubMed.
-
L. E. Limbird, Cell surface receptors: a short course on theory and methods: a short course on theory and methods, Springer Science & Business Media, 2012 Search PubMed.
-
U. Schwarz, Theoretical biophysics, Lecture notes, 2019, ch. 8 Search PubMed.
- R. M. Peltzer, H. B. Kolli, A. Stocker and M. Cascella, J. Phys. Chem. B, 2018, 122, 7066–7072 CrossRef CAS PubMed.
- C. Fasting, C. A. Schalley, M. Weber, O. Seitz, S. Hecht, B. Koksch, J. Dernedde, C. Graf, E.-W. Knapp and R. Haag, Angew. Chem., Int. Ed., 2012, 51, 10472–10498 CrossRef CAS.
-
A. J. Achazi, Theoretical Investigations of Multivalent Reactions, PhD thesis, Freie Universität Berlin, 2017.
- B. M. Mognetti, P. Cicuta and L. Di Michele, Rep. Prog. Phys., 2019, 82, 116601 CrossRef CAS PubMed.
-
S. Merminod, J. R. Edison, H. Fang, M. F. Hagan and W. B. Rogers, 2020, arXiv preprint arXiv:2008.07017.
- D. M. Crothers and H. Metzger, Immunochemistry, 1972, 9, 341–357 CrossRef CAS PubMed.
- E. N. Kaufman and R. K. Jain, Cancer Res., 1992, 52, 4157–4167 CAS.
- K. M. Müller, K. M. Arndt and A. Plückthun, Anal. Biochem., 1998, 261, 149–158 CrossRef PubMed.
- G. Vauquelin and S. J. Charlton, Br. J. Pharmacol., 2013, 168, 1771–1785 CrossRef CAS.
- E. T. Mack, P. W. Snyder, R. Perez-Castillejos and G. M. Whitesides, J. Am. Chem. Soc., 2011, 133, 11701–11715 CrossRef CAS PubMed.
- S. Liese and R. R. Netz, Beilstein J. Org. Chem., 2015, 11, 804–816 CrossRef CAS PubMed.
- D. Diestler and E. Knapp, Phys. Rev. Lett., 2008, 100, 178101 CrossRef CAS PubMed.
- D. Diestler and E. Knapp, J. Phys. Chem. C, 2010, 114, 5287–5304 CrossRef CAS.
- C. Hunter and H. Anderson, Angew. Chem., Int. Ed., 2009, 48, 7488–7499 CrossRef CAS PubMed.
- G. Ercolani and L. Schiaffino, Angew. Chem., Int. Ed., 2011, 50, 1762–1768 CrossRef CAS PubMed.
-
S. Di Stefano and G. Ercolani, Advances in Physical Organic Chemistry, Elsevier, 2016, vol. 50, pp. 1–76 Search PubMed.
- L. K. S. von Krbek, C. A. Schalley and P. Thordarson, Chem. Soc. Rev., 2017, 46, 2622–2637 RSC.
- S. J. Wodak, E. Paci, N. V. Dokholyan, I. N. Berezovsky, A. Horovitz, J. Li, V. J. Hilser, I. Bahar, J. Karanicolas and G. Stock,
et al.
, Structure, 2019, 27, 566–578 CrossRef CAS PubMed.
- W. A. Eaton, E. R. Henry, J. Hofrichter and A. Mozzarelli, Nat. Struct. Biol., 1999, 6, 351–358 CrossRef CAS PubMed.
- Z.-X. Wang, FEBS Lett., 1995, 360, 111–114 CrossRef CAS PubMed.
- A. S. Perelson and C. DeLisi, Math. Biosci., 1980, 48, 71–110 CrossRef.
- A. P. Minton, Mol. Pharmacol., 1981, 19, 1–14 CAS.
- J. A. Reynolds, Biochemistry, 1979, 18, 264–269 CrossRef CAS PubMed.
- S. K. Dower, C. DeLisi, J. A. Titus and D. M. Segal, Biochemistry, 1981, 20, 6326–6334 CrossRef CAS PubMed.
- M. Dembo and B. Goldstein, J. Immunol., 1978, 121, 345–353 CAS.
- A. S. Perelson and G. Weisbuch, Rev. Mod. Phys., 1997, 69, 1219–1268 CrossRef CAS.
- C. Guo and H. Levine, Biophys. J., 1999, 77, 2358–2365 CrossRef CAS PubMed.
- B. R. Caré and H. A. Soula, BMC Syst. Biol., 2011, 5, 1–13 CrossRef PubMed.
- D. T. Gillespie, J. Phys. Chem., 1977, 81, 2340–2361 CrossRef CAS.
- D. Gomez and S. Klumpp, Front. Phys., 2015, 3, 45 Search PubMed.
- G. Vauquelin, D. Hall and S. J. Charlton, Br. J. Pharmacol., 2015, 172, 2300–2315 CrossRef CAS PubMed.
- A. Simonsen, R. Lippe, S. Christoforidis, J.-M. Gaullier, A. Brech, J. Callaghan, B.-H. Toh, C. Murphy, M. Zerial and H. Stenmark, Nature, 1998, 394, 494–498 CrossRef CAS PubMed.
- C. Raiborg, E. M. Wenzel, N. M. Pedersen, H. Olsvik, K. O. Schink, S. W. Schultz, M. Vietri, V. Nisi, C. Bucci, A. Brech, T. Johansen and H. Stenmark, Nature, 2015, 520, 234–238 CrossRef CAS PubMed.
- E. T. Mack, L. Cummings and R. Perez-Castillejos, Anal. Bioanal. Chem., 2011, 399, 1641–1652 CrossRef CAS PubMed.
|
| This journal is © The Royal Society of Chemistry 2021 |
Click here to see how this site uses Cookies. View our privacy policy here.  Open Access Article
Open Access Article *ab,
Harald
Stenmark
b and
Andreas
Carlson
*ab,
Harald
Stenmark
b and
Andreas
Carlson
 *a
*a

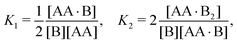
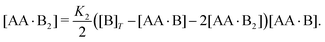
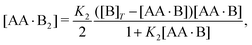
![[scr O, script letter O]](https://www.rsc.org/images/entities/char_e52e.gif) ([AA]T/[B]T). Last, Appendix E covers the case [AA]T ≫ [B]T. For this case, we solve eqn (6) with a power series approximation to [AA·B]. Our solutions to [AA·B] and [AA·B2] differ from Perelson and DeLisi's results27 from
([AA]T/[B]T). Last, Appendix E covers the case [AA]T ≫ [B]T. For this case, we solve eqn (6) with a power series approximation to [AA·B]. Our solutions to [AA·B] and [AA·B2] differ from Perelson and DeLisi's results27 from ![[scr O, script letter O]](https://www.rsc.org/images/entities/char_e52e.gif) ([B]T3/[AA]T3) onwards.
([B]T3/[AA]T3) onwards.
![[scr O, script letter O]](https://www.rsc.org/images/entities/char_e52e.gif) ([B]T3/[AA]T3). For [B]T/[AA]T = 0.2 and K1[B]T = 103, we evaluated that [AA] = 0.81[AA]T; hence, the assumption [AA] = [AA]T of ref. 27 is satisfied to some extend at this [B]T/[AA]T value. Comparing to our earlier evaluation of [B] at [B]T/[AA]T = 100, we see that, as anticipated in the introduction, the closer [B]T/[AA]T is to unity, the stronger the unbound species are depleted. Third, a salient feature of the curves in Fig. 2(a) are the plateaus for K1[B]T ≫ 1 and [B]T ≈ [AA]T. As we derive in Appendix C [specifically, eqn (C3)], their height is set by
([B]T3/[AA]T3). For [B]T/[AA]T = 0.2 and K1[B]T = 103, we evaluated that [AA] = 0.81[AA]T; hence, the assumption [AA] = [AA]T of ref. 27 is satisfied to some extend at this [B]T/[AA]T value. Comparing to our earlier evaluation of [B] at [B]T/[AA]T = 100, we see that, as anticipated in the introduction, the closer [B]T/[AA]T is to unity, the stronger the unbound species are depleted. Third, a salient feature of the curves in Fig. 2(a) are the plateaus for K1[B]T ≫ 1 and [B]T ≈ [AA]T. As we derive in Appendix C [specifically, eqn (C3)], their height is set by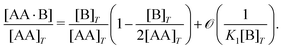

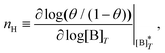
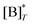 is the molecular concentration at half occupancy,
is the molecular concentration at half occupancy, 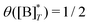 . Fig. 3(c) shows the K2/K1 dependence of nH for several [B]T/[AA]T. As such, Fig. 3(c) generalises Fig. 6 of ref. 20, where [B]T ≫ [AA]T was considered. In that case, nH is given by
. Fig. 3(c) shows the K2/K1 dependence of nH for several [B]T/[AA]T. As such, Fig. 3(c) generalises Fig. 6 of ref. 20, where [B]T ≫ [AA]T was considered. In that case, nH is given by 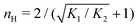 [cf.eqn (D4)], indicated in Fig. 3(c) with a thick grey solid line. We see that, for [B]T/[AA]T = 100, the numerically determined nH is close to predictions from eqn (D4). Conversely, we see that nH → 0 for [B]T/[AA]T → 1. Fig. 4(a) and (b) show that half occupancy (θ = 1/2) is not reached if [B]T/[AA]T < 1; hence, nH is undetermined for [B]T/[AA]T < 1. The symbols in Fig. 3(c) for K2 = K1 represent the analytical expression eqn (C8). These symbols match perfectly to the numerical nH predictions.
[cf.eqn (D4)], indicated in Fig. 3(c) with a thick grey solid line. We see that, for [B]T/[AA]T = 100, the numerically determined nH is close to predictions from eqn (D4). Conversely, we see that nH → 0 for [B]T/[AA]T → 1. Fig. 4(a) and (b) show that half occupancy (θ = 1/2) is not reached if [B]T/[AA]T < 1; hence, nH is undetermined for [B]T/[AA]T < 1. The symbols in Fig. 3(c) for K2 = K1 represent the analytical expression eqn (C8). These symbols match perfectly to the numerical nH predictions.


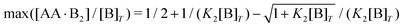 at K1[AA]T = 1/2 and that [AA·B2]/[B]T should be symmetric around this maximum when plotted against log(K1[AA]T).27 For K2/K1 = 10 and K2[B]T = [0.1,1,10] as used in Fig. 4(b), we find max([AA·B2]/[B]T) = [0.0857,0.268,0.410], which are close to the peak values observed there. For K1[B]T = 0.1, we see that eqn (E5) (grey lines) actually closely follows the numerical data for all K1[AA]T considered. Conversely, for K1[B]T = [1,10], the bell shape of [AA·B2]/[B]T becomes skewed and shifts away from K1[AA]T = 1/2 to larger K1[AA]T. For these K1[B]T values, the assumption [B]T ≪ [AA]T is incorrect for small K1[AA]T. For K1[AA]T = 1 and K1[B]T = 10, for example, one has that [B]T/[AA]T = 10, so the assumption [B]T ≪ [AA]T underlying eqn (E5) is not justified. For these K1[AA]T and K1[B]T values, it makes more sense to compare the numerical data to eqn (D2), which was derived under the opposite assumption [B]T ≫ [AA]T. Indeed, in the regime of small K1[AA]T, the numerical data in Fig. 4(b) is accurately described by eqn (D2) (black dashed lines). Hence, as the ratio [B]T/[AA]T varies during a titration experiment, the analytical expressions for [AA·B]/[B]T and [AA·B2]/[B]T for different [B]T/[AA]T limits hold in different K1[AA]T-regimes. Similar observations can be made in Fig. 4(a) and (c). For instance, we see that [AA·B]/[B]T is decently described by eqn (E4) for K1[B]T = 0.1 and all considered K1[AA]T. Conversely, for K1[B]T = [1,10], we see that [AA·B]/[B]T is described by eqn (D1) for small K1[AA]T and by eqn (E4) for large K1[AA]T. Similar to [AA·B2]/[AA]T, also [AA·B]/[AA]T shifts towards larger K1[AA]T for larger K1[B]T.
at K1[AA]T = 1/2 and that [AA·B2]/[B]T should be symmetric around this maximum when plotted against log(K1[AA]T).27 For K2/K1 = 10 and K2[B]T = [0.1,1,10] as used in Fig. 4(b), we find max([AA·B2]/[B]T) = [0.0857,0.268,0.410], which are close to the peak values observed there. For K1[B]T = 0.1, we see that eqn (E5) (grey lines) actually closely follows the numerical data for all K1[AA]T considered. Conversely, for K1[B]T = [1,10], the bell shape of [AA·B2]/[B]T becomes skewed and shifts away from K1[AA]T = 1/2 to larger K1[AA]T. For these K1[B]T values, the assumption [B]T ≪ [AA]T is incorrect for small K1[AA]T. For K1[AA]T = 1 and K1[B]T = 10, for example, one has that [B]T/[AA]T = 10, so the assumption [B]T ≪ [AA]T underlying eqn (E5) is not justified. For these K1[AA]T and K1[B]T values, it makes more sense to compare the numerical data to eqn (D2), which was derived under the opposite assumption [B]T ≫ [AA]T. Indeed, in the regime of small K1[AA]T, the numerical data in Fig. 4(b) is accurately described by eqn (D2) (black dashed lines). Hence, as the ratio [B]T/[AA]T varies during a titration experiment, the analytical expressions for [AA·B]/[B]T and [AA·B2]/[B]T for different [B]T/[AA]T limits hold in different K1[AA]T-regimes. Similar observations can be made in Fig. 4(a) and (c). For instance, we see that [AA·B]/[B]T is decently described by eqn (E4) for K1[B]T = 0.1 and all considered K1[AA]T. Conversely, for K1[B]T = [1,10], we see that [AA·B]/[B]T is described by eqn (D1) for small K1[AA]T and by eqn (E4) for large K1[AA]T. Similar to [AA·B2]/[AA]T, also [AA·B]/[AA]T shifts towards larger K1[AA]T for larger K1[B]T.
![[scr O, script letter O]](https://www.rsc.org/images/entities/char_e52e.gif) ([AA]T/[B]T) and
([AA]T/[B]T) and ![[scr O, script letter O]](https://www.rsc.org/images/entities/char_e52e.gif) ([B]T3/[AA]T3), respectively.
([B]T3/[AA]T3), respectively.
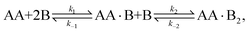
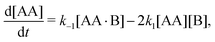
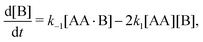
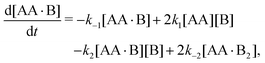
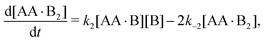
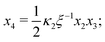
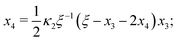
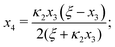
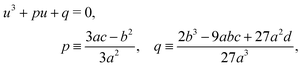
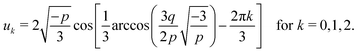
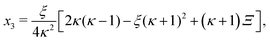
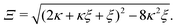
![[scr O, script letter O]](https://www.rsc.org/images/entities/char_e52e.gif) (κ−1).
(κ−1).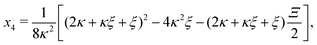
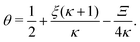
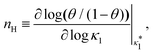
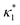 is such that
is such that 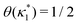 ; hence,
; hence,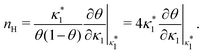
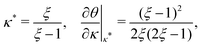
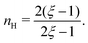
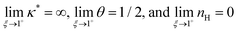 . For smaller ξ, the condition of half occupancy in the definition of the Hill coefficient is never fulfilled, leaving nH undefined for ξ ≤ 1.
. For smaller ξ, the condition of half occupancy in the definition of the Hill coefficient is never fulfilled, leaving nH undefined for ξ ≤ 1.
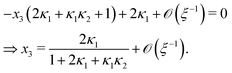
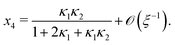
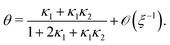
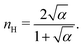
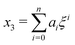 into eqn (B4), collect terms of equal order in ξ, and demand the coefficient of each successive order in ξ to be zero. For n = 3, we find
into eqn (B4), collect terms of equal order in ξ, and demand the coefficient of each successive order in ξ to be zero. For n = 3, we find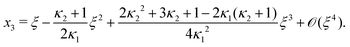
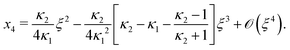
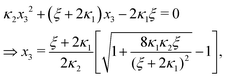
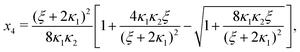
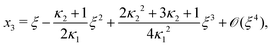
![[scr O, script letter O]](https://www.rsc.org/images/entities/char_e52e.gif) (ξ3). Practically, setting κ1 = κ2 = 102, the two approximations eqn (E1) and (E6) differ from the numerically found root by 0.0001% and 0.52% at ξ = 0.1 and 0.5% and 50% at ξ = 1, respectively. As expected: for small ξ, both approximations are decent and for ξ = 1, eqn (E1) performs better.
(ξ3). Practically, setting κ1 = κ2 = 102, the two approximations eqn (E1) and (E6) differ from the numerically found root by 0.0001% and 0.52% at ξ = 0.1 and 0.5% and 50% at ξ = 1, respectively. As expected: for small ξ, both approximations are decent and for ξ = 1, eqn (E1) performs better.
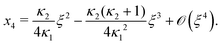
![[scr O, script letter O]](https://www.rsc.org/images/entities/char_e52e.gif) (ξ3). Concluding, eqn (19) and (20) of ref. 27, contain errors of
(ξ3). Concluding, eqn (19) and (20) of ref. 27, contain errors of ![[scr O, script letter O]](https://www.rsc.org/images/entities/char_e52e.gif) (ξ3).
(ξ3).