 Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Complex coacervation and metal–ligand bonding as synergistic design elements for aqueous viscoelastic materials†
Alexei D.
Filippov
 *a,
Joris
Sprakel
*a,
Joris
Sprakel
 a and
Marleen
Kamperman
a and
Marleen
Kamperman
 b
b
aLaboratory of Physical Chemistry and Soft Matter, Wageningen University & Research, Stippeneng 4, 6708WE Wageningen, The Netherlands. E-mail: adfilippov.work@protonmail.com
bZernike Institute for Advanced Materials, University of Groningen, P. O. Box 221, 9700AE Groningen, The Netherlands
First published on 3rd March 2021
Abstract
The application of complex coacervates in promising areas such as coatings and surgical glues requires a tight control of their viscous and elastic behaviour, and a keen understanding of the corresponding microscopic mechanisms. While the viscous, or dissipative, aspect is crucial at pre-setting times and in preventing detachment, elasticity at long waiting times and low strain rates is crucial to sustain a load-bearing joints. The independent tailoring of dissipative and elastic properties proves to be a major challenge that can not be addressed adequately by the complex coacervate motif by itself. We propose a versatile model of complex coacervates with customizable rheological fates by functionalization of polyelectrolytes with terpyridines, which provide transient crosslinks through complexation with metals. We show that the rheology of the hybrid complexes shows distinct footprints of both metal–ligand and coacervate dynamics, the former as a contribution very close to pure Maxwell viscoelasticity, the latter approaching a sticky Rouse fluid. Strikingly, when the contribution of metal–ligand bonds is dominant at long times, the relaxation of the overall complex is much slower than either the “native” coacervate relaxation time or the dissociation time of a comparable non-coacervate polyelectrolyte–metal–ligand complex. We recognize this slowing-down of transient bonds as a synergistic effect that has important implications for the use of complementary transient bonding in coacervate complexes.
Introduction
In synthetic coatings and adhesives, good adhesion and film formation is reliably found in hydrophobic, covalent bond-forming systems. Conversely, the polyelectrolyte-based adhesives of mussels and sandcastle worms are delivered in water-rich dispersions,1,2 and prominently feature transient bonds long into the curing process,2,3 whereas covalent bonds are important for long-term load bearing.4 Associative strategies from Nature are diverse, and compelling arguments are made for their incorporation into novel water-based adhesives, biomaterials for tissue engineering and implants, and other novel viscoelastics for use in biological contexts. First, the requirement of low surface tension for effective contact formation is met by mussels and sandcastle worms through the choice of highly hydrophilic constituents.3,5 Second, the seemingly contradictory requirement of non-solubility in the medium of use (water) is overcome in the same systems by the modification of macromolecules with transiently binding groups.2 Finally, Nature offers a vast range of bond strengths in transient bonds, allowing for the selection of appropriate stiffness and relaxation times. Unsurprisingly, the application of chemistry inspired by the underwater adhesion of water-dwelling animals is a tremendously active field.1,6,7 Since complex coacervation is a prominent feature in wet bio-adhesives,3 the use of coacervate matrices in the development of novel water-rich materials represents a natural choice. Complex coacervates are complexes of oppositely charged polyelectrolytes with a salt-dependent terminal relaxation time τR,8 and inevitably show creep when loaded for long times. Therefore, a central challenge of the field remains the incorporation of transient or covalent crosslinks into complex coacervates, ideally in response to a trigger. Examples are the thermostiffening block poly(N-isopropylacrylamide) (pNIPAm),9–11 catechol chemistry,12–14 or hydrophobic groups.12 Despite the reassuring progress, substantial questions in the design of the networks remain.For complex-coacervate based underwater adhesives, good adhesive performance occurs in a narrow range of salt concentration (cs) and temperatures,10 and it is not trivial to extend the parameter window towards arbitrary conditions, which has, for example, been attempted with extrusion.15 Similarly, the thermostiffening transition is strongly dependent on the blocks lengths, some compositions favouring micelles rather than continuous phases.16 Even in cases where a single lifetime τX can be ascribed to a crosslink, it is unknown how it impacts a pre-existing transient network of bonds of some lifetime τ0, which is a property of the complex coacervate matrix. The design of previous studies makes the elucidation of exact contributions due to crosslinking difficult – in an ideal case, this would be done with a design element that is structurally and temporally orthogonal to the coacervate, an idea rooted in the work of Holten-Andersen et al.17
The targeted design of responsively strengthened coacervate complexes requires predictable models of the emergence of viscoelasticity and elasticity in “bimodal” networks – those with two modes of thickening or stiffening. Therefore, we present a strategy to tailor the flow of coacervate-forming polyelectrolytes with metal–ligand complexes. The pairing is ideally suited to explore the combined effect of τR and a longer crosslink-associated timescale τX on coacervate viscoelasticity, as drawn in Fig. 1. We call the resulting materials transiently crosslinked complex coacervates (TC3s), in which the transient bonds we employ achieve transient crosslinks in the complex coacervate due to metal–ligand binding. To this end, we covalently attach terpyridines (tP) to polyelectrolytes poly(acrylic acid) (pA) and poly(N,N-dimethylaminoethyl methacrylate) (pD). The polyelectrolytes can then be bound to each other through complex coacervation, or by complexation with a range of metals, in which case a crosslink is formed by binding of one metal ion by two terpyridines. TC3s are models of underwater adhesives and their synthetic adaptations: instead of the complex behaviour of catechols18 or thermoresponsive blocks,9–11 we can analyze their phase behaviour and mechanics in terms of the well-defined relaxation times of coacervate and metal–ligand bonds. Furthermore, on account of the vast available range of terpyridine–metal ion equilibrium constants,19 TC3s offer a highly ion-specific viscoelastic response that complex coacervates natively lack.
In this paper, we reveal the effect of independently changing the relative magnitude of two relaxational timescales on viscoelasticity. We address TC3 flow through macrorheological measurements. Specifically, we search for the circumstances in which the coacervate could be expected to act unaware of the transient bonds, and vice versa. As such, we are able to assess to which extent transient bonds would suit to improve complex coacervate mechanics. The findings are relevant for those who seek to engineer novel water-rich materials, such as underwater glues and viscoelastics for use in a biological context. We show that the amount of transient crosslinks needed to thicken a complex coacervate is very low. Metal–ligand crosslinks are found to be able to entirely dominate the long-time mechanics of our hybrid complexes: TC3s can be tuned from low-viscosity fluids to indefinitely stable solids. Surprisingly, we find that the transient bonds are able to act over timescales that are often much longer than their “innate” lifetime, which we recognize as a form of synergy.
Experimental section
Notation
Throughout this work, we refer to polyelectrolytes as pXnϕ, with X either A for acrylic acid, D for N,N-dimethylaminomethyl methacrylate, or AMPS for 2-acrylamido-2-methyl-1-propanesulfonic acid. ϕ represents the molar percentage of repeat units that express a tP moiety, and n the polyelectrolyte degree of polymerization. The symbol ○ (instead of M2+) denotes the absence of metal.Materials
Unless stated otherwise, chemicals were used as received. Hydroxybenzotriazole hydrate (HOBt, 14% water, 98%), ethyl α-bromoisobutyrate (98%), concentrated hydrochloric acid (HCl 37%, aqueous, ACS reagent), N-(3-dimethylaminopropyl)-N′-ethylcarbodiimide hydrochloride (EDC, ≥98.0%), aluminum oxide (Al2O3, activated, basic), and, N,N-dimethylformamide (DMF, anhydrous, 99.8%) were obtained from Sigma-Aldrich, Germany. Tris[2-(dimethylamino)ethyl]amine (Me6TREN, Alfa Aesar, ≥ 99.0%), ethylenediamine tetraacetic acid (EDTA, MilliporeSigma), and, copper(II) bromide (CuBr2, 99%), were obtained from VWR. 2-(dimethylamino)ethyl methacrylate (DMAEMA, stabilized with MEHQ, >98.5%), tert-butyl acrylate (tBuAc, stabilized with MEHQ, >98.0%), and, methyl α-bromophenylacetate (MBPA, ≥98.0%) were obtained from TCI Europe. Methanol (MeOH, HPLC, ≥99.9%), 1,1,1,3,3,3-hexafluoro-2-propanol (HFIP, AR, ≥99.8%), acetonitrile (CH3CN, anhydrous, 99.8%), di-iso-propyl ether (∼0.001% BHT as stabilizer, ≥98.5%), and, n-hexane (HPLC), were obtained from Biosolve.CH3CN and DMF were stored on molecular sieves (4 Å). tBuAc and DMAEMA were stripped from inhibitor by filtration over a column of Al2O3. 3-Terpyridyloxy bromopropane and 4-terpyridyloxy butylamine were synthesized following literature procedures, and the corresponding Experimental section can be found in the ESI.†
Poly(N,N-dimethylethyl methacrylate) – 35 kDa (pD222, Đ = 1.12) and poly(acrylic acid) – 17 kDa (pA234, Đ = 1.12) were obtained from Polymer Source, Canada. Commercial pA was dried for several days on a high vacuum line, then dissolved in DMF and centrifuged at 2000g for 1 h to remove insoluble impurities. Poly(N,N-dimethylethyl methacrylate) (pD1k, Đ = 1.43) and poly(acrylic acid) (pA250, Đ = 1.13) were synthesized using copper-catalyzed polymerizations as reported below. pAMPS was synthesized as is described in the ESI.†
Terpyridylation of poly(N,N-dimethylethyl methacrylate)
In a representative example, pD (1.00 g, 6.36 mmol amines) was weighed into a round-bottomed flask and dissolved in dry acetonitrile (30 mL). To this was added 3-terpyridyloxy bromopropane (0.236 g, 0.64 mmol), and the mixture was stirred for three days at 55 °C. The mixture was concentrated in vacuo and purified by repeated precipitation in mixtures of diethyl ether and hexane. pD10 was obtained as faintly yellow glassy solid, 1.06 g (85%). 1H-NMR, 400 MHz: Fig. S7 (ESI†).pD01 was synthesized similarly, but precipitated in diisopropyl ether. It was obtained as a faintly yellow glassy solid, 0.80 g (50%). 1H-NMR, 400 MHz: Fig. S7 (ESI†).
Terpyridylation of poly(acrylic acid)
pA was terpyridylated as described by Aamer and Tew.20 In a representative example, pA (0.31 g, 4.3 mmol COOH) was dissolved in 10 mL dry DMF and bubbled with N2(g). EDC (0.0815 g, 0.424 mmol), HOBT (0.0659 g, 0.424 mmol) were each dissolved in minimal DMF in separate vials, and also sparged with N2(g). EDC and HOBT solutions were injected into the stirred pA solution, to which after 50 min was added a suspension of 4-terpyridyloxy butylamine (0.130 g) in minimal DMF. The mixture was left to stir for 16 h. pA with a terpyridylation extent of 10% (pA10) was recovered as a mixture with the EDC urea after centrifugation, neutralization to pH 7, and dialysis against Milli-Q followed by lyophilization. 0.433 g, as a purple powder. 1H-NMR, 400 MHz: Fig. S5 (ESI†).Synthesis of poly(N,N-dimethyl aminoethyl methacrylate) (pD1k)
To 60 mL DMF in a round-bottomed flask fitted with a magnetic stirrer were added CuIIBr2 (5.68 mg, 25.4 mmol), Me6TREN (40.8 mL, 152 mmol), and DMAEMA (60.0 mL, 0.356 mol), after which the solution was bubbled with Ar(g) for 15 min. MBPA was added (0.200 mL, 1.27 mmol), and the flask was sealed with a rubber septum and bubbled for 15 more min. The solution was then stirred for 37 h under UV light of 385 nm. The residue was precipitated thrice in hexane, and dried under high vacuum.SEC-MALLS (HFIP, 0.02 M KTFA): Mn = 161 kDa, Mw = 230 kDa, Đ = 1.43. The polymerization followed pseudo-first order kinetics strictly (Fig. S3, ESI†).
Synthesis of poly(tert-butyl acrylate)-32.5 kDa (pT250)
To a round-bottomed flask were added tert-butyl acrylate (57.1 mL, 0.390 mol), DMF (57 mL), ethyl α-bromoisobutyrate (0.229 mL, 1.56 mmol), CuIIBr2 (6.97 mg, 0.0312 mmol), and Me6TREN (50.1 μL, 0.2520 mmol). While the green solution was bubbled with Ar(g) for 30 min, 50 cm of copper wire was activated in 37% aqueous HCl, and subsequently rinsed with copious amounts of water. The wire was wrapped around a magnetic stirrer, and was added to the flask, which was then quickly sealed under postive Ar pressure with a rubber septum. The mixture was stirred for 5 h, after which a glassy residue was precipitated in ice-cold MeOH![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) water 2
water 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, which was redissolved in acetone and filtrated over a short plug of Al2O3. Thorough drying under high vacuum afforded a colourless, odorless glassy solid (38.2 g, 76%), which was de-tert-butylated to afford poly(acrylic acid).
1, which was redissolved in acetone and filtrated over a short plug of Al2O3. Thorough drying under high vacuum afforded a colourless, odorless glassy solid (38.2 g, 76%), which was de-tert-butylated to afford poly(acrylic acid).
SEC-MALLS (HFIP, 0.02 M KTFA): Mn = 32.511 kDa, Mw = 36.694 kDa, Đ = 1.13. Polymerization kinetics are given in Fig. S3 (ESI†).
Synthesis of poly(acrylic acid)-18 kDa (pA250)
Poly(tert-butyl acrylate (38.15 g, 0.2977 mol butyl ester) was dissolved in 220 mL of HFIP in a round-bottomed flask fitted with a magnetic stirrer. HCl (27.3 mL, 0.327 mol) in 100 mL of HFIP was slowly added using a dropping funnel. Immediately, a white precipitate formed, which was stirred for 3 d. The precipitate was collected by filtration, washed with fresh HFIP, and dried in vacuo to yield poly(acrylic acid) quantitatively. For use with terpyridines, it was further dialysed against large quantities of aqueous EDTA (10 mM) and then water.Size exclusion chromatography with multi-angle light scattering detection
Unmodified polyelectrolytes were characterized using size exclusion chromatography in tandem with multi-angle light scattering detector and viscometry, on an Omnisec Reveal system fitted with two PSS PFG columns. The mobile phase was HFIP with 0.02 M KTFA, at 0.7 ml min−1.Preparation of complexes
We added half an equivalent of MCl2 (with respect to terpyridyl content) to a solution of the non-modified polyelectrolyte, since two terpyridyl groups complex one metal ion. M2+ was either Mn2+, Zn2+, Co2+ or Ni2+. The polyelectrolyte was subsequently brought into a complex with the oppositely charged, terpyridylated chain. Polyelectrolytes were pipetted from stocks with a monomer concentration of 0.25 M with a background salt concentration of 0.1 M. After addition of a NaCl solution of a suitable concentration (between 0.5 and 1.5 M), the final polyelectrolyte concentration was brought to 0.1 M by addition of Milli-Q water. The protocol encourages a uniform concentration of M2+, minimizing distance from equilibrium. Complexes were equilibrated until transparent, which took an overnight wait for complexes with Mn2+ and Zn2+, but required prolonged centrifugation for Co2+ and Ni2+ at low gravitational fields. In the latter case, flat tubes with a diameter of 10 mm were used to allow yieldless loading of the sample, and the temperature was kept at 20 °C.To prepare polyelectrolyte gels of only pD, water was evaporated from a stock solution of pD with a terpyridyl content of 1% using a stream of nitrogen. Then, a quarter of an equivalent of either Mn2+, Zn2+, Co2+ or Ni2+ was added. The complexes were mixed on a turning rack for one week, and equilibrated as described above. The mass-over-volume fraction was chosen to match the fraction of polymers in a high-salt coacervate. To this end, we measured the coacervate volume using photographs of equilibrated samples. Subsequently we assumed that all of the polymer travels to the coacervate phase, setting the polymer mass-over-volume fraction to 16%.
Rheology
For mechanical characterization, we applied around 0.3 mL of dense phase onto the glass plate of an MCR-301 or MCR-501 (Anton Paar, Austria). For complexes that relaxed sufficiently fast, a 10 mm cone was used. For complexes characterized by a slow relaxation, a 10 mm plate was employed. After bringing the tool to trim gap and trimming, the dilute phase was poured over the geometry, and the tool was brought to gap. Geometries were closed off with a Peltier hood. Frequency sweeps between 0.1–100 Hz were performed at small strains in the linear viscoelastic regime (LVR, for our complexes, γ < 1). Step strain relaxation measurements were done at strains of 0.1–0.25. For samples that required prolonged measurement, a final frequency sweep was then recorded to assure evaporation did not alter the properties. Amplitude sweeps were conducted posteriorly, up to yield, to confirm that the prior measurements sampled the LVR.Results and discussion
We acquire unmodified polyelectrolytes pA and pD either commercially, or through synthesis under Cu-catalyzed conditions. We subsequently install tP groups by well-established derivatization chemistries. Complete experimental methods for synthesis of tP building blocks, polymerizations, and derivatization chemistry are given in ESI,† as well as characterization data for all polymers used (Fig. S7 and S5, ESI†). Fig. 2 portrays the resulting polymer inventory. | ||
| Fig. 2 A chemical toolbox for studying transiently crosslinked complex coacervates: coacervate-forming polyelectrolytes pA and pD, metal ions M2+, and terpyridines attached covalently to the polyelectrolytes allow to explore the dynamics sketched in Fig. 1. | ||
We prepare three families of complex: (1) complexes of unmodified polyelectrolytes (pA/pD), (2) complexes of divalent transition metals ions with only a single modified polyelectrolyte (pD01–M2+), (3) complexes in which one of the polyelectrolyte partners is modified (pA01/pD–M2+, pA/pD01–M2+), and (4) complexes in which both are terpyridylated (pA01/pD01–M2+). Non-TC3 complexes of families (1) and (2) know an extensive literature,20–22 whereas (3) and (4) have not been prepared nor studied.
Transient crosslinking of complex coacervates alters the phase diagram for ϕtP ≥ 10%
For a given pair of pA and pD, complex coacervation was found to occur up to some critical salt concentration cs*, typical for complexes of flexible polyelectrolytes, as is consistently reported in literature.21,23 For the pair pA250ϕ,A/pD1kϕ,B–Ni2+, with ϕA = 0, 0.42 or 1% and ϕB = 0 or 1%, we did not observe macroscopic complexes at salt strengths cs ≥ 1.0![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) M, regardless of the degree of terpyridylation on either polyelectrolyte or the addition of Ni2+. Similarly, for the pair pA23401/pD22201–M2+, we observed coacervation up to a cs of 0.9
M, regardless of the degree of terpyridylation on either polyelectrolyte or the addition of Ni2+. Similarly, for the pair pA23401/pD22201–M2+, we observed coacervation up to a cs of 0.9![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) M, regardless of the addition of even the stronger-binding Zn2+ or Ni2+ as metals. Thus, the added crosslinks do not strongly widen the two-phase region in the phase diagram, and neither do metal ions show any significant influence on complexes that present no terpyridine.
M, regardless of the addition of even the stronger-binding Zn2+ or Ni2+ as metals. Thus, the added crosslinks do not strongly widen the two-phase region in the phase diagram, and neither do metal ions show any significant influence on complexes that present no terpyridine.
However, we observed that even the addition of weakly binding Mn2+ to pA234/pD22210, which is non-complexing at 1.0![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) M
M![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) NaCl, separated a viscous phase. Hence, a plenitude of enthalpically attractive bonds can overrule the entropic unfeasibility24 of complex coacervation above cs*. The possibility to manipulate complex coacervate phase behaviour with even the weakest-binding metal ion suggests that TC3s have a particularly rich flow behaviour as well, the study of which is covered by the remainder.
NaCl, separated a viscous phase. Hence, a plenitude of enthalpically attractive bonds can overrule the entropic unfeasibility24 of complex coacervation above cs*. The possibility to manipulate complex coacervate phase behaviour with even the weakest-binding metal ion suggests that TC3s have a particularly rich flow behaviour as well, the study of which is covered by the remainder.
Rouse-like rheological signatures of complexes with short-lived transient crosslinks
We employ rheology to quantify the effect of non-covalent crosslinks on the transient network formed in coacervate complexes with added salt. The complexes are in the non-entangled regime (vide infra). Complex coacervates are distinguished from non-charged viscous polymer solution by the presence of inter-chain electrostatic interactions, the strength of which is controlled by the salt concentration. Non-crosslinked coacervates resist flow at short times because each chain forms multi-ion “ladder” bonds to several other chains,25 which act as a crosslink. Over time, the multi-ion pairs exchange between chains, initially enabling diffusion of small chain sections (“monomers”) at τ0, then larger chunks (τp), and finally entire chains at τR. The collective exchange act, at least for times longer than a few ms, yields behaviours consistent with the sticky Rouse model.8,26–28At long times, or low angular frequencies (ω < 2πτR−1), only whole-chain friction can contribute to the viscoelasticity. The coil density sets the modulus level GR, and for times much longer than τR, the shear relaxation modulus tends to a (Maxwellian) exponential decay
 | (1) |
The Fourier conjugate of G(t) is the frequency-dependent shear relaxation modulus G(ω), with real (storage) and imaginary (loss) parts G′(ω) and G′′(ω). Maxwell relaxation manifests itself as G′ ∝ ω2 and G′′ ∝ ω1 at low frequencies. At a certain ωc, G becomes equal to G′′. For a liquid with only one relaxation mode, ωc is the inverse of a characteristic relaxation time τc. For shorter times (higher frequencies), G′ plateaus at G0 and G′′ decreases rapidly with increasing frequency. However, viscoelastics with a broad relaxation spectrum typically give weak power laws in both G*(ω) and G(t).29,30 Such is also the case for complex coacervates.
Complex coacervates are Rouse-like, with signatures near to  and
and 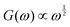 above the crossover frequency.8,31–34 The occurence of power laws of slope one-half is a feature of (sticky) Rouse theory,28 and can be seen as a result of the superposition of an array of Maxwell modes
above the crossover frequency.8,31–34 The occurence of power laws of slope one-half is a feature of (sticky) Rouse theory,28 and can be seen as a result of the superposition of an array of Maxwell modes  , with ωc,p evolving according to
, with ωc,p evolving according to
 | (2) |
The above slowest-mode analysis suffers from the weakness that only one relaxation time τR is treated (eqn (1)). At frequencies below ωc, this reproduces the frequency-dependent moduli sufficiently well to estimate the frequency of crossover. However, complex coacervates have a broad relaxation spectrum.8,32 Later, we will see that the effect of metal–ligand bonds on complex coacervates is profound when τX significantly outlives τR, broadening the relaxation spectrum even further. A number of previous authors has demonstrated the utility of Prony series, in which one takes the sum of a large number of Maxwell elements, which for complex coacervates can be viewed as having their origin in Rouse modes.8,17 Despite providing excellent agreement to data, the procedure requires iterative fitting, and is an ill-posed problem.
Here, we employ the fractional Maxwell liquid model (FMM). In the model, both stress and strain are fractional derivatives of time, which lead to forms for G(t) and G′, G′′(ω) that are able to capture highly broad relaxation spectra with excellent agreement with rheological data for complex liquids.29 Rouse dynamics are consistent with FMM in the sense that the Rouse model can be cast as a constitutive equation with a fractional time derivative of the stress of order one-half29,32 − Rouse relaxation can then be captured in only three parameters, without the need for a Prony series of N Rouse modes, and thus 2N free parameters. Moreover, recent work32 reveals that the scaling of the frequency-dependent storage and loss moduli deviates quite strongly from the  required by Rouse theory, whereas an FMM model provided an excellent fit. Whilst microscopic models and properties based on fractional constitutive equations reconcile uneasily,36 FMM proved more useful in our work than microscopic theories precisely because its flexibility allows a facile comparison between complex coacervate-dominated and metal–ligand dynamics.
required by Rouse theory, whereas an FMM model provided an excellent fit. Whilst microscopic models and properties based on fractional constitutive equations reconcile uneasily,36 FMM proved more useful in our work than microscopic theories precisely because its flexibility allows a facile comparison between complex coacervate-dominated and metal–ligand dynamics.
The fractional Maxwell model characterizes complex coacervate flow in three parameters
Sadman et al.32 outline the application of the fractional Maxwell model to complex coacervate rheology. For the complex modulus G(ω), FMM gives | (3) |
![[Doublestruck V]](https://www.rsc.org/images/entities/char_e179.gif) and
and ![[Doublestruck G]](https://www.rsc.org/images/entities/char_e16a.gif) are quasi-viscosities with units Pa sα and Pa sβ. As previously shown for complex coacervates,32α can be set to unity, which results in a simpler formulation of the model in terms of a viscosity (since then the power in
are quasi-viscosities with units Pa sα and Pa sβ. As previously shown for complex coacervates,32α can be set to unity, which results in a simpler formulation of the model in terms of a viscosity (since then the power in ![[Doublestruck V]](https://www.rsc.org/images/entities/char_e179.gif) is unity), a timescale and a modulus. Here, we use the traditional quasi-property36 formulation of eqn (3), but with α = 1, as suggested by Jaishankar.29 For β = 0, the equation reverts to the Maxwell model with
is unity), a timescale and a modulus. Here, we use the traditional quasi-property36 formulation of eqn (3), but with α = 1, as suggested by Jaishankar.29 For β = 0, the equation reverts to the Maxwell model with ![[Doublestruck G]](https://www.rsc.org/images/entities/char_e16a.gif) = E and
= E and ![[Doublestruck V]](https://www.rsc.org/images/entities/char_e179.gif) = η0, with E a plateau modulus and η0 a zero-shear viscosity. With α = 1 and
= η0, with E a plateau modulus and η0 a zero-shear viscosity. With α = 1 and  , the model gives Rouse dynamics.
, the model gives Rouse dynamics.
The time τc corresponding to the crossover frequency ωc can be written
 | (4) |
 ). The corresponding Gc can be calculated with Eqn 3. τc corresponds to the frequency 2πτc−1 at which G′ = G′′, and at which the relaxation modulus G(t) crosses over into an exponential decay. When a full measurement of either or both of these functions is not feasible due to slow relaxation, we shall use eqn (4) to provide an estimate. The procedure is validated in the Section on frequency sweeps of coacervates at cs*.
). The corresponding Gc can be calculated with Eqn 3. τc corresponds to the frequency 2πτc−1 at which G′ = G′′, and at which the relaxation modulus G(t) crosses over into an exponential decay. When a full measurement of either or both of these functions is not feasible due to slow relaxation, we shall use eqn (4) to provide an estimate. The procedure is validated in the Section on frequency sweeps of coacervates at cs*.
FMM gives the relaxation modulus G(t) as
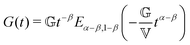 | (5) |
 | (6) |
![[Doublestruck V]](https://www.rsc.org/images/entities/char_e179.gif) ,
, ![[Doublestruck G]](https://www.rsc.org/images/entities/char_e16a.gif) as defined for eqn (3). We used a Python implementation of the ML function for the numerical work.37,38
as defined for eqn (3). We used a Python implementation of the ML function for the numerical work.37,38
Low-salt complexes at low terpyridyl content are largely unaffected by metal binding
We measure the mechanical relaxation spectrum of TC3s for different cs, M2+ identities, and degrees of terpyridylation. First, we turn to the limiting case of low-cs complexes with Mn2+, a metal that is weakly bound, and thus fast to associate and dissociate. The complex pA234/pD222–M2+ was prepared with various degrees of terpyridylation of pA and pD, and in presence and absence of Mn2+.At a cs of 0.2 and 0.6 M![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) NaCl, the frequency-dependent moduli exhibit features close to those expected for Rouse-like dynamics – loss and storage moduli tend to a scaling of respectively ω1 and ω2 at low frequencies, and cross at ωc, from which point on they increase with a slope below
NaCl, the frequency-dependent moduli exhibit features close to those expected for Rouse-like dynamics – loss and storage moduli tend to a scaling of respectively ω1 and ω2 at low frequencies, and cross at ωc, from which point on they increase with a slope below  . Fig. 3 shows G′,G′′(ω) of these complexes as black lines. At 0.2 M
. Fig. 3 shows G′,G′′(ω) of these complexes as black lines. At 0.2 M![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) NaCl (Fig. 3, two leftmost panels), we predominantly observe the effect of Rouse modes, whereas for 0.6 M
NaCl (Fig. 3, two leftmost panels), we predominantly observe the effect of Rouse modes, whereas for 0.6 M![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) NaCl we measure mostly in the terminal regime. Since Na+ and Cl− compete for bonds between the charges on pA and pD, the presence of salts speeds up polyelectrolyte complex relaxation.24,39 Multiple previous works have exploited this feature to access the entire relaxation spectrum8,33 through salt-time superposition: an increase in salt concentration is akin to an acceleration of dynamics through decrease of τ0 (eqn (2)).
NaCl we measure mostly in the terminal regime. Since Na+ and Cl− compete for bonds between the charges on pA and pD, the presence of salts speeds up polyelectrolyte complex relaxation.24,39 Multiple previous works have exploited this feature to access the entire relaxation spectrum8,33 through salt-time superposition: an increase in salt concentration is akin to an acceleration of dynamics through decrease of τ0 (eqn (2)).
 | ||
| Fig. 3 Storage (filled symbols) and loss (open symbols) moduli G′(ω) and G′′(ω) for TC3s with at low (left and center) to moderate (right) cs, with (large markers) and without (small dots) Mn2+. All symbols represent recorded data, lines are fits to eqn (3), vide infra. | ||
Inspection of loss and storage moduli gives direct access to the crossover frequency that defines a relaxation time for a given complex, τc (eqn (2), leftmost equality). We fitted the frequency-dependent moduli to eqn (3). The fits were always excellent (Fig. 3). We report the corresponding parameters in Table 1, along with crossover times and moduli τc and Gc. The fits now allow us to extrapolate to τc through eqn (4), for those cases where the crossover lies beyond the rheometric range.
![[Doublestruck V]](https://www.rsc.org/images/entities/char_e179.gif) and
and ![[Doublestruck G]](https://www.rsc.org/images/entities/char_e16a.gif) are in units of, respectively, (kPa s) and (kPa sβ). Crossover times are defined as 2πτc = ωc−1
are in units of, respectively, (kPa s) and (kPa sβ). Crossover times are defined as 2πτc = ωc−1
| Complex | M2+ | [NaCl] | β | ![[Doublestruck V]](https://www.rsc.org/images/entities/char_e179.gif) |
![[Doublestruck G]](https://www.rsc.org/images/entities/char_e16a.gif) |
τ c (ms) | G c (kPa) |
|---|---|---|---|---|---|---|---|
| pA234/pD22210 | ○ | 0.2 M | 0.43 | 42.3 | 28.8 | 90 | 66 |
| Mn2+ | 0.2 M | 0.45 | 86.1 | 33.5 | 79 | 55 | |
| pA23401/pD222 | ○ | 0.2 M | 0.35 | 9.0 | 19.3 | 55 | 32 |
| Mn2+ | 0.2 M | 0.36 | 10.8 | 11.8 | 176 | 12 | |
| pA23410/pD222 | ○ | 0.6 M | 0.45 | 0.5 | 3.9 | 0.8 | 80 |
| Mn2+ | 0.6 M | 0.40 | 2.5 | 10.3 | 9.0 | 40 |
For complexes with no additional crosslinks, we can equate τc to τR, the whole-chain Rouse time, which at 0.2 M NaCl is 55 ms, and at 0.6 M NaCl is reduced to 0.8 ms for pA234/pD22210. Reducing the amount of terpyridines on the chain reduces τR and GR to the levels of an unmodified complex at the same cs. Thus, we conclude that thickening of complexes due to hydrophobicity of terpyridine is a small yet significant effect.
We now turn to the question whether transient crosslinks with a lifetime τXbelow the coacervate relaxation time influence flow behaviour, i.e., whether transiently crosslinked coacervates are coacervate-like. At 0.2 M NaCl, the difference in terms of G′,G′′(ω) from the uncrosslinked complex is small for both lightly (1%) and heavily (10%) terpyridylated participants. However, at 0.6 M NaCl, as we approach cs*, the effect of Mn2+ is more pronounced. The transient bonds slow down relaxation, and contribute more strongly to the modulus at the crossover frequency. Fig. 3 shows frequency sweeps for Mn2+-crosslinked complexes with marked, colored lines. Nonetheless, short-lived transient crosslinks perturb pA/pD complexes only weakly.
Encouragingly, the addition of slower transient bonds did not hinder the ability of the FMM to capture the rheological behaviour over the complete frequency range employed. We see that the tPy–Mn2+ bonds are not consistently effective in slowing down relaxation at low salt strength. At higher salt (0.6 M), the effect of Mn2+ is to shift the crossover point slightly. β values were between 0.35 and 0.45, in accordance with the work of Sadman et al.32
The “ideal” case of Rousian chains corresponds to an FMM with α = 1 and β = 0.5, which manifests itself as a 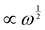 scaling in both loss and storage moduli (for “frozen” Rouse chains in between crosslinks, α = 0.5 and β = 1). The inclusion of hydrodynamics (Zimm model) facilitates relaxation,40 and increases β up to 0.67.41 The discrepancy in our data from a Rouse fluid is thus not likely attributable to a contribution from hydrodynamics. Rather, the disagreement could stem from the bias towards predominantly fluid-like (G′′ > G′) frequencies, which, however, is contradicted by the decrease of β as the bond lifetimes in the complex are lengthened by a decrease in salt. Alternatively, one could argue that we sample an excess of longer “ladder” bonds due to the slow equilibration of the complex coacervate. The suggestion of non-ergodicity does not agree with the near-Rouse dynamics of pA234/pD22210, which should be the slowest sample to equilibrate on account of low cs and high density of terpyridyl moieties.
scaling in both loss and storage moduli (for “frozen” Rouse chains in between crosslinks, α = 0.5 and β = 1). The inclusion of hydrodynamics (Zimm model) facilitates relaxation,40 and increases β up to 0.67.41 The discrepancy in our data from a Rouse fluid is thus not likely attributable to a contribution from hydrodynamics. Rather, the disagreement could stem from the bias towards predominantly fluid-like (G′′ > G′) frequencies, which, however, is contradicted by the decrease of β as the bond lifetimes in the complex are lengthened by a decrease in salt. Alternatively, one could argue that we sample an excess of longer “ladder” bonds due to the slow equilibration of the complex coacervate. The suggestion of non-ergodicity does not agree with the near-Rouse dynamics of pA234/pD22210, which should be the slowest sample to equilibrate on account of low cs and high density of terpyridyl moieties.
Returning to the influence of metal–ligand transient crosslinks on the linear viscoelasticity of complex coacervates, we hypothesize that the distance between the Rousian relaxation time τR and metal–ligand crosslink time τX dictates the effect of the latter. In the following sections, we take the tools outlined so far to examine the case of near-cs* complexes, where the crosslink times can be expected to significantly outlast τR.
Metal–ligand dissocation rates dictate relaxation times of complexes at high salt
We prepared complexes of pA250 and terpyridylated pD1k01 at a salt concentration very near to dissolution (0.9 M). Metal ions were either Mn2+, Zn2+, Co2+, or Ni2+, and were introduced as pre-mixed with pA. We employed step strain measurements of G(t) up to long waiting times (>24 h), combined with frequency sweeps to address the widest range of relaxation times. G(ω) and G(t) were recorded for all complexes but pD01–Mn2+, which did not give rise to enough torque to allow a meaningful measurement of G(t).Unlike the low-salt, fast-metal complexes seen in Fig. 3, the high-salt complexes pA/pD01–M2+ were dramatically changed by the choice of metal ion in the transient metal–ligand bonds. Whereas fast metals Mn2+ and Zn2+ showed the tail of a decaying function, slow metals Co2+ and Ni2+ gave decay only after prolonged waiting (>104 s). Fig. 4 (right) shows the pronounced effect of metal–ligand binding in terms of G(t) (marks represent data).
 | ||
| Fig. 4 Relaxation moduli G(t) for materials with different metal–ligand crosslinks for (left) non-coacervate samples and (right) coacervates at near-critical cs. Symbols represent (part of) the collected data, while solid lines are fits to eqn (5). | ||
Following literature on polymeric networks with metal–ligand crosslinks, we attempted to model the relaxations with Maxwell models (eqn (1)),42 and stretched exponentials.17 The Maxwell model approximated the data poorly, whereas the analysis with a sum of two stretched exponentials was complicated by multiple parameter sets offering similarly low residuals. The decays are not exponential, and are in fact power law-like in the initial several orders of magnitude in t. However, as is clear in the right-hand panel of Fig. 4, we were able to capture the entire relaxation for all samples with the FMM form for G(t) given by eqn (5).
As was the case for the mainly coacervate-like complex with Mn2+ and lower cs, α was always kept at 1, meaning that the complexes are ultimately fluids, albeit with sometimes extreme viscosities. Unlike the coacervate-like complexes, β was much closer to 0, indicating Maxwell-like response. In the case of near-zero β, the pseudo-property ![[Doublestruck G]](https://www.rsc.org/images/entities/char_e16a.gif) can be interpreted as close to a plateau modulus G0. We list the parameters used to achieve the fits of G(t) in Table 1. Using eqn (3) and (4), we calculated the crossover values for relaxation time and modulus. In the case of complexes with no metal–ligand bonds, an extrapolation was used, with τc assumed to be in exponential decay with cs.33 For Mn2+, we used a fit to G(ω).
can be interpreted as close to a plateau modulus G0. We list the parameters used to achieve the fits of G(t) in Table 1. Using eqn (3) and (4), we calculated the crossover values for relaxation time and modulus. In the case of complexes with no metal–ligand bonds, an extrapolation was used, with τc assumed to be in exponential decay with cs.33 For Mn2+, we used a fit to G(ω).
With all metals, the relaxation time is significantly lengthened by the presence of transient metal–ligand bonds. Fig. 4 confirms that the relaxation times follow the order of binding affinities (equilibrium constants) Mn2+ < Zn2+ < Co2+ < Ni2+.19,43 For the last three, the increase in measured τc is at least thousandfold. Ni2+ gives rise to particularly slow relaxation,  approaching 109 (Table 2).
approaching 109 (Table 2).
![[Doublestruck V]](https://www.rsc.org/images/entities/char_e179.gif) and
and ![[Doublestruck G]](https://www.rsc.org/images/entities/char_e16a.gif) are in units of, respectively, (kPa s) and (kPa sβ). A minus sign (−) means that an estimate is not meaningful, since the data are dominated by inertial effects or slip
are in units of, respectively, (kPa s) and (kPa sβ). A minus sign (−) means that an estimate is not meaningful, since the data are dominated by inertial effects or slip
| Complex | M2+ | [NaCl] | β | ![[Doublestruck V]](https://www.rsc.org/images/entities/char_e179.gif) |
![[Doublestruck G]](https://www.rsc.org/images/entities/char_e16a.gif) |
τ c (s) | G c (kPa) |
|---|---|---|---|---|---|---|---|
| pA250/pD1k01 | ○ | 0.9 M | — | — | — | ≤0.6 × 10−3 | <0.01 |
| Mn2+ | 0 | 0.6 × 10−3 | 0.4 | 1.5 × 10−3 | 0.2 | ||
| Zn2+ | 0.103 | 0.340 | 1.0 | 238 × 10−3 | 0.6 | ||
| Co2+ | 0.006 | 4.6 × 104 | 2.2 | 22.5 × 103 | 1.0 | ||
| Ni2+ | 0.009 | 2.8 × 105 | 1.9 | 0.16 × 106 | 0.9 | ||
| 0.8 M | 0.015 | 2.5 × 105 | 1.8 | 0.16 × 106 | 0.8 | ||
| pD1k01 | Mn2+ | 0 M | — | — | — | ≤1 × 10−3 | <0.01 |
| Zn2+ | 0.053 | 0.06 | 0.75 | 68 × 10−3 | 0.4 | ||
| Co2+ | 0.014 | 2.7 × 104 | 2.0 | 13.6 × 103 | 0.9 | ||
| Ni2+ | 0.015 | 2.1 × 104 | 1.4 | 20.9 × 103 | 0.5 | ||
We attribute the increase of relaxation times in complexes that contain pD01 and an M2+ species to the formation of a physical network inside the complex coacervate matrix, as pictured in Fig. 1. With the help of simple scaling theories,44 knowledge of the form factor from neutron scattering of pD in a pA/pD complex of similar degrees of polymerization45 allows to approximate the inter-terpyridine length Rx. Polyelectrolytes in coacervates obey Gaussian statistics,45Rx2 = Nlk2, with lk the persistence length and N the amount of Kuhn segments between crosslinks.45 Taking lk at 16 nm, we arrive at an Rx of 20 nm for 1% terpyridylated chains (100 chemical monomers between terpyridine units). Given one elastically active chain per Rx3, classical rubber elasticity predicts an elastic modulus of 0.5 kPa, which underestimates G0′ for complexes with the slow metals, but is a reasonable estimate for complexes with Mn2+ and Zn2+.
Additionally, scaling theory allows to estimate whether intra-chain crosslinks are expected to play a role in the network. The possibility for polymers to crosslink with themselves is often overlooked, but results in crosslinks that are elastically inactive.46–48 We assess the importance of self-crosslinks by counting the amount of terpyridines within one volume spanned by Rx – this is the bulk concentration of terpyridines ctPy multiplied by Rx3. Our coacervates near cs* have a ctPy of 5 mM, which corresponds to 25 terpyridines within the volume, indicating a self-crosslinking efficiency of 4%. Thus, while present in the complexes, inactive, or “self”, crosslinks do not likely have a dominant influence on G0′.
Importantly, the rather large internode spacing suggests that there is ample space to guarantee appropriate binding geometry for the [2+1] complex, which is on the order of 2 nm. While no deviation from the expected stoichiometry due to strain49 is expected, we did not quantify the stoichiometry, since the absolute number of crosslinks does not affect our comparison between metal identities. We note that the scaling analysis above is an order-of-magnitude estimate, and that a full structure study using deuterated “tracer” polyelectrolytes is appropriate to address the issue of structure fully. Since we focus on the dynamics of the hybrid complexes, such a study is beyond the scope of the present contribution.
In complex coacervates at high salt in which one polyelectrolyte is terpyridylated, the metal–ligand bond strengths dominate the rapid relaxation mechanisms that are native to complex coacervates. Only at frequencies so rapid to be inaccessible by rheology would one expect to retrieve a contribution of the coacervate. At frequencies measurable with a commercial rheometer, the linear viscoelasticity bears witness only to relaxation from metal–ligand dissocation. Transient bonds offer a salt-independent control over high-cs polyelectrolyte complexes: they can be tuned from viscous to indefinitely mechanically stable at one and the same salt concentration.
Non-coacervate complexes experience less slowing-down than their coacervate counterparts
We then turned to the question whether the extreme response to metal ion identity is intrinsic to pD1k01, or a result of participation of both pA and pD. We inquired into whether the non-dominant contribution of the coacervate (at ) is at all present in the rheology, or whether the coacervate merely provides a water-insoluble phase that then accepts metal–ligand viscoelasticity. First, we repeated the experiment with pA/pD–Ni2+ at a slightly lower cs of 0.8 M, which resulted in exactly the same relaxation time, and negligible differences in the FMM fits (Table 2). Thus, at long times, complexes with Ni2+ crosslinks are entirely dominated by the metal–ligand dissociation time.
) is at all present in the rheology, or whether the coacervate merely provides a water-insoluble phase that then accepts metal–ligand viscoelasticity. First, we repeated the experiment with pA/pD–Ni2+ at a slightly lower cs of 0.8 M, which resulted in exactly the same relaxation time, and negligible differences in the FMM fits (Table 2). Thus, at long times, complexes with Ni2+ crosslinks are entirely dominated by the metal–ligand dissociation time.
Moreover, we made non-coacervate metal complexes with terpyridylated pD, denoted pD01–M2+ (note the absence of pA). The polymer mass-over-volume fraction of the coacervate complexes at 0.9 M was estimated at 0.16, which was subsequently used as the polymer concentration in the pD01-M2+ complexes (see Experimental section for details).
Non-coacervate complexes pD01–M2+ showed strikingly similar linear viscoelasticity to the metalated coacervate samples (Fig. 4, leftmost panel), and were amenable to the same FMM analysis with eqn (5). In the bottom part of Table 2, we list fit parameters and crossover features. For Mn2+, it was difficult to assess the reliability of the data due to low torque: complexes with Mn2+ do not have a distinguishable contribution of terpyridylation at this level of analysis.
β values were close to zero for Zn2+, Co2 and Ni2+, which means that the response is nearly Maxwellian, and ![[Doublestruck G]](https://www.rsc.org/images/entities/char_e16a.gif) essentially a plateau modulus. Note that for an FMM liquid with β > 0, Gc <
essentially a plateau modulus. Note that for an FMM liquid with β > 0, Gc < ![[Doublestruck G]](https://www.rsc.org/images/entities/char_e16a.gif) – an analysis of crossover moduli in the Maxwellian sense is thus somewhat misleading. Rather,
– an analysis of crossover moduli in the Maxwellian sense is thus somewhat misleading. Rather, ![[Doublestruck G]](https://www.rsc.org/images/entities/char_e16a.gif) is proportional to the G(t) at t = 0 (eqn (5)).
is proportional to the G(t) at t = 0 (eqn (5)).
Due to the responses being close to Maxwellian, we can approximately compare τc and ![[Doublestruck G]](https://www.rsc.org/images/entities/char_e16a.gif) for pA/pD01–M2+ to the corresponding non-coacervate pD01–M2+ systems. The values of
for pA/pD01–M2+ to the corresponding non-coacervate pD01–M2+ systems. The values of ![[Doublestruck G]](https://www.rsc.org/images/entities/char_e16a.gif) agree up to a factor of 1.3, which indicates that the effective crosslinking densities are sufficiently close to allow a comparison of τc. The striking similarities in β and
agree up to a factor of 1.3, which indicates that the effective crosslinking densities are sufficiently close to allow a comparison of τc. The striking similarities in β and ![[Doublestruck G]](https://www.rsc.org/images/entities/char_e16a.gif) preclude major structural changes. Such a comparison of τc shows that each non-coacervate sample relaxes significantly faster than the corresponding high-salt coacervate sample. The difference is especially striking in the case of Ni2+, where τc is slowed down more than tenfold. We analyze the short-time response of the complexes more closely using G(ω) in the subsequent section.
preclude major structural changes. Such a comparison of τc shows that each non-coacervate sample relaxes significantly faster than the corresponding high-salt coacervate sample. The difference is especially striking in the case of Ni2+, where τc is slowed down more than tenfold. We analyze the short-time response of the complexes more closely using G(ω) in the subsequent section.
Entanglements have proven to be an important contribution to the slow relaxation of coacervate complexes of high molecular weight polyelectrolytes.33 However, we do not ascribe the plateaus in G(t) and high τ to entanglement-like phenomenology, at least not at the polymer concentration of 16% m/v. The pD01 complex with Mn2+ is a liquid of poor viscosity, and the corresponding coacervate complex pA/pD01–Mn2+ shares a very similar flow behaviour. While the higher Mn of the poly[cation] suggests that entanglements could be important, the relaxation times of pA234/pD222 and pA250/pD1k are in fact very close, more representative of the molecular weight derived from conversion during polymerization (see Fig. S8 (ESI†) and the accompanying discussion). Thus, slowed-down pA/pD01–M2+ complexes do not have a significant contribution of entanglements to their viscoelasticity.
Frequency-dependent moduli agree with the parameters determined from relaxation fits
Given the wide separation between τR and τc for complexes with metals slower than Mn2+, we would expect high similarities in the short-time responses in both families of complexes, pD01–M2+ and pA/pD01–M2+. On the other hand, any differences would signify a change in network structure on a rather short length scale. G(t) data are not reliable below 100 ms, and therefore we measured G′,G′′(ω) using oscillatory shear.Frequency sweeps were consistent with relaxation moduli. To demonstrate the correspondence on a quantitative level, we plotted graphs of G′, G′′(ω) calculated using Eqn 3 with the parameters previously obtained for the same samples in step shear (Table 2). Fig. 5, shows measured G′, G′′(ω) as marks, and calculated G′, G′′(ω) as black lines. Note that the black lines are not fits to the frequency-dependent data, they are merely the Fourier conjugate of eqn (5) with the appropriate parameters.
 | ||
| Fig. 5 Real and imaginary parts of frequency-dependent moduli G (filled symbols) and G′′(ω) (open symbols). Symbols are measured data, one in two or three points is marked. Molarities refer to cs. The high-frequency ends were not truncated, and the upturn in moduli is related to slip and tool inertia. Black lines are graphs of eqn (3) with parameters as fitted for the corresponding relaxation modulus G(t), i.e. measured in the same run. Coloured lines (bottom panels) are fits to a two-component fractional Maxwell liquid. | ||
The agreement was excellent for Zn2+, whereas it leaves something to be desired for the slower metals. This is a consequence of the fact that most of G(t) captures exclusively plateau-like regimes for Co2+ and Ni2+, so any sloping-up features are missed. Additionally, measurements of G(ω) were plagued by problems due to slip and inertia at higher frequencies, which manifests as the erratic increases in both curves at high frequencies. By using a sum of two FMM elements, we were able to fit the whole frequency range (colored lines in Fig. 5). However, the extracted parameters are of very limited use for our analysis, since they indicate β > 0.5. Complex coacervates have finite relaxation times, and therefore we attribute the high-frequency anomalies to slip and inertia.
However, G′ was reliably found to arrive to a plateau-like feature at the value predicted by the FMM fits of the step strain measurements. Additionally, we do not see evidence for a different short-time relaxation mechanism for coacervate and non-coacervate complexes from the frequency sweeps, since features in G(ω) and G(t) are highly similar.
Coacervate-metal–ligand synergy in transiently crosslinked complex coacervates
In the above, we have shown that metal–ligand complexation offers an attractive avenue to program the rheological fate of complex coacervates. Given the potential applicability of complex coacervates in underwater adhesives and other future technologies, ways of changing their modulus and relaxation behaviour “on demand” attract interest. For complex coacervates at low cs, thus with a long τR, with quickly-dissociating metals, we find that metal–ligand binding gives only a modest contribution to the rheology. The timescale of tPy–M2+-dissocation is not separated from the dissocation time of a carboxylate-dimethylammonium bond. However, when the distance between the coacervate relaxation time and the metal–ligand dissociation time is clearly separated, the linear viscoelasticity is strongly dominated by the latter.At near-critical salt concentrations, where the complex coacervate contributes to viscoelasticity only at extremely high frequencies, we retrieve similar behaviour for metal–ligand-only complexes of pD01 (without poly[anion] partner) and the coacervate-metal–ligand complexes. However, the relaxation times are vastly different, despite similar instantaneous and short-time moduli. Given the obvious benefits of having two faster (i.e. easily injectable) building blocks assemble into a much slower one for e.g. underwater adhesion, we identify the slowing-down effect of the coacervate on metal–ligand network formation as a synergistic effect. However, the elucidation of the structural cause is beyond the scope of the present contribution, and is a topic of ongoing investigation.
To widen the scope of the idea of metal–ligand-coacervate synergy, we took the tPy−Zn2+ motif into a complex of pD01 with not pA but poly(2-acrylamido-2-methylpropylsulfonic acid) (pAMPS), prepared near the critical salt strength (1.3 M for this pair) and at much lower salt (0.6 M). G(t) measurements again showed that coacervates without additional transient bonds have short relaxation times, untractable (<1 ms) at cs*, but easily estimable at 0.6 M (10 ms) (see Table 3 for relaxation times and FMM fit parameters and Fig. 6 for measured and fit G(t) data).
![[Doublestruck V]](https://www.rsc.org/images/entities/char_e179.gif) and
and ![[Doublestruck G]](https://www.rsc.org/images/entities/char_e16a.gif) are in units of, respectively, (kPa s) and (kPa sβ). A hyphen (−) means that any estimate is not meaningful, since the data are dominated by inertial effects or slip
are in units of, respectively, (kPa s) and (kPa sβ). A hyphen (−) means that any estimate is not meaningful, since the data are dominated by inertial effects or slip
| Complex | M2+ | [NaCl] | β | ![[Doublestruck V]](https://www.rsc.org/images/entities/char_e179.gif) |
![[Doublestruck G]](https://www.rsc.org/images/entities/char_e16a.gif) |
τ c (s) |
|---|---|---|---|---|---|---|
| pAMPS800/pD1k01 | ○ | 0.6 M | 0.211 | 0.29 | 6.6 | 10 × 10−3 |
| Zn2+ | 0.6 M | 0.094 | 53.5 × 103 | 6.6 | 8.3 | |
| ○ | 1.3 M | — | — | — | ≤1 × 10−3 | |
| Zn2+ | 1.3 M | 0.078 | 0.36 | 0.66 | 453 × 10−3 |
 | ||
| Fig. 6 Relaxation moduli G(t) at medium high cs for metal–ligand-coacervate system pAMPS–pD01–Zn2+. Symbols correspond to collected data, solid lines are fits to eqn (5). | ||
Both critical and medium-salt complexes were significantly slowed down by addition of Zn2+ with respect to the native relaxation time of the metal-less complex. The cs*-complex closely resembled the 0.9 M scenario for pA/pD–Zn2+ (compare Fig. 4, left), which shows that complex coacervates generally slow down tPy-metal bonds, even at the critical salt concentration. For the lower cs of 0.6 M, we witness a slowdown of almost three orders of magnitude in time with respect native dynamics, and a twenty-fold change as compared to the complex at critical salt.
Thus, the relaxation time of a coacervate-metal–ligand complex is not solely set by the dissociation time of the metal–ligand complex. Instead, the dissociation time is a limiting value that complexes approach as their viscosity decreases. Throughout two different poly(anion) chemistries, we show that the relaxation time of a complex can outlast both the native complex coacervate relaxation time, as well as the relaxation time of a complex with only one of the polyelectrolyte partners.
Conclusion
We demonstrate with pA/pD complexes in which tP groups are incorporated that complex coacervates can be stiffened through the use of metal–ligand complexes. While low tP contents do not increase the salt tolerance of the pA/pD complex, we show that the incorporation of 10% tP widens the complex coacervation window. This is attributable to the hydrophobic effect, given that terpyridine is insoluble in water. The effect of tP–M2+ complexes on the dynamics of the coacervate-metal–ligand complex depends on the stability of the metal–ligand bond, but also on the “native” relaxation time inherent in the coacervate. When the “native” timescale is longer than the metal–ligand dissociation time, effects are only seen for high tPy contents, which again could be explained by the hydrophobic effect. However, for metal–ligand bonds that significantly outlast the native relaxation times, we find a dramatic slowing-down of the coacervate-metal–ligand complex. This is attributed to the metal–ligand bonds now acting as an impermanent crosslink. In fact, the transient bonds can appear as rather permanent, with relaxation times in excess of 1 day for Ni2+ at a tPy content of only 1% on one of the coacervating partners.Owing to the far slower time signature of such bonds, the coacervate's native dynamics are mostly invisible in the rheology, and coacervate-metal pA/pD01–M2+ and non-coacervate-metal pD01–M2+ complexes appear highly similar in their high-frequency dynamics. However, we see unaccounted-for slowing-down in the long-time behaviour of the coacervate complexes with respect to their non-coacervate counterparts. We see this as a form of coacervate-metal–ligand synergy, in which two relatively fast elements come together to flow much more slowly together. The requirements of on-demand setting adhesives are highly compatible with the synergistic characteristics of transiently crosslinked complex coacervates. Future studies should point out whether ligands that offer better biocompatibility (such as histidine) or responsivity (catechols) offer similar benefits. A wider choice of ligands would also allow to address the influence of hydrophobicity.
In addition, we expose the utility of the fractional Maxwell model in capturing viscoelastic phenomena encountered in complex liquids with diverse mechanisms accounting for their constrained flow. All our results can be fitted with equations derived from one and the same constitutional equation. Thus, fractional Maxwell models can be successfully applied in the design of complex fluids.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
We thank Mariska Brüls for a part of the rheological work, and Jasper van der Gucht for helpful discussions. We acknowledge funding by the Dutch Research Council (NWO).References
- A. H. Hofman, I. A. van Hees, J. Yang and M. Kamperman, Adv. Mater., 2018, 1704640, 1704640 CrossRef PubMed.
- C. S. Wang and R. J. Stewart, Biomacromolecules, 2013, 14, 1607–1617 CrossRef CAS PubMed.
- R. J. Stewart, C. S. Wang and H. Shao, Adv. Colloid Interface Sci., 2011, 167, 85–93 CrossRef CAS.
- H. G. Silverman and F. F. Roberto, Mar. Biotechnol., 2007, 9, 661–681 CrossRef CAS PubMed.
- R. J. Stewart, T. C. Ransom and V. Hlady, J. Polym. Sci., Part B: Polym. Phys., 2011, 49, 757–771 CrossRef CAS.
- M. Cui, S. Ren, S. Wei, C. Sun and C. Zhong, APL Mater., 2017, 5, 116102 CrossRef.
- W. C. Blocher and S. L. Perry, J. Polym. Sci., Part B: Polym. Phys., 2017, 9, 76–78 Search PubMed.
- E. Spruijt, M. A. Cohen Stuart and J. Van Der Gucht, Macromolecules, 2013, 46, 1633–1641 CrossRef CAS.
- I. van Hees, A. H. Hofman, R. Fokkink and M. Kamperman, Macromolecules, 2021 Search PubMed , in preparation.
- M. Dompé, F. J. Cedano-serrano, O. Heckert, N. V. D. Heuvel, J. V. D. Gucht, Y. Tran, D. Hourdet, C. Creton and M. Kamperman, Adv. Mater., 2019, 31, 1808179 CrossRef PubMed.
- M. Dompé, F. J. Cedano-serrano, M. Vahdati, L. V. Westerveld, D. Hourdet, C. Creton, J. V. D. Gucht, T. Kodger and M. Kamperman, Adv. Mater. Interfaces, 2020, 7, 1901785 CrossRef.
- Q. Zhao, D. W. Lee, B. K. Ahn, S. Seo, Y. Kaufman, J. Israelachvili and J. H. Waite, Nat. Mater., 2016, 15, 407–412 CrossRef CAS PubMed.
- L. Zhang, V. Lipik and A. Miserez, J. Mater. Chem. B, 2016, 4, 1544–1556 RSC.
- S. Seo, S. Das, P. J. Zalicki, R. Mirshafian, C. D. Eisenbach, J. N. Israelachvili, J. H. Waite and B. K. Ahn, J. Am. Chem. Soc., 2015, 137, 9214–9217 CrossRef CAS PubMed.
- M. Dompe, M. Vahdati, F. V. Ligten, F. J. Cedano-serrano, D. Hourdet, C. Creton, M. Zanetti, P. Bracco, J. V. D. Gucht, T. Kodger and M. Kamperman, ACS Appl. Polym. Mater., 2020, 2, 1722–1730 CrossRef CAS.
- I. A. V. Hees, P. J. M. Swinkels, R. G. Fokkink, A. H. Velders, I. K. Voets, J. V. D. Gucht and M. Kamperman, Polym. Chem., 2019, 10, 3127–3134 RSC.
- S. C. Grindy, R. Learsch, D. Mozhdehi, J. Cheng, D. G. Barrett, Z. Guan, P. B. Messersmith and N. Holten-Andersen, Nat. Mater., 2015, 14, 1210–1216 CrossRef CAS PubMed.
- J. Yang, M. A. Cohen Stuart and M. Kamperman, Chem. Soc. Rev., 2014, 43, 8271–8298 RSC.
- R. H. Holyer, C. D. Hubbard, S. F. Kettle and R. G. Wilkins, Inorg. Chem., 1966, 5, 622–625 CrossRef CAS.
- K. A. Aamer and G. N. Tew, Macromolecules, 2007, 40, 2737–2744 CrossRef CAS.
- E. Spruijt, A. H. Westphal, J. W. Borst, M. A. Cohen Stuart and J. Van Der Gucht, Macromolecules, 2010, 43, 6476–6484 CrossRef CAS.
- J. Brassinne, F. D. Jochum, C. A. Fustin and J. F. Gohy, Int. J. Mol. Sci., 2015, 16, 990–1007 CrossRef CAS.
- L. Li, S. Srivastava, M. Andreev, A. B. Marciel, J. J. De Pablo and M. V. Tirrell, Macromolecules, 2018, 51, 2988–2995 CrossRef CAS.
- J. Fu and J. B. Schlenoff, J. Am. Chem. Soc., 2016, 138, 980–990 CrossRef CAS PubMed.
- J. A. Jaber and J. B. Schlenoff, J. Am. Chem. Soc., 2006, 128, 2940–2947 CrossRef CAS PubMed.
- F. G. Hamad, Q. Chen and R. H. Colby, Macromolecules, 2018, 51, 5547–5555 CrossRef CAS.
- C. S. Y. Tan, G. Agmon, J. Liu, D. Hoogland, E. R. Janeček, E. A. Appel and O. A. Scherman, Polym. Chem., 2017, 8, 5336–5343 RSC.
- M. Rubinstein and A. N. Semenov, Macromolecules, 1998, 31, 1386–1397 CrossRef CAS.
- A. Jaishankar and G. H. McKinley, Proc. R. Soc. A, 2013, 469, 20120284 CrossRef.
- P. Patricio, arXiv:1506.01934 (physics.bio-ph), 2015.
- P. C. Suarez-Martinez, P. Batys, M. Sammalkorpi and J. L. Lutkenhaus, Macromolecules, 2019, 52, 3066–3074 CrossRef CAS.
- K. Sadman, Q. Wang, Y. Chen, B. Keshavarz, Z. Jiang and K. R. Shull, Macromolecules, 2017, 50, 9417–9426 CrossRef CAS.
- M. Yang, J. Shi and J. B. Schlenoff, Macromolecules, 2019, 52, 1930–1941 CrossRef CAS.
- K. Sadman, Q. Wang and K. R. Shull, ACS Macro Lett., 2019, 8, 117–122 CrossRef CAS.
- P.-G. De Gennes, Introduction to Polymer Dynamics, Cambridge University Press, 1990 Search PubMed.
- G. W. Blair, B. C. Veinoglou and J. E. Caffyn, Proc. R. Soc. A, 1947, 189, 69–87 CAS.
- R. Garrappa, The Mittag-Leffler function, 2020 Search PubMed.
- K. Hinsen, The Mittag-Leffler function in Python, 2020, https://github.com/khinsen/mittag-leffler Search PubMed.
- Q. Wang and J. B. Schlenoff, Macromolecules, 2014, 47, 3108–3116 CrossRef CAS.
- P. G. De Gennes, Macromolecules, 1976, 9, 594–598 CrossRef CAS.
- R. L. Bagley and P. J. Torvik, J. Rheol., 1983, 27, 201–210 CrossRef CAS.
- T. Rossow and S. Seiffert, Polym. Chem., 2014, 5, 3018–3029 RSC.
- R. Hogg and R. G. Wilkins, J. Chem. Soc., 1962, 341–350 RSC.
- P.-G. De Gennes, Scaling concepts in polymer physics, Cornell University Press, Ithaca and London, 1979, p. 43 Search PubMed.
- E. Spruijt, F. A. Leermakers, R. Fokkink, R. Schweins, A. A. Van Well, M. A. Cohen Stuart and J. Van Der Gucht, Macromolecules, 2013, 46, 4596–4605 CrossRef CAS.
- P. J. Skrzeszewska, F. A. De Wolf, M. W. Werten, A. P. Moers, M. A. Cohen Stuart and J. Van Der Gucht, Soft Matter, 2009, 5, 2057–2062 RSC.
- D. Xu, J. L. Hawk, D. M. Loveless, S. L. Jeon and S. L. Craig, Macromolecules, 2010, 43, 3556–3565 CrossRef CAS.
- M. Zhong, R. Wang, K. Kawamoto, B. D. Olsen and J. A. Johnson, Science, 2016, 353, 1264–1268 CrossRef CAS PubMed.
- J. Wang, R. H. De Kool and A. H. Velders, Langmuir, 2015, 31, 12251–12259 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/d0sm02236e |
| This journal is © The Royal Society of Chemistry 2021 |

