DOI:
10.1039/D0SM02210A
(Review Article)
Soft Matter, 2021,
17, 4226-4253
Smoothed profile method for direct numerical simulations of hydrodynamically interacting particles
Received
16th December 2020
, Accepted 9th March 2021
First published on 17th March 2021
Abstract
A general method is presented for computing the motions of hydrodynamically interacting particles in various kinds of host fluids for arbitrary Reynolds numbers. The method follows the standard procedure for performing direct numerical simulations (DNS) of particulate systems, where the Navier–Stokes equation must be solved consistently with the motion of the rigid particles, which defines the temporal boundary conditions to be satisfied by the Navier–Stokes equation. The smoothed profile (SP) method provides an efficient numerical scheme for coupling the continuum fluid mechanics with the dispersed moving particles, which are allowed to have arbitrary shapes. In this method, the sharp boundaries between solid particles and the host fluid are replaced with a smeared out thin shell (interfacial) region, which can be accurately resolved on a fixed Cartesian grid utilizing a SP function with a finite thickness. The accuracy of the SP method is illustrated by comparison with known exact results. In the present paper, the high degree of versatility of the SP method is demonstrated by considering several types of active and passive particle suspensions.
1 Introduction
The dynamics of particles dispersed in a host solvent, i.e., how they react to and affect the motion of the fluid, is fundamental to many areas of the physical sciences and provides the basis for many engineering applications.1 A proper understanding of this dynamical behavior is required to explain the macroscopic physical properties of colloidal dispersions (e.g., viscosity, elastic modulus, and thermal conductivity), the mechanics of protein unfolding,2 the kinetics of bio-molecular reactions,3 and the tumbling motion of bacteria,4 among many other processes. All these examples share one common characteristic: as they move, the particles generate long-range disturbances in the fluid, resulting in long-range hydrodynamic interactions between all particles present in the system. The non-linear, many-body, and long-range nature of these interactions makes these systems incredibly challenging to study.
Theoretical approaches have been limited to simple idealized systems (i.e., spheroidal particles in dilute suspensions), while experiments can be difficult to analyze, leaving computer simulations as one of the preferred methods. While this still requires advanced simulation methods and considerable computational resources, significant progress has been made in the past few decades, and there are now several well-established numerical techniques to explicitly account for the hydrodynamic interactions in a suspension of particles.5–11 However, not all of these methods can be (easily) applied to dispersions with non-Newtonian host solvents, or solvents with internal degrees of freedom, which severely limits the physical and biological systems they can study. To address this issue, we have proposed a direct numerical simulation (DNS) method called the smoothed profile (SP) method,12,13 which simultaneously solves the coupled equations of motion for both the host fluid and the particles, and allows for complex non-Newtonian fluids at arbitrary Reynolds numbers. The basic idea behind our method, and the key to its simplicity and efficiency, is to replace the sharp particle interfaces with smoothed (diffuse) profiles. This allows us to directly couple the fluid and particle motions, effectively treating the system as a single component fluid. This leads to the main advantage of our model with respect to alternative approaches, which is the ability of using a fixed Cartesian grid to solve the fluid equations of motion, as this allows for improved accuracy and efficiency (e.g., by adopting pseudo-spectral solvers based on the Fast-Fourier transform). We note that our method is closely related to Araki and Tanaka's fluid particle dynamics (FPD) method,14 which models the particles as a highly viscous fluid. Furthermore, while a similar approach to deal with the solid–fluid interaction has been proposed in earlier work,15 our proposed method presents a more general and robust framework.
The SP method is our approach to include the hydrodynamic interactions in a colloidal suspension. As presented here, it uses a DNS in which the Navier–Stokes equation is solved numerically. However, it is also possible to achieve the same goal without solving this equation directly by using a proxy which yields the correct hydrodynamics. The three most popular of these alternative computational fluid dynamics (CFD) methods, often used to simulate soft matter, are the lattice Boltzmann method (LBM),10,16–20 the dissipative particle dynamics (DPD) method,21 and the multi-particle collision dynamics (MPC)22–27 method. While the implementation details and inherent approximations vary between each of these methods (LBM, DPD, MPC, and DNS), they all rely on the same physical principle to couple the particle and fluid motion: local conservation of momentum. In fact, the SP method has also been successfully used together with the LBM.28
Originally, we developed the SP method to simulate colloidal particles in liquid crystals29,30 and electrolyte solutions.13.,31–34 It has now been extended to study diffusion,35–37 coagulation,38,39 sedimentation,40–45 and rheological processes46–51 of colloidal particles in incompressible fluids. Recently, the method has also been adapted to allow for arbitrarily shaped rigid bodies,52 active particles,53 and self-propelled micro-swimmers.54–60 Extensions for complex host fluids such as compressible,61–63 viscoelastic,64,65 and multi-phase66–69 fluids have also been developed. Important contributions for further extending the SP method have also been published independently by other groups.70–72 The purpose of this paper is to provide a comprehensive summary of the SP method and its application to several problems of particulate systems in which the hydrodynamic interactions play crucial rules.
2 Simulation method
2.1 Basic equations for particulate systems in fluids
The SP method allows us to solve the motion of solid particles in a continuum medium.13 In principle, it can be applied to solid particles of arbitrary shape and is not limited to simple liquids, as we are free to use any constitutive equation for the stress, including multi-component complex fluids and rheological constitutive models discussed in the subsequent sections, as well as continuum models of active matter, such as an active turbulent fluid.73 To explain how the motion of the particles and the flow is coupled by the SP method, we will consider in this section the motion of arbitrarily shaped solid particles in a Newtonian fluid.52 A schematic representation of a freely moving disk is shown in Fig. 1, here represented as a rigid ensemble of spherical beads. The incompressible flow of the Newtonian medium is governed by the continuity and Navier–Stokes equations:| | | (∂t + uf·∇)uf = ρf−1∇·σ, | (2) |
| | | σ = −pI + η[∇uf + (∇uf)t] | (3) |
where uf, ρf, η, and σ are the velocity, mass density, viscosity and stress of the fluid, respectively; p the pressure; I the unit tensor; and (⋯)t indicates a transpose. Unless otherwise stated, we will assume a density-matched suspension, such that ρf = ρp = ρ. We apply the stick or no-slip condition at the solid–fluid interface, i.e., uf = up on the solid surface, where up is the particle velocity at the surface. The motion of an ensemble of N rigid particles, with the I-th particle (I = 1,…,N) having mass MI and moment of inertia II, is described by the Newton–Euler equations:74| | ṘI = VI, ![[Q with combining dot above]](https://www.rsc.org/images/entities/b_i_char_0051_0307.gif) I = skew(Ω)·QI, I = skew(Ω)·QI, | (4) |
| | MI![[V with combining dot above]](https://www.rsc.org/images/entities/b_i_char_0056_0307.gif) I = FHI + FCI + FEI + GVI, I = FHI + FCI + FEI + GVI, | (5) |
| | ![[J with combining dot above]](https://www.rsc.org/images/entities/b_i_char_004a_0307.gif) I = NHI + NCI + NEI + GΩI, I = NHI + NCI + NEI + GΩI, | (6) |
where RI and VI are the center of mass position and velocity vectors, respectively, QI and ΩI the corresponding orientation matrix and angular velocity, respectively, and JI = II·ΩI is the angular momentum. The orientation matrix associates the fixed (lab) coordinate system, {ei} (i = 1, 2, 3), with a time-dependent coordinate system that rotates with the particles, {ẽi} (i = 1, 2, 3) as 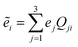 . The time-evolution of the rotation matrix is determined by the (skew-symmetric) angular velocity matrix, derived from the angular velocity vector,
. The time-evolution of the rotation matrix is determined by the (skew-symmetric) angular velocity matrix, derived from the angular velocity vector, 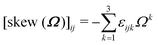 , where εijk is the Levi-Civita symbol, as
, where εijk is the Levi-Civita symbol, as| | 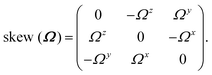 | (7) |
The particles will be subject to forces F and torques N coming from their environment. Here, we have separated out the contributions to the forces (torques) in terms of the interactions coming from the medium, which is composed of the hydrodynamic forces FH and the thermally fluctuating forces GV, the direct inter-particle interactions FC, and those due to external fields FE, such as gravity. Note that the precise form of these terms will depend on the system under consideration and will be discussed separately.
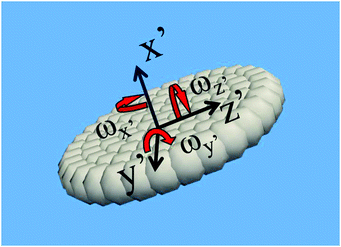 |
| | Fig. 1 Schematic representation of the motion of a disk-like object in a 3D domain where the motion is characterized by three translational and three rotational degrees of freedom. Primed variables refer to components measured in the co-rotating body reference frame. | |
We will now explain how to solve the system of coupled equations shown above with the SP method. In this approach, the velocity field is defined over the whole domain, in order to include both the host fluid and the solid particles, as
| | | u(x,t) = (1 − ϕ)uf(x,t) + ϕup(x,t), | (8) |
| | 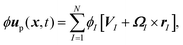 | (9) |
where
rI =
x −
RI is the distance from the center of mass and
ϕI =
ϕI(
x;
RI,
QI) ∈ [0, 1] defines an order parameter for the particle domain, which is 1 inside of the particle and 0 outside. In the SP method, instead of a sharp interface, a continuous diffuse interface domain of thickness
ξ is explicitly introduced in the
ϕ function. Setting the interface domain to have a finite width has two merits for achieving practical numerical calculations: first, the interface location is supported over the finite grid used in the fluid solver; second, the solid–fluid interactions can still be correctly described, as shown below.
There are two main difficulties when describing the whole domain, including the solid and fluid regions, as a continuum, which is what we propose for the SP method. First, the continuum field must satisfy the boundary condition at the particle surface. Second, the hydrodynamic forces need to be evaluated to solve for the particle dynamics. Here, it is crucial that the particle boundary conditions and the hydrodynamic forces be evaluated consistently with each other. To solve this problem, several methods have been developed. In the distributed Lagrange multiplier (DLM) method,75 a Lagrange multiplier field is introduced in the continuum equation, within the particle domain, in order to simultaneously solve for both the fluid velocity field and the particle velocity. In the fictitious boundary method based on a multi-grid finite element approach,76 hydrodynamic forces are explicitly calculated by introducing a fictitious boundary indicator. In the immersed-boundary method (IBM),77–79 markers distributed over the particle surface are used to apply frictional forces between the particle and the fluid velocity field near the surface. It is also possible to have a direct forcing of the particle velocity field in the particle domain, rather just at the particle surface, by adopting a volume-of-fluid representation for the particle.15 In the force coupling method (FCM),80 all forces on the particle, other than the hydrodynamic ones, are used to define a force field (assuming a Gaussian profile) that is then applied to the particle domain in the continuum equations. In the fluid particle dynamics (FPD) method,14,81 in addition to the particle force field, a large artificial viscosity is applied within the inner particle region to penalize fluid-like behaviour and thus enforce the rigid-body constraints on the velocity field. In the SP method, the calculation of the hydrodynamic forces and the boundary conditions are separated by using a fractional-step approach, without introducing an artificially large viscosity in the particle domain (in contrast to FPD).
2.2 Implementation of the SP method
The velocity field is governed by a modified version of the continuity and Navier–Stokes equations:| | | (∂t + u·∇)u = ρ−1∇·σ + ϕfp, | (11) |
where ϕfp acts as a penalty force to impose the rigid-body constraints within the particle domain, and where the stress tensor is defined exactly as in eqn (3), but now in terms of the total velocity u. The terms responsible for the coupling with the rigid-body dynamics, ϕfp, FHI and NHI, are determined at a temporally discretized level as follows. Let un be the velocity field at the n-th time step tn = nh with time increment h. First, eqn (11) is solved without the ϕfp-term and the particle positions and orientations are propagated as| | 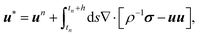 | (12) |
| | 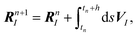 | (13) |
| | 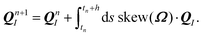 | (14) |
at which point the particle velocity field must also be updated even if the particle velocities remain unchanged. The hydrodynamic forces and torques are expressed in terms of the corresponding momentum impulses, by assuming momentum conservation for the unperturbed velocity u*| | 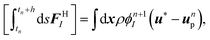 | (15) |
| | 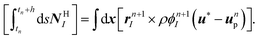 | (16) |
Then, the velocities of the particles are updated to Vn+1i and Ωn+1I, from which ϕn+1I, the final particle velocity field ϕn+1un+1p is obtained, by Eqn (9). Finally, the forcing needed to impose the rigid-body constraint on the particle velocity field is also applied as a momentum impulse| | 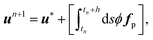 | (17) |
| | 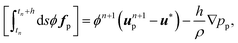 | (18) |
with the pressure due to the rigidity constraint obtained from the continuity equation ∇·un+1 = 0. Since the viscous stress is applied over the whole domain, the relevant no-slip condition on the particle surface will be satisfied within the limits of the interfacial scale ξ.
2.3 The smoothed profile function
We now explain how to construct the Smoothed Profile (SP) function ϕI for a particle of arbitrary shape. This function defines the particle domain, introducing an interface of finite width ξ, to smoothly connect the inner particle domain ϕ = 1 with the fluid domain ϕ = 0. For a spherical particle, several analytical forms of the SP function are presented in ref. 12. One example of such a SP function for spherical particles is14,29| | 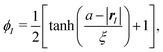 | (19) |
where a is the sphere radius. The interfacial scale ξ is a free parameter to be specified, though it is typically set to be one or two times the grid spacing for numerical stability. Fig. 2 shows a cross section of a sphere, with interfacial thickness ξ, to illustrate the separation between the particle and fluid domains.
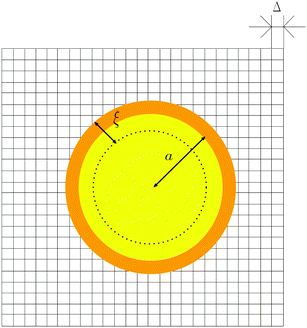 |
| | Fig. 2 Schematic representation of the cross section of a spherical SP particle. Δ is the lattice spacing, a is the particle radius, and ξ is the interfacial thickness. The particle surface now has a finite volume ∼πa2ξ supported by several grid points on a fixed 3D Cartesian grid. Reproduced from Phys. Rev. E, 71, 036707,12 Copyright 2005, with permission from the American Physical Society. | |
For non-spherical particles, Luo et al.70 have generalized the definition of the SP function to arbitrary geometries by replacing |rI(x, t)| − a with a signed distance function dI(x, t) to the surface of the I-th particle. However, to define dI, this requires that we define the position of the particle surface. Alternatively, complex shapes can be constructed using a set of spherical beads,52 which is the approach we have adopted.
For this, consider the I-th particle as being composed of a collection of nI spherical beads. Since the constituent beads can overlap, a large class of particle geometries can be easily represented as an assembly of spherical beads. The SP function for such an assembly of beads is constructed as
| | 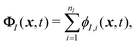 | (20) |
| | 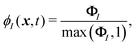 | (21) |
where
ϕI,i is the SP function of the
i-th spherical bead, belonging to the
I-th rigid particle.
Once the SP function of a complex shape has been defined, the hydrodynamic impulse on a particle and the corresponding momentum impulse on the medium are evaluated using eqn (15), (16) and (18).
Since the fluid inertia is solved for in the above SP algorithm, the added mass effect is accounted for in the hydrodynamic impulse in eqn (15). To specify the inertial effect, the integrand of the hydrodynamic impulse (15) is decomposed as
| | 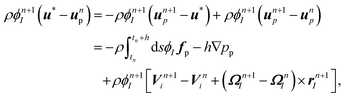 | (22) |
Spatial integration of this equation with
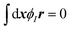
yields
| | 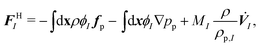 | (23) |
where
ρp,I is the mass density of the
I-th particle. From this equation, the hydrodynamic force in
eqn (15) is found to be composed of the counter-action of the rigidity constraint and the added mass force.
The accuracy of the flow field obtained from the SP method will depend on both the time increment h and the interfacial thickness ξ. Luo et al.70 reported that the accuracy does not improve monotonically as h decreases, but instead reaches an optimal value when ξ2 = O(ηh/ρ). This relation reflects the fact that a sufficiently large interfacial scale is required to resolve the viscous Stokes layer generated by the rigidity constraint impulse (18).
Due to the fractional step approach used in the SP method, it is relatively easy to apply different hydrodynamic solvers. In fact, the SP method has already been applied in combination with different flow solvers: the pseudo-spectral method,12,13,31,35–40,46–49,54,61 spectral element method,70,82 finite difference method,83 finite volume method,71 and LBM.28
3 Applications
3.1 Brownian motion and coagulation
3.1.1 Thermal fluctuations.
Let us consider the Brownian motion of spherical particles dispersed in an incompressible fluid. Following eqn (4)–(6), the motion of the i-th particle is now governed by a set of Langevin equations:| | Mi![[V with combining dot above]](https://www.rsc.org/images/entities/b_i_char_0056_0307.gif) i = FHi + FCi + GVi, i = FHi + FCi + GVi, | (25) |
| | 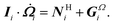 | (26) |
where the external forces/torques are set to be zero, and it is assumed that the inter-particle interactions are given by a central-force potential, such that NC = 0.
The stochastic forces GVi and torques GΩi satisfy the following properties:
| | | 〈Gni(t)〉 = 0, 〈Gni(t)Gnj(0)〉 = αnIδ(t)δij, | (27) |
where the square brackets denote an equilibrium ensemble average. Here,
αn represents the noise intensity associated with each of the translational (
n =
V) and rotational (
n =
Ω) degrees of freedom of the particles. The noise intensity is controlled in such a way that the variance in the linear and angular velocities is constant, that is, 〈
Vi2〉 =
C1 and 〈
Ωi2〉 =
C2, where
C1 and
C2 are constant parameters. The time evolution of the noise intensity is described by
αV(
t +
h) =
αV(
t)
e1−Vi2(t)/C1 and
αΩ(
t +
h) =
αΩ(
t)
e1−Ωi2(t)/C2, which play the role of a thermostat. The temperature of the system is defined by the diffusive motion of the dispersed particles. The translational particle temperature
kBTV is determined by the long-time diffusion coefficient
DV of a spherical particle, as given by the Stokes–Einstein relation,
kBTV = 6π
ηaDV, with
DV obtained from the simulations. Similarly, the rotational particle temperature
kBTΩ can be determined by the rotational diffusion coefficient
DΩ.
3.1.2 Velocity auto-correlation of a single particle.
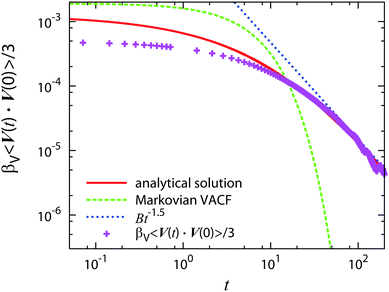
To test the validity of the present approach, we first consider the translational and rotational motions of a single Brownian particle in an incompressible Newtonian fluid. The translational velocity auto-correlation function βV〈Vi(t)·Vi(0)〉 is shown in Fig. 3. Our numerical data (+) clearly approach the analytical solution in the long-time limit, exhibiting the appropriate power law decay Bt−3/2. A similar trend is found for the rotational velocity auto-correlation function 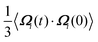 , as shown in Fig. 4.
, as shown in Fig. 4.
 |
| | Fig. 3 Pluses (+): translational velocity auto-correlation function for Brownian particles at βV = 1.2 and φ = 0.002. The solid line is obtained from the analytical solution for the translational particle velocity of the corresponding drag problem. The dotted line shows the power-law Bt−3/2, where B = 1/12ρf(πνf)3/2, whereas the dashed line shows the exponential decay obtained from the Markovian Langevin equation. Reproduced from J. Phys. Soc. Jpn., 77, 074007,35 Copyright 2008, with permission from the Physical Society of Japan. | |
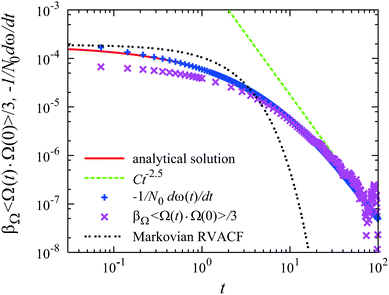 |
| | Fig. 4 Crosses (×): rotational velocity auto-correlation function for Brownian particles at βΩ = 1 and φ = 0.002. Pluses (+): the relaxation response of the angular velocity of a particle under a constant external torque N0. The solid line is obtained from the analytical solution for the angular velocity of the corresponding drag problem. The dashed line shows the power-law Ct−5/2, where C = π/32ρf(πνf)5/2, and the dashed-dotted line shows the exponential decay obtained from the Markovian Langevin equation. Reproduced from J. Phys. Soc. Jpn., 77, 074007,35 Copyright 2008, with permission from the Physical Society of Japan. | |
3.1.3 Brownian coagulation with hydrodynamics.
For over 100 years, ever since Smoluchowski presented his theory of Brownian coagulation in colloidal dispersions, there have been numerous theoretical, experimental, and simulation studies performed to assess the validity of this theory. Based on balance equations and a simple kinetic theory of coagulation, but ignoring the effect of inter-particle interactions, Smoluchowski's theory predicts a coagulation rate that is twice that of actual colloidal dispersions.84–88 To address this discrepancy, it has been suggested to introduce a correction factor into the coagulation rate, so as to account for the contributions from these missing inter-particle interactions.89–91 Several experimental evaluations of this correction factor have been performed, and they suggest that the reduction in the aggregation rate is mostly caused by the (repulsive) hydrodynamic lubrication forces between the particles.84–88,92 However, it should be noted that these examinations assume the validity of the correction factor itself. To understand the role played by the hydrodynamic interactions it is necessary to directly measure them.
We have performed simulations of monodisperse spherical particles of diameter σ = 2a, with a = 4Δ, ξ = 2Δ, in a Newtonian host fluid. All simulations have been performed in a 3D cubic box, of length L = 256, under periodic boundary conditions, starting from a random initial configuration of particles. The number of particles was set to Np = 187, 281, 375, 625, 938, 1877, 3754 and 6258. These conditions correspond to a particle volume fraction of φ = 0.003, 0.0045, 0.006, 0.01, 0.015, 0.03, 0.06 and 0.1, respectively, where φ = πσ3Np/6L3. The particles interact via a modified Lennard–Jones (LJ) potential, defined as
| | | VLJ(r) = 4ε[(σ/r)m − (σ/r)n] | (28) |
with
n![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif)
:
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) m
m = 200
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif)
:
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif)
100, where
r is the inter-particle distance and
ε is the interaction strength. The large value of the exponent in
eqn (28) results in a very short-range interaction, appropriate for the rapid coagulation of sticky particles. For the results presented here, we chose a strong enough attractive potential, so that coagulated particles were prevented from breaking apart due to thermal fluctuations. For this, the value of
ε was fixed to be 7.03
kBT. To improve the statistical significance of the data, five independent simulations were performed for each set of parameter values, and the results were averaged over.
The units of all variables are based on the three fundamental constants Δ, μ, and ρf. Accordingly, the unit of time is τ = ρfΔ2/μ, and the unit of energy is ε0 = Δμ2/ρf. Unless otherwise stated, we set Δ = 1, τ = 1, μ = 1, ρf = 1, ρp = 1, a = 4, σ = 8, ξ = 2, the Lennard–Jones time unit τM = ((Miσ2)/ε)1/2 ≈ 131. Assuming dispersions of neutrally buoyant particles of radius 1 μm in water at room temperature, our unit length Δ and time τ correspond to 0.25 μm and 0.0625 μs, respectively. The discretized time step is h = 0.07481. Although this value is chosen from the stability condition of the Navier–Stokes equation, it can be used safely for the particle's equations because h is smaller than the oscillation period of the particle in the potential well 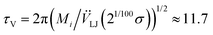 .
.
The volume fraction dependence of Smoluchowski's coagulation rate K, normalized by the early-stage coagulation rate K0, is shown in Fig. 5. This ratio is seen to asymptotically approach a fixed value in the dilute volume fraction limit, as φ → 0, whereas it gradually increases with increasing volume fraction. The coagulation rate we have obtained in the dilute limit is approximately 0.3–0.5 times smaller than that predicted by Smoluchowski's theory, in good agreement with previous experimental results (shown as open symbols in the figure), which reported values of K/K0 between 0.4 and 0.6.84–88 Likewise, the increase at higher volume fractions is in qualitative agreement with experiments and simulation results.85,93–95 The solid line in Fig. 5 shows the ratio of the coagulation rates K/K0 in the high-concentration limit, as given by the regression formula of Heine et al:93
| | 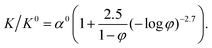 | (29) |
with
α0 = 1. This equation by Heine
et al. reduces to the Smoluchowski result
K/
K0 = 1 in the dilute volume fraction limit, when (−log
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) φ
φ)
−2.7 ≪ 1. However, since this formula was obtained from simulations using Langevin dynamics, it ignores the hydrodynamic interactions between the particles. To account for these missing contributions, we can treat
α0 as a scaling or correction factor. Using a least-squares fit of
α0 to our simulation results, we obtained
α0 = 0.326. This result agrees well with the form of
eqn (29), despite the differences in the way that the hydrodynamic interactions are considered. From this, we can conclude that while hydrodynamic interactions affect the magnitude of the coagulation rate, they do not affect the particle concentration dependency, at least in the dilute limit.
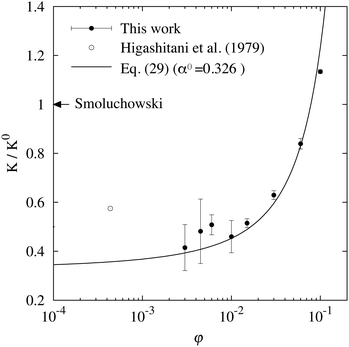 |
| | Fig. 5 The volume fraction dependence of the normalized coagulation rate K/K0. The filled symbols show our simulation results, and the open symbols the experimental results of Higashitani et al.86 The arrows indicate Smoluchowski's prediction, while the solid line shows the fit to the data using eqn (29). Reproduced from Phys. Rev. E, 86, 051403,39 Copyright 2012, with permission from the American Physical Society. | |
3.2 Hindered settling
3.2.1 Settling velocity at small Re.
We now consider the sedimentation of non-Brownian (T = 0) spherical particles interacting via a truncated LJ or Weeks–Chandler–Anderson potential| | 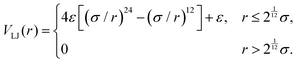 | (30) |
under a gravitational force FEI = (0, 0, −Fg). Simulations are performed using cubic simulation boxes, of length L = 64Δ, 128Δ or 256Δ, under periodic boundary conditions, with Δ being the grid spacing and our unit of length. The particle radius a is set to 4Δ and the particle volume fraction ranges from 0.01 to 0.5. To avoid any inertial effects, and remain within the Stokes regime, we perform all simulations at a particle Reynolds number of Re = ρfaVs/η = 0.14, with 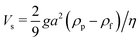 being the corresponding Stokes velocity for a single particle.
being the corresponding Stokes velocity for a single particle.
To account for the sedimentation of colloidal dispersions, we need to consider the fact that a sedimenting particle will experience a hindered settling due to the presence and the motion of the other particles. This includes the drag force induced by the back flow of the fluid, as well as any direct particle–particle interactions. The net effect of these interactions is to reduce the average settling velocity of the suspension, in comparison with the terminal velocity of a single isolated particle sedimenting under the same gravitational force. If a simulation is to reproduce this hindered settling, which has been amply studied, both theoretically96–101 and experimentally,102 it must accurately characterize the many-body hydrodynamic interactions at their origin. Thus, this hindered settling presents itself as a suitable parameter to assess whether or not the hydrodynamic interactions are properly described. We verify our SP method by comparing its predictions for the average settling velocity of a suspension, with theoretical,96–101 experimental102 and alternative simulation103,104 results, as shown in Fig. 6. The simplest semi-empirical relation to describe this behaviour is the power-law function proposed by Richardson and Zaki,96Vsed/Vs = (1 − φ)n, where Vsed = 〈Viz〉 is the average settling velocity of the particle and n is the power law exponent. Different studies97,101–105 have obtained different values for this exponent, ranging from 4.7 to 6.55 in the Stokes flow regime. From our results, we find that a value of 5.3 provides the best fit to the data, which is well within the range of previous values. Our results are also in good agreement with the theoretical work of Hayakawa et al.,99 which also considers the effect of the hydrodynamic interactions. The agreement of our simulation results with previous experimental, theoretical, and simulation studies further validates our method.
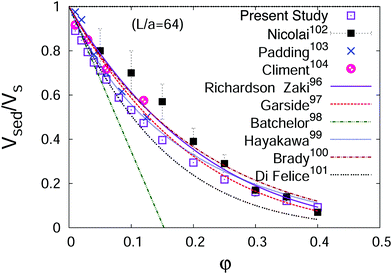 |
| | Fig. 6 Average particle settling velocity Vsed, normalized by the Stokes velocity Vs, as a function of the particle volume fraction. This observed reduction with volume fraction highlights the hindered settling of these particles. Solid lines show the various theoretical predictions,96,98–101 and the symbols represent the experimental102 and simulation103 data. Reproduced from Soft Matter, 9, 10056–10068,40 Copyright 2013, with permission from the Royal Society of Chemistry. | |
3.2.2 Settling velocity at Re > 1.
Let us now consider the inertial effects on the sedimentation of non-Brownian particles. For this, we vary the Reynolds number Re between 0.05 and 10, by increasing the strength of the gravitational force. In principle, our method is also applicable for Re > 10, but this requires that we reduce the time step and decrease the grid spacing, dramatically increasing the computational cost of our simulations. Our simulation results, presented in Fig. 7(a–c), show that the theoretical predictions obtained for the Stokes regime are no longer applicable due to the presence of inertial effects. To capture this deviation, one can use a modified expression for the sedimentation velocity, of the form:where the terminal velocity, as a function of Re, is computed according to Vt = Reη/ρfσ. Here, both the scaling factor k and the exponent n are allowed to vary with Re. Koch et al. have reported k values of 0.92 ± 0.03 and 0.86 ± 0.04 for Re = 1 and 10, respectively, and suggested to use the following quadratic polynomial for n:| | | n = 4.23 − 0.0526Re + 0.00111Re2. | (32) |
Previous work by Koch and Di Felice details the mechanism responsible for the initial decay in the hindered settling function at a low volume fraction, but their proposed mathematical expressions cannot be applied at φ ≃ 0. In order to include this missing information, we suggest a modified hindered settling expression:| | Vsed/Vt = k(1 − φ)n + (1 − k)![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(−φ/0.008), exp(−φ/0.008), | (33) |
where the values of k and n are, respectively, determined by| | 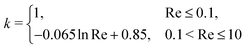 | (34) |
and| | 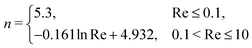 | (35) |
These simple fitting functions capture the behaviour of sedimenting particle dispersions as a function of Re and volume fraction. We note that these expressions are reduced to the Richardson and Zaki96 law at Re ≤ 0.1, whereas at 0.1 < Re ≤ 10 the second term (0.1 < Re ≤ 10) provides for the fast decay in the sedimentation velocity, as shown in Fig. 7.
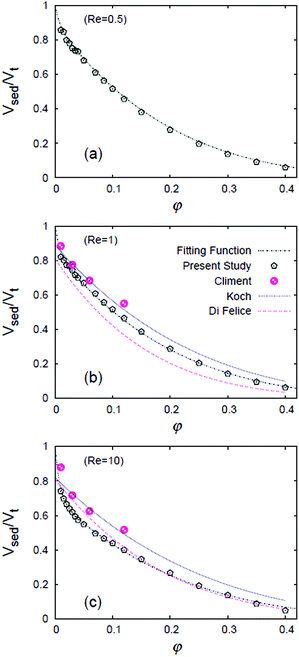 |
| | Fig. 7 Average sedimentation velocity Vsed, normalized by the terminal velocity Vt of an isolated sphere, as a function of the volume fraction for Re = 0.5, 1 and 10. Simulation results are fitted to the hindered settling function of eqn (33) and compared with other theoretical predictions101,106 and simulation results.104 Legends apply to all three figures. Reproduced from RSC Adv., 4, 53681–53693,43 Copyright 2014, with permission from the Royal Society of Chemistry. | |
3.3 Shear flow and rheology
3.3.1 Implementation of sheared boundary conditions.
Understanding the macroscopic rheological properties of colloidal dispersions remains a challenging problem in colloidal science, particularly when considering non-Newtonian host fluids and non-spherical particles. Of particular interest are the non-Newtonian behaviours that appear whenever the suspension is subjected to shear, such as shear thinning or shear thickening, both of which are strongly related to changes in the microstructure of the suspension. In addition to experiments, DNSs are left as the only viable tool to measure the rheology. The SP method is an ideal tool for these studies, as it allows us to directly solve the Navier–Stokes equation for (Brownian and non-Brownian) arbitrarily shaped rigid particles under shear. We can account for the fluid and particle inertial effects and do not require the separation of time scales between fluid and particle relaxation times.
The easiest way to introduce a simple shear flow U = ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) yex in the system is to add an external forcing term ρfs into the modified Navier–Stokes equation (11), the role of which is to maintain the target shear flow (
yex in the system is to add an external forcing term ρfs into the modified Navier–Stokes equation (11), the role of which is to maintain the target shear flow (![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) ). When performing bulk 3D simulations under periodic boundary conditions, a linear zig-zag (possibly time-dependent) profile with two kinks (where the force is applied) can be used to satisfy the boundary constraints.46,47 The results obtained using this external forcing are in good agreement with alternative DNS methods and theoretical predictions, but the method presents some considerable drawbacks: first, the shear rate is not a precisely controlled quantity; second, there are non-physical kinks where the velocity gradient changes sign (at which point particles translate with no net rotation); and third, the zero-wavevector transport coefficients cannot be obtained (as the technique uses a finite-wavelength perturbation). To overcome these difficulties, one can adopt Lees–Edwards boundary conditions, solving the continuum equations on an (oblique) time-dependent coordinate system whose points are advected by the shear flow. Fig. 8 presents a schematic illustration of this coordinate transform. At time t = t0, a solid spherical particle is shown dispersed in a solvent, which is discretized on a rectangular grid (Fig. 8(a)). After the shear-flow is applied (t > t0), both the particle and the grid points are convected by the flow, with the grid undergoing a shear-induced deformation, in contrast to the particle whose shape remains unchanged. This situation can be represented in a fixed coordinate system (Fig. 8(b)), as well as a time-dependent oblique coordinate system which tracks the shear-flow (Fig. 8(c)), and in which the particle shape is deformed. This formulation is equivalent to the SLLOD algorithm used in non-equilibrium MD simulations to model (arbitrary) homogeneous and divergence-free flows, but the implementation of this algorithm within a grid-based system requires a careful treatment.49,108,109 The appropriate contravariant form of the Navier–Stokes equation for the peculiar velocity ξ = u − U within this time-dependent oblique coordinate system, with basis vectors (Ê1 = ex + γ(t)ey, Ê2 = e2, Ê3 = e3), is given as51
). When performing bulk 3D simulations under periodic boundary conditions, a linear zig-zag (possibly time-dependent) profile with two kinks (where the force is applied) can be used to satisfy the boundary constraints.46,47 The results obtained using this external forcing are in good agreement with alternative DNS methods and theoretical predictions, but the method presents some considerable drawbacks: first, the shear rate is not a precisely controlled quantity; second, there are non-physical kinks where the velocity gradient changes sign (at which point particles translate with no net rotation); and third, the zero-wavevector transport coefficients cannot be obtained (as the technique uses a finite-wavelength perturbation). To overcome these difficulties, one can adopt Lees–Edwards boundary conditions, solving the continuum equations on an (oblique) time-dependent coordinate system whose points are advected by the shear flow. Fig. 8 presents a schematic illustration of this coordinate transform. At time t = t0, a solid spherical particle is shown dispersed in a solvent, which is discretized on a rectangular grid (Fig. 8(a)). After the shear-flow is applied (t > t0), both the particle and the grid points are convected by the flow, with the grid undergoing a shear-induced deformation, in contrast to the particle whose shape remains unchanged. This situation can be represented in a fixed coordinate system (Fig. 8(b)), as well as a time-dependent oblique coordinate system which tracks the shear-flow (Fig. 8(c)), and in which the particle shape is deformed. This formulation is equivalent to the SLLOD algorithm used in non-equilibrium MD simulations to model (arbitrary) homogeneous and divergence-free flows, but the implementation of this algorithm within a grid-based system requires a careful treatment.49,108,109 The appropriate contravariant form of the Navier–Stokes equation for the peculiar velocity ξ = u − U within this time-dependent oblique coordinate system, with basis vectors (Ê1 = ex + γ(t)ey, Ê2 = e2, Ê3 = e3), is given as51
| | 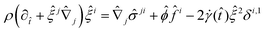 | (36) |
| | 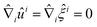 | (37) |
where a caret (
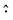
) is used here to denote tensorial components in the oblique frame. After the flow equations are solved, we transform back to the fixed laboratory frame to compute the particle–fluid interactions and solve for the particle dynamics.
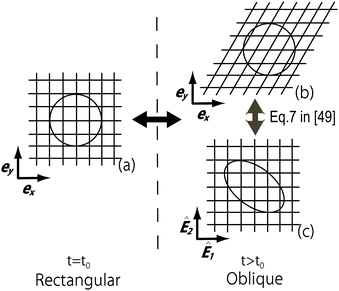 |
| | Fig. 8 A schematic representation of the coordinate transformation used to model the effect of shear-flow in the DNS simulations. (a) A solid spherical particle is discretized on a rectangular lattice at time t = t0. Both the particle and the solvent, represented by the grid points, are convected by the applied shear-flow (t > t0). While the grid is deformed, the shape of the solid particle remains unchanged. This is depicted in (b) the fixed or laboratory reference frame and (c) the transformed or oblique reference frame. The transformation between (b) and (c) is defined in eqn (7) of our earlier paper.49 Reproduced from J. Chem. Phys., 134, 064110,49 Copyright 2011, with the permission of AIP Publishing. | |
Within this formulation, the instantaneous volume-averaged stress of the flowing dispersion is defined in terms of the particle constraint force as
| | 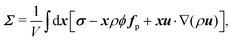 | (38) |
and the particle contribution to the stress can be obtained by subtracting the average fluid contribution,
s =
Σ − 〈
σ〉. In the case of zig-zag shear flow, a similar expression is obtained but with the external force field
ρfs appearing instead of the particle constraint force
ρϕfp. The apparent and intrinsic viscosities of the dispersions,
η and [
η], respectively, are defined as
| | 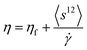 | (39) |
| | 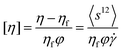 | (40) |
with
ηf = 〈
σ12〉/
![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif)
.
3.3.2 Rheology of dilute suspensions.
The suspension viscosity for dilute systems of spherical and non-spherical particles is calculated and compared with analytical results at zero Reynolds numbers, as well as the results obtained using alternative (high-precision) methods. SP method simulation results for a single particle under simple shear can reproduce the known analytical solutions for the fluid velocity, stress distribution and particle angular velocity.110 Furthermore, the results at finite Reynolds numbers (Re ≲ 10) are also in agreement with the detailed finite element simulations of Mikulencak and Morris107 (see Fig. 9). Simulations for two-particle systems give similarly accurate stress predictions, in agreement with Stokesian dynamics calculations, provided that the surface-to-surface distance between the particles is larger than the grid spacing. When this condition is violated, we cannot expect the SP method to correctly account for the lubrication forces. However, if required, such lubrication corrections can be directly incorporated into the inter-particle interactions.111 The results for rigid linear bead chains are also in good agreement with theoretical predictions and SD simulations, allowing us to reproduce Jeffery's orbits, as well as the time-varying particle contribution to the stress.112 Simulations of Brownian flexible and rigid bead chains have revealed a tumbling motion, with a frequency F that depends only on Pe, following F ∝ Peα, and which exhibits a crossover between Brownian α = 2/3 and shear-flow α = 1 dominated behaviour.48 Furthermore, this transition in the tumbling frequency is shown to correspond to the transition between shear thinning and the second Newtonian regime,50 as first predicted by Hinch and Leal.113,114
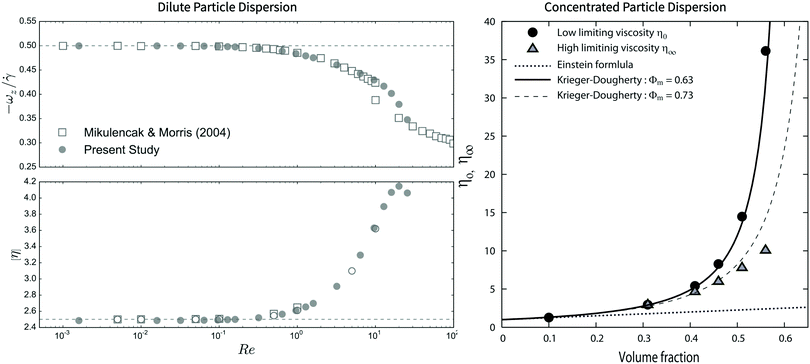 |
| | Fig. 9 (left) Angular velocity ωz and intrinsic viscosity [η] of a single spherical particle as a function of Re. Filled symbols are from SP method simulations using Lees–Edwards boundary conditions, with a particle radius-to-system size ratio of ε/L = 0.0625; open symbols are from the finite element simulations of Mikulencak and Morris,107 for ε = 0.01 (squares) and ε = 0.1 (circles). (right) SP method results, with ε = 0.0625 and 10−3 ≲ Re ≲ 1, under zig-zag shear for the low-shear η0- and high-shear η∞-limiting viscosity of concentrated particle dispersions as a function of the particle volume fraction. Solid and dashed lines show the fits to the data using the Krieger–Dougherty relations, with ΦM being the packing volume fraction at which the viscosity diverges. The left figure is reproduced from J. Fluid Mech., 792, 590–619,51 Copyright 2016, with permission from Cambridge University Press. The right figure is reproduced from Phys. Rev. E, 80, 061402,46 Copyright 2009, with permission from the American Physical Society. | |
3.3.3 Rheology of non-dilute suspensions.
To understand the relationship between the non-Newtonian viscosity of spherical particle dispersions and the underlying microstructural changes, we report simulation results over a wide range of volume fractions φ ≲ 0.56 and Peclet numbers Pe = 6πηfa3![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) /KBT (10−2 < Pe < 10). For low to intermediate particle volume fractions φ ≲ 0.3, the viscosities are constant over the examined range of Peclet numbers, signalling Newtonian behaviour. However, for higher volume fractions (φ ≳ 0.4), shear-thinning behaviour is obtained, with a sharp decrease in the viscosity at high Peclet numbers. The low- and high-shear limiting viscosities (shown in Fig. 9), both monotonically increasing functions of volume fraction, are in good agreement with the semi-empirical Krieger–Dougherty relationship. Analysis of the structural relaxation time τp, defined as the time required for the Brownian particles to diffuse a distance equal to their radius, shows that shear thinning starts at approximately τp
/KBT (10−2 < Pe < 10). For low to intermediate particle volume fractions φ ≲ 0.3, the viscosities are constant over the examined range of Peclet numbers, signalling Newtonian behaviour. However, for higher volume fractions (φ ≳ 0.4), shear-thinning behaviour is obtained, with a sharp decrease in the viscosity at high Peclet numbers. The low- and high-shear limiting viscosities (shown in Fig. 9), both monotonically increasing functions of volume fraction, are in good agreement with the semi-empirical Krieger–Dougherty relationship. Analysis of the structural relaxation time τp, defined as the time required for the Brownian particles to diffuse a distance equal to their radius, shows that shear thinning starts at approximately τp![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) ∼ 1, reminiscent of the non-Newtonian behaviour of supercooled liquids.115 Furthermore, to study the viscoelastic properties, we also consider an oscillatory shear flow and measure the storage and loss moduli, which are shown to be in excellent agreement with experimental data.47
∼ 1, reminiscent of the non-Newtonian behaviour of supercooled liquids.115 Furthermore, to study the viscoelastic properties, we also consider an oscillatory shear flow and measure the storage and loss moduli, which are shown to be in excellent agreement with experimental data.47
3.4 Colloids in compressible media
In this section, we review our studies on the propagation of hydrodynamic interactions using the SP method,12,13 which can be applied to both compressible and incompressible fluids.61 Considering the fluid compressibility allows us to capture the sound propagation. We consider a two-particle system in a compressible fluid and investigate the correlated motion of the particles. In particular, we estimate the velocity relaxation of the particles in response to the application of an impulsive force on one of the particles.
In contrast to incompressible fluids, for which the speed of sound is infinite and the hydrodynamic interactions propagate instantaneously, followed by a temporal evolution due to viscous diffusion, in compressible fluids the sound propagates at finite speeds. This difference strongly affects the time evolution of the hydrodynamic interactions. To quantify the relative importance of the sound propagation, compared to the viscous diffusion, we define the compressibility factor ε as
| | 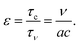 | (41) |
where
τν =
a2/
ν and
τc =
a/
c are the time-scales associated with the viscous diffusion and sound propagation over a distance equal to the particle size, respectively.
The fluid dynamics is now governed by the following hydrodynamic equations:
| | 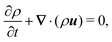 | (42) |
| | 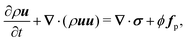 | (43) |
where
ρ(
r,
t) and
u(
r,
t) are the fluid mass density and velocity fields, respectively. The stress tensor is given by
| | 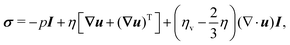 | (44) |
where
p(
r,
t) is the pressure,
η is the shear viscosity, and
ηv is the bulk viscosity. As before, a body force
ϕfp(
r,
t) is added to the Navier–Stokes equation in order to satisfy the particle rigidity constraint. We consider a barotropic fluid with
p =
p(
ρ) and assume a constant speed of sound
c, such that
| | 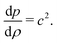 | (45) |
Eqn (42)–(45) constitute a closed system of equations for the variables
ρ,
u, and
p, without consideration of the conservation of energy.
We perform 3D simulations for two spherical particles (a = 4), labelled 1 and 2, in a cubic simulation box (L = 256), under periodic boundary conditions, for various compressibility factors. At t = 0 an impulsive force is exerted on particle 2, and their correlated motions are analyzed in order to characterize the hydrodynamic interactions between them. The cross-relaxation tensor γ12 is defined as the normalized change in the velocity of particle 1:
| | 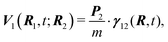 | (46) |
| | γ12(R, t) = γ‖12(R,t)![[R with combining circumflex]](https://www.rsc.org/images/entities/b_i_char_0052_0302.gif) ![[R with combining circumflex]](https://www.rsc.org/images/entities/b_i_char_0052_0302.gif) + γ⊥12(R,t)(I − + γ⊥12(R,t)(I − ![[R with combining circumflex]](https://www.rsc.org/images/entities/b_i_char_0052_0302.gif) ![[R with combining circumflex]](https://www.rsc.org/images/entities/b_i_char_0052_0302.gif) ). ). | (47) |
where
P2 is the impulsive force exerted on particle 2 at
t = 0. The cross-relaxation tensor can be characterized through its components along only two directions of motion, parallel and perpendicular to the center-to-center vector
R. From the fluctuation–dissipation theorem, the cross-relaxation tensor is equivalent to the velocity cross-correlation function of the fluctuating system:
| | 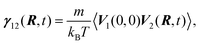 | (48) |
We examine both the parallel correlation
γ‖12 and the perpendicular correlation
γ⊥12 by adjusting the direction of the impulsive force
P2. We consider two cases, one in which the impulse is applied perpendicular to the line connecting the centre of mass of the particles and one in which it is parallel and pushes the particles apart. The velocity fields around the particles at
t/
τν = 6.25 × 10
−1, separated by
R* = 7, are shown in
Fig. 10, for compressibility factors of
ε = 0.1 and 0.6. An expanding doublet flow, with a strength given by the divergence of the velocity field
∇·
u, is observed. In the case of a small compressibility
ε = 0.1, the doublet flow has just arrived at the left particle at this time. In contrast, for the large compressibility
ε = 0.6, the doublet flow has not yet arrived at the left particle. Further discussions on the effect of compressibility on the velocity cross-correlation between two particles (
γ‖12 and
γ⊥12) are found in our earlier paper.
62
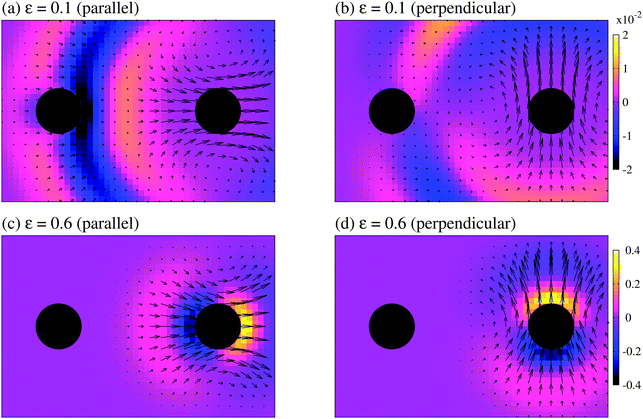 |
| | Fig. 10 Velocity field around particles in a compressible fluid after the application of an impulsive force on the right particle in the parallel (a and c) or perpendicular (b and d) direction. Simulation results at t/τν = 6.25 × 10−1 for compressibility factors with values (a and b) ε = 0.1 and (c and d) ε = 0.6. The divergence of the velocity field ∇·v is described by a colour scale extending from negative (darker) to positive (lighter) divergence. The value of divergence is normalized by τν/Rep. Reproduced from Phys. Fluids, 25, 046101,62 Copyright 2013, with the permission of AIP Publishing. | |
3.5 Particles in multi-phase fluids
3.5.1 A model for ternary systems.
We now consider the adsorption of solid particles at the fluidic interface of moving droplets, which is relevant to many industrial processes, including the stabilization of emulsions and foams,116 the armouring of droplets in capillary tubes,117 and the recovery of mineral particles by rising gas bubbles.118,119 The encapsulation of air bubbles in seawater presents another striking example in which the addition of solid particles dramatically changes the dynamics of these multi-phase systems.120 Performing DNS of such a ternary, fluid–fluid–particle system is challenging due to the complexity of capturing all the relevant physical mechanisms, including capillary effects, three-phase flow hydrodynamics, and inter-particle interactions. Most studies have focused on the dynamics of single particles trapped at planar fluidic interfaces121–123 or at the fluidic interface of an immobile spherical droplet.124,125
Consider a ternary system in which solid particles are dispersed in a binary fluid mixture. A schematic representation of this setup is given in Fig. 11. The field ϕ(x, t) will denote the volume fraction of the solid constituent at position x and time t. The binary fluid mixture will separate into its two immiscible fluid constituents, “A” and “B”. Constituent A represents the host fluid, whereas constituent B represents the fluid inside the droplet phase. The volume fractions of the two fluid constituents are denoted as ϕA(x, t) and ϕB(x, t). The separation of the binary fluid mixture into A and B phases is driven by the minimisation of the following free energy functional:
| | 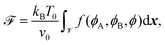 | (49) |
where
![[scr V, script letter V]](https://www.rsc.org/images/entities/char_e149.gif)
denotes the spatial extent of our ternary system,
kB is the Boltzmann constant,
T0 is the reference temperature,
v0 is the reference unit volume, and
f is the non-dimensional free energy density. The variables (
ϕ,
ϕA, and
ϕB) in the free energy density
f are usually referred to as “order parameters”.
126 Because the sum total of the volume fractions is constrained to be unity
ϕA +
ϕB +
ϕ = 1, the free energy density can be conveniently recast as a function of only two order parameters, which we take to be
ψ =
ϕA −
ϕB and
ϕ. For simplicity, We refer to
ψ as “the” order parameter and
ϕ as the particle or fibre (
i.e., bead-chain) volume fraction. Consistent with previous studies,
127,128 we adopt the following form for the free energy densities of the mixture:
| | 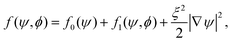 | (50) |
| | 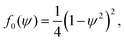 | (51) |
| | 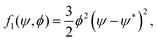 | (52) |
where
f0(
ψ) is a double well function with minima at
ψ = −1 and
ψ = +1,
f1(
ψ,
ϕ) is an energy penalty introduced to impose
ψ =
ψ0 inside the particles,
ψ* is a control parameter that sets the affinity of the beads to the fluid phases, and
ξ is the interfacial thickness defined in
eqn (19).
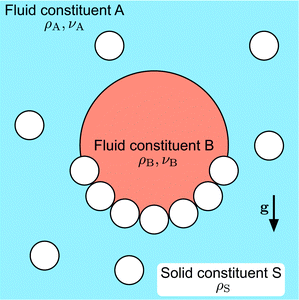 |
| | Fig. 11 Schematic representation of a reference ternary system, showing a fluid (B) droplet rising in the host fluid (A). The solid particles (S) adsorb at the fluidic interface of the binary fluid. Reproduced from Phys. Rev. Fluids, 3, 094002,68 Copyright 2018, with permission from the American Physical Society. | |
The bulk term fb = f0 + f1 is a function with a single minimum located at ψ = ψ0 inside the particle domain (see Fig. 12). This bulk term ensures that ψ = +1 in fluid A, ψ = −1 in fluid B, and ψ = ψ0 in each solid bead. The last term in eqn (50), ξ2|∇ψ|2/2, gives an excess energy contribution across each diffuse interface. We note that the control parameter ψ* and the position of the single well minimum ψ0 are dependent on each other. At equilibrium, δfb/δψ = 0, which results in the following dependency:
| | 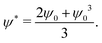 | (53) |
As suggested by Araki and Tanaka,
129 imposing
ψ =
ψ0 inside the solid domain determines the bead affinity. A positive value
ψ* > 0 results in a stronger affinity to fluid
A, whereas
ψ* < 0 results in a stronger affinity to fluid
B, and
ψ* = 0 results in an equal affinity to the two fluid phases. In fact, for the special case when
ψ* = 0, it can be shown that the bulk driving force term δ
fb/δ
ψ coincides with that suggested by Kim,
130 resulting in a factor of 3/2 for the
f1 term in
eqn (52). We stress the fact that
ψ* is an input parameter, while
ψ0 is an output parameter. In all the simulations we have performed, the value of
ψ0 coincides exactly with the theoretical prediction of
eqn (53). Because it is straightforward to verify that
ψ =
ψ0 from a contour of the order parameter, we only specify the value of
ψ0 in what follows.
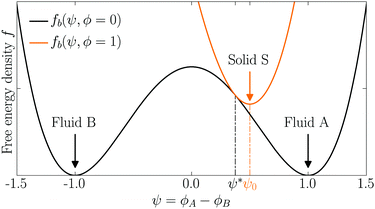 |
| | Fig. 12 Bulk free energy density fb = f0 + f1. Reprinted from J. Comp. Phys., 409, G. Lecrivain, T. B. P. Grein, R. Yamamoto, U. Hampel, and T. Taniguchi, Eulerian/Lagrangian formulation for the elasto-capillary deformation of a flexible fibre,69 109324, Copyright 2020, with permission from Elsevier. | |
The order parameter ψ(x, t) is updated in time following a modified Cahn–Hilliard equation:
| | 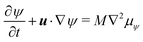 | (54) |
where
M is the mobility of the binary fluid,
u is the velocity field, and
μψ = δ
![[scr F, script letter F]](https://www.rsc.org/images/entities/char_e141.gif)
/δ
ψ is the chemical potential associated with the order parameter
ψ.
We use the SP method to solve for the coupled hydrodynamics and particle dynamics. For the type of system we are interested in, namely the deformation of flexible fibres, capillary effects provide the dominant contributions. Since a mismatch in the fluid densities or viscosities would only alter the transient dynamical behavior, but not the equilibrium steady-states, we will only consider the case of low-Reynolds number flows with equal densities and viscosities for all constituents, such that ρA = ρB = ρ and ηA = ηB = η. As such, the two volume fractions of the pure fluid phases, ϕA and ϕB, are not directly needed for our implementation. The total fluid velocity, satisfying the incompressibility condition ∇·u = 0, is advanced in time by solving the following modified Navier–Stokes equation:
| | 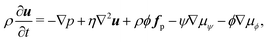 | (55) |
where
ϕfp is again the penalty term that enforces the rigid-body constraints on the beads and
μϕ = δ
![[scr F, script letter F]](https://www.rsc.org/images/entities/char_e141.gif)
/δ
ϕ is the chemical potential with respect to the fibre volume fraction
ϕ. The last source term
ϕ∇
μϕ is motivated by the ternary fluid studies of Boyer
et al.,
131 but our tests show that it is only necessary to improve the stability of the solution in 2D. For 3D simulations, remarkable agreement with theory can be achieved without it.
68
3.5.2 Elasto-capillary deformation of a fibre.
For simplicity, we have solved the equations in their non-dimensional form, using the Reynolds number Re, the Weber number We, the Peclet number Pe, and the elasto-capillary number Ec, defined as| | 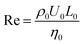 | (56) |
| | 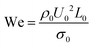 | (57) |
| | 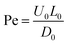 | (58) |
| | 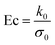 | (59) |
where ρ0 = ρ, η0 = η, L0 = Δ, and U0 are the reference density, viscosity, length and velocity scales, respectively. Here U0 can be the terminal velocity of a single particle in the reference/host fluid. The diffusion coefficient is defined as D0 = e0M, where e0 = kBT0/v0 is the reference free energy density of eqn (49). The reference surface tension is given by σ0 = e0L0. The term k0 is a measure of the fibre stiffness, with the axial beam force between adjacent beads at a separation r given by |Fb(r)| = k|(r − 2a)|. The two limiting cases of Ec = 0 and Ec → ∞ correspond to independent (non-attached) beads and a fully rigid fibre, respectively.69 We find that the dynamics of the ternary system is particularly sensitive to the ratio of the Weber number to the Reynolds number We/Re. For We/Re ≳ 1, we observe large amplitude oscillations in the motion of the fibre at the A/B fluidic interface, which can require long simulation times to reach equilibrium. For this reason, in what follows we set this ratio to be We/Re ≃ 10.
We report on simulations to study the capillary-induced tumbling of a fibre in a stratified fluid, which allow us to assess the validity of our ternary fluid model by checking the equilibrium orientation. We consider a stagnant fluid with no externally imposed flow, such that the fibre rotation is driven solely by the capillary effects at the three-phase contact line. Fig. 13 shows simulation snapshots illustrating the capillary-induced tumbling of a flexible fibre with equal affinity to the two fluid constituents in a stratified 3D system. The A/B fluidic interface is represented by the ψ = 0 isosurface, drawn here using a wire-frame representation. These results are obtained for a fiber with the number of beads Nb = 8, bead radius rb = 6, particle interfacial thickness ξ = 2Δ, in a rectangular system of size 120 × 120 × 32, under periodic boundary conditions. The Reynolds, Weber, Peclet, and elasto-capillary numbers are Re = 0.02, We = 0.1, Pe = 1, and Ec = 10, respectively. Further simulations can be found in ref. 69.
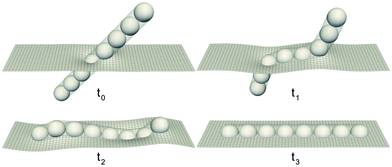 |
| | Fig. 13 Capillary-induced tumbling of a flexible fibre in a 3D stratified system. Reprinted from J. Comput. Phys., 409, G. Lecrivain, T. B. P. Grein, R. Yamamoto, U. Hampel, and T. Taniguchi, Eulerian/Lagrangian formulation for the elasto-capillary deformation of a flexible fibre,69 109324, Copyright 2020, with permission from Elsevier. | |
Next, we have considered the bending of a fibre at the interface of a fluid droplet. At time t = 0, the droplet is initialised to a sphere filled with the fluid constituent A, that is, ψ = 1. Fig. 14 shows the simulation snapshots of the equilibrium solutions, for a fibre with an equal affinity to both fluid constituents, ψ0 = 0. The droplet is represented by the ψ = 0 isosurface. Details regarding the unsteady dynamics leading up to the encapsulation process can be found in ref. 69. These results are obtained with Nb = 10, rb = 6, ξ = 2Δ, Re = 0.02, We = 0.1, Pe = 1, for a system size of 128 × 120 × 120.
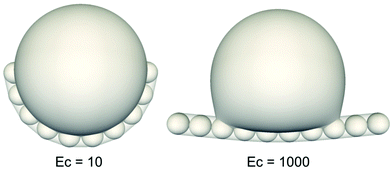 |
| | Fig. 14 3D equilibrium solutions of droplet encapsulation for high values of Ec. Reprinted from J. Comput. Phys., 409, G. Lecrivain, T. B. P. Grein, R. Yamamoto, U. Hampel, and T. Taniguchi, Eulerian/Lagrangian formulation for the elasto-capillary deformation of a flexible fibre,69 109324, Copyright 2020, with permission from Elsevier. | |
3.6 Electrophoresis of charged colloids
3.6.1 A model for charged colloidal dispersion.
The dynamics of charged colloidal dispersions is crucial to many physical, chemical, and biological systems, as well as of great importance for the engineering field.1 Among them, the electrophoresis of charged colloidal particles is one of the most salient examples. When a charged particle is placed in an electrolyte solution, it will develop an electric double layer (EDL), as a cloud of counter-ions is attracted to the surface of the particle. Upon the application of an external electric field, this charged particle will move with an electrophoretic mobility determined by the balance between the electrostatic driving force and the hydrodynamic frictional force acting on the particle. This mobility will depend strongly on the EDL whose distribution becomes anisotropic due to the external field and the friction between the ions and the fluid. The time evolution of the colloidal particles, the ions, and the host fluid are described by the coupled equations for the rigid-body dynamics, hydrodynamics (Navier–Stokes), and electrostatics (Poisson) with the appropriate boundary conditions on the surface of the colloidal particles. We briefly outline our numerical model for such charged colloidal dispersions and how it differs from the standard model discussed in the introduction, and then demonstrate the reliability of the SP method by comparing our numerical results with well-established approximate theories.132–135 Finally, the electrophoretic mobilities of dense dispersions, where simulation results deviate from mean-field type theories,136,137 as well as the field-induced pearl formation, are presented.
Let us consider N charged spherical particles of total charge Ze (e being the unit charge) distributed uniformly on its surface. We define the spatial distribution of the surface charge to be eq(r) = Ze|∇ϕ|/4πa2, with ϕ being the SP function. The particles are dispersed in a host fluid containing ions of species α, with charges Zαe. The local number density of the α-th ionic species is Cα(r, t) at time t, and the total charge density is smoothly defined over the entire domain by 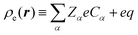 . The complete dynamics of the system is obtained by solving the following time evolution equations.12,13
. The complete dynamics of the system is obtained by solving the following time evolution equations.12,13
(i) The Navier–Stokes equation:
| | | ρ(∂t + v·∇)v = −∇p + η∇2v − ρe∇(Ψ + Ψex) + ϕfp, | (60) |
with the incompressibility condition ∇·
v = 0, where
Ψex = −
E·
r is the electrostatic potential due to the imposed external electric field
E. The electrostatic potential
Ψ(
r) is determined by solving the Poisson equation
ε∇
2Ψ = −
ρe with
ε being the dielectric constant of the host fluid. For simplicity we consider only dielectrically matched particles, such that
εf =
εp =
ε.
(ii) Newton's and Euler's equations of motions:
| | 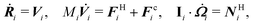 | (61) |
We include all the electrostatic interactions, which consist of the driving from the external electric field
E, as well as the forces due to the distribution of charges in the system, in
FHi.
(iii) Advection–diffusion equation:
| | 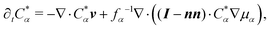 | (62) |
where
fα is the ionic friction coefficient,
I is the unit tensor, and
n is a unit-vector field defined by
n = −∇
ϕ/|∇
ϕ|. In our method, the physical ionic density fields are actually
Cα(
r,
t) = (1 −
ϕ(
r,
t))
Cα*(
r,
t), which are defined using the auxiliary density field
Cα*(
r,
t). This definition explicitly avoids the penetration of ions into the colloidal domains without using any artificial potentials, which would require smaller time increments. The operator (
I −
nn) in
eqn (62) ensures the conservation of
Cα by enforcing the no-penetration condition, as
n·∇
μα = 0 is directly assigned at the diffuse particle interface. In this way the total charge neutrality
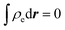
of the system is guaranteed. The chemical potential is defined as
138,139| | μα = kBT![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Cα* + Zαe(Ψ + Ψex), Cα* + Zαe(Ψ + Ψex), | (63) |
If we set
v = 0 in
eqn (62), the equilibrium (
t → ∞) ionic density corresponds to the Boltzmann equation:
| | Cα* = ![[C with combining macron]](https://www.rsc.org/images/entities/i_char_0043_0304.gif) α α![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp[−Zαe(Ψ + Ψex)/kBT]. exp[−Zαe(Ψ + Ψex)/kBT]. | (64) |
The bulk salt concentration
![[C with combining macron]](https://www.rsc.org/images/entities/i_char_0043_0304.gif) α
α is related to the Debye screening length
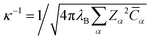
, where
λB =
e2/4π
εkBT is the Bjerrum length, which is approximately 0.72 nm in water at 25 °C.
Simulations are performed in a 3D cubic box, of length L = 64Δ (Δ = 4πλB is the grid spacing and our unit of length), under periodic boundary conditions. We use spherical particles of radius a = 5 and interfacial thickness ξ = 2. The host fluid contains a 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 electrolyte composed of monovalent counter-ions (α = +) and co-ions (α = −). The units of energy and electrostatic potential are kBT and kBT/e, respectively. The non-dimensional mobility parameter mα = 2εkBTfα/3ηe2 is set to be m+ = m− = 0.184, which corresponds to that of KCl solution at 25 °C. Finally, our unit of time τ = Δ2f+/kBT would correspond to 0.44 μs.
1 electrolyte composed of monovalent counter-ions (α = +) and co-ions (α = −). The units of energy and electrostatic potential are kBT and kBT/e, respectively. The non-dimensional mobility parameter mα = 2εkBTfα/3ηe2 is set to be m+ = m− = 0.184, which corresponds to that of KCl solution at 25 °C. Finally, our unit of time τ = Δ2f+/kBT would correspond to 0.44 μs.
3.6.2 Electrophoresis of charged colloids.
We first consider a single charged particle moving with velocity V = (−V, 0, 0) under a constant external electric field E = (E, 0, 0). The electrophoretic mobility V/E as a function of the zeta potential ζ, defined as the electrostatic potential on a slipping plane, is given byin the limit when ζ is small.1 The Smoluchowski equation, corresponding to f = 1, is valid in the limiting case when κa → ∞,132 while the Hückel equation, corresponding to f = 2/3, is valid in the opposite limit of κa → 0.133 An expression for f = fH(κa) that is valid for an arbitrary κa has been derived by Henry.134 These equations all predict a mobility that is proportional to ζ; however, this is not true for large values of ζ, when the relaxation effects due to deformation of the EDL can no longer be neglected. O’Brien and White have proposed an approximate theory that is also valid for larger values of ζ.135
We perform simulations for the electrophoresis of a single particle in the linear response regime E ≲ 0.15 and compare their results with the O’Brien–White theory. A constant uniform electric field of magnitude E = 0.1 is applied. The terminal velocity V is calculated as a function of the charge on the particle, for 50 ≤ −Z ≤ 750, with κ−1 = 10, which would correspond to a salt concentration of 11 μmol l−1 at 25 °C in water. In particular, we set the surface charges to be Z = −50, −100, −200, −300, −400, −500, and −750, corresponding to a dimensionless zeta potential of y ≡ eζ/kBT = 0.525, 1.044, 2.035, 2.927, 3.692, 4.332, and 5.510, respectively. We choose ν = η/ρ = 5 to maintain a small Reynolds number Re = aV/ν. In our simulations, as well as the O’Brien–White theory, the zeta potential is assumed to be the electrostatic potential at the particle surface, ζ = Ψ|surface. Our simulation results are in excellent agreement with the O’Brien–White theory, even in the non-linear regime y ≥ 2, with an error of only a few percent.31 This agreement is unprecedented when compared to alternative simulation methods at this level of description.
Our simulation method applies just as easily to dense dispersions, allowing us to examine the effect of particle concentration on the electrophoretic mobility. The linearized theory for the mobility of a single particle, as described by eqn (65), is still valid for dense dispersions, as long as E is small; however, f now depends on both κa and φ. Simulations for Z = −100 and E = 0.1, at various particle volume fractions φ ≡ 4πa3N/3L3, are performed to measure the value of f(κa, φ) = ηV/εζE. We consider Debye lengths κ−1 of 5 and 10, which correspond to κa = 1 and 0.5, and salt concentrations of 44 μmol l−1 and 11 μmol l−1, respectively. Fig. 15 shows typical simulation snapshots for systems with κa = 1 and (a) FCC, (b) BCC, and (c) random particle configurations.140 The colour map indicates the charge density, shown over a cross-sectional slab perpendicular to the z-axis. In the case of FCC and BCC, E is applied perpendicular to the (1, 0, 0) and (1, 1, 1) faces, but we obtain very small differences in the electrophoretic mobility (within only 1%).
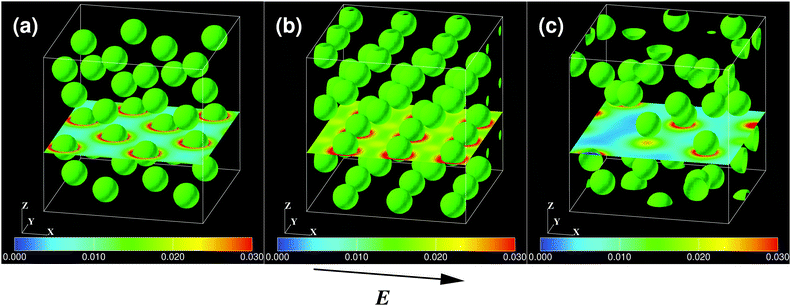 |
| | Fig. 15 Simulation snapshots for the electrophoresis of dense dispersions with (a) FCC, (b) BCC, and (c) random particle configurations. The colour map represents the total ionic charge density 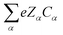 in a plane perpendicular to the z-axis. The electric field is applied in the +x direction, normal to the (1, 0, 0) face for the FCC and BCC lattices. Reproduced from Phys. Rev. Lett., 96, 208302,31 Copyright 2006, with permission from the American Physical Society. in a plane perpendicular to the z-axis. The electric field is applied in the +x direction, normal to the (1, 0, 0) face for the FCC and BCC lattices. Reproduced from Phys. Rev. Lett., 96, 208302,31 Copyright 2006, with permission from the American Physical Society. | |
The mobility coefficient f(κa, φ) for κa = 1 and 0.5 is plotted as a function of φ in Fig. 16(a and b), respectively. It is seen that f decreases rapidly with increasing φ. Furthermore, we see no significant difference in f with respect to the particle configurations (FCC, BCC, or random). A theoretical model for the electrophoretic mobility based on the cell model has been proposed by Levine and Neale.136 For this, they have studied a spherical particle (radius a) at the center of a spherical container or cell (radius b), and calculated the velocity V as a function of κa and φ = (a/b)3. A similar expression for the mobility coefficient f, also based on this cell model, has been proposed by Ohshima.137 Ohshima's prediction is shown in Fig. 16, together with our numerical results. The agreement between our simulations and Ohshima's theory is generally good for small Debye lengths (κ−1 = 5 = a), but shows considerable deviations at large Debye lengths (κ−1 = 10). In both cases, the simulation results predict larger values of f than Ohshima's theory as φ increases. We consider that this deviation arises because of the overlapping of the EDLs for larger φ, as this effect is completely neglected in the theory. To test this, we estimate the effective particle radius a + κ−1 of the ionically dressed particles and define an effective volume fraction φeff ≡ 4π(a + κ−1)3N/3L3 = (1 + (κa)−1)3φ. Fig. 16 clearly shows that our results agree well with Ohshima's theory for φeff ≤ 1, where the overlap effect is small. However, for φeff > 1, where the degree of EDL overlap is large, deviations between our simulations and the theory are notable. These are the first simulations to provide quantitative data necessary to examine the reliability of Ohshima's theory in dense colloidal dispersions. Our results are consistent with more recent studies that have taken EDL overlap into account.141–143
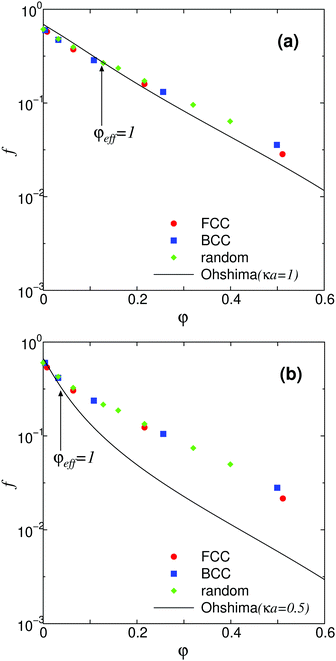 |
| | Fig. 16 The mobility coefficient f(κa, φ) as a function of the volume fraction φ for (a) κa = 1 and (b) κa = 0.5. The solid lines show the results given by the approximate theory proposed by Ohshima.137 This theory is confirmed to be accurate for φeff ≤ 1 but tends to deviate from our numerical results for φeff > 1, where the overlap of the EDLs becomes notable. Reproduced from Phys. Rev. Lett., 96, 208302,31 Copyright 2006, with permission from the American Physical Society. | |
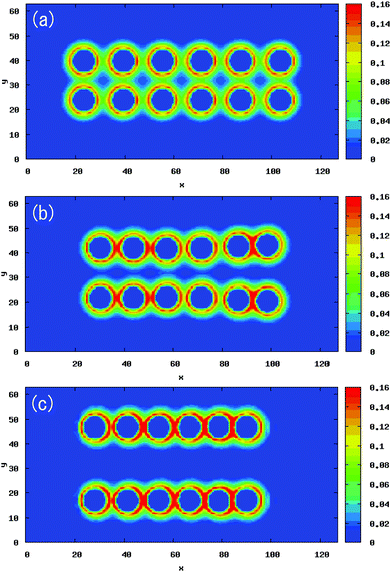 |
| | Fig. 17 Simulation snapshots depicting the time evolution of 12 free particles, initially configured as two stacked linear chains aligned parallel to the oscillating electric field, for ζ = 0.5, κa = 2.5, E = 0.3, and ω* = 0.001. Assuming a colloidal radius of 1 μm and an ionic diffusion constant of Dα = 2 × 10−9 m2 s−1, the simulation times t correspond to (a) 2.1 × 10−4 s, (b) 1.4 × 10−2 s and (c) 8.4 × 10−2 s. The colour map represents the charge density. Reproduced from Soft Matter, 14, 4520–4529,34 Copyright 2018, with permission from the Royal Society of Chemistry. | |
3.6.3 Field-induced order formation.
The field-induced anisotropic interactions between like-charged colloidal particles is studied using the SP method. In particular, we are able to include the polarization of the EDL under external AC electric fields (at frequency ω*) explicitly. Consider a field that is parallel to the distance vector between two particles, such that the induced dipoles (arising from the polarization of the EDL) are aligned in an end-to-end fashion, with the partial positive charge on one particle attracted to the partial negative charge of its neighbour. This situation is depicted in Fig. 17, where particles in the same row feel an attractive inter-particle force (whereas particles on opposite rows are repelled). If the induced dipoles are strong enough to overcome their Coulombic repulsion, i.e., if the field strength is large enough, the particles will experience an effective attraction. Since this attractive interaction depends on the polarization of the EDL, it will also depend strongly on ζ and κa. For a fixed value of the field strength E0, the interaction is attractive for small ζ but repulsive for large ζ. This is due to the fact that at large ζ (high surface potential) more counter-ions are attracted to the charged particle surface, leading to an increase in the charge density around the particle. In turn, this makes the particle more insensitive to external perturbations and more difficult to polarize. In the end, this results in smaller induced dipole–dipole interactions between the particles. Similarly, for thin double layers (large κa) the EDL is more difficult to polarize, compared to thick double layers (small κa), because the counter-ions are more strongly bound to the particle surface. Furthermore, we find that the dynamic response of the colloids and ions is frequency dependent. In particular, we observe two dynamically distinct regimes, corresponding to whether ω* is faster or slower than the ionic diffusion rate ωκ* over the size of the EDL. In the low-frequency regime ω* < ωκ*, the polarization of the EDL has enough time to develop in response to the electric field E(t) and can therefore induce a strong inter-particle force. In contrast, in the high-frequency regime ω* > ωκ* the ions cannot follow the field fast enough to fully polarize the EDL. This results in an inter-particle force that decreases with increasing ω*, up until the point where the system reproduces the results in the absence of an external electric field E0 = 0.
3.7 Colloids in viscoelastic media
In colloidal suspensions in Boger fluids, which are one class of viscoelastic fluids,144,145 shear thickening has been experimentally reported even at dilute concentrations.146–151 This sharply contrasts with Newtonian media, where shear thickening occurs only in concentrated suspensions. The shear rheology of suspensions in viscoelastic media has been studied by using DNS of many-particle systems, for both 2D152 and 3D systems64,153 under periodic boundary conditions, as well as 3D systems under wall-driven shear flow.150,154 Since DNS with surface-conforming meshes155–163 have a limit on the number of particles that can be considered, due to the increasing computational costs, DNS using a fluid mesh independent of the moving boundaries (particles)64,150,152,153,164–168 and smoothed-particle hydrodynamics (SPH) simulations, which employ a mesh-free method, are more suitable to suspensions in viscoelastic media.154
To characterize a viscoelastic suspending medium using the SP method, the viscoelastic stress is added to the continuum eqn (11):
| | | ρ(∂t + u·∇)u = ∇·σ + ∇·σp + ρϕfp, | (66) |
where
σp is a “polymer” stress that is governed by a certain constitutive equation.
169–173 If there is no specific interaction between the polymers in the suspending medium and the solid surface, then
ϕσp = 0 holds.
The shear rheology of a suspension in an Oldroyd-B fluid is investigated by using the SP method.64,65 The Oldroyd-B model exhibits a shear-rate-independent viscosity and finite elasticity, which serves as a model for Boger fluids. The polymer stress in the single-mode Oldroyd-B fluid is governed by
| | 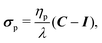 | (67) |
| | 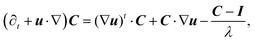 | (68) |
where
C,
ηp, and
λ are the conformation tensor, polymer viscosity, and relaxation time, respectively. The single-mode Oldroyd-B fluid is characterized by two non-dimensional parameters, namely, the viscosity ratio
β =
ηs/(
ηs +
ηp), where
ηs is the viscosity in Newtonian stress, and the Weissenberg number Wi =
λ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif)
. Suspension flow under simple shear flow is solved under periodic boundary conditions in the same way as described in Section 3.3.1.
51
Since shear thickening in Boger fluid media occurs at dilute concentrations, this thickening is attributed mainly to the interaction between a particle and the viscoelastic stress around the particle. The flow around a particle has been previously examined by different DNS studies.64,154,163 Since the flow is forced to circumvent the particle, the direction of the shear flow necessarily changes around the particle. Depending on the conformation orientation, the elastic stress caused by the stretched conformation contributes to an increase in either the macroscopic shear stress or the macroscopic first normal stress difference. Variations in several quantities along a recirculating streamline around a particle at Wi = 2 and β = 0.5 are shown in Fig. 18. The location in Fig. 18 is specified by the angle ϕs from the velocity gradient direction. When σp,xy/ηp![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) > 1, the elastic stress contributes to bulk shear thickening (Fig. 18(a)). For elastic thickening to occur, both the strong stretch of the conformation and the appropriate orientation of the conformation are necessary. For the conformation to be stretched, a large shear rate is not necessarily required (Fig. 18(b)), but the alignment of the major axes of the conformation and the strain-rate tensors, i.e., θC ≈ θD in Fig. 18(c), is important. The efficiency of the conformation stretch can be evaluated by the effective molecular elongation rate,174
> 1, the elastic stress contributes to bulk shear thickening (Fig. 18(a)). For elastic thickening to occur, both the strong stretch of the conformation and the appropriate orientation of the conformation are necessary. For the conformation to be stretched, a large shear rate is not necessarily required (Fig. 18(b)), but the alignment of the major axes of the conformation and the strain-rate tensors, i.e., θC ≈ θD in Fig. 18(c), is important. The efficiency of the conformation stretch can be evaluated by the effective molecular elongation rate,174![[small epsi, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a1.gif) p = n1n1:D shown in Fig. 18(d), where n1 and D are the primary directions of C and the strain-rate tensor, respectively.64 Furthermore, the flow modulated by a particle is almost irrotational in front of and behind the particles,64,154,163 which promotes conformation stretching because the vorticity induced misalignment of C from D is suppressed. These effects of a suspended particle do not depend on the particle shape; therefore, elastic thickening is expected to occur even in suspensions of non-spherical particles.
p = n1n1:D shown in Fig. 18(d), where n1 and D are the primary directions of C and the strain-rate tensor, respectively.64 Furthermore, the flow modulated by a particle is almost irrotational in front of and behind the particles,64,154,163 which promotes conformation stretching because the vorticity induced misalignment of C from D is suppressed. These effects of a suspended particle do not depend on the particle shape; therefore, elastic thickening is expected to occur even in suspensions of non-spherical particles.
 |
| | Fig. 18 Variations in several quantities along a recirculating streamline around a particle at Wi = 2 and β = 0.5: (a) the polymer stress normalized by ηp![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) , (b) the magnitude of the strain-rate tensor normalized by the applied shear rate, (c) the angles of the primary directions of D (red solid line) and C (blue dashed line) defined in the left inset, and (d) the effective elongation rate in the primary direction of C. The abscissa is the clockwise angle ϕs from the velocity gradient direction in the xy-plane, depicted in the right inset. , (b) the magnitude of the strain-rate tensor normalized by the applied shear rate, (c) the angles of the primary directions of D (red solid line) and C (blue dashed line) defined in the left inset, and (d) the effective elongation rate in the primary direction of C. The abscissa is the clockwise angle ϕs from the velocity gradient direction in the xy-plane, depicted in the right inset. | |
Simulations of multi-particle systems in an Oldroyd-B fluid succeeds in quantitatively reproducing the experimentally measured shear-thickening behaviour with a Boger fluid matrix up to φ ≤ 1 for the first time.65
3.8 Dynamics of micro-swimmers
3.8.1 A model for swimming systems.
Micro-swimmers, defined as particles that self-propel in a viscous fluid, among which we find spermatozoa, bacteria, and algae, are ubiquitous in biology and life sciences and are one of the main representatives of active matter systems. From a purely theoretical standpoint, the study of active matter presents itself as fertile ground on which to test and develop theories of non-equilibrium systems. From an applied perspective, particularly with the introduction of synthetic micro-swimmers, there is also the prospect of developing novel medical applications, such as cargo transport systems for targeted drug delivery. However, understanding the role played by hydrodynamic interactions in determining the physical properties of the system remains an incredibly challenging task.175
We focus here on a generic model for micro-swimmers called squirmers. Originally developed by Lighthill and Blake as a model for the ciliary propulsion of paramecia,176,177 this model has become standard for studying the hydrodynamic interactions of rigid micro-swimmers.178 Instead of modelling the synchronized beating of cilia at the surface, which would result in a computationally prohibitive description, one can reproduce the same effects (at the scale of the particle size) by imposing a prescribed boundary condition at the surface of the rigid particle. Here, we consider only spherical swimmers (radius a), but extensions of the squirmer model to spheroidal particles also exist.179,180 Let {ẽi} denote the ortho-normal basis vectors defining the body-axis reference frame, with ẽ3 = ẽ being the fixed swimming axis of the particle. A given point on the particle surface is parametrized in terms of the polar (colatitude) θ and azimuthal λ angles, with θ and λ being the corresponding unit tangent vectors, ϱ the unit vector in the radial direction and θ = arccos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ϱ·ẽ. The imposed “slip” velocity for the squirmer (assuming zero radial velocity) is181
ϱ·ẽ. The imposed “slip” velocity for the squirmer (assuming zero radial velocity) is181
| | 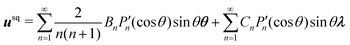 | (69) |
where
Pn′ is the derivative of the
n-order Legendre polynomial and
Bn and
Cn are the coefficients for the
n-th order polar and azimuthal modes, respectively. Most studies neglect the azimuthal modes (
Cn = 0) and all polar modes beyond the second order
Bn = 0 (
n > 2), as this results in the simplest non-trivial model that can represent both pushers (generating propulsion at the back) and pullers (generating propulsion at the front). In this case, the surface velocity becomes (
α =
B2/
B1)
| | 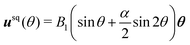 | (70) |
where
B1 determines the steady-state swimming speed for a single particle in an unbounded fluid (
U = 2/3
B1) and
B2 is the strength of the stresslet. The ratio of these modes
α (also denoted as
β in the literature) determines the type of swimmer, with
α > 0 and
α < 0 corresponding to pullers and pushers, respectively, and
α = 0 to the so-called neutral or potential swimmers. A schematic diagram of the squirmer representation for pushers/pullers, together with the different kinds of self-generated flows, is shown in
Fig. 19. The nature of swimming strongly affects the hydrodynamics of the generated flow, with the flow generated by neutral swimmers undergoing 3D decay as
r−3, while pullers (pushers) generate contractile (extensile) flows with a weaker decay as
r−2.
181 This has important consequences for collective behaviour, as shown below.
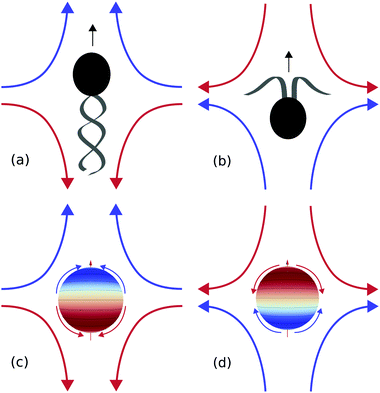 |
| | Fig. 19 Schematic representation of the propulsion mechanism and flow profiles of a pusher and a puller (a and b), respectively. These swimmers can be represented using Blake's squirming model, in which the detailed propulsion mechanism is replaced by a specified slip velocity at the surface of the particles for pushers and pullers (c and d), respectively. Reproduced from Soft Matter, 9, 4923–4936,54 Copyright 2013, with permission from the Royal Society of Chemistry. | |
To solve for the hydrodynamics of these micro-swimmer suspensions using the SP method, we introduce an additional constraint force ϕfsq to the continuum eqn (11) to enforce the slip velocity at the surface54,58
| | | ρ(∂t + u·∇)u = ∇·σ + ρϕfp + ρϕfsq | (71) |
To solve this equation, we incorporate an additional step in the fractional-step approach. After updating for the advection and viscous terms and obtaining
u*, but before enforcing the rigidity constraints through
ϕfp, we solve for the surface constraint force
ϕfsq to obtain an updated velocity field
u** that satisfies the squirmer boundary conditions. For this, we consider an additional SP function
ϕsq, which is non-zero only within the interface domain of the particle
| | 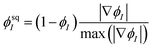 | (72) |
The new velocity field can then be obtained as
| | 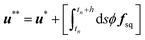 | (73) |
| | 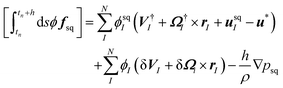 | (74) |
where the first term is the one that actually fixes the slip boundary conditions, the second term is added to ensure local momentum conservation (
i.e., the squirmer experiences a counteracting force if it pushes the fluid at the boundary), and the third term guarantees that the final fluid velocity field is incompressible. Since the updated particle velocities are not yet known at this point of the calculation, we adopt an iterative solution and enforce the slip velocity with respect to
VI† (
WI†) using the velocities at the previous time step at an initial guess. The hydrodynamic force and torque are computed as before, using
u** instead of
u*, and used to update the particle velocities. This procedure is iterated to ensure consistency between the velocities
V†I used to enforce the slip boundary conditions and the particle velocities at the next time step
Vn=1I. The method has been validated for the motion of a single swimmer, where both the particle velocity and the fluid velocity show good agreement with theoretical predictions.
54
3.8.2 Self-diffusion of a micro-swimmer.
Experiments of tracers in swimming suspensions show that hydrodynamic interactions with swimmers, which continuously stir the fluid, are responsible for enhancing the tracer diffusion (beyond that due to thermal fluctuations).182,183 Theoretical predictions based on a kinetic theory approach, as well as simulations and experiments, show that this induced diffusion scales with the flux of swimmers (∝UΦswimmer).184,185 Early simulations of squirmer suspensions indicated a similar diffusive behaviour for swimmers, but with a diffusion coefficient DT that decreases with increasing volume fraction (∝Φswimmer−1).186 This difference is due to the distinct dynamics of tracers and swimmers, where the former can move only as a result of interactions with other particles, while the latter propel themselves along straight paths, deviating only when interacting with other particles. These interactions can be either hydrodynamic or steric in nature. The hydrodynamic interactions, which give rise to rapidly decaying velocity fluctuations as the particles respond to the evolving configuration of the system, are expected to similarly affect both tracers and swimmers. This short time scale is given approximately by the average time it takes for a swimmer to move a distance equal to its diameter. In contrast, the velocity fluctuations caused by the steric interactions decay over a time scale determined by the average time between collisions, which can be estimated to be ∝Φswimmer−1 from kinetic theory arguments. Clearly, the contributions to the dynamics of the swimmers coming from the hydrodynamic interactions are completely masked by their intrinsic motion. This is the reason why the diffusion coefficients of tracers and swimmers show opposite tendencies.187 However, with a careful choice of reference system, it is possible to define an effective diffusion coefficient for the swimmers ![[D with combining tilde]](https://www.rsc.org/images/entities/i_char_0044_0303.gif) T, in which the contributions from the particle's self-propulsion have been removed. This effective diffusion is measuring only the contribution from the hydrodynamic interactions. This is done by computing the particle displacements in the rotating body frame and subtracting the average contribution of the swimming motion along ẽ. In this way, we can show the correspondence between tracer diffusion and (effective) swimmer diffusion (see Fig. 20).54,56 At high swimmer concentrations, both factors are essentially the same, while at low concentrations the asymmetry of the flow field generated by the swimmers gives rise to a negative correlation in the tracer velocity (as the swimmer moves past) and thus reduces the diffusion coefficient.
T, in which the contributions from the particle's self-propulsion have been removed. This effective diffusion is measuring only the contribution from the hydrodynamic interactions. This is done by computing the particle displacements in the rotating body frame and subtracting the average contribution of the swimming motion along ẽ. In this way, we can show the correspondence between tracer diffusion and (effective) swimmer diffusion (see Fig. 20).54,56 At high swimmer concentrations, both factors are essentially the same, while at low concentrations the asymmetry of the flow field generated by the swimmers gives rise to a negative correlation in the tracer velocity (as the swimmer moves past) and thus reduces the diffusion coefficient.
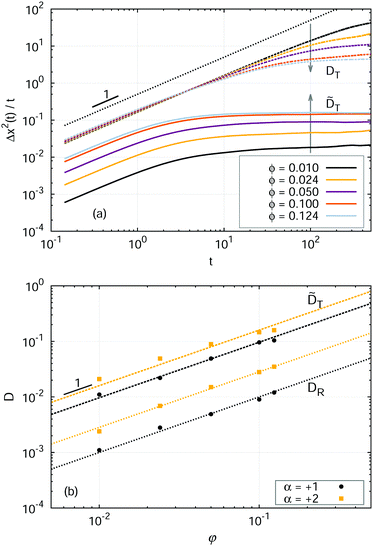 |
| | Fig. 20 (top) Mean-squared displacements for a suspension of pullers (α = +2) at various volume fractions. Dashed lines show the full mean-squared displacements, as measured in the laboratory frame, while solid lines show the effective mean-squared displacements (after removing the self-propulsion term) in the body frame of the swimmers. (bottom) Effective translational ![[D with combining tilde]](https://www.rsc.org/images/entities/i_char_0044_0303.gif) T and rotational DR diffusion coefficients as a function of volume fraction for pullers with α = +1, 2. Adapted from Soft Matter, 9, 4923–4936,54 Copyright 2013, with permission from the Royal Society of Chemistry. T and rotational DR diffusion coefficients as a function of volume fraction for pullers with α = +1, 2. Adapted from Soft Matter, 9, 4923–4936,54 Copyright 2013, with permission from the Royal Society of Chemistry. | |
3.8.3 Collective dynamics of micro-swimmers.
It is well known that squirmers in bulk fluid tend to exhibit polar order188 provided |α| is small, with the highest degree of order obtained for α = 0. As there are no direct alignment interactions, this collective behaviour is due exclusively to the hydrodynamic interactions among particles. Furthermore, this non-zero polar order is stronger at lower volume fractions, which suggests that it could arise from repeated binary interactions. Indeed, using collision data from dilute simulations, we have computed the transition probabilities for the incoming and outgoing angles of the particles and used them to develop a coarse-grained binary collision model.59 Using this simplified representation, we are able to predict the bulk polar order of swimmer suspensions arising from repeated binary collisions. Our results are in good agreement for dilute suspensions of pushers and neutral swimmers but show large discrepancies for pullers, particularly for intermediate α. This can be explained as a breakdown of the binary collision hypothesis, as these systems are known to form transient dynamic clusters in bulk fluid.189
In practice, swimmers usually move in complex environments near boundaries or interfaces, which strongly affects their dynamics and the nature of the hydrodynamic interactions.190 Studies indicate that varying the strength and type of confinement can give rise to dramatically different collective behaviours.191,192 Simulations of swimmers between flat parallel walls, with a narrow confinement ∼2σ that results in quasi-2D systems, show that neutral squirmers exhibit dense/dilute phase separation, whereas pushers and pullers tend to exhibit a hexagonal phase.193 Even though the hydrodynamics are strongly screened by the walls, the near-field hydrodynamic interactions play a crucial role in the particle alignment, and polar ordering is observed only for neutral particles.55 Upon increasing the separation of the wall, squirmers tend to accumulate at the boundary in a manner that depends on the swimmer type.191
We have performed simulations of squirmers under confinement between two flat parallel walls and shown that when the wall separation is large enough (≳40σ, i.e., larger than the characteristic size of the propagating flock), weak pullers develop travelling density waves that bounce back and forth between the walls.58 A similar travelling wave-like motion has been reported in systems with explicit alignment interactions between the particles,194,195 but our results show that hydrodynamic interactions alone are enough to yield this type of collective behaviour. We observe that the strength and type of swimming (pusher vs. puller) are crucial to observe this behaviour but not the degree of global alignment. Furthermore, this behaviour is a manifestation of the bulk behaviour of the suspension and is not due to the presence of walls. This is evidenced by the fact that the velocity of these waves is found to correspond to the sound velocity measured in the bulk fluid, which means that this phenomenon can be interpreted as a pseudo-sound property of the system.
The travelling wave-like motion is illustrated in Fig. 21, where we show simulation snapshots, together with the time evolution of the (local) density ρ, perpendicular polar order parameter Ql and velocity vl, as a function of the height in the channel (computed within parallel slabs of width 2Δ), for a dilute suspension of squirmers (volume fraction of 13%). These simulations are performed in a rectangular simulation box, with periodic boundaries in the x and z directions, but confined between two flat parallel walls along the y direction (at y = 1Δ and 159Δ). Here, for simplicity, the walls are constructed out of (inert) spherical particles of equal radius to the swimmers, which are pinned in place and unable to move or rotate from their initial configuration. Simulations for various α values are performed, with the most interesting results obtained for weak pullers satisfying 0 < α < 1. Fig. 21 shows that the pullers with α = ±0.5 show strong spatiotemporal density fluctuations, first developing two waves travelling in opposite directions, before they merge into a single persistent propagating wave, which bounces back and forth between the top and bottom walls. No such behaviour is observed for the pushers. The onset of this nontrivial collective behaviour is due purely to the differences in the hydrodynamic flow fields generated by the swimmers and their corresponding hydrodynamic interactions, as no direct alignment potential is used.
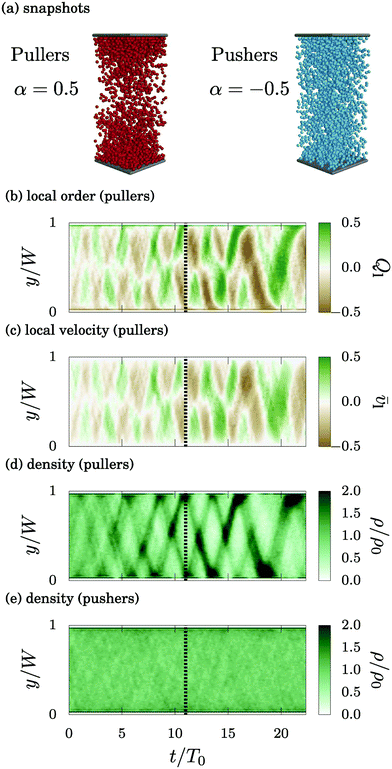 |
| | Fig. 21 Simulation results for pullers and pushers (α = ±0.5) at a volume fraction of 13% and wall separation W/a = 40. (a) Simulation snapshots at T = 11T0, (b) local order of pullers defined as Ql = 〈ẽy〉plane, (c) local velocity of pullers in the y direction (perpendicular to the walls) defined as ![[v with combining macron]](https://www.rsc.org/images/entities/i_char_0076_0304.gif) l = 〈Vy/U0〉plane, (d and e) plane averaged density for pushers and pullers at each height y/W. The density is normalized by the global average value, ρ0, and time and velocity are normalized by T0 = W/U0 and U0, where W represents the separation of parallel flat walls. The snapshots are at approximately t = 11T0, as marked by dashed lines. Reproduced from Phys. Rev. E, 93, 043114,57 Copyright 2016, with permission from the American Physical Society. l = 〈Vy/U0〉plane, (d and e) plane averaged density for pushers and pullers at each height y/W. The density is normalized by the global average value, ρ0, and time and velocity are normalized by T0 = W/U0 and U0, where W represents the separation of parallel flat walls. The snapshots are at approximately t = 11T0, as marked by dashed lines. Reproduced from Phys. Rev. E, 93, 043114,57 Copyright 2016, with permission from the American Physical Society. | |
Recently, we have extended this model to include the rotlet term, in addition to the pusher/puller term, and DNS were performed to study the single particle motion of a swimmer near a flat wall.60
4 Conclusions
We have developed the SP method to simulate the motion of hydrodynamically interacting particles in various kinds of host fluids. By utilizing a SP for the particle–fluid boundaries, the hydrodynamic interactions acting between the particles can be fully considered, yielding both accurate and efficient simulations. The reliability and performance of the method were confirmed to be very satisfactory through several critical tests. The SP method can be easily applied to many-particle systems and arbitrarily shaped particles. In the present paper, the high applicability of the SP method was illustrated for various examples of particle suspensions.
For Brownian particles, we have developed a numerical method for consistently implementing the thermal fluctuation in an incompressible host fluid.35 The validity of the method was confirmed by comparing our numerical results against the fluctuation–dissipation theorem for a single spherical system. Simulations for concentrated dispersions, as well as for a polymeric chain, were then performed. For the former, we found that the hydrodynamic long-time tail in the velocity auto-correlation function, which is clearly observed for a single-particle dispersion, becomes weaker as the volume fraction is increased. For the latter case, we found very good agreement with the theoretical predictions of the Zimm model.35 We have also investigated the rate of rapid Brownian coagulation over a range of volume fractions from φ = 0.003 to φ = 0.1. In the dilute regime the rate of rapid Brownian coagulation is reduced to approximately 0.3–0.5 times the theoretical value predicted by Smoluchowski. This is consistent with previous experimental and theoretical results taking the hydrodynamic effects into account. Because we explicitly include the exact hydrodynamic interactions in our simulations, the fact that we can reproduce this reduction in the coagulation rate is clear evidence for their hydrodynamic origin.39
We have considered non-Brownian sedimenting particles at small Reynolds number (Re ≈ 0.14) over a wide range of volume fractions (0.01 ≤ φ ≤ 0.5). The good agreement between our simulations and other theoretical, experimental and simulation results further illustrates the validity of our method.40 Upon increasing the Re, the inertial forces give rise to a drafting–kissing–tumbling (DKT) mechanism that results in a deficit of neighboring particles. This entails significant phenomenological changes and strongly affects the transport properties of the suspension. At small Reynolds number, Re = 0.1, the fluid exhibits a fore-aft symmetry around the particle, whereas at high Reynolds number, Re > 1, an asymmetric behaviour is clearly observed. The theoretical predictions for the settling velocity in the Stokes regime are no longer applicable when these inertial effects are relevant. To extend the predictive capabilities of previously proposed relations, we proposed an empirical formula valid for Re ≤ 10, which captures the rapid decay of the average sedimentation velocity at low volume fractions and the strong influence of the anisotropic local structure.43
To study the rheological behaviour of colloidal dispersions we have extended the SP method to systems under steady or oscillatory shear flow, by using the Lees–Edwards boundary conditions.49,51 In this way, all the relevant physical quantities, such as the local and total shear stress, can be directly computed during the simulation. We simulated three systems under simple-shear to test the validity of our model: a spherical particle, a rigid-bead chain, and the collision of two spherical particles. We compared the viscosity predicted by the simulations to theoretical predictions and Stokesian dynamics calculations and found good overall agreement. We are also able to capture the shear-thinning behaviour of concentrated colloidal dispersions.51
Hydrodynamic interactions are propagated by both viscous diffusion and sound propagation. To study the time evolution of the hydrodynamic interactions, and the relative importance of these two mechanisms, we have extended the SP method to perform DNS of particles in compressible media. In an incompressible fluid, with an infinite speed of sound, hydrodynamic interactions propagate instantaneously, followed by a temporal evolution due to viscous diffusion. On the other hand, in a compressible fluid, sound propagates at a finite speed, which affects the time evolution of the hydrodynamic interactions. This effect can be quantified by measuring the ratio of the time scales associated with viscous diffusion and sound propagation,62 which defines a compressibility factor. We quantify hydrodynamic interactions for a two-particle system in a compressible fluid through the velocity correlation of the particles. We observe excellent agreement with theoretical predictions.
We have considered multi-phase fluids, consisting of particles dispersed in an A/B fluid mixture, in order to study the attachments/detachments of particles to/from the fluid–fluid interfaces.66 We extended the SP method, within a Cahn–Hilliard framework, in order to simulate such multi-phase flows. The method was applied to perform DNS of a flexible fibre, represented as a chain of spherical beads, interacting with a fluidic interface. The fibre can undergo stretching, bending, and twisting deformations. The capillary force, acting at the three-phase contact line, is calculated using a ternary diffuse-interface model. First we validated the fibre deformation and ternary diffuse-interface model against theoretical solutions. We then performed 2D and 3D simulations for the elasto-capillary bending of the fibre by an immersed droplet. We were able to simulate both partial wrapping and complete encapsulation. We found that the fibre curvature increases linearly with the square of the elasto-capillary length, regardless of the degree of structural deformation.69
We have simulated electrohydrodynamic phenomena in charged colloidal dispersions through a suitable extension of the SP method. The time evolution of the colloidal particles, ions, and host fluid were simultaneously computed by solving the Newton–Euler, advection–diffusion, and Navier–Stokes equations, allowing us to fully capture the electrohydrodynamic coupling of the system.13 We have calculated the electrophoretic mobilities of charged spherical particles under several conditions. Comparisons with approximate theories showed quantitative agreement for dilute dispersions, without requiring any fitting parameters; however, our predictions exhibit considerable deviations for dense dispersions.31 Next, we considered the field-induced anisotropic interactions between like-charged colloidal particles, where the polarization of the electric double layer was explicitly computed under external AC electric fields.34 These interactions were found to depend on the magnitude E0 and frequency ω of the applied field, as well as the zeta potential, the Debye length, and the relative orientation of the particles. We also performed simulations for systems of six and twelve colloidal particles to study the stability of pearl-chain-like configurations.
We have simulated particle dispersions in viscoelastic media. The shear-thickening behaviour in dilute suspensions was investigated utilizing an Oldroyd-B model.64 Here, the fluid elasticity is determined by the Weissenberg number Wi and the relative contribution of the polymer stress that is measured by the viscosity ratio 1 − β = ηp/(ηs + ηp), where ηp and ηs are the polymer and solvent viscosities, respectively. As 1 − β increases, while the suspension viscosity increases, the growth rate of the normalized polymer stress with Wi is suppressed. An analysis of the flow and the conformation dynamics around a particle reveals that, for large values of 1 − β, the conformation stretching is suppressed because of the modulated flow by the polymer stress. This effect of β on the polymer stress is indicative of a complex coupling between the fluid elasticity and the flow. The experimental shear thickening in a Boger fluid matrix was quantitatively reproduced by multi-particle calculations using an Oldroyd-B fluid matrix up to φ ≤ 1.65
The hydrodynamic interactions of a suspension of self-propelled particles were studied using a modified version of the SP method that represents micro-swimmers as squirmers.54 The diffusive behaviour that arises due to the swimming motion of the particles reveals that there are two basic mechanisms at play: the hydrodynamic interactions caused by the squirming motion of the particles and the particle–particle collisions. This dual nature gives rise to two distinct time and length scales, and thus to two distinct diffusion coefficients, which we obtained by a suitable analysis of the swimming motion within the co-rotating reference frame of the particles. These results have allowed us to gain a better understanding of the complex hydrodynamic interactions of self-propelled swimmers. In addition, simulations were performed to study the collective motion of model swimmers in confinement.57 We showed that certain swimming mechanisms can lead to travelling wave-like collective motion, even without any direct alignment interactions between the particles. It was also shown that, by varying the swimming mechanism, this collective motion can be suppressed, contrary to the common perception that hydrodynamic effects are completely screened at high volume fractions. From an analysis of bulk systems, it was shown that this travelling wave-like motion, which can be characterized as a pseudo-acoustic mode, is due mainly to the intrinsic swimming property of the particles.
Conflicts of interest
There are no conflicts to declare.
Appendix A: numerical implementation
We briefly describe the basic computational implementation for a single-component fluid, as found in the KAPSEL simulation package.196
Fluid solver
As mentioned in the Simulation Method section, we use a fractional step approach. First, the modified Navier–Stokes equation without the ϕfp term is evolved to determine u*. This allows us to solve for the advection and hydrodynamic viscous stress. However, for computational simplicity, we do not solve for the fluid velocity u directly but for the vorticity ω = ∇ × u. Assuming a fixed Cartesian coordinate system, under periodic boundary conditions, the corresponding vorticity equation for an incompressible fluid (∇·u = 0) is given by| | 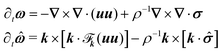 | (75) |
where ![[scr F, script letter F]](https://www.rsc.org/images/entities/char_e141.gif) k(f) =
k(f) = ![[f with combining circumflex]](https://www.rsc.org/images/entities/i_char_0066_0302.gif) (k) denotes a Fourier transform, with k being the wave vector. The fluid velocity is obtained from the definition of the vorticity and the divergence-free condition as
(k) denotes a Fourier transform, with k being the wave vector. The fluid velocity is obtained from the definition of the vorticity and the divergence-free condition as| | 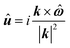 | (76) |
The benefit of solving for the vorticity comes from the fact that we do not need to consider the Poisson equation for the pressure whose only role is to ensure that the final velocity field is incompressible. This can be enforced directly in Fourier space by projecting out the components of û parallel to k such that| | 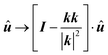 | (77) |
Furthermore, to reduce the memory requirements of the code, we can take advantage of the fact that the three components of the curl are not linearly independent and solve for only two of them (for every given wave vector). Let â = ![[scr F, script letter F]](https://www.rsc.org/images/entities/char_e141.gif) k(∇ × A) = ik × Â be the Fourier transform of the curl of some arbitrary vector field A. We define the following invertible mapping (†: C3 → C2) such that
k(∇ × A) = ik × Â be the Fourier transform of the curl of some arbitrary vector field A. We define the following invertible mapping (†: C3 → C2) such that
| | 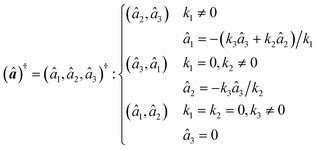 | (78) |
for all
k ≠ 0. The value of
â(
k = 0), which corresponds to the volume integral of the total velocity field, cannot be obtained from
↠and should therefore be propagated independently. We apply the mapping to both sides of
eqn (75) to yield an equation for
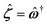
and a subsequent one-third reduction in the computational requirements needed to update the fluid velocity.
The form of the integrator depends on the particular stress tensor s that is used. For the case of a Newtonian fluid, for which ∇·s = η∇2u, the vorticity equation becomes
| | 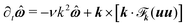 | (79) |
which is of the form
| | ∂ta = ![[script L]](https://www.rsc.org/images/entities/char_e144.gif) a − a − ![[scr N, script letter N]](https://www.rsc.org/images/entities/char_e52d.gif) (t,a(t)) (t,a(t)) | (80) |
with
![[script L]](https://www.rsc.org/images/entities/char_e144.gif)
being a time-independent linear operator and
![[scr N, script letter N]](https://www.rsc.org/images/entities/char_e52d.gif)
being a non-linear operator. This equation has a general solution given by
| | 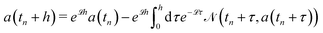 | (81) |
in which the linear part is solved exactly. The integral over the non-linear term can be approximated in many ways, giving rise to the family of exponential time difference (ETD) methods.
197,198 In particular, a first-order approximation
N(
tn +
τ,
a(
tn +
τ)) =
N(
tn,
a(
tn)) results in
| | a(tn + h) = eh[a(tn) − ![[script L]](https://www.rsc.org/images/entities/char_e144.gif) −1(1 − e−h −1(1 − e−h![[script L]](https://www.rsc.org/images/entities/char_e144.gif) ) )![[scr N, script letter N]](https://www.rsc.org/images/entities/char_e52d.gif) (tn,a(tn))] (tn,a(tn))] | (82) |
| | = a(tn) + (e−h![[script L]](https://www.rsc.org/images/entities/char_e144.gif) − 1)(a(tn) + − 1)(a(tn) + ![[script L]](https://www.rsc.org/images/entities/char_e144.gif) −1 −1![[scr N, script letter N]](https://www.rsc.org/images/entities/char_e52d.gif) (tn,a(tn))) (tn,a(tn))) | (83) |
which reduces to the Euler method in the limit when |
![[script L]](https://www.rsc.org/images/entities/char_e144.gif)
| → 0.
Particle solver
The particle configurations (position, orientation, velocity, and angular velocity) are updated using a two-step Adams–Bashforth method (and Euler method for the initial step). Let YI denote the dynamical variable of interest, with YnI = YI(tn)| | 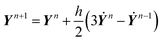 | (84) |
The Euler equations are solved for in the body (principal-axis) reference frame, in which the moment of inertia Ĩ is diagonal, with74| | 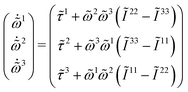 | (85) |
Furthermore, for improved numerical accuracy, the orientations are updated using rotation quaternions q (normalized at the end of every step) instead of rotational matrices R. The dynamical equations for the orientation are then given by199| | 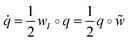 | (86) |
where ° denotes quaternion multiplication and 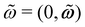 and ω = (0, ω) are the quaternion equivalents of the angular velocity in the lab ω and body reference frames
and ω = (0, ω) are the quaternion equivalents of the angular velocity in the lab ω and body reference frames 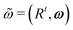 , respectively.
, respectively.
B Validation
The validity of our method to describe the hydrodynamic interactions of non-spherical particle dispersions in complex host solvents is established by comparing our results with exact analytical expressions (when available) as well as with the results obtained using alternative high-precision simulations. To verify that we are able to accurately account for the fluid–particle interactions, we compute the mobility/friction factors for a wide variety of geometrical shapes and compare them with exact solutions to the Stokes equation (SE). As is well known, in the over-damped stationary limit, the force/torque exerted by the fluid on the particles is linear in the velocities. For a system with N particles, this is expressed as200where F = (F1,…,FN, N1,…,NN) and U = (V1,…,Vn, W1,…,WN) are the 6 − N-dimensional force and velocity vectors, respectively, and Z = M−1 is the friction matrix (M is the mobility matrix). The friction/mobility matrices couple the translational (T) and rotational (R) motions of all the particles; in block form, they can be expressed as| | 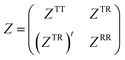 | (88) |
For the special case of a single spherical particle (radius a) in an unbounded fluid, under stick-boundary conditions, the friction matrix can be obtained from an exact solution to the SE as| | 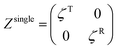 | (89) |
where ζT = 6πηa and ζR = 8πηa3 are the translational and rotational friction coefficients, respectively.
Simulations at Re ≃ 0 for a single non-spherical particle, constructed as a rigid assembly of non-overlapping beads of equal radius a, are performed with a fixed particle velocity U = (Vx, Vy, Vz, 0, 0, 0). The hydrodynamic forces at steady-state F are measured to compute the friction coefficients. We consider six families of axisymmetric regularly shaped particle agglomerates: (even/odd) v-shaped, h-shaped, hexagonal, and rectangular arrays (see Fig. 22(1–f)). Except for the v- and w-shaped particles, for which there is a weak coupling between translation and rotation, the friction matrices are all diagonal. In all cases, however, the translational friction matrix KTT is diagonal.
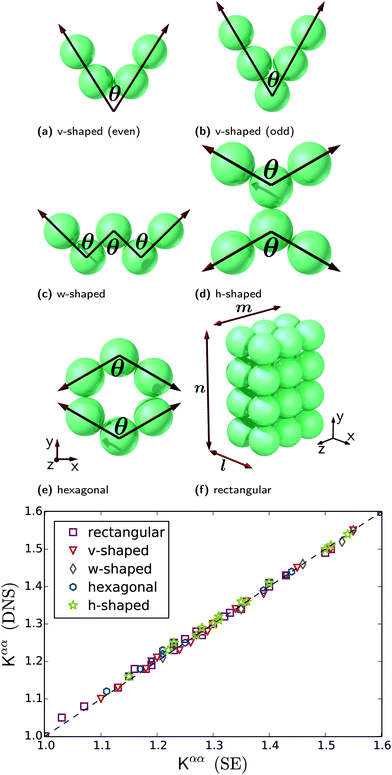 |
| | Fig. 22 (a–f) Non-spherical regular-shaped agglomerates used in the simulations. (g) Correlation between the friction coefficients obtained from the SP method (DNS) simulations and the exact solutions to the SE (as given by HYDROLIB). Adapted from J. Chem. Phys., 139, 234105,52 Copyright 2013, with the permission of AIP publishing. | |
We vary the number of beads and relative bead configuration while keeping the same geometrical shape for a total of 84 different geometric configurations. For simplicity, we report the kinetic form factors K, defined in terms of the friction coefficients by
| | 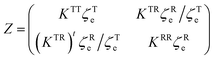 | (90) |
with
ζT,Re being the friction coefficients for a single spherical particle of equal volume (with effective radius
ae), translating (rotating) with the same velocity (angular velocity) and subject to the same boundary conditions. We compare our results with those of the HYDROLIB package, which uses an induced force method truncated to third order.
201 When compared with experimental results, the HYDROLIB results show errors less than 1%
202 and can be considered to correspond to the exact solution of the SE for the current purposes.
Fig. 22(g) shows our results for the friction coefficient with respect to the exact solution to the SE. We obtain excellent agreement, with an error ≲2%. A similar level of agreement is obtained for chiral structures, as well as close-packed (HCP and FCC) arrays of spherical particles (with up to 167 constituent beads), allowing us to resolve the difference in the friction factors for particles that differ in volume by only a few percent.
52
We now consider the lubrication interactions between nearby particles moving relative to each other. These are one of the most important and difficult to capture hydrodynamic effects. We computed the squeeze lubrication interaction between two approaching spheres in a finite system. The velocity and pressure distributions are shown in Fig. 23(a). Fig. 23(b) shows the normalized approach velocity for a pair of particles of equal radius (a), versus the normalized gap distance (h/a) between them, obtained using the SP method (black circles) as well as three different theoretical predictions. Our simulation data accurately reproduce the expected crossover from the near-field (h/a<1)204 to the far-field (h/a > 1)2,203 behaviour around h/a∼ 0.7. It is found that SD5 tends to underestimate the mobility in the crossover regime. The validity of the SP method has been further confirmed using other critical tests, such as the friction coefficient of chiral objects52 where the coupling between translational and rotational motions becomes important, the volume fraction13 and Reynolds number43 dependence of the drag coefficient, the motion and stresslet of a sphere under shear flow,51 the electrokinetics in charged colloidal systems,13,31 and the pair interaction between two squirmers,54 among others.
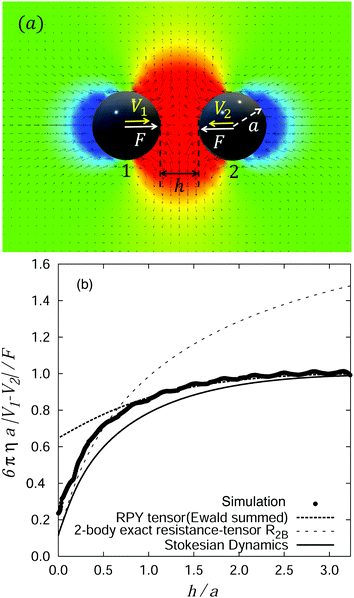 |
| | Fig. 23 (a) Snapshot of two approaching colloidal particles of radius a = 4, under a constant attractive force F. The black arrows indicate the velocity field and density map represents the pressure field (a change in color from red to blue corresponds to a change from high to low pressure). (b) The normalised relative velocity of approaching spheres versus the normalised gap distance between them (h/a). A small oscillating behaviour seen in the present simulation data (black circles) is due to the numerical artifacts of using a finite grid size (Δ). The solid curves correspond to three different theoretical predictions: far-field asymptotics computed using the Ewald summed Rotne–Prager–Yamakawa tensor (dotted line),2,203 near-field exact solution (dashed line),204 and the Stokesian Dynamics predictions (solid line).5 Reproduced from Eur. Phys. J. E Soft Matter, 26, 361–368,13 Copyright 2008, with kind permission of The European Physical Journal (EPJ). | |
C Software availability
We have developed the DNS software KAPSEL that implements the SP method. KAPSEL is designed to simulate the dynamics of solid particles dispersed in simple and complex fluids in various situations, and we performed all the simulations presented in this paper using KAPSEL. The source code of KAPSEL is fully open to the public on KAPSEL-HP196 and can be freely downloaded and used by anyone who agrees to the license. KAPSEL works with the GUI library Gourmet, which is included in the integrated simulator package OCTA205 for soft materials, to provide input/output of simulation parameters and visualize the data. For details on how to obtain and install KAPSEL and OCTA, see KAPSEL-HP.196
Acknowledgements
The authors express their gratitude to Prof. Kang Kim, Prof. Takuya Iwashita, Dr Hideki Kobayashi, Dr Yuki Matsuoka, Dr Rei Tatsumi, Dr Chunyu Shih, Dr Adnan Hamid, Dr Norihiro Oyama, Dr Gregory Lecrivain, Dr Federico Fadda, Prof. Takashi Taniguchi, and Prof. Ko Higashitani for collaboration. This work was supported by the Japan Science and Technology Agency (JST) through their PRESTO and CREST projects as well as Grants-in-Aid for Scientific Research (JSPS KAKENHI) under grant no. JP 23244087, 26247069, 17H01083, 18K03563, 20K03786, 20H00129 and 20H05619. The numerical calculations were partly carried out using the computer facilities at the Research Institute for Information Technology, Kyushu University.
References
-
W. B. Russel, W. Russel, D. A. Saville and W. R. Schowalter, Colloidal dispersions, Cambridge University Press, 1991 Search PubMed
 .
.
-
H. Yamakawa, Modern theory of polymer solutions, Harper & Row, 1971 Search PubMed
 .
.
- C. Y. Son and S. Lee, J. Chem. Phys., 2011, 135, 224512 CrossRef PubMed
 .
.
- A. Sokolov and I. S. Aranson, Phys. Rev. Lett., 2012, 109, 248109 CrossRef PubMed
 .
.
- J. F. Brady and G. Bossis, Annu. Rev. Fluid Mech., 1988, 20, 111–157 CrossRef
 .
.
- B. Cichocki, B. Felderhof, K. Hinsen, E. Wajnryb and J. Bl/awzdziewicz, J. Chem. Phys., 1994, 100, 3780–3790 CrossRef CAS
 .
.
- A. Malevanets and R. Kapral, J. Chem. Phys., 1999, 110, 8605–8613 CrossRef CAS
 .
.
- H. H. Hu, N. A. Patankar and M. Zhu, J. Comput. Phys., 2001, 169, 427–462 CrossRef CAS
 .
.
- R. Glowinski, T.-W. Pan, T. I. Hesla, D. D. Joseph and J. Periaux, J. Comput. Phys., 2001, 169, 363–426 CrossRef CAS
 .
.
- A. Ladd and R. Verberg, J. Stat. Phys., 2001, 104, 1191–1251 CrossRef CAS
 .
.
- M. Cates, K. Stratford, R. Adhikari, P. Stansell, J. Desplat, I. Pagonabarraga and A. Wagner, J. Phys.: Condens. Matter, 2004, 16, S3903 CrossRef CAS
 .
.
- Y. Nakayama and R. Yamamoto, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2005, 71, 036707 CrossRef PubMed
 .
.
- Y. Nakayama, K. Kim and R. Yamamoto, Eur. Phys. J. E: Soft Matter Biol. Phys., 2008, 26, 361–368 CrossRef CAS PubMed
 .
.
- H. Tanaka and T. Araki, Phys. Rev. Lett., 2000, 85, 1338–1341 CrossRef CAS PubMed
 .
.
- T. Kajishima and S. Takiguchi, Int. J. Heat Fluid Flow, 2002, 23, 639–646 CrossRef CAS
 .
.
- A. J. Ladd, Phys. Fluids A, 1993, 5, 299–310 CrossRef CAS
 .
.
- A. J. Ladd, Phys. Rev. Lett., 1996, 76, 1392 CrossRef CAS PubMed
 .
.
- A. J. Ladd, Phys. Fluids, 1997, 9, 491–499 CrossRef CAS
 .
.
- A. Ladd, Phys. Rev. Lett., 2002, 88, 048301 CrossRef CAS PubMed
 .
.
- N.-Q. Nguyen and A. J. Ladd, J. Fluid Mech., 2005, 525, 73 CrossRef
 .
.
- P. Hoogerbrugge and J. Koelman, Europhys. Lett., 1992, 19, 155 CrossRef
 .
.
- J. Padding and A. Louis, Phys. Rev. Lett., 2004, 93, 220601 CrossRef CAS PubMed
 .
.
- S. H. Lee and R. Kapral, J. Chem. Phys., 2004, 121, 11163–11169 CrossRef CAS PubMed
 .
.
- M. Hecht, J. Harting, T. Ihle and H. J. Herrmann, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2005, 72, 011408 CrossRef PubMed
 .
.
- I. O. Götze, H. Noguchi and G. Gompper, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2007, 76, 046705 CrossRef PubMed
 .
.
- S. Poblete, A. Wysocki, G. Gompper and R. G. Winkler, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2014, 90, 033314 CrossRef PubMed
 .
.
- P. D. Godfrin, N. E. Valadez-Pérez, R. Castaneda-Priego, N. J. Wagner and Y. Liu, Soft Matter, 2014, 10, 5061–5071 RSC
 .
.
- S. Jafari, R. Yamamoto and M. Rahnama, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2011, 83, 026702 CrossRef PubMed
 .
.
- R. Yamamoto, Phys. Rev. Lett., 2001, 87, 075502 CrossRef CAS PubMed
 .
.
- R. Yamamoto, Y. Nakayama and K. Kim, J. Phys.: Condens. Matter, 2004, 16, S1945–S1955 CrossRef CAS
 .
.
- K. Kim, Y. Nakayama and R. Yamamoto, Phys. Rev. Lett., 2006, 96, 208302 CrossRef PubMed
 .
.
- C. Shih and R. Yamamoto, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2014, 89, 062317 CrossRef PubMed
 .
.
- C. Shih, J. J. Molina and R. Yamamoto, Mol. Phys., 2015, 113, 2511–2522 CrossRef CAS
 .
.
- C. Shih, J. J. Molina and R. Yamamoto, Soft Matter, 2018, 14, 4520–4529 RSC
 .
.
- T. Iwashita, Y. Nakayama and R. Yamamoto, J. Phys. Soc. Jpn., 2008, 77, 074007 CrossRef
 .
.
- T. Iwashita and R. Yamamoto, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2009, 79, 031401 CrossRef PubMed
 .
.
- T. Iwashita, Y. Nakayama and R. Yamamoto, Prog. Theor. Phys. Suppl., 2009, 178, 86–91 CrossRef CAS
 .
.
- R. Yamamoto, K. Kim, Y. Nakayama, K. Miyazaki and D. R. Reichman, J. Phys. Soc. Jpn., 2008, 77, 084804 CrossRef
 .
.
- Y. Matsuoka, T. Fukasawa, K. Higashitani and R. Yamamoto, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2012, 86, 051403 CrossRef PubMed
 .
.
- A. Hamid, J. J. Molina and R. Yamamoto, Soft Matter, 2013, 9, 10056 RSC
 .
.
- A. Hamid and R. Yamamoto, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2013, 87, 022310 CrossRef PubMed
 .
.
- A. Hamid and R. Yamamoto, J. Phys. Soc. Jpn., 2013, 82, 024004 CrossRef
 .
.
- A. Hamid, J. J. Molina and R. Yamamoto, RSC Adv., 2014, 4, 53681–53693 RSC
 .
.
- A. Hamid, J. J. Molina and R. Yamamoto, Mol. Simul., 2015, 41, 968–973 CrossRef CAS
 .
.
- M. Shakeel, A. Hamid, A. Ullah, J. J. Molina and R. Yamamoto, J. Phys. Soc. Jpn., 2018, 87, 064402 CrossRef
 .
.
- T. Iwashita and R. Yamamoto, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2009, 80, 061402 CrossRef PubMed
 .
.
- T. Iwashita, T. Kumagai and R. Yamamoto, Eur. Phys. J. E: Soft Matter Biol. Phys., 2010, 32, 357–363 CrossRef CAS PubMed
 .
.
- H. Kobayashi and R. Yamamoto, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2010, 81, 041807 CrossRef PubMed
 .
.
- H. Kobayashi and R. Yamamoto, J. Chem. Phys., 2011, 134, 064110 CrossRef PubMed
 .
.
- H. Kobayashi and R. Yamamoto, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2011, 84, 051404 CrossRef PubMed
 .
.
- J. J. Molina, K. Otomura, H. Shiba, H. Kobayashi, M. Sano and R. Yamamoto, J. Fluid Mech., 2016, 792, 590–619 CrossRef CAS
 .
.
- J. J. Molina and R. Yamamoto, J. Chem. Phys., 2013, 139, 234105 CrossRef PubMed
 .
.
- N. Oyama, K. Teshigawara, J. J. Molina, R. Yamamoto and T. Taniguchi, Phys. Rev. E, 2018, 97, 032611 CrossRef CAS PubMed
 .
.
- J. J. Molina, Y. Nakayama and R. Yamamoto, Soft Matter, 2013, 9, 4923 RSC
 .
.
- J. B. Delfau, J. Molina and M. Sano, EPL, 2016, 114, 24001 CrossRef
 .
.
- J. J. Molina and R. Yamamoto, Mol. Phys., 2014, 112, 1389–1397 CrossRef CAS
 .
.
- N. Oyama, J. J. Molina and R. Yamamoto, Phys. Rev. E, 2016, 93, 043114 CrossRef PubMed
 .
.
- N. Oyama, J. J. Molina and R. Yamamoto, J. Phys. Soc. Jpn., 2017, 86, 101008 CrossRef
 .
.
- N. Oyama, J. J. Molina and R. Yamamoto, Eur. Phys. J. E: Soft Matter Biol. Phys., 2017, 40, 95 CrossRef PubMed
 .
.
- F. Fadda, J. J. Molina and R. Yamamoto, Phys. Rev. E, 2020, 101, 052608 CrossRef CAS PubMed
 .
.
- R. Tatsumi and R. Yamamoto, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2012, 85, 066704 CrossRef PubMed
 .
.
- R. Tatsumi and R. Yamamoto, Phys. Fluids, 2013, 25, 046101 CrossRef
 .
.
- R. Tatsumi and R. Yamamoto, J. Chem. Phys., 2013, 138, 184905 CrossRef PubMed
 .
.
- Y. Matsuoka, Y. Nakayama and T. Kajiwara, Soft Matter, 2020, 16, 728–737 RSC
 .
.
- Y. Matsuoka, Y. Nakayama and T. Kajiwara, J. Fluid Mech., 2021, 913, A38 CrossRef CAS
 .
.
- G. Lecrivain, R. Yamamoto, U. Hampel and T. Taniguchi, Phys. Fluids, 2016, 28, 83301–123305 CrossRef
 .
.
- G. Lecrivain, R. Yamamoto, U. Hampel and T. Taniguchi, Phys. Rev. E, 2017, 95, 063107 CrossRef PubMed
 .
.
- G. Lecrivain, Y. Kotani, R. Yamamoto, U. Hampel and T. Taniguchi, Phys. Rev. Fluids, 2018, 3, 094002 CrossRef
 .
.
- G. Lecrivain, T. B. P. Grein, R. Yamamoto, U. Hampel and T. Taniguchi, J. Comput. Phys., 2020, 409, 109324 CrossRef
 .
.
- X. Luo, M. R. Maxey and G. E. Karniadakis, J. Comput. Phys., 2009, 228, 1750–1769 CrossRef
 .
.
- M. Fujita and Y. Yamaguchi, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2008, 77, 026706 CrossRef PubMed
 .
.
- F. Balboa Usabiaga, I. Pagonabarraga and R. Delgado-Buscalioni, J. Comput. Phys., 2012, 235, 701–722 CrossRef
 .
.
- H. H. Wensink, J. Dunkel, S. Heidenreich, K. Drescher, R. E. Goldstein, H. Löwen and J. M. Yeomans, Proc. Natl. Acad. Sci. U. S. A., 2012, 109, 14308–14313 CrossRef CAS PubMed
 .
.
-
J. V. José and E. J. Saletan, Classical Dynamics: A Contemporary Approach, Cambridge University Press, 1998 Search PubMed
 .
.
- R. Glowinski, T. W. Pan, T. I. Hesla and D. D. Joseph, Int. J. Multiphase Flow, 1999, 25, 755–794 CrossRef CAS
 .
.
- D. Wan and S. Turek, Int. J. Numer. Methods Fluids, 2006, 51, 531–566 CrossRef
 .
.
- C. S. Peskin, Acta Numer., 2002, 11, 479–517 CrossRef
 .
.
- M. Uhlmann, J. Comput. Phys., 2005, 209, 448–476 CrossRef
 .
.
- P. Atzberger, P. Kramer and C. Peskin, J. Comput. Phys., 2007, 224, 1255–1292 CrossRef
 .
.
- S. Lomholt and M. R. Maxey, J. Comput. Phys., 2003, 184, 381–405 CrossRef
 .
.
- S. Vincent, J. C. B. De Motta, A. Sarthou, J.-L. Estivalezes, O. Simonin and E. Climent, J. Comput. Phys., 2014, 256, 582–614 CrossRef
 .
.
- X. Luo, A. Beskok and G. E. Karniadakis, J. Comput. Phys., 2010, 229, 3828–3847 CrossRef CAS PubMed
 .
.
- S. Gallier, E. Lemaire, L. Lobry and F. Peters, J. Comput. Phys., 2014, 256, 367–387 CrossRef
 .
.
- J. Lichtenbelt, C. Pathmamanoharan and P. Wiersema, J. Colloid Interface Sci., 1974, 49, 281–285 CrossRef CAS
 .
.
- W. Hatton, P. Mcfadyen and A. Smith, J. Chem. Soc., Faraday Trans. 1, 1974, 655–660 RSC
 .
.
- K. Higashitani and Y. Matsuno, J. Chem. Eng. Jpn., 1979, 12, 460–465 CrossRef CAS
 .
.
-
H. Sonntag and K. Strenge, Coagulation kinetics and structure formation, Plenum, New York, 1987 Search PubMed
 .
.
- H. Holthoff, S. U. Egelhaaf, M. Borkovec, P. Schurtenberger and H. Sticher, Langmuir, 1996, 12, 5541–5549 CrossRef CAS
 .
.
- N. Fuchs, Z. Phys., 1934, 87, 736–743 CrossRef
 .
.
- L. Spielman, J. Colloid Interface Sci., 1970, 33, 562–571 CrossRef CAS
 .
.
- E. Honig, G. Roebersen and P. Wiersema, J. Colloid Interface Sci., 1971, 36, 97–109 CrossRef CAS
 .
.
- K. Higashitani, T. Tanaka and Y. Matsuno, J. Colloid Interface Sci., 1978, 63, 551–560 CrossRef CAS
 .
.
- M. Heine and S. Pratsinis, Langmuir, 2007, 23, 9882–9890 CrossRef CAS PubMed
 .
.
- G. Urbina-Villalba, J. Toro-Mendoza, A. Lozsán and M. García-Sucre, J. Phys. Chem. B, 2004, 108, 5416–5423 CrossRef CAS
 .
.
-
T. Trzeciak, A. Podgóski and J. Marijnissen, In 5th World Congress on Particle Technology, Orlando, FL, 2006, p. 202d Search PubMed
 .
.
- J. Richardson and W. Zaki, Chem. Eng. Sci., 1954, 3, 65–73 CrossRef CAS
 .
.
- J. Garside and M. R. Al-Dibouni, Ind. Eng. Chem. Proc. Des. Dev., 1977, 16, 206–214 CrossRef CAS
 .
.
- G. Batchelor, J. Fluid Mech., 1972, 52, 245–268 CrossRef
 .
.
- H. Hayakawa and K. Ichiki, Phys. Rev. E: Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top., 1995, 51, R3815 CrossRef CAS PubMed
 .
.
- J. F. Brady and L. J. Durlofsky, Phys. Fluids, 1988, 31, 717–727 CrossRef CAS
 .
.
- R. Di Felice, Int. J. Multiphase Flow, 1999, 25, 559–574 CrossRef CAS
 .
.
- H. Nicolai, B. Herzhaft, E. Hinch, L. Oger and E. Guazzelli, Phys. Fluids, 1995, 7, 12–23 CrossRef CAS
 .
.
- J. Padding and A. Louis, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2008, 77, 011402 CrossRef CAS
 .
.
- E. Climent and M. Maxey, Int. J. Multiphase Flow, 2003, 29, 579–601 CrossRef CAS
 .
.
- F. Cunha, G. Abade, A. Sousa and E. Hinch, J. Fluids Eng., 2002, 124, 957–968 CrossRef
 .
.
- X. Yin and D. L. Koch, Phys. Fluids, 2007, 19, 093302 CrossRef
 .
.
- D. R. Mikulencak and J. F. Morris, J. Fluid Mech., 2004, 520, 215–242 CrossRef
 .
.
- A. Onuki, J. Phys.: Condens. Matter, 1997, 9, 6119 CrossRef CAS
 .
.
- S. Toh, K. Ohkitani and M. Yamada, Phys. D, 1991, 51, 569–578 CrossRef
 .
.
- C. J. Lin, J. H. Peery and W. R. Schowalter, J. Fluid Mech., 1970, 44, 1–17 CrossRef
 .
.
- N. Q. Nguyen and A. J. Ladd, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2002, 66, 12 Search PubMed
 .
.
- G. B. Jeffery, R. Soc., 1922, 102, 161–179 Search PubMed
 .
.
- L. G. Leal and E. J. Hinch, J. Fluid Mech., 1971, 46, 685–703 CrossRef
 .
.
- E. J. Hinch and L. G. Leal, J. Fluid Mech., 1972, 52, 683–712 CrossRef
 .
.
- R. Yamamoto and A. Onuki, Phys. Rev. E: Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top., 1998, 58, 3515–3529 CrossRef CAS
 .
.
- N. Taccoen, F. m. c. Lequeux, D. Z. Gunes and C. N. Baroud, Phys. Rev. X, 2016, 6, 011010 Search PubMed
 .
.
- Y. E. Yu, S. Khodaparast and H. A. Stone, Soft Matter, 2017, 13, 2857–2865 RSC
 .
.
- S.-Y. Tan, S. Ata and E. J. Wanless, J. Phys. Chem. B, 2013, 117, 8579–8588 CrossRef CAS PubMed
 .
.
- G. Lecrivain, G. Petrucci, M. Rudolph, U. Hampel and R. Yamamoto, Int. J. Multiphase Flow, 2015, 71, 83–93 CrossRef CAS
 .
.
- B. D. Johnson and R. C. Cooke, Science, 1981, 213, 209–211 CrossRef CAS
 .
.
- K. Stratford, R. Adhikari, I. Pagonabarraga and J. C. Desplat, J. Stat. Phys., 2005, 121, 163–178 CrossRef
 .
.
- G. B. Davies, T. Krüger, P. V. Coveney and J. Harting, J. Chem. Phys., 2014, 141, 154902 CrossRef PubMed
 .
.
- H. Mehrabian, J. Harting and J. H. Snoeijer, Soft Matter, 2016, 12, 1062–1073 RSC
 .
.
- T. Krüger, S. Frijters, F. Günther, B. Kaoui and J. Harting, Eur. Phys. J.: Spec. Top., 2013, 222, 177–198 Search PubMed
 .
.
- X.-C. Luu and A. Striolo, J. Phys. Chem. B, 2014, 118, 13737–13743 CrossRef CAS PubMed
 .
.
- D. M. Anderson, G. B. McFadden and A. A. Wheeler, Annu. Rev. Fluid Mech., 1998, 30, 139–165 CrossRef
 .
.
- H. Shinto, Adv. Powder Technol., 2012, 23, 538–547 CrossRef CAS
 .
.
- T. Araki and S. Fukai, Soft Matter, 2015, 11, 3470–3479 RSC
 .
.
- T. Araki and H. Tanaka, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2006, 73, 061506 CrossRef PubMed
 .
.
- J. Kim, Comput. Methods Appl. Mech. Eng., 2007, 196, 4779–4788 CrossRef
 .
.
- F. Boyer, C. Lapuerta, S. Minjeaud, B. Piar and M. Quintard, Transp. Porous Media, 2010, 82, 463–483 CrossRef
 .
.
- M. v. Smoluchowski, Z. Phys. Chem., 1918, 93, 129 CrossRef
 .
.
- E. Huckel, Phys. Z., 1924, 25, 204–210 Search PubMed
 .
.
- D. Henry, Proc. R. Soc. London, Ser. A, 1931, 133, 106–129 CAS
 .
.
- R. W. O'Brien and L. R. White, J. Chem. Soc., Faraday Trans. 2, 1978, 1607–1626 RSC
 .
.
- S. Levine and G. H. Neale, J. Colloid Interface Sci., 1974, 47, 520–529 CrossRef
 .
.
- H. Ohshima, J. Colloid Interface Sci., 1997, 188, 481–485 CrossRef CAS
 .
.
- J.-P. Hansen and H. Löwen, Annu. Rev. Phys. Chem., 2000, 51, 209–242 CrossRef CAS PubMed
 .
.
-
J.-L. Barrat and J.-P. Hansen, Basic concepts for simple and complex liquids, Cambridge University Press, 2003 Search PubMed
 .
.
- EPAPS Document No. E-PRLTAO-96-051621, http://www.aip.org/pubservs/epaps.html.
- F. Carrique, F. J. Arroyo, M. L. Jiménez and Á. V. Delgado, J. Phys. Chem. B, 2003, 107, 3199–3206 CrossRef CAS
 .
.
- V. Lobaskin, B. Dünweg, M. Medebach, T. Palberg and C. Holm, Phys. Rev. Lett., 2007, 98, 176105 CrossRef PubMed
 .
.
- T. Palberg, M. Medebach, N. Garbow, M. Evers, A. B. Fontecha, H. Reiber and E. Bartsch, J. Phys.: Condens. Matter, 2004, 16, S4039 CrossRef CAS
 .
.
- D. Boger, J. Non-Newtonian Fluid Mech., 1977, 3, 87–91 CrossRef CAS
 .
.
- D. F. James, Annu. Rev. Fluid Mech., 2009, 41, 129–142 CrossRef
 .
.
- I. E. Zarraga, D. A. Hill and D. T. Leighton, J. Rheol., 2001, 45, 1065–1084 CrossRef CAS
 .
.
- R. Scirocco, J. Vermant and J. Mewis, J. Rheol., 2005, 49, 551–567 CrossRef CAS
 .
.
- S.-C. Dai, F. Qi and R. I. Tanner, J. Rheol., 2014, 58, 183–198 CrossRef CAS
 .
.
- R. I. Tanner, J. Non-Newtonian Fluid Mech., 2015, 222, 18–23 CrossRef CAS
 .
.
- M. Yang and E. S. G. Shaqfeh, J. Rheol., 2018, 62, 1379–1396 CrossRef CAS
 .
.
- S. Dai and R. I. Tanner, Rheol. Acta, 2020, 59, 477–486 CrossRef CAS
 .
.
- W. R. Hwang, M. A. Hulsen and H. E. Meijer, J. Non-Newtonian Fluid Mech., 2004, 121, 15–33 CrossRef CAS
 .
.
- G. D'Avino, F. Greco, M. A. Hulsen and P. L. Maffettone, J. Rheol., 2013, 57, 813–839 CrossRef
 .
.
- A. Vázquez-Quesada, P. Español, R. I. Tanner and M. Ellero, J. Fluid Mech., 2019, 880, 1070–1094 CrossRef
 .
.
- N. A. Patankar and H. H. Hu, J. Non-Newtonian Fluid Mech., 2001, 96, 427–443 CrossRef CAS
 .
.
- M. Ahamadi and O. G. Harlen, J. Comput. Phys., 2008, 227, 7543–7560 CrossRef
 .
.
- M. Ahamadi and O. G. Harlen, J. Non-Newtonian Fluid Mech., 2010, 165, 281–291 CrossRef CAS
 .
.
- Y. J. Choi, M. A. Hulsen and H. E. Meijer, J. Non-Newtonian Fluid Mech., 2010, 165, 607–624 CrossRef CAS
 .
.
- Y. J. Choi and M. A. Hulsen, J. Non-Newtonian Fluid Mech., 2012, 175-176, 89–103 CrossRef CAS
 .
.
- N. O. Jaensson, M. A. Hulsen and P. D. Anderson, J. Non-Newtonian Fluid Mech., 2016, 235, 125–142 CrossRef CAS
 .
.
- N. O. Jaensson, M. A. Hulsen and P. D. Anderson, J. Non-Newtonian Fluid Mech., 2015, 225, 70–85 CrossRef CAS
 .
.
- M. Yang, S. Krishnan and E. S. Shaqfeh, J. Non-Newtonian Fluid Mech., 2016, 233, 181–197 CrossRef CAS
 .
.
- M. Yang and E. S. G. Shaqfeh, J. Rheol., 2018, 62, 1363–1377 CrossRef CAS
 .
.
- W. R. Hwang and M. A. Hulsen, Macromol. Mater. Eng., 2011, 296, 321–330 CrossRef CAS
 .
.
- R. Pasquino, G. D'Avino, P. L. Maffettone, F. Greco and N. Grizzuti, J. Non-Newtonian Fluid Mech., 2014, 203, 1–8 CrossRef CAS
 .
.
- S. Krishnan, E. S. Shaqfeh and G. Iaccarino, J. Comput. Phys., 2017, 338, 313–338 CrossRef
 .
.
- Y. K. Lee and K. H. Ahn, J. Non-Newtonian Fluid Mech., 2017, 244, 75–84 CrossRef CAS
 .
.
- C. Fernandes, S. A. Faroughi, O. S. Carneiro, J. M. Nóbrega and G. H. McKinley, J. Non-Newtonian Fluid Mech., 2019, 266, 80–94 CrossRef CAS
 .
.
-
R. B. Bird, C. F. Curtiss, R. C. Armstrong and O. Hassager, Dynamics of Polymeric Liquids, Volume 2: Kinetic Theory, Wiley, 1987 Search PubMed
 .
.
-
R. G. Larson, Constitutive equations for polymer melts and solutions: Butterworths series in chemical engineering, Butterworth-Heinemann, Boston, 1988 Search PubMed
 .
.
-
C. W. Macosko, Rheology: Principles, Measurements, and Applications, VCH Publishes, 1994 Search PubMed
 .
.
-
R. I. Tanner, Engineering rheology, OUP, Oxford, 2000, vol. 52 Search PubMed
 .
.
-
R. G. Owens and T. N. Phillips, Computational rheology, Imperial College Press, London, 2002, vol. 14 Search PubMed
 .
.
- M. Pasquali and L. Scriven, J. Non-Newtonian Fluid Mech., 2002, 108, 363–409 CrossRef CAS
 .
.
- M. C. Marchetti, J. F. Joanny, S. Ramaswamy, T. B. Liverpool, J. Prost, M. Rao and R. A. Simha, Rev. Mod. Phys., 2013, 85, 1143–1189 CrossRef CAS
 .
.
- M. J. Lighthill, Annu. Rev. Fluid Mech., 1969, 1, 413 CrossRef
 .
.
- J. R. Blake, J. Fluid Mech., 1971, 46, 199–208 CrossRef
 .
.
- M. R. Shaebani, A. Wysocki, R. G. Winkler, G. Gompper and H. Rieger, Nat. Rev. Phys., 2020, 2, 181–199 CrossRef
 .
.
- S. R. Keller and T. Y. Wu, J. Fluid Mech., 1977, 80, 259 CrossRef
 .
.
- K. Kyoya, D. Matsunaga, Y. Imai, T. Omori and T. Ishikawa, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2015, 92, 1–6 CrossRef PubMed
 .
.
- O. S. Pak and E. Lauga, J. Eng. Math., 2014, 88, 1–28 CrossRef
 .
.
- X. L. Wu and A. Libchaber, Phys. Rev. Lett., 2000, 84, 3017–3020 CrossRef CAS PubMed
 .
.
- K. C. Leptos, J. S. Guasto, J. P. Gollub, A. I. Pesci and R. E. Goldstein, Phys. Rev. Lett., 2009, 103, 1–4 CrossRef PubMed
 .
.
- G. L. Miño, J. Dunstan, A. Rousselet, E. Clément and R. Soto, J. Fluid Mech., 2013, 729, 423–444 CrossRef
 .
.
- A. Jepson, V. A. Martinez, J. Schwarz-Linek, A. Morozov and W. C. Poon, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2013, 88, 3–7 CrossRef PubMed
 .
.
- T. Ishikawa and T. J. Pedley, J. Fluid Mech., 2007, 588, 437–462 CrossRef
 .
.
- T. Ishikawa, J. T. Locsei and T. J. Pedley, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2010, 82, 1–15 CrossRef PubMed
 .
.
- A. A. Evans, T. Ishikawa, T. Yamaguchi and E. Lauga, Phys. Fluids, 2011, 23, 111702 CrossRef
 .
.
- F. Alarcón and I. Pagonabarraga, J. Mol. Liq., 2013, 185, 56–61 CrossRef
 .
.
- C. Bechinger, R. Di Leonardo, H. Löwen, C. Reichhardt, G. Volpe and G. Volpe, Rev. Mod. Phys., 2016, 88, 045006 CrossRef
 .
.
- G. J. Li and A. M. Ardekani, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2014, 90, 1–12 Search PubMed
 .
.
- L. Zhu, E. Lauga and L. Brandt, J. Fluid Mech., 2013, 726, 285 CrossRef
 .
.
- A. Zöttl and H. Stark, Phys. Rev. Lett., 2014, 112, 1–5 CrossRef PubMed
 .
.
- H. Chaté, F. Ginelli, G. Grégoire, F. Peruani and F. Raynaud, Eur. Phys. J. B, 2008, 64, 451–456 CrossRef
 .
.
- T. Ohta and S. Yamanaka, Prog. Theor. Exp. Phys., 2014, 2014, 1–7 Search PubMed
 .
.
- KAPSEL Home Page, https://kapsel-dns.com.
- S. M. Cox and P. C. Matthews, J. Comput. Phys., 2002, 176, 430–455 CrossRef CAS
 .
.
- M. Hochbruck and A. Ostermann, Acta Numer., 2010, 19, 209–286 CrossRef
 .
.
-
M. P. Allen and D. J. Tildesley, Computer Simulation of Liquids, Oxford Science Publications, 1987 Search PubMed
 .
.
-
S. Kim and S. J. Karrila, Microhydrodynamics: Principles and Selected Applications, Dover Publications, 2005 Search PubMed
 .
.
- K. Hinsen, Comput. Phys. Commun., 1995, 88, 327–340 CrossRef CAS
 .
.
- B. Cichocki and K. Hinsen, Phys. Fluids, 1995, 7, 285–291 CrossRef CAS
 .
.
- C. Beenakker, J. Chem. Phys., 1986, 85, 1581–1582 CrossRef CAS
 .
.
- D. J. Jeffrey and Y. Onishi, J. Fluid Mech., 1984, 139, 261–290 CrossRef
 .
.
- OCTA Home Page, http://octa.jp.
|
| This journal is © The Royal Society of Chemistry 2021 |
Click here to see how this site uses Cookies. View our privacy policy here.  Open Access Article
Open Access Article *a,
John J.
Molina
*a,
John J.
Molina
 a and
Yasuya
Nakayama
a and
Yasuya
Nakayama
 b
b
![[Q with combining dot above]](https://www.rsc.org/images/entities/b_i_char_0051_0307.gif) I = skew(Ω)·QI,
I = skew(Ω)·QI,![[V with combining dot above]](https://www.rsc.org/images/entities/b_i_char_0056_0307.gif) I = FHI + FCI + FEI + GVI,
I = FHI + FCI + FEI + GVI,![[J with combining dot above]](https://www.rsc.org/images/entities/b_i_char_004a_0307.gif) I = NHI + NCI + NEI + GΩI,
I = NHI + NCI + NEI + GΩI,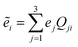 . The time-evolution of the rotation matrix is determined by the (skew-symmetric) angular velocity matrix, derived from the angular velocity vector,
. The time-evolution of the rotation matrix is determined by the (skew-symmetric) angular velocity matrix, derived from the angular velocity vector, 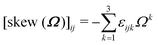 , where εijk is the Levi-Civita symbol, as
, where εijk is the Levi-Civita symbol, as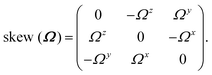
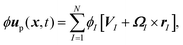
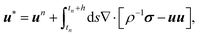
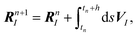
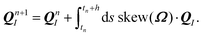
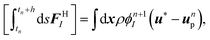
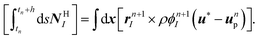
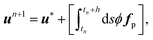
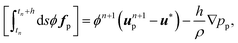
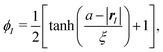

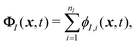
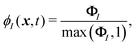
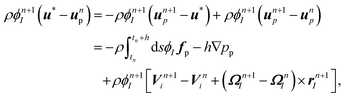
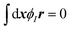 yields
yields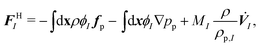
![[V with combining dot above]](https://www.rsc.org/images/entities/b_i_char_0056_0307.gif) i = FHi + FCi + GVi,
i = FHi + FCi + GVi,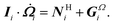
 , as shown in Fig. 4.
, as shown in Fig. 4.


![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) m = 200
m = 200![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 100, where r is the inter-particle distance and ε is the interaction strength. The large value of the exponent in eqn (28) results in a very short-range interaction, appropriate for the rapid coagulation of sticky particles. For the results presented here, we chose a strong enough attractive potential, so that coagulated particles were prevented from breaking apart due to thermal fluctuations. For this, the value of ε was fixed to be 7.03kBT. To improve the statistical significance of the data, five independent simulations were performed for each set of parameter values, and the results were averaged over.
100, where r is the inter-particle distance and ε is the interaction strength. The large value of the exponent in eqn (28) results in a very short-range interaction, appropriate for the rapid coagulation of sticky particles. For the results presented here, we chose a strong enough attractive potential, so that coagulated particles were prevented from breaking apart due to thermal fluctuations. For this, the value of ε was fixed to be 7.03kBT. To improve the statistical significance of the data, five independent simulations were performed for each set of parameter values, and the results were averaged over.
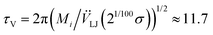 .
.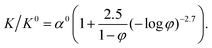
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) φ)−2.7 ≪ 1. However, since this formula was obtained from simulations using Langevin dynamics, it ignores the hydrodynamic interactions between the particles. To account for these missing contributions, we can treat α0 as a scaling or correction factor. Using a least-squares fit of α0 to our simulation results, we obtained α0 = 0.326. This result agrees well with the form of eqn (29), despite the differences in the way that the hydrodynamic interactions are considered. From this, we can conclude that while hydrodynamic interactions affect the magnitude of the coagulation rate, they do not affect the particle concentration dependency, at least in the dilute limit.
φ)−2.7 ≪ 1. However, since this formula was obtained from simulations using Langevin dynamics, it ignores the hydrodynamic interactions between the particles. To account for these missing contributions, we can treat α0 as a scaling or correction factor. Using a least-squares fit of α0 to our simulation results, we obtained α0 = 0.326. This result agrees well with the form of eqn (29), despite the differences in the way that the hydrodynamic interactions are considered. From this, we can conclude that while hydrodynamic interactions affect the magnitude of the coagulation rate, they do not affect the particle concentration dependency, at least in the dilute limit.

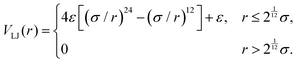
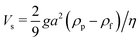 being the corresponding Stokes velocity for a single particle.
being the corresponding Stokes velocity for a single particle.

![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(−φ/0.008),
exp(−φ/0.008),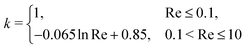
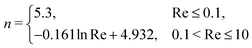

![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) yex in the system is to add an external forcing term ρfs into the modified Navier–Stokes equation (11), the role of which is to maintain the target shear flow (
yex in the system is to add an external forcing term ρfs into the modified Navier–Stokes equation (11), the role of which is to maintain the target shear flow (![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) ). When performing bulk 3D simulations under periodic boundary conditions, a linear zig-zag (possibly time-dependent) profile with two kinks (where the force is applied) can be used to satisfy the boundary constraints.46,47 The results obtained using this external forcing are in good agreement with alternative DNS methods and theoretical predictions, but the method presents some considerable drawbacks: first, the shear rate is not a precisely controlled quantity; second, there are non-physical kinks where the velocity gradient changes sign (at which point particles translate with no net rotation); and third, the zero-wavevector transport coefficients cannot be obtained (as the technique uses a finite-wavelength perturbation). To overcome these difficulties, one can adopt Lees–Edwards boundary conditions, solving the continuum equations on an (oblique) time-dependent coordinate system whose points are advected by the shear flow. Fig. 8 presents a schematic illustration of this coordinate transform. At time t = t0, a solid spherical particle is shown dispersed in a solvent, which is discretized on a rectangular grid (Fig. 8(a)). After the shear-flow is applied (t > t0), both the particle and the grid points are convected by the flow, with the grid undergoing a shear-induced deformation, in contrast to the particle whose shape remains unchanged. This situation can be represented in a fixed coordinate system (Fig. 8(b)), as well as a time-dependent oblique coordinate system which tracks the shear-flow (Fig. 8(c)), and in which the particle shape is deformed. This formulation is equivalent to the SLLOD algorithm used in non-equilibrium MD simulations to model (arbitrary) homogeneous and divergence-free flows, but the implementation of this algorithm within a grid-based system requires a careful treatment.49,108,109 The appropriate contravariant form of the Navier–Stokes equation for the peculiar velocity ξ = u − U within this time-dependent oblique coordinate system, with basis vectors (Ê1 = ex + γ(t)ey, Ê2 = e2, Ê3 = e3), is given as51
). When performing bulk 3D simulations under periodic boundary conditions, a linear zig-zag (possibly time-dependent) profile with two kinks (where the force is applied) can be used to satisfy the boundary constraints.46,47 The results obtained using this external forcing are in good agreement with alternative DNS methods and theoretical predictions, but the method presents some considerable drawbacks: first, the shear rate is not a precisely controlled quantity; second, there are non-physical kinks where the velocity gradient changes sign (at which point particles translate with no net rotation); and third, the zero-wavevector transport coefficients cannot be obtained (as the technique uses a finite-wavelength perturbation). To overcome these difficulties, one can adopt Lees–Edwards boundary conditions, solving the continuum equations on an (oblique) time-dependent coordinate system whose points are advected by the shear flow. Fig. 8 presents a schematic illustration of this coordinate transform. At time t = t0, a solid spherical particle is shown dispersed in a solvent, which is discretized on a rectangular grid (Fig. 8(a)). After the shear-flow is applied (t > t0), both the particle and the grid points are convected by the flow, with the grid undergoing a shear-induced deformation, in contrast to the particle whose shape remains unchanged. This situation can be represented in a fixed coordinate system (Fig. 8(b)), as well as a time-dependent oblique coordinate system which tracks the shear-flow (Fig. 8(c)), and in which the particle shape is deformed. This formulation is equivalent to the SLLOD algorithm used in non-equilibrium MD simulations to model (arbitrary) homogeneous and divergence-free flows, but the implementation of this algorithm within a grid-based system requires a careful treatment.49,108,109 The appropriate contravariant form of the Navier–Stokes equation for the peculiar velocity ξ = u − U within this time-dependent oblique coordinate system, with basis vectors (Ê1 = ex + γ(t)ey, Ê2 = e2, Ê3 = e3), is given as51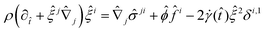
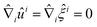
 ) is used here to denote tensorial components in the oblique frame. After the flow equations are solved, we transform back to the fixed laboratory frame to compute the particle–fluid interactions and solve for the particle dynamics.
) is used here to denote tensorial components in the oblique frame. After the flow equations are solved, we transform back to the fixed laboratory frame to compute the particle–fluid interactions and solve for the particle dynamics.

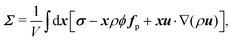
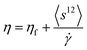
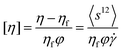
![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) .
.

![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) /KBT (10−2 < Pe < 10). For low to intermediate particle volume fractions φ ≲ 0.3, the viscosities are constant over the examined range of Peclet numbers, signalling Newtonian behaviour. However, for higher volume fractions (φ ≳ 0.4), shear-thinning behaviour is obtained, with a sharp decrease in the viscosity at high Peclet numbers. The low- and high-shear limiting viscosities (shown in Fig. 9), both monotonically increasing functions of volume fraction, are in good agreement with the semi-empirical Krieger–Dougherty relationship. Analysis of the structural relaxation time τp, defined as the time required for the Brownian particles to diffuse a distance equal to their radius, shows that shear thinning starts at approximately τp
/KBT (10−2 < Pe < 10). For low to intermediate particle volume fractions φ ≲ 0.3, the viscosities are constant over the examined range of Peclet numbers, signalling Newtonian behaviour. However, for higher volume fractions (φ ≳ 0.4), shear-thinning behaviour is obtained, with a sharp decrease in the viscosity at high Peclet numbers. The low- and high-shear limiting viscosities (shown in Fig. 9), both monotonically increasing functions of volume fraction, are in good agreement with the semi-empirical Krieger–Dougherty relationship. Analysis of the structural relaxation time τp, defined as the time required for the Brownian particles to diffuse a distance equal to their radius, shows that shear thinning starts at approximately τp![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) ∼ 1, reminiscent of the non-Newtonian behaviour of supercooled liquids.115 Furthermore, to study the viscoelastic properties, we also consider an oscillatory shear flow and measure the storage and loss moduli, which are shown to be in excellent agreement with experimental data.47
∼ 1, reminiscent of the non-Newtonian behaviour of supercooled liquids.115 Furthermore, to study the viscoelastic properties, we also consider an oscillatory shear flow and measure the storage and loss moduli, which are shown to be in excellent agreement with experimental data.47
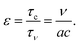
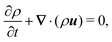
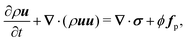
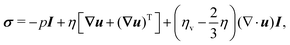
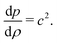
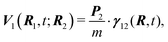
![[R with combining circumflex]](https://www.rsc.org/images/entities/b_i_char_0052_0302.gif)
![[R with combining circumflex]](https://www.rsc.org/images/entities/b_i_char_0052_0302.gif) + γ⊥12(R,t)(I −
+ γ⊥12(R,t)(I − ![[R with combining circumflex]](https://www.rsc.org/images/entities/b_i_char_0052_0302.gif)
![[R with combining circumflex]](https://www.rsc.org/images/entities/b_i_char_0052_0302.gif) ).
).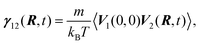

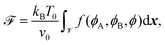
![[scr V, script letter V]](https://www.rsc.org/images/entities/char_e149.gif) denotes the spatial extent of our ternary system, kB is the Boltzmann constant, T0 is the reference temperature, v0 is the reference unit volume, and f is the non-dimensional free energy density. The variables (ϕ, ϕA, and ϕB) in the free energy density f are usually referred to as “order parameters”.126 Because the sum total of the volume fractions is constrained to be unity ϕA + ϕB + ϕ = 1, the free energy density can be conveniently recast as a function of only two order parameters, which we take to be ψ = ϕA − ϕB and ϕ. For simplicity, We refer to ψ as “the” order parameter and ϕ as the particle or fibre (i.e., bead-chain) volume fraction. Consistent with previous studies,127,128 we adopt the following form for the free energy densities of the mixture:
denotes the spatial extent of our ternary system, kB is the Boltzmann constant, T0 is the reference temperature, v0 is the reference unit volume, and f is the non-dimensional free energy density. The variables (ϕ, ϕA, and ϕB) in the free energy density f are usually referred to as “order parameters”.126 Because the sum total of the volume fractions is constrained to be unity ϕA + ϕB + ϕ = 1, the free energy density can be conveniently recast as a function of only two order parameters, which we take to be ψ = ϕA − ϕB and ϕ. For simplicity, We refer to ψ as “the” order parameter and ϕ as the particle or fibre (i.e., bead-chain) volume fraction. Consistent with previous studies,127,128 we adopt the following form for the free energy densities of the mixture: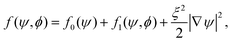
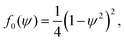
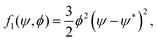

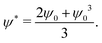

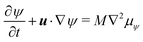
![[scr F, script letter F]](https://www.rsc.org/images/entities/char_e141.gif) /δψ is the chemical potential associated with the order parameter ψ.
/δψ is the chemical potential associated with the order parameter ψ.
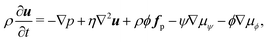
![[scr F, script letter F]](https://www.rsc.org/images/entities/char_e141.gif) /δϕ is the chemical potential with respect to the fibre volume fraction ϕ. The last source term ϕ∇μϕ is motivated by the ternary fluid studies of Boyer et al.,131 but our tests show that it is only necessary to improve the stability of the solution in 2D. For 3D simulations, remarkable agreement with theory can be achieved without it.68
/δϕ is the chemical potential with respect to the fibre volume fraction ϕ. The last source term ϕ∇μϕ is motivated by the ternary fluid studies of Boyer et al.,131 but our tests show that it is only necessary to improve the stability of the solution in 2D. For 3D simulations, remarkable agreement with theory can be achieved without it.68
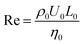
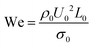
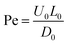
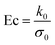


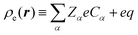 . The complete dynamics of the system is obtained by solving the following time evolution equations.12,13
. The complete dynamics of the system is obtained by solving the following time evolution equations.12,13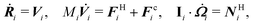
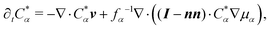
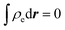 of the system is guaranteed. The chemical potential is defined as138,139
of the system is guaranteed. The chemical potential is defined as138,139![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln
ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Cα* + Zαe(Ψ + Ψex),
Cα* + Zαe(Ψ + Ψex),![[C with combining macron]](https://www.rsc.org/images/entities/i_char_0043_0304.gif) α
α![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp[−Zαe(Ψ + Ψex)/kBT].
exp[−Zαe(Ψ + Ψex)/kBT].![[C with combining macron]](https://www.rsc.org/images/entities/i_char_0043_0304.gif) α is related to the Debye screening length
α is related to the Debye screening length 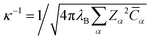 , where λB = e2/4πεkBT is the Bjerrum length, which is approximately 0.72 nm in water at 25 °C.
, where λB = e2/4πεkBT is the Bjerrum length, which is approximately 0.72 nm in water at 25 °C.
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 electrolyte composed of monovalent counter-ions (α = +) and co-ions (α = −). The units of energy and electrostatic potential are kBT and kBT/e, respectively. The non-dimensional mobility parameter mα = 2εkBTfα/3ηe2 is set to be m+ = m− = 0.184, which corresponds to that of KCl solution at 25 °C. Finally, our unit of time τ = Δ2f+/kBT would correspond to 0.44 μs.
1 electrolyte composed of monovalent counter-ions (α = +) and co-ions (α = −). The units of energy and electrostatic potential are kBT and kBT/e, respectively. The non-dimensional mobility parameter mα = 2εkBTfα/3ηe2 is set to be m+ = m− = 0.184, which corresponds to that of KCl solution at 25 °C. Finally, our unit of time τ = Δ2f+/kBT would correspond to 0.44 μs.
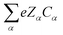 in a plane perpendicular to the z-axis. The electric field is applied in the +x direction, normal to the (1, 0, 0) face for the FCC and BCC lattices. Reproduced from Phys. Rev. Lett., 96, 208302,31 Copyright 2006, with permission from the American Physical Society.
in a plane perpendicular to the z-axis. The electric field is applied in the +x direction, normal to the (1, 0, 0) face for the FCC and BCC lattices. Reproduced from Phys. Rev. Lett., 96, 208302,31 Copyright 2006, with permission from the American Physical Society.

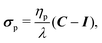
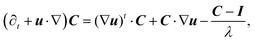
![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) . Suspension flow under simple shear flow is solved under periodic boundary conditions in the same way as described in Section 3.3.1.51
. Suspension flow under simple shear flow is solved under periodic boundary conditions in the same way as described in Section 3.3.1.51
![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) > 1, the elastic stress contributes to bulk shear thickening (Fig. 18(a)). For elastic thickening to occur, both the strong stretch of the conformation and the appropriate orientation of the conformation are necessary. For the conformation to be stretched, a large shear rate is not necessarily required (Fig. 18(b)), but the alignment of the major axes of the conformation and the strain-rate tensors, i.e., θC ≈ θD in Fig. 18(c), is important. The efficiency of the conformation stretch can be evaluated by the effective molecular elongation rate,174
> 1, the elastic stress contributes to bulk shear thickening (Fig. 18(a)). For elastic thickening to occur, both the strong stretch of the conformation and the appropriate orientation of the conformation are necessary. For the conformation to be stretched, a large shear rate is not necessarily required (Fig. 18(b)), but the alignment of the major axes of the conformation and the strain-rate tensors, i.e., θC ≈ θD in Fig. 18(c), is important. The efficiency of the conformation stretch can be evaluated by the effective molecular elongation rate,174![[small epsi, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a1.gif) p = n1n1:D shown in Fig. 18(d), where n1 and D are the primary directions of C and the strain-rate tensor, respectively.64 Furthermore, the flow modulated by a particle is almost irrotational in front of and behind the particles,64,154,163 which promotes conformation stretching because the vorticity induced misalignment of C from D is suppressed. These effects of a suspended particle do not depend on the particle shape; therefore, elastic thickening is expected to occur even in suspensions of non-spherical particles.
p = n1n1:D shown in Fig. 18(d), where n1 and D are the primary directions of C and the strain-rate tensor, respectively.64 Furthermore, the flow modulated by a particle is almost irrotational in front of and behind the particles,64,154,163 which promotes conformation stretching because the vorticity induced misalignment of C from D is suppressed. These effects of a suspended particle do not depend on the particle shape; therefore, elastic thickening is expected to occur even in suspensions of non-spherical particles.![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ϱ·ẽ. The imposed “slip” velocity for the squirmer (assuming zero radial velocity) is181
ϱ·ẽ. The imposed “slip” velocity for the squirmer (assuming zero radial velocity) is181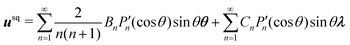
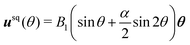

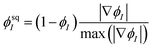
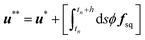
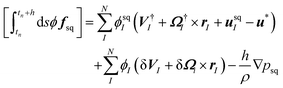
![[D with combining tilde]](https://www.rsc.org/images/entities/i_char_0044_0303.gif) T, in which the contributions from the particle's self-propulsion have been removed. This effective diffusion is measuring only the contribution from the hydrodynamic interactions. This is done by computing the particle displacements in the rotating body frame and subtracting the average contribution of the swimming motion along ẽ. In this way, we can show the correspondence between tracer diffusion and (effective) swimmer diffusion (see Fig. 20).54,56 At high swimmer concentrations, both factors are essentially the same, while at low concentrations the asymmetry of the flow field generated by the swimmers gives rise to a negative correlation in the tracer velocity (as the swimmer moves past) and thus reduces the diffusion coefficient.
T, in which the contributions from the particle's self-propulsion have been removed. This effective diffusion is measuring only the contribution from the hydrodynamic interactions. This is done by computing the particle displacements in the rotating body frame and subtracting the average contribution of the swimming motion along ẽ. In this way, we can show the correspondence between tracer diffusion and (effective) swimmer diffusion (see Fig. 20).54,56 At high swimmer concentrations, both factors are essentially the same, while at low concentrations the asymmetry of the flow field generated by the swimmers gives rise to a negative correlation in the tracer velocity (as the swimmer moves past) and thus reduces the diffusion coefficient.

![[D with combining tilde]](https://www.rsc.org/images/entities/i_char_0044_0303.gif) T and rotational DR diffusion coefficients as a function of volume fraction for pullers with α = +1, 2. Adapted from Soft Matter, 9, 4923–4936,54 Copyright 2013, with permission from the Royal Society of Chemistry.
T and rotational DR diffusion coefficients as a function of volume fraction for pullers with α = +1, 2. Adapted from Soft Matter, 9, 4923–4936,54 Copyright 2013, with permission from the Royal Society of Chemistry.
![[v with combining macron]](https://www.rsc.org/images/entities/i_char_0076_0304.gif) l = 〈Vy/U0〉plane, (d and e) plane averaged density for pushers and pullers at each height y/W. The density is normalized by the global average value, ρ0, and time and velocity are normalized by T0 = W/U0 and U0, where W represents the separation of parallel flat walls. The snapshots are at approximately t = 11T0, as marked by dashed lines. Reproduced from Phys. Rev. E, 93, 043114,57 Copyright 2016, with permission from the American Physical Society.
l = 〈Vy/U0〉plane, (d and e) plane averaged density for pushers and pullers at each height y/W. The density is normalized by the global average value, ρ0, and time and velocity are normalized by T0 = W/U0 and U0, where W represents the separation of parallel flat walls. The snapshots are at approximately t = 11T0, as marked by dashed lines. Reproduced from Phys. Rev. E, 93, 043114,57 Copyright 2016, with permission from the American Physical Society.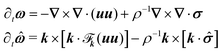
![[scr F, script letter F]](https://www.rsc.org/images/entities/char_e141.gif) k(f) =
k(f) = ![[f with combining circumflex]](https://www.rsc.org/images/entities/i_char_0066_0302.gif) (k) denotes a Fourier transform, with k being the wave vector. The fluid velocity is obtained from the definition of the vorticity and the divergence-free condition as
(k) denotes a Fourier transform, with k being the wave vector. The fluid velocity is obtained from the definition of the vorticity and the divergence-free condition as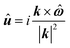
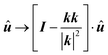
![[scr F, script letter F]](https://www.rsc.org/images/entities/char_e141.gif) k(∇ × A) = ik × Â be the Fourier transform of the curl of some arbitrary vector field A. We define the following invertible mapping (†: C3 → C2) such that
k(∇ × A) = ik × Â be the Fourier transform of the curl of some arbitrary vector field A. We define the following invertible mapping (†: C3 → C2) such that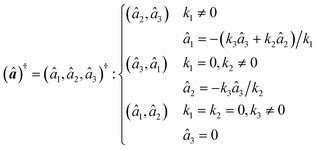
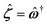 and a subsequent one-third reduction in the computational requirements needed to update the fluid velocity.
and a subsequent one-third reduction in the computational requirements needed to update the fluid velocity.
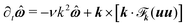
![[script L]](https://www.rsc.org/images/entities/char_e144.gif) a −
a − ![[scr N, script letter N]](https://www.rsc.org/images/entities/char_e52d.gif) (t,a(t))
(t,a(t))![[script L]](https://www.rsc.org/images/entities/char_e144.gif) being a time-independent linear operator and
being a time-independent linear operator and ![[scr N, script letter N]](https://www.rsc.org/images/entities/char_e52d.gif) being a non-linear operator. This equation has a general solution given by
being a non-linear operator. This equation has a general solution given by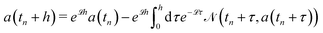
![[script L]](https://www.rsc.org/images/entities/char_e144.gif) −1(1 − e−h
−1(1 − e−h![[script L]](https://www.rsc.org/images/entities/char_e144.gif) )
)![[scr N, script letter N]](https://www.rsc.org/images/entities/char_e52d.gif) (tn,a(tn))]
(tn,a(tn))]![[script L]](https://www.rsc.org/images/entities/char_e144.gif) − 1)(a(tn) +
− 1)(a(tn) + ![[script L]](https://www.rsc.org/images/entities/char_e144.gif) −1
−1![[scr N, script letter N]](https://www.rsc.org/images/entities/char_e52d.gif) (tn,a(tn)))
(tn,a(tn)))![[script L]](https://www.rsc.org/images/entities/char_e144.gif) | → 0.
| → 0.
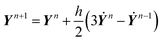
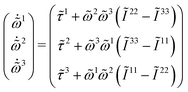
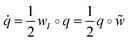
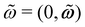 and ω = (0, ω) are the quaternion equivalents of the angular velocity in the lab ω and body reference frames
and ω = (0, ω) are the quaternion equivalents of the angular velocity in the lab ω and body reference frames 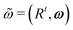 , respectively.
, respectively.
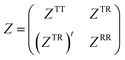
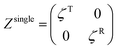

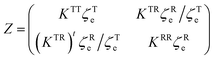

.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.


