Fabrication of strong magnetic micron-sized supraparticles with anisotropic magnetic properties for magnetorheology

Abstract

We propose three different techniques to synthesize anisotropic magnetic supraparticles for their incorporation in the formulation of magnetorheological fluids with novel potential applications. The techniques include microtransfer molding, electrodeposition and microfluidic flow-focusing devices. Although the yield of these methods is not large, with their use, it is possible to synthesize supraparticles with anisotropy in both their magnetic content and shape. The magnetorheological characteristics (yield stress) of the resulting field-induced structures were computed using finite element method simulations and demonstrated to be strongly dependent on the microstructural anisotropy of the supraparticles. In anisotropic particles, the simulated yield stress is always larger than that of the isotropic ones consisting of magnetically homogeneous spherical particles.

---

Introduction

Magnetorheological fluids are field-responsive colloidal suspensions that exhibit a large rheological change upon the application of an external magnetic field.^1–3 The reason for this is the directional/anisotropic assembly of the particulates under the superposition of the field. Magnetic field-guided colloidal assembly can be controlled through the field configuration (DC, AC, and DC + AC)⁴ and colloidal building blocks.⁵ For the given field configuration and strength, it is the morphology and structure of the field-induced colloidal aggregates (dictated by the building blocks and their concentration) that govern the rheological performance of these fluids: yield stress and elasticity. In most cases, magnetorheological fluids consist of building blocks that are magnetically homogeneous carbonyl iron (CI) microparticles (i.e. isotropic magnetic particles) and their performance is improved by increasing the particle concentration.²

Alternative routes to improve the rheological response imply modifications in the shape and magnetic content of the building blocks. In this work, we follow three different approaches to synthesize particles that can feature these modifications at the same time. This is in contrast to previously reported publications where anisotropy always comes from non-spherical shapes.^6–10

Currently, there is great interest in the fabrication of magnetic anisotropic particles that combine surface, bulk and/or shape anisotropies to generate novel colloidal assemblies with improved rheological properties and functionalities.⁵ Some examples are Janus particles,¹¹ shifted dipoles¹² and patchy structures.¹³ Of outstanding interest is the control of the magnetic anisotropy within the bulk of the dispersed particles because it determines the magnetic field-directed assembly through directional bonding.^14,15 With this, multipolar configurations become possible; the simplest case being the quadrupolar one where the magnetization pattern can be described with a pair of induced dipoles within the particle.

Most of the anisotropic magnetic particles reported in the literature consist of magnetic nanoparticles encapsulated in a polymer matrix. Using bulk methods, it is extraordinarily difficult to control the distribution of the nanoparticles within the matrix. However, template assisted methods constitute a very useful technique for the generation of anisotropic magnetic particles.¹⁴ Apart from magnetorheological applications, these composite particles may be of interest in many other applications where complex hierarchical structures are needed¹⁶ and control over the particle rotation is required.¹⁷

In this work, we aim to establish new template-assisted fabrication methodologies (involving microtransfer molding, electrodeposition and microfluidic techniques) to obtain micron-sized supraparticles with anisotropic magnetic properties and tunable morphology (spherical and non-spherical shapes). Both, microtransfer molding and microfluidic techniques will make use of the same materials to synthesize shape an-/isotropic supraparticles, respectively. In this way, the generated supraparticles will differentiate only in their shape. This will allow studying shape effects in future works and decoupling them from other factors such as surface chemistry, particle–carrier interactions, particle density and particle rigidity. Finally, electrodeposition will be used to synthesize particles with extraordinarily large aspect ratios, much larger than those obtained using microtransfer molding techniques.

Different from the previously reported approaches, the presented methods will yield strong magnetic supraparticles, suitable for magnetorheological applications, as they are based on strongly magnetic particles (namely, CI).

Results and discussion

Non-spherical magnetic supraparticles using microtransfer molding techniques

Isotropic. A method that is based on the microtransfer molding technique¹⁸ has been implemented for the production of monodisperse non-spherical magnetic composite supraparticles (see below). We show here that this is a versatile synthesis method that provides control over geometry, dimensions and magnetic content of the particles. A schematic description of this methodology is described in Fig. 1. To demonstrate the utility and generality of this technique for the fabrication of supraparticles for magnetorheological applications, we used poly(dimethylsiloxane) (PDMS) elastomers as the template similar to Tavacoli et al.¹⁵ and Garstecki et al.¹⁹

Fig. 1 Schematics of the particle fabrication by microtransfer molding technique. (a) The process begins with a polydimethylsiloxane (PDMS) mold previously treated with plasma and activated with chlorosilane. (b) The mold wells were filled with a suspension of carbonyl iron (CI) particles in ethoxylated trimethylolpropane triacrylate (ETPTA) and a photoinitiator (2-hydroxy-2-mehtyl-1-phenyl-propan-1-one). (c) The excess suspension was removed by scraping off the surface of the mold with a razor blade and gently pressing the mold against a glass slide several times. (d) The dispersion was reticulated using a 254 nm light. (e) The PDMS block was cleaned again; this time rinsing in ethanol and with a stream of dry air. (f) A water solution of poly(vinyl alcohol) (PVA) was spread on top of the PDMS mold. (g) Once the polymer was solidified, the PDMS mold was carefully peeled off from the polymer. (h) To release the particles from the PVA film, the polymer was dissolved in water. Finally, the particles were collected by magnetic decantation and rinsed with water.

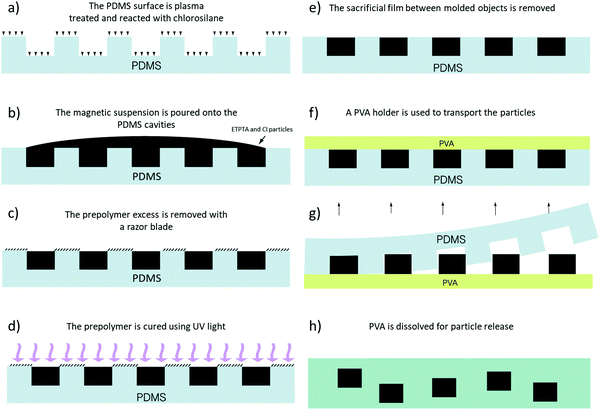
PDMS substrates were prepared using soft lithography techniques and used as templates for the fabrication of the magnetic supraparticles (for details see the Experimental section below). Briefly, the process consists of the following steps. First, a predesigned motif was transferred from a photomask to a SU8 photoresist which was then exposed to UV light and later developed to dissolve the unexposed parts. A PDMS mold was later obtained from the photoresist by replication. Once the PDMS templates were prepared, a suspension containing magnetic microparticles in a UV-curable monomer was poured in the PDMS cavities and subsequently reticulated. A fast polymerization rate allowed trapping the structure of the cavities. The motifs used in this work consist of cubes (aspect ratio 1), rods (>1), cylinders (1) and disks (<1). The shape and dimensions of these cavities within the PDMS molds controlled the morphology and size of the supraparticles. Using this technique, it is possible to fabricate particles of a reasonably large height/width aspect ratio (up to 6 : 1).¹⁸

The magnetic microparticles used in the suspension formulation were polydisperse silica-coated CI particles. The silica coating (refractive index n = 1.45) together with the UV-curable monomer used (ethoxylated trimethylolpropane triacrylate, ETPTA, n = 1.4689) ensured colloidal stability and prevented CI particles from aggregating.²⁰ Also, the high polydispersity level of the CI particles allowed us to closely pack the CI particles within the PDMS wells and thus to improve the magnetic response of the supraparticles. The expected magnetic response is at least four times larger than that previously reported for similar supraparticles (see ESI†). It is noteworthy that, considering these precautions, the particle concentration used in this work could be astonishingly large (50 vol%; 84 wt%). This content is very large compared to the same volumetric concentrations reported in the literature (e.g. Tavacoli et al.¹⁵).

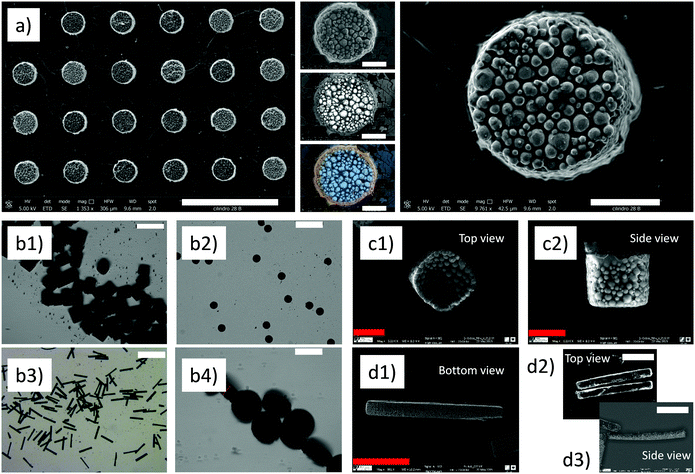
After UV-curing the supraparticles (solidification within approximately 4 h), the scum layer was carefully removed (see Experimental section below). Then, the particles were harvested from the PDMS mold. For this, we used a waxing technique using polyvinyl alcohol (PVA) as the extractor holder. Next, the particles embedded within the PVA polymer were released by dissolution of the wax in water at 40 °C. Taking advantage of the optical transparency of polymerized ETPTA, the distribution of magnetic microparticles within the supraparticles could be easily observed using optical microscopy. Additionally, the SEM images obtained from retrodispersed electrons allowed us to obtain high-magnification images of the microparticle distribution near the surfaces. To demonstrate the versatility of this method, in Fig. 2, we show some representative images of the fabricated supraparticles obtained using SEM (Fig. 2a, c and d) and bright-field optical microscopy (Fig. 2b). We show examples of supraparticles having cubic, rod-like and cylindrical shapes. The CI microparticle distribution is homogeneous within the generated supraparticles and therefore the latter are magnetically isotropic.

Fig. 2 Microscopy images of the isotropic magnetic supraparticles generated using microtransfer molding techniques. (a) Bottom view of the supraparticles cured within the cylindrical PDMS microwells (25 μm diameter) still within the PVA holder. Observed spherical inclusions within the supraparticles correspond to the CI microparticles. Array of supraparticles, scale bar: 100 μm. Individual supraparticle scale bar: 10 μm. (b) Typical optical microscopy images corresponding to released: (b1, scale bar 50 μm) cubes, (b2, 200 μm) cylinders, (b3, 500 μm) rods and (b4, 50 μm) disks. (c) Detail of the cubic particles, scale bar 10 μm: (c1) top view and (c2) side view. (d) Detail of the rods, scale bar 100 μm: (d1) bottom, (d2) top and (d3) side views.

Non-isotropic. In order to generate a magnetic anisotropy in the supraparticles, we prepositioned the CI particles within the PDMS wells prior to UV curing following two different approaches: (i) convective driven self-assembly and (ii) magnetic field guided self-assembly. Typical images of the particles obtained using these techniques are shown in Fig. 3.

Fig. 3 Left column: Schematics of convective deposition technique: (a1) the size of the magnetic region can be controlled by the concentration of ethanol, (a2) the size of the central hollow cylinder can be controlled by the evaporation rate. (b) Typical optical microscopy pictures of the transverse view corresponding to the cylindrical supraparticles with different concentrations of ethanol (25 vol% and 50 vol%). Scale bar: 25 μm. (c) SEM micrographs of the horizontal cut carried out to an array of cubic supraparticles within a PVA holder. Scale bar: 50 μm. (d) SEM micrographs of arrays of cubic supraparticles under (d1) slow and (d2) fast evaporation rates. Scale bars: 100 μm and 10 μm (inset). Right column: Optical microscopy pictures corresponding to magnetic field-guided self-assembly under uniaxial DC fields in (e1) one-step process and (e2) two-step process. Scale bar: 25 μm.

(i) One possibility is to use convective deposition in a two-step process. This consists of the following. First, a given amount of ethanol is added to the CI suspension. Next, the suspension is loaded into the PDMS mold and ethanol is evaporated to leave the wells partially empty. Then, the carrier is reticulated as normal. Finally, a certain amount of the carrier (without particles or ethanol) is added to fully cover the wells. Upon reticulation, the two parts comprising the wells merge together. The result is the formation of Janus particles having one part that is non-magnetic and another region that is magnetic (see Fig. 3a). By simply tuning the initial ethanol concentration in the mixture it is possible to control the size of the magnetic and non-magnetic regions (see Fig. 3a-1). This is demonstrated in Fig. 3b where particles are observed from the side and the dark region (containing CI particles) becomes thinner for a large concentration of ethanol. In addition, because of the presence of a triple line, CI particles migrate to the sides leaving a particle depleted region (“magnetically” hollow) in the center of the particles (see Fig. 3a-2). This is demonstrated in Fig. 3c where a transversal section of the transferred holder (PVA containing the supraparticles) is observed under an electron microscope to demonstrate the internal structure of the supraparticles.

Interestingly, iron particles can be driven slowly or speedily to the contact line of the suspension/well interface depending on the evaporation rate of ethanol. The evaporation rate can be easily controlled by tuning the temperature of the substrate during the evaporation of ethanol. In this way, we can control the size of the central depleted region (see Fig. 3a-2). For this, a wettability control is important because wettability determines the evaporation rate (lower contact angle results in a larger evaporation rate):²¹ (i) a slow evaporation rate results in lesser particle migration towards the walls of the cavities and therefore a smaller (or even negligible) central region (see Fig. 3d-1); (ii) in contrast, a fast evaporation rate results in important capillary-driven convective flows that push the CI particles towards the triple line in the cavities increasing the size of the central region (see Fig. 3d-2). As a result, under these conditions, the particles do not sediment much in the bottom of the wells. Hence, CI microparticles are not observed in SEM images shown in Fig. 3d-2 in contrast to the slow evaporation case where the particles are clearly sedimented and the central hole is not observed (Fig. 3d-1).

The mechanism behind the particle migration towards the periphery of the cavity in the first stage is the convective driven self-assembly coming from the greater rate of evaporation at the triple line. This mechanism occurs because of the sufficiently large pinning time (the contact line is pinned on the PDMS walls) and contact angle hysteresis. When the evaporation flow is weak, deposition can be suppressed if the particle diffusion overcomes convection flow. In contrast, if evaporation is strong, convection dominates and particles migrate to the triple line.²² It is important to note here that the proposed mechanism to generate magnetic anisotropy within the particles is valid for CI concentrations below a certain value. When the particle concentration is too large (approx. 40 vol%) the central hole is not observed. Interestingly, both the size ratio between the magnetic and non-magnetic regions and also the size of the depleted internal region can be controlled using only two independent parameters: the initial ethanol concentration and the evaporation rate.

(ii) An alternative approach for the fabrication of non-isotropic magnetic particles involves the superposition of external magnetic fields during reticulation (right column in Fig. 3). Depending on the pattern of the magnetic field lines, the CI microparticles may redistribute and segregate into different configurations (Janus, patched, etc.) resulting in tunable magnetic anisotropies. Here, we consider the simplest case that involves the superposition of uniaxial DC fields perpendicular to the substrates.

Under uniaxial magnetic fields, the particles tend to aggregate in the field direction and migrate to the sides of the cavities giving place to the formation of “magnetically hollow” cylinders similar to those observed using convective deposition (i.e. the particles are concentrated on the sides of the cylinders). In this case, the physical mechanism is different. This is now due to the magnetic-induced repulsion between chains of particles confined in the well (see Fig. 3e).²³ Again, Janus particles can be generated using the two-step process described above (see Fig. 3e-1,2) with the difference that the magnetic region is not homogeneous when self-assembled under magnetic fields. Obviously, multiaxial magnetic fields would allow greater freedom by introducing other control parameters such as frequency and strength in various directions.

Non-spherical magnetic particles using electrodeposition techniques

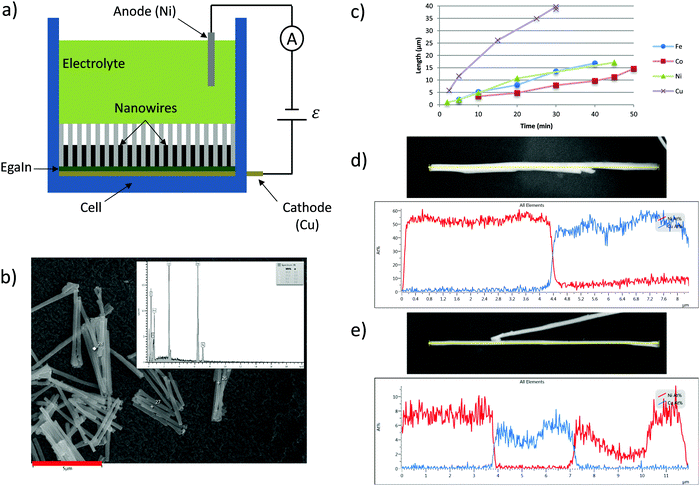
Non-spherical micron sized particles can also be fabricated using electrodeposition techniques. This is a well-known, very simple, versatile and inexpensive technique for the manufacture of dense and uniform films made of almost any metal or conductive alloy and also nanostructures.²⁴ In this work we are particularly interested in magnetic materials. Electrodeposition techniques have the advantage that a larger degree of miniaturization can be obtained in one dimension, when compared to the microtransfer molding techniques. Therefore, the aspect ratio of the produced particles can be significantly larger and this is of much interest in steady-state²⁵ and dynamic-oscillatory²⁶ magnetorheological applications as already demonstrated in the specialized literature.

Isotropic. Magnetic particles having a very large aspect ratio (microwires) can be prepared using electrodeposition by molding. According to this methodology, a porous membrane serves as the template for the synthesis of the particles. Typically, prior to electrodeposition, a metallic layer is sputtered on one side of the membrane. Instead, in this work, we applied a thin layer of eutectic gallium–indium (EGaIn) what results in a cheaper, faster and easier protocol. Since the mold is not conductive, this layer functions as a cathode in the electrodeposition process.

Basically, the procedure involves the reduction of the cations of a particular electrolyte within the pores of the membrane when an electric current is applied to the solution. Thus, the electrodeposition begins at the conductive face adhered to the membrane and advances into the pores (Fig. 4a). The particle diameter is determined by the size of the pores, while the length of the particles can be simply controlled by adjusting the deposition time.

Fig. 4 (a) Schematics of the transverse view of the electrodeposition setup. The cell is filled with an electrolyte and contains the porous alumina template in the bottom. This template is in contact on one side with the EGaIn cathode and on the other side with the solution. (b) SEM image and EDX spectrum of typical 5 μm long iron microwires. Scale bar: 5 μm. (c) Experimental particle length versus time curves for iron (circles), cobalt (squares), nickel (triangles) and copper (crosses). (d and e) EDX microanalysis of multisegmented microwires: (d) Ni/Cu and (e) Ni/Cu/Ni.

By employing the electrodeposition technique and making use of EGaIn as the cathode, we have successfully synthesized iron, cobalt and nickel particles. Fig. 4b shows the typical particles obtained from iron solutions. As stated above, using this technique, the length of the particles can be easily controlled by adjusting the reaction time as shown in Fig. 4c.

Non-isotropic. It is also feasible to fabricate compositionally anisotropic particles by electrodeposition. To achieve this, we repeatedly implemented the process described above several times alternating the electrolyte and voltage according to the material to be deposited. In this work, we demonstrate this possibility by fabricating microwires having segments of different magnetic character: ferromagnetic/non-ferromagnetic. We manufactured different combinations of segments: specifically of iron, cobalt and nickel. Fig. 4d and e show some of the fabricated multisegmented microwires.

Spherical magnetic supraparticles: microfluidic-based synthesis

Wet self-assembly techniques, and in particular droplet templated colloidal assembly, are a topic of recent interest. The latter encompasses the fabrication of colloidal structures within droplets suspended in a second immiscible liquid phase (e.g. Rastogi et al.²⁷). This is an alternative strategy for the fabrication of monodisperse colloids through the formation of monodisperse emulsion drops by coflowing immiscible fluids at low Reynolds numbers.²⁸

Isotropic. Isotropic spherical supraparticles were prepared using microfluidic techniques with a flow focusing device and two immiscible liquids. The device consists of four channels arranged in an X-junction: the continuous phase (sodium dodecyl sulfate – SDS–aqueous solution) is flowed through the outer channels whereas the dispersed phase (a suspension of CI particles in ETPTA and a photoinitiator) is fed in the inner channel. Both phases meet at the junction where the continuous one gets around the dispersed one, becoming unstable and breaking periodically in droplets which are collected from the drainage channel (see Fig. 5a). Depending on the flow rate of the continuous and dispersed phases (Q_c, Q_d), different patterns were observed as summarized in Fig. 5b.

Fig. 5 (a1) Schematics of the microfluidic flow focusing system. The dispersed phase is flowed through the inner channel whereas the continuous phase is flowed through the outer channels. (a2) Photograph of the experimental flow focusing system. Scale bar: 1 mm. (b) Observed flow regimes as a function of the dispersed Q_d and continuous Q_c flow rates. Monodisperse droplets were only obtained in the dripping regime. (c) Isotropic supraparticles with different CI contents and diameters were obtained by varying the CI concentration and flow rates of both phases. Scale bar: 50 μm. Anisotropic magnetic content was obtained by (d) photopolymerizing droplets once the CI particles have settled down or (e) superimposing an uniaxial DC external magnetic field during photopolymerization.

Monodisperse droplets with an adjustable diameter, smaller than the junction's orifice (100 μm, see Experimental section), were obtained in the dripping regime by varying flow rates in both channels: as Q_c (Q_d) increases, smaller (larger) droplets are produced. By changing Q_c between 40 and 110 μL min⁻¹ and Q_d between 0.2 and 1 μL min⁻¹, droplets with a diameter from 25 to 60 μm were obtained. In the dripping regime, the break-off of droplets is governed by the competition between viscous stress and surface tension²⁹ or equivalently by the Capillary number Ca = μ_cv_c/γ where μ_c and v_c are the viscosity and velocity of the continuous phase, respectively, and γ is the interfacial tension between both phases. Increasing the flow rate in the continuous phase also implies an increase in Ca. As a consequence, the shear stress exerted by this phase on the dispersed one promotes the development of a jet which eventually breaks into droplets. Depending on the flow rate of the dispersed phase, jetting or tip streaming patterns were found.³⁰ In both cases generated droplets were smaller than in the dripping regime, though polydispersity and satellite droplets were also observed. Because of this, the dripping regime was preferred to get monodisperse droplets. Finally, if the flow rates were reduced, droplets were not produced because the continuous phase could not break the dispersed one (annular flow), droplets were larger than the channel width (plug) or generated droplets stick together in the drainage channel (coalescence).

Once the droplets were produced in the dripping regime, they were next collected in a Petri dish and exposed to UV light for 1 to 4 h for solidification. To compensate for the strong UV absorption from the dispersed CI microparticles UV polymerization was performed inside a box that was covered with an aluminum foil. At this stage, it was also important to maintain a low amplitude vibration of the emulsion to avoid CI sedimentation and clustering between droplets. The final supraparticles obtained for different flow rates of continuous and dispersed phases are shown in Fig. 5c. Once polymerized, the magnetic supraparticles were robust and could be washed, dried and re-dispersed into water. Microfluidic-based techniques allow us to synthesize supraparticles in a continuous way. However, it does not allow us to use highly concentrated CI suspensions (in contrast to the microtransfer molding technique) because of clogging limitations.

Anisotropic. Anisotropic spherical particles were simply fabricated using the same process as described in the section above. However, in this case the suspensions were left to sediment or under external magnetic fields for a sufficiently long time prior to exposing the droplets to UV light and full polymerization (see Fig. 5d and e).

Finite element method simulations

One of the main shortcomings of the three proposed methods is that their yield is not large (see ESI†). This makes its very difficult to perform statistically relevant experiments using conventional torsional magnetorheometers (the resultant samples have a magnetic content usually below 1 vol%). As a result, finite element method simulations were carried out to interrogate the influence of the particle anisotropy on the mechanical strength (i.e. the yield stress) of the field-induced structures. A large number of different anisotropic supraparticles, similar to the experimental ones, were simulated: cubes, Janus cubes, rods, cylinders and disks with and without an inner hole, and Janus spheres (i.e. spheres with only a magnetic pole).

First, the equilibrium orientation of the supraparticles was determined in the presence of magnetic fields. For this, the magnetostatic energy of the supraparticle was computed when subjected to homogeneous magnetic fields with different orientations. Then, the equilibrium orientation was identified with the one that minimizes the energy similar to Gangwal et al.³¹

For the equilibrium orientation, the magnetic field was found to be parallel to the supraparticle's major polarization axis as it has been previously reported in the literature.^5,15,31 The major polarization axis corresponds to the longest magnetic side of rods and Janus cubes, the height of the cylinders (w / and w/o a hole) and the diameter of the disks (w / and w/o a hole). For a Janus sphere, the field was parallel to the plane between the magnetic and non-magnetic parts. In the case of the cubes, the field tended to align them along the diagonal of a cube face. Nevertheless, the energetic difference from the different field orientations were very small (within 0.016%) indicating that a cubic shape is not anisotropic enough to clearly define a main polarization axis, in good agreement with Tavacoli et al.¹⁵ For this reason, in the following, it will be considered that the cube polarization axis is normal to one of its faces. Finally, it should be highlighted that for the cubes (Janus or not) and rods, the azimuthal orientation of the field did not have a significant influence on the particle energy.

In a second step, anisotropic supraparticles were assembled into single-width infinite chains aligned with the applied field. The chains were affinely strained fixing the field direction as reported by Morillas and de Vicente.³² For each applied strain, the supraparticles were rotated in the chain till they minimized their magnetostatic energy. Then, for that minimum configuration, the shear stress was computed. Eventually, the yield stress was identified with the maximum of the stress–strain curve. Results for the yield stress (normalized by the magnetic volume fraction) of the different supraparticle chains are summarized in Table 1 together with the strain and orientation angle where the yield stress occurs; the case of a homogeneous sphere is also shown as a reference. As it can be seen, all anisotropic supraparticles exhibit a normalized yield stress that is larger than the spherical case. This enhancement seems to be due to two main reasons. First, thanks to their long axis being aligned with the field, the anisotropic supraparticles show a lower demagnetization factor and thus can reach larger magnetization levels than spheres for the same field strength applied. Secondly, the yield stress is also enhanced for supraparticles that contact neighboring ones with plane faces, i.e. cubes (Janus or not), rods and cylinders (w / and w/o a hole). This fact has been already reported experimentally.³³

Table 1 Simulated yield stress τ₀ with supraparticles having a different anisotropy. The yield strain (γ₀), equilibrium orientation angle (φ₀) with respect to the magnetic field direction, magnetic content (ϕ), particle magnetization (M) and yield stress normalized by the magnetic content (τ₀/ϕ) are also shown. In all cases, the applied magnetic field was 30 kA m⁻¹

Particle	τ 0 (Pa)	γ 0	φ 0 (rad)	ϕ	M (kA m^−1)	τ 0/ϕ (kPa)
Cube	70.79	0.46	0	0.03	158	2.36
Janus cube	54.45	0.46	0	0.015	146	3.63
Rod	141.43	0.12	0.1	0.03	183	4.71
Cylinder	77.58	0.46	0	0.03	154	2.59
Hollow cylinder	80.82	0.24	0	0.022	168	3.67
Disk	71.66	0.24	—	0.03	134	2.39
Hollow disk	39.37	0.24	—	0.022	133	1.79
Sphere	52.40	0.26	—	0.03	104	1.75

---

Finally, it should be commented that the yield stress generated in a chain of Janus spheres was not evaluated. In this case, supraparticles form staggered chains trying to put as closer as possible their magnetic poles, aligning them along the centerline of the chain parallel to the applied magnetic field.³⁴ These configurations avoid shearing the chains under affine motion and thus computing the yield stress with the previous method. Following Smoukov et al.,³⁵ the equilibrium angle θ between Janus spheres in an infinite chain (see simulation cell in Fig. 6a) was computed using minimization energy principles again. Fig. 6b shows the results of Janus supraparticles with different plane-to-pole heights of the magnetic part (h_p). It can be seen that, the thicker the magnetic pole, the smaller the angle θ. In this figure, angles that yield a perfect alignment between the magnetic poles of the particles (magnetic lane configuration)^31,35 are pointed using straight vertical lines. It can be seen that these angles are approximately the equilibrium configurations for each case. Note that for the thinnest magnetic poles, h_p = 5 μm, the equilibrium configuration occurs at an angle larger than 60°. However, these angles are not allowed because they would imply supraparticle overlapping. Therefore, the thinnest Janus spheres will ensemble forming 60° in a kinetically arrested state. Also note that for the thickest magnetic poles (h_p = 25 μm), occupying one half of the sphere, simulations predict an equilibrium state (θ ∼ 25°) and a metastable one (θ = 60°). Similar results with two preferred states can be found in the literature.³⁵

Fig. 6 (a) Simulation cell to model an infinite staggered chain. θ stands for the angle between consecutive spheres and h_p is the plane-to-pole height of the magnetic part. (b) Particle energy for an infinite staggered chain of Janus spheres of different h_p values as a function of θ. Solid lines correspond to the angle that yields a perfect alignment of the magnetic poles. The maximum angle that is allowed to avoid particle overlapping (60°) is pointed using a dashed line.

Conclusions

This manuscript reports the possibility of fabricating a wide range of anisotropic magnetic supraparticles starting from CI microparticles and multisegmented microwires. Although the yields of the considered methods are not large, the generated particles are expected to be of interest for magnetorheological applications, especially those developed for highly confined devices (e.g. microfluidics), and for the formulation of dimorphic magnetorheological fluids with an enhanced rheological response due to their shape and magnetic content anisotropy. To our knowledge, this is the first demonstration of the fabrication of micron sized anisotropic magnetic particles including CI particles.

We show some representative examples of the types of supraparticles that can be built. Magnetically anisotropic supraparticles are fabricated with non-spherical shapes, using microtransfer molding, or with a spherical shape, using a microfluidic flow-focusing device. The magnetic anisotropic character is induced via convective deposition and magnetic field driven self-assembly of the CI particles within microcavities. In this way, CI microparticles are sequestered within specific regions in the supraparticle volume. As a result of the strong magnetic anisotropy of the particles, all of them can be easily manipulated and subjected to both forced translation and rotation in the presence of magnetic fields.

The methodologies described in this work can be extended to a wide range of composites comprising polymeric and metallic materials in order to prepare particles with various anisotropies. This is so because the processing parameters are uncoupled with the particular formulation of the composites. Furthermore, examples provided in this manuscript open new routes for the fabrication of magnetic particles with complex multipolar configurations, where the relative angular and spatial orientation of the dipoles can be controlled at will. Simple examples are the cases of shifted dipoles, Janus and patchy particles.

Finally, the strength of the resulting suprastructures (i.e. the yield stress) is quantified through finite element simulations. We demonstrate that the yield stress is strongly dependent on the internal magnetic anisotropy of the supraparticles. Specifically, particles having a long axis align it according to the applied field direction, showing lower demagnetization factors and enhancing their magnetization level and magnetic interactions. In addition, particles showing a plane surface against neighboring particles also develop larger yield stress.

Experimental

Preparation of PDMS templates

Polydimethylsiloxane (PDMS) elastomeric templates were prepared using conventional soft-lithography techniques.³⁶ First, the rapid prototyping technique was used to produce the master.³⁷ The pattern array was designed using a CAD program. This design was printed onto a transparent polymer films using a high-resolution commercial image setter. A silicon wafer was spin-coated with a SU photoresist (Microchem) and exposed on a Karl SÜS mask aligner to 365 nm light. The transparency serves as photolithographic mask to produce a positive relief of the photoresist on the silicon wafer. The photoresist was developed using a mr Dev-600 system (Microresist).

Once the master was fabricated, the pattern was transferred to a PDMS block by negative replica molding.³⁸ For this, a liquid silicone base and its crosslinker (Sylgard 184, Dow Corning) were mixed in a given weight ratio (10 : 1 w/w base : cross-linker). After manually mixing the two components, the mixture was degassed under vacuum for 15 min. Then, it was poured over the master and subsequently cured at room temperature for 24 h. Because the PDMS block becomes brittle when it is too thin, its thickness was always larger than 3 mm. After curing, the PDMS mold was carefully peeled off from the master to be afterwards treated with oxygen plasma using a K1050X Plasma Asher, for 15 min, to activate its surface. Finally, the elastomeric mold was reacted with trichloro(1H,1H,2H,2H-perfluoro-octyl)silane (Sigma Aldrich) via vapor deposition for 30 min. This later treatment was applied to facilitate the removal of supraparticles from the PDMS wells in subsequent steps.

Preparation of magnetically homogeneous supraparticles by microtransfer molding

Once the elastomeric mold was manufactured, the wells of the PDMS were filled with a magnetic suspension. First, a small amount of photoinitiator 2-hydroxy-2-mehtyl-1-phenyl-propan-1-one was mixed with ethoxylated trimethylolpropane triacrylate (ETPTA) (10 : 1 w/w ETPTA : photoinitiator, Sigma-Aldrich). The densities of the photoinitiator and ETPTA were 1.077 g mL⁻¹ and 1.11 g mL⁻¹, respectively. Next, carbonyl iron (CI) particles (density 7.86 g mL⁻¹, grade EW BASF SE, Germany) at a volume fraction of 50 vol% were mechanically dispersed in the mixture using a centrifugal mixer. Then, the CI suspensions were spread over the PDMS mold with a spoon spatula. Most of the excess suspension was removed by scraping off the surface of the mold with a razor blade. Next, the mold was pressed gently onto a glass slide several times in order to completely clean the excess material. Afterwards, the filled PDMS wells were degassed for 5 minutes and reticulated for 4 hours under a UV-lamp (UVGL-58, UVP, UK) with wavelength of 254 nm and power of 6 Watt. Finally, the mold was rinsed with ethanol and then a stream of air was used to dry the surface.

Convective driven self-assembly

Anisotropic magnetic supraparticles were prepared following a two-step protocol. First, a certain amount of ethanol was added to the CI suspension. After loading into the PDMS molds the blocks were cleaned using a standard method (see above). Then, the ethanol was evaporated at a commanded rate, for 30 minutes, leaving the wells partially filled. Next, the wells were reticulated under UV light. In a second step, an ETPTA solution, containing the photoinitiator, was then loaded above, where, on reticulation, it bonded to the magnetic region below. In this second step, the block was cleaned again using a standard method prior to reticulation. By controlling the evaporation rate of ethanol it is possible to tune the magnetic anisotropic character of the particles.

Magnetic guided self-assembly

In this case, magnetically homogeneous supraparticles were placed in the presence of magnetic fields during reticulation. As a proof of concept, a uniaxial DC magnetic field superimposed. This was generated using an open coil that was capable of generating a magnetic field strength of 16 kA m⁻¹.

Extraction of supraparticles from PDMS templates

A certain amount of poly(vinyl alcohol) (PVA) aqueous solution was spread on top of the PDMS mold. Next, the polymerization was allowed to progress for 12 h. After this, the supraparticles were strongly attached to the polymeric PVA film but they could be easily detached from the PDMS mold. To proceed, we took advantage of the flexibility of the PDMS block. The polymer-covered-side was placed on a flat surface and then, the elastomer was gently peeled off from the polymer. Finally, to release the supraparticles from the PVA film, the polymer film was immersed in water at 40 °C for 20 min. The supraparticles were carefully collected using low field-gradient magnetic separation and rinsed with water. In order to thoroughly clean them, the PVA dissolution process was repeated three more times (now reducing the dissolution time to 5 min). Finally, the supraparticles were collected by magnetic separation and rinsed with isopropanol.

Fabrication of multisegmented rodlike particles using electrodeposition

The electrodeposition process was carried out in a homemade electrolytic cell. Commercial porous anodized alumina membranes (Whatman) with a thickness of 60 μm and a pore diameter of 200 nm were used as templates. A thin layer of eutectic gallium–indium (EGaIn, Sigma-Aldrich) was applied to one surface of the membrane. Then, the EGaIn coated side was placed in contact with a thin cooper plate to serve as the cathode, and the other uncovered side was exposed to the electrolyte. In this way, the electrolyte solution penetrates the pores of the membrane until it encounters the EGaIn layer (Fig. 4a). The electrodeposition was performed at room temperature under controlled pH and applied voltage. Table 2 summarizes the pH values and voltages employed in this work, for the different electrolyte solutions investigated. After deposition, the microwires were released by dissolving the alumina membrane in 4 M NaOH for 24 h.

Table 2 Electrolytes, pH values and voltages used in the fabrication of the microwires reported in this work

Material	Electrolyte solution	pH	Voltage (V)
Ni	NiSO4·6H2O 300 g L^−1, NiCl2 × 6H2O 45 g L^−1, H3BO3 45 g L^−1	3.5	1.3
Co	CoSO4 238.5 g L^−1, H3BO3 30 g L^−1	2.0	−0.95
Fe	FeSO4 × 7H2O 120 g L^−1, H3BO3 40 g L^−1	2.0	2.5
Cu	CuSO4 × 5H2O 125 g L^−1, H3BO3 40 g L^−1	3.0	0.9

---

The electrodeposition of multisegmented microwires was performed by alternating the electrolytes and voltages for each segment. The particles were fabricated without using a reference electrode and the particle growth was controlled by adjusting the electrodeposition time. Particle length versus deposition time curves were constructed for each material investigated under the particular experimental condition (pH and voltage).

Fabrication of supraparticles using flow-focusing devices

The system setup for droplet generation was purchased from Dolomite Microfluidics (UK) and consisted of two pressure pumps to flow both phases, two flow rate sensors, a sample injection valve (to avoid the flow of particulate suspensions through the flow rate sensors) and a droplet X-junction chip. The chip is made of glass and has got a hydrophilic coating to fabricate oil-in-water emulsions. Due to this fact, no additional surface treatment was necessary to generate droplets.

The channels were 100 μm in depth and 300 μm in width but, as can be seen in Fig. 5, they narrow at the junction to 105 μm width. Due to this narrowing, the pressure and elongational strain gradient are maximized fixing the point of the channel where the droplets break off. This, together with the use of pulseless pumps, improves the control on the droplet size.³⁹ The droplet generation process at the X-junction was observed and recorded using a high speed camera (PL-B742F-R, PixeLink, Japan) mounted on a Nikon microscope SMZ745-T.

A first nonpolar fluid was injected to the central (inner) channel, and a second polar fluid was injected to the side (outer) channels. The first fluid consisted of the same CI suspension used in the microtransfer molding technique, but at 0.5–1 vol% of CI particles. The second fluid consisted of a water solution of sodium dodecylsulfate (SDS) at 2 wt%. This SDS concentration was appropriate to stabilize the droplets. The later were next transferred to a Petri dish. The photopolymerization of the generated droplets was carried out using the same UV-lamp used in microtransfer molding. The distance between the lamp and the Petri dish was 15 cm. In Table 3, the diameters of some representative particles are summarized together with the experimental conditions of the synthesis. As it can be seen in this table, supraparticle diameters are smaller than the channel orifice and similar to the supraparticle size obtained with microtransfer molding. In previously reported works involving ETPTA in water emulsions, typical droplet diameters are above the values reported in Table 3.^40–42 In our case, these small diameters were possible thanks to the use of a glass chip, which allowed us to impose the required large flow rates/pressures (due to the large viscosity of ETPTA, 90 mPa s) avoiding channel–substrate detachment commonly seen in the PDMS microfluidic devices.

Table 3 Diameters of the spherical supraparticles created with the microfluidic flow-focusing device shown in Fig. 5a. For each synthesis, the experimental conditions are also provided

Q c (μL min^−1)	Q d (μL min^−1)	UV exposure time (h)	CI concentration (%)	Diameter (μm)
40	0.2	0	1	60
50	0.2	4	0.5	25
55	0.4	0	0.5	15
110	0.7	0.67	0.5	40
110	1	4	0.5	60

---

Finite element method simulations

Simulations were carried out using COMSOL Multiphysics. Although experimental supraparticles were heterogeneous and consisted of discrete CI microparticles, the continuum hypothesis was used and magnetic regions in the simulations were supposed to be uniform and homogeneous. The simulated dimensions of the magnetic regions (representative of the experimental ones) are summarized in Table 4. As a constitutive equation, the Fröhlich–Kennelly model was used with an initial magnetic permeability of 8.07 and a saturation magnetization of 1853 kA m⁻¹. These parameters were obtained from fitting the model to the experimental magnetization curve of CI particles in a powder.

Table 4 Dimensions of the magnetic domains within the simulated supraparticles

Particle	Width (μm)	Height (μm)	Length (μm)
Cube	25	25	25
Janus cube	25	25	12.5
Rod	25	25	250

---

Particle	Diameter (μm)	Inner (hollow) diameter (μm)	Height (μm)
Cylinder	25	—	25
Hollow cylinder	25	12.5	25
Disk	56	—	25
Hollow disk	56	28	25

---

Particle	Diameter (μm)	Plane-to-pole height, hp (μm)
Janus sphere	50	{5, 15, 25}
Sphere	25	—

---

To compute the equilibrium orientation of the supraparticles in a homogeneous magnetic field, the magnetic regions within the supraparticles were centered in a cubic computational box with periodic boundary conditions. The side of the box was 15 times the typical length of the supraparticles. No significant differences were seen when the box side was doubled. Applied field was imposed using a reduced field formulation. Its magnitude was fixed to 30 kA m⁻¹ and its direction was varied till a minimum in the particle magnetostatic energy was found.

Individual chains of anisotropic supraparticles were simulated to evaluate their yield stress. For this, the method reported by Morillas and de Vicente³² was adapted to allow supraparticle rotation inside the chain at low concentrations (see Table 1). A linear dependence of the yield stress with the particle concentration has been previously demonstrated.⁴³ Hence, simulations at low concentrations are equivalent to simulations for isolated chains when normalized by the particle volume fraction. Among the many different simulated supraparticles, it is noted that once a chain of Janus cubes is formed with one of their long sides (for example, its width) aligned with the field direction, the chain can be strained parallel to the other long side (its height) or parallel to the short side (its length). Since, from an experimental point of view, it is not expected to get all particles in the same orientation, results for this kind of particle are the average for these two shear directions.

To compute the magnetostatic energy of the Janus spheres arranged in staggered chains, the cell plotted in Fig. 6a was used. Note that the cell width is not shown in full-scale. The cell height was changed according to θ. Periodic boundary conditions are imposed in all cell boundaries and the field is applied using the aforementioned reduced field formulation. In all simulations, an interparticle gap of 15 nm was used to prevent close contact. From an experimental point of view, this gap could be attributed to particle roughness, oxidation or a thin ETPTA layer coating the CI particles. In addition, straight corners and edges were slightly rounded so that the magnetic field keeps on being continuous in these places. Finally, the mesh size was fine enough to discard any dependence of the results. Differences were always below 0.016%.

Conflicts of interest

There are no conflicts to declare. 

Acknowledgements

Dr Tavacoli is acknowledged for useful discussions. This work was supported by MICINN PID2019-104883GB-I00 project (Spain), Junta de Andalucía P18-FR-2465 project and European Regional Development Fund (ERDF). J. R. M. acknowledges FPU14/01576 fellowship. E. C.-G. acknowledges financial support by CONACYT (Ref. #232347).

References

1. G. Bossis, O. Volkova, S. Lacis and A. Meunier, in Ferrofluids. Magnetically Controllable Fluids and Their Applications, ed. S. Odenbach, Springer-Verlag, Berlin Heidelberg, Germany, 2002, vol. 11, pp. 202–230.
2. J. de Vicente, D. J. Klingenberg and R. Hidalgo-Álvarez, Soft Matter, 2011, 7, 3701–3710.
3. N. Wereley, Magnetorheology: Advances and Applications, Royal Society of Chemistry: RSC Smart Materials, London, 2013.
4. J. E. Martin, Soft Matter, 2016, 12, 5636–5644.
5. B. Bharti and O. D. Velev, Langmuir, 2015, 31, 7897–7908.
6. J. de Vicente, F. Vereda, J. P. Segovia-Gutiérrez, M. P. Morales and R. Hidalgo-Álvarez, J. Rheol., 2010, 54, 1337–1362.
7. A. J. F. Bombard, F. R. Gonçalves, J. R. Morillas and J. de Vicente, Smart Mater. Struct., 2014, 23, 125013.
8. J. R. Morillas, E. Carreón-González and J. de Vicente, Smart Mater. Struct., 2015, 24, 125005.
9. A. V. Anupama, V. Kumaran and B. Sahoo, Soft Matter, 2018, 14, 5407–5419.
10. M. S. Pisuwala, K. H. Parekh and R. V. Upadhyay, Rheol. Acta, 2020, 59, 887–904.
11. M. Lattuada and T. A. Hatton, J. Am. Chem. Soc., 2007, 129, 12878–12889.
12. A. B. Yener and S. H. L. Klapp, Soft Matter, 2016, 12, 2066–2075.
13. A. B. Pawar and I. Kretzschmar, Macromol. Rapid Commun., 2010, 31, 150–168.
14. P. Tierno, Phys. Chem. Chem. Phys., 2014, 16, 23515–23528.
15. J. W. Tavacoli, P. Bauer, M. Fermigier, D. Bartolo, J. Heuvingh and O. du Roure, Soft Matter, 2013, 9, 9103–9110.
16. N. Pamme, Lab Chip, 2006, 6, 24–38.
17. C. H. Chen, A. R. Abate, D. Lee, E. M. Terentjev and D. A. Weitz, Adv. Mater., 2009, 21, 3201–3204.
18. X. M. Zhao, Y. Xia and G. M. Whitesides, Adv. Mater., 1996, 8, 837–840.
19. P. Garstecki, P. Tierno, D. B. Weibel, F. Sagués and G. M. Whitesides, J. Phys.: Condens. Matter, 2009, 21, 204110.
20. S. H. Kim, S. J. Jeon, W. C. Jeong, H. S. Park and S. M. Yang, Adv. Mater., 2008, 20, 4129–4134.
21. R. D. Deegan, O. Bakajin, T. F. Dupont, G. Huber, S. R. Nagel and T. A. Witten, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2000, 62, 756.
22. L. Frastia, A. J. Archer and U. Thiele, Phys. Rev. Lett., 2011, 106, 077801.
23. M. Mohebi, N. Jamasbi and J. Liu, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 1996, 54, 5407.
24. F. Nasirpouri, Electrodeposition of Nanostructured Materials, Springer International Publishing, Cham, 2017.
25. R. C. Bell, E. D. Miller, J. O. Karli, A. N. Vavreck and D. T. Zimmerman, Int. J. Mod. Phys. B, 2007, 21, 5018–5025.
26. J. de Vicente, J. P. Segovia-Gutiérrez, E. Andablo-Reyes, F. Vereda and R. Hidalgo-Álvarez, J. Chem. Phys., 2009, 131, 194902.
27. V. Rastogi, A. A. García, M. Marquez and O. D. Velev, Macromol. Rapid Commun., 2010, 31, 190–195.
28. R. F. Shepherd, J. C. Conrad, S. K. Rhodes, D. R. Link, M. Marquez, D. A. Weitz and J. A. Lewis, Langmuir, 2006, 22, 8618–8622.
29. D. Dendukuri, K. Tsoi, T. A. Hatton and P. S. Doyle, Langmuir, 2005, 21, 2113–2116.
30. S. L. Anna and H. C. Mayer, Phys. Fluids, 2006, 18, 121512.
31. S. Gangwal, O. J. Cayre and O. D. Velev, Langmuir, 2008, 24, 13312–13320.
32. J. R. Morillas and J. de Vicente, Composites, Part B, 2019, 160, 626–631.
33. G. Bossis, J. A. Marins, P. Kuzhir, O. Volkova and A. Zubarev, J. Intell. Mater. Syst. Struct., 2015, 26, 1871–1879.
34. C. W. Shields IV, S. Zhu, Y. Yang, B. Bharti, J. Liu, B. B. Yellen, O. D. Velev and G. P. López, Soft Matter, 2013, 9, 9219–9229.
35. S. K. Smoukov, S. Gangwal, M. Marquez and O. D. Velev, Soft Matter, 2009, 5, 1285–1292.
36. Y. Xia and G. M. Whitesides, Angew. Chem., Int. Ed., 1998, 37, 550–575.
37. D. Qin, Y. Xia and G. M. Whitesides, Adv. Mater., 1996, 8, 917–919.
38. Y. Xia, J. J. McClelland, R. Gupta, D. Qin, X. M. Zho, L. L. Sohn, R. J. Celotta and G. M. Whitesides, Adv. Mater., 1997, 9, 147–149.
39. Y. C. Tan, V. Cristini and A. P. Lee, Sens. Actuators, B, 2006, 114, 350–356.
40. S. H. Kim and D. A. Weitz, Angew. Chem., 2011, 123, 8890–8893.
41. Y. Zhao, H. C. Shum, H. Chen, L. L. A. Adams, Z. Gu and D. A. Weitz, J. Am. Chem. Soc., 2011, 133, 8790–8793.
42. T. Li, L. Zhao, W. Liu, J. Xu and J. Wang, Lab Chip, 2016, 16, 4718–4724.
43. J. R. Morillas and J. de Vicente, Soft Matter, 2019, 15, 3330–3342.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: 10.1039/d0sm02178d

---