Near-surface rheology and hydrodynamic boundary condition of semi-dilute polymer solutions
Gabriel
Guyard
ab,
Alexandre
Vilquin
 a,
Nicolas
Sanson
a,
Nicolas
Sanson
 cd,
Stéphane
Jouenne
ef,
Frédéric
Restagno
cd,
Stéphane
Jouenne
ef,
Frédéric
Restagno
 b and
Joshua D.
McGraw
b and
Joshua D.
McGraw
 *a
*a
aGulliver UMR CNRS 7083, ESPCI Paris, Université PSL, 10 rue Vauquelin, 75005 Paris, France. E-mail: joshua.mcgraw@espci.fr
bUniversité Paris-Saclay, CNRS, Laboratoire de Physique des Solides, 91405, Orsay, France
cSIMM UMR CNRS 7615, ESPCI Paris, Université PSL, 10 rue Vauquelin, 75005 Paris, France
dLaboratoire Physico-Chimie des Interfaces Complexes, ESPCI Paris, 10 rue Vauquelin, F-75231 Paris, France
eTOTAL SA, Pôle dÉtudes et de Recherche de Lacq, BP47, 64170 Lacq, France
fLaboratoire Physico-Chimie des Interfaces Complexes, Bâtiment CHEMSTARTUP, Route Départemental 817, 64170 Lacq, France
First published on 3rd March 2021
Abstract
Understanding confined flows of complex fluids requires simultaneous access to the mechanical behaviour of the liquid and the boundary condition at the interfaces. Here, we use evanescent wave microscopy to investigate near-surface flows of semi-dilute, unentangled polyacrylamide solutions. By using both neutral and anionic polymers, we show that monomer charge plays a key role in confined polymer dynamics. For solutions in contact with glass, the neutral polymers display chain-sized adsorbed layers, while a shear-rate-dependent apparent slip length is observed for anionic polymer solutions. The slip lengths measured at all concentrations collapse onto a master curve when scaled using a simple two-layer depletion model with non-Newtonian viscosity. A transition from an apparent slip boundary condition to a chain-sized adsorption layer is moreover highlighted by screening the charge with additional salt in the anionic polymer solutions. We anticipate that our study will be a starting point for more complex studies relating the polymer dynamics at interfaces to their chemical and physical composition.
1 Introduction
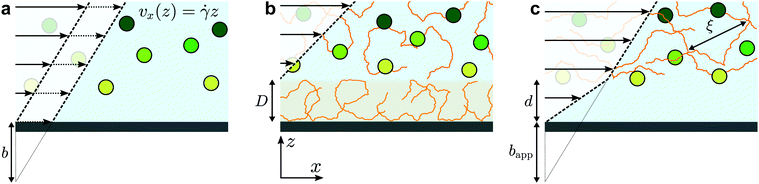
The physics of polymers near interfaces is encountered in many fundamental and applied problems, from industrial to biological processes. In this context, interfacial interactions are a key feature.1 Attractive surfaces, for example, may lead to irreversible adsorption of polymer chains,2,3 but chains may also be repelled from surfaces4 leading to a depletion layer. Such structural effects can have major consequences on dynamics in confined systems. Adsorption leads to decreased permeability in porous media, which is a major issue in enhanced oil recovery;5 depletion enhances flows via the formation of a low-viscosity lubrication layer close to the surface.6,7 As will be studied here, polymer/surface interactions impact nanoscale flows by modifying the boundary condition for polymeric fluids, and non-trivial rheology also plays an important role.The classic, no-slip boundary condition, schematically depicted in Fig. 1(a), assumes that the hydrodynamic velocity profile vanishes at the wall. While this condition is the simplest to treat analytically, there is no a priori reason for its validity. Slip at the wall was thus hypothesised in the early stages of hydrodynamics,8 and the velocity at the wall is typically characterised by a slip length, b, defined as the distance at which the flow profile linearly extrapolates to zero (see Fig. 1(a)). For simple liquids on hydrophobic surfaces, slip lengths are just a few nanometres.9–11 For complex fluids,12 however, these extrapolation lengths can reach many microns; this is notably the case for polymer melts and solutions.13
Slip of polymer melts has indeed been extensively studied over several decades,14–16 and the case of ideal surfaces was explained in the seminal paper of de Gennes.17 There, arguing from the standpoint of stress balance at the interface, a cubic dependence on the molar mass of the slip length was predicted for smooth, non-adsorbing surfaces. This prediction was confirmed recently in studies of dewetting thin polymer films18 and using velocimetry measurements.19,20 For adsorbing surfaces or surfaces with grafted chains, the field is still active21,22 but a mature understanding both on the experimental14 and theoretical sides23 has been reached to capture the main picture. The dynamics of dilute polymer solutions near interfaces has also received significant attention.24 In this situation, the chains can be considered as independent. The typical relevant force is a repulsive hydrodynamic interaction with the wall under flow,25 along with molecular forces which can lead to complex relationships between the shear rate and a depletion layer at the wall.26
In between the extremes of dilute polymer solutions and polymer melts, the semi-dilute solution regime is encountered in which polymer chains overlap, but where the solvent still plays an important role. For these cases, relatively little is known about the boundary conditions and near-wall transport.24 On one hand, attractive interactions can lead to adsorbed layers as described above, leading to an immobile layer of thickness D (Fig. 1(b)). Such a layer can be interpreted as providing a “negative” slip length. On the other hand, for repulsive surfaces, apparent slip lengths of many micrometers7 are thought to arise due to the depletion layers schematically indicated in Fig. 1(c). More recent experimental studies27 showed suppressed apparent slip for polymers confined to regions smaller than the bulk chain size, which was recovered lately in surface forces apparatus experiments of entangled, semi-dilute solutions.28 Relatively few studies have been performed on semi-dilute, unentangled polymer solutions where the slip lengths may be smaller. Indeed, some of the most recent velocimetry techniques for the investigation of near-wall polymer dynamics29,30 are limited to micron-scale slip lengths. As will be shown below, however, there is a rich phenomenology below micrometric scales.
Semi-dilute polymer solutions, both entangled and unentangled, are also commonly observed to be non-Newtonian fluids.31 Such fluids particularly display shear viscosities that decrease with the imposed shear rate.32 In the bulk and for neutral polymers in good solvents, universal behaviour for this non-linearity has been demonstrated for a variety of polymer/solvent pairs;33,34 however, it is not obvious that such universality should be preserved near the interface. A consequence of this non-trivial rheological behaviour is that slip measurements should be accompanied with simultaneous rheometry measurements, and that this rheology should be done near the surface. Indeed, when complex interfacial phenomena occur, usual macroscopic rheometry tools could be subject to subtle effects that make the interpretation of data difficult.6,35,36 This sets the need for experimental setups able to distinguish near-surface rheology from the boundary condition. One way to achieve both at the same time is to map the polymer flow near the wall using particle-tracking velocimetry.37,38
In this paper, we use total internal reflection fluorescence microscopy (TIRFM) to perform 3-dimensional velocimetry in semi-dilute unentangled, unmodified and partially-hydrolized polyacrylamide (PAM and HPAM, respectively) solutions. We recover the near-wall velocity profiles of PAM solutions and capture their shear-thinning behaviour in good agreement with bulk rheometry. In the same experiment, we measure complex boundary conditions that depend on the presence of polymer chains, their charge and the electrolyte concentration. We demonstrate that neutral polymer chains adsorb at the surface of the channel, while solutions containing negatively-charged chains display apparent slip at the glass wall with a shear rate dependent slip length ranging between a few and 2000 nm.
2 Materials and methods
2.1 Polymers, microfluidics, and rheometry
The polymers used in this study were neutral and anionic, monodisperse PAMs synthesised by controlled-radical polymerisation as described elsewhere.39,40 For anionic polymers, negative charges were introduced by 10% random copolymerisation of acrylic acid. Table 1 lists the characteristics and nomenclatures for all of the polymers used here.| Designation | M w (kg mol−1) | c* (mg mL−1) | Đ | Electric charge |
|---|---|---|---|---|
| PAM(1284k) | 1284 | 4.0 | 1.05 | Neutral |
| PAM(2082k) | 2082 | 2.8 | 1.07 | Neutral |
| HPAM(817k[−]) | 817 | 1.5 × 10−2 | 1.09 | [−], 10% |
Aqueous solutions were prepared by dissolving PAM in ultrapure deionised water (18.2 MΩ cm−1, Milli-Q Advantage A10) at different mass fractions ranging from c = 2 to 10 mg mL−1 for neutral PAM and from 0.1 to 2 mg mL−1 for the anionic polymers; these concentrations can be compared to our estimates of the overlap concentration, c*, of the different polymers in water (see Table 1). The overlap concentrations for the neutral PAMs were evaluated based on the hydrodynamic radius of the neutral polymers (50 nm and 66 nm for PAM(1284k) and PAM(2082k)) and standard scaling laws for polyelectrolyte chains.41 For the anionic polymers, here called HPAM(817k[−]), we performed experiments with and without added salt, the former using 28 mM NaCl (Sigma Aldrich). For viscous, Newtonian liquids, deionised water/glycerol mixtures (Sigma Aldrich, ≥99%) with composition between 0 and 60 wt% glycerol were used. Finally, in order to probe the near-surface flow using TIRFM, 110 nm-diameter carboxylate-modified fluorescent microspheres (Invitrogen F8803, 2% solid) were added to the PAM solutions as received by the manufacturer at a volume fraction of 3 μL mL−1. The resulting tracer concentration in the samples is approximately 8.6 × 1013 L−1 and the average distance between particles, verified by image analysis, is approximately 2 μm. For 55 nm-radius particles and at this low concentration, interactions between the particles were verified to be insignificant.
The tracer-containing solutions described above were injected in a microfluidic device prepared using standard soft lithography methods.42 The chips were prepared with polydimethylsiloxane (Momentive RTV615 A) mixed with 10% cross-linking agent (Momentive RTV615 B). The reticulated elastomers were treated under O2 plasma (Femto Science CUTE) to be covalently bonded to a glass coverslip and were used immediately after bonding with no further treatment. The chips consisted of a single microchannel with dimensions {L, w, h} = {8.8 cm, 180 μm, 18 μm}, with the long dimension consisting of several U-turns. Flows were driven by a pressure controller (Fluigent MFCS-4C) allowing for pressure drops ΔP ≤ 1000 mbar.
For each polymer solution tested, reference velocimetry measurements were performed with a solution containing tracer particles in ultrapure water, before the polymer solution was injected into the same microfluidic chip. The TIRF velocimetry measurements were complimented with bulk rheology measurements (Anton Paar, MCR 302) performed in continuous-shear mode in a Couette cell. Strain sweeps were performed with shear rates in the range 1 ≤ ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) ≤ 1000 s−1 with corresponding measurements of the shear stress, σ.
≤ 1000 s−1 with corresponding measurements of the shear stress, σ.
2.2 TIRF microscopy and image processing
The TIRF microscopy setup along with alignment procedure are described in ref. 43. For our system, a 10×-expanded, continuous-wave laser (Coherent Sapphire, λ = 488 nm, 150 mW) was piloted off the optical axis and focused onto the back focal plane of a high-numerical-aperture, high-magnification objective (Leica, oil immersion HCX PL APO, NA = 1.46, M = 100×). The beam thus exits the objective at an angle which could be measured using the method described in the appendix. Total internal reflection was achieved when the exiting angle, θ, was larger than θc = arcsin(n/ng) where ng = 1.518 is the index of refraction of the glass coverslip and n is that of the solution used. These latter indices were all measured using a refractometer (Atago PAL-RI). Under TIRF conditions particles in the near-surface region emit44,45 a fluorescence intensityI(z) = I0![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(−z/Π), exp(−z/Π), | (1) |
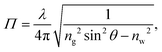 | (2) |
Fluorescence images were collected with an sCMOS-based camera (Andor Neo) under flow in the microfluidic devices described above. For all the tracer-containing flows presented here, 2000-frame movies were recorded at 400 Hz in rolling shutter mode. Four to seven such videos were recorded for each experimental condition comprising a given polymer solution and driving pressure. This volume of data ensured that at least 104 particle positions were measured for each experimental realisation of a polymer concentration at a given imposed pressure. Tracers appear as Gaussian-shaped diffraction-limited spots with approximately 10 pixel (approximately 400 nm) diameters, giving a precision of ca. 10 nm for the lateral (x, y) particle positions. The fluorescence intensity ranged from 100 to 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 on the 16-bit camera gray scale and were sorted into bins of approximately 0.25 units of log(I) (here the natural logarithm), corresponding to a roughly 20 nm spread in vertical position for an 80 nm evanescent decay length. Tracking these binned tracer positions over time allowed to obtain the velocity profiles.
000 on the 16-bit camera gray scale and were sorted into bins of approximately 0.25 units of log(I) (here the natural logarithm), corresponding to a roughly 20 nm spread in vertical position for an 80 nm evanescent decay length. Tracking these binned tracer positions over time allowed to obtain the velocity profiles.
3 Results and discussion
3.1 Near-wall velocity profiles
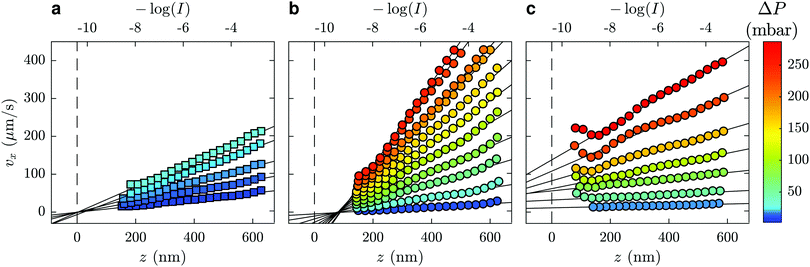
The velocity vx along the pressure gradient, computed as the mean displacement of the tracers within an intensity bin divided by the time elapsed during one frame (2.5 ms), is plotted as a function of z in Fig. 2(a), where we use the apparent altitude z = Π![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) log(I0/I) according to eqn (1). In the appendix, we discuss the possible systematic errors46–48 that affect this determination of the altitude along with that of the tracer velocity. The standard error associated to the estimate of vx and z is smaller than the symbol size, and thus errorbars are not displayed for clarity. Despite the minor aforementioned limitations, and for each pressure used, a linear regression describes the data well. Here, we take the slope of this data as the near-wall shear rate,
log(I0/I) according to eqn (1). In the appendix, we discuss the possible systematic errors46–48 that affect this determination of the altitude along with that of the tracer velocity. The standard error associated to the estimate of vx and z is smaller than the symbol size, and thus errorbars are not displayed for clarity. Despite the minor aforementioned limitations, and for each pressure used, a linear regression describes the data well. Here, we take the slope of this data as the near-wall shear rate,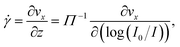 | (3) |
3.2 Near-wall rheology
To extract mechanical properties of the fluid from the above-described shear rate measurements, the local shear stress close to the interface is needed. In a rectangular geometry with h ≪ w ≪ L as satisfied here, a force balance implies that the shear stress is σ(z) = ΔP(h/2 − z)/L. Therefore, close to the wall one has σ = hΔP/2L.Combining the shear rate and the shear stress, we have the viscosity of the fluid which is defined through
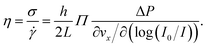 | (4) |
To this end, we turn our attention to the velocity profiles of neutral PAM(2082k) and anionic HPAM(817k[−]) that are shown in Fig. 2(b) and (c), respectively. As with the profiles for the water flows, the near-wall velocity profiles are well-described by linear regressions, the shear rate obtained through eqn (3) also increasing with the pressure drop. We note however, that the pressure drops required to reach a given velocity are larger than those used for water, which is a reflection of the fact that these liquids are more viscous than water. While not shown here, similar trends are seen for water/glycerol mixtures ranging from 0 to 60 wt% glycerol.
In Fig. 3(a) is shown the viscosity as a function of the shear rate for such water/glycerol mixtures, obtained through eqn (4). These viscosities were normalised by the average TIRFM-measured water viscosity for a calibration experiment done in the same chip; the TIRFM-derived data are represented with the circles. Using the viscosity ratio, η/ηw, the geometric prefactor of eqn (4) cancels. The remaining ratio of the penetration depths is estimated using eqn (2). These liquids are expected to be Newtonian on the range of shear rates accessed by the near-wall velocimetry experiments, and we indeed find that the near-wall nanovelocimetry results do not vary within error over the shear rate range measured. The small points in Fig. 3(a) were obtained using bulk rheometry, and were normalized by the constant water viscosity also measured using bulk rheometry. It is found within error that the data obtained from near-wall TIRFM velocimetry is in agreement with the constant viscosities measured in the bulk.
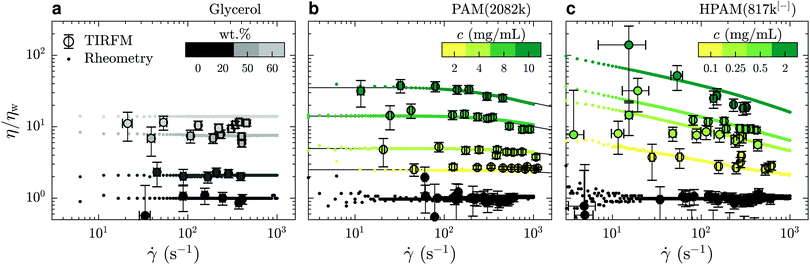 | ||
| Fig. 3 Comparison of the mechanical behaviours of: (a) water/glycerol mixtures; (b) PAM(2082k) solutions; and (c) HPAM(817k[−]) solutions. TIRFM velocimetry data are plotted in circles and rotational rheometry data are plotted using dots; black lines in panel (b) indicate predictions of the universal model of ref. 34. The color bars indicate the concentration of each solution and water is always represented in black. All the data shown here were collected without added salt. | ||
In Fig. 3(b) and (c) are shown η/ηw – for neutral PAM(2082k) and anionic HPAM(817k[−]) – as a function of the measured shear rates. As with the data in panel (a), the TIRFM-derived data (larger circles) are normalised by the average, constant, water viscosity through eqn (4). In contrast to the water/glycerol mixtures, however, these solutions contain at most 0.1 wt% polymer in water. With such a small amount of polymer, the indices of refraction are almost identical (no more than 0.2% difference), and thus, according to eqn (4), this normalisation cancels all of the experimental length scales on the y-axis.
For the neutral polymers in Fig. 3(b), we observe shear thinning, i.e. a viscosity decreasing with shear rate, at the highest concentrations and the highest shear rates. Associated rotational rheometry data, performed with the same solution and normalised in the same way, are superimposed for comparison. The black lines in Fig. 3(b) show a universal rheological model34 applied to the bulk rheology data, with only one fitting parameter. This parameter is the relaxation time of a polymer chain in the dilute regime λ0 = 1.8 ± 0.2 ms, which is proportional to the Zimm time50τZ. The model gives λ0 = 1.5τZ, which suggests τZ = 1.2 ms, that is close to the theoretical estimation for a coil of radius R = 66 nm in water τZ = 6πηwR3/kT ≈ 1.3 ms. The other parameter required by the model, the intrinsic viscosity, [η], was evaluated as 0.52 ± 0.03 mL mg−1 by measuring the bulk viscosity as a function of concentration for c < c* ≈ 2.8 mg mL−1 (data not shown). The agreement between the model and the bulk rheology is excellent, as is the agreement between bulk rheology and the TIRFM-derived rheology.
Lastly, the anionic HPAM(817k[−]) of Fig. 3(c) shows shear thinning in the bulk (small data points) even at the lowest concentrations and shear rates. These solutions being roughly a factor of ten less concentrated than the neutral-PAM solutions, the viscosity nevertheless decreases by almost a decade in the 10 to 1000 s−1 range. As with the neutral-chain solutions, we note a good agreement between the TIRFM-derived results (larger circles, eqn (3) and (4)) and the bulk rheology (smaller points). In the appendix, we show that the bulk results at the lowest shear rate (roughly 5 s−1) are in agreement with the classical scaling results51 for the zero-shear values of the viscosity as a function of polymer and electrolyte concentration.
We conclude this subsection generally by noting that for all the liquids we have investigated here, the rheology in the range 150 ≲ z ≲ 600 nm is consistent with that in the bulk. In the following section, we will use this information to unify our description, in particular, of apparent slip boundary conditions for the unentangled semi-dilute solutions of anionic polymers.
3.3 Boundary conditions
Focusing on the upper horizontal scale in Fig. 2(a), and under our no-slip assumption, the dashed vertical line corresponds with the fluorescence intensity of a particle at the wall in water, Iwater0. In Fig. 2(b), for a solution of PAM(2082k) with c = 2.0 mg mL−1, we draw the same vertical dashed line centred on the same logarithmic intensity, Iwater0, as for the water flow in the same microfluidic chip and for the same incident laser angle. While the velocity profiles for this polymer-laden flow remarkably extrapolate to zero at the same point on the horizontal axis, there is a shift in the extrapolated value of I0 as compared to Iwater0.
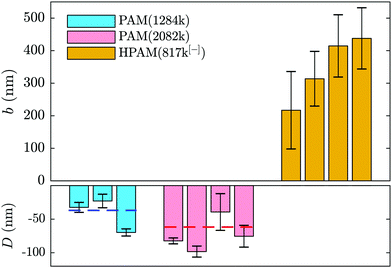
Such a shifted value of I0 for the polymer-laden flow is consistent with the presence of an adsorbed layer of polymer on the glass–water interface that serves as a no-slip boundary plane. Using the exponential relation for I(z) and the penetration depth, Π, associated to the angle measured in the same experiment (cf.eqn (1) and (2) as well as the appendix), we estimate the adsorbed layer here to be of thickness D = 77 ± 6 nm. Such a value is within order unity of the expected chain size in the bulk solution for PAM(2082k).
Adsorption of neutral PAM on oxide-based surfaces has been observed for decades in various systems such as nanopores (see e.g.ref. 5) or at the surface of colloids.54–56 Additionally, it was predicted that such an adsorbed layer would impact the hydrodynamic boundary condition57 in the way depicted in Fig. 1(b) and revealed by the boundary conditions displayed in Fig. 2 and 4. The parameters influencing the adsorbed-layer size are notably the surface's affinity for the polymer, the molar mass, and the solvent; kinetics is also likely to play a role, yet here the incubation time of the polymer solution in the chip prior to velocimetry measurements was not systematically controlled, varying from a few minutes to an hour. While it is beyond the scope of this study to do a detailed analysis of the structure and dynamics of adsorbed chains, the measurements presented here are compatible with de Gennes' theory for polymer adsorption on weakly adsorbing surfaces.1
In this model, three regions of increasing distance from the substrate are distinguished: the proximal, central and distal regions. The monomer density in the so-called proximal and central regions, fixing the adsorbed layer thickness, is shown to be independent of the bulk concentration and independent of the chain length as indicated by Bessaies-Bey et al.5 Such a result is in seeming contradiction with the molar mass dependence in Fig. 4. Nevertheless, the entire adsorbed-chain monomer density profile – through to the distal region of order the chain size – is expected to impact hydrodynamic flow.1 Since our nanovelocimetry measurement is a hydrodynamic one, we expect that the distal region size is the one to which our measurements are sensitive. The measured thicknesses are compatible with this picture and the ratio of these lengths, 〈D2082〉/〈D1284〉 = 1.8 ± 0.6, is, within error, the ratio of the expected chain sizes, R ∼ N1/2, in semi-dilute solution,50 where N is the number of repeat units. Specifically, we have R2082/R1284 ≈ (2082/1284)1/2 ≈ 1.3, the prefactor being a weak power law in the concentration50 for semi-dilute solutions.
In order to rationalise the results for charged chains in Fig. 4, we apply an apparent slip model that is applicable to systems with a stratified viscosity profile; here we suppose that such stratification is due to an electrostatically-mediated depletion layer. Indeed unlike neutral chains, the interaction between negatively charged PAM and the glass surface is repulsive since glass develops negative charges in aqueous solution.58 If d is the typical length scale associated with the low-viscosity depletion layer near the glass/water interface, a simple two-layer model may be proposed. Based on the continuity of stress across the two layers, assuming no slip at the solid/liquid boundary, and considering the geometry shown in Fig. 1(c), the apparent slip length is given by:
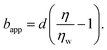 | (5) |
To estimate d, we assume that the depletion layer thickness is on the order of the solution's correlation length, ξ, defined as the average distance between neighbouring polymer chains in solution, see Fig. 1(c). This result was predicted by Joanny and co-workers59 for equilibrium situations, balancing monomeric interactions with the wall and the entropic penalty of the chain which results from its exclusion from the volume near the interface; this typical depletion layer size was confirmed in measurements by Lee and coworkers.60 Following the scaling theory of Dobrynin et al.41 for salt-free, semi-dilute polyelectrolyte solutions in a good solvent, we have
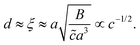 | (6) |
![[c with combining tilde]](https://www.rsc.org/images/entities/i_char_0063_0303.gif) is the volumetric monomer concentration, and B = (a
is the volumetric monomer concentration, and B = (a![[small script l]](https://www.rsc.org/images/entities/i_char_e146.gif) B−1f−2)2/7 is the ratio of the chain's contour length and its size in dilute solution for an athermal solvent with f the fraction of charged monomers. Finally, the Bjerrum length,
B−1f−2)2/7 is the ratio of the chain's contour length and its size in dilute solution for an athermal solvent with f the fraction of charged monomers. Finally, the Bjerrum length, ![[small script l]](https://www.rsc.org/images/entities/i_char_e146.gif) B = e2/εkT, is defined as the distance over which the electrostatic energy of two elementary charges (e) in a medium of dielectric permittivity, ε, is equal to kT, the thermal energy at room temperature. For our estimations, we here use a = 1 nm, f = 0.1, and ε = 80ε0 for water with ε0 the vacuum permittivity.
B = e2/εkT, is defined as the distance over which the electrostatic energy of two elementary charges (e) in a medium of dielectric permittivity, ε, is equal to kT, the thermal energy at room temperature. For our estimations, we here use a = 1 nm, f = 0.1, and ε = 80ε0 for water with ε0 the vacuum permittivity.
In Fig. 5(a), we test the scaling predictions of eqn (5) and (6) collecting data from all concentrations of HPAM(817k[−]) and all of the imposed pressures. There we show the normalised slip length as a function of the TIRFM-derived specific viscosity (see Fig. 3(c)), noting that the specific viscosity changes with the driving pressure. Scaled in this way, we find that all of the data collapse onto a single master curve that is well-described by linear power law in accordance with eqn (5). The prefactor is furthermore of order unity, indicating that the depletion layer thickness in these steady shear flows is approximately twice the scaling prediction for the depletion layer thickness at equilibrium, regardless of the shear rate and well into the shear-thinning regime.
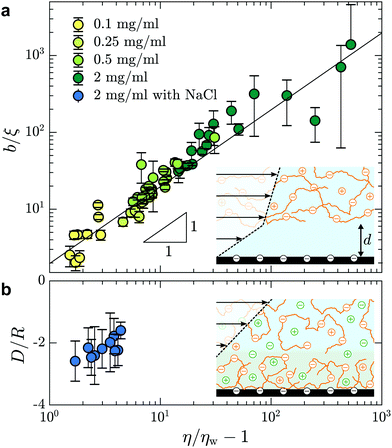 | ||
| Fig. 5 (a) Slip length, normalised by the correlation length, as a function of the specific viscosity for different HPAM(817k[−]) solutions measured at each imposed pressure. For concentrations c = {0.1,0.25,0.5,2} mg mL−1, we have used ξ = {62,39,27,14} nm according to eqn (6). The black line shows b/ξ ≈ (η/ηw − 1) where the prefactor is 2.0 ± 0.1. (b) Adsorbed layer thickness, normalised by the chain size, as a function of specific viscosity for HPAM(817k[−]) with concentration of NaCl of cs = 28 mM. For this solution, we used R = 151 nm according to ref. 41 for chains in a good solvent and with added salt. | ||
Screening the charges on the anionic polymers and on the glass/water interface is one way to test the validity of our assumption that electrostatic repulsion mediates the apparent slip displayed in Fig. 5(a). To this end, we prepared a solution at the highest concentration of anionic polymer (i.e. 2.0 mg mL−1), in parallel and from the same parent solution as displayed in Fig. 5(a), with added salt. The salt concentration, cs = 28 mM, was chosen to give roughly ten times the number of charges needed to complement each of the anions on the polymer backbone. In Fig. 5(b) are shown the results from this TIRFM-based, combined rheological/boundary condition experiment. As with the unscreened solutions, the viscosity varied as a result of changes in the shear rate attained with changes in the imposed pressure. However, the viscosities are significantly smaller as compared to the unscreened solutions. As for neutral polymers, we find a chain-sized adsorbed layer that varies at most weakly with the imposed pressure (cf.Fig. 2(b)).
We thus find that screening the charges on the polymer backbone in a polyelectolyte solution enables to tune the boundary condition in microfluidic contexts with simple control parameters: the polymer concentration and the imposed pressure. By controlling added electrolyte concentration, we are furthermore able to cross the threshold from adsorbed layers of several tens of nanometres, to positive slip length values in the range of one or two hundred nanometres to several microns.
4 Conclusion
Using evanescent wave microscopy and calibrations based on well-known properties of water, we characterise near-surface flows of semi-dilute, neutral and anionic acrylamide-based polymer solutions with macromolecular resolution. The shear rates were extracted from near-wall velocity profiles and measured as a function of the imposed pressure across a microfluidic channel. Such measurements provide the viscosity of the solutions over a wide range of polymer concentration. The rheological properties determined within the first micrometer of the surface, are similar to those obtained from bulk rheology measurements, for Newtonian water/glycerol mixtures as well as shear-thinning PAM and HPAM solutions.In addition to rheological information, extrapolation of the velocity profiles highlights various boundary conditions for the semi-dilute polymer solutions. The neutral solutions display a chain-sized adsorbed layer wherein the no-slip plane is shifted above the solid/liquid interface; in contrast, anionic polymer solutions exhibit shear-dependant slip lengths. These steady-shear slip lengths are consistent with a bilayer fluid model, wherein viscosity stratification is due to electrostatically-mediated polymer depletion between the glass and polymer. In this model, the near-surface layer has a thickness proportional to the equilibrium value of the correlation length for semi-dilute polyelectrolytes. Lastly, we showed that the apparent slip boundary condition of the anionic PAM solutions is due to the monomer charges: adding salt to screen the charges on the polymer backbone and the glass/water interface, we recover a macromolecular-sized adsorbed layer as for the neutral polymer solutions.
Finally, these experiments show that TIRFM is well-suited to study interfacial phenomena in complex fluids, and especially the underlying mechanism at stake in the friction and slip for semi-dilute polymer solutions. Indeed, it allows to disentangle the two quantities involved in both phenomena: the local viscosity of the fluid and the friction coefficient for the fluid on the substrate. Our method opens perspectives to describe a rich phenomenology of polymer/substrate interactions under flow.
Conflicts of interest
There are no conflicts to declare.Appendix
Angle measurement
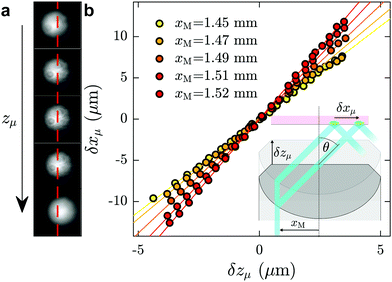
Here we describe the procedure used for measuring the angle of incidence of the laser, which was performed after each data acquisition and in the same microfluidic chip as was used for the investigation of a given fluid of interest. First, a fluorescent dye, typically fluorescein at mass fraction of 10−4 in ultrapure water, was injected into the channel. With the laser turned on, a fluorescence spot was observed with full camera resolution (field of view 113 × 94 μm, see Fig. 6(a)). Using a piezoelectric objective mount (Physik Instrument, P-721 PIFOC controlled by E-662 LVPZT), the objective was moved vertically in a controlled way, so that the objective position zμ could be tuned. Taking the position for which the fluorescence spot is in focus as a reference, zμ was shifted from −5 μm to 5 μm with a 0.4 μm increment, and for each position a snapshot was collected. When the focusing plane moved a distance δzμ upward, the fluorescence spot shifted a distance δxμ to the right, as schematically shown in the inset of Fig. 6(b); corresponding shifts of the fluorescence spot for different focusing positions are shown in (a). The position xμ of the spots were determined by 2D-Gaussian-fitting their intensity profiles. In Fig. 6(b) are shown δxμ as a function of δzμ for different values of xM, the off-axis shift of the laser beam (see inset of Fig. 6(b)), corresponding to different values of θ.As seen in the Fig. 6(b), for a given value of xM, δxμ grows linearly with δzμ, with a slope dδxμ/dδzμ increasing with θ (see for instance ref. 48 and 61). The relation δxμ = tan(θ)δzμ can be derived from the geometry shown in the inset. The angles, θ, predicted from these slopes allow for a prediction of the evanescent penetration depth (cf.eqn (2)), which are validated by the agreement of our measured water viscosity using TIRFM with accepted values. More directly, and while not shown here, we have verified that the angles thus measured in situ are in agreement with the typical method of projecting the laser through a half sphere placed atop the objective,48,62 with the horizontal position of the laser measured as a function of xM.
Limitations of the particle altitude determination
Here we discuss how experimental artefacts may affect the velocity profiles displayed in Fig. 2. The error on individual tracer position, determined by Gaussian fitting of the intensity profile of the particle, is approximately one quarter of a pixel. At our level of magnification, this corresponds to 11 nm or, over one frame of 2.5 ms, approximately 9 μm s−1. While this effect becomes negligible on mean value estimation for large data sets, the velocimetry data nevertheless display small deviations from linearity. These are mainly due to optical aberrations: because of the finite depth of field of the objective (415 nm), off-focal-plane tracers appear relatively less bright than their in-focus counterparts. Expanding the typical62 Lorentzian multiplicative factor for the intensity as a function of the particle's distance from the focal plane, and considering that the focal plane is typically a few hundred nanometres from the surface, we do not expect that the near-wall linear profile exhibits more than 10% change in the shear rate due to this defocusing effect. Polydispersity is also expected to play a role in tracer altitude estimation. At a given z position, a bigger particle appears brighter, and is interpreted as closer to the wall than a smaller particle. To investigate the effects of defocussing and polydispersity, we have used63 the signal intensity distribution analyses of ref. 62, simultaneously fitting the distribution of intensities and velocity profiles and find good agreement with the slopes measured here, within 10% or so and not varying systematically with the imposed pressure.Lastly, we note particular deviations from the linear profile are present at the smallest z, especially for part (c) of Fig. 2. These deviations may arise from Brownian wandering of the tracer particles in the wall-normal direction during the exposure time (2.5 ms),46–48 coupled with the exponential dependence of the evanescent decay. Because of lubrication, the diffusion coefficient is not isotropic nor homogeneous at smallest z such that the Brownian noise on particles' displacement does not cancel out upon time averaging. This results in an overestimation of the velocity close to the wall as described in detail by several authors.64 Since our particles are at the closest roughly two radii away from the wall, we expect this effect to be minor. Nevertheless, to prevent this bias in the shear rate determination, the data points of Fig. 2 are weighted by a factor proportional to the standard error on the individual velocities. This way, when doing the linear fit, an order of magnitude less emphasis is put on the tails of the curves, where fewer tracers are observed and where this effect is the strongest.
Bulk rheology for HPAM(817k[−]) – comparison to scaling theory
Here we make a simple comparison between the bulk, steady-shear rheology measured for HPAM(817k[−]) and the scaling theory of Dobrynin et al.41 Without added salt, the specific viscosity, ηs,0 = η/ηw − 1, is expected to scale with the polymer concentration as ηs,0 ∼![[c with combining tilde]](https://www.rsc.org/images/entities/i_char_0063_0303.gif) 1/2. Including the ionic strength, an additional term counting the (monovalent) ions is needed, such that
1/2. Including the ionic strength, an additional term counting the (monovalent) ions is needed, such that 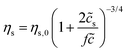 , where
, where ![[c with combining tilde]](https://www.rsc.org/images/entities/i_char_0063_0303.gif) s is added ion concentration. For large salt concentrations, the scaling becomes ηs ∼
s is added ion concentration. For large salt concentrations, the scaling becomes ηs ∼ ![[c with combining tilde]](https://www.rsc.org/images/entities/i_char_0063_0303.gif) 5/4. In Fig. 7 is shown the specific viscosity measured at the lowest accessed shear rates (5 s−1) as a function of the variable just described. The data for all of the polymer and salt concentrations fall on a single curve with a straight line describing well the relationship. We thus conclude that the bulk rheology is consistent with standard theories.
5/4. In Fig. 7 is shown the specific viscosity measured at the lowest accessed shear rates (5 s−1) as a function of the variable just described. The data for all of the polymer and salt concentrations fall on a single curve with a straight line describing well the relationship. We thus conclude that the bulk rheology is consistent with standard theories.
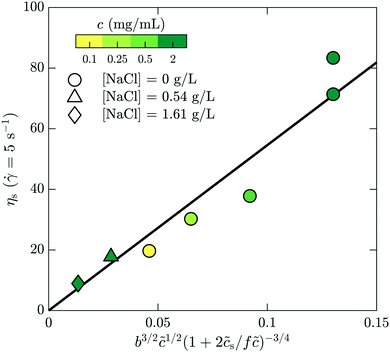 | ||
| Fig. 7 Bulk rheology measurements of the steady-shear viscosity for HPAM(817k[−]) at a shear rate of 5 s−1, as a function of the scaling variable developed by Dobrynin and coworkers.41 | ||
Acknowledgements
The authors thank Mathias Destarac for providing the polymers used here. They also benefited from the financial support of CNRS, ESPCI, the Agence Nationale de la Recherche (ANR) under the ENCORE (ANR-15-CE06-005) and CoPinS (ANR-19-CE06-0021) grants, and of the Institut Pierre-Gilles de Gennes (Equipex ANR-10-EQPX-34 and Labex ANR-10-LABX-31), PSL Research University (Idex ANR-10-IDEX-0001-02). Total is also gratefully acknowledged for financial support under contract TOTAL DS3700 – CNRS 2019200804.References
- P. G. De Gennes, Macromolecules, 1981, 14, 1637–1644 CrossRef CAS.
- Z. Fu and M. M. Santore, Colloids Surf., A, 1998, 135, 63–75 CrossRef CAS.
- L. Léger, E. Raphaël and H. Hervet, in Polymers in Confined Environments, ed. S. Granick, K. Binder, P.-G. de Gennes, E. P. Giannelis, G. S. Grest, H. Hervet, R. Krishnamoorti, L. Léger, E. Manias, E. Raphaël and S.-Q. Wang, Springer, Berlin, Heidelberg, 1999, pp. 185–225 Search PubMed.
- L. Lee, O. Guiselin, A. Lapp, B. Farnoux and J. Penfold, Phys. Rev. Lett., 1991, 67, 2838 CrossRef CAS PubMed.
- H. Bessaies-Bey, J. Fusier, S. Harrisson, M. Destarac, S. Jouenne, N. Passade-Boupat, F. Lequeux, J.-B. d'Espinose de Lacaillerie and N. Sanson, J. Colloid Interface Sci., 2018, 531, 693–704 CrossRef CAS PubMed.
- H. A. Barnes, J. Nonnewton. Fluid Mech., 1995, 56, 221–251 CrossRef CAS.
- H. Müller-Mohnssen, D. Weiss and A. Tippe, J. Rheol., 1990, 34, 223–244 CrossRef.
- C. Navier, Mémoires de l'Académie Royale des Sciences de l'Institut de France, 1823, 6, 389–440 Search PubMed.
- C. Neto, D. R. Evans, E. Bonaccurso, H.-J. Butt and V. S. J. Craig, Rep. Prog. Phys., 2005, 68, 2859–2897 CrossRef CAS.
- E. Lauga, M. Brenner and H. Stone, in Microfluidics: The No-Slip Boundary Condition, ed. C. Tropea, A. L. Yarin and J. F. Foss, Springer Berlin Heidelberg, Berlin, Heidelberg, 2007, pp. 1219–1240 Search PubMed.
- L. Bocquet and E. Charlaix, Chem. Soc. Rev., 2010, 39, 1073–1095 RSC.
- S. G. Hatzikiriakos, Soft Matter, 2015, 11, 7851–7856 RSC.
- V. Mhetar and L. A. Archer, Macromolecules, 1998, 31, 8607–8616 CrossRef CAS.
- L. Léger, H. Hervet, G. Massey and E. Durliat, J. Phys.: Condens. Matter, 1997, 9, 7719–7740 CrossRef.
- O. Bäumchen, R. Fetzer, M. Klos, M. Lessel, L. Marquant, H. Hähl and K. Jacobs, J. Phys.: Condens. Matter, 2012, 24, 325102 CrossRef PubMed.
- S. G. Hatzikiriakos, Prog. Polym. Sci., 2012, 37, 624–643 CrossRef CAS.
- P.-G. de Gennes, C. R. Seances Acad. Sci., Ser. B, 1979, 288, 219 CAS.
- O. Bäumchen, R. Fetzer and K. Jacobs, Phys. Rev. Lett., 2009, 103, 247801 CrossRef PubMed.
- M. Hénot, E. Drockenmuller, L. Léger and F. Restagno, ACS Macro Lett., 2018, 7, 112–115 CrossRef.
- M. Hénot, M. Grzelka, J. Zhang, S. Mariot, I. Antoniuk, E. Drockenmuller, L. Léger and F. Restagno, Phys. Rev. Lett., 2018, 121, 177802 CrossRef PubMed.
- M. Ilton, T. Salez, P. D. Fowler, M. Rivetti, M. Aly, M. Benzaquen, J. D. McGraw, E. Raphaël, K. Dalnoki-Veress and O. Bäumchen, Nat. Commun., 2018, 9, 1172 CrossRef PubMed.
- M. Hamieh, S. Al Akhrass, T. Hamieh, P. Damman, S. Gabriele, T. Vilmin, E. Raphaël and G. Reiter, J. Adhes., 2007, 83, 367–381 CrossRef CAS.
- F. Brochard-Wyart, C. Gay and P.-G. de Gennes, Macromolecules, 1996, 29, 377–382 CrossRef CAS.
- M. D. Graham, Annu. Rev. Fluid Mech., 2011, 43, 273–298 CrossRef.
- Y.-L. Chen, M. D. Graham, J. J. de Pablo, K. Jo and D. C. Schwartz, Macromolecules, 2005, 38, 6680–6687 CrossRef CAS PubMed.
- S. J. Park, A. Shakya and J. T. King, Proc. Natl. Acad. Sci. U. S. A., 2019, 116, 16256–16261 CrossRef CAS PubMed.
- A. Cuenca and H. Bodiguel, Phys. Rev. Lett., 2013, 110, 108304 CrossRef PubMed.
- C. Barraud, B. Cross, C. Picard, F. Restagno, L. Léger and E. Charlaix, Soft Matter, 2019, 15, 6308–6317 RSC.
- M. Hénot, A. Chennevière, E. Drockenmuller, L. Léger and F. Restagno, Macromolecules, 2017, 50, 5592–5598 CrossRef.
- M. Grzelka, I. Antoniuk, E. Drockenmuller, A. Chennevière, L. Léger and F. Restagno, ACS Macro Lett., 2020, 9, 924–928 CrossRef CAS.
- R. G. Larson, The structure and rheology of complex fluids, Oxford University Press, 1999 Search PubMed.
- R. H. Colby, D. C. Boris, W. E. Krause and S. Dou, Rheol. Acta, 2007, 46, 569–575 CrossRef CAS.
- Y. Heo and R. G. Larson, Macromolecules, 2008, 41, 8903–8915 CrossRef CAS.
- S. Jouenne and B. Levache, J. Rheol., 2020, 64, 1295–1313 CrossRef CAS.
- T. Kiljański, Rheol. Acta, 1989, 28, 61–64 CrossRef.
- K. Bertula, L. Martikainen, P. Munne, S. Hietala, J. Klefström, O. Ikkala and Nonappa, ACS Macro Lett., 2019, 8, 670–675 CrossRef CAS.
- S.-Q. Wang, S. Ravindranath and P. E. Boukany, Macromolecules, 2011, 44, 183–190 CrossRef CAS.
- P. Nghe, E. Terriac, M. Schneider, Z. Z. Li, M. Cloitre, B. Abecassis and P. Tabeling, Lab Chip, 2011, 11, 788–794 RSC.
- E. Read, A. Guinaudeau, D. James Wilson, A. Cadix, F. Violleau and M. Destarac, Polym. Chem., 2014, 5, 2202–2207 RSC.
- H. Bessaies-Bey, J. Fusier, M. Hanafi, S. Zhang, M. Destarac, S. Jouenne, N. Passade-Boupat, F. Lequeux, J.-B. dEspinose de Lacaillerie and N. Sanson, Colloids Surf., A, 2019, 579, 123673 CrossRef CAS.
- A. V. Dobrynin, R. H. Colby and M. Rubinstein, Macromolecules, 1995, 28, 1859–1871 CrossRef CAS.
- Y. Xia and G. M. Whitesides, Angew. Chem., Int. Ed., 1998, 37, 550–575 CrossRef CAS.
- P. R. Selvin, T. Lougheed, M. T. Hoffman, H. Park, H. Balci, B. H. Blehm and E. Toprak, Single-Molecule Techniques: A Laboratory Manual, In vitro and in vivo FIONA and other acronyms for watching molecular motors walk, Cold Spring Harbor Laboratory Press, 2008, ch. 3, pp. 37–71 Search PubMed.
- D. Axelrod, T. P. Burghardt and N. L. Thompson, Annu. Rev. Biophys. Bioeng., 1984, 13, 247–268 CrossRef CAS PubMed.
- K. D. Kihm, A. Banerjee, C. K. Choi and T. Takagi, Exp. Fluids, 2004, 37, 811–824 CrossRef CAS.
- R. Sadr, H. Li and M. Yoda, Exp. Fluids, 2005, 38, 90–98 CrossRef.
- M. Yoda and Y. Kazoe, Phys. Fluids, 2011, 23, 111301 CrossRef.
- Z. Li, L. D’eramo, C. Lee, F. Monti, M. Yonger, P. Tabeling, B. Chollet, B. Bresson and Y. Tran, J. Fluid Mech., 2015, 766, 147–171 CrossRef CAS.
- L. Korson, W. Drost-Hansen and F. J. Millero, J. Phys. Chem., 1969, 78, 6 Search PubMed.
- M. Rubinstein and R. Colby, Polymer Physics, OUP, Oxford, 2003 Search PubMed.
- A. Dobrynin and M. Rubinstein, Prog. Polym. Sci., 2005, 30, 1049–1118 CrossRef CAS.
- C. Cottin-Bizonne, S. Jurine, J. Baudry, J. Crassous, F. Restagno and E. Charlaix, Eur. Phys. J. E: Soft Matter Biol. Phys., 2002, 9, 47–53 CrossRef CAS PubMed.
- D. Lasne, A. Maali, Y. Amarouchene, L. Cognet, B. Lounis and H. Kellay, Phys. Rev. Lett., 2008, 100, 214502 CrossRef CAS.
- Y. Otsubo and K. Umeya, J. Colloid Interface Sci., 1983, 95, 279–282 CrossRef CAS.
- L. T. Lee and P. Somasundaran, Langmuir, 1989, 5, 854–860 CrossRef CAS.
- P. Auroy, L. Auvray and L. Leger, Macromolecules, 1991, 24, 5158–5166 CrossRef CAS.
- H. J. Ploehn, W. B. Russel and C. K. Hall, Macromolecules, 1988, 21, 1075–1085 CrossRef CAS.
- S. H. Behrens and D. G. Grier, J. Chem. Phys., 2001, 115, 6716–6721 CrossRef CAS.
- J. F. Joanny, L. Leibler and P. G. D. Gennes, J. Polym. Sci., Polym. Phys. Ed., 1979, 17, 1073–1084 CrossRef CAS.
- L. T. Lee, O. Guiselin, A. Lapp, B. Farnoux and J. Penfold, Phys. Rev. Lett., 1991, 67, 2838–2841 CrossRef CAS PubMed.
- K. N. Fish, Curr. Protoc. Cytom., 2009, 50, 12.18.1–12.18.13 Search PubMed.
- X. Zheng, F. Shi and Z. Silber-Li, Microfluid. Nanofluid., 2018, 22, 127 CrossRef.
- A. Vilquin, V. Bertin, P. Soulard, G. Guyard, E. Raphaël, F. Restagno, T. Salez and J. McGraw, arXiv:2007.08261 [cond-mat, physics:physics], 2020.
- R. Sadr, C. Hohenegger, H. Li, P. J. Mucha and M. Yoda, J. Fluid Mech., 2007, 577, 443–456 CrossRef CAS.
| This journal is © The Royal Society of Chemistry 2021 |