Open Access Article
Open Access ArticleThermal dissipation as both the strength and weakness of matter. A material failure prediction by monitoring creep†
Tom
Vincent-Dospital
 *ab,
Renaud
Toussaint
*ab,
Renaud
Toussaint
 *ab,
Alain
Cochard
*ab,
Alain
Cochard
 a,
Eirik G.
Flekkøy
a,
Eirik G.
Flekkøy
 b and
Knut Jørgen
Måløy
b and
Knut Jørgen
Måløy
 b
b
aUniversité de Strasbourg, CNRS, ITES UMR 7063, Strasbourg F-67084, France. E-mail: renaud.toussaint@unistra.fr
bSFF Porelab, The Njord Centre, Department of Physics, University of Oslo, N-0316 Oslo, Norway. E-mail: tom.vincent-dospital@fys.uio.no
First published on 18th March 2021
Abstract
In any domain involving some stressed solids, that is, from seismology to general engineering, the strength of matter is a paramount feature to understand. We here discuss the ability of a simple thermally activated sub-critical model, which includes the auto-induced thermal evolution of cracks tips, to predict the catastrophic failure of a vast range of materials. It is in particular shown that the intrinsic surface energy barrier, for breaking the atomic bonds of many solids, can be easily deduced from the slow creeping dynamics of a crack. This intrinsic barrier is however higher than the macroscopic load threshold at which brittle matter brutally fails, possibly as a result of thermal activation and of a thermal weakening mechanism. We propose a novel method to compute this macroscopic energy release rate of rupture, Ga, solely from monitoring slow creep, and we show that this reproduces the experimental values within 50% accuracy over twenty different materials, and over more than four decades of fracture energy.
1 Introduction: from slow creep to abrupt rupture
Although seminal, the early theoretical descriptions of crack dynamics, such as Griffith's2 or Slepyan's,3,4 were somewhat binary: beyond a critical mechanical load, matter suddenly breaks. It is however acknowledged that, at load levels below the critical one, a far slower crack propagation already occurs, that will here be referred to as ‘creep’. This phenomenon was successfully modelled with Arrhenius-like sub-critical growth laws,1,5 and is hence sometimes called ‘stress corrosion’. With the increasing number of experimental work, the description of such a slow dynamics was quickly refined, and five propagation stages were notably distinguished.1 Let us start this manuscript by summarising them. Fig. 1 illustrates these stages in a V–G plot, where V is the crack velocity for a given load G, which is the ‘energy release rate’, that is, the energy that the fracture consumes to advance by unit surface.2 At stage 0, while under only a mild mechanical input, cracks do not actually propagate forward. This was notably explained by the existence of some healing processes, that there efficiently compete with the failure ones.5 From this state, when the load is increased above a given threshold, some slow fracture growth starts to be observed (stage I). The propagation velocity V increases exponentially with the crack's energy release rate G. In a sub-critical (i.e., Arrhenius-like) description, it implies that V is to first order explained by an activation mechanism dependent on G, in a chemical-like rupture reaction.6 Logically, this regime was observed to also depend on the surrounding temperature and on the fluid which is present in the fracture,7 which affects the chemical reaction involved in molecular bond breaking. When reaching a faster propagation, some velocity plateau might then hold (stage II), possibly as the transport of fluid corrosive elements toward the tip cannot efficiently cope with the crack advance. Such plateau is, in this case, only a transition to a sub-critical growth ‘in-vacuum-condition’, where the dynamics becomes notably insensitive to the fracture fluid (stage III). Finally, when a particular threshold is reached for the energy release rate, the velocity jumps to a far quicker regime: the material fails (stage IV). We will denote‡ this threshold Ga in J m−2, with ‘a’ standing for ‘avalanche’.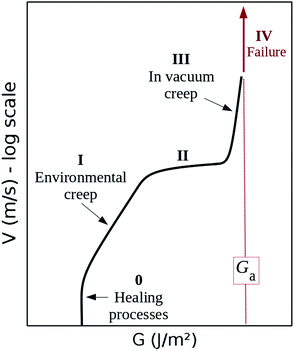 | ||
| Fig. 1 Summary of the different forward crack velocity regions observed in experimental velocity curves. After Fracture of Brittle Solids, Lawn.1 | ||
In this work, we will show how studying the slow creep regime allows to predict this particular failure load. This can lead to methods to characterise natural or lowly controlled materials, where the critical energy release rate Ga is not well known a priori, but where the monitoring of creep allows to infer it. In a previous study,8 we indeed proposed a unifying model of the slow creep and the fast regime, holding a precise quantification of the energy budget and the heating of the crack tip, which is coupled with an Arrhenius-type activation law. We have shown how it accounts, in some polymers,9 for seven decades of propagation velocities and for the transition, at the avalanche load, from creep to sudden failure. Here, we present how well this thermodynamics based model can predict the threshold Ga for a broad range of materials, by comparing its forecasts to actual experimental failure thresholds from twenty data sets from the literature. By doing so, one can actually identify the microscopic rupture energy of the breaking bonds, Gc, and show how this quantity is related to, yet different from, the macroscopic Ga. The agreement between the predictions and the realisation is obtained for materials spanning more than 4 orders of magnitude in energy release rate, indicating the robustness of this description among different types of materials and the versatility of the theoretical framework.
2 The thermal weakening model
We consider that the propagation of a crack follows an Arrhenius sub-critical growth law, in which the temperature term accounts for the induced heat generated at the plastic crack tip.10,11 Such a model, introduced in ref. 8 and 9, writes as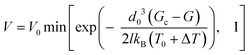 | (1) |
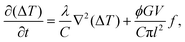 | (2) |
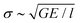 (e.g., see ref. 1), where E is the materials Young's modulus. This assumption is the reason why l also intervenes in eqn (1), where the elastic energy stored in the rupturing link typically writes as d03σ2/(2E), and is thus similar to d03G/(2l). In this framework, an acceleration of a fracture is thus both related to an increase of stress at the tip, which reduces the rupture energy barrier d03(Gc − G)/(2l), and to a related increase in volumetric internal energy (CΔT) at the fracture's head.
(e.g., see ref. 1), where E is the materials Young's modulus. This assumption is the reason why l also intervenes in eqn (1), where the elastic energy stored in the rupturing link typically writes as d03σ2/(2E), and is thus similar to d03G/(2l). In this framework, an acceleration of a fracture is thus both related to an increase of stress at the tip, which reduces the rupture energy barrier d03(Gc − G)/(2l), and to a related increase in volumetric internal energy (CΔT) at the fracture's head.
Note that it was shown9,13 that, at low velocities (i.e., the creep velocities we are interested in), ΔT computed from eqn (2) can, more simply, be approximated to
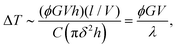 | (3) |
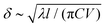 is the skin depth of heat diffusion upon the same time. According to eqn (3), ΔT does not depend on C or l, notably because if the crack advances slowly enough, the temperature elevation is constrained by the heat diffusion skin depth δ rather than by the size of the heat production zone, as the former is, in this case, big compared to the latter.
is the skin depth of heat diffusion upon the same time. According to eqn (3), ΔT does not depend on C or l, notably because if the crack advances slowly enough, the temperature elevation is constrained by the heat diffusion skin depth δ rather than by the size of the heat production zone, as the former is, in this case, big compared to the latter.
Approximating eqn (1) and (2) by their steady state solutions, two stable propagation branches are derived from this model,8 as shown in Fig. 2: a fast phase, which is obtained for a hot crack tip and corresponds to the catastrophic failure of matter, and a slow one corresponding to the creep regime, when ΔT ≪ T0. In between these two branches, a hysteresis situation holds with a third unstable phase. In this study, we are mainly interested in the slow to fast regime transition (i.e., that leads to quick material failure).
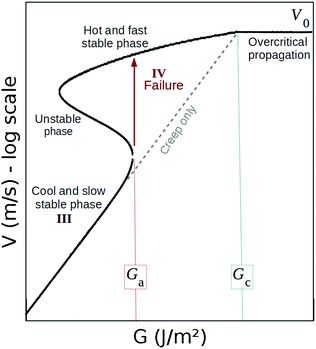 | ||
| Fig. 2 Modelled crack velocity as a function of energy release rate, as per eqn (1) and (2). Stages III and IV correspond to those labelled in Fig. 1. As explained in the text, stages 0, I and II are here not covered. In our model, the failure occurs when the cracks becomes hot enough, that is, when ΔT ∼ T0. The dashed line corresponds to a cold case ΔT ≪ T0 in eqn (1). | ||
When approaching this transition, the velocity deviates from its negligible heating asymptotic expression, which is a simple exponential increase with the load G:
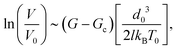 | (4) |
Although rarely regarded today, such an importance of the auto-induced heat to explain brittleness was early developed.14–16 These studies reckon that the dissipated energy favours failure by locally softening the material at the tip (i.e., a decrease of its elastic moduli with temperature), in particular in the case of soft rubber-like materials. In the formalism of eqn (1), this view would correspond to a brutal reduction of the energy barrier d03(Gc − G)/(2l) at the onset of the instability, rather to (or maybe in addition to) a dramatic increase in temperature, due to chemicophysical phase changes of the matrix. Our model neglects such a softening effect and instead considers that the reaction rate for rupture is increased from the elevated temperature, only as understood by statistical physics. Of course, both views are not mutually exclusive, and one of the two mechanisms may prevail depending on the considered material, or depending on the crack velocity. Indeed, for a softening effect to be at stake, the typical time for a material temperature-related change in phase must be less than the typical warming time l/V of a given location of the crack trajectory. By contrast, a change in velocity, as understood by statistical physics, should be as quick as a few atomic vibrations6 (∼1013 Hz) and, hence, should be more likely to explain fast cracks in hard solids. Such a qualitative discussion underlines the importance of knowing the actual rheology close to crack tips in given materials, and its sensibility to eventual temperature bursts. Note that in both approaches of thermal weakening here discussed, the G value of interest (i.e., Ga) remains similar in its concept: the threshold for which ΔT is high enough so that a quick avalanche can be generated by a given mechanism. In the rest of this manuscript, we will focus on the thermally activated, statistical, model that we have developed above, where the accurate rheology at the tip is actually considered to be of second order on the crack dynamics, and only the increase of ΔT is considered.
3 Model predictions versus reported failures
Extensive fracturing experiments on numerous materials can be found in the literature. Hence, we can compare the model predictions of Ga to some experimentally reported avalanche thresholds, that are often referred to as ‘critical energy release rate’ or ‘material toughness’, although it does not correspond to what is here denoted Gc, which is an intrinsic (microscopic) medium property not directly measurable at lab scale. In our framework, Gc is called the critical energy release rate because it differentiates between an actual subcritical propagation (at G < Gc), where thermal activation is required for the crack to advance, and an overcritical propagation (at G > Gc), where enough mechanical energy is given to the crack so that thermal activation is not strictly needed. In this latter case, eqn (1) simplifies to V = V0. A fast ‘dynamical’ crack can be subcritical (see Fig. 2), in particular when Ga < G < Gc, and we thus refrained to call Ga a critical energy release rate.Note that eqn (1) does not account for all of the creep regimes summarized in Fig. 1, that one can meet with an experimental test, but displays a unique low velocity slope (i.e., from eqn (4)). We have indeed discarded any healing processes, needed to explain stage 0, as they are beyond the topic of the current study. Such processes can however be included in the model.9 We have also assumed no rate-limiting environmental factor, that is, no significant chemical interaction of the matrix with the fracture fluid (i.e., no stage I or II). We have hence restricted our comparison to experimental data to such a non-environmental creep case (stage III), although distinguishing it with certitude is not always straightforward. When available, we have notably preferred data sets of in-vacuum or dry (in air) experiments or with lowly corrosive (e.g., neutral pH) fracture fluids (see the creep plots in the ESI† for an exhaustive list of the considered experiments, and their environmental conditions).
Indeed, high fluid pH or moisture tend to increase the creep dynamics of given materials (e.g., ref. 17), presumably by altering the chemistry of the rupture process at the tip (i.e., stages I and II), and such effects are not included in our model. Note however that, when some fluid–matrix interaction does take place, the model could still be somewhat applied, if failure is preceded by a unique slope (i.e., if it occurs before the slope break between stages I and II), or after it, once clearly having entered in regime III. In the former case, the definition of the surface energy barrier Gc may slightly change: from an intrinsic strength of the solid to an equivalent (lower) strength under a given chemical environment.
To predict Ga, it is of course needed to know, for each material, the values of the model constitutive parameters, that is, the parameters of eqn (1) and (2), which describe the evolution of the crack velocity as a function of the applied energy release rate. Although they are not many, most of these parameters are not usually considered, and are hence unknown. It is however possible to estimate their order of magnitude from known material properties, or to assess them from the slow (creep) part of the loading curve. We have first considered that V0 is of the order the mechanical wave velocity. It could ideally be that of the Rayleigh waves,12 but it is often simpler to instead estimate the – similar – shear wave velocity of solids, 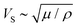 , as the shear modulus μ and the density ρ of most materials are easily available. The heat conductivity λ is also known in most cases, and T0 is nothing but the room temperature at which a given reported experiment took place. We assume the inter-atomic space d0 to be 1 Å. While it could be two or three times larger depending on the materials, which would have an order of magnitude effect on the term d03, this uncertainty would only impact the estimation of l, as the ratio d03/l is here of importance. We indeed have to deduce l and Gc from the slope and intercept of the slow sub-critical growth, that is, from the two terms of eqn (4) fitted to the experimental curves with the fit parameters Vnull and b: ln(V/Vnull) = bG, Vnull being the velocity a crack would have at a null load (G = 0), in the absence of fluid corrosion or healing effects and b the slope of the creep curve of dimension m3 s−1 J−1. This gives
, as the shear modulus μ and the density ρ of most materials are easily available. The heat conductivity λ is also known in most cases, and T0 is nothing but the room temperature at which a given reported experiment took place. We assume the inter-atomic space d0 to be 1 Å. While it could be two or three times larger depending on the materials, which would have an order of magnitude effect on the term d03, this uncertainty would only impact the estimation of l, as the ratio d03/l is here of importance. We indeed have to deduce l and Gc from the slope and intercept of the slow sub-critical growth, that is, from the two terms of eqn (4) fitted to the experimental curves with the fit parameters Vnull and b: ln(V/Vnull) = bG, Vnull being the velocity a crack would have at a null load (G = 0), in the absence of fluid corrosion or healing effects and b the slope of the creep curve of dimension m3 s−1 J−1. This gives
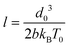 | (5) |
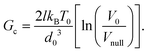 | (6) |
Note that, while the velocity is often reported in relation to the stress intensity factor K rather than the energy release rate G, we have here converted from one to the other with the following relation:1G ∼ K2/E to derive a and b, and then l and Gc. Backwardly, with the here proposed method, we will thus predict the toughness, 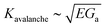 , based on the creep measurement. All the introduced parameters can now be estimated, and we did so for twenty materials for which the creeping behaviour was studied in the literature.9,17–34 The corresponding G to V curves and a table of all the inferred parameters values are shown in the ESI.† We can then solve numerically the two non linear eqn (1) and (2), now taking into account the temperature rise ΔT. In other words, for any value of the energy release rate G, we can compute the possible crack propagation velocities according to the model, as for instance shown in Fig. 2, where, depending on G, one to three velocities are possible. The inflection of the obtained curve, where ∂V/∂G → +∞ (see Fig. 2), can be identified as Ga and compared to the reported experimental thresholds. The detailed procedure is discussed and applied to two materials (PMMA and Pressure Sensitive Adhesive) in ref. 9. This comparison is summarised for all the media in Fig. 3, and our model displays there a good general description of catastrophic failure. In the same figure, the surface energy barrier Gc is also displayed for comparison, as well as the relative error made in the estimation of Ga.
, based on the creep measurement. All the introduced parameters can now be estimated, and we did so for twenty materials for which the creeping behaviour was studied in the literature.9,17–34 The corresponding G to V curves and a table of all the inferred parameters values are shown in the ESI.† We can then solve numerically the two non linear eqn (1) and (2), now taking into account the temperature rise ΔT. In other words, for any value of the energy release rate G, we can compute the possible crack propagation velocities according to the model, as for instance shown in Fig. 2, where, depending on G, one to three velocities are possible. The inflection of the obtained curve, where ∂V/∂G → +∞ (see Fig. 2), can be identified as Ga and compared to the reported experimental thresholds. The detailed procedure is discussed and applied to two materials (PMMA and Pressure Sensitive Adhesive) in ref. 9. This comparison is summarised for all the media in Fig. 3, and our model displays there a good general description of catastrophic failure. In the same figure, the surface energy barrier Gc is also displayed for comparison, as well as the relative error made in the estimation of Ga.
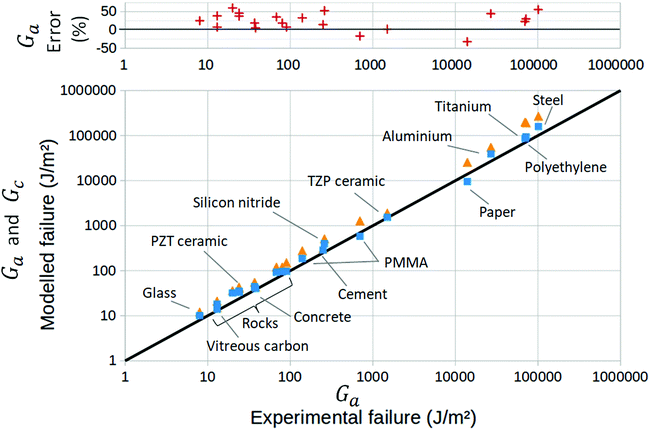 | ||
| Fig. 3 (bottom) Modelled Ga thresholds (squares) and modelled surface energy barrier Gc (triangles) compared to the experimental thresholds from the literature. The black line is the identity. The labels locate different materials. The unlabelled rock materials are quartz, sapphire, granite and andesite. See the ESI† for an exhaustive list. (top) Relative error on the avalanche threshold. | ||
4 Analytical approximation
While, to derive the modelled Ga, one should compute the full crack dynamics (i.e., as displayed in Fig. 2), and search for the points where ∂G/∂V = 0, we explain in the ESI† how eqn (1) and (2) also approximately lead to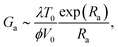 | (7) |
We show, in the ESI,† how the approximation of eqn (7) is a slight overestimation of the real solution, by about 0 to 10%. It however gives further insight on the influence of each parameter. The remaining dependence on (Gc − Ga) shows that, to obtain thermal weakening, one must already be close to the actual microscopic energy barrier of rupture Gc. The stress at the tip thus remains an important driving mechanism of the crack propagation. The brutal failure threshold Ga increases with the ambient temperature T0, as a higher temperature elevation ΔT is then required at the tip to significantly overcome a higher thermal bath. Similarly, Ga increases with the λ/ϕ ratio, as a high λ/ϕ indicates a rather cool crack tip, either because little energy is converted into heat (i.e., a small ϕ) or because this energy is efficiently evacuated away from the crack (i.e., a high λ). The failure threshold also decreases with V0, as, at a given load, a higher V0 means a faster (and then hotter) creeping crack from a higher atomic collision frequency V0/d0.
5 Microscopic vs. macroscopic fracture energy, and local vs. bulk energy dissipation
In Fig. 3, one can notice that the surface energy barrier Gc is always similar in order of magnitude to the rupture threshold Ga. Yet, the rupture always occurs at a load less than Gc, with Ga being about twice lower in average for all the displayed solids. We have here explained how a weakening mechanism, as the thermal view that we have here developed, allows to account for this discrepancy.Having gathered various exponential creep data, and derived l and Gc from their slope and intercept in their ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) V − G representations, we can notably infer the intrinsic crack energy barrier in each material: Uc = d03Gc/(2l) = kBT0
V − G representations, we can notably infer the intrinsic crack energy barrier in each material: Uc = d03Gc/(2l) = kBT0![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln(V0/Vnull). As shown in Fig. 4, this quantity is always in the order of 10−19 J–1 eV, logically comparable to the energy level necessary to unbind single atomic covalent bounds,35 which confirms the relevance of a simple thermally activated model for the description of stage III (in-vacuum-like) creep. The actual values of Uc are yet often slightly smaller than the typical covalent strength. This could derive from an averaging effect. Indeed, the Arrhenius law of eqn (1) is a mesoscopic statistical law, which we have fitted to some macroscopic measurements of crack propagation (i.e., the creep experiments). With cracks that are prone to follow the weakest paths, that possibly include weak inter-molecular bonds (such as van der Waals and hydrogen links) and dislocations or atomic voids (i.e., when the distance between two consecutive breaking bonds is more than a few Ångströms), Uc is likely representative of the average rupture energy in a disordered landscape. For instance, in polymers, part of the rupture shall be inter-molecular, and, in rock-type materials, the crack dynamics might benefit from the intrinsic porosity. However, due to the simplicity of the model, care should be taken when interpreting Uc beyond its order of magnitude.
ln(V0/Vnull). As shown in Fig. 4, this quantity is always in the order of 10−19 J–1 eV, logically comparable to the energy level necessary to unbind single atomic covalent bounds,35 which confirms the relevance of a simple thermally activated model for the description of stage III (in-vacuum-like) creep. The actual values of Uc are yet often slightly smaller than the typical covalent strength. This could derive from an averaging effect. Indeed, the Arrhenius law of eqn (1) is a mesoscopic statistical law, which we have fitted to some macroscopic measurements of crack propagation (i.e., the creep experiments). With cracks that are prone to follow the weakest paths, that possibly include weak inter-molecular bonds (such as van der Waals and hydrogen links) and dislocations or atomic voids (i.e., when the distance between two consecutive breaking bonds is more than a few Ångströms), Uc is likely representative of the average rupture energy in a disordered landscape. For instance, in polymers, part of the rupture shall be inter-molecular, and, in rock-type materials, the crack dynamics might benefit from the intrinsic porosity. However, due to the simplicity of the model, care should be taken when interpreting Uc beyond its order of magnitude.
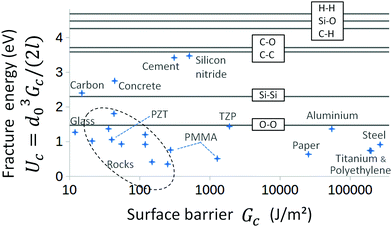 | ||
| Fig. 4 Microscopic fracture energy Uc = d03Gc/(2l) as a function of the macroscopic energy barrier Gc, for the same materials as in Fig. 3. See the ESI† for the exhaustive list. Note that the accuracy of Uc is not better than an order of magnitude. The horizontal lines show some typical covalent cohesion energies for comparison.35 | ||
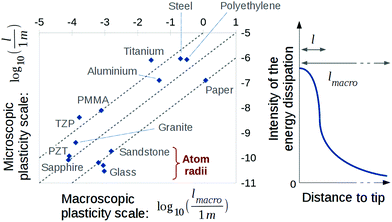
It is clear however that the value of Gc varies by a factor 104 for different materials, while its counterpart Uc does not. As most materials have the same Uc and d0, in order of magnitude, the large variability in Gc (and hence in Ga) which is observed is, in this description, attributable entirely to the variability in the scale for the release of heat. We indeed infer that l varies from the radius of a single atom, for the weakest materials, up to 1 μm, for the ones with the highest Gc (see Fig. 5). The wider the plastic area that shields crack tips, the stronger matter is. But backwardly, we have discussed how the heat dissipation might be the root cause for dramatic ruptures in brittle solids, if the heat is not efficiently evacuated away from the rupture front. Overall, eqn (1) should be understood as:
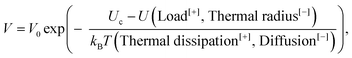 | (8) |
We can compare the values of l with the more typical plastic radius predicted by a Dugdale view36 of the process zone, lmacro ∼ GcE/σy2, where σy is the tensile yield stress, beyond which macroscopic samples lose their elasticity. As shown in Fig. 5, the latter is consistently five to seven orders of magnitude higher than what we predict for l. This likely translates to the fact that plasticity (here understood as the dissipation of mechanical energy in any form) ought to be a rather heterogeneous phenomenon, with a greater density of energy dissipation close to the front than away from it. A higher density of energy is indeed likely to be dissipated close to the tip singularity than at the edge of the lmacro plastic radius. Thus, the scale of a process zone can be characterised either by its core radius l, where most of the heating due to the dissipation takes place, or by its full extent lmacro, where the rheology becomes non elastic. While the former is to include significant thermal losses (quantified by ϕG), the latter can also encompass various other dissipation mechanisms for another portion of G, namely, the nucleation of dislocations, the release of extra heat over a greater volume around the tip, the emission of phonons and photons, or even some material change in phase (e.g., softening). In our formalism, l is also the main parameter that describes the shielding of the stress near the crack tip, and this stress is indeed likely to be higher at the centre of the process zone than at its periphery, calling for l < lmacro. Large scale bulk energy losses (e.g., ref. 37 and 38) are hence permitted by our model, and we only state that it is of second order effect on the temperature elevation and the stress level at the crack front and, hence, on the crack dynamics.
Besides its straight derivation from a canonical kinetics law (i.e., eqn (1)), there are various indicators suggesting that, although smaller than the more common lmacro, the sizes l that we have inverted bear a strong physical significance. For materials where l is here computed to be relatively large (i.e., in the micrometer range) infrared emissions can easily be recorded around (hot) crack tips by standard resolution infrared cameras, such as in paper13 or steel.39 In the case of paper, we inferred l close to the micrometric domain, which is about the dimension of the fibril forming this media. For running cracks in materials with a smaller l, such as PMMA or even glass, a hot temperature could also be derived by the characterisation of light emission,40,41 although its observation is not as straightforward. In glass,41 in particular, the light emission lies in the visible domain, calling for blackbody42 temperatures elevations of thousands of kelvins, and the light emitting zone was shown to have a nanometric radius. In PMMA, secondary microcracks tend to nucleate ahead of fast fronts from cavities/bubbles of about 100 nm in radius,9 possibly initiated by sublimation at hot temperature of the solid matrix. In rocky materials, nanometric damages can be observed43 on fault planes. These planes are sometimes referred to as fault mirrors, due to their glossy appearance arising from their very low roughness at the visible light wavelengths. Intense thermal effects, often referred to as ‘flash heating’, are notably suspected for the instability of some seismic faults.44,45
Overall, some intense, extremely localised (i.e., l), dissipation processes close to rupture fronts are thus likely to explain these various observations, and, in our framework, could also explain the brittleness of matter.
6 Discussion and conclusion
We have thus presented a model that gives reasonable predictions of the rupture load, over a broad range of materials. We did this with a full expression (eqn (1) and (2)), or in simplified forms (eqn (1) and (3) or eqn (7)). This predicted load is still, however, overestimated by about 25% (in average for all media, see the errors in Fig. 3). This could derive from numerous causes. First, most of our parameters were only broadly estimated, when not arbitrarily fixed. We have in particular assumed that Gc is a homogeneously distributed constant, whereas it is likely to hold some level of quenched disorder.46,47 In this case, the overall creep dynamics (i.e. the slow branch of Fig. 2, described by eqn (4)) would not be strongly affected, as it shall mainly depend on an average value of Gc. The failure, however, would be prone to occur on weaker locations,8 that are controlled by a lower Gc, which would explain our overestimation of Ga. It corresponds to the common idea that the overall strength of a material is highly dependent on its heterogeneities. As discussed in Section 5, our computation of the microscopic energy barrier Uc likely represents the average of a disordered landscape in dissociation energy, as its value lies in between that of an actual covalence energy and those of weaker interactions. Additionally, we derived Gc from the mean fit to experimental creep curves that, in some materials, hold some significant data dispersion (see the ESI†). Some of this dispersion could arise from mesoscopic fluctuations of macroscopic fracture energy Gc in these materials, and the avalanche threshold Ga could be highly dependent on the standard deviation of these fluctuations. Another explanation for the overestimation of Ga could be that the experimental error on the measurement of this parameter may in practice be important, as the avalanches occur in a regime where the crack velocity diverges with G, just before test samples snap at a velocity comparable to that of the mechanical waves. Hence, the last mechanical load accurately measured before rupture is, by essence, to be slightly below the actual physical threshold. Note also that, sometimes, the actual creep stage (i.e., 0 to III in Fig. 1) that we fit to derive our parameters is not unambiguously identifiable on the experimental curves, while our theory does not encompass fluid-to-matrix interactions. Besides these considerations, the model is extremely simple, applying mesoscopic laws (i.e., Fourier conductivity and Arrhenius growth) at atomic scales. For instance, a propagative description48 of the heat transport (i.e., not assuming, such as Fourier diffusion, an infinite transport velocity) could be needed, due to the small time and space scales that are here considered. Overall, a transposition of the model into a, more complicated, atomistic solver49 would be beneficial.Of course, the fact that the model reproduces an instability does not necessarily mean that it is the only explanation for britleness. Other models (e.g., the thermal softening of the matrix around the tip,16 or the perturbation of the stress field ahead of the crack by the rupture-induced emission of high frequency phonons3) have been proposed for this instability, and, in practice, depending on the materials, more than one physical process could here be at stake. Still, the model we propose gave, in some instances,9 a comprehensive explanation of the full dynamics of failure. Additionally, we have here shown how Gc, the intrinsic surface energy barrier of materials, shall only depend on a heat dissipation scale around the crack tip, and that the accumulation of this induced heat is effectively reducing the mechanical resistance of matter (Ga < Gc).
Countering this latter effect could be a key to design advanced strong materials, in particular as some intriguingly tough solids such as graphene50,51 or arachnid silks,52 are indeed very conductive. Interestingly, the conductivity of spider threads even increases with deformation,52 which could be a nature made adaptive defence mechanism for the stability of nets, whenever they are pressurized. Replicating such a behaviour with a man-made material would then be an important achievement that could lead to high performance cables or bulk materials. For instance, a first step could be the engineering of highly conductive atomic networks, integrated into strong solid matrices, thus limiting any local rise in temperature that could weaken matter. A more down-to-earth application of the model could be the monitoring of structures and infrastructures, as we have shown how their creep rate can be used to predict their failure. This would be of particular interest for bodies that have aged in uncontrolled conditions, in which the change in mechanical properties becomes uncertain with time, but could be inverted from their creep.
Finally, and although we have only treated about fracture in mode I, we suggest that most of the effects that we have discussed shall be valid for mixed-mode fracturing and solid friction. The latter is also suspected to hold some non negligible, thermal related, weakening mechanisms,44,45 which could notably be a key in geophysics and in understanding the stability of seismic faults. In particular, when increasing the background temperature T0, it was shown that the model holds a critical point, beyond which not enough heat can be generated to trigger instabilities in the dynamics of cracks,8 which may physically explain the brittle-ductile transition in the Earth's crust,53,54 below which rocks tend to flow rather than break.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
The authors declare no competing financial interests in the publishing of this work and acknowledge the support of the IRP France-Norway D-FFRACT, of the Universities of Strasbourg and Oslo and of the CNRS INSU ALEAS program. We thank the Research Council of Norway through its Centres of Excellence funding scheme, project number 262644.References
- B. Lawn, Fracture of Brittle Solids, Cambridge University Press, 2nd edn, 1993 Search PubMed.
- A. Griffith, Philos. Trans. R. Soc. London, Ser. A, 1921, 221, 163–198 Search PubMed.
- L. Slepyan, Sov. Phys., Dokl., 1981, 26, 538–540 Search PubMed.
- M. Marder, Philos. Trans. R. Soc., A, 2019, 20190098 CrossRef CAS.
- J. Rice, J. Mech. Phys. Solids, 1978, 26, 61–78 CrossRef CAS.
- G. G. Hammes, Principles of Chemical Kinetics, Academic Press, 1978 Search PubMed.
- N. Brantut, M. J. Heap, P. G. Meredith and P. Baud, J. Struct. Geol., 2013, 52, 17–43 CrossRef.
- T. Vincent-Dospital, R. Toussaint, A. Cochard, K. J. Måløy and E. G. Flekkøy, Phys. Rev. Mater., 2020, 023604 CrossRef CAS.
- T. Vincent-Dospital, R. Toussaint, S. Santucci, L. Vanel, D. Bonamy, L. Hattali, A. Cochard, K. J. Måløy and E. G. Flekkøy, Soft Matter, 2020, 9590–9602 RSC.
- E. Orowan, Energy criteria of fracture, Massachusetts institute of technology, cambridge departement of mechanical engineering technical report, 1954.
- G. R. Irwin, J. Appl. Mech., 1957, 24, 361–364 CrossRef.
- L. B. Freund, J. Mech. Phys. Solids, 1972, 20, 129–152 CrossRef.
- R. Toussaint, O. Lengliné, S. Santucci, T. Vincent-Dospital, M. Naert-Guillot and K. J. Måløy, Soft Matter, 2016, 12, 5563–5571 RSC.
- G. P. Marshall, L. H. Coutts and J. G. Williams, J. Mater. Sci., 1974, 9, 1409–1419 CrossRef CAS.
- D. Maugis, J. Mater. Sci., 1985, 20, 3041–3073 CrossRef CAS.
- G. Carbone and B. N. J. Persson, Phys. Rev. Lett., 2005, 95, 114301 CrossRef CAS.
- P. M. Dove, J. Geophys. Res.: Solid Earth, 1995, 100, 22349–22359 CrossRef CAS.
- O. Lengliné, R. Toussaint, J. Schmittbuhl, J. E. Elkhoury, J. P. Ampuero, K. T. Tallakstad, S. Santucci and K. J. Måløy, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2011, 84, 036104 CrossRef.
- S. Santucci, PhD thesis, Ecole Normale Supérieure de Lyon, 2004, http://www.theses.fr/2004ENSL0288.
- M. Yoda, M. Nabetani and W. Shim, Int. J. Fract., 2001, 112, 21–26 CrossRef.
- S. M. Wiederhorn, J. Am. Ceram. Soc., 1967, 50, 407–414 CrossRef CAS.
- S. Wiederhorn and R. J. Krause, Ceramic Engineering and Science Proceedings, 2002, pp. 71–82 Search PubMed.
- P. Meredith and B. Atkinson, Phys. Earth Planet. Inter., 1985, 39, 33–51 CrossRef.
- Y. Nara and K. Kaneko, Int. J. Rock Mech. Min. Sci., 2005, 42, 521–530 CrossRef.
- J. Holder, J. E. Olson and Z. Philip, Geophys. Res. Lett., 2001, 28, 599–602 CrossRef.
- W. Wang, T. Tong and Q. Yu, 9th International Conference on Fracture Mechanics of Concrete and Concrete Structures, 2016.
- Y. Nara, M. Takada, D. Mori, H. Owada, T. Yoneda and K. Kaneko, Int. J. Fract., 2010, 164, 57–71 CrossRef CAS.
- W. S. Oates, C. S. Lynch, D. C. Lupascu, A. B. K. Njiwa, E. Aulbach and J. Rödel, J. Am. Ceram. Soc., 2004, 87, 1362–1364 CrossRef CAS.
- J. Chevalier, C. Olagnon and G. Fantozzi, J. Am. Ceram. Soc., 1999, 82, 3129–3138 CrossRef CAS.
- A. G. Evans and S. M. Wiederhorn, J. Mater. Sci., 1974, 9, 270–278 CrossRef CAS.
- G. Hénaff, G. Odemer and B. Journet, Aluminium Alloys, Theory and Applications, IntechOpen, 2011, pp. 259–282 Search PubMed.
- J. H. Huang and C. J. Altstetter, Metall. Trans. A, 1991, 22, 2605–2618 CrossRef.
- S. M. L. Sastry, R. J. Lederich and B. B. Rath, Metall. Trans. A, 1981, 12, 83–94 CrossRef CAS.
- J. S. Nadeau, J. Am. Ceram. Soc., 1974, 57, 303–306 CrossRef CAS.
- G. B. Kaufman, J. Chem. Educ., 1993, 70, A279 CrossRef.
- D. Dugdale, J. Mech. Phys. Solids, 1960, 8, 100–104 CrossRef.
- J. Slootman, V. Waltz, C. J. Yeh, C. Baumann, R. Göstl, J. Comtet and C. Creton, Phys. Rev. X, 2020, 10, 041045 CAS.
- J. Samaca Martinez, E. Toussaint, X. Balandraud, J.-B. Le Cam and D. Berghezan, Mech. Mater., 2015, 81, 62–71 CrossRef.
- D. Palumbo, R. De Finis, F. Ancona and U. Galietti, Eng. Fract. Mech., 2017, 181, 65–76 CrossRef.
- K. N. G. Fuller, P. G. Fox and J. E. Field, Proc. R. Soc. London, Ser. A, 1975, 341, 537–557 Search PubMed.
- G. Pallares, C. L. Rountree, L. Douillard, F. Charra and E. Bouchaud, Europhys. Lett., 2012, 99, 28003 CrossRef.
- P. Jain and L. Sharma, J. Appl. Sci. South Afr., 1998, 4, 80–101 Search PubMed.
- S. Siman-Tov, E. Aharonov, A. Sagy and S. Emmanuel, Geology, 2013, 41, 703–706 CrossRef.
- J. R. Rice, J. Geophys. Res.: Solid Earth, 2006, 111, B05311 Search PubMed.
- G. A. Prieto, M. Florez, S. A. Barrett, G. C. Beroza, P. Pedraza, J. F. Blanco and E. Poveda, Geophys. Res. Lett., 2013, 40, 6064–6068 CrossRef.
- K. T. Tallakstad, R. Toussaint, S. Santucci, J. Schmittbuhl and K. J. Måløy, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2011, 83, 046108 CrossRef.
- A. Cochard, O. Lengliné, K. J. Måløy and R. Toussaint, Philos. Trans. R. Soc., A, 2018, 20170399 Search PubMed.
- D. W. Tang and N. Araki, Int. J. Thermophys., 1997, 18, 493 CrossRef CAS.
- C. L. Rountree, R. K. Kalia, E. Lidorikis, A. Nakano, L. Van Brutzel and P. Vashishta, Annu. Rev. Mater. Res., 2002, 32, 377–400 CrossRef CAS.
- Y. Hwangbo, C.-K. Lee, S.-M. Kim, J.-H. Kim, K.-S. Kim, B. Jang, H.-J. Lee, S.-K. Lee, S. Kim, J.-H. Ahn and S.-M. Lee, Sci. Rep., 2014, 4, 4439 CrossRef.
- A. Balandin, S. Ghosh, W. Bao, I. Calizo, D. Teweldebrhan, F. Miao and J. Lau, Nano Lett., 2008, 8, 902–907 CrossRef CAS.
- X. Huang, G. Liu and X. Wang, Adv. Mater., 2012, 24, 1482–1486 CrossRef CAS.
- C. H. Scholz, Geol. Rundsch., 1988, 77, 319–328 CrossRef.
- E. Aharonov and C. H. Scholz, J. Geophys. Res.: Solid Earth, 2019, 124, 2721–2737 CrossRef CAS.
Footnotes |
| † Electronic supplementary information (ESI) available: Derivation of eqn (7), sensitivity of the ϕ parameter, creep data for the presented materials, inverted parameters summary. See DOI: 10.1039/d0sm02089c |
| ‡ This is usually referred to as Gc in experiments, since it corresponds to the value of the macroscopic energy release rate at which the velocity of fracture propagation jumps to much higher values. By contrast, in this article and our previous works, we made the choice to design as Gc a microscopic property, which corresponds to an actual energy barrier in the rupture process, and we consequently used a different notation, Ga, for the load at which cracks avalanche to a fast phase, as a result of a boosted thermal activation (i.e., see Section 2). This notation choice is further discussed in Section 3. |
| This journal is © The Royal Society of Chemistry 2021 |