Force chains in crystalline and frustrated packing visualized by stress-birefringent spheres

Abstract

Force networks play an important role in the stability of configurations when granular material is packed into a container. These networks can redirect part of the weight of grains inside a container to the side walls. We employ monodisperse stress-birefringent spheres to visualize the contact forces in a quasi-2D and a nearly-2D configuration of these spheres in a thin cuboid cell. The packing structures are particularly simple: a hexagonal lattice in the ground state when the cell width is equal to the sphere diameter, and a frustrated, slightly distorted lattice in thicker cells. The force redistribution is substantially changed by this geometrical modification. In both cases, we observe an ‘inverse’ Janssen effect with the pressure decreasing from the top to the bottom of the container when the material is loaded with a weight on top of the vessel.

---

1 Introduction

The packing of monodisperse disks in two dimensions (2D) is quite well understood,¹ and in 3D, substantial progress has been made in the understanding of regular packing (proof of Kepler's conjecture)² and random packing in large containers where geometrical restrictions can be disregarded.³ However, many challenging open questions still remain.⁴ Among these questions is the problem of sphere packing under geometrical restrictions. In 2D, the hexagonal lattice optimizes the packing density both locally and globally.^1,5 Thus, gravitational filling a flat cell with spheres of a diameter d that is equal to the cell gap D (quasi-2D cell) produces a hexagonal (or, triangular) lattice with few distortions. Defects can be largely annealed by agitating (shaking) the cell appropriately. A perfect lattice requires that the lateral extension of the cell is either large with respect to the particle diameters or the cell has an appropriate width. In our experiments, the mismatch is small enough for a perfect lattice to form. In three dimensions, filling a container by pouring in spheres never leads to an optimal packing, but instead of the ≈74% of densest packing in HCP or FCC crystal configurations, only a random close packing (RCP) with about 60% to 64% space filling is reached. Even external agitation does not improve the packing substantially.⁶

Flat cuboid cells with thicknesses not much larger than the sphere diameter are an example of an interesting restricted geometry on the way from 2D to 3D (dimension 2 +ε). When spheres are packed in a cuboid cell that are only slightly thicker than their diameter (1 <D/d < 1.5), they form a distorted triangular lattice which is characterized by 13 possible structurally different configurations of the six neighbors of each sphere.^7–11 After filling the cell, these configurations are distributed randomly with particular statistical weights.^7,8 A ‘crystalline’ ground state is not reached even under long-term external agitation. On the other hand, the structure that is formed is far from random. We note that there is a structural similarity to packing of colloidal systems in thin layers,^9–14 but it is essential to emphasize that the granular system is athermal, in contrast to the latter. It shall also be mentioned in passing that the system has some resemblance to antiferromagnetic spin systems on a triangular lattice:¹⁵ The local configurations of neighboring spheres in a triangle are frustrated. Two spheres can occupy opposite cell plates to optimize packing, but the third one has to choose a site at the same plate as one of the other two. The positions of the spheres (contacting the front or rear container walls) determine a two-state system similar to spin-up and spin-down states in the antiferromagnet.

The original purpose of this study was to verify a hypothesis that the force network in the frustrated lattice is mainly established between spheres that touch the same (rear or front) container plate. In a single unit cell of the frustrated triangular lattice, when one of the spheres touches the opposite plate than the other two, the spheres on the same side have a larger mutual in-plane distance. Thus, one may naturally assume that such contacts carry larger loads in this structure than those between spheres occupying opposite sides. We anticipate here that this assumption is not correct as we will demonstrate in this study. However, the applied optical method revealed other interesting features of the confined packing structures.

We employ stress-birefringent spheres† to visualize the distribution of force chains in this (2 + ε)D geometry. This system is sufficiently different from the trivial hexagonal lattice, which already presents a challenge for the prediction of stable force networks,^16,17 but it is still of manageable complexity to allow the quantitative analysis of the quasi-2D force network structure in the cell plane using optical imaging. In particular, we will show that the conformation of the force network is strongly related to the dimensionality of the packing structure.

Force networks play an important role in the stability of configurations not only when granular material is packed into a container. In heaps of grains, the pressure distribution at the bottom can be counter-intuitive¹⁸ and depends, among other features, on the method the pile is created.^19–25 In containers, such networks can redirect the load on the grains to the container walls, so that the pressure in the granular bed does not increase linearly (hydrostatically) with fill height. It saturates in a certain depth below the granular bed surface. This effect was described more than a century ago by Hagen and Janssen.^26–29 We will demonstrate this redirection of forces to the side walls and measure the pressure saturation (Janssen's law) in a quantitative way.

It is challenging to reconstruct the complete network of interparticle forces in a 3D granular ensemble. In some emulsions, it is possible to employ confocal microscopy to detect particle contacts and local deformations of droplets, which can be used as a measure of force distributions.³⁰ A similar approach may be employed with soft, transparent granular spheres.³¹ For harder particles, this straightforward method fails. A substantial step forward in the qualitative and even quantitative determination of forces between particles was achieved with so-called photoelastic disks, at least in quasi-twodimensional systems. Stress-birefringent transparent material, commonly disk shaped, is used in these experiments.³² The disks are placed between polarizers in order to detect birefringent regions in the transmitted light. Preferentially, circular polarizers are employed since linear polarizers are not able to detect deformations in certain directions. Recent reviews of this technique can be found in ref. 33–36.

In absence of forces, the disk material is optically isotropic. In dark-field configuration of the polarizers, these disks appear black. Under stress, the material becomes locally birefringent. Changes of the transmission intensity indicate local distortions of the material. The optical transmission images can then be used to extract qualitative, and even quantitative information³⁹ on the strength and direction of contact forces. A certain disadvantage of this approach is that, while it works excellently for quasi-2D objects, the evaluation of forces in 3D packed “photoelastic” spheres is substantially more complicated.

A short discussion of the terminology may be appropriate here: The attribute “photoelastic”, even though it is commonly used in the community, does not quite accurately describe the nature of such materials. The grains do not change their shapes under optical illumination (like thermoelastic samples that deform at temperature changes). Instead, they change their optical properties under strain. We thus prefer the term “stress-birefringent” spheres in this paper.

The distribution of forces in granular packing has been analyzed not only theoretically in numerical simulations (e.g.ref. 16, 17, 40, 41 and 42) but also experimentally (e.g.ref. 32, 37, 38 and 43). Such experimental studies, however, are essentially restricted to 2D systems, with few exceptions.^44–46 Our stress-birefringent spheres in a flat cell may be considered as an extension of the previous work with disks. There are several quantitatively different and new aspects when one uses spheres: First, the optical analysis requires an immersion fluid, otherwise the polarization by refraction at the sphere surfaces would obscure the stress-induced birefringence. Second, since the contacts start point-like with spheres, the distortions are much more localized than in the case of disks. Third, the optical path differences cannot be obtained by simple multiplication of the stress-induced birefringence with the disk thickness but need to be integrated along the light path. Nevertheless, the step from disks to spheres is inevitable if one attempts to apply the stress-birefringence method to real 3D ensembles.

2 Experimental

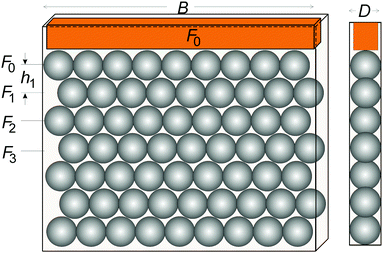
Spheres with diameter d = 12 ± 0.5 mm were prepared in appropriate cast moulds from stress-birefringent epoxy PL-3 (Vishay). Special care was taken to avoid entrapped air bubbles in the spheres (which was not possible in all cases) and to prepare them without pre-stresses during the polymerization process. These spheres were filled into cuboid boxes of width B = 170 mm and height H = 195 mm to monitor the force distributions in the lattices formed in the restricted geometry. Two different cell types were in investigated: One with a thickness D equal to the sphere diameter (D/d = 1.0, quasi-2D), and another one with a thickness 30% larger (D/d = 1.3, frustrated cell).

After filling a cell with spheres, we exposed it to vertical vibrations in order to compact the material and to reach a stationary packing fraction, similar to earlier experiments with monodisperse glass beads.⁸ A frustrated triangular lattice is formed in the cell with D > d, while in the quasi-2D cell with D = d, a triangular lattice with few defects is achieved. We prepared a refractive index matching immersion fluid, an oversaturated 80% aqueous sugar solution, initially prepared at 90 °C and slowly cooled down to room temperature. This fluid is not only refractive-index matching, but also nearly density matching. The polymer spheres have a refractive index n_p = 1.55 and a density ρ_p = 1.13 g cm⁻³. The index matching fluid is slightly heavier, with a density ρ_{[small script l]} = 1.40 g cm⁻³ and refractive index n_{[small script l]} = 1.49. Therefore, the spheres swim, but are nearly neutrally buoyant. An external force is needed to keep the spheres at the bottom of the container. The situation is comparable to that of hydrogel spheres in index-matching immersion fluids³¹ that were studied by means of optical imaging with a Laser sheet method: buoyancy almost completely compensates the weight of the hydrogel beads, and forces between them have to be generated externally. In order to suppress particle rearrangements after the packing preparation, the sucrose solution was carefully filled into the cell while the packing was kept confined under load by a piston.

We applied homogeneous vertical forces between 2 N and 30 N, transmitted by a horizontal bar, onto the upper layer of beads. A load of 6 N turned out to be optimal for our experiments. The pressure generated by the 6 N weight is 2.9 kPa, it corresponds to the pressure below a 44 cm high stack of (not density-matched) stress-birefringent spheres in perfect hexagonal packing without lateral walls.

The cell was illuminated with uniform parallel white light and photographed, using circular polarizers in front of and behind the cell. Optical transmission images were evaluated for the determination of stress-induced birefringence. Reference images were taken without polarizers. From these images, we can extract the positions of the spheres (in contact with the front or rear glass plates) in order to identify the 13 basic local configurations.⁸ This allows us to correlate the force network structure with the distribution of frustrated and non-frustrated bonds⁷ in the triangular unit cells.

We performed a total number of ten experiments at a cell thickness D = 1.3 d and four experiments with the quasi-2D cell (D = d). For each experiment, the cell was first emptied and then freshly filled. Images were taken in dark-field (Fig. 1(b)) and bright-field polarizer configurations as well as reference images in unpolarized light (Fig. 1(a)). Fig. 2 shows a detail of one lattice site and its six neighbors observed with circular polarizers in bright-field configuration. The stress-birefringence patterns at the contact points are well resolved.

Fig. 1 Visualization of interparticle forces by means of stress-birefringent spheres in frustrated monolayers of spheres: (a) Reference image in unpolarized light. (b) Same configuration of spheres under circular polarizers in dark-field configuration. (c) Image of the squared greyscale gradient of the same configuration. (d) Force chains shown as lines with thicknesses proportional to the forces.

Fig. 2 Detail of an Image taken with white light between circular polarizers in bright-field configuration (same handedness). Forces in the contact region manifest themselves as color changes via yellow, red and purple to dark blue and light blue back to the next order yellow. (magnified detail of Fig. 4 below).

3 Evaluation of forces from optical images

Before analyzing the experimental geometry of the triangular lattice, we calibrated the forces by optical images of single spheres under load. Fig. 3 shows the optical transmission images of a sphere that was exposed to different normal forces with a punch above the top pole, while being supported on a horizontal plate at the bottom pole. The top row is a sequence recorded during loading, the bottom row shows the same sphere during unloading. The two processes are symmetric, there is no noticeable hysteresis. With this tool, it is possible to obtain the quantitative forces in reasonable accuracy already by visual inspection of individual contacts. A similar calibration can be performed with circular polarizers in bright-field configuration. Information extracted from either types of images is fully equivalent. The index matching fluid has some optical rotatory power, which is not relevant in our experiments. We can neglect its presence in the following analysis of transmission images.

Fig. 3 Calibration of the optical images of a sphere with two point contacts (top and bottom) under circular polarizers in dark-field configuration.

For a quantitative analysis of multisphere structures, the judgement of individual contacts is in principle possible, but an automatized procedure is preferable, even with some loss in accuracy. In contrast to the analysis of monochromatic images, which we found severly affected by artifacts from defects, sphere overlap and inhomogeneities of the illumination, we used the following procedure based on images using white light: The bright-field image was divided by the corresponding dark-field image. The result was converted to a pseudo-greyscale image I using a linear combination of the RGB color channels I = 200R − 45G − 45B. This combination provided the best compromise between low sensitivity to particle defects and high contrast of the stress birefringence patterns. This greyscale image was then inverted, then artifacts in the form of isolated bright pixels were removed. An evaluation procedure was employed to create an image corresponding to the square of the grey value gradient (g² image, see Fig. 1(c)).

Particle positions were extracted from the reference images by means of straightforward image analysis. The integrated grey-value within circles corresponding to the spheres within the thresholded, inverted hue-channel image is analyzed. After varying the circle position, the local maxima give a first estimate of the sphere positions. Using these as new initial values, optimization of the positions is done with the same method but in the inverted hue-channel image without thresholding. We found this method to work reasonably well for slightly overlapping spheres. Visual comparison with the raw images shows an accuracy of ±3 pixels for spheres of 185 pixels diameter that are slightly overlapping with neighboring spheres or with the sample cell border. Together with the gradient image, the contact forces were now determined as follows: Based on the distance between two particles, a list of possible neighbors was created for each particle. For each pair of neighboring particles, an image selection around the suspected contact point was defined, corresponding to a union of three circles whose centers lie on the line joining the particle centers. The circle radius was chosen one third of the particle radius. One circle was centered around the contact point, the other two were shifted by their radius into the first and the second particle, respectively. Within the combined area of all three circles, the mean grey value of the g² image was determined. This region-of-interest covers points close to the contact point, whose contribution dominates at very small contact forces, as well as points inside the particles, whose contribution still allows a distinction of large contact forces. The mean grey value is proportional to the number of visible rings of the stress birefringence pattern and proportional to the contact force. This was established in the calibration measurements with diametrically stressed particles (Fig. 3). In the frustrated system, neighboring spheres that occupy opposite sides of the cell partly overlap in the images, so that a certain region near the contact cannot be used for evaluation. For the present experimental parameters, this overlap is small enough to be negligible in the evaluations.

The main uncertainty of the resulting contact forces stems from randomly distributed small defects of the spheres. They affect both the g² image as well as the estimated sphere positions and contact positions, the latter leading to a random shift of the region-of-interest. The force error is estimated to be no larger than ± 15%. For forces ≪0.1 N, the defects may lead to falsely identified contacts that are actually not present. Therefore we imposed a threshold of 0.1 N to suppress them.

In this work we consider a force chain a series of at least three particles in pairwise contact whose centers lie on approximately parallel connecting lines (up to a deviation of 58 degrees). Fig. 1(d) shows a typical network structure extracted from the stress-birefringence measurements. Force chains are marked as lines whose widths are proportional to the normalized contact force. Pairs of particles with a contact force below a threshold of 10% of the maximum contact force were not considered.

4 Results

4.1 Local particle arrangements and force network structure

First, we compare the force network structure in a quasi two-dimensional geometry, where the cell thickness D is equal to the sphere diameter d, with that in a container with width D = 1.3 d. Fig. 4(a and b) show two independent experiments in the same cell, where the individual filling procedures produced different particle arrangements (a) and (b). These individual packing structures generate force networks with similar global features but different local details.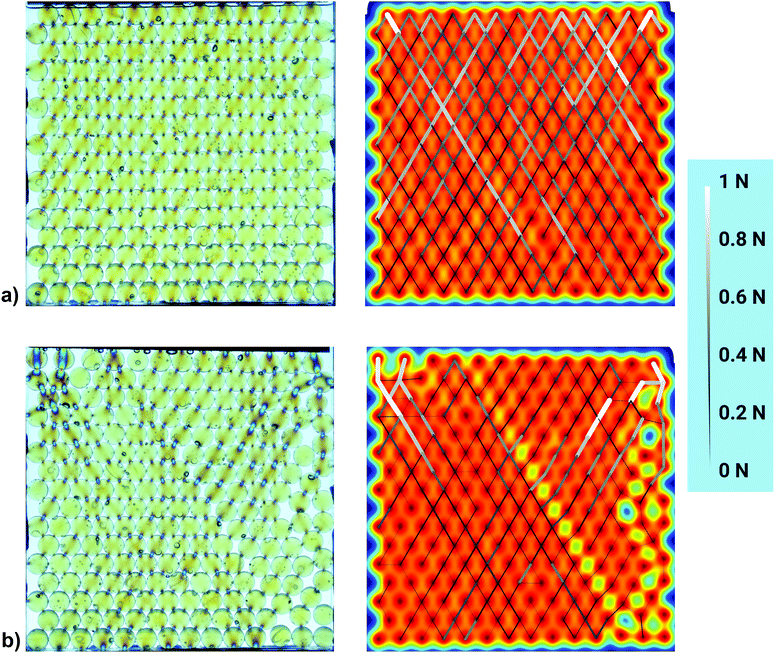

Fig. 4 Interparticle forces in two independent measurements in a cell with thickness D = d by means of stress-birefringent spheres. In case (a) the spheres form a perfect triangular lattice, while in case (b) a dislocation line separates two crystalline domains and the lattice contains numerous defects at the right hand side. Left: Bright-field transmission images with circular polarizers. The stress-birefringent spheres appear light yellowish where they are not deformed. Forces near the contact points manifest themselves in color changes (see details in Fig. 2). Right: Same packing with pseudocolors indicating the particle positions (blue for empty, red for the particle center) and force chains. The thickness of the lines symbolizes the strength. Note the absence of horizontal force segments in both configurations.

Fig. 5(a and b) show two independent experiments with the frustrated cell, D = 1.3 d, with non-planar packing. Again, two different particle arrangements (a) and (b) are shown as examples. The different local packing structures generate different force networks.

Fig. 5 Interparticle forces in two independent measurements in the D = 1.3 d cell by means of stress-birefringent spheres. The photos at the left are bright-field transmission images with circular polarizers. In the images at the right, spheres at the front and rear cell plate are differently colored. In case (a), the spheres form a distorted regular triangular lattice, except close to the bottom right corner. In case (b), several defects affect the force network. Spheres touching the front plate are coloured in red, while those touching the back plate are coloured in blue. The thickness of the lines indicates the strength of the force. Note that in both configurations there is a region in the lower cell center that is almost stress-free.

When the vertical force on the top row of spheres is varied, as shown in Fig. 6, the force network structure is not changed. This behavior is anticipated as long as the particular arrangement of the spheres and their contacts remains unaltered. The forces in the network are uniformly increased proportional to the increment of the top load. Its stepwise release led to exactly the same pictures in reverse sequence (from (f) to (a)).

Fig. 6 Evolution of the force network structure inside the frustrated cell (D = 1.3 d) depending on the vertical pressure applied on the top particle layer. The vertical force is progressively increased from (a) 0 N, (b) 2 N, (c) 6 N, (d) 10 N, (e) 20 N to a maximum of (f) 30 N. Subsequent stepwise reduction of the weight results in identical images without any hysteresis.

It is obvious in Fig. 4–6 that the forces act primarily at contacts between spheres in different horizontal layers. Their interconnection vectors (center-center) form angles α close to ±60° respective to the horizontal. A quantitative evaluation is given in Fig. 7 and 8. They show histograms of the angular distributions of interparticle forces. Fig. 7 reveals that in the quasi-2D cell, 90% of the contacts fall in a range of α = (60 ± 2)°. Forces between neighboring spheres in the same layers (α ≈ 0°) are found with a probability of less than 5% of all detected contacts. In contrast, the frustrated cell shows a much broader distribution of the contact angles, and roughly 15% of the forces are horizontal (α ≤ 4°).

Fig. 7 Relative frequency of contact forces depending on the angle between neighboring spheres. The bin width is 2°. We compare the experiments in the quasi-2D cell (blue) with those in the frustrated cell (green). In the 2D case, a sharp peak at 60° is visible. In contrast, almost no horizontal forces were observed. In the frustrated cell, there is a broader angle distribution around 60°, and horizontal forces are much more present (by a factor of 2.5).

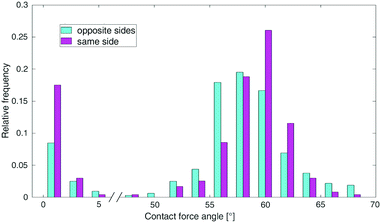Fig. 8 Relative frequency of contact forces depending on the angle between neighboring spheres. The bin width is 2°. We analyze experiments in the frustrated cell, comparing spheres on the same side (magenta) to spheres on opposite cell walls (cyan). Horizontal forces are much more often distributed between spheres located at the same side of the cell. Additionally, in comparison to the 2D case, there is a broader distribution of contact angles around 60°, due to the distorted triangular lattice (see ref. 8 for a detailed explanation).

In the frustrated packing, one can discriminate forces between spheres on the same side (front or back) of the cell, and spheres on opposite cell plates. This is detailed in Fig. 8. The conclusion drawn from this figure is that the differences between both local configurations are not very large. Two minor details are found. The first one is that horizontal force contacts of spheres on the same side of the cell are much more probable than those between spheres in opposite positions. The second observation is that the angles of forces near the 60° peak are noticeably shifted to smaller α. This is reasonable, because the projected angle between two spheres in neighboring horizontal layers decreases from 60° to about 58.4° when D = 1.3 d. This shifts the force distribution by about 2 degrees to lower α.

One additional feature is evident when the quasi-2D cells with perfect crystalline packing are compared to the thicker, frustrated cells: In the crystalline lattice of the former, the forces are rather uniformly distributed among all spheres in a given layer (cf., for example, Fig. 4). This is noticeably different in the frustrated, non-perfect lattices of the thicker cell. There, the outer spheres carry significantly more load than those in the cell middle part. This is particularly well reflected in Fig. 6. In the deeper layers, the forces are concentrated on the lateral spheres, while those in the center experience much less load. This feature is characteristic for all experiments with the frustrated cell, see for example Fig. 5.

4.2 Janssen's law

One of the interesting aspects of this experiment that is not directly related to the perfect or frustrated triangular lattice, but is conveniently accessible with our approach, is the redistribution of weight forces to the container walls, the so-called Janssen effect.²⁸ Friction of the grains with the container side walls, generated by the normal forces on the contacts, are responsible for the saturation of the pressure in the granular bed. In our experimental geometry of the quasi-2D cell, the spheres are stacked exactly in-plane, and thus there are ideally no relevant contact force components out of the stacking plane. So only the side walls of the container need to be taken into account. Then, one can perform, in reasonable approximation, a discrete mathematical analogue to Janssen's approach. One computes the forces on a horizontal layer of spheres in different heights of the container, setting the force onto the first (upper) layer to F₀. This is in good approximation the force of the upper bar in our experiment. We will start the computation with a simplified system that has no immersion fluid. Then, the force acting onto the next layer below is found by

F_n+1 = F_n + DBρgh₁ − γF_n (1)

Here, ρ = ρ_pϕ is the product of the polymer density and the filling fraction ϕ ≈ 0.6 of the spheres in the container. B and D are the dimensions of the container as sketched in Fig. 9, h₁ is the vertical distance of the centers of mass of subsequent layers (see sketch), and g is the gravitational acceleration. The coefficient γ contains a proportionality constant between the vertical force F_n on the n-th layer and the normal force at the contact of a sphere with the wall, multiplied by its coefficient of static friction at the glass wall. In Janssen's model, γ essentially contains the coefficient of static friction of the grains at the walls and a ratio of horizontal and vertical pressures in the silo. In our case, we assume that in each layer, one sphere has contact to one of the side walls (see sketch). When the cell width is an integer multiple of the sphere diameter, then two or no spheres are in contact with the side walls alternating, and the computation is still good on a coarse-grain scale.

Fig. 9 Sketch of the quasi-2D cell with definition of the geometric quantities for the determination of the force and pressure profiles. The image on the left shows the front view of the cell, the right image is the side view. Forces F_i are defined for horizontal layers of spheres, see text.

One finds by iteration of F_n+1 = aF_n + b with a= 1 − γ < 1 and b = DBρgh₁, the series

which yieldswith the limitwhich is of the order of 1 N for our material.

When one is not interested in the details of force structures for individual layers but defines a mean pressure dependence p(h) = F(h)/(BD) in the granular structure (in analogy to Janssen), one can find an integral form of eqn (2)–(4) with F₀ = F(h₀),

with a saturation pressure ρ_pϕgh₁/γ ≈ 650 Pa. It corresponds to a hydrostatic pressure at the bottom of a 6.5 cm high water column.

Now, we discuss our actual experiment where the spheres are immersed in a liquid. Then, buoyancy influences the force network. When the liquid is heavier, the vertical force components in the granular packing will reverse sign at some depth. In the liquid, we have of course the hydrostatic pressure p_{[small script l]} = ρ_{[small script l]}g(h₀ − h). In the granular material, we have to set the forces acting on the n-th row of spheres to

F^(p)_n+1 = F^(p)_n − DBΔρϕgh₁ − γF_n (6)

with the density mismatch Δρ = (ρ_{[small script l]} − ρ_p) and obtain an equation similar to eqn (3) where ρ_p is replaced by Δρ.which for large n reacheswhich is of the order of a few dozen mN. For the present experiment with the top weight F₀ of ≥6 Newton, the force drop in the first few layers is practically equivalent to that of eqn (3)–(5). In larger depths, one would indeed find a sign reversal of the vertical components of the contact forces because of the buoyancy effect. The saturation force F_∞ is negative and, because of Δρ ≈ 0.1ρ_p, one order lower than in the non-immersed spheres. The same holds for the saturation pressure.

Fig. 10 compares the results of this calculation with the experimentally measured force chains. We have summed up the vertical components of the forces determined from the optical images in each horizontal layer. Three individual measurements were averaged, both for the 2D cell (D = d) and for the frustrated cell with D = 1.3 d. The dashed lines correspond to interpolations of the discrete values that were determined with eqn (7). The coefficient γ was found from a least squares fit. For the experimentally determined values we assume a relative error of ±5% for the 2D system. Due to the higher uncertainty in the determination of the exact contact points between the particles, the maximum relative error is somewhat higher in the frustrated system. Still, the calculated values from eqn (7) are in very good agreement with the experimental ones, see Fig. 10.

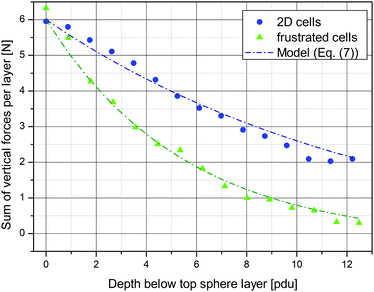Fig. 10 Height dependence of the sum of the vertical components of forces in each particle layer. The blue dots represent an average over three individual experiments with the quasi-2D cell. The green triangles correspond to an average over three experiments within the frustrated cell (D = 1.3 d). The dashed lines show fits according to eqn (7). We found γ = 0.0625 for the quasi-2D cell from a mean square deviations fit. The pressure at the top is higher than the saturation pressure, thus the pressure decreases towards deeper layers. A force saturation due to this ‘inverse’ Janssen effect is expected at F_∞ ≈ −0.50 N. In the frustrated cell, forces are additionally transferred to the front and back cell plates, resulting in a steeper drop than in the 2D case. Therefore, γ′ = 0.150 is higher than in the 2D case, resulting also in a smaller value for the force saturation, F_∞ ≈ −0.21 N.

Fig. 10 also shows the vertical force characteristics of the frustrated D = 1.3 d cell. The decay is steeper there. One can find the expected vertical force characteristics with the same ansatz as in eqn (1)–(3). However, one has to take into account the forces at the front and rear sides of the container. This can be summarized in an additional term −γ′F_n on the right hand side of in eqn (1). In the subsequent equations, γ = 0.0625 must be replaced by a larger coefficient γ′ = 0.150. Fig. 10 shows that indeed, the friction with the rear and front walls has a crucial influence on the Janssen effect. The coefficient γ is more than twice as large as in the quasi-2D cell where forces transmitted to the rear and front plates are negligible. In addition, the absolute value of the saturation force is consequently substantially smaller.

5 Summary

We have employed stress-birefringent spheres for a quantitative characterization of force networks in thin cells. The two geometries compared in this study are those of a quasi-2D cell where forces act essentially in the cell plane, and a slightly thicker cell with a frustrated triangular lattice configuration of the spheres. This has significant consequences for the vertical dependence of the pressure in the granular bed.

The peculiarities of our study, compared to conventional investigations of Janssen's effect, are that first, the material is submerged in a liquid of higher density, which has the consequence that the buoyancy forces pointing upward overcompensate the weight of the material. Second, we have placed a weight on the top of the granular bed to prevent the spheres from moving up. The consequence is that the pressure in the upper layers is larger than the saturation pressure, even if the grains were not immersed in a denser liquid. The Janssen effect is therefore inverted, the pressure in the granular bed approaches the saturation value from ‘above’. The direction of forces on the top layer is downward, whereas buoyancy leads to a saturation force F_∞ directed upward. Thus, in a sufficient depth within a high container, we predict the existence of a neutral layer where the forces compensate, and the direction of vertical forces on the beads changes sign. This depth was not reached in our experiments because of the limited amount of available stress-birefringent spheres.

The existence of this neutral layer has an interesting consequence for the stability of this configuration of buoyant grains carrying a load: When the load is larger than the saturation force |F_∞| of the sphere packing, then a sufficiently deep layer of buoyant grains can carry this load irrespective of a potential contact to a container bottom. Sufficiently deep in this sense means that the neutral layer exists inside the container, above the bottom. The position of this layer can be derived, e.g. from eqn (5). If the load is of the same order as the saturation force, the necessary depth of the buoyant grain layer is of the order of h₁/γ.

In the frustrated packing of the thicker cell, there is no clear preference of forces acting between grains positioned at the same side of the cell, as compared to grains occupying opposite positions, front and rear. Frustrated and non-frustrated bonds contribute, statistically, in the same measure to the force network.

There is, however, an obvious difference between quasi-2D and frustrated cells in the lateral distribution of forces: In the regular 2D lattice, the forces are nearly equally distributed among the spheres in the same layer. In contrast, the distribution of forces in the frustrated system is non-uniform. The lateral spheres carry more of the weight of the overlying material than the spheres in the middle. This, qualitatively, is reminiscent of the non-intuitive pressure distributions below heaps of grains that were mentioned in the introduction. While we have no explanation for this feature, we assume that must be related to the randomness of the particle arrangement in the frustrated lattice in contrast to the regular lattice of the quasi-2D structure.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

The authors acknowledge funding by the German Science Foundation within projects STA 425/38-1 and STA 425/46-1, and from Deutsches Zentrum für Luft- und Raumfahrt within projects 50WM1945 and 50WM2071.

References

1. László Fejes Tóth, Commentarii Mathematici Helvetici, 1949, 23, 342.
2. T. C. Hales, Ann. Mathematics, 2005, 162, 1065–1185.
3. S. Torquato, T. M. Truskett and P. G. Debenedetti, Phys. Rev. Lett., 2000, 84, 2064–2067.
4. M. P. Ciamarra, P. Richard, M. Schröter and B. P. Tighe, Soft Matter, 2012, 8, 9731.
5. A. Thue, Christiania Vid.-Selsk. Skr, 1910, 1, 9.
6. F. Rietz, C. Radin, H. L. Swinney and M. Schröter, Phys. Rev. Lett., 2018, 120, 055701.
7. K. Harth, A. Mauney and R. Stannarius, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2015, 91, 030201(R).
8. S. Lévay, D. Fischer, R. Stannarius, B. Szabó, T. Börzsönyi and J. Török, Soft Matter, 2018, 14, 396.
9. Y. Han, Y. Shokef, A. M. Alsayed, P. Yunker, T. C. Lubensky and A. G. Yodh, Nature, 2008, 456, 898.
10. Y. Shokef and T. C. Lubensky, Phys. Rev. Lett., 2009, 102, 048303.
11. Y. Shokef, A. Souslov and T. C. Lubensky, Proc. Natl. Acad. Sci. U. S. A., 2011, 108, 11804.
12. P. Pieranski, L. Strzelecki and B. Pansu, Phys. Rev. Lett., 1983, 50, 900.
13. M. Schmidt and H. Löwen, Phys. Rev. Lett., 1996, 76, 4552.
14. H. Löwen, Phys. Rep., 1994, 237, 249.
15. G. Wannier, Phys. Rev., 1950, 79, 357 ; Phys. Rev. B: Solid State, 1973, 7 5017.
16. J. H. Snoeijer, T. J. H. Vlugt, M. van Hecke and W. van Saarloos, Phys. Rev. Lett., 2004, 92, 054302.
17. P. Tighe, J. H. Snoeijer, T. J. H. Vlugt and M. van Hecke, Soft Matter, 2010, 6, 2908.
18. T. Jotaki and R. Moriyama, J. Soc. Powder Technol., Jpn., 1979, 16, 184.
19. J. P. Wittmer, P. Claudin, M. E. Cates and J.-P. Bouchaud, Nature, 1996, 382, 336.
20. D. M. Mueth, H. M. Jaeger and S. R. Nagel, Phys. Rev. E: Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top., 1998, 57, 3164.
21. G. Løvoll, K. J. Måløy and E. G. Flekkøy, Phys. Rev. E: Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top., 1999, 60, 5872.
22. J. Ai, J. Y. Ooi, J.-F. Chen, J. M. Rotter and Z. Zhong, Mechanics of Materials, 2013, 66, 160.
23. J. Y. Ooi, Z. Zhong, J.-F. Chen and J. Michael Rotter, Conference: Structures and Granular Solids: From Scientific Principles to Engineering Applications, DOI: 10.1201/9780203884447.ch8.
24. H.-G. Matuttis, Granular Matter, 1998, 1, 83.
25. H.-G. Matuttis and A. Schinner, Granular Matter, 1999, 1, 195.
26. G. H. L. Hagen, Bericht über die zur Bekanntmachung geeigneten Verhandlungen der Königlich Preußischen Akademie der Wissenschaften zu Berlin. 1852, p. 35 (Berlin: Verl. d. Kgl. Akad. d. Wiss.).
27. B. P. Tighe and M. Sperl, Granular Matter, 2007, 9, 141.
28. H. A. Janssen, Zeitschr. d. Vereines deutscher Ingenieure, 1895, 39, 1045.
29. M. Sperl, Granular Matter, 2006, 8, 59.
30. J. Brujic, S. F. Edwards, D. V. Grinev, I. Hopkinson, D. Brujic and H. A. Makse, Faraday Discuss., 2003, 123, 207.
31. D. M. Walker, A. Tordesillas, N. Brodu, J. A. Dijksman, R. P. Behringer and G. Froyland, Soft Matter, 2015, 11, 2157.
32. T. S. Majmudar and R. P. Behringer, Nature, 2005, 435, 2079.
33. J. Zhang, T. S. Majmudar, M. Sperl and R. P. Behringer, Soft Matter, 2010, 6, 2982.
34. K. E. Daniels, J. E. Kollmer and J. G. Puckett, Rev. Sci. Instrum., 2017, 88, 051808.
35. L. Papadopoulos, M. A. Porter, K. E. Daniels and D. S. Bassett, J. Complex Networks, 2018, 6, 485.
36. A. A. Zadeh, et al. , Granular Matter, 2019, 21, 83.
37. K. E. Daniels and N. W. Hayman, J. Geophys. Research, 2008, 113, B11411.
38. P. Yu and R. P. Behringer, Chaos, 2005, 15, 041102.
39. T. S. Majmudar, M. Sperl, S. Luding and R. P. Behringer, Phys. Rev. Lett., 2007, 98, 058001.
40. J. H. Snoeijer, T. J. H. Vlugt, M. van Hecke and W. van Saarloos, Phys. Rev. Lett., 2004, 92, 054302.
41. B. P. Tighe, A. R. T. van Eerd and T. J. H. Vlugt, Phys. Rev. Lett., 2008, 100, 238001.
42. G. Bi, J. Rock Mech. Geotech. Eng., 2017, 9, 135.
43. J. Zhang, T. S. Majmudar, A. Tordesillas and R. P. Behringer, Jamming for a 2D granular material, Granular Matter, 2010, 12, 159–172.
44. C.-H. Liu, et al. , Science, 1995, 269, 513.
45. P. Yu, S. Frank-Richter, A. Börngen and M. Sperl, Granular Matter, 2014, 16, 165.
46. D. Leśniewska, M. Nitka, J. Tejchman and M. Pietrzak, Granular Matter, 2020, 22, 71.

---

Footnote

† In literature, the term “photoelastic” grains has become customary for such objects.

---