DOI:
10.1039/D0SM02045A
(Paper)
Soft Matter, 2021,
17, 2062-2070
Transport of neutral and charged nanorods across varying-section channels
Received
17th November 2020
, Accepted 26th December 2020
First published on 4th January 2021
Abstract
We study the dynamics of neutral and charged rods embedded in varying-section channels. By means of systematic approximations, we derive the dependence of the local diffusion coefficient on both the geometry and charge of the rods. This microscopic insight allows us to provide predictions for the permeability of varying-section channels to rods with diverse lengths, aspect ratios and charge. Our analysis shows that the dynamics of charged rods is sensitive to the geometry of the channel and that their transport can be controlled by tuning both the shape of the confining walls and the charge of the rod. Interestingly, we find that the channel permeability does not depend monotonically on the charge of the rod. This opens the possibility of a novel mechanism to separate charged rods.
I Introduction
The transport of molecules, proteins and small particles across pores, channels and, in general, porous materials is of paramount relevance in several biological, environmental and technological scenarios.1 In biology and technological applications, ions and molecules are transported across membrane pores,2–4 RNA is transported across the nuclear membrane5–7 and the crowded environment of cell cytoplasm provides dynamical obstacles to the motion of organelles and vesicles.8 Similarly, in environmental sciences, pollutants and plant nutrients spread across the porous matrix of rocks and soil. In this perspective, substantial effort has been dedicated to the synthesis9,10 and characterization11 of anisotropic nano-colloids and stiff filaments.12,13 Finally, in recent years the development of experimental techniques such as DNA14,15 and protein16 sequencing, resistive-pulse sensing techniques17–20 and chromatography21–23 have been developed by exploiting transport across pores.
On the theoretical side, tackling these problems is typically complicated since it requires detailed numerical simulations that take into account the interactions between the suspended object and the confining walls. Recently, several groups have contributed developing the so-called Fick–Jacobs approximation.24–29 This scheme relies on the assumption that when the net longitudinal velocity is slow enough, the transported object will explore the directions transverse to the motion with a probability distribution that is very close to the equilibrium one. Thanks to this approximation, the geometry of the pore as well as the interaction with the walls can be accounted for by the local equilibrium free energy. This approach has been shown to be applicable to the transport of colloids,30–34 ions,35–39 and polymers40–42 just to mention a few among others (see recent review articles29,43 for a more comprehensive list).
In this article we study the dynamics of charged rods confined in varying section channels. In particular, we propose an extension of the Fick–Jacobs approximation that allows us to account for both the geometry of the rod as well as for its net charge. From this perspective, our work goes beyond a recent contribution (see ref. 44) in which an approximated equation governing the transport of uncharged rods across varying section channels has been proposed. First, we test our approach against known experimental results45 for neutrally charged rods. Our model retrieves both the local dependence of the diffusion coefficient as well as the dependence of the Mean First Passage Time (MFPT) profile. Second, we use our model to predict the dependence of the diffusion coefficient on the geometry of both the channel and the rod as well as on the charge of the rod. For neutrally charged rods, in agreement with ref. 45, we find that the local diffusion coefficient maximizes at the channel bottleneck, i.e. where the rod is mainly oriented along the channel axes. Interestingly, the modulation of the local diffusion coefficient is maximized when the length of the rod major axis is comparable to the channel average section and it becomes vanishing small when these two length scales differ. Finally, our data show that such a dependence can be even amplified by the electrostatic interaction between the rod and the channel walls.
II Model
We characterize the transport of rigid rods across a 2D varying-section channel whose half-section is given by| |  | (1) |
where h0 is the average section, h1 is the amplitude of the section modulation and L0 is the period of the channel. The position and orientation of the rod are encoded in the position of the center of mass (with coordinates (x,z)) and in the angle θ between the rod and the x-axis. Accordingly, the 2D-Smoluchowski equation reads| | | ∂tρ(x,z,θ,t) = ∂xJx+ ∂zJz+ ∂θJθ, | (2) |
with| | 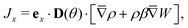 | (3) |
| |  | (4) |
where ρ is the probability distribution function, β−1 = kBT is the inverse thermal energy, kB is the Boltzmann constant, T is the absolute temperature. Moreover,| |  | (6) |
is the translational diffusion matrix that accounts for the fact that the diffusion along the major axis of the rod differs from that perpendicular to it, Dθ is the rotational diffusion coefficient and W accounts for the both, the conservative forces acting on the rod and the confinement. In the following, we focus on the case in which the local radius of curvature is much larger than the length of the rod. In such a regime the channel walls can be approximated as locally parallel to the longitudinal axis. Accordingly we have that the potential W reads| |  | (7) |
with| |  | (8) |
| | 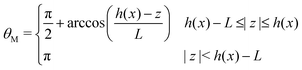 | (9) |
where ϕ(x,z,θ) accounts for the equilibrium conservative forces and f for the longitudinal force responsible for the transport along the channel. In eqn (8) and (9) we assume that the aspect ratio between the long axis, 2L, and the minor axis, 2l, of the rod is such that L ≫ l and hence we can disregard the geometric corrections to eqn (8) and (9) due to the finiteness of l.
We further assume that translation along the channel axis is slow enough such that ρ retains its equilibrium profiles along z and θ, which implies the absence of fluxes in z and θ, i.e.
Accordingly, we perform the standard Fick–Jacobs approximation24–28
| |  | (12) |
where
| |  | (13) |
is the local equilibrium free energy.
24,25 We remark that
p(
x) (see
eqn (12)) is proportional to the probability of finding the center of mass at a position
x. In the frame of reference of the rod we have
| |  | (14) |
where

is the diffusion coefficient along the minor axis of the rod (of size
l),
α encodes for the geometric correction,
e⊥, and
D0 is the diffusion coefficient along the major axis of the rod (of size 2
L),
e‖, and the off-diagonal terms are zero due to the axial symmetry of the rod.
46 Since
α depends on the geometry of the rod and there is no closed formula for it, in the following we assume the same value for the geometric prefactor along both axes,
i.e. we assume
α = 1. Integrating
eqn (3) along
z and
θ and using
eqn (10)–(12) we obtain
| |  | (15) |
Here,
| |  | (16) |
is the effective local diffusion coefficient. According to
Fig. 1 we have
ex = cos
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θe‖
θe‖ − sin
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θe⊥
θe⊥ which leads to the following expression for the local diffusion coefficient,
| |  | (17) |
which, once substituted into
eqn (16), leads to
| |  | (18) |
 |
| | Fig. 1 Top: Scheme of a rod (orange) with major axis of length 2L tilted by an angle θ and embedded in a plane channel with half section h0. The minimum, θmin(z) and maximum, θmax(z) angles for a given position of the center of mass are reported. Bottom: A rod in a varying-section channel with half-section h(x). | |
We remark that for l = Leqn (18) reduces to  , which is the diffusion coefficient of spherical particles of size l.24,25 Finally, integrating eqn (2) along z and θ and using eqn (15) leads to
, which is the diffusion coefficient of spherical particles of size l.24,25 Finally, integrating eqn (2) along z and θ and using eqn (15) leads to
| |  | (19) |
This is the extension of the Fick–Jacobs approximation to the case of rigid rods embedded in varying-section channels. The steady-state solution of eqn (19) reads
| |  | (20) |
where
J and
Π are integration constants. For periodic boundary conditions and imposing the normalization of the probability we obtain
| |  | (21) |
| |  | (22) |
Finally we define the dimensionless permeability as
| |  | (23) |
where
f is the magnitude of the external force and
J0 =
βD0f/
L is the flux of a spherical colloid of radius
l in a flat channel of half-width
h0.
III Results
A Neutral rods
At first we focus on neutral rods for which the potential W reads| |  | (24) |
and the local free energy reads| | 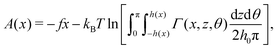 | (25) |
with| | | Γ(x,z,θ) = Θ(θ − θm(x,z))Θ(θM(x,z) − θ), | (26) |
where Θ(θ) is the Heaviside step function. Accordingly, the effective diffusion coefficient reads| |  | (27) |
where L is the half-length of the major axis of the rod (see Fig. 1).
1 Diffusion.
At first we compare our analytical predictions for the diffusion coefficient against experimental results. As already shown in ref. 45, the diffusion coefficient is maximum at the channel bottleneck where the rod is mainly parallel to the axis of the channel. Fig. 2a shows that predictions of eqn (27) qualitatively agree with the experimental data. In particular, the model properly captures the enhancement of the sensitivity of the local diffusion coefficient upon increasing the length of the rod. Indeed, we remark that for longer rods, for which the dependence of the diffusion coefficient is more significant, the predictions of the model are quantitatively reliable, whereas the agreement with the experimental data becomes weaker when the dependence of D on x becomes milder (possibly due to the absence of hydrodynamic coupling with the walls in the model). Once the agreement for the diffusion coefficient has been assessed we focus on the validity of the Fick–Jacobs approximation for what concerns the MFPT between the origin and an arbitrary position x:| |  | (28) |
Interestingly, the predictions of eqn (28) match well with the data reported in ref. 45 in the case of more corrugated channels whereas it is just qualitative for more shallow shapes (see Fig. 2b). Interestingly, this trend is similar to that of the model (based on finite-element numerical simulations) reported in ref. 45.
 |
| | Fig. 2 Validation of the model (solid lines) against experimental data taken from ref. 45 (dots). (a) Dependence of the diffusion coefficient  normalized by the value at the bottleneck. In order to check the validity of the model the values of the parameters are chosen to be close to those used in Fig. 3a of ref. 45. Accordingly, we have: L0 = 12 μm, h0 = 3 μm, l = 0.15 μm and L = 1, 1.2, 1.6 μm. Lighter colors stand for larger values of L. We remark the agreement between the model and the experimental data improves upon increasing the length of the rods. (b) Mean first passage time (MFPT) with reflecting boundary conditions at the origin and absorbing at x for L = 1.04 μm, h0 = μm, h1 = μm (black), L = 1.14 μm, h0 = μm, h1 = μm (dark green), L = 1.18 μm, h0 = μm, h1 = μm (light grey). As shown in the panel, the agreement improves upon increasing the corrugation of the channel. normalized by the value at the bottleneck. In order to check the validity of the model the values of the parameters are chosen to be close to those used in Fig. 3a of ref. 45. Accordingly, we have: L0 = 12 μm, h0 = 3 μm, l = 0.15 μm and L = 1, 1.2, 1.6 μm. Lighter colors stand for larger values of L. We remark the agreement between the model and the experimental data improves upon increasing the length of the rods. (b) Mean first passage time (MFPT) with reflecting boundary conditions at the origin and absorbing at x for L = 1.04 μm, h0 = μm, h1 = μm (black), L = 1.14 μm, h0 = μm, h1 = μm (dark green), L = 1.18 μm, h0 = μm, h1 = μm (light grey). As shown in the panel, the agreement improves upon increasing the corrugation of the channel. | |
Next, we characterize the dependence of the ratio between the maximum and the minimum local diffusion coefficients on the length of the rod. As expected, Fig. 3 shows that in the asymptotic limits, L/h0 ≪ 1 and L/h0 ≫ 1, the rods either reduce to a spherical particle of radius l = L or to a very long stiff filament that, due to the confinement is almost always aligned with the channel axis. In both cases the effective diffusion coefficient reduces to  . In contrast, for L ≃ h0, Fig. 3 shows that increasing the corrugation of the channel increases the range of values of the rod length for which the local diffusion coefficient is sensitive to the local channel section. Clearly, if the aspect ratio L/l approaches unity the diffusion coefficient becomes homogeneous along the channel.
. In contrast, for L ≃ h0, Fig. 3 shows that increasing the corrugation of the channel increases the range of values of the rod length for which the local diffusion coefficient is sensitive to the local channel section. Clearly, if the aspect ratio L/l approaches unity the diffusion coefficient becomes homogeneous along the channel.
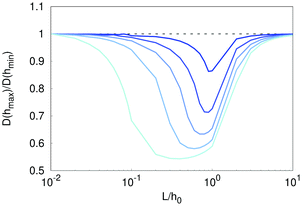 |
| | Fig. 3 Ratio of the effective diffusion coefficient at the maximum channel amplitude (D(hmax)) and at the bottleneck (D(hmin)) as a function of L and for different values of βΔAgas = 0, 0.2, 0.6, 1.1, 1.7, 2.9 (from blue to cyan). Rods have a fixed magnitude of the small axis l/h0 = 0.01. | |
2 Free energy barrier.
Having an explicit formula for the free energy, it allows us to discuss the dependence of the equilibrium (f = 0) free energy barrier defined as the difference between the free energy at the bottleneck and the one at the channel's widest section (see Fig. 4a and b):| | | ΔAeq = A(hmin, f = 0) − A(hmax, f = 0) | (29) |
For comparison we recall that the free energy difference for an ideal gas depends solely on the geometry of the channel:25| |  | (30) |
Our model shows that the dependence of the free energy barrier of rods strongly depends on their length (see Fig. 4c). Indeed, while for shorter rods, L/h0 ≲ 0.5, the free energy barrier of the rod increases upon increasing channel corrugation (i.e. increasing ΔAgas) for longer rods, L/h0 ≳ 1, the free energy barrier of the rod decreases upon increasing ΔAgas, as shown in Fig. 4. Additionally, for every geometry of the channel the maximum departure of ΔA from ΔAgas is attained when the length of the rod is comparable to the channel average section, L ≃ h0. Interestingly, for rods much longer than the channel section we have that ΔA → 2ΔAgas. In particular, very long rods L ≫ h0 imply that z ≃ 0, i.e. that the center of mass is confined close to the channel axis. Hence, this asymptotic behavior can be understood by expanding eqn (25) about z = 0. Indeed, for L/h0 ≫ 1 the integrand of eqn (25) can be approximated by h(x)/L and hence we obtain that A(x) ∝ 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln[h(x)] which eventually leads to ΔA → 2ΔAgas.
ln[h(x)] which eventually leads to ΔA → 2ΔAgas.
 |
| | Fig. 4 Equilibrium free energy barrier ΔA. (a) and (b) depict the dependence of the free energy barrier, ΔA, for rods of different length L/h0 = 0.05, 0.1, 0.5, 0.7, 1, 2 (from blue to cyan) as a function of the free energy barrier of the ideal gas. (c) Dependence of the free energy barrier on the length, L, of the rod for different channel corrugations ΔAgas ≃ 0.4, 0.6, 1.1, 1.7, 3. | |
3 Transport.
Next, we analyze the transport of rods under the action of a constant force. In order to simplify the analysis we assume that the fluid rods are suspended and keep at rest, i.e. there is no advection of rods due to fluid motion. In such a regime, Fig. 5 shows that the dependence of the dimensionless permeability μ on the length of the major axis of the rod, L, is quite complex. Indeed, for flat channels (βΔAgas = 0) the transport is determined solely by the effective diffusion coefficient. In particular, for L ≫ h0 the rod is almost aligned with the axis of the channel and the effective diffusion coefficient approaches the one of the minor axis (see Fig. 3) and, according to eqn (23)μ → 1 for L ≫ h0. In contrast, for βΔAgas = 0 and L ≪ h0 the rod can freely rotate and it experiences a reduction in the effective diffusion coefficient (see Fig. 3). For βΔAgas ≠ 0, the channel is not flat and the dependence of the dimensionless permeability μ on L becomes more involved. Indeed, Fig. 5 shows that for intermediate values of βΔAgas, μ displays a non-monotonous dependence on L/h0. This behavior is similar to that observed for polymers confined between corrugated plates (see ref. 40). Finally, for larger values of βΔAgas, μ monotonically decreases upon increasing L/h0.
 |
| | Fig. 5 Dimensionless channel permeability, μ, to non-charged rods as function of the normalized length of the major axis of the rods, L/h0 for rods with l = 10−2h0 and for different values of βΔAgas = 0.2, 0.6, 1.1, 1.7, 2.9 (from blue to cyan), whereas the grey dots are for βΔAgas = 0. | |
B Charged rods
Next, we analyze the case of charged rods. For simplicity we assume that the charge, q, is localized at the center of the rod and that the channel walls are characterized by a constant charge density σ. In addition, we assume that a dilute monovalent electrolyte is suspended in the fluid phase so that the system is electrically neutral. In this regard, the rod brings an extra charge, whose magnitude is assumed to be much smaller than that of the charge of the double layer such that it does not affect significantly the local electrostatic field.† Accordingly, the (unperturbed) electrostatic potential inside the channel reads| |  | (31) |
with  . The local free energy becomes
. The local free energy becomes| |  | (32) |
where the diffusion coefficient reads| |  | (33) |
The dependence of the channel permeability on the electrostatic interaction of the rods with the walls is shown in Fig. 6a. In particular, Fig. 6a shows that the dependence of μ on the interaction potential of the rods with the walls is non-monotonous. For a given charge density on the walls, when the magnitude of the charge is very large (for both signs of the charge) the permeability becomes vanishingly small. Indeed, for such cases the effective free energy barrier to be overcome is very large and hence μ becomes very small. In contrast, upon reducing the magnitude of the charge, μ increases and it reaches its maximum for weakly negatively charged rods, i.e. when rods are attracted by the channel walls. As shown in Fig. 6a the optimal value of the charge depends on the channel corrugation and it decreases upon increasing the channel corrugation. This non-monotonous dependence, and in particular the location of the maximum, can be understood by looking at the equilibrium free energy difference βΔAeq. Indeed, Fig. 6b shows that the maxima observed in Fig. 6a occur for values of q for which βΔAeq = 0 (see Fig. 6b) i.e., when the equilibrium overall free energy barrier drops and the rods have only to overcome smaller local free energy barriers.
 |
| | Fig. 6 Dimensionless channel permeability, μ, as function of the charge of the rods. (a): μ as a function of βqϕ0 for different values of the channel corrugation, βΔAgas = 1.1, 1.7, 2.2, 2.9, with κh0 = 1. Lighter colors stand for larger values of βΔAgas, whereas the grey solid line stands for βΔAgas = 0. The force is proportional to the charge and, for a unit charge, it amounts to βfeL = 0.1. (b): βΔAeq (see eqn (29)) as function of the interaction potential with the walls βqϕ0. Note that the maxima in panel (a) occur for values of q for which βΔAeq ≃ 0. | |
Fig. 6a shows that the geometry of the channel can be used to tune the sorting of rods depending on their charge. In order to exploit the geometry of the channel and to separate charged rods depending on their length, it is mandatory to find the set of parameters for which the sensitivity of the dimensionless channel permeability on the channel geometry is maximized. As discussed, our model highlights a direct correlation between the equilibrium free energy barrier ΔAeq and the dimensionless channel permeability μ. This implies that the region of the parameter space in which μ is likely to be sensitive to the geometry, ΔAgas, can be guessed by inspecting the equilibrium free energy difference ΔAeq. Fig. 7 shows that for kh0 ≳ 1, the isolines βΔAeq = 0 are parallel to the ordinate axis for L ≳ h0. Hence, all rods with length L ≳ h0 are expected to have relatively similar values of μ. Accordingly, for this set of parameters only rods with length L ≲ h0 can be separated. In contrast, for kh0 ≃ 0.5 and for βΔAgas ≃ 0.75 the contour line βΔAeq = 0 bends. This can be the signal of a strong dependence of the velocity on the rod size. Fig. 8a shows that for larger values of βΔAgas of and βqϕ0 ≳ − 0.1, μ is sensitive to L/h0 only for L ≲ h0 whereas μ shows a plateau for L ≳ h0, in agreement with our argument based on βΔAeq. In contrast, for smaller values of βΔAgas, Fig. 8b shows that for βqϕ0 ≲ − 0.1, μ is more sensitive to L for the full range of values explored in Fig. 8b, again in agreement with our argument.
 |
| | Fig. 7 Contour lines of βΔAeq = 0 for kh0 = 0.5 (dashed lines) and kh0 = 1 (solid lines). Different colors are for diverse values of βqϕ0 = −0.6, −0.8, −1 where lighter colors stand for larger values of the absolute value of βqϕ0. | |
 |
| | Fig. 8 Absolute value of the dimensionless channel permeability, μ, to charged rods as function of the normalized length of the major axis of the rods, L/h0, for κh0 = 0.5, βΔAgas = 1.7 (panel (a)), βΔAgas = 0.6 (panel (b)), L/l = 100 and for different values of the wall potential, βqϕ0 = −0.5, −0.3, −0.1, 0, 0.1, 0.3, 0.5, that is color coded: blue (red) lines stand for negative (positive) charges and lighter colors stands for smaller magnitudes of the wall potential. The black solid line stands for z = 0. All results are for βqfL = 0.1. | |
Finally we have studied the dependence of the flux of charged rods as a function of the Debye length. Interestingly, Fig. 9 shows that the flux of negatively charged rods (hence attracted by the channel walls) has a non-monotonous dependence on the dimensionless inverse Debye length κh0 and it displays a maximum around κh0 ≲ 1 for all the geometries of the channel that we have explored. In contrast, the net flow of positively charged rods increases monotonously with the inverse Debye length κh0.
 |
| | Fig. 9 Absolute value of the dimensionless channel permeability, μ, to charged rods upon varying the inverse dimensionless Debye length, κh0, for βΔAgas = 1.7, L/l = 100 and for βqϕ0 = − 0.5 (blue lines) and βqϕ0 = 0.5 (red lines). In blue colors lighter colors stands for larger values of L/h0 = 0.3, 0.5, 1 and βqϕ0 = 0.5 in red colors lighter colors stands for larger values of L/h0 = 0.3, 0.5, 1. All results are for βqfL = 0.1. | |
IV Conclusions
We have studied the dynamics of charged rods embedded in varying-section channels. Under the assumption of slowly varying channel sections, ∂xh(x) ≪ 1 we have extended the Fick–Jacobs approximation to the case of charged rods. Our approximation allows us to derive an expression for the local diffusion coefficient,  (see eqn (18)). We have tested our prediction for the case of neutrally charged rods against experimental and numerical results (see ref. 45). Interestingly, our predictions (see Fig. 2) match well with the experimental/numerical data for both the local diffusion coefficient as well as for the mean first passage time. We remark that, while in experiments hydrodynamic coupling between the rods and the channel walls is naturally accounted for, it is not so in our model. Hence, a first result of our analysis is that, in the regime under study, hydrodynamic coupling plays a minor role in the diffusion of rods within corrugated channels.
(see eqn (18)). We have tested our prediction for the case of neutrally charged rods against experimental and numerical results (see ref. 45). Interestingly, our predictions (see Fig. 2) match well with the experimental/numerical data for both the local diffusion coefficient as well as for the mean first passage time. We remark that, while in experiments hydrodynamic coupling between the rods and the channel walls is naturally accounted for, it is not so in our model. Hence, a first result of our analysis is that, in the regime under study, hydrodynamic coupling plays a minor role in the diffusion of rods within corrugated channels.
In order to grasp the relevance of the rod geometry on the free energy barrier, ΔA, we have compared it to that of point particles, ΔAgas. Interestingly, we found that the enhancement in the free energy difference, ΔA, is at most twofold (see Fig. 4c). Next, we have characterized the channel permeability, μ, to neutral rods as a function of their length and found that for intermediate values of βΔAeq, μ displays a non-monotonous dependence (see Fig. 5) on the major axis of the rod, L, similarly to what has been observed for confined polymers.40
Finally, we have characterized the channel permeability to charged rods. In particular, we have focused on the dependence of μ on the rod size and charge. Interestingly, we found that μ displays a non-monotonous dependence on the rod charge and that the value of the charge that maximizes μ is the one for which the overall equilibrium free energy barrier, ΔAeq vanishes. Hence, our model allows us to rationalize the non-monotonous dependence of μ with respect to the charge of the rod. We have exploited this feature to identify those set of parameters for which μ is likely to be more sensitive to the length, L, of the major axis of the rods. Interestingly, this approach has revealed to be reliable in identifying those regimes for which the sensitivity of μ on L is maximized. All in all our results show that μ can be tuned by properly combining the channel geometry and the length and charge of the rod. Moreover, our model allows to rationalize the appearance of non-monotonous dependence of μ on both, the charge of the rod and its length. Our results can be useful for the design of novel micro- and nano-fluidic devices aiming at sorting stiff filaments.
Conflicts of interest
There are no conflicts to declare.
Acknowledgements
This work was supported by the Deutsche Forschungsgemeinschaft (DFG, German Research Foundation) – Project-ID 416229255 – SFB 1411. Open Access funding provided by the Max Planck Society.
References
- P. Malgaretti, G. Oshanin and J. Talbot, Special issue on transport in narrow channels, J. Phys.: Condens. Matter, 2019, 31, 270201 CrossRef CAS.
- C. Calero, J. Faraudo and M. Aguilella-Arzo, First-passage-time analysis of atomic-resolution simulations of the ionic transport in a bacterial porin, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2011, 83, 021908, DOI:10.1103/PhysRevE.83.021908.
- A. Peyser, D. Gillespie, R. Roth and W. Nonner, Domain and Interdomain Energetics Underlying Gating in Shaker-Type KV Channels, Biophys. J., 2014, 107, 1841 CrossRef CAS.
- H. Lee, D. Segets, S. Süβ, W. Peukert, S. C. Chen and D. Y. H. Pui, Liquid filtration of nanoparticles through track-etched membrane filters under unfavorable and different ionic strength conditions: Experiments and modeling, J. Membr. Sci., 2017, 524, 682 CrossRef CAS.
- D. V. Melnikov, Z. K. Hulings and M. E. Gracheva, Electro-osmotic flow through nanopores in thin and ultrathin membranes, Phys. Rev. E, 2017, 95, 063105 CrossRef.
- P. Bacchin, Membranes: A Variety of Energy Landscapes for Many Transfer Opportunities, Membranes, 2018, 8, 10 CrossRef.
- A. M. Berezhkovskii, L. Dagdug and S. M. Bezrukov, Two-site versus continuum diffusion model of blocker dynamics in a membrane channel: Comparative analysis of escape kinetics, J. Chem. Phys., 2019, 151, 054113 CrossRef.
-
B. Alberts, A. Johnson, J. Lewis, M. Raff, K. Roberts and P. Walter, Molecular Biology of the Cell, Garland Science, Oxford, 2007 Search PubMed.
- Q. Yu, K. Wang, J. Zhang, M. Liu, Y. Liu and C. Cheng, Synthesis of anisotropic silica colloids, RSC Adv., 2017, 7, 37542 RSC.
- C. Chen, L. Xie and Y. Wang, Recent advances in the synthesis and applications of anisotropic carbon and silica-based nanoparticles, Nano Res., 2019, 12, 1267 CrossRef CAS.
- L. Yang, Z. Zhou, J. Song and X. Chen, Anisotropic nanomaterials for shape-dependent physicochemical and biomedical applications, Chem. Soc. Rev., 2019, 48, 5140 RSC.
- N. Fakhri, F. C. MacKintosh, B. Lounis, L. Cognet and M. Pasquali, Brownian Motion of Stiff Filaments in a Crowded Environment, Science, 2010, 330, 1804 CrossRef CAS.
-
Nanocolloids, ed. M. S. Domínguez and C. R. Abreu, Elsevier, Amsterdam, 2016 Search PubMed.
- D. J. Bonthuis, C. Meyer, D. Stein and C. Dekker, Conformation and dynamics of DNA confined in slitlike nanofluidic channels, Phys. Rev. Lett., 2008, 101(10), 108303 CrossRef.
- T. Sakaue, Compressing a confined DNA: from nano-channel to nano-cavity, J. Phys.: Condens. Matter, 2018, 30, 244004 CrossRef.
- M. Chinappi and F. Cecconi, Protein sequencing via nanopore based devices: a nanofluidics perspective, J. Phys.: Condens. Matter, 2018, 30(20), 204002 CrossRef.
- O. A. Saleh and L. L. Sohn, Capacitance cytometry: Measuring biological cells one by one, Proc. Natl. Acad. Sci. U. S. A., 2003, 100, 820 CrossRef CAS.
- T. Ito, L. Sun, M. A. Bevan and R. M. Crooks, Comparison of nanoparticle size and electrophoretic mobility measurements using a carbon-nanotube-based Coulter counter, dynamic light scattering, transmission electron microscopy, and phase analysis light scattering, Langmuir, 2004, 20, 6940 CrossRef CAS.
- E. A. Heins, Z. S. Siwy, L. A. Baker and R. C. Martin, Detecting Single Porphyrin Molecules in a Conically Shaped Synthetic Nanopore, Nano Lett., 2005, 5, 1824 CrossRef CAS.
- N. Arjmandi, W. Van Roy, L. Lagae and G. Borghs, Measuring the electric charge and zeta potential of nanometer-sized objects using pyramidal-shaped nanopores, Anal. Chem., 2012, 84, 8490 CrossRef CAS.
- C. A. Martinez Cristancho and A. Seidel-Morgenstern, Purification of single-chain antibody fragments exploiting pH-gradients in simulated moving bed chromatography, J. Chromatogr. A, 2016, 1434, 29 CrossRef CAS.
- R. Ghosh, Protein separation using membrane chromatography: opportunities and challenges, J. Chromatogr. A, 2002, 952(1), 13 CrossRef CAS.
- S. Swernath, M. Kaspereit and A. Kienle, Coupled continuous chromatography and racemization processes for the production of pure enantiomers, Chem. Eng. Technol., 2014, 37, 643 CrossRef CAS.
- R. Zwanzig, Diffusion past an entropy barrier, J. Phys. Chem., 1992, 96, 3926 CrossRef CAS.
- D. Reguera and J. M. Rubi, Kinetic equations for diffusion in the presence of entropic barriers, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2001, 64, 061106 CrossRef CAS.
- P. Kalinay and J. K. Percus, Approximations of the generalized Fick-Jacobs equation, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2008, 78, 021103 CrossRef.
- S. Martens, G. Schmidt, L. Schimansky-Geier and P. Hänggi, Entropic particle transport: Higher-order corrections to the Fick-Jacobs diffusion equation, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2011, 94, 2492 Search PubMed.
- G. Chacón-Acosta, I. Pineda and L. Dagdug, Diffusion in narrow channels on curved manifolds, J. Chem. Phys., 2013, 139(21), 214115 CrossRef.
- P. Malgaretti, I. Pagonabarraga and J. M. Rubi, Entropic transport in confined media: a challenge for computational studies in biological and soft-matter systems, Front. Phys., 2013, 1, 21 Search PubMed.
- D. Reguera, G. Schmid, P. S. Burada, J. M. Rubi, P. Reimann and P. Hänggi, Entropic Transport: Kinetics, Scaling, and Control Mechanisms, Phys. Rev. Lett., 2006, 96, 130603 CrossRef CAS.
- D. Reguera, A. Luque, P. S. Burada, G. Schmid, J. M. Rubi and P. Hänggi, Entropic Splitter for Particle Separation, Phys. Rev. Lett., 2012, 108, 020604 CrossRef CAS.
- U. Marini Bettolo Marconi, P. Malgaretti and I. Pagonabarraga, Effective electrodiffusion equation for non-uniform nanochannels, J. Chem. Phys., 2015, 143, 184501 CrossRef.
- P. Malgaretti, I. Pagonabarraga and J. M. Rubi, Rectification and non-Gaussian diffusion in heterogeneous media, Entropy, 2016, 18, 394 CrossRef.
- A. M. Puertas, P. Malgaretti and I. Pagnabarraga, Active microrheology in corrugated channels, J. Chem. Phys., 2018, 149, 174908 CrossRef.
- P. Malgaretti, I. Pagonabarraga and J. M. Rubi, Entropic electrokinetics, Phys. Rev. Lett., 2014, 113, 128301 CrossRef.
- P. Malgaretti, I. Pagonabarraga and J. M. Rubi, Geometrically Tuned Channel Permeability, Macromol. Symp., 2015, 357, 178 CrossRef CAS.
- P. Malgaretti, I. Pagonabarraga and J. Miguel Rubi, Entropically induced asymmetric passage times of charged tracers across corrugated channels, J. Chem. Phys., 2016, 144, 034901 CrossRef.
- M. Chinappi and P. Malgaretti, Charge polarization, local electroneutrality breakdown and eddy formation due to electroosmosis in varying-section channels, Soft Matter, 2018, 14, 9083 RSC.
- P. Malgaretti, M. Janssen, I. Pagonabarraga and J. M. Rubi, Driving an electrolyte through a corrugated nanopore, J. Chem. Phys., 2019, 151, 084902 CrossRef.
- V. Bianco and P. Malgaretti, Non-monotonous polymer translocation time across corrugated channels: Comparison between Fick-Jacobs approximation and numerical simulations, J. Chem. Phys., 2016, 145, 114904 CrossRef.
- P. Malgaretti and G. Oshanin, Polymer Translocation Across a Corrugated Channel: Ficks-Jacobs Approximation Extended Beyond the Mean First-Passage Time, Polymers, 2019, 11, 251 CrossRef.
- I. V. Bodrenko, S. Salis, S. Acosta-Gutierrez and M. Ceccarelli, Diffusion of large particles through small pores: From entropic to enthalpic transport, J. Chem. Phys., 2019, 150, 211102 CrossRef.
- P. S. Burada, P. Hänggi, F. Marchesoni, G. Schmid and P. Talkner, Diffusion in Confined Geometries, ChemPhysChem, 2009, 10(1), 45–54 CrossRef CAS.
- H. Karimi, M. R. Setare and A. Moradian, Rod separation by sawtooth channel, Phys. Rev. E, 2020, 102, 012610, DOI:10.1103/PhysRevE.102.012610.
- X. Yang, Q. Zhu, C. Liu, W. Wang, Y. Li and F. Marchesoni,
et al., Diffusion of colloidal rods in corrugated channels, Phys. Rev. E, 2019, 99, 020601 CrossRef CAS.
-
J. Happel and H. Brenner, Low Reynolds number hydrodynamics, Kluwer, The Hague, 1983 Search PubMed.
Footnote |
| † Such an approximation becomes exact in the limit of vanishing charge of the rod. |
|
| This journal is © The Royal Society of Chemistry 2021 |
Click here to see how this site uses Cookies. View our privacy policy here.  Open Access Article
Open Access Article *abc and
Jens
Harting
*abc and
Jens
Harting
 cd
cd

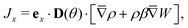




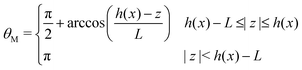



 is the diffusion coefficient along the minor axis of the rod (of size l), α encodes for the geometric correction, e⊥, and D0 is the diffusion coefficient along the major axis of the rod (of size 2L), e‖, and the off-diagonal terms are zero due to the axial symmetry of the rod.46 Since α depends on the geometry of the rod and there is no closed formula for it, in the following we assume the same value for the geometric prefactor along both axes, i.e. we assume α = 1. Integrating eqn (3) along z and θ and using eqn (10)–(12) we obtain
is the diffusion coefficient along the minor axis of the rod (of size l), α encodes for the geometric correction, e⊥, and D0 is the diffusion coefficient along the major axis of the rod (of size 2L), e‖, and the off-diagonal terms are zero due to the axial symmetry of the rod.46 Since α depends on the geometry of the rod and there is no closed formula for it, in the following we assume the same value for the geometric prefactor along both axes, i.e. we assume α = 1. Integrating eqn (3) along z and θ and using eqn (10)–(12) we obtain

![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θe‖ − sin
θe‖ − sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θe⊥ which leads to the following expression for the local diffusion coefficient,
θe⊥ which leads to the following expression for the local diffusion coefficient,

 , which is the diffusion coefficient of spherical particles of size l.24,25 Finally, integrating eqn (2) along z and θ and using eqn (15) leads to
, which is the diffusion coefficient of spherical particles of size l.24,25 Finally, integrating eqn (2) along z and θ and using eqn (15) leads to





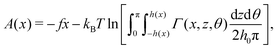



 normalized by the value at the bottleneck. In order to check the validity of the model the values of the parameters are chosen to be close to those used in Fig. 3a of ref. 45. Accordingly, we have: L0 = 12 μm, h0 = 3 μm, l = 0.15 μm and L = 1, 1.2, 1.6 μm. Lighter colors stand for larger values of L. We remark the agreement between the model and the experimental data improves upon increasing the length of the rods. (b) Mean first passage time (MFPT) with reflecting boundary conditions at the origin and absorbing at x for L = 1.04 μm, h0 = μm, h1 = μm (black), L = 1.14 μm, h0 = μm, h1 = μm (dark green), L = 1.18 μm, h0 = μm, h1 = μm (light grey). As shown in the panel, the agreement improves upon increasing the corrugation of the channel.
normalized by the value at the bottleneck. In order to check the validity of the model the values of the parameters are chosen to be close to those used in Fig. 3a of ref. 45. Accordingly, we have: L0 = 12 μm, h0 = 3 μm, l = 0.15 μm and L = 1, 1.2, 1.6 μm. Lighter colors stand for larger values of L. We remark the agreement between the model and the experimental data improves upon increasing the length of the rods. (b) Mean first passage time (MFPT) with reflecting boundary conditions at the origin and absorbing at x for L = 1.04 μm, h0 = μm, h1 = μm (black), L = 1.14 μm, h0 = μm, h1 = μm (dark green), L = 1.18 μm, h0 = μm, h1 = μm (light grey). As shown in the panel, the agreement improves upon increasing the corrugation of the channel. . In contrast, for L ≃ h0, Fig. 3 shows that increasing the corrugation of the channel increases the range of values of the rod length for which the local diffusion coefficient is sensitive to the local channel section. Clearly, if the aspect ratio L/l approaches unity the diffusion coefficient becomes homogeneous along the channel.
. In contrast, for L ≃ h0, Fig. 3 shows that increasing the corrugation of the channel increases the range of values of the rod length for which the local diffusion coefficient is sensitive to the local channel section. Clearly, if the aspect ratio L/l approaches unity the diffusion coefficient becomes homogeneous along the channel.
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln[h(x)] which eventually leads to ΔA → 2ΔAgas.
ln[h(x)] which eventually leads to ΔA → 2ΔAgas.

 . The local free energy becomes
. The local free energy becomes


 (see eqn (18)). We have tested our prediction for the case of neutrally charged rods against experimental and numerical results (see ref. 45). Interestingly, our predictions (see Fig. 2) match well with the experimental/numerical data for both the local diffusion coefficient as well as for the mean first passage time. We remark that, while in experiments hydrodynamic coupling between the rods and the channel walls is naturally accounted for, it is not so in our model. Hence, a first result of our analysis is that, in the regime under study, hydrodynamic coupling plays a minor role in the diffusion of rods within corrugated channels.
(see eqn (18)). We have tested our prediction for the case of neutrally charged rods against experimental and numerical results (see ref. 45). Interestingly, our predictions (see Fig. 2) match well with the experimental/numerical data for both the local diffusion coefficient as well as for the mean first passage time. We remark that, while in experiments hydrodynamic coupling between the rods and the channel walls is naturally accounted for, it is not so in our model. Hence, a first result of our analysis is that, in the regime under study, hydrodynamic coupling plays a minor role in the diffusion of rods within corrugated channels.







