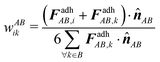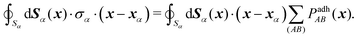Open Access Article
Open Access ArticleDistribution and propagation of mechanical stress in simulated structurally heterogeneous tissue spheroids
Maxim
Cuvelier
 *ab,
Jiří
Pešek
ac,
Ioannis
Papantoniou
bde,
Herman
Ramon
a and
Bart
Smeets
a
*ab,
Jiří
Pešek
ac,
Ioannis
Papantoniou
bde,
Herman
Ramon
a and
Bart
Smeets
a
aMeBioS, KU Leuven, Heverlee, Belgium. E-mail: Maxim.Cuvelier@kuleuven.be
bPrometheus, Division of Skeletal Tissue Engineering, KU Leuven, Leuven, Belgium
cTeam MAMBA, Inria de Paris, Paris, France
dInstitute of Chemical Engineering Sciences (ICEHT), Foundation for Research and Technology – Hellas (FORTH), Patras, Greece
eSkeletal Biology and Engineering Research Center, Department of Development and Regeneration, KU Leuven, Leuven, Belgium
First published on 18th June 2021
Abstract
The mechanical microenvironment of cells has been associated with phenotypic changes that cells undergo in three-dimensional spheroid culture formats. Radial asymmetry in mechanical stress – with compression in the core and tension at the periphery – has been analyzed by representing tissue spheroids as homogeneous visco-elastic droplets under surface tension. However, the influence of the granular microstructure of tissue spheroids in the distribution of mechanical stress in tissue spheroids has not been accounted for in a generic manner. Here, we quantify the distribution and propagation of mechanical forces in structurally heterogeneous multicellular assemblies. For this, we perform numerical simulations of a deformable cell model, which represents cells as elastic, contractile shells surrounding a liquid incompressible cytoplasm, interacting by means of non-specific adhesion. Using this model, we show how cell-scale properties such as cortical stiffness, active tension and cell–cell adhesive tension influence the distribution of mechanical stress in simulated tissue spheroids. Next, we characterize the transition at the tissue-scale from a homogeneous liquid droplet to a heterogeneous packed granular assembly.
Introduction
Spheroids – small self-assembled cell aggregates – are an often used culture format to produce micro-tissues and organoids with applications in disease modeling, drug discovery and tissue engineering. They serve as a model to study the mechanisms that govern the organization of cells into tissue, providing in vitro analogues to biological processes that occur during tissue development such as cell condensation, jamming, collective migration and sorting.1,2 Spheroid culture has been shown to alter cell fate compared to two-dimensional cell culture, due to differences in cell morphology resulting in the development of diverse mechanical microenvironments.3 As cell-generated contractile forces establish the overall mechanical state of tissue spheroids, the resulting force balance is frequently modeled based on the mechanics of a homogeneous viscous or visco-elastic droplet.4–6 This allows for a straightforward interpretation of mechanical stress, with a compressed core and a tensed periphery that provides surface tension. However, at the cellular scale, tissue structure is heterogeneous and may feature pores of varying size in a foam-like architecture.7 At high porosity, tissues more resemble a granular packing, which is mechanically characterized by a heterogeneous and anisotropic stress distribution.8,9 Experimental measurements of in situ mechanical stress in tissue spheroids have revealed the existence of large heterogeneity and radial anisotropy in mechanical stress.10–13 It is not known to what extent this heterogeneity and radial anisotropy result from different mechanical properties at the sub-cellular scale, and to what extent they can be explained from the shape and topology of the cells as they accommodate the spherical tissue geometry. Similarly, it remains to be understood how measurable mechanical properties of single cells, through the establishment of tissue microstructure, determine the appropriate parameterization of mechanical stress at the tissue scale.In this work, we quantify mechanical stress in structurally heterogeneous tissue spheroids using a computational modeling approach. Virtual tissue spheroids are generated using a Deformable Cell Model (DCM). The DCM simulates the visco-elastic deformation of the cell cortex and formulates explicit contact forces to model adhesive interactions between cells.14,15 Similar to vertex models, it is tuned using a small set of experimentally accessible mechanical parameters such as interfacial tension and active tension.16 At the same time, its contact-centered implementation allows for the simulation of loose cell packing, dynamic cell rearrangements and the open boundaries that typify early stage cell aggregates. As such, it bridges the gap between two limiting tissue descriptions: granular packing in the colloidal limit and fully confluent tissues in the adhesive limit.17 Based on DCM simulations, we quantify how the distribution and propagation of mechanical stress in various microstructural configurations relates to theoretical models of granular assemblies and homogeneous visco-elastic materials.
Methods
Mechanical model
Cells are approximated as visco-elastic and contractile shells that surround a near-incompressible cytoplasm. Mechanically, the shell represents the acto-myosin cortex, which is parameterized by its Young's modulus E, Poisson's ratio ν, thickness t, viscosity η and active tension γ.14 We assume that the force-deformation response of a single cell is dominated by the acto-myosin cortex. Cell–cell interactions are implemented by means of a fixed uniform adhesive tension ω on the surface of the shells,15 see Fig. 1. This effective adhesive tension defines the work needed to separate a pair of adhering cells and can be estimated from pull-off force experiments.18 It should be noted that ω also incorporates the reduction of active cortical tension at cell–cell contacts, and may be significantly larger than the total binding energy density of adhesion molecules shared by an adhering pair, see Appendix A.19,20Computationally, the mechanical model of a single cell is implemented as a triangulated surface mesh, representing the acto-myosin cortex. The node positions in this network represent the degrees of freedom in our system and govern how the cells deform and interact.9,14,15 The motion of these nodes is governed by a system of overdamped equations
 | (1) |
where Fel represent an in-plane cortex elasticity, cf. (8), while Fbend describe cortex bending rigidity (10), Fact originates from an active cortical tension (11), Fcyt is a cytosolic response (13) and Fadh is adhesion between multiple cells (7). Γij can similarly be deconstructed into contact friction ΓfricAB, cf. (18), cortical friction Γcij due to cortex viscosity, cf. (16), and Stokes drag Γfii representing friction of the surrounding fluid, cf. (14). Due to the non-trivial weighting of these different contributions, we refer to the Appendix A for a more in-depth description.
The generated virtual tissue spheroids are relaxed over time by solving eqn (1) for vi and integrating the nodal positions accordingly. A detailed description of the computational model, including expressions for the individual force contributions is provided in Appendix A.
Within the simulated virtual tissue spheroids, we compute three mechanical measures, each related to distinct biological mechanisms of mechanosensing:
(1) The planar stress in the cortex-membrane complex, which affects tension sensing machinery of the cell such as stretch-activated membrane channels,21 is parameterized by the in-plane net surface tension
 | (2) |
(2) The mechanical stress at cell–cell junctions, which affects various mechanosensing pathways associated to cadherin complexes,22 is parameterized by the normal contact stress σcnn,
σcnn = ![[n with combining circumflex]](https://www.rsc.org/images/entities/b_i_char_006e_0302.gif) ·σc· ·σc·![[n with combining circumflex]](https://www.rsc.org/images/entities/b_i_char_006e_0302.gif) , , | (3) |
![[n with combining circumflex]](https://www.rsc.org/images/entities/b_i_char_006e_0302.gif) is the normal direction on the cell surface.
is the normal direction on the cell surface.
(3) The average mechanical stress inside the cell, associated to nucleus mechanotransduction pathways such as YAP/TAZ, and affects mechanisms that control cell volume,23,24 is estimated by a measure of the hydrostatic stress σh (derivation provided in Appendix B),
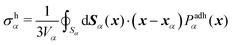 | (4) |
The computational approximation of these mechanical measures, in a virtual tissue spheroid generated using the DCM, is detailed in Appendix C.
Simulation procedure
Our simulation setups consist of a seeding, aggregation and loading phase. During seeding, stiff non-adherent beads are randomly generated in a target volume and a simulated annealing procedure25 is used to generate compact granular piles, see Fig. 1b and Appendix E. Bead sizes are polydisperse and sampled from a gamma distribution with shape parameter k ≈ 37.75 and scale parameter θ ≈ 0.24, based on experimental data from Smeets et al.9Next, beads are replaced with deformable cells with corresponding positions and radii. During aggregation simulations, cells are initially compacted until a confluent state is reached. The confining pressure is released, allowing the system to relax until a new (local) energetic minimum state is found, see Fig. 1c. Mechanical measures are extracted, before starting the loading phase.
In the final phase, spheroids are subjected to a confined indentation simulation to quantify how mechanical loads propagate through the tissue, see Fig. 1d and Appendix G. Similar to the unloaded tissues, mechanical measures are extracted once the system reaches a steady-state. For each configuration, which requires a computation time of ≃80 h we performed five independent replicates per setup and pool the data per configuration.
Results
Heterogeneity and anisotropy of mechanical stress
Simulations of spheroids were performed using the DCM to assess the spatial distribution of mechanical stress. Fig. 2 shows a comparison of simulated spheroids between reference conditions (Table 1, A), cells with decreased adhesion strength (B) and cells with decreased cortical stiffness (C). With decreased adhesion, a loose granular aggregate is observed, whereas a decrease in cortical stiffness results in compact, nearly confluent micro-tissues. In all three conditions, the mechanical measures γeff, σcnn and σh are spatially heterogeneous across the spheroids, indicating a large variance of the mechanical microenvironment between individual cells. Moreover, a distinct radial anisotropy separates the core from the periphery. The effective surface tension is highly tensile at the periphery and lower at the inner surface of the periphery (Fig. 2b). Intermediate tensions are observed at the core. Cell–cell junctions between peripheral cells are under tensile stress (Fig. 2c), while the average junction stress at the core is lower. The average intercellular stress is tensile towards the periphery of the spheroid (Fig. 2d). These conditions parallel the apico-basal asymmetry and mechanical state of a typical epithelium.26 Conversely, cells in the core are compressed and display a large variance in cortical tension and intercellular stress. Inter-cellular variation in mechanical conditions are caused by the granular nature of the spheroid, whereas further inter-cellular variation results from microscopic pores near triple junctions, which demonstrate elevated levels of tensile stress.| Parameter | Symbol | Case A | Case B | Case C | Units | Source |
|---|---|---|---|---|---|---|
| Mean cell radius | R cell | 9.0 | μm | 9 | ||
| Effective cortical thickness | t | 200 | nm | 15, 27 and 28 | ||
| Cortical stiffness | E | 20 | 5 | 0.3125 | kPa | 15 and 27 |
| Poisson's ratio cortex | ν | 1/3 | — | 29 | ||
| Cortical tension | γ | 0.5 | nN μm−1 | 15, 27, 30 and 31 | ||
| Adhesive tension | ω | 0.5 | 0.125 | 0.5 | nN μm−1 | 19 |
| Cell count | N | 150 | — |
To put these results in context of experimental findings, we first compare the distribution of σcnn on the surface of individual cells to experimental measurements of cell-generated stress using in situ pressure probes. In growing undifferentiated melanoma tumor-repopulating cell colonies, Mohagheghain et al. observe a heterogeneous distribution of normal and shear stresses in the range of −358 Pa and 49 Pa respectively.32 For reference case A, we obtain comparable values (Fig. 3b and c). Unlike on our ‘virtual cells’, Fig. 3a, Mohagheghain et al. did not observe any tensile stress on their pressure probes, possibly due to the use of encapsulating hydrogels that favor a global compressed state in the spheroid, or due to the reduced adhesive tension in passive pressure probes. Still, our simulations indicate that the existence of a radial gradient combined with the granular micro-architecture inside of the spheroid are sufficient to explain the overall observed heterogeneity of mechanical stress. For comparison to the work of Campàs et al., we compute the “maximum anisotropic stress”, defining it as the difference between 95th and 5th percentile of σcnn per cell.10 We find values in the measured range between 1.5 kPa and 3.6 kPa, see Fig. 3d. Changing mechanical properties (A, B, C) has a strong influence on the estimated maximum anisotropic stress, which is in line with the observations when changing the cell type. In a follow-up study, Lucio et al. computed the “Mean anisotropic stress” as the standard deviation of the stress distribution per cell.12 In contrast to our observations when computing this measure, Fig. 3e, they found no significant radial asymmetry. However, in our simulations, the mean anisotropic stress is only elevated in the outer cell layer, whereas no pressure sensors where observed in the outer cell layers in the study of Lucio et al.
 | ||
Fig. 3 Comparison to experimental data (a) visualization of normal stress σcnn = ![[n with combining circumflex]](https://www.rsc.org/images/entities/b_i_char_006e_0302.gif) ·σc· ·σc·![[n with combining circumflex]](https://www.rsc.org/images/entities/b_i_char_006e_0302.gif) on a simulated cell inside of the virtual tissue. (b) Radial distribution of mean shear stress |σc· on a simulated cell inside of the virtual tissue. (b) Radial distribution of mean shear stress |σc·![[n with combining circumflex]](https://www.rsc.org/images/entities/b_i_char_006e_0302.gif) − ( − (![[n with combining circumflex]](https://www.rsc.org/images/entities/b_i_char_006e_0302.gif) ·σc· ·σc·![[n with combining circumflex]](https://www.rsc.org/images/entities/b_i_char_006e_0302.gif) ) )![[n with combining circumflex]](https://www.rsc.org/images/entities/b_i_char_006e_0302.gif) | per cell. (c) Radial distribution of the mean normal stress σcnn per cell. (d) Radial distribution of maximal anisotropic stress, calculated as the difference between the 95th and 5th percentile of σcnn acting on an individual cell. Experimentally measured limits of 1.5 kPa and 3.6 kPa are represented by the grey dotted lines.10 (e) Radial profile of the mean anisotropic stress std(p(σcnn)) acting on an individual cell. Experimentally measured limits of 200 Pa and 350 Pa are represented by the grey dotted lines.12 | per cell. (c) Radial distribution of the mean normal stress σcnn per cell. (d) Radial distribution of maximal anisotropic stress, calculated as the difference between the 95th and 5th percentile of σcnn acting on an individual cell. Experimentally measured limits of 1.5 kPa and 3.6 kPa are represented by the grey dotted lines.10 (e) Radial profile of the mean anisotropic stress std(p(σcnn)) acting on an individual cell. Experimentally measured limits of 200 Pa and 350 Pa are represented by the grey dotted lines.12 | ||
Applicability of liquid droplet force balance
The observed radial dependency of the mean normal stress (Fig. 3c) hints at the existence of a non-uniform bulk tissue pressure, which is measured by the hydrostatic pressure σh. In analogy to liquid droplets, the Young–Laplace equation is commonly used to describe the relation between tissue surface tension and the pressure drop across its interface.33 Given our observations, the apparent surface tension of the tissue is established by the adhesive tension ω, similar to the cohesion energy between the constituent elements of an isotropic material, see Appendix F.34,35 Hence, given the minimal confluent spheroid radius , the theoretical pressure drop over the interface is
, the theoretical pressure drop over the interface is| σhth = 2ω/Raggrth. | (5) |
Fig. 4 shows how the local hydrostatic stress σhα in simulations compares to σhth for varying cell mechanical properties. Fixing Et/ω = 1/8 and decreasing/results in spheroids with an increasingly tensile periphery, and a compressed core in which σhα converges to σhth (Fig. 4a). The same trend can be observed when fixing γ/ω = 1/2 while decreasing Et/ω. However, at high γ/ω, the simulated spheroids fail to establish a periphery that is sufficiently well connected to generate a net surface tension and the clear distinction between cells in the core and at the periphery breaks down (Fig. 4b).
To determine how the relative size of tensile and compressed regions changes with spheroid size, we performed simulations with varying cell counts, Fig. 4c. These demonstrate that the thickness of the tensile periphery does not scale with the total spheroid size, but remains constant and roughly corresponds to one cell diameter. Similarly, the peak in tensile stress occurs at a distance of one cell radius from the outer surface. This observation is consistent with the liquid droplet model, in which a microscopically thin tensile layer envelops a continuous isotropic compressed core. A notable discrepancy with liquid theory is that the magnitude of hydrostatic stress decreases towards the spheroid center. We propose that this behavior can be attributed to mechanical shielding effects, as the granular architecture of the spheroids allows for the formation of force bridges that shield underlying cells from compressive loads. Indeed, as the spheroid structure becomes confluent with increasing adhesion, this effect disappears and a clear plateau in σh is observed, Fig. 4b.
To quantify the accordance to liquid theory, we calculate the mean hydrostatic stress 〈σh〉 for all cells with a radial position r < Raggrth − 2Rcell. From this, we define the relative error εYL = 1 − 〈σh〉/σhth as a measure for the applicability of the Young–Laplace law. Fig. 4d shows that for sufficiently large values of cell–cell adhesion, the Young–Laplace law provides a good approximation of the global mechanical balance in the spheroid.
Distribution and propagation of external forces
Tissues are frequently subjected to external loads which alter the self-established microenvironment of constituent cells. We investigated the distribution of mechanical forces in a simulated mechanical loading experiment. For this, simulated spheroids were confined by a convex hull before being subjected to a load of 15 nN, applied by a spherical probe with radius 3Rcell, see Appendix G. Cell–cell connectivity and the distribution of normalized cell–cell contact normal forces f = −Fc/〈F6c〉 were extracted, with 〈Fc〉 as the mean magnitude of contact normal forces in the system. Fig. 5a visualizes the contact force distribution throughout the tissue, using a network representation of the tissue with cells as nodes and cell–cell contacts as edges. Tissues consisting of soft adhesive cells (Fig. 5a left) exhibit a higher connectivity than tissues consisting of stiff non-adherent cells (Fig. 5a right). This difference in connectivity is reflected in the mean coordination number Z, see Fig. 5b. In granular piles, a value of Z close to the critical coordination number Zc is linked to the presence of force chains in the system.† These pronounced force chains are responsible for the highly anisotropic propagation of loads. Given the accordance to granular theory, as Z increases, loads are distributed increasingly even as the network connectivity improves.8 Apart from tissue connectivity we also analyzed the scaling of the probability density function of contact forces P(f) between different configurations, see Fig. 5c. In the limit of granular particles, an exponential decay is expected, where high contact forces are increasingly rare P(f) ∝ exp(−f). As the spheroids become progressively compressible, the expected scaling approaches the normal distribution P(f) ∝ exp(−f2) as forces are more evenly distributed in the network.8 In order to locate the simulated spheroids in this range, we fit P(f) ∝ exp(−fβ), estimating β by using an unconstrained curve fitting procedure, see Fig. 5d. We observe a transition from β ≈ 2 to β ≈ 1 as adhesion decreased or as cortical stiffness increased.Discussion
In this work, we presented a mechanical model of multi-cellular tissue spheroids that takes into account the microscopic structure of the cellular material. The distribution and propagation of mechanical forces inside virtual tissue spheroids were quantified and compared to experimental measurements and theoretical limits. For a reference configuration based on typical cell-like mechanical properties, we obtain similar estimates for the magnitude and heterogeneity of shear and normal stress measures as experimentally measured.10,12,32Simulations revealed an inherent core-periphery asymmetry established by the force-balance at the tissue boundary. We demonstrated that in the limit of soft and adhesive cells, this asymmetry can be well approximated using the model of a liquid droplet, which balances the tissue's internal pressure with surface tension at the periphery. The asymmetry between cells in the core and at the periphery is reflected in the properties of the mechanical microenvironment, and is established even in absence of mechanical heterogeneity in the underlying cell population. This is of importance in the context of micro-tissues, since no prior biochemical gradient is required to establish this asymmetry. At the same time, cells experience different mechanical conditions depending on their location in the spheroid: cells at the periphery are under pronounced lateral tension that is reminiscent of the mechanical state of an epithelium, whereas cells at the core are generally under compression, of which the magnitude and heterogeneity depend on cell mechanical properties. Eventually, mechanotransduction pathways may consolidate these differences in discrepancies in cell fate.36 For example, we observed that for larger spheroids, the relative size of the peripheral region decreases, and shielding effects may decrease compression at the core. Hence, it could be expected that the altered distribution of mechanical states results in a different composition of cell types, even in absence of mass transport effects.37,38 Recent experiments support this notion.39 However, given the limitations of our model and current experimental techniques, more data is still needed to validate this claim.
Finally, we showed that two regimes of force distribution occur, depending on the loading conditions and cell mechanical properties: stiff granular spheroids exhibit force bridges and highly heterogeneous force distributions, whereas soft, adhesive and confluent tissues behave like a compressible granular material with a normal distribution of internal mechanical forces. In the stiff granular regime, the heterogeneity in the mechanical microenvironment may be very large, even for adjacent cells. As such, in absence of other control mechanisms, mechanotransduction processes could amplify heterogeneity in cell fate for spheroids in these configurations. Loaded conditions on small multicellular assemblies are common in many biological applications, for example in growing spheroids encapsulated in elastic materials.40,41 Hence, it may be opportune to identify the loading regime, which is reflected in the microscopic architecture of the cellular packing through the cell–cell connectivity number.
This work approximated cellular properties based on a mechanical description that focuses on the cell cortex. Comparing to realistic cells, this approach has some evident limitations, the implication of which will be discussed here. First of all, we assumed cellular properties to be static over time, whereas in reality, many cellular properties are dynamic, responsive, and often timescale dependent.33 Moreover, by not including active motility, simulated cells are effectively frozen in a jammed state. These limitations prevent us from analyzing tissue rheology and dynamics. Still, in many biological systems, both in vivo and in vitro, cells are not very motile, and remain in a jammed configuration.42 Secondly, our model considers mechanical properties to be uniform across the cell. For example, we assumed constant non-specific adhesive tension. In reality, adhesive ligands tend to be strongly clustered near the edges of cell–cell contacts, a phenomenon that could alter the distribution of inter-cellular stress.43 However, the modeled ‘adhesive tension’, expressed in the force balance at an intercellular junction, stems from the combination of adhesion energy and differential interfacial tension, see Appendix A. The latter originates from a decrease of acto-myosin contractility near cell–cell interfaces and has been shown to dominate the energy contribution in the net adhesive tension.19,20,44
Finally, our model does not take into account the presence of extracellular matrix, which is expected to contribute heavily to force transmission and distribution. This limits the applicability of the model predictions to immature artificial spheroids and early developmental structures, where the pericellular matrix is absent or sufficiently thin to justify its exclusion.45 Future developments that take into account the contribution of the aforementioned phenomena in a similar modeling strategy will allow the quantification of mechanical effects due to tissue dynamics, and of changes in the mechanical microenvironment during tissue maturation.
Author contributions
M. C., H. R. and B. S. conceived the project. M. C. and B. S. designed and conducted the simulations, M. C., J. P. and B. S. performed data analysis. M. C., J. P., I. P. and B. S. wrote the manuscript. All authors commented on the manuscript.Conflicts of interest
There are no conflicts to declare.Appendix A: deformable cell model
The acto-myosin cortex of a cell is represented by a visco-elastic shell. We approximate this shell by a triangulated surface mesh with effective thickness t, and nodal positions xi as the relevant degrees of freedom. First, contact mechanics are briefly summarized, after which implementation of the visco-elastic cortical shell model is discussed.Contact mechanics
In the mechanical cell model, we assume a fixed and uniform adhesive tension ω across the cell surface. The adhesive tension incorporates cell–cell adhesive interactions as well as the effect of cortical tension reduction at the cell–cell interface: ωA = ωint + γ − γi, where ωint[J m−2] represents the adhesive energy density due to adhesion molecule interactions and depletion forces at the interface, γ [N m−1] is the cortical tension or equivalently the cell-medium interfacial tension and γi [N m−1] is the cell–cell interfacial tension.19,20,40 The total adhesive tension ω acting on interface (AB) is given by ω = ωA + ωB.A linear force, scaling with contact overlap δ, was introduced to represent repulsive interactions between surfaces and ensure stable contacts. The contact potential for contact-pair (AB) with contact area SAB is then given by
The resulting contact pressure PadhAB is estimated with a linear contact pressure model where no energy is stored in deformation at equilibrium
| PadhAB(x) = kABδAB(x) − P0AB, |
δAB(x) = max{0; 2(x − sAB)·(![[n with combining circumflex]](https://www.rsc.org/images/entities/b_i_char_006e_0302.gif) AB × ÎAB)tan AB × ÎAB)tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ}, θ}, |
![[n with combining circumflex]](https://www.rsc.org/images/entities/b_i_char_006e_0302.gif) AB ∝ (
AB ∝ (![[n with combining circumflex]](https://www.rsc.org/images/entities/b_i_char_006e_0302.gif) B −
B − ![[n with combining circumflex]](https://www.rsc.org/images/entities/b_i_char_006e_0302.gif) A) × ÎAB the contact normal and sAB is an arbitrary point on the intersection line defined by ÎAB ∝
A) × ÎAB the contact normal and sAB is an arbitrary point on the intersection line defined by ÎAB ∝ ![[n with combining circumflex]](https://www.rsc.org/images/entities/b_i_char_006e_0302.gif) A ×
A × ![[n with combining circumflex]](https://www.rsc.org/images/entities/b_i_char_006e_0302.gif) B, as reported by Smeets et al.,47 see also Fig. 6. The resulting contact forces and moment are obtained by integrating the total contact pressure over the oriented contact area SAB,
B, as reported by Smeets et al.,47 see also Fig. 6. The resulting contact forces and moment are obtained by integrating the total contact pressure over the oriented contact area SAB, | (6) |
To distribute the contact forces acting on the contact plains to the nodal contact forces FadhAB,i, it is assumed that the nodal forces are collinear with the contact normal ![[n with combining circumflex]](https://www.rsc.org/images/entities/b_i_char_006e_0302.gif) AB. This results in a system of linear equations per contact pair (AB)
AB. This results in a system of linear equations per contact pair (AB)
 | (7) |
Cortex elasticity
Passive mechanical properties dominate cortex behavior at short time-scales (<5 min). As cortex deformation is assumed to be small, a linear elastic model is used to capture in-plane stretching and compression energy. For nodes (ij) this giveswhere dij = ‖xj − xi‖ and
 represent the current and equilibrium distance between nodes i and j with positions xi and xj respectively. The linear spring force between the connected nodes is then given by
represent the current and equilibrium distance between nodes i and j with positions xi and xj respectively. The linear spring force between the connected nodes is then given by | (8) |
The linear spring stiffness kel, under our assumption of an isotropic linear elastic material model, can be approximated by using Van Gelder's formula:
in which (SA,ij + SB,ij) is the area of the connected triangle pair (AB) associated with spring (ij) ∈ A ∩ B.49E and t are cortex specific parameters, representing the Young's modulus and effective thickness of the cortex.
Due to its non-zero thickness, the cortex also has bending rigidity. The energy required to bend connected triangles (AB) is given by
 | (9) |
 represent the instantaneous and spontaneous angles between a pair of adjacent triangles (AB). Derived from the macroscopic (continuum) flexural rigidity of a sheet, we estimate
represent the instantaneous and spontaneous angles between a pair of adjacent triangles (AB). Derived from the macroscopic (continuum) flexural rigidity of a sheet, we estimatewith ν as the Poisson ratio of the cortex. To be consistent with the assumption of an isotropic linear elastic material, ν is fixed at a value of 1/3.29 The bending force
 | (10) |
Active cellular properties
Tension generated in the cortex results from acto-myosin contractility which we represent as an effective surface tension γ in the cortical shell model. Using the derivation of Fedosov et al.,51 the direct force contribution of surface tension γ is given by | (11) |
Since the cytoplasm is assumed to be incompressible, active volume control is implemented via a cytoplasmic pressure. We assume the equilibrium volume  of a cell α is constant at short timescales and implemented a proportional–integral–derivative (PID) pressure controller to enforce this. The cytoplasmic pressure Pcytα(t) due to the volume controller is then estimated as
of a cell α is constant at short timescales and implemented a proportional–integral–derivative (PID) pressure controller to enforce this. The cytoplasmic pressure Pcytα(t) due to the volume controller is then estimated as
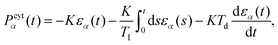 | (12) |
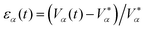 . TI and Td are typically chosen as one order of magnitude larger than the time-resolution with which the system is updated. In the main text Fig. 1 we used K′ to represent the effective bulk modulus of a cell, lumping the different contributions of eqn (12) into a single parameter.
. TI and Td are typically chosen as one order of magnitude larger than the time-resolution with which the system is updated. In the main text Fig. 1 we used K′ to represent the effective bulk modulus of a cell, lumping the different contributions of eqn (12) into a single parameter.
The total pressure acting on a node
| Fcyti(t) = SiPi(t). | (13) |
Dissipative forces
Apart from conservative forces, dissipative forces are considered as well. A general drag force| Fdragi = −Γfii·vi, |
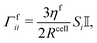 | (14) |
A much larger contribution to energy dissipation arises from cortex viscosity. The viscous damping force between two connected nodes is given by
| Fviscij = Γcij·(vj − vi) | (15) |
 | (16) |
 is the second-order identity tensor. This cortical damper works in parallel with the cortical springs defined in eqn (8).
is the second-order identity tensor. This cortical damper works in parallel with the cortical springs defined in eqn (8).
Finally a viscous contact force is included to account for drag between contacting triangles. The contact drag force acting on node i of triangle A of the contact pair (AB)
 | (17) |
is used as an approximation. ΓfricAB for a given contact area SAB is estimated as
with normal and tangential friction coefficients γ⊥ and γ‖ respectively.
Note that (17) can be equivalently formulated as
| ΓfricAB,ik = wABikΓfricAB. | (18) |
Equation of motion
In the overdamped cellular environment, inertial forces may be neglected.53 Based on the different contributions described above, the force balance for node i giveswhich can be abbreviated as
for a system consisting of N nodes, where
The Cartesian components of the overall force vectors can be represented as a single (3N × 1) column matrix, while the friction matrices can be assembled to a single (3N × 3N) sparse symmetric positive definite friction matrix.14,54 The conjugate gradient method is then used to efficiently solve the system for {vj} at each iteration. Positions of the nodes are subsequently updated using a forward Euler integration scheme.
We estimated  as the characteristic timescale and used it to determine simulation time-step δt = ζ/N. In order to minimize computational time without sacrificing accuracy, a small study was performed with varying N. Based on the convergence of output measures, N = 25 was chosen.
as the characteristic timescale and used it to determine simulation time-step δt = ζ/N. In order to minimize computational time without sacrificing accuracy, a small study was performed with varying N. Based on the convergence of output measures, N = 25 was chosen.
A full simulation procedure took on average 60–80 h for a single setup, this was however heavily influenced by tissues size and tissue connectivity.
Appendix B: tissue stress estimation
In order to estimate the macroscopic stress induced inside the tissue during compression, we need to find a suitable continuous representation of our discrete system. The typical approach how to describe a stress distribution in a continuous mechanics is to distribution of forces on a suitable elementary volume. On the tissue scale, a single cell is a natural choice for such an elementary volume.We further assume that the Cauchy stress theorem is still valid for a macroscopic stress. Namely, we assume that the external force applied on a surface S of the cell α can be fully characterized by cellular macroscopic stress σα,
 | (19) |
 ,
, | (20) |
The macroscopic stress σα on the cell α is then a suitable candidate simultaneously fulfilling set of eqn (19) and (20). An obvious choice is the normal contact pressure
A suitable candidate for an error function, inspired by the functional form of the virial stress, is
Note, that unlike in the naive approach where contact pressures were weighted by the contact area, in this approach they are weighted by (triple) the volume of the conical section from the center of the cell to the contact area.
Assuming the macroscopic stress tensor is symmetric, σα = σTα, and contact pressure on the cell surface  the equation can be further simplified to
the equation can be further simplified to
which leads to constraint
 | (21) |
Appendix C: mechanical measures
To obtain the reported mechanical measures, we perform five independent repeats for each experimental condition. A statistical ensemble is generated by pooling the end states of these repeats. This ensemble is then used to determine the mean value and variances. To generate radial profiles, spatially distributed quantities were binned based on their relative position vector.(1) For each node i of the triangulated representation of the cell, connected to NΔt triangles, the in-plane cortex tension eqn (2) is estimated as
![[n with combining circumflex]](https://www.rsc.org/images/entities/b_i_char_006e_0302.gif) ij/dij, cf. (8), from all connected nodes j.14
ij/dij, cf. (8), from all connected nodes j.14
(2) The contact stress, eqn (3), is estimated for each triangle A by summing the contact forces FadhAB for all contact pairs (AB), cf.(6),
![[n with combining circumflex]](https://www.rsc.org/images/entities/b_i_char_006e_0302.gif) A and SA are the normal unit vector and area of triangle A. The total contact force magnitude acting on the interface of cell pair (αβ) is then estimated as
A and SA are the normal unit vector and area of triangle A. The total contact force magnitude acting on the interface of cell pair (αβ) is then estimated asprojecting all forces at the interface of cells α and β to the direction
![[n with combining circumflex]](https://www.rsc.org/images/entities/b_i_char_006e_0302.gif) αβ ∝ xα − xβ.
αβ ∝ xα − xβ.
(3) We estimate the hydrostatic stress expressed in eqn (4) (derivation provided in Appendix B) as
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 probes were used to estimate the σh for a given location, interpolating between the values of the cellular nearest neighbors. This was done independently for the 5 replicas per setup. The results were binned based on the radial position inside of the tissue spheroid to generate the radial profiles reported in the main text.
000 probes were used to estimate the σh for a given location, interpolating between the values of the cellular nearest neighbors. This was done independently for the 5 replicas per setup. The results were binned based on the radial position inside of the tissue spheroid to generate the radial profiles reported in the main text.
Appendix D: list of model parameters
Appendix E: simulated annealing
Simulated annealing-based approaches have been used to optimize 3D packing in general components layout problems. During the seeding phase, a simulated annealing procedure was used to generate compact granular piles. These piles were then used to initialize the aggregation simulations.Our simulated annealing procedures are initialized by randomly seeding beads in the selected geometry with a density slightly lower than the close-packing density. Due to the distribution of cell radii and random placement, overlapping beads will be present. A linear repulsive force model was used to describe bead-bead contacts, minimizing bead overlaps. Random forces were introduced to agitate the beads, unjamming the system. The annealing procedure is achieved by an exponential decay of the mean magnitude of the random (Gaussian) force, while at the same time the stiffness of the repulsive potential is linearly increased. This means that the system effectively cools down to a (global) potential minimum, with a reduced chance of getting caught in local minima caused by bead jamming.
Appendix F: the adhesive limit
In the soft adhesive limit, adhesive forces balanced by volume conservation forces dominate the system. In the bulk of the tissue, symmetry conditions (cell–cell contact in all directions) assure that the mean total adhesive force acting on a cell has no net direction. At the periphery, a net inward facing force (pointing towards the core of the aggregate) emerges as the adhesive forces over the cell surface are not symmetric at the tissue boundary. This is very analogous to how the surface tension of an isotropic material results from an imbalance of cohesive forces between the molecules. With this analogy, it can be seen that the cell–cell property (adhesive tension) emerges as a tissue-scale property (effective surface tension of the tissue) in this soft adhesive limit.As σh represents the bulk tissue pressure, the relation between σh and adhesive tension ω is then the result of the geometrical boundary conditions: mean tissue curvature 2/Raggrth. This relation is described by the young-Laplace law σhth = 2ω/Raggrth.
However, and importantly, this only holds for very specific cases, where no external loads are applied on the tissue and when cell mechanical properties are within the adhesive limit, where the confluent tissue behaves as an isotropic material.
To investigate how σh converged to σhth, a full parameter sweep was performed, see Fig. 7. As the trend scaled smoothly, a subset of the data was used in the main text as to not over-saturate the graph, see Fig. 4a and b.
Appendix G: indentation simulations
To mechanically probe the spheroids generated in the aggregation phase, indentation simulations were performed. In our work we opted to perform confined indentation experiments where a convex hull was fitted around the samples before being probed. The contact stiffness of these hulls should be sufficiently high to confine the samples during compression, while not being to high as too introduce numerical artifacts. As a probe we used a stiff bead with radius Rbead = 3Rcell. A Hertzian contact model with slip boundary conditions was used to model both cell-hull and cell probe interactions.Using a force based controller, we indented the samples with a force of 15 nN, generating a force–displacement curve as the simulation progressed. Once the probe reached a stable position, cell–cell contact forces were extracted for further analysis, see main text.
Acknowledgements
This work is part of Prometheus, the KU Leuven R&D Division for Skeletal Tissue Engineering. M. C. acknowledges support form the Research Foundation Flanders (FWO), grant 1S46817N. B. S. acknowledges support from the Research Foundation Flanders (FWO) grant 12Z6118N, and KU Leuven internal funding C14/18/055.Notes and references
- F. Hirschhaeuser, H. Menne, C. Dittfeld, J. West, W. Mueller-Klieser and L. A. Kunz-Schughart, J. Biotechnol., 2010, 148, 3–15 Search PubMed.
- E.-M. Schoetz, M. Lanio, J. A. Talbot and M. L. Manning, J. R. Soc., Interface, 2013, 10, 20130726 Search PubMed.
- K. Duval, H. Grover, L.-H. Han, Y. Mou, A. F. Pegoraro, J. Fredberg and Z. Chen, Physiology, 2017, 32, 266–277 Search PubMed.
- K. Guevorkian, M.-J. Colbert, M. Durth, S. Dufour and F. Brochard-Wyart, Phys. Rev. Lett., 2010, 104, 218101 Search PubMed.
- D. Jaiswal, N. Cowley, Z. Bian, G. Zheng, K. P. Claffey and K. Hoshino, PLoS One, 2017, 12, e0188346 Search PubMed.
- S. Ehrig, B. Schamberger, C. M. Bidan, A. West, C. Jacobi, K. Lam, P. Kollmannsberger, A. Petersen, P. Tomancak and K. Kommareddy, et al. , Sci. Adv., 2019, 5, eaav9394 Search PubMed.
- S. Kim, M. Pochitaloff, G. Stooke-Vaughan and O. Campas, Nat. Phys., 2021, 1–8, DOI:10.1038/s41567-021-01215-1.
- D. M. Mueth, H. M. Jaeger and S. R. Nagel, Phys. Rev. E: Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top., 1998, 57, 3164 Search PubMed.
- B. Smeets, J. Pešek, T. Deckers, G. N. Hall, M. Cuvelier, S. Ongenae, V. Bloemen, F. P. Luyten, I. Papantoniou and H. Ramon, Matter, 2020, 1283–1295 Search PubMed.
- O. Campàs, T. Mammoto, S. Hasso, R. A. Sperling, D. O'connell, A. G. Bischof, R. Maas, D. A. Weitz, L. Mahadevan and D. E. Ingber, Nat. Methods, 2014, 11, 183 Search PubMed.
- M. Dolega, M. Delarue, F. Ingremeau, J. Prost, A. Delon and G. Cappello, Nat. Commun., 2017, 8, 14056 Search PubMed.
- A. A. Lucio, A. Mongera, E. Shelton, R. Chen, A. M. Doyle and O. Campàs, Sci. Rep., 2017, 7, 12022 Search PubMed.
- W. Lee, N. Kalashnikov, S. Mok, R. Halaoui, E. Kuzmin, A. J. Putnam, S. Takayama, M. Park, L. McCaffrey and R. Zhao, et al. , Nat. Commun., 2019, 10, 144 Search PubMed.
- T. Odenthal, B. Smeets, P. Van Liedekerke, E. Tijskens, H. Van Oosterwyck and H. Ramon, PLoS Comput. Biol., 2013, 9, e1003267 Search PubMed.
- B. Smeets, M. Cuvelier, J. Pešek and H. Ramon, Biophys. J., 2019, 116, 930–937 Search PubMed.
- S. Alt, P. Ganguly and G. Salbreux, Philos. Trans. R. Soc., B, 2017, 372, 20150520 Search PubMed.
- P. Van Liedekerke, J. Neitsch, T. Johann, E. Warmt, I. G. Valverde, S. Grosser, S. Hoehme, J. Kaes and D. Drasdo, bioRxiv, 2019 DOI:10.1101/470559.
- Y.-S. Chu, S. Dufour, J. P. Thiery, E. Perez and F. Pincet, Phys. Rev. Lett., 2005, 94, 028102 Search PubMed.
- J.-L. Matre, H. Berthoumieux, S. F. G. Krens, G. Salbreux, F. Jülicher, E. Paluch and C.-P. Heisenberg, Science, 2012, 338, 253–256 Search PubMed.
- H. Turlier and J.-L. Maître, Semin. Cell Dev. Biol., 2015, 47-48, 110–117 Search PubMed.
- J. B. Lansman, T. J. Hallam and T. J. Rink, Nature, 1987, 325, 811–813 Search PubMed.
- D. E. Leckband and J. De Rooij, Annu. Rev. Cell Dev. Biol., 2014, 30, 291–315 Search PubMed.
- J. Gao, L. He, Y. Shi, M. Cai, H. Xu, J. Jiang, L. Zhang and H. Wang, Nanoscale, 2017, 9, 16993–17003 Search PubMed.
- D.-H. Kim, B. Li, F. Si, J. M. Phillip, D. Wirtz and S. X. Sun, J. Cell Sci., 2015, 128, 3375–3385 Search PubMed.
- J. Pannetier, J. Bassas-Alsina, J. Rodriguez-Carvajal and V. Caignaert, Nature, 1990, 346, 343 Search PubMed.
- L. Sui, S. Alt, M. Weigert, N. Dye, S. Eaton, F. Jug, E. W. Myers, F. Jülicher, G. Salbreux and C. Dahmann, Nat. Commun., 2018, 9, 1–13 Search PubMed.
- A. X. Cartagena-Rivera, J. S. Logue, C. M. Waterman and R. S. Chadwick, Biophys. J., 2016, 110, 2528–2539 Search PubMed.
- A. G. Clark, K. Dierkes and E. K. Paluch, Biophys. J., 2013, 105, 570–580 Search PubMed.
- M. Kot, H. Nagahashi and P. Szymczak, Vis. Comput., 2015, 31, 1339–1350 Search PubMed.
- J.-Y. Tinevez, U. Schulze, G. Salbreux, J. Roensch, J.-F. Joanny and E. Paluch, Proc. Natl. Acad. Sci. U. S. A., 2009, 106, 18581–18586 Search PubMed.
- M. Krieg, Y. Arboleda-Estudillo, P.-H. Puech, J. Käfer, F. Graner, D. Müller and C.-P. Heisenberg, Nat. Cell Biol., 2008, 10, 429 Search PubMed.
- E. Mohagheghian, J. Luo, J. Chen, G. Chaudhary, J. Chen, J. Sun, R. H. Ewoldt and N. Wang, Nat. Commun., 2018, 9, 1–14 Search PubMed.
- K. Guevorkian, M.-J. Colbert, M. Durth, S. Dufour and F. Brochard-Wyart, Phys. Rev. Lett., 2010, 104, 218101 Search PubMed.
- R. Winklbauer, J. Cell Sci., 2015, 128, 3687–3693 Search PubMed.
- R. Shuttleworth, Proc. Phys. Soc., London, Sect. A, 1950, 63, 444 Search PubMed.
- M. A. Wozniak and C. S. Chen, Nat. Rev. Mol. Cell Biol., 2009, 10, 34–43 Search PubMed.
- J. J. Northey, L. Przybyla and V. M. Weaver, Cancer Discovery, 2017, 7, 1224–1237 Search PubMed.
- G. Cheng, J. Tse, R. K. Jain and L. L. Munn, PLoS One, 2009, 4, e4632 Search PubMed.
- I. C. Berg, E. Mohagheghian, K. Habing, N. Wang and G. H. Underhill, bioRxiv, 2021 DOI:10.1101/2020.10.28.355875.
- C.-P. Heisenberg and Y. Bellache, Cell, 2013, 153, 948–962 Search PubMed.
- T. Lecuit, P.-F. Lenne and E. Munro, Annu. Rev. Cell Dev. Biol., 2011, 27, 157–184 Search PubMed.
- M. Sadati, N. T. Qazvini, R. Krishnan, C. Y. Park and J. J. Fredberg, Differentiation, 2013, 86, 121–125 Search PubMed.
- R. Changede and M. Sheetz, BioEssays, 2017, 39, 1–12 Search PubMed.
- P.-F. Lenne, J.-F. Rupprecht and V. Viasnoff, Dev. Cell, 2021, 56, 202–212 Search PubMed.
- R. Winklbauer, J. Cell Sci., 2019, 132, jcs231597 Search PubMed.
- J. N. Israelachvili, Intermolecular and surface forces, Academic Press, 2011 Search PubMed.
- B. Smeets, T. Odenthal, S. Vanmaercke and H. Ramon, Comput. Methods Appl. Mech. Eng., 2015, 290, 277–289 Search PubMed.
- L. Zhang, T. Cui and H. Liu, J. Comput. Math., 2009, 27, 89–96 Search PubMed.
- A. V. Gelder, J. Graph. Tools, 1998, 3, 21–41 Search PubMed.
- D. Fedosov, B. Caswell and G. Karniadakis, Comput. Methods Appl. Mech. Eng., 2010, 199, 1937–1948 Search PubMed.
- D. Fedosov, PhD thesis, Brown University, 2010.
- P. Van Liedekerke, B. Smeets, T. Odenthal, E. Tijskens and H. Ramon, Comput. Phys. Commun., 2013, 184, 1686–1696 Search PubMed.
- E. M. Purcell, Am. J. Phys., 1977, 45, 3–11 Search PubMed.
- P. Van Liedekerke, M. M. Palm, N. Jagiella and D. Drasdo, Comput. Part. Mech., 2015, 2, 401–444 Search PubMed.
Footnote |
| † The specific value of Zc is determined by the dimensionality of the system and the relative contribution of contact friction; for our setups we estimated Zc ≈ 6, given the low contact friction in the simulated setups. |
| This journal is © The Royal Society of Chemistry 2021 |






![[small beta, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e114.gif)