Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Spatial inhomogeneity, interfaces and complex vitrification kinetics in a network forming nanocomposite†
Paulina
Szymoniak
 a,
Xintong
Qu
a,
Mozhdeh
Abbasi
b,
Brian R.
Pauw
a,
Sven
Henning
c,
Zhi
Li‡
a,
Xintong
Qu
a,
Mozhdeh
Abbasi
b,
Brian R.
Pauw
a,
Sven
Henning
c,
Zhi
Li‡
 d,
De-Yi
Wang
d,
De-Yi
Wang
 d,
Christoph
Schick
d,
Christoph
Schick
 ef,
Kay
Saalwächter
ef,
Kay
Saalwächter
 b and
Andreas
Schönhals
b and
Andreas
Schönhals
 *a
*a
aBundesanstalt für Materialforschung und -prüfung (BAM), Unter den Eichen 87, 12205 Berlin, Germany. E-mail: Andreas.Schoenhals@bam.de
bInstitut für Physik – NMR, Martin-Luther-Universität Halle-Wittenberg, Betty-Heimann-Str. 7, 06120 Halle, Germany
cFraunhofer-Institut für Mikrostruktur von Werkstoffen und Systemen IMWS, Walter-Hülse-Str. 1, 06120 Halle, Germany
dIMDEA Materials Institute, Eric Kandel 2, 28906 Getafe, Madrid, Spain
eUniversity of Rostock, Institute of Physics and Competence Center CALOR, Albert-Einstein-Str. 23-24, 18059 Rostock, Germany
fA. M. Butlerov Institute of Chemistry, Kazan Federal University, Kremlevskaya 18, 420008 Kazan, Russian Federation
First published on 14th January 2021
Abstract
A detailed calorimetric study on an epoxy-based nanocomposite system was performed employing bisphenol A diglycidyl ether (DGEBA) cured with diethylenetriamine (DETA) as the polymer matrix and a taurine-modified MgAL layered double hydroxide (T-LDH) as the nanofiller. The –NH2 group of taurine can react with DGEBA improving the interaction of the polymer with the filler. The combined X-ray scattering and electron microscopy data showed that the nanocomposite has a partially exfoliated morphology. Calorimetric studies were performed using conventional DSC, temperature modulated DSC (TMDSC) and fast scanning calorimetry (FSC) in the temperature modulated approach (TMFSC) to investigate the vitrification and molecular mobility dependent on the filler concentration. First, TMDSC and NMR were used to estimate the amount of the rigid amorphous fraction which consists of immobilized polymer segments at the nanoparticle surface. It was found to be 40 wt% for the highest filler concentration, indicating that the interface dominates the overall macroscopic properties and behavior of the material to a great extent. Second, the relaxation rates of the α-relaxation obtained by TMDSC and TMFSC were compared with the thermal and dielectric relaxation rates measured by static FSC. The investigation revealed that the system shows two distinct α-relaxation processes. Furthermore, two separate vitrification mechanisms were also found for a bulk network-former without geometrical confinement as also confirmed by NMR. This was discussed in terms of the intrinsic spatial heterogeneity on a molecular scale, which becomes more pronounced with increasing nanofiller content.
Introduction
In the field of polymer nanocomposites (PNCs), it is widely discussed that the addition of inorganic nanoparticles (NPs) to the polymer matrix often alters the fundamental polymer characteristics such as the mechanical, thermal and electrical properties.1 The possibility of producing advanced tailor-made materials, as well as their light weight and low cost, inspired academic and applied research towards potential applications in the electronics, construction, and automotive industries as a few examples.2,3 Many of these improvements are due to the fact that the NPs add functionality without affecting the polymer processability4 because only low nanofiller contents are required to enhance the material properties. Nevertheless, successful tailoring of the nanocomposites remains challenging,5,6 since the property enhancement is determined not only by the nature of the used components. It is generally accepted that the interfacial layer between the nanofiller and the polymer matrix substantially affects the macroscopic behavior of the PNCs as well. Some studies suggest that tailoring of the PNC's properties can be improved through manipulating the interface.5,7–9 So far, several parameters were identified which might influence the interfacial layer, such as the phase morphology of the nanocomposites, the size and distribution of the nanoparticles, and the interfacial interaction between the NPs and the matrix.10,11Such an interphase, for attractive polymer–particle interactions denoted as the rigid amorphous fraction (RAF), is formed by polymer segments physically adsorbed or chemically bonded to the surface of the NPs. The behavior of the polymer segments within the RAF differ from that of the bulk polymer in their structure, conformation and molecular mobility (dynamics)12–18 as, for instance, RAF is immobilized with respect to the cooperative segmental mobility (α-relaxation). This is attributed to entropic (presence of a solid boundary) and energetic (difference between polymer–polymer and polymer–particle interactions) contributions. Moreover, compared to conventional scaled composites, where the particle dimensions are in the micrometer scale, for nanoparticles, their surface-to-volume ratio increases significantly, yielding a high volume fraction of the interphase.19,20 It should be noted that the formation of RAF is due to the physical or chemical adsorption of the segments at the surface of the nanoparticles. This region is, therefore, also called the adsorbed layer.15–18 The rigid amorphous fraction and the polymer/matrix interphase have been investigated in the literature employing a variety of different systems and techniques.21–31 A considerable amount of work has been carried out to study the structure and properties of the PNCs, as well as the interfacial layer employing calorimetry. This method is useful to investigate, for instance, the NP- and the interface-related changes of the glass transition temperature (Tg), changes in the molecular mobility and temperature dependence of the heat flow.32–37 Moreover, absolute values of the specific heat capacity can provide further information about the system.38,39 As discussed in the literature, RAF can be quantified from the analysis of the calorimetric strength, i.e., the change of the specific heat capacity at the glass transition (Δcp) as the number of segments which did not participate in the glass transition, in comparison with the unfilled system.40–45 The formalism to calculate RAF has been already discussed in the literature for semicrystalline polymers, pioneered by Wunderlich et al.,46,47 and was further extended to nanocomposites.48,49 It should be noted that the question of whether RAF can devitrify at temperatures above the glass transition temperature is discussed in the literature for a longer time for both semicrystalline polymers and polymer-based nanocomposites. For a semicrystalline polymer, a devitrification of RAF is expected to take place at temperatures close to the melting of the crystallites which makes it difficult to observe.50 For polymer-based nanocomposites, in some cases, an adsorbed layer is observed which shows some molecular mobility at higher temperatures17,18 where a second step in the specific heat capacity is also found corresponding to the devitrification of RAF. In most cases, no devitrification of RAF is evidenced.40,41
Most of the calorimetric studies of the interface for PNCs are based on model systems, where the matrix is an uncrosslinked polymer and the polymer–nanoparticle interactions are relatively simple. More complex PNCs, which might be more important for applications, are only scarcely addressed in the literature. Therefore, a detailed understanding of such materials is required.
Epoxy-based materials have received increasing attention in both fundamental and applied research because of their properties such as high toughness, low shrinkage, good adhesion, and high mechanical stability which make them stand out among other polymers.51 While the chemistry of epoxidation is generally understood, there is still a considerable need to understand their structure–property relationship, as well as to engineer their properties for an increasing range of desired applications. Due to their superior characteristics and high processability of epoxies, they are promising materials for applications in automotive, aerospace and shipbuilding industries, as well as for coatings, adhesives, laminates and electrical insulators.52–54 However, one main disadvantage of epoxy-based polymers is their relatively high flammability, which can be reduced by incorporating nanofillers, such as layer doubled hydroxides (LDH), into the matrix.55,56 Because of the high amount of tightly bound water in the interlayer galleries of LDHs,57 as well as their endothermic decomposition that takes place at high temperatures,58 the flame retardancy of polymeric materials can be significantly enhanced.59,60
Epoxy-based materials are prepared via a curing reaction where a network is formed. The resulting crosslinking density affects significantly their macroscopic properties. The addition of nanoparticles might affect the curing reaction, as discussed in the literature.61–63 Recently, it was shown that the introduction of boehmite nanoparticles to an anhydride crosslinked epoxy-based matrix yields simultaneous mobilization and immobilization effects of the segmental dynamics64 resulting from changes in the crosslinking density and the formation of an immobilized interface.
Here, temperature modulated DSC (TMDSC) and fast scanning calorimetry (FSC) in the temperature modulated mode (TMFSC) are combined with NMR to study the vitrification kinetics and the molecular mobility of an amine crosslinked epoxy-based nanocomposite with an LDH as the nanofiller. A relaxation process was found by dielectric spectroscopy which was assigned to localized fluctuations in the interfacial region.25 Therefore, the interphase should be studied in more detail by means of advanced calorimetry and NMR, since due to the localized character of the dielectric relaxation process, it is expected that the interphase is immobilized with respect to the cooperative segmental fluctuations. The data were compared to the preliminary results obtained for the same system by dielectric spectroscopy and static FSC.25 This concerns a detailed comparison of the static FSC results with that of the TMDSC and TMFSC presented here. Furthermore, a detailed comparison is made to an anhydride crosslinked epoxy nanocomposite system where boehmite was employed as the nanofiller.64
Materials and methods
Materials
Layered double hydroxides (LDH) are anionic clays with the chemical formula [[M1−x2+Mx3+(OH)2]x+(Az−)x/z·mH2O]x−, where Mg2+ and Al3+ are the divalent (M2+) and trivalent (M3+) metal cations, respectively. Az− is an exchangeable interlayer anion. The LDH resembles in its structure brucite layered crystals (Mg(OH)2), where magnesium is octahedrally surrounded by hydroxyl groups. For the employed LDH, a partial isomorphous replacement of Mg2+ by Al3+ was carried out, which results in positively charged layers. The charge is compensated by additional anions between the layers. A modification of the LDH by exchanging the interlayer anions is mostly carried out to enlarge the basal spacing between the layers and to change the surface energy and hydrophilicity to facilitate better incorporation in the polymer matrix. Here, the relatively small molecule taurine (for the chemical structure, see left inset Fig. 1) was incorporated as an interlayer anion in the clay directly during its synthesis (T-LDH). Taurine, due to its –NH2 group, can react with the epoxy resin to improve the interaction between the LDH and the polymer matrix.Mg(NO3)2·6H2O, Al(NO3)3·9H2O, sodium hydroxide and taurine were purchased from Sigma-Aldrich Chemical Co. Bisphenol A diglycidyl ether (DGEBA) and diethylenetriamine (DETA; Epoxidharz C) were supplied by R&G Faserverbundwerkstoffe GmbH, Germany.
In parallel to the unfilled sample (EP), nanocomposites were prepared by mixing fractions of 6, 9, 12, 15 and 18 wt% of the T-LDH (EP/T-LDH6–EP/T-LDH18) with DGEBA. Further DETA was added for the curing process. A detailed description of the synthesis of the T-LDH, as well as epoxy/T-LDH nanocomposites, can be found elsewhere.55,58
Experimental
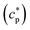 of the system can be extracted from the ratio of the area under the heat-flow peak and the height of the temperature step.67 Absolute values of
of the system can be extracted from the ratio of the area under the heat-flow peak and the height of the temperature step.67 Absolute values of 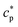 were obtained using synthetic sapphire (α-Al2O3) as a reference material. Here, the modulus of complex specific heat capacity
were obtained using synthetic sapphire (α-Al2O3) as a reference material. Here, the modulus of complex specific heat capacity 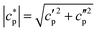 (the so-called reversing heat capacity) is considered, where
(the so-called reversing heat capacity) is considered, where 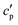 and
and 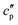 are the real and the imaginary parts of
are the real and the imaginary parts of 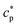 , respectively.
, respectively.
Here, the Flash DSC1 was used in the temperature modulated approach (dynamic measurements, TMFSC), where analogously to TMDSC, step response analysis was employed with alternating isothermal and heating steps.73–76 In the measurement 2 K up-steps at the heating rates (Ṫ) of 200 and 2000 K s−1 were followed by the isothermal periods (tp) of 1 and 0.1 s. The frequency-dependent complex heat capacity 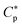 was calculated from the ratio of the Fourier transformations of the instantaneous heat flow (HF) and the instantaneous heating rate75,77 using eqn (1):
was calculated from the ratio of the Fourier transformations of the instantaneous heat flow (HF) and the instantaneous heating rate75,77 using eqn (1):
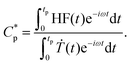 | (1) |
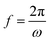 , ω – angular frequency) corresponds, like for TMDSC, to the length of the isothermal period, where higher harmonics were also extracted from one base frequency in the range of 1–11 Hz for tp = 1 s and 10–110 Hz for tp = 0.1 s.
, ω – angular frequency) corresponds, like for TMDSC, to the length of the isothermal period, where higher harmonics were also extracted from one base frequency in the range of 1–11 Hz for tp = 1 s and 10–110 Hz for tp = 0.1 s. 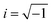 is the imaginary unit.
is the imaginary unit.
A high viscosity silicone oil AK 60![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 (Wacker Chemie AG) was used to establish the thermal contact between the crosslinked samples and the sensors and to minimize thermal lags.78 To compensate for the additional heat capacity of the silicone oil, it was additionally placed on the heating area of the reference side. The sensors were conditioned and calibrated according to the procedure of the manufacturer. Nitrogen was used as a purge gas at a flow rate of 40 ml min−1.
000 (Wacker Chemie AG) was used to establish the thermal contact between the crosslinked samples and the sensors and to minimize thermal lags.78 To compensate for the additional heat capacity of the silicone oil, it was additionally placed on the heating area of the reference side. The sensors were conditioned and calibrated according to the procedure of the manufacturer. Nitrogen was used as a purge gas at a flow rate of 40 ml min−1.
The data obtained for EP and PNCs at heating rates in the range of 0.5 to 4 × 104 K s−1 measured by the Flash DSC1 were taken from ref. 25.
The NMR experiments, recording simple proton free-induction decay (FID) signals, exploit the dominant multiple orientation-dependent proton–proton dipolar couplings. In the absence of molecular motion, the FID decay is Gaussian and reflects the static second moment M2 of the dipolar-broadened spectral line FID ∼ exp(−0.5×M2×tacq2) with M2 = (9/20) × Deff2. Here, Deff2 is the average effective dipolar coupling constant. Molecular rotations reduce the intra- and internuclear couplings and lead to a lengthening and a shape change of the FID decay. The transition takes place in a range of correlation times of ca. 2 decades centered around 1/Deff (roughly 10 μs in the static limit) and the FID can then be fitted using one or a combination of two modified exponential functions ∼exp{−(tacq/T2)β}. In the “rigid limit” with β = 2, 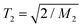 holds. The noted relaxation effects during the MSE are the strongest in the mentioned transition regime which enables an estimation of the time scale of the segmental motion29 to be employed below.
holds. The noted relaxation effects during the MSE are the strongest in the mentioned transition regime which enables an estimation of the time scale of the segmental motion29 to be employed below.
Results and discussion
X-ray and TEM investigations
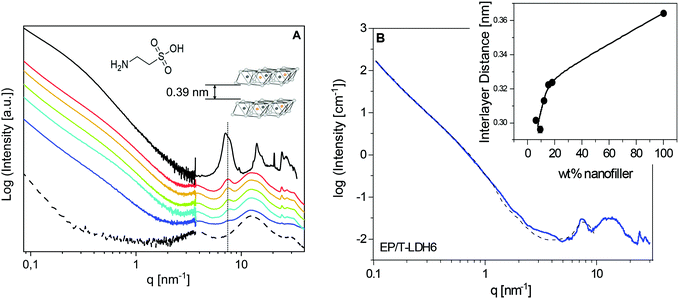
The structure of the pure material and of the PNCs was first studied employing X-ray scattering techniques. The characteristic scattering patterns are depicted in Fig. 1A. For the investigated system, a detailed comparison of the taurine modified and pristine LDH was published elsewhere.25 It was found that the T-LDH shows similar equidistant reflections like the pure LDH at 7.1 and 14.11 nm−1. In the first approach, from the reflection at the lower q value, the lamellar repeat distance (basal repeat distance) was calculated by the Bragg approximation to 0.88 nm. By subtracting the thickness of the LDH layer, the interlayer distance was estimated to be 0.39 nm (left inset in Fig. 1). This point will be reconsidered by detailed analysis of the SAXS data using a model function. One significant difference between the modified and the unmodified LDH is that for the T-LDH, a double-peak structure was observed, indicating the coexistence of polymorphs or layers of the same type with a different interlamellar distance.81 The so-called interstratification effect probably results from the presence of the taurine anion and the different amount of water molecules in the interlayer galleries. Nevertheless, the T-LDH resembles the interlamellar distance of the unmodified LDH. This proves that taurine, as a small molecule, did not enlarge the interlayer distances.For the unfilled epoxy (EP), the scattering pattern shows three distinct scattering features in the high q region, located at 4, 12.6 and 29.6 nm−1. Generally, for the amorphous materials with no long-range order, broad bumps in the X-ray scattering patterns can be taken as a fingerprint for short-range correlations.82 A detailed analysis of the three-peak structure for an anhydride epoxy material was published elsewhere.64 It was debated that such an X-ray pattern represents evidence for an inherent spatial heterogeneity of thermosetting networks on a molecular scale.83,84 In short, the intermediate bump with the highest intensity, here at q = 12.6 nm−1, was assigned as an amorphous halo, corresponding to the most frequently occurring intermolecular distances. In addition, the low-q and high-q peaks were taken as a manifestation of inhomogeneities in the epoxy network. For instance, the peak at q = 4 nm−1 was assigned to isopropylidene groups between the phenyl rings forming elongated clusters in an average size of ca. 1.5 nm, according to the Bragg approximation.
In comparison with the unfilled EP, the position of the amorphous halo, as well as the two other broad features in the X-ray pattern, remains unaffected for the nanocomposites, which indicates that the X-ray investigations did not detect large differences in the structure of the matrix in the PNCs compared to that of the pure EP. However, considering that X-ray scattering curves show only averaged intermolecular distances, the nanoparticle-related changes in the matrix are studied further employing advanced calorimetry. Moreover, the sharp peaks, related to the crystal structure of the nanoparticles, are also found at the same positions as for the pure LDH. This is evidence that polymer segments are not intercalated into the interlayer galleries.
Recently, a new procedure for the analysis of X-ray scattering data of polymer-based nanocomposites was developed for an anhydride-cured epoxy system filled with boehmite nanofiller.25 In the first step, the procedure is based on a linear combination of the scattering curves of the pure nanofiller and the pure epoxy to confirm the weight fractions of the nanofiller in the nanocomposites. For the system investigated here, an attempt was made to employ a similar approach. Surprisingly, the data for the nanocomposites cannot be described by a linear combination of both the pure components. This is probably due to a stronger interaction between the polymer and the filler for the system discussed here, in comparison with the anhydride-cured epoxy with the boehmite nanoparticles.
The SAXS region of the X-ray measurements was further analysed using SasView 5.0.3, with SasModels 1.0.3. To model the nanofiller structure, a “stacked disks”-model was chosen, which is applicable for clay-like materials.85 The used scattering length densities of the nanoparticles and their calculation are given in the ESI.† Furthermore, a Porod law was added to that model to phenomenologically describe the scattering from larger agglomerates. An example of the fit is given in Fig. 1B for EP/T-LDH6. The data are reasonably described by this analysis besides the q range from ca. 3 nm−1 to 4 nm−1. This might point to the presence of a considerable adsorbed layer. For the higher filler concentrations, similar fits are obtained.
For the pure T-LDH, the increase in the scattering intensity with decreasing q shows a change of the slope at ca. 0.3 nm−1. For the nanocomposites, this change is shifted strongly to higher q values. In the framework of the model, this effect is described as a reduction of the average number of layers in the particles from 7 for T-LDH to 3 for the nanocomposites. This strongly suggests that the clay partially exfoliates when it is placed into the epoxy. This line of argumentation is further supported by a reduction of the height of the interlayer peak and its broadening. The exfoliation is most likely due to the amine groups of taurine. It probably reacts with the resin, leading to the partial exfoliation of the T-LDH layers.
Finally, the interlayer thickness (lamellar repeat distance) can be extracted from the fit of the model function to the SAXS data. For the pure T-LDH, an average value of 0.36 nm is obtained from the fit. This is quite close to the value extracted from the maximum of the peak (0.39 nm). For the nanocomposites, the values are smaller than that for the pure T-LDH and increase with increasing LDH concentration (see the inset in Fig. 1B). Generally, the interlayer distances in the nanofiller are subjected to a distribution. Assuming that the layers with the largest distances are located at the edges of the particles, these layers are most prone to exfoliation. Consequently, the corresponding distances are not involved in the average interlayer distance anymore calculated from the SAXS data. Therefore, the decreased value of the interlayer distances for the nanocomposites can be explained in terms of increasing exfoliation of the nanoparticles. For a higher filler concentration, the nanoparticles come spatially closer to each other. This will hinder the exfoliation of the layers. Therefore, the interlayer distances increase with increasing filler concentration (see the inset in Fig. 1B).
The structure of the composites was further investigated by TEM (see Fig. 2 as an example, further images are given in ref. 25). The images show that T-LDH is distributed mostly homogenously in the polymer matrix in the form of small agglomerates, where the filler kept its layered structure to a certain extent, which agrees with the X-ray data. Higher magnifications show that a part of the T-LDH is distributed in the matrix as completely exfoliated layers which is also consistent with the interpretation of the SAXS data. From the structural investigations employing a combination of X-ray scattering and TEM, it is concluded that the nanocomposite system has a partially exfoliated morphology.
 | ||
| Fig. 2 TEM pictures for the EP/T-LDH12 sample. The scale bars represent 0.2 μm (left) and 50 nm (right). Similar images were obtained for the other concentrations of the nanofiller. For TEM pictures with different concentrations of T-LDH, see ref. 25. | ||
Overview of the calorimetric investigations
A combination of different calorimetric techniques was applied to study the thermal properties of the EP and the PNCs. First, their vitrification kinetics was characterized employing conventional DSC, where a constant heating rate of 20 K min−1 was applied, emphasizing the influence of the nanofiller on the glass transition behavior. Second, identical samples were measured by temperature modulated DSC (TMDSC) to investigate the segmental dynamics (α-relaxation) independent of the filler concentration. Moreover, this technique was also used to quantify the amount of the interface, which was detected for this system by dielectric spectroscopy.25 Furthermore, similar investigations on the segmental dynamics were performed employing fast scanning calorimetry (FSC) in the temperature modulated mode (TMFSC), extending the frequencies accessible by the conventional methods. All calorimetric data are taken from the second and further heating runs, where the material is fully cured, because in the first heating run, an exothermic post-curing peak in the heat flow curve was observed.Conventional DSC investigations
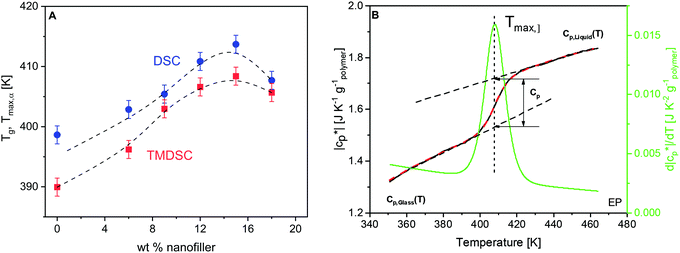
From the heat flow curves obtained by DSC, the glass transition temperature (Tg) values were estimated. In the literature, a variety of methods are known for the determination of Tg. Here, the derivative of the heat flow with respect to temperature is calculated and the maximum temperature of the obtained peak is defined as Tg (ESI,† Fig. S1). Tg increases first with increasing concentration of the nanofiller until ca. 15 wt%, followed by a decrease for higher filler contents (Fig. 3A). This dependence can be discussed by a competition of two effects, both related to the crosslinking density. For epoxy-based materials, where during the curing reaction a crosslinked network is formed, the introduction of the nanoparticles to the reacting mixture might result in changes in the polymer matrix, compared to that of the unfilled material. This is due to the spatial obstacles introduced by the NPs in the diffusion-controlled curing reaction, or due to the preferential adsorption of the components of the reaction mixture onto the NPs, altering the stoichiometry. In both cases, this may yield a lower crosslinking density of the network, and thus a lower glass transition temperature as observed by us for an anhydride crosslinked epoxy system nano-filled with boehmite.64 Here Tg increases for low filler contents. This is probably due to the additional amine groups of the taurine-modified nanofiller which can react with the DGEBA. Due to the acid group of taurine, it is strongly adsorbed to the LDH. Therefore, the reaction of DEBA with taurine will lead to an immobilization of the segments which percolate through the matrix due to the partly exfoliated structure and cause an increase of Tg. Moreover, besides the network structure of the bulk matrix, one important aspect affecting the vitrification is the interfacial behavior in the PNCs. The polymer segments are confined there due to the adsorption at the particle surface and/or the formation of covalent bonds with the –NH2 group from the nanofiller. This effect leads to a lower molecular mobility and higher energy barriers for their conformational changes, and thus higher Tg values. With increasing LDH content, the nanofiller hinders the diffusion of the reaction partners more and more, weakening the increase of Tg and causing the observed maximum at 15 wt%. For high concentrations of the nanofiller, the slowing down of the diffusion of the reaction partners becomes dominating, leading to a decrease in the crosslinking density and hence a decrease of Tg. Finally, it should be noted that the free volume and its distribution are also changed by the nanoparticles. In addition, the influence of the crosslinking density on the glass transition temperature is corroborated with additional experimental results in ref. 64. This supports the interpretation given here.Estimation of RAF by calorimetry
Temperature modulated DSC (TMDSC) was further employed to measure the absolute values of the modulus of complex specific heat capacity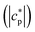 . The TMDSC data were analyzed by fitting a sigmoidal function to it, which is further differentiated with respect to temperature, resulting in a peak. The temperatures of the maxima of the obtained peaks are taken as the frequency-dependent glass transition temperatures, Tmax,α (α-relaxation). An example of the analysis is shown in Fig. 3B. The concentration dependence of Tmax,α resembles that of the Tg, as shown in Fig. 3A.
. The TMDSC data were analyzed by fitting a sigmoidal function to it, which is further differentiated with respect to temperature, resulting in a peak. The temperatures of the maxima of the obtained peaks are taken as the frequency-dependent glass transition temperatures, Tmax,α (α-relaxation). An example of the analysis is shown in Fig. 3B. The concentration dependence of Tmax,α resembles that of the Tg, as shown in Fig. 3A.
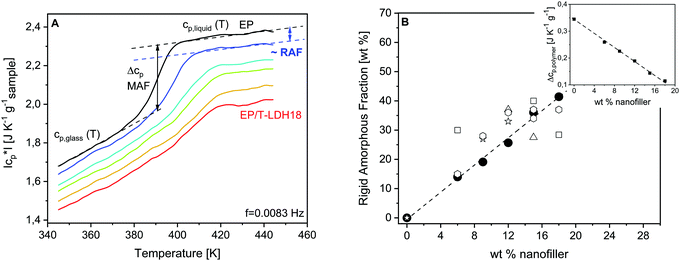
Fig. 4A gives the specific heat capacity curves of EP and PNCs. The specific heat capacity in the glassy state cp,glass decreases systematically with the content of the nanofiller (see also Fig. S2, ESI†). This decrease of cp,glass is related to the lower specific heat capacity of the nanofiller and similar changes have been reported in the literature.41,86,87 The specific heat capacity in the glassy state is due to vibrations. It seems unlikely that quite localized vibrations will be influenced by a change of the crosslinking density. For the correct estimation of the specific heat of the polymer in the nanocomposite, the specific heat capacity of the nanofiller must be considered.41 Nevertheless, further investigations are necessary to clarify this point.
Moreover, the step height of the specific heat capacity at the glass transition Δcp = cp,liquid − cp,glass (calorimetric strength) provides information about the amount of the rigid amorphous fraction. The cooperative segmental motions are immobilized in the RAF. Therefore, Δcp is expected to decrease with the increasing amount of RAF, with respect to the unfilled material. As depicted in the inset of Fig. 4B, Δcp normalized by the mass of the polymer (Δcp,polymer) decreases linearly with increasing filler content. It is concluded that the amount of interface increases proportionally with the T-LDH concentration.
The amount of RAF can be estimated from the TMDSC measurements according to a three-phase model. For an amorphous nanocomposite, the system is composed of a mobile amorphous fraction (MAF), which is the bulk-like polymer matrix, the RAF and the nanoparticles. Thus, RAF is given by,41,88
| RAF = 1 − filler content − MAF. | (2) |
MAF = Δcp,polymer,i/Δcp,pure![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) polymer, polymer, | (3) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) polymer are the calorimetric strengths for the nanocomposite i and the pure polymer, respectively. It should be noted that this calculation assumes that RAF does not devitrify until the highest temperature is measured. The devitrification of RAF would result in an additional glass transition to be observed at higher temperatures than the glass transition of the matrix. Such a glass transition is not observed even for the highest concentration of the nanofiller.
polymer are the calorimetric strengths for the nanocomposite i and the pure polymer, respectively. It should be noted that this calculation assumes that RAF does not devitrify until the highest temperature is measured. The devitrification of RAF would result in an additional glass transition to be observed at higher temperatures than the glass transition of the matrix. Such a glass transition is not observed even for the highest concentration of the nanofiller.
According to eqn (2) and (3), RAF was calculated and depicted in Fig. 4Bversus the concentration of the nanofiller. As indicated by the concentration dependence of Δcp,polymer, RAF increases proportionally to the particle concentration. It reaches up to 40% of the sample mass for the highest filler content, meaning that the macroscopic properties of the PNCs are dominated or strongly affected by the properties of the interface. The amount of interface is particularly high, compared to the other PNCs, which might be due to the –NH2 groups introduced by the taurine modification of the LDH nanofiller. These amine functionalities react with the DGEBA enhancing the interaction of the matrix with the filler because, due to its acid group, taurine is strongly adsorbed to the LDH.
Molecular dynamics by temperature modulated DSC and FSC in the temperature modulated mode
Fig. 5 shows the thermal relaxation rates obtained by static fast scanning calorimetry taken from ref. 25 for the pure epoxy, EP/T-LDH6 and EP/T-LDH15. The procedure to convert heating rates into a thermal relaxation rate in the framework of the fluctuation model to the glass transition89 is described in detail in ref. 25.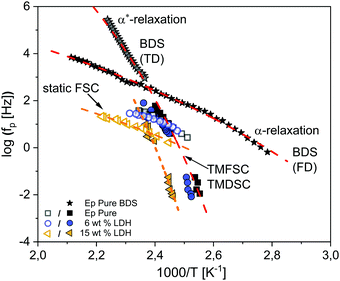 | ||
| Fig. 5 Relaxation map for the pure epoxy (black squares) and epoxy/T-LDH nanocomposites obtained from the static (open symbols) and dynamic fast scanning calorimetry measurements (filled symbols), as well as the temperature modulated DSC data (filled symbols) for two concentrations: EP/T-LDH6 – dark blue circles and EP/T-LDH15 – orange left-sided triangles. The dashed lines are VFT fits to the corresponding data (color coded). The black stars represent the broadband dielectric spectroscopy data taken from ref. 25. The red dashed lines indicate VFT fits to the dielectric data. | ||
Moreover, the relaxation rates of the dielectric α-relaxation taken from ref. 25 are also added to the activation plot for comparison. Furthermore, the dielectric data published in ref. 25 were revisited for the pure epoxy, employing the analysis of the isochronal scans of the conduction free dielectric loss (for more details see the ESI,† Fig. S3). This analysis revealed the presence of an additional relaxation process at temperatures lower than the α-relaxation. The new relaxation is denoted as the α*-relaxation.
First, the data for the pure epoxy will be addressed. As discussed in ref. 25, the temperature dependence of the relaxation rates of the α-relaxation is curved when plotted versus 1/T and can be described by the Vogel–Fulcher–Tammann (VFT) equation. It reads90
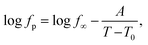 | (4) |
Moreover, the relaxation rates of the second dielectrically active process, α*-relaxation, show a different temperature dependence than the α-relaxation which is also curved when plotted versus 1/T, indicating a different molecular origin.
Furthermore, in Fig. 5, the dielectric data are compared to the calorimetric ones including static FSC from ref. 25, dynamic FSC (TMFSC) and TMDSC for EP, EP/T-LDH6 and EP/T-LDH15. In ref. 25, only preliminary TMDSC data at one frequency are given.91 Therefore, here the frequency range of the TMDSC measurements is extended by one decade. The relaxation maps for the other filler concentrations are given in the ESI,† Fig. S4–S6.
Compared to dielectric spectroscopy, FSC could be measured only in a limited frequency range. Therefore, for the first comparison of the temperature dependence of the relaxation rates of the dielectric α-relaxation with those obtained by static FSC, they are approximated by the Arrhenius equation that yields an apparent activation energy which is 108 kJ mol−1 for the dielectric α-relaxation and 127 kJ mol−1 for static FSC. It turns out that both values are quite similar. Therefore, it is concluded that the process probed by the static FSC measurements and the dielectric α-process have a similar molecular origin.
Therefore, here to extend the calorimetric investigations further, TMDSC and TMFSC measurements were employed to probe the segmental dynamics. It is worth noting that the dynamic TMFSC measurements were performed on the identical sample as the static FSC ones. Examples of the 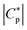 data are shown in the ESI,† Fig. S7 and S8. The data were analyzed similar to the TMDSC measurements (Fig. 3B) and the estimated Tmax,α values were added to the relaxation plot (Fig. 5). Firstly, the TMFSC and TMDSC data follow the same temperature dependence as the dielectric α*-relaxation. Therefore, it is concluded that the three techniques probe the same process. A common VFT function is fitted to both sets of the data. The estimated VFT parameters are given in the ESI† (Table S1). Secondly, it seems that the temperature dependence measured by the modulated calorimetric measurements is different from that of the α-relaxation measured by the static FSC and dielectric measurements. Moreover, Fig. 5 also shows that the temperature dependence of the relaxation rates of the α*-relaxation crosses that of the α-relaxation.
data are shown in the ESI,† Fig. S7 and S8. The data were analyzed similar to the TMDSC measurements (Fig. 3B) and the estimated Tmax,α values were added to the relaxation plot (Fig. 5). Firstly, the TMFSC and TMDSC data follow the same temperature dependence as the dielectric α*-relaxation. Therefore, it is concluded that the three techniques probe the same process. A common VFT function is fitted to both sets of the data. The estimated VFT parameters are given in the ESI† (Table S1). Secondly, it seems that the temperature dependence measured by the modulated calorimetric measurements is different from that of the α-relaxation measured by the static FSC and dielectric measurements. Moreover, Fig. 5 also shows that the temperature dependence of the relaxation rates of the α*-relaxation crosses that of the α-relaxation.
For the nanocomposites, as discussed in detail in ref. 25, the α-process detected by BDS shifts by 9–25 K (depending on the nanofiller concentration) to higher temperatures, compared to the bulk. But in general, the curvature versus 1/T remains similar, indicating again that BDS and static FSC probe the same process (α-relaxation). Also, similar to the pure epoxy, the TMDSC and TMFSC data follow the same temperature dependence, different than the α-relaxation, indicating the presence of the α*-process also for the nanocomposites.
There are different possibilities when discussing the observed behavior. Firstly, the two segmental relaxations for the pure epoxy and the nanocomposites are due to their structural inhomogeneity on a molecular level related to the regions with different crosslinking densities. The α*-relaxation is assigned to the glassy dynamics of the spatial regions with a higher crosslinking density, where the α-process is related to the glass transition of regions with a lower than average crosslinking density or dangling ends or other unreacted parts of the system. Secondly, the observation of the two glassy dynamics could be due to the confinement effects which might be present in the highly crosslinked systems. This would open a more general understanding of the observed behavior. It should be noted that a corresponding behavior was also observed for polystyrene.92 Nevertheless, in light of the spatial inhomogeneity observed by the X-ray measurements, the first interpretation is preferrable. Moreover, the assignment of the observed two glassy dynamics to a spatial heterogeneity is in agreement with the common view that only one α-relaxation is responsible for vitrification. This means that the both α-relaxations belong to different spatial regions with their own vitrification.
It should be noted that two α-processes have been reported elsewhere by us for an anhydride epoxy system by dielectric spectroscopy63 and dynamic mechanical analysis (DMA).65 Nevertheless, in that work, the two processes were found by dielectric investigations only, where here a combination of dielectric and specific heat spectroscopy was required to obtain a complete picture of the material structure. The different behavior of the two systems can be assigned to the different epoxy structures due to the hardeners employed for the network formation. However, in a broader sense, similar conclusions can be extracted on the structural heterogeneity.
Estimation of the cooperativity length scale
There is some agreement in the literature that the glass transition is a cooperative process with an underlying length scale of 1 nm to 3 nm.93 Here, the cooperativity length scale (ξ) of the glass transition for the α*-relaxation was estimated from the TMDSC data employing the fluctuation approach to the glass transition94 by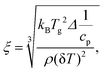 | (5) |
Unfortunately, the cooperativity length scale could not be estimated for the α-relaxation because no values of the specific heat capacity can be obtained due to the unknown sample mass. The dominating factor in eqn (5) is the width of the glass transition δT which is larger for the FSC than for the TMDSC curves. Therefore, it is concluded that ξ is smaller for the α-process than for the α*-process.
Detailed analysis of the heat flow curves
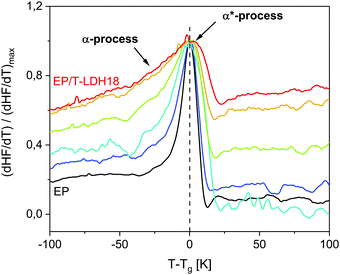
To further investigate the vitrification behavior, the first derivative of the heat flow normalized by its maximum value (dHF/dT)/(dHF/dT)max is plotted versus temperature reduced by Tg in Fig. 6. Commonly, dHF/dT is expected to be rather symmetrical for materials, which are dynamically homogeneous. For the considered system, even the pure EP shows a slight low-temperature bump indicating the presence of segments with a higher molecular mobility than the average. Consequently, the low temperature wing, evidenced also by the temperature modulated measurements (ESI,† Fig. S10), is assigned to the α-process.For the nanocomposites, the low temperature wing increases in intensity systematically with increasing concentration of the nanoparticles (see Fig. 6). As the low temperature wing of the derivative of the heat flow is assigned to the α-relaxation, this result means that the relative contribution of the α-process to the whole response increases. As discussed above, the diffusion of the reaction during the curing process is slowed down by the nanoparticles. This effect will affect the crosslinking density, leading to more loose ends and/or higher heterogeneity and therefore more regions with lower than average crosslinking density, both having a higher molecular mobility. With increasing concentration of the nanofiller, this effect will increase and therefore the amount of the fraction having a higher mobility will increase. At first glance, this disagrees with the concentration dependence of Tg. However, one has to recall that the increase of the glass transition temperature with increasing filler content is due to the amine groups of taurine that react with DGEBA close to the nanoparticles. This does not exclude a decrease of the crosslinking density in the polymer matrix considering also the decreased available DGEBA functionalities. The Tg measured by DSC is a complicated average of all these effects.
Interestingly, this process is significantly more pronounced for static measurements, extending over 50 K below the found glass transition temperature. This agrees with the low temperature broadening being more pronounced for the heat flow curves obtained by DSC, compared to the specific heat capacity curves from TMDSC (ESI,† Fig. S10).
Estimation of RAF by low field NMR
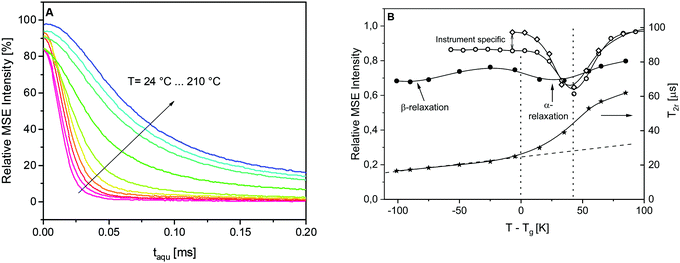
It should be noted that in principle, the amount of RAF can also be estimated from the dielectric measurements.96 However, that is not possible for the dielectric data given for the system discussed here in ref. 25, because the dielectric α-relaxation is strongly overlaid by conductivity. Therefore, low field NMR was employed to estimate RAF from a second experimental perspective.29To understand the estimation first, it is focused on the glass transition as observed by NMR. In the case of the α-relaxation in common polymers seen by NMR, the motion is characterized by the ultimately isotropic segmental rearrangements leading to a near-zero average Deff. Upon heating, the center point of the transition is located at ∼40 K above Tg. The signal decays can be roughly fitted by the theoretical expressions,29 but due to the complexity of the epoxy material, a more quantitative analysis is not carried out here. Rather, the data for the pure epoxy are fitted with a combination of the two modified exponentials ∼exp{−(tacq/T2)β}. The FID and MSE signals are fitted simultaneously to quantify and control the expected loss of signal during the MSE80 as discussed above. Signal losses arise due to instrumental imperfections and actual transverse relaxation due to the motions on the MSE timescale, the latter being the strongest in the 10 μs correlation time range. In these fits, T2 and β values are shared while the amplitudes can vary for FID and MSE. The FID-based amplitude fractions are a quantitative measure of the relative proton number ratio.
The phenomenology of the “NMR glass transition” of common polymers such as the PS reference sample or a poly(ethyl acrylate) elastomer (PEA) was studied previously in the literature (see Fig. 2 in ref. 29). In the static limit, the fitted T2 is about 15–20 μs and β = 2. Upon heating, the decays become increasingly stretched, requiring two fitting components, but become a single component again with β ≤ 1 and T2 reaching a value of the order of 500 μs or more, which is the isotropic limit depending on the resolution limit of the instrument. Fig. 7A depicts the MSE-refocused signals at different temperatures for the pure epoxy. In the high temperature limit considered here, the signal decays converge to a ca. 60%![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 40% mixture of a near-Gaussian (β ≥ 1.6) and a more exponential decay, where the T2r of the dominant, more “rigid” component is only about 60–70 μs. (Please note that the high temperature cannot be completely reached due to instrumental limitations.) This comparably low limiting value range is a consequence of the high crosslinking density of the epoxy, which only allows for highly anisotropic rather than near-isotropic segmental motions above Tg. Fig. 7B illustrates the loss of the first-point signal as discussed in the Experimental section. For the two model polymers, the intensity minimum is indeed found at Tg + 40 K. The differences between PS and PEA in the low-temperature branch arise from the differences in the instruments used (the MSE sequence suffers most from finite pulse lengths when Deff is large at low temperatures). In contrast, the signal loss for the epoxy is more pronounced over the whole range, and the minimum associated with the alpha process is much shallower and found already at Tg + 30 K, indicating a much more significant dynamic heterogeneity. The width of the shallow minima of the NMR signal might be due to the two relaxation processes as evidenced by the dielectric and calorimetric experiments.
40% mixture of a near-Gaussian (β ≥ 1.6) and a more exponential decay, where the T2r of the dominant, more “rigid” component is only about 60–70 μs. (Please note that the high temperature cannot be completely reached due to instrumental limitations.) This comparably low limiting value range is a consequence of the high crosslinking density of the epoxy, which only allows for highly anisotropic rather than near-isotropic segmental motions above Tg. Fig. 7B illustrates the loss of the first-point signal as discussed in the Experimental section. For the two model polymers, the intensity minimum is indeed found at Tg + 40 K. The differences between PS and PEA in the low-temperature branch arise from the differences in the instruments used (the MSE sequence suffers most from finite pulse lengths when Deff is large at low temperatures). In contrast, the signal loss for the epoxy is more pronounced over the whole range, and the minimum associated with the alpha process is much shallower and found already at Tg + 30 K, indicating a much more significant dynamic heterogeneity. The width of the shallow minima of the NMR signal might be due to the two relaxation processes as evidenced by the dielectric and calorimetric experiments.
Notably also, another minimum around Tg – 100 K, i.e., around room temperature, is found. This is the temperature range of the β-process discussed in ref. 25, which is here demonstrated to be associated with a significant amplitude of the proton motions. Rotational motions of the para-substituted phenyl rings of the DGEBA molecule come to mind. The β-process thus provides a pre-averaging of the rigid-limit Deff, which explains the comparably strong increase of the shortest value of T2r ∼ 1/Deff above 20 μs which is plotted in Fig. 7B (right y-scale). This near-linear increase, indicated by the dashed line, is more significant than the increase expected from thermal expansion (which increases the inter-proton distances). In the temperature range below Tg, the signal decays are essentially two components with a dominant (>90%) Gaussian with a decay time constant T2r. The dashed line extrapolation emphasizes that the additional sigmoidal increase in the crosslinking induced rather a low final value of T2r upon going through the “NMR glass transition”.
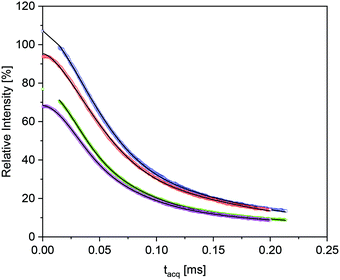
The RAF estimation was performed first in the high temperature range, where the epoxy matrix has the longest overall transversal relaxation time T2, and a component which is shifted with regard to Tg would be the most apparent. Fig. 8 shows the “isochronal” comparison of the FID and MSE data for the pure epoxy and the nanocomposite EP/T-LDH15 at a temperature which has the same difference to the corresponding Tg values (T + ΔTg).97
The two data sets in Fig. 8 are rather similar, but the data for the composites show a systematic tendency to somewhat accelerated initial decay for increasing LDH fractions. As compared to the previous work,29 the comparably low high-temperature T2r values and the two-component nature of the pure-epoxy response pose challenges for extracting the amount of Tg shifted material or RAF for the filled samples. Despite the inherent limitations to separate the relaxation components with too similar T2, it was possible to fit the data obtained from the composites with 9 wt% or more T-LDH with three components, where the only fixed parameter was the β exponent for the most “rigid” component, held constant at β = 2 (i.e., the Gaussian expected in the absence of sufficiently fast α-relaxation). Gratifyingly, these free fits always reproduced a component ratio of the components with an intermediate and a longest T2 of about 60![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 40 and the two β exponents found for the neat epoxy. Thus, the additional component with somewhat lower T2r can safely be associated with the RAF. This lower T2r was always around 37–41 μs. This is somewhat larger, but still close to the value expected from the increase of T2r arising from the thermal expansion and the more significant pre-averaging arising from the β-process25 as discussed above. Thus, it is concluded that the RAF also exhibits the β-process, but there is no indication of a significant Tg gradient as observed previously.29 The RAF for the nanocomposite with 6 wt% LDH was obtained by fixing T2r for this sample to the value obtained for the other nanocomposites.
40 and the two β exponents found for the neat epoxy. Thus, the additional component with somewhat lower T2r can safely be associated with the RAF. This lower T2r was always around 37–41 μs. This is somewhat larger, but still close to the value expected from the increase of T2r arising from the thermal expansion and the more significant pre-averaging arising from the β-process25 as discussed above. Thus, it is concluded that the RAF also exhibits the β-process, but there is no indication of a significant Tg gradient as observed previously.29 The RAF for the nanocomposite with 6 wt% LDH was obtained by fixing T2r for this sample to the value obtained for the other nanocomposites.
In a first attempt, it was tried to hold the relaxation parameters (T2, β) of the two components needed for pure epoxy fixed and fit only a fraction and T2r of RAF. This approach failed, as the intermediate and longest T2 values (associated with the two components needed to describe the signal decay of neat epoxy) were always about 10–20% higher than in the composites than in the neat epoxy. This can be correlated to a reduced crosslinking density in the composites discussed above (see also ref. 98 and 99) whereby the motional amplitude of the α-process increases somewhat.
In order to obtain an insight into the (likely significant) fitting ambiguities, RAF is estimated from two sets of data, i.e., the isothermal results for all samples measured at 190 °C (463 K) and the isochronal results measured at T + ΔTg. Two fitting strategies to each set of data were applied: first, a fully free fit (fixing only β = 2 for the RAF) and second, a fit in which we constrained the intermediate and long T2 components associated with the epoxy matrix at a fixed amplitude ratio of 60![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 40 (without fixing, the ratio only a few percent on average). The obtained values show a gratifying similarity to the result obtained from TMDSC (see Fig. 4B) despite the scatter, proving the consistency of the RAF estimation.
40 (without fixing, the ratio only a few percent on average). The obtained values show a gratifying similarity to the result obtained from TMDSC (see Fig. 4B) despite the scatter, proving the consistency of the RAF estimation.
Conclusion
In this work, an epoxy-based nanocomposite system was studied, based on bisphenol A diglycidyl ether cured with diethylenetriamine as the polymer matrix and a taurine-modified MgAL layered double hydroxide as the nanofiller. The –NH2 group of taurine can react with the DGEBA, improving the interaction of the polymer with the filler. The combined small- and wide-angle X-ray scattering data, as well as the TEM, showed that the nanocomposites have a partially exfoliated structure.A detailed calorimetric study combining DSC, TMDSC and TMFSC on the vitrification kinetics and molecular mobility of the nanocomposite system was performed. First, the glass transition temperature (Tg) was found to increase with increasing concentration of the nanofiller until a maximum at ca. 15 wt% was reached followed by a decrease for higher filler contents. This dependence results from two effects. On one hand, the amine group of the T-LDH leads to an immobilization of the polymer segments which percolated through to the epoxy matrix. The polymer/particle interface, denoted as the rigid amorphous fraction (RAF), was further studied by TMDSC, showing that the amount of RAF increases linearly with increasing nanofiller content, reaching up to 40% for the nanocomposite with the highest concentration. This indicates that the interface dominates the macroscopic material properties for this system to a larger extent. Furthermore, the RAF was also estimated from the low field NMR measurements and agree quantitatively with the calorimetric data.
Secondly, the molecular mobility was studied employing TMDSC and TMFSC in a broad frequency range. The obtained calorimetric relaxation rates for the found process (α*-relaxation) obtained from the two techniques can be described by a common Vogel–Fulcher–Tammann fit. The relaxation rates of the α*-relaxation was further compared with the thermal and dielectric relaxation rates obtained by FSC (α-relaxation) from the literature. It was found that the relaxation rates of the α*- and α-relaxation have different temperature dependencies, indicating a different molecular origin. The two processes were also evidenced as the low temperature broadening of the glass transition region probed by DSC and FSC, pointing towards two distinct mechanisms of vitrification as well. The origin of the two separate vitrification and relaxation mechanisms was discussed relying upon the intrinsic structural heterogeneity of the epoxy matrix. Thermosetting network formers can have regions with lower crosslinking density and/or uncrosslinked dangling ends in the network which are expected to have a higher mobility than the average one, thus vitrifying at lower temperatures than the average Tg. Consequently, the α*-relaxation was assigned to the glassy dynamics of a fully crosslinked epoxy network, where the α-process is related to the glass transition of the dangling ends or other unreacted parts of the system. The dynamical heterogeneity of the epoxy network was further confirmed by the investigation of the glass transition with NMR.
For the nanocomposites, the α-relaxation becomes more pronounced with increasing filler content, indicating that the contribution of the α-process to the whole calorimetric response increases. Considering that the introduction of the nanoparticles to the polymer matrix during the curing process slows down the diffusion of the reaction partners, as a result, compared to the bulk, the PNCs have more loose ends and a more heterogeneous structure (more regions with lower than average crosslinking density) with a higher molecular mobility in the network. This effect increases with increasing concentration of the nanofiller, and therefore a higher amount of the fraction has a higher mobility, causing the observed more pronounced α-relaxation.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
Mr M. Elert is thanked for his help with the graphical abstract. The German Science Foundation DFG (Grant Research Unit FOR 2021) is acknowledged for the financial support. CS gratefully acknowledges the financial support from the Ministry of Science and Higher Education of the Russian Federation (Grant No. 14.Y26.31.0019). The polystyrene reference sample was kindly provided by Manfred Wilhelm (KIT Karlsruhe).References
- R. Bogue, Nanocomposites: a review of technology and applications, Assembly Automation, 2011, 31(2), 106 CrossRef
.
- P. H. C. Camargo, K. G. Satyanarayana and F. Wypych, Nanocomposites: synthesis, structure, properties and new application opportunities, Mater. Res., 2009, 12(1), 1 CrossRef CAS
.
-
V. Patel and Y. Mahajan, Polymer Nanocomposites: Emerging Growth Driver for the Global Automotive Industry, in Handbook of Polymernanocomposites. Processing, Performance and Application, ed. J. K. Pandey, K. R. Reddy, A. K. Mohanty and M. Misra, Springer, Berlin, 2014, vol. A, pp. 511–538 Search PubMed
.
- A.-L. Goffin, J.-M. Raquez, E. Duquesne, G. Siqueira, Y. Habibi, A. Dufresne and P. Dubois, Poly (ε-caprolactone) Based Nanocomposites Reinforced by Surface-grafted Cellulose Nanowhiskers via Extrusion Processing: Morphology, Rheology, and Thermo-mechanical Properties, Polymer, 2011, 52(7), 1532 CrossRef CAS
.
- L. S. Schadler, S. K. Kumar, B. C. Benicewicz, S. L. Lewis and S. E. Harton, Designed Interfaces in Polymer Nanocomposites: A Fundamental Viewpoint, MRS Bull., 2007, 32(04), 335 CrossRef CAS
.
- J. Jancar, J. F. Douglas, F. W. Starr, S. K. Kumar, P. Cassagnau, A. J. Lesser, S. S. Sternstein and M. J. Buehler, Current issues in research on structure-property relationships in polymer nanocomposites, Polymer, 2010, 51(15), 3321 CrossRef CAS
.
- S. Cheng, B. Carroll, W. Lu, F. Fan, J.-M. Y. Carrillo, H. Martin, A. P. Holt, N.-G. Kang, V. Bocharova, J. W. Mays, B. G. Sumpter, M. Dadmun and A. P. Sokolov, Interfacial Properties of Polymer Nanocomposites: Role of Chain Rigidity and Dynamic Heterogeneity Length Scale, Macromolecules, 2017, 50(6), 2397 CrossRef CAS
.
- S. Cheng, B. Carroll, V. Bocharova, J.-M. Carrillo, B. G. Sumpter and A. P. Sokolov, Focus: Structure and dynamics of the interfacial layer in polymer nanocomposites with attractive interactions, J. Chem. Phys., 2017, 146(20), 203201 CrossRef
.
- S. K. Kumar, B. C. Benicewicz, R. A. Vaia and K. I. Winey, 50th Anniversary Perspective: Are Polymer Nanocomposites Practical for Applications?, Macromolecules, 2017, 50, 714 CrossRef CAS
.
- A. Papon, H. Montes, M. Hanafi, F. Lequeux, L. Guy and K. Saalwächter, Glass-Transition Temperature Gradient in Nano-composites: Evidence from Nuclear Magnetic Resonance and Differential Scanning Calorimetry, Phys. Rev. Lett., 2012, 108(6), 065702 CrossRef
.
- G. P. Baeza, C. Dessi, S. Costanzo, D. Zhao, S. Gong, A. Alegria, R. H. Colby, M. Rubinstein, D. Vlassopoulos and S. K. Kumar, Network dynamics in nanofilled polymers, Nat. Commun., 2016, 7, 11368 CrossRef
.
- D. Fragiadakis, P. Pissis and L. Bokobza, Glass transition and molecular dynamics in poly (dimethylsiloxane)/silica nanocomposites, Polymer, 2005, 46(16), 6001 CrossRef CAS
.
- M. Böhning, H. Goering, A. Fritz, K. W. Brzezinka, G. Turky, A. Schönhals and B. Schartel, Dielectric study of molecular mobility in poly(propylene-graft-maleic anhydride)/clay nanocomposites, Macromolecules, 2005, 38(7), 2764 CrossRef
.
- G. Z. Papageorgiou, Z. Terzopoulou, D. Biakiaris, K. S. Triantafyllidis, E. Diamanti, D. Gournis, P. Klonos, E. Giannoulidis and P. Pissis, Evaluation of the formed interface in biodegradable poly(L-lactic acid)/graphene oxide nanocomposites and the effect of nanofillers on mechanical and thermal properties, Thermochim. Acta, 2014, 597, 48 CrossRef CAS
.
- D. Fragiadakis and P. Pissis, Glass transition and segmental dynamics in poly(dimethylsiloxane)/silica nanocomposites studied by various techniques, J. Non-Cryst. Solids, 2007, 353, 4344 CrossRef CAS
.
- S. Cheng, B. Carroll, W. Lu, F. Fan, J.-M. Y. Carrillo, H. Martin, A. P. Holt, N.-G. Kang, V. Bocharova, J. W. Mays, B. G. Sumpter, M. Dadmun and A. P. Sokolov, Interfacial Properties of Polymer Nanocomposites: Role of Chain Rigidity and Dynamic Heterogeneity Length Scale, Macromolecules, 2017, 50(6), 2397 CrossRef CAS
.
- A. P. Holt, V. Bocharova, S. Cheng, A. M. Kisliuk, B. T. White, T. Saito, D. Uhrig, J. P. Mahalik, R. Kumar, A. E. Imel, T. Etampawala, H. Martin, N. Sikes, B. G. Sumpter, M. D. Dadmun and A. P. Sokolov, Controlling Interfacial Dynamics: Covalent Bonding versus Physical Adsorption in Polymer Nanocomposites, ACS Nano, 2016, 10(7), 6843 CrossRef CAS
.
- M. Füllbrandt, P. J. Purohit and A. Schönhals, Combined FTIR and Dielectric Investigation of Poly(vinyl acetate) Adsorbed on Silica Particles, Macromolecules, 2013, 46(11), 4626 CrossRef
.
- S. K. Kumar, B. C. Benicewicz, R. A. Vaia and K. I. Winey, 50th Anniversary Perspective: Are Polymer Nanocomposites Practical for Applications?, Macromolecules, 2017, 50, 714 CrossRef CAS
.
- R. A. Vaia and E. P. Giannelis, Polymer nanocomposites: Status and opportunities, MRS Bull., 2001, 26(5), 394 CrossRef CAS
.
- D. Ciprari, K. Jacob and R. Tannenbaum, Characterization of polymer nanocomposite interphase and its impact on mechanical properties, Macromolecules, 2006, 39(19), 6565 CrossRef CAS
.
- G. Giusca, M. Baibarac, S. Lefrant, O. Chauvet, I. Baltog, A. Devenyi and R. Manaila, C-60-polymer nanocomposites: evidence for interface interaction, Carbon, 2002, 40(9), 1565 CrossRef
.
- K. S. Wilson, A. J. Allen, N. R. Washburn and J. M. Antonucci, Interphase effects in dental nanocomposites investigated by small-angle neutron scattering, J. Biomed. Mater. Res., Part A, 2007, 81A(1), 113 CrossRef CAS
.
- P. J. Purohit, D.-Y. Wang, A. Wurm, C. Schick and A. Schönhals, Comparison of thermal and dielectric spectroscopy for nanocomposites based on polypropylene and Layered Double Hydroxide - Proof of interfaces, Eur. Polym. J., 2014, 55, 48 CrossRef CAS
.
- P. Szymoniak, Z. Li, D.-Y. Wang and A. Schönhals, Dielectric and flash DSC investigations on an epoxy based nanocomposite system with MgAl layered double hydroxide as nanofiller, Thermochim. Acta, 2019, 677, 151 CrossRef CAS
.
- J. Leng, N. Kang, D.-Y. Wang, J. Falkenhagen, A. F. Thünemann and A. Schönhals, Structure-Property Relationships of Nanocomposites Based on Polylactide and Layered Double Hydroxides - Comparison of MgAl and NiAl LDH as Nanofiller, Macromol. Chem. Phys., 2017, 218(20), 1700232 CrossRef
.
- J. Leng, P. J. Purohit, N. J. Kang, D.-Y. Wang, J. Falkenhagen, F. Emmerling, A. F. Thünemann and A. Schönhals, Structure-property relationships of nanocornposites based on polylactide and MgAl layered double hydroxides, Eur. Polym. J., 2015, 68, 338 CrossRef CAS
.
- S. Peng, Q. B. Zeng, X. Yang, J. Hu, X. Qiu and J. L. He, Local Dielectric Property Detection of the Interface between Nanoparticle and Polymer in Nanocomposite Dielectrics, Sci. Rep., 2016, 6, 38978 CrossRef CAS
.
- A. Papon, K. Saalwächter, K. Schäler, L. Guy, F. Lequeux and H. Montes, Low-Field NMR Investigations of Nanocomposites: Polymer Dynamics and Network Effects, Macromolecules, 2011, 44(4), 913 CrossRef CAS
.
- M.-L. Trutschel, A. Mordvinkin, F. Furtado, L. Willner and K. Saalwächter, Time-Domain NMR Observation of Entangled Polymer Dynamics: Focus on All Tube-Model Regimes, Chain Center, and Matrix Effects, Macromolecules, 2018, 51(11), 4108 CrossRef CAS
.
- K. Saalwächter and A. Heuer, Chain dynamics in elastomers as investigated by proton multiple-quantum NMR, Macromolecules, 2006, 39(9), 3291 CrossRef
.
- A. Bansal, H. Yang, C. Li, K. Cho, B. C. Benicewich, S. K. Kumar and L. S. Schadler, Quantitative equivalence between polymer nanocomposites and thin polymer films, Nat. Mater., 2005, 4, 693 CrossRef CAS
.
- P. Rittigstein, R. D. Priestley, L. J. Broadbelt and J. M. Torkelson, Model polymer nanocomposites provide an understanding of confinement effects in real nanocomposites, Nat. Mater., 2007, 6, 278 CrossRef CAS
.
- O. Bera, B. Pilic, J. Pavlicevic, M. Jovicic, B. Hollo, K. M. Szecsenyi and M. Spirkova, Preparation and thermal properties of polystyrene/silica nanocomposites, Thermochim. Acta, 2011, 515, 1 CrossRef CAS
.
- G. P. Baeza, C. Dessi, S. Costanzo, D. Zhao, S. Gong, A. Alegria, R. H. Colby, M. Rubinstein, D. Vlassopoulos and S. K. Kumar, Network dynamics in nanofilled polymers, Nat. Commun., 2016, 7, 11368 CrossRef
.
- D. Fragiadakis, P. Pissis and L. Bokobza, Glass transition and molecular dynamics in poly(dimethylsiloxane)/silica nanocomposites, Polymer, 2005, 46, 6001 CrossRef CAS
.
- H. Xia and M. Song, Characteristic length of dynamic glass transition based on polymer/clay intercalated nanocomposites, Thermochim. Acta, 2005, 429, 1 CrossRef CAS
.
- V. P. Privalko, Y. S. Lipatov and Y. Y. Kercha, Calorimetric Studies of Effect of Interphase on Behavior of Oligoethyleneglycoleadipate, Polym. Sci. U. S. S. R., 1970, 12(6), 1520 CrossRef
.
- Y. S. Lipatov and V. P. Privalko, Glass-Transition in Filled Polymeric Systems, Polym. Sci. U.S.S.R., 1972, 14(7), 1643 CrossRef CAS
.
- A. Wurm, M. Ismail, B. Kretzschmar, D. Pospiech and C. Schick, Retarded Crystallization in Polyamide/Layered Silicates Nanocomposites caused by an Immobilized Interphase, Macromolecules, 2010, 43(3), 1480 CrossRef CAS
.
- A. Sargsyan, A. Tonoyan, S. Davtyan and C. Schick, The amount of immobilized polymer in PMMA SiO(2) nanocomposites determined from calorimetric data, Eur. Polym. J., 2007, 43(8), 3113 CrossRef CAS
.
- J. Leng, N. J. Kang, D.-Y. Wang, A. Wurm, C. Schick and A. Schönhals, Crystallization behavior of nanocomposites based on poly(L-lactide) and MgAl layered double hydroxides - Unbiased determination of the rigid amorphous phases due to the crystals and the nanofiller, Polymer, 2017, 108, 257 CrossRef CAS
.
- P. Klonos, S. Kripotou, A. Kyritsis, G. Z. Papageorgiou, D. Bikiaris, D. Gournis and P. Pissis, Glass transition and segmental dynamics in poly(l-lactic acid)/graphene oxide nanocomposites, Thermochim. Acta, 2015, 617, 44 CrossRef CAS
.
- S. Koutsoumpis, K. N. Raftopoulos, O. Oguz, C. M. Papadakis, Y. Z. Menceloglu and P. Pissis, Dynamic glass transition of the rigid amorphous fraction in polyurethane-urea/SiO2 nanocomposites, Soft Matter, 2017, 13, 4580 RSC
.
- P. Klonos, S. N. Tegopoulos, C. S. Koutsiara, E. Kontou, P. Pissis and A. Kyritsis, Effects of CNTs on thermal transitions, thermal diffusivity and electrical conductivity in nanocomposites: comparison between an amorphous and a semicrystalline polymer matrix, Soft Matter, 2019, 15, 1813 RSC
.
- H. Suzuki, J. Grebowicz and B. Wunderlich, Glass transition of poly(oxymethylene), Br. Polym. J., 1985, 17(1), 1 CrossRef CAS
.
- B. Wunderlich, Reversible crystallization and the rigid amorphous phase in semicrystalline macromolecules, Prog. Polym. Sci., 2003, 28(3), 383 CrossRef CAS
.
- J. Leng, N. J. Kang, D.-Y. Wang, A. Wurm, C. Schick and A. Schönhals, Crystallization behavior of nanocomposites based on poly(L-lactide) and MgAl layered double hydroxides - unbiased determination of the rigid amorphous phases due to the crystals and the nanofiller, Polymer, 2017, 108, 257 CrossRef CAS
.
- J. Martin, N. Stingelin and D. Cangialosi, Direct Calorimetric Observation of the Rigid Amorphous Fraction in a Semiconducting Polymer, J. Phys. Chem. Lett., 2018, 9, 990 CrossRef CAS
.
- C. Schick, A. Wurm and A. Mohamed, Vitrification and devitrification of the rigid amorphous fraction of semicrystalline polymers revealed from frequency-dependent heat capacity, Colloid Polym. Sci., 2001, 279, 800 CrossRef CAS
.
- T. F. Irzhak and V. I. Irzhak, Epoxy nanocomposites, Polym. Sci., Ser. A, 2017, 59(6), 791 CrossRef CAS
.
- X. Wang, Y. Hu, L. Song, W. Y. Xing, H. D. Lu, P. Lv and G. X. Jie, Flame retardancy and thermal degradation mechanism of epoxy resin composites based on a DOPO substituted organophosphorus oligomer, Polymer, 2010, 51(11), 2435 CrossRef CAS
.
- N. Kinjo, M. Ogata, K. Nishi and A. Kaneda, Epoxy Molding Compounds as Encapsulation Materials for Microelectronic Devices, Adv. Polym. Sci., 1989, 88, 1–48 CrossRef CAS
.
- G. H. Chen, B. Yang and Y. Z. Wang, A novel flame retardant of spirocyclic pentaerythritol bisphosphorate for epoxy resins, J. Appl. Polym. Sci., 2006, 102(5), 4978 CrossRef CAS
.
- E. N. Kalali, X. Wang and D.-Y. Wang, Functionalized layered double hydroxide-based epoxy nanocomposites with improved flame retardancy and mechanical properties, J. Mater. Chem. A, 2015, 3(13), 6819 RSC
.
- C. H. Tseng, H. B. Hsueh and C. Y. Chen, Effect of reactive layered double hydroxides on the thermal and mechanical properties of LDHs/epoxy nanocomposites, Compos. Sci. Technol., 2007, 67(11), 2350 CrossRef CAS
.
- L. Frunza, A. Schönhals, S. Frunza, V. I. Parvulescu, B. Cojocaru, D. Carriazo, C. Martin and V. Rives, Rotational fluctuations of water confined to layered oxide materials: Nonmonotonous temperature dependence of relaxation times, J. Phys. Chem. A, 2007, 111(24), 5166 CrossRef CAS
.
- D.-Y. Wang, A. Das, A. Leuteritz, R. N. Mahaling, D. Jehnichen, U. Wagenknecht and G. Heinrich, Structural characteristics and flammability of fire retarding EPDM/layered double hydroxide (LDH) nanocomposites, RSC Adv., 2012, 2(9), 3927 RSC
.
- D.-Y. Wang, A. Leuteritz, Y. Z. Wang, U. Wagenknecht and G. Heinrich, Preparation and burning behaviors of flame retarding biodegradable poly (lactic acid) nanocomposite based on zinc aluminum layered double hydroxide, Polym. Degrad. Stab., 2010, 95(12), 2474 CrossRef CAS
.
- D.-Y. Wang, A. Das, F. R. Costa, A. Leuteritz, Y. Z. Wang, U. Wagenknecht and G. Heinrich, Synthesis of Organo Cobalt Aluminum Layered Double Hydroxide via a Novel Single-Step Self-Assembling Method and Its Use as Flame Retardant Nanofiller in PP, Langmuir, 2010, 26(17), 14162 CrossRef CAS
.
- M. Ghasem Zadeh Khorasani, D. Silbernagl, P. Szymoniak and V.-D. Hodoraba, The effect of boehmite nanoparticles (γ-AlOOH) on nanomechanical and thermomechanical properties correlated to crosslinking density of epoxy, Polymer, 2019, 164, 174 CrossRef CAS
.
- K. W. Putz, M. J. Palmeri, R. B. Cohn, R. Andrews and C. Brinson, L. ffect of Cross-Link Density on Interphase Creation in Polymer Nanocomposites, Macromolecules, 2008, 41(18), 6752 CrossRef CAS
.
- H. Rastin, M. R. Saeb, M. Nonahal, M. Shabanian, H. Vahabi, K. Formela, X. Gabrion, F. Seidi, P. Zarrintaj, M. Ganjaee Sari and P. Laheurte, Transparent nanocomposite coatings based on epoxy and layered double hydroxide: nonisothermal cure kinetics
band viscoelastic behavior assessments, Prog. Org. Coat., 2017, 113, 126 CrossRef CAS
.
- P. Szymoniak, R. P. Pauw, X. Qu and A. Schönhals, Competition of nanoparticle-induced mobilization and immobilization effects on segmental dynamics of an epoxy-based nanocomposite, Soft Matter, 2020, 16, 5406–5421 RSC
.
- J. Filik, A. W. Ashton, P. C. Y. Chang, P. A. Chater, S. J. Day, M. Drakopoulos, M. W. Gerring, M. L. Hart, O. V. Magdysyuk, S. Michalik, A. Smith, C. C. Tang, N. J. Terrill, M. T. Wharmby and H. J. Wilhelm, Processing two-dimensional X-ray diffraction and small-angle scattering data in DAWN 2, Appl. Crystallogr., 2017, 50(3), 959 CrossRef CAS
.
- B. R. Pauw, A. J. Smith, T. Snow, N. J. Terrill and A. F. Thünemann, The modular small-angle X-ray scattering data correction sequence, J. Appl. Crystallogr., 2017, 50, 1800 CrossRef CAS
.
-
C. Schick, in Handbook of Thermal Analysis and Calorimetry, ed. Cheng, Elsevier, Amsterdam, 2002, vol. 3, pp. 713–810 Search PubMed
.
- V. Mathot, M. Pyda, T. Pijpers, G. Van den Poel, E. van de Kerkhof, S. van Herwaarden, F. van Herwaarden and A. Leenaers, The Flash DSC 1, a power compensation twin-type, chip-based fast scanning calorimeter (FSC): First findings on polymers, Thermochim. Acta, 2011, 522(1), 36 CrossRef CAS
.
- J. E. K. J. Schawe, Influence of processing conditions on polymer crystallization measured by fast scanning DSC Therm, Anal. Calorim., 2014, 116(3), 1165 CrossRef CAS
.
- S. A. Adamovsky, A. A. Minakov and C. Schick, Scanning microcalorimetry at high cooling rate, Thermochim. Acta, 2003, 403(1), 55 CrossRef CAS
.
- A. A. Minakov, S. A. Adamovsky and C. Schick, Non-adiabatic thin-film (chip) nanocalorimetry, Thermochim. Acta, 2005, 432(2), 177 CrossRef CAS
.
- S. van Herwaarden, E. Iervolino, F. van Herwaarden, T. Wijffels, A. Leenaers and V. Mathot, Design, performance and analysis of thermal lag of the UFS1 twin-calorimeter chip for fast scanning calorimetry using the Mettler-Toledo Flash DSC 1, Thermochim. Acta, 2011, 522(1), 46 CrossRef CAS
.
- M. Merzlyakov and C. Schick, Step response analysis in DSC: a fast way to generate heat capacity spectra, Thermochim. Acta, 2001, 380, 5 CrossRef CAS
.
- E. Shoifet, G. Schulz and C. Schick, Temperature modulated differential scanning calorimetry extension to high and low frequencies, Thermochim. Acta, 2015, 603, 227 CrossRef CAS
.
- B. R. Hernandez, X. Monnier, J. A. Pomposo, M. Gonzales-Burgos, D. Cangialosi and A. Alegria, Glassy Dynamics of an All-Polymer Nanocomposite Based on Polystyrene Single-Chain Nanoparticles, Macromolecules, 2019, 52, 6868 CrossRef
.
- N. G. Perez-de-Eulate, V. D. Lisio and D. Cangialosi, Glass Transition and Molecular Dynamics in Polystyrene Nanospheres by Fast Scanning Calorimetry, ACS Macro Lett., 2017, 6, 859 CrossRef CAS
.
- P. Kamasa, M. Merzlyakov, M. Pyda, J. Pak, C. Schick and B. Wunderlich, Multi-frequency Heat Capacity Measured with different types of TMDSC, Thermochim. Acta, 2002, 392–393, 195 CrossRef CAS
.
- J. E. K. Schawe, Practical aspects of the Flash DSC 1: Sample prepataion for measurements of polymers in Thermal Analysis UserCom 36, https://www.mt.com/de/en/home/library/usercoms/lab-analytical-instruments/thermal-analysis-usercom-36.html.
- K. Schäler, M. Roos, P. Micke, Y. Golitsyn, A. Seidlitz, T. Thurn-Albercht, H. Schneider, G. Hemple and K. Saalwächter, Basic principles of static proton low-resolution spin diffusion in nanophase-separated materials with mobility contrast, Solid State Nucl. Magn. Reson., 2015, 205(72), 50 CrossRef
.
- A. Wittmer, R. Wellen, K. Saalwächter and K. Koschek, Moisture-mediated self-healing kinetics and molecular dynamics in modified polyurethane urea polymers, Polymer, 2018, 151, 125 CrossRef CAS
.
-
V. Rives, Layered Double Hydroxides: Present and Future, Nova Science Publishers, New York, 2001 Search PubMed
.
- G. W. Stewart, Theory of X-ray diffraction in liquids, Phys. Rev., 1928, 32, 558 CrossRef CAS
.
- J. Duchet and P. Pascault, Do epoxy–amine networks become inhomogeneous at the nanometric scale?, J. Polym. Sci., Part B: Polym. Phys., 2003, 41, 2422 CrossRef CAS
.
- K. Dusek, J. Plestil, F. Lednicky and S. Lunak, Are cured epoxy resins inhomogeneous?, Polymer, 1978, 19, 393 CrossRef CAS
.
- http://www.sasview.org/docs/user/models/stacked_disks.html .
- S. Swier, G. Van Assche, A. Van Hemelrijck, H. Rahier, E. Verdonck and B. Van Mele, Characterization of reacting polymer systems by temperature-modulated differential scanning calorimetry, J. Therm. Anal., 1998, 54, 585 CrossRef CAS
.
- B. Van Mele and S. Swier, Reaction-induced phase separation in polyethersulfone-modified epoxy-amine systems studied by temperature modulated differential scanning calorimetry, Thermochim. Acta, 1999, 330, 175 CrossRef
.
- J. Leng, P. Szymoniak, N.-J. Kang, D.-Y. Wang, A. Wurm, C. Schick and A. Schönhals, Influence of interfaces on the crystallization behavior and the rigid amorphous phase of poly(l-lactide)-based nanocomposites with different layered doubled hydroxides as nanofiller, Polymer, 2019, 184(5), 121929 CrossRef CAS
.
-
E. Donth, Glasübergang, Akademieverlag, Berlin, 1981 Search PubMed
.
- H. Vogel, The temperature dependence law of the viscosity of fluids, Phys. Z., 1921, 22, 645 Search PubMed
; G. S. Fulcher, Analysis of recent measurements of the viscosity of glasses, J. Am. Ceram. Soc., 1925, 8, 339 CrossRef CAS
; G. Tammann and G. Hesse, The dependency of viscosity on temperature in hypothermic liquids, Z. Anorg. Allg. Chem., 1926, 156(4), 245 CrossRef
.
- By an error wrong TMDSC data have been plotted in Fig. 11 of ref. 25.
- V. Lapascu, S. J. Picken and M. Wübbenhorst, Dynamics of T2G2 Helices in Atactic and Syndiotactic Polystyrene: New Evidence from Dielectric Spectroscopy and FTIR, Macromolecules, 2006, 39, 5152 CrossRef
.
-
A. Schönhals and F. Kremer, Amorphous Polymers in Polymer Science: A Comprehensive Reference, ed. K. Matyjaszewski and M. Möller, Elsevier, 2012, vol. 1 Search PubMed
.
- E. Donth, The Size of Cooperatively Rearranging Regions at the Glass Transition, J. Non-Cryst. Solids, 1982, 53, 325 CrossRef CAS
.
- T. Sasaki, T. Uchida and K. Sakurai, Effect of Crosslink on the Characteristic Length of GlassTransition of Network Polymers, J. Polym. Sci., Part B: Polym. Phys., 1958, 2006, 44 Search PubMed
.
- E. Schlosser and A. Schönhals, Recent development in dielectric relaxation spectroscopy of polymers, Colloid Polym. Sci., 1989, 267, 963–969 CrossRef CAS
.
- Although the Tg shifts are noticeable, the effect on the comparison was small if not negligible, as the NMR results are not a strong function of temperature in this range, due to the limited dynamic range of the method.
- J. L. Valentin, I. Mora-Barrantes, M. A. Carretero-González, P. Sotta, D. R. Long and K. Saalwächter, Novel experimental approach to evaluate filler-elastomer interactions, Macromolecules, 2010, 43, 334–346 CrossRef CAS
.
- A. Mujtaba, M. Keller, S. Illisch, H.-J. Radusch, T. Thurn-Albrecht, K. Saalwächter and M. Beiner, Mechanical properties and cross-linking density of styrene-butadiene model composites containing fillers with bimodal particle size distribution, Macromolecules, 2012, 45, 6504–6515 CrossRef CAS
.
Footnotes |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/d0sm01992e |
| ‡ Current address: China-Spain Collaborative Research Center for Advanced Materials, School of Materials Science and Engineering, Chongqing Jiaotong Univeristy, Chongqing, 400074, China. |
| This journal is © The Royal Society of Chemistry 2021 |