Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
SANS quantification of bound water in water-soluble polymers across multiple concentration regimes†
Helen
Yao
 and
Bradley D.
Olsen
and
Bradley D.
Olsen
 *
*
Department of Chemical Engineering, Massachusetts Institute of Technology, Cambridge, Massachusetts 02139, USA. E-mail: bdolsen@mit.edu; Tel: +1 617 715 4548
First published on 20th May 2021
Abstract
Contrast-variation small-angle neutron scattering (CV-SANS) is a widely used technique for quantifying hydration water in soft matter systems, but it is predominantly applied in the dilute regime or for systems with a well-defined structure factor. Here, CV-SANS was used to quantify the number of hydration water molecules associating with three water-soluble polymers with different critical solution temperatures and types of water–solute interactions in dilute, semidilute, and concentrated solution through the exploration of novel methods of data fitting and analysis. Multiple SANS fitting workflows with varying levels of model assumptions were evaluated and compared to give insight into SANS model selection. These fitting pathways ranged from general, model-free algorithms to more standard form and structure factor fitting. In addition, Monte Carlo bootstrapping was evaluated as a method to estimate parameter uncertainty through simulation of technical replicates. The most robust fitting workflow for dilute solutions was found to be form factor fitting without CV-SANS (i.e. polymer in 100% D2O). For semidilute and concentrated solutions, while the model-free approach can be mathematically defined for CV-SANS data, the addition of a structure factor imposes physical constraints on the optimization problem, suggesting that the optimal fitting pathway should include appropriate form and structure factor models. The measured hydration numbers were consistent with the number of tightly bound water molecules associated with each monomer unit, and the concentration dependence of the hydration number was largely governed by the chemistry-specific interactions between water and polymer. Polymers with weaker water–polymer interactions (i.e. those with fewer hydration water molecules) were found to have more bound water at higher concentrations than those with stronger water–polymer interactions due to the increase in the number of forced water–polymer contacts in the concentrated system. This SANS-based method to count hydration water molecules can be applied to polymers in any concentration regime, which will lead to improved understanding of water–polymer interactions and their impact on materials design.
Introduction
Water plays a central role in the design and application of polymer-based materials in areas such as therapeutics,1,2 anti-biofouling,3,4 enzyme catalysis,5 and separations.6 For example, in anti-biofouling coatings made of zwitterionic polymers, the hydration layer is believed to enhance the repulsion between contaminant proteins and the surface of interest.7 The existence of hydration water layers is also relevant to biocompatible polymer materials that must be placed into the human body without attracting unwanted adsorbents that can lead to adverse effects.8 As a result, water interactions can impact the design of medical materials such as hemocompatible polymers,9 dialyzers,10 and hydrogel tissue scaffolds.11,12 In drug delivery applications, tuning the thermoresponsive properties of polymers such as poly(N-isopropylacrylamide) (PNIPAM)13 or elastin-like polypeptides (ELPs)14 requires understanding of polymer–water interactions. Water can also change the phase behavior of protein–polymer bioconjugates which self-assemble into nanostructures similar to those observed in synthetic block copolymers.15In a system of water and polymer, there are often multiple populations of solvent. Water is typically divided into three populations: bound water, intermediate water, and bulk water.8,9,16 These three populations have been identified by numerous groups based on mobility,17–19 freezing point,20–23 and thermal expansion.16,24 Bound water consists of water molecules that are directly and strongly associated to the polymer via hydrogen bonds or electrostatic interactions.25–27 These molecules can often stay bound to the polymer even through state changes, such as freezing21 or macrophase separation.28 Intermediate water is characterized by weaker interactions, such as dipole–dipole interactions or hydrophobic interactions.26 This population often contributes to desirable properties such as anti-biofouling and protein repulsion.8 The remainder of the water in the system is bulk water, whose molecules can diffuse around freely like molecules in pure water.
The differences in the types of interactions and the dynamics present in each of the three water populations allow for the characterization of water using a multitude of techniques, including dielectric relaxation spectroscopy,29–32 nuclear magnetic resonance (NMR),18,33–35 attenuated total reflection Fourier transform infrared (ATR-FTIR) and Raman spectroscopy,28,36–38 and neutron scattering.39–42 In particular, small-angle neutron scattering (SANS) is widely known to have utility in quantifying hydration water populations, as the contrast can be directly manipulated via water and deuterium oxide blends to provide information on water partitioning. However, a challenge that arises in these studies is making measurements in the poorly understood but highly relevant concentrated solution regime, a challenge which persists for different types of macromolecules, including proteins43,44 and polymers.45 In many SANS studies, the experiments are often done in the dilute regime, or at best, in the semidilute regime.46,47 In other cases, assumptions that parameters such as the size of the hydration layer, hydration number, or scattering length density are not dependent on concentration must be made to fit experimental data to various form and structure factor models.39,48 The existence of a structure factor that describes the system is also important when there are interparticle interactions in non-dilute regimes.49–51 In some cases, the choice of structure factor does not allow for the direct quantification of hydration number and only provides an indirect indication of hydration level through structural information, necessitating the use of supplementary techniques to obtain hydration number.52,53
Here, the contrast variation SANS (CV-SANS) method used by Nickels et al.39 is adapted to quantify the hydration number of three polymers for concentration regimes ranging from dilute to concentrated with minimal model-related assumptions. Three industrially relevant polymers that span different polymer chemistries (PNIPAM, poly(hydroxypropyl acrylate) (PHPA), and poly(3-[N-(2-methacroyloyethyl)-N,N-dimethylammonio]propane sulfonate) (PDMAPS)) are studied. PNIPAM and PHPA are non-ionic hydrogen bond acceptors and donors, and PDMAPS is a zwitterionic polymer. Different fitting methods are applied and compared for each concentration and for each polymer in solution. The results of this study provide insight into SANS model selection, performance, and generalizability for different water-soluble polymers over a wide range of concentration regimes. SANS is shown to measure a very specific population of hydration water and is used to illustrate the effect of polymer chemistry on the concentration dependence of hydration water.
Experimental
Polymer synthesis
The three polymers used in the study (Scheme 1) were synthesized by reversible addition–fragmentation chain-transfer (RAFT) polymerization, as described previously.15,54,55 Poly(N-isopropylacrylamide) (PNIPAM) and poly(hydroxypropyl acrylate) (PHPA) were synthesized using 2-(ethylsulfanylthiocarbonylsulfanyl)-2-methylpropionic acid (EMP) as a chain transfer agent (CTA), whereas poly(3-[N-(2-methacroyloyethyl)-N,N-dimethylammonio]propane sulfonate) (PDMAPS) was synthesized using 4-cyano-4-(phenylcarbonothioylthio)pentanoic acid (CPP) as a CTA. Molecular properties of all polymers can be found in Table 1. Molar mass and purity were assessed by gel permeation chromatography (GPC, Fig. S1–S3, ESI†) and proton nuclear magnetic resonance spectroscopy (NMR), respectively (Fig. S4–S6, ESI†).| Polymer | Molar mass, Mn [g mol−1] | Dispersity, Đ | Pure NSLDa [× 10−4 nm−2] | Volume of monomer unit [nm3] | Densityb [g cm−3] | Overlap concentrationc, φ* |
|---|---|---|---|---|---|---|
| a From NIST scattering calculator.56 b Densities taken from Thomas et al.54 (PNIPAM), Chang et al.15 (PHPA), and Chang and Olsen55 (PDMAPS). c See method of calculation in ESI. | ||||||
| PNIPAM | 28![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 050 050 |
1.03 | 0.8140 | 0.1790 | 1.05 | 0.038 |
| PHPA | 27![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 960 960 |
1.07 | 1.0689 | 0.1863 | 1.16 | 0.030 |
| PDMAPS | 32![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 500 500 |
1.18 | 1.2020 | 0.3386 | 1.37 | 0.034 |
Contrast-variation small-angle neutron scattering (CV-SANS)
For dilute (13.75 mg mL−1) and semidilute (50 mg mL−1) conditions, polymers were dissolved in stock solutions of water and deuterium oxide. Stock solutions of PDMAPS at 50 mg mL−1 and PHPA and PNIPAM at both 13.75 and 50 mg mL−1 were blended at D2O![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) H2O ratios of 10
H2O ratios of 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 90, 25
90, 25![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 75, 40
75, 40![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 60, 60
60, 60![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 40, 70
40, 70![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 30, 80
30, 80![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 20, 90
20, 90![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 10, and 100
10, and 100![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0 by volume. Stock solutions of PDMAPS at 13.75 mg mL−1 were blended at D2O
0 by volume. Stock solutions of PDMAPS at 13.75 mg mL−1 were blended at D2O![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) H2O ratios of 10
H2O ratios of 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 90, 25
90, 25![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 75, 40
75, 40![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 60, 70
60, 70![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 30, 80
30, 80![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 20, and 100
20, and 100![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0 by volume. For concentrated polymers (250 and 300 mg mL−1), blends were prepared at D2O
0 by volume. For concentrated polymers (250 and 300 mg mL−1), blends were prepared at D2O![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) H2O ratios of 0
H2O ratios of 0![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 100, 15
100, 15![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 85, 30
85, 30![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 70, 45
70, 45![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 55; 60
55; 60![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 40, 80
40, 80![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 20, 90
20, 90![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 10, and 100
10, and 100![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0. Due to the high viscosity of these solutions, D2O and H2O were added to pre-weighed polymer instead of blending stock solutions. Solvent backgrounds at the same blend ratios were prepared for all SANS configurations.
0. Due to the high viscosity of these solutions, D2O and H2O were added to pre-weighed polymer instead of blending stock solutions. Solvent backgrounds at the same blend ratios were prepared for all SANS configurations.
SANS experiments were conducted at the NIST Center for Neutron Research (NCNR) NG-B 30 m instrument and the Oak Ridge National Laboratory High Flux Isotope Reactor (ORNL HFIR) Bio-SANS CG3 instrument. Preliminary experiments were conducted at the EQ-SANS instrument at ORNL Spallation Neutron Source (SNS). At NIST, the 9CB sample environment, a standard sample holder with Peltier temperature control available for NG-B 30 m, was used for dilute PDMAPS solutions. PDMAPS solutions were loaded into demountable titanium cells with quartz windows spaced 1 mm apart. After loading, samples were allowed to equilibrate at 60 °C (>UCST, see cloud point curves in Fig. S7, ESI†) in an oven for 12 hours. After transferring samples to the 9CB holder, they were incubated for an additional 20 min at 60 °C prior to collecting data. SANS intensities were recorded at three configurations using detector distances of 11 m (3 guides), 4 m (5 guides), and 1 m (7 guides), spanning a q-range of 0.045–4.5 nm−1. The neutron wavelength, λ, was 6 Å, with a spread (Δλ/λ) of 13.8%. Data from the three configurations were reduced and stitched together using the NCNR reduction package in the Igor platform.
HFIR scattering patterns for PHPA, PNIPAM, and semidilute and concentrated PDMAPS solutions were measured using a neutron wavelength of 6.0 ± 0.8 Å. A q-range of 0.03–8 nm−1 was achieved using a single configuration with two simultaneous detectors at 1.1 m (offset wing) and 15.5 m. The beam aperture was restricted to 14 mm for all samples. PHPA and PNIPAM solutions were loaded into quartz Suprasil banjo cells with a 1 mm path length (Hellma, 120-QS). These solutions were equilibrated at 5 °C (<LCST, Fig. S7, ESI†) for at least 12 hours prior to data collection at 5.5 ± 0.5 °C. PDMAPS solutions were loaded into demountable titanium cells with quartz windows spaced 1 mm apart. These were equilibrated at 60 °C in an oven for at least 12 hours prior to data collection at 60 °C ± 0.5 °C. The sample cell holder was fitted with a quartz chamber with dry air flow to prevent condensation. All solvent backgrounds were measured using banjo cells. Conversion between titanium cell and banjo cell backgrounds was done by normalizing the signal from the 100% H2O solvent sample. 2D scattering patterns were reduced using the Mantid reduction package57 and corrected for the quartz background from an empty sample cell and dark field scattering. Absolute scaling was obtained using a scattering standard. To eliminate instrument-related artifacts, only data collected at q > 0.1 nm−1 were included for fitting.
Results and discussion
Model fitting and error estimation
The hydration number is defined as the number of bound water molecules associated with a monomer repeat unit. For a polymer dissolved in a solvent blend of water and deuterium oxide, it is related to the neutron scattering length density (SLD) by eqn (1).39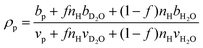 | (1a) |
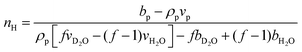 | (1b) |
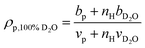 when the polymer is dissolved in pure D2O, as is typically done for maximal contrast. In general, the scattering lengths can be obtained from tabulated values. The molecular volume of H2O is calculated as 0.0299 nm3, and the molecular volume of D2O is taken to be 0.0304 nm3 (from experiment58). The molecular volume of a polymeric repeat unit can either be calculated from molar mass and density (as shown in Table 1) or measured from the contrast matching SANS experiment.39 The SLD of polymer is likewise obtained from SANS, though the method of calculation depends on the concentration regime of the polymer solution, as illustrated in Fig. 1.
when the polymer is dissolved in pure D2O, as is typically done for maximal contrast. In general, the scattering lengths can be obtained from tabulated values. The molecular volume of H2O is calculated as 0.0299 nm3, and the molecular volume of D2O is taken to be 0.0304 nm3 (from experiment58). The molecular volume of a polymeric repeat unit can either be calculated from molar mass and density (as shown in Table 1) or measured from the contrast matching SANS experiment.39 The SLD of polymer is likewise obtained from SANS, though the method of calculation depends on the concentration regime of the polymer solution, as illustrated in Fig. 1.
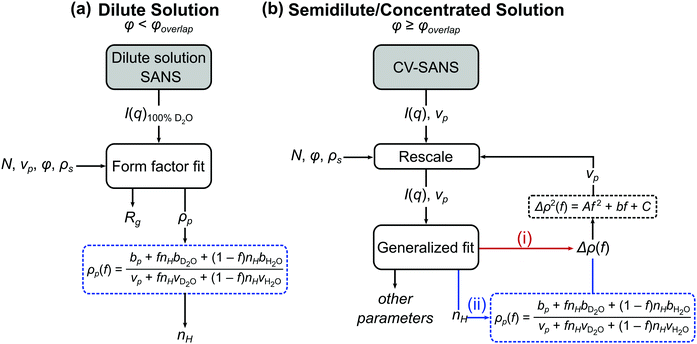 | ||
| Fig. 1 Process flow diagram for calculating hydration number (nH) from (a) dilute and (b) semidilute and concentrated solutions of polymers. For the generalized fit used in semidilute and concentrated solutions, there are two pathways to obtaining the hydration number: (i) fitting Δρ(f) and solving for nH through eqn (1) or (ii) fitting for nH directly. In both cases, Δρ(f) is needed for the contrast matching procedure (eqn (7)) to obtain the volume vp. | ||
The basis for obtaining SLD from contrast matching is described by Nickels et al. for phytoglycogen.39 Here, the analysis is extended to account for effects of polymer solution concentration. As shown in Fig. 1, dilute solution polymers can be analyzed through a SANS experiment in 100% D2O paired with a form factor fit, yielding SLD and radius of gyration; once SLD is obtained, nH can be calculated through eqn (1b). For polymer solutions with a concentration above that of overlap, contrast variation and matching can be leveraged to perform a generalized fit with or without a structure factor. Within this analysis workflow, the fit can be performed for SLD or directly for nH. The data analysis pathways shown in Fig. 1 are summarized in Table 2 and described in detail in subsequent sections.
| Name of method | Identifier | Concentration regime | G(q) functional form | Input parameters | Fitting parameters | Fig. 1 pathway |
|---|---|---|---|---|---|---|
| Note: the methods are named as [SANS experiment]–[G(q)]–[main fitting parameter], where the choices are D (dilute solution SANS), CV (CV-SANS), FF (form factor), SF (structure factor), SLD (scattering length density, ρp), and nH (hydration number).a ρP is a vector, where each element represents SLD at a certain D2O volume fraction, f.b Does not converge when fitting for nH directly.c Requires initial input but changes upon iteration. | ||||||
| Dilute SANS Debye/SLD | D-FF-SLD | Dilute | Debye form factor | N, ϕ, ρs, vp | ρ p (f = 1), Rg | a |
| CV-SANS Model-free/SLDb | CV-MF-SLD | All | None | N, ϕ, ρs, vpc | ρ p | bi |
| CV-SANS Debye/SLD | CV-FF-SLD | Dilute | Debye form factor | N, ϕ, ρs, vpc | ρ p,aRg | bi |
| CV-SANS Debye/nH | CV-FF-nH | Dilute | Debye form factor | N, ϕ, ρs, vpc | n H, Rg | bii |
| CV-SANS Zimm/SLD | CV-SF-SLD | All | Zimm structure factor | N, ϕ, ρs, vp,cRg | ρ p,avex/V | bi |
| CV-SANS Zimm/nH | CV-SF-nH | All | Zimm structure factor | N, ϕ, ρs, vp,cRg | n H, vex/V | bii |
Parameter uncertainty for all fitting pathways illustrated in Fig. 1 was quantified using Monte Carlo bootstrapping.59 In this technique, which is well-suited for high-cost, low-replicate experiments, experimental (technical) replicates, termed replicas, of the scattering intensity were simulated by drawing samples from a normal distribution centered around the measured scattering intensity at each q with a variance defined by the squared error in the scattering intensity measured at each q (Ireplica ∼ ![[scr N, script letter N]](https://www.rsc.org/images/entities/char_e52d.gif) (Imeas, (dImeas)2)). The normality of the scattering intensities was verified using Q–Q plots (Fig. S8–S19, ESI†). For each polymer, concentration, and solvent blend studied, 99 replicas were generated and input into the fitting scheme shown in Fig. 1b for a total of 100 replicas, with the first replica being the original measured data. All parameters obtained through fit or calculation were averaged, and the standard deviation in the 100 samples was taken as the parameter uncertainty. For the hydration number, the standard error of the mean is reported as well.
(Imeas, (dImeas)2)). The normality of the scattering intensities was verified using Q–Q plots (Fig. S8–S19, ESI†). For each polymer, concentration, and solvent blend studied, 99 replicas were generated and input into the fitting scheme shown in Fig. 1b for a total of 100 replicas, with the first replica being the original measured data. All parameters obtained through fit or calculation were averaged, and the standard deviation in the 100 samples was taken as the parameter uncertainty. For the hydration number, the standard error of the mean is reported as well.
For dilute solutions, form factor fitting was used to obtain the scattering length density of the polymer and the hydration number. This is similar to the approach taken by Nickels et al.39 For all polymer solutions at 13.75 mg mL−1, SANS intensity curves taken in 100% D2O were fit using the Debye form factor for Gaussian chains, shown in eqn (2), where q is the scattering vector, and Rg is the radius of gyration of the polymer.
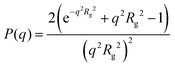 | (2) |
| Ifit(q) = NvpϕΔρ2G(q) + B | (3) |
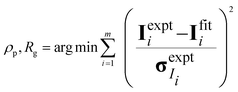 | (4) |
For polymers in semidilute (50 mg mL−1) and concentrated solution (250, 300 mg mL−1), intermolecular interactions are no longer negligible, necessitating an alternate approach to obtain ρp and nH shown in Fig. 1b. The semidilute and concentrated solution approach is more general and can in theory be applied to the dilute solution regime as well. There are two main components to this approach, as shown in Fig. 1—a contrast variation SANS (CV-SANS) experiment and a generalized fit. By changing the blend ratio of D2O to H2O in the solvent, contrast variation (CV) allows the measurement of a family of SANS intensity curves without significantly changing the structure of the polymers or the interactions that are present in the system. In a CV-SANS experiment, for a single polymer at a single concentration, there are n solvent blends, each with an associated ρp, which is a function of f, the volume fraction of D2O in the solvent. The hydration number can be obtained through a fit using eqn (1). This fit assumes that N, vp, φ, and G(q) are the same across all n blends at the same concentration. Thus, CV-SANS leads to the following matrix representation of eqn (3), where I ∈ ![[Doublestruck R]](https://www.rsc.org/images/entities/char_e175.gif) m×n, Δρ ∈
m×n, Δρ ∈ ![[Doublestruck R]](https://www.rsc.org/images/entities/char_e175.gif) 1×n, G ∈
1×n, G ∈ ![[Doublestruck R]](https://www.rsc.org/images/entities/char_e175.gif) m×1, B ∈
m×1, B ∈ ![[Doublestruck R]](https://www.rsc.org/images/entities/char_e175.gif) m×n, and m is the number of q-values.
m×n, and m is the number of q-values.
| I = Nvpϕ(Δρ)⊙2⊙G + B | (5) |
![[Doublestruck R]](https://www.rsc.org/images/entities/char_e175.gif) m×n and ⊙ denotes a Hadamard (element-wise) operation.
m×n and ⊙ denotes a Hadamard (element-wise) operation.| Ifit = 10−20(Nvpϕ)−1(Δρ)⊙2⊙G | (6) |
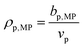 , where bp,MP is the scattering length of the polymer at the match point, taking into consideration exchangeable hydrogens, and ρp,MP is the SLD of the polymer at the match point. Typically, the match point can be obtained by plotting I(q) at one q as a function of f to identify the point at which I(q) equals zero50 or by fitting the total scattering invariant Q* to a quadratic function of f.39 Here, the contrast match point was obtained directly through Δρ2 (shorthand for (Δρ)⊙2), as the scattering invariant could not be reliably obtained at high q due to noise. The vector of Δρ2 can be fit directly to a quadratic function of f using linear least-squares regression, and the point where Δρ2 is minimized can be found via the first derivative of this quadratic function.
, where bp,MP is the scattering length of the polymer at the match point, taking into consideration exchangeable hydrogens, and ρp,MP is the SLD of the polymer at the match point. Typically, the match point can be obtained by plotting I(q) at one q as a function of f to identify the point at which I(q) equals zero50 or by fitting the total scattering invariant Q* to a quadratic function of f.39 Here, the contrast match point was obtained directly through Δρ2 (shorthand for (Δρ)⊙2), as the scattering invariant could not be reliably obtained at high q due to noise. The vector of Δρ2 can be fit directly to a quadratic function of f using linear least-squares regression, and the point where Δρ2 is minimized can be found via the first derivative of this quadratic function.| Δρ2(f) = Af2 + Bf + C | (7) |
CV-SANS intensities collected for semidilute and concentrated polymers were fit to eqn (6). This fitting problem can be described mathematically as eqn (8), where the output polymer SLD ρp is a vector of length n:
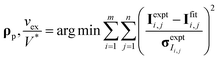 | (8a) |
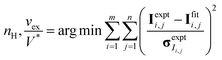 | (8b) |
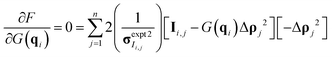 | (9) |
Once the derivative is computed and set equal to 0, it is possible to solve for G(q) at each q-value as eqn (10) in matrix format (all operations are element-wise):
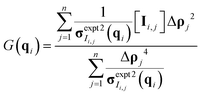 | (10) |
After fitting for polymer SLD, nH can be calculated viaeqn (1). The optimization problem was solved in MATLAB using an interior point method implemented in fmincon. The model-free approach is potentially very powerful, as it can be generalized to many systems beyond polymers and the dilute solution regime.
In the second approach, the Zimm solution structure factor (eqn (11)) was used as G(q), adding the interaction term vex/V as a fitting parameter.49 The form factor was taken to be the Debye form factor (eqn (2)), with the radius of gyration constrained to be that found from dilute solution SANS. The assumption that the radius of gyration can be taken from the dilute solution Debye form factor fit was adopted to simplify the fitting process.
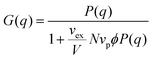 | (11) |
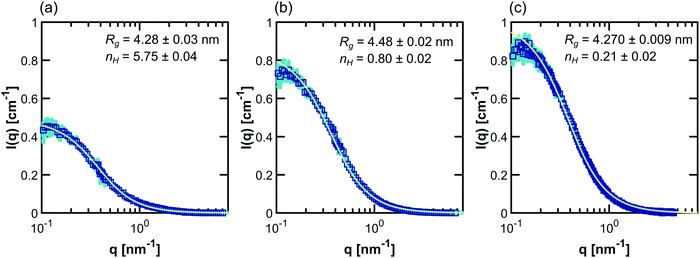
Example fits using the methods listed in Table 2 for PNIPAM in dilute solution are shown in Fig. 3. Fits for other polymers and concentrations can be found in the ESI,† where Fig. S20–S33 depict intensity as a function of q, Fig. S34–S47 depict SLD as a function of D2O volume fraction, and Fig. S48–S59 depict form and structure factors for each polymer at each concentration obtained from each method in Table 2. For CV-SANS methods, there are a panel of SANS intensities, each corresponding to a different H2O/D2O blend; for clarity, only a single replica (i.e. the original experimental intensity) is shown in Fig. 3. Relevant fitting parameters are summarized in subsequent sections in Tables 3 and 5 for all polymers and concentration regimes, with statistics summarized for dilute solutions in Table 4, in the context of model performance. Reported hydration numbers obtained through SLD (CV-MF-SLD, CV-FF-SLD, and CV-SF-SLD methods) are calculated from eqn (1) using the SLD of polymer in 100% D2O, as is done in other literature.39 However, the dependence of nH on the fraction of D2O in the blend is also analyzed for all SLD-based fits in subsequent sections.
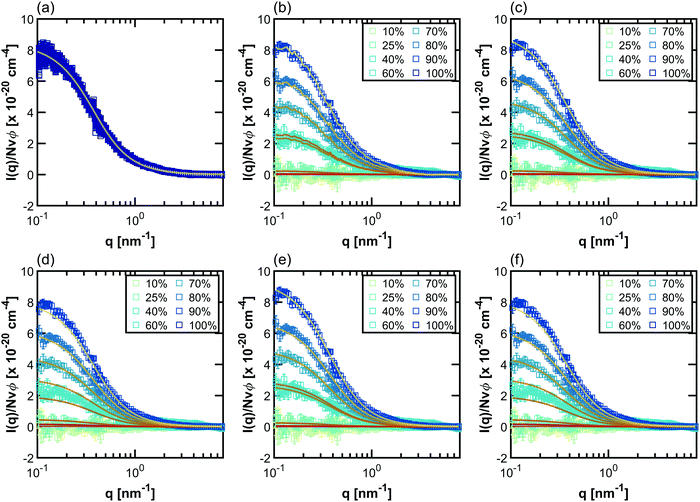 | ||
| Fig. 3 Scaled SANS intensity curves taken for dilute solution PNIPAM (13.75 mg mL−1) fit using the methods described in Table 2: (a) D-FF-SLD, (b) CV-MF-SLD, (c) CV-FF-SLD, (d) CV-FF-nH, (e) CV-SF-SLD and (f) CV-SF-nH. The subplot for the D-FF-SLD method includes all 100 replicas of the SANS intensity curve taken in 100% D2O (dark blue squares), with the solid line representing the Debye fit. For clarity, methods (b)–(f) include only replica 1 (the original experiment, squares), with solid lines representing the fits. Error bars are standard deviation from the instrument. | ||
| Polymer | Method | R g [nm] | Nv p φ(vex/V) | v p [nm3] | n H | |
|---|---|---|---|---|---|---|
| Error bars represent ±1σ over 100 bootstrapped replicates.a Fixed from D-FF-SLD fit (for computational efficiency in linked, bootstrapped fits).b Ideal volume. | ||||||
| PNIPAM | D-FF-SLD | 4.28 ± 0.03 | 0.17896b | 5.75 ± 0.04 | ||
| CV-MF-SLD | 0.168 ± 0.008 | 3.2 ± 0.4 | ||||
| CV-FF-SLD | 4.36 ± 0.02 | 0.168 ± 0.007 | 3.7 ± 0.5 | |||
| CV-FF-nH | 4.58 ± 0.03 | 0.17706 ± 2 × 10−5 | 4.58 ± 0.03 | |||
| CV-SF-SLD | 4.28a | −0.036 ± 0.009 | 0.161 ± 0.007 | 3.4 ± 0.4 | ||
| CV-SF-nH | 4.28a | −0.0367 ± 0.01 | 0.1750 ± 6 × 10−4 | 4.64 ± 0.04 | ||
| PHPA | D-FF-SLD | 4.48 ± 0.02 | 0.1863b | 0.8 ± 0.02 | ||
| CV-MF-SLD | 0.187 ± 0.005 | 0.35 ± 0.06 | ||||
| CV-FF-SLD | 4.336 ± 0.01 | 0.183 ± 0.004 | 0.8 ± 0.2 | |||
| CV-FF-nH | 4.35 ± 0.02 | 0.186325 ± 1 × 10−6 | 0.903 ± 0.01 | |||
| CV-SF-SLD | 4.48a | 0.063 | 0.008 | 0.188 ± 0.005 | 0.7 ± 0.2 | |
| CV-SF-nH | 4.48a | 0.000115 | 0.00001 | 0.186331 ± <0.001 | 0.7 ± 0.02 | |
| PDMAPS | D-FF-SLD | 4.270 ± 0.009 | 0.3386b | 0.2 ± 0.02 | ||
| CV-MF-SLD | 0.297 ± 0.004 | −0.4 ± 0.05 | ||||
| CV-FF-SLD | 4.269 ± 0.009 | 0.320 ± 0.008 | −0.7 ± 0.2 | |||
| CV-FF-nH | 4.209 ± 0.004 | 0.338623 ± <1 × 10−6 | 2 × 10−4 ± 3 × 10−9 | |||
| CV-SF-SLD | 4.27a | −0.014 ± 0.004 | 0.317 ± 0.008 | −0.7 ± 0.2 | ||
| CV-SF-nH | 4.27a | −0.025 ± 0.002 | 0.338623 ± <1 × 10−6 | 2 × 10−4 ± 2 × 10−5 | ||
| Comparison | PNIPAM | PHPA | PDMAPS | ||||
|---|---|---|---|---|---|---|---|
| Pair 1 | Pair 2 | p-Value | Cohen's d | p-Value | Cohen's d | p-Value | Cohen's d |
| D-FF-SLD | CV-MF-SLD | <0.001 | 9.15 | <0.001 | 9.74 | <0.001 | 15.90 |
| D-FF-SLD | CV-FF-SLD | <0.001 | 6.35 | 1 | 0.01 | <0.001 | 6.33 |
| D-FF-SLD | CV-FF-nH | <0.001 | 30.03 | <0.001 | −7.01 | <0.001 | 20.00 |
| D-FF-SLD | CV-SF-SLD | <0.001 | 7.41 | <0.001 | 0.84 | <0.001 | 6.49 |
| D-FF-SLD | CV-SF-nH | <0.001 | 26.71 | <0.001 | 6.40 | <0.001 | 20.00 |
| CV-MF-SLD | CV-FF-SLD | <0.001 | −1.08 | <0.001 | −3.79 | <0.001 | 1.88 |
| CV-MF-SLD | CV-FF-nH | <0.001 | −5.01 | <0.001 | −12.03 | <0.001 | −10.82 |
| CV-MF-SLD | CV-SF-SLD | 0.001 | −0.57 | <0.001 | −2.92 | <0.001 | 2.06 |
| CV-MF-SLD | CV-SF-nH | <0.001 | −5.21 | <0.001 | −7.66 | <0.001 | −10.82 |
| CV-FF-SLD | CV-FF-nH | <0.001 | −2.83 | <0.001 | −0.93 | <0.001 | −4.83 |
| CV-FF-SLD | CV-SF-SLD | 0.006 | 0.51 | 0.001 | 0.60 | 0.922 | 0.14 |
| CV-FF-SLD | CV-SF-nH | <0.001 | −3.01 | <0.001 | 0.87 | <0.001 | −4.83 |
| CV-FF-nH | CV-SF-SLD | <0.001 | 3.71 | <0.001 | 1.73 | <0.001 | 4.99 |
| CV-FF-nH | CV-SF-nH | <0.001 | −1.68 | <0.001 | 14.12 | 0.132 | −0.35 |
| CV-SF-SLD | CV-SF-nH | <0.001 | −3.90 | 1 | 0.02 | <0.001 | −4.99 |
Hypothesis testing and effect sizes
Statistical comparisons of hydration numbers obtained from the various fitting methods applied to bootstrapped datasets were performed using hypothesis testing and effect sizes. Bootstrapping gives access to simulated technical replicates. It allows for comparison within a single polymer and concentration group, assuming that the SANS instrument performs consistently given a desired number of total counts (typically 500![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 above background for this set of experiments). Here, the null hypothesis is that all the fitting methods described in Table 2 yield the same hydration number. To select an appropriate test, the distribution of the hydration numbers obtained from each fit (per polymer, per concentration) was verified to be Gaussian using Q–Q plots (Fig. S8–S19, ESI†). However, a Bartlett test showed that each set of hydration numbers obtained from different fitting methods had unequal variances. Thus, a Welch's one-way ANOVA test followed by a post-hoc Games–Howell test was chosen to evaluate the differences between fitting methods. The Games–Howell test was implemented in R from the userfriendlyscience package. This analysis is valid for normally distributed data with unequal variances. Since bootstrapping enables the use of large sample sizes (here, 99 replicas were simulated from the original experimental dataset for a total of 100 datasets), statistical significance may be achieved even with small effect sizes. Thus, effect size between pairs of fitting methods was calculated using Cohen's d, shown in eqn (12),63 which is more representative of the meaningful variation between measurements. Here, for dataset i,
000 above background for this set of experiments). Here, the null hypothesis is that all the fitting methods described in Table 2 yield the same hydration number. To select an appropriate test, the distribution of the hydration numbers obtained from each fit (per polymer, per concentration) was verified to be Gaussian using Q–Q plots (Fig. S8–S19, ESI†). However, a Bartlett test showed that each set of hydration numbers obtained from different fitting methods had unequal variances. Thus, a Welch's one-way ANOVA test followed by a post-hoc Games–Howell test was chosen to evaluate the differences between fitting methods. The Games–Howell test was implemented in R from the userfriendlyscience package. This analysis is valid for normally distributed data with unequal variances. Since bootstrapping enables the use of large sample sizes (here, 99 replicas were simulated from the original experimental dataset for a total of 100 datasets), statistical significance may be achieved even with small effect sizes. Thus, effect size between pairs of fitting methods was calculated using Cohen's d, shown in eqn (12),63 which is more representative of the meaningful variation between measurements. Here, for dataset i, 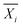 is the sample mean, Ni is the sample size, and σi is the sample standard deviation.
is the sample mean, Ni is the sample size, and σi is the sample standard deviation.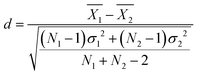 | (12) |
Model performance in dilute solution
Since all proposed fitting pathways apply generally to the dilute solution regime, dilute solution SANS intensities were fit using all methods listed in Table 2. In this concentration regime, the Zimm interaction parameter is relatively small, indicating that the data can simply be described with the Debye form factor, as expected (Table 3 and Fig. S48–S50, ESI†). The resulting hydration numbers are compared across methods for each polymer in Fig. 4 (see Fig. S60 for the same data on different scales, ESI†). For those methods that fit ρp(f) instead of nH directly, hydration number was also calculated by averaging across all replicas from high D2O blends (>60%), as represented by the light blue bars in Fig. 4.The dilute solution SANS Debye fit (D-FF-SLD), which only uses the SANS intensity taken in 100% D2O, results in hydration numbers with very small standard deviations, shown in Table 3. For PNIPAM and PDMAPS, this hydration number is higher than those calculated from other methods, whereas for PHPA, the hydration number is similar to those obtained from other methods. This method, however, overestimates the data in the low-q region for PHPA and PDMAPS (Fig. 2b and c). This deviation in the fit may be due to PHPA and PDMAPS being slightly non-Gaussian in dilute solution. The model-free approach (CV-MF-SLD) produces a hydration number that is slightly lower than the hydration numbers obtained from other SLD-based fits for PNIPAM and PHPA; for PDMAPS, the model-free approach gives a hydration number closer to those predicted by the nH-based methods.
In general, the SLD-based fits paired with a form or structure factor (CV-FF-SLD, CV-SF-SLD) yielded hydration numbers that were within a standard deviation (Table 3) of each other. For PHPA, the SLD-based Zimm fits also yielded hydration numbers that were within error of results from nH-based fits (CV-SF-SLD, CV-SF-nH). For PDMAPS, SLD-based fits yielded negative hydration numbers, which are not physical. The observation of both small (<|1|) positive and negative hydration numbers in PDMAPS suggests that it likely has a hydration number close to 0, as indicated by the nH-based fits, and that the negative values are fluctuations around 0.
For all polymers, the hydration numbers obtained from SLD-based fits after averaging across high D2O blends are similar to those obtained from only the SLD in 100% D2O, indicating that the optimizer has converged to the same hydration number, as dictated by eqn (1), despite the high number of degrees of freedom when fitting for the SLD vector ρp. One consequence of this relatively unconstrained fitting method was that the hydration numbers obtained through SLD-based fits had a larger spread (Fig. 5 and Fig. S61, ESI†). The low D2O blends could not be used for this analysis due to a low signal-to-noise ratio from H2O incoherent scattering. For CV-SANS experiments, all SLD-based methods did in fact yield a lower value for the objective function, and the model-free approach had the lowest objective functions. This is largely due to the relatively unconstrained nature of these fits compared to a direct fit for the hydration number. While these methods allow for the fluctuation of the hydration number across different H2O/D2O blends, this freedom can also lead to issues when SANS intensity curves are flat in low D2O blends.
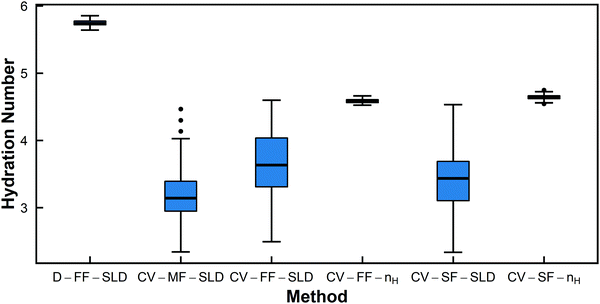 | ||
| Fig. 5 Box-and-whisker plots for hydration number of PNIPAM in dilute solution (13.75 mg mL−1) from the six different fitting methods. | ||
The Welch's one-way ANOVA test showed that for all polymers in dilute solution, the hydration numbers obtained from different methods were statistically not equivalent (p < 0.01), but statistical significance was dominated by large sample size. For PNIPAM, the Welch's ANOVA and Games-Howell tests indicate that the null hypothesis that there is no difference between fitting methods should be rejected in all pairwise comparisons (p < 0.01 in all cases) (Table 4). However, Fig. 5 shows that several of the methods have overlapping distributions (i.e. CV-MF-SLD/CV-SF-SLD and CV-FF-SLD/CV-SF-SLD). This is because statistical significance does not necessarily imply a large effect size, as shown in Table 4. Though the pairs of CV-MF-SLD/CV-SF-SLD and CV-FF-SLD/CV-SF-SLD appear to yield hydration numbers that are significantly different from each other (p < 0.01), these differences have only a medium effect size (∼|0.5|).63 For PHPA, methods D-FF-SLD and CV-FF-SLD yielded statistically the same hydration number (p = 1, d = 0.01), as did methods CV-SF-SLD and CV-SF-nH (p = 1, d = 0.02). In addition, the difference between hydration numbers obtained from CV-FF-SLD and CV-SF-SLD are statistically significant, but the effect size is moderate (p = 0.001, d = 0.60). For PDMAPS, the pairs CV-FF-SLD/CV-SF-SLD (p = 0.922, d = 0.14) and CV-FF-nH/CV-SF-nH (p = 0.132, d = −0.35) yielded the same hydration number statistically. Though most of the methods yielded statistically distinct hydration numbers, on a practical level, many of these quantities are very similar and fall within 1 water molecule per repeat unit of each other.
In addition to hydration number, the volume of the monomer unit, vp, presents another metric by which to gauge the performance of the six fitting methods. The volume vP as obtained from contrast-matching SLD-based fits deviated the most from the ideal volumes shown in Table 1. For dilute solution PNIPAM, SLD-based methods gave volumes that deviated from the ideal volume by at most 10%. For PDMAPS, the greatest deviation from the ideal volume was from the model-free approach, at 12% difference. However, PHPA did not have any large deviations from the ideal volume in any fitting method (the largest was <2%, from CV-FF-SLD). This agreement is likely dependent on the ideal volume assumption and the quality of the data in the low D2O blends, since the match point occurs in this region; of the three polymers, PHPA had the highest signal-to-noise ratio in low-D2O blends, whereas the other polymers had largely flat intensity curves in blends with less than 40% D2O (Fig. S20, ESI†). For the other polymers, there may also be a true deviation in the actual volume compared to the ideal volume.
In assessing which fitting method performs the best in dilute solution, it appears that either single-solution dilute SANS form factor fitting (D-FF-SLD) or CV-SANS paired with a Debye form factor fitting for nH (CV-FF-nH) yields the most consistent hydration numbers. The benefit of using the latter is that the Debye form factor is essentially fit to multiple replicates (i.e. the different blends). However, the assumption that the form factor is constant across all H2O/D2O blends must hold. If the polymer interacts differently with water compared to heavy water, this assumption breaks down. If the restriction on the functional form of ρp is relaxed (i.e. fitting for SLD instead of nH), reasonable hydration numbers can still be obtained for certain cases, as long as there is a functional form for the form factor. Additionally, the Zimm structure factor generally reduces to the Debye form factor in dilute solution, as expected (small interaction parameters in Table 3). Finally, while the model-free approach is theoretically powerful, it produced inconsistent results across the three polymers. It performs fairly well in the case of PNIPAM but underestimates hydration numbers for the other two polymers, indicating the need for constraints to restrict the optimizer to a physical search space. This is mainly caused by the inverse correlation between the SLD and the form/structure factor, G(q), as shown in eqn (3). When G(q) has no functional form, its value can vary freely as a function of q. With only the vector of SLDs as the fitting parameters, the optimizer can compensate for a smaller SLD by increasing the magnitude of G(q). For PHPA and PDMAPS, the model-free approach gives a G(q) that deviates from the Debye form factor from D-FF-SLD in the same direction as the imposed Zimm structure factor in the CV-SF-SLD and CV-SF-nH methods but to a greater degree (see Fig. S49 and S50, ESI†). Despite these limitations, in all cases, the model-free approach does yield hydration numbers within 1 water molecule of other approaches.
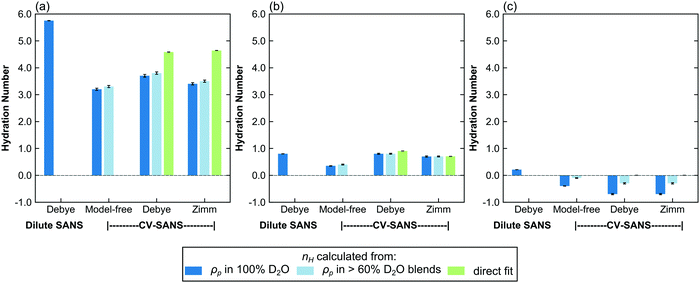
Model performance in the semidilute and concentrated regimes
In contrast to polymer hydration number in the dilute regime, the hydration numbers of polymers in the semidilute and concentrated regimes are not well characterized. The determination of the hydration number requires a structure factor that does not have any scaling constants apart from NvφΔρ2. Here, three fitting methods are applied to data in the non-dilute regime: CV-MF-SLD, CV-SF-SLD, and CV-SF-nH, corresponding to model-free CV-SANS fitting SLD, CV-SANS with Zimm structure factor fitting SLD, and CV-SANS with Zimm structure factor fitting nH, respectively. The resulting hydration numbers are plotted in bar graphs in Fig. 6, with box-and-whisker plots in Fig. S62–S64 (ESI†). In the semidilute regime, Zimm interaction parameters are slightly negative for PHPA and PDMAPS but positive for PNIPAM, suggesting that PNIPAM molecules are repulsive to each other. In this regime, the Welch's ANOVA test shows that the differences in the hydration numbers obtained from each method are statistically significant for all three polymers. However, some of these differences are less than 1 water molecule per repeat unit. In PNIPAM, both SLD-based methods produce hydration numbers that were within 1 standard deviation of each other, yielding a Cohen's d value of −0.56 (medium effect size), but the nH-based method yielded a much lower hydration number (Table S1, ESI†). The structure factors predicted by the SLD-based methods are also similar for PNIPAM (Fig. S51, ESI†), and they led to larger monomer volumes from contrast matching. For PHPA, the SLD-based Zimm fit did not converge, but the model-free fit gave a result that was less than 1 water molecule from the hydration number obtained through the nH-based Zimm fit, though this difference had a large effect size (d = −13.57) since the spread of the hydration number from each method was very narrow (Table S1, ESI†).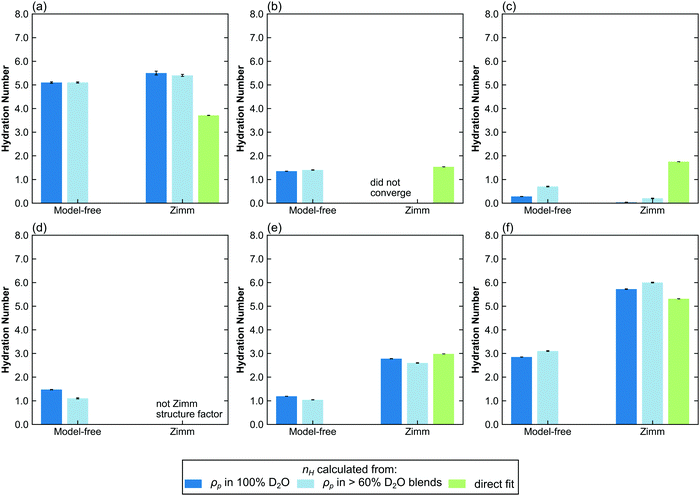 | ||
| Fig. 6 Bar charts comparing the hydration number obtained through different fitting methods in the semi-dilute and concentrated regimes. Top row: (a) PNIPAM, (b) PHPA, and (c) PDMAPS in semidilute solution (50 mg mL−1). Bottom row: (d) PNIPAM, (e) PHPA, and (f) PDMAPS in concentrated solution (250 mg mL−1). Hydration numbers for 300 mg mL−1 solutions can be found in Fig. S65 (ESI†). The hydration numbers obtained from SLD (dark and light blue bars) are from the CV-SANS approach (i), and directly fit hydration numbers are from approach (ii). The light blue bars represent hydration numbers averaged across high D2O blends. Error bars represent standard error of the mean from 100 replicas. | ||
For PDMAPS, the results vary across all the models, though the SLD-based models generally predict a hydration number closer to 0. The PDMAPS structure factors are mostly consistent across the three models, but the contrast matched volumes deviate from the ideal volume by as much as 13%, in contrast to the nH-based method, which matches with the ideal volume. Perturbations in the volume can propagate to the SLD in two ways, causing it to deviate from the functional form of eqn (1). Changes in the volume affect both the rescaling of the scattering intensities and the calculation of the SLD itself from 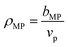 . The deviation in SLD is evident in the averaged nH across the high-D2O blends in Fig. 6c, which diverges from the hydration number calculated from the 100% D2O SLD.
. The deviation in SLD is evident in the averaged nH across the high-D2O blends in Fig. 6c, which diverges from the hydration number calculated from the 100% D2O SLD.
In the concentrated regime (250, 300 mg mL−1), PHPA and PDMAPS begin to experience repulsive intermolecular interactions, as evidenced by the positive Zimm interaction parameter (Table 5). Here, the model-free approach consistently underestimates the hydration number compared to the models that include a Zimm structure factor (Fig. 6d–f and Fig. S63–S65, ESI†). For PHPA and PDMAPS, the difference in the hydration numbers obtained from a SLD- versus nH-based Zimm fit is statistically significant (p < 0.01), with very large effect sizes (d ≥ 1) (Tables S2 and S3, ESI†). However, these numbers are physically similar, since they are within 1 water molecule per repeat unit of each other. Furthermore, the structure factors obtained from both Zimm methods are similar, indicating that these fits are consistent with each other. This suggests that the model-free approach breaks down in this regime for PDMAPS and PHPA. Unfortunately, in this regime, PNIPAM takes on a different structure factor with a mid-q shoulder and thus, a reliable hydration number cannot be extracted from the CV-SF-SLD and CV-SF-nH methods. The hydration number obtained from the Zimm methods was used as an initial guess for the model-free method, which assumes that while the Zimm structure factor is the wrong functional form, the asymptotic behavior of the Zimm structure factor at low q provides a reasonable estimate for the asymptotic behavior of the true structure factor, but the optimizer converged to a much lower hydration number, as shown in Fig. 6d and Fig. S65a (ESI†). The hydration numbers obtained from the Zimm methods are very close to the upper limit on the hydration number, which is calculated by assuming all water molecules in the solution are bound water.
| Polymer | Method | R g [nm] | Nv p φ(vex/V) | v p [nm3] | n H |
|---|---|---|---|---|---|
| Error bars represent ± 1σ over 100 bootstrapped replicates.a Fixed from D-FF-SLD fit (for computational efficiency in linked, bootstrapped fits). | |||||
| Semidilute regime: 50 mg mL−1 | |||||
| PNIPAM | CV-MF-SLD | 0.205 ± 0.008 | 5.2 ± 0.3 | ||
| CV-SF-SLD | 4.28a | 1.86 ± 0.02 | 0.205 ± 0.01 | 5.5 ± 0.8 | |
| CV-SF-nH | 4.28a | 1.83 ± 0.02 | 0.1776 ± 0.0002 | 3.72 ± 0.02 | |
| PHPA | CV-MF-SLD | 0.158 ± 0.007 | 1.35 ± 0.02 | ||
| CV-SF-SLD | 4.48a | No convergence, likely due to shape of low-q region | |||
| CV-SF-nH | 4.48a | −0.396 ± 0.002 | 0.186283 ± 1 × 10−6 | 1.532 ± 0.008 | |
| PDMAPS | CV-MF-SLD | 0.320 ± 0.002 | 0.28 ± 0.02 | ||
| CV-SF-SLD | 4.27a | −0.393 ± 0.002 | 0.293 ± 0.003 | 0.03 ± 0.09 | |
| CV-SF-nH | 4.27a | −0.369 ± 0.002 | 338.652 ± <1 × 10−6 | 1.75 ± 0.01 | |
| Concentrated regime: 250 mg mL−1 | |||||
| PNIPAM | CV-MF-SLD | 0.151 ± 0.003 | 1.47 ± 0.07 | ||
| CV-SF-SLD | 4.28a | Not Zimm structure factor | |||
| CV-SF-nH | 4.28a | ||||
| PHPA | CV-MF-SLD | 0.1786 ± 0.0007 | 1.19 ± 0.02 | ||
| CV-SF-SLD | 4.48a | 0.261 ± 0.01 | 0.181 ± 0.008 | 2.78 ± 0.04 | |
| CV-SF-nH | 4.48a | 0.245 ± 0.004 | 0.186512 ± 1 × 10−6 | 2.98 ± 0.01 | |
| PDMAPS | CV-MF-SLD | 0.3602 ± 0.001 | 2.85 ± 0.02 | ||
| CV-SF-SLD | 4.27a | 0.173 ± 0.005 | 0.348 ± 0.002 | 5.72 ± 0.1 | |
| CV-SF-nH | 4.27a | 0.179 ± 0.004 | 0.339004 ± 1 × 10−6 | 5.31 ± 0.02 | |
In the semidilute regime, the most consistent method to obtain hydration number is through the CV-SF-nH method, which is the Zimm method paired with a direct nH fit, though for the most part, CV-MF-SLD and CV-SF-SLD provide similar hydration numbers, except for PDMAPS. At 50 mg mL−1, the signal-to-noise ratio in the scattering intensities taken in low D2O blends remains an issue, which affects the contrast matching and the SLD fits to a greater extent than direct nH fits. In the concentrated regime, the CV-SF-SLD and CV-SF-nH methods both provide consistent hydration numbers, as well as contrast matched volumes. This is likely due to the improved signal in SANS intensities taken in low D2O blends. However, the Zimm structure factor does not apply to PNIPAM in this regime.
The analysis of the concentration dependence of the hydration number in the next section is done with hydration numbers taken from CV-FF-nH (dilute) and CV-SF-nH (non-dilute), with the exception of hydration numbers of PNIPAM in concentrated solution, which were extracted from the CV-MF-SLD method.
SANS detects and quantifies the strongly bound hydration water
The behavior of the hydration number as a function of concentration varies across polymer chemistries (Fig. 7). In dilute solution, PNIPAM has the highest hydration number, followed by PHPA, with PDMAPS having a hydration number of 0. In semidilute solution, PNIPAM still has the highest hydration number, but PDMAPS and PHPA now have similar hydration numbers that are higher than in dilute solution (Fig. 7a). For PHPA, this change may not be significant, as the hydration number increased by less than 1 water molecule. Since PDMAPS has a much larger monomer compared to the other polymers, the hydration number was also scaled by the monomer volume (Fig. 7b). When scaled, the hydration number for PDMAPS drops below that of PHPA. In concentrated solution, the raw hydration number continues to increase for PDMAPS and PHPA; when scaled, the hydration numbers for PDMAPS and PHPA collapse to between 15–20 water molecules per cubic nm. For PNIPAM, the hydration number decreases to ∼1.5 water molecules, which amounts to ∼10 water molecules per cubic nm. For all polymers, the change in hydration number within the concentrated regime from 250 to 300 mg mL−1 is almost negligible and less than 1 water molecule per monomer unit, but in the transition from semidilute to concentrated, the hydration number changes by more than 1 water molecule per monomer.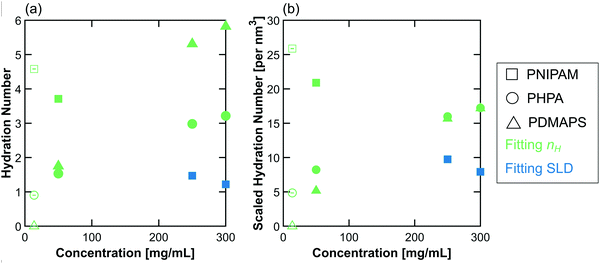 | ||
| Fig. 7 (a) Hydration number and (b) scaled hydration number as a function of polymer concentration in solution. The colors are chosen to match those in Fig. 4 and 6, where green represents nH-based fitting methods (here, CV-FF-nH and CV-SF-nH), and blue represents SLD-based methods (here, CV-MF-SLD). Open symbols are hydration numbers obtained from CV-FF-nH, and closed symbols are hydration numbers obtained from the CV-MF-SLD or CV-SF-nH fits. Error bars (standard error of the mean over 100 replicas) are smaller than the symbols. | ||
Comparison of the hydration numbers measured here using CV-SANS to those available in the literature suggests that the CV-SANS method captures not all of the water molecules in the first hydration shell but the most strongly bound water molecules. Though many hydration measurement techniques do not leverage the same physics to probe interactions with water, comparison among them can both provide a check for hydration numbers obtained through scattering fits and give insight into the interactions that are detected by neutron scattering. Using dielectric relaxation spectroscopy, Ono and Shikata showed that linear PNIPAM has a hydration number of 11, with little concentration and molar mass dependence.30 The same technique revealed that the bare monomer NIPAM has a hydration number of 5–6,64 cyclic PNIPAM has a hydration number of 12, and linear PNIPAM with azido and alkyne end groups has a hydration number of 13.29 All-atom simulations of isotactic-rich PNIPAM 30-mers show that in the first hydration shell (defined based on the radial distribution function between relevant interacting groups), the hydrophobic group interacts with 5.9 ± 0.2 water molecules, and the hydrophilic group interacts with 1.9 ± 0.08 water molecules at 278 K.65 In contrast, all-atom simulations of atactic PNIPAM 30-mers suggest that the first hydration shell contains 14 ± 1 water molecules.66 These measurements of the number of water molecules in the first hydration shell are larger than those found in this study at any concentration (maximum 4.5 in dilute solution). However, the hydration number measured in these experiments does align with the number of water molecules that are bound to molecules of NIPAM64 in aqueous solution via direct hydrogen bonding to the amide group (3 water molecules) and via H-bonding to these directly bound waters (∼2 water molecules). Ono and Shikata hypothesize that the much higher hydration number measured by dielectric relaxation spectroscopy for PNIPAM compared to NIPAM could be from bridging of water molecules between monomers.64 Since the scattering length density defined in the SANS experiments is calculated per monomer (eqn (1)), it is not surprising that the hydration number matches more closely with the NIPAM monomer result. The SANS experiments thus detect the strongly bonded subset of the first hydration water shell that surrounds PNIPAM.
There is evidence for different populations of hydration water surrounding PNIPAM in both experiment and simulation, with different population sizes. In a quasielastic neutron scattering (QENS) study of PNIPAM in 250 mg mL−1 of H2O, the total hydration number under the transition temperature was measured to be 8; when PNIPAM undergoes a phase transition, some of these water molecules become very strongly bound (∼2 water molecules, attributed to those H-bonded to the amide group).41 In simulation, each monomer is found to have 2.6 H-bonds with water at 5 °C, with 1.4–1.5 water–water H-bonds per water molecule in the first hydration shell. Furthermore, clusters of 2–3 water molecules are most commonly found around the hydrophilic groups of PNIPAM within the first hydration shell.66 Hydration numbers from dielectric relaxation spectroscopy can also be decomposed into three populations, with the strongly bound group of “frozen” water molecules having the smallest population size (∼1, with fairly large spread at low concentrations).67 The numbers measured by SANS for dilute and semidilute concentration fall within the error bars of this measurement. They are also consistent with the expected number of H-bonded water molecules measured from simulation.
The hydration numbers measured for PHPA (∼1–3) also support the idea that the CV-SANS method counts the most strongly bound water. While the hydration of PHPA is not commonly studied, polymers with similar structures such as poly(hydroxyethyl methacrylate) (PHEMA), poly(hydroxyethyl acrylate) (PHEA), and poly(methoxyethyl acrylate) (PMEA, with caveat that this is not a hydrogen bond donor) are widely studied as hydrogel materials.16,26,32,68–71 As stated in the introduction, water may be grouped into three populations. In this framework, the bound population of hydration water is said to share dynamic and thermodynamic properties with the polymer chain.68 For PMEA, ATR-FTIR shows that the most common type of non-freezing water is one water molecule shared by the carbonyl oxygen between two consecutive monomers.72 Thermogravimetric analysis (TGA) of PHEMA films after soaking in liquid water showed that 3.2 water molecules/monomer were sorbed into the film at equilibrium.73 Simulations of PHEA hydrogels indicate that depending on the concentration of water in the system, water can form 0–3 hydrogen bonds per monomer, mostly between water and the hydroxyl group.74 Thus, like for PNIPAM, SANS appears to measure the population of strongly bound water directly hydrogen-bonded to donors and acceptors on PHPA monomer units.
For PDMAPS, the hydration number varies from ∼0–6 depending on the concentration, which is surprising in light of other studies on this polymer. By NMR, the hydration number for PDMAPS is measured to be 6.67–8.75 This aligns with the high concentration hydration number measured by SANS. The hydration number measured by NMR most likely corresponds to the water molecules that associate with the negatively charged group of PDMAPS, which has been shown by simulation to have 7.08 ± 0.01 hydration water molecules in the first hydration shell.76 In contrast, the positively charged group associates with 18.64 ± 0.01 hydration water molecules in the first hydration shell. However, water molecules that associate with the negative group are more structured and have a longer residence time.76 Although zwitterionic polymers with sulfobetaine (such as PDMAPS) and carboxybetaine monomers are generally considered to have a stronger interaction with water molecules than non-ionic polymers, such as poly(ethylene glycol) (PEG), the SANS study shows that at least in dilute solution, PDMAPS does not appear to associate as strongly with water compared to PNIPAM and PHPA. Unlike PEG, PNIPAM and PHPA both have hydrogen bond donors. These groups may enhance water–polymer interactions in these non-ionic polymers relative to PDMAPS. There may also be small differences in interactions with D2O compared to H2O.
Concentration dependence of hydration number
As shown in Fig. 7, as concentration increases, the hydration number of PNIPAM decreases, and the hydration numbers of PHPA and PDMAPS increase. This discrepancy can be attributed to chemistry-specific water–polymer interactions. PNIPAM has an especially high affinity for water, with a cooperative hydration process, where water molecules tend to hydrogen bond to those monomers that already have existing associations with water.77 This cooperative hydration mechanism leads to a flat phase diagram also shown here using cloud point measurements (Fig. S7, ESI†). Thus, even in dilute solution, PNIPAM has a high hydration number. The presence of an extensive hydration network surrounding each PNIPAM molecule contributes to the repulsive intermolecular interactions measured in the Zimm structure factor in semidilute solution (Table 5). However, as concentration increases, the polymer chains are forced more closely together, disrupting the hydration network and lowering the hydration number.41 In fact, the hydration number as measured by the model-free approach for the concentrated solutions is very close to the theoretical value if the only bound waters are those H-bonded to the amide group.41 These hydration water molecules have been shown to be bound to PNIPAM even above the coil-to-globule transition.28 In addition, PNIPAM takes on a very different structure factor compared to the other polymers at high concentration, where a shoulder appears in the mid-q region (Fig. S66, ESI†). This second characteristic length scale has been attributed to the formation of PNIPAM microglobules at high concentration, which are also observable by small and wide-angle X-ray scattering (SWAXS).78 Fitting the PNIPAM scattering intensities taken at 250 and 300 mg mL−1 to a sum of the Ornstein–Zernike and pseudo-Voight Lorentzian functions (eqn (S3) and (S4), ESI†) allows for the estimation of both blob correlation length and microglobule correlation length (Tables S5 and S6, ESI†).67,78 These microglobules are dispersed in the matrix of polymer chains and have been hypothesized to weaken the structure of the hydration water network when the PNIPAM undergoes its thermally driven phase transition.78,79 The appearance of these microglobules at high concentration even below the PNIPAM LCST may explain the trend in hydration number. As the solution transitions from semidilute to concentrated, microglobules begin to form, with the distance between microglobules decreasing as concentration increases (Table S6, ESI†), crowding out the hydration water network and leaving only the amide H-bonded water molecules bound to the monomer units.In contrast to PNIPAM, PHPA and PDMAPS experience an increase in the hydration number as concentration increases. This is likely a consequence of the inherently weaker interaction between water and polymer in these systems compared to the PNIPAM/water system. As shown in Fig. 7, PHPA and PDMAPS have a similarly low hydration number in dilute solution. However, as concentration increases, water molecules and polymer chains are forced to interact more closely. This behavior has been shown to occur for water and PHEA hydrogels in simulation, where at high water content, water molecules preferred to H-bond with each other in clusters, but at low water content, water molecules interacted instead with H-bonding groups on the HEA monomer.74 The trend in the hydration number correlates with the increase in the Zimm interaction parameter, suggesting that as the number of bound water molecules increases, the polymers become more repulsive to each other. Thus, the concentration dependence of bound water is strongly governed by the polymer chemistry and specific interactions with water molecules.
Conclusion
Contrast-variation small-angle neutron scattering (CV-SANS) was used to investigate the hydration of three water-soluble polymers in dilute, semidilute, and concentrated solution. Multiple fitting pathways were presented, and model performance was compared using a combination of hypothesis testing, effect sizes, physical insight, and literature-based validation. Appropriate model fitting pathways can be selected based on several criteria including data quality, concentration regime, and the need for physical constraints. In the dilute regime, if all polymer blends have the same form factor, a form factor fit paired with direct fitting of the hydration number gives the most consistent results. In the semidilute and concentrated regimes, if a structure factor is available, the most reliable analysis is a structure factor fit with the hydration number as a fitting parameter. If a structure factor is not available, and all CV-SANS data have a high signal-to-noise ratio, the model-free algorithm can provide a good estimate of the hydration number. In all cases, Monte Carlo bootstrapping can be implemented to quantify uncertainty in these types of high-cost, low-replicate neutron scattering experiments.The CV-SANS method is shown to detect and measure only strongly bound water molecules and not all the water inside the first hydration shell. This indicates that neutron scattering can be used to study direct interactions between solvent and solute. The concentration dependence of the hydration number was highly correlated with polymer chemistry. As polymer concentration increased, polymers with a weaker interaction with water (PHPA, PDMAPS) gained bound water molecules, while PNIPAM, which interacts more strongly with water, lost bound water molecules. Thus, the CV-SANS method has great utility for measuring reliable and consistent hydration numbers (or generally, solvent numbers) for polymers across multiple concentration regimes. Furthermore, concentration was shown to have a major impact on the strength of interactions between water and polymer, which has implications for the design of polymeric materials that interface with water and indicates that dilute solution measurements of hydration may not be reflective of the relevant properties in higher concentration systems.
Conflicts of interest
There are no conflicts to report.Acknowledgements
This work was supported by the Department of Energy Office of Basic Energy Sciences Neutron Scattering Program (award number DE-SC0007106). CV-SANS experiments were conducted at the NIST Center for Neutron Research (NCNR) NG7 and NGB 30 m instruments with the help of Dr Susan Krueger, Dr Jeff Krzywon, and Dr Cedric Gagnon. Dilute solution SANS and additional CV-SANS experiments were run at Oak Ridge National Lab (ORNL) EQ-SANS with the help of Dr Changwoo Do and Dr William Heller and Bio-SANS with the help of Dr Shuo Qian. We thank Professor James Swan for enlightening discussions on the weighted low-rank approximation method used in the model-free fitting approach. We thank Professor Gregory Rutledge for the suggestion to explore bootstrapping-based methods for error quantification. We thank Dr Michelle Calabrese, Dr Aaron Huang, Dr Danielle Mai, and Dr Carolyn Mills for assistance with neutron scattering experiments. Additionally, we thank Takuya Suguri for assistance with polymer synthesis and the Johnson group in the Department of Chemistry at MIT for use of their DMF GPC.References
- R. Duncan, Nat. Rev. Drug Discovery, 2003, 2, 347–360 CrossRef CAS PubMed.
- S. Liu, R. Maheshwari and K. L. Kiick, Macromolecules, 2009, 42, 3–13 CrossRef CAS PubMed.
- C. M. Magin, S. P. Cooper and A. B. Brennan, Mater. Today, 2010, 13, 36–44 CrossRef CAS.
- L. D. Blackman, P. A. Gunatillake, P. Cass and K. E. S. Locock, Chem. Soc. Rev., 2019, 48, 757–770 RSC.
- M. A. Gauthier and H.-A. Klok, Polym. Chem., 2010, 1, 1352–1373 RSC.
- H.-C. Yang, K.-J. Liao, H. Huang, Q.-Y. Wu, L.-S. Wan and Z.-K. Xu, J. Mater. Chem. A, 2014, 2, 10225–10230 RSC.
- Z. Wang, E. van Andel, S. P. Pujari, H. Feng, J. A. Dijksman, M. M. J. Smulders and H. Zuilhof, J. Mater. Chem. B, 2017, 5, 6728–6733 RSC.
- M. Tanaka, T. Hayashi and S. Morita, Polym. J., 2013, 45, 701–710 CrossRef CAS.
- M. A. Bag and L. M. Valenzuela, Int. J. Mol. Sci., 2017, 18, 1422 CrossRef PubMed.
- M. Tanaka, Contrib. Nephrol., 2017, 189, 137–143 Search PubMed.
- S. Ahadian, R. B. Sadeghian, S. Salehi, S. Ostrovidov, H. Bae, M. Ramalingam and A. Khademhosseini, Bioconjugate Chem., 2015, 26, 1984–2001 CrossRef CAS PubMed.
- J. Zhu and R. E. Marchant, Expert Rev. Med. Devices, 2011, 8, 607–626 CrossRef CAS PubMed.
- S. Ashraf, H.-K. Park, H. Park and S.-H. Lee, Macromol. Res., 2016, 24, 297–304 CrossRef CAS.
- T. Luo, M. A. David, L. C. Dunshee, R. A. Scott, M. A. Urello, C. Price and K. L. Kiick, Biomacromolecules, 2017, 18, 2539–2551 CrossRef CAS PubMed.
- D. Chang, C. N. Lam, S. Tang and B. D. Olsen, Polym. Chem., 2014, 5, 4884–4895 RSC.
- M. S. Jhon and J. D. Andrade, J. Biomed. Mater. Res., 1973, 7, 509–522 CrossRef CAS PubMed.
- O. Hechter, T. Wittstruck, N. McNiven and G. Lester, Proc. Natl. Acad. Sci. U. S. A., 1960, 46, 783–787 CrossRef CAS PubMed.
- V. J. McBrierty, S. J. Martin and F. E. Karasz, J. Mol. Liq., 1999, 80, 179–205 CrossRef CAS.
- C. Sterling and M. Masuzawa, Macromol. Chem. Phys., 1968, 116, 140–145 CrossRef CAS.
- Y. Hirata, Y. Miura and T. Nakagawa, J. Membr. Sci., 1999, 163, 357–366 CrossRef CAS.
- M. Tanaka, T. Motomura, N. Ishii, K. Shimura, M. Onishi, A. Mochizuki and T. Hatakeyama, Polym. Int., 2000, 49, 1709–1713 CrossRef CAS.
- H. Hatakeyama and T. Hatakeyama, Thermochim. Acta, 1998, 308, 3–22 CrossRef CAS.
- A. Higuchi and T. Iijima, Polymer, 1985, 26, 1833–1837 CrossRef CAS.
- M. Aizawa and S. Suzuki, Bull. Chem. Soc. Jpn., 1971, 44, 2967–2971 CrossRef CAS.
- H. B. Lee, M. S. Jhon and J. D. Andrade, J. Colloid Interface Sci., 1975, 51, 225–231 CrossRef CAS.
- G. Smyth, F. X. Quinn and V. J. McBrierty, Macromolecules, 1988, 21, 3198–3204 CrossRef CAS.
- D. G. Pedley and B. J. Tighe, Br. Polym. J., 1979, 11, 130–136 CrossRef CAS.
- Y. Maeda, T. Higuchi and I. Ikeda, Langmuir, 2000, 16, 7503–7509 CrossRef CAS.
- Y. Satokawa, T. Shikata, F. Tanaka, X.-P. Qiu and F. M. Winnik, Macromolecules, 2009, 42, 1400–1403 CrossRef CAS.
- Y. Ono and T. Shikata, J. Am. Chem. Soc., 2006, 128, 10030–10031 CrossRef CAS PubMed.
- P. Pissis, in Electromagnetic Aquametry: Electromagnetic Wave Interaction with Water and Moist Substances, ed. K. Kupfer, Springer Berlin Heidelberg, Berlin, Heidelberg, 2005, pp. 39–70 DOI:10.1007/3-540-26491-4_3.
- A. Kyritsis, P. Pissis, J. L. Gómez Ribelles and M. Monleón Pradas, J. Non-Cryst. Solids, 1994, 172–174, 1041–1046 CrossRef CAS.
- E. Liepinsh, G. Otting and K. Wüthrich, Nucleic Acids Res., 1992, 20, 6549–6553 CrossRef CAS PubMed.
- K. Wüthrich, NMR of Proteins and Nucleic Acids, Wiley, New York, 1986 Search PubMed.
- J. Keeler, Understanding NMR Spectroscopy, John Wiley and Sons, Chichester, UK, 2nd edn, 2010 Search PubMed.
- M. Grossutti and J. R. Dutcher, Biomacromolecules, 2016, 17, 1198–1204 CrossRef CAS PubMed.
- P. Schmidt, J. Dybal and M. Trchová, Vib. Spectrosc., 2006, 42, 278–283 CrossRef CAS.
- Y. Maeda and H. Kitano, Spectrochim. Acta, Part A, 1995, 51, 2433–2446 CrossRef.
- J. D. Nickels, J. Atkinson, E. Papp-Szabo, C. Stanley, S. O. Diallo, S. Perticaroli, B. Baylis, P. Mahon, G. Ehlers, J. Katsaras and J. R. Dutcher, Biomacromolecules, 2016, 17, 735–743 CrossRef CAS PubMed.
- K. Kyriakos, M. Philipp, L. Silvi, W. Lohstroh, W. Petry, P. Müller-Buschbaum and C. M. Papadakis, J. Phys. Chem. B, 2016, 120, 4679–4688 CrossRef CAS PubMed.
- M. Philipp, K. Kyriakos, L. Silvi, W. Lohstroh, W. Petry, J. K. Krüger, C. M. Papadakis and P. Müller-Buschbaum, J. Phys. Chem. B, 2014, 118, 4253–4260 CrossRef CAS PubMed.
- S. Perticaroli, G. Ehlers, C. B. Stanley, E. Mamontov, H. O’Neill, Q. Zhang, X. Cheng, D. A. A. Myles, J. Katsaras and J. D. Nickels, J. Am. Chem. Soc., 2017, 139, 1098–1105 CrossRef CAS PubMed.
- C. Ota, S. Noguchi and K. Tsumoto, Biopolymers, 2015, 103, 237–246 CrossRef CAS PubMed.
- M. A. Blanco, T. Perevozchikova, V. Martorana, M. Manno and C. J. Roberts, J. Phys. Chem. B, 2014, 118, 5817–5831 CrossRef CAS PubMed.
- I. Teraoka, Polymer Solutions: An Introduction to Physical Properties, John Wiley & Sons, New York, 2002 Search PubMed.
- D. I. Svergun, S. Richard, M. H. J. Koch, Z. Sayers, S. Kuprin and G. Zaccai, Proc. Natl. Acad. Sci. U. S. A., 1998, 95, 2267–2272 CrossRef CAS PubMed.
- C. Stanley, S. Krueger, V. A. Parsegian and D. C. Rau, Biophys. J., 2008, 94, 2777–2789 CrossRef CAS PubMed.
- C. F. Wu and S. H. Chen, J. Chem. Phys., 1987, 87, 6199–6205 CrossRef CAS.
- B. Hammouda, Probing Nanoscale Structures: The SANS Toolbox, NIST, Gaithersburg, MD, 2010 Search PubMed.
- R.-J. Roe, Methods of X-ray and Neutron Scattering in Polymer Science, Oxford University Press, New York, 2000 Search PubMed.
- B. Hammouda, Eur. Polym. J., 2010, 46, 2275–2281 CrossRef CAS.
- A. Luk, N. S. Murthy, W. Wang, R. Rojas and J. Kohn, Acta Biomater., 2012, 8, 1459–1468 CrossRef CAS PubMed.
- V. Lebedev, G. Török, L. Cser, W. Treimer, D. Orlova and A. Sibilev, J. Appl. Crystallogr., 2003, 36, 967–969 CrossRef CAS.
- C. S. Thomas, M. J. Glassman and B. D. Olsen, ACS Nano, 2011, 5, 5697–5707 CrossRef CAS PubMed.
- D. Chang and B. D. Olsen, Polym. Chem., 2016, 7, 2410–2418 RSC.
- N. C. f. N. Research, Neutron activation and scattering calculator, https://www.ncnr.nist.gov/resources/activation/.
- Mantid, Manipulation and Analysis Toolkit for Instrument Data, http://dx.doi.org/10.5286/SOFTWARE/MANTID, 2013, DOI: http://dx.doi.org/10.5286/SOFTWARE/MANTID.
- H. I. Petrache, S. E. Feller and J. F. Nagle, Biophys. J., 1997, 72, 2237–2242 CrossRef CAS PubMed.
- R. Navarro Pérez, J. E. Amaro and E. Ruiz Arriola, Phys. Lett. B, 2014, 738, 155–159 CrossRef.
- C. N. Lam, D. Chang, M. Wang, W.-R. Chen and B. D. Olsen, J. Polym. Sci., Part A: Polym. Chem., 2016, 54, 292–302 CrossRef CAS.
- N. Srebro and T. Jaakkola, presented in part at the Twentieth International Conference on Machine Learning (ICML-2003), Washington, D.C., 2003.
- P.-G. de Gennes, Scaling Concepts in Polymer Physics, Cornell University Press, Ithaca, New York, 1979 Search PubMed.
- J. Cohen, Statistical Power Analysis for the Behavioral Sciences, Routledge, New York, 2nd edn, 1988 Search PubMed.
- Y. Ono and T. Shikata, J. Phys. Chem. B, 2007, 111, 1511–1513 CrossRef CAS PubMed.
- S. A. Deshmukh, S. K. R. S. Sankaranarayanan, K. Suthar and D. C. Mancini, J. Phys. Chem. B, 2012, 116, 2651–2663 CrossRef CAS PubMed.
- L. Tavagnacco, E. Zaccarelli and E. Chiessi, Phys. Chem. Chem. Phys., 2018, 20, 9997–10010 RSC.
- K. Yanase, R. Buchner and T. Sato, J. Mol. Liq., 2020, 302, 112025 CrossRef CAS.
- P. Pissis and A. Kyritsis, J. Polym. Sci., Part B: Polym. Phys., 2013, 51, 159–175 CrossRef CAS.
- A. S. Hoffman, Adv. Drug Delivery Rev., 2012, 64, 18–23 CrossRef.
- A. Stathopoulos, P. Klonos, A. Kyritsis, P. Pissis, C. Christodoulides, J. C. Rodriguez Hernández, M. Monleón Pradas and J. L. Gómez Ribelles, Eur. Polym. J., 2010, 46, 101–111 CrossRef CAS.
- C. Pandis, A. Spanoudaki, A. Kyritsis, P. Pissis, J. C. R. Hernández, J. L. Gómez Ribelles and M. Monleón Pradas, J. Polym. Sci., Part B: Polym. Phys., 2011, 49, 657–668 CrossRef CAS.
- S. Morita, M. Tanaka and Y. Ozaki, Langmuir, 2007, 23, 3750–3761 CrossRef CAS PubMed.
- M. Ide, T. Mori, K. Ichikawa, H. Kitano, M. Tanaka, A. Mochizuki, H. Oshiyama and W. Mizuno, Langmuir, 2003, 19, 429–435 CrossRef CAS.
- S. Mani, F. Khabaz, R. V. Godbole, R. C. Hedden and R. Khare, J. Phys. Chem. B, 2015, 119, 15381–15393 CrossRef CAS PubMed.
- J. Wu, W. Lin, Z. Wang, S. Chen and Y. Chang, Langmuir, 2012, 28, 7436–7441 CrossRef CAS PubMed.
- Q. Shao, Y. He, A. D. White and S. Jiang, J. Phys. Chem. B, 2010, 114, 16625–16631 CrossRef CAS PubMed.
- Y. Okada and F. Tanaka, Macromolecules, 2005, 38, 4465–4471 CrossRef CAS.
- K. Yanase, R. Buchner and T. Sato, Phys. Rev. Mater., 2018, 2, 085601 CrossRef CAS.
- K. Mochizuki and D. Ben-Amotz, J. Phys. Chem. Lett., 2017, 8, 1360–1364 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/d0sm01962c |
| This journal is © The Royal Society of Chemistry 2021 |