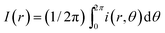Controlling uniform patterns by evaporation of multi-component liquid droplets in a confined geometry†
Jeongsu
Pyeon
and
Hyoungsoo
Kim
 *
*
Department of Mechanical Engineering, Korea Advanced Institute of Science and Technology, Daejeon 34141, Republic of Korea. E-mail: hshk@kaist.ac.kr; Fax: +82-042-350-3049; Tel: +82 042-350-3049
First published on 7th December 2020
Abstract
Surface-coating technologies are important for a variety of applications, e.g. ink-jet printing, micro-electronic engineering and biological arrays. In this study, we introduce a novel idea to obtain uniform patterns with multi-component solution in a confined geometry. When a droplet of the multi-component liquid evaporates in the confined area, the evaporated vapors are stagnated inside the confined chamber where the evaporated liquid molecule is much heavier than the ambient air. These vapors change internal flow in the droplet by generating Marangoni effects during evaporation, which help to obtain uniform deposition. Finally, we show that a coffee-ring is totally suppressed and a uniformly dried pattern is achieved. For a potential application as display panels, we use quantum dots and create a uniform light-emitting layer.
1 Introduction
Understanding of the evaporation mechanism of a particle-laden droplet is crucial to control a final dried pattern, which has been receiving enormous attention in coating and electronics industries. The uniform coating results can be useful for various applications, such as light-emitting diode (LED) displays, electronic wiring, biological engineering for tissues and vasculature and radio-frequency identification (RFID).1–7 In particular, the maximum illumination efficiency of LEDs can be increased by improving the thickness uniformity of the LED layer.8,9 Also, the resistivity of the electronic wiring can be optimized when the printed electronic pattern has uniform morphology.4 Furthermore, uniform conductive patterns can contribute to long-term stability for the performance of an electronic device such as RFID.10To date, diverse deposition patterns were observed under different drying conditions, e.g., coffee-ring patterns,11 dual-ring patterns,12,13 multiple ring patterns13,14 and uniform patterns,15–25 after a droplet was completely evaporated. The coffee-ring pattern is commonly observed from the evaporation of a single liquid component droplet with a low contact angle (<90°) where the evaporatively driven capillary flow occurs. If the contact line is pinned, there is a single ring. In contrast, dual and multiple rings are observed, if there are strong Marangoni flows and stick-and-slip contact line motion during the evaporation. In order to obtain uniform dried patterns, the coffee-ring effect should be effectively suppressed. However, it is still difficult to obtain perfectly uniform particle patterns using evaporation of a droplet on a substrate due to the coffee-ring effect. To suppress this coffee-ring and to achieve uniformly deposited particle patterns, several ways were introduced; adding surfactants into droplets,15 increasing the evaporation rate by the thermal effect,16 changing the surface tension gradient by transfer of volatile vapors (i.e., solutal Marangoni effect17–20), changing pH concentration,21 controlling the elasticity and stiffness of the substrate22–24 and using elongated ellipsoidal particles.25 Most of the preceding studies on the uniform particle deposition are mainly done by applying additional chemical additives or external effects. However, the geometry effect on the dried pattern during evaporation has been rarely investigated.
There are some studies on evaporating droplets in a confined system. They simply observed the change of contact lines and contact angles under different geometrical conditions26–29 and a final dried pattern was investigated between two parallel plates.30,31 However, to date, studies of the final dried pattern inside the confined system have not been sufficiently done although some applications such as display diodes have a confined chamber containing quantum dots or other functional materials. In this sense, it is important to examine how a drop evaporates in a confined system and what kind of final dried pattern can be obtained.
If the droplet evaporates in a finite space, the ambient boundary conditions could be changed in time due to the evaporation of the droplet. The evaporated vapors will remain in the confined area. Recently, some studies have demonstrated that changes in boundary conditions around a droplet directly influence an internal flow pattern inside the droplet during evaporation. For example, a neighboring droplet changes internal flow patterns inside an adjacent binary-mixture droplet.32 Furthermore, external point sources of volatile vapors located near the droplet locally can generate Marangoni flows driven by surface tension gradient along a liquid–vapor interface inside a droplet33,34 and also can control a particle distribution after the droplet is completely dried.35 From these vapor-driven solutal Marangoni problems, we realized that the boundary conditions play an important role in changing internal flows and final dried patterns.
In this paper, we focus on the evaporation phenomenon of multi-component droplets composed of ethanol and distilled (DI) water in a confined geometry. We presume that evaporated vapors from the droplet remain in the confined chamber. The captured vapors stagnate around the droplet because the molecular weight of the volatile vapor component is much heavier than that of the ambient air.36 We examine how the stagnant vapors affect internal flows inside the droplet during evaporation using particle image velocimetry (PIV). From PIV results, we found that stagnant volatile vapors induce all suspension particles to move towards the middle of the droplet and the particles gather with a circular shape, which is defined as particle accumulation. Also, we investigate flow transitions inside the droplet of multi-component solutions, i.e., the binary or ternary mixture, under the confined conditions using PIV. We compare this result with an open system as well. Moreover, the uniformity of the final deposition patterns after the droplets completely dried in the confined chamber is examined in this study.
2 Experiments
2.1 Experimental set-up
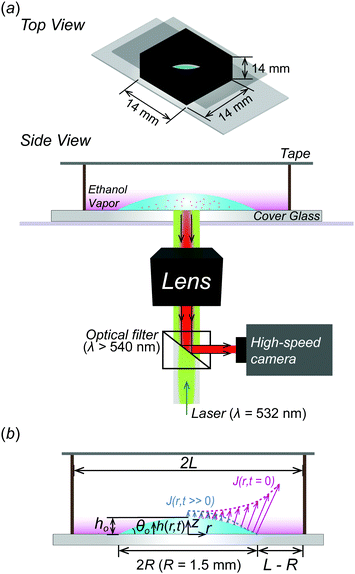
In the experiment, we use a binary mixture droplet composed of ethanol (≥99.5% purity, Sigma-Aldrich, USA.) and distilled (DI) water (Direct-Q3 UV, Sungwoo Genetech, Korea), which is widely used in a drying study.37–40 As shown in Fig. 1, the droplet of the binary mixture is evaporated in a confined chamber fabricated by 3D printing (3DWOX 1, polylactic acid, Sindoh, Korea) at room temperature (T ≈ 293 K). Here, a 2 ± 0.04 μl droplet (Vo) is deposited on a cover glass and the radius R of the droplet is kept constant at around 1.5 mm by hydrophilic surface treatment using a plasma gun (BD-10ASV, Electro-Technic Products, INC., USA) with a shadow mask having a circular hole with R = 1.5 mm. The initial contact angle θo and droplet height ho are 32 ± 2° and 0.37 ± 0.01 mm, respectively. The confined chamber is completely sealed with a tape on top after placing the binary mixture droplet on the cover glass. Evaporated vapors are not allowed to diffuse out to the ambient environment due to the confined chamber so that the ethanol vapors are forced to remain in the chamber as sketched in Fig. 1.2.2 Flow visualization
To visualize internal flows inside droplets using particle image velocimetry (PIV), fluorescent particles (PS-FluoRed-Fi320, micro-particles GmbH, Germany) with a diameter of 1.9 ± 0.09 μm are used, whose concentration is 1% v/v in the binary mixture solution. Images of fluorescent particles during evaporation were recorded with 50 frames per second using a high-speed camera (Photron Fastcam Mini-AX200, Japan) and a 5× magnification lens. Also, the focal plane was set to the vicinity of the bottom part of the droplet where the depth of field is 150–200 μm from the substrate of the cover glass. Here, the droplet height ho is much smaller than the droplet radius R (ho/R ≈ 0.25 < 1). Flow field calculation is conducted by the PIVlab tool in Matlab.41 To obtain vector fields, we apply iterative 2D cross-correlation of the particle images with multiple interrogation windows of 128 × 128 pixels (first) and 64 × 64 pixels (second) with 50% overlaps, where the signal-to-noise ratio (SNR > 3) is large enough for the reliable PIV.422.3 Deposition patterns
We evaluated uniformity of dried patterns after a completed evaporation in the confined geometry with various combinations of solvents [see Table 1]. All the solvents used in this experiment are much more volatile than DI-water and have heavier molecular weight than the ambient air as listed in Table 1. Not only fluorescent particles, but also greenish quantum dots (CZM-530W QDs, ZEUS, Korea) were tested whether a surface-coating method newly proposed in this paper can obtain a uniform pattern. Eventually, it can be utilized in relevant applications, such as light-emitting devices,43 solar cells44 and color filters in displays.45–47 In the experiment, water-soluble QDs with a particle concentration of 5 mg ml−1 in water and a size of 10.5 ± 1.5 nm are used where they can emit light in the λ = 450 nm wavelength range with full width at half maximum (FWHM) ≤35 nm when they are exposed to ultraviolet rays (Photo Luminescence, PL) or current (Electron Luminescence, EL). QD particles are stably dispersed in the solution with ζ-potential −20 to −40 mV. In this study, the final deposition of QDs was visualized by using an ultraviolet ray lamp (PL) where we mixed ethanol, DI-water and QDs with weight ratio, 44.1%![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 55.7%
55.7%![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.2% in the solution.
0.2% in the solution.
3 Results and discussion
3.1 Theoretical background
In this study, during the experiment, ethanol evaporation is relatively predominant compared to water because the vapor pressure of ethanol (Pv = 5.95 kPa) is about 2 times higher than that of water (Pv = 2.34 kPa). Thus, we mainly consider an evaporative flux of the ethanol along an air–liquid interface, which varies with space (r) and time (t) due to the confinement effect. In this problem, initially, h(r, t = 0, 0)/R < 1 and h(r, t)/R become smaller as the droplet evaporates so that we can use lubrication approximation for a thin droplet. As a result, the evaporative flux can be expressed as follows48–51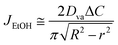 | (1) |
Here, in the case of evaporation for an open substrate, ethanol vapor concentration Ce might be constant (here, Ce ≈ 0) because the ethanol vapors can freely discharge into the ambient atmosphere in a relatively infinite area. In other words, if they are not constrained by geometries, the ethanol vapor concentration gradient could be constant, i.e. (ΔC = Cs − Ce ≈ Cs). However, in a confined system, evaporated ethanol vapors cannot diffuse out to the ambient environment due to the fabricated confined chamber and they stagnate in the chamber where the molecular weight of ethanol (MEtOH = 46.07 g mol−1) is much heavier than the ambient air (Mair = 28.93 g mol−1), so the vapors sink down to the bottom direction, as shown in the pink gradation in Fig. 1. Simultaneously, the stagnant ethanol vapors result in an increase of ethanol vapor concentration Ce in the vicinity of the droplet. Consequently, the ethanol vapor concentration gradient diminishes as the droplet evaporates, i.e. (ΔC = Cs − Ce), which induces a decreased evaporative flux profile based on the following relational formula,
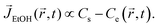 | (2) |
In a confined system, as the ethanol vapor concentration ΔC along a droplet surface changes, the evaporative flux profile J varies based on eqn (1) and (2). At the same time, the surface tension gradient along a liquid–vapor interface also changes with space and time. Consequently, time-dependent Marangoni flows inside the droplets in the confined system would be differently developed compared to the experimental results of the open substrate.
3.2 Flow field
To investigate the internal flow pattern, we perform PIV and the results are summarized in Fig. 2. We find that the internal flows of binary mixture (ethanol![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) DI-water = 70
DI-water = 70![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
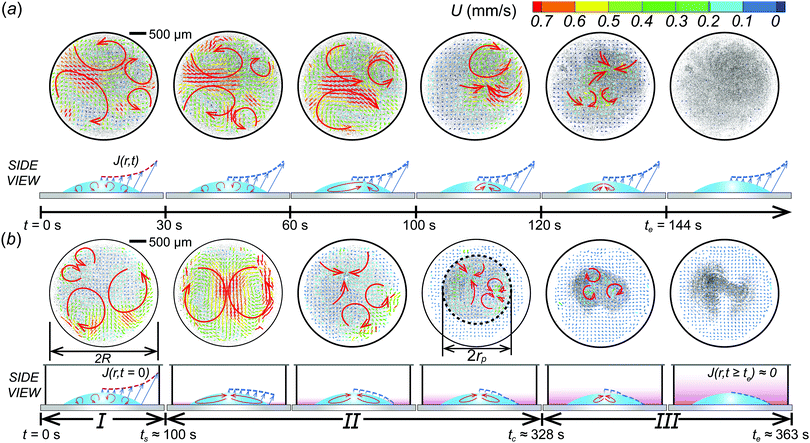
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 30 vol%) in a confined chamber can be classified into three stages: Stage I, complicated Marangoni-driven convection flow, Stage II, continuous inward flow, and Stage III, gradually diminishing Marangoni flow as shown in Fig. 2(b). At stage I, complicated mixing flows are observed everywhere inside the droplet, which is a similar result to initial evaporative flow patterns on an open substrate [Fig. 2(a and b)], where the typical flow speed U ≈ O(0.1 mm s−1). At stage II, the inward circulation flow pattern is developed and maintained for longer time compared to the droplet on an open substrate (see the ESI,† Movies S1 and S2). The long-lasting inward circulation flows in the confined chamber is due to stagnant ethanol vapors around droplets that can continuously generate a surface tension gradient at a liquid–vapor interface, which contributes to the development of Marangoni flow inside droplets in a confined system for a much longer period of time than that of the open system. The typical inward flow induces particle accumulation in the middle of the droplet, which forms a certain circular area with the smallest radius rp at tc ≈ 328 s in Fig. 2(b). We defined the smallest radius rp as a critical radius in this study. At stage III, Marangoni flow inside the droplet is gradually diminished as the ethanol components in the droplet evaporate.
30 vol%) in a confined chamber can be classified into three stages: Stage I, complicated Marangoni-driven convection flow, Stage II, continuous inward flow, and Stage III, gradually diminishing Marangoni flow as shown in Fig. 2(b). At stage I, complicated mixing flows are observed everywhere inside the droplet, which is a similar result to initial evaporative flow patterns on an open substrate [Fig. 2(a and b)], where the typical flow speed U ≈ O(0.1 mm s−1). At stage II, the inward circulation flow pattern is developed and maintained for longer time compared to the droplet on an open substrate (see the ESI,† Movies S1 and S2). The long-lasting inward circulation flows in the confined chamber is due to stagnant ethanol vapors around droplets that can continuously generate a surface tension gradient at a liquid–vapor interface, which contributes to the development of Marangoni flow inside droplets in a confined system for a much longer period of time than that of the open system. The typical inward flow induces particle accumulation in the middle of the droplet, which forms a certain circular area with the smallest radius rp at tc ≈ 328 s in Fig. 2(b). We defined the smallest radius rp as a critical radius in this study. At stage III, Marangoni flow inside the droplet is gradually diminished as the ethanol components in the droplet evaporate.
If the droplet evaporates on an open substrate, complicated mixing flows are observed in the beginning of evaporation. When ethanol completely evaporates, the mixing flows stop and it shows a coffee-ring flow pattern. For the open system, the time duration of the mixing flow regime is relatively shorter than the confined system (t ≈ 60 s). From PIV results, we see that the confinement effect can obviously change the flow structure in time and in space. Hereby, we conclude that the confined system changes the boundary condition related to the evaporation mechanism.
3.3 Effect of stagnant ethanol vapors
To further investigate the particle accumulation phenomenon, we control an initial ethanol concentration CEtOH in a droplet and a distance L−R between the droplet and inner walls and initial droplet height ho. Fig. 3(a) shows that the critical radius rp decreases as the ethanol concentration CEtOH inside the droplet increases from 30 to 50 and 70% with a volume ratio in the droplet. The reason is that the amount of ethanol vapors around the droplet increases with the ethanol concentration so that it helps to make long-lasting continuous inward flow, which plays a role in accumulating all suspended particles in the middle of the droplet.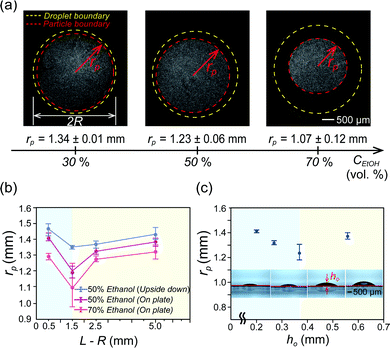 | ||
Fig. 3 Comparison of particle accumulation by Marangoni flow by varying different ethanol concentrations and geometry conditions. (a) Images of the particle distribution region in the binary mixture droplet with 30, 50, and 70% ethanol concentration CEtOH in water, respectively. Initial droplet diameters are the same as 2R. The critical radius rp is defined when all the particles are gathered in the smallest region (red-dashed line). (b) Effect of the distance L–R (see Fig. 1(b)) between the wall and the droplet with ethanol–water (50![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 50 vol%) and ethanol–water (70 50 vol%) and ethanol–water (70![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 30 vol%) (purple and orange line) on the critical radius rp. The blue line is for the upside down droplet case. (c) Effect of initial droplet height ho (0.5, 1, 2, and 3 μl volume of the droplet) on critical radius rp. Here, the initial contact angle θo and droplet height ho are measured as 20 ± 1° and 0.20 ± 0.01 mm for a 0.5 μl drop, 23 ± 2° and 0.28 ± 0.01 mm for 1.0 μl, 32 ± 2° and 0.37 ± 0.01 mm for 2.0 μl and 37 ± 2° and 0.56 ± 0.01 mm for 3.0 μl, respectively. 30 vol%) (purple and orange line) on the critical radius rp. The blue line is for the upside down droplet case. (c) Effect of initial droplet height ho (0.5, 1, 2, and 3 μl volume of the droplet) on critical radius rp. Here, the initial contact angle θo and droplet height ho are measured as 20 ± 1° and 0.20 ± 0.01 mm for a 0.5 μl drop, 23 ± 2° and 0.28 ± 0.01 mm for 1.0 μl, 32 ± 2° and 0.37 ± 0.01 mm for 2.0 μl and 37 ± 2° and 0.56 ± 0.01 mm for 3.0 μl, respectively. | ||
We have shown that the ethanol concentration is proportional to the duration of Marangoni flow, which can help to concentrate the particles in the middle further. In a similar manner, we consider the relation between the amount of the evaporated volatile liquid vapors and the chamber space. To examine this, we varied the L–R space. As shown in Fig. 3(b), we noticed that distance L–R is also an important factor to determine the critical radius rp. From the result, the minimal radius rp is observed with L–R = 1.5 mm. This indicates that there is an optimized chamber size to achieve the long-lasting Marangoni flow condition. On the other hand, for L–R = 0.5 mm [blue-shaded area in Fig. 3(b)], if the space between the droplet and solid inner wall is relatively small, the ethanol vapor can easily and uniformly cover the entire droplet so that the Marangoni effect caused by a surface tension gradient at a droplet surface rapidly disappears and it cannot make smaller rp. Actually, the duration time of the inward circulation flow is te ≈ 36 s for L–R = 0.5 mm for an ethanol concentration CEtOH = 50 vol% in water. However, the duration time for internal circulation flows also increases as L–R increases because they are less likely to be covered by the stagnant ethanol vapors due to a large area (L–R = 1.5 mm: te ≈ 180 s, L–R= 2.5 mm: te ≈ 330 s, L–R = 5.0 mm: te ≈ 380 s). Also, as L–R gradually increases [the yellow-shaded area in Fig. 3(b)], the confinement effects on the droplet evaporation become weaker by losing the surface tension gradient along the droplet interface as the ethanol evaporates. Thus, the critical radius rp increases.
In addition, to prove the gravity effect due to the density difference between an ethanol vapor and ambient air, we measure and compare critical radius rp for sessile and upside down droplet evaporation in a confined system. We expect that the larger critical radius rp will be obtained if the droplet is placed under the substrate because a molecular weight of ethanol vapors is much heavier than that of the ambient air so that the ethanol vapors leave away from the droplet surface. From the experimental result [blue line in Fig. 3], in the case of upside down, they have larger critical radius rp than other cases. From this, we can conclude that the evaporated ethanol vapors sink down onto the bottom by the gravity effect driven by the density difference and, therefore, the inversely suspended droplet does not have a strong Marangoni effect during evaporation.
Moreover, in order to check the effect of a droplet height on critical radius rp, we control a droplet volume, 0.5, 1.0, 2.0 and 3.0 μl in the same confined chamber [see insets in Fig. 3(c)] while fixing the constant radius R and the same initial concentration of ethanol in the droplet (R = 1.5 mm and ethanol 50% in water with a volume ratio). We found that a critical condition is ho ≈ 0.37 mm (2 μl droplet) in Fig. 3(c) to distinguish two regimes. First, in the blue-shaded area, they have relatively very shallow droplet height ho so that they can be easily covered by an stagnant ethanol vapor within a short moment and then Marangoni flows inside the droplet cannot be continued for a long time (actually, te ≈ 60–80 s). Eventually, relatively larger critical radius rp is observed [blue-shaded area in Fig. 3(c)]. On the other hand, in the yellow-shaded area, this case has a sufficient droplet height not to be easily covered with the ethanol vapors and there is an enough space for the evaporated ethanol vapors diffused into the ambient environment. Therefore, under the same conditions, as the droplet height ho increases, the contact angle gets larger. Then, the influenced area near the contact line becomes narrower so that the larger critical radius rp is developed as shown in the yellow-shaded area in Fig. 3(c). We found that the optimal conditions for the smallest rp are for ho ≈ 0.37 mm (a droplet volume 2 μl) and L–R is 1.5 mm. In this study, we find the droplet height ho ≈ 0.37 mm is an optimal condition for minimal critical radius rp.
As a result, we observe that there is an optimal condition to have a long-lasting Marangoni flow and a smaller rp, which can be determined by the concentration of the evaporated vapors, the confinement space, and the droplet shape.
3.4 Results of the deposition pattern
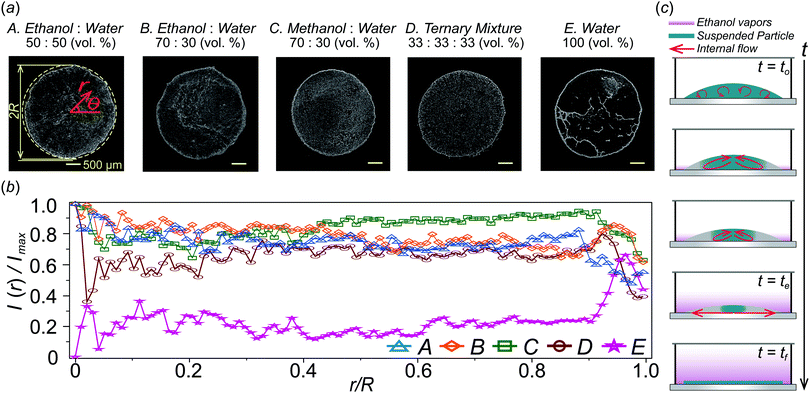
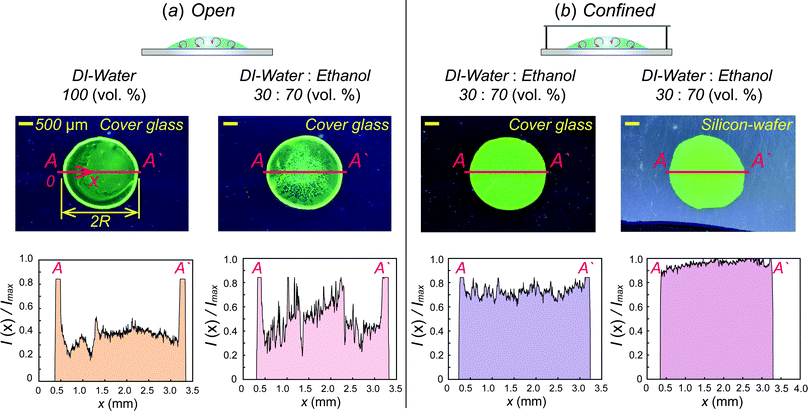
As shown in Fig. 4(a), we compare dried patterns in a confined chamber by using various solvents; ethanol, methanol, 1,4-dioxane and DI-water. The dried patterns of binary (A–C) and ternary (D) solution that consist of the abovementioned solvents. We observed that (A–D) shows uniformly distributed particle patterns compared to the coffee-ring pattern produced by evaporation of pure water (E) in Fig. 4. To quantitatively compare the uniformity, we measured the averaged particle image density as a function of the radial direction and the result can clearly show uniformly deposited patterns [Fig. 4(b)]. The intensity profile I(r) is normalized with the maximum Imax where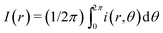 and i(r,θ) is the local light intensity.
and i(r,θ) is the local light intensity.
The procedure of drying of the droplet in a confined chamber is summarized in Fig. 4(c). Initially (0 ≤ t ≤ te), all suspended particles congregate towards the center of the droplet due to inward Marangoni flows in the middle of the droplet induced by evaporated ethanol vapors stagnant near the droplet [see also Fig. 2b], where te is the final time for the Marangoni flow to disappear. After that (te < t), the ethanol vapor concentration near the droplet surface, is saturated by stagnant ethanol vapors and gathered particles in the middle of the droplet start to spread out towards the contact line because the strong Marangoni flow disappears. However, the ethanol vapors next to the droplet surface help to suppress the coffee-ring pattern by vapor-driven solutal Marangoni effects.33,34 Finally, we can achieve relatively uniform deposition without coffee-ring patterns [Fig. 4(a) and (b)].
For a real application, we use water-soluble QDs as a coating material. As shown in Fig. 5, uniform surface-coating was obtained where the solvent consists of ethanol, DI-water and QDs with weight ratio; 44.1%![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 55.7%
55.7%![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.2%, respectively, while the coffee-ring pattern is clearly formed when a DI-water or binary mixture droplet evaporates in an open system [Fig. 5(a)]. We test two different substrates as a potential substrate. There is a slight difference between two cases (i.e., glass and silicon-wafer) from the intensity distribution. However, the illumination results excited by UV light (λ = 395 nm) provide a uniform green color everywhere [Fig. 5(b)]. We believe that the current method would be a reliable QD printing method for a display element.
0.2%, respectively, while the coffee-ring pattern is clearly formed when a DI-water or binary mixture droplet evaporates in an open system [Fig. 5(a)]. We test two different substrates as a potential substrate. There is a slight difference between two cases (i.e., glass and silicon-wafer) from the intensity distribution. However, the illumination results excited by UV light (λ = 395 nm) provide a uniform green color everywhere [Fig. 5(b)]. We believe that the current method would be a reliable QD printing method for a display element.
4 Conclusions
We investigate how a multi-component liquid droplet evaporates in a confined chamber and we observe a final deposit pattern. As a consequence, uniformly dried patterns are achieved using the proposed method. To understand this result, by using the PIV technique, we monitor and compare internal flow fields between droplet evaporation on an open substrate and in a confined system. It is confirmed that long-lasting continuous inward circulation flows in the middle of the droplet generate in the confined chamber and these flows play a leading role in inducing the particle accumulation phenomenon. Eventually, we obtain uniform dried patterns without the coffee-ring. For some specific patterning, the evaporation in the confined system based on ink-jet printing is commonly used when color filters are manufactured in display fields.52,53 Then, it is crucial that uniform surface-coating technologies are still required for high luminous quality and efficiency. Therefore, to check the potential of the proposed method for being applicable to practical applications, we also test QDs deposition patterns and obtain uniformly illuminated spots on two different substrates, i.e., a cover glass and silicon–wafer. We expect that the proposed surface-coating method can be widely applied in various relevant industrial areas without any external energy sources and adding special additives to achieve uniform coating with a restrained coffee-ring effect.Conflicts of interest
There are no conflicts to declare.References
- B.-J. De Gans, P. C. Duineveld and U. S. Schubert, Adv. Mater., 2004, 16, 203–213 CrossRef CAS.
- Y. L. Kong, I. A. Tamargo, H. Kim, B. N. Johnson, M. K. Gupta, T.-W. Koh, H.-A. Chin, D. A. Steingart, B. P. Rand and M. C. McAlpine, Nano Lett., 2014, 14, 7017–7023 CrossRef CAS PubMed.
- B. Chen, T. Cui, Y. Liu and K. Varahramyan, Solid-State Electron., 2003, 47, 841–847 CrossRef CAS.
- E. B. Secor, P. L. Prabhumirashi, K. Puntambekar, M. L. Geier and M. C. Hersam, J. Phys. Chem. Lett., 2013, 4, 1347–1351 CrossRef CAS.
- L. Yang, A. Rida, R. Vyas and M. M. Tentzeris, IEEE Trans. Microwave Theory Tech., 2007, 55, 2894–2901 Search PubMed.
- X. Cui and T. Boland, Biomaterials, 2009, 30, 6221–6227 CrossRef CAS.
- T. Xu, W. Zhao, J.-M. Zhu, M. Z. Albanna, J. J. Yoo and A. Atala, Biomaterials, 2013, 34, 130–139 CrossRef CAS.
- X. Yu, R. Xing, Z. Peng, Y. Lin, Z. Du, J. Ding, L. Wang and Y. Han, Chin. Chem. Lett., 2019, 30, 135–138 CrossRef CAS.
- C. Jiang, Z. Zhong, B. Liu, Z. He, J. Zou, L. Wang, J. Wang, J. Peng and Y. Cao, ACS Appl. Mater. Interfaces, 2016, 8, 26162–26168 CrossRef CAS PubMed.
- R. Singh, E. Singh and H. S. Nalwa, RSC Adv., 2017, 7, 48597–48630 RSC.
- R. D. Deegan, O. Bakajin, T. F. Dupont, G. Huber, S. R. Nagel and T. A. Witten, Nature, 1997, 389, 827–829 CrossRef CAS.
- X. Zhong and F. Duan, Phys. Chem. Chem. Phys., 2016, 18, 20664–20671 RSC.
- M. Parsa, S. Harmand, K. Sefiane, M. Bigerelle and R. Deltombe, Langmuir, 2015, 31, 3354–3367 CrossRef CAS PubMed.
- L. Shmuylovich, A. Q. Shen and H. A. Stone, Langmuir, 2002, 18, 3441–3445 CrossRef CAS.
- H. Kim, F. Boulogne, E. Um, I. Jacobi, E. Button and H. A. Stone, Phys. Rev. Lett., 2016, 116, 124501 CrossRef PubMed.
- Y. Li, Q. Yang, M. Li and Y. Song, Sci. Rep., 2016, 6, 1–8 CrossRef PubMed.
- S. Bekki, M. Vignes-Adler, E. Nakache and P. Adler, J. Colloid Interface Sci., 1990, 140, 492–506 CrossRef CAS.
- C. Sternling and L. Scriven, AIChE J., 1959, 5, 514–523 CrossRef CAS.
- K. Schwarzenberger, T. Köllner, H. Linde, T. Boeck, S. Odenbach and K. Eckert, Adv. Colloid Interface Sci., 2014, 206, 344–371 CrossRef CAS PubMed.
- M. Majumder, C. S. Rendall, J. A. Eukel, J. Y. Wang, N. Behabtu, C. L. Pint, T.-Y. Liu, A. W. Orbaek, F. Mirri and J. Nam, et al. , J. Phys. Chem. B, 2012, 116, 6536–6542 CrossRef CAS PubMed.
- R. Bhardwaj, X. Fang, P. Somasundaran and D. Attinger, Langmuir, 2010, 26, 7833–7842 CrossRef CAS PubMed.
- R. Iqbal, A. Matsumoto, A. Sudeepthi, A. Q. Shen and A. Sen, Appl. Phys. Lett., 2019, 114, 253701 CrossRef.
- Y. Chen, A. Askounis, V. Koutsos, P. Valluri, Y. Takata, S. K. Wilson and K. Sefiane, Langmuir, 2019, 36, 204–213 CrossRef PubMed.
- M. C. Lopes and E. Bonaccurso, Soft Matter, 2013, 9, 7942–7950 RSC.
- P. J. Yunker, T. Still, M. A. Lohr and A. Yodh, Nature, 2011, 476, 308–311 CrossRef CAS PubMed.
- L. Bansal, S. Chakraborty and S. Basu, Soft Matter, 2017, 13, 969–977 RSC.
- J. Li, L. Shan, B. Ma, X. Jiang, A. Solomon, M. Iyengar, J. Padilla and D. Agonafer, J. Colloid Interface Sci., 2019, 555, 583–594 CrossRef CAS PubMed.
- F. Clément and J. Leng, Langmuir, 2004, 20, 6538–6541 CrossRef PubMed.
- J. Leng, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2010, 82, 021405 CrossRef PubMed.
- P. J. Yunker, M. Gratale, M. A. Lohr, T. Still, T. C. Lubensky and A. G. Yodh, Phys. Rev. Lett., 2012, 108, 228303 CrossRef PubMed.
- R. Mondal and M. G. Basavaraj, Soft Matter, 2020, 16, 3753–3761 RSC.
- T. K. Pradhan and P. K. Panigrahi, Colloids Surf., A, 2016, 500, 154–165 CrossRef CAS.
- J. Ryu, J. Kim, J. Park and H. Kim, Int. J. Heat Mass Transfer, 2021, 164, 120499 CrossRef CAS.
- J. Park, J. Ryu, H. J. Sung and H. Kim, J. Colloid Interface Sci., 2020, 561, 408–415 CrossRef CAS PubMed.
- R. Malinowski, G. Volpe, I. P. Parkin and G. Volpe, J. Phys. Chem. Lett., 2018, 9, 659–664 CrossRef CAS PubMed.
- P. Kelly-Zion, C. J. Pursell, N. Hasbamrer, B. Cardozo, K. Gaughan and K. Nickels, IInt. J. Heat Mass Transfer, 2013, 65, 165–172 CrossRef CAS.
- J. R. Christy, Y. Hamamoto and K. Sefiane, Phys. Rev. Lett., 2011, 106, 205701 CrossRef PubMed.
- C. H. Ooi, E. Bormashenko, A. V. Nguyen, G. M. Evans, D. V. Dao and N.-T. Nguyen, Langmuir, 2016, 32, 6097–6104 CrossRef CAS PubMed.
- X. Zhong and F. Duan, Eur. Phys. J. E: Soft Matter Biol. Phys., 2016, 39, 1–6 CrossRef CAS PubMed.
- C. Diddens, H. Tan, P. Lv, M. Versluis, J. Kuerten, X. Zhang and D. Lohse, J. Fluid Mech., 2017, 823, 470–497 CrossRef CAS.
- W. Thielicke and E. Stamhuis, J. Open Res., 2014, 2 Search PubMed.
- L. Adrian, R. J. Adrian and J. Westerweel, Particle Image Velocimetry, Cambridge University Press, 2011 Search PubMed.
- Y. Shirasaki, G. J. Supran, M. G. Bawendi and V. Bulović, Nat. Photonics, 2013, 7, 13 CrossRef CAS.
- Z. Yang, M. Wang, J. Li, J. Dou, H. Qiu and J. Shao, ACS Appl. Mater. Interfaces, 2018, 10, 26387–26395 CrossRef CAS PubMed.
- J. Han, D. Ko, M. Park, J. Roh, H. Jung, Y. Lee, Y. Kwon, J. Sohn, W. K. Bae and B. D. Chin, J. Soc. Inf. Disp., 2016, 24, 545–551 CrossRef CAS.
- B. Bao, M. Li, Y. Li, J. Jiang, Z. Gu, X. Zhang, L. Jiang and Y. Song, Small, 2015, 11, 1649–1654 CrossRef CAS.
- P. Yang, L. Zhang, D. J. Kang, R. Strahl and T. Kraus, Adv. Opt. Mater., 2020, 8, 1901429 CrossRef CAS.
- R. D. Deegan, O. Bakajin, T. F. Dupont, G. Huber, S. R. Nagel and T. A. Witten, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2000, 62, 756 CrossRef CAS PubMed.
- H. Hu and R. G. Larson, J. Phys. Chem. B, 2002, 106, 1334–1344 CrossRef CAS.
- Y. O. Popov, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2005, 71, 036313 CrossRef.
- H. Gelderblom, A. G. Marin, H. Nair, A. Van Houselt, L. Lefferts, J. H. Snoeijer and D. Lohse, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2011, 83, 026306 CrossRef.
- H.-S. Koo, M. Chen and P.-C. Pan, Thin Solid Films, 2006, 515, 896–901 CrossRef CAS.
- C.-T. Chen, K.-H. Wu, C.-F. Lu and F. Shieh, J. Micromech. Microeng., 2010, 20, 055004 CrossRef.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/d0sm01872d |
| This journal is © The Royal Society of Chemistry 2021 |