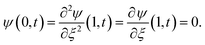Electrostatic wrapping of a microfiber around a curved particle†
Janine K.
Nunes
 *a,
Jiang
Li
*a,
Jiang
Li
 b,
Ian M.
Griffiths
b,
Ian M.
Griffiths
 c,
Bhargav
Rallabandi
c,
Bhargav
Rallabandi
 d,
Jia
Man
d,
Jia
Man
 e and
Howard A.
Stone
e and
Howard A.
Stone
 a
a
aDepartment of Mechanical and Aerospace Engineering, Princeton University, Princeton, NJ 08544, USA. E-mail: nunes@princeton.edu
bSchool of Mechanical Engineering, University of Science and Technology Beijing, Beijing 100083, China
cMathematical Institute, University of Oxford, Oxford, OX2 6GG, UK
dDepartment of Mechanical Engineering, University of California, Riverside, California 92521, USA
eSchool of Mechanical Engineering, Key Laboratory of High Efficiency and Clean Mechanical Manufacture (Ministry of Education), Shandong University, Jinan 250061, China
First published on 13th January 2021
Abstract
The dynamics of the wrapping of a charged flexible microfiber around an oppositely charged curved particle immersed in a viscous fluid is investigated. We observe that the wrapping behavior varies with the radius and Young's modulus of the fiber, the radius of the particle, and the ionic strength of the surrounding solution. We find that wrapping is primarily a function of the favorable interaction energy due to electrostatics and the unfavorable deformation energy needed to conform the fiber to the curvature of the particle. We perform an energy balance to predict the critical particle radius for wrapping, finding reasonably good agreement with experimental observations. In addition, we use mathematical modeling and observations of the deflected shape of the free end of the fiber during wrapping to extract a measurement of the Young's modulus of the fiber. We evaluate the accuracy and potential limitations of this in situ measurement when compared to independent mechanical tests.
1 Introduction
There are many examples of spontaneous self-organization or control over spatial arrangement at the nanoscale that require the bending of one object around a second object driven by attractive interactions. Two examples of this type of phenomenon that are essential for biological function are DNA wrapping around histone proteins to form nucleosomes, and a cell membrane wrapping around objects for transport into the cell during endocytosis.1–3 While this spontaneous self-assembly is ubiquitous at the nanoscale, it is not commonly observed at larger, non-Brownian length scales. At larger length scales, a related liquid–solid phenomenon has been studied where the attractive interaction is provided by capillary forces, such that if the reduction of surface energy upon contacting a liquid drop to a deformable object is greater than the energetic costs of deforming the object, wrapping may occur. For example, a soft fiber or membrane can wrap or fold around the surface of a droplet.4–6 Such capillary-induced behaviors have been studied as a potential pathway for the self-assembly of complex structures. Both classes of examples, which span multiple length scales, highlight the common underlying physics of a strong attractive interaction (capillary, electrostatic, etc.) causing deformations—often large-scale relative to the size of the deforming object.For polyelectrolyte systems, such as DNA–protein systems, the formation of stable wrapped complexes due to electrostatic interactions is determined by numerous parameters. The most important of these parameters include the length of the polymer, its linear charge distribution, its persistence length, the size, charge and curvature of the complexing object, and salt concentration.1 While the resulting thermodynamically stable conformations of these complexes have been investigated, the dynamics of this wrapping process can be challenging to study at such small dimensions. Inspired by macromolecular wrapping behavior, we describe a model experimental system to study the dynamics of spontaneous electrostatic wrapping of a slender high-aspect-ratio object around a curved oppositely charged solid object at micrometer to millimeter length scales, and use both analytical and numerical analyses to extract useful properties of the system.
The dynamics of flexible fibers moving in a viscous fluid is an important aspect of the rich class of problems involving fluid–structure interactions, and is essential for understanding, for example, microscopic biological motion involving slender flexible filaments (e.g., cilia, flagella), the development of micro-actuators, and many industrial practices involving flexible fiber suspensions.7,8 In the self-driven wrapping motion of a fiber around an oppositely charged curved particle, the microfiber sweeps through the fluid with decreasing length, and it adopts a unique deflected shape during wrapping. We model this behavior to enable an in situ “measurement” of the Young's modulus of the fiber, which we compare with independent mechanical testing.
2 Experimental procedure
This experiment comprises two charged non-Brownian objects in an aqueous environment—a microfiber and a disk-shaped particle, both of which are hydrogels containing isotropically distributed ionizable functional groups covalently bonded to a poly(ethylene glycol) diacrylate network. Carboxylic acid groups confer a negative net charge to the fibers; fabrication of the microfibers is described in Section 2.1. Tertiary amine groups in the particle yield a positive charge; fabrication of the particles is described in Section 2.2.2.1 Fabricating microfibers
Negatively charged microfibers were prepared using a two-phase microfluidic method described previously.9–11 Microfluidic channels were prepared using standard methods of soft lithography.12 Polydimethylsiloxane (PDMS, Dow Corning Sylgard 184, Ellsworth Adhesives) channels were plasma-bonded to PDMS-coated glass slides using a Corona Surface Treater (Electro-Technic Products, Inc.). The microfluidic focusing device had two inlets, one each for the oil continuous phase and the oligomer solution. A cylindrical aqueous oligomer jet, sheathed by the oil continuous phase, flowed through the main channel with width = 200 μm and height = 120 μm. The oil continuous phase was composed of 62 vol% heavy mineral oil (Fisher Scientific), 27 vol% hexadecane and 11 vol% Span 80. Two types of microfibers were produced for this study, which we refer to as “soft” and “rigid”, the latter achieved due to a higher level of crosslinking. The oligomer solution for the soft microfibers contained 57 vol% poly(ethylene glycol) diacrylate (PEG-DA; molecular weight = 575 g mol−1), 20 vol% 2-carboxyethyl acrylate (CEA), 10 vol% de-ionized (DI) water, 8 vol% 2-hydroxy-2-methylpropiophenone (photoinitiator, PI), and 5 vol% dye solution (20 mg ml−1 acryloxyethyl thiocarbamoyl rhodamine B, polysciences, in dimethyl sulfoxide). The solution composition used to prepare the rigid microfibers was 67 vol% PEG-DA, 20 vol% CEA, 8 vol% PI, and 5 vol% dye solution. The oligomer and oil phases were infused at constant flow rates Q1 and Q2, respectively, using syringe pumps (Harvard Apparatus), as summarized in Table 1. Unless otherwise stated, all chemicals were purchased from Sigma-Aldrich.| Fiber designation | a (μm) | Q 1 (mL h−1) | Q 2 (mL h−1) |
|---|---|---|---|
| Soft | 17.5 | 0.16 | 1.8 |
| Soft | 20 | 0.16 | 1.2 |
| Soft | 22.5 | 0.16 | 1.0 |
| Soft | 27.5 | 0.16 | 0.8 |
| Rigid | 20 | 0.1 | 0.75 |
Ultraviolet (UV) light was used to initiate the cross-linking reaction in the flowing oligomer solution. The UV light was supplied by a fluorescence light source (120 W mercury short arc lamp) on a Leica DMI4000B inverted microscope via the 20× magnification objective lens; spot size = 1.4 mm. No optical filters were used to modify the broad spectrum of light supplied from the lamp. For fiber fabrication, we measured the UV light intensity to be 35 ± 5 mW cm−2 using a UVA/B digital light meter (spectrum range 290–370 nm), based on a sensor area = 0.8 cm2. The oligomer solution was exposed to 200 ms pulses of UV light.
The fibers were collected in DI water and washed 3 times in 1 wt% aqueous solution of Tween 80 non-ionic surfactant, followed by at least 2 washes in 0.1 wt% Tween 80 solution. To limit excessive adhesion to all surfaces, both fibers and particles were stored in a 0.1 wt% aqueous solution of Tween 80. After cleaning, a dye adsorption assay (see ESI†) was used to estimate the amount of bound carboxyl groups in the fibers. Lastly, to ensure that the entire length of the fiber was in the field of view during the wrapping measurements, the fibers were manually cut immediately before experiments. The fiber lengths were 3–5 mm, and the fiber radii a ranged from 17.5–27.5 μm. Polymerization conditions were selected to minimize variations in the Young's modulus among the fibers with different radii. However, the fiber modulus is not constant in this study, and increases slightly with increasing a.
2.2 Fabricating disk-shaped particles
We made both positively charged and uncharged disk-shaped particles. The oligomer solution for the positively charged disk-shaped particle was composed of 57 vol% PEG-DA, 20 vol% 2-(dimethylamino)ethyl acrylate (DMAEA), 15 vol% DI water, 8 vol% PI, and 5 mg ml−1 fluorescein o-acrylate. The oligomer solution for the uncharged particle was composed of 57 vol% PEG-DA, 30 vol% DI water, 8 vol% PI, and 5 vol% dye solution (20 mg ml−1 acryloxyethyl thiocarbamoyl rhodamine B, Polysciences, in dimethyl sulfoxide). The particles were prepared using microscope projection photolithography13 in a PDMS chamber with height = 240 μm. Using the field diaphragm in the Leica DMI4000B inverted microscope as a mask, circular spots of UV light with the desired dimensions were projected onto the stationary oligomer solution. The size of the UV spot, and therefore the particle diameter, was controlled by the objective magnification and the size of the diaphragm opening. Disk-shaped particles with four different radii r were produced: 0.125 mm, 0.25 mm, 0.5 mm and 1 mm. The particles were removed easily from the PDMS chamber because of oxygen inhibition at the PDMS walls.14 The particles were washed repeatedly in Tween 80 solution (same cleaning procedure described above for the fibers), and stored in 0.1 wt% Tween 80. For experiments in sodium chloride (NaCl) solution, the fibers and particles were stored separately in the desired concentration of NaCl solution for at least 24 hours prior to testing.2.3 Nanoindendation measurements
The Young*s moduli of the fibers E and particles in water were measured using a bench-top PIUMA nanoindenter (Optics 11, The Netherlands). The PIUMA Dataviewer software was used to estimate the samples' Young's moduli, applying the Hertzian model to the loading curves in the linear visco-elastic regime of the stress strain curve.15 Specifically we report results from fitting the data for small penetration depths (500 nm). The performance of the PIUMA nanoindenter was first verified with a calibrated sheet of PDMS before the measurements on the samples of fibers and particles. The measured value was 2.6 ± 0.1 MPa, which matched the Young*s modulus of 2.5 MPa provided by the vendor.A probe with a spherical indentation tip was used to deform the samples of the fibers and the particles immersed in water. The radius of the spherical tip of the probe was 39.5 μm, and the spring constant of the cantilever was 3.56 N m−1. Though the spherical tip is of comparable size to the fibers, the contact area is expected to be small with a small indentation depth, so we utilize the traditional Hertzian model; this approach is consistent with measurement of spindle-shaped cells where reasonable values were obtained for the reported elastic modulus.16 A single force curve was generated per particle or fiber for at least 4 different particles or fibers in the batch, and an average Young's modulus, E, per batch was determined. The Young's moduli of the soft and rigid fibers (a = 20 μm) were measured to be 82 ± 5 kPa and 210 ± 30 kPa, respectively. The modulus of the disk-shaped particles was found to be 2500 ± 900 kPa.
2.4 Initializing contact between fiber and particle
In a typical wrapping experiment, the microfiber and the particle were transferred to an untreated polystyrene Petri dish containing a solution of 0.1 wt% Tween 80, where they settled to the bottom of the dish separately, and were completely immersed in the liquid. The fiber and particle do not make contact until an external force is provided. A home-made micromanipulator apparatus with a copper wire probe was used to gently push the particle into contact with the fiber. We tested different positions along the fiber length to initiate contact, and observed similar results regardless of where the particle was positioned. The results presented herein were obtained from particle placement roughly centered along the fiber length. The probe was quickly removed once contact was achieved, and the dish was covered and left undisturbed to allow the two objects to rearrange into their final configuration. The progress was recorded with a laser scanning confocal microscope (Leica SP5).3 Results and discussion
3.1 Effect of particle and fiber radius on fiber wrapping
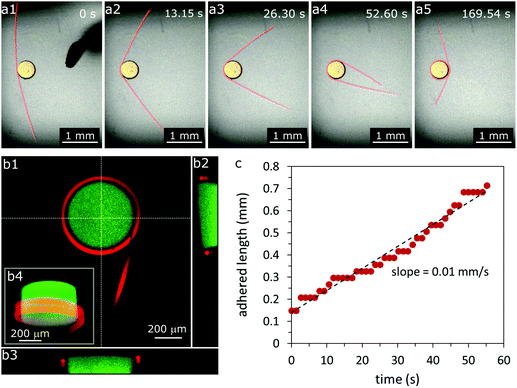
When we manually contact the curved surface of the positively charged particle to the negatively charged fiber, the fiber may spontaneously wrap around the particle for some conditions, which we describe below (Fig. 1a). In such cases, the fiber wraps continuously until it is obstructed or runs out of available surface on the particle. The fiber is able to make multiple revolutions by wrapping around the particle at different levels, as seen in the cross-sectional views in Fig. 1b2–4. For example, in Fig. 1, a fiber with radius a = 20 μm makes two revolutions around a particle with radius r = 250 μm (see also Video SV1, ESI†). For the conditions tested, the fiber–particle aggregate is irreversibly adhered, that is, the fiber remains adhered to the particle upon agitation or manipulation with the wire probe. If the same experiment is conducted with an uncharged particle (r = 250 μm), we observe adhesion but no continuous wrapping of the fiber around the particle (Fig. S1, ESI†), indicating that wrapping requires relatively strong electrostatic interactions, but the objects can adhere without charge–charge interactions if forced into close contact. We also note that the particles do not deform for any conditions considered in this work; the modulus of the particle is at least 10 times larger than that of the fiber (refer to Section 2.3).During the first revolution of fiber wrapping, we record the length of fiber adhering to the particle (from one free end), and we find that the length varies linearly with time (Fig. 1c). Moreover, within the limits of experimental error, this constant wrapping rate is independent of the initial length of the free end of the fiber for the range of lengths tested (1–3 mm) (Fig. S2, ESI†). This result suggests that viscous drag over the length of the fiber plays a negligible role in the dynamics of this wrapping process, and so the wrapping rate is determined by a dissipative mechanism close to the contact point.
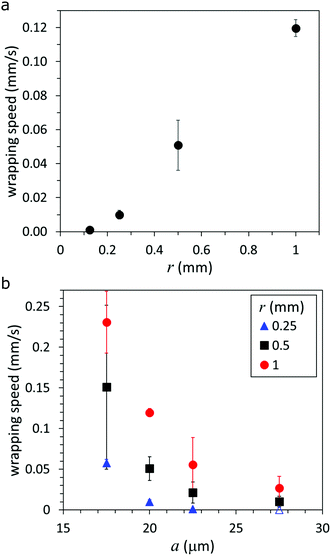
Since the fiber wraps with a constant speed, we measure the wrapping rate (in mm s−1) to study the effects of the radius of the “soft” fiber a and the particle radius r, which is shown in Fig. 2. The wrapping rate can also be presented in terms of an angular frequency, which is shown in ESI† (Fig. S3). For constant a, we observe a roughly linear increase in the wrapping speed with increasing r, for 125 μm ≤ r ≤ 1 mm, as shown in Fig. 2a. From the trend, we expect a positive horizontal intercept (corresponding to a wrapping rate = 0 mm s−1), indicating that there is a critical radius rc below which the fiber cannot wrap; in this case, rc ≲ 125 μm. In Section 4.2, we develop a theory to predict rc for different particle, fiber and solution properties.
In contrast, we observe an inverse relationship between the wrapping speed and a when r is constant (Fig. 2b). The trends in wrapping rate as a function of fiber and particle radii indicate that the fiber wraps if the gain in interaction energy outweighs the energetic cost of bending—the difference is dissipated due to motion through the fluid. Viscous dissipation occurs both as a result of having the free end of the fiber sweep through the fluid and by the squeezing out of fluid through the small gap as the surfaces make contact. The bending energy per unit length scales as Ea4/r2, where E is the Young's modulus of the fiber, thus we expect that, as the radius of the particle increases (decreasing curvature), less energy is required to deform the fiber, which may lead to an increase in the rate of wrapping (Fig. 2a). Similarly, we expect that the wrapping rate may decrease if the radius of the fiber increases, i.e., the bending rigidity of the fiber increases, and so more energy is required to bend a larger radius fiber around a particle of a given radius (Fig. 2b).
3.2 Effect of salt concentration on fiber wrapping
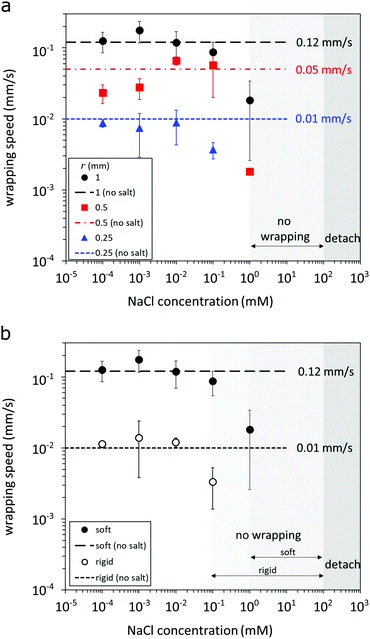
We dissolve salt in the surrounding liquid to vary the interaction energy between the fiber and the particle. The wrapping rate as a function of NaCl concentration is displayed in Fig. 3; the results for three particle radii are presented in Fig. 3a, and two fiber moduli in Fig. 3b. We observe three distinct interaction regimes as salt concentration varies. At low salt concentrations (<0.1 mM NaCl) we observe the first regime—wrapping—where the wrapping rate is comparable to that in 0 mM NaCl. For higher salt concentrations (≳0.1 mM NaCl) the wrapping rate decreases with increasing salt concentration until the wrapping behavior is no longer reproducible. We observe a transition to fibers that are weakly deformed or not deformed at all above a critical value of 1 mM NaCl. For the concentration range 1 mM < [NaCl] < 100 mM, wrapping does not occur (i.e., the no-wrapping regime), however, the fiber and the particle are well-adhered and do not separate upon agitation or manipulation with the wire probe (see SV2, ESI†). In contrast, when the fiber and particle are forced into contact in solutions containing >100 mM NaCl, they detach readily upon agitation or manipulation with the probe.For the results shown in Fig. 3b, we consider the behavior of the soft and rigid fibers. We observe that the rigid fiber can only wrap around the largest particle in our study, r = 1 mm. Otherwise, the trend in wrapping rate due to salt concentration for the rigid fiber is the same as the soft fiber, except that the transition to the no-wrapping regime occurs at a lower concentration of NaCl (0.1 mM). Though the Young's modulus of the rigid fiber is approximately 2.6 times larger than that of the soft fiber (based on nanoindentation measurements; refer to Section 2.3), the wrapping rate is about one order of magnitude smaller than that of the soft fiber (dashed lines in Fig. 3b). This result suggests a significant effect of fiber Young's modulus on the dynamics of the wrapping rate. We explore this dependence in more detail in the subsequent section by deriving a model to quantify the Young's modulus of the fiber from the deflected shape in situ during wrapping for more convenient characterization and a theory to predict the critical radius for wrapping.
Our experiments demonstrate the role of salt in screening the electrostatic interaction between the fiber and particle, inhibiting wrapping above one critical concentration, and inhibiting adhesion (without wrapping) above a second higher critical concentration. However, we note that if salt is added after the fiber has wrapped around the particle (initially in a salt-free medium), there is no observable effect of added salt concentration. Moreover, we note that an adhered fiber does not unwrap from the particle for any of the conditions tested in this study.
4 Modeling
In the following sections we derive a theory for the wrapping dynamics. We first derive a model for the shape assumed by the fiber and show how this may be used to extract the Young's modulus (Section 4.1). We follow this by a model to predict the critical radius for wrapping (Section 4.2).4.1 Modeling fiber shape
As the fiber wraps around the particle, it deflects due to the viscous drag exerted by the surrounding fluid. We postulate that, for a given wrapping rate and Young's modulus of the fiber, the shape assumed by the fiber is unique. Thus, by proposing a mathematical model for the fiber configuration as it wraps, we hypothesize that we may be able to make a prediction for the Young's modulus of the fiber. In this section, we propose such a model and test its predictive power on the soft and rigid fibers considered experimentally.We define a coordinate system (x,z) such that the origin lies at the particle center (see Fig. 4 for a schematic). We model only the part of the wrapping fiber above the contact point, which wraps in a clockwise fashion. We model the fiber shape with angle from the x-axis, θ, and arclength, s, coordinates, where s ∈ [0,L] is the arclength of the fiber measured from the first contact point (s = 0) to the end (s = L) (Fig. 4). We suppose that immediately before contact, in the absence of any motion, the fiber's initial state is described by θp(s) with θp(0) = 0. This information is extracted from the experiment (see ESI† for details). We set t = 0 to be the time at which the fiber first makes contact with the particle, of radius r, and without loss of generality assume this is at the far-left point of the particle. The initial fiber configuration is thus θ(s,0) = π/2 + θp(s). We suppose that the fiber subsequently wraps around the particle in a clockwise fashion and, based on the experimental observations, we assume it wraps with constant and known angular frequency ω. At time t, the fiber will have thus wrapped an angle αw = ωt. At this time, the part of the fiber described by 0 ≤ s ≤ sw(t) = rαw(t) is wrapped while the part of the fiber described by sw(t) ≤ s ≤ L is free; the total length of the detached fiber is Ld(t) = L − sw.
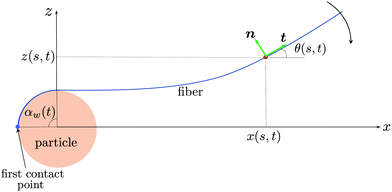 | ||
| Fig. 4 Schematic illustrating the wrapping motion of the fiber. The fiber is parameterized using angle-arclength coordinates θ(s,t). | ||
The x and z coordinates of the fiber at time t are then given by
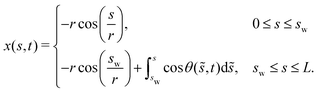 | (1) |
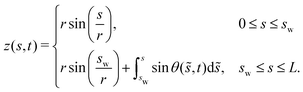 | (2) |
The fiber is observed to detach from the particle tangentially to the surface. In the experiments, the deflection of the fiber is typically small compared with the deflection of the prestressed state. As a result, it is convenient to work with the deflections from the prestressed configuration. Letting ψ denote the free-fiber configuration relative to the deflection from the prestressed state, we may write the fiber configuration as
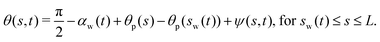 | (3) |
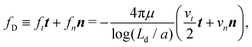 | (4) |
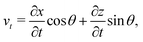 | (5a) |
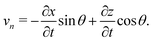 | (5b) |
A force balance in the directions parallel and perpendicular to the fiber and a balance of moments on the fiber yields, respectively,
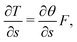 | (6a) |
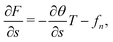 | (6b) |
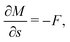 | (6c) |
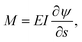 | (7) |
At t = 0, the fiber makes first contact with the particle. Prior to this, the fiber is stationary, so no external forces act and thus ft = fn = 0, and the fiber will be in its prestressed configuration, θ(s,0) = π/2 + θp(s). The initial x and z coordinates are determined by (1) and (2), and F = T = M = 0 from (6).
At time t > 0, the fiber described by 0 ≤ s ≤ sw wraps onto the particle and its location is thus known trivially. For sw(t) ≤ s ≤ L, we must solve for the fiber shape using (3), (6) and (7). The system is solved subject to the following boundary conditions
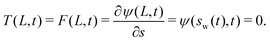 | (8) |
| vt ≈ 0, vn ≈ −(s − sw)ω, | (9) |
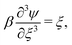 | (10) |
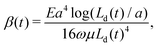 | (11) |
The system behavior is thus characterized entirely by the dimensionless parameter β(t), given by (11). We note that the time dependence of the parameter β arises due to the change in the free-fiber length Ld as it wraps during the experiment and that all other parameters in (11) remain constant during the experiment. This equation can be rearranged to provide a prediction for the Young's modulus in terms of physical parameters
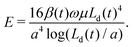 | (13) |
The final deflection of the profile from the prestressed state is
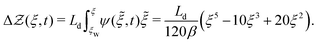 | (14) |
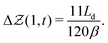 | (15) |
We may use this expression as a simple way of determining the Young's modulus when the deflection from the prestressed state is not too large and the prestressed state is close to flat. In dimensional terms, this result may be rearranged to give a prediction for the Young's modulus,
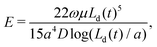 | (16) |
While the above strategy provides an estimate of the Young's modulus, we may obtain a more accurate estimate from determining the parameter β(t) from (11) if we are able to fit the entire experimental fiber profile to the model eqn (10). Then, (13) provides the Young's modulus for the fiber. In the following section we shall show how in practice both of these strategies are helpful to obtain a prediction for the Young's modulus, depending on the experimental setup and in each case we compare this with measurements made using nanoindentation.
In Fig. 5, we show the experimental fiber deflection after accommodating for the prestressed state and the prediction from the theory (14) and observe a good agreement in the shape. For completeness, we also compare this with the full theory in which we make no assumption on the prestressed fiber shape and the subsequent deflection (see ESI† for details). We observe almost no discernible difference between this prediction and the full numerical system, which confirms the validity of the simplified theory to describe the fiber dynamics.
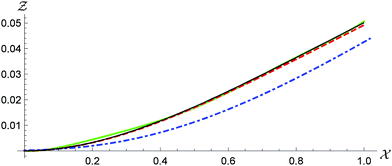 | ||
| Fig. 5 Comparison of the prediction of the deflection of a soft fiber wrapping around a 0.25 mm radius particle in 0.1 mM NaCl for the fiber configuration given by the solution to the reduced model for small-deflection prestressed states (14) (red dashed) and the experimental data (green solid). The match between the data and the theory is excellent. We also show in blue dot dashed the prestressed state and in black the solution to the full model presented in the Model equations section (see ESI† for details). The difference between the two theories is barely discernible, supporting the use of the simplified model (14). | ||
We use three independent snapshots and match the experimental profiles with the theoretical model and obtain a prediction of E = 71 ± 6 kPa, where the error here corresponds to one standard deviation (see Fig. S6, ESI† as an example). The smallness in the error and the good fit to the experimental shape provides confidence in the reliability of this method. This also emphasizes the fact that in (13), although both β and Ld vary with time, the predicted Young's modulus remains constant. Nano-indentation measurements give a Young's modulus of this fiber of 82 ± 5 kPa, which is not too dissimilar to the prediction.
We now attempt a similar approach for a rigid fiber wrapping around a particle of radius 1 mm in 0.1 mM NaCl. In this case, the rotation rate of the fiber is more than five times slower than in the soft fiber case (ω = 0.0067 s−1). Coupled with the fact that this fiber is more rigid, we observe only marginal deflection of the fiber, which is at the level of the pixel resolution of the images (see Fig. S7, ESI†). Indeed, for an experiment conducted on the rigid fiber, we observe a deflection of a single pixel from the prestressed state due to the viscous drag forces. As a result, it is unwise to match the shape of the fiber as we did in the case of the soft fiber. In this case, we instead use (16), to give an estimate of the Young's modulus. However, when determining the error bounds in this case we know that the deflection is at least 0.5 pixels and less than 1.5 pixels. Thus we obtain an estimate for the Young's modulus of 134 ± 67 kPa. For comparison, the Young's modulus of the rigid fiber was measured to be 210 ± 30 kPa by nanoindentation. While we acknowledge the reduced accuracy within which we can predict the Young's modulus in this case, we observe that this predicts a higher Young's modulus than that of the soft fiber, and so we are able to distinguish between the two fibers.
4.2 Critical particle radius to wrap
In this section we consider an energy balance to estimate the minimum particle radius for wrapping to occur. Electrostatic attraction between the fiber and particle drives wrapping at the energetic cost of bending the fiber. To estimate the size of the smallest particle round which a fiber will wrap, we model their surfaces as carrying surface charge densities ±σ. Interactions are screened over the Debye length, defined by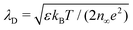 in a monovalent solution with concentration n∞ and permittivity ε, where kB is the Boltzmann constant, T is the temperature and e is the charge on an electron.18 Assuming constant-charge interactions,18,19 the energy of interaction per area between the two oppositely charged surfaces has a characteristic scale φ = σ2λD/ε. We assume tangential contact between the fiber and the particle, so the horizontal length over which the surfaces interact is 2
in a monovalent solution with concentration n∞ and permittivity ε, where kB is the Boltzmann constant, T is the temperature and e is the charge on an electron.18 Assuming constant-charge interactions,18,19 the energy of interaction per area between the two oppositely charged surfaces has a characteristic scale φ = σ2λD/ε. We assume tangential contact between the fiber and the particle, so the horizontal length over which the surfaces interact is 2![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) where
where 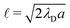 . The electrostatic work per length therefore scales as ∼φ(2
. The electrostatic work per length therefore scales as ∼φ(2![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) ). A detailed calculation using the Derjaguin approximation in the Debye–Huckel limit (see p. 294 of ref. 19) confirms this scaling relation up to a prefactor
). A detailed calculation using the Derjaguin approximation in the Debye–Huckel limit (see p. 294 of ref. 19) confirms this scaling relation up to a prefactor ![[k with combining circumflex]](https://www.rsc.org/images/entities/i_char_006b_0302.gif) ≈ 1.07, finding that the electrostatic work per wrapped length is
≈ 1.07, finding that the electrostatic work per wrapped length is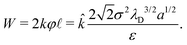 | (17) |
This favorable energetic contribution is offset by the bending energy which, per wrapped length, is EI(1/r − 1/rp)2/2, where 1/rp = −∂θp/∂s is the signed curvature of the fiber in its initial (prestressed) configuration.20 In our experiments, the curvature of the initial state is typically small relative to that of the particle and will be neglected below. The net energy cost per unit time to wrap the fiber around the particle at a speed ṡw = ωr is then
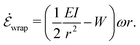 | (18) |
 . Using this condition, we find that the fiber can only wrap around particles whose radius exceeds a critical value
. Using this condition, we find that the fiber can only wrap around particles whose radius exceeds a critical value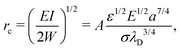 | (19) |
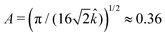 . As intuitively expected, thicker and more rigid fibers can only wrap relatively larger particles due to their higher bending energy cost. We also note that the critical radius to wrap increases with salt concentration (via λD; rc ∝ n∞3/8) due to electrostatic screening.
. As intuitively expected, thicker and more rigid fibers can only wrap relatively larger particles due to their higher bending energy cost. We also note that the critical radius to wrap increases with salt concentration (via λD; rc ∝ n∞3/8) due to electrostatic screening.
We estimate σ as the charge corresponding to the first few molecular-thickness layers at the fiber surface. Denoting the bulk carboxylate ion density by ne and the radius of a carboxylate ion by ai = 0.35 nm (based on the size of the formate anion21), the outermost k layers of the fiber surface carry a charge ke(2ai)ne. For the 20 μm radius soft particle, we measure ne ≈ 0.017 ions per nm3 (see ESI†), yielding that the top one to two “layers” of ions carry a charge in the range σ ≈ 1.8–3.6 mC m−2. We note that this range of surface charge corresponds to zeta potentials σλD/ε in the range 25–50 mV at a 1 mM NaCl concentration, which is typical of similar charged hydrogels.22,23 For simplicity, we use the mean value within the range of surface charge estimated above, σ = 2.7 mC m−2. We note that σ is expected to remain relatively independent of concentration since the fibers and particles are seeded with bulk charges at a fixed density.
We now estimate rc for a soft fiber (E = 82 kPa) with radius a = 20 μm wrapping in pure (deionized) water (corresponding to Fig. 2a). We use n∞ = 10−7 M (the concentration of ions in deionized water) to calculate λD and, with the value of σ estimated above, find rc ≈ 0.2 mm, consistent with the experimental observation for the initiation of wrapping. Alternatively, the expression (19) can be inverted to obtain a prediction for the radius of the thickest fiber, ac, that will wrap a particle of radius r, given by
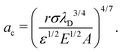 | (20) |
To predict ω one needs to balance the energy gained from wrapping with the rate of dissipation. While the mechanism of dissipation remains unclear, we make some estimates of viscous dissipation here. The energy dissipated due to the drag on the fiber is estimated as 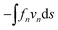 [see (4) and (9)] and is approximately μω2Ld3/log(Ld/a). Very close to the contact point, there is an additional lubrication force associated with squeezing the fluid between the fiber and the particle. This force per unit length of the fiber scales as flub ∼ −μa3/2h−3/2vn, where h is the separation distance between the surfaces.24 Assuming a weakly curved fiber consistent with (9), we estimate h ∝ x2/r and obtain an energy dissipation rate
[see (4) and (9)] and is approximately μω2Ld3/log(Ld/a). Very close to the contact point, there is an additional lubrication force associated with squeezing the fluid between the fiber and the particle. This force per unit length of the fiber scales as flub ∼ −μa3/2h−3/2vn, where h is the separation distance between the surfaces.24 Assuming a weakly curved fiber consistent with (9), we estimate h ∝ x2/r and obtain an energy dissipation rate 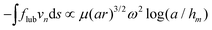 , where hm is a molecular cutoff length.
, where hm is a molecular cutoff length.
For the experimentally measured parameters we find that both of these sources of dissipation are of similar magnitude, but both are smaller than the rate of energy gained from wrapping. However, the experimental observation that the wrapping rate is independent of the detached length Ld (see ESI†) indicates that the actual dissipation mechanism in the experiments must be local to the region around the contact point. Such a mechanism may involve an interplay of electrostatic, elastic and viscous forces on length scales much smaller than the fiber radius.25 For example, viscous dissipation is likely amplified by a local flattening of the fiber cross-section by the lubrication pressure26 or by electrostatic or adhesive forces. Energy may also be dissipated within the hydrogel matrix of the fiber as the contact point moves along it.27 Quantifying these sources of dissipation requires a detailed analysis of the near-contact dynamics and is an interesting line of future inquiry.
5 Conclusions
Using a non-Brownian two-object system that spontaneously self-organizes via an electrostatic adhesion-wrapping mechanism, we quantify the speed of wrapping with respect to the microfiber and particle radii, the fiber modulus, and the ionic strength of the surrounding liquid. The experimental wrapping trends support a mechanistic understanding based on competing effects from the electrostatic attraction between the oppositely charged microfiber and curved particle and the bending energy to wrap the fiber around the particle. From these energetic considerations, we are able to predict the critical particle radius rc for wrapping, which is consistent with experimental observations. Characterization of the wrapping rate and critical properties, such as rc, can provide useful design criteria for controlling aggregates and assemblies of fibers and curved particles or fibers and curved substrates with strong adhesive interactions.In addition, we present a model to describe the shape of a fiber as it wraps around a particle due to an attractive force between the fiber and particle. This model provides a convenient and useful approach to estimating the modulus of the fiber in situ. The full model comprising integro-differential equations can describe arbitrarily large deflections of the fiber from its original prestressed state. By making the assumption that the deflections are not too large simplifies the model to a set of coupled partial differential equations. Making the further assumption that the initial prestressed state is close to straight enables us to write down the profile shape explicitly. The shape of the fiber is characterized by a single dimensionless parameter β, which corresponds to a balance between the viscous forces exerted on the fiber and the resistance to deformations through the bending stiffness. Matching the theoretical model to the experimental images provides a prediction of β, which in turn gives a prediction for the Young's modulus.
For soft fibers that deflect by a measurable amount we are able to extract a prediction for the Young's modulus that does not differ significantly from snapshot to snapshot. For stiffer fibers, or for experiments in which the wrapping rate is slower, the deflections are more difficult to measure accurately. In this case the model is still able to make a prediction, but with necessarily larger associated errors. This model is applicable in a wide range of other scenarios in which a fiber is deflected due to an external viscous flow, and may be useful in probing the material properties in scenarios in which other invasive methods are difficult.
Author contributions
JKN and HAS conceived the original idea and supervised the work. JL and JKN planned the experiments. JL, JM and JKN carried out the experiments and collected and analyzed data. IMG, BR and HAS developed the models. IMG performed numerical analysis. All authors discussed the results. IMG, JKN and BR wrote the manuscript with input from all authors.Conflicts of interest
There are no conflicts to declare.Acknowledgements
We thank Mr Yuzhen Feng and Mr Zhenhao Jiang for helping with nanoindentation measurements. JKN and HAS acknowledge NSF CMMI-1661672. IMG gratefully acknowledges support from the Royal Society through a University Research Fellowship. This research was partially supported by NSF through the Princeton University Materials Research Science and Engineering Center DMR-2011750.References
- R. G. Winkler and A. G. Cherstvy, in Strong and Weak Polyelectrolyte Adsorption onto Oppositely Charged Curved Surfaces, ed. M. Müller, Springer Berlin Heidelberg, Berlin, Heidelberg, 2014, pp. 1–56 Search PubMed.
- X. Yi, X. Shi and H. Gao, Phys. Rev. Lett., 2011, 107, 098101 CrossRef.
- P. Guo, D. Liu, K. Subramanyam, B. Wang, J. Yang, J. Huang, D. T. Auguste and M. A. Moses, Nat. Commun., 2018, 9, 1–9 CrossRef.
- B. Roman and J. Bico, J. Phys.: Condens. Matter, 2010, 22, 493101 CrossRef CAS.
- R. D. Schulman, A. Porat, K. Charlesworth, A. Fortais, T. Salez, E. Raphaël and K. Dalnoki-Veress, Soft Matter, 2017, 13, 720–724 RSC.
- C. Py, P. Reverdy, L. Doppler, J. Bico, B. Roman and C. N. Baroud, Phys. Rev. Lett., 2007, 98, 156103 CrossRef.
- A. Lindner and M. Shelley, Fluid-Structure Interactions in Low-Reynolds-Number Flows, The Royal Society of Chemistry, 2016, pp. 168–192 Search PubMed.
- P. Katsamba and E. Lauga, Phys. Rev. E, 2019, 99, 053107 CrossRef CAS.
- J. K. Nunes, K. Sadlej, J. I. Tam and H. A. Stone, Lab Chip, 2012, 12, 2301–2304 RSC.
- A. Perazzo, J. K. Nunes, S. Guido and H. A. Stone, Proc. Natl. Acad. Sci. U. S. A., 2017, 114, E8557–E8564 CrossRef CAS.
- M. Slutzky, H. A. Stone and J. K. Nunes, Soft Matter, 2019, 15, 9553–9564 RSC.
- D. Qin, Y. Xia and G. M. Whitesides, Nat. Protoc., 2010, 5, 491–502 CrossRef CAS.
- J. C. Love, D. B. Wolfe, H. O. Jacobs and G. M. Whitesides, Langmuir, 2001, 17, 6005–6012 CrossRef CAS.
- D. Dendukuri, P. Panda, R. Haghgooie, J. M. Kim, T. A. Hatton and P. S. Doyle, Macromolecules, 2008, 41, 8547–8556 CrossRef CAS.
- L. Cheng, X. Xia, L. Scriven and W. Gerberich, Mech. Mater., 2005, 37, 213–226 CrossRef.
- S.-A. Xie, T. Zhang, J. Wang, F. Zhao, Y.-P. Zhang, W.-J. Yao, S. S. Hur, Y.-T. Yeh, W. Pang, L.-S. Zheng, Y.-B. Fan, W. Kong, X. Wang, J.-J. Chiu and J. Zhou, Biomaterials, 2018, 155, 203–216 CrossRef CAS.
- H. A. Stone and C. Duprat, Fluid-Structure Interactions in Low-Reynolds-Number Flows, The Royal Society of Chemistry, 2016, pp. 25–77 Search PubMed.
- J. N. Israelachvili, Intermolecular and Surface Forces, Academic Press, San Diego, 3rd edn, 2011, pp. 253–289 Search PubMed.
- H. Ohshima, Biophysical Chemistry of Biointerfaces, John Wiley & Sons, 2011 Search PubMed.
- B. Audoly and Y. Pomeau, Elasticity and geometry: from hair curls to the non-linear response of shells, Oxford University Press, 2010 Search PubMed.
- N. A. Lange and J. G. Speight, Lange's Handbook of Chemistry, McGraw-Hill Education, New York, 16th edn, 2005 Search PubMed.
- S. Schmidt, H. Wang, D. Pussak, S. Mosca and L. Hartmann, Beilstein J. Org. Chem., 2015, 11, 720–729 CrossRef CAS.
- A. H. Faraji, J. J. Cui, Y. Guy, L. Li, C. A. Gavigan, T. G. Strein and S. G. Weber, Langmuir, 2011, 27, 13635–13642 CrossRef CAS.
- D. Jeffrey and Y. Onishi, Q. J. Mech. Appl. Math., 1981, 34, 129–137 CrossRef.
- T. Tang, C.-Y. Hui and A. Jagota, J. Appl. Phys., 2006, 99, 054906 CrossRef.
- R. H. Davis, J.-M. Serayssol and E. Hinch, J. Fluid Mech., 1986, 163, 479–497 CrossRef.
- B. Andreotti and J. H. Snoeijer, Annu. Rev. Fluid Mech., 2020, 52, 285–308 CrossRef.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/d0sm01857k |
| This journal is © The Royal Society of Chemistry 2021 |