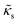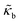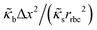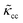Open Access Article
Open Access ArticleEmergent cell-free layer asymmetry and biased haematocrit partition in a biomimetic vascular network of successive bifurcations†
Qi
Zhou
 *a,
Joana
Fidalgo
b,
Miguel O.
Bernabeu
*a,
Joana
Fidalgo
b,
Miguel O.
Bernabeu
 c,
Mónica S. N.
Oliveira
c,
Mónica S. N.
Oliveira
 b and
Timm
Krüger
b and
Timm
Krüger
 *a
*a
aSchool of Engineering, Institute for Multiscale Thermofluids, University of Edinburgh, Edinburgh EH9 3FB, UK. E-mail: q.zhou@ed.ac.uk; timm.krueger@ed.ac.uk
bJames Weir Fluids Laboratory, Department of Mechanical and Aerospace Engineering, University of Strathclyde, Glasgow G1 1XJ, UK
cCentre for Medical Informatics, Usher Institute, University of Edinburgh, Edinburgh EH16 4UX, UK
First published on 6th January 2021
Abstract
Blood is a vital soft matter, and its normal circulation in the human body relies on the distribution of red blood cells (RBCs) at successive bifurcations. Understanding how RBCs are partitioned at bifurcations is key for the optimisation of microfluidic devices as well as for devising novel strategies for diagnosis and treatment of blood-related diseases. We report the dynamics of RBC suspensions flowing through a biomimetic vascular network incorporating three generations of microchannels and two classical types of bifurcations at the arteriole level. Our microfluidic experiments with dilute and semidilute RBC suspensions demonstrate the emergence of excessive heterogeneity of RBC concentration in downstream generations upon altering the network's outflow rates. Through parallel simulations using the immersed-boundary-lattice-Boltzmann method, we reveal that the heterogeneity is attributed to upstream perturbations in the cell-free layer (CFL) and lack of its recovery between consecutive bifurcations owing to suppressed hydrodynamic lift under reduced flow conditions. In the dilute/semidilute regime, this perturbation dominates over the effect of local fractional flow at the bifurcation and can lead to inherently unfavourable child branches that are deprived of RBCs even for equal flow split. Our work highlights the importance of CFL asymmetry cascading down a vascular network, which leads to biased phase separation that deviates from established empirical predictions.
1 Introduction
The human microcirculation is a network of microvessels (involving arterioles, venules and capillaries) perfused by blood to maintain the normal function of organs and tissues.1 A main feature of the microcirculatory blood flow is its highly heterogeneous haematocrit (or volume fraction of RBCs, Ht). This heterogeneity is a direct consequence of disproportionate partitioning of RBCs (relative to the flow split) at successive bifurcations, governed by the well-known Zweifach–Fung effect owing to prevalent CFLs in microvessels.2,3 Under extreme conditions, some child branches may only receive the plasma from the CFL of the feeding branch and are completely deprived of RBCs, the phenomenon of which is coined by Krogh as plasma skimming.4Extensive studies have explored factors that could potentially affect the partitioning of RBCs at vascular/artificial bifurcations, either in vivo5–8 or in vitro.9–15 By using bioplastic bifurcating channels ranging from 20–100 μm in diameter, Fenton et al. identified three key variables: the feeding haematocrit, the diameter of vessels, and the fractional flows in respective child branches.9 The dominance of these variables was further confirmed by Pries et al.8via examination of multiple arteriolar bifurcations in rat mesentery. Thanks to the abundance of in vivo data, Pries et al. developed a robust empirical model that provides quantitative description of the phase-separation process at microvascular bifurcations (hereafter referred to as phase-separation model, PSM). Over time, the PSM evolves with refined parametric formulation16–19 and has been widely applied to elaborate microcirculatory blood flow.
Experimentally speaking, in vivo investigation of the phase-separation process is inherently subject to various uncertainties (e.g. photometric accuracy, physiological compensation, or regulatory responses). On the other hand, critical challenges also remain to be satisfactorily resolved for in vitro experiments (e.g. geometric reality, concentration constriction, independent plasma/cell velocimetry and haematocrit determination) to accurately imitate and quantify the process using microfluidic bifurcations composed of comparably small channels.12,13,20,21 These experimental limitations can be potentially overcome by increasingly realistic computational simulations, which can query multiple aspects that are otherwise inconvenient or inaccessible to experiments, such as microscopic cell dynamics in a dense suspension, emergent cell orderings on the cross-sectional plane and spatio-temporal RBC flow properties (e.g. evolving CFLs22,23).
However, there is a lack of coordination between experimental and computational studies to converge towards a mutual understanding of the phase-separation process within overlapping parameter space (e.g. channel dimension, fluid inertia, cell concentration, RBC deformability) and under justifiable assumptions (e.g. ideal Poiseuille flow, centralised haematocrit profile, symmetric CFLs). One such discrepancy in understanding haematocrit partition at a bifurcation is about the existence/strength of a potential preference of RBC populations moving towards the orthogonal side branch (rather than the continuation of the parent branch) in the typical right-angle T-bifurcation, for which previous microfluidic12 and computational24 studies offered conflicting answers.
For a mechanistic understanding of the phase-separation process, two-dimensional (2D) in silico models have been widely employed to study the microscopic behaviour of individual RBCs at a bifurcation.25–28 Several underlying effects have been proposed, such as the vessel obstruction effect,29 the unbalanced shear–force effect,30 the branching angle effect,31 and the low-flow attraction effect.32 Recently, three-dimensional (3D) computer simulations considering more realistic cell–wall interactions24,33–38 emerged to overcome the inherent limitations of 2D models.
Apart from the interaction between RBCs and the bifurcation geometry, the breakdown and recovery of CFLs in pre-/post-bifurcation branches is also an increasing focus of in silico studies.39–41 The RBC core is usually disturbed at a bifurcation, leading to asymmetric CFL associated with transient haematocrit profiles. If the inter-bifurcation distances are short or only moderate (e.g. less than 10 vessel-diameter long as postulated by ref. 8), the transverse organisation of RBCs bears a memory of the transient flow from last bifurcation and the CFL symmetry may not be restored upon reaching the next bifurcation.23,42,43 Indeed, recent RBC simulations in a microvascular network demonstrated increasingly asymmetric CFL that develop along curved vessels without apparent recovery of symmetry.22 In line with an earlier in vitro study,12 these simulations also highlighted the profound impact of haematocrit-profile skewness on the partitioning of RBCs at bifurcations in the vascular network.44 As the symmetry assumption for haematocrit profile in the parent branch of a bifurcation is central to the empirical formulation of PSM,8 uncertainties arise when applying PSM to bifurcations in a network where time-dependent effects are prevailing, for instance, with underdeveloped cellular flow between successive bifurcations (more likely to occur with smaller inter-bifurcation distances and lower RBC concentrations).
The present study aims to elucidate the phase separation of blood flow in bifurcating networks by inspecting the partitioning of dilute/semidilute RBC suspensions through successive bifurcations under controlled outflow conditions, where cell–cell interactions are weak and the microscopic behaviour of individual RBCs can be tracked experimentally. We perform experiments and simulations of a biomimetically designed artificial vascular network that comprises three generations of microchannels with two classical types of bifurcations. Through cross-validation of experimental and simulation data, we uncover an emerging heterogeneity of haematocrit partition within the network that substantially deviates from empirical predictions of the PSM. We attribute this heterogeneity to the perturbed CFLs between bifurcations and analyse the underlying RBC dynamics subject to network outflows. It is found in the dilute/semidilute regime, upstream CFL perturbations persist and can lead to severely biased phase-separation at a bifurcation under reduced flow conditions, even with equal fractional flow for the child branches. Furthermore, we identify consistent patterns of haematocrit reduction/enrichment in the network against varying outflow ratios for different systemic haematocrits, which may provide insights into the elusive microvascular blood flow, and inspire the optimisation of existing microfluidic devices for handling RBC suspensions.
2 Materials and methods
2.1 Microfluidic experiments
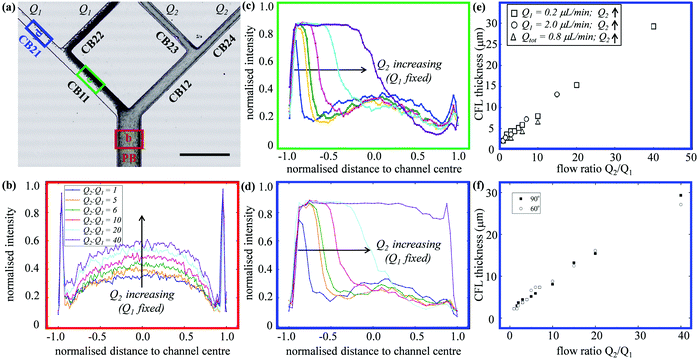
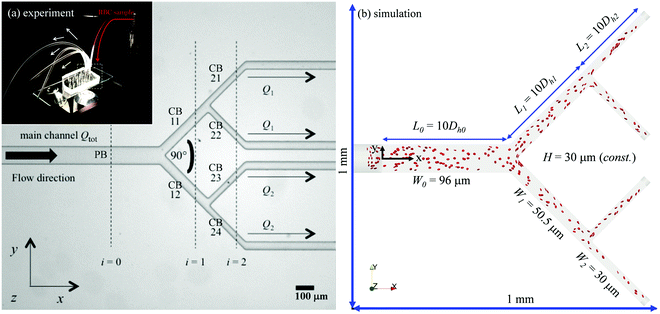
Fig. 1a shows a typical microfluidic network used in this work. The planar microdevice was manufactured in PDMS (polydimethylsiloxane, Sylgard 184, Dow Corning) by soft-lithography using an SU8 mould produced by photo-lithography (microLIQUID), and was sealed with a glass slide substrate using oxygen plasma treatment (Zepto, Diener). Each network is composed of three generations. The 0th generation (i = 0) has one main channel, which is hereafter referred to as the network parent branch (PB). The PB bifurcates into two child branches (CBs) in the 1st generation (i = 1), which are denoted CB11 and CB12, respectively. CB11 and CB12 themselves further bifurcate in the 2nd generation (i = 2), leading to four child branches denoted CB21, CB22, CB23 and CB24, respectively. All channels have a constant depth H = 30 μm. The channel width Wi = 96, 50.5, 30 μm varies following the biomimetic rule proposed by45,46 so that a generalised Murray's law for microfluidic manifolds is observed, which yields a constant wall shear stress in the fully developed regions throughout the network (see Fig. S1 in the ESI† for numerical validation). The segment length Li is designed as Li = 10Dh,i, where Dh,i = 2WiH/(Wi + H) is the hydraulic diameter of a given branch (except i = 0, where L0 = 30Dh,0). The main difference between the current design and the ones proposed in ref. 45 and 46 is the bifurcation angle, which is chosen as 90 degrees, rather than 180 degrees, to avoid sharp bends within child branches.47,48 A second device with an angle of 60 degrees at all bifurcations has also been fabricated to test the effect of bifurcation angle (see Fig. S2a in the ESI†).The blood samples consist of RBC suspensions in Dextran40, prepared using horse blood in anticoagulant EDTA (TCS Biosciences, 1.5 mg mL−1). The sample-processing procedures have been detailed in our previous work49 and are therefore not repeated here for brevity. The steady shear rheology of Dextran 40 was determined by a rotational rheometer (DHR2, TA Instruments, with minimum resolvable torque 0.1 nN m) using a cone-plate geometry of 60 mm diameter and angle θ = 1° (CP60/1), 30 μm truncation gap. The density and shear viscosity are 1.07 × 103 kg m−3 and 5.0 mPa s, respectively.
The flow of the RBC suspensions through the device was imposed using two syringe pump modules (Nemesys, Cetoni) connected to the outlets. These modules can be operated independently (one for Q1, the other for Q2 as depicted in Fig. 1a) and each module controls two coupled syringes continuously withdrawing the RBC sample from the single inlet. Flow visualisation was performed using an inverted microscope (Olympus IX71) equipped with a halogen lamp. Videos/images were acquired by a sensitive monochrome CCD camera (Olympus, XM10) using a 10× magnification objective with numerical aperture of 0.25 to guarantee that the depth of field and image depth are large enough to observe cell trajectories across the entire channel height.
2.2 Numerical simulation
The computational domain for numerical simulations is reconstructed using design dimensions of the microfluidic device (see Fig. 1b and Table 1). The flow inlets/outlets are modelled as cylindrical regions with the same geometry as the CTRACT-S configuration (“smaller inflow contraction”) of the microchannel simulated in our previous work.49 This geometric feature enables an RBC distribution with considerate initial CFLs upon entry into the main channel, therefore a much shorter length of the parent branch PB (≈10Dh,0) than its experimental counterpart (= 30Dh,0) is needed for the CFL to fully develop before reaching the first bifurcation. This treatment is crucial, as an equivalent length of the numerical PB to the experimental one would be prohibitively expensive for cellular simulation. To initialise the simulation, a plasma flow (without RBCs) is pulled from left to right with a fixed volume flow rate Qtot = 4 μL min−1 in PB with varying outflow ratio Q1/Q2. This is realised by imposing parabolic velocity profiles (assuming Poiseuille flow in the cylindrical extensions, with no-slip condition on the channel wall) at each outlet. After the steady flow has been established within the whole network, RBCs are randomly inserted from the cylindrical entry region in a continuous manner with fixed feeding haematocrit of 1%, 2% or 10%.| Network geometry | ||
|---|---|---|
| Channel width | W i (i = 0, 1, 2) | 96, 50.5, 30 μm |
| Channel depth | H | 30 μm |
| Network length | L | 1 mm |
| Hydraulic diameter | D h,i | 2WiH/(Wi + H) |
| RBC model | ||
|---|---|---|
| Cell radius | r rbc | 4 μm |
| Viscosity contrast | λ | 1.0 |
| Feeding haematocrit | H F | 1%, 2%, 10% |
| Local haematocrit | ϕ | variable |
The numerical model for simulating blood flow as a suspension of deformable RBCs as in our recent work49 employs the immersed-boundary-lattice-Boltzmann method (IB-LBM50). The model is implemented in the parallel flow simulator HemeLB51,52 (open source at https://github.com/hemelb-codes/hemelb) by incorporating a new module for discrete deformable cells. The fluid flow governed by the Navier–Stokes equations is solved by the lattice-Boltzmann method with standard D3Q19 lattice,53 BGK collision operator,54 Guo's forcing scheme55 and the Bouzidi–Firdaouss–Lallemand (BFL) implementation of no-slip boundary condition at the walls.56 To precisely control the volume flow rates at various inlets/outlets, inflow/outflow open boundary conditions are implemented with the Ladd velocity boundary condition.57
The RBCs are modelled as Lagrangian membranes through a finite element approach, which are further coupled with the fluid flow using the immersed-boundary method58 for the interpolation of velocities and the spreading of forces. Each RBC is modelled as a closed finite-element membrane consisting of 720 triangular facets (with the membrane mesh matching the lattice resolution Δx for numerical stability and accuracy59). The unstressed RBC shape is assumed as a biconcave discoid. The RBC membrane is elastic, with its mechanical properties controlled by five moduli which govern different energy contributions. They are the strain modulus κs, the bending modulus κb, the dilation modulus κα, the surface modulus κS and the volume modulus κV. To tackle potential close-contact of cells or between a cell and the wall, a repulsion potential decaying with inverse distance between neighbouring surfaces is implemented (characterised by interaction strengths κcc and κcw as in Table 1).
The flow behaviour of RBCs is determined by the particle Reynolds number Rep and the capillary number Ca. Rep represents the ratio of particle inertia to fluid viscous forces and is defined based on the channel Reynolds number Rec:
| Rep = Rec(2rrbc/Dh)2, Rec = ρexūDh/ηex | (1) |
Ca = τrbc![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) c, τrbc = ηexrrbc/κs, c, τrbc = ηexrrbc/κs, ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) c = 8ū/Dh c = 8ū/Dh | (2) |
![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) c is the characteristic wall shear rate in equivalent Poiseuille flow. Both Ca and the viscosity contrast λ (between RBC cytosol and the suspending fluid) are kept the same for experiments and simulations (see Table 1).
c is the characteristic wall shear rate in equivalent Poiseuille flow. Both Ca and the viscosity contrast λ (between RBC cytosol and the suspending fluid) are kept the same for experiments and simulations (see Table 1).
2.3 Cell-counting procedure
The quantification of RBC fluxes Qrbc in the network relies on a cell-counting procedure that records cells crossing designated planes of interest, which are placed perpendicular to the channel axis of individual branches. To satisfy mass conservation, the counting procedure only considers RBCs outwith the transient state of a simulation, i.e. when the total number of cells in the simulated network has become quasi-constant. The obtained Qrbc values are then used to calculate the discharge haematocrit HD in each branch based on the local volume flow rate of blood Qblood. To describe the systematic variation of RBC concentration within the vascular network, we follow the approach of Pries et al.60 and compare the HD value of a given child branch against that of PB (referred to as HD,inflow). Note that HD,inflow should not be confused with HF, which is the feeding haematocrit from our numerical inlet imitating a RBC reservoir and may differ slightly from HD,inflow. If HD/HD,inflow < 1 for the child branch, this is defined as haematocrit reduction; if HD/HD,inflow > 1, this is defined as haematocrit enrichment. For the calculation of local haematocrits ϕ, which are needed to construct cross-sectional haematocrit profiles, cells are extracted at given time intervals (sufficiently large to minimise the effect of cell sampling) from the simulation after steady state has been reached.3 Results
3.1 Outflow-tuned RBC distribution and CFL asymmetry
In experiments with HF = 1%, where Q1 = 0.2 μL min−1 is kept constant while gradually increasing Q2 to achieve higher flow ratios (Q2/Q1 = 1–40, see the variation of flow pathlines in Fig. S4a–c, ESI†), diverse patterns of RBC distribution are achieved at successive bifurcations (Fig. 2c). Fig. 3a details the RBC distribution at Q2/Q1 = 40 (as in the last panel of Fig. 2c). Notably, despite an even flow split for CB21 and CB22, a marked discrepancy in RBC concentration exists between them, potentially caused by the one-sided RBC core in CB11. Inspection of the intensity profiles reveals that the CFLs measured at a fixed location in the PB remain constant and symmetric, regardless of the varying outflow ratio (see the overlapping intensity peaks in Fig. 3b for Q2/Q1 = 1–40). On the contrary, in CB11 (Fig. 3c) and CB21 (Fig. 3d), a sharp CFL asymmetry develops, with pronounced CFLs present near one side of the channel wall and virtually no CFLs near the other. At Q2/Q1 = 20, the outward CFL in CB21 occupies nearly half of the channel width (see blue curve in Fig. 3d). Further increasing the flow ratio to Q2/Q1 = 40 leads to the expansion of the CFL across the whole channel width (see purple curve in Fig. 3d), corresponding to the complete depletion of cells observed in Fig. 3a. Subsequent quantification shows that the trend of CFL expansion in CB21 versus the network outflow ratio is almost linear (Fig. 3e).
An identical trend is observed if Q1 = 2.0 μL min−1 is fixed instead while increasing Q2, or having Qtot = 0.8 μL min−1 fixed while changing both Q1 and Q2 to achieve the desired Q2/Q1 (Fig. 3e). Experiments conducted in the microfluidic device with 60-degree bifurcations also present the same trend (Fig. 3f and Fig. S2b, c, ESI†). These findings suggest that neither the flow rate in the parent branch nor the bifurcation angles play an important role in the RBC partitioning within the designed bifurcating network, at least for Q1 between 0.2 and 2.0 μL min−1, and the bifurcation angle between 60 and 90 degrees.
As Q2/Q1 increases, we find similar variation of the RBC fluxes (represented by cell trajectories) within the bifurcating network to experiments (Fig. 4a–d). The RBC fluxes in the upper-half child branches of the network (CB11, CB21 and CB22), where the flow rates are considerably smaller than their counterparts in the lower-half child branches (CB12, CB23 and CB24), gradually diminish as Q2/Q1 increases. At Q2/Q1 = 19, the terminal branch CB21 is completely devoid of cells (Fig. 4c). Further increasing the flow ratio to Q2/Q1 = 39 leaves both branches CB21 and CB22 free of cells (Fig. 4d).
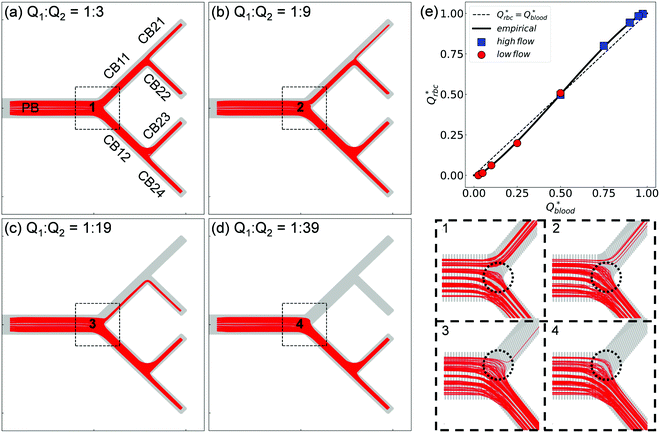 | ||
| Fig. 4 (Simulation) RBC fluxes in the network under different flow conditions at HF = 1%. (a–d) Show the superimposed RBC trajectories for flow ratios Q2/Q1 = 3, 9, 19, and 39, respectively. The panels labelled “1”—“4” show enlarged views of the Y-bifurcation region (marked with black dashed square boxes) with a reduced number of trajectories (about 150 randomly selected cell paths) for better clarity. (e) Comparison of the simulated distribution of RBC fluxes against the empirical model.17Qrbc* and Qblood* are the fractional RBC flux and fractional blood flow in a child branch relative to its parent branch. The circles and squares represent the relatively lower-/higher-flow child branches within a given bifurcation, respectively. The solid line is the empirical prediction, and the dotted line indicates a linear correlation. | ||
Next, we quantify the distribution of RBC fluxes at the primary Y-bifurcation (referred to as BifY hereafter). The fractional RBC fluxes Qrbc* in the child branches CB11 and CB12 (relative to the RBC flux in PB) are calculated and evaluated against the empirical PSM17 as described in eqn (S1)–(S4) (see Section S6 of the ESI†). Good agreement is found between the simulation data and the empirical predictions, with the relative errors under all tested flow conditions below 1% (see Table S2 in the ESI†). The quantitative match suggests that our simulated RBC partitioning at BifY sensibly reproduces the Zweifach–Fung effect. Furthermore, it can be inferred that for the present channel dimensions at BifY (Dh = 30–50 μm), where the cells are not strongly confined, the effect of fractional flow on RBC distribution dominates over that of channel geometry (rectangular instead of circular here).
One intriguing feature found in the RBC trajectories at the geometrically symmetric BifY is a protrusion cap into the lower-flow branch (marked with dotted circles in panels “1”–“4”' of Fig. 4). Such protrusion of cell trajectories indicates a diversion of RBC fluxes occurring near the bifurcation apex (or bifurcating point), with cells intending to enter the lower-flow branch abruptly pulled away and diverted towards the higher-flow branch instead. The size of this trajectory protrusion is seemingly correlated with the flow split at BifY (to be elaborated in Section 3.2) and increases with Q2/Q1 until complete absence of RBCs in CB11 at Q2/Q1 = 39, causing the deprivation of cells in the entire upper half of the network (CB11, CB21 and CB22).
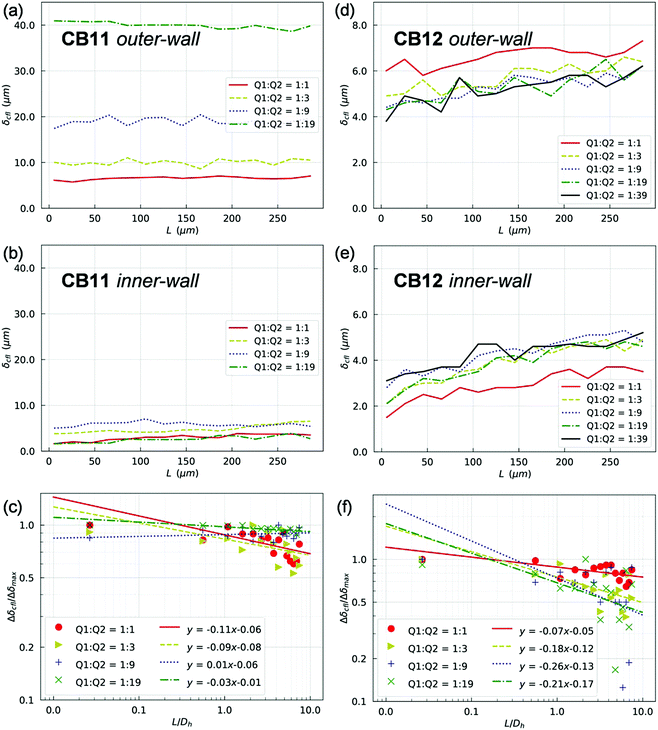
In line with the experimental findings, two lateral CFLs symmetric about the channel axis exist in the PB at HF = 1% (see Fig. S6 and S7 in the ESI†). CFLs are also found near the top/bottom walls in the depth direction, which is inaccessible to experimental observation with the present set-up. The CFLs in PB appear independent of the outflow ratio Q2/Q1, either in terms of absolute magnitude and spatial development (which is expected given the fixed flow in PB). Conversely, CFLs in branches of the first generation (namely CB11 and CB12) show a clear dependence on Q2/Q1 (Fig. 5). Also, the CFL symmetry between opposite walls appears broken after BifY.
For quantification of the CFL asymmetry, we have defined “inner wall” as the side of a child branch directly connected to the bifurcation apex, and “outer wall” as the opposite side of the same channel. The outer wall of a child branch naturally inherits the CFL from its upstream parent and therefore has initially large CFL thickness. Contrarily, the inner wall usually experiences the re-establishment of a CFL from zero, which results from direct collision of the core of RBCs in the parent branch with the apex of the bifurcation. The difference between the inner-/outer-wall CFLs (defined as CFL asymmetry) of CB11 is found prominent at high flow ratios, e.g. Q2/Q1 = 9 or Q2/Q1 = 19 (Fig. 5a and b). Furthermore, this asymmetry decreases slowly along CB11 (Fig. 5c) and practically persists throughout the whole branch. On the contrary, CB12 (which receives higher fraction of blood flow than its counterpart CB11) experiences substantially smaller CFL asymmetry (Fig. 5d and e) and faster recovery of CFL symmetry (Fig. 5f).
3.2 Diversion of RBC flux at primary Y-bifurcation
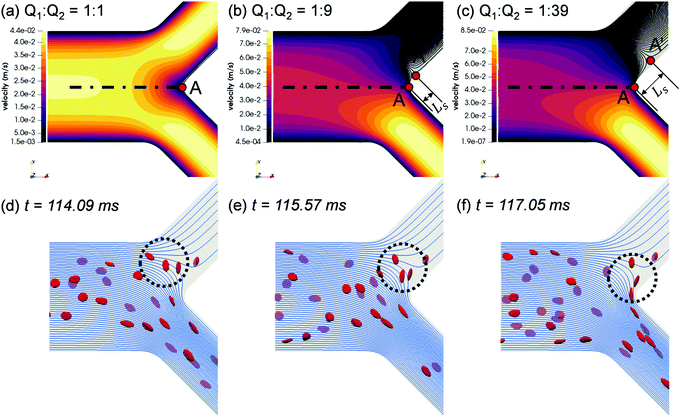
To elucidate the occurrence of RBC flux diversion at the primary BifY and the post-bifurcation CFL asymmetry as revealed in Section 3.1.2, we investigate the flow patterns underpinning the RBC motion. From the unperturbed flow field (Fig. 6a–c), the breakdown of flow symmetry and emergence of disrupted streamlines near the bifurcation apex (branching point A in Fig. 6a) is evident as Q2/Q1 gradually increases from 1. One notable feature is the appearance of a different separation point A′ on the channel mid-plane (located at Ls away from the branching point A), where the stagnation streamline meets the wall. All streamlines to the right of the stagnation streamline (“right” and “left” determined by a forward view along the flow direction) enter the high-flow branch (i.e. bottom branch in the figure), whereas those to its left end in the low-flow branch (i.e. top branch in the figure). As Q2/Q1 increases, A′ shifts towards the low-flow branch, thus increasing the separation distance Ls, and an enlarged nose tip of curved streamlines in the bifurcation region emerges, which matches the protrusion cap observed in the RBC trajectories (see panels “1”–“4” of Fig. 4).The RBCs approaching the bifurcation essentially follow the streamlines, and no evident cross-streamline migration of RBC populations is observed from the simulation (see Fig. S4d–f in the ESI†). This explains why the partitioning of RBCs at the Y-bifurcation (where the CFL is symmetric and confinement is small) obeys the classic Zweifach–Fung effect. Consequently, the PSM,8,16 as an empirical representation of the Zweifach–Fung effect derived from in vivo data, can correctly predict the distribution of RBC fluxes at the BifY (see Fig. 4e).
Under high flow ratios Q2/Q1, only a small proportion of streamlines originally close to the PB wall are directed into the low-flow branch CB11, which causes excessive bending of streamlines to satisfy flow continuity (see Fig. S4f in the ESI† for Q2/Q1 = 39). The streamlines ending in the low-flow branch CB11 largely originate from the outer-wall CFL in PB and therefore carry only a few RBCs. As demonstrated in Fig. 6d–f, due to the severely bent streamlines at Q2/Q1 = 19, the single RBC entering CB11 traverses across the whole channel width of CB11 and moves along its inner wall thereafter. Meanwhile, the protrusion zone is so profound that the other two RBCs already travelling deep into CB11 revert their paths, linger against the bifurcation and eventually proceed towards the higher-flow branch CB12. As the flow ratio increases to Q2/Q1 = 39 and the flow rate in the lower-flow branch further drops, all streamlines entering CB11 are from the upstream CFL and carry no RBCs at all (see Fig. S4f in the ESI†).
3.3 Biased phase separation at secondary T-bifurcations
Contrary to what happens at the primary BifY, the partitioning of RBC fluxes at the two secondary T-type bifurcations (referred to as BifT1 and BifT2 hereafter) considerably deviates from the empirical predictions based on the Zweifach–Fung effect (see Fig. 7a for BifT1 and Fig. S8 in the ESI† for BifT2). The deviation is particularly severe at BifT1 (Fig. 7a), for which one of the two downstream child branches can be completely depleted of RBCs whereas RBC perfusion is still visible in the other branch (compare CB21 and CB22 in Fig. 4c, where Q2/Q1 = 19). This severely biased partitioning of RBCs would appear counterintuitive if we simply focused on the local flow split at the bifurcation, which is even for CB21 and CB22.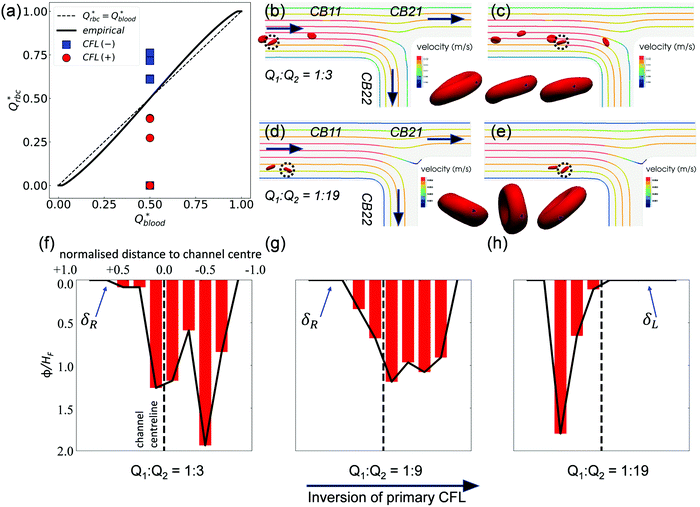 | ||
| Fig. 7 (Simulation) (a) Comparison of the simulated distribution of RBC fluxes at BifT1 against the empirical model,17 following the same convention as Fig. 4e. (b and c) RBC motion in CB11 for Q2/Q1 = 3. The highlighted cell (dotted circle) spins forward with nearly fixed orientation. (d and e) RBC motion in CB11 for Q2/Q1 = 19. The highlighted cell tumbles in a rigid-body fashion. The black spot (triangle-shaped) on the highlighted cell in (b and c) and in (d and e) tracks a fixed mass element on the RBC membrane. An additional time instant between (b and c) and between (d and e) is also shown in the time sequence to better reflect the motion regime of the cell. (f–h) Haematocrit profiles (time-averaged distribution of local RBC concentration ϕ, normalised by the feeding haematocrit HF) in channel CB22 under Q2/Q1 = 3, 9, and 19, respectively. The CFL is defined as the region where ϕ/HF = 0. The primary CFL labelled as δR or δL indicates the side possessing a larger CFL within a channel, where “R”' (right) or “L” (left) is relative to the flow direction (see black arrows in (b and d)). | ||
Underlying this deviation from the empirical approximation at BifT1 is the substantially asymmetric CFL in its feeding branch CB11 (see Fig. 5a–c) as a consequence of the upstream disruption to the cross-sectional RBC distribution by BifY. Recalling our analysis in Section 3.2, this asymmetry primarily arises from the manner how RBCs enter CB11 at BifY, which is sensitive to the outflow ratio Q2/Q1 of the network. At sufficiently high Q2/Q1, the RBCs entering branch CB11 (if any) are found diverted towards the inner wall, leaving a substantial CFL near the outer wall (Fig. 6d–f). One would expect the RBCs to migrate towards the channel centreline under hydrodynamic lift when travelling along CB11 (even with minimal shear-induced diffusion of cells in the dilute regime), therefore gradually recovering the inner-wall CFL and reducing the CFL asymmetry. However, there are two reasons why the CFL symmetry is not yet restored on arriving at BifT1. First, the length of CB11 is just 10 times its hydraulic diameter. Second, as Q2/Q1 increases, the flow velocity and the associated shear rate decreases in CB11. If the shear rate that RBCs experience becomes exceedingly low, RBCs appear rigid and tumble (resembling rigid-body rotation), rather than tank-tread. Tumbling RBCs experience a lower lift force than tank-treading RBCs.64
To examine whether the above conjecture is the case, we compare the motion of RBCs at a moderate Q2/Q1 = 3 (Fig. 7b and c) with a high Q2/Q1 = 19 (Fig. 7d and e). A notable difference in the RBC entry position in CB11 between Q2/Q1 = 3 (near channel centre) and Q2/Q1 = 19 (near inner wall) can be observed, which directs the cells to flow towards a different downstream branch or different sides of the same downstream branch. For Q2/Q1 = 3, the cells perform a “frisbee-like” spinning motion with nearly fixed orientation relative to the streamlines, accompanied by a slight increase in cell–wall distance (see the inset between Fig. 7b and c). This spinning behaviour has been previously captured in RBC experiments using simple shear flow, and is a transient motion regime towards tank-treading under increasing shear.65 For Q2/Q1 = 19, the cells in CB11 are tumbling all the way along streamlines, and no sign of cross-streamline migration can be observed (see the inset between Fig. 7d and e). The above two differences – the role of initial position and the dynamic mode of RBCs – both depend on the ratio of outflow rates Q2/Q1 and co-determine the RBC trajectories at the T-bifurcation.
Notably, an inversion of the primary CFL location in CB22 occurs as the flow ratio is increased from Q2/Q1 = 9 to 19 (Fig. 7g and h). This inversion primarily arises from the difference in the initial position of RBCs upon entering CB11, because the nominal shear rates in CB11 for Q2/Q1 = 9 to Q2/Q1 = 19 are designed in a way that the capillary number Ca is nearly the same under both flow conditions (see Table S1 in the ESI†).
3.4 Haematocrit reduction/enrichment in network
The partitioning of RBCs at successive bifurcations gives rise to a heterogeneity in the cell concentration throughout the network, especially with the presence of excessive outflow ratios (see Fig. 4b–d). To systematically quantify the RBC fluxes within the network and determine the preferential paths of RBCs, we calculate the discharge haematocrits HD in all branches using a cell-counting procedure as stated in Section 2.3, and compare HD to the discharge haematocrit HD,inflow in the feeding branch of the whole network, i.e. PB (Table 2, see raw data in Table S3, ESI†). It is important to note that HD itself is not a conserved quantity at a bifurcation (e.g. HPBD ≠ HCB11D + HCB12D); instead, the RBC flux Qrbc is (e.g. QPBrbc = QCB11rbc + QCB12rbc), provided that the system is in a quasi steady state.| Q 2/Q1 | Individual branches | Generation mean | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| PB | CB11 | CB12 | CB21 | CB22 | CB23 | CB24 | 0th | 1st | 2nd | |
| 1 | 1 | 1.02 | 0.99 | 0.78 | 1.24 | 1.21 | 0.78 | 1 | 1.00 | 1.00 |
| 3 | 1 | 0.79 | 1.07 | 0.61 | 0.97 | 1.13 | 0.98 | 1 | 0.93 | 0.93 |
| 9 | 1 | 0.61 | 1.05 | 0.33 | 0.88 | 1.24 | 0.86 | 1 | 0.83 | 0.83 |
| 19 | 1 | 0.28 | 1.03 | 0.00 | 0.43 | 1.19 | 0.88 | 1 | 0.66 | 0.62 |
| 39 | 1 | 0.00 | 1.02 | 0.00 | 0.00 | 1.10 | 0.94 | 1 | 0.51 | 0.51 |
| 9 (HF = 2%) | 1 | 0.59 | 1.04 | 0.33 | 0.88 | 1.22 | 0.87 | 1 | 0.82 | 0.83 |
| 9 (HF = 10%) | 1 | 0.67 | 1.03 | 0.45 | 0.88 | 1.12 | 0.96 | 1 | 0.85 | 0.85 |
Earlier on in Section 3.2, we have covered that when RBCs encounter the BifY with uneven fractional flows downstream (i.e. Q2/Q1 ≠ 1 at the outlets), asymmetric phase-separation between CB11 and CB12 occurs (Fig. 6). As Q2/Q1 increases from 3 to 39, the degree of haematocrit reduction in CB11 is found to surge, with HD/HD,inflow dropping from 0.79 to zero (Table 2). The haematocrit enrichment in CB12 is not enhanced, but slightly decreased (HD/HD,inflow dropping from 1.07 to 1.02). Among the branches in the second generation of the network, CB21 is the most diluted branch under all investigated flow ratios, whereas CB23 is always most concentrated. The discharge haematocrits in CB23 and CB24 vary non-monotonically with Q2/Q1.
We further evaluate the HD data at all three bifurcations separately using the PSM.17 This empirical model matches well with simulation data at the BifY (Fig. 8a), but it breaks down at BifT1 and BifT2 (Fig. 8b and c). These findings are in line with our results in Sections 3.1–3.3 which demonstrated that the partitioning of RBCs at the BifY adheres to the Zweifach–Fung effect, whereas that at both BifTs is substantially biased due to the persisting CFL asymmetry in the respective feeding branches (CB11 and CB12). Notably, the range of haematocrit partition in branches downstream of BifT1 under even flow split is much wider than for BifT2, as a result of the stronger CFL asymmetry in CB11 compared to CB12 (see Fig. 5).
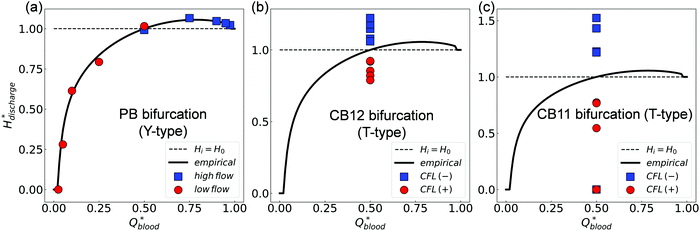 | ||
| Fig. 8 (Simulation) Comparison of simulated discharge haematocrits in each pair of child branches against the empirical PSM17 for HF = 1% (raw data in Table S3, ESI†). (a) Y-type BifY (data corresponding to Fig. 4e). (b) T-type BifT2. (c) T-type BifT1 (data corresponding to Fig. 7a). In (a-c), Hdischarge* and Qblood* represent the fractional discharge haematocrit and fractional blood flow in a given child branch relative to its parent branch within a bifurcation. In (a), the circles and squares represent the relatively lower-flow and higher-flow child branches, respectively. In (b) and (c), the circles and squares represent the CFL-favoured and CFL-unfavoured child branches (determined by the relative magnitude of CFL they inherit from the upstream feeding branch), respectively. The solid lines in (a–c) are the empirical predictions. | ||
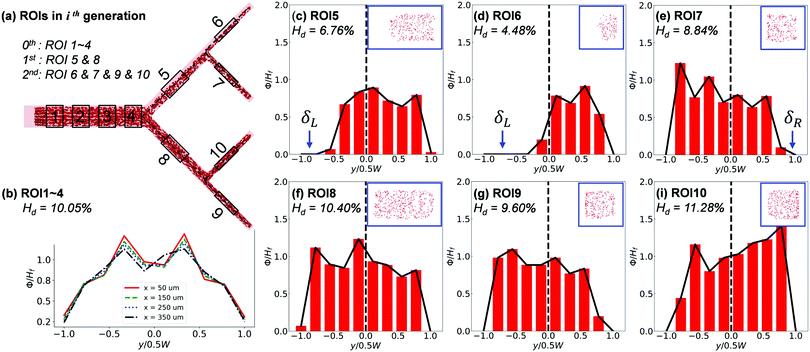
The cross-sectional haematocrit profiles (characterised through local RBC concentration ϕ) further reveal rich behaviour of the RBC distribution cascading down the network. Taking Q2/Q1 = 9, HF = 10% as example (Fig. 9), the profile of ϕ remains symmetric about the channel centreline in the main channel until approaching BifY, where an asymmetry starts to develop (see x = 350 μm in Fig. 9b). The asymmetry embedded in the ϕ profile significantly grows in CB11 (see ROI5), resulting from distinct CFLs formed near opposite walls (Fig. 9c). Due to the low-shear environment and negligible hydrodynamic lift of RBCs in CB11, the CFL asymmetry persists throughout the inter-bifurcation segment until BifT1 is met and consequently leads to asymmetric RBC partitioning despite an even flow split (HD = 4.48% in CB21 versus HD = 8.84% in CB22, Fig. 9d and e). The ϕ profile and accompanying CFL in CB21 (see ROI6) are even more asymmetric (Fig. 9d). Contrary to CB11, CB12 (see ROI8) appears less disturbed and presents a pseudo-symmetric ϕ profile with the lateral CFLs slightly favouring the outer wall (Fig. 9f). The partitioning of RBCs into CB24 (see ROI9) and CB23 (see ROI10) downstream of CB12 is still uneven, with HD = 9.60% for CB24 and HD = 11.28% for CB23. For both CB24 and CB23, the asymmetry in the ϕ profile is amplified compared with their immediate parent CB12 (Fig. 9g–i).
4 Discussion
4.1 Simulated RBC morphology and dynamics
The simulated RBC morphology in our arteriole-level network (see Fig. S5 in the ESI†) agrees with recent observations of human RBCs under microcirculatory flow conditions with physiological viscosity contrast (λ ≥ 5) between the RBC cytosol and the suspending medium.61,62 However, complex shapes such as the RBC polylobe are reproduced in the present simulations without viscosity contrast (λ = 1), whereas recently attempted RBC simulations in microchannels with λ = 5 failed to capture the polylobe structure.63 This is counterintuitive because a high viscosity contrast (e.g. λ > 3.2) was asserted as crucial for the formation of multi-lobed structures on the RBC membrane.62 It is worth noting that previous simulations which reproduced the polylobe shape were either for simple shear flow61,62,70 or planar Poiseuille flow71 without the confinement of lateral walls.A potential reason behind this disagreement is the confinement level χ = ![[D with combining macron]](https://www.rsc.org/images/entities/i_char_0044_0304.gif) rbc/Dh, ratio of the RBC effective diameter (
rbc/Dh, ratio of the RBC effective diameter (![[D with combining macron]](https://www.rsc.org/images/entities/i_char_0044_0304.gif) rbc = 6.5 μm, diameter of a sphere with the same volume) to the channel hydraulic diameter. Whereas the confinement considered by the square-channel simulations in ref. 63 was between χ = 0.4–0.75 (same confinement levels as their microfluidic experiments), the equivalent χ in our current simulations is much lower, ranging between 0.14–0.22. Another source of the mismatch may be the membrane viscosity neglected by our simulations. Last but not least, a possible explanation for the polylobed RBCs observed in the present study could be the existence of transient secondary flows in the vicinity of a bifurcation, which is clearly absent in the configuration of simple or planar shear flows. Answering these questions with further observation from carefully designed experiments will advance our understanding of the mechanisms for dynamic RBC shapes in arteriole-level networks.
rbc = 6.5 μm, diameter of a sphere with the same volume) to the channel hydraulic diameter. Whereas the confinement considered by the square-channel simulations in ref. 63 was between χ = 0.4–0.75 (same confinement levels as their microfluidic experiments), the equivalent χ in our current simulations is much lower, ranging between 0.14–0.22. Another source of the mismatch may be the membrane viscosity neglected by our simulations. Last but not least, a possible explanation for the polylobed RBCs observed in the present study could be the existence of transient secondary flows in the vicinity of a bifurcation, which is clearly absent in the configuration of simple or planar shear flows. Answering these questions with further observation from carefully designed experiments will advance our understanding of the mechanisms for dynamic RBC shapes in arteriole-level networks.
Apart from their evolving shapes, the motion regimes for RBCs observed in the simulated network is also rich, even for nearly unstressed cells with a biconcave shape. In addition to the commonly reported tumbling (in low shear) and tank-treading (in moderate/high shear) regimes, the intriguing “frisbee-like” spinning (a transient state between the rolling motion and tank-treading motion of RBCs under increasing shear as reported in ref. 65) is also reproduced by our simulations.
4.2 CFL development between arteriole-level bifurcations
Owing to its primary influence on the flow resistance as well as platelet/particle transport in microcirculatory blood flow, CFL has been extensively researched through in vivo, in vitro and in silico studies.72–74 However, until recently most studies were focused on the variation of CFLs subject to different blood flow conditions in a single straight vessel/channel, and these discrete findings on CFL development may not be applicable to the microcirculation environment where bifurcations/junctions of diverse geometries are frequently met.22 Our cell-scale simulation at successive arteriole-level bifurcations matching a microfluidic design of artificial vascular network provides a possibility of cross-validating numerical/experimental results with regard to CFL breakdown/recovery in complex geometries under finely-controlled flow conditions. This approach can be readily applied to query the spatio-temporal dynamics of heterogeneous RBC flow in more intricate microfluidic vascular networks presented earlier20,75 and ultimately contribute to the formulation of reduced-order models for tractable blood flow simulation at larger scales, e.g. in tissue-level or organ-level vasculature.Our simulated CFLs qualitatively agree with the experimental results, featuring symmetric CFL at opposite walls in the network feeding branch (see Fig. S6 in the ESI†) and increasingly asymmetric CFL in branches of downstream generations, especially under high network outflow ratios (see Fig. 3 for experimental observation and Fig. 5 for simulation data). The origin of the CFL asymmetry observed here is rooted in the underdeveloped RBC flow between consecutive bifurcations, as their distance falls short for the perturbed haematocrit profile (i.e. transverse organisation of RBCs) to be sufficiently restored so that the symmetry of CFL can be re-established.
Whilst Pries et al. originally postulated a recovery length of 10D (vessel diameter D ∈ [10,30] μm, in vivo measurements for rat mesenteric arterioles), Katanov et al.76 revealed via 3D simulations that a length up to 25D is needed for the CFL to fully develop in cylindrical microchannels (D ∈ [15,80] μm, haematocrit Ht ∈ [15%,45%]). Also through simulations, Shaqfeh and co-workers71,77 demonstrated moderately larger recovery lengths (beyond 36Dh) for the CFL to saturate in rectangular channels with comparable dimension and haematocrit levels (channel hydraulic diameter Dh ∈ [20,30] μm, Ht ∈ [10%,20%]). Under the circumstances of locally reduced flow or diluted RBC concentration in individual branches, the CFL recovery process may be further prolonged due to weakened hydrodynamic lift or lack of shear-induced diffusion. In our previous study of dilute RBC suspensions in low-inertia channel flow (Dh ≈ 46 μm, Ht ∈ [1%, 5%]), a stationary CFL was not established even after 46Dh.49 The length required for the haematocrit profile to achieve equilibrium is in general more demanding, which can go beyond 78Dh (Dh ≈ 29 μm) according to ref. 78.
4.3 Partitioning of RBCs at microvascular bifurcations
There are two main approaches for studies in the context of RBC partitioning at bifurcations. The first examines the relative motion of individual RBCs (or their biomimetic counterpart, vesicles or capsules) against the background flow in different bifurcation geometries (e.g.ref. 29, 30, 31, 32, 35, 36 and 79), typically aimed at microfluidic design optimisation for cell sorting or enrichment. The second approach focuses on quantifying the split of RBC fluxes or discharge haematocrits within a flowing RBC suspension at bifurcations (e.g.ref. 12, 13, 15, 21, 23 and 24), aimed at elucidating the fundamental process of phase separation occurring in vivo which may inspire not only enhanced blood-on-a-chip devices, but also novel strategies for treating microcirculatory disorders arising from abnormal blood flow.Our cellular blood simulations involving successive bifurcations at the arteriole scale, in parallel with corroborating microfluidic experiments, provide exhaustive data for in-depth examination of the RBC partitioning behaviour through cross-validation between experimental and computational data. In particular, we investigate whether or not the classic phase separation of blood as stipulated by the Zweifach–Fung effect2 and the empirical model8 is observed, and how these observations are related to the individual motion of RBCs and the symmetry/asymmetry of CFLs preceding a bifurcation. We also validate a straightforward means of manipulating the RBC partitioning within a bifurcating network, i.e. by varying the flow ratios between network outlets, which consistently leads to certain branches developing excessive haematocrit reduction or enrichment at feeding haematocrits HF = 1%–10%.
4.4 Implications and limitations
In summary, our computational model of cellular blood flow with highly resolved RBCs flowing in an artificial microvascular network satisfactorily reproduces the phenomenon of biased RBC partitioning observed in the corroborating microfluidic experiments. The simulations elucidate in detail the microscopic behaviour of RBCs at arteriole-level bifurcations (channel hydraulic diameter Dh = 30–50 μm) subject to different outflow ratios at terminal branches of the network. Furthermore, our findings suggest the prominent effect of CFL asymmetry on the phase separation process. Such CFL asymmetry arises from upstream disturbances and can persist for more than 10 times the hydraulic channel diameter, which plays a key role in the partitioning of RBCs in downstream branches.Some important implications are: (I) Artificial microvascular networks consisting of rectangular microchannels designed following the biomimetic rule proposed by Zografos et al.46 can capture the phase-separation process of RBC suspensions in realistic microvascular networks with quantitative accuracy (see Fig. 4e, evaluation performed against the established empirical model based on in vivo data from rat arteriolar bifurcations8), provided that equivalent dimensional descriptions are used, e.g. hydraulic channel diameter versus vessel diameter. (II) In low-inertia flows (Re < 1) with arteriole-level confinement (relatively small Drbc/Dh), RBCs in dilute/semidilute suspensions follow the fluid streamlines in the vicinity of a bifurcation and behave like point particles, with no evident migration of RBC populations crossing the stagnation streamline (see Fig. S4d–f, ESI†). Therefore, the obstruction effect proposed by45 or the low-flow attraction effect proposed by32 is irrelevant, and the partitioning of RBCs obeys the classic Zweifach–Fung effect provided that the symmetry of haematocrit profile or CFL is preserved. Under such conditions, reduced models without involving RBCs may be sufficient to capture the phase-separation process. (III) Under high outflow ratios, RBCs near the stagnation streamline (separation surface or separatrix in 3D, which divides the fluid layers entering different branches) tend to be drawn towards the lower-flow branch first and linger for a while. They are then pulled away and eventually flow into the higher-flow branch (see Fig. 6d–f). This observation is in line with the finding of a previous numerical study in 2D, where similar behaviour was found for an elastic capsule.31 An earlier microfluidic study of bifurcating channels at 180 degrees also presented similar pattern of RBC fluxes at a high ratio of fractional flows.48 (IV) Significant asymmetry in both the CFL and haematocrit profile prevails in a vascular network as suggested by22,44 earlier, owing to disrupted cross-sectional distribution of RBCs in downstream branches by the disturbance of upstream bifurcations (see Fig. 9). As a consequence, the partitioning of RBCs at successive bifurcations can be substantially biased and would give rise to excessive haematocrit reduction in downstream child branches, even under equal flow splits (see Fig. 8). (V) The lateral migration of RBCs, which arises from the hydrodynamic lift and contributes to the recovery of disrupted CFL, is largely suppressed in branches of low flow due to the absence of tank-treading motion. This leads to negligible recovery of CFL symmetry between certain consecutive bifurcations.
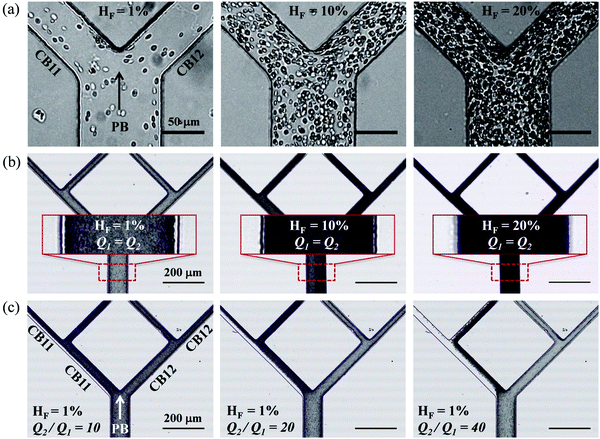
There are several limitations for the present study. (1) While horse RBCs were used in experiments, the numerical model simulates human RBCs. This may have caused a certain degree of quantitative discrepancy between the simulation and experiments. However, the influence on results of the suspension behaviour should be limited to quantitative instead of qualitative differences (see evidence from our previous paper49). (2) Quantitative agreement of the CFL thickness as well as the critical outflow ratio for complete RBC depletion in low-flow fraction of the network between experiments and simulations remains challenging due to our numerical treatment of the flow entry region (required for tractable computational cost), where geometric contraction in the width direction is deliberately removed to enable the generation of an artificial CFL immediately after the inlet (see Section 2.2 for the reason behind this particular treatment). This numerical treatment is justified against our previous findings of CFL development of dilute RBC suspensions in low-inertia channel flow49 (see Section S5 of the ESI†). (3) So far, only dilute/semidilute RBC suspensions (HF = 1%, 2%, 10%) are simulated, primarily aimed at a mechanistic understanding of RBC partitioning behaviour in bifurcating microchannels. The performance of the biomimetic microfluidic network in terms of separating RBCs and plasma is subject to scrutiny if the haematocrit is to be further increased to a level when cell–cell interactions become dominant. As previously reported by ref. 13, the degree of phase-separation is expected to decrease with increasing haematocrit, especially for symmetric bifurcations. Our preliminary experiments with higher RBC concentration (HF = 10%, 20%) suggest less pronounced phase-separation even under extreme flow conditions (see Fig. S3 in the ESI†). The reduction/enrichment effect through controlling outflow ratios reported in the present study remains to be further inspected before applications are possible, e.g. handling dense RBC suspensions for separation, sorting or purification purposes.
5 Concluding remarks
This work studies the partitioning of RBCs in an artificial vascular network designed following a biomimetic rule that generalises Murray's law for microfluidic manifolds. The microscopic behaviour of RBCs flowing within are reported in detail, including their morphological deformation, motion regime, and temporal paths. We find the RBC partitioning at the primary bifurcation, where the symmetry of cross-sectional cell distribution in the feeding branch are preserved, quantitatively agreeing with the established phase-separation model8,17 as an empirical approximation of the classic Zweifach–Fung effect. Contrarily at secondary bifurcations, a biased partitioning that substantially deviates from the empirical model is observed under moderate or high network outflow ratios, leading to excessive haematocrit reduction/enrichment in downstream child branches. The biased phase separation is attributed to the complex spatio-temporal dynamics of RBC flow within a successively bifurcating network, featured by the post-bifurcation breakdown of CFL symmetry due to upstream disturbances on the cell distribution and the lack of symmetry recovery due to negligible hydrodynamic lift of cells tumbling in low-shear environments.Whilst the Zweifach–Fung effect has been widely tested and validated to predict the partitioning of RBCs at individual bifurcations, our current results draw attention to exceptions in a network of bifurcations for which CFL asymmetries prevail in the system when the haematocrits are considerably lower than the physiological level and the flow rates in certain fraction of the network are small. Caution is therefore needed when applying the empirical phase-separation model8,17 to describe blood flow in a hierarchical network, especially under non-physiological flow conditions as in the case of many microfluidic experiments. The qualitative and quantitative agreement between our simulations and experiments in an arteriole-level artificial network is important to validate the 3D computational model for studying the haemodynamics of cellular blood flow in diverse microfluidic devices or reconstructed microvascular networks. Our findings of the RBC partitioning within the bifurcating geometry may also find application in manipulating blood samples for biomedical purposes.
Author contributions
QZ organised the research, performed the simulations, analysed the data and wrote the article. JF designed and conducted the experiments, processed the experimental data and analysed the results. MOB discussed the results and revised the manuscript. MSNO and TK conceived the research idea, supervised the study and edited the manuscript.Conflicts of interest
The authors declare that they have no competing financial interests.Acknowledgements
The authors would like to acknowledge the contribution of the HemeLB development team. QZ thanks the University of Edinburgh for the award of a Principal's Career Development Scholarship and an Edinburgh Global Research Scholarship. TK's and MOB's contributions have been sponsored through two Chancellor's Fellowships at the University of Edinburgh and funded by EPSRC (grant EP/T008806/1). TK is also funded by the European Commission (grant agreement No 803553). MOB is supported by grants from EPSRC (EP/R029598/1, EP/R021600/1), Fondation Leducq (17 CVD 03), and the European Unions Horizon 2020 research and innovation programme under grant agreement No. 801423. Supercomputing time on the ARCHER UK National Supercomputing Service (http://www.archer.ac.uk) was provided by the “UK Consortium on Mesoscale Engineering Sciences (UKCOMES)” under the EPSRC Grant No. EP/R029598/1. Processing and disposal of the blood sample were performed following the Ethics Committee for Animal Experimentation at University of Strathclyde.References
- A. S. Popel and P. C. Johnson, Annu. Rev. Fluid Mech., 2005, 37, 43–69 CrossRef.
- K. Svanes and B. W. Zweifach, Microvasc. Res., 1968, 1, 210–220 CrossRef.
- Y.-C. Fung, Microvasc. Res., 1973, 5, 34–48 CrossRef CAS.
- A. Krogh, J. Physiol., 1921, 55, 412–422 CrossRef CAS.
- G. W. Schmid-Schönbein, R. Skalak, S. Usami and S. Chien, Microvasc. Res., 1980, 19, 18–44 CrossRef.
- G. Mchedlishvili and M. Varazashvili, Biorheology, 1982, 19, 613–620 CAS.
- B. Klitzman and P. C. Johnson, Am. J. Physiol., 1982, 242, H211–H219 CAS.
- A. R. Pries, K. Ley, M. Claassen and P. Gaehtgens, Microvasc. Res., 1989, 38, 81–101 CrossRef CAS.
- B. M. Fenton, R. T. Carr and G. R. Cokelet, Microvasc. Res., 1985, 29, 103–126 CrossRef CAS.
- R. T. Carr and L. L. Wickham, Microvasc. Res., 1991, 41, 184–196 CrossRef CAS.
- S. Yang, A. Ündar and J. D. Zahn, Lab Chip, 2006, 6, 871–880 RSC.
- J. M. Sherwood, D. Holmes, E. Kaliviotis and S. Balabani, PLoS One, 2014, 9, e100473 CrossRef.
- S. Roman, A. Merlo, P. Duru, F. Risso and S. Lorthois, Biomicrofluidics, 2016, 10, 034103 CrossRef.
- Z. Shen, G. Coupier, B. Kaoui, B. Polack, J. Harting, C. Misbah and T. Podgorski, Microvasc. Res., 2016, 105, 40–46 CrossRef.
- K. Yamamoto, H. Abe, C. Miyoshi, H. Ogura and T. Hyakutake, J. Med. Biol. Eng., 2020, 40, 53–61 CrossRef.
- A. R. Pries, T. W. Secomb, P. Gaehtgens and J. F. Gross, Circ. Res., 1990, 67, 826–834 CrossRef CAS.
- A. R. Pries, B. Reglin and T. W. Secomb, Am. J. Physiol., 2003, 284, H2204–H2212 CAS.
- A. R. Pries and T. W. Secomb, Am. J. Physiol., 2005, 289, H2657–H2664 CAS.
- P. M. Rasmussen, T. W. Secomb and A. R. Pries, Microcirculation, 2018, 25, e12445 CrossRef.
- O. Forouzan, X. Yang, J. M. Sosa, J. M. Burns and S. S. Shevkoplyas, Microvasc. Res., 2012, 84, 123–132 CrossRef.
- A. Mantegazza, F. Clavica and D. Obrist, Biomicrofluidics, 2020, 14, 014101 CrossRef CAS.
- P. Balogh and P. Bagchi, J. Fluid Mech., 2019, 864, 768–806 CrossRef CAS.
- M. O. Bernabeu, J. Köry, J. A. Grogan, B. Markelc, A. Beardo, M. d’Avezac, R. Enjalbert, J. Kaeppler, N. Daly, J. Hetherington, T. Krüger, P. K. Maini, J. M. Pitt-Francis, R. J. Muschel, T. Alarcón and H. M. Byrne, Proc. Natl. Acad. Sci. U. S. A., 2020, 117, 27811–27819 CrossRef CAS.
- T. Hyakutake and S. Nagai, Microvasc. Res., 2015, 97, 115–123 CrossRef.
- G. Enden and A. S. Popel, J. Biomech. Eng., 1994, 116, 79–88 CrossRef CAS.
- J. O. Barber, J. M. Restrepo and T. W. Secomb, Cardiovascular Engineering and Technology, 2011, 2, 349–360 CrossRef.
- H. Ye, H. Huang and X.-Y. Lu, Comput. Fluids, 2015, 114, 110–120 CrossRef.
- T. Wang, U. Rongin and Z. Xing, Sci. Rep., 2016, 6, 20262 CrossRef CAS.
- J. O. Barber, J. P. Alberding, J. M. Restrepo and T. W. Secomb, Ann. Biomed. Eng., 2008, 36, 1690–1698 CrossRef.
- W. Xiong and J. Zhang, Biomech. Model. Mechanobiol., 2012, 11, 575–583 CrossRef.
- H. C. Woolfenden and M. G. Blyth, J. Fluid Mech., 2011, 669, 3–31 CrossRef.
- V. Doyeux, T. Podgorski, S. Peponas, M. Ismail and G. Coupier, J. Fluid Mech., 2011, 674, 359–388 CrossRef CAS.
- K. Lykov, X. Li, H. Lei, I. V. Pivkin and G. E. Karniadakis, PLoS Comput. Biol., 2015, 11, e1004410 CrossRef.
- T. Ye, L. Peng and Y. Li, J. Appl. Phys., 2018, 123, 064701 CrossRef.
- Z. Wang, Y. Sui, A.-V. Salsac, D. Barthès-Biesel and W. Wang, J. Fluid Mech., 2016, 806, 603–626 CrossRef CAS.
- Z. Wang, Y. Sui, A.-V. Salsac, D. Barthès-Biesel and W. Wang, J. Fluid Mech., 2018, 849, 136–162 CrossRef CAS.
- T. Ye, L. Peng and G. Li, Biomech. Model. Mechanobiol., 2019, 18, 1821–1835 CrossRef.
- Z. L. Liu, J. R. Clausen, J. L. Wagner, K. S. Butler, D. S. Bolintineanu, J. B. Lechman, R. R. Rao and C. K. Aidun, Phys. Rev. E, 2020, 102, 013310 CrossRef CAS.
- X. Yin, T. Thomas and J. Zhang, Microvasc. Res., 2013, 89, 47–56 CrossRef.
- S. S. Ye, M. Ju and S. Kim, Microvasc. Res., 2016, 106, 14–23 CrossRef.
- C. Bächer, A. Kihm, L. Schrack, L. Kaestner, M. W. Laschke, C. Wagner and S. Gekle, Biophys. J., 2018, 115, 411–425 CrossRef.
- P. K. Ong, S. Jain and S. Kim, Microvasc. Res., 2012, 83, 118–125 CrossRef.
- Y. C. Ng, B. Namgung, S. L. Tien, H. L. Leo and S. Kim, Am. J. Physiol., 2016, 311, H487–H497 Search PubMed.
- P. Balogh and P. Bagchi, Phys. Fluids, 2018, 30, 051902 CrossRef.
- R. W. Barber and D. R. Emerson, Microfluid. Nanofluid., 2008, 4, 179–191 CrossRef.
- K. Zografos, R. W. Barber, D. R. Emerson and M. S. N. Oliveira, Microfluid. Nanofluid., 2015, 19, 737–749 CrossRef.
- J. Fidalgo, K. Zografos, L. Casanellas, A. Lindner and M. S. N. Oliveira, Biomicrofluidics, 2017, 11, 064106 CrossRef.
- J. Fidalgo, D. Pinho, R. Lima and M. S. N. Oliveira, VipIMAGE 2017, Cham, 2018, pp. 945–953 Search PubMed.
- Q. Zhou, J. Fidalgo, L. Calvi, M. O. Bernabeu, P. R. Hoskins, M. S. N. Oliveira and T. Krüger, Biophys. J., 2020, 118, 2561–2573 CrossRef CAS.
- T. Krüger, Computer Simulation Study of Collective Phenomena in Dense Suspensions of Red Blood Cells under Shear, Vieweg + Teubner Verlag, 2012 Search PubMed.
- M. D. Mazzeo and P. V. Coveney, Comput. Phys. Commun., 2008, 178, 894–914 CrossRef CAS.
- M. O. Bernabeu, M. L. Jones, J. H. Nielsen, T. Krüger, R. W. Nash, D. Groen, S. Schmieschek, J. Hetherington, H. Gerhardt, C. A. Franco and P. V. Coveney, J. R. Soc., Interface, 2014, 11, 20140543 CrossRef.
- Y. H. Qian, D. D’Humières and P. Lallemand, EPL, 1992, 17, 479 CrossRef.
- P. L. Bhatnagar, E. P. Gross and M. Krook, Phys. Rev., 1954, 94, 511–525 CrossRef CAS.
- Z. Guo, C. Zheng and B. Shi, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2002, 65, 046308 CrossRef.
- M. Bouzidi, M. Firdaouss and P. Lallemand, Phys. Fluids, 2001, 13, 3452–3459 CrossRef CAS.
- A. J. C. Ladd, J. Fluid Mech., 1994, 271, 285–309 CrossRef CAS.
- C. S. Peskin, Acta Numerica, 2002, 11, 479–517 CrossRef.
- T. Krüger, F. Varnik and D. Raabe, Computers & Mathematics with Applications, 2011, 61, 3485–3505 Search PubMed.
- A. R. Pries, T. W. Secomb and P. Gaehtgens, Am. J. Physiol., 1996, 270, H545–H553 CAS.
- L. Lanotte, J. Mauer, S. Mendez, D. A. Fedosov, J.-M. Fromental, V. Claveria, F. Nicoud, G. Gompper and M. Abkarian, Proc. Natl. Acad. Sci. U. S. A., 2016, 201608074 Search PubMed.
- J. Mauer, S. Mendez, L. Lanotte, F. Nicoud, M. Abkarian, G. Gompper and D. A. Fedosov, Phys. Rev. Lett., 2018, 121, 118103 CrossRef CAS.
- F. Reichel, J. Mauer, A. A. Nawaz, G. Gompper, J. Guck and D. A. Fedosov, Biophys. J., 2019, 117, 14–24 CrossRef CAS.
- A. Nait-Ouhra, A. Guckenberger, A. Farutin, H. Ez-Zahraouy, A. Benyoussef, S. Gekle and C. Misbah, Phys. Rev. Fluids, 2018, 3, 123601 CrossRef.
- J. Dupire, M. Socol and A. Viallat, Proc. Natl. Acad. Sci. U. S. A., 2012, 109, 20808–20813 CrossRef CAS.
- A. R. Pries, T. W. Secomb and P. Gaehtgens, Am. J. Physiol., 1995, 269, H1713–H1722 CAS.
- K. H. Albrecht, P. Gaehtgens, A. R. Pries and M. Heuser, Microvasc. Res., 1979, 18, 33–47 CrossRef CAS.
- R. Skalak and S. Chien, Biorheology, 1981, 18, 307–330 CAS.
- A. R. Pries, K. Ley and P. Gaehtgens, Am. J. Physiol., 1986, 251, H1324–H1332 CAS.
- N. Takeishi, M. E. Rosti, Y. Imai, S. Wada and L. Brandt, J. Fluid Mech., 2019, 872, 818–848 CrossRef CAS.
- A. Saadat, C. J. Guido and E. S. G. Shaqfeh, bioRxiv:10.1101/572933, 2019.
- S. Kim, P. K. Ong, O. Yalcin, M. Intaglietta and P. C. Johnson, Biorheology, 2009, 46, 181–189 CAS.
- D. A. Fedosov, B. Caswell, A. S. Popel and G. E. Karniadakis, Microcirculation, 2010, 17, 615–628 CrossRef.
- S. Tripathi, Y. V. B. V. Kumar, A. Prabhakar, S. S. Joshi and A. Agrawal, J. Micromech. Microeng., 2015, 25, 083001 CrossRef.
- N. Z. Piety, W. H. Reinhart, J. Stutz and S. S. Shevkoplyas, Transfusion, 2017, 57, 2257–2266 CrossRef CAS.
- D. Katanov, G. Gompper and D. A. Fedosov, Microvasc. Res., 2015, 99, 57–66 CrossRef.
- Q. M. Qi and E. S. G. Shaqfeh, Phys. Rev. Fluids, 2018, 3, 034302 CrossRef.
- H. Zhao, E. S. G. Shaqfeh and V. Narsimhan, Phys. Fluids, 2012, 24, 011902 CrossRef.
- G. Li, T. Ye, S. Wang, X. Li and R. UI Haq, Phys. Fluids, 2020, 32, 031903 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/d0sm01845g |
| This journal is © The Royal Society of Chemistry 2021 |

![[small tau, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e5.gif)