Open Access Article
Open Access ArticleMore than just a barrier: using physical models to couple membrane shape to cell function
Felix
Frey
 and
Timon
Idema
and
Timon
Idema
 *
*
Department of Bionanoscience, Kavli Institute of Nanoscience, Delft University of Technology, Delft, The Netherlands. E-mail: T.Idema@tudelft.nl
First published on 21st January 2021
Abstract
The correct execution of many cellular processes, such as division and motility, requires the cell to adopt a specific shape. Physically, these shapes are determined by the interplay of the plasma membrane and internal cellular driving factors. While the plasma membrane defines the boundary of the cell, processes inside the cell can result in the generation of forces that deform the membrane. These processes include protein binding, the assembly of protein superstructures, and the growth and contraction of cytoskeletal networks. Due to the complexity of the cell, relating observed membrane deformations back to internal processes is a challenging problem. Here, we review cell shape changes in endocytosis, cell adhesion, cell migration and cell division and discuss how by modeling membrane deformations we can investigate the inner working principles of the cell.
1 Introduction
Cellular processes such as endocytosis, cell adhesion, cell migration and cell division depend crucially on the ability of cells to adapt and control their shape. The shape of a cell is determined by its complex internal structure. Eukaryotic cells are surrounded by a plasma membrane that forms a barrier and separates the cell's interior from its environment.1 Contained within this barrier is the cytoskeleton, a dynamical scaffold of different polymer networks that organizes cell shape.2,3 In order to determine the driving factors that control cell shape and reduce the system's complexity, a rewarding approach is to simplify the system by reconstituting it “bottom up”, with the ultimate goal of building a synthetic cell.4,5 One of the aims of such a reductionist approach is to disentangle the mechanisms and contributions of the different intracellular processes.6 However, to experiment with a complex system, like a cell, is technically challenging, even when considering a simplified version. Therefore, it is helpful to take complementary approaches.Already back in 1917 D'Arcy Thompson suggested in his book On Growth and Form that the shape of biological organisms, including cells, is determined by physical forces.7 Using this idea in reverse, it is also possible to determine intracellular forces and processes that lead to a particular shape by examining the cell shape and the dynamics of shape changes. Since the plasma membrane surrounds the cell, it mirrors both the activity inside the cell and the response of the cell to its environment.8 In particular, the plasma membrane is not static but highly dynamic because it is vital for the cell to be able to adapt its shape quickly.
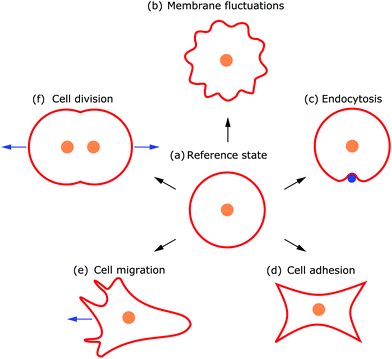
Deformations appear in a huge variety because diverse driving factors frequently deform the membrane in various cellular processes.9 Thus, both the shape and dynamics of deformations contain information about the generating forces and driving factors. Because cells are under osmotic pressure, due to differences in ion concentrations between the inside and outside of the cell, in solution they take on a spherical shape.3 In the absence of external perturbations, the spherical shape therefore defines the reference shape with which all deformations are compared (cf.Fig. 1a). For instance, processes like membrane fluctuations, endocytosis, cell adhesion, cell migration, and cell division deform the plasma membrane in a characteristic manner compared to the spherical reference state (cf.Fig. 1b–f).
Observing shape changes and membrane deformations is relatively simple, because they act on a mesoscopic length scale (∼μm) and therefore are experimentally accessible. This makes it possible to determine either the membrane properties or the cellular functions. While the investigation of passive membrane fluctuations makes the membrane properties measurable, the investigation of membrane deformations in processes such as active membrane fluctuations, endocytosis, cell adhesion, cell migration or cell division provides information about cell functions. The challenge is then to infer the driving forces from membrane deformations. While we go through the different examples (cf.Fig. 1), we also review various modeling strategies. These strategies include both continuum and discrete models. Examples of the first type consider cytoskeletal networks as fields of active fluids or liquid crystals, whereas examples of the second type consider ligand–receptor contacts as discrete binding sites or triangulate the membrane. In addition to these approaches, particle based coarse-grained molecular dynamics simulations are used to study the shape and dynamics of membranes, for example to investigate how membrane-bound protein clusters deform the membrane during assembly.
This review is structured as follows: In Section 2 we give a short biophysical background on the plasma membrane and the cytoskeleton, which are the two main determinants of cell shape. We then introduce the central modeling concept, the Helfrich Hamiltonian, which forms the basis for most of the membrane models that we discuss. In Section 3 we discuss how thermal and active fluctuations impact cell shape, while in Sections 4–7 we investigate what can be learnt by modeling membrane deformations in endocytosis, cell adhesion, cell migration and cell division. In Section 8 we conclude by a discussion of future challenges and open questions. In particular, we highlight throughout the review how modeling membrane deformations is an important tool to investigate the inner workings of the cell.
2 Defining cell shape: the plasma membrane and the cytoskeleton
2.1 Biophysical background
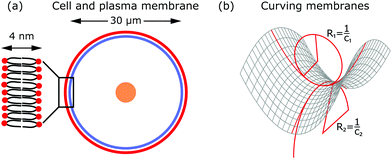
The shape of the cell is largely determined by the plasma membrane and the cytoskeleton.1,2 Since the plasma membrane separates the cell from its environment, it mirrors the activity within the cell, but also indicates the response of the cell to its surroundings. Compared to the dimensions of a cell (∼30 μm), the plasma membrane is relatively thin (∼4 nm). The plasma membrane is a fluid lipid bilayer, made of different lipid molecules with hydrophobic tails and hydrophilic heads, in which diverse proteins are embedded (cf.Fig. 2a).1,9 The plasma membrane is supported by the underlying actin cortex, which is around 100 nm thick and made of a layer of branched and crosslinked actin filaments.10,11 Although the plasma membrane is anchored to the actin cortex by linker molecules of the ERM family (ezrin, radixin, moesin), it can still fluctuate due to the large distances of 10–20 nm between the membrane and the cortex.12,13 Other important protein classes that are embedded in the plasma membrane are ion pumps (transporters that actively shuttle ions across the membrane) and ion channels (gates that are either open or closed). Since they pump water out of the cell and modulate ion concentrations within the cell, they ensure that the osmotic pressure is neither too low nor too high.3 Because of their activity, they also exert forces on the membrane.In addition to these forces generated by ion pumps and channels, the cytoskeleton can also exert forces that deform the membrane. The cytoskeleton is a composite meshwork, made of polymer networks, crosslinker proteins and molecular motors. The three main components building up the polymer networks are actin filaments, microtubules and intermediate filaments.14 In addition, septin filaments have been described as another cytoskeletal component that can assemble into hierarchical structures, sense membrane curvature and, hence, stabilize membrane deformations (as for example in cell division).15,16 Of particular interest in this context are actin filaments and molecular motors, because together they are probably the most important sources that generate active membrane deformations.17
Actin filaments grow by the addition of actin monomers. The growth mainly happens at the plus (or barbed) end, where ATP-actin, i.e. monomers to which ATP is bound, attaches, after which the ATP is hydrolyzed. Thus, the growth of actin filaments is an active process.10 Actin filaments can organize into adaptive higher-order structures of various architectures such as parallel bundles or branched networks.17 Depending on the architecture of the growing actin network, different cell shapes and membrane deformations evolve. For example in phagocytosis and cell migration the plasma membrane gets deformed by the growth of branched actin networks.
Polymerizing actin structures and contractile ones are both able to deform the plasma membrane.18 The contraction of actin networks is caused by molecular motors that consume energy by hydrolyzing ATP.17 Myosin molecular motors form a protein family that is associated with actin filaments. Myosin II motors can assemble and form myosin II mini-filaments, which are able to contract branched or bundled actin networks. For instance, in cell migration the membrane is deformed due to polymerizing actin filaments at the front of the cell while the back of the cell is contracted by actin stress fibers (crosslinked and contractile actin bundles). In contrast, in cell division the membrane is deformed due to the contracting actin cortex.
Deformations of the plasma membrane can be caused by both passive and active processes. Membrane deformations caused by passive processes either occur in equilibrium or drive the system towards equilibrium, i.e., they minimize the free energy of the system, without additional energy consumption. Examples are membrane fluctuations due to thermal random kicks of the surrounding medium, endocytosis driven by adhesion or the assembly of protein superstructures. Moreover, membrane deformations and fluctuations can be driven by active processes. Following the usual definition, active processes consume energy, i.e., they run out of equilibrium and are capable of converting free energy into systematic activity.19–21 Examples of such processes are active membrane fluctuations, phagocytosis, cell migration and cell division. Here, the activity originates for instance from ion channels or pumps, growing and contracting actomyosin or septin networks, and other protein families such as clathrin, caveolin-1 or ESCRT-III.15,17,22,23
2.2 Modeling deformations of the plasma membrane: the Helfrich Hamiltonian
From a physical point of view the plasma membrane can be modeled as a surface in three-dimensional space that is described locally by its two principal curvatures C1 and C2 (cf.Fig. 2b). The usual starting point for continuum models describing membrane deformations is the Helfrich Hamiltonian.24 The Helfrich Hamiltonian describes the elastic energy of the plasma membrane, with the most relevant contribution being the out-of-plane bending energy. In contrast, the shear modulus vanishes due to the fluid nature of the lipid bilayer.25 Because the lipids of the membrane are closely packed, the compression modulus is large, and thus the contribution from compression is also negligible. In addition, there is an entropic contribution to the free energy of the plasma membrane, quantifying the energetic cost to pull out excess area as for instance membrane fluctuations, effectively acting as a tension energy. Hence, the free energy of the membrane reads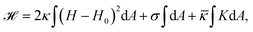 | (1) |
![[small kappa, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0cb.gif) . The tension σ can be interpreted either as the chemical potential for membrane area quantifying the energetic cost to pull out excess area, or as a Lagrange multiplier to constrain the membrane area.25 For any processes that do not involve topological changes (as e.g. fusing or splitting cells), the term containing the Gaussian curvature is constant due to the Gauss–Bonnet theorem and thus can be neglected.25 When the volume enclosed within the membrane is fixed, a term
. The tension σ can be interpreted either as the chemical potential for membrane area quantifying the energetic cost to pull out excess area, or as a Lagrange multiplier to constrain the membrane area.25 For any processes that do not involve topological changes (as e.g. fusing or splitting cells), the term containing the Gaussian curvature is constant due to the Gauss–Bonnet theorem and thus can be neglected.25 When the volume enclosed within the membrane is fixed, a term 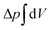 , with Δp the pressure difference between inside and outside, is added to eqn (1).
, with Δp the pressure difference between inside and outside, is added to eqn (1).
An alternative description to the Helfrich Hamiltonian or spontaneous curvature model is the bilayer-couple model that assumes fixed but different numbers of lipids in the inner and outer monolayers of the membrane and thus different monolayer areas.26,27 The resulting energy functional is similar to eqn (1) without including a contribution from spontaneous curvature. The approach can be extended in the Area Difference Elasticity (ADE) model where one assumes that the monolayers can also stretch.26,28 In this case one finds an energy functional identical to eqn (1) but now also including a stretching energy term that takes the area difference between the monolayers into account. Although the ADE model describes transitions of membrane shapes more accurately,27,28 for simplicity most authors use the Helfrich Hamiltonian, as we will do in the following.
In equilibrium, the shape of the plasma membrane is the one that minimizes its energy. To find this equilibrium shape, we calculate the variation of eqn (1) with respect to the membrane shapes, which gives us the shape equation of the membrane, akin to the Euler–Lagrange equation for the action in classical mechanics. In its general form (now including Δp) the shape equation reads29
| Δp − 2σH + κ(2H + 2H0)(2H2 − 2K − 2H0H) + 2κΔH = 0. | (2) |
To conclude, by modeling plasma membranes, using the framework of the Helfrich Hamiltonian in eqn (1), it is possible to predict equilibrium membrane shapes and thus the shapes of simple biological cells such as red blood cells, and to relate membrane shapes to measurable material properties.
3 Membrane fluctuations
The plasma membrane is always affected by fluctuations, which cause transient deformations that survive for only a short period of time (∼1–104 ms). Originally they were thought to be generated by thermal noise only, however, today we know that there are also several active origins that could drive membrane flickering, as reviewed by Turlier and Betz.22Fig. 3a shows the spherical reference state (dashed) and a deformed state (solid) of the plasma membrane (red) and the actin cortex (blue) due to fluctuations of various origins. | ||
| Fig. 3 Membrane deformations due to fluctuations of various origins. (a) Schematics of membrane fluctuations, caused by thermal random kicks from the environment, ion channels, ion pumps, and the coupling of plasma membrane and cytoskeleton. The spherical reference state of the cell (dashed) and a deformed state (solid) are shown. Membrane: red, actin cortex: blue and cell nucleus: orange. (b) Simulation snapshot of a triangulated membrane exhibiting active fluctuations. The mechanical properties of the membrane and the surrounding fluid are represented by the shear modulus μ, the bending rigidity κ and the fluid viscosity η. The forces with amplitude F0 are activated and inactivated with rates ka and ki and deform the membrane (red arrows). The surrounding fluid counteracts the active forces (green arrows). Reproduced from ref. 44 with permission from Springer Nature, copyright (2016). | ||
First, thermal random kicks of the surrounding medium drive membrane fluctuations.38 Second, and roughly equally important, several active processes drive membrane fluctuations, including the action of ion pumps and ion channels. Both pumps and channels can generate ion gradients and electric potentials that help the cell to control osmotic pressure and excitability. At the same time, as a consequence of Newton's third law, they exert additional forces onto the membrane, that lead to active fluctuations.22
By investigating membrane fluctuations, both the elastic properties of the plasma membrane and the possible active origin of the fluctuations can be studied. Membrane fluctuations are most easily characterized in red blood cells, since red blood cells lack a nucleus and thus represent a simple experimental model system. In red blood cells the actomyosin cortex and the spectrin network (another polymer network attached to the membrane) introduce additional sources of activity, which exert forces onto the membrane and lead to active fluctuations.39,40 The fluctuation spectrum of the membrane is typically observed with video microscopy or fluctuation spectroscopy. The elastic properties of the membrane such as the membrane tension or bending rigidity can then be determined by fitting the fluctuation spectrum.38,41,42 Moreover, by fitting membrane shapes to simulated triangulated surfaces the spontaneous curvature of the membrane can be determined as well.43 In addition, differences between the measured fluctuation spectrum and the prediction of the spectrum for purely thermally driven fluctuations suggest that the fluctuations are driven by active processes.44 For example, the time scale for thermally or actively induced fluctuations differs. While thermally induced fluctuations act on all time scales, actively induced fluctuations mostly enhance the amplitude for fluctuations acting on the time scale of 102–104 ms. In the following sections, we discuss how passive and active membrane fluctuations can be modeled.
3.1 Passive fluctuations
Because the plasma membrane is always affected by thermal fluctuations, a background of membrane deformations develops, which gives rise to a whole spectrum of membrane fluctuations. Since membrane fluctuations deform the plasma membrane only weakly, it is useful to describe the membrane by a height function h(x,y), that is a scalar field of the internal membrane coordinates x and y. This parametrization of membrane shape is known as the Monge gauge.45 For small deformations, we can expand eqn (1) to second order in h and its derivatives: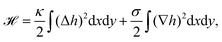 | (3) |
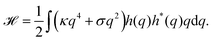 | (4) |
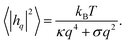 | (5) |
For passive systems the main driver of membrane fluctuations are random thermal kicks of the surrounding fluid. Thus, in order to describe the dynamics of the membrane and the fluid, the Navier–Stokes equation has to be coupled to eqn (3). The emerging Langevin equation then governs the dynamics of membrane deformations.47–49 Because we are mostly interested in the behavior for low Reynolds numbers, we can neglect inertia, and the fluid is represented by the Stokes equation
| ηΔv(r) − ∇p(r) = F (r), | (6) |
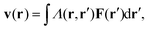 | (7) |
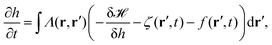 | (8) |
3.2 Active membrane fluctuations
In order to explain active processes, such as irreversible chemical reactions or active transport across the membrane, we have to go beyond the description given by equilibrium statistical physics. We can integrate activity into the membrane by either including an active force f(r′,t) in eqn (8) or by modifying eqn (3). Prost and Bruinsma treated the embedded proteins as two-state systems that can be either active or passive and either exert forces (due to momentum exchange with the surrounding fluid) or no forces on the membrane.47 The additional forces then lead to a modified Langevin equation, predicting a modified fluctuation spectrum compared to the passive case. Following this approach, it has been theoretically shown that active membrane fluctuations are amplified in front of a wall.48The effect of active proteins such as ion channels and ion pumps was explored in a series of papers.50–53 It has been suggested that ion channels affect the diffusion behavior in membranes, for instance that over long timescales diffusivity is increased.50 Moreover, the interplay between membrane undulations and ion pumps has been modeled, suggesting that membrane undulations travel with a velocity that is determined by the pump activity, that undulations are proportional to the inverse of the viscosity of the surrounding fluid, and that the statistical distribution of active membrane fluctuations is non-Gaussian.51–53 The interplay between excess area contained in membrane fluctuations and tension has furthermore been explored theoretically by Loubet et al. for a membrane that is subject to active fluctuations caused by a force resulting from pushing, spontaneous curvature, or permeation.54 They suggest that active fluctuations change the fluctuation spectrum and effect the relation between tension and excess area.
The growth, binding dynamics, and contraction of the cytoskeleton also lead to active membrane deformations. Interactions of the plasma membrane with the cytoskeleton, modeled as spring networks, suggest that the coupled cytoskeleton produces large membrane fluctuations that help to regulate membrane area,55 that cytoskeletal defects56 and the membrane–cortex bond density57 influence the fluctuation spectrum, and that the dynamics of the cytoskeletal network alters the elastic properties of the membrane.58
At large scales, cells show a tendency to form wavelike or unstable membrane deformations. The emergence of these patterns can be understood in a system with a feedback loop between the recruitment of membrane-bound activators and increased actin polymerization. The resulting shapes then depend on the induced spontaneous curvature of the activators.59–61
Active membrane fluctuations have been studied experimentally using various observation techniques.62 It has been shown that membrane-embedded ion pumps increase shape fluctuations and excess area,63 and decrease membrane tension64 compared to the passive case. Moreover, the amplitudes of membrane fluctuations are reduced in red blood cells that are depleted of ATP65,66 and changed in red blood cells that are infected by malaria parasites.67 Additional insight into how activity can change membrane shapes was provided by the recent experimental observation and numerical simulation of lipid vesicles that enclose bacteria,68 and lipid vesicles that contain active Janus particles.69 Both studies theoretically predicted, in agreement with the experimental data, that the observed active membrane fluctuation spectrum shows increased amplitudes for deformations acting on long wave lengths compared to the passive fluctuation spectrum.
The work by Turlier and coworkers is an illustrative example on how cellular processes can be theoretically inferred from these membrane deformations.44 By analyzing the red blood cell fluctuation spectrum, they showed that it deviates from what one would expect for a membrane in equilibrium, suggesting that active processes contribute to these membrane deformations. Analytical calculations and simulations of a triangulated membrane on which active forces act (cf.Fig. 3b), support this finding. However, the nature of the processes leading to these active forces remains elusive, since simulations with both monopole and dipole forces agree equally well with the data.
To conclude, while the analysis of passive membrane fluctuations can inform us about material properties of the membrane that would otherwise be difficult to measure with the same ease and precision, the extension to active membrane fluctuations also gives us insight into cellular functioning, since the changed fluctuation spectrum is due to active processes inside the cell.
4 Endocytosis
After membrane fluctuations, endocytosis is conceptually the simplest cellular process that causes membrane deformations. In endocytosis extracellular material is brought into the cell, or simply speaking the cell wraps a particle in its plasma membrane in order to take it up. Compared to the other examples discussed in this review, membrane deformations in endocytosis act on smaller length scales which makes it more challenging to access them experimentally, because with standard light microscopy we cannot resolve the relevant details of the membrane shape. Various modes of endocytosis occur in the cell. Here, we discuss the three main cases, namely adhesion driven particle uptake, clathrin-mediated endocytosis, and phagocytosis (cf.Fig. 4a, d and g).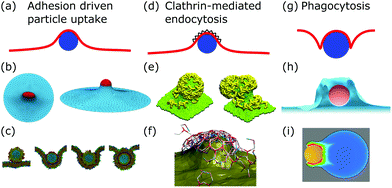 | ||
| Fig. 4 Membrane deformations in endocytosis. (a) Schematics of adhesion driven particle uptake. Membrane: red, particle: blue. (b) Simulated triangulated membrane, deformed by an adhered particle. Reproduced from ref. 80 with permission from The Royal Society of Chemistry. (c) Particle-based membrane simulation of particle uptake. Reproduced from ref. 91 with permission from Elsevier, copyright (2012). (d) Schematics of clathrin-mediated endocytosis. Membrane: red, particle: blue, clathrin lattice: black wedges. (e and f) Particle-based simulation of assembling clathrin triskelia deforming a membrane. (e) Reproduced from ref. 123 with permission from The Royal Society of Chemistry. (f) Reproduced from ref. 124 with permission from AIP Publishing. (g) Schematics of phagocytosis with the characteristic membrane deformation of the phagocytic cup. Membrane: red, particle: blue. (h) Simulation of particle engulfment in phagocytosis. Reproduced from ref. 128 with permission from Springer Nature, copyright (2010). (i) Simulation of engulfment of an antibody coated particle. The coloring shows the density of the actin cytoskeleton from blue (low) to red (high). Reproduced from ref. 129 under the terms of the Creative Commons Attribution License (CC BY 4.0). | ||
4.1 Adhesion driven particle uptake
While various entry modes exist in the cell, such as clathrin-mediated endocytosis or caveolar endocytosis, arguably the simplest case of endocytosis is particle uptake driven by adhesion energy (cf.Fig. 4a). Examples include viruses and nanoparticles that are typically ten to several hundred nanometers large,70 as well as micrometer-sized pathogens such as malaria parasites.71–74 The adhesion energy, which the particle experiences upon making contact with the membrane, can be of various origins, including electrostatic interactions, ligand–receptor binding, and entropic, van der Waals, or hydrophobic forces.70The uptake process starts if the energetic gain upon particle adhesion overcomes the energetic cost of bending the membrane and pulling out the excess area necessary to wrap the particle. Afterwards, adhesion driven uptake is an energetic downhill process that only stops if the energy minimum (i.e. a stable equilibrium) is reached. Since the connection of a fully wrapped particle to a membrane by means of a membrane neck costs approximately zero bending energy due to the saddle-shape of the neck (H = 0 in eqn (1)), we immediately understand that after uptake, membrane scission has to be driven by an active process such as membrane constriction by dynamin.75,76
The adhesion process can be incorporated in our membrane model by adding the adhesion energy to eqn (1),
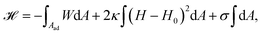 | (9) |
The main results of uptake models based on eqn (9) are that membrane tension, bending rigidity and adhesion strength determine whether one has full uptake, partial uptake or no uptake (cf.Fig. 4b).75,77,79–81 For example, for an intermediate adhesion energy and low membrane tension one has full uptake, while for an intermediate adhesion energy and large membrane tension one has partial uptake. In general, the competition between adhesion energy and membrane tension determines if partial uptake occurs, while the competition between adhesion energy (dependent on particle size) and bending energy (independent of particle size) defines a critical particle radius 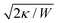 below which uptake is not possible.78,82 Uptake dynamics and membrane deformations are also studied for non-spherical particle shapes,79,81,83 for particles with elastic properties,84,85 for membranes with spontaneous curvature,86 for active particles87 and for particles with discrete and stochastic ligand–receptor binding.88–90 Specifically, the chemical and physical properties of the ligands have been investigated (cf.Fig. 4c).91 For instance, simulations suggest that for longer ligands, initial membrane attachment is easier while full uptake becomes more difficult.
below which uptake is not possible.78,82 Uptake dynamics and membrane deformations are also studied for non-spherical particle shapes,79,81,83 for particles with elastic properties,84,85 for membranes with spontaneous curvature,86 for active particles87 and for particles with discrete and stochastic ligand–receptor binding.88–90 Specifically, the chemical and physical properties of the ligands have been investigated (cf.Fig. 4c).91 For instance, simulations suggest that for longer ligands, initial membrane attachment is easier while full uptake becomes more difficult.
Particle wrapping not only deforms the adhered membrane parts, attached to the particle, but also the non-adhered free membrane parts, adjacent to the particle (cf.Fig. 4b). The two membrane parameters κ and σ define a length scale 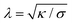 , characterizing the deformations in the free membrane parts during uptake.75 Using typical parameter values (κ = 25kBT and σ = 10−5–10−3 N m−1) one finds λ = 10–100 nm.90,92 In order to characterize membrane deformations one considers the ratio λ/R, with R the particle radius, that determines how far deformations can penetrate into the free membrane parts.75,90,92 For λ/R ≪ 1 we get a tense membrane where the deformation stays close to the particle, whereas for λ/R ≫ 1 we get a floppy membrane where the deformation reach is large. Inversely, the membrane parameters or the strength of adhesion can be predicted from the observation of the uptake state and the deformations of the membrane.
, characterizing the deformations in the free membrane parts during uptake.75 Using typical parameter values (κ = 25kBT and σ = 10−5–10−3 N m−1) one finds λ = 10–100 nm.90,92 In order to characterize membrane deformations one considers the ratio λ/R, with R the particle radius, that determines how far deformations can penetrate into the free membrane parts.75,90,92 For λ/R ≪ 1 we get a tense membrane where the deformation stays close to the particle, whereas for λ/R ≫ 1 we get a floppy membrane where the deformation reach is large. Inversely, the membrane parameters or the strength of adhesion can be predicted from the observation of the uptake state and the deformations of the membrane.
Apart from size and shape, the particle number affects the shape of membrane deformations during uptake.93,94 If there are multiple particles present on the membrane, they can interact with each other through the deformations they induce, which can lead to an attractive interaction and the emergence of collective behavior.95–100 Cooperative wrapping is a result of the interplay of bending and adhesion energy such that multiple wrapped particles can self-assemble into membrane tubes101 linear aggregates,102 hexagonal arrays103 or rings.104 In contrast, long parallel cylinders in globally flat membranes are predicted to repel each other.105
Some of these theoretical predictions on multiple-particle interactions on membranes still have to be confirmed by experimental studies, while others have been verified in recent years. These experiments typically involve giant lipid vesicles that wrap micrometer-sized particles because here membrane deformations are more easily accessible due to their larger sizes. For example this setup has been used to show that particles at membranes aggregate to reduce membrane deformations,98,106 assemble into 2D crystals with hexagonal order,107 and to measure the state digram of wrapping in the tensionless regime.108
4.2 Clathrin-mediated endocytosis
Particle wrapping is often assisted by protein–membrane interactions and the assembly of protein superstructures, providing additional mechanisms to curve the membrane.109 The most important example is clathrin-mediated endocytosis (CME).110 In CME, clathrin triskelia with tripod shapes bind to membrane-embedded adaptor proteins, which leads to the formation of clathrin lattices (protein assemblies) at the cell membrane (cf.Fig. 4d). As a result of clathrin assembly, the membrane gets deformed and a clathrin-coated vesicle is created.111,112 The sequence of assembly, membrane deformation and vesicle formation is regulated and before progression occurs several check-points have to be passed.112,113 The timing of clathrin induced membrane deformations relative to the timing of lattice assembly, however, is still elusive and two models explaining the extreme cases of the invagination process exist: the constant curvature model and the constant area model.114,115In the constant curvature model the clathrin coat grows with constant curvature, implying that the membrane is continuously deformed. In contrast, in the constant area model the clathrin coat first grows flat without curvature. Only after the coat has reached a sufficient size the membrane is deformed and a flat-to-curved transition occurs.110 To transform a flat lattice into a curved clathrin coat, however, a topological barrier has to be overcome, since Euler's polyhedron criterion dictates that the number of faces and vertices minus the number of edges has to equal two for closed polyhedra. Therefore, twelve pentagons (or possibly more pentagons accompanied by equally many more heptagons) have to be incorporated into the otherwise hexagonal clathrin lattice.116,117
Accessing the assembly process of clathrin coats experimentally is difficult, because the involved length scales are below the diffraction limit, therefore standard light microscopy techniques cannot resolve the assembly process. However, significant steps have been taken in modeling and simulations. In order to investigate how clathrin coats deform the membrane, additional terms have been added to eqn (1), representing polymerization energy, line tension or bending energy of the clathrin coat.118–122 In addition, simulations show how the assembly of clathrin triskelia deforms the membrane (cf.Fig. 4e and f).123,124 The assembly of flat and invaginated clathrin lattices was suggested to result from triskelia which occur in a flat and curved configuration and from lattices that exhibit lattice vacancies.125,126 The dynamics of clathrin coat assembly can be modeled by kinetic growth equations. A comparison of this model with the experimentally measured size and shape distribution of clathrin coated membranes suggests that clathrin coats first assemble flat before they start to curve.127 However, it is still unresolved how this transition from flat to curved could take place precisely on a microscopic level.
While under normal conditions CME can occur without the contribution of polymerizing actin filaments, the situation changes if membrane tension is high, or for cells with turgor pressure (e.g. yeast).130,131 Now polymerizing actin filaments can prevent CME from being stalled and support the invagination process of a flat membrane into a curved vesicle.132,133 It has been suggested by a combination of experiments and simulations that accessory proteins, triggering actin polymerization, organize in a ring-like manner around the endocytic site to optimize the efficiency of membrane invagination driven by actin134 and that bent actin filaments contribute to internalization by releasing elastic energy upon getting straight.135 To determine the rigidity of the clathrin coat and the force, generated by polymerizing actin filaments, in yeast cells, a shape equation, based on eqn (1), was fitted to registered membrane profiles.136 Using this approach the rigidity of the clathrin coat and the generated force were determined to be between 400–2000kBT and 1000–5000 pN, respectively. It remains unclear, however, how and where the point force of the model, generated by the actin network, is exerted and distributed on the membrane (cell wall) in the cell.
4.3 Phagocytosis
Phagocytosis is the main pathway in which cells take up large particles (≥0.5 μm) such as microbes (cf.Fig. 4g). For mammals the ability to phagocytose particles is mainly limited to immune cells to clear out pathogens, whereas single-cell organisms use it to take up nutrients.137–139 Although the actual dynamics have not been fully resolved experimentally, phagocytosis can be modeled by a zipper mechanism, implying that phagocytosis is the collective interplay of many particle–membrane adhesion contacts. In detail, first particles adhere to the plasma membrane through sequential ligand–receptor binding. Second, the plasma membrane encloses the particle due to actin polymerization, which also leads to further ligand–receptor binding. Finally, the membrane fuses around the particle to enable the separation of the enveloped particle from the plasma membrane.137,139In contrast to adhesion driven particle uptake, the particle size does not seem to play an important role for the effectiveness of phagocytosis,140 suggesting that active processes are the dominant players involved. Indeed large particles are engulfed not just by the membrane but also by the growing actin cortex.128,139 The polymerizing actin network leads to a particular type of membrane deformation, the so-called phagocytic cup, a membrane protrusion exhibiting increased membrane curvature since the membrane is deformed both in- and outwards.
Modeling the effect of ligand–receptor binding on the uptake dynamics suggests that the first half of engulfment is slow whereas the second half is fast.141 Moreover, particle shape and orientation influences the uptake dynamics. For instance, oblate shaped particles are engulfed fastest when the flat surface is presented to the membrane first.142 Surprisingly, for small particles phagocytosis has also been observed in systems where actin activity was inhibited, facilitated by ratcheted ligand–receptor binding alone, although the uptake rate is three to four times slower under such circumstances.128 We note that the interpretation of this observation is still under debate.143
Actin polymerization renders the shape of the phagocytic cup more regular (cf.Fig. 4h). From the shape of phagocytic cup the necessary engulfment forces have been calculated.144 The model predicts that two kinds of forces are at work: a repulsive force between the actin cytoskeleton and the membrane that leads to the engulfment of the particle and a flattening force that leads to the shape of the phagocytic cup. Furthermore, the shape and position of the phagocytic cup were investigated for a zymosan particle (made from yeast cell walls), where the membrane protrusion flows around the particle, leading to outward particle motion prior to engulfment, and for an antibody coated particle, where the membrane forms thin protrusions at all sides, leading to inward particle motion.129 Simulations suggest that for the zymosan particle, the membrane is pushed by actin and does not adhere to the particle, whereas for the antibody coated particle, the membrane lacks protrusion and adheres to the particle (cf.Fig. 4i). Moreover, by observing the shapes of deformable hydrogel particles during phagocytosis with confocal microscopy, it is possible to calculate the tensile forces from the deformation of the particles.145 Using this method, it was estimated that the cells exert a total tensile force of approximately 1 nN on the particle at the base of the phagocytic cup.
To conclude, modeling and observing endocytosis reveals amongst others how material properties of the membrane change the uptake behavior of particles and which particle shapes perform best, considering the uptake dynamics. Therefore, modeling could inform us on how to avoid undesirable uptake of harmful nanoparticles or pathogens but also which shapes should be used as potential drug carriers for therapeutical applications.
5 Cell adhesion
When a eukaryotic cell encounters a surface, it will spread upon and adhere to it, if the surface properties are favorable for the cell to form specific adhesion sites. The cell can also non-specifically interact with the surface, either by attractive Coulomb or van der Waals forces, or due to the repulsive effect of the glycocalyx (a cover of sugar molecules) and membrane fluctuations that both weaken the unspecific adhesion by electrostatic or steric (entropic) repulsion.146The adhesion process along specific adhesion sites consists of multiple steps, in which the cell adapts to the changed environment, affecting both the plasma membrane and the cytoskeleton, and thus leading to dramatic cell shape changes.12 In the first step, cell adhesion molecules or receptors, which are transmembrane proteins embedded in the plasma membrane, form bonds with ligands of the substrate or the extracellular matrix (ECM). Together, ligands and receptors work like lock-and-key. The most important protein family that conveys adhesion in humans are integrins, that bind to the corresponding ligands of the ECM, for example collagen or fibronectin.12,146
Due to the dynamic nature of cells, cell adhesion has to be a reversible process. Therefore, individual bonds are weak and contribute only a few kBT of adhesion energy. However, an ensemble of many bonds provides sufficient energy to establish strong cell–surface adhesion.12,146 For instance, integrins can assemble into focal adhesions, which are supra-molecular adhesion sites that strongly couple the actin cytoskeleton to the ECM.
During the initial spreading phase of adhesion, the cell surface area increases by about 50% due to the formation of adhesion sites, while the volume of the cell remains constant.147 The excess membrane area originates from wrinkles or exocytosis.148 The area gain is actively driven because the plasma membrane is pushed outwards by polymerizing actin filaments, creating a branched and cross-linked network of actin filaments at the leading edge of the cell. Between adhesion sites, cells develop actin stress fibers, that can be contracted by molecular motors. The generated forces are then transmitted via focal adhesion to the substrate.
Fig. 5a and b show a schematic view of an adhering cell after the internal remodeling process. In side view, the cell is essentially flat with only the cell nucleus sticking out (Fig. 5a). In the top view, the shape of the cell is characterized by invaginated arcs that span between focal adhesions (Fig. 5b).
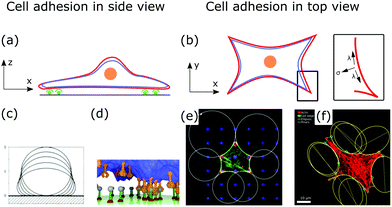 | ||
| Fig. 5 Membrane deformations in cell adhesion. (a) Schematic of cell adhesion in side view. A cell (nucleus: orange, membrane: red, actin cortex: blue) adheres to a surface at adhesion sites (green). (b) Schematic of cell adhesion in top view (nucleus: orange, membrane: red, actin cortex: blue). On patterned substrates cell shapes of adherent cells can be described by contour models. Inset: The contour of the cell shape can be described by the competition of surface and line tension. (c) Computed shapes of a membrane that adheres to a surface. By increasing the adhesion energy the contact area between membrane and surface increases. Reproduced from ref. 149 with permission from the American Physical Society, copyright (1990). (d) Simulated shape of a fluctuating membrane (blue) that adheres to a surface by binding receptors (orange) to ligands (grey). Reproduced from ref. 153 under the terms of the Creative Commons Attribution License (CC BY 3.0). (e) Theoretically predicted circular arcs fitted to the contour of adherent cells. Reproduced from ref. 155 with permission from Elsevier, copyright (2008). (f) Ellipses fitted to the contour of adherent cells. Reproduced from ref. 163 with permission from the American Physical Society, copyright (2018). | ||
5.1 Adhesion of membrane patches
The starting point to model specific cell adhesion is usually a continuum approach. In the basic model a spherical vesicle interacts by adhesion energy with the substrate, similar to the description of particle uptake (cf.eqn (9)). By minimizing the energy, the equilibrium membrane shape is determined (cf.Fig. 5c).149 The approach can be extended straightforwardly to an adhered vesicle from which a tether is pulled.150 Inversely, the adhesion energy density can be determined by fitting the shape equations to experimentally observed membrane contours.Since cells specifically adhere to a substrate by forming discrete ligand–receptor bonds, the model can be improved by incorporating the discrete nature of the adhesion sites. Ligand–receptor bonds can be modeled as springs. The adhesion part of the energy functional (in the Monge gauge) then reads
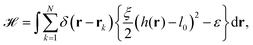 | (10) |
5.2 Shapes and contours of adherent cells
After a cell has spread, its shape is determined by the tension that acts on invaginated membrane arcs that span between focal adhesions (cf.Fig. 5b).154 These arcs are especially prominent in cells cultured on patterned substrates,155,156 as shown in Fig. 5e and f. Micropatterns then define adhesive and non-adhesive areas, regulating where and how cells adhere to surfaces.156,157To model the membrane shapes of adherent cells on patterned substrates, continuum models, discrete network models and cell contour models are employed.158–162 The basis of all contour models is the simple tension model, relating tensions within the cell contour to membrane deformations or cell shapes.12,155 After spreading, the cell is essentially flat, hence, it is described as a surface bound within a contour r(s), that is parametrized by its arc length s. If the cell is in equilibrium, the contractile forces of the actin cytoskeleton locally balance the force of the actin cortex at the cell contour. In the model, the surface tension σ is then locally balanced by the line tension λ (cf.Fig. 5b, inset). A tangent t(s) and a normal vector n(s) are defined at any point of the contour. If both vectors are normalized they are related by dt(s)/ds = n(s)/R(s), with R(s) the local radius of curvature. If σ and λ are independent of s, the force balance on a contour element ds can be expressed by
| σn(s)ds = λ(t(s + ds) − t(s)), | (11) |
Alternatively, cell shapes can be described on the level of energies, connecting contour models with the framework derived for membrane shapes in Section 2. Similar to eqn (1), the energy functional then reads
 | (12) |
To conclude, modeling cell shape during cell adhesion contributes to our understanding of how the cytoskeletal network architecture and molecular motor contractility regulate cell shapes. Inversely, from observed cell shapes, especially on patterned surfaces, we can infer mechanical properties not just of the membrane, but also of the underlying cortical cytoskeleton.
6 Cell migration
Cell motility is another example of a cellular process where the plasma membrane is strongly deformed from the spherical reference state, affecting cell shape globally.165 In general, cell motility can be classified into swimming motility and substrate-based motility, including cell gliding and crawling. For both swimmers and gliders the overall cell shape does not change much.166 Thus, here, we focus on cell crawling where cell shape changes are most important, requiring continuous remodeling of the interior of the cell.167The diversity of the shapes of migrating cells is huge and depends, among others, on the environment in which cells move. The same cell will assume vastly different shapes if it moves along a one-dimensional collagen fiber, a two-dimensional epithelial tissue, or through three-dimensional interstitial tissue.168 The most common cell shapes that develop in cell crawling are lamellipodia (2D sheets of a branched actin network), filopodia (protrusions of parallel actin bundles), blebs (membrane bulges, driven by hydrostatic pressure and a weak connection to the actin cortex) and lobopodia (blunt protrusions, driven by hydrostatic pressure).169
The mechanism underlying lamellipodia based cell migration consists of several steps. First, cell polarity is established, i.e., the front and back of the cell form. Second, the plasma membrane and the leading edge of the lamellipodium are pushed outwards trough actin polymerization and branching. The actin system is linked to the substrate at focal adhesions that form at the front and dissolve at the back of the cell. Therefore, traction forces are exerted to the substrate leading to forward motion of the cell. Finally, the back of the cell is pulled forwards because the actomyosin cytoskeleton contracts.169 Thus, cell migration is achieved by constant internal remodeling of the cell causing steady shape changes (cf.Fig. 6a).
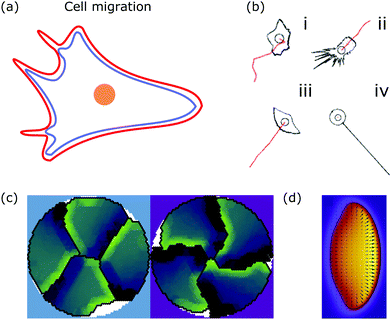 | ||
| Fig. 6 Membrane deformations in cell migration. (a) Schematic of a crawling cell (nucleus: orange, membrane: red, actin cortex: blue) that exhibits continuous internal remodeling affecting overall cell shape, including the lamellipodium and filopodia. (b) Phenomenological model that produces different cell shapes by changing the model parameters. Modeled cell shapes (black), paths of migration (red) and starting point of migration (black circle) for (i) dictyostelium cells, (ii) fibroblasts, (iii) keratocytes, and (iv) neurons. Reproduced from ref. 172 with permission from Elsevier, copyright (2008). (c) Shapes of four confined crawling cells modeled in a cellular Potts model. Reproduced from ref. 173 under the terms of the Creative Commons Attribution License (CC BY 4.0). (d) Crawling cell in the phase-field model. The heat map encodes the value of the phase-field from zero (purple) to one (yellow). Reproduced from ref. 174 with permission from The Royal Society of Chemistry. | ||
In the most basic model of cell migration, both the cell shape and the microscopic origins of motility are neglected and migration is described purely in terms of persistent random walks,170 which is indeed observed for individual cells in a uniform environment. In a complementary approach, the interplay between cell migration, mediated through actin polymerization, and cell adhesion, mediated by stochastic linkers, has been theoretically studied recently. Focusing on the microscopic driving factors while still neglecting cell shape, it was found that the stick-slip dynamics of the traction force can explain both steady cell crawling and bipedal cell motion.171
A more detailed phenomenological approach is to reproduce the shape of different cell types in a rule-based “shape machine”, where different cell shapes can be generated by tuning model parameters that summarize many molecular interactions (cf.Fig. 6b).172,175 For instance, one rule is that protrusions are formed at the leading edge whereas protrusions are suppressed anywhere else. By using cell shape as input information such models can make predictions about the internal structure of the cell. Results include the prediction that microtubule depolymerization increases the rate with which cells retract,172 and a relation between the dynamics of the actin cytoskeleton, such as the capping rate and the stall force, and the observed shape of fish keratocytes.175 Furthermore, computer simulations of the motion of flexocytes (vesicles with enclosed filaments) suggest that cell shape and the persistence of trajectories of migrating cells correlate.176
Another method to address the shape of migrating cells are cellular Potts models,173,177–179 in which crawling cells are discretized on a lattice. Individual lattice sites can be added or removed from cells, allowing the cells to fluctuate and move over (simulation) time. Equilibrium configurations are typically determined from the minimization of an appropriate energy functional using Monte Carlo methods. Using such a model it was suggested that cell shape is not only a consequence of cellular signaling but also that these signaling processes are influenced by cell shape changes.177 The approach can also be used to predict the shape of cells moving in ensembles (cf.Fig. 6c).173
Phase-field models are another approach to study cell migration.180 The basic idea here is to represent the cell by a continuous field, the phase-field ρ, at the position r and time t, which is ρ = 1 inside the cell, and ρ = 0 outside the cell. Consequently, the cell membrane or interface of the cell is represented by a smooth change of the phase-field. Similar to eqn (1) the bending and tension energy of the cell membrane can be formulated in terms of the phase-field by180
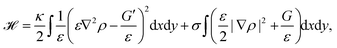 | (13) |
From eqn (13) a line density force for bending and tension can be calculated by Fben + Ften = (δ![[script letter H]](https://www.rsc.org/images/entities/char_e142.gif) /δρ)(∇ρ)/(ε|∇ρ|2). Adding contributions for area conservation Farea, protrusion and retraction forces of actin filaments, Fprot and Fretr, and a friction force Ffr, one finds the total force Ftot = Fben + Ften + Farea + Fprot + Fretr + Ffr. At steady state there is no total force (Ftot = 0) and from ∂ρ/∂t = v·∇ρ, with v the local speed of the membrane or phase-field, the time evolution of the membrane follows as180
/δρ)(∇ρ)/(ε|∇ρ|2). Adding contributions for area conservation Farea, protrusion and retraction forces of actin filaments, Fprot and Fretr, and a friction force Ffr, one finds the total force Ftot = Fben + Ften + Farea + Fprot + Fretr + Ffr. At steady state there is no total force (Ftot = 0) and from ∂ρ/∂t = v·∇ρ, with v the local speed of the membrane or phase-field, the time evolution of the membrane follows as180
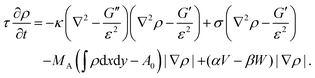 | (14) |
Alternatively, the phase-field can be coupled to a vector field p, describing polymerizing actin filaments.181 Most importantly, the phase-field approach predicts the steady state shape of moving cells (cf.Fig. 6d).174,180,181 Similar to the cellular Potts model the phase-field approach can be used to study the cell migration of cell ensembles.182 In addition, it can be used to predict the shape of cells migrating in a 3D environment with different surface topographies.183
To conclude, theoretical modeling of cell migration reveals how driving factors on the molecular level regulate motility and shape changes on the cellular level. In addition, modeling shows how interactions between a cell and its environment affect shape dynamics, which can lead to emergent collective bahavior with implications for wound healing and metastasis.
7 Cell division
From the viewpoint of shape, when animal cells divide, one sphere is transformed into two spheres, which fundamentally affects both the plasma membrane and the internal cellular components. To disentangle the underlying mechanisms cell division can be split up into multiple steps. In the first step, the cell rounds up and chromosomes assemble in the middle of the cell. In the second step, the chromosomes are pulled apart by mitotic spindles. In the third step, known as cytokinesis, the cell content is distributed between the two daughter cells.184,185 Here we focus on symmetrical cytokinesis (cf.Fig. 7a).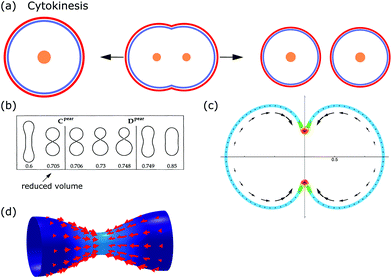 | ||
| Fig. 7 Membrane deformations in cell division. (a) Schematics of cytokinesis, the last step of cell division, where the cytoplasm is distributed over two daughter cells. Cell nucleus: orange, membrane: red, and actin cortex: blue. (b) Sequence of membrane shapes for constant spontaneous curvature and increasing reduced volume. Reproduced from ref. 31 with permission from the American Physical Society, copyright (1991). (c) Calculated cell shape during membrane constriction. The color code represents the activity within the cortex and the arrows show the cortical flow towards the equator. Reproduced from ref. 189 with permission from Elsevier, copyright (2014). (d) Shape of a constricting membrane tube due to the self-organizing flow of an active fluid (red arrows). Reproduced from ref. 190 under Creative Commons Attribution-NonCommercial-NoDerivatives License 4.0 (CC BY-NC-ND). | ||
During cytokinesis the cellular volume V0 is conserved to a good approximation, i.e. V0 = 2VD, where VD is the volume of a daughter cell.186 Thus, by assuming spherical shapes it follows that 2AD ≈ 1.26A0, implying that the surface area of the daughter cells has to increase during cytokinesis. The necessary extra area is provided by exocytosis and membrane remodeling.23,187 Moreover, the shape of the membrane changes drastically during cytokinesis. In order to model deformations of a cell of volume V and surface area A, one usually defines the reduced volume
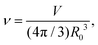 | (15) |
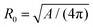 is the radius of a sphere of the same surface area. While spherical shapes have ν = 1, all other shapes have smaller values. In animal cells this shape change is driven by ATP-consuming activity within a ring of actomyosin that is anchored to the cell membrane, generating the necessary forces that constrict the membrane.188
is the radius of a sphere of the same surface area. While spherical shapes have ν = 1, all other shapes have smaller values. In animal cells this shape change is driven by ATP-consuming activity within a ring of actomyosin that is anchored to the cell membrane, generating the necessary forces that constrict the membrane.188
From a physical point of view, the problem of cell division is similar to endocytosis, the main difference being that the parts created are the same size. Hence, the starting point for modeling cell division is again eqn (1). The membrane shapes, which are reminiscent of dividing cells, are then determined by solving the corresponding shape equation. One finds the sequence from spherical to splitting cells either by changing spontaneous curvature while keeping the reduced volume ν constant, or by keeping spontaneous curvature constant while changing the reduced volume (cf.Fig. 7b).31 Similar to this idea, a sequence of shapes reminiscent of dividing cells was found in a phase-field model as a result of a time-dependent spontaneous curvature.191 Complementary, it has been demonstrated experimentally that vesicles could be split by changing their spontaneous curvature.192
Cell division in animal cells however is an active process, driven by the constriction of an actomyosin ring. Further details must therefore be included in the theoretical description.193 From a conceptual point of view, probably the simplest way is to include the constriction force as a boundary condition at the midplane of the cell, and calculate the corresponding energy-minimizing shapes. However, these calculations suggest that symmetric division is unstable at constant volume.194,195 The approach can be generalized to include the effect of membrane tension, spontaneous curvature and osmotic pressure.196,197 A related approach is to represent the constriction force by a line tension energy, added to eqn (1). By fitting the solution of the corresponding shape equation to the shapes of dividing cells, the bending rigidity, the contractile force and the line tension could be determined.198
The models discussed above consider only the plasma membrane. These could be useful for the future development of artificial cells with a minimal internal structure. However, in animal cells the cytoskeleton cannot be neglected when considering large-scale changes. As a first step towards including the effects of the cytoskeleton, the contractile forces acting on the membrane can be modeled to originate from a gradient in membrane tension during cytokinesis.199,200 Building on this idea, cell shapes during cytokinesis were examined in a model that represents the composite of plasma membrane and actomyosin cortex as an active gel, which can restrict the initial spherical cell shape due to the internal activity within the gel.189 A gradient in surface contractility from the poles to the equator then drives cytokinesis and, for example, reproduces the experimentally observed cortical flow to the equator (cf.Fig. 7c).
The constriction of the membrane can also be modeled by a contractile network that couples the network density with the spontaneous curvature of the membrane. In a framework similar to the one explained in Section 3 the dispersion and, hence, the stability of membrane constriction can be determined.201 Moreover, the role of stress of different origins (adhesion, protrusion, contraction) acting on the membrane during cytokinesis has been investigated.202–204
As cytokinesis progresses, a cell–cell interface begins to form between the two daughter cells. The dynamics of this interface can be examined by balancing its viscous friction and active stresses. As a result, the model predicts the corresponding changes in cell shape.205 Finally, curved surfaces can be coupled with active gels to study the interplay between different membrane shapes and contractile forces,190 resulting for example in the formation of contractile rings on tubular membranes (cf.Fig. 7d).
To conclude, theoretical modeling of membrane deformations during cytokinesis predicts how membrane constriction might be initiated, how large constriction forces have to be and where they act. Therefore, modeling deformations in cell division contributes to our basic understanding necessary to build artificial cells.
8 Conclusion
The shape of the cell and the plasma membrane surrounding it are deformed in many cellular processes. The variety of the resulting membrane shapes shows the diversity of underlying driving factors. At the same time, this morphological variety allows us to extract a large amount of information about the inner workings of the cell. In this review we have outlined how modeling cell shape and membrane deformations can contribute to our understanding of the mechanisms that drive membrane fluctuations, endocytosis, cell adhesion, cell migration and cell division. We have demonstrated that modeling cell shape and membrane deformations is an important tool to investigate the cell, even on the microscopic scale.The properties of a pure lipid bilayer membrane are well described by the Helfrich Hamiltonian (eqn (1)). Membrane deformations in a living cell however predominantly originate from active processes, which result in additional fluctuations, driven deformations, and large-scale shape and topological changes. To explain these shape changes, models can be built that include localized adhesion, changes in spontaneous curvature, or variation in stress, due to the interaction of the membrane with proteins and polymer networks. Inversely, the calculated shapes can be fitted to experimental data to both verify the model predictions and extract material properties of the other cellular components involved, such as the magnitude of exerted forces or the adhesion energy of linker molecules.
In some cases, the experimental resolution in time or space is not yet high enough to distinguish between competing models, as for example in the two possible assembly pathways of a clathrin-coated pit discussed in section 4. While one of the proposed models might be ruled out by future experimental insight, it is also possible that both methods are employed. Life tends to be creative, and find a use for any pathway that is physically allowed, which is of course also why we can observe the large variety in membrane shapes we have explored here.
The discussed examples demonstrate how theoretical modeling can relate membrane deformations and shapes to cell function and thus lead to biological insight. In general, through modeling, the cell's complexity can be reduced and therefore modeling can identify key players, responsible for specific deformations. Moreover, modeling can couple theoretical concepts such as material parameters to observables such as fluctuation amplitudes or membrane invaginations, hence making the cell more quantifiable. Both these aspects show how theoretical modeling can reduce some of the cell's complexity by making predictions or hypotheses quantifiable.
We need not stop at the surface though. The insights we have gained about the inner workings of the cell by studying how it behaves in well-controlled situations like adhesion or phagocytosis allow us to also build models for more complex processes like cell migration and division. Because of the high complexity of cells, these models are by necessity more phenomenological; however, they can continually be refined as more detailed studies provide new information. Moreover, they provide a bridge from the fundamental study of lifeless components like lipid bilayers and proteins to full-fledged living cells, with promising applications in biology and medicine.
A well-known example is the difference between healthy and tumorigenic cells, which differ strongly in their material properties, allowing tumor cells to metastasize and invade healthy tissue. In this context, there is still a large array of questions to be answered, of which many center on the role of the membrane. For instance, while for reconstituted membranes or extracted membrane vesicles the membrane tension is uniform, recent experiments suggest that it is not in living cells.206
Recapitulating the different examples of this review, there are many more open questions to be answered. Membranes in living cells contain many different types of lipids, as well as transmembrane and membrane-associated proteins, which all affect membrane properties and shapes. There is still a large gap between experimentally reconstituted and theoretically modeled membranes with just a few, or just one component, and those we know to exist in living cells. Likewise, it is still quite elusive what the physiological role of active membrane fluctuations is. It is also still unknown what the minimal necessary requirements are for cells to divide, which might be especially important when engineering an artificial cell. Finally, there is a need to develop integrated models that bridge multiple scales, for instance when studying the interplay between cell adhesion and cell migration.
To answer these questions, we need new experiments, but also new models, that take the interactions between the plasma membrane and cellular driving factors into account. More importantly, experimentalist and theorists need to continue working together, as these open questions can only be answered jointly.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
We thank Rachel Los, Ulrich Schwarz and Falko Ziebert for critical comments on the manuscript.References
- B. Alberts, A. Johnson, J. Lewis, D. Morgan, M. Raff, K. Roberts and P. Walter, Molecular biology of the cell: Sixth edition, Garland Science, New York, 2015 Search PubMed.
- D. H. Boal, Mechanics of the Cell, Cambridge University Press, Cambridge, 2nd edn, 2012 Search PubMed.
- R. Phillips, J. Kondev, J. Theriot and H. Garcia, Physical biology of the cell, Garland Science, New York, 2012 Search PubMed.
- P. Schwille, J. Spatz, K. Landfester, E. Bodenschatz, S. Herminghaus, V. Sourjik, T. J. Erb, P. Bastiaens, R. Lipowsky, A. Hyman, P. Dabrock, J.-C. Baret, T. Vidakovic-Koch, P. Bieling, R. Dimova, H. Mutschler, T. Robinson, T.-Y. D. Tang, S. Wegner and K. Sundmacher, Angew. Chem., Int. Ed., 2018, 57, 13382–13392 CrossRef CAS.
- F. Fanalista, A. Birnie, R. Maan, F. Burla, K. Charles, G. Pawlik, S. Deshpande, G. H. Koenderink, M. Dogterom and C. Dekker, ACS Nano, 2019, 13, 5439–5450 CrossRef CAS.
- Y. Mulla, A. Aufderhorst-Roberts and G. H. Koenderink, Phys. Biol., 2018, 15, 041001 CrossRef.
- D. W. Thompson, On Growth and Form, Cambridge University Press, 1917 Search PubMed.
- A.-L. Le Roux, X. Quiroga, N. Walani, M. Arroyo and P. Roca-Cusachs, Philos. Trans. R. Soc., B, 2019, 374, 20180221 CrossRef CAS.
- P. Bassereau and P. Sens, Physics of Biological Membranes, Springer, 2018 Search PubMed.
- L. Blanchoin, R. Boujemaa-Paterski, C. Sykes and J. Plastino, Physiol. Rev., 2014, 94, 235–263 CrossRef CAS.
- P. Chugh and E. K. Paluch, J. Cell Sci., 2018, 131, jcs186254 CrossRef.
- U. S. Schwarz and S. A. Safran, Rev. Mod. Phys., 2013, 85, 1327–1381 CrossRef CAS.
- M. P. Clausen, H. Colin-York, F. Schneider, C. Eggeling and M. Fritzsche, J. Phys. D: Appl. Phys., 2017, 50, 064002 CrossRef CAS.
- F. Huber, A. Boire, M. P. López and G. H. Koenderink, Curr. Opin. Cell Biol., 2015, 32, 39–47 CrossRef CAS.
- S. Mostowy and P. Cossart, Nat. Rev. Mol. Cell Biol., 2012, 13, 183–194 CrossRef CAS.
- A. A. Bridges, M. S. Jentzsch, P. W. Oakes, P. Occhipinti and A. S. Gladfelter, J. Cell Biol., 2016, 213, 23–32 CrossRef CAS.
- S. Banerjee, M. L. Gardel and U. S. Schwarz, Annu. Rev. Condens. Matter Phys., 2020, 11, 421–439 CrossRef.
- M. Murrell, P. W. Oakes, M. Lenz and M. L. Gardel, Nat. Rev. Mol. Cell Biol., 2015, 16, 486–498 CrossRef CAS.
- S. Ramaswamy, Annu. Rev. Condens. Matter Phys., 2010, 1, 323–345 CrossRef.
- M. C. Marchetti, J.-F. Joanny, S. Ramaswamy, T. B. Liverpool, J. Prost, M. Rao and R. A. Simha, Rev. Mod. Phys., 2013, 85, 1143 CrossRef CAS.
- M. R. Shaebani, A. Wysocki, R. G. Winkler, G. Gompper and H. Rieger, Nat. Rev. Phys., 2020, 2, 181–199 CrossRef.
- H. Turlier and T. Betz, Annu. Rev. Condens. Matter Phys., 2019, 10, 213–232 CrossRef.
- F. Rizzelli, M. G. Malabarba, S. Sigismund and M. Mapelli, Open Biol., 2020, 10, 190314 CrossRef CAS.
- W. Helfrich, Z. Naturforsch., C: J. Biosci., 1973, 28, 693–703 CAS.
- M. Deserno, Chem. Phys. Lipids, 2015, 185, 11–45 CrossRef CAS.
- S. Svetina and B. Žekš, Eur. Biophys. J., 1989, 17, 101–111 CrossRef CAS.
- S. Svetina and B. Žekš, Anat. Rec., 2002, 268, 215–225 CrossRef CAS.
- L. Miao, U. Seifert, M. Wortis and H.-G. Döbereiner, Phys. Rev. E: Stat. Phys., Plasmas, Fluids, Relat. Interdiscip., 1994, 49, 5389–5407 CrossRef CAS.
- O.-Y. Zhong-can and W. Helfrich, Phys. Rev. A: At., Mol., Opt. Phys., 1989, 39, 5280–5288 CrossRef.
- R. Lipowsky, Nature, 1991, 349, 475–481 CrossRef CAS.
- U. Seifert, K. Berndl and R. Lipowsky, Phys. Rev. A: At., Mol., Opt. Phys., 1991, 44, 1182–1202 CrossRef CAS.
- H. W. Gerald Lim, M. Wortis and R. Mukhopadhyay, Proc. Natl. Acad. Sci. U. S. A., 2002, 99, 16766–16769 CrossRef CAS.
- T. Baumgart, S. Das, W. W. Webb and J. T. Jenkins, Biophys. J., 2005, 89, 1067–1080 CrossRef CAS.
- S. Semrau, T. Idema, L. Holtzer, T. Schmidt and C. Storm, Phys. Rev. Lett., 2008, 100, 088101 CrossRef.
- I. Derényi, F. Jülicher and J. Prost, Phys. Rev. Lett., 2002, 88, 238101 CrossRef.
- T. R. Powers, G. Huber and R. E. Goldstein, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2002, 65, 12 Search PubMed.
- P. Bassereau, B. Sorre and A. Lévy, Adv. Colloid Interface Sci., 2014, 208, 47–57 CrossRef CAS.
- F. Brochard and J. Lennon, J. Phys., 1975, 36, 1035–1047 CrossRef.
- A. Biswas, A. Alex and B. Sinha, Biophys. J., 2017, 113, 1768–1781 CrossRef CAS.
- S. E. Lux, Blood, 2016, 127, 187–199 CrossRef CAS.
- H. Duwe, J. Kaes and E. Sackmann, J. Phys., 1990, 51, 945–961 CrossRef CAS.
- T. Betz and C. Sykes, Soft Matter, 2012, 8, 5317–5326 RSC.
- H.-G. Döbereiner, G. Gompper, C. K. Haluska, D. M. Kroll, P. G. Petrov and K. A. Riske, Phys. Rev. Lett., 2003, 91, 048301 CrossRef.
- H. Turlier, D. A. Fedosov, B. Audoly, T. Auth, N. S. Gov, C. Sykes, J.-F. Joanny, G. Gompper and T. Betz, Nat. Phys., 2016, 12, 513–519 Search PubMed.
- U. Seifert, Adv. Phys., 1997, 46, 13–137 CrossRef CAS.
- W. Helfrich and R.-M. Servuss, Il Nuovo Cimento D, 1984, 3, 137–151 CrossRef.
- J. Prost and R. Bruinsma, Europhys. Lett., 1996, 33, 321–326 CrossRef CAS.
- J. Prost, J.-B. Manneville and R. Bruinsma, Eur. Phys. J. B, 1998, 1, 465–480 CrossRef CAS.
- L. C.-L. Lin and F. L. H. Brown, J. Chem. Theory Comput., 2006, 2, 472–483 CrossRef CAS.
- R. Granek and S. Pierrat, Phys. Rev. Lett., 1999, 83, 872–875 CrossRef CAS.
- S. Ramaswamy, J. Toner and J. Prost, Phys. Rev. Lett., 2000, 84, 3494–3497 CrossRef CAS.
- N. Gov, Phys. Rev. Lett., 2004, 93, 268104 CrossRef CAS.
- L. C.-L. Lin, N. Gov and F. L. H. Brown, J. Chem. Phys., 2006, 124, 074903 CrossRef.
- B. Loubet, U. Seifert and M. A. Lomholt, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2012, 85, 031913 CrossRef.
- J.-B. Fournier, D. Lacoste and E. Raphaél, Phys. Rev. Lett., 2004, 92, 018102 CrossRef.
- C. Dubus and J.-B. Fournier, Europhys. Lett., 2006, 75, 181–187 CrossRef CAS.
- R. Alert, J. Casademunt, J. Brugués and P. Sens, Biophys. J., 2015, 108, 1878–1886 CrossRef CAS.
- R. Zhang and F. L. H. Brown, J. Chem. Phys., 2008, 129, 065101 CrossRef.
- N. S. Gov and A. Gopinathan, Biophys. J., 2006, 90, 454–469 CrossRef CAS.
- R. Shlomovitz and N. S. Gov, Phys. Rev. Lett., 2007, 98, 168103 CrossRef CAS.
- A. Maitra, P. Srivastava, M. Rao and S. Ramaswamy, Phys. Rev. Lett., 2014, 112, 258101 CrossRef.
- C. Monzel and K. Sengupta, J. Phys. D: Appl. Phys., 2016, 49, 243002 CrossRef.
- J.-B. Manneville, P. Bassereau, D. Lévy and J. Prost, Phys. Rev. Lett., 1999, 82, 4356–4359 CrossRef CAS.
- M. D. E. A. Faris, D. Lacoste, J. Pécréaux, J.-F. Joanny, J. Prost and P. Bassereau, Phys. Rev. Lett., 2009, 102, 038102 CrossRef.
- T. Betz, M. Lenz, J.-F. Joanny and C. Sykes, Proc. Natl. Acad. Sci. U. S. A., 2009, 106, 15320–15325 CrossRef CAS.
- Y. Park, C. A. Best, T. Auth, N. S. Gov, S. A. Safran, G. Popescu, S. Suresh and M. S. Feld, Proc. Natl. Acad. Sci. U. S. A., 2010, 107, 1289–1294 CrossRef CAS.
- Y. Park, M. Diez-Silva, G. Popescu, G. Lykotrafitis, W. Choi, M. S. Feld and S. Suresh, Proc. Natl. Acad. Sci. U. S. A., 2008, 105, 13730–13735 CrossRef CAS.
- S. C. Takatori and A. Sahu, Phys. Rev. Lett., 2020, 124, 158102 CrossRef CAS.
- H. R. Vutukuri, M. Hoore, C. Abaurrea-Velasco, L. van Buren, A. Dutto, T. Auth, D. A. Fedosov, G. Gompper and J. Vermant, Nature, 2020, 586, 52–56 CrossRef CAS.
- S. Zhang, H. Gao and G. Bao, ACS Nano, 2015, 9, 8655–8671 CrossRef CAS.
- P. Cossart and A. Helenius, Cold Spring Harbor Perspect. Biol., 2014, 6, a016972 CrossRef.
- L. Shang, K. Nienhaus and G. Nienhaus, J. Nanobiotechnol., 2014, 12, 5 CrossRef.
- T. Wiegand, M. Fratini, F. Frey, K. Yserentant, Y. Liu, E. Weber, K. Galior, J. Ohmes, F. Braun, D.-P. Herten, S. Boulant, U. S. Schwarz, K. Salaita, E. A. Cavalcanti-Adam and J. P. Spatz, Nat. Commun., 2020, 11, 32 CrossRef CAS.
- S. Dasgupta, T. Auth, N. Gov, T. Satchwell, E. Hanssen, E. Zuccala, D. Riglar, A. Toye, T. Betz, J. Baum and G. Gompper, Biophys. J., 2014, 107, 43–54 CrossRef CAS.
- M. Deserno, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2004, 69, 031903 CrossRef.
- Z. A. McDargh, P. Vázquez-Montejo, J. Guven and M. Deserno, Biophys. J., 2016, 111, 2470–2480 CrossRef CAS.
- M. Deserno and W. M. Gelbart, J. Phys. Chem. B, 2002, 106, 5543–5552 CrossRef CAS.
- H. Gao, W. Shi and L. B. Freund, Proc. Natl. Acad. Sci. U. S. A., 2005, 102, 9469–9474 CrossRef CAS.
- R. Vácha, F. J. Martinez-Veracoechea and D. Frenkel, Nano Lett., 2011, 11, 5391–5395 CrossRef.
- S. Dasgupta, T. Auth and G. Gompper, Soft Matter, 2013, 9, 5473–5482 RSC.
- S. Dasgupta, T. Auth and G. Gompper, Nano Lett., 2014, 14, 687–693 CrossRef CAS.
- R. Lipowsky and H.-G. Döbereiner, Europhys. Lett., 1998, 43, 219–225 CrossRef CAS.
- C. Huang, Y. Zhang, H. Yuan, H. Gao and S. Zhang, Nano Lett., 2013, 13, 4546–4550 CrossRef CAS.
- X. Yi, X. Shi and H. Gao, Phys. Rev. Lett., 2011, 107, 098101 CrossRef.
- C. Zeng, M. Hernando-Pérez, B. Dragnea, X. Ma, P. van der Schoot and R. Zandi, Phys. Rev. Lett., 2017, 119, 038102 CrossRef.
- J. Agudo-Canalejo and R. Lipowsky, ACS Nano, 2015, 9, 3704–3720 CrossRef CAS.
- P. Chen, Z. Xu, G. Zhu, X. Dai and L.-T. Yan, Phys. Rev. Lett., 2020, 124, 198102 CrossRef CAS.
- X. Yi and H. Gao, Nanoscale, 2017, 9, 454–463 RSC.
- F. Frey, F. Ziebert and U. S. Schwarz, Phys. Rev. Lett., 2019, 122, 088102 CrossRef CAS.
- F. Frey, F. Ziebert and U. S. Schwarz, Phys. Rev. E, 2019, 100, 052403 CrossRef CAS.
- H.-M. Ding and Y.-G. Ma, Biomaterials, 2012, 33, 5798–5802 CrossRef CAS.
- L. Foret, Eur. Phys. J. E: Soft Matter Biol. Phys., 2014, 37, 42 CrossRef.
- A. Chaudhuri, G. Battaglia and R. Golestanian, Phys. Biol., 2011, 8, 046002 CrossRef.
- A. H. Bahrami, M. Raatz, J. Agudo-Canalejo, R. Michel, E. M. Curtis, C. K. Hall, M. Gradzielski, R. Lipowsky and T. R. Weikl, Adv. Colloid Interface Sci., 2014, 208, 214–224 CrossRef CAS.
- M. Goulian, R. Bruinsma and P. Pincus, Europhys. Lett., 1993, 22, 145–150 CrossRef CAS.
- B. J. Reynwar, G. Illya, V. A. Harmandaris, M. M. Müller, K. Kremer and M. Deserno, Nature, 2007, 447, 461–464 CrossRef CAS.
- A. Šarić and A. Cacciuto, Soft Matter, 2013, 9, 6677 RSC.
- C. van der Wel, A. Vahid, A. Šarić, T. Idema, D. Heinrich and D. J. Kraft, Sci. Rep., 2016, 6, 32825 CrossRef CAS.
- A. Vahid, A. Šarić and T. Idema, Soft Matter, 2017, 13, 4924–4930 RSC.
- T. Idema and D. J. Kraft, Curr. Opin. Colloid Interface Sci., 2019, 40, 58–69 CrossRef CAS.
- A. H. Bahrami, R. Lipowsky and T. R. Weikl, Phys. Rev. Lett., 2012, 109, 188102 CrossRef.
- A. Šarić and A. Cacciuto, Phys. Rev. Lett., 2012, 109, 188101 CrossRef.
- A. Šarić and A. Cacciuto, Phys. Rev. Lett., 2012, 108, 118101 CrossRef.
- A. Vahid and T. Idema, Phys. Rev. Lett., 2016, 117, 138102 CrossRef.
- M. M. Müller, M. Deserno and J. Guven, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2005, 72, 061407 CrossRef.
- C. van der Wel, D. Heinrich and D. J. Kraft, Biophys. J., 2017, 113, 1037–1046 CrossRef CAS.
- M. Wang, A. M. Mihut, E. Rieloff, A. P. Dabkowska, L. K. Månsson, J. N. Immink, E. Sparr and J. J. Crassous, Proc. Natl. Acad. Sci. U. S. A., 2019, 116, 5442–5450 CrossRef CAS.
- H. T. Spanke, R. W. Style, C. François-Martin, M. Feofilova, M. Eisentraut, H. Kress, J. Agudo-Canalejo and E. R. Dufresne, Phys. Rev. Lett., 2020, 125, 198102 CrossRef CAS.
- J. Zimmerberg and M. M. Kozlov, Nat. Rev. Mol. Cell Biol., 2006, 7, 9–19 CrossRef CAS.
- M. Kaksonen and A. Roux, Nat. Rev. Mol. Cell Biol., 2018, 19, 313 CrossRef CAS.
- A. Picco and M. Kaksonen, Curr. Opin. Cell Biol., 2018, 53, 105–110 CrossRef CAS.
- M. Mettlen, P.-H. Chen, S. Srinivasan, G. Danuser and S. L. Schmid, Annu. Rev. Biochem., 2018, 87, 871–896 CrossRef CAS.
- R. T. Pedersen, J. E. Hassinger, P. Marchando and D. G. Drubin, J. Cell Biol., 2020, 219, e202002160 CrossRef CAS.
- M. Lampe, S. Vassilopoulos and C. Merrifield, J. Struct. Biol., 2016, 196, 48–56 CrossRef CAS.
- K. A. Sochacki and J. W. Taraska, Trends Cell Biol., 2019, 29, 241–256 CrossRef CAS.
- R. J. Mashl and R. F. Bruinsma, Biophys. J., 1998, 74, 2862–2875 CrossRef CAS.
- T. Kohyama, D. M. Kroll and G. Gompper, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2003, 68, 061905 CrossRef CAS.
- R. Lipowsky, J. Phys. II, 1992, 2, 1825–1840 CrossRef CAS.
- A. Banerjee, A. Berezhkovskii and R. Nossal, Biophys. J., 2012, 102, 2725–2730 CrossRef CAS.
- M. Saleem, S. Morlot, A. Hohendahl, J. Manzi, M. Lenz and A. Roux, Nat. Commun., 2015, 6, 6249 CrossRef CAS.
- J. E. Hassinger, G. Oster, D. G. Drubin and P. Rangamani, Proc. Natl. Acad. Sci. U. S. A., 2017, 114, E1118–E1127 CrossRef CAS.
- F. Frey and U. S. Schwarz, Soft Matter, 2020, 16, 10723–10733 RSC.
- R. Matthews and C. N. Likos, Soft Matter, 2013, 9, 5794 RSC.
- M. Giani, W. K. den Otter and W. J. Briels, J. Chem. Phys., 2017, 146, 155102 CrossRef CAS.
- W. K. den Otter and W. J. Briels, Traffic, 2011, 12, 1407–1416 CrossRef CAS.
- F. Frey, D. Bucher, K. A. Sochacki, J. W. Taraska, S. Boulant and U. S. Schwarz, New J. Phys., 2020, 22, 073043 CrossRef CAS.
- D. Bucher, F. Frey, K. A. Sochacki, S. Kummer, J.-P. Bergeest, W. J. Godinez, H.-G. Kräusslich, K. Rohr, J. W. Taraska and U. S. Schwarz, et al. , Nat. Commun., 2018, 9, 1109 CrossRef.
- S. Tollis, A. E. Dart, G. Tzircotis and R. G. Endres, BMC Syst. Biol., 2010, 4, 149 CrossRef.
- M. Herant, C.-Y. Lee, M. Dembo and V. Heinrich, PLoS Comput. Biol., 2011, 7, e1001068 CrossRef CAS.
- S. Boulant, C. Kural, J.-C. Zeeh, F. Ubelmann and T. Kirchhausen, Nat. Cell Biol., 2011, 13, 1124–1131 CrossRef CAS.
- L. Johannes, R. G. Parton, P. Bassereau and S. Mayor, Nat. Rev. Mol. Cell Biol., 2015, 16, 311–321 CrossRef CAS.
- A. E. Carlsson, Curr. Opin. Cell Biol., 2018, 50, 1–7 CrossRef CAS.
- F. Baschieri, K. Porshneva and G. Montagnac, J. Cell Sci., 2020, 133, jcs240861 CrossRef CAS.
- M. Mund, J. A. van der Beek, J. Deschamps, S. Dmitrieff, P. Hoess, J. L. Monster, A. Picco, F. Nédélec, M. Kaksonen and J. Ries, Cell, 2018, 174, 884–896 CrossRef CAS . e17.
- M. Akamatsu, R. Vasan, D. Serwas, M. A. Ferrin, P. Rangamani and D. G. Drubin, eLife, 2020, 9, e49840 CrossRef CAS.
- S. Dmitrieff and F. Nédélec, PLoS Comput. Biol., 2015, 11, e1004538 CrossRef.
- J. A. Swanson, Nat. Rev. Mol. Cell Biol., 2008, 9, 639–649 CrossRef CAS.
- D. M. Richards and R. G. Endres, Rep. Prog. Phys., 2017, 80, 126601 CrossRef.
- V. Jaumouillé and C. M. Waterman, Front. Immunol., 2020, 11, 1097 CrossRef.
- J. A. Champion and S. Mitragotri, Proc. Natl. Acad. Sci. U. S. A., 2006, 103, 4930–4934 CrossRef CAS.
- D. M. Richards and R. G. Endres, Biophys. J., 2014, 107, 1542–1553 CrossRef CAS.
- D. M. Richards and R. G. Endres, Proc. Natl. Acad. Sci. U. S. A., 2016, 113, 6113–6118 CrossRef CAS.
- V. Heinrich, Biophys. J., 2015, 109, 469–476 CrossRef CAS.
- M. Herant, J. Cell Sci., 2006, 119, 1903–1913 CrossRef CAS.
- D. Vorselen, Y. Wang, M. M. de Jesus, P. K. Shah, M. J. Footer, M. Huse, W. Cai and J. A. Theriot, Nat. Commun., 2020, 11, 20 CrossRef CAS.
- K. Sengupta and A.-S. Smith, Physics of Biological Membranes, Springer, 2018, pp. 499–535 Search PubMed.
- N. C. Gauthier, O. M. Rossier, A. Mathur, J. C. Hone and M. P. Sheetz, Mol. Biol. Cell, 2009, 20, 3261–3272 CrossRef CAS.
- N. C. Gauthier, M. A. Fardin, P. Roca-Cusachs and M. P. Sheetz, Proc. Natl. Acad. Sci. U. S. A., 2011, 108, 14467–14472 CrossRef CAS.
- U. Seifert and R. Lipowsky, Phys. Rev. A: At., Mol., Opt. Phys., 1990, 42, 4768–4771 CrossRef CAS.
- A.-S. Smith, E. Sackmann and U. Seifert, Phys. Rev. Lett., 2004, 92, 208101 CrossRef.
- T. R. Weikl, M. Asfaw, H. Krobath, B. Różycki and R. Lipowsky, Soft Matter, 2009, 5, 3213 RSC.
- T. Bihr, U. Seifert and A.-S. Smith, Phys. Rev. Lett., 2012, 109, 258101 CrossRef.
- T. Bihr, U. Seifert and A.-S. Smith, New J. Phys., 2015, 17, 083016 CrossRef.
- R. Bar-Ziv, T. Tlusty, E. Moses, S. A. Safran and A. Bershadsky, Proc. Natl. Acad. Sci. U. S. A., 1999, 96, 10140–10145 CrossRef CAS.
- I. B. Bischofs, F. Klein, D. Lehnert, M. Bastmeyer and U. S. Schwarz, Biophys. J., 2008, 95, 3488–3496 CrossRef CAS.
- P. J. Albert and U. S. Schwarz, Cell Adhes. Migr., 2016, 10, 516–528 CrossRef CAS.
- C. S. Chen, Science, 1997, 276, 1425–1428 CrossRef CAS.
- S. Banerjee and M. Cristina Marchetti, New J. Phys., 2013, 15, 035015 CrossRef.
- V. S. Deshpande, R. M. McMeeking and A. G. Evans, Proc. Natl. Acad. Sci. U. S. A., 2006, 103, 14015–14020 CrossRef CAS.
- M. F. Coughlin and D. Stamenović, Biophys. J., 2003, 84, 1328–1336 CrossRef CAS.
- P. Guthardt Torres, I. B. Bischofs and U. S. Schwarz, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2012, 85, 011913 CrossRef CAS.
- L. Giomi, Cell Migrations: Causes and Functions, Springer, Cham, 2019, pp. 13–29 Search PubMed.
- W. Pomp, K. Schakenraad, H. E. Balcıoğlu, H. van Hoorn, E. H. J. Danen, R. M. H. Merks, T. Schmidt and L. Giomi, Phys. Rev. Lett., 2018, 121, 178101 CrossRef CAS.
- S. Banerjee and L. Giomi, Soft Matter, 2013, 9, 5251 RSC.
- A. Mogilner and K. Keren, Curr. Biol., 2009, 19, R762–R771 CrossRef CAS.
- D. A. Fletcher and J. A. Theriot, Phys. Biol., 2004, 1, T1–T10 CrossRef CAS.
- P. Sens and J. Plastino, J. Phys.: Condens. Matter, 2015, 27, 273103 CrossRef.
- V. te Boekhorst, L. Preziosi and P. Friedl, Annu. Rev. Cell Dev. Biol., 2016, 32, 491–526 CrossRef CAS.
- D. L. Bodor, W. Pönisch, R. G. Endres and E. K. Paluch, Dev. Cell, 2020, 52, 550–562 CrossRef CAS.
- D. Selmeczi, L. Li, L. I. Pedersen, S. F. Nrrelykke, P. H. Hagedorn, S. Mosler, N. B. Larsen, E. C. Cox and H. Flyvbjerg, Eur. Phys. J.-Spec. Top., 2008, 157, 1–15 CrossRef.
- P. Sens, Proc. Natl. Acad. Sci. U. S. A., 2020, 202011785 Search PubMed.
- J. Satulovsky, R. Lui and Y.-l. Wang, Biophys. J., 2008, 94, 3671–3683 CrossRef CAS.
- F. Thüroff, A. Goychuk, M. Reiter and E. Frey, eLife, 2019, 8, e46842 CrossRef.
- J. Löber, F. Ziebert and I. S. Aranson, Soft Matter, 2014, 10, 1365–1373 RSC.
- K. Keren, Z. Pincus, G. M. Allen, E. L. Barnhart, G. Marriott, A. Mogilner and J. A. Theriot, Nature, 2008, 453, 475–480 CrossRef CAS.
- C. Abaurrea-Velasco, T. Auth and G. Gompper, New J. Phys., 2019, 21, 123024 CrossRef.
- A. F. M. Maré, V. A. Grieneisen and L. Edelstein-Keshet, PLoS Comput. Biol., 2012, 8, e1002402 CrossRef.
- P. J. Albert and U. S. Schwarz, Biophys. J., 2014, 106, 2340–2352 CrossRef CAS.
- F. Zhou, S. A. Schaffer, C. Schreiber, F. J. Segerer, A. Goychuk, E. Frey and J. O. Rädler, PLoS One, 2020, 15, e0230679 CrossRef CAS.
- D. Shao, W.-J. Rappel and H. Levine, Phys. Rev. Lett., 2010, 105, 108104 CrossRef.
- F. Ziebert, S. Swaminathan and I. S. Aranson, J. R. Soc., Interface, 2012, 9, 1084–1092 CrossRef.
- J. Löber, F. Ziebert and I. S. Aranson, Sci. Rep., 2015, 5, 9172 CrossRef.
- B. Winkler, I. S. Aranson and F. Ziebert, Commun. Phys., 2019, 2, 82 CrossRef.
- J. G. Carlton, H. Jones and U. S. Eggert, Nat. Rev. Mol. Cell Biol., 2020, 21, 151–166 CrossRef CAS.
- R. A. Green, E. Paluch and K. Oegema, Annu. Rev. Cell Dev. Biol., 2012, 28, 29–58 CrossRef CAS.
- J. Sedzinski, M. Biro, A. Oswald, J.-Y. Tinevez, G. Salbreux and E. Paluch, Nature, 2011, 476, 462–466 CrossRef CAS.
- M. Fürthauer and M. González-Gaitán, Cell Cycle, 2009, 8, 3311–3318 CrossRef.
- A. L. Miller, Curr. Biol., 2011, 21, R976–R978 CrossRef CAS.
- H. Turlier, B. Audoly, J. Prost and J.-F. Joanny, Biophys. J., 2014, 106, 114–123 CrossRef CAS.
- A. Mietke, F. Jülicher and I. F. Sbalzarini, Proc. Natl. Acad. Sci. U. S. A., 2019, 116, 29–34 CrossRef CAS.
- R. A. Barrio, T. Alarcon and A. Hernandez-Machado, PLoS One, 2020, 15, e0227562 CrossRef CAS.
- J. Steinkühler, R. L. Knorr, Z. Zhao, T. Bhatia, S. M. Bartelt, S. Wegner, R. Dimova and R. Lipowsky, Nat. Commun., 2020, 11, 905 CrossRef.
- D. B. Cortes, A. Dawes, J. Liu, M. Nickaeen, W. Strychalski and A. S. Maddox, J. Cell Sci., 2018, 131, jcs203570 CrossRef.
- V. G. Almendro-Vedia, F. Monroy and F. J. Cao, PLoS One, 2013, 8, e69750 CrossRef CAS.
- V. G. Almendro-Vedia, F. Monroy and F. J. Cao, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2015, 91, 012713 CrossRef.
- E. Beltrán-Heredia, V. G. Almendro-Vedia, F. Monroy and F. J. Cao, Front. Physiol., 2017, 8, 312 CrossRef.
- E. Beltrán-Heredia, F. Monroy and F. J. Cao-García, Phys. Rev. E, 2019, 100, 052408 CrossRef.
- H. Koyama, T. Umeda, K. Nakamura, T. Higuchi and A. Kimura, PLoS One, 2012, 7, e31607 CrossRef CAS.
- H. Greenspan, J. Theor. Biol., 1977, 65, 79–99 CrossRef CAS.
- J. White and G. Borisy, J. Theor. Biol., 1983, 101, 289–316 CrossRef CAS.
- R. Shlomovitz and N. S. Gov, Biophys. J., 2008, 94, 1155–1168 CrossRef CAS.
- C. C. Poirier, W. P. Ng, D. N. Robinson and P. A. Iglesias, PLoS Comput. Biol., 2012, 8, e1002467 CrossRef CAS.
- J. F. Dorn, L. Zhang, T.-T. Phi, B. Lacroix, P. S. Maddox, J. Liu and A. S. Maddox, Mol. Biol. Cell, 2016, 27, 1286–1299 CrossRef CAS.
- J. Zhao and Q. Wang, Int. J. Numer. Methods Biomed. Eng., 2016, 32, e02774 CrossRef.
- A. Sain, M. M. Inamdar and F. Jülicher, Phys. Rev. Lett., 2015, 114, 048102 CrossRef.
- Z. Shi, Z. T. Graber, T. Baumgart, H. A. Stone and A. E. Cohen, Cell, 2018, 175, 1769–1779 CrossRef CAS . e13.
| This journal is © The Royal Society of Chemistry 2021 |