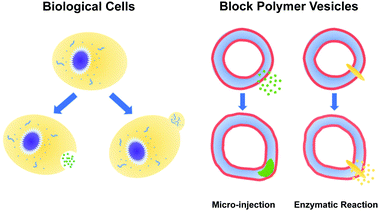
Using reactive dissipative particle dynamics to understand local shape manipulation of polymer vesicles†
Qinyu
Zhu
 ,
Timothy R.
Scott
and
Douglas R.
Tree
,
Timothy R.
Scott
and
Douglas R.
Tree
 *
*
Chemical Engineering Department, Brigham Young University, Provo, Utah, USA. E-mail: tree.doug@byu.edu
First published on 28th October 2020
Abstract
Biological cells have long been of interest to researchers due to their capacity to actively control their shape. Accordingly, there is significant interest in generating simplified synthetic protocells that can alter their shape based on an externally or internally generated stimulus. To date, most progress has been made towards controlling the global shape of a protocell, whereas less is known about generating a local shape change. Here, we seek to better understand the possible mechanisms for producing local morphological changes in a popular protocell system, the block copolymer vesicle. Accordingly, we have combined Dissipative Particle Dynamics (DPD) and the Split Reactive Brownian Dynamics algorithm (SRBD) to produce a simulation tool that is capable of modeling the dynamics of self-assembled polymer structures as they undergo chemical reactions. Using this Reactive DPD or RDPD method, we investigate local morphological change driven by either the microinjection of a stimulus or an enzymatically-produced stimulus. We find that sub-vesicle-scale morphological change can be induced by either a solvent stimulus that swells the vesicle membrane, or by a reactant stimulus that alters the chemistry of the block polymer in the membrane corona. Notably, the latter method results in a more persistent local deformation than the former, which we attribute to the slower diffusion of polymer chains relative to the solvent. We quantify this deformation and show that it can be modulated by altering the interaction parameter of the parts of the polymer chain that are affected by the stimulus.
Introduction
From a soft materials perspective, living cells are a technological wonder. Each cell is an active material with metabolic processes and an internal instruction set that gives it control over its shape and motion.1–3 Collectively, cells communicate and engage in far-from-equilibrium assembly to form remarkable higher-order structures such as tissues, organs, and complete organisms.4 Clearly, there would be numerous scholarly and practical benefits if one could create synthetic analogues to the cell, i.e. a synthetic protocell.Given the extensive overlap between the fields of biology and soft matter,5 researchers in both fields are vigorously pursuing the creation of protocells that perform functions similar to biological cells.6 The polymer vesicle—a solvent-filled spherical bilayer composed of either natural lipids (liposome) or synthetic amphiphilic block polymers (polymersome)—is a popular platform for creating protocells.7,8 However, even with recent attention, the most advanced polymer vesicles still lack basic functions that are essential to biological cells.9
In particular, we focus here on the challenge of actively controlling the shape and morphology of a polymer vesicle. We distinguish between two different scales of control that biological systems exert over shape. First, cells are able to control their global shape, by which we mean differences on the scale of the entire cell (e.g. the difference between rod-like, spherical, or cup-shaped). Even setting aside the drastic differences between the different types of specialized cells (e.g. nerve cells are incredibly complicated compared to the spheres and rods that are the most common cell shapes in animals10), individual cells can actively change their global morphology. For example, the familiar biconcave shape of red blood cells becomes cup-like when traveling in the narrowest blood vessels.5 Because the shape of a cell is a balance between the forces exerted on the cell membrane from both intracellular components and the external environment,1 it can be actively manipulated by osmotic forces that swell or shrink the cell, or by the introduction of membrane disrupting agents that cause the total dissolution of the cell leading to cell death.11 It is interesting to note that the latter mechanisms can be utilized beneficially by the immune system11 or hijacked to cause diseases such as Alzheimer's.12
Second, cells exert control over their local shape, through localized osmotic swelling and processes such as cell division, exocytosis, and endocytosis.13 In contrast with global shape changes, these processes occur on the sub-cellular scale, affecting for example only one side of the cell or cell membrane. For example, fine-tuned local protrusions assist cellular motility when a neutrophil (i.e. white blood cell) navigates through red blood cells to chase a bacterium or travel directly to a wound site.14,15 Such local deformation also happens within the cells, where mitochondria change the structure of their inner cristae membrane in response to metabolic needs, adjusting ATP production through shape control.16
Biological cells rely heavily on signaling and feedback processes to actively control both local and global shape.2,5,14 Concomitantly, researchers have spent considerable effort on achieving stimuli-responsive shape manipulation of vesicles. Most of the reported progress has been on achieving stimuli-responsive manipulation of the global shape. To cite a few examples, Huo et al. utilized liquid crystalline block copolymers to change ellipsoidal assemblies to spheres or faceted spheres, programming them through temperature control.17 Eloi et al. created fully reversible assembly and disassembly of spherical and rod-like micelles with redox reactive polymers.18 Lagzi et al. used a pH oscillator to reversibly alternate between spherical micelles and vesicles assembled from fatty acids.19 Finally, by changing solvent selectivity, concentration, or osmotic pressure, several authors have collapsed vesicles into cup-shaped stomatocytes, which have potential as micro-reactors, and when loaded with platinum can be used in catalytic hydrogen peroxide reactions to create motors.20–23 While each of these cases use a different stimulus to achieve distinct morphological features, the general paradigm of using a stimuli-responsive amphiphilic polymer to induce global shape change is the same.
By contrast, less is known about the local shape control of synthetic vesicles, but several approaches have recently emerged. One paradigm focuses on manipulating pH gradients near a pH-responsive lipid membrane. A straightforward technique for doing so is to “microinject” an acid or base into a localized region near the membrane.24–26 Alternatively, a pH gradient can be created by synthesizing or re-hydrating a vesicle in a basic solution, and then decreasing the environmental pH using an acid, thereby creating local pH gradients at the membrane.27 Bitbol et al. used the former method to locally change the pH near a lipid vesicle, resulting in a reversible local membrane deformation.24–26 Khalifat et al. also performed similar experiments and observed membrane invaginations that resemble those found in the cristae membrane of mitochondria mentioned earlier.28,29 Though Bibtol et al. studied effects on the outer membrane and Khalifat et al. studied the inner, in both cases, the authors attributed the spontaneous change in curvature to a chemical modification and subsequent dynamic redistribution of the lipids in the respective monolayers.
Other paradigms for achieving local morphological control focus on the use of either a hybrid membrane or in situ chemical reactions. Passos Gibson et al. used a hybrid membrane composed of both pH-inert block copolymer amphiphiles and pH-responsive lipids to trigger a variety of local conformational changes including tubular protrusions, membrane fluctuations, and internalized vesicles.30 Using the latter approach, Miele et al. reported that the urease-catalyzed hydrolysis of urea inside the lumen of a vesicle led to spontaneous vesicle fission, again driven by pH gradients.31 Other reaction-driven approaches are also possible, including methods that directly modify the molecular weight of the membrane polymer including polymerization32 and chain scission.33
The paradigms that employ pH gradients and reaction-driven morphological manipulation are especially exciting developments, as they enable autonomous far-from-equilibrium processes that echo Nature's use of reaction-driven signalling pathways. As shown in Fig. 1, in the present manuscript, we seek to give these approaches a more firm theoretical footing by adopting polymer vesicles as protocells that can mimic the cellular local morphological changes in responses to microinjected or enzymatically-produced chemical signals. In particular, we focus on modeling a polymersome composed of a coarse-grained representation of a diblock copolymer vesicle with solvophobic and solvophilic blocks.
Computer simulations have been used extensively in the past two decades to study the behavior of block polymer vesicles with both generic coarse-grained models,34–36 and models whose parameters mimic a specific experimental system.33,37,38 There have been many studies focused on the equilibrium (or metastable) morphology of block polymer micelles and vesicles and connecting molecular properties (e.g. block length, solvent/polymer interaction parameter) to the final self-assembled structure (e.g. micelle core radius).36,39–46
More interesting for our present purposes, several researchers have recently simulated kinetically-driven morphology changes in polymer vesicles.33,47 Wright et al. performed coarse grained DPD simulations investigating enzyme-induced kinetic control over the self-assembly behavior of a polymer-peptide diblock in solution.33 They studied the morphological evolution of spherical micelles following the addition of a protolytic enzyme that cleaves the peptide block, reducing the fraction of the hydrophilic block. In quite a different system, Gumus et al. studied the effects of “fast-quenching” or multi-stage quenching simulations on the morphology of micellar structures of bottlebrush polymers in solution.47 They found a series of non-equilibrium nanostructures that could potentially be realized in experiments by inducing a change in solvent quality in response to an external stimulus. Though different physical systems, both approaches found that kinetics could indeed induce morphological transformation of micellar structures. Additionally, both approaches relied on an instantaneously applied stimulus effected by a change of a simulation parameter (e.g. block length or interaction parameter) at a certain time in the simulation to induce morphological change.
By contrast, in order to study the far-from-equilibrium regulation of local structure inherent to living systems, one must properly account for the kinetics as part of the simulation. Indeed, one of the primary challenges to mimicking the above experimental systems is the need to incorporate chemical kinetics, as there are few established simulation methods that are able to capture both solution-phase amphiphilic polymer self-assembly and the type of stochastic chemical kinetics that are appropriate for these systems. Accordingly, we introduce a method below that combines dissipative particle dynamics (DPD) with a model for stochastic chemical kinetics that mirrors the Split Reactive Brownian Dynamics (SRBD) method by Donev et al.48 We call this combined method reactive DPD (RDPD). Following its description, we use RDPD to explore morphological change driven by (i) microinjection of a stimulus and (ii) a stimulus generated via chemical reactions at membrane embedded-catalysts. We subsequently describe and quantify the resulting morphological change and speculate on the implications for experiments. Notably, we believe this is the first theoretical or simulation approach that explicitly accounts for the effects of chemical kinetics on polymer vesicle assembly and morphology dynamics. Subsequently, this is the first simulation to demonstrate local morphological manipulation via these mechanisms.
Methods: reactive dissipative particle dynamics
Simulating reaction-driven local morphology change in a polymer vesicle is not an easy task. The first key challenge is to properly model block polymer self-assembly and dynamics. Models of block polymer self-assembly are notoriously subtle, and a vast array of approaches for simulating polymer vesicles spanning length and times scale from atoms49–52 to continuous fields53–55 have been used. The timescale of atomistic simulations limit their applicability here, and though there are emerging field-based approaches of interest,55–58 field theory-based simulations are typically challenging due to the need to capture both dynamics and the strong composition fluctuations present in micellar systems.53 A mesoscopic particle model such as DPD is a practical alternative as it splits the difference between molecular dynamics (MD) and field-based methods, allowing for relatively fast relaxation times compared to MD and a facile incorporation of dynamics and fluctuations compared to field-based approaches.41,59The second key challenge is to model chemical kinetics appropriately. Models of chemical kinetics can be categorized as either (i) nonspatial or spatial and (ii) deterministic or stochastic.60–63 Nonspatial models are valid for a chemically homogeneous (i.e. well-mixed) system, and deterministic models are valid when the concentration is large enough for concentration fluctuations to have a negligible effect on the kinetics.64 Neither is the case for reaction-driven morphology change in polymer vesicles, where inhomogeneities are inherent, and the small concentration of reactants and catalysts can lead to important stochastic effects. One pragmatic approach is to use a particle-based chemical reaction model. This approach offers spatially resolved, non-deterministic chemical kinetics based on collision theory,65 and is compatible with a particle-based model of polymer self-assembly such as DPD.
Accordingly, we report here a DPD method for simulating local morphology changes in polymer vesicles that incorporates a collision-based model of chemical kinetics that we term Reactive Dissipative Particle Dynamics or RDPD. A classical DPD algorithm is used to simulate the self-assembly thermodynamics and transport behavior. An efficient, event-driven algorithm called Split Reactive Brownian Dynamics (SRBD) is used to model the stochastic chemical reactions.48 While there are multiple open source software packages for performing classical DPD simulation (e.g. HOOMD-Blue66,67), we are not aware of any that have the capacity to simultaneously perform stochastic reaction kinetics. As such, we describe in detail our approach below, which we have subsequently implemented in a custom developed GPU-accelerated Python code.
Dissipative particle dynamics
Our DPD model is based on the classic work by Groot and Warren,68 which models Nt particles driven by Newton's equations of motion68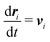 | (1) |
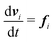 | (2) |
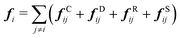 | (3) |
| fCij = aijωC(rij)eij | (4) |
| fDij = −γωD(rij)(eij·vij)eij | (5) |
| fRij = σωR(rij)ζijΔt−0.5eij | (6) |
| fSij = Cspring(|rij|)eij | (7) |
| σ2 = 2γkBT | (8) |
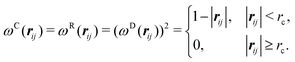 | (9) |
| Parameter | Value | Description |
|---|---|---|
| Δt | 0.05 | Time step |
| σ | 3.0 | Coefficient of random force |
| γ | 4.5 | Coefficient of dissipative force |
| C spring | 100.0 | Spring constant |
| N t | 3 × 106 | Total number of beads |
| x p | 0.08376 | Mole fraction of polymer beads |
| f a | 0.2 | Block fraction of A |
| N b | 60 | Diblock chain length |
| ρ | 3 | Bead number density |
Our block polymer solution consists of Ns solvent beads and Np polymer beads, the latter consisting of Nc chains of an AmBn diblock copolymer with block lengths m and n respectively. In our convention, A represents a solvophilic block and B represents a solvophobic block. The chain length of the diblock is given by Nb = m + n, and the block fraction of the solvophilic block is defined as 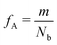 . Additionally, we define the mole fraction of the total number of monomers in polymer chains as xp = Np/Nt and the total solvent mole fraction as xs = Ns/Nt. Typical simulation parameters associated with the solvent and polymer model are again specified in Table 1 unless otherwise noted in the text below.
. Additionally, we define the mole fraction of the total number of monomers in polymer chains as xp = Np/Nt and the total solvent mole fraction as xs = Ns/Nt. Typical simulation parameters associated with the solvent and polymer model are again specified in Table 1 unless otherwise noted in the text below.
In addition to solvent (SA) beads, and beads for the AB diblock (A, B), we introduce three additional bead types. Enzyme (E) beads are separate particles which are completely compatible with A beads and SA beads, but act as reaction catalysts. We introduce a second solvent type (SB) which are equivalent to B beads. We also have a third solvent type (SA′) which act as the external stimulus to change polymer properties. We set the repulsive parameter between beads of the same type to aii = 25. The repulsive parameter between compatible beads is also set to aij = 25, and the parameter between incompatible beads is set to aij = 160, unless otherwise noted. A summary of the matrix of interaction parameters between the different beads is given in Table 2. The cutoff radius is the same for all simulation particles, rc. Following Groot and Warren, we set the number density of beads in the simulation box to ρ = 3. At this number density, an effective Flory–Huggins interaction parameter can be estimated from the DPD interaction parameter,
| χ = (0.286 ± 0.002)(aij − aii) | (10) |
| A | B | SA | SA′ | SB | E | |
|---|---|---|---|---|---|---|
| A | 25 | 160 | 25 | 25 | 160 | 25 |
| B | 160 | 25 | 160 | 160 | 25 | 160 |
| SA | 25 | 160 | 25 | 25 | 160 | 25 |
| SA′ | 25 | 160 | 25 | 25 | — | — |
| SB | 160 | 25 | 160 | — | 25 | 160 |
| E | 25 | 160 | 25 | — | 160 | 25 |
We numerically integrate eqn (1) and (2) using a modified Velocity-Verlet algorithm71
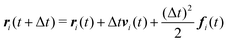 | (11) |
| ṽi(t + Δt) = vi(t) + λΔtfi(t) | (12) |
| fi(t + Δt) = fi(r(t + Δt),ṽ(t + Δt)) | (13) |
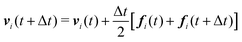 | (14) |
We use a cell list to efficiently calculate the pairwise interactions between particles. We chose a cell list, rather than another technique such as a Verlet list, because it is compatible with the SRBD technique described below. In our approach, we use a traditional algorithm that divides the simulation domain into uniform cells of size rc and stores particle indices in a linked list.71 One must pay particular attention to the algorithm for creating and populating this linked list in order to achieve efficient parallelism and to preserve O(Nt) scaling when running on a GPU. We provide details for this procedure in the ESI.†
Stochastic chemical kinetics
To the classical DPD simulation described above, we add a model of spatially heterogeneous, stochastic reaction kinetics. There are a variety of alogrithms for simulating particle-based stochastic reaction kinetics including Meredys,73 Green's function reaction dynamics,74 hybrid smoothed dissipative particle dynamics (SDPD), the spatial stochastic simulation algorithm (SSA),75 first passage kinetic Monte Carlo (FPKMC),76,77 and split reactive Brownian dynamics (SRBD).48 The SRBD48 algorithm stands out amongst these methods for a number of reasons, including its compatibility with DPD and its ability to simulate reversible reactions.All of the above methods are based on collision theory, which postulates that reactive particles need to approach one another within some distance in order for a reaction to occur.65 Doi added an important model onto collision theory, making a reaction a probabilistic event (a Poisson process) that may or may not occur even when particles are inside the reaction radius.78 Consequently, simulations based on Doi's model makes it easier to achieve detailed balance (reversibility), which is rather important for real systems. Doi's model also provides a means for calculating an expected reaction time for a given reaction rate parameter.
It is easy to imagine a naive algorithm for simulating chemical kinetics based on collision theory and Doi's model. Namely, one searches the simulation box for pairs of beads within some reaction radius, and a decision is made whether or not to execute a reaction event based on the reaction rate parameter and a draw of a random time increment. (This time increment needs to be less than the diffusion time step Δt, or the reaction will not happen.) While certainly correct, this method is computationally expensive, because one needs to repeatedly search for reactive pairs throughout the entire simulation box following each reaction.
The SRBD algorithm48 solves this problem by dividing the system into reactive subvolumes where each reaction is processed based on the Doi model.78 This approach makes SRBD similar to solving a local reaction–diffusion master equation in each subvolume.63,79 Notably, such a cell-based method is also compatible with efficient implementations of DPD. On top of the spatial discretization, SRBD implements an event-driven method for processing the reactions in each cell, increasing the efficiency of the algorithm. In our implementation of the method, we have replaced the uncorrelated Brownian particles discussed in ref. 48 with DPD particles, making it more suitable for simulating a liquid system.
To illustrate the method more specifically, we consider here the SRBD method with the binary reaction,
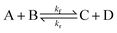 | (15) |
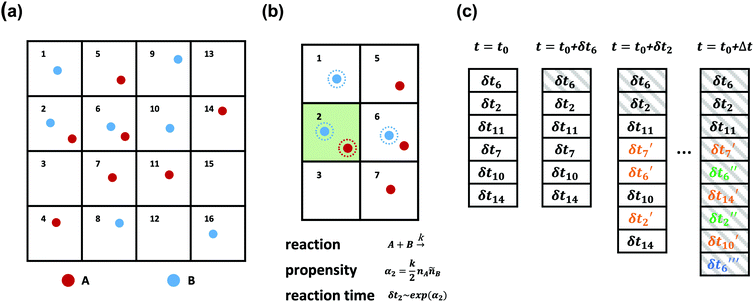
SRBD is implemented as shown in the schematic in Fig. 2. First, the simulation box is divided into reactive cells of size rc (see Fig. 2a), and a reaction time is calculated for each cell based on its current condition. This reaction time is the scheduled time for the next reaction that will happen in the cell, and is calculated using a propensity function based on the local concentration of reactants in the cell (see Fig. 2b). The propensity function for the forward reaction in eqn (15) in cell i is given by,
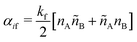 | (16) |
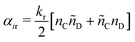 | (17) |
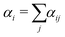 | (18) |
As is characteristic of a Poisson process, the reaction time δti for cell i is obtained by a draw from an exponential distribution with a rate parameter αi.80 Once the δti are calculated for each cell, they are arranged into an event queue in ascending order, as illustrated in Fig. 2c. The cell with the smallest δti (i.e. the top of the event queue) is chosen first, and either the forward or reverse reaction is chosen according to the SSA algorithm.64,80,81 In the latter algorithm, a uniformly distributed random number between 0 and 1, ξ, is generated and the forward reaction is selected if ξ < αif/αi. Otherwise, the reverse reaction is selected.
Once a reaction is chosen, beads of the appropriate reactive species are randomly chosen inside cell i. If the interbead distance rij between the reactive species is less than the reaction radius rc, the particles undergo the selected reaction and their identities are converted to those of the products. If the chosen particles are too far apart, then no reaction takes place. Regardless of whether the reaction occurs or not, the global time t is advanced to t + δti, where δti is the reaction time of the first cell in the event queue. We then proceed to deal with the next shortest reaction time, as suggested at in Fig. 2c. The reactions are processed by iterating this procedure until the global time reaches t + Δt (the length of one time step in the velocity Verlet algorithm) or until the event queue is empty.
The simple “one event per cell” procedure is complicated by the fact that a reaction changes the state of a cell and its neighbors, meaning the next event that will take place in the reacting cell and its neighbors has changed. Thus, when a reaction takes place, a new reaction time δti′ is calculated for both the reacting cell and its neighboring cells by again evaluating the propensity function using eqn (16)–(18) and generating a random number from an exponential distribution rate αi. Note that the new reaction times δti′ may update the reaction time for a cell that has not yet processed an event, or it may re-insert a cell into the queue that has previously experienced an event (whether or not the event resulted in a successful reaction). The event queue is then re-sorted with the new reaction times, as visualized in Fig. 2c.
We implemented the above version of SRBD in our custom GPU-accelerated DPD code described above. In the original algorithm, Donev et al. used a second-order Strang splitting method to integrate their Brownian dynamics code.48 That is, they executed a diffusive half-step, then processed the reactions over a full time step Δt, and then completed another half-step. For our DPD algorithm, we found that we required a time step size at least one order of magnitude smaller than Donev et al., making the second-order scheme unnecessary for accuracy. Accordingly, in our approach, we first diffuse for a full time step Δt, and then react over Δt. This process results in fewer evaluations of the interbead forces, increasing our efficiency relative to the second order method.
Additionally, analogous to our cell list for evaluating pairwise interactions between DPD particles, we parallelized the reactive cell calculations of δti on the GPU. This does not represent a full parallelization of SRBD, because the event queue is still processed sequentially. As noted by Donev et al., parallelizing the event queue remains an open methodological challenge.48
Results and discussion: validation of RDPD
Vesicle self-assembly via DPD
While numerous DPD simulations of polymer vesicles have been achieved,34,37,82 and much has been said about the equilibrium morphology of micellar polymer solutions,35,83 the literature does not provide simple, universal relationships between model parameters and vesicle morphology. Indeed such an endeavor is complicated by the formation of neighboring metastable morphologies and defective states that have similar free energies. As such, achieving a polymer vesicle of a desired size at a given chain length and block fraction remains somewhat of an art form.Additionally, in the present work, we require a polymer vesicle that is large enough to sustain meaningful gradients in the simulation box for times that are long enough to drive local morphological change. As we show below, such a simulation requires a large simulation box, requiring an efficient, parallelized DPD simulation. Here we show some basic results demonstrating the formation of a large polymer vesicle in our DPD model. These results provide the primary validation that our model is (i) fast enough to reach these large scales and (ii) capable of capturing the relevant polymer phase behavior.
To demonstrate that our code is capable of running large scale jobs, Fig. 3 compares the simulation time of our code with that of a popular MD package, HOOMD-Blue.66 These simulations were performed in a diblock copolymer solution with xp = 0.2 and xs = 0.8, as the box size is increased from L = Lx = Ly = Lz = 30rc to L = 80rc with the other DPD parameters given in Table 1. The computational time scales linearly with Nt, demonstrating that the cell list appropriately accounts for pairwise interactions.
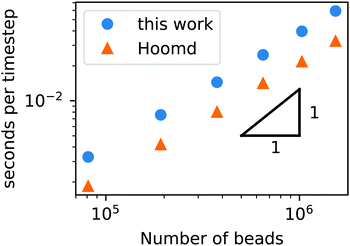 | ||
| Fig. 3 Simulation time of a GPU-accelerated DPD model (without chemical reactions) as a function of the number of beads for the RDPD code and HOOMD-Blue. | ||
Our DPD code is between 1.58 and 1.75 times slower than the HOOMD-Blue code under the same conditions. This is not an insignificant slowdown, but the result is in fact remarkable given our code platform and development path. HOOMD-Blue is a highly optimized CUDA/C++ code developed and maintained over several years with many users. Our code is developed in native Python and is optimized with the Numba just-in-time (JIT) compiler with the accompanying CUDA Toolkit that enables GPU-accelerated calculations.84 Numba is an open source compiler for Python numerical calculations that generates optimized machine code from pure Python, and its CUDA Toolkit provides the ability to develop GPU-accelerated code with speeds that are competitive with C++. With these tools, our code development process took a single graduate student less than three months.
We now turn our attention to equilibrating a large polymer vesicle. Since our simulations are carried out in a large simulation box, it is computationally costly to relax and equilibrate a vesicle from random initial conditions. Additionally, because of nearby metastable states the final morphology of a given simulation is sensitive to the initial condition and is therefore kinetically determined, making it even harder to obtain our desired vesicle structure. Accordingly, we used an external field to guide the formation of vesicle structure.85 The guiding field is in the shape of the vesicle morphology and consists of ghost particles at fixed positions that only interact with the solvophilic blocks through a Gaussian potential,
| UGuass = −ae−b|rij|2 | (19) |
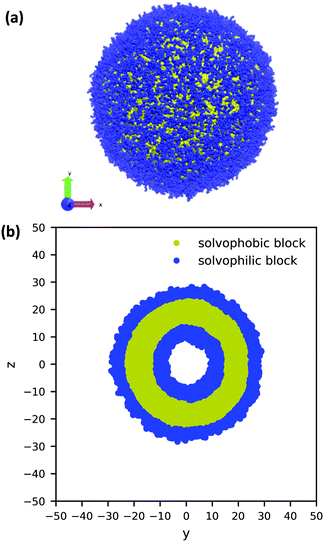
Using the guiding field, we equilibrated the vesicle in Fig. 4 using the following procedure. We first performed a DPD simulation in a L = 60rc box with the guiding field to get a roughly spherical vesicle morphology. We then expanded the box size to L = 100rc using the previous morphology as an initial condition (filling the rest of the space with solvent particles), and ran another DPD simulation without the guiding field for 106 steps to ensure that the system reached equilibrium. As the system equilibrated, some polymer chains were ejected from the vesicle. At the conclusion of the simulation, these chains were converted to solvent particles, and the final system was again relaxed for another 106 steps. These stray chains were converted into solvent to ensure that no extra chains in the solution could interfere with the vesicle and to keep the system density fixed at ρ = 3. Further details of the relaxation time of our system are provided in the ESI.† The final polymer vesicle was obtained using Nc = 60, fA = 0.2 and xp = 0.08376. The average size of the vesicle is 56.8 rc in diameter, and the lumen is approximately 17.2 rc in diameter.
Stochastic reaction diffusion model
As discussed above, the SRBD algorithm enables the simulation of chemical reaction kinetics in DPD. To validate the reaction kinetics, we performed simulations of the binary chemical reaction of the conversion of solvent A into solvent B mediated by catalyst particles E,| SA + E ⇌ SB + E. | (20) |
The results from the irreversible reaction are shown in Fig. 5a. To interpret the RDPD results, it is instructive to compare to a model of a non-stochastic first order rate equation,
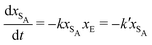 | (21) |
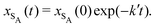 | (22) |
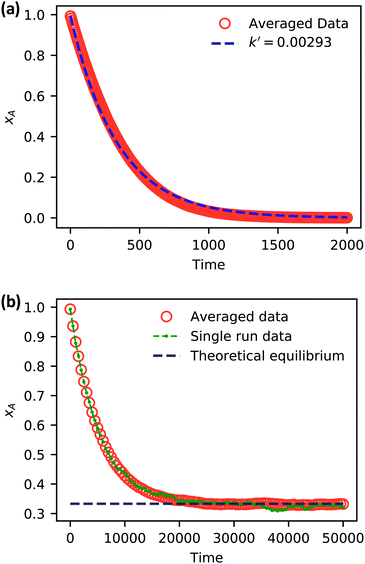 | ||
| Fig. 5 Simulation data of xA as a function of time for (a) an irreversible catalytic conversion, and (b) a reversible catalytic conversion. The average of 20 replicates are plotted for both simulations. Additionally, the blue dashed line in panel (a) shows eqn (22) using the predicted value k′ = 0.00293, and the gray dashed line in panel (b) shows the theoretical equilibrium mole fraction of 0.333. The green points in panel (b) show a single simulation, illustrating the stochastic nature of the reaction. | ||
As expected, 〈xSA〉 obtained from the RDPD simulation decays exponentially in time starting from the initial mole fraction of xSA(0) = 0.993 as predicted by eqn (22). However, a non-linear fit to the rate of decay gives a value of k′ = 0.0029, which does not match the microscopic reaction rate of kfxE = 7 × 10−4. This apparent contradiction is resolved by more carefully mapping the microscopic reaction rate onto the effective macroscopic rate k′. In the SRBD algorithm, the macroscopic reaction rate is determined by the propensity function, i.e.eqn (16) and (17). The propensity function depends on the number of particles within the reactive distance, rc, and therefore the effective macroscopic reaction rate is given by,
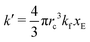 | (23) |
Turning our attention to the case of the reversible reaction, Fig. 5b shows the mole fraction of SA as a function of time obtained from RDPD, again averaged over 20 replicates. At long times we expect this system to reach an equilibrium value of xSA = 0.333. We observe that the value of 〈xSA〉 fluctuates around an equilibrium mole fraction of 0.33 after t = 1500. This is of course in excellent agreement with the prediction, suggesting that we are reaching the equilibrium value determined by the forward and reverse rate constants as expected.
It is also informative to compare the performance of the various algorithms discussed in the previous section for simulating chemical kinetics. Fig. 6 shows the run-time of classical DPD (our code), the “naive” algorithm, and the SRBD algorithm in both serial and parallel (i.e. GPU) schemes. These simulations were performed using the same parameters as those above, namely for monomers in a box of size L = 15rc, though here each simulation is only run for 2 × 104 time step. The particles were randomly placed in the simulation box, and were subjected to the catalytic conversion reaction in eqn (20).
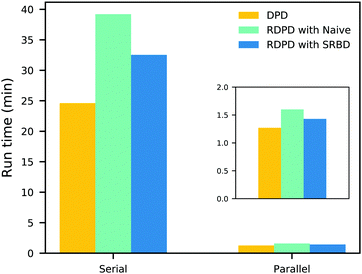 | ||
| Fig. 6 Comparison of the run time of three algorithms in both serial and parallel: bare DPD, RDPD using the “naive” algorithm, and RDPD using SRBD. The inset shows the parallel results on a re-scaled axis. Numerical values of these run times are provided in the ESI.† | ||
We draw several conclusions from the results in Fig. 6. First, as expected, the parallel versions are considerably faster than the serial versions, even when executing chemical reactions. In fact, the SRBD algorithm is over 22× faster when using the GPU. Second, including chemical reaction kinetics slows down the simulation, which is also expected. When executing the serial version code, the SRBD code runs 32.2% slower than the basic DPD code, and in parallel the SRBD code is only 12.6% slower. Finally, we see that SRBD brings modest performance gains over the naive algorithm. SRBD is 20% faster than the naive algorithm in serial and 12% faster in parallel. Again we note that we did not parallelize the SRBD event queue, but this could bring additional performance gains.
In addition to characterizing the rate of chemical reactions, it is useful to know the species diffusivity in chemically reacting systems. Accordingly, we performed a calculation of the tracer diffusion by calculating the mean squared displacement (MSD) of DPD solvent beads as a function of time and fitting the data points to
| MSD = 6DSAt | (24) |
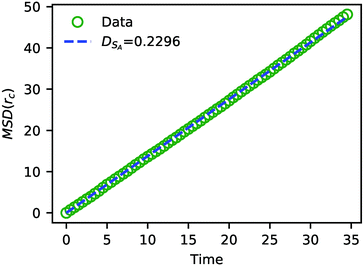 | ||
| Fig. 7 The MSD of solvent beads as a function of time. The green circles are the MSD obtained from the simulation, and the blue dashed line is a fit to eqn (24) with DSA = 0.2296. | ||
The value of DSA obtained above is a simple calculation of the bare tracer diffusion and does not include interactions between solvents that must be accounted for in the mutual diffusivity when considering a mixture that contains beads with disparate values of aij. Additionally, in their paper on SRBD,48 Donev et al. reported a curious enhancement of diffusion during reversible reactions where the number of particles are not conserved, such as
| A + B ⇌ C. | (25) |
In addition to the solvent diffusivity, we also calculated the diffusivity of polymer chains inside the vesicle membrane to be Dpolymer = 0.0073. As expected, chains move significantly slower than solvent, especially when co-located in the vesicle membrane. Additional details related to these latter results are given in the ESI.†
Results and discussion: stimulus-responsive local morphology
We highlighted above two generic experimental paradigms for manipulating the local shape of vesicles: microinjection of a solvent and local chemical reactions. These paradigms are not mutually exclusive, since a local chemical reaction can proceed from either a microinjected reactant or from a localized catalyst, such as an embedded enzyme.In this section, we explore two mechanisms using both microinjection and local chemical reactions that can induce morphological change in a vesicle. The first mechanism is local morphology change due to solvent swelling. Here a solvent can either be microinjected or can be produced by a local chemical reaction. If this solvent interacts favorably or unfavorably with the monomers that compose the polymer vesicle, this can result in swelling or deswelling respectively. The second mechanism of morphology change comes from alteration of the chemistry of the polymer blocks inside the vesicle, leading to a local change in the “shape parameter” of these blocks.86 Here a reactant that is microinjected near the vesicle or produced locally via enzymatic reaction can react with a polymer block, resulting in a new local block chemistry or molecular weight that can subsequently alter the local morphology. We explore both of these mechanisms here, starting with solvent swelling and then discussing changes to the polymer shape parameter.
For both mechanisms, we explore a case with an instantaneous change in either solvent or polymer properties and a case with finite reaction kinetics. The simulations of the latter case are performed with a significantly shorter timescale than those of the former. We keep these simulations short because the fast reaction kinetics lead to a rapid conversion of solvent or polymer respectively that can obscure the localized deformation at longer times as the reaction proceeds.
Local morphology change by solvent swelling
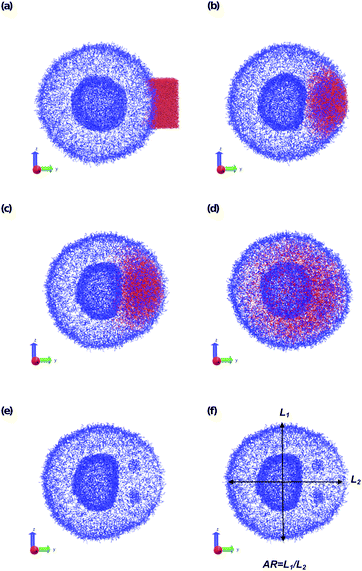
To understand how local solvent gradients can alter the morphology of a polymer vesicle, we performed two different sets of in silico experiments, one mimicking solvent microinjection and the other simulating solvent production by a membrane-embedded enzyme. Both sets of calculations were preceded by the creation and equilibration of a large AB polymer vesicle with Nb = 60, fA = 0.2 in the solvent SA as described above.We first mimicked solvent microinjection by “instantaneously injecting” a droplet of B-selective solvent SB near the vesicle membrane at the beginning of the simulation. Recall that B is the majority block that comprises the bilayer of the vesicle membrane. As shown in Fig. 8a and b, microinjection was achieved by converting a portion of SA to a droplet of SB near the surface of the vesicle. We varied the size of this droplet, ranging from 1.65% of the vesicle volume (2058 beads) to 8.07% (15![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 584 Beads) of the vesicle volume and examined the swelling behavior as a function of time up to t = 2.5 × 104.
584 Beads) of the vesicle volume and examined the swelling behavior as a function of time up to t = 2.5 × 104.
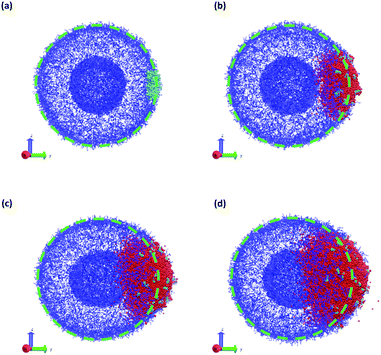
The vesicle dynamics following microinjection followed a similar pattern for all of the simulated cases, and therefore in Fig. 8 we highlight a single example. Fig. 8a shows the initial state of the simulation immediately following the microinjection event, where a droplet of SB that is 8.07% (15![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 584 beads) of the vesicle volume is injected. Following their introduction, the beads of SB are all systematically drawn into the vesicle, with no SB escaping into the bulk solvent, as shown in Fig. 8b. These beads segregate into the vesicle membrane where they associate with the polymer B-blocks. As shown in Fig. 8c, this leads to a noticeable flattening of the internal compartment of the vesicle co-localized with a swelling of the outer vesicle wall. At long times, the SB beads diffuse more evenly throughout the vesicle membrane, and as shown in Fig. 8d, the vesicle returns to its spherical shape with slightly increased size due to the solvent swelling.
584 beads) of the vesicle volume is injected. Following their introduction, the beads of SB are all systematically drawn into the vesicle, with no SB escaping into the bulk solvent, as shown in Fig. 8b. These beads segregate into the vesicle membrane where they associate with the polymer B-blocks. As shown in Fig. 8c, this leads to a noticeable flattening of the internal compartment of the vesicle co-localized with a swelling of the outer vesicle wall. At long times, the SB beads diffuse more evenly throughout the vesicle membrane, and as shown in Fig. 8d, the vesicle returns to its spherical shape with slightly increased size due to the solvent swelling.
The different droplet sizes all follow the pattern in Fig. 8, but there is some noticeable variation. At large enough droplet sizes (3.3% of the vesicle volume and greater) small portions of the outer vesicle wall are carried with the droplet into the vesicle and form micelles within the vesicle membrane as can be seen in Fig. 8e. For intermediate droplet sizes (3.3% to 4.73% of the vesicle volume), these micelles are transient and merge with the internal wall of the vesicle at long times. However, for the largest droplet sizes (6.46% and 8.07% of the vesicle volume), these micelles appear to be metastable, and persist through the end of our longest simulations (t = 2.5 × 104).
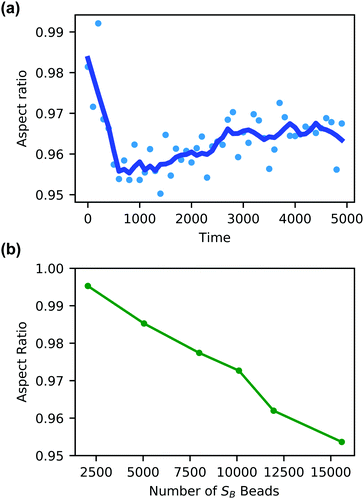
Additionally, the degree of local swelling and its effect on the shape of the vesicle also varies with the size of the microinjected droplet. To characterize this swelling, we calculate the aspect ratio of the outer vesicle wall as a function of time for each size of SB droplet. Fig. 9a shows this calculation for the SB droplet that is 8.08% the size of the vesicle, where the blue points represent the calculated aspect ratio at each time point, and the curve applies the Savitzky–Golay filter to smooth the data points and better demonstrate the tendency.87 As expected from Fig. 8, the aspect ratio initially decreases in time as the vesicle anisotropically swells. After a short period, the aspect ratio then increases, as the microinjected solvent diffuses throughout the vesicle membrane.
There is a curve analogous to Fig. 9a for each droplet size, and the minimum of this curve represents the maximum degree of local swelling. The aspect ratio at t = 800, at which the vesicles display the maximum degree of local swelling, is shown in Fig. 9b as a function of droplet size. The larger injected droplets produce smaller aspect ratios, indicating more dramatic changes to the vesicle. This is supported by our qualitative observation that the outer wall increasingly swells and the inner wall increasingly flattens as the droplet size increases.
In our second set of in silico experiments, we observed local solvent swelling driven by membrane-embedded “enzyme” particles E that catalyze the conversion of SA into SB according to
| SA + E ⇌ SB + E. | (26) |
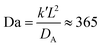 | (27) |
Fig. 10 gives a time-series of the local morphology change as SB is produced. Similar to the microinjection case, the vesicle quickly absorbs nearly all of the SB, and the vesicle begins to swell locally. Due to the rapid production of SB, the accumulation and swelling happens quickly within the vesicle membrane that contains the B-blocks and is already apparent at t = 75 in Fig. 10b. Furthermore, due to the rapid production of SB, the degree of deformation increases with time as more particles of SB are produced before they could diffuse out, as shown in Fig. 10c and d. This can be seen from the dashed circle which outlines the spherical shape of the initial vesicle in each panel. Finally, note that particles of SB largely remain near the B-blocks in the vesicle membrane, despite the deceptive appearance of Fig. 10d. The figure shows the 2D projections of a 3D object, and the solvent particles are also diffusing into the foreground obscuring one's view of the vesicle interior.
It is interesting to consider the similarities and differences between the microinjection and embedded-enzyme cases. In both cases, the SB particles prefer to aggregate in the vesicle membrane, and there is a sequence where SB is first absorbed into the vesicle before distributing throughout. However, in the enzymatically-driven case, the SB particles remain “bunched up” throughout the entire simulation because the reaction rate is producing them faster than diffusion can disperse them. Additionally, there are also more SB particles generated in the enzymatically-driven case than the pre-allocated droplets in the microinjection case. These two effects combine to give a larger degree of swelling for the enzyme-driven case relative to microinjection. However, we expect that if we stop the reaction at a given time and let the SB particles diffuse, they would distribute uniformly in within the vesicle membrane and would produce global swelling at long times similar to the microinjection case.
Local morphology change by altering polymer packing parameter
In addition to modifying the local vesicle morphology by solvent swelling, another mode for inducing changes to the vesicle structure is to directly alter the block polymer that makes up the vesicle. This modality has precedence for example in experiments that use pH-responsive polymers in polymersomes.88,89 A simplistic way to conceptualize the local morphology change is via modification of the so-called packing parameter of the polymer, which has been widely used in explaining the self-assembly behavior of amphiphilic molecules.90 The packing parameter of an amphiphile is given by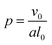 | (28) |
For block polymers, it has been argued that p is a function of the block fraction fA, i.e. the ratio of the size of the hydrophilic block to the hydrophobic block.91 For a fixed molecular weight, the a parameter increases with fA, meaning that small fA corresponds to lower curvature structures such as vesicles, while a larger fA corresponds to higher curvature structures such as micelles. Accordingly, we hypothesize that it is possible to alter the curvature in a localized region of a vesicle by modifying the block fraction of a polymer in that region.
To test this hypothesis, we performed two different types of simulations. First, starting from an equilibrated vesicle obtained using the procedure described previously (Nb = 60, fA = 0.2 and xp = 0.08376), we instantaneously changed the block fraction of a series of vesicles. Though unphysical, this instantaneous change allows us to study the infinitely fast kinetic limit without the complication of finite reaction kinetics. Second, we simulate a more realistic scenario where we “microinject” a chemical stimulant SA′ that converts beads in the solvophobic B-block in the polymer chain into beads of A according to
| SA′ + B ⇌ SA + A | (29) |
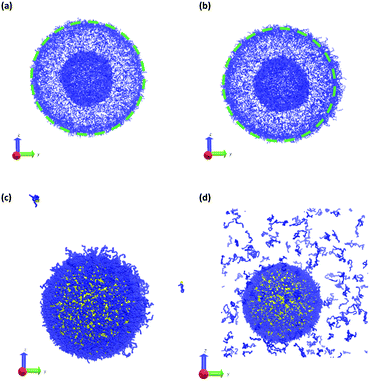
Fig. 11 summarizes the results of the first class of simulations, where we instantaneously vary fA of several chains on one side of the outer corona of the polymer vesicle. In these calculations we chose 174 co-localized chains, which is about 4% of the total number of chains in the vesicle structure, and varied fA from 0.1 to 1.0 while retaining the chain position and orientation. In other words, the bead positions remain the same and the A block is still located in the outer corona. Recall that the original block fraction of the vesicle was fA = 0.2. All simulations were performed for 5 × 105 steps in order to fully observe any changes in morphology.
We observed four qualitatively different behaviors as a function of fA. For 0.1 < fA < 0.3, there is little or no change in the morphology, and as shown in Fig. 11a the vesicle retains its spherical shape. For 0.4 < fA < 0.7, the vesicle remains largely spherical, but as seen in Fig. 11b there is an increase in curvature of the outer corona in the region where the chain block fraction was altered. For 0.7 < fA < 1.0, local swelling does not occur, and the chains are only weakly attached to the vesicle. Indeed, as is apparent in Fig. 11c, some chains do not remain bound to the vesicle, but escape into the bulk solvent. Finally, for fA = 1.0 (i.e. a homopolymer of A) there is no longer a thermodynamic force holding these fully solvophilic chains inside the vesicle, and as shown in Fig. 11d they eventually completely escape the structure. Note however that this does not destabilize the rest of the vesicle, and the unconverted chains remain.
Notably, the change to the polymer chemistry results in a longer-lived local deformation than the solvent swelling case. Local deformations persist in Fig. 11d until at least t = 2.5 × 104, which is our longest run time for these simulations. By contrast, the local deformation in the solvent swelling case in Fig. 8d has completely disappeared by t = 7.5 × 103. We attribute this difference in time to the relative rates of diffusion between solvent inside the vesicle membrane and the polymer chains that compose the vesicle.
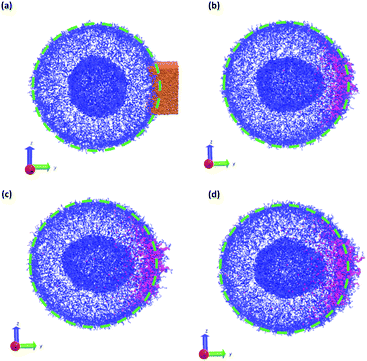
In a more realistic scenario, Fig. 12 shows the results of the microinjection of a solvent stimulus followed by the chemical conversion of monomers on the B-block of the polymers inside the vesicle according to eqn (29). We performed this calculation by instantaneously converting a droplet containing 11343 SA beads (equivalent to about 5.54% of the volume of the vesicle) into beads of SA′ near one side of the vesicle surface at t = 0. We then ran the simulation with the reaction given in eqn (29) where kf = 5 and kr = 0.2 giving a diffusion limited process with Da≈3450 similar to the reactions performed previously. An additional plot characterizing the number of monomers that are converted as a function of time is given in Fig. S5 in the ESI.†
Fig. 12 gives snapshots of a typical simulation as a function of time. Following the initial state in Fig. 12a, Fig. 12b–d show a locally swollen vesicle where the local curvature increases as a function of time. Notably, the change in polymer chemistry results in an increased positive curvature for both the outer vesicle wall and the boundary separating the lumen and the membrane. This is in contrast with the solvent swelling seen for example in Fig. 8, where the boundary between the lumen and membrane was flattened as it was pushed by excess solvent.
We claimed above that it was possible to alter the local curvature of a vesicle and create a more persistent local deformation by altering the polymer chemistry. To justify this claim more quantitatively, we calculate the curvature of a 2D projection of the vesicle before and after reaction to demonstrate the localized shape change. We do so by calculating a local concentration of monomers of B as a function of space, xB(r), using a grid. After smoothing this concentration function, we define the vesicle wall as the contour xB(r) = C and project it onto the y–z plane to define a two-dimensional space curve γ(s). Parameterizing this curve as γ(s) = (y(s),z(s)) permits us to define a curvature92
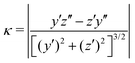 | (30) |
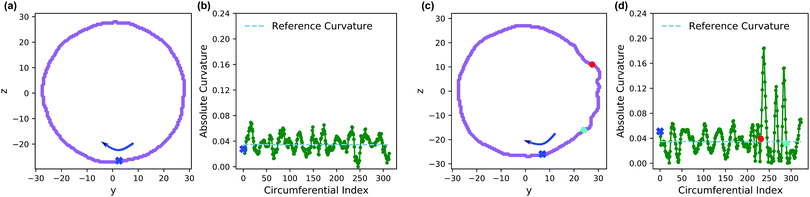
Fig. 13 shows an analysis of the curvature of the initial and final vesicles from Fig. 12. Fig. 13a and b shows a projection of the initial vesicle shape and the absolute curvature as a function of an index that traces the circumference of the shape. Clearly, the projection is circular, and the curvature fluctuates about 0.035, the curvature for a circle with average diameter 56.8rc. There are significant fluctuations about κ = 0.035 despite our smoothing techniques because of (i) thermal fluctuations that make the vesicle an imperfect sphere, (ii) discrete DPD beads and a grid mapping that yields noisy concentration fields, and (iii) an amplification of noise due to the numerical calculation of first and second derivatives in eqn (30).
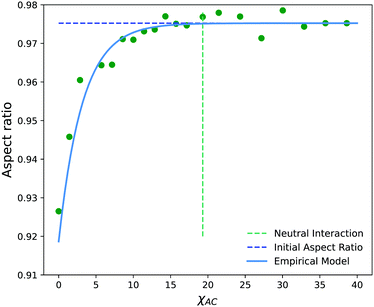
Fig. 13c shows the projection of the vesicle at t = 500 after the reaction has occurred and clearly shows a local deformation of the vesicle structure in the positive y-direction. Concomitantly, the curvature in Fig. 13d shows a sharp increase at these circumferential indices, but is otherwise similar to the original vesicle in other locations. Interestingly, the curvature does not increase smoothly, but shows significant fluctuations in the region where the reaction occured. This heterogeneity may be simply a consequence of noise or of the scale of the curvature calculation. Alternatively, because the reaction forms random copolymers, these fluctuations may be inherent to the reaction-driven change and may have important physical effects. We leave the latter hypothesis to future investigation.
To better understand how to modulate the extent of deformation, we also performed a series of simulations with a generalization of eqn (29),
| SA′ + B ⇌ SA + C | (31) |
Fig. 14 shows the average aspect ratio of 10 replicate runs at t = 500 after the initiation of the reaction versus the Flory–Huggins parameter χAC. The aspect ratios are calculated by sweeping orthogonal directions with an increment of π/10 and locating the direction with the smallest aspect ratio. The values of χAC were obtained from the aij parameters using eqn (10).
As expected, the aspect ratio is the smallest, i.e. the vesicles are the most deformed, when χAC approaches 0. As χAC increases, the aspect ratio also increases and then levels off at the aspect ratio of the original vesicle, AR0 = 0.975. Interestingly, the aspect ratio first reaches AR0 near the point of neutral interaction where χAC = χBC = 19.3. It seems plausible that this value of the interaction parameter marks the point where a newly created monomer of C no longer creates a significant driving force for expulsion from the solvophobic vesicle membrane to create extra curvature. Additionally, we fit the aspect ratio data in Fig. 14 to a three-parameter empirical model,
| AR = AR0 − aeb(χAC+c) | (32) |
Conclusion
We have developed and validated a GPU-accelerated RDPD code that combines a DPD model and an SRBD reaction kinetics model to simulate the dynamics of self-assembled polymer solutions due to chemical reactions. Notably, our use of just-in-time compiled Python tools has allowed us to create this tool in a relatively short time with speeds that approach those of the much more sophisticated HOOMD-Blue.66After validating the code, we performed a series of RDPD simulations to study the manipulation of local shape change of polymer vesicles. We first investigate the local morphology change due to solvent swelling. We performed two different sets of in silico experiments, one mimicking solvent microinjection and the other simulating solvent production by a membrane-embedded enzyme. Our results suggest that the generated solvophobic SB particles tend to aggregate within the B blocks, causing a local swelling at the injection site or reactive site, and that the extent of deformation increases with the number of injected or converted SB particles. However, introducing SB particles does not result in a persistent local deformation, since the SB particles rapidly disperse throughout the solvophobic membrane layer, resulting in a globally swollen morphology.
We also demonstrated local morphology change in the vesicle structure by altering the solvophobicity of the block polymer either instantaneously or with the introduction of external stimuli. Similar to the solvent swelling case, the polymer vesicle also displays an obvious localized swelling due to the decrease of solvophobicity of the B blocks. Here the local deformation has a longer time-scale that we attribute to the relatively long diffusion time for a polymer chain in the outer vesicle corona. We also showed that this deformation is tunable, based on the interaction parameter of the newly created monomer. These latter results imply that changing the polymer solvophobicity is a more practical approach for creating a persistent local deformation.
Even with the current progress, much remains to be studied in the present system. Experiments show more extensive local deformations such as large protrusions and vesicle fission, and the related parameter space for simulations has yet to be explored. For example, diblock copolymers of different molecular weight and block fraction may exhibit different membrane elasticities or diffusivities that could be highly relevant for such processes. Additionally, the results presented here are qualitative, and could benefit enormously from a more rigorous attempt to connect to experimental values. Finally, more complex systems such as vesicles that interact and communicate via chemical signals present many additional opportunities.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
We gratefully acknowledge financial support from Brigham Young University and the Simmons Research Endowment at Brigham Young University. We also acknowledge computational resources from the BYU Office of Research Computing.References
- E. Paluch and C. P. Heisenberg, Curr. Biol., 2009, 19, R790–R799 CrossRef CAS.
- S. M. Saporito-Irwin, C. E. Birse, P. S. Sypherd and W. A. Fonzi, Mol. Cell. Biol., 1995, 15, 601–613 CrossRef CAS.
- S. J. Vainio, P. V. Itaranta, J. P. Perasaari and M. S. Uusitalo, Int. J. Dev. Biol., 2003, 43, 419–423 Search PubMed.
- H. Weinans and P. J. Prendergast, Bone, 1996, 19, 143–149 CrossRef CAS.
- I. Hamley and V. Castelletto, Angew. Chem., Int. Ed., 2007, 46, 4442–4455 CrossRef CAS.
- R. V. Solé, A. Munteanu, C. Rodriguez-Caso and J. Macía, Philos. Trans. R. Soc., B, 2007, 362, 1727–1739 CrossRef.
- E. Rideau, R. Dimova, P. Schwille, F. R. Wurm and K. Landfester, Chem. Soc. Rev., 2018, 47, 8572–8610 RSC.
- N. P. Kamat, J. S. Katz and D. A. Hammer, J. Phys. Chem. Lett., 2011, 2, 1612–1623 CrossRef CAS.
- B.-Y. Xu, J. Xu and T. Yomo, Biochem. Soc. Trans., 2019, 47, 1909–1919 CrossRef CAS.
- P. C. Letourneau, Nerve cell shape, Academic Press, Inc, New York, 1989 Search PubMed.
- D. R. Green and F. Llambi, Cold Spring Harbor Perspect. Biol., 2015, 7, a006080 CrossRef.
- M. F. M. Sciacca, S. A. Kotler, J. R. Brender, J. Chen, D.-k. Lee and A. Ramamoorthy, Biophys. J., 2012, 103, 702–710 CrossRef CAS.
- Q. F. Ahkong and J. A. Lucy, J. Cell Sci., 1988, 91, 597–601 Search PubMed.
- A. F. M. Marée, V. A. Grieneisen and L. Edelstein-Keshet, PLoS Comput. Biol., 2012, 8, e1002402 CrossRef.
- S. K. Yoo, Q. Deng, P. J. Cavnar, Y. I. Wu, K. M. Hahn and A. Huttenlocher, Dev. Cell, 2010, 18, 226–236 CrossRef CAS.
- H. M. Heath-Engel and G. C. Shore, Biochim. Biophys. Acta, Mol. Cell Res., 2006, 1763, 549–560 CrossRef CAS.
- M. Huo, G. Song, J. Zhang, Y. Wei and J. Yuan, ACS Macro Lett., 2018, 7, 956–961 CrossRef CAS.
- J. C. Eloi, D. A. Rider, G. Cambridge, G. R. Whittell, M. A. Winnik and I. Manners, J. Am. Chem. Soc., 2011, 133, 8903–8913 CrossRef CAS.
- I. Lagzi, D. Wang, B. Kowalczyk and B. A. Grzybowski, Langmuir, 2010, 26, 13770–13772 CrossRef CAS.
- I. A. B. Pijpers, L. K. E. A. Abdelmohsen, D. S. Williams and J. C. M. van Hest, ACS Macro Lett., 2017, 6, 1217–1222 CrossRef CAS.
- K. T. Kim, J. Zhu, S. A. Meeuwissen, J. J. L. M. Cornelissen, D. J. Pochan, R. J. M. Nolte and J. C. M. van Hest, J. Am. Chem. Soc., 2010, 132, 12522–12524 CrossRef CAS.
- S. A. Meeuwissen, K. T. Kim, Y. Chen, D. J. Pochan and J. C. van Hest, Angew. Chem., 2011, 123, 7208–7211 CrossRef.
- D. A. Wilson, R. J. M. Nolte and J. C. M. van Hest, Nat. Chem., 2012, 4, 268–274 CrossRef CAS.
- A. F. Bitbol, J. B. Fournier, M. I. Angelova and N. Puff, J. Phys.: Condens. Matter, 2011, 23, 284102 CrossRef.
- A.-F. Bitbol, N. Puff, Y. Sakuma, M. Imai, J.-B. Fournier and M. I. Angelova, Biophys. J., 2012, 102, 33a CrossRef.
- A. F. Bitbol and J. B. Fournier, Biochim. Biophys. Acta, Biomembr., 2013, 1828, 1241–1249 CrossRef CAS.
- W. F. Paxton, D. Price and N. J. Richardson, Soft Matter, 2013, 9, 11295–11302 RSC.
- N. Khalifat, N. Puff, S. Bonneau, J. B. Fournier and M. I. Angelova, Biophys. J., 2008, 95, 4924–4933 CrossRef CAS.
- N. Khalifat, J. B. Fournier, M. I. Angelova and N. Puff, Biochim. Biophys. Acta, Biomembr., 2011, 1808, 2724–2733 CrossRef CAS.
- V. Passos Gibson, M. Fauquignon, E. Ibarboure, J. Leblond Chain and J.-F. Le Meins, Polymers, 2020, 12, 637 CrossRef.
- Y. Miele, Z. Medveczky, G. Holló, B. Tegze, I. Derényi, Z. Hórvölgyi, E. Altamura, I. Lagzi and F. Rossi, Chem. Sci., 2020, 11, 3228–3235 RSC.
- H. Maemichi, K. Shikinaka, A. Kakugo, H. Furukawa, Y. Osada and J. P. Gong, Langmuir, 2008, 24, 11975–11981 CrossRef CAS.
- D. B. Wright, A. Ramírez-Hernández, M. A. Touve, A. S. Carlini, M. P. Thompson, J. P. Patterson, J. J. De Pablo and N. C. Gianneschi, ACS Macro Lett., 2019, 8, 676–681 CrossRef.
- X. Li, I. V. Pivkin, H. Liang and G. E. Karniadakis, Macromolecules, 2009, 42, 3195–3200 CrossRef CAS.
- S. H. Chou, D. T. Wu, H. K. Tsao and Y. J. Sheng, Soft Matter, 2011, 7, 9119–9129 RSC.
- T. L. Rodgers, J. E. Magee, T. Amure and F. R. Siperstein, Soft Matter, 2016, 12, 9014–9024 RSC.
- X. Li, Soft Matter, 2013, 9, 11663–11670 RSC.
- Z. Luo, Y. Li, B. Wang and J. Jiang, Macromolecules, 2016, 49, 6084–6094 CrossRef CAS.
- P. Sun, Y. Yin, B. Li, Q. Jin and D. Ding, Int. J. Mod. Phys. B, 2003, 17, 241–244 CrossRef CAS.
- X. He, H. Liang, L. Huang and C. Pan, J. Phys. Chem. B, 2004, 108, 1731–1735 CrossRef CAS.
- V. Ortiz, S. O. Nielsen, M. L. Klein and D. E. Discher, J. Polym. Sci., Part B: Polym. Phys., 2006, 44, 1907–1918 CrossRef CAS.
- N. K. Li, W. H. Fuss, L. Tang, R. Gu, A. Chilkoti, S. Zauscher and Y. G. Yingling, Soft Matter, 2015, 11, 8236–8245 RSC.
- J. A. Mysona, A. V. McCormick and D. C. Morse, Phys. Rev. E, 2019, 100, 012602 CrossRef.
- J. A. Mysona, A. V. McCormick and D. C. Morse, Phys. Rev. E, 2019, 100, 012603 CrossRef.
- M. Xiao, J. Liu, J. Yang, R. Wang and D. Xie, Soft Matter, 2013, 9, 2434–2442 RSC.
- S. Ma, M. Xiao and R. Wang, Langmuir, 2013, 29, 16010–16017 CrossRef CAS.
- B. Gumus, M. Herrera-Alonso and A. Ramírez-Hernández, Soft Matter, 2020, 16, 4969–4979 RSC.
- A. Donev, C.-Y. Yang and C. Kim, J. Chem. Phys., 2018, 148, 034103 CrossRef.
- R. M. Elder, T. Emrick and A. Jayaraman, Biomacromolecules, 2011, 12, 3870–3879 CrossRef CAS.
- R. M. Elder and A. Jayaraman, J. Phys. Chem. B, 2013, 117, 11988–11999 CrossRef CAS.
- A. H. de Vries, A. E. Mark and S. J. Marrink, J. Am. Chem. Soc., 2004, 126, 4488–4489 CrossRef CAS.
- G. Srinivas, D. E. Discher and M. L. Klein, Nat. Mater., 2004, 3, 638–644 CrossRef CAS.
- G. H. Fredrickson, The Equilibrium Theory of Inhomogeneous Polymers, Oxford University Press, 2006 Search PubMed.
- Y. Jiang, S. Li and J. Z. Chen, Eur. Phys. J. E: Soft Matter Biol. Phys., 2016, 39, 91 CrossRef.
- L. Zhang, A. Sevink and F. Schmid, Macromolecules, 2011, 44, 9434–9447 CrossRef CAS.
- D. R. Tree, K. T. Delaney, H. D. Ceniceros, T. Iwama and G. H. Fredrickson, Soft Matter, 2017, 13, 3013–3030 RSC.
- S. Qi and F. Schmid, Macromolecules, 2017, 50, 9831–9845 CrossRef CAS.
- H. Chao, J. Koski and R. A. Riggleman, Soft Matter, 2017, 13, 239–249 RSC.
- G. D. Smith and D. Bedrov, J. Polym. Sci., Part B: Polym. Phys., 2007, 45, 627–643 CrossRef CAS.
- A. Marciniak-Czochra and M. Kimmel, Math. Modell. Nat. Phenom., 2008, 3, 90–114 CrossRef.
- A. Mahmutovic, D. Fange, O. G. Berg and J. Elf, Nat. Methods, 2012, 9, 1163 CrossRef CAS.
- K. Takahashi, S. N. V. Arjunan and M. Tomita, FEBS Lett., 2005, 579, 1783–1788 CrossRef CAS.
- N. G. Van Kampen, Stochastic Processes in Physics and Chemistry, Elsevier, Amsterdam, 1992, vol. 1 Search PubMed.
- R. Erban and S. J. Chapman, Phys. Biol., 2009, 6, 046001 CrossRef.
- M. Davis and R. Davis, Fundamentals of Chemical Reaction Engineering, Dover Publications, 2013 Search PubMed.
- J. A. Anderson, J. Glaser and S. C. Glotzer, Comput. Mater. Sci., 2020, 173, 109363 CrossRef CAS.
- C. L. Phillips, J. A. Anderson and S. C. Glotzer, J. Comput. Phys., 2011, 230, 7191–7201 CrossRef CAS.
- R. D. Groot and P. B. Warren, J. Chem. Phys., 1997, 107, 4423–4435 CrossRef CAS.
- P. Español and P. Warren, Europhys. Lett., 1995, 30, 191–196 CrossRef.
- P. Medapuram, J. Glaser and D. C. Morse, Macromolecules, 2015, 48, 819–839 CrossRef CAS.
- M. Allen and D. Tildesley, Computer Simulation of Liquids, Clarendon Press, 1987 Search PubMed.
- W. Humphrey, A. Dalke and K. Schulten, et al. , J. Mol. Graphics, 1996, 14, 33–38 CrossRef CAS.
- D. P. Tolle and N. Le Novère, BMC Syst. Biol., 2010, 4, 24 CrossRef.
- L. Sbailò and F. Noé, J. Chem. Phys., 2017, 147, 184106 CrossRef.
- B. Drawert, B. Jacob, Z. Li, T. M. Yi and L. Petzold, J. Comput. Phys., 2019, 378, 1–17 CrossRef CAS.
- T. Opplestrup, V. V. Bulatov, G. H. Gilmer, M. H. Kalos and B. Sadigh, Phys. Rev. Lett., 2006, 97, 230602 CrossRef.
- T. Oppelstrup, V. V. Bulatov, A. Donev, M. H. Kalos, G. H. Gilmer and B. Sadigh, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2009, 80, 066701 CrossRef.
- M. Doi, J. Phys. A: Math. Gen., 1976, 9, 1479–1495 CrossRef.
- M. Malek-Mansour and G. Nicolis, J. Stat. Phys., 1975, 13, 197–217 CrossRef.
- D. T. Gillespie, Annu. Rev. Phys. Chem., 2007, 58, 35–55 CrossRef CAS.
- D. T. Gillespie, A. Hellander and L. R. Petzold, J. Chem. Phys., 2013, 138, 170901 CrossRef.
- S. Yamamoto, Y. Maruyama and S.-a. Hyodo, J. Chem. Phys., 2002, 116, 5842–5849 CrossRef CAS.
- H. Tan, C. Yu, Z. Lu, Y. Zhou and D. Yan, Soft Matter, 2017, 13, 6178–6188 RSC.
- S. K. Lam, A. Pitrou and S. Seibert, Proceedings of the Second Workshop on the LLVM Compiler Infrastructure in HPC, 2015, pp. 1–6.
- C. Nowak and F. A. Escobedo, J. Chem. Theory Comput., 2018, 14, 5984–5991 CrossRef CAS.
- P. C. Hiemenz and R. Rajagopalan, Principles of Colloid and Surface Chemistry, CRC Press, 3rd edn, 1997 Search PubMed.
- A. Savitzky and M. J. Golay, Anal. Chem., 1964, 36, 1627–1639 CrossRef CAS.
- S. H. R. Shin, P. T. McAninch, I. M. Henderson, A. Gomez, A. C. Greene, E. C. Carnes and W. F. Paxton, Chem. Commun., 2018, 54, 9043–9046 RSC.
- G. Kocak, C. Tuncer and V. Bütün, Polym. Chem., 2017, 8, 144–176 RSC.
- J. N. Israelachvili, Intermolecular and Surface Forces, Academic Press, San Diego, 3rd edn, 2011, ch. 20, pp. 535–576 Search PubMed.
- M. Antonietti and S. Förster, Adv. Mater., 2003, 15, 1323–1333 CrossRef CAS.
- S. Kobayashi and K. Nomizu, Foundations of Differential Geometry, New York, London, 1963, vol. 1 Search PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/d0sm01654c |
| This journal is © The Royal Society of Chemistry 2021 |