Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Optical quantification of intracellular mass density and cell mechanics in 3D mechanical confinement†
Sadra
Bakhshandeh
a,
Hubert M.
Taïeb
a,
Raimund
Schlüßler
b,
Kyoohyun
Kim
bc,
Timon
Beck
bc,
Anna
Taubenberger
b,
Jochen
Guck
*bc and
Amaia
Cipitria
 *a
*a
aDepartment of Biomaterials, Max Planck Institute of Colloids and Interfaces, Potsdam, Germany. E-mail: amaia.cipitria@mpikg.mpg.de
bBiotechnology Center, Center for Molecular and Cellular Bioengineering, Technische Universität Dresden, Dresden, Germany
cMax Planck Institute for the Science of Light & Max-Planck-Zentrum für Physik und Medizin, Erlangen, Germany. E-mail: jochen.guck@mpl.mpg.de
First published on 20th November 2020
Abstract
Biophysical properties of cells such as intracellular mass density and cell mechanics are known to be involved in a wide range of homeostatic functions and pathological alterations. An optical readout that can be used to quantify such properties is the refractive index (RI) distribution. It has been recently reported that the nucleus, initially presumed to be the organelle with the highest dry mass density (ρ) within the cell, has in fact a lower RI and ρ than its surrounding cytoplasm. These studies have either been conducted in suspended cells, or cells adhered on 2D substrates, neither of which reflects the situation in vivo where cells are surrounded by the extracellular matrix (ECM). To better approximate the 3D situation, we encapsulated cells in 3D covalently-crosslinked alginate hydrogels with varying stiffness, and imaged the 3D RI distribution of cells, using a combined optical diffraction tomography (ODT)-epifluorescence microscope. Unexpectedly, the nuclei of cells in 3D displayed a higher ρ than the cytoplasm, in contrast to 2D cultures. Using a Brillouin-epifluorescence microscope we subsequently showed that in addition to higher ρ, the nuclei also had a higher longitudinal modulus (M) and viscosity (η) compared to the cytoplasm. Furthermore, increasing the stiffness of the hydrogel resulted in higher M for both the nuclei and cytoplasm of cells in stiff 3D alginate compared to cells in compliant 3D alginate. The ability to quantify intracellular biophysical properties with non-invasive techniques will improve our understanding of biological processes such as dormancy, apoptosis, cell growth or stem cell differentiation.
Introduction
The biophysical properties of cells hold important physiological information.1,2 This can be gathered from different levels of structural hierarchy, spanning from cellular-level mechanics and cytoskeletal organization to sub-cellular level spatial distribution and the physicochemical state of organelles and sub-organelles. It has been shown that biophysical properties such as cell stiffness, can be altered during physiological processes such as stem cell differentiation3,4 and tissue morphogenesis5,6 as well as pathological conditions like cardiovascular diseases,7,8 tumour growth, migration and metastasis.9–12 At the sub-cellular level, liquid–liquid phase separation of cytoplasmic stress granules or nuclear chromatin condensation, are examples of physical changes that have also been linked to cellular states and processes such as dormancy,13 apoptosis14 and cell growth.15 These biological phenomena have also been associated with changes in mass density (ρ) distribution within the cell. The refractive index (RI), reported to vary at the sub-cellular level, is linearly proportional to protein concentration in most in most biological materials,16,17 which can be in turn correlated with good approximation to ρ and has been proposed as a suitable parameter in cell sorting and diagnostic devices.18Earlier optical studies on two-dimensional (2D) cell cultures reported higher RI for the nucleus compared to the cytoplasm.19–22 Interestingly, recent studies using a variety of microscopy techniques such as quantitative phase imaging,23,24 orientation-independent differential interference microscopy,25 plasmon resonance microscopy26 and transport-of-intensity microscopy,27 have shown the opposite. Furthermore, using a combined optical diffraction tomography (ODT) and epifluorescence microscope, it was reported that such relationship, meaning the cytoplasm having a higher RI and ρ than the nucleus, is robustly conserved not only throughout the whole cell cycle, but also after actin and microtubule depolymerization and chromatin condensation or decondensation.28 Upon drug perturbations, the cell morphology, including shape, volume and dry mass changed, while the relative mass densities among sub-cellular compartments was preserved.28
Most of these studies have been performed on 2D substrates or suspended cells, neglecting the third dimension (3D) provided by the extracellular matrix (ECM) in physiological environments. Changes in the ECM have been associated to phenotypic and genotypic alterations in cell properties such as morphology,29 differentiation,30 signal transduction,31 migration and proliferation.32 To our knowledge, no study has investigated the effect of the dimensionality provided by the ECM on sub-cellular mass distribution. For this purpose, we employed a covalently-crosslinked 3D alginate hydrogel, which allows for versatile and independent tuning of various biophysical properties such as adhesion,33 stiffness,33,34 viscoelasticity35–37 and degradation.38,39 Using a custom-made combined ODT-epifluorescence microscope, we quantitatively mapped the 3D RI distribution of human breast cancer cells MDA-MB-231, encapsulated in 3D hydrogels with different stiffness, and compared the resulting ρ with cells on 2D substrates.
While optical properties of cells are accessible in 2D and 3D using optical techniques, mechanical testing of cells has mostly been performed using mechanical or particle probes such as atomic force microscopy (AFM) indentation,40 micropipette aspiration41 or optical tweezers.42 However, with the more recent availability of optical techniques such as Brillouin spectroscopy,43,44 it is now possible to measure mechanical properties of cells in a contact-free fashion. Its ability to map at high resolution 3D (visco)elastic properties45,46 in terms of longitudinal modulus M and viscosity η, has made Brillouin spectroscopy an attractive tool in the biomechanical analysis of biological samples, in this case cells encapsulated in 3D hydrogels.
This is, to our knowledge, the first study where the effect of dimensionality and matrix stiffness on intracellular ρ distribution and sub-cellular mechanics have been assessed in a 3D, contact-free fashion using ODT-epifluorescence and confocal Brillouin-epifluorescence microscopes. We show that the nuclei of MDA-MB-231 cells in 3D hydrogels display higher RI and ρ compared to the cytoplasm, differently to what is commonly found on 2D substrates. In addition, the nuclei reveal higher M and η compared to the cytoplasm. Moreover, cells encapsulated in stiff alginate hydrogels show a higher M for both the nucleus and cytoplasm compared to cells in compliant 3D alginate hydrogels.
Materials and methods
Fabrication of covalently-crosslinked norbornene-modified alginate hydrogels
Covalently-crosslinked alginate hydrogels were fabricated as previously reported.38 Briefly, 1% w/v high guluronic acid sodium alginate (265 kDa Pronova MVG; NovaMatrix) was dissolved in 0.1 M 2-(N-morpholino)ethanesulfonic acid (MES; Sigma-Aldrich), 0.3 M NaCl (EMD Millipore) buffer (pH 6.5) overnight. N-Hydroxysuccinimide (NHS; Sigma-Aldrich) and 1-ethyl-3-(3-dimethylaminopropyl)-carbodiimide hydrochloride (EDC; Sigma-Aldrich) were added drop-wise at 5000 molar equivalents to the alginate solution while stirring. To functionalize the polymer backbone with norbornene, 5-norbornene-2-methylamine (TCI Deutschland GmbH) was added to the solution. The theoretical degree of substitution (DStheo) was aimed at 300 molecules per alginate chain. The reaction (final concentration 0.6% w/v) was run for 20 h stirring at 700 rpm and quenched with hydroxylamine (Sigma-Aldrich). After 3 days dialysis (Spectra/Por 6, MWCO 3.5 kDa; Spectrum) with 3–4 changes per day against a salt gradient (6 g L−1 to 0 g L−1; Sigma-Aldrich), purification followed using activated charcoal (Sigma-Aldrich). Finally, the solution was sterile-filtered (0.22 μm; Steriflip-GP; Merck) and lyophilized.Thiol–ene crosslinking and casting of norbornene-modified alginate hydrogels
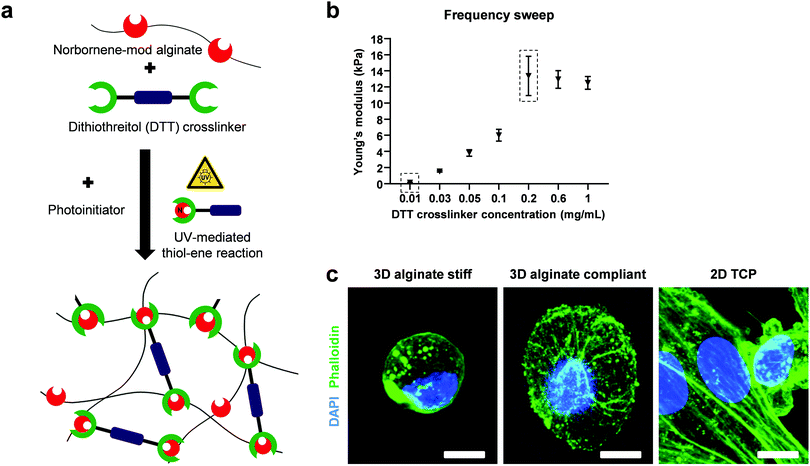
Norbornene-modified alginate and the photoinitiator (PI, Irgacure 2959; Sigma-Aldrich) were dissolved in PBS overnight at 50 °C under shaking. The crosslinker dithiothreitol (DTT, Sigma-Aldrich) was mixed just before casting for a final concentration of 2% w/v alginate and 0.5% w/v PI. The solution was then pipetted on glass plates using positive displacement pipettes, covered with a dichloromethylsilane-coated glass slide (≥99.5%; Sigma-Aldrich) with 2 mm spacers, placed in a custom-built chamber and exposed to UV light (365 nm) for 10 min at 10 mW cm−2 (OmniCure S2000). The coated glass slide was then carefully removed and the gels were punched out using biopsy punches (Integra Miltex) with 8 mm in diameter. The reaction of double cysteine-containing DTT with the alkene-containing molecules of norbornene in the presence of a photoinitiator, yielded covalently-crosslinked non degradable 3D hydrogels after UV exposure (Fig. 1a). The fast and high efficiency of this click reaction results in an increased yield of functionalization without side products. A final washing step with PBS to remove residual and unreacted material preceded the mechanical characterization.Mechanical characterization of hydrogels
Norbornene-modified alginate (2% w/v) with different concentration of DTT (0.01–0.1 mg mL−1) was casted to yield hydrogels with different stiffness. Following overnight incubation in PBS, a frequency sweep from 0.01 to 10 Hz over 30 min was performed at constant 1% shear strain using a rheometer (Physica MCR 301; Anton Paar) with a 8 mm flat plate (PP08; Anton Paar). The temperature was kept at 25 °C using a Peltier cooling module. The elastic modulus (E) was calculated using the following equations:47E = 2G(1 + ϑ) and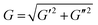 . G, G′ and G′′ are the shear, storage and loss moduli respectively. E is the Young's modulus and ϑ = 0.5 is the Poisson's ratio in hydrogels.48
. G, G′ and G′′ are the shear, storage and loss moduli respectively. E is the Young's modulus and ϑ = 0.5 is the Poisson's ratio in hydrogels.48
Cell culture and generation of FUCCI2 cell reporters
MDA-MB-231 highly metastatic human breast cancer cells (HTB-26; ATCC) were cultured in Dulbecco's Modified Eagle's Medium (D6046; Sigma-Aldrich) supplemented with 10% v/v fetal bovine serum (Biochrom), and 1% penicillin/streptomycin (Gibco). The cells were incubated in a 5% CO2 environment at 37 °C and passaged every 3–5 days. MDA-MB-231 FUCCI2 cell cycle reporter was generated using lentiviral transduction and employed as nucleus reporter as previously reported.49 Briefly, lentiviral particles were produced by co-transfecting HEK-293TN cells (System Biosciences) with mCherry-hCdt1 (30/120)/pCSII-EF-MCS (DDBJ/EMBL/GenBank, AB512478) or mVenus-hGeminin (1/100)/pCSII-EF-MCS (DDBJ/EMBL/GenBank, AB512479) lentiviral vectors in the presence of packaging and envelope plasmids psPAX2 (Addgene plasmid, #12260) and pMD2.G (Addgene plasmid, #12259). Subsequently, parental MDA-MB-231 cell line was transfected with the previously produced particles and sorted via FACSAria™ II flow cytometer (Becton Dickinson) for mCherry and mVenus fluorescence. For 2D experiments, cells were seeded on 2D glass bottom dishes (FluoroDish, WPI).3D cell encapsulation, viability and morphological characterization
Norbornene-modified alginate with two different DTT concentrations (0.01 and 0.2 mg mL−1) were selected to yield compliant (300 Pa) and stiff (13 kPa) hydrogels, respectively. For 3D cell encapsulation, MDA-MB-231 cells were mixed with the gel precursor solution as a cell suspension (106 cells per mL). To visualize the nucleus and actin cytoskeleton, 3D encapsulated cells were fixed with paraformaldehyde 4% (Boster), permeabilized with 0.1% wt/v Triton-X-100 (Sigma-Aldrich), blocked with 3% wt/v bovine serum albumin (Sigma-Aldrich) in phosphate buffer solution (PBS) and stained with DAPI (1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1000, Roche) and Alexa Fluor 488 Phalloidin (1
1000, Roche) and Alexa Fluor 488 Phalloidin (1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 50, Invitrogen). Due to camera limitations resulting in the FUCCI2 signal not being detectable for cells in 3D hydrogels, Hoechst 33342 (8 μM, Molecular Probes) was used for live nuclear staining following manufacturer's indications. To assess viability, cells were stained with 1.6 μM calcein AM (C125400; TRC) and 4 μM ethidium homodimer-1 (L3224; Thermo Fisher Scientific) for live and dead, respectively. Images were acquired using either a Zeiss AxioObserver 7 fluorescence microscope and a 10×, 0.3 NA objective or a Leica SP8 confocal microscope with 63×, 1.4 NA oil-immersion objective.
50, Invitrogen). Due to camera limitations resulting in the FUCCI2 signal not being detectable for cells in 3D hydrogels, Hoechst 33342 (8 μM, Molecular Probes) was used for live nuclear staining following manufacturer's indications. To assess viability, cells were stained with 1.6 μM calcein AM (C125400; TRC) and 4 μM ethidium homodimer-1 (L3224; Thermo Fisher Scientific) for live and dead, respectively. Images were acquired using either a Zeiss AxioObserver 7 fluorescence microscope and a 10×, 0.3 NA objective or a Leica SP8 confocal microscope with 63×, 1.4 NA oil-immersion objective.
Optical diffraction tomography: setup, tomogram reconstruction and analysis
The combined ODT and epifluorescence microscope setup has been previously described.50 Briefly, to measure the 3D RI distribution, a Mach–Zehnder interferometer was used (Fig. 2). A laser beam (λ = 532 nm, frequency-doubled Nd-YAG laser, Torus, Laser Quantum Inc.) and an optical fiber were coupled and then separated into two beams using a 2 × 2 single-mode fiber-optic coupler. These beams were used as sources for sample illumination and reference through a tube lens (f = 175 mm) on a custom-made inverted microscope equipped with a water immersion objective lens (NA = 1.0, 40×, Carl Zeiss AG).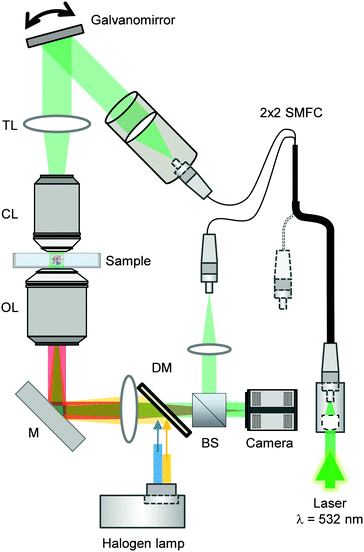 | ||
| Fig. 2 Combined optical diffraction tomography and epifluorescence microscope setup. Abbreviations correspond to BS = beam splitter, DM = dichroic mirror, M = mirror, OL = objective lens, CL = condenser lens, TL = tube lens, SMFC = single-mode fiber coupler. Image adapted from ref. 28. | ||
The samples were illuminated from 150 different incident angles using a dual-axis galvano-mirror (GVS012/M, Thorlabs Inc.) in order to reconstruct the 3D RI tomograms of cells.
A high-numerical aperture objective lens (NA = 1.2, 63×, water immersion, Carl Zeiss AG) and a tube lens (f = 200 mm) were employed for collection of the diffracted beam. The total magnification was set at 57×.
Interference between the reference and the diffracted beam at an image plane resulted in a spatially modulated hologram which was recorded using a CCD camera (FL3-U3-13Y3M-C, FLIR Systems, Inc.). Temperature of the glass bottom Petri dish and the objective lenses were kept at 37 °C with resistant foil heaters (Thorlabs Inc.).
For epifluorescence measurements, a three-channel dichroic mirror (FF409/493/596-Di01-25×36, Semrock Inc.) was employed to couple an incoherent light from a halogen lamp (DC-950, Dolan-Jenner Industries Inc.) into the same path as the ODT beam. To image the nuclei with Hoechst staining, a corresponding bandpass filter was employed.
The Fourier transform-based field retrieval algorithm was applied to obtain the complex optical fields of the scattered light from the recorded holograms, which were then used to reconstruct the 3D RI distribution using the Fourier diffraction theorem.51–53 More detailed descriptions can be found elsewhere.54,55
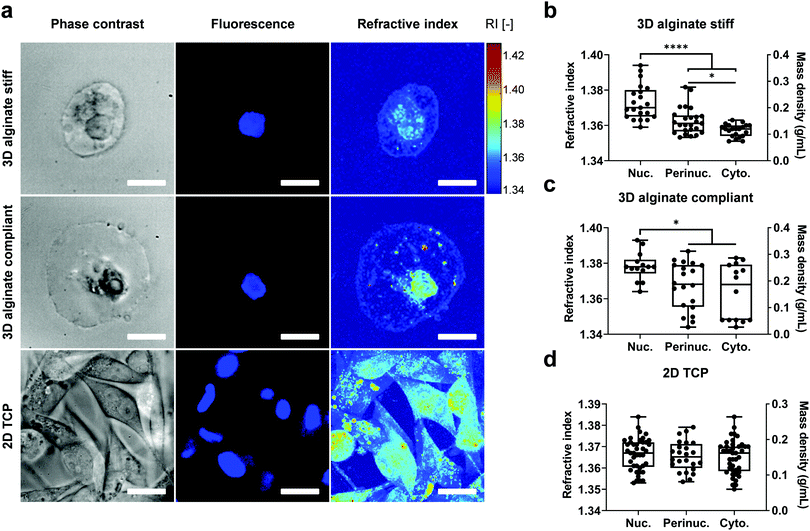
Based on the reconstructed tomograms, the nucleus was then segmented using the Hoechst or FUCCI2 fluorescence image, while the boundaries for the cytoplasm were defined by the plasma membrane and double-checked with phase contrast images (Fig. 3).
In addition, the perinuclear region was segmented separately as the neighbouring region within 2 μm distance from the nuclear membrane by expanding the nuclear binary mask.
The mass density ρ, is linearly proportional to the RI in most biological samples16,17 and was calculated using the following equation:28ρ = (n − nm)/α, where n is the sample RI, nm the RI of the empty hydrogel which was measured using an Abbe refractometer (2WAJ, Arcarda GmbH) and found to be 1.3370 at λ = 532 nm, and α = 0.190 mL g−1 as the RI increment for proteins and nucleic acids.56,57 To calculate the cell volume, ODT-derived binary masks were segmented using AMIRA ZIB software and the cell volume was extracted by counting the number of voxels.
Data acquisition and analysis were done using custom-written MATLAB scripts (R2019b, MathWorks, Inc.).
Confocal Brillouin epifluorescence microscopy: scattering, setup, imaging and analysis
Brillouin images were acquired employing a two-stage VIPA spectrometer based on the design by Scarcelli et al.58 The spectrometer was attached to a custom-built confocal unit employing a Zeiss Axiovert 200 M microscope stand (Carl Zeiss AG, Germany). A frequency-modulated diode laser with a wavelength of 780.24 nm was used as illumination source. The laser was stabilized to the D2 transition line of Rubidium 85 to block the elastically scattered light. Amplified spontaneous emission (ASE) was suppressed by a Fabry–Pérot interferometer (FPI) (Light Machinery, CA) and a Bragg grating (Ondax NoiseBlock, Ondax, CA). The utilized setup was described in detail by Schlüßler et al.,46 and was slightly modified for the measurements performed here. To further improve the ratio of the intensity of the central laser line to the ASE intensity the alignment of the FPI was changed from a one-pass to a two-pass configuration (Fig. 4), which improved the ASE ratio to 95 dB. The Brillouin setup was controlled with a custom acquisition software written in C++, which stores the data as HDF5 files (https://github.com/BrillouinMicroscopy/BrillouinAcquisition). All images were obtained with a 40×/0.95 air objective (Carl Zeiss AG, Germany). The sample temperature was controlled to 37 °C by a Petri dish heater (JPK BioAFM). Longitudinal modulus and viscosity were derived as previously described.46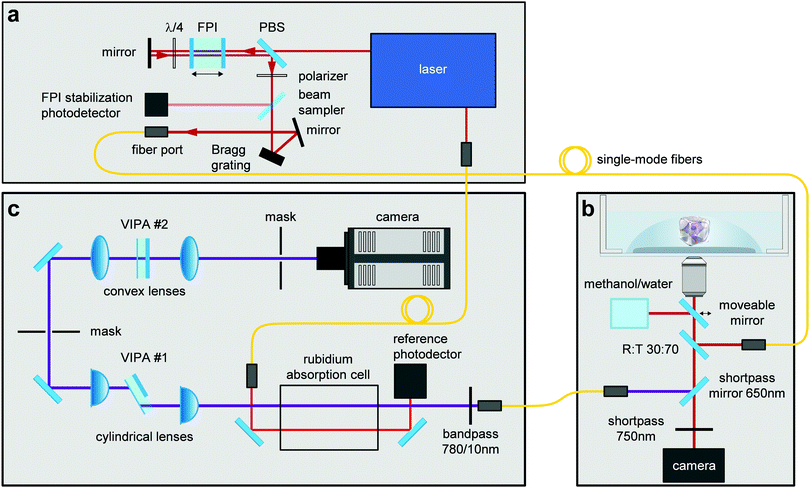 | ||
| Fig. 4 Combined confocal Brillouin and epifluorescence microscope setup. The different components of this custom-built microscope consist of: (a) illumination source, (b) confocal microscope, (c) Brillouin spectrometer. Abbreviations correspond to FPI = Fabry–Pérot interferometer, PBS = polarizing beam splitter, VIPA = virtually imaged phased array. Image adapted from ref. 46. | ||
Statistical analysis
Experiments were performed with cells on 2D tissue culture plate and 3D encapsulated cells in compliant vs. stiff alginate hydrogels. At least three samples per hydrogel group, and multiple cell measurements within each group, were analysed. Box plots showing minimum, maximum, median and interquartile range were used to illustrate the results. Two-tailed student's t-test or Mann–Whitney U-test were used to statistically compare between normally-distributed or non-parametric groups, respectively (*: p ≤ 0.05, **: p ≤ 0.01, ***: p ≤ 0.001, ****: p ≤ 0.0001). For multiple group comparison one-way Anova with Tukey's correction or Kruskal–Wallis test with Dunn's correction was conducted. GraphPad Prism 8 software was used to plot the data and for statistical analysis.Results
Mechanical characterization of 3D alginate hydrogels
To investigate the mechanical and rheological properties of norbornene-modified alginate, frequency sweep experiments were conducted (Fig. 1b). By changing the concentration of the DTT, a stiffness range between 300 Pa and 13 kPa was achieved. The minimum and maximum stiffness-yielding concentrations were selected for further cell encapsulation and will be referred to as compliant and stiff hydrogels, respectively.3D cell encapsulation, viability and morphological characterization
MDA-MB-231 highly metastatic human breast cancer cells encapsulated in 3D alginate hydrogels remained viable as evidenced by calcein/ethidium homodimer-1 stainings (Fig. S1, ESI†). They remained as single cells, displaying a round morphology after 5 days of encapsulation compared to the more elongated shape of cells on 2D TCP (Fig. 1c).Refractive index and mass density
To determine intracellular mass density distribution in 3D confined single cells, ODT measurements were performed after staining for the nuclei with Hoechst for cells encapsulated in 3D alginate hydrogels. Following RI tomogram reconstruction, regions associated with nucleus, perinuclear region and cytoplasm were segmented by colocalizing RI tomograms with epifluorescence images (Fig. 3a). Subsequently, the RI and ρ of the segmented compartments were calculated (Fig. 3b–d). The nuclei in the cells encapsulated in 3D alginate hydrogels displayed higher RI and ρ compared to cytoplasm independent from their stiffness (Fig. 3b and c). In addition, the perinuclear region of cells encapsulated in stiff but not compliant 3D alginate hydrogels was characterised by a higher RI and ρ compared to the cytoplasmic region (Fig. 3b). Notably, RI and ρ values in the cytoplasm and perinuclear regions of cells encapsulated in 3D alginate compliant displayed considerably high variability and dispersion as evidenced by the larger interquartile range (Fig. 3c). Nonetheless, no difference was detected between the absolute values of RI of nuclei, perinucleus or cytoplasm of cells encapsulated in either stiff or compliant 3D alginate hydrogels (Fig. S2a, ESI†). Volume analysis revealed significantly higher volume for cells encapsulated in compliant compared to stiff 3D alginate hydrogels (Fig. S2b, ESI†). The RI and ρ from different sub-cellular regions of cells on 2D TCP did not show any statistical difference (Fig. 3d). Noteworthy, no difference between the nuclear to cytoplasmic ratio of RI and ρ of cells in neither 3D alginate compliant or stiff was detected (Fig. S2c, ESI†).Longitudinal modulus and viscosity
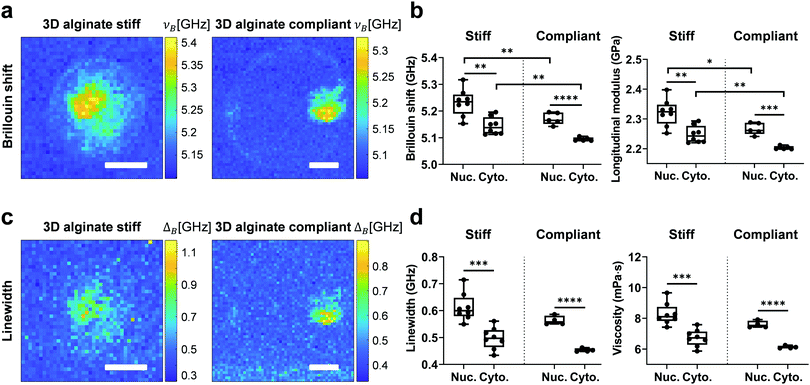
To investigate the mechanical properties of 3D confined single cells in a non-invasive way, Brillouin measurements were performed after staining for the nucleus. After map reconstruction, regions associated with the nucleus and cytoplasm were segmented based on fluorescence images and their respective Brillouin shift (νB) and linewidth (ΔB) were calculated (Fig. 5a and c). Longitudinal modulus (M) and viscosity (η) were calculated as described previously.46 Like for RI and ρ, νB and the corresponding M of the nucleus for both stiff and compliant 3D alginate were higher than the corresponding values for the cytoplasm (Fig. 5b). Those values were on average greater for both the nucleus and cytoplasm of cells in stiff than in compliant 3D alginate hydrogels (Fig. 5b). The ΔB and corresponding η of the nucleus was also significantly higher than the values of the cytoplasm for cells in both stiff and compliant hydrogels (Fig. 5d). Noteworthy, in contrast to νB, ΔB and η did not differ between the compliant and stiff 3D alginate hydrogels (Fig. 5d). In addition, the nuclear to cytoplasmic ratio of the νB and ΔB did not reveal any statistical difference among stiff and compliant 3D alginate hydrogels (Fig. S3a and b, ESI†), resembling RI and ρ behaviour. Noteworthy, νB, M, ΔB and η of the nucleus and cytoplasm of cells seeded on 2D TCP didn’t display any statistical difference, even though a trend for higher values of the nucleus compared to the cytoplasm could be observed (Fig. S4, ESI†).Discussion
Using a combined ODT-epifluorescence microscope, to our surprise, we found that human breast cancer cells MDA-MB-231 encapsulated in 3D hydrogels displayed a significantly higher nuclear RI and ρ compared to the cytoplasm, irrespective of matrix stiffness. This is different from our 2D results as well as compared to recent 2D data on RI distribution across various cell lines including MDA-MB-231, where it was shown that cells cytoplasm have higher RI than their nuclei using a wide variety of microscopy techniques.23–28,59,60 Such discrepancy might be attributed to differences in cytoskeletal and/or nuclear morphologies in 2D compared to 3D. Cells on 2D substrates spread out and elongate, displaying a forced ventral-dorsal polarity compared to the non-polarized shape of cells in 3D.32 Moreover, attachment and spreading on 2D surfaces is accompanied by more pronounced stress fiber formation along the ventral plane, compared to the cortical arrangement of F-actin in 3D.32 In this scenario, the force sensed by the cell's focal adhesions is tangentially-oriented to the substrate which results in stress propagation along the basal fibers.61,62 This is in stark contrast to the 3D context, where the less mature focal adhesions and stress fibers are associated to an unpolarized and more round morphology.32 Here, the cell is exposed to external forces mainly perpendicular to its membrane, which will result in a more isotropic propagation of the stress up to the nucleus.32 Previous works have shown that cells adherent on 2D substrates display higher nuclear volume and cross-sectional size as well as a more elongated nucleus shape compared to cells encapsulated in 3D hydrogels or on loosely adherent surfaces.63,64 These differences in cytoskeletal architecture and nuclear shape have distinct signalling implications. In this regard, it has been previously shown that in weakly adhered cells which have reduced stress fiber formation and actomyosin contractility, the histone deacetylases (HDACs) translocates from the cytoplasm to nucleus.63,65,66 This results in chromatin condensation and compaction with fluid exiting from the nucleus.63,65,66 Whether this is the reason for the higher nuclear RI and ρ in 3D compared to 2D seen in this study remains to be elucidated. Indeed, it was recently reported that inhibition of chromatin condensation in HeLa cells on 2D substrates results in a reduction of RI and ρ, while inducing chromatin condensation results in the opposite effect.28It has been widely reported that external osmotic pressure modulates chromatin structure and aberrations67–69 and more recently intracellular mass density.15 In addition, it was shown that cancer cells under mechanical compression, actively efflux ions to decrease their intracellular tonicity in order to improve their chances of survival.70 A recent work by the Chaudhuri group showed that stiffer 3D alginate hydrogels induce a tumorigenic phenotype in MCF10A breast epithelial cells by making chromatin sites more accessible.34 These observations motivate the assumption that 3D matrix-mediated compression could exert an analogous effect as external hyperosmotic pressure. Within this line of reasoning, our study is providing evidence for the effect of alginate-provided 3D mechanical confinement on intracellular mechanical properties, which is reflected in a higher M for both the nucleus and cytoplasm of cells encapsulated in stiff compared to compliant hydrogels. This is in agreement with a recent study where AFM measurements were conducted on isolated MCF-7 spheroids and constituent cells that had been grown in 3D compliant and stiff polyethylene glycol-heparin hydrogels.12 Both single cells and spheroids displayed a higher Young's modulus after growth in stiff compared to compliant hydrogels. Interestingly, this effect was mitigated when cells were perturbed with cytochalasin D (F-actin depolymerisation) and Y-27632 (ROCK inhibitor), underlining the importance of F-actin cytoskeleton adaptations in modulating cell mechanics.12
Another aspect that can explain the different M between compliant and stiff hydrogels is the cell volume. In a seminal paper from the Weitz group, Guo et al.71 showed that cell cortical and cytoplasmic stiffness scales inversely with their volume in a 2D set-up. Specifically, by increasing external osmotic pressure or substrate stiffness, they observed an increase in cytoplasmic and cortical stiffness coupled with a decrease in cell volume.71 Similarly, here we show that cells encapsulated in 3D stiff hydrogels display a smaller volume compared to 3D compliant hydrogels, which is reflected in a higher M for both the nucleus and cytoplasm in the former. Remarkably, we show that cells in 2D display an almost double value for M and η compared to cells encapsulated in 3D hydrogels, stressing again on the importance of dimensionality provided by the ECM when assessing mechanical properties of cells.
Noteworthy, viscosity η did not show any statistical difference for the nucleus nor the cytoplasm between compliant and stiff hydrogels. This indicates that, depending on the type of microenvironmental alteration, elastic and viscous properties of the cell might be influenced differently. Indeed, microviscosity of cellular organelles was shown to affect intracellular diffusion and macromolecular crowding.72 In an elegant study employing molecular rotor-based optical imaging, Chambers et al.72 demonstrated that subjecting cells to hypotonic or hypertonic culture conditions resulted in a respective decrease or increase in the viscosity of the endoplasmic reticulum (ER), mirroring changes in the cytoplasm, while the mitochondria remained relatively unaffected. Interestingly, we show that the cytoplasm of cells adherent on 2D substrates display a considerably higher viscosity compared to cells encapsulated in 3D hydrogels, presumably due to an enhanced stress fiber formation and actomyosin contractility. A similar explanation might hold true for cells embedded in stiff compared to compliant 3D hydrogels, where the cytoplasm in the former group displays higher trends in viscosity than the latter, even though the difference is not statistically significant.
Apart from being contact-free, an important feature of Brillouin spectroscopy is the possibility to extract multiple readouts from both elastic and viscous regimes, which offers additional opportunities not accessible by current conventional methods. Still, care must be taken when interpreting M and η from Brillouin shift measurements. As extensively discussed elsewhere,43 the spatial and temporal scales of Brillouin measurements are much shorter than conventional AFM, questioning as to whether the frequency range (GHz) at which biomechanical properties are probed is indeed physiologically relevant. In addition, the type of ‘stiffness’ provided by Brillouin measurements is fundamentally different from the Young's modulus (E). The latter considers the resistance to shape changes where the material is not confined in the direction orthogonal being tested. In contrast, the longitudinal modulus test the elastic resistance while the material is constrained laterally and therefore not allowed to expand. This results in differences between M and E for highly hydrated (>90%) materials,73 as M is more sensitive to changes in the mechanical properties of the liquid component in a material than E. Nonetheless, cells do not fall under this category (∼60–80% water content).43 This was shown by a comparative study, where fibroblasts were subjected to mechanical and cytoskeletal perturbations, after which they displayed comparable variation of Brillouin shifts and AFM Young's moduli.45 That being said, improving instrument sensitivity will increasingly facilitate the detection of even small variations in the compressibility properties of different components.43,74
Recent efforts are pointing towards liquid–solid-like transition processes participating in the local increase of intracellular ρ, which was shown to contribute to the stiffening of the cytoplasm and growth arrest in yeast cells.13,15 Likewise, how the nucleus and cytoplasm in cells interact with each other, and in what way such an interplay is influenced by extracellular cues, is still an underexplored field. One reason is the practical inaccessibility in a non-invasive way using conventional instruments. With the advent of state-of-the-art optical techniques such as ODT and Brillouin microscopy, it will become easier to address such questions in a non-invasive manner.
Conclusions
The effect of ECM-provided dimensionality is being increasingly recognized in cell biology. Nonetheless, less is known about its effect on sub-cellular ρ distribution and the potential physiological changes it might accompany. Using a combined epifluorescence-ODT setup, we showed that MDA-MB-231 cells encapsulated in 3D alginate hydrogels display a higher RI and ρ in the nucleus than the cytoplasm, which is different to the situation where the cells adhere to 2D substrates. This RI and ρ distribution coincides with a higher M and η for the nucleus than the cytoplasm, measured using a confocal Brillouin-epifluorescence microscope. Furthermore, the nucleus and cytoplasm of cells encapsulated in stiff 3D alginate hydrogels displayed higher M and η compared to cells in compliant 3D alginate hydrogels. Changes in biophysical properties such as intracellular osmolarity, cytoplasmic/nuclear stiffening and mass distribution have been associated with alterations of cell growth and division. Deregulation of these processes have been linked to various diseases; nevertheless, little is known about the underlying mechanisms governing such alterations. Even less is understood about the role of microenvironmental changes in this context. The ability to visualize and quantify intracellular biophysical properties at the single-cell level with non-invasive techniques is a first and important step towards better understanding of a wide variety of biological processes, in particular those associated with alterations in ρ distribution, such as dormancy, apoptosis, cell growth or stem cell differentiation.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was funded by the Deutsche Forschungsgemeinschaft (DFG) Emmy Noether grant (CI 203/2-1 to A. C.), a DFG research grant (GU 612/8-1 to J. G.), a “Life? A Fresh Scientific Approach to the Basic Principles of Life” research grant from the Volkswagen Foundation (92847 to J. G.), and an Alexander von Humboldt Professorship (to J. G.). A. T. is fellow of the Mildred Scheel Early Career Center Dresden funded by the German Cancer Aid (Deutsche Krebshilfe). H. M. T. thanks the International Max Planck Research School (IMPRS) on Multiscale Bio Systems for financial support. Additionally, the authors would like to acknowledge Peter Fratzl for scientific discussion.References
- D. Di Carlo, J. Lab. Autom., 2012, 17, 32–42 CrossRef CAS.
- E. M. Darling and D. Di Carlo, Annu. Rev. Biomed. Eng., 2015, 17, 35–62 CrossRef CAS.
- M. Urbanska, M. Winzi, K. Neumann, S. Abuhattum, P. Rosendahl, P. Müller, A. Taubenberger, K. Anastassiadis and J. Guck, Development, 2017, 144, 4313–4321 CrossRef CAS.
- J. Lin, D. Kim, H. T. Tse, P. Tseng, L. Peng, M. Dhar, S. Karumbayaram and D. Di Carlo, Microsyst. Nanoeng., 2017, 3, 17013 CrossRef CAS.
- C. J. Chan, C.-P. Heisenberg and T. Hiiragi, Curr. Biol., 2017, 27, R1024–R1035 CrossRef CAS.
- T. Mammoto and D. E. Ingber, Development, 2010, 137, 1407–1420 CrossRef CAS.
- J. C. Benech, N. Benech, A. I. Zambrana, I. Rauschert, V. Bervejillo, N. Oddone and J. P. Damián, Am. J. Physiol.: Cell Physiol., 2014, 307, C910–C919 CrossRef CAS.
- A. E. Ekpenyong, G. Whyte, K. Chalut, S. Pagliara, F. Lautenschläger, C. Fiddler, S. Paschke, U. F. Keyser, E. R. Chilvers and J. Guck, PLoS One, 2012, 7, e45237 CrossRef CAS.
- J. Guck, S. Schinkinger, B. Lincoln, F. Wottawah, S. Ebert, M. Romeyke, D. Lenz, H. M. Erickson, R. Ananthakrishnan, D. Mitchell, J. Käs, S. Ulvick and C. Bilby, Biophys. J., 2005, 88, 3689–3698 CrossRef CAS.
- C. N. Holenstein, A. Horvath, B. Schär, A. D. Schoenenberger, M. Bollhalder, N. Goedecke, G. Bartalena, O. Otto, M. Herbig, J. Guck, D. A. Müller, J. G. Snedeker and U. Silvan, Mol. Biol. Cell, 2019, 30, 887–898 CrossRef CAS.
- V. Swaminathan, K. Mythreye, E. T. O’Brien, A. Berchuck, G. C. Blobe and R. Superfine, Cancer Res., 2011, 71, 5075–5080 CrossRef CAS.
- A. V. Taubenberger, S. Girardo, N. Träber, E. Fischer-Friedrich, M. Kräter, K. Wagner, T. Kurth, I. Richter, B. Haller, M. Binner, D. Hahn, U. Freudenberg, C. Werner and J. Guck, Adv. Biosyst., 2019, 1900128, 1900128 CrossRef.
- M. C. Munder, D. Midtvedt, T. Franzmann, E. Nüske, O. Otto, M. Herbig, E. Ulbricht, P. Müller, A. Taubenberger, S. Maharana, L. Malinovska, D. Richter, J. Guck, V. Zaburdaev and S. Alberti, eLife, 2016, 5, 1–30 CrossRef.
- S. Toné, K. Sugimoto, K. Tanda, T. Suda, K. Uehira, H. Kanouchi, K. Samejima, Y. Minatogawa and W. C. Earnshaw, Exp. Cell Res., 2007, 313, 3635–3644 CrossRef.
- S. Abuhattum, K. Kim, T. M. Franzmann, A. Eßlinger, D. Midtvedt, R. Schlüßler, S. Möllmert, H.-S. Kuan, S. Alberti, V. Zaburdaev and J. Guck, Front. Phys., 2018, 6, 131 CrossRef.
- G. Popescu, Y. Park, N. Lue, C. Best-Popescu, L. Deflores, R. R. Dasari, M. S. Feld and K. Badizadegan, Am. J. Physiol.: Cell Physiol., 2008, 295, C538–C544 CrossRef CAS.
- H. G. Davies and M. H. F. Wilkins, Nature, 1952, 169, 541 CrossRef CAS.
- P. Y. Liu, L. K. Chin, W. Ser, H. F. Chen, C.-M. Hsieh, C.-H. Lee, K.-B. Sung, T. C. Ayi, P. H. Yap, B. Liedberg, K. Wang, T. Bourouina and Y. Leprince-Wang, Lab Chip, 2016, 16, 634–644 RSC.
- P. M. A. Sloot, A. G. Hoekstra and C. G. Figdor, Cytometry, 1988, 9, 636–641 CrossRef CAS.
- A. Brunsting and P. F. Mullaney, Biophys. J., 1974, 14, 439–453 CrossRef CAS.
- R. Drezek, M. Guillaud, T. Collier, I. Boiko, A. Malpica, C. Macaulay, M. Follen and R. R. Richards-Kortum, J. Biomed. Opt., 2003, 8, 7 CrossRef.
- V. V. Tuchin, J. Biomed. Opt., 1997, 2, 401 CrossRef CAS.
- M. Schürmann, J. Scholze, P. Müller, J. Guck and C. J. Chan, J. Biophotonics, 2016, 9, 1068–1076 CrossRef.
- Z. A. Steelman, W. J. Eldridge, J. B. Weintraub and A. Wax, J. Biophotonics, 2017, 10, 1714–1722 CrossRef CAS.
- R. Imai, T. Nozaki, T. Tani, K. Kaizu, K. Hibino, S. Ide, S. Tamura, K. Takahashi, M. Shribak and K. Maeshima, Mol. Biol. Cell, 2017, 28, 3349–3359 CrossRef CAS.
- H. Hassani and E. Kreysing, Opt. Lett., 2019, 44, 1359 CrossRef CAS.
- N. J. Mudrak, P. S. Rana and M. A. Model, Cytometry, Part A, 2018, 93, 297–304 CrossRef.
- K. Kim and J. Guck, Biophys. J., 2020, 119(10), 1946–1957 CrossRef CAS.
- P. A. Kenny, G. Y. Lee, C. A. Myers, R. M. Neve, J. R. Semeiks, P. T. Spellman, K. Lorenz, E. H. Lee, M. H. Barcellos-Hoff, O. W. Petersen, J. W. Gray and M. J. Bissell, Mol. Oncol., 2007, 1, 84–96 CrossRef CAS.
- N. Huebsch, P. R. Arany, A. S. Mao, D. Shvartsman, O. A. Ali, S. A. Bencherif, J. Rivera-Feliciano and D. J. Mooney, Nat. Mater., 2010, 9, 518–526 CrossRef CAS.
- S. Raghavan, C. J. Shen, R. A. Desai, N. J. Sniadecki, C. M. Nelson and C. S. Chen, J. Cell Sci., 2010, 123, 2877–2883 CrossRef CAS.
- B. M. Baker and C. S. Chen, J. Cell Sci., 2012, 125, 3015–3024 CrossRef CAS.
- N. Huebsch, P. R. Arany, A. S. Mao, D. Shvartsman, O. A. Ali, S. A. Bencherif, J. Rivera-Feliciano and D. J. Mooney, Nat. Mater., 2010, 9, 518–526 CrossRef CAS.
- R. S. Stowers, A. Shcherbina, J. Israeli, J. J. Gruber, J. Chang, S. Nam, A. Rabiee, M. N. Teruel, M. P. Snyder, A. Kundaje and O. Chaudhuri, Nat. Biomed. Eng., 2019, 3(12), 1009–1019 CrossRef.
- O. Chaudhuri, L. Gu, M. Darnell, D. Klumpers, S. A. Bencherif, J. C. Weaver, N. Huebsch and D. J. Mooney, Nat. Commun., 2015, 6, 6365 CrossRef CAS.
- O. Chaudhuri, L. Gu, D. Klumpers, M. Darnell, S. A. Bencherif, J. C. Weaver, N. Huebsch, H. Lee, E. Lippens, G. N. Duda and D. J. Mooney, Nat. Mater., 2016, 15, 326–334 CrossRef CAS.
- O. Chaudhuri, J. Cooper-White, P. A. Janmey, D. J. Mooney and V. B. Shenoy, Nature, 2020, 584, 535–546 CrossRef CAS.
- A. Lueckgen, D. S. Garske, A. Ellinghaus, D. J. Mooney, G. N. Duda and A. Cipitria, Biomaterials, 2019, 217, 119294 CrossRef CAS.
- A. Lueckgen, D. S. Garske, A. Ellinghaus, R. M. Desai, A. G. Stafford, D. J. Mooney, G. N. Duda and A. Cipitria, Biomaterials, 2018, 181, 189–198 CrossRef CAS.
- M. Krieg, G. Fläschner, D. Alsteens, B. M. Gaub, W. H. Roos, G. J. L. Wuite, H. E. Gaub, C. Gerber, Y. F. Dufrêne and D. J. Müller, Nat. Rev. Phys., 2019, 1, 41–57 CrossRef.
- R. M. Hochmuth, J. Biomech., 2000, 33, 15–22 CrossRef CAS.
- H. Zhang and K.-K. Liu, J. R. Soc., Interface, 2008, 5, 671–690 CrossRef CAS.
- R. Prevedel, A. Diz-Muñoz, G. Ruocco and G. Antonacci, Nat. Methods, 2019, 16, 969–977 CrossRef CAS.
- G. Antonacci, T. Beck, A. Bilenca, J. Czarske, K. Elsayad, J. Guck, K. Kim, B. Krug, F. Palombo, R. Prevedel and G. Scarcelli, Biophys. Rev., 2020, 12(3), 615–624 CrossRef.
- G. Scarcelli, W. J. Polacheck, H. T. Nia, K. Patel, A. J. Grodzinsky, R. D. Kamm and S. H. Yun, Nat. Methods, 2015, 12, 1132–1134 CrossRef CAS.
- R. Schlüßler, S. Möllmert, S. Abuhattum, G. Cojoc, P. Müller, K. Kim, C. Möckel, C. Zimmermann, J. Czarske and J. Guck, Biophys. J., 2018, 115, 911–923 CrossRef.
- O. Chaudhuri, S. T. Koshy, C. Branco da Cunha, J.-W. Shin, C. S. Verbeke, K. H. Allison and D. J. Mooney, Nat. Mater., 2014, 13, 970–978 CrossRef CAS.
- S. T. Gould, N. J. Darling and K. S. Anseth, Acta Biomater., 2012, 8, 3201–3209 CrossRef CAS.
- A. Sakaue-Sawano, T. Kobayashi, K. Ohtawa and A. Miyawaki, BMC Cell Biol., 2011, 12, 2 CrossRef CAS.
- K. Kim, W. S. Park, S. Na, S. Kim, T. Kim, W. Do Heo and Y. Park, Biomed. Opt. Express, 2017, 8, 5688 CrossRef CAS.
- E. Cuche, P. Marquet and C. Depeursinge, Appl. Opt., 2000, 39, 4070 CrossRef CAS.
- E. Wolf, Opt. Commun., 1969, 1, 153–156 CrossRef.
- Y. Sung, W. Choi, C. Fang-Yen, K. Badizadegan, R. R. Dasari and M. S. Feld, Opt. Express, 2009, 17, 266 CrossRef CAS.
- K. Kim, H. Yoon, M. Diez-Silva, M. Dao, R. R. Dasari and Y. Park, J. Biomed. Opt., 2013, 19, 1 Search PubMed.
- P. Müller, M. Schürmann and J. Guck, The Theory of Diffraction Tomography, 2016, arXiv:1507.00466v3 Search PubMed.
- H. Zhao, P. H. Brown and P. Schuck, Biophys. J., 2011, 100, 2309–2317 CrossRef CAS.
- T. A. Zangle and M. A. Teitell, Nat. Methods, 2014, 11, 1221–1228 CrossRef CAS.
- G. Scarcelli and S. H. Yun, Opt. Express, 2011, 19, 10913 CrossRef.
- J. Lee, H. Kim, H. Cho, Y. Jo, Y. Song, D. Ahn, K. Lee, Y. Park and S.-J. Ye, IEEE Access, 2019, 7, 83449–83460 Search PubMed.
- W. Sung, Y. Jeong, H. Kim, H. Jeong, C. Grassberger, S. Jung, G.-O. Ahn, I. H. Kim, J. Schuemann, K. Lee and S.-J. Ye, Radiat. Res., 2018, 190, 558 CAS.
- M. Dembo and Y.-L. Wang, Biophys. J., 1999, 76, 2307–2316 CrossRef CAS.
- J. L. Tan, J. Tien, D. M. Pirone, D. S. Gray, K. Bhadriraju and C. S. Chen, Proc. Natl. Acad. Sci. U. S. A., 2003, 100, 1484–1489 CrossRef CAS.
- F. Alisafaei, D. S. Jokhun, G. V. Shivashankar and V. B. Shenoy, Proc. Natl. Acad. Sci. U. S. A., 2019, 116, 13200–13209 CrossRef CAS.
- J. Y. Lee, J. K. Chang, A. A. Dominguez, H. Lee, S. Nam, J. Chang, S. Varma, L. S. Qi, R. B. West and O. Chaudhuri, Nat. Commun., 2019, 10, 1848 CrossRef.
- K. Damodaran, S. Venkatachalapathy, F. Alisafaei, A. V. Radhakrishnan, D. Sharma Jokhun, V. B. Shenoy and G. V. Shivashankar, Mol. Biol. Cell, 2018, 29, 3039–3051 CrossRef CAS.
- N. Jain, K. V. Iyer, A. Kumar and G. V. Shivashankar, Proc. Natl. Acad. Sci. U. S. A., 2013, 110, 11349–11354 CrossRef CAS.
- S. M. Galloway, D. A. Deasy, C. L. Bean, A. R. Kraynak, M. J. Armstrong and M. O. Bradley, Mutat. Res., 1987, 189, 15–25 CAS.
- A. L. Olins, T. J. Gould, L. Boyd, B. Sarg and D. E. Olins, Nucleus, 2020, 11, 1–18 CrossRef.
- A. F. Lima, G. May, J. Díaz-Colunga, S. Pedreiro, A. Paiva, L. Ferreira, T. Enver, F. J. Iborra and R. Pires das Neves, Sci. Rep., 2018, 8, 7210 CrossRef CAS.
- D. J. McGrail, K. M. McAndrews, C. P. Brandenburg, N. Ravikumar, Q. M. N. Kieu and M. R. Dawson, Biophys. J., 2015, 109, 1334–1337 CrossRef CAS.
- M. Guo, A. F. Pegoraro, A. Mao, E. H. Zhou, P. R. Arany, Y. Han, D. T. Burnette, M. H. Jensen, K. E. Kasza, J. R. Moore, F. C. Mackintosh, J. J. Fredberg, D. J. Mooney, J. Lippincott-Schwartz and D. A. Weitz, Proc. Natl. Acad. Sci. U. S. A., 2017, 114, E8618–E8627 CrossRef CAS.
- J. E. Chambers, M. Kubánková, R. G. Huber, I. López-Duarte, E. Avezov, P. J. Bond, S. J. Marciniak and M. K. Kuimova, ACS Nano, 2018, 12, 4398–4407 CrossRef CAS.
- P.-J. Wu, I. V. Kabakova, J. W. Ruberti, J. M. Sherwood, I. E. Dunlop, C. Paterson, P. Török and D. R. Overby, Nat. Methods, 2018, 15, 561–562 CrossRef CAS.
- P. Shao, T. G. Seiler, A. M. Eltony, A. Ramier, S. J. J. Kwok, G. Scarcelli, R. Pineda II and S.-H. Yun, Invest. Ophthalmol. Vis. Sci., 2018, 59, 3020 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/d0sm01556c |
| This journal is © The Royal Society of Chemistry 2021 |