Viscosity of cohesive granular flows†
Matthew
Macaulay
 *a and
Pierre
Rognon
b
*a and
Pierre
Rognon
b
aSchool of Civil Engineering, The University of Sydney, Sydney, NSW 2006, Australia. E-mail: matthew.macaulay@sydney.edu.au
bSchool of Civil Engineering, The University of Sydney, Sydney, NSW 2006, Australia. E-mail: pierre.rognon@sydney.edu.au; Tel: +61 2 9351 5402
First published on 29th October 2020
Abstract
Cohesive granular materials such as wet sand, snow, and powders can flow like a viscous liquid. However, the elementary mechanisms of momentum transport in such athermal particulate fluids are elusive. As a result, existing models for cohesive granular viscosity remain phenomenological and debated. Here we use discrete element simulations of plane shear flows to measure the viscosity of cohesive granular materials, while tuning the intensity of inter-particle adhesion. We establish that two adhesion-related, dimensionless numbers control their viscosity. These numbers compare the force and energy required to break a bond to the characteristic stress and kinetic energy in the flow. This progresses the commonly accepted view that only one dimensionless number could control the effect of adhesion. The resulting scaling law captures strong, non-Newtonian variations in viscosity, unifying several existing viscosity models. We then directly link these variations in viscosity to adhesion-induced modifications in the flow micro-structure and contact network. This analysis reveals the existence of two modes of momentum transport, involving either grain micro-acceleration or balanced contact forces, and shows that adhesion only affects the latter. This advances our understanding of rheological models for granular materials and other soft materials such as emulsions and suspensions, which may also involve inter-particle adhesive forces.
Continuum fluid mechanics models are of considerable interest to predict the dynamics of natural and industrial granular flows. However, they hinge on the knowledge of the shear viscosity of granular fluids.
A robust scaling law for granular viscosity has been established for dry grains which have no contact adhesive force. By analogy with Newtonian fluids, the apparent granular viscosity η was defined as the ratio of the shear stress τ and shear rate ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) : η = τ/|
: η = τ/|![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) |. A major breakthrough was the identification of a frictional constitutive law relating the bulk shear stress to the pressure P, τ = μP. Like Coulomb friction, it involves a coefficient of friction μ. The complexity of granular flows is rationalised by a unique friction law μ(I) relating the friction coefficient to a single dimensionless number, called the inertial number
|. A major breakthrough was the identification of a frictional constitutive law relating the bulk shear stress to the pressure P, τ = μP. Like Coulomb friction, it involves a coefficient of friction μ. The complexity of granular flows is rationalised by a unique friction law μ(I) relating the friction coefficient to a single dimensionless number, called the inertial number 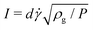 , involving the grain size d and density ρg. This led to establishing a general scaling law for granular viscosity:1–4
, involving the grain size d and density ρg. This led to establishing a general scaling law for granular viscosity:1–4
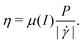 | (1) |
This law captures complex non-Newtonian features of granular flows, including shear-thinning and a viscosity divergence when flows stop. Its domain of validity has been extended to granular materials submerged in a fluid of viscosity ηf, by introducing a second dimensionless number J = ηf/P contributing to a friction law that became μ(I,J).5,6
However, there is no consensus on extending this viscosity scaling to the vast range of granular materials featuring inter-granular adhesion. These typically include materials with grain size smaller than 100 μm which tend to adhere via van der Waals surface interactions or wet grains of all sizes which stick via capillary forces. The difficulty in establishing a cohesive granular viscosity is that these modes of adhesion have different physical characteristics. Nonetheless, they all involve two elementary contact parameters: an adhesion force f0 and an adhesion energy w0. These correspond to the minimum force and energy needed to unstick two grains.
Adhesive forces are known to strongly affect the micro-structure of granular flows. They induce the formation of large clusters in the flow,7–9 which enhances the process of shear-induced dilation.10–15 These micro-structural changes generally coincide with an increase in friction. The usual approach to rationalise this effect is to express a friction law, which depends on the inertial number and a dimensionless number 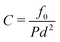 . This compares the contact tensile strength f0 to the typical force scale related to the pressure P. Various phenomenological expressions for μ(I,C) were introduced, which capture measurements made in many flow configurations and with different modes of adhesion.7,8,12,16–21 The consensus is that the friction is not significantly enhanced at low values of C ≲ 1 and then increases with C. This transition delineates between a non-cohesive and a cohesive flow regime. However, several observations indicate that the viscosity of cohesive granular flows is not solely controlled by the number C: at a fixed value of C, grains that are softer or more dissipative lead to larger friction,22 while a faster shear rate induces a decrease in friction.16,17
. This compares the contact tensile strength f0 to the typical force scale related to the pressure P. Various phenomenological expressions for μ(I,C) were introduced, which capture measurements made in many flow configurations and with different modes of adhesion.7,8,12,16–21 The consensus is that the friction is not significantly enhanced at low values of C ≲ 1 and then increases with C. This transition delineates between a non-cohesive and a cohesive flow regime. However, several observations indicate that the viscosity of cohesive granular flows is not solely controlled by the number C: at a fixed value of C, grains that are softer or more dissipative lead to larger friction,22 while a faster shear rate induces a decrease in friction.16,17
We propose that the apparent discrepancies in existing scaling laws for cohesive granular viscosity reflect the existence of different cohesive flow regimes controlled either by the strength f0 or the energy w0 of adhesive forces. In this paper, we assess this assumption using a set of simulations of steady plane shear flows of adhesive grains, with varying combinations of these two adhesive parameters. The goal of these numerical experiments is to simultaneously measure the material viscosity and to identify the internal mechanisms of momentum transport controlling it.
Methods
Measuring viscosity in simulated plane shear flows
To measure the viscosity of cohesive granular flows, we used a discrete element method to simulate bi-dimensional plane shear flows of 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 sticky grains. This section presents the key physical properties of the grains and of the flows configuration.
000 sticky grains. This section presents the key physical properties of the grains and of the flows configuration.
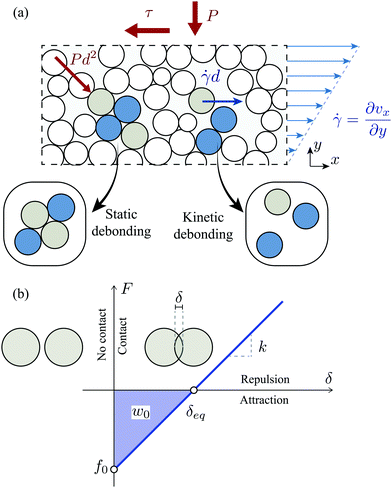
The plane shear flow configuration is illustrated in Fig. 1a. It involves prescribing both the normal stress P and the shear rate ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) . This is achieved using Lees–Edwards periodic boundary conditions to avoid any solid boundaries and subsequent flow heterogeneities they would induce.23 The normal stress is controlled by allowing the cell height to expand or contract during the flow. The advantage of this configuration is to produce steady flows characterised by a homogeneous shear rate
. This is achieved using Lees–Edwards periodic boundary conditions to avoid any solid boundaries and subsequent flow heterogeneities they would induce.23 The normal stress is controlled by allowing the cell height to expand or contract during the flow. The advantage of this configuration is to produce steady flows characterised by a homogeneous shear rate ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) , normal stress P and shear stresses τ. It thus enables us to prescribe a single value of I and to directly measure the resulting friction coefficient μ(I).
, normal stress P and shear stresses τ. It thus enables us to prescribe a single value of I and to directly measure the resulting friction coefficient μ(I).
Grains are disks of diameter d ± 20%. This slight polydispersity is introduced to prevent shear-induced crystallisation. Grains interact via direct contacts with their neighbours. Contact forces are comprised of friction, elastic repulsion, dissipation and adhesion. The inter-granular friction coefficient is 0.5 and the normal, non-cohesive coefficient of restitution is 0.5 in all simulations. The effect of these parameters on the flow properties can be found in ref. 2 for non-cohesive flows and in ref. 22 and 24 for cohesive flows.
The elastic repulsion follows a Hookean law Fe(δ) = kδ where δ measures the interpenetration of two contacting grains and k is an elastic stiffness parameter. An elementary dimensionless number measuring the softness of the grains is:
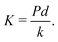 | (2) |
The adhesion model is chosen to be the simplest: a constant attractive normal force Fa(δ) = −f0 is active while two grains are in contact. The resulting normal force between two immobile contacting grains F = Fe + Fa is illustrated in Fig. 1b. It is characterised by an equilibrium position 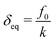 , a maximum strength f0 and an adhesion energy
, a maximum strength f0 and an adhesion energy 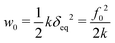 . Accordingly, two elementary dimensionless numbers characterise the intensity of adhesion in such flows:
. Accordingly, two elementary dimensionless numbers characterise the intensity of adhesion in such flows:
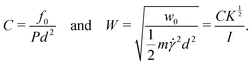 | (3) |
The cohesion energy number W compares the cohesion energy to the characteristic kinetic energy of grains colliding at a relative velocity ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) d. This dimensional analysis points out two processes by which a pair of contacting grains may be pulled apart, which we called static and kinetic de-bonding. An illustration of these processes is shown in Fig. 1a. Static de-bonding is likely at low cohesion strength (C ≲ 1), when sustained forces of magnitude Pd2 exceed the adhesion strength f0. Kinetic de-bonding is likely at low values of cohesion energy (W ≲ 1), when colliding grains have enough kinetic energy to overcome the adhesion energy w0.
d. This dimensional analysis points out two processes by which a pair of contacting grains may be pulled apart, which we called static and kinetic de-bonding. An illustration of these processes is shown in Fig. 1a. Static de-bonding is likely at low cohesion strength (C ≲ 1), when sustained forces of magnitude Pd2 exceed the adhesion strength f0. Kinetic de-bonding is likely at low values of cohesion energy (W ≲ 1), when colliding grains have enough kinetic energy to overcome the adhesion energy w0.
Results
Cohesion strength and energy control viscosity
In order to quantify the effect of adhesive forces of granular viscosity, we simulated a series of plane shear flows, selecting a value of inertial number, cohesion-strength number and stiffness number in the ranges 5 × 10−3 ≤ I ≤ 0.3, 0 ≤ C ≤ 10, and 10−5 ≤ K ≤ 10−3. With no cohesion, these values of K are small enough to not affect the rheology;2 the rheology of softer grains is discussed in ref. 12, 14 and 24. The choice of these three numbers determines the value of the cohesive-energy number W(C,I,K), which ranges from 0 to 63.Once steady and homogeneous shear flow developed, the friction μ was measured by averaging the stresses across the entire shear cell during 15 shear deformation. Fig. 2a shows the resulting set of friction laws μ(I,C), obtained at a fixed stiffness K = 10−3. At low cohesion strength (C ≲ 1), the friction law is similar to that of non-cohesive grains (C = 0). It follows the established empirical law:1–4
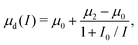 | (4) |
 | ||
| Fig. 2 Viscosity measurements. (a) Friction law μ(I) measured at different cohesion strengths C (the stiffness number is fixed at K = 10−3 in a, b, d): markers are the simulation results and solid lines represent the proposed phenomenological model eqn (5) and (6); some flows developed heterogenous shear state in the form of a persistent shear bands (see the ESI†). (b) Quasi-static friction μ(I → 0): markers represent the friction measured at the lowest value of the inertial number I = 5 × 10−3; the solid line is the best linear fit of this data: μ(I → 0) = 0.29 + 0.066C. (c) Friction enhancement factor g scaling with particle softness; the lines represents the proposed model in eqn (5) and (6). (d) Viscosity regimes: markers colours indicate measured values of the friction enhancement factor g(I,C) = μ/μd using eqn (4); background colour is the model in eqn (6) calculated for various value of W corresponding to different combinations of C and I; the white lines at C = 1 and W = 1 delineates the cohesive and non-cohesive regimes; the dashed line C = W delineates the cohesive-strength and cohesive-energy regimes. | ||
In contrast, the friction may be significantly increased at higher cohesion strengths (C ≳ 1). Then, the friction law μ(I) measured at a constant value of C are qualitatively different from their non-cohesive counterpart μd(I). Strikingly, a phenomenon of shear-rate weakening occurs at the highest values of C, by which the friction coefficient decreases as the inertial number is increased.
We propose a phenomenological scaling law to capture the measured cohesive friction μ(I,C) that involves not only C but also the cohesion energy W. We choose the following functional form:
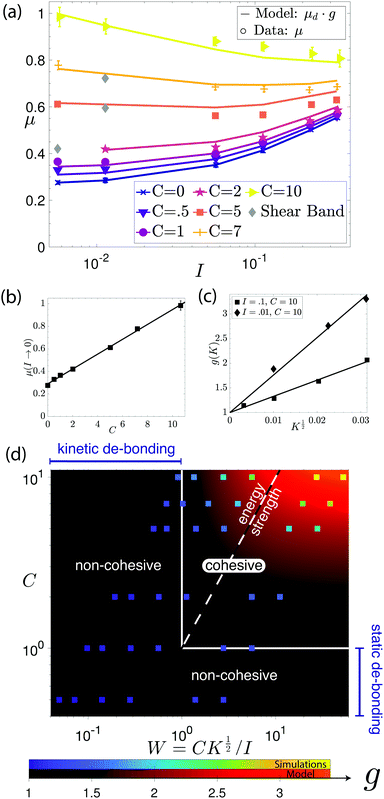
| μ = μd(I)g(W,I) | (5) |
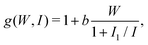 | (6) |
This chosen functional form is not derived from a physical process and other choices could possibly capture the data equally well. Nonetheless, it conveniently highlights three ways cohesion might affect granular viscosity. Firstly, any effect of adhesion is included into the term g(W,I), which may be seen as a friction enhancing factor induced by adhesion. This readily distinguishes a regime of low cohesion (g(W,I) ≈ 1) where friction is unaffected and similar to that of non-cohesive grains, to a regime of high cohesion (g(W,I) > 1) where adhesion significantly enhances friction. This criterion delineates the non-cohesive and cohesive flow regimes.
The law in eqn (6) quantifies the friction enhancement in the cohesive flow regime and indicates a transition between two cohesive regimes. At low inertial number, it reduces to
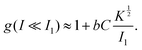 | (7) |
The effect of adhesion on friction is then independent from the cohesion energy W and from the inertial number. At a fixed grain stiffness, it is solely controlled by the cohesion strength C. Fig. 2b confirms that in the limit of I → 0, the friction μ increases linearly with C for a fixed value of stiffness K. We call this flow regime cohesive-strength. This linear increase of the friction with C is consistent with several existing results.7,8,10–12,21 Furthermore, this friction scaling with the stiffness number K is qualitatively consistent with the observation that softer grains (larger K) lead to an increase in friction.22
In contrast, at high inertial numbers eqn (6) reduces to:
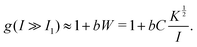 | (8) |
The effect of adhesion on friction is then controlled by the adhesion energy W. We call this flow regime cohesive-energy. The scaling in eqn (8) is qualitatively consistent with the observations that softer grains lead to an increase in friction;22 that at high inertial numbers, the scale of kinetic energy is important,25 and may induce a decrease in friction for cohesive flows with a fixed value of C,16,17 as with granular suspensions.26Fig. 2b shows the friction μ measured in flows performed at a fixed value of I and C, and with differing stiffness number K. It confirms that g linearly increases with K½.
According to eqn (6), the transition between the cohesion-strength and cohesion-energy regimes occurs at I ≈ I1. The cohesion energy is then 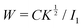 . Our results indicate that the ratio K½/I1 is of the order of unity (I1 = 0.063, and K½ = 0.03). As a first order approximation, we then propose a regime transition for C = W. The cohesive-strength regime develops for C < W, and the mechanism of static de-bonding is typically the weakest way to pull grains apart and therefore controls the effect of adhesion. Reciprocally, the cohesive-energy regime develops for C > W.
. Our results indicate that the ratio K½/I1 is of the order of unity (I1 = 0.063, and K½ = 0.03). As a first order approximation, we then propose a regime transition for C = W. The cohesive-strength regime develops for C < W, and the mechanism of static de-bonding is typically the weakest way to pull grains apart and therefore controls the effect of adhesion. Reciprocally, the cohesive-energy regime develops for C > W.
Fig. 2d maps the occurrence of these three regimes (non-cohesive, cohesive-strength and cohesive energy), by plotting the measured friction enhancement 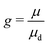 as a function of the cohesion strength C and energy W, keeping the stiffness K = 10−3 constant. It confirms that g becomes significantly larger than one only if both cohesion strength and energy are greater than one. This progresses the view that cohesive and non-cohesive regimes may be delineated by only one dimensionless number.
as a function of the cohesion strength C and energy W, keeping the stiffness K = 10−3 constant. It confirms that g becomes significantly larger than one only if both cohesion strength and energy are greater than one. This progresses the view that cohesive and non-cohesive regimes may be delineated by only one dimensionless number.
Section 3 of the ESI† presents a detailed analysis of previously proposed model of friction laws. It provides evidence that previous models successfully captured either cohesive-strength or the cohesive-energy regime, but not both. The rheology proposed here distinguishes these two cohesive regimes, enabling one to reconcile the apparent differences in these models.
Internal mechanisms of momentum transport
We now seek to understand the behaviour of cohesive viscosity by establishing the elementary mechanisms of momentum transport controlling it. As a starting point, we consider the basic definition of stress in granular materials in terms of individual contact force fc and contact branch vector lc, which joins the centre of a grain to the point of contact. The average stress tensor σ is given by: σαβ = nc〈sym(fαclβc)〉. nc is the contact density or number of contacts per unit volume; sym(fαlβ) is the symmetric part of an individual contact moment tensor fαclβc. 〈·〉 is the averaging operator including all contacts in the flow. As we observed that the moment tensor is symmetrical, the shear stress may be expressed as τ = nc〈fylx〉 = nc〈fxly〉.The shear stress represents the flux of momentum through the flow. This expression relates it to individual contacts, which readily bridges the continuum scale to micro-dynamical properties. However, it does not reveal any specific mechanism of momentum transport. To highlight them, we use a mathematical expansion of this expression introduced in ref. 27: 〈fylx〉 = 〈fy〉〈lx〉 + ![[f with combining circumflex]](https://www.rsc.org/images/entities/i_char_0066_0302.gif) y
y![[l with combining circumflex]](https://www.rsc.org/images/entities/i_char_006c_0302.gif) x
x![[capital script C]](https://www.rsc.org/images/entities/char_e522.gif) , where
, where ![[f with combining circumflex]](https://www.rsc.org/images/entities/i_char_0066_0302.gif) y and
y and ![[l with combining circumflex]](https://www.rsc.org/images/entities/i_char_006c_0302.gif) x are the standard deviation of the force and branch vector components, and
x are the standard deviation of the force and branch vector components, and ![[capital script C]](https://www.rsc.org/images/entities/char_e522.gif) is their correlation. Since the average force 〈fy〉 is null in steady flows, this reduces to 〈fylx〉 =
is their correlation. Since the average force 〈fy〉 is null in steady flows, this reduces to 〈fylx〉 = ![[f with combining circumflex]](https://www.rsc.org/images/entities/i_char_0066_0302.gif) y
y![[l with combining circumflex]](https://www.rsc.org/images/entities/i_char_006c_0302.gif) x
x![[capital script C]](https://www.rsc.org/images/entities/char_e522.gif) . We further observed that the term
. We further observed that the term ![[l with combining circumflex]](https://www.rsc.org/images/entities/i_char_006c_0302.gif) x is proportional to the grain size:
x is proportional to the grain size: ![[l with combining circumflex]](https://www.rsc.org/images/entities/i_char_006c_0302.gif) x ≈ αld with a constant αl ≈ 0.71 that we found to be virtually independent on adhesion and inertial number. This leads to the following expression:
x ≈ αld with a constant αl ≈ 0.71 that we found to be virtually independent on adhesion and inertial number. This leads to the following expression:
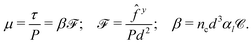 | (9) |
Hereafter, we refer to the dimensionless number ![[scr F, script letter F]](https://www.rsc.org/images/entities/char_e141.gif) as force fluctuations. This expression shows how macroscopic friction, and hence granular viscosity, is directly related to three measurable microscopic quantities: the contact density, the force fluctuations and the force correlation. The following presents how adhesion affects each of them.
as force fluctuations. This expression shows how macroscopic friction, and hence granular viscosity, is directly related to three measurable microscopic quantities: the contact density, the force fluctuations and the force correlation. The following presents how adhesion affects each of them.
Adhesion enhances contact density
This counter-intuitive observation is evidenced in Fig. 3a: at a given inertial number, the contact density of a cohesive flow is equal or larger than in a non-cohesive flow. This is unexpected as cohesion simultaneously enhances the process of shear-induced dilation. This discord reflects the potential for granular matter to form fragile force networks28 and the fact that the solid fraction ϕ decreases when the inertial number is increased. Fig. 3b shows that the solid fraction is significantly lower in cohesive flows than in non-cohesive flows, as previously observed.7,8,12–14 In a first approximation, we propose to capture these variations by the following dilatancy law:| ϕ = ϕd(I)h(C); | (10) |
| ϕd(I) ≈ ϕ0 − bϕI; h(C) ≈ 1 − cϕC. | (11) |
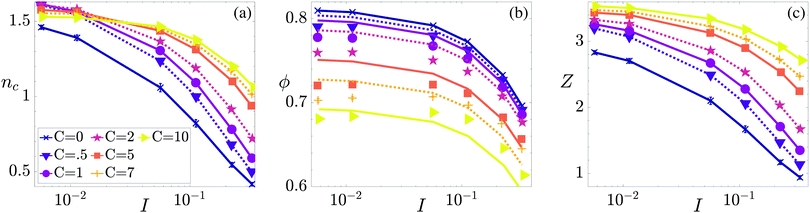 | ||
| Fig. 3 Microstructure of cohesive flows. (a) Contact density nc; (b) solid fraction ϕ; and (c) coordination number Z at a function of the flows’ inertial number I and cohesion strength C. Grain stiffness is constant K = 10−3. Markers are numerical results; lines in (b) are the best linear fits obtained using eqn (10) and (11). | ||
Having a higher contact density with a lower solid fraction is made possible by an increase in coordination number, which measures the average number of contacts per grain. The relation between these three quantities is nc = ϕZ. Fig. 3c shows that flows at high cohesion-strength, for instance C = 10, can keep a high coordination number even at large inertial number. Nonetheless, even flows with the highest cohesion-strength exhibit a drop in coordination number at high inertial numbers, which coincides with the onset of the cohesive-kinetic regime. This decrease may therefore be attributed to the process of kinetic de-bonding, which becomes effective at separating grains in this regime.
Adhesion enhances force fluctuations
Fig. 4a shows that the force fluctuations are generally enhanced in the presence of adhesive forces. This enhancement, which is very pronounced at low inertial numbers, vanishes at high inertial numbers. This can be understood by estimating the range of force magnitude that contacts transmit. This is illustrated in the contact network snapshots shown in Fig. 4d.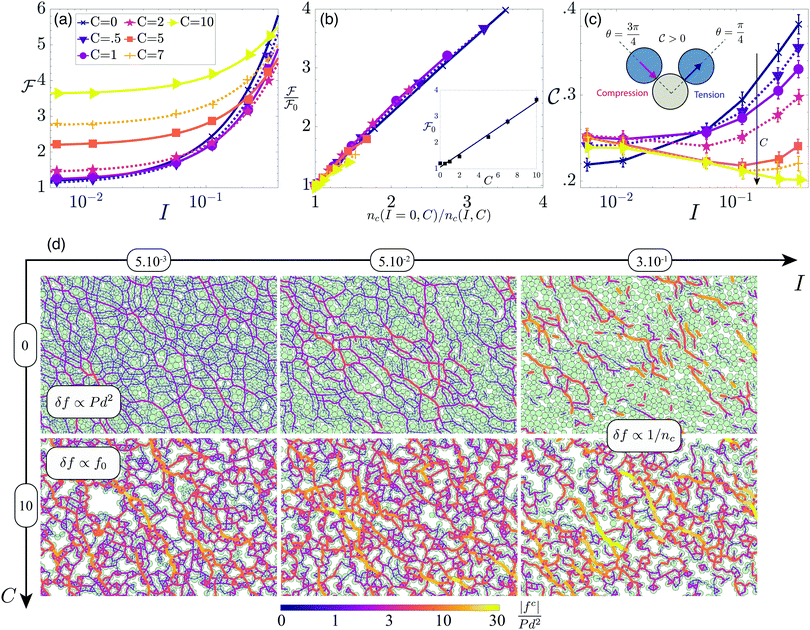 | ||
Fig. 4 Contact forces in cohesive flows at different inertial number and cohesion strength (constant grain stiffness K = 10−3). (a) Force fluctuations measuring the standard deviation of contact force y-component. (b) Force fluctuations as a function of the contact density; ![[scr F, script letter F]](https://www.rsc.org/images/entities/char_e141.gif) 0 = (I → 0) and nc(I → 0) are the quasi-static limit of the force fluctuations and contact density, which are approximated here by the value measured at the lowest inertial number I = 5 × 10−3. The inset shows how this quasi-static limit of force fluctuations increases linearly with cohesion; the line represents the best linear fit: 0 = (I → 0) and nc(I → 0) are the quasi-static limit of the force fluctuations and contact density, which are approximated here by the value measured at the lowest inertial number I = 5 × 10−3. The inset shows how this quasi-static limit of force fluctuations increases linearly with cohesion; the line represents the best linear fit: ![[scr F, script letter F]](https://www.rsc.org/images/entities/char_e141.gif) 0 = 1 + 0.26C. (c) Correlation between contact force and branch vector cross-components. The inset illustrate two contact orientations that maximise this term. (d) Snapshots of contact forces fc taken during steady and homogeneous shear flows. Lines join pairs of grains in contact with a width and colour representing the magnitude of the contact force on a logarithmic scale. The ESI† contains corresponding movies. 0 = 1 + 0.26C. (c) Correlation between contact force and branch vector cross-components. The inset illustrate two contact orientations that maximise this term. (d) Snapshots of contact forces fc taken during steady and homogeneous shear flows. Lines join pairs of grains in contact with a width and colour representing the magnitude of the contact force on a logarithmic scale. The ESI† contains corresponding movies. | ||
With no cohesion, the high solid fraction and coordination number enable a contact network to percolate through the packing and connect virtually every grain. This means that most grains and contacts are involved in carrying the stresses, which scale with P. Accordingly, the force fluctuations is of the order of ![[scr F, script letter F]](https://www.rsc.org/images/entities/char_e141.gif) ≈ 1. As the inertial number increases, more and more grains are disconnected from the network and have no contacts. The stresses are then supported by fewer bearing contacts, each of which must transmit a larger force. This qualitatively explains why the force fluctuations increases with I.
≈ 1. As the inertial number increases, more and more grains are disconnected from the network and have no contacts. The stresses are then supported by fewer bearing contacts, each of which must transmit a larger force. This qualitatively explains why the force fluctuations increases with I.
With cohesion, the contact force magnitude is no longer driven by the normal stress, as it can vary from 0 to the adhesive strength f0 while pairs of grains are pulled apart. At low inertial numbers, this yields the following scaling for force fluctuation: ![[scr F, script letter F]](https://www.rsc.org/images/entities/char_e141.gif) ∝ C. At higher inertial numbers, as with non-cohesive grains, a process of stress concentration onto fewer bearing contacts leads to an increase in
∝ C. At higher inertial numbers, as with non-cohesive grains, a process of stress concentration onto fewer bearing contacts leads to an increase in ![[scr F, script letter F]](https://www.rsc.org/images/entities/char_e141.gif) (I).
(I).
We propose to capture the evolution of force fluctuations with the following model:
![[scr F, script letter F]](https://www.rsc.org/images/entities/char_e141.gif) 0(C) = 0(C) = ![[scr F, script letter F]](https://www.rsc.org/images/entities/char_e141.gif) (I → 0) ≈ 1 + αcC (I → 0) ≈ 1 + αcC | (12) |
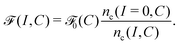 | (13) |
Fig. 4b confirms the inverse proportionality between the force fluctuations and the contact density ![[scr F, script letter F]](https://www.rsc.org/images/entities/char_e141.gif) ∝ nc−1. It also confirms the linear increase of
∝ nc−1. It also confirms the linear increase of ![[scr F, script letter F]](https://www.rsc.org/images/entities/char_e141.gif) 0(C) as in eqn (12), with fitted constant αc = 0.26 ± 0.01. This force fluctuation
0(C) as in eqn (12), with fitted constant αc = 0.26 ± 0.01. This force fluctuation ![[scr F, script letter F]](https://www.rsc.org/images/entities/char_e141.gif) 0 provides a coarse metric of correlated motions close to the jamming transition.29
0 provides a coarse metric of correlated motions close to the jamming transition.29
Adhesion reduces force correlations
Adhesion tends to enhance the contact density and the contact force fluctuations, which both enhance the friction. In contrast, Fig. 4c shows that it leads to a drop in the correlation C at high inertial numbers, which hinders the increase in friction.The force correlation term ![[capital script C]](https://www.rsc.org/images/entities/char_e522.gif) measures how efficient contact forces are, on average, at supporting the shear stress.27,30 Considering contacts carrying a normal force only, the correlation term is driven by the contact orientation θ, as
measures how efficient contact forces are, on average, at supporting the shear stress.27,30 Considering contacts carrying a normal force only, the correlation term is driven by the contact orientation θ, as ![[capital script C]](https://www.rsc.org/images/entities/char_e522.gif) ∝ 〈fc
∝ 〈fc![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos
cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ
θ![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sin
sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ〉/
θ〉/![[f with combining circumflex]](https://www.rsc.org/images/entities/i_char_0066_0302.gif) , where fc is the value of the normal contact force which can be negative if the contact is in compression or positive if it is in tension. Ignoring any covariance between force magnitude and orientation angle gives an approximation for this expression
, where fc is the value of the normal contact force which can be negative if the contact is in compression or positive if it is in tension. Ignoring any covariance between force magnitude and orientation angle gives an approximation for this expression ![[capital script C]](https://www.rsc.org/images/entities/char_e522.gif) ∝ 〈cos
∝ 〈cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ
θ![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sin
sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ〉, depending only on the orientation angle. Accordingly, two orientations that maximise the efficiency of such contacts in terms of contribution to the shear stress τ are: θ = 3π/4 for compressive contacts and θ = π/4 for contacts in tensions, as illustrated in Fig. 4c. Any other orientation would lessen
θ〉, depending only on the orientation angle. Accordingly, two orientations that maximise the efficiency of such contacts in terms of contribution to the shear stress τ are: θ = 3π/4 for compressive contacts and θ = π/4 for contacts in tensions, as illustrated in Fig. 4c. Any other orientation would lessen ![[capital script C]](https://www.rsc.org/images/entities/char_e522.gif) , and an isotropic force distribution would lead to
, and an isotropic force distribution would lead to ![[capital script C]](https://www.rsc.org/images/entities/char_e522.gif) = 0 and no shear stress. This result is consistent with the finding of an increase in force anisotropy by cohesion.31
= 0 and no shear stress. This result is consistent with the finding of an increase in force anisotropy by cohesion.31
Without cohesion, all contacts are in compression. As the inertial number is increased, Fig. 4d shows that the remaining contacts are preferentially aligned at θ = 3π/4, which drives the increase in correlation ![[capital script C]](https://www.rsc.org/images/entities/char_e522.gif) . With cohesion, these compressive contacts also develop at high inertial numbers. However, many contacts with seemingly random orientations remain, which contribute to lessening
. With cohesion, these compressive contacts also develop at high inertial numbers. However, many contacts with seemingly random orientations remain, which contribute to lessening ![[capital script C]](https://www.rsc.org/images/entities/char_e522.gif) . This means that not all contacts actively contribute to the transport of momentum.
. This means that not all contacts actively contribute to the transport of momentum.
Adhesion enhances only one mode of momentum transport
Expressing the friction μ in terms of force fluctuations in (9) enables us to further the analysis of elementary mechanisms of momentum transport. Following the approach introduced in ref. 27, we seek to decompose the force fluctuations into two components. The first component arises from balanced forces on a grain and do not lead to the grain's acceleration. The second component arises from the remaining unbalanced forces, which drives grain acceleration. Fig. 5c illustrates this decomposition.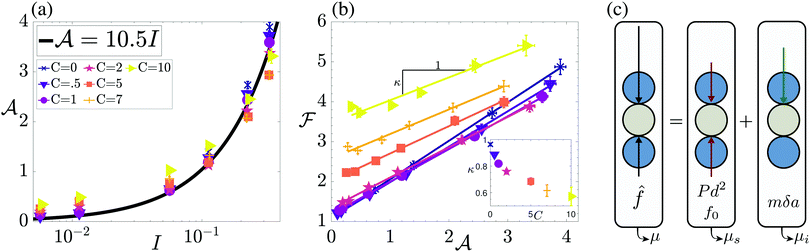 | ||
Fig. 5 Grain micro-acceleration (constant grain stiffness K = 10−3). (a) Acceleration fluctuations at different inertial number and cohesion strength; the black line shows the fitted function ![[scr A, script letter A]](https://www.rsc.org/images/entities/char_e520.gif) = 10.5I. Relation between fluctuation in grain acceleration = 10.5I. Relation between fluctuation in grain acceleration ![[scr A, script letter A]](https://www.rsc.org/images/entities/char_e520.gif) and contact force and contact force ![[scr F, script letter F]](https://www.rsc.org/images/entities/char_e141.gif) ; markers are the simulated data and lines are the best linear fit using (15), obtained for a value of ; markers are the simulated data and lines are the best linear fit using (15), obtained for a value of ![[scr F, script letter F]](https://www.rsc.org/images/entities/char_e141.gif) 0(C) given by eqn (12) and a value of κ shown on the inset. (c) Illustration of the decomposition of the contact force fluctuations into a balanced and an unbalanced part, controlling the static and inertial components of the friction μ respectively. 0(C) given by eqn (12) and a value of κ shown on the inset. (c) Illustration of the decomposition of the contact force fluctuations into a balanced and an unbalanced part, controlling the static and inertial components of the friction μ respectively. | ||
To establish the relative importance of these components, we measured the standard deviation of grain acceleration â. By sampling over the ensemble, localised transient bursts of grain acceleration32 are averaged out. We call its normalised counterpart ![[scr A, script letter A]](https://www.rsc.org/images/entities/char_e520.gif) = â/(d/ti2) acceleration fluctuation or micro-acceleration, where ti = I/
= â/(d/ti2) acceleration fluctuation or micro-acceleration, where ti = I/![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) is the inertial time. Fig. 5a shows that acceleration fluctuation is proportional to the inertial number, with only a marginal effect of adhesion:
is the inertial time. Fig. 5a shows that acceleration fluctuation is proportional to the inertial number, with only a marginal effect of adhesion:
![[scr A, script letter A]](https://www.rsc.org/images/entities/char_e520.gif) (I,C) ≈ 10.5I. (I,C) ≈ 10.5I. | (14) |
Accordingly, the acceleration standard deviation scales like: â∝Id/ti2 = d![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) /ti, which involves a length scale d and a time scale
/ti, which involves a length scale d and a time scale 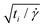 that are both adhesion independent, and similar to those involved in the diffusion of mass.33,34
that are both adhesion independent, and similar to those involved in the diffusion of mass.33,34
Fig. 5b shows the contribution of balanced and unbalanced forces to the force fluctuation. It provides evidence for an approximately linear relation between the force and acceleration fluctuations:
![[scr F, script letter F]](https://www.rsc.org/images/entities/char_e141.gif) = = ![[scr F, script letter F]](https://www.rsc.org/images/entities/char_e141.gif) 0(C) + κ(C) 0(C) + κ(C)![[scr A, script letter A]](https://www.rsc.org/images/entities/char_e520.gif) . . | (15) |
We translate this force decomposition into a friction decomposition by combining eqn (15) and eqn (9):
| μ = μs + μi; | (16) |
μs = β![[scr F, script letter F]](https://www.rsc.org/images/entities/char_e141.gif) 0; 0;![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) μi = κβ μi = κβ![[scr A, script letter A]](https://www.rsc.org/images/entities/char_e520.gif) . . | (17) |
We call μs the static component of the friction, as it arises from balanced contact forces only. We call μi the inertial component of the friction as it arises from unbalanced forces only, and therefore from grain accelerations. Fig. 6a confirms the validity of this decomposition by comparing the measured friction coefficient μ to the sum μs + μi as per eqn (17).
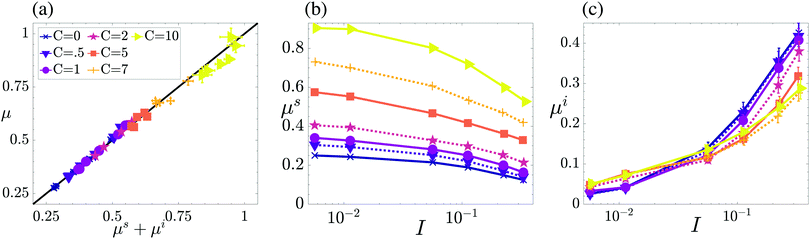 | ||
| Fig. 6 Two mechanisms of momentum transport (constant grain stiffness K = 10−3). (a) Assessment of the proposed decomposition of the friction μ into static and inertial components in eqn (16) and (17): markers show the coefficient of friction μ measured in the flows versus the sum of the components μs and μi calculated from micro-structural quantities as per eqn (17). The line shows the function μ = μs + μi. (b and c) Static and inertial components of the friction calculated by eqn (17). | ||
Fig. 6b and c show the effect of adhesion on the two components μs and μi. The inertial component μi is not greatly influenced by the cohesion strength, and increases approximately linearly with the inertial number. This component drives the shear-rate strengthening effect. In contrast, the static component μs is strongly enhanced by adhesive forces. The enhancement is most pronounced at low inertial numbers. However, increasing the inertial number leads to a reduction in μs for a fixed value of cohesion strength C. Accordingly, this component drives the shear-rate weakening effect as cohesive flows transition from the cohesive regime to the non-cohesive regime with increasing shear rate.
Discussion and conclusion
This study introduced a framework that rationalises the effect of adhesive contact forces on the viscosity of granular materials. The framework includes a new scaling law for the cohesive granular viscosity that can readily be used in continuum fluid mechanics modelling, and some evidence of the micro-mechanical processes controlling it.The phenomenological scaling law for cohesive granular viscosity that we propose is based on the frictional model eqn (4) established for non-cohesive grains. The effect of adhesion is to enhance the friction μ by a factor g given in eqn (6). The major advance of this finding is to show that the effect of adhesion on friction is controlled by two dimensionless numbers, namely the cohesion-strength C and the cohesion-energy W, which compare the adhesive contact strength and energy to the characteristic force and kinetic energy in the flow. This progresses the commonly accepted view that only one adhesion-related dimensionless number could control the viscosity and reconciles the apparent discrepancies of several existing scaling laws.
In particular, our results indicate that the transition between non-cohesive and cohesive regimes is controlled by these two numbers – adhesion does not significantly increase the viscosity of granular flows if either C or W is less than unity. In this non-cohesive regime, we propose that the stresses and shear rate are sufficient to pull apart adhesive grains by an epitomised process of static or kinetic de-bonding. Reciprocally, the viscosity increases linearly with C or W provided that both numbers are greater than 1. We further define two cohesive regimes, which we call the cohesive-strength (for C < W) and cohesive-energy (for W > C) regimes, where the viscosity is controlled by the weakest way that two grains can be pulled apart. We found that the existence of these two rheological regimes enables a reconciliation between a number of previously proposed rheological models.
The finding that the cohesion-energy number W is inversely proportional to the inertial number I captures the development of a shear-rate weakening behaviour, whereby the friction decreases as the inertial number is increased for a fixed value of C. This behaviour constitutes a promising potential explanation for the existing observations that adhesion induces heterogeneous flows.10,15,17,35–38 A possible analysis would compare the energy dissipated in a cohesive flow that is homogeneously sheared (uniform friction), to that in a flow featuring a localised shear band (reduced friction) separating two zones with no shear (no dissipation).39,40
We expect this viscous scaling law to apply to more realistic models of adhesion, such as capillary-bridge models, the JKR model or DTM model, which include non-linear Hertz repulsion and a contact area dependent adhesive force. This expectation is supported by the finding in ref. 41 that different models of adhesion lead to the same rheology given that f0 and w0 match. We anticipate that the scaling of W with the grain stiffness K may then involve a slightly different power law, as discussed in the ESI.†
We also expect that this scaling law could be extended to incorporate the effect of the contact dissipation, which was kept constant in our study, possibly by incorporating it into a generalised energy number W in a way similar to ref. 22. Doing so may explain their remark on the usefulness of the equilibrium grain overlap δeq, since it is inbuilt into the energy scale W.
To further understand the origin of this viscosity scaling law, this study presented an analysis of the internal processes of momentum transport. This led us to pinpoint the micro-structural and micro-dynamical processes affected by adhesion that control the variation in viscosity. These include contact density, force fluctuation, and a measure of force anisotropy. We further developed this micro-mechanical analysis to show that the viscosity arises from two mechanisms of momentum transfer using two distinct pathways: either through balanced contact forces or grain micro-accelerations. This analysis evidenced that adhesion only affects (enhances) momentum transport through balanced contacts. In contrast, it does not significantly affect momentum transport by grain-micro acceleration.
Without cohesion, non-local effects develop at low inertial numbers.23,42–45 These effects occur in heterogeneous flows, where the friction law eqn (4) becomes affected by the nature of the flow within a typical distance of influence. This distance increases and diverges as the inertial number tends to zero. Little is known on non-locality in cohesive granular flows. Nonetheless, our results indicate that adhesion may strongly affect the prevalent mode of momentum transport at low inertial numbers. This suggests that adhesion may also affect non-local behaviours. The framework introduced in this study may be used as a basis to explore such behaviours.
Conflicts of interest
There are no conflicts to declare.References
- G. MiDi, Eur. Phys. J. E, 2004, 14, 341–365 CrossRef CAS
.
- F. Da Cruz, S. Emam, M. Prochnow, J.-N. Roux and F. Chevoir, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2005, 72, 021309 CrossRef
.
- P. Jop, Y. Forterre and O. Pouliquen, Nature, 2006, 441, 727 CrossRef CAS
.
- Y. Forterre and O. Pouliquen, Annu. Rev. Fluid Mech., 2008, 40, 1–24 CrossRef
.
- P. G. Rognon, I. Einav and C. Gay, J. Fluid Mech., 2011, 689, 75–96 CrossRef CAS
.
- E. DeGiuli, G. Düring, E. Lerner and M. Wyart, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2015, 91, 062206 CrossRef CAS
.
- P. Rognon, J.-N. Roux, D. Wolf, M. Naam and F. Chevoir, EPL, 2006, 74, 644 CrossRef CAS
.
- P. G. Rognon, J.-N. Roux, M. Naaim and F. Chevoir, J. Fluid Mech., 2008, 596, 21–47 CrossRef CAS
.
- M. Macaulay and P. Rognon, J. Fluid Mech., 2019, 858, R2 CrossRef CAS
.
- I. Iordanoff, N. Fillot and Y. Berthier, Powder Technol., 2005, 159, 46–54 CrossRef CAS
.
- S. Khamseh, J.-N. Roux and F. Chevoir, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2015, 92, 022201 CrossRef
.
- S. Roy, S. Luding and T. Weinhart, New J. Phys., 2017, 19, 043014 CrossRef
.
- D. J. Koeze and B. P. Tighe, Phys. Rev. Lett., 2018, 121, 188002 CrossRef CAS
.
- H. Shi, S. Roy, T. Weinhart, V. Magnanimo and S. Luding, Granular Matter, 2019, 22, 14 CrossRef
.
- E. Irani, P. Chaudhuri and C. Heussinger, Phys. Rev. Lett., 2014, 112, 188303 CrossRef
.
- L. Aarons and S. Sundaresan, Powder Technol., 2006, 169, 10–21 CrossRef CAS
.
- Y. Gu, S. Chialvo and S. Sundaresan, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2014, 90, 032206 CrossRef
.
- R. Brewster, G. S. Grest, J. W. Landry and A. J. Levine, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2005, 72, 061301 CrossRef
.
- J.-F. Métayer, P. Richard, A. Faisant and R. Delannay, J. Stat. Mech.: Theory Exp., 2010, 2010, P08003 Search PubMed
.
- N. Berger, E. Azéma, J.-F. Douce and F. Radjai, EPL, 2016, 112, 64004 CrossRef
.
- T. T. Vo, S. Nezamabadi, P. Mutabaruka, J.-Y. Delenne and F. Radjai, Nat. Commun., 2020, 11, 1–8 Search PubMed
.
- S. Mandal, M. Nicolas and O. Pouliquen, Proc. Natl. Acad. Sci. U. S. A., 2020, 117, 8366–8373 CrossRef CAS
.
- P. G. Rognon, T. Miller, B. Metzger and I. Einav, J. Fluid Mech., 2015, 764, 171–192 CrossRef
.
- A. Singh, V. Magnanimo, K. Saitoh and S. Luding, New J. Phys., 2015, 17, 043028 CrossRef
.
- S. Gonzalez, A. R. Thornton and S. Luding, Eur. Phys. J.: Spec. Top., 2014, 223, 2205–2225 Search PubMed
.
- H. Perrin, C. Clavaud, M. Wyart, B. Metzger and Y. Forterre, Phys. Rev. X, 2019, 9, 031027 CAS
.
- M. Macaulay and P. Rognon, Phys. Rev. E, 2020, 101, 050901 CrossRef
.
- D. Bi, J. Zhang, B. Chakraborty and R. P. Behringer, Nature, 2011, 480, 355 CrossRef CAS
.
- E. I. Corwin, H. M. Jaeger and S. R. Nagel, Nature, 2005, 435, 1075 CrossRef CAS
.
- T. S. Majmudar and R. P. Behringer, Nature, 2005, 435, 1079 CrossRef CAS
.
- A. Singh, V. Magnanimo, K. Saitoh and S. Luding, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2014, 90, 022202 CrossRef
.
- A. Wautier, S. Bonelli and F. Nicot, Int. J. Numer. Anal. Methods Geomech., 2018, 42, 1037–1056 CrossRef
.
- P. Kharel and P. Rognon, Phys. Rev. Lett., 2017, 119, 178001 CrossRef
.
- P. Kharel and P. Rognon, EPL, 2018, 124, 24002 CrossRef
.
- A. W. Alexander, B. Chaudhuri, A. Faqih, F. J. Muzzio, C. Davies and M. S. Tomassone, Powder Technol., 2006, 164, 13–21 CrossRef CAS
.
- J. F. Klausner, D. Chen and R. Mei, Powder Technol., 2000, 112, 94–101 CrossRef CAS
.
- Y. Yamaguchi, S. Takada and T. Hatano, J. Phys. Soc. Jpn., 2018, 87, 094802 CrossRef
.
- K. Kamrin and G. Koval, Phys. Rev. Lett., 2012, 108, 178301 CrossRef
.
- T. Divoux, M. A. Fardin, S. Manneville and S. Lerouge, Annu. Rev. Fluid Mech., 2016, 48, 81–103 CrossRef
.
- E. DeGiuli and M. Wyart, Proc. Natl. Acad. Sci. U. S. A., 2017, 114, 9284–9289 CrossRef CAS
.
- S. Roy, A. Singh, S. Luding and T. Weinhart, Computational Particle Mechanics, 2016, 3, 449–462 CrossRef
.
- K. Kamrin, Front. Phys., 2019, 7, 116 CrossRef
.
- P. Kharel and P. Rognon, EPJ Web of Conferences, 2017, p. 03060.
- Q. Zhang and K. Kamrin, Phys. Rev. Lett., 2017, 118, 058001 CrossRef
.
- M. Bouzid, M. Trulsson, P. Claudin, E. Clément and B. Andreotti, Phys. Rev. Lett., 2013, 111, 238301 CrossRef
.
Footnote |
| † Electronic supplementary information (ESI) available: Online movie illustrates the evolution of the force networks for non-cohesive and cohesive (C = 10) simulations at three inertial numbers I = {0.005, 0.05, 0.3}, data-sets for every figure, and detailed methods with a discussion on other cohesion models. See DOI: 10.1039/d0sm01456g |
| This journal is © The Royal Society of Chemistry 2021 |