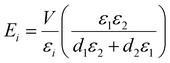Open Access Article
Open Access ArticleMagnetic propulsion of colloidal microrollers controlled by electrically modulated friction†
Ahmet F.
Demirörs
 *a,
Alex
Stauffer
a,
Carmen
Lauener
a,
Jacopo
Cossu
*a,
Alex
Stauffer
a,
Carmen
Lauener
a,
Jacopo
Cossu
 a,
Shivaprakash N.
Ramakrishna
a,
Shivaprakash N.
Ramakrishna
 b,
Joost
de Graaf
b,
Joost
de Graaf
 c,
Carlos C. J.
Alcantara
d,
Salvador
Pané
c,
Carlos C. J.
Alcantara
d,
Salvador
Pané
 d,
Nicholas
Spencer
d,
Nicholas
Spencer
 b and
André R.
Studart
*a
b and
André R.
Studart
*a
aComplex Materials, Department of Materials, ETH Zurich, 8093 Zurich, Switzerland. E-mail: Ahmet.demiroers@mat.ethz.ch; Andre.studart@mat.ethz.ch
bLaboratory for Surface Science and Technology, Department of Materials, ETH Zurich, 8093 Zurich, Switzerland
cInstitute for Theoretical Physics, Center for Extreme Matter and Emergent Phenomena, Utrecht University, Princetonplein 5, 3584 CC Utrecht, The Netherlands
dMulti-Scale Robotics Lab, Institute of Robotics and Intelligent Systems, ETH Zurich, 8092 Zurich, Switzerland
First published on 26th November 2020
Abstract
Precise control over the motion of magnetically responsive particles in fluidic chambers is important for probing and manipulating tasks in prospective microrobotic and bio-analytical platforms. We have previously exploited such colloids as shuttles for the microscale manipulation of objects. Here, we study the rolling motion of magnetically driven Janus colloids on solid substrates under the influence of an orthogonal external electric field. Electrically induced attractive interactions were used to tune the load on the Janus colloid and thereby the friction with the underlying substrate, leading to control over the forward velocity of the particle. Our experimental data suggest that the frictional coupling required to achieve translation, transitions from a hydrodynamic regime to one of mixed contact coupling with increasing load force. Based on this insight, we show that our colloidal microrobots can probe the local friction coefficient of various solid surfaces, which makes them potentially useful as tribological microsensors. Lastly, we precisely manipulate porous cargos using our colloidal rollers, a feat that holds promise for bio-analytical applications.
Introduction
The vast majority of motile creatures move themselves by mechanisms such as walking, swimming, slithering, or crawling. Some animals are also observed to roll, although this is a far less common displacement mechanism. Examples of this can be found in medium-size mammals (e.g., hedgehog and pangolin), small amphibia (pebble toad), and arachnids (cartwheeling spider).1 Rolling motion is used by these organisms to escape when they feel threatened.1 All of the above mechanisms of displacement, including rolling, rely on contact friction with the surface over which the animal is moving. In contrast to these macroscale mechanisms, motion at the microscale is influenced by different forces and phenomena. When fully immersed in a viscous Newtonian fluid, namely at low Reynolds number,2,3 microoganisms must overcome the restrictions imposed by the Scallop theorem4 on achieving translational motion. This is why these organisms often possess flagella, which allow for a time-reversal symmetry break and thus enable net displacement. Near a surface, crawling is also a common strategy to achieve forward motion. However, even at these small scales, examples of rolling are found in cells, such as leukocytes and keratocytes,5,6 which migrate by rolling motion over tissues to combat infections or heal wounds, respectively.Inspired by nature, researchers have engineered several small-scale architectures, known as micro- and nanorobots, that can move in fluids by mimicking the mechanisms of living microorganisms and cells. These man-made micromotors use different types of stimuli to achieve motion, such as magnetic fields,7–9 electric fields,10–12 ultrasound,13 or light.14 Rolling motion has been mainly reported for magnetically responsive micro- and nanostructures that are manipulated on substrates using rotating magnetic fields. Such magnetically driven small-scale rollers have been proposed for environmental,15,16 medical17,18 and robotic applications.19–21 The ability to program motion at small scales22 is a crucial requirement for precise biomedicine, such as therapeutic cargo delivery, or in vitro and in vivo chemical gradient formation and manipulation thereof. Recently, we have demonstrated that magnetodielectric particles can be used as colloidal shuttles to trap, transport and release cargos under external magnetic and electric fields.10,23 Trapping and releasing of cargo was achieved by switching on and off a high-frequency electric field that induced dielectrophoretic attractive forces between the shuttle and the cargo through field-induced polarization. In these systems, both magnetic-field gradients23 and an electrically induced self-propelling mechanism10 were explored to spatially control shuttles in the form of uniform or Janus colloidal particles, respectively. The speed of Janus shuttles was shown to scale quadratically with the applied electric field strength.10
Being immersed in a fluid, yet close to a substrate, raises the question: how do these particles achieve motion? The macroscopic picture suggests a contact-based interaction, for which load-force arguments can be made to describe the motion. Unfortunately, the situation for microscopic particles immersed in a fluid is more complex. Even if there is a substantial fluid gap, hydrodynamic lubrication theory states that a smooth sphere moving parallel to a smooth no-slip wall, will start to spin,24 and conversely, a spinning sphere will also achieve net forward motion. In the limit of vanishing separation, a sphere of radius R will move forward with velocity V = ωR/4 if forced to spin with angular velocity ω. In view of electrostatic effects in the fluid, which can cause colloids to ‘hover’ with a small, yet finite separation above the surface—comparable to the Debye length25,26—it is often assumed that rolling colloidal spheres move by a hydrodynamic coupling to the wall.
However, load-force arguments have been recently combined with shear in the fluid-gap arguments to describe the motion of fluid-immersed, self-assembled wheels rolling over a wall.27 This kind of argument is more in line with a mixed or even contact-friction argument, than it is with the above hydrodynamic description. Yet, it should also be noted, that ‘load forces’ can play a role even in the fully hydrodynamic description, when interpreted as the balance between gravity, electrostatics, and other surface forces present in the system. These collectively control the fluid gap size, which is the key parameter in setting the amount of hydrodynamic translation–rotation coupling. Presently, there is an increased interest in contact friction phenomena on the colloidal length scale.28–30 Our Janus shuttles fall into the size regime where contact friction arguments are debated and it is therefore important to know whether the load description27 applies to our particles and what this description's limitations are.
Here, we investigate in detail the motion of magnetically propelled Janus shuttles to test the accuracy of the hydrodynamic and load-based predictions. We used an external electric field to induce reversible dipolar interactions between the microroller and the substrate, by which we are able to increase the load on our particles and modulate the coupling between translation and rotation. This expressed itself in a greater or smaller, even vanishing, forward velocity, depending on whether we pushed the microrollers toward the substrate or away from it, respectively. The role of hydrodymamic and contact-friction forces on the motion of the microrollers is examined to identify possible mechanisms to control the speed of our Janus shuttles. We explore the behavior of our microrollers further by varying the surface chemistry of the underlying substrate. These findings provide insights on the potential use of Janus particles as microrobots to probe the friction properties of surfaces. Lastly, we report on additional pick-and-place experiments that feature our Janus shuttle's ability to control the distribution of diffusive colloidal particles using orthogonal electric and magnetic fields.
The experimental system
Janus particles were used as microrollers, also referred to as Janus shuttles, while uniform polystyrene particles played the role of model cargo in our study. The Janus particles were fabricated by metal coating one hemisphere of silica particles with diameter (2R, with R the radius) in the range 3.3–7.8 μm. This partial coating consisted of an initial 200 nm thick nickel layer covered with a second 200 nm thick magnesium layer on top. The resulting Janus colloids were suspended together with cargo particles in double deionized (DI) water at a volume fraction of 1–3% to perform pick-and-place experiments. The gravitational length of the Janus colloids was estimated to be on the order of a nanometer (ESI,† Table S1). Therefore, our particles are expected to sediment to the bottom of the sample within the timeframe of the reported experiments.The ferromagnetic nature of nickel provides the magnetic torque necessary for the motion and guidance of the microrollers. That is, applying a rotating magnetic field proved sufficient to roll the Janus particles contactless (ESI,† Fig. S1a). This type of rolling mechanism is well established and has been previously used to propel a variety of colloidal systems ranging from spherical31 to anisotropic particles,32–35 and even living bacteria.36 Importantly, the direction of the moving colloidal particle can be controlled by changing the orientation of the rotating magnetic field, which allows us to program the path that the particle undertakes on top of the substrate (ESI,† Fig. S1c). We note that the magnesium layer in our Janus colloid is crucial, because it is oxidized on the surface in contact with the water phase. The electrical charges formed on this oxidized layer in water leads to electrostatic repulsion between the particle and the substrate, thus preventing sticking and enabling effective rolling of the Janus colloid (see ESI,† for additional details).
Cargo trapping and transport is possible due to the electrically induced formation of dipoles of opposite orientations in the dielectric cargo and in the metallic layer of the Janus colloid. Thus, the combination of magnetic guiding and dipolar trapping, can be used to transport and release other cargo colloids from one place to another23 (ESI,† Fig. S1 and Movie S1).
The role of friction on the motion of the Janus microrollers
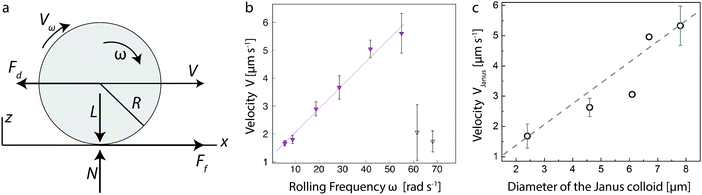
We investigate the role of friction on the translational motion of the microroller by first performing rolling experiments with Janus particles of different sizes under varying frequencies of the rotating magnetic field. The ability to magnetically control the motion of our Janus particles was first demonstrated by optically tracking the velocity of the microroller under a rotating magnetic field of increasing frequency. The rolling experiment shows that the velocity of the microroller increased linearly with the frequency of the rotating magnetic field up to the critical value known as the step-out frequency. We report this step-out frequency in terms of the equivalent critical angular velocity ωc (Fig. 1b).35 When the angular velocity of the magnetic field ωm is greater than ωc, the microroller's speed was observed to rapidly decrease, in agreement with previous work on similar colloidal systems.37 This results from the fact that the viscous force exerted by the surrounding fluid is such that the rolling sphere is no longer able to follow the external magnetic field.33 The step-out frequency depends on the microroller's size and magnetization, the viscosity of the fluid and the strength of the applied field. In the absence of an external electric field, ωc was found to be equal to 58 rad s−1 for a 4.6 μm Janus particle in water.The critical angular velocity can also be estimated using the following expression: ωc = m0B/(8πηR3), where m0 is the magnetic dipole moment of the roller, B is the applied magnetic field, and η is the viscosity of the liquid medium.38,39 Note that this expression assumes bulk fluid friction acting on the rotating sphere. Based on previous works,38–40 we estimate the roller's magnetic dipole moment m0 to be equal to 5 × 10−13 A m−2. Using this estimated value in the above expression, we find ωc= 1270 rad s−1, which is significantly higher than the experimentally measured value of 58 rad s−1. Hydrodynamic forces due to the presence of the wall24 are expected to only weakly increase the rotational friction on the sphere even at very thin fluid layers. For the size of our colloid, such hydrodynamic forces should increase by at most a factor of 5 for nanometric separations, reducing the predicted ωc by the same factor. This suggests that the metal-coated particle is not only opposed by hydrodynamic friction during rolling. Contact friction or a mixed-lubrication response could lead to additional friction that is not accounted for in the above expression for ωc.
The effect of particle size on the motion of the Janus microroller was subsequently assessed by performing experiments under a rotating magnetic field operated well below the step-out angular velocity ωc. Experiments conducted at a constant angular velocity of 5.55 rad s−1 showed that the translational velocity of the microroller increased significantly with the diameter of the Janus particle (Fig. 1c).
To interpret our experimental results, we will now examine in more details the relevant models that have been used to describe the rolling response of colloidal particles. Pure hydrodynamic rolling24 is described by the lubrication-limit result:
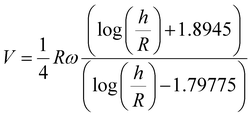 | (1) |
We will now also discuss the model used for describing the motion of microscopic self-assembled wheels.27 This model assumes that in-plane translational motion is caused by a mixed-lubrication or contact-friction force (Ff) between the rolling object and the surface of the underlying substrate (Fig. 1a). The argument is that for colloidal particles immersed in a liquid and close to a substrate, the (contact) friction-induced translational force is counteracted by the drag force (Fd) exerted by the surrounding liquid phase in the opposite direction. These two forces should cancel each other such that: Ff − Fd = 0. Here, the friction force is given by Ff = μkL, where μk is the friction coefficient and L is the load applied by the particle on the solid surface along the normal direction (Fig. 1a). The hydrodynamic drag force can be approximated by Stokes’ law, which for spherical particles reads Fd = 6πηRV with V being the speed of the particle. It is implicitly assumed that the effect of the near-wall hydrodynamic and possible contact aspects are small. The former is reasonably justified on the basis of the lubrication results reported in Goldman,24 while the latter is an uncontrolled approximation.
The friction force relates to the imposed angular velocity via the velocity of the particle's surface, as follows (see ESI,†):
| μk = KωR, | (2) |
Implementing these relations into the equation for the contact-frictional force and balancing this with the drag force imposed by the fluid, allows us to relate V and L:
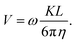 | (3) |
Since the viscosity of the medium is constant in our experiments, the above analysis indicates that the product KL should be proportional to the particle radius in order for eqn (3) to describe the observed dependence of the translational velocity on the size of the Janus colloid (Fig. 1c). Clearly, expression (3) is very different from eqn (1) in terms of its functional form. Yet, under certain assumptions, both formalisms are able to capture the trend in Fig. 1c. To emphasize that they are, however, describing fundamentally incommensurate regimes of friction, we note that K is typically viscosity dependent, whilst eqn (1) does not have such a dependence. eqn (1) also matches our data without the need for a fit parameter, provided the microrollers are deep within the lubrication regime; the height h can, however, be used a fit parameter to improve the fit. Our analysis indicates that both models can be used to describe the observed experimental results, but that the velocity of the shuttle in the absence of an electric field is likely governed by hydrodynamic friction.
Tuning friction using an electric field
The application of an electric field to our system allows us to impose an additional tunable electrostatic load on the Janus colloid. In the next experimental series, we use an electric field to deliberately adjust the applied load. That is, the size-dependent gravitational load can be offset by applying an external electric field to the colloid, leading to attraction or repulsion, because of the strong polarizability of the metallic hemisphere. The Janus particle polarizes in the same direction as the imposed external electric field. The type of interaction of the Janus particle with the substrate will therefore depend on the direction of the electric dipole generated at the surface of the electrode. If the conductive ITO layer is in close contact with the Janus colloid (normal configuration), the induced electric dipoles will display a head-to-tail arrangement that results in attractive interactions between the particle and the substrate.43 By contrast, changing the ITO-coated glass slide to a flipped configuration puts the 150 μm thick dielectric glass in closer proximity to the microroller. Since the electric dipole induced in the glass exhibits opposite direction with respect to the applied electric field, the dipoles induced in the particles and in the substrate acquire a head-to-head configuration that gives rise to repulsive interactions.Thus, depending on the electrode configuration, we expect that the external electric field can be used to speed up or slow down the motion of the Janus particle, either by modifying the gap height or by further increasing the load on the colloid beyond that exerted by gravitational forces alone. These two possible scenarios can be demonstrated by simply flipping one of the ITO-coated glass slides used in our experimental setup (Fig. 2a and d). Our results show that the alternating electric field applied in our system serves not only as a switch for the trapping and release of cargo particles (ESI,† Fig. S1d–g), but is also a convenient input to control the speed of the colloidal microroller.
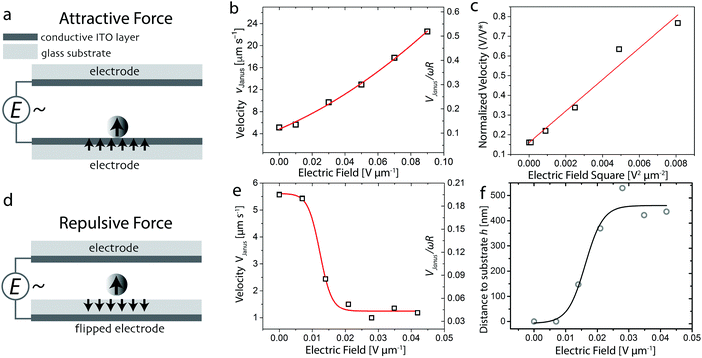 | ||
| Fig. 2 Control of Janus microroller velocity via electrically-tuned friction forces. (a and d) Schematics of the electrode configurations used to induce (a) attractive and (d) repulsive dipolar forces between the colloidal microroller and the underlying substrate. Attractive interactions are generated when the colloidal particle is in direct contact with the conductive side of the electrode (ITO), whereas repulsive interactions develop if the electrode is flipped to place the thick glass substrate in close proximity to the particle. (b and e) Rolling velocity of a Janus colloid as a function of the electric field strength, E, for (b) attractive and (e) repulsive interactions with the substrate. The secondary y-axis shows the speed normalized by ωR, where R is the radius of the particle and ω is the angular frequency of the magnet rotation in radians. (c) Correlation between the normalized speed of the Janus colloid and the square of the electric field strength. (f) Estimation of the distance, h, between the colloid and the substrate as a function of the electric field strength, assuming lubrication regime conditions outlined by Goldman et al.24 All experiments were conducted using a Janus particle with a radius of 3.9 μm on bare ITO substrates and applying a rotating magnetic field with a constant angular frequency at 8.2 rad s−1. The lines here are guides to the eye, except for the linear fit shown in (c). | ||
We quantify the effect of electrically-induced attractive and repulsive interactions on the motion of the Janus particles by measuring the speed of the microroller as a function of the applied electric field in the two electrode configurations (Fig. 2b and e). Our results show that the attractive interactions created in the normal electrode configuration increase the microroller's speed by a factor of 5 when an electric field of 0.090 V μm−1 is applied. Using the flipped configuration, we found that the induced repulsive interactions reduce abruptly the translational velocity of Janus particle to nearly zero when the applied electric field surpasses a threshold value around 0.015 V μm−1. We estimate this threshold field to correspond to an electric repulsive force on the order of 10 pN (see ESI†). This force is comparable to the forces exerted by gravitational forces on our particles or even van der Waals forces at short separations. Regardless of the configuration used, the application of an electric field was found to align the Janus particle in the field direction and to reduce the wiggling of the colloid in the direction orthogonal to the motion, thus enabling straight and well-defined motion (see ESI,† Movies S2 and S3).
To shed light on the physics underlying these effects, we computed V/ωR values from the experimentally measured velocity data (Fig. 2b and e). The fact that the normalized velocity of the colloid in the non-inverted configuration (Fig. 2b) can reach levels far above the upper theoretical limit predicted by the hydrodynamic model (V/ωR = 1/4) is a clear sign that our microroller's motion is not governed by hydrodynamic lubrication (eqn (1)), when strong attractive dielectric forces are applied. However, the situation without additional attractions still appears to fall within the regime of applicability of the hydrodynamic theory (Fig. 2e). Contrasting the two scenarios and the previously discussed effect of gravitational forces (Fig. 1c), it appears that our Janus shuttles live on the edge of hydrodynamic theory's range of applicability.
Further analysis of our experimental data using the relevant physical models allows us to quantitatively explain the motion of the Janus colloid under the applied electric field. By increasing the repulsive interactions, we expect the separation between the substrate and the roller to become sufficiently large to eliminate most of the hydrodynamic coupling. This behavior is borne out by our data on the velocity of the particle in the flipped configuration (Fig. 2e). Assuming that the particle and substrate are indeed not in contact, we can invert eqn (1) to predict the distance h of the microroller to the wall at different electric fields applied (see the ESI† and Fig. S2). This analysis reveals that the distance h increases sharply from nearly zero to around 400 nm when the applied electric field exceeds 0.015 V μm−1 (Fig. 2f). Such a qualitative prediction was experimentally confirmed by the observation that the Janus colloid moved away from the focal plane of the microscopy, when the electric field is increased above this threshold value. This rapid increase suggests that a short-ranged attraction between the substrate and microroller is broken, which could be a van der Waals attraction, as hydrophobic interactions are limited in this system.
In the configuration where the field induces attraction and V > ωR/4, we can instead rationalize the motion in terms of a transition toward a contact-friction regime, for which the increased load on the particle governs the rolling behavior (eqn (3)). The transition between a hydrodynamic and a mixed wet contact friction regime appears to be smooth, although we should note that flipping the substrate induces a discontinuity in our data set (Fig. 2b and e). Assuming the contact-frictional model to be more appropriate to describe the motion of the colloid in the normal configuration, we assume the load L (eqn (3)) to be the attractive force generated by the electric field Fe = (3α2E2)/(8εmr4),43 where α is the polarizability of the colloid, εm is the relative permittivity of the liquid medium, and r is the distance between the dipole (colloid) and the electrode.53,54 Straightforward algebra shows that this results in:
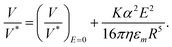 | (4) |
We tested the applicability of the above expression to our data by plotting V/V* against the square of the applied electric field, E2, for a 7.8 μm particle subjected to a constant magnetic rotational frequency (Fig. 2c). The resulting plot reveals a linear relationship between V/V* and E2, indicating that our simple analytical model captures the underlying physics that governs the Janus particle's motion under the range of electric fields applied in the attraction experiment. According to the model, the slope of the linear fit depends on physical properties of the particles (R, α) and the fluid (η, εm), as well as on the proportionality factor, K, used to correlate the friction coefficient with the fluid velocity (eqn (1)). We will next exploit this dependence to study the interaction between the roller and the surface.
Microroller motion on substrates with tailored surface chemistry
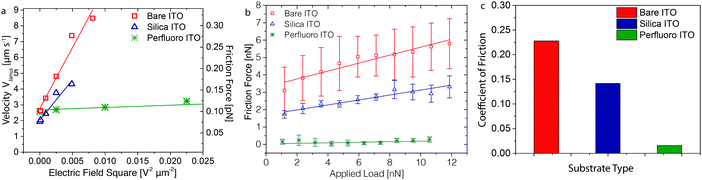
The surface chemistry of the substrate is expected to affect the motion of the microroller by changing the frictional properties between the colloid and the substrate, provided we are in the mixed contact-friction regime. The van der Waals attraction and thereby the load and colloid-substrate separation might potentially also be influenced by chemical modifications on the solid surface. To investigate the effect of the substrate surface chemistry on the velocity of the Janus microroller, we performed experiments on bare ITO electrodes and on electrodes coated either with a nanometric silica layer or with perfluorinated molecules. A 15 nm silica layer was created on top of the substrate by electron beam deposition,12 whereas perfluorinated substrates were prepared by adsorbing perfluorodecylchlorosilane (PFDCS) molecules on the electrode surface via the vapor phase.The speed of our microroller was found to clearly increase linearly with the square of the electric field for two of the investigated substrates (Fig. 3a), indicating that we are in the correct response regime to apply the load-based analytical model. Because the experiments were carried out using the same microroller, the dependence of the speed on the electric field reflects the changes in the friction properties of the substrate. Strong friction is manifested as steep linear trends in the V versus E2 plots (high K values). Coating of the substrate with a thin silica layer slightly reduces the friction on the ITO substrate. This is possibly due to a higher density of electric charges resulting from the deprotonation of hydroxyl groups on the silica surface,44 which affects the total load that is experienced. The shallow slope observed for the perfluorinated surfaces is in line with the low friction expected for this substrate. However, only a minor effect of the field was observed for the perfluorinated surface, which could also be indicative of the microroller not yet moving in the mixed contact regime in this particular case.
The empirical correlation observed between the microroller velocity and the applied electric field allows us to quantify the factor K (eqn (4)) and estimate an apparent coefficient of friction, μk, (eqn (1)) between the Janus particle and each of the investigated substrates, assuming our particles are in the mixed contact-friction regime. The K factor was found to decrease from 14 s m−1 for the bare electrodes to 7 s m−1 and 0.3 s m−1 for the silica-coated and perfluorinated substrates, respectively. From these K values and the experimentally measured particles velocities, we estimate the apparent coefficient of friction of the Janus particle on the bare, silica-coated and fluorinated substrates to vary within the ranges 2 × 10−4 to 3 × 10−4, 1 × 10−4 to 2 × 10−4 and 3 × 10−6 to 4 × 10−6, respectively. However, the absolute values of the coefficient of friction estimated here should be taken with caution, since they still need to be corrected by calibrating our data against measurements on the same system using established protocols under comparable conditions. Importantly, we expect this correction to shift the absolute coefficient values without significantly affecting the scaling relations proposed. If this is confirmed, colloidal microrollers may offer a useful tool to remotely probe the friction properties and interaction forces between particles and surfaces.
To strengthen our physical interpretation and shed further light on the effect of the surface chemistry of the substrate on the friction of the microroller, we conducted independent lateral force measurements on the distinct particle–substrate pairs using a colloidal probe atomic force microscopy (CP-AFM). A magnesium-coated 4.6 μm silica particle was utilized in these measurements to represent the rolling Janus colloid, while the substrates were the same as those previously employed for the microroller velocity measurements. In the AFM experiment, the coated silica particle was fixed at the tip of a microcantilever and scanned over the substrate surface while subjected to a normal force of controlled magnitude. By measuring the lateral force exerted on the particle (Ff) as a function of the applied normal force (L), the friction properties of different particle–substrate pairs were quantified (Fig. 3b).
Low lateral velocities and high normal forces on the particle were deliberately applied to probe the friction behavior of the particle–substrate pairs in the boundary regime. Under these measuring conditions, we expect to amplify differences in the friction coefficient of the investigated substrates. The close contact between the particle and the underlying substrate was confirmed by the observation that the AFM colloidal probe strongly adheres to the silica-coated and bare ITO substrates (see ESI,† Fig. S3). Our experiments confirm that the normal and friction forces probed in the AFM and microrolling experiments differ by several orders of magnitude (Fig. 3a and c). The coefficient of friction of the particle under the high normal forces exerted by the AFM cantilever was found to decrease from 0.23 for bare ITO to 0.14 and 0.016 for substrates coated with silica and perfluorinated molecules, respectively. Such values lie within the typical range expected for these types of surface chemistries under the boundary regime.45,46 Importantly, the results of the lateral force analysis revealed that the friction of the particles on substrates with different surface chemistries follows the same trend observed in the microrolling experiments. This qualitative agreement suggests that substrate friction is indeed important for the motion of the Janus microroller (Fig. 3a).
Generalized model
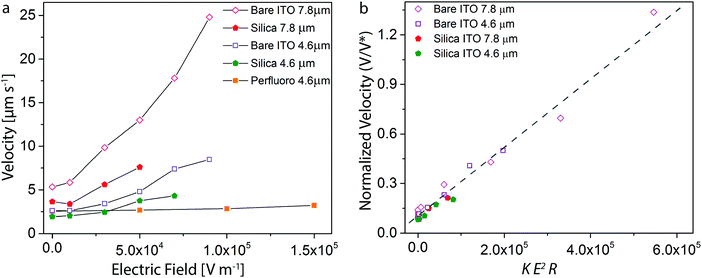
Our systematic analysis of the motion of magnetically driven Janus microrollers using different particle sizes and substrates under a broad range of electric fields allows us to derive quantitative scaling relations to predict and deliberately control the behavior of such particles in microscale environments. To test the predictive nature of such scaling relations, we combine in a single master plot all the experimental data obtained in our study (Fig. 4a). The axes of the master plot are chosen based on the physical quantities expressed in our simple analytical model (eqn (4)). According to the model, the normalized velocity V/V* is expected to scale linearly with the ratio Kα2E2/R5. Since the polarizability α varies with the cube of the particle size (R3), we plotted the normalized velocity as a function of the product KE2R to assess the validity of the model for experiments performed with different particle sizes (R), substrates (K) and electric fields (E).Our analysis shows that a wide range of velocity data (V) collapse into a single line in the master plot if the relevant physical parameters are grouped according to the proposed model (Fig. 4b). The scaling relation was found to be applicable to all the investigated experimental series, except for the measurements conducted on the perfluorinated substrates. The velocity of the particle on the perfluoro-coated ITO substrate deviates slightly from the theoretically predicted trend (ESI,† Fig. S4). This discrepancy could be explained by the particle being in the fully hydrodynamic regime due to surface slip, or by possible changes in the dielectric properties of the substrate resulting from the presence of the coating. Nonetheless, the fact that the other substrates follow our curve indicates that the previously proposed simplified description27 can be applied to our Janus shuttles for a wide range of particle sizes, electric fields, and substrates. However, systems for which the motion is less (or not) dependent on load-based frictional forces might not be governed by this model. Importantly, the proposed master plot can be used as a guideline for the design of microrollers for programmed manipulation tasks at the microscopic scale or for the remote assessment of the friction properties of surfaces using the Janus particle as a microprobe.
Programmable pick-and-place of porous cargo particles
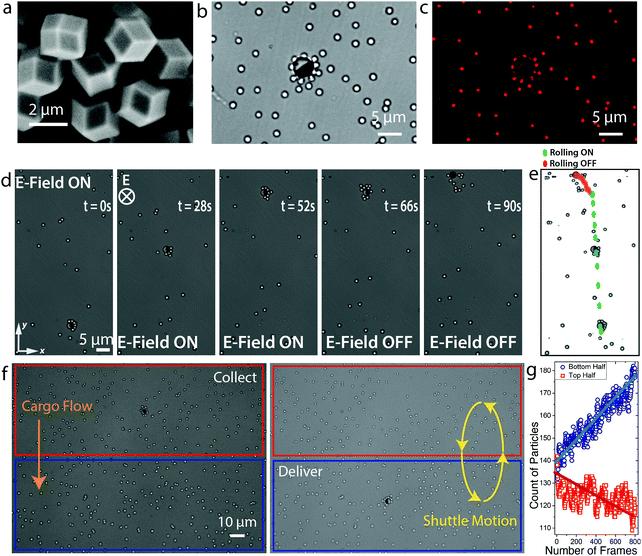
The magnetic propulsion of a Janus microroller via electrically controlled friction offers an enticing mechanism to manipulate particles and chemical species at the microscale. In one possible scenario, this manipulation platform might be used to build chemical gradients in an otherwise diffusion-controlled environment. This can be potentially realized by locally releasing porous cargo particles hosting a large concentration of functional molecules in their internal pores.To explore this concept, we designed a manipulation platform consisting of a Janus microroller and two types of porous cargo colloids, namely metal–organic framework (MOF) crystals or mesoporous silica particles (Fig. 5). MOF crystals and mesoporous silica particles are known for their high surface area, tunable pore sizes and the ability to host and controllably release functional molecules.47,48 The MOF crystals used in our manipulation experiment were synthesized following an established protocol49 and showed a distinct polyhedral morphology with particle size between 3 and 4 μm (Fig. 5a). For the mesoporous silica, we selected a commercially available grade that can be loaded with high concentrations of the hydrophilic fluorescent dye Rhodamine B (Fig. 5b). Such fluorescent dye facilitates visualization of the mesoporous silica particles by optical microscopy (Fig. 5c) and serves as a model molecular species that can be passively released from the cargo particle into the aqueous medium.
In our manipulation experiment, a Janus colloidal microrobot and a large quantity of MOF cargo particles are suspended in ethanol and placed between transparent ITO electrodes. A combination of electrically induced pick-up and magnetic steering was used to transport the cargo-laden microrobot over large distances without losing the trapped MOF crystals (Fig. 5c and d). While the electric field is on, the MOF crystals remain attached to the colloidal shuttle and can be moved using the magnetic field. By turning the electric field off, the dipolar interactions are terminated and the porous cargo particles are released. During cargo transport, the effect of the trapped cargo particles on the microrobot velocity can be accounted for by considering the effective size of the cargo-robot combo, as discussed in our earlier work.10
Because the timescales for diffusion of particles and chemical species are much longer than the timespan needed for cargo transport under the imposed electric field, multiple consecutive shuttling cycles can eventually be applied to build concentration gradients and thus store potential energy in the system. We illustrate this possibility by transporting dye-laden mesoporous silica particles between two distant locations of our chip in multiple shuttling cycles (Fig. 5e and ESI,† Movie S4). The difference in number density of particles between the two sides of the chip was tracked via image analysis (Fig. 5f). Such difference was found to increase linearly with the number of cycles. After only 7 cycles, an excess of ∼60 particles could be accumulated on one side of the chip. When the cargo particles are loaded with dye molecules that are locally released after the shuttle cycles, it is possible to create chemical potential gradients within the liquid medium. Taking reasonable assumptions for the dye load and volume of the chip, we estimate that the gradient built in our experiment would be able to generate an osmotic pressure on the order of 100 Pa. This corresponds to a column of water on the order of millimeters (see ESI,† for calculation).
Conclusions
The rolling motion of magnetically propelled Janus microparticles on a solid substrate can be controlled via electrically tunable friction forces. Friction can be enhanced under an electric field due to an increase of the normal load on the particle resulting from attractive dipolar forces between the particle and the underlying substrate. The rolling velocity of the Janus particle was found to scale with the square of the applied electric field, which can be interpreted using a simple analytical model based on a force balance between friction and drag forces exerted on the particle. The load-based model also explains the effect of the surface chemistry of the substrate on the motion of the Janus particle. Rolling experiments on substrates with distinct coatings show that the surface chemistry of the electrode affects the microrobot velocity by changing the apparent friction coefficient between the Janus particle and the substrate. By combining results from experiments with different particle sizes, substrate coatings and applied electric fields, we derive a scaling relation that can be used to estimate the apparent friction coefficient of surfaces using the Janus particle. This unique feature allows us to use the Janus colloid as a remotely controlled colloidal probe to interrogate the tribological properties of a wide variety of surfaces at forces down to tenths of picoNewtons. Interestingly, the rolling motion studied here appears to be at the edge of the range of applicability for pure hydrodynamic coupling when no field is applied, suggesting that it does not take much to take colloidal matter into the contact-friction regime. The controlled rolling response of the Janus microrobot can be harvested to manipulate cargo particles at the microscale, if the electric field is utilized for reversible cargo trapping and release. In combination with porous cargo particles loaded with functional molecules, the Janus microrobots can be exploited to create microscale chemical gradients or to achieve programmable release with spatiotemporal control. These unique functionalities might find applications in bio-analytical platforms for drug screening, medical diagnosis or fundamental biology studies.Materials and methods
Janus colloids
Janus particles were fabricated via the deposition of a metal coating on pre-dried colloidal particles.12 In a typically coating procedure, a 2–3 vol% suspension of 4.64 μm or 7.8 μm diameter silica particles (Microparticles GmbH, SiO2-R-KM277, SiO2-R-SC33-2) is spread on a glass slide and dried to form a sub-monolayer. Next, a 200 nm thick nickel layer is deposited vertically followed by a 200 nm of magnesium using an electron beam deposition setup (Plassys II, Plassys Bestek) at 2 × 10−6 mbar applying a deposition rate of 0.5–0.7 Å s−1. The sample is then sonicated in 30 mL DI water for 30 minutes to collect the particles. The suspension is finally centrifuged to concentrate the resulting Janus particles.Cargo colloids
Polystyrene colloids with particle size of 1.0 μm were purchased from Microparticles GmbH (PS-R-KM392-2) and used as model cargo. Mesoporous silica particles of 2.0 μm and pore size of 4 nm were acquired from Sigma Aldrich (grade 806900). Suspensions were prepared by mixing these cargo particles with Janus particles in deionized water. A small quantity (∼10−4 M) of nonionic surfactant (Tween 20, Sigma-Aldrich) was added to the suspension to minimize adhesion to the electrode.Synthesis of MOF particles
Zeolitic Imidazolate Framework (ZIF-8) crystals were synthesized by modifying the method described by Yanai et al.49 Stock solutions of zinc nitrate hexahydrate (aber; 98%), 2-methylimidazole (acros organics), 1-methylimidazole (abcr) and poly(vinyl pyrrolidone) (Sigma Aldrich, Mw = 360![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 g mol−1) prepared in an equal volume methanol:ethanol mixture. These solutions were mixed at a ratio to allow for the following concentrations; 25 mM zinc nitrate hexahydrate, 100 mM 2-methylimidazole, 150 mM 1-methylimidazole and 3.2 wt% poly(vinyl pyrrolidone). After vigorous mixing for 10 s, the resulting solution was incubated at room temperature for 20 h. This resulted in 3 to 4 μm particles that were large enough to be observed in an optical microscope. To modify the surface properties of the MOF crystals, we used a solution of lauryl gallate. The lauryl gallate solution was prepared by dissolving 0.525 wt% lauryl gallate in 25 ml ethanol. 2 ml of this solution was then mixed with 2 ml of the MOF suspension cleaned from its mother liquor with repetitive centrifugation cycles in ethanol. The resulting mixture was vortexed and sonicated for 2 h before the micromanipulation experiments.
000 g mol−1) prepared in an equal volume methanol:ethanol mixture. These solutions were mixed at a ratio to allow for the following concentrations; 25 mM zinc nitrate hexahydrate, 100 mM 2-methylimidazole, 150 mM 1-methylimidazole and 3.2 wt% poly(vinyl pyrrolidone). After vigorous mixing for 10 s, the resulting solution was incubated at room temperature for 20 h. This resulted in 3 to 4 μm particles that were large enough to be observed in an optical microscope. To modify the surface properties of the MOF crystals, we used a solution of lauryl gallate. The lauryl gallate solution was prepared by dissolving 0.525 wt% lauryl gallate in 25 ml ethanol. 2 ml of this solution was then mixed with 2 ml of the MOF suspension cleaned from its mother liquor with repetitive centrifugation cycles in ethanol. The resulting mixture was vortexed and sonicated for 2 h before the micromanipulation experiments.
Electrode and sample fabrication
Transparent and conductive indium tin oxide (ITO) cover slips (SPI supplies, 18 × 18 mm, #1, 8–12 ohms resistance) were used as electrodes in the micromanipulation cells. Cells were fabricated by sandwiching spacers with thicknesses of 0.09–0.12 mm (#0 cover slips) between two ITO cover slips. During the experiments, an AC electric field at a frequency of 1 MHz was applied to the electrodes while keeping the conductive sides facing each other. For the preparation of silica-modified electrodes, the conductive surface of the ITO cover slip was coated with a 15 nm thick layer of silica via e-beam deposition.12 Substrates coated with perfluorinated molecules were prepared by placing an ITO electrode in a desiccator that hosts a vial with a droplet of 1H,1H,2H,2H-perfluorodecyltrichlorosilane (PFDCS, 97%, Sigma Aldrich). While keeping the desiccator under vacuum overnight, the vapor of PFDCS reacted with the oxide groups on the ITO surface, thus changing its surface hydrophilicity and friction properties.Electric field estimations for different electrodes
For the case of two electrodes facing each other (Fig. 2a), a simple capacitor with only one type of dielectric between the plates was used to estimate the field strength using the relation: E = V/ε, where V is the voltage applied and ε is the dielectric constant of water. For the case of flipped electrodes (Fig. 2d), we assumed two parallel capacitors to be stacked in series. One of such capacitors has the dielectric constant of the glass while the other has the dielectric constant of the suspending medium, namely water. To estimate the electric field in the suspension, we used the following formula:where Ei is the effective electric field strength, εi is the dielectric constant, and di is the thickness of the ith layer. In our system, i = 1 was taken as the glass layer, whereas i = 2 refers to the suspension medium layer.
Microscopic imaging
Our imaging and shuttling experiments were performed using a Leica fluorescence microscope equipped with an inverted DM6000 stage, a mercury lamp (Leica), and a PL APO 63×/1.40 NA oil objective.Magnetic guidance of Janus colloids
The ferromagnetic nature of the 200 nm thick nickel layer deposited on one hemisphere of the Janus colloid allows for its magnetic alignment and propulsion when exposed to a rotating magnet. In the aligned configuration, the plane dividing the nickel-coated and the uncoated hemispheres is always orthogonal to the substrate surface. This helps control the direction of the Janus particle motion. For magnetic manipulation we used a 20 × 20 × 5 mm3 permanent neodymium magnet (SuperMagnete, Switzerland) that exhibits a magnetic field of 0.2 T on its surface. The magnet was kept at the same height as the cell but at a distance of 4 cm. The rotating magnetic field was generated by turning the magnet at pre-defined frequencies with the help of an electric motor.Lateral force microscopy (LFM) experiments
An AFM from Asylum Research (MFP 3D, Oxford Instruments) was used to measure the frictional properties between the substrate and a 4.6 μm magnesium-coated silica colloid. Bare, silicon-coated or perfluorinated ITO electrodes were used as substrates. The magnesium-coated silica colloid was glued to an end of a tipless cantilever (CSC38, micromasch, Bulgaria) by using a homebuilt micromanipulator. The normal and torsional spring constants of the cantilever were calibrated prior to the attachment of the colloid by using thermal noise50 and Saders51 methods, respectively. The friction measurements were carried out in air by moving the sample perpendicular to the cantilever axis. A scanning distance of 2 μm and a scanning rate of 4 μm s−1 was used for the friction measurements. Approximately 5 friction loops were recorded and averaged to measure the true friction and standard deviation values for each applied load. Lateral calibration was performed by using an improved wedge method described by Hutter et al.52 The coefficient of friction values were obtained by the slope of the friction vs load curves.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This research was supported by the Swiss National Science Foundation through the National Centre of Competence in Research Bio-Inspired Materials. We also thank the microscopy center ScopeM and the cleanroom facility FIRST at ETH Zurich for instrumental support. J. d. G. thanks NWO for funding through Start-Up Grant 740.018.013 and through association with the EU-FET project NANOPHLOW (766972) within Horizon 2020.References
- R. H. Armour and J. F. V. Vincent, J. Bionic Eng., 2006, 3, 195–208 CrossRef.
- T. S. Yu, E. Lauga and A. E. Hosoi, Phys. Fluids, 2006, 18, 091701 CrossRef.
- A. Shapere and F. Wilczek, J. Fluid Mech., 1989, 198, 557–585 CrossRef.
- E. M. Purcell, Am. J. Phys., 1977, 45, 3–11 CrossRef.
- P. Sundd, M. K. Pospieszalska, L. S.-L. Cheung, K. Konstantopoulos and K. Ley, Biorheology, 2011, 48, 1–35 Search PubMed.
- C. Dong and X. X. Lei, J. Biomech., 2000, 33, 35–43 CrossRef CAS.
- L. Zhang, J. J. Abbott, L. Dong, B. E. Kratochvil, D. Bell and B. J. Nelson, Appl. Phys. Lett., 2009, 94, 064107 CrossRef.
- Y. Alapan, B. Yigit, O. Beker, A. F. Demirörs and M. Sitti, Nat. Mater., 2019, 18, 1244–1251 CrossRef CAS.
- W. Hu, G. Z. Lum, M. Mastrangeli and M. Sitti, Nature, 2018, 554, 81–85 CrossRef CAS.
- A. F. Demirörs, M. T. Akan, E. Poloni and A. R. Studart, Soft Matter, 2018, 14, 4741–4749 RSC.
- A. Boymelgreen, G. Yossifon and T. Miloh, Langmuir, 2016, 32, 9540–9547 CrossRef CAS.
- J. Yan, M. Han, J. Zhang, C. Xu, E. Luijten and S. Granick, Nat. Mater., 2016, 15, 1095 CrossRef CAS.
- D. Ahmed, M. Lu, A. Nourhani, P. E. Lammert, Z. Stratton, H. S. Muddana, V. H. Crespi and T. J. Huang, Sci. Rep., 2015, 5, 9744 CrossRef.
- H. Zeng, P. Wasylczyk, D. S. Wiersma and A. Priimagi, Adv. Mater., 2018, 30, 1703554 CrossRef.
- L. Soler, V. Magdanz, V. M. Fomin, S. Sanchez and O. G. Schmidt, ACS Nano, 2013, 7, 9611–9620 CrossRef CAS.
- B. Jurado-Sánchez, S. Sattayasamitsathit, W. Gao, L. Santos, Y. Fedorak, V. V. Singh, J. Orozco, M. Galarnyk and J. Wang, Small, 2015, 11, 499–506 CrossRef.
- X. Ma and S. Sánchez, Self-propelling micro-nanorobots, https://www.futuremedicine.com/doi/full/10.2217/nnm-2017-0104, accessed September 6, 2017.
- T. Patino, R. Mestre and S. Sánchez, Lab Chip, 2016, 16, 3626–3630 RSC.
- H.-W. Huang, M. S. Sakar, A. J. Petruska, S. Pané and B. J. Nelson, Nat. Commun., 2016, 7, 12263 CrossRef CAS.
- Y. Alapan, U. Bozuyuk, P. Erkoc, A. C. Karacakol and M. Sitti, Sci. Robot., 2020, 5(42), eaba5726 CrossRef.
- T. Yang, A. Tomaka, T. O. Tasci, K. B. Neeves, N. Wu and D. W. M. Marr, Sci. Robot., 2019, 4(32), eaaw9525 CrossRef.
- R. Niu, D. Botin, J. Weber, A. Reinmüller and T. Palberg, Langmuir, 2017, 33, 3450–3457 CrossRef CAS.
- A. F. Demirörs, F. Eichenseher, M. J. Loessner and A. R. Studart, Nat. Commun., 2017, 8, 1872 CrossRef.
- A. J. Goldman, R. G. Cox and H. Brenner, Chem. Eng. Sci., 1967, 22, 637–651 CrossRef CAS.
- S. G. Flicker and S. G. Bike, Langmuir, 1993, 9, 257–262 CrossRef CAS.
- A. Rashidi and C. L. Wirth, J. Chem. Phys., 2017, 147, 224906 CrossRef.
- T. O. Tasci, P. S. Herson, K. B. Neeves and D. W. M. Marr, Nat. Commun., 2016, 7, 10225 CrossRef CAS.
- B. M. Guy, C. Ness, M. Hermes, L. J. Sawiak, J. Sun and W. C. K. Poon, Soft Matter, 2020, 16, 229–237 RSC.
- N. Y. C. Lin, B. M. Guy, M. Hermes, C. Ness, J. Sun, W. C. K. Poon and I. Cohen, Phys. Rev. Lett., 2015, 115, 228304 CrossRef.
- C.-P. Hsu, S. N. Ramakrishna, M. Zanini, N. D. Spencer and L. Isa, Proc. Natl. Acad. Sci. U. S. A., 2018, 115, 5117–5122 CrossRef CAS.
- R. R. Agayan, R. G. Smith and R. Kopelman, J. Appl. Phys., 2008, 104, 054915 CrossRef.
- M. Driscoll, B. Delmotte, M. Youssef, S. Sacanna, A. Donev and P. Chaikin, Nat. Phys., 2017, 13, 375–379 Search PubMed.
- P. Tierno, R. Golestanian, I. Pagonabarraga and F. Sagués, Phys. Rev. Lett., 2008, 101, 218304 CrossRef.
- S.-H. Kim, J. Y. Sim, J.-M. Lim and S.-M. Yang, Angew. Chem., Int. Ed., 2010, 49, 3786–3790 CrossRef CAS.
- F. Martinez-Pedrero, H. Massana-Cid and P. Tierno, Small, 2017, 13, 1603449 CrossRef.
- S. Schuerle, A. P. Soleimany, T. Yeh, G. M. Anand, M. Häberli, H. E. Fleming, N. Mirkhani, F. Qiu, S. Hauert, X. Wang, B. J. Nelson and S. N. Bhatia, Sci. Adv., 2019, 5, eaav4803 CrossRef CAS.
- A. W. Mahoney, N. D. Nelson, K. E. Peyer, B. J. Nelson and J. J. Abbott, Appl. Phys. Lett., 2014, 104, 144101 CrossRef.
- A. Cēbers and M. Ozols, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2006, 73, 021505 CrossRef.
- I. Sinn, P. Kinnunen, S. N. Pei, R. Clarke, B. H. McNaughton and R. Kopelman, Appl. Phys. Lett., 2011, 98, 024101 CrossRef.
- J. Yan, K. Chaudhary, S. Chul Bae, J. A. Lewis and S. Granick, Nat. Commun., 2013, 4, 1516 CrossRef.
- S. H. Behrens and D. G. Grier, J. Chem. Phys., 2001, 115, 6716–6721 CrossRef CAS.
- A. Z. Szeri, Fluid Film Lubrication, Cambridge University Press, 2011 Search PubMed.
- B. W. Kwaadgras, T. H. Besseling, T. J. Coopmans, A. Kuijk, A. Imhof, A. van Blaaderen, M. Dijkstra and R. van Roij, Phys. Chem. Chem. Phys., 2014, 16, 22575–22582 RSC.
- M. Polin, D. G. Grier and Y. Han, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2007, 76, 041406 CrossRef.
- F. Sadeghi, in Tribology and Dynamics of Engine and Powertrain, ed. H. Rahnejat, Woodhead Publishing, 2010, pp. 171e–226e Search PubMed.
- J. E. Otero, E. de la, G. Ochoa, E. C. Tanarro and B. del R. López, Adv. Mech. Eng., 2017, 9(7), 1–11 Search PubMed.
- M.-X. Wu and Y.-W. Yang, Adv. Mater., 2017, 29, 1606134 CrossRef.
- Y. Wang, Q. Zhao, N. Han, L. Bai, J. Li, J. Liu, E. Che, L. Hu, Q. Zhang, T. Jiang and S. Wang, Nanomedicine, 2015, 11, 313–327 CrossRef CAS.
- N. Yanai, M. Sindoro, J. Yan and S. Granick, J. Am. Chem. Soc., 2013, 135, 34–37 CrossRef CAS.
- H.-J. Butt and M. Jaschke, Nanotechnology, 1995, 6, 1–7 CrossRef.
- C. P. Green, H. Lioe, J. P. Cleveland, R. Proksch, P. Mulvaney and J. E. Sader, Rev. Sci. Instrum., 2004, 75, 1988–1996 CrossRef CAS.
- J. L. Hutter and J. Bechhoefer, Rev. Sci. Instrum., 1993, 64, 1868–1873 CrossRef CAS.
- J. Zhang, J. Yan and S. Granick, Angew. Chem., Int. Ed., 2016, 55, 5166–5169 CrossRef CAS.
- J. Yan, S. C. Bae and S. Granick, Adv. Mater., 2015, 27, 874–879 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/d0sm01449d |
| This journal is © The Royal Society of Chemistry 2021 |